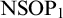1 Introduction
Two intensely studied generalisations of the class of simple theories are that of rosy theories (introduced by Onshuus in [Reference Onshuus30] and developed further by Onshuus and Ealy in [Reference Ealy and Onshuus16, Reference Onshuus29]) and that of
$\text {NSOP}_1$
theories (introduced by Džamonja and Shelah in [Reference Džamonja and Shelah15]). A common characteristic of both theories is the presence of a “canonical” independence relation whose properties determine the class. The connection of these classes with notions of independence was something present in the study of rosy theories from the start, but appeared in the context of
$\text {NSOP}_1$
theories more recently, first in the work of Chernikov and Ramsey in [Reference Chernikov and Ramsey11], and then explicitly in terms of the notion of Kim-independence in several papers of Kaplan, Shelah, and Ramsey in [Reference Kaplan and Ramsey20–Reference Kaplan, Ramsey and Shelah22].
The following natural question regarding the relationship between these two classes was posed by Christian d’Elbée and Byungham Kim, independently of each other, in 2021.
Question 1.1 (cf. [Reference d’Elbée13, Reference Kim25])
Is there an
$\text {NSOP}_1$
rosy theory which is not simple?
In this article, we show that an answer to this question can be obtained in connection with another conjecture coming out of the study of simple theories.
Recall that we say a formula
$\phi (x,y)$
is stable if there are no sequences
$(a_i)_{i<\omega }$
and
$(b_i)_{i < \omega }$
such that, for all
$i,j < \omega $
, we have
$\models \phi (a_i, b_j)$
iff
$i < j$
. In analogy to the stable forking conjecture proposed by Hart, Kim, and Pillay (cf. [Reference Kim23]), and which also relates to the dependent dividing conjecture stated by Chernikov (cf. [Reference Chernikov9, Proposition 4.14]), Bossut has recently introduced, in [Reference Bossut4], what we call here the stable Kim-forking conjecture. Our main result (Theorem 4.6) says that, if the stable Kim-forking conjecture holds, every
$\text {NSOP}_1$
rosy theory T must be simple. In fact, we prove something slightly stronger, since we only require that
$T^{\text {eq}}$
has stable Kim-forking over models.
The structure of the article is as follows. After some notation and terminology in Section 2, we introduce in Section 3 the stable Kim-forking conjecture and discuss several important
$\text {NSOP}_1$
examples where it has been verified. We include in that section a proof that the conjecture holds in the theory of a Frobenius field (Proposition 3.10). Then, in Section 4, we prove our main result and, as an application, we conclude that, if the stable Kim-forking conjecture holds, there is no strictly
$\text {NSOP}_1$
pregeometric theory with geometric elimination of imaginaries.
2 Preliminaries
2.1 Abstract independence relations
Let T be a complete theory with infinite models and
$\mathbb {M} \models T$
a monster model. We are interested in
$\text {Aut}(\mathbb {M})$
-invariant ternary relations on small subsets of our fixed monster model, i.e., 
(read as “A is independent from B over C”) iff 
for all
$\sigma \in \text {Aut}(\mathbb {M})$
. We will freely call each such relation an independence relation. Many abstract properties that independence relations may satisfy appear already in [Reference Shelah32], and more explicitly, in [Reference Baldwin3]. We follow Adler’s modern presentation in [Reference Adler1]:
-
• Existence: For all
$A, B \subset \mathbb {M}$
, . -
• Right monotonicity: For all
$A, B, C \subset \mathbb {M}$
, if and
$B' \subseteq B$
, then . -
• Right base monotonicity: For all
$A \subset \mathbb {M}$
and
$D \subseteq C \subseteq B \subset \mathbb {M}$
, if , then . -
• Right extension: For all
$A, B, C \subset \mathbb {M}$
, if and
$B \subseteq B' \subset \mathbb {M}$
, there is some
$A' \equiv _{BC} A$
such that . -
• Symmetry: For all
$A, B, C \subset \mathbb {M}$
, iff . -
• Right transitivity: For all
$A \subset \mathbb {M}$
and
$D \subseteq C \subseteq B\subset \mathbb {M}$
, if and , then . -
• Local character: For all
$A \subset \mathbb {M}$
, there is some cardinal
$\kappa (A)$
such that, for any
$B \subset \mathbb {M}$
, there is some
$C \subseteq B$
of cardinality
$< \kappa (A)$
such that .
.
and 
.
, then 
.
and 
.
iff 
.
and 
, then 
.
.We also have left-sided versions for each of the right-sided properties above. We omit the side if both left and right versions of the property hold. We say an independence relation 
is defined over models if its base can only be a model, i.e., if 
is only defined if C is a model of T. Given independence relations 
and 
, we write 
if 
implies 
.
2.2 Rosy and
$\text {NSOP}_1$
theories
In [Reference Onshuus30], Onshuus introduced the notions of þ-forking (read as “thorn-forking”) and rosy theories, a class that generalises both simple and o-minimal theories. We start by recalling all the relevant definitions from that paper. We follow the conventions in [Reference Hoffmann and Pillay18].
Definition 2.1. Let
$\phi (x,y)$
be a formula, b a tuple, and C a set of parameters.
-
(i) We say that
$\phi (x,b)$
strongly divides over C if the set of images of
$\phi (\mathbb {M},b)$
under elements of
$\text {Aut}(\mathbb {M}/C)$
is infinite and k-inconsistent for some
$k < \omega $
. -
(ii) We say that
$\phi (x,b)$
þ-divides over C if there is a tuple c such that
$\phi (x,b)$
strongly divides over
$Cc$
. -
(iii) We say that
$\phi (x,b)$
þ-forks over C if there exist formulas
$\psi _i(x, c_i)$
for
$i < n$
such that
$\phi (x,b) \vdash \bigvee _{i < n} \psi _i(x, c_i)$
and each
$\psi _i(x,c_i)$
þ-divides over C. -
(iv) We say A is þ-independent from B over C if, for some (equiv., any) enumeration a of A,
$\operatorname {\mathrm {tp}}(a/CB)$
does not contain a formula that þ-forks over C. We denote this directly for tuples by .
.Definition 2.2. We say a theory T is rosy if 
in
$T^{\text {eq}}$
satisfies local character.
Fact 2.3. In any theory, 
satisfies monotonicity, right base monotonicity, left transitivity, and right extension. If T is rosy, then, in
$T^{\mathrm{eq}}$
, 
also satisfies symmetry.
Another independence relation that has become widespread in the literature appears in the work of Kaplan and Ramsey in [Reference Kaplan and Ramsey20], who introduced the notion of Kim-independence. Recall that, for a set
$A \subset \mathbb {M}$
, we say a global type
$q \in S(\mathbb {M})$
is A-invariant if, whenever
$b \equiv _A b'$
and
$\phi (x,y)$
is an
$\mathcal {L}(A)$
-formula, we have
$\phi (x,b) \in q$
iff
$\phi (x,b') \in q$
.
Definition 2.4. Let
$\phi (x,y)$
be a formula, b a tuple,
$(b_i)_{i < \omega }$
a sequence, and
$M \models T$
.
-
(i) For a global type q, we say
$(b_i)_{i < \omega }$
is a Morley sequence in q over M if
$b_i \models q|_{Mb_{<i}}$
for all
$i \in \omega $
. If q is M-invariant, we call
$(b_i)_{i < \omega }$
an M-invariant Morley sequence. -
(ii) We say that
$\phi (x,b)$
Kim-divides over M if there is some M-invariant Morley sequence
$(b_i)_{i < \omega }$
with
$b_0 = b$
such that
$\{\phi (x, b_i) : i < \omega \}$
is inconsistent. -
(iii) We say that
$\phi (x,b)$
Kim-forks over M if there exist formulas
$\psi _i(x, c_i)$
for
$i < n$
such that
$\phi (x,b) \vdash \bigvee _{i < n} \psi _i(x, c_i)$
and each
$\psi _i(x,c_i)$
Kim-divides over M. -
(iv) We say that A is Kim-independent from B over M if, for some (equiv., any) enumeration a of A,
$\operatorname {\mathrm {tp}}(a/MB)$
does not contain any formula that Kim-forks over M. We denote this by . -
(v) We say that
$(b_i)_{i < \omega }$
is an -Morley sequence over M if it is M-indiscernible and for all i.
.
-Morley sequence over M if it is M-indiscernible and 
for all i. One of the main results from [Reference Kaplan and Ramsey20] characterises the class of
$\text {NSOP}_1$
theories, which had been defined combinatorially by Džamonja and Shelah in [Reference Džamonja and Shelah15], in terms of Kim-independence. We omit the combinatorial definition of
$\text {NSOP}_1$
, as we will not need it for what follows, but the following result is useful.
Theorem 2.5 [Reference Kaplan and Ramsey20, Theorem 5.16]
A theory T is
$\text {NSOP}_1$
iff Kim-independence is symmetric.
Remark 2.6. Another independence relation which will be useful for us is the following: Given a model
$M \models T$
, we define 
iff, for some (equiv., any) enumeration a of A,
$\operatorname {\mathrm {tp}}(a/MB)$
extends to a global M-invariant type. It is folklore that, in any theory, 
satisfies all of the properties listed in Section 2.1 except perhaps symmetry and right transitivity. Moreover, in any theory, we have 
and 
.
3 The stable Kim-forking conjecture
In [Reference Bossut4], Bossut introduces the following property of theories.
Definition 3.1. Let T be a complete
$\mathcal {L}$
-theory. We say that T has the stable Kim-forking property over models if, for any model
$M \models T$
and
$B \supseteq M$
, whenever
$p(x) \in S(B)$
Kim-forks over M, there is some stable formula
$\phi (x,y) \in \mathcal {L}(M)$
and some
$b \in B$
such that
$\phi (x,b) \in p(x)$
Kim-forks over M.
Conjecture 3.2 (Stable Kim-forking, cf. [Reference Baldwin, Freitag and Mutchnik2, Question 7.3])
Every
$\text {NSOP}_1$
theory has the stable Kim-forking property over models.
Remark 3.3. Bossut calls the above property the “weak stable Kim-forking property,” in order to distinguish it from a stronger version. However, he shows in [Reference Bossut4, Corollary 3.8] that having the stronger version implies that the theory is simple. Since we focus on the version of the conjecture that applies to (strictly)
$\text {NSOP}_1$
theories, we omit this stronger version and follow the terminology in [Reference Baldwin, Freitag and Mutchnik2].
In what follows, we discuss three of the most studied
$\text {NSOP}_1$
examples, which we will see all have the stable Kim-forking property. This provides some evidence toward Conjecture 3.2.
Example 3.4. Let
$\mathcal {L}$
be a two-sorted language with sorts P and O, and a ternary relation
$E \subseteq P \times O^2$
. Let
$T_{feq}^*$
be the model completion of the theory saying:
-
• P and O partition the structure.
-
• For all
$p \in P$
,
$E(p, x, y)$
defines an equivalence relation on O.
Chernikov and Ramsey show in [Reference Chernikov and Ramsey11, Corollary 6.20] that
$T_{feq}^*$
is
$\text {NSOP}_1$
. Adler proves directly in [Reference Adler1, Example 2.6] that
$T_{feq}^*$
is not rosy. Bossut explains that
$T_{feq}^*$
has stable Kim-forking in [Reference Bossut4, discussion after Corollary 4.11].
Example 3.5. Let
$T_\infty $
be the model companion of the theory of an infinite-dimensional vector space over an algebraically closed field with an alternating or symmetric bilinear form, in the two-sorted language with a sort for the vector space and another sort for the underlying field.
Chernikov and Ramsey show that
$T_\infty $
is
$\text {NSOP}_1$
in [Reference Chernikov and Ramsey11, Corollary 6.4], and Granger shows it is not simple in [Reference Granger17, Proposition 7.4.1]. In [Reference Kim and Kim26] a proof of non-rosiness is suggested. Finally, by [Reference Kaplan and Ramsey20, Proposition 9.37], 
coincides with algebraic independence in
$T_\infty $
, that is, linear independence of the algebraic closures in the vector space sort, and algebraic freeness in the field sort. This implies that
$T_\infty $
has the stable Kim-forking property.
Example 3.6. We say a field F is pseudo-algebraically closed (or PAC) if every absolutely irreducible variety defined over F has an F-rational point.
Let us denote by
$\mathcal {G}(F)$
the absolute Galois group of F, viewed as a topological group in the usual fashion. We say that F is Frobenius if
$\mathcal {G}(F)$
satisfies the Iwasawa property, i.e., if
$\phi \colon \mathcal {G}(F) \to A$
and 
are continuous epimorphisms and B is a finite quotient of
$\mathcal {G}(F)$
, then there is a continuous epimorphism
$\psi \colon \mathcal {G}(F) \to B$
making the following diagram commute:
In particular, whenever F is e-free (i.e.,
$\mathcal {G}(F) \cong \hat {\mathbb {F}}_e$
, the free profinite group on e many generators) for some
$e \in \omega $
, or
$\omega $
-free (i.e.,
$\mathcal {G}(F) \cong \hat {\mathbb {F}}_\omega $
), it is Frobenius.
The theory of a Frobenius field F in
$\mathcal {L} = \{+, -, \cdot , 0,1\}$
is
$\text {NSOP}_1$
(see [Reference Kaplan and Ramsey20, Section 9.3]). If F is an e-free PAC field, it is simple (see [Reference Hrushovski19]), and hence rosy, whereas if it is
$\omega $
-free it is
$\text {NSOP}_1$
(see [Reference Chernikov and Ramsey11, Corollary 6.2]) and not simple (see [Reference Chatzidakis7, Theorem 3.9]). A proof that the theory of an
$\omega $
-free PAC field is not rosy is hinted at in [Reference Chatzidakis8, Section 3] and written explicitly (and in more generality) in [Reference Montenegro28].
In what follows, we will show that the theory of a Frobenius field has the stable Kim-forking property over models. We use in our proof the notion of an equation, first introduced by Srour in [Reference Pillay and Srour31]. We take as a definition an equivalent characterisation of equations which follows by compactness (cf. [Reference Martin-Pizarro and Ziegler27]).
Definition 3.7. A formula
$\phi (x,y)$
is an equation if, for every indiscernible sequence
$(a_i, b_i)_{i < \omega }$
, if
$\models \phi (a_i, b_j)$
for all
$i < j$
, then
$\models \phi (a_i, b_i)$
for all
$i < \omega $
.
Fact 3.8 [Reference Pillay and Srour31, Proposition 2.6]
If
$\phi (x,y)$
is an equation, then it is stable.
Remark 3.9. We use the characterisation of Kim-independence for the theory T of a Frobenius field, which comes from [Reference Kaplan and Ramsey20, Theorem 9.32]: for any
$\operatorname {\mathrm {acl}}$
-closed subfields
$C \subseteq A,B$
of a sufficiently saturated field
$F \models T$
, 
iff 
and 
, where 
is nonforking independence in the
$\omega $
-sorted theory of the inverse system of
$\mathcal {G}(F)$
(for more details, see [Reference Chatzidakis6]).
In [Reference Chernikov and Ramsey11, Lemma 6.2], Chernikov and Ramsey explicitly give the formula witnessing strong finite character for Kim-independence in the theory of an
$\omega $
-free PAC field, which they attribute to Zoé Chatzidakis. We note here that the same formula proves strong finite character in the theory of any Frobenius field. In what follows, we briefly describe this formula.
Suppose, towards proving stable Kim-forking, that 
with
$A,B,C$
acl-closed and
$C \subseteq A,B$
contained in a large saturated field
$F \models T$
. If 
, this is witnessed by an equation and an inequation, which are always stable formulas. So it suffices to consider the case where 
and 
. Using finite character and [Reference Chatzidakis6, Proposition 4.1], it follows that we can find open normal subgroups
$M_1 \lhd \mathcal {G}(A)$
and
$M_2 \lhd \mathcal {G}(B)$
such that, if N is the smallest open normal subgroup of
$\mathcal {G}(F)$
containing
$M_1$
and
$M_2$
, then
$N \not \subseteq \mathcal {G}(C)$
.
Using some Galois theory and the fact that F is a regular extension of A and B, this means that there are some
$\alpha \in \langle AC \rangle ^{\text {alg}}$
and
$\beta \in \langle BC \rangle ^{\text {alg}}$
not in F such that
$F(\alpha ) = F(\beta )$
is Galois over F and
$\beta \notin F\langle C \rangle ^{\text {alg}}$
. We may choose some
$b' \in \operatorname {\mathrm {acl}}(CB)$
such that
$\langle CB\beta \rangle \cap F \subseteq \langle CBb' \rangle $
and
$\langle CBb' \rangle $
is closed under
$\text {Aut}(\operatorname {\mathrm {acl}}(CB)/\langle CB \rangle )$
. Similarly, we can pick
$a' \in \operatorname {\mathrm {acl}}(AC)$
such that
$\langle CA \alpha \rangle \cap F \subseteq \langle CAa' \rangle $
and
$\langle CAa'\rangle $
is closed under
$\text {Aut}(\operatorname {\mathrm {acl}}(CA)/\langle CA \rangle )$
. (Note:
$\alpha , \beta , a', b'$
can be taken as singletons by the Primitive Element Theorem.)
Fix some enumerations
$a,b,c$
of
$A,B,C$
, respectively. The idea now is to find a formula that captures the behaviour of
$a,b,\alpha , \beta $
as described above. In order to do so, let:
-
•
$P(Y, b, c)$
be the minimal polynomial of
$b'$
over
$\langle BC \rangle $
. -
•
$Q(Z, Y, b, c)$
be such that
$Q(Z, b', b, c)$
is the minimal polynomial of
$\beta $
over
$\langle CB b' \rangle $
. -
•
$R(W, a, c)$
be the minimal polynomial of
$a'$
over
$\langle AC \rangle $
. -
•
$S(W, T, a, c)$
be such that
$S(W, a', a, c)$
is the minimal polynomial of
$\alpha $
over
$\langle CAa' \rangle $
.
We now take
$\phi (t,b,c)$
(with variable t) to be the formula saying: “there exists some
$y \equiv _{bc} b'$
and a solution w of
$R(W, t, c) = 0$
such that (i)
$S(X, w, t, c)$
is irreducible over F of degree
$[\langle CA\alpha \rangle : \langle CAa' \rangle ]$
and (ii) for every solution z of
$Q(Z, y,b,c) = 0$
,
$F(z)$
contains a solution of
$S(X, w, t, c) = 0$
.” This can indeed be expressed using a first-order formula (for more details, see Chernikov and Ramsey’s paper). In [Reference Chernikov and Ramsey11, Lemma 6.2], it is shown that
$\phi (t,b,c)$
Kim-forks over C.
Proposition 3.10. The theory of a Frobenius field has the stable Kim-forking property over algebraically closed sets.
Proof. It is enough to show that the formula
$\phi (t, s, c)$
(in variables
$t, s$
) from the previous remark is stable. We prove something stronger (cf., Fact 3.8): namely, we will show that
$\phi (t,s,c)$
is an equation in Srour’s sense.
Suppose
$(a_i,b_i)_{i < \omega }$
is a C-indiscernible sequence such that
$\models \phi (a_i, b_j, c)$
for all
$i < j$
. Let us choose, for each
$i < j$
,
$d_{ij}$
and
$e_{ij}$
to be witnesses to y and w as stipulated by each appropriate instance of
$\phi $
, and also pick
$f_{ij}$
to be a solution to
$Q(Z, d_{ij}, b_j, c) = 0$
. Since by choice they are all roots of Q, it follows that, for all
$i < j$
,
$F(f_{ij})$
is a proper Galois extension of F of degree
$[\langle CB\beta \rangle : \langle CBb' \rangle ]$
which is not contained in
$F\langle C \rangle ^{\text {alg}}$
. Note that, by definition of
$\phi $
, for each
$i < j$
,
$F(f_{ij})$
is precisely the field generated by any of its roots of
$S(X, e_{ij}, a_i, c) = 0$
over F.
Claim 1. There exist
$k < i < j$
such that
$e_{ki} = e_{kj}$
and
$d_{kj} = d_{ij}$
.
Proof of Claim 1
Suppose that
$P(Y, b_0, c) = 0$
has m solutions and
$R(W, a_0, c) = 0$
has n solutions. By C-indiscernibility, we get the same number of solutions for any indices
$i,j < \omega $
. Thus, our choice of
$d_{ij}$
and
$e_{ij}$
defines an
$mn$
-colouring on
$\omega ^{(2)}$
. Hence, by Ramsey’s Theorem, there is an infinite subset
$X \subseteq \omega $
such that
$X^{(2)}$
is monochromatic. Pick
$k,i,j \in X$
with
$k < i < j$
. Then
$\{k,i\}, \{k,j\}, \{i,j\} \in X^{(2)}$
, so it follows that
$e_{ki} = e_{kj}$
and
$d_{kj} = d_{ij}$
, as required.
Let
$d_j := d_{kj} = d_{ij}$
and
$e_k := e_{ki} = e_{kj}$
. Then
$F(f_{ki})$
and
$F(f_{kj})$
both contain solutions to
$S(X, e_k, a_k, c) = 0$
, and since they are Galois, by our earlier remarks we get
$F(f_{ki}) = F(f_{kj})$
. Moreover,
$F(f_{kj})$
and
$F(f_{ij})$
also contain all solutions of
$Q(Z, d_j, b_j, c) = 0$
, so we get
$F(f_{kj}) = F(f_{ij})$
. Therefore,
$F(f_{ki}) = F(f_{ij})$
.
Claim 2.
$\models \phi (a_i, b_i, c)$
.
Proof. Assume not, for contradiction. So we can find a solution
$f_{ii}$
of
$Q(Z, d_{ki}, b_i, c) = 0$
such that
$F(f_{ii})$
contains no solutions of
$S(X, e_{ij}, a_i, c) = 0$
. But note that, by this choice of
$f_{ii}$
and the above remarks, it follows that
$f_{ii} \in F(f_{ki}) = F(f_{ij})$
, and hence,
$F(f_{ii})$
contains a solution to
$S(X, e_{ij}, a_i, c) = 0$
, a contradiction.
It follows from Claim 2 by C-indiscernibility of
$(a_ib_i)_{i < \omega }$
that this holds for all
$i < \omega $
, as required.
4 On the relation between
$\text {NSOP}_1$
and rosy theories
A frequent question in neostability theory concerns the relationship between the “canonical” independence relations arising from different classes of theories. One example is how 
relates to 
in simple theories. A partial answer to this question appears in [Reference Onshuus30, Corollary 5.1.3].
Theorem 4.1. Suppose that the stable forking conjecture holds. If T is simple, then 
.
More recently, Christian d’Elbée and Byungham Kim posed independently (in [Reference d’Elbée13, Section 3.4] and [Reference Kim25, Question 6.2], resp.) the following question.
Question 4.2. Is there any
$\text {NSOP}_1$
rosy theory which is not simple?
In what follows, we give a partial answer to this question under the assumption of the stable Kim-forking conjecture. This resembles Onshuus’ result for simple theories (cf. Theorem 4.1). But first, we need to collect some results from the literature.
A close inspection of the proof appearing in [Reference Hoffmann and Pillay18, Proposition 3.3] shows the following result, first proved by Onshuus in [Reference Onshuus30, Theorem 5.1.1].
Fact 4.3. Let
$M \prec N$
be models of
$T = T^{\text {eq}}$
, and
$p(x) \in S(N)$
. If there is some
$\phi (x,n) \in p(x)$
that forks over M such that
$\phi (x,y) \in \mathcal {L}(M)$
is stable, then 
-forks over M.
Recall that
$(M_i)_{i < \kappa }$
is a continuous chain of models if
$M_i \models T$
for all i,
$M_i \subseteq M_j$
for all
$i < j$
, and
$M_\alpha = \bigcup _{\beta < \alpha } M_\beta $
for
$\alpha $
limit. We assume that our continuous chains are always increasing. We will use the following version of the local character.
Lemma 4.4. Suppose
$T = T^{\text {eq}}$
is rosy. Then 
satisfies local character over models, that is: Let
$\kappa> \lvert T \rvert ^+$
be regular,
$(M_i)_{i < \kappa }$
be a continuous chain of models of T such that
$\lvert M_i \rvert < \kappa $
for all i, and let
$M := \bigcup _{i < \kappa } M_i$
be such that
$\lvert M \rvert = \kappa $
. Let a be a finite tuple. Then there is
$i < \kappa $
such that 
.
Proof. For an abstract proof of this result at the level of independence relations, see, e.g., [Reference Dobrowolski and Kamsma14, Lemma 9.6] (using the properties listed in Fact 2.3).
We also require some important facts about
$\text {NSOP}_1$
theories.
Fact 4.5.
-
(i) [Reference Kaplan and Ramsey20, Proposition 8.8] An
$\text {NSOP}_1$
theory T is simple iff satisfies base monotonicity over models. -
(ii) (This is a corollary to [Reference Kaplan and Ramsey20, Theorem 6.5]) Let T be
$\text {NSOP}_1$
and
$M \models T$
. If and
$I = (b_i)_{i < \omega }$
is a -Morley sequence over M with
$b_0 = b$
, then there is
$a' \equiv _{Mb} a$
such that
$a'b_i \equiv _M ab$
for all
$i < \omega $
.
satisfies base monotonicity over models.
and 
-Morley sequence over M with 
We also adapt the terminology from [Reference Dobrowolski and Kamsma14]: if 
satisfies existence and right extension, then, given a model
$M \models T$
and a tuple a, there exist a sequence
$(a_i)_{i < \kappa }$
with
$a_i \equiv _M a$
for all
$i < \kappa $
and a continuous chain of models
$(M_i)_{i < \kappa }$
such that
$M \subseteq M_0$
,
$a_{<i} \subset M_i$
, and 
for all
$i < \kappa $
. We will call this sequence
$(M_i)_{i < \kappa }$
a 
-independence chain for
$(a_i)_{i < \kappa }$
over M.
Theorem 4.6. If T is
$\text {NSOP}_1$
and rosy, and
$T^{\text {eq}}$
has the stable Kim-forking property over models, then T is simple.
Proof. Let T be
$\text {NSOP}_1$
and rosy. Recall (see, e.g., [Reference Kim24, Remark and Example 2.3.8], which can also be adapted for
$\text {NSOP}_1$
) that T is
$\text {NSOP}_1$
(resp., simple) iff
$T^{\text {eq}}$
is
$\text {NSOP}_1$
(resp., simple), so without loss of generality we may assume
$T = T^{\text {eq}}$
. In particular, by assumption, T has the stable Kim-forking property over models.
Claim.
over models.
Proof. (
$\Leftarrow $
) Suppose that 
but 
. By the stable Kim-forking property, there is some
$\mathcal {L}(M)$
-formula
$\phi (x,y)$
that is stable such that
$\phi (x,b) \in \operatorname {\mathrm {tp}}(a/Mb)$
Kim-forks over M. By right extension, we can find some
$N \supset M \cup \{b\}$
such that 
and
$N \models T$
. Then
$\phi (x,b) \in \operatorname {\mathrm {tp}}(a/N)$
, and in particular
$\phi (x,b)$
forks over M. Thus, by Fact 4.3,
$\operatorname {\mathrm {tp}}(a/N)$
þ-forks over M, a contradiction.
(
$\Rightarrow $
) We adapt the proof from [Reference Dobrowolski and Kamsma14, Theorem 9.1] (which is in turn based on the original proof from [Reference Chernikov, Kim and Ramsey10]). So suppose that 
. By the above remark, we can find a long M-indiscernible sequence
$(b_i)_{i < \kappa }$
with
$b_i \equiv _M b$
for all
$i < \kappa $
and an 
-independence chain
$(M_i)_{i < \kappa }$
for
$(b_i)_{i<\kappa }$
over M. In particular, we have 
for all
$i < \kappa $
, and so, by monotonicity,
$(b_i)_{i < \kappa }$
is 
-Morley over M. Hence, since T is
$\text {NSOP}_1$
, we can apply Fact 4.5(ii) to find some
$a' \equiv _{Mb} a$
such that
$a'b_i \equiv _M ab$
for all
$i < \omega $
.
By monotonicity and downwards Löwenheim–Skolem, we may assume
$\kappa = (\lvert T \rvert + \lvert M \rvert )^+$
and
$(M_i)_{i \in \kappa }$
is a continuous chain with
$\lvert M_i \rvert < \kappa $
. Let
$M_\kappa := \bigcup _{i \in \kappa } M_i$
. Since T is rosy, by Lemma 4.4, 
satisfies local character over models. Therefore, there is
$i_0 < \kappa $
such that 
, and so by monotonicity, 
. But also 
. Hence, by symmetry and transitivity, 
, so 
by invariance, as required.
This equality implies that 
satisfies base monotonicity over models. Therefore, by Fact 4.5(i), T is simple. This concludes the proof.
Corollary 4.7. Suppose that the stable Kim-forking conjecture holds. If T is
$\text {NSOP}_1$
and rosy, then T is simple.
Remark 4.8. It is an open problem whether, in order to conclude that
$T^{\text {eq}}$
has stable Kim-forking over models, it suffices to prove stable Kim-forking for types over real parameters (see [Reference Bossut5, Section 5] for more details).
Let us note that this pattern fails for higher levels of the
$\text {SOP}_n$
hierarchy: for instance, the generic triangle-free graph, which is
$\text {NSOP}_4$
but
$\text {SOP}_3$
, is rosy.
A corollary of this result emphasizes the distinction between simple and
$\text {NSOP}_1$
theories. Recall that T is said to be pregeometric if
$\operatorname {\mathrm {acl}}$
satisfies exchange, i.e., whenever
$a \in \operatorname {\mathrm {acl}}(Ab) \setminus \operatorname {\mathrm {acl}}(A)$
, we have
$b \in \operatorname {\mathrm {acl}}(Aa)$
. This large class of theories contains those of strongly minimal and o-minimal theories, plus a plethora of other
$\text {NIP}$
examples, such as the theory of p-adically closed fields. We can also find several examples of simple pregeometric theories, such as simple free amalgamation theories (cf. [Reference Conant12]) and pseudofinite fields (cf. [Reference Hrushovski19]).
Generally speaking, if T is pregeometric,
$T^{\text {eq}}$
need not be so. However, all that is required to extend the notion of dimension given by algebraic closure to the imaginary case is the weakest form of elimination of imaginaries, namely, geometric elimination of imaginaries, i.e., for any imaginary e, there is some real tuple a such that
$e \in \operatorname {\mathrm {acl}}^{\text {eq}}(a)$
and
$a \in \operatorname {\mathrm {acl}}(e)$
. This is the main idea underlying the proof of the following result, due to Ealy and Onshuus.
Fact 4.9 [Reference Ealy and Onshuus16, Theorem 4.12]
If T is pregeometric and has geometric elimination of imaginaries, then T is rosy.
Thus, together with Theorem 4.6, this implies the following.
Corollary 4.10. Suppose the stable Kim-forking conjecture holds. Then there is no strictly
$\text {NSOP}_1$
pregeometric theory with geometric elimination of imaginaries.
Example 4.11. Let us note that there are known strictly
$\text {NSOP}_1$
examples with exactly one of each of the two properties in the conclusion. We thank Christian d’Elbée for suggesting the following example: Consider
$\text {ACFG}$
, the theory of an algebraically closed field of characteristic
$p> 0$
expanded by a predicate for an additive subgroup. This theory is strictly
$\text {NSOP}_1$
and pregeometric, but does not have pregeometric elimination of imaginaries (see [Reference d’Elbée13]). We can (weakly) eliminate imaginaries by adding a new sort for the quotient group
$K/G$
and a function symbol for the quotient map
$\pi \colon K \to K/G$
, but the resulting two-sorted theory is not pregeometric.
Acknowledgments
The present work was completed during my Ph.D. at Imperial College London. I am deeply grateful to my supervisors, David Evans and Charlotte Kestner, for their guidance, suggestions, and constant support. The contents of the article were developed during a research visit to the University of Notre Dame. I thank Anand Pillay and Nicholas Ramsey for many useful comments and improvements, as well as Atticus Stonestrom for drawing my attention to the class of pregeometric theories. Finally, I thank the anonymous referee for several improvements throughout.
Funding
This project was completed during my Ph.D. and funded by the EPSRC (EP/W524323/1). The visit to the University of Notre Dame was jointly funded by a Dean’s Fund Award from Imperial College London and the University of Notre Dame.
Open access
