We dedicate this article to our esteemed colleague and friend Dimiter Vakarelov.
1 Introduction
Possibility-sufficiency algebras (PS-algebras), as Boolean algebras expanded with unary operators of possibility and sufficiency, were first studied in [Reference Düntsch and Orłowska5]. The latter operator is an algebraic counterpart of the window modality, whose provenance can be traced back to [Reference Gargov, Passy and Tinchev8, Reference Goranko9, Reference Humberstone11], and also [Reference van Benthem1] in the framework of deontic logic. The theory of PS-algebras was refined and developed further in [Reference Düntsch and Orłowska6, Reference Düntsch, Orłowska and Tinchev7], with particular emphasis on two subclasses of PS-algebras: mixed and weak mixed algebras, which force a relationship between the—otherwise independent—operators of possibility and sufficiency.
Building on the aforementioned works, we initiated in [Reference Düntsch, Gruszczyński and Menchón4] a theory of betweenness algebras (b-algebras), which were thought of as an approach to study the most general algebraic and logical properties of the ternary relation of betweenness well-known from ordered geometry. Being ternary, betweenness calls for binary operators, and for this reason, our PS-algebras are Boolean algebras with binary operators of possibility and sufficiency. To guarantee the interplay between the two operators, we focused on weak mixed algebras, which we enriched with equalities expressing the basic and well-motivated properties of betweenness. The approach turned out to be fruitful and allowed for the development of both representation and canonical extensions of algebras arising from betweenness relations. For these, the canonical frames of b-algebras are triples of the form
$\langle W,R,S \rangle $
, where S and R are ternary relations on W obtained in the standard way from sufficiency and possibility operators, respectively, with
$S\subseteq R$
. In a certain sense, R and S together simulate the betweenness relation. We showed that this cannot be avoided, in the sense that, in general, the canonical frame of a b-algebra cannot have just one ternary relation which is a betweenness. This was a negative result, as the starting point of our research was precisely frames
$\langle W,B \rangle $
, where B is a betweenness, and the properties of the complex algebras of such frames gave rise to the axiomatization presented in the article. However, the negative finding did not exclude the existence of a more general ternary relation that could allow for a representation theorem for b-algebras, and finding such a relation was formulated as problem (1) in [Reference Düntsch, Gruszczyński and Menchón4].
With the problem in focus, we concentrate below on a general study of frames
$\langle W,R,S \rangle $
with
$S\subseteq R$
(wMIA frames). We develop a logic
$K^{\#}$
with binary operators of possibility and sufficiency (window modality) that is sound and complete with respect to the class of wMIA frames. To this end, we adapt for our needs the copying method from [Reference Gargov, Passy and Tinchev8, Reference Vakarelov, Meyer and Zalessky14], which allows for the transformation of wMIA frames into frames with a single ternary relation. Further, we study algebraic models of
$K^{\#}$
, i.e., PS-algebras determined by an equational theory
$\Sigma $
. We prove that the variety
${\mathbf {V}}(\Sigma )$
is precisely the variety generated by the class of weak mixed algebras (which does not form a variety itself).
The techniques and results mentioned above allow us to prove that every weak mixed algebra can be embedded into a frame of the form
$\langle W,R \rangle $
, and in consequence, solve the problem (1) for b-algebras. In the article’s final section, we demonstrate how «far from» betweenness the ternary relation R is.
2 Notation and first definitions
2.1 Boolean algebras
Throughout,
$\langle A,+, \cdot , -, \mathbf {0}, \mathbf {1} \rangle $
is a non-trivial Boolean algebra, usually denoted by A. For
$a,b \in A$
we define the symmetric sum
which is the complement of the symmetric difference
$(a \cdot -b) + (b \cdot -a)$
and corresponds to logical equivalence. Clearly,
$a = b$
if and only if
$a \mathrel {\nabla } b = \mathbf {1}$
.
Lemma 2.1 [Reference Koppelberg, Monk and Bonnet13, Lemma 5.22].
If F is a filter on A, then the relation on A defined by
$$\begin{align*}a \mathrel{\theta_F} b \text{ if and only if } a \mathrel{\nabla} b \in F \end{align*}$$
is a Boolean congruence relation. Conversely, if
$\theta $
is a Boolean congruence on A, then 
is a filter on A. Furthermore,
$\theta _{F_\theta } = \theta $
and
$F_{\theta _F} = F$
.
2.2 PS-algebras
A binary possibility operator on A is a mapping
$f: A \times A \to A$
which satisfies for all
$a,b,a',b' \in A,$
$$ \begin{align} &f(a, \mathbf{0}) = f(\mathbf{0},a) = \mathbf{0}, && \text{Normality} \end{align} $$
$$ \begin{align} &f(a,b) + f(a,b') = f(a,b+b'), && \text{Additivity}, &f(a,b) + f(a',b) = f(a+a',b). \nonumber \end{align} $$
The dual
$f^\partial $
of f is the mapping defined by 
, often called a binary necessity operator.
A binary sufficiency operator on A is a mapping
$g: A \times A \to A$
which satisfies for all
$a,b,a',b' \in A,$
$$ \begin{align} &g(a, \mathbf{0}) = g(\mathbf{0},a) = \mathbf{1}, && \text{Co-normality} \end{align} $$
$$ \begin{align} &g(a,b) \cdot g(a,b') = g(a,b+b'), &&\text{Co-additivity}, \\ &g(a,b) \cdot g(a',b) = g(a+a',b). \nonumber \end{align} $$
It is well known that f is isotone in each component and that g is antitone in each component. A PS-algebra is a structure 
where f is a possibility operator and g is a sufficiency operator.
We prepare the description of the congruences on a PS-algebra
$\mathfrak {A}$
with a few known facts. The Boolean congruences on A were described earlier in Lemma 2.1. Congruences with respect to a binary necessity operator were characterized in [Reference Venema, Blackburn, Benthem and Wolter15].
Lemma 2.2 [Reference Venema, Blackburn, Benthem and Wolter15, Theorem 29].
If m is a binary necessity operator on
$\mathfrak {A}$
and F is a filter of A, then
$\theta _F$
preserves m if and only if
$a \in F$
implies
$m(a, \mathbf {0}) \cdot m(\mathbf {0},a) \in F$
.
To apply these results, we first define for a sufficiency operator
$g: A \times A \to A$
a mapping
$g^*: A \times A \to A$
by
$g^*(a,b) = g(-a,-b)$
. The operator
$g^*$
is a binary necessity operator, and a Boolean congruence preserves g if and only if it preserves
$g^*$
, since g and
$g^*$
are mutually term definable. We now define an auxiliary mapping
$u\colon A \times A \to A$
Footnote
1
$$\begin{align} u(a,b) = f^\partial(a,b) \cdot g^*(a,b). \end{align} $$
Clearly, u is a binary necessity operator on A.
Given a Boolean algebra A with binary necessity operators
$m_i$
(for some index set I), a filter of F of A is a congruence filter if and only if
$\theta _F$
preserves each
$m_i$
.
Theorem 2.3. Let 
be a PS-algebra. Suppose that F is a filter of A. Then, F is a congruence filter (i.e.,
$\theta _F$
preserves
$f^\partial $
and
$g^\ast $
) if and only if
$u(a, \mathbf {0}) \cdot u(\mathbf {0},a) \in F$
for all
$a \in F$
.
Proof. (
$\Rightarrow $
) Let F be a congruence filter and
$a \in F$
. Then,
$f^\partial (a,\mathbf {0}) \cdot {f^\partial (\mathbf {0},a) \in F}$
and
$g^*(a,\mathbf {0}) \cdot g^*(\mathbf {0},a) \in F$
by Lemma 2.2. Thus,
$$ \begin{align*} u(a, \mathbf{0}) \cdot u(\mathbf{0},a) = f^\partial(a,\mathbf{0}) \cdot g^*(a,\mathbf{0}) & \cdot f^\partial(\mathbf{0},a) \cdot g^*(\mathbf{0},a) = \\ & f^\partial(a,\mathbf{0})\cdot f^\partial(\mathbf{0},a) \cdot g^*(a,\mathbf{0}) \cdot g^*(\mathbf{0},a) \in F. \end{align*} $$
(
$\Leftarrow $
) If
$a \in F$
and
$u(a, \mathbf {0}) \cdot u(\mathbf {0},a) \in F$
, then
$$ \begin{align*} f^\partial(a,\mathbf{0}) \cdot g^*(a,\mathbf{0}) \cdot f^\partial(\mathbf{0},a) \cdot g^*(\mathbf{0},a) \in F, \end{align*} $$
and thus,
$f^\partial (a,\mathbf {0}) \cdot f^\partial (\mathbf {0},a) \in F$
and
$g^*(a,\mathbf {0}) \cdot g^*(\mathbf {0},a) \in F$
since F is a filter.
2.3 Complex algebras and canonical frames
The canonical frame of
$\mathfrak {A}$
is the structure 
, where
$R_f$
and
$S_g$
are ternary relations on
$\operatorname {\mathrm {Ult}} A$
defined by
$$\begin{align} R_f(\mathscr{U}_1,\mathscr{U}_2,\mathscr{U}_3) &\;\mathrel{\mathord{:}\mathord{\Leftrightarrow}}\; f[\mathscr{U}_1 \times \mathscr{U}_3] \subseteq \mathscr{U}_2, \end{align} $$
$$\begin{align} S_g(\mathscr{U}_1,\mathscr{U}_2,\mathscr{U}_3) &\;\mathrel{\mathord{:}\mathord{\Leftrightarrow}}\; g[\mathscr{U}_1\times\mathscr{U}_3]\cap\mathscr{U}_2\neq\emptyset. \end{align} $$
Additionally, we define an auxiliary operator
$h\colon A \times A \to A$
by
and we set
$$\begin{align} T_h(\mathscr{U}_1,\mathscr{U}_2,\mathscr{U}_3) \;\mathrel{\mathord{:}\mathord{\Leftrightarrow}}\; h[\mathscr{U}_1 \times \mathscr{U}_3] \subseteq \mathscr{U}_2. \end{align} $$
Lemma 2.4.
$T_h = R_f \cup -S_g$
.
Proof. (
$\subseteq $
) Suppose
$h[\mathscr {U}_1\times \mathscr {U}_3]\subseteq \mathscr {U}_2$
and
$g[\mathscr {U}_1\times \mathscr {U}_3]\cap \mathscr {U}_2\neq \emptyset $
. Let
$\langle a,b \rangle \in \mathscr {U}_1\times \mathscr {U}_3$
be such that
$g(a,b)\in \mathscr {U}_2$
. Pick
$x\in \mathscr {U}_1$
and
$y\in \mathscr {U}_3$
. As
$x\cdot a\in \mathscr {U}_1$
and
$y\cdot b\in \mathscr {U}_3$
, it must hold that
$h(x\cdot a,y\cdot b)\in \mathscr {U}_2$
. As g is antitone, also
${g(x\cdot a,y\cdot b)}\in \mathscr {U}_2$
. Thus by the definition of h we obtain
$f(x\cdot a,y\cdot b)\in \mathscr {U}_2$
. Now, f is isotone, so
$f(x,y)\in \mathscr {U}_2$
, as required.
(
$\supseteq $
) Let
$\mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3 \in \operatorname {\mathrm {Ult}} A$
, and
$a \in \mathscr {U}_1, b \in \mathscr {U}_3$
. If
$R_f(\mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3)$
, then,
$f(a,b) \in \mathscr {U}_2$
, and it follows that
$h(a,b) = f(a,b)+-g(a,b) \in \mathscr {U}_2$
. If
$\langle \mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3 \rangle $
is not an element of
$S_g$
, then
$g[\mathscr {U}_1\times \mathscr {U}_3]\cap \mathscr {U}_2 = \emptyset $
, hence,
$g(a,b) \not \in \mathscr {U}_2$
, which implies
$-g(a,b) \in \mathscr {U}_2$
. It follows that
$h(a,b) = f(a,b)+-g(a,b) \in \mathscr {U}_2$
.
In this article, a frame is a structure 
where W is a nonempty set, and R and S are ternary relations on W. The full complex algebra of
$\mathfrak {F}$
is the structure 
where
$\langle { R \rangle }$
and
$[[ S ]]$
are binary operators (of possibility and sufficiency, respectively) on
$2^W$
defined by
A subalgebra of
$\operatorname {{\mathsf {Cm}}}(\mathfrak {F})$
is called a complex algebra.
3 The binary logic
$K^{\#}$
We will develop the logic
$K^{\#}$
for the binary case using the copying construction from [Reference Vakarelov, Meyer and Zalessky14] adapted for our needs. This is a Boolean logic with a set
$\mathsf {Var}$
of propositional variables, a constant
$\top $
, and two extra binary modalities
$\Diamond $
and 
with duals
$\Box $
and 
. Formulas have the form:
where
$p \in \mathsf {Var}$
. We use the usual definitions of the Boolean connectives
$\bot $
,
$\lor $
,
$\rightarrow $
,
$\leftrightarrow $
. The axioms are those for classical propositional logic plus the following modal axioms:
$$ \begin{align} \neg\Diamond(\bot, \phi)\qquad\neg\Diamond(\phi, \bot), \end{align} $$
$$ \begin{align} \begin{aligned} \Diamond(\phi, \psi) \lor \Diamond(\phi, \chi) &{}\leftrightarrow \Diamond(\phi, \psi \lor \chi)\\ \Diamond(\phi, \psi) \lor \Diamond(\chi, \psi ) &{}\leftrightarrow \Diamond(\phi \lor \chi, \psi), \end{aligned} \end{align} $$
The auxiliary operator
$\langle U \rangle \!\rangle $
is defined by
Its dual is denoted by
$[ U ]]$
:
We consider the following additional axioms:
$$\begin{align} &\langle U \rangle\!\rangle(\phi,\top) \land \langle U \rangle\!\rangle(\psi, \top)\rightarrow \langle U \rangle\!\rangle(\phi,\psi), \end{align} $$
$$\begin{align} &\phi \rightarrow \langle U \rangle\!\rangle(\phi,\top), \end{align} $$
$$\begin{align} &\langle U \rangle\!\rangle(\langle U \rangle\!\rangle(\phi,\top),\top) \rightarrow \langle U \rangle\!\rangle(\phi,\top), \end{align} $$
$$\begin{align} &\phi \rightarrow [ U ]]\left(\langle U \rangle\!\rangle(\phi,\top),\bot\right). \end{align} $$
The names (T U ), (4 U ), and (B U ) are motivated in an obvious way by reference to the standard unary modal axioms corresponding to reflexivity, transitivity, and symmetry. The name for (C U ) is justified by the axiom postulating a non-standard behavior of possibility with respect to conjunction.
$K^{\#}$
is the smallest set of formulas that contains propositional tautologies, all instances of (M1)–(M4), (C
U
)–(B
U
), and is closed under modus ponens, uniform substitution, and the following rules for
$\Diamond $
and 
:
We have that
$$\begin{align} K^{\#}\vdash{}& \langle U \rangle\!\rangle(\phi,\psi)\rightarrow\langle U \rangle\!\rangle(\psi,\phi). \end{align} $$
3.1 Relational semantics
is called a weak MIA frame (wMIA frame, for short), if
$S \subseteq R$
. The class of weak MIA frames is decisive in the determination of the relational models of the logic
$K^{\#}$
.
Generalizing the notion of complex algebras of weak MIA frames we arrive at the following definition. A PS-algebra
$\mathfrak {A}$
is a weak MIA (wMIA) if it satisfies
$$ \begin{align} (\forall a,b\in A)\,[a \neq \mathbf{0} \text{ and } b \neq \mathbf{0} \Rightarrow g(a,b) \leq f(a,b)]. \end{align} $$
The class of weak MIAs is denoted by wMIA. Note that wMIA is a first-order positive universal class, and so it is closed under subalgebras and homomorphic images. The following establishes a relationship between weak MIAs and weak MIA frames.
Lemma 3.1 [Reference Düntsch, Gruszczyński and Menchón4].
-
(1) The complex algebra of a wMIA frame is a weak MIA.
-
(2) The canonical frame of a weak MIA is a weak MIA frame.
Theorem 3.2 [Reference Düntsch, Gruszczyński and Menchón4].
-
(1) Each wMIA frame is embeddable into the canonical frame of its complex algebra.
-
(2) Each weak MIA is embeddable into the complex algebra of its canonical frame.
Notation not explained here can be found in [Reference Blackburn, de Rijke and Venema2, Section 5] and [Reference Burris and Sankappanavar3, Reference Düntsch, Gruszczyński and Menchón4], in particular, II Section 10 of [Reference Burris and Sankappanavar3].
Models are structures 
where 
is a wMIA frame, and
$v\colon \mathsf {Var} \to 2^W$
is a valuation, extended over the Boolean connectives in the usual way, and over the modal operators as follows:
We call
$\mathfrak {F}$
the base of the model. A formula
$\phi $
is satisfied at
$x \in W$
with respect to
$\mathfrak {M}$
, written as
$\mathfrak {M},x \models \phi $
, if
$x \in v(\phi )$
. Then,
$$ \begin{align} \mathfrak{M}, x \models \Diamond(\phi,\psi) &{}\Leftrightarrow (v(\phi) \times \{x\} \times v(\psi)) \cap R \neq \emptyset, \end{align} $$
Consequently,
$$ \begin{align} \begin{aligned} \mathfrak{M},x\models \langle U \rangle\!\rangle(\varphi,\psi)\Leftrightarrow{}&(v(\phi) \times \{x\} \times v(\psi)) \cap R \neq \emptyset \text{ or }\\ &\phantom{aaaaaa}(v(\phi) \times \{x\} \times v(\psi)) \cap-S \neq \emptyset. \nonumber \end{aligned} \end{align} $$
Thus,
$$ \begin{align} \mathfrak{M},x\models \langle U \rangle\!\rangle(\varphi,\psi)&{}\Leftrightarrow v(\phi) \neq\emptyset\text{ and } v(\psi)\neq\emptyset, \end{align} $$
$$ \begin{align} \mathfrak{M},x\models [ U ]](\varphi,\psi)&{}\Leftrightarrow v(\phi) = W\text{ or } v(\psi)=W. \end{align} $$
and—thanks to these—with
$\langle U \rangle \!\rangle $
and
$[ U ]]$
we can associate global modalities, existential and universal, respectively
$$\begin{align} \mathfrak{M}, x \models \langle U \rangle\!\rangle(\phi,\top)& {}\Leftrightarrow (\exists y\in W)\,\mathfrak{M},y\models \phi, \end{align} $$
$$\begin{align} \mathfrak{M}, x \models [ U ]](\phi,\bot)& {}\Leftrightarrow (\forall y\in W)\,\mathfrak{M},y\models \phi. \end{align} $$
3.2 The canonical frame for
$\boldsymbol {K^{\#}}$
The main objectives for this section are proofs of soundness and completeness of
$K^{\#}$
with respect to the class of wMIA frames. For these, we use the standard notion of validity in a frame, i.e., a formula
$\varphi $
is valid in
$\mathfrak {F}$
if for any model
$\mathfrak {M}$
based on
$\mathfrak {F}$
and any
$x\in W$
,
$\mathfrak {M},x\models \varphi $
.
Soundness, as usual, is easy.
Theorem 3.3 (Soundness).
$K^{\#}$
is sound with respect to wMIA frames.
Proof. Let 
be a model with the base 
. It is easy to see that the axioms (M1)–(M4) are satisfied at all
$x\in W$
.
Straightforward computations show that for all
$x\in W$
,
$\mathfrak {M}, x\models (T_{U})$
,
$\mathfrak {M},x\models (4_{U})$
, and
$\mathfrak {M},x\models (B_{U})$
. For (C
U
), observe that if
$x\in W$
is such that
$\mathfrak {M}, x\models \langle U \rangle \!\rangle (\phi ,\top )\land \langle U \rangle \!\rangle (\psi ,\top )$
, then there exist
$y,z\in W$
such that
$\mathfrak {M}, y\models \phi $
and
$\mathfrak {M}, z\models \psi $
, i.e.,
$v(\phi )\neq \emptyset \neq v(\psi )$
. Therefore,
$\mathfrak {M},x\models \langle U \rangle \!\rangle (\phi ,\psi )$
by (3.7).
Since the valuation is arbitrary, we have shown that the axiomatization of
$K^{\#}$
is sound with respect to wMIA frames.
For completeness, we will need several definitions and lemmas. The key notion will be that of the canonical frame of the logic
$K^{\#}$
.
Let
$W^{K^{\#}}$
be the collection of all maximal consistent theories of
$K^{\#}$
. The canonical frame
Footnote
2
for
$K^{\#}$
is the structure
where
$$\begin{align} R^{K^{\#}}(x,y,z) &\;\mathrel{\mathord{:}\mathord{\Leftrightarrow}}\; \Diamond[x \times z] \subseteq y, \end{align} $$
We also define
$$\begin{align} T^{K^{\#}}(x,y,z) \;\mathrel{\mathord{:}\mathord{\Leftrightarrow}}\; \langle U \rangle\!\rangle[x \times z] \subseteq y. \end{align} $$
In analogy to Lemma 2.4 it can be shown that:
Lemma 3.4. In the canonical frame
$\mathfrak {F}^{K^{\#}}$
,
$T^{K^{\#}} =R^{K^{\#}}\cup -S^{K^{\#}}$
.
To simplify the notation we usually omit the superscripts in those situations which will not lead to any ambiguities.
We will prove the following.
Lemma 3.5. In
$\mathfrak {F}^{K^{\#}}$
the relation T satisfies the following properties:
-
(T1)
$T(x,x,x)$
. -
(T2) If
$T(x,y,z)$
, then
$T(z,y,x)$
. -
(T3) If
$T(x_1,y,z_1)$
,
$T(x_2,y,z_2),$
and
$T(x_3,y,z_3)$
, then
$T(a,b,c)$
for every triple
$\langle a,b,c \rangle $
in
$\{x_1,x_2,x_3\}^3\cup \{z_1,z_2,z_3\}^3$
.
Proof. For (T1), consider
$\phi ,\psi \in x$
. So
$\phi \land \psi \in x$
and, since x is a maximal theory, by (T
U
) and (C
U
) we obtain
$\langle U \rangle \!\rangle (\phi \land \psi ,\phi \land \psi )\in x$
. It follows that
$\langle U \rangle \!\rangle (\phi ,\psi )\in x$
, and therefore
$\langle U \rangle \!\rangle [x\times x]\subseteq x$
.
For (T2), suppose that
$\langle U \rangle \!\rangle [x\times z]\subseteq y$
. Let
$\phi \in z$
and
$\psi \in x$
. By assumption,
$\langle U \rangle \!\rangle (\psi ,\phi )\in y$
, and thus
$\langle U \rangle \!\rangle (\phi ,\psi )\in y$
by (S
U
) as required.
For (T3), suppose that
$\langle U \rangle \!\rangle [x_1\times z_1]\subseteq y$
,
$\langle U \rangle \!\rangle [x_2\times z_2]\subseteq y,$
and
$\langle U \rangle \!\rangle [x_3\times z_3]\subseteq y$
. Let
$\phi \in x_1$
and
$\psi \in x_3$
. By assumption, we know that
$\langle U \rangle \!\rangle (\phi ,\top )\in y$
and
$\langle U \rangle \!\rangle (\psi ,\top )\in y$
. By (B
U
)
$$\begin{align*}[ U ]](\langle U \rangle\!\rangle(\langle U \rangle\!\rangle(\psi,\top),\top),\bot)\in y \end{align*}$$
and by (4 U )
$$\begin{align*}[ U ]](\langle U \rangle\!\rangle(\psi,\top),\bot)\in y. \end{align*}$$
By the same argument
$[ U ]](\langle U \rangle \!\rangle (\phi ,\top ),\bot )\in y$
. Since
$$\begin{align*}[ U ]](\langle U \rangle\!\rangle(\phi,\top),\bot)\land [ U ]](\langle U \rangle\!\rangle(\psi,\top),\bot) \Leftrightarrow [ U ]](\langle U \rangle\!\rangle(\phi,\top)\land \langle U \rangle\!\rangle(\psi,\top),\bot), \end{align*}$$
from this and (C U ) it follows that
$$\begin{align*}[ U ]](\langle U \rangle\!\rangle(\phi,\psi),\bot)\in y,\quad\text{i.e.,}\quad \neg \langle U \rangle\!\rangle(\neg\langle U \rangle\!\rangle(\phi,\psi),\top)\in y. \end{align*}$$
In consequence
$\neg \langle U \rangle \!\rangle (\phi ,\psi )\notin x_1\cup x_2\cup x_3$
because otherwise
$$\begin{align*}\langle U \rangle\!\rangle(\neg\langle U \rangle\!\rangle(\phi,\psi),\top)\in y, \end{align*}$$
a contradiction. As we are dealing with maximal consistent theories of
$K^{\#}$
, we obtain
$\langle U \rangle \!\rangle (\phi ,\psi )\in x_1\cap x_2\cap x_3$
, and therefore
$T(x_1,x_1,x_3)$
,
$T(x_1,x_2,x_3),$
and
$T(x_1,x_3,x_3)$
.
All remaining possibilities are shown using the previous two points and choosing
$\varphi $
and
$\psi $
suitably.
Lemma 3.6. Let
$\mathfrak {F}^{K^{\#}}$
be the canonical frame for
$K^{\#}$
. For
$x\in W$
, let
If
$y\in W_x$
and
$T(a,y,b)$
, then
$a,b\in W_x$
.
Proof. Assume
$z\in W$
is such that
$T(y,x,z)$
and that
$T(a,y,b)$
. By (T1) we have that
$T(x,x,x)$
, and from (T3) we obtain
$T(x,y,x)$
. Applying (T3) again, but this time to
$T(a,y,b)$
and
$T(x,y,x)$
, we obtain that
$T(a,x,a)$
and
$T(b,x,b)$
, so both a and b are in
$W_x$
.
Lemma 3.7. If
$x\in W^{K^{\#}}$
, then 
such that and 
and 
is a wMIA frame (and a subframeFootnote
3
of
$\mathfrak {F}^{K^{\#}}$
).
Proof. Let
$\langle r,s,t \rangle \in S_x$
. By the definition of
$W_x$
and by (T3) we obtain
$T(r,s,t)$
, so
$\langle r,s,t \rangle \in R\cup -S$
by Lemma 3.4. By assumption,
$\langle r,s,t \rangle \in S$
so we obtain
$\langle r,s,t \rangle \in R\cap W_x^3$
, i.e.,
$\langle r,s,t \rangle \in R_x$
, as required.
Theorem 3.8 (Completeness).
If
$K^{\#}\nvdash \delta $
, then there is a model of
$K^{\#}$
based on a wMIA subframe of
$\mathfrak {F}^{K^{\#}}$
at which
$\delta $
fails. Thus, if
$\delta $
is valid in the class of wMIA frames, then
$K^{\#}\vdash \delta $
.
Proof. Suppose that
$K^{\#} \not \vdash \delta $
, and let x be a maximal consistent theory of the logic with
$\delta \notin x$
. Let
$V\colon \mathsf {Fml}\to 2^{W^{K^{\#}}}$
be the following mapping on the canonical frame
$\mathfrak {F}^{K^{\#}}$
:
$y\in V(\varphi )$
if and only if
$\varphi \in y$
. So
$x\notin V(\delta )$
. Take the weak MIA subframe
$\mathfrak {F}_x$
and consider the function
$v\colon \mathsf {Fml}\to 2^{W_x}$
defined by
Let us show that v is a valuation on the frame
$\mathfrak {F}_x$
, and in consequence of this and Theorem 3.3, 
is a model of
$K^{\#}$
(in which
$\delta $
fails at x, of course).
For the Boolean connectives, the proofs are straightforward, e.g., for negation, we have
For the possibility operator
$$ \begin{align*} y\in v(\Diamond(\varphi,\psi))&{}\;\mathrel{\mathord{:}\mathord{\Leftrightarrow}}\; y\in W_x\cap V(\Diamond(\varphi,\psi))\\ &{}\;\mathrel{\mathord{:}\mathord{\Leftrightarrow}}\; (V(\varphi)\times\{y\}\times V(\psi))\cap R\neq\emptyset\text{ and } y\in W_x \end{align*} $$
so, from the first conjunct, we obtain that there are
$a\in V(\varphi )$
and
$b\in V(\psi )$
such that (i)
$R(a,y,b)$
and from the second one that (ii)
$y\in W_x$
. From (i) and Lemma 3.4 it follows that
$T(a,y,b)$
, so (ii) and Lemma 3.6 entail that
$a,b\in W_x$
. Thus,
$$ \begin{align*} y\in v(\Diamond(\varphi,\psi))&{}\Leftrightarrow (V(\varphi)\cap W_x)\times\{y\}\times (V(\psi)\cap W_x)\cap R\neq\emptyset\text{ and } y\in W_x\\ &{}\Leftrightarrow (v(\varphi)\times\{y\}\times v(\psi))\cap R_x\neq\emptyset. \end{align*} $$
For the sufficiency operator we have to demonstrate that
$$\begin{align*}\{y\in W:V(\varphi)\times\{y\}\times V(\psi)\subseteq S\}\cap W_x=\{y\in W_x:v(\varphi)\times\{y\}\times v(\psi)\subseteq S_x\}. \end{align*}$$
(
$\subseteq $
) If
$V(\varphi )\times \{y\}\times V(\psi )\subseteq S$
,
$y\in W_x$
and
$\langle a,y,b \rangle \in v(\varphi )\times \{y\}\times v(\psi )$
, then also
$a,b\in W_x$
and thus the triple is in
$S_x$
as required.
(
$\supseteq $
) Let
$y\in W_x$
be such that
$v(\varphi )\times \{y\}\times v(\psi )\subseteq S_x$
. By the definition of
$W_x$
we have that there is
$z\in W$
such that
$T(y,x,z)$
. Take
$\langle a,b,c \rangle \in V(\varphi )\times \{y\}\times V(\psi )$
, and assume towards a contradiction that
$\langle a,y,b \rangle \notin S$
. By Lemma 3.4 it is the case that
$T(a,y,b)$
. By Lemma 3.6,
$a,b\in W_x$
, so
$\langle a,y,b \rangle \in S_x\subseteq S$
, which contradicts our assumption.
3.3 Special frames and models
A weak MIA frame 
is called special if
$R=S$
. Similarly, a model
$\mathfrak {M}$
based on a wMIA frame
$\mathfrak {F}$
is special if
$\mathfrak {F}$
itself is special.
Two models 
and 
are called modally equivalent if the same formulas are true in both, i.e., if for all
$\phi \in \mathsf {Fml}$
,
$$\begin{align*}\mathfrak{M} \models \phi \Leftrightarrow \mathfrak{M}' \models \phi. \end{align*}$$
OurFootnote
4
next aim is to construct—given
$\langle W,R,S,v \rangle $
—a special model
$\langle \underline {W}, \underline {R}, \underline {S}, \underline {v} \rangle $
, that is modally equivalent to
$\langle W,R,S,v \rangle $
. The idea of the construction of
$\underline {R}$
and
$\underline {S}$
is to “separate” triples
$\langle x,y,z \rangle $
which are in the intersection of R and
$-S$
, i.e., to remove those triples which prevent
$R = S$
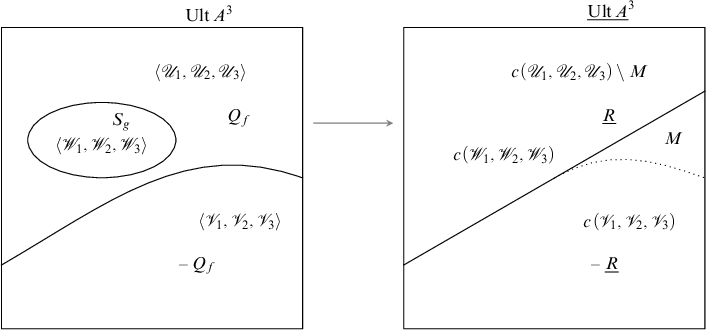
(see Figure 1).
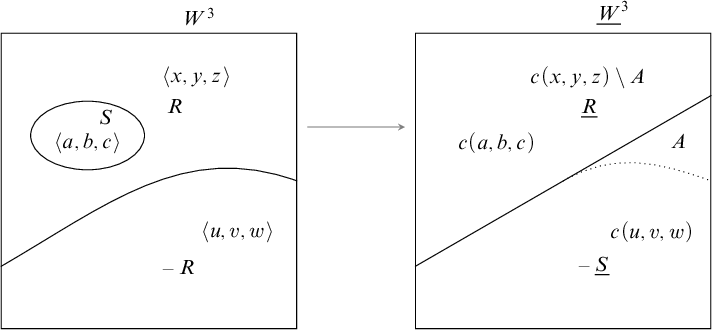
Figure 1 A visual presentation of the construction of the special frame of a frame
$\langle W,R,S\rangle $
with
$S\subseteq R$
. Observe that 
.
Let us start with a fixed frame 
. Let
$\mathfrak {F}\uplus \mathfrak {F}'$
be the disjoint union of
$\mathfrak {F}$
with its isomorphic copy 
whose domain is disjoint from that of
$\mathfrak {F}$
. Thus,
Clearly,Footnote
5
if both frames are wMIA frames, then
$S\cup S'\subseteq R\cup R'$
, so the disjoint union is a wMIA frame as well.
For 
, there are triples in
$\underline {W}^3$
such that:
-
(1) all coordinates are from either W or
$W'$
, which we call pure, or -
(2) at least one coordinate is from W and at least one from
$W'$
; these triples will be called mixed.
For a fixed pure triple
$\langle x,y,z \rangle \in W^3$
(or its copy
$\langle x',y',z' \rangle \in (W')^3$
), in
$\underline {W}^3$
there are eight “variants” of
$\langle x,y,z \rangle $
: the triple itself and
$$ \begin{align*} \langle x',y,z \rangle,\ \langle x,y',z \rangle,\ \langle x,y,z' \rangle,\ \langle x',y',z \rangle,\ \langle x',y,z' \rangle,\ \langle x,y',z' \rangle,\ \langle x',y',z' \rangle. \end{align*} $$
We denote the collection of these by
and we call it the cell determined by
$\langle x,y,z \rangle $
.
Let
$i\colon W\to W'$
be the bijection that assigns to any element of the domain its copy 
. Let
$i^{\ast }$
be the function inverse to i. By means of these we define an onto function
$j\colon W\cup W'\to W$
such that
Clearly, for
$x\in W$
,
$j^{-1}(x)=\{x,x'\},$
and
$\underline {W}=\bigcup _{x\in W}j^{-1}(x)$
. Moreover
$$\begin{align*}c(x,y,z)=\{\langle r,s,t \rangle: x=j(r)\text{ and } y=j(s)\text{ and } z=j(t)\}. \end{align*}$$
The next lemma justifies the name cell.
Lemma 3.9 (Partition Lemma).
The collection
is a partition of
$\underline {W}^3$
.
Proof. Let
$\langle r,s,t \rangle \in \underline {W}^3$
. Then, there are
$x,y,z \in W$
such that
$x=j(r)$
and
$y=j(s)$
and
$z=j(t)$
, and thus
$\langle r,s,t \rangle \in c(x,y,z)$
.
If
$\langle r,s,t \rangle \in c(x_0,y_0,z_0)\cap c(x_1,y_1,z_1)$
, then
$$\begin{align*}x_0=j(r)=x_1\quad\text{and}\quad y_0=j(s)=y_1\quad\text{and}\quad z_0=j(t)=z_1 \end{align*}$$
and so
$c(x_0,y_0,z_0)=c(x_1,y_1,z_1)$
.
For
$P\subseteq W^3$
, let
$P'$
be its copy. P and
$P'$
are relations that contain pure triples only. For relations that are subsets of
$\underline {W}^3$
(and may therefore contain mixed triples), we are going to use underlined letters, e.g.,
$\underline {P}$
,
$\underline {R}$
, and
$\underline {S}$
.
Given a relation
$\underline {P}\subseteq \underline {W}^3$
, we define the mixture of
$\underline {P}$
as the value of the function
$m\colon 2^{\underline {W}^3}\to 2^{\underline {W}^3}$
defined by
In consequence, for
$P\subseteq W^3$
and its copy
$P'\subseteq W^{\prime 3}$
we have
$$\begin{align*}m(P)=\bigcup_{\langle x,y,z \rangle\in P} c(x,y,z)\quad\text{and}\quad m(P')=\bigcup_{\langle x',y',z' \rangle\in P'} c(x,y,z). \end{align*}$$
Lemma 3.10. For all relations P and Q from
$W^3$
we have
$$ \begin{align} m(P)&{}=m(P')=m(P\cup P'), \end{align} $$
$$ \begin{align} m(W^3)&{}=\underline{W}^3, \end{align} $$
$$ \begin{align} P\subsetneq m(P)\quad&{}\text{ and }\quad P'\subsetneq m(P'), \end{align} $$
$$ \begin{align} P\subseteq Q&{}\Rightarrow m(P)\subseteq m(Q), \end{align} $$
$$ \begin{align} \underline{W}^3\setminus m(P)=m(W^3\setminus P)\quad&{}\text{ and }\quad \underline{W}^3\setminus m(P')=m(W^{\prime3}\setminus P') \end{align} $$
$$ \begin{align} m(P\cap Q)&{}=m(P)\cap m(Q), \end{align} $$
$$ \begin{align} m(P\cup Q)&{}=m(P)\cup m(Q). \end{align} $$
Proof. (3.9), (3.11), (3.12), and (3.15) have routine proofs that we leave to the reader.
(3.10) By the Partition Lemma.
(3.13) (
$\subseteq $
) Let
$\tau $
be a triple not in
$m(P)$
. Thus, for all
$\langle x,y,z \rangle \in P$
,
$\tau \notin c(x,y,z)$
. By the Partition Lemma there is a triple
$\langle x_0,y_0,z_0 \rangle \in W^3$
such that
$\tau \in c(x_0,y_0,z_0)$
. Clearly,
$\langle x_0,y_0,z_0 \rangle \notin P$
, so
$\tau \in m(W^3\setminus P)$
.
$(\supseteq )$
If
$\tau \in m(W^3\setminus P)$
, then there is
$\langle x,y,z \rangle \notin P$
such that
$\tau \in c(x,y,z)$
. If there were
$\langle r,s,t \rangle \in m(P)$
such that
$\tau \in c(j(r),j(s),j(t))$
, then P and
$W^3\setminus P$
would have a non-empty intersection, which is impossible.
The proof for the copy of P is similar.
(3.14) The left-to-right inclusion holds as m is isotone. For the reverse inclusion, pick
$\tau \in m(P)\cap m(Q)$
. Then, there are triples
$\langle x_0,y_0,z_0 \rangle \in P$
and
$\langle x_1,y_1,z_1 \rangle \in Q$
such that
$$\begin{align*}\tau\in c(x_0,y_0,z_0)\cap c(x_1,y_1,z_1). \end{align*}$$
By the Partition Lemma, these triples must be identical, and so
$\langle x_0,y_0,z_0 \rangle \in P\cap Q$
, which entails that
$\tau \in m(P\cap Q)$
.
The frame 
—obtained from the disjoint union of
$\mathfrak {F}$
and its copy
$\mathfrak {F}'$
—will be called the mixture of
$\mathfrak {F}$
. By (3.12), it is a wMIA frame, provided that
$\mathfrak {F}$
itself is.
The mixture
$m(\mathfrak {F})$
of any wMIA frame
$\mathfrak {F}$
can be turned into a special frame via the following construction of
$\underline {R}$
and
$-\underline {S}$
(below,
$-R$
and
$-S$
are the complements of the two relations in
$W^3$
):
Lemma 3.11. If
$\mathfrak {F}$
is a wMIA frame, then
$\underline {R} = \underline {S}$
.
Proof. We are going to show that
$\underline {R}\cup -\underline {S}=\underline {W}^3$
and
$\underline {R}\cap -\underline {S}=\emptyset $
.
For the first equality, we have to prove that
$$\begin{align*}\underline{W}^3=m(S)\cup[m(R\setminus S)\setminus(R\cup R')]\cup m(-R)\cup[(R\cup R')\setminus(S\cup S')]. \end{align*}$$
$$\begin{align*}\underline{W}^3=m(W^3)=m(S) \cup m(R \setminus S) \cup m(-R), \end{align*}$$
so it is enough to show that
$$\begin{align*}m(R \setminus S)=[m(R\setminus S)\setminus(R\cup R')]\cup[(R\cup R')\setminus(S\cup S')]. \end{align*}$$
Indeed,
$S\cup S'\subseteq R\cup R'$
and
$m(S)\cap (R\cup R')=S\cup S'$
, while from Lemma 3.10 it follows that
$m(S)\subseteq m(R)$
,
$S\cup S'\subseteq m(S)$
, and
$R\cup R'\subseteq m(R)$
. Together these imply
$$\begin{align*}m(R) \setminus m(S)=[(m(R)\setminus m(S))\setminus(R\cup R')]\cup[(R\cup R')\setminus(S\cup S')]. \end{align*}$$
UsingFootnote
6
Lemma 3.10 again, we obtain
$m(R\setminus S)=m(R) \setminus m(S)$
.
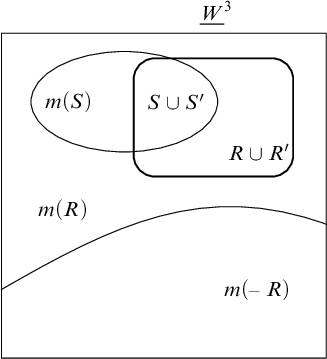
Figure 2
$m(R)\setminus m(S)$
is equal to the union of
$[m(R)\setminus m(S)]\setminus (R\cup R')$
and
$(R\cup R')\setminus (S\cup S')$
.
For the second equality, observe that each of the following four sets is empty (again, see Figure 2 for diagrammatic representation):
$$ \begin{align*} &\qquad\qquad\qquad m(S)\cap m(-R),\\ &\qquad\,\quad m(S)\cap [(R\cup R')\setminus(S\cup S')],\\ &\qquad\!\!\quad [m(R\setminus S)\setminus(R\cup R')]\cap m(-R),\\ & [m(R\setminus S)\setminus(R\cup R')]\cap [(R\cup R')\setminus(S\cup S')]. \end{align*} $$
The first one is empty by (3.14), since
$S\cap -R=\emptyset $
. The second one is empty since
$(R\cup R')\setminus (S\cup S')$
has only pure triples that are in
$R\cup R'$
, but not in
$m(S)$
. The emptiness of the third follows from (3.13), and the fourth one has a purely set-theoretical justification.
This concludes the proof.
Lemma 3.12. If 
is a wMIA frame, then
$\langle r,s,t \rangle \in \underline {R}$
implies
$\langle j(r),j(s),j(t) \rangle \in R$
.
Proof. Assume that
$\langle j(r),j(s),j(t) \rangle \in -R$
. By the relevant definitions,
$$\begin{align*}c(j(r),j(s),j(t))\subseteq m(-R)\subseteq-\underline{S}, \end{align*}$$
so by Lemma 3.11 we have that
$c(j(r),j(s),j(t))\subseteq -\underline {R}$
. Consequently,
$\langle r,s,t \rangle $
is in the complement of
$\underline {R}$
as required.
Theorem 3.13. If 
is a model of
$K^{\#}$
, based on a wMIA frame 
, then there is a special model 
such that
$\mathfrak {M}$
and
$\underline {\mathfrak {M}}$
are modally equivalent.
Proof. Fix a model 
. Let
$\mathfrak {F}'$
be an isomorphic and disjoint copy of
$\mathfrak {F}$
. Put 
where 
. Let 
be the special frame obtained from
$m(\mathfrak {F})$
. Let 
for every propositional variable p, and extend it to the valuation of all formulas
$\underline {v}\colon \mathsf {Fml}\to 2^{\underline {W}}$
in the standard way. We will prove by induction on the complexity of the formulas that for any
$\varphi \in \mathsf {Fml}$
,
$\underline {v}(\varphi )=v(\varphi )\cup v'(\varphi )$
.
For the negation, we have
Other Boolean connectives are straightforward, so we move to the modal operators.
Suppose
$\underline {v}(\varphi )=v(\varphi )\cup v'(\varphi )$
and
$\underline {v}(\psi )=v(\psi )\cup v'(\psi )$
, we will prove that
$$\begin{align*}\underline{v}(\Diamond (\varphi,\psi))=v(\Diamond (\varphi,\psi))\cup v'(\Diamond (\varphi,\psi)) \end{align*}$$
and
Let
$s\in \underline {W}$
be such that
$s\in \underline {v}(\Diamond (\varphi ,\psi ))$
, i.e.,
$(\underline {v}(\varphi )\times \{s\}\times \underline {v}(\psi ))\cap \underline {R}\neq \emptyset $
. By the induction hypothesis, we have that
$$\begin{align*}[(v(\varphi)\cup v'(\varphi))\times \{s\}\times (v(\psi)\cup v'(\psi))]\cap\underline{R}\neq\emptyset. \end{align*}$$
If
$\langle r,s,t \rangle $
is in the intersection, then by Lemma 3.12 the triple
$\langle j(r),j(s),j(t) \rangle $
is in R. Clearly,
$j(r)\in v(\varphi )$
and
$j(t)\in v(\psi )$
. So, if
$s\in W$
, then
$j(s)=s$
and
$\langle j(r),s,j(t) \rangle \in (v(\varphi )\times \{s\}\times v(\psi ))\cap R$
. If
$s\in W'$
, then
$j(s)'=s$
and
$\langle j(r)',s,j(t)' \rangle \in (v'(\varphi )\times \{s\}\times v'(\psi ))\cap R'$
. Thus
$s\in v(\Diamond (\varphi ,\psi ))\cup v'(\Diamond (\varphi ,\psi ))$
.
Let
$s\in v(\Diamond (\varphi ,\psi ))\cup v'(\Diamond (\varphi ,\psi ))$
, and consider the case that s is in the first component of the union. Then
$s\in W$
and
$(v(\varphi )\times \{s\}\times v(\psi ))\cap R\neq \emptyset $
. So, there exist
$y\in v(\varphi )$
and
$z\in v(\psi )$
such that
$\langle y,s,z \rangle \in R$
. By definition,
$\langle y',s,z' \rangle \in \underline {R}$
and, by the induction hypothesis,
$(\underline {v}(\varphi )\times \{s\}\times \underline {v}(\psi ))\cap \underline {R}\neq \emptyset $
. Therefore
$s\in \underline {v}(\Diamond (\varphi ,\psi ))$
. The proof is analogous for
$s\in v'(\Diamond (\varphi ,\psi ))$
.
For the case of the sufficiency operator, let 
, i.e.,
$\underline {v}(\varphi )\times \{s\}\times \underline {v}(\psi )\subseteq \underline {R}$
. If
$s\in W$
, let
$y\in v(\varphi )$
and
$z\in v(\psi )$
. By the induction hypothesis,
$\langle y,s,z \rangle \in \underline {R}$
. As the triple is pure, by the construction of
$\underline {R}$
it must be an element of S. Consequently, we obtain
$v(\varphi )\times \{s\}\times v(\psi )\subseteq S$
, i.e., 
. If
$s\in W'$
, it follows by a similar reasoning that 
.
Let 
. If 
, then
$v(\varphi )\times \{s\}\times v(\psi )\subseteq S$
. Let
$r\in \underline {v}(\varphi )=v(\varphi )\cup v'(\varphi )$
and
$t\in \underline {v}(\psi )=v(\psi )\cup v'(\psi )$
. So,
$j(r)\in v(\varphi )$
and
$j(t)\in v(\psi )$
, and the assumption entails that
$\langle j(r),s,j(t) \rangle \in S$
. By the construction of
$\underline {R}$
, we have
$c(j(r),s,j(t))\subseteq \underline {R}$
, and as the triple
$\langle r,s,t \rangle $
is in the cell, it must be in
$\underline {R}$
, too. The proof is analogous for 
.
Since
$\mathfrak {M}$
and
$\mathfrak {M}'$
are copies of each other, it is easy to see that the model 
is modally equivalent to
$\mathfrak {M}$
and by Lemma 3.11, we have
$\underline {R}=\underline {S}$
.
4 The class
${\textbf{V}}(\textbf{wMIA})$
In this section we shall exhibit an axiom system for the equational class of algebraic models of
$K^{\#}$
. To this end, consider the following equations for the operator u introduced by (
df u
) in Section 2:Footnote
7
$$ \begin{align} & u(a,\mathbf{0}) \leq a, \end{align} $$
$$ \begin{align} & u(a,\mathbf{0}) \leq u(u(a,\mathbf{0}),\mathbf{0}), \end{align} $$
$$ \begin{align} & a \leq u(u^{\partial}(a,\mathbf{0}),\mathbf{0}), \end{align} $$
$$ \begin{align} &u(a,a)=u(a,\mathbf{0})=u(\mathbf{0},a), \end{align} $$
$$ \begin{align} & u(a,b) = u(a,\mathbf{0}) + u(\mathbf{0},b). \end{align} $$
Recall that the class of wMIAs was defined as a subclass of the class of PS-algebras incorporating as an axiom the condition (wMIA), which is not an identity. We consider the class
${\mathbf {V}}(\mathbf {wMIA})$
, the smallest variety containing
$\mathbf {wMIA}$
.
Suppose that
and let
$\mathbf {V}(\Sigma )$
be the subvariety of PS-algebras generated by equations (4.1)–(4.5).
We will prove that the two varieties coincide.
Theorem 4.1.
$\mathbf {V}(\Sigma ) = {\mathbf {V}}(\mathbf {wMIA})$
.
Along the way we shall exhibit a larger class of algebras, which is relevant to our considerations.
In the case of unary modalities investigated in [Reference Düntsch, Orłowska and Tinchev7] a unary PS-algebra
$\langle A,f,g \rangle $
is a weak MIA if and only if the mapping defined by 
is the dual of the unary discriminator. We have shown in [Reference Düntsch, Gruszczyński and Menchón4] that for binary modalities such equivalence does not hold any more, and the weaker condition
$$\begin{align} (\forall a,b \in A)[a \cdot b \neq \mathbf{0} \Rightarrow g(a,b) \leq f(a,b)] \end{align} $$
isFootnote 8 necessary and sufficient for the discriminator to exist.
Lemma 4.2 [Reference Düntsch, Gruszczyński and Menchón4, Lemma 6.13].
Suppose that 
is a PS-algebra. Then, 
is the unary discriminator if and only if
$\mathfrak {A}$
satisfies (
di
).
Clearly, every wMIA satisfies ( di ). On the other hand, Table 1 from [Reference Düntsch, Gruszczyński and Menchón4] shows that (wMIA) is not equivalent to ( di ).
Let 
be a PS-algebra. We say that
$\mathfrak {A}$
is a dMIA if it satisfies (
di
). The class of all dMIAs will be denoted by
$\mathbf {dMIA}$
.
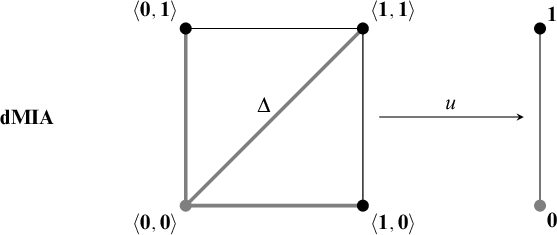
Lemma 4.3. Let 
be a dMIA. Then,
$\mathfrak {A}$
satisfies (4.4) (see Figure 3).
Figure 3 Assume that
$\langle A,\mathord {\leq _\ell }\rangle $
is a linearization (i.e.,
$\leq _\ell $
is an extension of
$\leq $
which is a linear order compatible with
$\leq $
) of a dMIA A, and take its binary product. Then, according to Lemmas 4.2 and 4.3, the binary operator u always sends the three black pairs to
$\mathbf {1}$
, and the gray ones to
$\mathbf {0}$
.
Proof. Firstly, assume that
$a=\mathbf {1}$
. Then,
$$\begin{align*}u(a,\mathbf{0})=u(\mathbf{1},\mathbf{0})=f^\partial(\mathbf{1},\mathbf{0})\cdot g(\mathbf{0},\mathbf{1})=\mathbf{1}\cdot\mathbf{1}=\mathbf{1}. \end{align*}$$
By analogous reasoning
$u(\mathbf {0},a)=\mathbf {1}$
and
$u(a,a)=\mathbf {1}$
.
Secondly, let
$a\neq \mathbf {1}$
, i.e.,
$-a\cdot \mathbf {1}\neq \mathbf {0}$
. Then by (
di
) we have
$g(-a,\mathbf {1})\leq f(-a,\mathbf {1})$
, and thus
$$\begin{align*}u(a,\mathbf{0})=-f(-a,\mathbf{1})\cdot g(-a,\mathbf{1})=\mathbf{0.} \end{align*}$$
In a similar way we show that
$u(\mathbf {0},a)=\mathbf {0}$
and
$u(a,a)=\mathbf {0}$
.
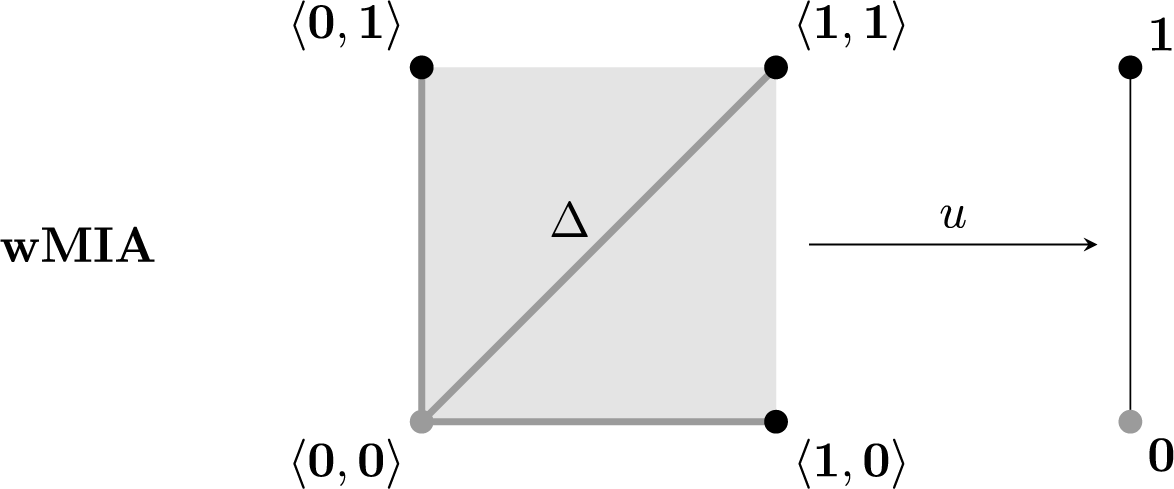
Lemma 4.4. Suppose that 
is a weak MIA. Then,
$\mathfrak {A}$
satisfies (4.5), and the range of the u operator is
$\{\mathbf {0},\mathbf {1}\}$
(see Figure 4).
Figure 4 This time let
$\langle A,\mathord {\leq _\ell }\rangle $
be a linearization of a wMIA A, and consider its binary product. Then, according to Lemma 4.4, the binary operator u sends the three black pairs to
$\mathbf {1}$
, and all the remaining ones to
$\mathbf {0}$
. The less saturated fragment of the rectangle indicates the area of possible differences between the behavior of u for dMIAs and wMIAs.
Proof. If
$a=\mathbf {1}$
or
$b=\mathbf {1}$
, then by the mere fact that u is a necessity operator we obtain
$u(a,b)=u(a,\mathbf {0})+u(\mathbf {0},b)$
.
If
$a\neq \mathbf {1}$
and
$b\neq \mathbf {1}$
, then
$-a\neq \mathbf {0}$
and
$-b\neq \mathbf {0}$
, and by (wMIA),
$g(-a,-b)\leq f(-a,-b)$
. Therefore,
$$\begin{align*}u(a,b)=g(-a,-b)\cdot -f(-a,-b)=\mathbf{0}.\end{align*}$$
In particular
$u(a,a)=\mathbf {0}$
and
$u(b,b)=\mathbf {0}$
. By Lemma 4.3,
$u(a,\mathbf {0})=u(a,a)$
and
$u(\mathbf {0},b)=u(b,b)$
, so the claim follows.
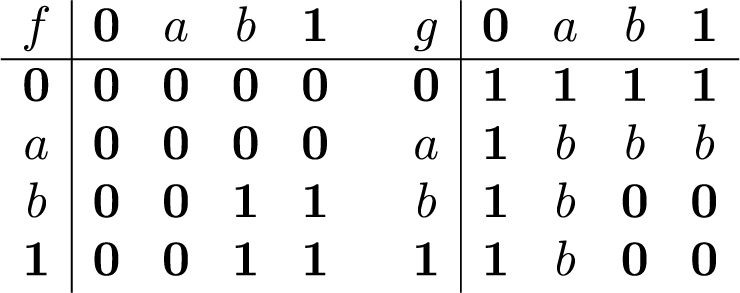
The algebra in Figure 5 is an example of a PS-algebra that satisfies (4.5) but not (wMIA), which shows that the condition is strictly weaker than (wMIA).
Figure 5 A PS-algebra that satisfies (4.5) but is not a weak MIA.
Proposition 4.5. Let 
be a PS-algebra. Then,
$\mathfrak {A}$
is a wMIA if and only if it satisfies both (4.5) and (
di
).
Proof. Suppose that
$\mathfrak {A}$
satisfies (4.5) and (
di
). Observe that
$$\begin{align*}\text{if}\ x\neq \mathbf{1},\ \text{then}\ u(x,\mathbf{0})=\mathbf{0}. \end{align*}$$
Indeed, if
$x\neq \mathbf {1}$
, then
$-x\neq \mathbf {0}$
and by (
di
) we have
$g(-x,\mathbf {1})\leq f(-x,\mathbf {1})$
, and so:
$u(x,\mathbf {0})=g(-x,\mathbf {1})\cdot -f(-x,\mathbf {1})=\mathbf {0}$
, as required.
To show that wMIA holds, assume that
$a\neq \mathbf {0}$
and
$b\neq \mathbf {0}$
, i.e.,
$-a\neq \mathbf {1}$
and
$-b\neq \mathbf {1}$
. By the above we have
$u(-a,\mathbf {0})=\mathbf {0}$
and
$u(-b,\mathbf {0})=\mathbf {0}$
. By (4.5) and (4.4) (which is a consequence of (
di
) by Lemma 4.3)
$u(-a,-b)=\mathbf {0}+\mathbf {0}=\mathbf {0}$
. Thus,
$-f(a,b)\cdot g(a,b)=\mathbf {0}$
, i.e.,
$g(a,b)\leq f(a,b)$
. Therefore,
$\mathfrak {A}$
is a weak MIA.
The other direction is immediate by Lemma 4.4.
Using again the algebra in Figure 5 we can see in light of Proposition 4.5 that (4.5) does not entail ( di ). Also, the algebra from Table 1 of [Reference Düntsch, Gruszczyński and Menchón4] shows that ( di ) is strictly weaker than (wMIA), and thus ( di ) cannot entail (4.5) either. Therefore, we obtain the following.
Lemma 4.7. Suppose that 
is a weak MIA. Then,
$\mathfrak {A}$
satisfies (4.1)–(4.3), and for all
$a,b\in A$
,
$u(a,b)=u(b,a)$
.
Proof. For commutativity, by (4.5) and (4.4),
$u(a,b)=u(a,\mathbf {0})+ u(\mathbf {0},b)=u(b,\mathbf {0})+ u(\mathbf {0},a)=u(b,a)$
.
(4.1) If
$a\neq \mathbf {1}$
, then by Lemma 4.3,
$u(a,\mathbf {0})=\mathbf {0}\leq a$
.
(4.2) If
$a=\mathbf {1}$
, then
$u(\mathbf {1},\mathbf {0})=\mathbf {1}=u(u(\mathbf {1},\mathbf {0}),\mathbf {0})$
. If
$a\neq \mathbf {1}$
then
$u(a,\mathbf {0})=\mathbf {0}$
and the result follows.
(4.3) If
$a=\mathbf {1}$
,
$u^\partial (\mathbf {1},\mathbf {1})=-u(\mathbf {0},\mathbf {0})=-\mathbf {0}=\mathbf {1}$
. So,
$\mathbf {1}\leq u(\mathbf {1},\mathbf {0})=\mathbf {1}$
. If
$\mathbf {0}<a<\mathbf {1}$
,
$u^\partial (a,\mathbf {1})=-u(-a,\mathbf {0})=-\mathbf {0}=\mathbf {1}$
. Thus,
$a\leq u(\mathbf {1},\mathbf {0})=\mathbf {1}$
.
Remark 4.8. Note that Condition (4.4) contains two identities,
$u(a,\mathbf {0})=u(\mathbf {0},a)$
and
$u(a,a)=u(\mathbf {0},a)$
. We need the second identity to prove that simple algebras in the variety generated by (4.1)–(4.4) are exactly the elements of the class
$\mathbf {dMIA}$
. In Figure 6, there is an example of a PS-algebra in the variety generated by (4.1)–(4.3) that satisfies the first but not the second identity.
Let
$u^1\colon A \to A$
be the unary necessity operator defined by:
$$ \begin{align*} u^1(a)=u(a,\mathbf{0}). \end{align*} $$
It is easy to see that the dual
${u^1}^\partial $
is the possibility operator defined by
$$ \begin{align*} {u^1}^\partial(a)=u^\partial(a,\mathbf{1}). \end{align*} $$
Indeed,
$-{u^1}(-a)=-u(-a,\mathbf {0})=u^\partial (a,\mathbf {1})={u^1}^\partial (a)$
.
So, by Lemma 4.7, we obtain that
$u^1$
is the standard S5 operator.
Lemma 4.9. Let 
be a PS-algebra that satisfies (4.2) and (4.4). If
$a\in A$
, then
$\mathop {\uparrow }u(a,\mathbf {0})$
is a congruence filter on
$\mathfrak {A}$
.
Proof. If
$u(a,\mathbf {0})\leq x$
, then
$u(u(a,\mathbf {0}),\mathbf {0})\leq u(x,\mathbf {0})$
. By (4.2) we have that
$u(a,\mathbf {0})\leq u(x,\mathbf {0})$
. By (4.4) we have that
$u(x,\mathbf {0})\cdot u(\mathbf {0},x)\in \mathop {\uparrow }u(a,\mathbf {0})$
, and so Theorem 2.3 entails that
$\mathop {\uparrow }u(a,\mathbf {0})$
is a congruence filter.
Lemma 4.10. Suppose that 
is a subdirectly irreducible PS-algebra in the variety generated by (4.1)–(4.4). Then
$\mathfrak {A}$
is simple, and 
is the dual discriminator.
Proof. We first show that
$\mathfrak {A}$
is simple. Since
$\mathfrak {A}$
is subdirectly irreducible, there is the smallest non-identity congruence
$\theta $
. In consequence,
$F_\theta $
is a non-trivial (i.e.,
${}\neq \{\mathbf {1}\}$
) congruence filter, which is the smallest among the non-trivial congruence filters of A. From the latter, we obtain that
$F_{\theta }$
is principal, say
$F_{\theta } = \mathop {\uparrow }c$
. Indeed, let
$x\in F_{\theta }\setminus \{\mathbf {1}\}$
. Then
$\mathop {\uparrow }u(x,\mathbf {0})\subseteq F_{\theta }$
, since
$F_{\theta }$
is a congruence filter, and
$F_{\theta }\subseteq \mathop {\uparrow }u(x,\mathbf {0})$
by the lemma above and the fact that
$F_{\theta }$
is the smallest non-trivial congruence filter on
$\mathfrak {A}$
.
Clearly,
$c\neq \mathbf {1}$
. Furthermore,
$c\leq u(c,\mathbf {0})$
, since
$u(c,\mathbf {0})\in F_{\theta }$
, and so
$$ \begin{align} c=u(c,\mathbf{0}) \end{align} $$
by (4.1). Also,
$$ \begin{align} u(a,\mathbf{0}) \leq c\quad \text{for all}\ a \neq \mathbf{1}. \end{align} $$
For this, observe that in the case
$a\neq \mathbf {1}$
,
$\mathop {\uparrow }u(a,\mathbf {0})$
is a congruence filter for which
$F_{\theta }\subseteq \mathop {\uparrow }u(a,\mathbf {0})$
, and so
$c\in \mathop {\uparrow }u(a,\mathbf {0})$
.
Assume
$c \neq \mathbf {0}$
. Then,
$$ \begin{align*} \begin{array}{l@{\qquad}l} -c \leq u(-u(c,\mathbf{0}),\mathbf{0}) &\text{by}\ ({4.3}) \\ \phantom{-c}= u(-c,\mathbf{0}) &\text{by } (\dagger)\\ \phantom{-c}\leq c &\text{by (}\ddagger\text{), since }-c\neq \mathbf{1}. \end{array}\end{align*} $$
This contradicts
$c \neq \mathbf {1}$
. Thus,
$F_{\theta }=A$
and
$\theta =A\times A$
, which means that
$\mathfrak {A}$
is simple.
Simplicity of
$\mathfrak {A}$
implies that
$$ \begin{align} u(a,\mathbf{0}) = \begin{cases} \mathbf{1}, &\text{if } a = \mathbf{1}, \\ \mathbf{0}, &\text{otherwise}. \end{cases} \end{align} $$
Indeed, if
$a=\mathbf {1}$
, then
$u(a,\mathbf {0})=\mathbf {1}$
, since u is a necessity operator. On the other hand, if
$a\neq \mathbf {1}$
, then
$u(a,\mathbf {0})\neq \mathbf {1}$
by (4.1). So, since for the congruence filter 
,
$\theta _F$
is either the identity or the universal relation, it must be the case that
$\theta _F=A\times A$
, and using Lemma 2.1 we obtain
$F_{\theta _{F}}=F=A$
. Thus,
$u(a,\mathbf {0})=\mathbf {0}$
.
This completes the proof.
Lemma 4.11. If
$\mathfrak {A}$
is a subdirectly irreducible PS-algebra in the variety generated by (4.1)–(4.4), then (
di
) holds in
$\mathfrak {A}$
. In particular, if
$\mathfrak {A}$
is a subdirectly irreducible PS-algebra in the variety generated by (4.1)–(4.5), then
$\mathfrak {A}\in \mathbf {wMIA}$
.
Proof. Let
$\mathfrak {A}$
be a subdirectly irreducible PS-algebra in the above-mentioned variety. By Lemma 4.10 and (4.4),
$$ \begin{align} u(a,a) = \begin{cases} \mathbf{1}, &\text{if } a = \mathbf{1}, \\ \mathbf{0}, &\text{otherwise}. \end{cases} \end{align} $$
Then,
$d(a)=-u(-a,-a)=f(a,a)+-g(a,a)$
is the unary discriminator. From Lemma 4.2, we obtain (
di
) holds in
$\mathfrak {A}$
. If in addition
$\mathfrak {A}$
satisfies (4.5), then by Proposition 4.5,
$\mathfrak {A}\in \mathbf {wMIA}$
.
We can now prove Theorem 4.1.
Proof. (
$\subseteq $
) From Lemma 4.11 we know that every subdirectly irreducible
$\mathfrak {A}$
in the variety
${\mathbf {V}}(\Sigma )$
is a wMIA. In consequence
${\mathbf {V}}(\Sigma )\subseteq {\mathbf {V}}$
(wMIA).
(
$\supseteq $
) (4.1)–(4.5) hold in wMIA by Lemmas 4.7 and 4.3. So if
$\mathfrak {A}$
is in
${\mathbf {V}}$
(wMIA), then
$\mathfrak {A}$
must satisfy these equations too.
Finally in this section we will show an analogon to [Reference Düntsch, Orłowska and Tinchev7, Theorem 8.5]. Let
$T(\mathsf {Var})$
be the term algebra over the language of
$K^{\#}$
with the set
$\mathsf {Var}$
of variables. Then, each formula
$\phi (p_1,\ldots ,p_n)$
of
$K^{\#}$
can be regarded as an element of
$T(\mathsf {Var})$
via the natural translation
$\tau $
. If
$\mathfrak {A}$
is an algebra with the signature of
$K^{\#}$
, we say that
$\phi (p_1,\ldots ,p_n)$
is valid in
$\mathfrak {A}$
—written as
$\mathfrak {A} \models \phi (p_1,\ldots ,p_n)$
—if
$\tau (\phi (v(p_1), \ldots , v(p_n))) = \mathbf {1}$
for all valuations
$v: \mathsf {Var} \to A$
.
Lemma 4.12. Let 
be a model of
$K^{\#}$
, and
$B_v = \{v(\phi ): \phi \in \mathsf {Fml}\}$
. Then:
-
(1)
$\mathfrak {B}_v = \langle B_v, \cap , \cup ,\, \emptyset , X, \langle { R \rangle }, [[ S ]] \rangle $
satisfies (wMIA). -
(2) If
$\mathfrak {B}$
is a subalgebra of
$\operatorname {{\mathsf {Cm}}}(\mathfrak {M})$
and
$v$
is a mapping onto a set of generators of
$\mathfrak {B}$
, then
$\mathfrak {B} = \mathfrak {B}_v$
.
Proof. 1. By definition, the extension of v over
$T(\mathsf {Var})$
is a homomorphism
$T(\mathsf {Var}) \to \operatorname {{\mathsf {Cm}}}(\mathfrak {M})$
, thus,
$\mathfrak {B}_v$
is a subalgebra of
$\operatorname {{\mathsf {Cm}}}(\mathfrak {M})$
. Since
$\operatorname {{\mathsf {Cm}}}(\mathfrak {M})$
satisfies (wMIA), and this is a universal sentence, we obtain that
$\mathfrak {B}_v$
satisfies (wMIA).
2. This follows from the definition of the extension of
$v$
and the fact that v maps
$\mathsf {Var}$
onto a set of generators.
Figure 7 An application of the construction of the special frame to the canonical frame
$\operatorname {{\mathsf {Cf}}}^{ps}(\mathfrak {A})=\langle \operatorname {\mathrm {Ult}} A,Q_f,S_g\rangle $
of the wMIA
$\mathfrak {A}$
. 
, where
$\langle \mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3\rangle \in Q_f\setminus S_g$
.
5 3-frames for weak MIAs
By a 3-frame, we mean any Kripke frame 
in which R is a ternary relation on W. In [Reference Düntsch, Gruszczyński and Menchón4] we asked the following question: is there for each betweenness algebra
$\mathfrak {A}$
a 3-frame
$\mathfrak {F}$
such that
$\mathfrak {A}$
is embeddable into
$\operatorname {{\mathsf {Cm}}}(\mathfrak {F})$
? Below, we answer this question positively by showing a stronger statement: any weak mixed algebra
$\mathfrak {A}$
can be embedded into the complex algebra of a 3-frame, which is the special frame of the canonical frame of
$\mathfrak {A}$
. To this end we follow the construction developed in Section 3.3.
Theorem 5.1. Let 
be a
$\mathbf {wMIA}$
. Then, there exists a 3-frame
$\mathfrak {F}$
such that
$\mathfrak {A}$
is isomorphic to a subalgebra of
$\operatorname {{\mathsf {Cm}}}(\mathfrak {F})$
.
Proof. Let
$\operatorname {{\mathsf {Cf}}}(\mathfrak {A})=\langle \operatorname {\mathrm {Ult}} A, Q_f, S_g \rangle $
be the canonical frame of
$\mathfrak {A}$
. Since
$\operatorname {{\mathsf {Cf}}}(\mathfrak {A})$
is a wMIA frame, we construct its special frame following the method from Section 3.3 (see Figure 8). To this end, let us consider an isomorphic copy
$\operatorname {{\mathsf {Cf}}}'(\mathfrak {A})=\langle \operatorname {\mathrm {Ult}} A', Q^{\prime }_f, S^{\prime }_g \rangle $
of
$\operatorname {{\mathsf {Cf}}}(\mathfrak {A}),$
where
$\operatorname {\mathrm {Ult}} A$
and
$\operatorname {\mathrm {Ult}} A'$
are disjoint sets. We put 
, and define
$\underline {R}\subseteq \underline {\operatorname {\mathrm {Ult}} A}^3$
and its complement as before:
Fix 
. We will prove that
$\mathfrak {A}$
embeds into the complex algebra
$\operatorname {{\mathsf {Cm}}}(\mathfrak {F})$
via the mapping
$s\colon A\to 2^{\underline {\operatorname {\mathrm {Ult}} A}}$
defined by
First, note that
$s(\mathbf {0})=\emptyset $
and
$s(\mathbf {1})=\underline {\operatorname {\mathrm {Ult}} A}$
. It is easy to check that
$s(a\cdot b)=s(a)\cap s(b)$
,
$s(a+ b)=s(a)\cup s(b),$
and
$s(-a)=\underline {\operatorname {\mathrm {Ult}} A}\setminus s(a)$
. We will prove that
$s(f(a,b))=\langle { \underline {R} \rangle }(s(a),s(b))$
and
$s(g(a,b))=[[ \underline {R} ]](s(a),s(b))$
.
Let
$\mathscr {U}^{\kern2.4pt\epsilon }$
denote either the ultrafilter
$\mathscr {U}$
or its copy
$\mathscr {U}^{\kern1.5pt\prime }$
. Assume that
$\mathscr {U}^{\kern2.4pt\epsilon} \in s(f(a,b))$
. By the definition, we have that
$f(a,b)\in \mathscr {U}$
. Thus, there exist
$\mathscr {U}_a,\mathscr {U}_b\in \operatorname {\mathrm {Ult}} A$
such that
$a\in \mathscr {U}_a$
,
$b\in \mathscr {U}_b$
and
$f[\mathscr {U}_a\times \mathscr {U}_b]\subseteq \mathscr {U}$
,Footnote
9
i.e.,
$\langle \mathscr {U}_a,\mathscr {U},\mathscr {U}_b \rangle \in Q_f$
. By construction,
$\langle \mathscr {U}^{\kern1.5pt\prime }_a,\mathscr {U}^{\kern2.4pt\epsilon} ,\mathscr {U}_b \rangle \in \underline {R}$
. It follows that
$(s(a)\times \{\mathscr {U}^{\kern2.4pt\epsilon} \}\times s(b))\cap \underline {R}\neq \emptyset $
and therefore
$\mathscr {U}^{\kern2.4pt\epsilon} \in \langle { \underline {R} \rangle }(s(a),s(b))$
.
For the other direction, let
$\mathscr {U}^{\kern2.4pt\epsilon} \in \langle { \underline {R} \rangle }(s(a),s(b))$
, i.e.,
$(s(a)\times \{\mathscr {U}^{\kern2.4pt\epsilon} \}\times s(b))\cap \underline {R}\neq \emptyset $
. Then, there exist
$\mathscr {U}_a,\mathscr {U}_b\in \operatorname {\mathrm {Ult}} A$
such that
$\mathscr {U}^{\kern2.4pt\epsilon} _a\in s(a)$
,
$\mathscr {U}^{\kern2.4pt\epsilon} _b\in s(b)$
and
$\langle \mathscr {U}^{\kern2.4pt\epsilon} _a,\mathscr {U}^{\kern2.4pt\epsilon} ,\mathscr {U}^{\kern2.4pt\epsilon} _b \rangle \in \underline {R}$
. By construction,
$\langle \mathscr {U}_a,\mathscr {U},\mathscr {U}_b \rangle \in S_g$
or
${\langle \mathscr {U}_a,\mathscr {U},\mathscr {U}_b \rangle \in Q_f\cap -S_g}$
. In both cases,
$\langle \mathscr {U}_a,\mathscr {U},\mathscr {U}_b \rangle \in Q_f$
, which implies that
$f[\mathscr {U}_a\times \mathscr {U}_b]\subseteq \mathscr {U}$
and therefore
$f(a,b)\in \mathscr {U}$
. By definition, we obtain
$\mathscr {U}^{\kern2.4pt\epsilon} \in s(f(a,b))$
.
Let
$\mathscr {U}^{\kern2.4pt\epsilon} \in s(g(a,b))$
, which is to say that
$g(a,b)\in \mathscr {U}$
. To prove that
$s(a)\times \{\mathscr {U}^{\kern2.4pt\epsilon} \}\times s(b)\subseteq \underline {R}$
, let us consider
$\mathscr {U}^{\kern2.4pt\epsilon} _a\in s(a)$
and
$\mathscr {U}^{\kern2.4pt\epsilon} _b\in s(b)$
. By definition,
$a\in \mathscr {U}_a$
and
$b\in \mathscr {U}_b$
and we have
$g[\mathscr {U}_a\times \mathscr {U}_b]\cap \mathscr {U}\neq \emptyset $
, i.e.,
$\langle \mathscr {U}_a,\mathscr {U},\mathscr {U}_b \rangle \in S_g$
. By construction,
$c(\mathscr {U}_a,\mathscr {U},\mathscr {U}_b)\subseteq \underline {R}$
, so
$\langle \mathscr {U}^{\kern2.4pt\epsilon} _a,\mathscr {U}^{\kern2.4pt\epsilon} ,\mathscr {U}^{\kern2.4pt\epsilon} _b \rangle \in \underline {R}$
. It follows that
$\mathscr {U}^{\kern2.4pt\epsilon} \in [[ \underline {R} ]](s(a),s(b))$
.
For the reverse inclusion, assume that
$\mathscr {U}^{\kern2.4pt\epsilon} \in [[ \underline {R} ]](s(a),s(b))$
, that is,
$s(a)\times \{\mathscr {U}^{\kern2.4pt\epsilon} \}\times s(b)\subseteq \underline {R}$
. Let
$\mathscr {U}_a,\mathscr {U}_b\in \operatorname {\mathrm {Ult}} A$
be such that
$a\in \mathscr {U}_a$
and
$b\in \mathscr {U}_b$
. Then,
$\langle \mathscr {U}_a,\mathscr {U}^{\kern2.4pt\epsilon} ,\mathscr {U}_b \rangle \in \underline {R}$
. Suppose that
$\langle \mathscr {U}_a,\mathscr {U},\mathscr {U}_b \rangle \notin S_g$
. By construction we have that
$\langle \mathscr {U}_a,\mathscr {U},\mathscr {U}_b \rangle \in Q_f$
but then
$\langle \mathscr {U}_a,\mathscr {U},\mathscr {U}_b \rangle \notin \underline {R}$
and
$\langle \mathscr {U}^{\kern1.5pt\prime }_a,\mathscr {U}^{\kern1.5pt\prime },\mathscr {U}^{\kern1.5pt\prime }_b \rangle \notin \underline {R}$
. This contradicts the fact that
$s(a)\times \{\mathscr {U}^{\kern2.4pt\epsilon} \}\times s(b)\subseteq \underline {R}$
, and thus,
$\langle \mathscr {U}_a,\mathscr {U},\mathscr {U}_b \rangle \in S_g$
. Since
$\mathscr {U}_a,\mathscr {U}_b$
are arbitrary ultrafilters that contain a and b, respectively, we obtain
$g(a,b)\in \mathscr {U}$
. We conclude that
$\mathscr {U}^{\kern2.4pt\epsilon} \in s(g(a,b))$
.
Therefore s is a homomorphism of Boolean algebras. Injectivity follows immediately from the properties of the Stone mapping.
The following corollary is a counterpart of [Reference Düntsch, Orłowska and Tinchev7, Theorem 8.5].
Theorem 5.2. Suppose that 
. Then, there is a 3-frame 
such that
$\mathfrak {A}$
and a subalgebra of
$\operatorname {{\mathsf {Cm}}}(\mathfrak {F})$
satisfy the same equations.
6 Applications to b-algebras
We will show now how the results obtained in this article can be applied to betweenness algebras introduced and studied in [Reference Düntsch, Gruszczyński and Menchón4]. We begin by recalling the key concepts from the article.
Definition 6.1. Let
$\langle W,B\rangle $
be a 3-frame. B is called a betweenness relation if it satisfies the following (universal) axioms:
$$ \begin{align} B(a,a,a), \end{align} $$
$$ \begin{align} B(a,b,c)\rightarrow B(c,b,a), \end{align} $$
$$ \begin{align} B(a,b,c)\rightarrow B(a,a,b), \end{align} $$
$$ \begin{align} B(a,b,c)\wedge B(a,c,b)\rightarrow b=c\,. \end{align} $$
A 3-frame
$\langle W,B \rangle $
satisfying these axioms is called a betweenness frame (or just a b-frame).
Definition 6.2. A weak MIA 
is a betweenness algebra (b-algebra for short) if
$\mathfrak {A}$
satisfies the following axioms:
$$ \begin{align} x\leq f(x,x), \end{align} $$
$$\begin{align} f(x,y)\leq f(y,x), \end{align} $$
$$\begin{align} g(x,y) \leq g(y,x), \end{align} $$
$$ \begin{align} y\cdot f(x,z)\leq f(x\cdot f(x,y),z), \end{align} $$
$$ \begin{align} f(x,g(x,-y)\cdot y)\leq y. \end{align} $$
Assuming that
${\mathbf {Abtw}}$
is the class of betweenness algebras and putting
from Theorem 4.1 we obtain the following.
Corollary 6.3.
${\mathbf {V}}\left (\Sigma ^B\right )={\mathbf {V}}({\mathbf {Abtw}})$
.
In [Reference Düntsch, Gruszczyński and Menchón4, Example 8.4] we demonstrated that there is a b-algebra that cannot be embedded into the complex algebra of any b-frame. However, as a consequence of Theorem 5.1 we have the following.
Corollary 6.4. Every b-algebra is isomorphic to a subalgebra of the complex algebra of a 3-frame.
As mentioned before, this answers problem (1) from [Reference Düntsch, Gruszczyński and Menchón4, Section 9]. We know from Example 8.4 of this paper that the ternary relation
$\underline {R}$
from Theorem 5.1 cannot be a betweenness relation, yet we may ask about its general properties. On the positive side, we have that
$\underline {R}$
satisfies (BT1)
$$ \begin{align*} \underline{R}({\mathscr{V}}^{\epsilon}_1,{\mathscr{V}}^{\epsilon}_2,{\mathscr{V}}^{\epsilon}_3)\rightarrow \underline{R}({\mathscr{V}}^{\epsilon}_3,{\mathscr{V}}^{\epsilon}_2,{\mathscr{V}}^{\epsilon}_1). \end{align*} $$
Proof. Indeed, assume that
$\underline {R}({\mathscr {V}}^{\epsilon }_1,{\mathscr {V}}^{\epsilon }_2,{\mathscr {V}}^{\epsilon }_3)$
. By construction, we have that either there is a triple
$\langle \mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3 \rangle \in S_g$
such that
$$\begin{align*}\langle {\mathscr{V}}^{\epsilon}_1,{\mathscr{V}}^{\epsilon}_2,{\mathscr{V}}^{\epsilon}_3 \rangle\in c(\mathscr{U}_1,\mathscr{U}_2,\mathscr{U}_3) \end{align*}$$
or there is a triple
$\langle \mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3 \rangle \in Q_f\cap -S_g$
such that
$$\begin{align*}\langle {\mathscr{V}}^{\epsilon}_1,{\mathscr{V}}^{\epsilon}_2,{\mathscr{V}}^{\epsilon}_3 \rangle\in c(\mathscr{U}_1,\mathscr{U}_2,\mathscr{U}_3)\setminus\{\langle \mathscr{U}_1,\mathscr{U}_2,\mathscr{U}_3 \rangle,\langle \mathscr{U}_1',\mathscr{U}_2',\mathscr{U}_3' \rangle\}. \end{align*}$$
In the first case, by [Reference Düntsch, Gruszczyński and Menchón4, Lemma 7.2] we obtain that the triple
$\langle \mathscr {U}_3,\mathscr {U}_2,\mathscr {U}_1 \rangle $
is in
$S_g$
, so
$$\begin{align*}\langle {\mathscr{V}}^{\epsilon}_3,{\mathscr{V}}^{\epsilon}_2,{\mathscr{V}}^{\epsilon}_1 \rangle\in c(\mathscr{U}_3,\mathscr{U}_2,\mathscr{U}_1)\subseteq\underline{R}. \end{align*}$$
In the second case, by the same lemma, we obtain
$\langle \mathscr {U}_3,\mathscr {U}_2,\mathscr {U}_1 \rangle \in Q_f\cap -S_g$
. In consequence, by the construction of
$\underline {R}$
and by the fact that
$\langle {\mathscr {V}}^{\epsilon }_1,{\mathscr {V}}^{\epsilon }_2,{\mathscr {V}}^{\epsilon }_3 \rangle $
is not pure we obtain
$\langle {\mathscr {V}}^{\epsilon }_3,{\mathscr {V}}^{\epsilon }_2,{\mathscr {V}}^{\epsilon }_1 \rangle $
is not pure either and
$$\begin{align*}\langle {\mathscr{V}}^{\epsilon}_3,{\mathscr{V}}^{\epsilon}_2,{\mathscr{V}}^{\epsilon}_1 \rangle\in c(\mathscr{U}_3,\mathscr{U}_2,\mathscr{U}_1)\setminus\{\langle \mathscr{U}_3,\mathscr{U}_2,\mathscr{U}_1 \rangle,\langle \mathscr{U}_3',\mathscr{U}_2',\mathscr{U}_1' \rangle\}\subseteq\underline{R}.\\[-33pt] \end{align*}$$
However, as subsequent propositions show, this is as far as we can, in general, get with the properties of
$\underline {R}$
shared with the betweenness.
Proposition 6.5. For no free ultrafilter
$\mathscr {U}$
,
$\underline {R}(\mathscr {U}^{\kern2.4pt\epsilon },\mathscr {U}^{\kern2.4pt\epsilon },\mathscr {U}^{\kern2.4pt\epsilon })$
, so in general
$\underline {R}$
does not meet (BT0).
Proof. By the construction of
$\underline {R}$
, the triples of the form
$\langle \mathscr {U}^{\kern2.4pt\epsilon },\mathscr {U}^{\kern2.4pt\epsilon },\mathscr {U}^{\kern2.4pt\epsilon } \rangle $
that are in
$\underline {R}$
can only be in the cells of triples in
$S_g$
. However, by [Reference Düntsch, Gruszczyński and Menchón4, Theorem 6.10], if
$S_g(\mathscr {U},\mathscr {U},\mathscr {U})$
, then
$\mathscr {U}$
must be a principal ultrafilter. Therefore, if
$\underline {R}(\mathscr {U}^{\kern2.4pt\epsilon },\mathscr {U}^{\kern2.4pt\epsilon },\mathscr {U}^{\kern2.4pt\epsilon })$
, then
$\mathscr {U}^{\kern2.4pt\epsilon }$
is either a principal ultrafilter or a copy of a principal ultrafilter.
Proof. The proof is based on [Reference Düntsch, Orłowska and Tinchev7, Example 8.6]. We take the 3-frame
$\mathfrak {N}=\langle \omega ,B_{\leqslant } \rangle ,$
where
$B_{\leqslant }$
is the betweenness relation obtained from the standard binary order
$\leqslant $
on the set
$\omega $
of natural numbers. Let
$2^\omega $
be the set of all sets of natural numbers. We consider the complex algebra
$\operatorname {{\mathsf {Cm}}}(\mathfrak {N})=\langle 2^\omega ,Q_{\langle { B_\leqslant \rangle }},S_{[[ B_\leqslant ]]} \rangle $
, its canonical frame
$\operatorname {{\mathsf {Cf}}}(\operatorname {{\mathsf {Cm}}}(\mathfrak {N}))=\langle \operatorname {\mathrm {Ult}} 2^\omega ,Q_{\langle { B_\leqslant \rangle }},S_{[[ B_\leqslant ]]} \rangle $
, and its special frame
$\langle \underline {\operatorname {\mathrm {Ult}} 2^\omega },\underline {R} \rangle $
.
For any triple of free ultrafilters
$\mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3$
it is the case that
$Q_{\langle { B_\leqslant \rangle }}(\mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3)$
. Recall that also
$-S_{[[ B_\leqslant ]]}(\mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3)$
for any such triple. Therefore
$\underline {R}(\mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3')$
, since
$$\begin{align*}c(\mathscr{U}_1,\mathscr{U}_2,\mathscr{U}_3)\setminus\{\langle \mathscr{U}_1,\mathscr{U}_2,\mathscr{U}_3 \rangle,\langle \mathscr{U}_1',\mathscr{U}_2',\mathscr{U}_3 \rangle\}\subseteq\underline{R}. \end{align*}$$
But
$-\underline {R}(\mathscr {U}_1,\mathscr {U}_1,\mathscr {U}_2)$
, as
$Q_{\langle { B_\leqslant \rangle }}(\mathscr {U}_1,\mathscr {U}_1,\mathscr {U}_2)$
and
$-S_{[[ B_\leqslant ]]}(\mathscr {U}_1,\mathscr {U}_1,\mathscr {U}_2)$
. Consequently, (BT2) fails for the special frame
$\langle \underline {\operatorname {\mathrm {Ult}} 2^\omega },\underline {R} \rangle $
.
We use the same construction to show the failure of (BT3). Again, fix a triple of free ultrafilters
$\mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3$
. From the above it follows that
$\underline {R}(\mathscr {U}_1,\mathscr {U}_2,\mathscr {U}_3')$
and
$\underline {R}(\mathscr {U}_1,\mathscr {U}_3',\mathscr {U}_2)$
, but obviously
$\mathscr {U}_2\neq \mathscr {U}_3'$
.
In [Reference Düntsch, Orłowska and Tinchev7] we also considered two more axioms for the betweenness:
$$ \begin{align} B(a,b,a)\rightarrow a=b, \end{align} $$
$$ \begin{align} B(a,a,b). \end{align} $$
The reader will easily check that the special model
$\langle \underline {\operatorname {\mathrm {Ult}} 2^\omega },\underline {R} \rangle $
does not satisfy any of them.
Funding
This research was funded by the National Science Center (Poland), grant number 2020/39/B/HS1/00216, “Logico-Philosophical Foundations of Geometry and Topology.” Ivo Düntsch would like to thank Nicolaus Copernicus University in Toruń for supporting him through the “Excellence Initiative–Research University” Program.
is a subframe of 
if 
.
Akademii Nauk. Comptes Rendus de l’Académie Bulgare des Sciences
, vol. 
Open access
