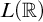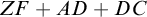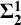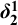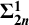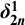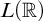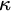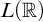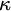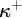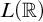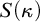1 Introduction
Definition 1.1. For a boldface pointclass
![]() $\boldsymbol {\Gamma }$
, we say
$\boldsymbol {\Gamma }$
, we say
![]() $\lambda $
is
$\lambda $
is
![]() $\boldsymbol {\Gamma }$
-reachable if there is a sequence of distinct
$\boldsymbol {\Gamma }$
-reachable if there is a sequence of distinct
![]() $\boldsymbol {\Gamma }$
sets of length
$\boldsymbol {\Gamma }$
sets of length
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda $
is
$\lambda $
is
![]() $\boldsymbol {\Gamma }$
-unreachable if
$\boldsymbol {\Gamma }$
-unreachable if
![]() $\lambda $
is not
$\lambda $
is not
![]() $\boldsymbol {\Gamma }$
-reachable.
$\boldsymbol {\Gamma }$
-reachable.
The problem of unreachability is to determine the minimal
![]() $\lambda $
which is
$\lambda $
which is
![]() $\boldsymbol {\Gamma }$
-unreachable for each pointclass
$\boldsymbol {\Gamma }$
-unreachable for each pointclass
![]() $\boldsymbol {\Gamma }$
. As this problem is trivial assuming the axiom of choice, unreachability is exclusively studied under determinacy assumptions. Under
$\boldsymbol {\Gamma }$
. As this problem is trivial assuming the axiom of choice, unreachability is exclusively studied under determinacy assumptions. Under
![]() $AD$
, unreachability yields an interesting measure of the complexity of a pointclass. An early result in this area is Harrington’s theorem that there is no injection of
$AD$
, unreachability yields an interesting measure of the complexity of a pointclass. An early result in this area is Harrington’s theorem that there is no injection of
![]() $\omega _1$
into any pointclass strictly below the pointclass of Borel sets in the Wadge hierarchy (see [Reference Harrington2]).
$\omega _1$
into any pointclass strictly below the pointclass of Borel sets in the Wadge hierarchy (see [Reference Harrington2]).
Theorem 1.2 (Harrington).
If
![]() $\beta < \omega _1$
, then
$\beta < \omega _1$
, then
![]() $\omega _1$
is
$\omega _1$
is
![]() $\boldsymbol {\Pi ^0_\beta }$
-unreachable.
$\boldsymbol {\Pi ^0_\beta }$
-unreachable.
A recent application of Harrington’s theorem was the resolution of the decomposability conjecture by Marks and Day (see [Reference Day and Marks1]).
Prior work on unreachability has focused on levels of the projective hierarchy. Kechris gave a lower bound on the complexity of the pointclass needed to reach
![]() $\boldsymbol {\delta ^1_{2n+2}}$
(see [Reference Kechris, Macintyre, Pacholski and Paris5]).
$\boldsymbol {\delta ^1_{2n+2}}$
(see [Reference Kechris, Macintyre, Pacholski and Paris5]).
Theorem 1.3 (Kechris).
Assume
![]() $ZF + AD + DC$
.
$ZF + AD + DC$
.
![]() $\boldsymbol {\delta ^1_{2n+2}}$
is
$\boldsymbol {\delta ^1_{2n+2}}$
is
![]() $\boldsymbol {\Delta ^1_{2n+1}}$
-unreachable.
$\boldsymbol {\Delta ^1_{2n+1}}$
-unreachable.
In [Reference Kechris, Macintyre, Pacholski and Paris5], Kechris conjectured his own result could be strengthened to
![]() $\boldsymbol {\delta ^1_{2n+2}}$
is
$\boldsymbol {\delta ^1_{2n+2}}$
is
![]() $\boldsymbol {\Delta ^1_{2n+2}}$
-unreachable. He also made a second, stronger conjecture that
$\boldsymbol {\Delta ^1_{2n+2}}$
-unreachable. He also made a second, stronger conjecture that
![]() $\boldsymbol {\delta ^1_{2n+2}}$
is
$\boldsymbol {\delta ^1_{2n+2}}$
is
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
-unreachable. Jackson proved the former in [Reference Jackson4].
$\boldsymbol {\Sigma ^1_{2n+2}}$
-unreachable. Jackson proved the former in [Reference Jackson4].
Theorem 1.4 (Jackson).
Assume
![]() $ZF + AD + DC$
.
$ZF + AD + DC$
.
![]() $\boldsymbol {\delta ^1_{2n+2}}$
is
$\boldsymbol {\delta ^1_{2n+2}}$
is
![]() $\boldsymbol {\Delta ^1_{2n+2}}$
-unreachable.
$\boldsymbol {\Delta ^1_{2n+2}}$
-unreachable.
Jackson [Reference Jackson4] also made progress on Kechris’s second conjecture by showing there is no strictly increasing sequence of
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
sets of length
$\boldsymbol {\Sigma ^1_{2n+2}}$
sets of length
![]() $\boldsymbol {\delta ^1_{2n+2}}$
. In fact, Jackson and Martin proved the following more general theorem.
$\boldsymbol {\delta ^1_{2n+2}}$
. In fact, Jackson and Martin proved the following more general theorem.
Theorem 1.5 (Jackson).
Assume
![]() $ZF +AD +DC$
. Suppose
$ZF +AD +DC$
. Suppose
![]() $\kappa $
is a Suslin cardinal, and
$\kappa $
is a Suslin cardinal, and
![]() $\kappa $
is either a successor cardinal or a regular limit cardinal. Then there is no strictly increasing (or strictly decreasing) sequence
$\kappa $
is either a successor cardinal or a regular limit cardinal. Then there is no strictly increasing (or strictly decreasing) sequence
![]() $\langle A_\alpha : \alpha < \kappa ^+\rangle $
contained in
$\langle A_\alpha : \alpha < \kappa ^+\rangle $
contained in
![]() $S(\kappa )$
.
$S(\kappa )$
.
But the resolution of Kechris’s second conjecture eluded the traditional techniques of descriptive set theory. Hjorth pioneered the use of inner model theory in this area to resolve one case of Kechris’s second conjecture (see [Reference Hjorth3]).
Theorem 1.6 (Hjorth).
Assume
![]() $ZF + AD + DC$
.
$ZF + AD + DC$
.
![]() $\boldsymbol {\delta ^1_{2}}$
is
$\boldsymbol {\delta ^1_{2}}$
is
![]() $\boldsymbol {\Sigma ^1_{2}}$
-unreachable.
$\boldsymbol {\Sigma ^1_{2}}$
-unreachable.
Kechris also pointed out the following corollary of Hjorth’s result.
Corollary 1.7. Assume
![]() $ZF + AD + DC$
. A
$ZF + AD + DC$
. A
![]() $\boldsymbol {\Pi ^1_2}$
equivalence relation has either
$\boldsymbol {\Pi ^1_2}$
equivalence relation has either
![]() $2^{\aleph _0}$
or
$2^{\aleph _0}$
or
![]() $\leq \aleph _1$
equivalence classes.
$\leq \aleph _1$
equivalence classes.
Hjorth’s proof of Theorem 1.6 involved an application of the Kechris–Martin Theorem, which precluded an easy generalization of his technique to other projective pointclasses. The rest of Kechris’s second conjecture survived another two decades, until Sargsyan found a modification of Hjorth’s proof which generalized to the rest of the projective hierarchy (see [Reference Sargsyan11]).
Theorem 1.8 (Sargsyan).
Assume
![]() $ZF + AD + DC$
.
$ZF + AD + DC$
.
![]() $\boldsymbol {\delta ^1_{2n+2}}$
is
$\boldsymbol {\delta ^1_{2n+2}}$
is
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
-unreachable.
$\boldsymbol {\Sigma ^1_{2n+2}}$
-unreachable.
The following result of Kechris shows Sargsyan’s theorem is optimal.
Theorem 1.9 (Kechris).
Assume
![]() $ZF + AD + DC$
. Suppose
$ZF + AD + DC$
. Suppose
![]() $\kappa $
is a Suslin cardinal. Then there is a strictly increasing sequence
$\kappa $
is a Suslin cardinal. Then there is a strictly increasing sequence
![]() $\langle A_\alpha : \alpha < \kappa \rangle $
contained in
$\langle A_\alpha : \alpha < \kappa \rangle $
contained in
![]() $S(\kappa )$
.
$S(\kappa )$
.
Sargsyan’s theorem resolves the problem of unreachability for every level of the projective hierarchy. He conjectured an analogous result holds for every regular Suslin pointclass.
Conjecture 1.10 (Sargsyan).
Assume
![]() $AD^+$
. Suppose
$AD^+$
. Suppose
![]() $\kappa $
is a regular Suslin cardinal. Then
$\kappa $
is a regular Suslin cardinal. Then
![]() $\kappa ^+$
is
$\kappa ^+$
is
![]() $S(\kappa )$
-unreachable.
$S(\kappa )$
-unreachable.
Below, we prove part of Conjecture 1.10.
Theorem 1.11. Assume
![]() $ZF + AD + DC + V=L(\mathbb {R})$
. Suppose
$ZF + AD + DC + V=L(\mathbb {R})$
. Suppose
![]() $\kappa $
is a regular Suslin cardinal and
$\kappa $
is a regular Suslin cardinal and
![]() $S(\kappa )$
is inductive-like. Then
$S(\kappa )$
is inductive-like. Then
![]() $\kappa ^+$
is
$\kappa ^+$
is
![]() $S(\kappa )$
-unreachable.
$S(\kappa )$
-unreachable.
![]() $ZF + AD + DC + V=L(\mathbb {R})$
implies
$ZF + AD + DC + V=L(\mathbb {R})$
implies
![]() $AD^+$
, so Theorem 1.11 is a special case of Conjecture 1.10. Theorem 1.9 demonstrates that this is the optimal result for inductive-like pointclasses.
$AD^+$
, so Theorem 1.11 is a special case of Conjecture 1.10. Theorem 1.9 demonstrates that this is the optimal result for inductive-like pointclasses.
Let
![]() $\boldsymbol {\Gamma } = S(\kappa )$
for
$\boldsymbol {\Gamma } = S(\kappa )$
for
![]() $\kappa $
as in Theorem 1.11. Then
$\kappa $
as in Theorem 1.11. Then
![]() $\kappa = \boldsymbol {\delta _\Gamma }$
.
$\kappa = \boldsymbol {\delta _\Gamma }$
.
![]() $ZF + AD + DC + V=L(\mathbb {R})$
also implies any inductive-like pointclass
$ZF + AD + DC + V=L(\mathbb {R})$
also implies any inductive-like pointclass
![]() $\boldsymbol {\Gamma }$
is of the form
$\boldsymbol {\Gamma }$
is of the form
![]() $S(\kappa )$
for some regular Suslin cardinal
$S(\kappa )$
for some regular Suslin cardinal
![]() $\kappa $
. So an equivalent formulation of Theorem 1.11 is the following.
$\kappa $
. So an equivalent formulation of Theorem 1.11 is the following.
Theorem 1.12. Assume
![]() $ZF + AD + DC + V=L(\mathbb {R})$
. Suppose
$ZF + AD + DC + V=L(\mathbb {R})$
. Suppose
![]() $\boldsymbol {\Gamma }$
is an inductive-like pointclass. Then
$\boldsymbol {\Gamma }$
is an inductive-like pointclass. Then
![]() $\boldsymbol {\delta _{\Gamma }^+}$
is
$\boldsymbol {\delta _{\Gamma }^+}$
is
![]() $\boldsymbol {\Gamma }$
-unreachable.
$\boldsymbol {\Gamma }$
-unreachable.
Our proof of Theorem 1.12 extends the inner model theory approach pioneered in [Reference Hjorth3]. Our technique also gives an alternative proof of Theorem 1.8.
2 Background
We will assume the reader is familiar with the basics of descriptive set theory espoused in [Reference Moschovakis8] and the theory of iteration strategies for premice covered in [Reference Steel, Foreman and Kanamori19]. The rest of the necessary background is covered below. In Section 2.1, we summarize Steel’s classification of the scaled pointclasses and Suslin pointclasses in
![]() $L(\mathbb {R})$
. Section 2.2 reviews the relationship between Woodin cardinals and iteration trees. Two inner model constructions are covered in Sections 2.3 and 2.4. In Section 2.5, we review results from the core model induction demonstrating the existence of mice corresponding to inductive-like pointclasses in
$L(\mathbb {R})$
. Section 2.2 reviews the relationship between Woodin cardinals and iteration trees. Two inner model constructions are covered in Sections 2.3 and 2.4. In Section 2.5, we review results from the core model induction demonstrating the existence of mice corresponding to inductive-like pointclasses in
![]() $L(\mathbb {R})$
.
$L(\mathbb {R})$
.
2.1 The pointclasses of
 $L(\mathbb {R})$
$L(\mathbb {R})$
We will assume for this section
![]() $ZF + DC + AD + V = L(\mathbb {R})$
. All of the results in this section are due to Steel and are proven outright or else implicit in [Reference Steel, Kechris, Martin and Moschovakis15].
$ZF + DC + AD + V = L(\mathbb {R})$
. All of the results in this section are due to Steel and are proven outright or else implicit in [Reference Steel, Kechris, Martin and Moschovakis15].
The boldface pointclasses we are interested in all appear in a hierarchy we will now define. If
![]() $\boldsymbol {\Gamma }$
and
$\boldsymbol {\Gamma }$
and
![]() $\boldsymbol {\Lambda }$
are non-selfdual pointclasses, say
$\boldsymbol {\Lambda }$
are non-selfdual pointclasses, say
![]() $\{\boldsymbol {\Gamma },\boldsymbol {\Gamma ^c}\} <_w \{\boldsymbol {\Lambda }, \boldsymbol {\Lambda ^c}\}$
if
$\{\boldsymbol {\Gamma },\boldsymbol {\Gamma ^c}\} <_w \{\boldsymbol {\Lambda }, \boldsymbol {\Lambda ^c}\}$
if
![]() $\boldsymbol {\Gamma } \subset \boldsymbol {\Lambda } \cap \boldsymbol {\Lambda ^c}$
. This is a wellordering by Wadge’s Lemma. For
$\boldsymbol {\Gamma } \subset \boldsymbol {\Lambda } \cap \boldsymbol {\Lambda ^c}$
. This is a wellordering by Wadge’s Lemma. For
![]() $\alpha < \Theta $
, consider the
$\alpha < \Theta $
, consider the
![]() $\alpha $
th pair
$\alpha $
th pair
![]() $\{\boldsymbol {\Gamma },\boldsymbol {\Gamma ^c}\}$
in this wellordering such that
$\{\boldsymbol {\Gamma },\boldsymbol {\Gamma ^c}\}$
in this wellordering such that
![]() $\boldsymbol {\Gamma }$
or
$\boldsymbol {\Gamma }$
or
![]() $\boldsymbol {\Gamma ^c}$
is closed under projection. Let
$\boldsymbol {\Gamma ^c}$
is closed under projection. Let
![]() $\boldsymbol {\Sigma ^1_\alpha }$
denote whichever of the two is closed under projection—if both are,
$\boldsymbol {\Sigma ^1_\alpha }$
denote whichever of the two is closed under projection—if both are,
![]() $\boldsymbol {\Sigma ^1_\alpha }$
denotes whichever has the separation property. Let
$\boldsymbol {\Sigma ^1_\alpha }$
denotes whichever has the separation property. Let
![]() $\boldsymbol {\Pi ^1_\alpha } = (\boldsymbol {\Sigma ^1_\alpha })^c$
.
$\boldsymbol {\Pi ^1_\alpha } = (\boldsymbol {\Sigma ^1_\alpha })^c$
.
For any pointclass
![]() $\boldsymbol {\Gamma }$
, we define
$\boldsymbol {\Gamma }$
, we define
 $$ \begin{align*} \boldsymbol{\Delta_\Gamma} &= \boldsymbol{\Gamma} \cap \boldsymbol{\Gamma^c} \text{ and} \\\boldsymbol{\delta_\Gamma} &= sup \{|\leq^*| :\, \leq^* \text{ is a prewellordering in } \boldsymbol{\Delta_\Gamma}\}. \end{align*} $$
$$ \begin{align*} \boldsymbol{\Delta_\Gamma} &= \boldsymbol{\Gamma} \cap \boldsymbol{\Gamma^c} \text{ and} \\\boldsymbol{\delta_\Gamma} &= sup \{|\leq^*| :\, \leq^* \text{ is a prewellordering in } \boldsymbol{\Delta_\Gamma}\}. \end{align*} $$
Let
![]() $\boldsymbol {\delta ^1_\alpha } = \boldsymbol {\delta _{\Sigma ^1_\alpha }}$
. The pointclasses
$\boldsymbol {\delta ^1_\alpha } = \boldsymbol {\delta _{\Sigma ^1_\alpha }}$
. The pointclasses
![]() $\{\boldsymbol {\Sigma ^1_n}: n\in \omega \}$
and
$\{\boldsymbol {\Sigma ^1_n}: n\in \omega \}$
and
![]() $\{\boldsymbol {\Pi ^1_n}: n\in \omega \}$
are the usual levels of the projective hierarchy. We will refer to the collection of pointclasses
$\{\boldsymbol {\Pi ^1_n}: n\in \omega \}$
are the usual levels of the projective hierarchy. We will refer to the collection of pointclasses
![]() $\{\boldsymbol {\Sigma ^1_\alpha }: \alpha \in ON \} \cup \{\boldsymbol {\Pi ^1_\alpha }: \alpha \in ON\}$
as the extended projective hierarchy.
$\{\boldsymbol {\Sigma ^1_\alpha }: \alpha \in ON \} \cup \{\boldsymbol {\Pi ^1_\alpha }: \alpha \in ON\}$
as the extended projective hierarchy.
We now define a hierarchy slightly coarser than the one above. If
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $\alpha \in ON$
, we say a pointset A is in the pointclass
$\alpha \in ON$
, we say a pointset A is in the pointclass
![]() $\boldsymbol {\Sigma _n}(J_\alpha (\mathbb {R}))$
if there is a
$\boldsymbol {\Sigma _n}(J_\alpha (\mathbb {R}))$
if there is a
![]() $\Sigma _n$
formula
$\Sigma _n$
formula
![]() $\phi $
with real parameters such that
$\phi $
with real parameters such that
![]() $A = \{x : J_\alpha (\mathbb {R}) \models \phi [x]\}$
.
$A = \{x : J_\alpha (\mathbb {R}) \models \phi [x]\}$
.
![]() $\boldsymbol {\Pi _n}(J_\alpha (\mathbb {R}))$
is defined analogously with
$\boldsymbol {\Pi _n}(J_\alpha (\mathbb {R}))$
is defined analogously with
![]() $\Pi _n$
-formulas.Footnote
1
The Levy hierarchy consists of all pointclasses of the form
$\Pi _n$
-formulas.Footnote
1
The Levy hierarchy consists of all pointclasses of the form
![]() $\boldsymbol {\Sigma _n}(J_\alpha (\mathbb {R}))$
or
$\boldsymbol {\Sigma _n}(J_\alpha (\mathbb {R}))$
or
![]() $\boldsymbol {\Pi _n}(J_\alpha (\mathbb {R}))$
for some n and
$\boldsymbol {\Pi _n}(J_\alpha (\mathbb {R}))$
for some n and
![]() $\alpha $
. It is clear any pointclass in the Levy hierarchy equals
$\alpha $
. It is clear any pointclass in the Levy hierarchy equals
![]() $\boldsymbol {\Sigma ^1_\alpha }$
or
$\boldsymbol {\Sigma ^1_\alpha }$
or
![]() $\boldsymbol {\Pi ^1_\alpha }$
for some
$\boldsymbol {\Pi ^1_\alpha }$
for some
![]() $\alpha $
, but the converse is false.
$\alpha $
, but the converse is false.
In this section, we will classify the scaled pointclasses within the Levy hierarchy, relate the Levy hierarchy to the extended projective hierarchy, and classify the regular Suslin pointclasses.
2.1.1 Classification of scaled pointclasses.
A
![]() $\Sigma _1$
-gap is a maximal interval
$\Sigma _1$
-gap is a maximal interval
![]() $[\alpha ,\beta ]$
such that for any real x, the
$[\alpha ,\beta ]$
such that for any real x, the
![]() $\Sigma _1$
-theory of x is the same in
$\Sigma _1$
-theory of x is the same in
![]() $J_\alpha (\mathbb {R})$
and
$J_\alpha (\mathbb {R})$
and
![]() $J_\beta (\mathbb {R})$
.
$J_\beta (\mathbb {R})$
.
We say the gap
![]() $[\alpha ,\beta ]$
is admissible if
$[\alpha ,\beta ]$
is admissible if
![]() $J_\alpha (\mathbb {R})\models KP$
, equivalently, if the pointclass
$J_\alpha (\mathbb {R})\models KP$
, equivalently, if the pointclass
![]() $\boldsymbol {\Sigma _1}(J_\alpha (\mathbb {R}))$
is closed under coprojection. Suppose
$\boldsymbol {\Sigma _1}(J_\alpha (\mathbb {R}))$
is closed under coprojection. Suppose
![]() $[\alpha ,\beta ]$
is an admissible gap. Let
$[\alpha ,\beta ]$
is an admissible gap. Let
![]() $n_\beta \in \mathbb {N}$
be least such that the pointclass
$n_\beta \in \mathbb {N}$
be least such that the pointclass
![]() $\boldsymbol {\Sigma _{n_\beta }}(J_\beta (\mathbb {R}))$
is not contained in
$\boldsymbol {\Sigma _{n_\beta }}(J_\beta (\mathbb {R}))$
is not contained in
![]() $J_\beta (\mathbb {R})$
. We say
$J_\beta (\mathbb {R})$
. We say
![]() $[\alpha ,\beta ]$
is a strong gap if for any
$[\alpha ,\beta ]$
is a strong gap if for any
![]() $b\in J_\beta (\mathbb {R})$
, there is
$b\in J_\beta (\mathbb {R})$
, there is
![]() $\beta ' < \beta $
and
$\beta ' < \beta $
and
![]() $b' \in J_{\beta '}(\mathbb {R})$
such that the
$b' \in J_{\beta '}(\mathbb {R})$
such that the
![]() $\Sigma _{n_\beta }$
and
$\Sigma _{n_\beta }$
and
![]() $\Pi _{n_\beta }$
theories of
$\Pi _{n_\beta }$
theories of
![]() $b'$
in
$b'$
in
![]() $J_{\beta '}(\mathbb {R})$
are the same as the
$J_{\beta '}(\mathbb {R})$
are the same as the
![]() $\Sigma _{n_\beta }$
and
$\Sigma _{n_\beta }$
and
![]() $\Pi _{n_\beta }$
theories of b in
$\Pi _{n_\beta }$
theories of b in
![]() $J_{\beta }(\mathbb {R})$
. Otherwise, we say
$J_{\beta }(\mathbb {R})$
. Otherwise, we say
![]() $[\alpha ,\beta ]$
is weak.
$[\alpha ,\beta ]$
is weak.
Theorem 2.1. Suppose
![]() $\boldsymbol {\Gamma }$
is a pointclass in the Levy hierarchy. If
$\boldsymbol {\Gamma }$
is a pointclass in the Levy hierarchy. If
![]() $\boldsymbol {\Gamma }$
is scaled, then one of the following holds:
$\boldsymbol {\Gamma }$
is scaled, then one of the following holds:
-
1.
 $\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_{2k+1}(J_\alpha (\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_{2k+1}(J_\alpha (\mathbb {R}))$
for some
 $k\in \omega $
and some
$k\in \omega $
and some
 $\alpha $
beginning an inadmissible gap.
$\alpha $
beginning an inadmissible gap. -
2.
 $\boldsymbol {\Gamma } = \boldsymbol {\Pi }_{2k+2}(J_\alpha (\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Pi }_{2k+2}(J_\alpha (\mathbb {R}))$
for some
 $k\in \omega $
and some
$k\in \omega $
and some
 $\alpha $
beginning an inadmissible gap.
$\alpha $
beginning an inadmissible gap. -
3.
 $\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_1(J_\alpha (\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_1(J_\alpha (\mathbb {R}))$
for some
 $\alpha $
beginning an admissible gap.
$\alpha $
beginning an admissible gap. -
4.
 $\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_{n_{\beta }+2k}(J_\beta (\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_{n_{\beta }+2k}(J_\beta (\mathbb {R}))$
for some
 $k\in \omega $
and some
$k\in \omega $
and some
 $\beta $
ending a weak gap.
$\beta $
ending a weak gap. -
5.
 $\boldsymbol {\Gamma } = \boldsymbol {\Pi }_{n_{\beta }+2k + 1}(J_\beta (\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Pi }_{n_{\beta }+2k + 1}(J_\beta (\mathbb {R}))$
for some
 $k\in \omega $
and some
$k\in \omega $
and some
 $\beta $
ending a weak gap.
$\beta $
ending a weak gap.
Definition 2.2. A self-justifying system (sjs) is a countable set
![]() $\mathcal {B} \subseteq \mathcal {P}(\mathbb {R})$
which is closed under complements and has the property that every
$\mathcal {B} \subseteq \mathcal {P}(\mathbb {R})$
which is closed under complements and has the property that every
![]() $B\in \mathcal {B}$
admits a scale
$B\in \mathcal {B}$
admits a scale
![]() $\vec {\psi }$
such that
$\vec {\psi }$
such that
![]() $\leq _{\psi _n} \in \mathcal {B}$
for all n.
$\leq _{\psi _n} \in \mathcal {B}$
for all n.
Definition 2.3. Let
![]() $z\in \mathbb {R}$
and
$z\in \mathbb {R}$
and
![]() $\gamma \in ON$
.
$\gamma \in ON$
.
![]() $OD^{<\gamma }(z)$
is the set of pointsets which are ordinal definable from the parameter z in
$OD^{<\gamma }(z)$
is the set of pointsets which are ordinal definable from the parameter z in
![]() $J_\xi (\mathbb {R})$
for some
$J_\xi (\mathbb {R})$
for some
![]() $\xi <\gamma $
.
$\xi <\gamma $
.
![]() $OD^{<\gamma }$
denotes
$OD^{<\gamma }$
denotes
![]() $OD^{<\gamma }(0)$
.
$OD^{<\gamma }(0)$
.
The proof of Theorem 2.1 also gives the following theorem.
Theorem 2.4. Suppose
![]() $[\alpha ,\beta ]$
is an admissible gap. Let
$[\alpha ,\beta ]$
is an admissible gap. Let
![]() $\beta '$
be the least ordinal such that there is a scale for a universal
$\beta '$
be the least ordinal such that there is a scale for a universal
![]() $\boldsymbol {\Pi _1}(J_\alpha (\mathbb {R}))$
-set definable over
$\boldsymbol {\Pi _1}(J_\alpha (\mathbb {R}))$
-set definable over
![]() $J_{\beta '}(\mathbb {R})$
. Then there is
$J_{\beta '}(\mathbb {R})$
. Then there is
![]() $z\in \mathbb {R}$
and a sjs
$z\in \mathbb {R}$
and a sjs
![]() $\mathcal {B} \subset OD^{<\beta '}(z)$
such that a universal
$\mathcal {B} \subset OD^{<\beta '}(z)$
such that a universal
![]() $\boldsymbol {\Pi _1}(J_\alpha (\mathbb {R}))$
-set is in
$\boldsymbol {\Pi _1}(J_\alpha (\mathbb {R}))$
-set is in
![]() $\mathcal {B}$
and either:
$\mathcal {B}$
and either:
-
1.
 $[\alpha ,\beta ]$
is weak and
$[\alpha ,\beta ]$
is weak and
 $\beta ' = \beta $
or
$\beta ' = \beta $
or -
2.
 $[\alpha ,\beta ]$
is strong and
$[\alpha ,\beta ]$
is strong and
 $\beta ' = \beta +1$
.
$\beta ' = \beta +1$
.
Remark 2.5. Suppose
![]() $\boldsymbol {\Gamma }$
is a boldface inductive-like pointclass in
$\boldsymbol {\Gamma }$
is a boldface inductive-like pointclass in
![]() $L(\mathbb {R})$
. Then
$L(\mathbb {R})$
. Then
-
1.
 $\boldsymbol {\Gamma } = \boldsymbol {\Sigma _1}(J_\alpha (\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Sigma _1}(J_\alpha (\mathbb {R}))$
for some
 $\alpha $
beginning an admissible gap,
$\alpha $
beginning an admissible gap, -
2. there is
 $x\in \mathbb {R}$
such that letting
$x\in \mathbb {R}$
such that letting
 $\Gamma $
be the class of pointsets which are
$\Gamma $
be the class of pointsets which are
 $\Sigma _1$
-definable over
$\Sigma _1$
-definable over
 $J_\alpha (\mathbb {R})$
from the parameter x,
$J_\alpha (\mathbb {R})$
from the parameter x,
 $\boldsymbol {\Gamma }$
is the closure of
$\boldsymbol {\Gamma }$
is the closure of
 $\Gamma $
under preimages by continuous functions, and
$\Gamma $
under preimages by continuous functions, and -
3.
 $\boldsymbol {\Gamma } = (\boldsymbol {\Sigma ^2_1})^{\boldsymbol {\Delta _\Gamma }}$
.Footnote
2
$\boldsymbol {\Gamma } = (\boldsymbol {\Sigma ^2_1})^{\boldsymbol {\Delta _\Gamma }}$
.Footnote
2
2.1.2 Relationship between the Levy hierarchy and the extended projective hierarchy.
Definition 2.6. Suppose
![]() $\lambda < \Theta $
is a limit ordinal. We say
$\lambda < \Theta $
is a limit ordinal. We say
-
•
 $\lambda $
is type I if
$\lambda $
is type I if
 $\boldsymbol {\Sigma ^1_\lambda }$
is closed under finite intersection but not countable intersection,
$\boldsymbol {\Sigma ^1_\lambda }$
is closed under finite intersection but not countable intersection, -
•
 $\lambda $
is type II if
$\lambda $
is type II if
 $\boldsymbol {\Sigma ^1_\lambda }$
is not closed under finite intersection,
$\boldsymbol {\Sigma ^1_\lambda }$
is not closed under finite intersection, -
•
 $\lambda $
is type III if
$\lambda $
is type III if
 $\boldsymbol {\Sigma ^1_\lambda }$
is closed under countable intersection but not coprojection, and
$\boldsymbol {\Sigma ^1_\lambda }$
is closed under countable intersection but not coprojection, and -
•
 $\lambda $
is type IV if
$\lambda $
is type IV if
 $\boldsymbol {\Sigma ^1_\lambda }$
is closed under coprojection.
$\boldsymbol {\Sigma ^1_\lambda }$
is closed under coprojection.
Let
![]() $\langle \delta _\alpha : \alpha < \Theta \rangle $
enumerate the ordinals
$\langle \delta _\alpha : \alpha < \Theta \rangle $
enumerate the ordinals
![]() $\delta $
such that there exist sets of reals in
$\delta $
such that there exist sets of reals in
![]() $J_{\delta +1}(\mathbb {R}) \backslash J_\delta (\mathbb {R})$
. Let
$J_{\delta +1}(\mathbb {R}) \backslash J_\delta (\mathbb {R})$
. Let
![]() $n_\alpha $
be minimal such that
$n_\alpha $
be minimal such that
![]() $\boldsymbol {\Sigma _{n_\alpha }}(J_{\delta _\alpha }(\mathbb {R})) \not \subset J_{\delta _\alpha }(\mathbb {R})$
.
$\boldsymbol {\Sigma _{n_\alpha }}(J_{\delta _\alpha }(\mathbb {R})) \not \subset J_{\delta _\alpha }(\mathbb {R})$
.
Theorem 2.7. Suppose
![]() $\alpha < \Theta $
.
$\alpha < \Theta $
.
-
1. If
 $\omega {\alpha }$
is type I, then
$\omega {\alpha }$
is type I, then
 $\boldsymbol {\Sigma ^1_{\omega \alpha + k}} = \boldsymbol {\Sigma _{n_\alpha +k}}(J_{\delta _{\alpha }}(\mathbb {R}))$
for all
$\boldsymbol {\Sigma ^1_{\omega \alpha + k}} = \boldsymbol {\Sigma _{n_\alpha +k}}(J_{\delta _{\alpha }}(\mathbb {R}))$
for all
 $k\in \omega $
.
$k\in \omega $
. -
2. If
 $\omega \alpha $
is type II or III, then
$\omega \alpha $
is type II or III, then
 $\boldsymbol {\Sigma ^1_{\omega \alpha + k + 1}} = \boldsymbol {\Sigma _{n_\alpha +k}}(J_{\delta _{\alpha }}(\mathbb {R}))$
for all
$\boldsymbol {\Sigma ^1_{\omega \alpha + k + 1}} = \boldsymbol {\Sigma _{n_\alpha +k}}(J_{\delta _{\alpha }}(\mathbb {R}))$
for all
 $k\in \omega $
.
$k\in \omega $
. -
3. If
 $\omega \alpha $
is type IV, then
$\omega \alpha $
is type IV, then
 $\boldsymbol {\Pi ^1_{\omega \alpha }} = \boldsymbol {\Sigma _{n_\alpha }}(J_{\delta _{\alpha }}(\mathbb {R}))$
and
$\boldsymbol {\Pi ^1_{\omega \alpha }} = \boldsymbol {\Sigma _{n_\alpha }}(J_{\delta _{\alpha }}(\mathbb {R}))$
and
 $\boldsymbol {\Sigma ^1_{\omega \alpha + k+1}} = \boldsymbol {\Sigma _{n_{\alpha }+k}}(J_{\delta _{\alpha }}(\mathbb {R}))$
for all
$\boldsymbol {\Sigma ^1_{\omega \alpha + k+1}} = \boldsymbol {\Sigma _{n_{\alpha }+k}}(J_{\delta _{\alpha }}(\mathbb {R}))$
for all
 $k\in \omega {\backslash }\{0\}$
.
$k\in \omega {\backslash }\{0\}$
.
2.1.3 Classification of Suslin pointclasses.
There is a related classification of the Suslin pointclasses. For
![]() $\alpha < \Theta $
, let
$\alpha < \Theta $
, let
![]() $\kappa _\alpha $
be the
$\kappa _\alpha $
be the
![]() $\alpha $
th Suslin cardinal. Let
$\alpha $
th Suslin cardinal. Let
![]() $\nu _\alpha $
be the
$\nu _\alpha $
be the
![]() $\alpha $
th ordinal
$\alpha $
th ordinal
![]() $\nu $
such that
$\nu $
such that
![]() $\boldsymbol {\Sigma ^1_\nu }$
or
$\boldsymbol {\Sigma ^1_\nu }$
or
![]() $\boldsymbol {\Pi ^1_\nu }$
is scaled.
$\boldsymbol {\Pi ^1_\nu }$
is scaled.
Theorem 2.8. Let
![]() $\lambda < \boldsymbol {\delta ^2_1}$
be a limit cardinal and
$\lambda < \boldsymbol {\delta ^2_1}$
be a limit cardinal and
![]() $\nu = sup\{\nu _\alpha : \alpha < \lambda \}$
.
$\nu = sup\{\nu _\alpha : \alpha < \lambda \}$
.
-
1. If
 $\nu $
is type I, then for all
$\nu $
is type I, then for all
 $k\in \omega $
$k\in \omega $
-
•
 $\boldsymbol {\Sigma ^1_{\nu +2k}}$
and
$\boldsymbol {\Sigma ^1_{\nu +2k}}$
and
 $\boldsymbol {\Pi ^1_{\nu +2k+1}}$
are scaled,
$\boldsymbol {\Pi ^1_{\nu +2k+1}}$
are scaled, -
•
 $S(\kappa _{\lambda + k}) = \boldsymbol {\Sigma ^1_{\nu +k+1}}$
,
$S(\kappa _{\lambda + k}) = \boldsymbol {\Sigma ^1_{\nu +k+1}}$
, -
•
 $\kappa _{\lambda +2k+1} = \boldsymbol {\delta ^1_{\nu +2k+1}} = (\kappa _{\lambda +2k})^+$
, and
$\kappa _{\lambda +2k+1} = \boldsymbol {\delta ^1_{\nu +2k+1}} = (\kappa _{\lambda +2k})^+$
, and -
•
 $cof(\kappa _{\lambda +2k}) = \omega $
.
$cof(\kappa _{\lambda +2k}) = \omega $
.
-
-
2. If
 $\nu $
is type II or III, then for all
$\nu $
is type II or III, then for all
 $k\in \omega $
$k\in \omega $
-
•
 $\boldsymbol {\Sigma ^1_{\nu +2k+1}}$
and
$\boldsymbol {\Sigma ^1_{\nu +2k+1}}$
and
 $\boldsymbol {\Pi ^1_{\nu +2k}}$
are scaled,
$\boldsymbol {\Pi ^1_{\nu +2k}}$
are scaled, -
•
 $S(\kappa _{\lambda + k}) = \boldsymbol {\Sigma ^1_{\nu +k+1}}$
,
$S(\kappa _{\lambda + k}) = \boldsymbol {\Sigma ^1_{\nu +k+1}}$
, -
•
 $\kappa _{\lambda +2k+2} = \boldsymbol {\delta ^1_{\nu +2k+2}} = (\kappa _{\lambda +2k+1})^+$
, and
$\kappa _{\lambda +2k+2} = \boldsymbol {\delta ^1_{\nu +2k+2}} = (\kappa _{\lambda +2k+1})^+$
, and -
•
 $cof(\kappa _{\lambda +2k+1}) = \omega $
.
$cof(\kappa _{\lambda +2k+1}) = \omega $
.
-
-
3. If
 $\nu $
is type IV, then
$\nu $
is type IV, then
 $\boldsymbol {\Pi ^1_\nu }$
is scaled,
$\boldsymbol {\Pi ^1_\nu }$
is scaled,
 $S(\kappa _\lambda ) = \boldsymbol {\Pi ^1_\nu }$
, and for all
$S(\kappa _\lambda ) = \boldsymbol {\Pi ^1_\nu }$
, and for all
 $k\in \omega $
, letting
$k\in \omega $
, letting
 $\mu = \nu _{\lambda +1}$
,
$\mu = \nu _{\lambda +1}$
,-
•
 $\boldsymbol {\Sigma ^1_{\mu +2k}}$
and
$\boldsymbol {\Sigma ^1_{\mu +2k}}$
and
 $\boldsymbol {\Pi ^1_{\mu +2k+1}}$
are scaled,
$\boldsymbol {\Pi ^1_{\mu +2k+1}}$
are scaled, -
•
 $S(\kappa _{\lambda + k + 1}) = \boldsymbol {\Sigma ^1_{\mu +k+1}}$
,
$S(\kappa _{\lambda + k + 1}) = \boldsymbol {\Sigma ^1_{\mu +k+1}}$
, -
•
 $\kappa _{\lambda +2k+2} = \boldsymbol {\delta ^1_{\mu +2k+1}} = (\kappa _{\lambda +2k+1})^+$
, and
$\kappa _{\lambda +2k+2} = \boldsymbol {\delta ^1_{\mu +2k+1}} = (\kappa _{\lambda +2k+1})^+$
, and -
•
 $cof(\kappa _{\lambda +2k+1}) = \omega $
.
$cof(\kappa _{\lambda +2k+1}) = \omega $
.
-
Corollary 2.9. Suppose
![]() $\boldsymbol {\Gamma } = S(\kappa )$
for a regular Suslin cardinal
$\boldsymbol {\Gamma } = S(\kappa )$
for a regular Suslin cardinal
![]() $\kappa \leq \boldsymbol {\delta ^2_1}$
. Then one of the following holds:
$\kappa \leq \boldsymbol {\delta ^2_1}$
. Then one of the following holds:
-
1.
 $\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_{2k+1}(J_\alpha (\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_{2k+1}(J_\alpha (\mathbb {R}))$
for some
 $k\in \omega $
and some
$k\in \omega $
and some
 $\alpha $
beginning an inadmissible gap.
$\alpha $
beginning an inadmissible gap. -
2.
 $\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_1(J_\alpha (\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_1(J_\alpha (\mathbb {R}))$
for some
 $\alpha $
beginning an admissible gap.
$\alpha $
beginning an admissible gap. -
3.
 $\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_{n_{\beta }+2k}(J_\beta (\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Sigma }_{n_{\beta }+2k}(J_\beta (\mathbb {R}))$
for some
 $k\in \omega $
and some
$k\in \omega $
and some
 $\beta $
ending a weak gap.
$\beta $
ending a weak gap.
2.2 Woodin cardinals and iterations
We borrow most of the notation of premice and iteration trees from [Reference Steel, Foreman and Kanamori19]. In addition to the lightface premice defined in [Reference Steel, Foreman and Kanamori19], we will also consider premice built over some
![]() $a\in HC$
. We write an a-premouse as
$a\in HC$
. We write an a-premouse as
![]() $M = (J_\alpha ^{\vec {E}},\in ,\vec {E}\upharpoonright \alpha ,E_\alpha ,a)$
, for a fine extender sequence
$M = (J_\alpha ^{\vec {E}},\in ,\vec {E}\upharpoonright \alpha ,E_\alpha ,a)$
, for a fine extender sequence
![]() $\vec {E} = \langle E_\eta : \eta \leq \alpha \rangle $
. If
$\vec {E} = \langle E_\eta : \eta \leq \alpha \rangle $
. If
![]() $\beta \leq \alpha $
,
$\beta \leq \alpha $
,
![]() $M|\beta $
represents the premouse
$M|\beta $
represents the premouse
![]() $(J_\beta ^{\vec {E}},\in ,\vec {E}\upharpoonright \beta ,E_\beta ,a)$
. Unless otherwise specified, an iteration strategy will refer to an
$(J_\beta ^{\vec {E}},\in ,\vec {E}\upharpoonright \beta ,E_\beta ,a)$
. Unless otherwise specified, an iteration strategy will refer to an
![]() $(\omega _1,\omega _1)$
-iteration strategy and a mouse will refer to a premouse with such a strategy. Under
$(\omega _1,\omega _1)$
-iteration strategy and a mouse will refer to a premouse with such a strategy. Under
![]() $ZF + AD$
,
$ZF + AD$
,
![]() $\omega _1$
is measurable, so an
$\omega _1$
is measurable, so an
![]() $(\omega _1,\omega _1)$
-iteration strategy induces an
$(\omega _1,\omega _1)$
-iteration strategy induces an
![]() $(\omega _1,\omega _1+1)$
-iteration strategy. In particular, the theorems in this section requiring an
$(\omega _1,\omega _1+1)$
-iteration strategy. In particular, the theorems in this section requiring an
![]() $\omega _1+1$
-iteration strategy will all apply to the mice we use in Section 3.
$\omega _1+1$
-iteration strategy will all apply to the mice we use in Section 3.
Additionally, if
![]() $\mathcal {T}$
is an iteration tree of limit length and b is a cofinal, non-dropping branch through
$\mathcal {T}$
is an iteration tree of limit length and b is a cofinal, non-dropping branch through
![]() $\mathcal {T}$
, we let
$\mathcal {T}$
, we let
![]() $M_b^{\mathcal {T}}$
be the direct limit of the models on b and let
$M_b^{\mathcal {T}}$
be the direct limit of the models on b and let
![]() $i_b^{\mathcal {T}}: M_0^{\mathcal {T}} \to M_b^{\mathcal {T}}$
be the associated direct limit embedding.
$i_b^{\mathcal {T}}: M_0^{\mathcal {T}} \to M_b^{\mathcal {T}}$
be the associated direct limit embedding.
For a model M, let
![]() $\delta _M$
denote the least Woodin cardinal of M (if one exists) and
$\delta _M$
denote the least Woodin cardinal of M (if one exists) and
![]() $Ea_M$
denote Woodin’s extender algebra in M at
$Ea_M$
denote Woodin’s extender algebra in M at
![]() $\delta _M$
. Let
$\delta _M$
. Let
![]() $\kappa _M$
be the least cardinal of M which is
$\kappa _M$
be the least cardinal of M which is
![]() $<\delta _M$
-strong in M.
$<\delta _M$
-strong in M.
![]() $ea$
will refer to the generic over
$ea$
will refer to the generic over
![]() $Ea_M$
. When considering the product extender algebra
$Ea_M$
. When considering the product extender algebra
![]() $Ea_M \times Ea_M$
, we will write
$Ea_M \times Ea_M$
, we will write
![]() $ea_l \times ea_r$
for the generic.
$ea_l \times ea_r$
for the generic.
![]() $ea_r$
will typically code a pair which we shall write
$ea_r$
will typically code a pair which we shall write
![]() $(ea^1_r,ea^2_r)$
. For posets of the form
$(ea^1_r,ea^2_r)$
. For posets of the form
![]() $Col(\omega ,X)$
,
$Col(\omega ,X)$
,
![]() $\dot {g}$
denotes a name for the generic.
$\dot {g}$
denotes a name for the generic.
Suppose M is a premouse with iteration strategy
![]() $\Sigma $
. We say N is a complete iterate of M if N is the last model of an iteration tree
$\Sigma $
. We say N is a complete iterate of M if N is the last model of an iteration tree
![]() $\mathcal {T}$
on M such that
$\mathcal {T}$
on M such that
![]() $\mathcal {T}$
is according to
$\mathcal {T}$
is according to
![]() $\Sigma $
and the branch through
$\Sigma $
and the branch through
![]() $\mathcal {T}$
from M to N is non-dropping.Footnote
3
$\mathcal {T}$
from M to N is non-dropping.Footnote
3
Theorem 2.10. Let M be a countable premouse with an
![]() $\omega _1+1$
-iteration strategy such that
$\omega _1+1$
-iteration strategy such that
![]() $M \models $
“There is a Woodin cardinal.” Then
$M \models $
“There is a Woodin cardinal.” Then
![]() $Ea_M$
is a
$Ea_M$
is a
![]() $\delta _M$
-c.c. Boolean algebra and for any
$\delta _M$
-c.c. Boolean algebra and for any
![]() $x\in \mathbb {R}$
, there is a countable, complete iterate N of M such that x is
$x\in \mathbb {R}$
, there is a countable, complete iterate N of M such that x is
![]() $Ea_N$
-generic over N.
$Ea_N$
-generic over N.
Corollary 2.11. Let M be a countable premouse with an
![]() $\omega _1+1$
-iteration strategy such that
$\omega _1+1$
-iteration strategy such that
![]() $M \models $
“There is a Woodin cardinal.” Then for any
$M \models $
“There is a Woodin cardinal.” Then for any
![]() $x\in \mathbb {R}$
, there is a countable, complete iterate N of M and g which is
$x\in \mathbb {R}$
, there is a countable, complete iterate N of M and g which is
![]() $Col(\omega ,\delta _N)$
-generic over N such that
$Col(\omega ,\delta _N)$
-generic over N such that
![]() $x\in N[g]$
.
$x\in N[g]$
.
See Section 7.2 of [Reference Steel, Foreman and Kanamori19] for a proof of Theorem 2.10 and its corollary.
Definition 2.12. For
![]() $\kappa <\delta $
and
$\kappa <\delta $
and
![]() $A\subseteq \delta $
, we say
$A\subseteq \delta $
, we say
![]() $\kappa $
is A-reflecting in
$\kappa $
is A-reflecting in
![]() $\delta $
if for every
$\delta $
if for every
![]() $\nu < \delta $
, there is an extender E with critical point
$\nu < \delta $
, there is an extender E with critical point
![]() $\kappa $
such that
$\kappa $
such that
![]() $i_E(\kappa )>\nu $
and
$i_E(\kappa )>\nu $
and
![]() $i_E(A) \cap \nu = A \cap \nu $
.
$i_E(A) \cap \nu = A \cap \nu $
.
Theorem 2.13. Suppose b and c are distinct wellfounded branches of a normal iteration tree
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $A\subseteq \delta (\mathcal {T})$
is in
$A\subseteq \delta (\mathcal {T})$
is in
![]() $M^{\mathcal {T}}_b \cap M^{\mathcal {T}}_c$
. Then there is
$M^{\mathcal {T}}_b \cap M^{\mathcal {T}}_c$
. Then there is
![]() $\kappa < \delta (\mathcal {T})$
such that
$\kappa < \delta (\mathcal {T})$
such that
![]() $M^{\mathcal {T}}_b \models $
“
$M^{\mathcal {T}}_b \models $
“
![]() $\kappa $
is A-reflecting in
$\kappa $
is A-reflecting in
![]() $\delta (\mathcal {T})$
,” and this is witnessed by a sequence of extenders on the extender sequence of
$\delta (\mathcal {T})$
,” and this is witnessed by a sequence of extenders on the extender sequence of
![]() $\mathcal {M}(\mathcal {T})$
.
$\mathcal {M}(\mathcal {T})$
.
See Definition 6.9 and Theorem 6.10 of [Reference Steel, Foreman and Kanamori19] for definitions of
![]() $\delta (\mathcal {T})$
and
$\delta (\mathcal {T})$
and
![]() $\mathcal {M}(\mathcal {T})$
and a proof of Theorem 2.13. The theorem justifies the following definitions.
$\mathcal {M}(\mathcal {T})$
and a proof of Theorem 2.13. The theorem justifies the following definitions.
Definition 2.14. Suppose b is a wellfounded branch through a normal iteration tree
![]() $\mathcal {T}$
. Let
$\mathcal {T}$
. Let
![]() $\mathcal {Q}(b,\mathcal {T})$
be the least initial segment of
$\mathcal {Q}(b,\mathcal {T})$
be the least initial segment of
![]() $M^{\mathcal {T}}_b$
extending
$M^{\mathcal {T}}_b$
extending
![]() $\mathcal {M}(\mathcal {T})$
such that there is
$\mathcal {M}(\mathcal {T})$
such that there is
![]() $A\subset \delta (\mathcal {T})$
which is definable over
$A\subset \delta (\mathcal {T})$
which is definable over
![]() $\mathcal {Q}(b,\mathcal {T})$
and realizes
$\mathcal {Q}(b,\mathcal {T})$
and realizes
![]() $\delta (\mathcal {T})$
is not Woodin via extenders in
$\delta (\mathcal {T})$
is not Woodin via extenders in
![]() $\mathcal {M}(\mathcal {T})$
, if such an initial segment exists.
$\mathcal {M}(\mathcal {T})$
, if such an initial segment exists.
Definition 2.15. Suppose M is a premouse and
![]() $\eta \in M$
. We say
$\eta \in M$
. We say
![]() $\eta $
is a cutpoint of M if there is no extender on the fine extender sequence of M with critical point less than
$\eta $
is a cutpoint of M if there is no extender on the fine extender sequence of M with critical point less than
![]() $\eta $
and length greater than
$\eta $
and length greater than
![]() $\eta $
.
$\eta $
.
![]() $\eta $
is a strong cutpoint if there is no extender on the fine extender sequence of M with critical point less than or equal to
$\eta $
is a strong cutpoint if there is no extender on the fine extender sequence of M with critical point less than or equal to
![]() $\eta $
and length greater than
$\eta $
and length greater than
![]() $\eta $
.
$\eta $
.
Definition 2.16. Suppose
![]() $\mathcal {T}$
is a normal iteration tree. Let
$\mathcal {T}$
is a normal iteration tree. Let
![]() $\mathcal {Q}(\mathcal {T})$
be the least
$\mathcal {Q}(\mathcal {T})$
be the least
![]() $\delta (\mathcal {T})$
-sound,
$\delta (\mathcal {T})$
-sound,
![]() $\omega _1+1$
-iterable premouse extending
$\omega _1+1$
-iterable premouse extending
![]() $\mathcal {M}(\mathcal {T})$
and projecting to
$\mathcal {M}(\mathcal {T})$
and projecting to
![]() $\delta (\mathcal {T})$
such that
$\delta (\mathcal {T})$
such that
![]() $\delta (\mathcal {T})$
is a strong cutpoint of
$\delta (\mathcal {T})$
is a strong cutpoint of
![]() $\mathcal {Q}(\mathcal {T})$
and there is
$\mathcal {Q}(\mathcal {T})$
and there is
![]() $A\subset \delta (\mathcal {T})$
which is definable over
$A\subset \delta (\mathcal {T})$
which is definable over
![]() $\mathcal {Q}(\mathcal {T})$
and realizes
$\mathcal {Q}(\mathcal {T})$
and realizes
![]() $\delta (\mathcal {T})$
is not Woodin via extenders in
$\delta (\mathcal {T})$
is not Woodin via extenders in
![]() $\mathcal {M}(\mathcal {T})$
, if one exists.
$\mathcal {M}(\mathcal {T})$
, if one exists.
It follows from Theorem 2.13 that there is at most one wellfounded branch b through
![]() $\mathcal {T}$
such that
$\mathcal {T}$
such that
![]() $\mathcal {Q}(\mathcal {T})\trianglelefteq M^{\mathcal {T}}_b$
. In many cases, we will be able to locate the branch a strategy
$\mathcal {Q}(\mathcal {T})\trianglelefteq M^{\mathcal {T}}_b$
. In many cases, we will be able to locate the branch a strategy
![]() $\Sigma $
chooses as the unique branch which absorbs
$\Sigma $
chooses as the unique branch which absorbs
![]() $\mathcal {Q}(\mathcal {T})$
in this sense.
$\mathcal {Q}(\mathcal {T})$
in this sense.
Note that an
![]() $\omega _1$
-iteration strategy on a countable premouse can be coded by a set of reals. For
$\omega _1$
-iteration strategy on a countable premouse can be coded by a set of reals. For
![]() $a\in HC$
and a pointclass
$a\in HC$
and a pointclass
![]() $\Gamma $
, this allows us to define
$\Gamma $
, this allows us to define
 $$ \begin{align*} Lp^\Gamma(a) = \, \bigcup\{N :\, &N \text{ is an } \omega\text{-sound } a\text{-premouse projecting to } a \\ & \text{ with an } \omega_1\text{-iteration strategy in } \boldsymbol{\Delta_{\Gamma}}\}. \end{align*} $$
$$ \begin{align*} Lp^\Gamma(a) = \, \bigcup\{N :\, &N \text{ is an } \omega\text{-sound } a\text{-premouse projecting to } a \\ & \text{ with an } \omega_1\text{-iteration strategy in } \boldsymbol{\Delta_{\Gamma}}\}. \end{align*} $$
![]() $Lp^\Gamma (a)$
can be reorganized as an a-premouse, which is what we will typically use
$Lp^\Gamma (a)$
can be reorganized as an a-premouse, which is what we will typically use
![]() $Lp^\Gamma (a)$
to refer to.
$Lp^\Gamma (a)$
to refer to.
Closely related to
![]() $Lp^\Gamma $
is the operator
$Lp^\Gamma $
is the operator
![]() $C_\Gamma $
. For
$C_\Gamma $
. For
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
And for
![]() $a\in HC$
,
$a\in HC$
,
Here
![]() $b_x$
codes b relative to x. See [Reference Steel, Kechris, Löwe and Steel20] for more details.
$b_x$
codes b relative to x. See [Reference Steel, Kechris, Löwe and Steel20] for more details.
Theorem 2.17. Assume
![]() $AD^{L(\mathbb {R})}$
. Suppose
$AD^{L(\mathbb {R})}$
. Suppose
![]() $\Gamma $
is a (lightface) inductive-like pointclass in
$\Gamma $
is a (lightface) inductive-like pointclass in
![]() $L(\mathbb {R})$
and
$L(\mathbb {R})$
and
![]() $a\in HC$
. Then
$a\in HC$
. Then
![]() $C_\Gamma (a) = Lp^\Gamma (a) \cap P(a)$
.
$C_\Gamma (a) = Lp^\Gamma (a) \cap P(a)$
.
Remark 2.18. Suppose a and b are countable, transitive sets and
![]() $a\in b$
. It is easy to see from the definition of
$a\in b$
. It is easy to see from the definition of
![]() $C_\Gamma $
that
$C_\Gamma $
that
![]() $C_\Gamma (a)\subseteq C_\Gamma (b)$
. This, and the theorem above, implies
$C_\Gamma (a)\subseteq C_\Gamma (b)$
. This, and the theorem above, implies
![]() $Lp^\Gamma (a)\subseteq Lp^\Gamma (b)$
.
$Lp^\Gamma (a)\subseteq Lp^\Gamma (b)$
.
2.3 The Mitchell–Steel construction
We shall require a method of building an a-premouse inside a premouse M which contains a. Our main tool for this purpose is the fully backgrounded Mitchell–Steel construction developed in [Reference Mitchell and Steel7]. This section reviews the construction and its properties.
We say a premouse M is reliable if
![]() $\mathcal {C}_\omega (M)$
exists and is universal and solid. As we shall see in a moment, we will end the Mitchell–Steel construction if we reach a premouse which is not reliable. Mitchell and Steel [Reference Mitchell and Steel7] define reliable to include the stronger property that
$\mathcal {C}_\omega (M)$
exists and is universal and solid. As we shall see in a moment, we will end the Mitchell–Steel construction if we reach a premouse which is not reliable. Mitchell and Steel [Reference Mitchell and Steel7] define reliable to include the stronger property that
![]() $\mathcal {C}_\omega (M)$
is iterable. But the weaker properties of universality and solidity are enough to propagate the construction, and our weaker requirement ensures the construction does not end prematurely when performed inside a mouse. The definitions of universality and solidity can be found in [Reference Steel, Foreman and Kanamori19]. In all of the cases relevant to us, universality and solidity are guaranteed and the reader will lose little by taking on faith that the construction does not end.
$\mathcal {C}_\omega (M)$
is iterable. But the weaker properties of universality and solidity are enough to propagate the construction, and our weaker requirement ensures the construction does not end prematurely when performed inside a mouse. The definitions of universality and solidity can be found in [Reference Steel, Foreman and Kanamori19]. In all of the cases relevant to us, universality and solidity are guaranteed and the reader will lose little by taking on faith that the construction does not end.
For the moment we will work in V and assume
![]() $ZFC$
. Fix
$ZFC$
. Fix
![]() $z\in \mathbb {R}$
. Define a sequence of z-premice
$z\in \mathbb {R}$
. Define a sequence of z-premice
![]() $\langle \mathcal {M}_\xi : \xi \in On\rangle $
inductively as follows:
$\langle \mathcal {M}_\xi : \xi \in On\rangle $
inductively as follows:
-
1.
 $\mathcal {M}_0 = (V_\omega ,\in ,\emptyset ,\emptyset ,z).$
$\mathcal {M}_0 = (V_\omega ,\in ,\emptyset ,\emptyset ,z).$
-
2. Suppose we have constructed
 $\mathcal {M}_\xi = (J_\alpha ^{\vec {E}},\in ,\vec {E},\emptyset ,z)$
. Note that
$\mathcal {M}_\xi = (J_\alpha ^{\vec {E}},\in ,\vec {E},\emptyset ,z)$
. Note that
 $\mathcal {M}_\xi $
is a passive premouse. Suppose also there is an extender
$\mathcal {M}_\xi $
is a passive premouse. Suppose also there is an extender
 $F^*$
over V, an extender F over
$F^*$
over V, an extender F over
 $\mathcal {M}_\xi $
, and
$\mathcal {M}_\xi $
, and
 $\nu <\alpha $
such that
$\nu <\alpha $
such that-
(a)
 $V_{\nu +\omega } \subset Ult(V,F^*)$
,
$V_{\nu +\omega } \subset Ult(V,F^*)$
, -
(b)
 $\nu $
is the support of F,
$\nu $
is the support of F, -
(c)
 $F\upharpoonright \nu = F^*\cap ([\nu ]^{<\omega } \times \mathcal {M}_\xi )$
, and
$F\upharpoonright \nu = F^*\cap ([\nu ]^{<\omega } \times \mathcal {M}_\xi )$
, and -
(d)
 $\mathcal {N}_{\xi +1} = (J_\alpha ^{\vec {E}},\in ,\vec {E},F,z)$
is a premouse.
$\mathcal {N}_{\xi +1} = (J_\alpha ^{\vec {E}},\in ,\vec {E},F,z)$
is a premouse.
If
 $\mathcal {N}_{\xi +1}$
is reliable, let
$\mathcal {N}_{\xi +1}$
is reliable, let
 $\mathcal {M}_{\xi +1} = \mathcal {C}_\omega (\mathcal {N}_{\xi +1})$
. Otherwise, the construction ends. If there are multiple such
$\mathcal {M}_{\xi +1} = \mathcal {C}_\omega (\mathcal {N}_{\xi +1})$
. Otherwise, the construction ends. If there are multiple such
 $F^*$
, we pick one which minimizes the support of F. We say
$F^*$
, we pick one which minimizes the support of F. We say
 $F^*$
is the extender used as a background at step
$F^*$
is the extender used as a background at step
 $\xi +1$
.
$\xi +1$
. -
-
3. Suppose we have constructed
 $\mathcal {M}_\xi = (J_\alpha ^{\vec {E}},\in ,\vec {E},E_\alpha ,z)$
and either
$\mathcal {M}_\xi = (J_\alpha ^{\vec {E}},\in ,\vec {E},E_\alpha ,z)$
and either
 $\mathcal {M}_\xi $
is active or
$\mathcal {M}_\xi $
is active or
 $\mathcal {M}_\xi $
is passive and there is no extender
$\mathcal {M}_\xi $
is passive and there is no extender
 $F^*$
as above. Let
$F^*$
as above. Let
 $\mathcal {N}_{\xi +1} = (J_{\alpha +1}^{\vec {E}^\frown E_\alpha }, \in ,\vec {E}^\frown E_\alpha ,\emptyset ,z)$
. If
$\mathcal {N}_{\xi +1} = (J_{\alpha +1}^{\vec {E}^\frown E_\alpha }, \in ,\vec {E}^\frown E_\alpha ,\emptyset ,z)$
. If
 $\mathcal {N}_{\xi +1}$
is reliable, let
$\mathcal {N}_{\xi +1}$
is reliable, let
 $\mathcal {M}_{\xi +1} = \mathcal {C}_\omega (\mathcal {N}_{\xi +1})$
. Otherwise, the construction ends.
$\mathcal {M}_{\xi +1} = \mathcal {C}_\omega (\mathcal {N}_{\xi +1})$
. Otherwise, the construction ends. -
4. Suppose we have constructed
 $\langle \mathcal {M}_\xi : \xi < \lambda \rangle $
for
$\langle \mathcal {M}_\xi : \xi < \lambda \rangle $
for
 $\lambda $
a limit ordinal. Let
$\lambda $
a limit ordinal. Let
 $\eta = lim\,inf_{\xi < \lambda } (\rho _\omega (\mathcal {M}_\xi )^+)^{\mathcal {M}_\xi }$
. Let
$\eta = lim\,inf_{\xi < \lambda } (\rho _\omega (\mathcal {M}_\xi )^+)^{\mathcal {M}_\xi }$
. Let
 $\mathcal {N}_\lambda $
be the passive premouse of height
$\mathcal {N}_\lambda $
be the passive premouse of height
 $\eta $
such that
$\eta $
such that
 $\mathcal {N}_\lambda |\beta = lim_{\xi <\lambda }\, \mathcal {M}_\xi |\beta $
for all
$\mathcal {N}_\lambda |\beta = lim_{\xi <\lambda }\, \mathcal {M}_\xi |\beta $
for all
 $\beta < \eta $
. If
$\beta < \eta $
. If
 $\mathcal {N}_\lambda $
is reliable, let
$\mathcal {N}_\lambda $
is reliable, let
 $\mathcal {M}_\lambda = \mathcal {C}_\omega (\mathcal {N}_\lambda )$
. Otherwise, the construction ends.
$\mathcal {M}_\lambda = \mathcal {C}_\omega (\mathcal {N}_\lambda )$
. Otherwise, the construction ends.
Suppose the construction never breaks down. That is,
![]() $\mathcal {M}_\xi $
is defined for all
$\mathcal {M}_\xi $
is defined for all
![]() $\xi \in On$
.
$\xi \in On$
.
Theorem 2.19. Suppose
![]() $\zeta _0$
and
$\zeta _0$
and
![]() $\xi $
are ordinals such that
$\xi $
are ordinals such that
![]() $\zeta _0 < \xi $
and
$\zeta _0 < \xi $
and
![]() $\kappa = \rho _\omega (\mathcal {M}_\xi ) \leq \rho _\omega (\mathcal {M}_\zeta )$
for all
$\kappa = \rho _\omega (\mathcal {M}_\xi ) \leq \rho _\omega (\mathcal {M}_\zeta )$
for all
![]() $\zeta \geq \zeta _0$
. Then
$\zeta \geq \zeta _0$
. Then
![]() $\mathcal {M}_\xi \trianglelefteq \mathcal {M}_\eta $
for all
$\mathcal {M}_\xi \trianglelefteq \mathcal {M}_\eta $
for all
![]() $\eta \geq \xi $
. Moreover,
$\eta \geq \xi $
. Moreover,
![]() $\mathcal {M}_{\xi +1} \models $
“every set has cardinality at most
$\mathcal {M}_{\xi +1} \models $
“every set has cardinality at most
![]() $\kappa $
.”
$\kappa $
.”
Let
![]() $\mathcal {M}$
be the class-sized model such that whenever
$\mathcal {M}$
be the class-sized model such that whenever
![]() $\xi \in On$
satisfies
$\xi \in On$
satisfies
![]() $\mathcal {M}_\xi \trianglelefteq \mathcal {M}_\eta $
for all
$\mathcal {M}_\xi \trianglelefteq \mathcal {M}_\eta $
for all
![]() $\eta \geq \xi $
,
$\eta \geq \xi $
,
![]() $\mathcal {M}_\xi $
is an initial segment of
$\mathcal {M}_\xi $
is an initial segment of
![]() $\mathcal {M}$
. We call
$\mathcal {M}$
. We call
![]() $\mathcal {M}$
the output of the Mitchell–Steel construction over z. For
$\mathcal {M}$
the output of the Mitchell–Steel construction over z. For
![]() $\delta \in On$
, we call
$\delta \in On$
, we call
![]() $\mathcal {M}_\delta $
the output of the Mitchell–Steel construction of length
$\mathcal {M}_\delta $
the output of the Mitchell–Steel construction of length
![]() $\delta $
over z.
$\delta $
over z.
Theorem 2.20. Assume
![]() $ZFC$
. Suppose
$ZFC$
. Suppose
![]() $\delta $
is the least ordinal such that
$\delta $
is the least ordinal such that
![]() $\delta $
is Woodin in
$\delta $
is Woodin in
![]() $L(V_\delta )$
. Suppose the Mitchell–Steel construction in
$L(V_\delta )$
. Suppose the Mitchell–Steel construction in
![]() $V_\delta $
does not break down, and let
$V_\delta $
does not break down, and let
![]() $\mathcal {M}$
be the output of the construction. Then
$\mathcal {M}$
be the output of the construction. Then
![]() $\delta $
in Woodin in
$\delta $
in Woodin in
![]() $L(\mathcal {M})$
.
$L(\mathcal {M})$
.
See the proof of Theorem 11.3 of [Reference Mitchell and Steel7].
Theorem 2.21 (Universality).
Assume
![]() $ZFC$
. Let
$ZFC$
. Let
![]() $\delta $
be Woodin and
$\delta $
be Woodin and
![]() $z\in \mathbb {R}$
. Assume the Mitchell–Steel construction of length
$z\in \mathbb {R}$
. Assume the Mitchell–Steel construction of length
![]() $\delta $
over z does not break down. Let N be the output of the construction. Suppose no initial segment of N satisfies “there is a superstrong cardinal.” Let W be a premouse over x of height
$\delta $
over z does not break down. Let N be the output of the construction. Suppose no initial segment of N satisfies “there is a superstrong cardinal.” Let W be a premouse over x of height
![]() $\leq \delta $
, and suppose P and Q are the final models above W and N, respectively, in a successful coiteration. Then
$\leq \delta $
, and suppose P and Q are the final models above W and N, respectively, in a successful coiteration. Then
![]() $P\trianglelefteq Q$
.
$P\trianglelefteq Q$
.
See Theorem 11.1 of [Reference Steel18].
Theorem 2.22. Suppose M is an
![]() $\omega _1+1$
-iterable mouse with Woodin cardinal
$\omega _1+1$
-iterable mouse with Woodin cardinal
![]() $\delta $
satisfying enough of
$\delta $
satisfying enough of
![]() $ZFC$
and
$ZFC$
and
![]() $z\in M\cap \mathbb {R}$
. Then the Mitchell–Steel construction of length
$z\in M\cap \mathbb {R}$
. Then the Mitchell–Steel construction of length
![]() $\delta $
over z done inside M does not break down. Let N be the output of the construction. Then N is a z-mouse of height
$\delta $
over z done inside M does not break down. Let N be the output of the construction. Then N is a z-mouse of height
![]() $\delta $
.
$\delta $
.
The proof of Theorem 2.22 is well known. To show the construction does not break down, by [Reference Mitchell and Steel7] it suffices to show universality and solidity of the models
![]() $\langle \mathcal {M}_\xi : \xi < \delta \rangle $
built during the construction. Mitchell and Steel [Reference Mitchell and Steel7] further reduce this to showing iterability for each
$\langle \mathcal {M}_\xi : \xi < \delta \rangle $
built during the construction. Mitchell and Steel [Reference Mitchell and Steel7] further reduce this to showing iterability for each
![]() $\mathcal {M}_\xi $
. An iteration strategy for
$\mathcal {M}_\xi $
. An iteration strategy for
![]() $M_\xi $
can be defined by lifting iteration trees on
$M_\xi $
can be defined by lifting iteration trees on
![]() $\mathcal {M}_\xi $
to trees on (an initial segment of) M and selecting the branch picked by the strategy for M.
$\mathcal {M}_\xi $
to trees on (an initial segment of) M and selecting the branch picked by the strategy for M.
![]() $\omega _1+1$
-iterability of M suffices to obtain the required iterability for each
$\omega _1+1$
-iterability of M suffices to obtain the required iterability for each
![]() $\mathcal {M}_\xi $
. Similarly, N being a z-mouse follows from iterability of M.
$\mathcal {M}_\xi $
. Similarly, N being a z-mouse follows from iterability of M.
For a premouse M satisfying enough of
![]() $ZFC$
and
$ZFC$
and
![]() $z\in M\cap \mathbb {R}$
, we write
$z\in M\cap \mathbb {R}$
, we write
![]() $Le[M,z]$
for the output of the Mitchell–Steel construction in M over z (assuming the construction does not break down).
$Le[M,z]$
for the output of the Mitchell–Steel construction in M over z (assuming the construction does not break down).
![]() $Le[M]$
will refer to
$Le[M]$
will refer to
![]() $Le[M,\emptyset ]$
.
$Le[M,\emptyset ]$
.
![]() $Le[M,z]$
is a z-premouse. If M is iterable, so is
$Le[M,z]$
is a z-premouse. If M is iterable, so is
![]() $Le[M,z]$
.
$Le[M,z]$
.
We are most interested in cases in which M is a mouse with a Woodin cardinal
![]() $\delta $
, no largest cardinal, and no total extenders above
$\delta $
, no largest cardinal, and no total extenders above
![]() $\delta $
. Then
$\delta $
. Then
![]() $Le[M|\delta ,z]$
is equal to the Mitchell–Steel construction of length
$Le[M|\delta ,z]$
is equal to the Mitchell–Steel construction of length
![]() $\delta $
over z, done inside M, and
$\delta $
over z, done inside M, and
![]() $Le[M,z]$
is an initial segment of
$Le[M,z]$
is an initial segment of
![]() $L(Le[M|\delta .z])$
.
$L(Le[M|\delta .z])$
.
Remark 2.23. Suppose M is an
![]() $\omega _1+1$
-iterable premouse,
$\omega _1+1$
-iterable premouse,
![]() $z\in M\cap \mathbb {R}$
, and
$z\in M\cap \mathbb {R}$
, and
![]() $\kappa $
is inaccessible in M. Let
$\kappa $
is inaccessible in M. Let
![]() $\langle \mathcal {M}_\xi : \xi < \kappa \rangle $
be the models of the Mitchell–Steel construction in M of length
$\langle \mathcal {M}_\xi : \xi < \kappa \rangle $
be the models of the Mitchell–Steel construction in M of length
![]() $\kappa $
over z. Suppose an extender is added at step
$\kappa $
over z. Suppose an extender is added at step
![]() $\xi +1$
in the construction. Let
$\xi +1$
in the construction. Let
![]() $F^*$
, F, and
$F^*$
, F, and
![]() $\nu $
be as in Case 2 of the construction. Then there is
$\nu $
be as in Case 2 of the construction. Then there is
![]() $F'\in M|\kappa $
such that
$F'\in M|\kappa $
such that
![]() $M\models V_{\nu +\omega }\subset Ult(M,F')$
and
$M\models V_{\nu +\omega }\subset Ult(M,F')$
and
![]() $F'\cap ([\nu ]^{<\omega } \times \mathcal {M}_\xi ) = F\upharpoonright \nu $
. So we may assume if
$F'\cap ([\nu ]^{<\omega } \times \mathcal {M}_\xi ) = F\upharpoonright \nu $
. So we may assume if
![]() $F^*$
is used as a background in the construction of length
$F^*$
is used as a background in the construction of length
![]() $\kappa $
, then
$\kappa $
, then
![]() $F^*\in M|\kappa $
.
$F^*\in M|\kappa $
.
In particular, if M is an
![]() $\omega _1+1$
-iterable premouse,
$\omega _1+1$
-iterable premouse,
![]() $z\in M\cap \mathbb {R}$
, and
$z\in M\cap \mathbb {R}$
, and
![]() $\kappa $
is inaccessible in M, then
$\kappa $
is inaccessible in M, then
![]() $Le[M|\kappa ,z]$
equals the Mitchell–Steel construction of length
$Le[M|\kappa ,z]$
equals the Mitchell–Steel construction of length
![]() $\kappa $
over z, done in M.
$\kappa $
over z, done in M.
2.4 S-constructions
Below we outline the S-construction (this was introduced as the P-construction in [Reference Schindler and Steel12]).
Suppose
![]() $M = (J_\gamma ^{\vec {E}},\in ,\vec {E}\upharpoonright \gamma ,E_\gamma ,a)$
is a countable a-premouse and
$M = (J_\gamma ^{\vec {E}},\in ,\vec {E}\upharpoonright \gamma ,E_\gamma ,a)$
is a countable a-premouse and
![]() $\delta \in M$
is a cardinal and cutpoint of M. Suppose
$\delta \in M$
is a cardinal and cutpoint of M. Suppose
![]() $ON \cap \bar {S} = \delta + \omega $
,
$ON \cap \bar {S} = \delta + \omega $
,
![]() $\delta $
is a Woodin cardinal of
$\delta $
is a Woodin cardinal of
![]() $\bar {S}$
,
$\bar {S}$
,
![]() $\bar {S}$
is definable over M, and there is a generic G (for the version of Woodin’s extender algebra with
$\bar {S}$
is definable over M, and there is a generic G (for the version of Woodin’s extender algebra with
![]() $\delta $
propositional letters) such that
$\delta $
propositional letters) such that
![]() $\bar {S}[G] = M|\delta +1$
. Inductively define a sequence
$\bar {S}[G] = M|\delta +1$
. Inductively define a sequence
![]() $\langle S_\alpha : \delta + 1 \leq \alpha \leq \gamma \rangle $
as follows.
$\langle S_\alpha : \delta + 1 \leq \alpha \leq \gamma \rangle $
as follows.
![]() $S_{\delta +1}$
is set to be
$S_{\delta +1}$
is set to be
![]() $\bar {S}$
. At a limit
$\bar {S}$
. At a limit
![]() $\lambda $
,
$\lambda $
,
![]() $S_\lambda = \bigcup _{\alpha < \lambda } S_\alpha $
. If
$S_\lambda = \bigcup _{\alpha < \lambda } S_\alpha $
. If
![]() $M|\lambda $
is active, add a predicate for
$M|\lambda $
is active, add a predicate for
![]() $E_{\lambda } \cap S_\lambda $
to
$E_{\lambda } \cap S_\lambda $
to
![]() $S_\lambda $
. For the successor step, we define
$S_\lambda $
. For the successor step, we define
![]() $S_{\alpha + 1}$
by constructing one more level over
$S_{\alpha + 1}$
by constructing one more level over
![]() $S_\alpha $
. The construction proceeds until we construct
$S_\alpha $
. The construction proceeds until we construct
![]() $S_\gamma $
, or we reach some
$S_\gamma $
, or we reach some
![]() $S_\alpha $
such that
$S_\alpha $
such that
![]() $\delta $
is not Woodin in
$\delta $
is not Woodin in
![]() $S_\alpha $
. We refer to
$S_\alpha $
. We refer to
![]() $S_\gamma $
as the maximal S-construction in M over
$S_\gamma $
as the maximal S-construction in M over
![]() $\bar {S}$
if the construction reaches
$\bar {S}$
if the construction reaches
![]() $\gamma $
. We are primarily interested in cases where
$\gamma $
. We are primarily interested in cases where
![]() $\delta $
is Woodin in M, in which case the construction is guaranteed to reach
$\delta $
is Woodin in M, in which case the construction is guaranteed to reach
![]() $\gamma $
.
$\gamma $
.
Lemma 2.24. Suppose
![]() $M,\bar {S},\delta ,\gamma ,$
and G are as above. Assume also M is
$M,\bar {S},\delta ,\gamma ,$
and G are as above. Assume also M is
![]() $(\omega _1,\omega _1+1)$
-iterable,
$(\omega _1,\omega _1+1)$
-iterable,
![]() $\omega $
-sound, and
$\omega $
-sound, and
![]() $\rho _\omega (M)\geq \delta $
. If the construction reaches
$\rho _\omega (M)\geq \delta $
. If the construction reaches
![]() $\gamma $
, then for each
$\gamma $
, then for each
![]() $\alpha $
such that
$\alpha $
such that
![]() $\delta +1\leq \alpha \leq \gamma $
,
$\delta +1\leq \alpha \leq \gamma $
,
![]() $S_\alpha $
is an
$S_\alpha $
is an
![]() $\bar {S}$
-mouse and
$\bar {S}$
-mouse and
![]() $S_\alpha [G] = M|\alpha $
. If also
$S_\alpha [G] = M|\alpha $
. If also
![]() $\alpha < \gamma $
, or
$\alpha < \gamma $
, or
![]() $\alpha = \gamma $
and
$\alpha = \gamma $
and
![]() $\delta $
is definably Woodin over
$\delta $
is definably Woodin over
![]() $S_\alpha $
, then
$S_\alpha $
, then
![]() $\rho _n(S_\alpha ) = \rho _n(M|\alpha )$
for all n and
$\rho _n(S_\alpha ) = \rho _n(M|\alpha )$
for all n and
![]() $S_\alpha $
is
$S_\alpha $
is
![]() $\omega $
-sound.
$\omega $
-sound.
Lemma 1.5 of [Reference Schindler and Steel12] gives everything in Lemma 2.24 except the iterability of
![]() $S_\gamma $
. The iteration strategy for
$S_\gamma $
. The iteration strategy for
![]() $S_\gamma $
in Lemma 2.24 comes from lifting an iteration tree on
$S_\gamma $
in Lemma 2.24 comes from lifting an iteration tree on
![]() $S_\gamma $
to iteration trees on M above
$S_\gamma $
to iteration trees on M above
![]() $\delta $
. In particular, we have the following fact.
$\delta $
. In particular, we have the following fact.
Fact 2.25. Suppose
![]() $M,\bar {S},\delta ,\gamma ,$
and G are as in Lemma 2.24. Then the iteration strategy for
$M,\bar {S},\delta ,\gamma ,$
and G are as in Lemma 2.24. Then the iteration strategy for
![]() $S_\gamma $
(as an
$S_\gamma $
(as an
![]() $\bar {S}$
-premouse) is projective in the iteration strategy for M restricted to iteration trees above
$\bar {S}$
-premouse) is projective in the iteration strategy for M restricted to iteration trees above
![]() $\delta $
.
$\delta $
.
The S-construction serves two purposes in what follows. It allows us to “undo” generic extensions from Woodin’s extender algebra. And combined with the fully-backgrounded Mitchell–Steel construction, it provides an inner model of a premouse with convenient properties.
Definition 2.26. Let M be an
![]() $\omega _1+1$
-iterable premouse with a Woodin cardinal and
$\omega _1+1$
-iterable premouse with a Woodin cardinal and
![]() $z\in M \cap \mathbb {R}$
. Let
$z\in M \cap \mathbb {R}$
. Let
![]() $\bar {S}$
be the result of constructing one level of the
$\bar {S}$
be the result of constructing one level of the
![]() $\mathcal {J}$
-hierarchy over
$\mathcal {J}$
-hierarchy over
![]() $Le[M|\delta _M,z]$
. Let
$Le[M|\delta _M,z]$
. Let
![]() $StrLe[M,z]$
denote the maximal S-construction in M over
$StrLe[M,z]$
denote the maximal S-construction in M over
![]() $\bar {S}$
.
$\bar {S}$
.
2.5 Suitable mice
We now review some results from the core model induction. Most of the concepts below are from [Reference Schindler and Steel13], with some minor additions. We need to work with mice with an inaccessible cardinal above a Woodin, so in Definition 2.28 we introduce a modification of the standard notion of a suitable premouse. Schindler and Steel [Reference Schindler and Steel13] prove the existence of terms in suitable mice capturing certain sets of reals. We will need analogous lemmas for our modified definition. In fact we require more than is stated in [Reference Schindler and Steel13]—it is essential for our purposes that there is a canonical term capturing each set. Fortunately, this stronger claim is already implicit in the proofs of [Reference Schindler and Steel13].
For the remainder of this section, we will assume
![]() $ZF + AD + DC + V=L(\mathbb {R})$
and fix a boldface inductive-like pointclass
$ZF + AD + DC + V=L(\mathbb {R})$
and fix a boldface inductive-like pointclass
![]() $\boldsymbol {\Gamma }$
such that
$\boldsymbol {\Gamma }$
such that
![]() $\boldsymbol {\Gamma }\neq \boldsymbol {\Sigma ^2_1}$
. We then have
$\boldsymbol {\Gamma }\neq \boldsymbol {\Sigma ^2_1}$
. We then have
![]() $\boldsymbol {\Gamma } = \boldsymbol {\Sigma _1}(J_{\alpha _0}(\mathbb {R}))$
for some
$\boldsymbol {\Gamma } = \boldsymbol {\Sigma _1}(J_{\alpha _0}(\mathbb {R}))$
for some
![]() $\alpha _0$
beginning an admissible
$\alpha _0$
beginning an admissible
![]() $\Sigma _1$
-gap
$\Sigma _1$
-gap
![]() $[\alpha _0,\beta _0]$
. Fix a lightface pointclass
$[\alpha _0,\beta _0]$
. Fix a lightface pointclass
![]() $\Gamma $
as in Remark 2.5 such that
$\Gamma $
as in Remark 2.5 such that
![]() $\boldsymbol {\Gamma }$
is the closure of
$\boldsymbol {\Gamma }$
is the closure of
![]() $\Gamma $
under preimages by continuous functions.
$\Gamma $
under preimages by continuous functions.
Definition 2.27. Suppose
![]() $x\in HC$
. Say an x-premouse N is
$x\in HC$
. Say an x-premouse N is
![]() $\Gamma $
-suitable if N is countable and
$\Gamma $
-suitable if N is countable and
-
1.
 $N \models $
there is exactly one Woodin cardinal
$N \models $
there is exactly one Woodin cardinal
 $\delta _N$
.
$\delta _N$
. -
2. Letting
 $N_0 = Lp^\Gamma (N|\delta _N)$
and
$N_0 = Lp^\Gamma (N|\delta _N)$
and
 $N_{i+1} = Lp^\Gamma (N_i)$
, we have that
$N_{i+1} = Lp^\Gamma (N_i)$
, we have that
 $N = \bigcup _{i<\omega } N_i$
.
$N = \bigcup _{i<\omega } N_i$
. -
3. If
 $\xi < \delta _N$
, then
$\xi < \delta _N$
, then
 $Lp^\Gamma (N|\xi ) \models \xi $
is not Woodin.
$Lp^\Gamma (N|\xi ) \models \xi $
is not Woodin.
Definition 2.28. Suppose
![]() $x\in HC$
. Say an x-premouse N is
$x\in HC$
. Say an x-premouse N is
![]() $\Gamma $
-super-suitable (
$\Gamma $
-super-suitable (
![]() $\Gamma $
-ss) if N is countable and
$\Gamma $
-ss) if N is countable and
-
1.
 $N \models $
There is exactly one Woodin cardinal
$N \models $
There is exactly one Woodin cardinal
 $\delta _N$
.
$\delta _N$
. -
2.
 $N \models $
There is exactly one inaccessible cardinal above
$N \models $
There is exactly one inaccessible cardinal above
 $\delta _N$
. We denote this inaccessible by
$\delta _N$
. We denote this inaccessible by
 $\nu _N$
.
$\nu _N$
. -
3. Letting
 $N_0 = Lp^\Gamma (N|\nu _N)$
and
$N_0 = Lp^\Gamma (N|\nu _N)$
and
 $N_{i+1} = Lp^\Gamma (N_i)$
, we have that
$N_{i+1} = Lp^\Gamma (N_i)$
, we have that
 $N = \bigcup _{i<\omega } N_i$
.
$N = \bigcup _{i<\omega } N_i$
. -
4. For each
 $\xi \geq \delta _N$
,
$\xi \geq \delta _N$
,
 $N|(\xi ^+)^N = Lp^\Gamma (N|\xi )$
.
$N|(\xi ^+)^N = Lp^\Gamma (N|\xi )$
. -
5. If
 $\xi < \delta _N$
, then
$\xi < \delta _N$
, then
 $Lp^\Gamma (N|\xi ) \models \xi $
is not Woodin.
$Lp^\Gamma (N|\xi ) \models \xi $
is not Woodin.
Definition 2.29. Let N be a mouse and
![]() $\delta \in N$
. We say
$\delta \in N$
. We say
![]() $\delta $
is a
$\delta $
is a
![]() $\Gamma $
-Woodin of N if
$\Gamma $
-Woodin of N if
![]() $\delta $
is Woodin in
$\delta $
is Woodin in
![]() $Lp^\Gamma (N|\delta )$
.
$Lp^\Gamma (N|\delta )$
.
A
![]() $\Gamma $
-suitable premouse is a minimal premouse with a
$\Gamma $
-suitable premouse is a minimal premouse with a
![]() $\Gamma $
-Woodin cardinal which is closed under
$\Gamma $
-Woodin cardinal which is closed under
![]() $Lp^{\Gamma }$
, in that none of its initial segments have this property. Similarly, a
$Lp^{\Gamma }$
, in that none of its initial segments have this property. Similarly, a
![]() $\Gamma $
-ss premouse can be considered a minimal premouse with a
$\Gamma $
-ss premouse can be considered a minimal premouse with a
![]() $\Gamma $
-Woodin which is closed under
$\Gamma $
-Woodin which is closed under
![]() $Lp^\Gamma $
and has an inaccessible cardinal above its
$Lp^\Gamma $
and has an inaccessible cardinal above its
![]() $\Gamma $
-Woodin. The existence of a
$\Gamma $
-Woodin. The existence of a
![]() $\Gamma $
-suitable (or
$\Gamma $
-suitable (or
![]() $\Gamma $
-ss) premouse is not any stronger than the existence of a premouse with a
$\Gamma $
-ss) premouse is not any stronger than the existence of a premouse with a
![]() $\Gamma $
-Woodin cardinal. For suppose
$\Gamma $
-Woodin cardinal. For suppose
![]() $N = Lp^{\Gamma }(N|\delta )$
,
$N = Lp^{\Gamma }(N|\delta )$
,
![]() $\delta $
is Woodin in N, and no
$\delta $
is Woodin in N, and no
![]() $\xi < \delta $
is a
$\xi < \delta $
is a
![]() $\Gamma $
-Woodin of N. If
$\Gamma $
-Woodin of N. If
![]() $Q \triangleright N$
,
$Q \triangleright N$
,
![]() $\rho (Q) \leq \delta $
, Q is
$\rho (Q) \leq \delta $
, Q is
![]() $\delta $
-sound, and a set definable over Q witnesses that
$\delta $
-sound, and a set definable over Q witnesses that
![]() $\delta $
is not Woodin, then Q must have a
$\delta $
is not Woodin, then Q must have a
![]() $\Gamma $
-Woodin cardinal above
$\Gamma $
-Woodin cardinal above
![]() $\delta $
. Otherwise, Q would be iterable by Q-structures in
$\delta $
. Otherwise, Q would be iterable by Q-structures in
![]() $\boldsymbol {\Delta _\Gamma }$
and hence in
$\boldsymbol {\Delta _\Gamma }$
and hence in
![]() $Lp^\Gamma (N|\delta )$
. Then we may build a
$Lp^\Gamma (N|\delta )$
. Then we may build a
![]() $\Gamma $
-suitable (
$\Gamma $
-suitable (
![]() $\Gamma $
-ss) premouse by closing under
$\Gamma $
-ss) premouse by closing under
![]() $Lp^\Gamma $
as many times as is necessary, since this will never construct a
$Lp^\Gamma $
as many times as is necessary, since this will never construct a
![]() $\Gamma $
-Woodin.
$\Gamma $
-Woodin.
Definition 2.30. Let
![]() $A \subseteq \mathbb {R}$
, N a countable premouse,
$A \subseteq \mathbb {R}$
, N a countable premouse,
![]() $\eta $
an uncountable cardinal of N, and
$\eta $
an uncountable cardinal of N, and
![]() $\tau \in N^{Col(\omega ,\eta )}$
. We say that
$\tau \in N^{Col(\omega ,\eta )}$
. We say that
![]() $\tau $
weakly captures A over N if whenever g is
$\tau $
weakly captures A over N if whenever g is
![]() $Col(\omega ,\eta )$
-generic over N,
$Col(\omega ,\eta )$
-generic over N,
![]() $\tau [g] = A \cap N[g]$
.
$\tau [g] = A \cap N[g]$
.
Lemma 2.31. Suppose
![]() $\mathcal {B}$
is a self-justifying system and N and M are transitive models of enough of ZFC such that
$\mathcal {B}$
is a self-justifying system and N and M are transitive models of enough of ZFC such that
![]() $N\in M$
. Let
$N\in M$
. Let
![]() $\mathcal {C}$
be a comeager set of
$\mathcal {C}$
be a comeager set of
![]() $Col(\omega ,N)$
generics over M and suppose for each
$Col(\omega ,N)$
generics over M and suppose for each
![]() $B\in \mathcal {B}$
there is a term
$B\in \mathcal {B}$
there is a term
![]() $\tau _B\in M$
such that if
$\tau _B\in M$
such that if
![]() $g\in \mathcal {C}$
, then
$g\in \mathcal {C}$
, then
![]() $\tau _B[g] = B \cap M[g]$
. Let
$\tau _B[g] = B \cap M[g]$
. Let
![]() $\pi : \bar {M} \to M$
be elementary with
$\pi : \bar {M} \to M$
be elementary with
![]() $\{N\} \cup \{\tau _B: B \in \mathcal {B}\}\subset ran(\pi )$
. Let
$\{N\} \cup \{\tau _B: B \in \mathcal {B}\}\subset ran(\pi )$
. Let
![]() $(N,\tau _B) = \pi (\bar {N},\bar {\tau }_B)$
. Then whenever g is
$(N,\tau _B) = \pi (\bar {N},\bar {\tau }_B)$
. Then whenever g is
![]() $Col(\omega ,\bar {N})$
-generic over
$Col(\omega ,\bar {N})$
-generic over
![]() $\bar {M}$
,
$\bar {M}$
,
![]() $\bar {\tau }_B[g] = B \cap \bar {M}[g]$
.
$\bar {\tau }_B[g] = B \cap \bar {M}[g]$
.
See Lemma 3.7.2 of [Reference Schindler and Steel13].
Let
![]() $\beta '$
be the least ordinal greater than
$\beta '$
be the least ordinal greater than
![]() $\alpha _0$
such that there is a scale for a universal
$\alpha _0$
such that there is a scale for a universal
![]() $\boldsymbol {\Pi _1}(J_{\alpha _0}(\mathbb {R}))$
set definable over
$\boldsymbol {\Pi _1}(J_{\alpha _0}(\mathbb {R}))$
set definable over
![]() $J_{\beta '}(\mathbb {R})$
. By Theorem 2.4,
$J_{\beta '}(\mathbb {R})$
. By Theorem 2.4,
![]() $\beta '= \beta _0$
or
$\beta '= \beta _0$
or
![]() $\beta '=\beta _0+1$
and there is a self-justifying system
$\beta '=\beta _0+1$
and there is a self-justifying system
![]() $\mathcal {G} = \{ G_n : n\in \omega \}$
such that
$\mathcal {G} = \{ G_n : n\in \omega \}$
such that
 $$ \begin{align*} G_0 = \{(x,y):\, & x \text{ codes some transitive set } a \text{ and } y \text{ codes an } \omega\text{-sound } \\ & a\text{-premouse } R \text{ such that } R \text{ projects to } a \text{ and } R \text{ has an } \\ & \omega_1\text{-iteration strategy in } \boldsymbol{\Delta}\}, \end{align*} $$
$$ \begin{align*} G_0 = \{(x,y):\, & x \text{ codes some transitive set } a \text{ and } y \text{ codes an } \omega\text{-sound } \\ & a\text{-premouse } R \text{ such that } R \text{ projects to } a \text{ and } R \text{ has an } \\ & \omega_1\text{-iteration strategy in } \boldsymbol{\Delta}\}, \end{align*} $$
and
![]() $\mathcal {G}$
is contained in
$\mathcal {G}$
is contained in
![]() $OD^{<\beta '}(z)$
for some
$OD^{<\beta '}(z)$
for some
![]() $z\in \mathbb {R}$
. Note that
$z\in \mathbb {R}$
. Note that
![]() $G_0\in \boldsymbol {\Gamma }$
, by part 3 of Remark 2.5. In fact,
$G_0\in \boldsymbol {\Gamma }$
, by part 3 of Remark 2.5. In fact,
![]() $G_0$
is a universal
$G_0$
is a universal
![]() $\boldsymbol {\Gamma }$
-set (we will not need this property specifically for
$\boldsymbol {\Gamma }$
-set (we will not need this property specifically for
![]() $G_0$
, but we will use that
$G_0$
, but we will use that
![]() $\mathcal {G}$
contains some universal
$\mathcal {G}$
contains some universal
![]() $\boldsymbol {\Gamma }$
-set). For ease of notation, assume
$\boldsymbol {\Gamma }$
-set). For ease of notation, assume
![]() $\mathcal {G}\subset OD^{<\beta '}$
.
$\mathcal {G}\subset OD^{<\beta '}$
.
Definition 2.32. Suppose
![]() $B \subset \mathbb {R}$
, N is a premouse, and
$B \subset \mathbb {R}$
, N is a premouse, and
![]() $\eta $
is a cardinal of N. Let
$\eta $
is a cardinal of N. Let
![]() $\tau ^N_{B,\eta }$
be the set of pairs
$\tau ^N_{B,\eta }$
be the set of pairs
![]() $(\sigma ,p)\in N$
such that
$(\sigma ,p)\in N$
such that
-
1.
 $\sigma $
is a
$\sigma $
is a
 $Col(\omega ,\eta )$
-standard term for a real,
$Col(\omega ,\eta )$
-standard term for a real, -
2.
 $p\in Col(\omega ,\eta )$
, and
$p\in Col(\omega ,\eta )$
, and -
3. for comeager many
 $g\subset Col(\omega ,\eta )$
which are
$g\subset Col(\omega ,\eta )$
which are
 $Col(\omega ,\eta )$
-generic over N such that
$Col(\omega ,\eta )$
-generic over N such that
 $p\in g$
,
$p\in g$
,
 $\sigma [g]\in B$
.
$\sigma [g]\in B$
.
For
![]() $n\in \omega $
, let
$n\in \omega $
, let
![]() $\tau ^N_{n,\eta } = \tau ^N_{G_n,\eta }$
and if N has a Woodin cardinal let
$\tau ^N_{n,\eta } = \tau ^N_{G_n,\eta }$
and if N has a Woodin cardinal let
![]() $\tau ^N_n = \tau ^N_{n,\delta _N}$
.
$\tau ^N_n = \tau ^N_{n,\delta _N}$
.
Lemma 2.33. Suppose N is a
![]() $\Gamma $
-suitable or
$\Gamma $
-suitable or
![]() $\Gamma $
-ss premouse,
$\Gamma $
-ss premouse,
![]() $z\in N$
,
$z\in N$
,
![]() $B\in OD^{<\beta '}(z)$
, and
$B\in OD^{<\beta '}(z)$
, and
![]() $\eta $
is a cardinal of N. Then
$\eta $
is a cardinal of N. Then
![]() $\tau ^N_{B,\eta }$
is in N.
$\tau ^N_{B,\eta }$
is in N.
See the proof of Lemma 3.7.5 of [Reference Schindler and Steel13]. In Lemma 5.4.3 of [Reference Schindler and Steel13], Lemma 2.31 is used to show the following.
Lemma 2.34 (Woodin).
Suppose
![]() $z\in \mathbb {R}$
, N is a
$z\in \mathbb {R}$
, N is a
![]() $\Gamma $
-suitable (or
$\Gamma $
-suitable (or
![]() $\Gamma $
-ss) z-premouse, and
$\Gamma $
-ss) z-premouse, and
![]() $\mathcal {B}$
is a sjs containing a universal
$\mathcal {B}$
is a sjs containing a universal
![]() $\boldsymbol {\Sigma _1}(J_{\alpha _0}(\mathbb {R}))$
-set such that each
$\boldsymbol {\Sigma _1}(J_{\alpha _0}(\mathbb {R}))$
-set such that each
![]() $B\in \mathcal {B}$
is
$B\in \mathcal {B}$
is
![]() $OD^{<\beta '}(z)$
. Suppose
$OD^{<\beta '}(z)$
. Suppose
![]() $\pi :M\to N$
is
$\pi :M\to N$
is
![]() $\Sigma _1$
-elementary and for every
$\Sigma _1$
-elementary and for every
![]() $B\in \mathcal {B}$
and
$B\in \mathcal {B}$
and
![]() $\eta \geq \delta _N$
,
$\eta \geq \delta _N$
,
![]() $\tau ^N_{B,\eta }\in range(\pi )$
. Then
$\tau ^N_{B,\eta }\in range(\pi )$
. Then
-
1. M is
 $\Gamma $
-suitable (
$\Gamma $
-suitable (
 $\Gamma $
-ss) and
$\Gamma $
-ss) and -
2.
 $\pi (\tau ^M_{B,\bar {\eta }}) = \tau ^N_{B,\eta }$
, where
$\pi (\tau ^M_{B,\bar {\eta }}) = \tau ^N_{B,\eta }$
, where
 $\bar {\eta }$
is such that
$\bar {\eta }$
is such that
 $\pi (\bar {\eta }) = \eta $
.
$\pi (\bar {\eta }) = \eta $
.
As a result of Lemmas 2.31 and 2.33 we have the following.
Corollary 2.35. If N is
![]() $\Gamma $
-suitable or
$\Gamma $
-suitable or
![]() $\Gamma $
-ss and
$\Gamma $
-ss and
![]() $\eta $
is an uncountable cardinal of N, then
$\eta $
is an uncountable cardinal of N, then
![]() $\tau ^N_{n,\eta }$
weakly captures
$\tau ^N_{n,\eta }$
weakly captures
![]() $G_n$
.
$G_n$
.
Definition 2.36. Let
![]() $\mathcal {T}$
be a normal iteration tree on a
$\mathcal {T}$
be a normal iteration tree on a
![]() $\Gamma $
-suitable (or
$\Gamma $
-suitable (or
![]() $\Gamma $
-ss) premouse N. Suppose also
$\Gamma $
-ss) premouse N. Suppose also
![]() $\mathcal {T}$
is below
$\mathcal {T}$
is below
![]() $\delta _N$
. Say
$\delta _N$
. Say
![]() $\mathcal {T}$
is
$\mathcal {T}$
is
![]() $\Gamma $
-short if for all limit
$\Gamma $
-short if for all limit
![]() $\xi \leq lh(\mathcal {T})$
,
$\xi \leq lh(\mathcal {T})$
,
![]() $Lp^\Gamma (\mathcal {M}(\mathcal {T}\upharpoonright \xi ))\models \delta (\mathcal {T}\upharpoonright \xi )$
is not Woodin. Otherwise, say
$Lp^\Gamma (\mathcal {M}(\mathcal {T}\upharpoonright \xi ))\models \delta (\mathcal {T}\upharpoonright \xi )$
is not Woodin. Otherwise, say
![]() $\mathcal {T}$
is
$\mathcal {T}$
is
![]() $\Gamma $
-maximal.
$\Gamma $
-maximal.
Definition 2.37. Let N be a
![]() $\Gamma $
-suitable (
$\Gamma $
-suitable (
![]() $\Gamma $
-ss) premouse with an
$\Gamma $
-ss) premouse with an
![]() $(\omega _1,\omega _1)$
-iteration strategy
$(\omega _1,\omega _1)$
-iteration strategy
![]() $\Sigma $
. Say
$\Sigma $
. Say
![]() $\Sigma $
is fullness-preserving if whenever P is an iterate of N by
$\Sigma $
is fullness-preserving if whenever P is an iterate of N by
![]() $\Sigma $
via an iteration below
$\Sigma $
via an iteration below
![]() $\delta _N$
, then
$\delta _N$
, then
-
1. if the branch to P does not drop, then P is
 $\Gamma $
-suitable (
$\Gamma $
-suitable (
 $\Gamma $
-ss), and
$\Gamma $
-ss), and -
2. if the branch to P does drop, then P has an
 $\omega _1$
-iteration strategy in
$\omega _1$
-iteration strategy in
 $J_{\alpha _0}(\mathbb {R})$
.
$J_{\alpha _0}(\mathbb {R})$
.
Remark 2.38. Let N be a
![]() $\Gamma $
-suitable (or
$\Gamma $
-suitable (or
![]() $\Gamma $
-ss) mouse with a fullness-preserving iteration strategy
$\Gamma $
-ss) mouse with a fullness-preserving iteration strategy
![]() $\Sigma $
. Suppose
$\Sigma $
. Suppose
![]() $P\triangleleft N|\delta _N$
, and
$P\triangleleft N|\delta _N$
, and
![]() $\Sigma '$
is the iteration strategy for P given by restricting the domain of
$\Sigma '$
is the iteration strategy for P given by restricting the domain of
![]() $\Sigma $
to trees on P. Suppose
$\Sigma $
to trees on P. Suppose
![]() $\mathcal {T}$
is an iteration tree on P according to
$\mathcal {T}$
is an iteration tree on P according to
![]() $\Sigma '$
. Then the branch b through
$\Sigma '$
. Then the branch b through
![]() $\mathcal {T}$
chosen by
$\mathcal {T}$
chosen by
![]() $\Sigma '$
can be determined from
$\Sigma '$
can be determined from
![]() $\mathcal {Q}(\mathcal {T})$
. And
$\mathcal {Q}(\mathcal {T})$
. And
![]() $\mathcal {Q}(\mathcal {T})$
is the unique
$\mathcal {Q}(\mathcal {T})$
is the unique
![]() $\mathcal {M}(\mathcal {T})$
-mouse projecting to
$\mathcal {M}(\mathcal {T})$
-mouse projecting to
![]() $\omega $
with an iteration strategy in
$\omega $
with an iteration strategy in
![]() $\boldsymbol {\Delta }$
. It follows from Remark 2.5 and the uniqueness of
$\boldsymbol {\Delta }$
. It follows from Remark 2.5 and the uniqueness of
![]() $\mathcal {Q}(\mathcal {T})$
that
$\mathcal {Q}(\mathcal {T})$
that
![]() $\Sigma '$
is coded by a set in
$\Sigma '$
is coded by a set in
![]() $\boldsymbol {\Delta }$
.
$\boldsymbol {\Delta }$
.
Definition 2.39. Let
![]() $\mathcal {T}$
be a
$\mathcal {T}$
be a
![]() $\Gamma $
-maximal iteration tree on a
$\Gamma $
-maximal iteration tree on a
![]() $\Gamma $
-suitable (or
$\Gamma $
-suitable (or
![]() $\Gamma $
-ss) premouse N and let b be a cofinal branch through
$\Gamma $
-ss) premouse N and let b be a cofinal branch through
![]() $\mathcal {T}$
. Say b respects
$\mathcal {T}$
. Say b respects
![]() $\vec {G}_n$
if
$\vec {G}_n$
if
![]() $i^{\mathcal {T}}_b(\tau ^N_{k,\eta }) = \tau ^{M^{\mathcal {T}}_b}_{k,i_b(\eta )}$
for all
$i^{\mathcal {T}}_b(\tau ^N_{k,\eta }) = \tau ^{M^{\mathcal {T}}_b}_{k,i_b(\eta )}$
for all
![]() $k < n$
and every cardinal
$k < n$
and every cardinal
![]() $\eta $
of N above
$\eta $
of N above
![]() $\delta _N$
.
$\delta _N$
.
Definition 2.40. Let N be a
![]() $\Gamma $
-suitable (or
$\Gamma $
-suitable (or
![]() $\Gamma $
-ss) mouse with a fullness-preserving iteration strategy
$\Gamma $
-ss) mouse with a fullness-preserving iteration strategy
![]() $\Sigma $
. Say
$\Sigma $
. Say
![]() $\Sigma $
is guided by
$\Sigma $
is guided by
![]() $\mathcal {G}$
if whenever
$\mathcal {G}$
if whenever
![]() $\mathcal {T}$
is an iteration tree according to
$\mathcal {T}$
is an iteration tree according to
![]() $\Sigma $
of limit length and
$\Sigma $
of limit length and
![]() $b = \Sigma (\mathcal {T})$
, then
$b = \Sigma (\mathcal {T})$
, then
-
1. if
 $\mathcal {T}$
is
$\mathcal {T}$
is
 $\Gamma $
-short, then
$\Gamma $
-short, then
 $\mathcal {Q}(b,\mathcal {T})$
exists and
$\mathcal {Q}(b,\mathcal {T})$
exists and
 $\mathcal {Q}(b,\mathcal {T}) \in Lp^\Gamma (\mathcal {M}(\mathcal {T}))$
, and
$\mathcal {Q}(b,\mathcal {T}) \in Lp^\Gamma (\mathcal {M}(\mathcal {T}))$
, and -
2. if T is
 $\Gamma $
-maximal, then
$\Gamma $
-maximal, then
 $\Sigma (b)$
respects
$\Sigma (b)$
respects
 $\vec {G}_n$
for all
$\vec {G}_n$
for all
 $n\in \omega $
.
$n\in \omega $
.
Lemma 2.41. If N is
![]() $\Gamma $
-suitable (or
$\Gamma $
-suitable (or
![]() $\Gamma $
-ss) and
$\Gamma $
-ss) and
![]() $\Sigma $
is an iteration strategy for N which is guided by
$\Sigma $
is an iteration strategy for N which is guided by
![]() $\mathcal {G}$
, then
$\mathcal {G}$
, then
![]() $\Sigma $
is not in
$\Sigma $
is not in
![]() $\boldsymbol {\Gamma }$
.
$\boldsymbol {\Gamma }$
.
Proof. There is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $G_n$
is a universal
$G_n$
is a universal
![]() $\boldsymbol {\Gamma ^c}$
-set. Then
$\boldsymbol {\Gamma ^c}$
-set. Then
![]() $y\in G_n$
if and only if there exists a countable, complete iterate
$y\in G_n$
if and only if there exists a countable, complete iterate
![]() $N^*$
of N according to
$N^*$
of N according to
![]() $\Sigma $
and
$\Sigma $
and
![]() $g\in \mathbb {R}$
which is
$g\in \mathbb {R}$
which is
![]() $Col(\omega ,\mathbb {R})$
-generic over
$Col(\omega ,\mathbb {R})$
-generic over
![]() $N^*$
such that
$N^*$
such that
![]() $y\in \tau ^{N^*}_n[g]$
. Since
$y\in \tau ^{N^*}_n[g]$
. Since
![]() $\boldsymbol {\Gamma }$
is closed under projection, if
$\boldsymbol {\Gamma }$
is closed under projection, if
![]() $\Sigma $
were in
$\Sigma $
were in
![]() $\boldsymbol {\Gamma }$
,
$\boldsymbol {\Gamma }$
,
![]() $G_n$
would also be in
$G_n$
would also be in
![]() $\boldsymbol {\Gamma }$
.
$\boldsymbol {\Gamma }$
.
Theorem 2.42 (Woodin).
For any
![]() $x\in HC$
, there is a (unique)
$x\in HC$
, there is a (unique)
![]() $\omega $
-sound,
$\omega $
-sound,
![]() $\Gamma $
-suitable x-mouse
$\Gamma $
-suitable x-mouse
![]() $W_x$
projecting to x with a (unique) iteration strategy that is fullness-preserving, condenses well,Footnote
4
and is guided by
$W_x$
projecting to x with a (unique) iteration strategy that is fullness-preserving, condenses well,Footnote
4
and is guided by
![]() $\mathcal {G}$
. Similarly, there is a (unique)
$\mathcal {G}$
. Similarly, there is a (unique)
![]() $\omega $
-sound,
$\omega $
-sound,
![]() $\Gamma $
-ss x-mouse
$\Gamma $
-ss x-mouse
![]() $M_x$
projecting to x with a (unique) iteration strategy that is fullness-preserving, condenses well, and is guided by
$M_x$
projecting to x with a (unique) iteration strategy that is fullness-preserving, condenses well, and is guided by
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Chapter 5 of [Reference Schindler and Steel13] demonstrates the existence of such a
![]() $\Gamma $
-suitable mouse. It is not difficult to see this gives the existence of the required
$\Gamma $
-suitable mouse. It is not difficult to see this gives the existence of the required
![]() $\Gamma $
-ss mouse as well.
$\Gamma $
-ss mouse as well.
For any
![]() $\Gamma $
-suitable (or
$\Gamma $
-suitable (or
![]() $\Gamma $
-ss) premouse N and any
$\Gamma $
-ss) premouse N and any
![]() $n\in \omega $
, let
$n\in \omega $
, let
The regularity of
![]() $\delta _N$
in N implies each
$\delta _N$
in N implies each
![]() $\gamma ^N_n$
is an ordinal. Lemma 2.34 can be used to show the following fact.
$\gamma ^N_n$
is an ordinal. Lemma 2.34 can be used to show the following fact.
Fact 2.43.
![]() $\langle \gamma ^N_n : n \in \omega \rangle $
is cofinal in
$\langle \gamma ^N_n : n \in \omega \rangle $
is cofinal in
![]() $\delta _N$
.
$\delta _N$
.
Lemma 2.44. Let
![]() $\mathcal {T}$
be a normal iteration tree on a
$\mathcal {T}$
be a normal iteration tree on a
![]() $\Gamma $
-suitable (or
$\Gamma $
-suitable (or
![]() $\Gamma $
-ss) premouse N and let b and c be branches through
$\Gamma $
-ss) premouse N and let b and c be branches through
![]() $\mathcal {T}$
which respect
$\mathcal {T}$
which respect
![]() $\vec {G}_n$
. Then
$\vec {G}_n$
. Then
![]() $i^{\mathcal {T}}_b\upharpoonright \gamma ^N_n = i^{\mathcal {T}}_c\upharpoonright \gamma ^N_n$
. Moreover, if b and c both respect
$i^{\mathcal {T}}_b\upharpoonright \gamma ^N_n = i^{\mathcal {T}}_c\upharpoonright \gamma ^N_n$
. Moreover, if b and c both respect
![]() $\vec {G}_n$
for all n, then
$\vec {G}_n$
for all n, then
![]() $b=c$
.
$b=c$
.
See Lemma 6.25 of [Reference Steel, Woodin, Kechris, Löwe and Steel21].
Lemma 2.44 implies if b is the branch through
![]() $\mathcal {T}$
chosen by the nice iteration strategy for a
$\mathcal {T}$
chosen by the nice iteration strategy for a
![]() $\Gamma $
-suitable premouse given by Theorem 2.42 and c is any branch respecting
$\Gamma $
-suitable premouse given by Theorem 2.42 and c is any branch respecting
![]() $\vec {G}_n$
, then
$\vec {G}_n$
, then
![]() $i^{\mathcal {T}}_b$
and
$i^{\mathcal {T}}_b$
and
![]() $i^{\mathcal {T}}_c$
agree up to
$i^{\mathcal {T}}_c$
agree up to
![]() $\gamma ^N_n$
. In particular, to track the iteration of a
$\gamma ^N_n$
. In particular, to track the iteration of a
![]() $\Gamma $
-suitable mouse up to some point below its least Woodin, it is sufficient to know finitely many of the sets in
$\Gamma $
-suitable mouse up to some point below its least Woodin, it is sufficient to know finitely many of the sets in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Suppose M is a countable premouse with an
![]() $(\omega _1,\omega _1+1)$
-iteration strategy.Footnote
5
Together, the Comparison Lemma and the Dodd–Jensen Lemma imply the collection of countable, complete iterates of M, together with the iteration maps between them, forms a directed system.
$(\omega _1,\omega _1+1)$
-iteration strategy.Footnote
5
Together, the Comparison Lemma and the Dodd–Jensen Lemma imply the collection of countable, complete iterates of M, together with the iteration maps between them, forms a directed system.
Steel [Reference Steel17] presents work of Steel and Woodin analyzing the direct limit of all countable, complete iterates of
![]() $M^\#_\omega $
. This direct limit cut to its least Woodin is
$M^\#_\omega $
. This direct limit cut to its least Woodin is
![]() $(HOD||\Theta )^{L(\mathbb {R})}$
. Steel and Woodin [Reference Steel, Woodin, Kechris, Löwe and Steel21] go further in showing that the entire class
$(HOD||\Theta )^{L(\mathbb {R})}$
. Steel and Woodin [Reference Steel, Woodin, Kechris, Löwe and Steel21] go further in showing that the entire class
![]() $HOD^{L(\mathbb {R})}$
is a strategy mouse. The iteration maps through trees on
$HOD^{L(\mathbb {R})}$
is a strategy mouse. The iteration maps through trees on
![]() $M^\#_\omega $
are approximated using indiscernibles, analogously to the use of terms in Lemma 2.44. These approximations are merged to give an ordinal definable definition of the direct limit in
$M^\#_\omega $
are approximated using indiscernibles, analogously to the use of terms in Lemma 2.44. These approximations are merged to give an ordinal definable definition of the direct limit in
![]() $L(\mathbb {R})$
. In particular, initial segments of the direct limit maps are definable from finitely many indiscernibles.
$L(\mathbb {R})$
. In particular, initial segments of the direct limit maps are definable from finitely many indiscernibles.
In place of
![]() $M^\#_\omega $
, we shall analyze the direct limit of a
$M^\#_\omega $
, we shall analyze the direct limit of a
![]() $\Gamma $
-suitable mouse and prove that portions of the direct limit maps are definable within a
$\Gamma $
-suitable mouse and prove that portions of the direct limit maps are definable within a
![]() $\Gamma $
-ss mouse.
$\Gamma $
-ss mouse.
Our task is simpler in that we only need to reach up to
![]() $\boldsymbol {\delta _\Gamma ^+}$
, which we show in Section 3.1 is below the least Woodin of our direct limit. So a single approximation using only finitely many sets from
$\boldsymbol {\delta _\Gamma ^+}$
, which we show in Section 3.1 is below the least Woodin of our direct limit. So a single approximation using only finitely many sets from
![]() $\mathcal {G}$
will suffice. Another advantage we have is that there is no harm in working over a real parameter, so we can work in a
$\mathcal {G}$
will suffice. Another advantage we have is that there is no harm in working over a real parameter, so we can work in a
![]() $\Gamma $
-ss mouse over a real which codes
$\Gamma $
-ss mouse over a real which codes
![]() $W_0$
. On the other hand, we will have some extra work to do in Section 3.2 ensuring enough information about
$W_0$
. On the other hand, we will have some extra work to do in Section 3.2 ensuring enough information about
![]() $\Gamma $
and
$\Gamma $
and
![]() $\mathcal {G}$
is definable in a
$\mathcal {G}$
is definable in a
![]() $\Gamma $
-ss mouse before we internalize the directed system in Section 3.3.
$\Gamma $
-ss mouse before we internalize the directed system in Section 3.3.
Steel and Woodin [Reference Steel, Woodin, Kechris, Löwe and Steel21] also make use of the fact that the derived model of
![]() $M^\#_\omega $
is essentially
$M^\#_\omega $
is essentially
![]() $L(\mathbb {R})$
. So for
$L(\mathbb {R})$
. So for
![]() $x\in M^\#_\omega \cap \mathbb {R}$
, a
$x\in M^\#_\omega \cap \mathbb {R}$
, a
![]() $\Sigma ^2_1$
statement about x is true if and only if it holds in the derived model of
$\Sigma ^2_1$
statement about x is true if and only if it holds in the derived model of
![]() $M^\#_\omega $
. In particular, there is a natural way to ask about
$M^\#_\omega $
. In particular, there is a natural way to ask about
![]() $\Sigma ^2_1$
truth inside of
$\Sigma ^2_1$
truth inside of
![]() $M^\#_\omega $
. A second, though minor, inconvenience of having to use a
$M^\#_\omega $
. A second, though minor, inconvenience of having to use a
![]() $\Gamma $
-suitable mouse is we cannot talk about its derived model, since it only has one Woodin. Instead we will use the fine-structural witness condition of [Reference Schindler and Steel13].
$\Gamma $
-suitable mouse is we cannot talk about its derived model, since it only has one Woodin. Instead we will use the fine-structural witness condition of [Reference Schindler and Steel13].
Remark 2.45. We can associate to any
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\phi $
a sequence of formulas
$\phi $
a sequence of formulas
![]() $\langle \phi ^k:k<\omega \rangle $
such that for any ordinal
$\langle \phi ^k:k<\omega \rangle $
such that for any ordinal
![]() $\gamma $
and any real z,
$\gamma $
and any real z,
![]() $J_{\gamma +1}(\mathbb {R})\models \phi [z] \iff (\exists k) J_\gamma (\mathbb {R}) \models \phi ^k[z]$
. Moreover, the map
$J_{\gamma +1}(\mathbb {R})\models \phi [z] \iff (\exists k) J_\gamma (\mathbb {R}) \models \phi ^k[z]$
. Moreover, the map
![]() $\phi \to \langle \phi ^k:k<\omega \rangle $
is recursive.
$\phi \to \langle \phi ^k:k<\omega \rangle $
is recursive.
Definition 2.46. Suppose
![]() $\phi (v)$
is a
$\phi (v)$
is a
![]() $\Sigma _1$
-formula and
$\Sigma _1$
-formula and
![]() $z\in \mathbb {R}$
. A
$z\in \mathbb {R}$
. A
![]() $\langle \phi ,z\rangle $
-witness is an
$\langle \phi ,z\rangle $
-witness is an
![]() $\omega $
-sound z-mouse N in which there are
$\omega $
-sound z-mouse N in which there are
![]() $\delta _0 < \cdots < \delta _9$
,
$\delta _0 < \cdots < \delta _9$
,
![]() $\mathcal {S}$
, and
$\mathcal {S}$
, and
![]() $\mathcal {T}$
such that N satisfies the formulae expressing
$\mathcal {T}$
such that N satisfies the formulae expressing
-
1. ZFC,
-
2.
 $\delta _0 < \cdots < \delta _9$
are Woodin,
$\delta _0 < \cdots < \delta _9$
are Woodin, -
3.
 $\mathcal {S}$
and
$\mathcal {S}$
and
 $\mathcal {T}$
are trees on some
$\mathcal {T}$
are trees on some
 $\omega \times \eta $
which are absolutely complementing in
$\omega \times \eta $
which are absolutely complementing in
 $V^{Col(\omega ,\delta _9)}$
, and
$V^{Col(\omega ,\delta _9)}$
, and -
4. for some
 $k < \omega $
,
$k < \omega $
,
 $\rho [T]$
is the
$\rho [T]$
is the
 $\Sigma _{k+3}$
-theory (in the language with names for each real) of
$\Sigma _{k+3}$
-theory (in the language with names for each real) of
 $J_\gamma (\mathbb {R})$
, where
$J_\gamma (\mathbb {R})$
, where
 $\gamma $
is least such that
$\gamma $
is least such that
 $J_\gamma (\mathbb {R}) \models \phi ^k[z]$
.
$J_\gamma (\mathbb {R}) \models \phi ^k[z]$
.
Other than iterability, the rest of the properties of being a
![]() $\langle \phi ,z\rangle $
-witness are first order. The following two lemmas illustrate the usefulness of this definition.
$\langle \phi ,z\rangle $
-witness are first order. The following two lemmas illustrate the usefulness of this definition.
Lemma 2.47. If there is a
![]() $\langle \phi ,z\rangle $
-witness, then
$\langle \phi ,z\rangle $
-witness, then
![]() $L(\mathbb {R})\models \phi [z]$
.
$L(\mathbb {R})\models \phi [z]$
.
Lemma 2.48. Suppose
![]() $\phi $
is a
$\phi $
is a
![]() $\Sigma _1$
-formula,
$\Sigma _1$
-formula,
![]() $z\in \mathbb {R}$
,
$z\in \mathbb {R}$
,
![]() $\gamma $
is a limit ordinal, and
$\gamma $
is a limit ordinal, and
![]() $J_\gamma (\mathbb {R})\models \phi [z]$
. Then there is a
$J_\gamma (\mathbb {R})\models \phi [z]$
. Then there is a
![]() $\langle \phi ,z\rangle $
-witness N such that the iteration strategy for N restricted to countable trees is in
$\langle \phi ,z\rangle $
-witness N such that the iteration strategy for N restricted to countable trees is in
![]() $J_\gamma (\mathbb {R})$
. By taking a Skolem hull, we can also ensure
$J_\gamma (\mathbb {R})$
. By taking a Skolem hull, we can also ensure
![]() $\rho _\omega (N) = \omega $
.
$\rho _\omega (N) = \omega $
.
3 The inductive-like case
In this section we will prove Theorem 1.12. We now assume
![]() $ZF + AD + DC + V=L(\mathbb {R})$
and fix a boldface inductive-like pointclass
$ZF + AD + DC + V=L(\mathbb {R})$
and fix a boldface inductive-like pointclass
![]() $\boldsymbol {\Gamma }$
. By a reflection argument, we may assume
$\boldsymbol {\Gamma }$
. By a reflection argument, we may assume
![]() $\boldsymbol {\Gamma } \neq \boldsymbol {\Sigma ^2_1}$
.Footnote
6
$\boldsymbol {\Gamma } \neq \boldsymbol {\Sigma ^2_1}$
.Footnote
6
Let
![]() $\boldsymbol {\Delta } = \boldsymbol {\Delta _{\Gamma }}$
and let
$\boldsymbol {\Delta } = \boldsymbol {\Delta _{\Gamma }}$
and let
![]() $[\alpha _0,\beta _0],\beta '$
,
$[\alpha _0,\beta _0],\beta '$
,
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\mathcal {G}$
be as in Section 2.5. We will also refer to the mouse operators
$\mathcal {G}$
be as in Section 2.5. We will also refer to the mouse operators
![]() $x\to W_x$
and
$x\to W_x$
and
![]() $x\to M_x$
from Theorem 2.42 and use the notation for standard terms from Definition 2.32.
$x\to M_x$
from Theorem 2.42 and use the notation for standard terms from Definition 2.32.
In Sections 3.1–3.3 we analyze the directed system of iterates of a suitable mouse and show the directed system can be approximated inside a larger suitable mouse. Section 3.4 covers some lemmas about the StrLe construction inside a suitable mouse. Section 3.5 contains a lemma we will use to obtain witnesses for
![]() $\Sigma _1$
statements inside an initial segment of a suitable mouse. Finally, Theorem 1.12 is proven in Section 3.6.
$\Sigma _1$
statements inside an initial segment of a suitable mouse. Finally, Theorem 1.12 is proven in Section 3.6.
One of the key ideas to our proof of Theorem 1.12 is a different coding than the one used in [Reference Hjorth3, Reference Sargsyan11]. In [Reference Sargsyan11],
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
sets are coded by conditions in the extender algebra at the least Woodin of some complete iterate N of
$\boldsymbol {\Sigma ^1_{2n+2}}$
sets are coded by conditions in the extender algebra at the least Woodin of some complete iterate N of
![]() $M^\#_{2n+1}$
. The reflection argument from [Reference Hjorth3] ensures a code for each
$M^\#_{2n+1}$
. The reflection argument from [Reference Hjorth3] ensures a code for each
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
set appears below the least
$\boldsymbol {\Sigma ^1_{2n+2}}$
set appears below the least
![]() $<\delta _N$
-strong cardinal
$<\delta _N$
-strong cardinal
![]() $\kappa _N$
of some iterate N (in fact it gives a uniform bound below
$\kappa _N$
of some iterate N (in fact it gives a uniform bound below
![]() $\kappa _N$
). But this reflection argument depends upon the pointclass
$\kappa _N$
). But this reflection argument depends upon the pointclass
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
not being closed under coprojection.
$\boldsymbol {\Sigma ^1_{2n+2}}$
not being closed under coprojection.
Our proof of Theorem 1.12 instead codes
![]() $\boldsymbol {\Gamma }$
-sets by sets of conditions in the extender algebra of some
$\boldsymbol {\Gamma }$
-sets by sets of conditions in the extender algebra of some
![]() $\Gamma $
-suitable mouse N. A weaker reflection argument than the one in [Reference Hjorth3] is used to contain each code in
$\Gamma $
-suitable mouse N. A weaker reflection argument than the one in [Reference Hjorth3] is used to contain each code in
![]() $N|\kappa _N$
. This weaker reflection is sufficient for the proof.
$N|\kappa _N$
. This weaker reflection is sufficient for the proof.
3.1 The direct limit
Let
![]() $W = W_0$
and let
$W = W_0$
and let
![]() $\mathcal {I}$
be the directed system of countable, complete iterates of W according to its
$\mathcal {I}$
be the directed system of countable, complete iterates of W according to its
![]() $(\omega _1,\omega _1)$
-iteration strategy. Let
$(\omega _1,\omega _1)$
-iteration strategy. Let
![]() $M_\infty $
be the direct limit of
$M_\infty $
be the direct limit of
![]() $\mathcal {I}$
. For
$\mathcal {I}$
. For
![]() $M,N\in \mathcal {I}$
and N an iterate of M, let
$M,N\in \mathcal {I}$
and N an iterate of M, let
![]() $\pi _{M,N}: M \to N$
be the iteration map and
$\pi _{M,N}: M \to N$
be the iteration map and
![]() $\pi _{M,\infty }: M \to M_\infty $
the direct limit map. Here we demonstrate a few properties of
$\pi _{M,\infty }: M \to M_\infty $
the direct limit map. Here we demonstrate a few properties of
![]() $M_\infty $
. The proofs of this section are generalizations of arguments in [Reference Steel, Foreman and Kanamori19, Reference Steel, Woodin, Kechris, Löwe and Steel21] giving analogous properties of the direct limit of all countable, complete iterates of
$M_\infty $
. The proofs of this section are generalizations of arguments in [Reference Steel, Foreman and Kanamori19, Reference Steel, Woodin, Kechris, Löwe and Steel21] giving analogous properties of the direct limit of all countable, complete iterates of
![]() $M^\#_\omega $
.
$M^\#_\omega $
.
Lemma 3.1.
![]() $\kappa _{M_\infty } \leq \boldsymbol {\delta _\Gamma }$
.Footnote
7
$\kappa _{M_\infty } \leq \boldsymbol {\delta _\Gamma }$
.Footnote
7
Proof. Suppose
![]() $\xi < \kappa _{M_\infty }$
. Let
$\xi < \kappa _{M_\infty }$
. Let
![]() $M\in \mathcal {I}$
and
$M\in \mathcal {I}$
and
![]() $\bar {\xi }\in M$
be such that
$\bar {\xi }\in M$
be such that
![]() $\pi _{M,\infty }(\bar {\xi }) = \xi $
. Let P be an initial segment of M such that
$\pi _{M,\infty }(\bar {\xi }) = \xi $
. Let P be an initial segment of M such that
![]() $\bar {\xi }\in P$
and the largest cardinal of P is both a cutpoint and a cardinal of M. The iteration strategy
$\bar {\xi }\in P$
and the largest cardinal of P is both a cutpoint and a cardinal of M. The iteration strategy
![]() $\Sigma $
for P is in
$\Sigma $
for P is in
![]() $\boldsymbol {\Delta }$
by Remark 2.38. Let
$\boldsymbol {\Delta }$
by Remark 2.38. Let
![]() $\mathcal {I}_P$
be the directed system of countable, complete iterates of P by
$\mathcal {I}_P$
be the directed system of countable, complete iterates of P by
![]() $\Sigma $
. Then
$\Sigma $
. Then
![]() $\bar {\xi }$
is sent to
$\bar {\xi }$
is sent to
![]() $\xi $
by the direct limit map of this system, since the largest cardinal of P is a cutpoint and a cardinal of M. So a prewellordering of height
$\xi $
by the direct limit map of this system, since the largest cardinal of P is a cutpoint and a cardinal of M. So a prewellordering of height
![]() $\xi $
is projective in
$\xi $
is projective in
![]() $\Sigma $
and therefore
$\Sigma $
and therefore
![]() $\boldsymbol {\delta _\Gamma }> \xi $
.
$\boldsymbol {\delta _\Gamma }> \xi $
.
Lemma 3.2.
![]() $\delta _{M_\infty }> (\boldsymbol {\delta _\Gamma })^+$
.
$\delta _{M_\infty }> (\boldsymbol {\delta _\Gamma })^+$
.
Proof. Let
![]() $\Sigma $
be the
$\Sigma $
be the
![]() $(\omega _1,\omega _1)$
-iteration strategy for W. Recall
$(\omega _1,\omega _1)$
-iteration strategy for W. Recall
![]() $\Sigma $
is not in
$\Sigma $
is not in
![]() $\boldsymbol {\Gamma }$
. We will show
$\boldsymbol {\Gamma }$
. We will show
![]() $\Sigma $
is in
$\Sigma $
is in
![]() $S(\delta _{M_\infty })\backslash S(\boldsymbol {\delta _\Gamma }^+)$
.
$S(\delta _{M_\infty })\backslash S(\boldsymbol {\delta _\Gamma }^+)$
.
Claim 3.3.
![]() $\Sigma $
is
$\Sigma $
is
![]() $\delta _{M_\infty }$
-Suslin.
$\delta _{M_\infty }$
-Suslin.
Proof. Let
![]() $\mathcal {T}$
be a tree on
$\mathcal {T}$
be a tree on
![]() $(\omega \times \omega ) \times \delta _{M_\infty }$
such that
$(\omega \times \omega ) \times \delta _{M_\infty }$
such that
![]() $(x,y,f)\in [\mathcal {T}]$
if and only if x codes a countable iteration tree
$(x,y,f)\in [\mathcal {T}]$
if and only if x codes a countable iteration tree
![]() $\mathcal {S}$
on W of limit length, y codes a cofinal, wellfounded branch b through
$\mathcal {S}$
on W of limit length, y codes a cofinal, wellfounded branch b through
![]() $\mathcal {S}$
, and f codes an embedding
$\mathcal {S}$
, and f codes an embedding
![]() $\pi : M_b^{\mathcal {S}} \to M_\infty $
such that
$\pi : M_b^{\mathcal {S}} \to M_\infty $
such that
![]() $\pi \circ i^{\mathcal {S}}_b = \pi _{W,\infty }$
. Let
$\pi \circ i^{\mathcal {S}}_b = \pi _{W,\infty }$
. Let
![]() $\Sigma ' = \rho [\mathcal {T}]$
.
$\Sigma ' = \rho [\mathcal {T}]$
.
If
![]() $(x,y)\in \Sigma $
, then x codes an iteration tree
$(x,y)\in \Sigma $
, then x codes an iteration tree
![]() $\mathcal {S}$
on W according to
$\mathcal {S}$
on W according to
![]() $\Sigma $
and y codes the cofinal, wellfounded branch b through
$\Sigma $
and y codes the cofinal, wellfounded branch b through
![]() $\mathcal {S}$
chosen by
$\mathcal {S}$
chosen by
![]() $\Sigma $
. And
$\Sigma $
. And
![]() $\pi _{M^{\mathcal {S}}_b,\infty }\circ i^{\mathcal {S}}_b = \pi _{W,\infty }$
. So if
$\pi _{M^{\mathcal {S}}_b,\infty }\circ i^{\mathcal {S}}_b = \pi _{W,\infty }$
. So if
![]() $f:\omega \to \delta _{M_\infty }$
codes the embedding
$f:\omega \to \delta _{M_\infty }$
codes the embedding
![]() $\pi _{M^{\mathcal {S}}_b,\infty }$
, then
$\pi _{M^{\mathcal {S}}_b,\infty }$
, then
![]() $(x,y,f)\in [\mathcal {T}]$
. Thus
$(x,y,f)\in [\mathcal {T}]$
. Thus
![]() $(x,y)\in \Sigma '$
.
$(x,y)\in \Sigma '$
.
On the other hand, suppose
![]() $(x,y) \in \Sigma '$
and x codes an iteration tree
$(x,y) \in \Sigma '$
and x codes an iteration tree
![]() $\mathcal {S}$
according to
$\mathcal {S}$
according to
![]() $\Sigma $
. Fix
$\Sigma $
. Fix
![]() $f:\omega \to \delta _{M_\infty }$
such that
$f:\omega \to \delta _{M_\infty }$
such that
![]() $(x,y,f)\in [\mathcal {T}]$
. Let b be the branch coded by y and
$(x,y,f)\in [\mathcal {T}]$
. Let b be the branch coded by y and
![]() $\pi $
the embedding coded by f.
$\pi $
the embedding coded by f.
Subclaim 3.4. For all n,
![]() $\pi ^{\mathcal {S}}_b(\tau ^W_n) = \tau ^{M^{\mathcal {S}}_b}_n$
.
$\pi ^{\mathcal {S}}_b(\tau ^W_n) = \tau ^{M^{\mathcal {S}}_b}_n$
.
Proof. Let
![]() $Q \in \mathcal {I}$
be such that
$Q \in \mathcal {I}$
be such that
![]() $range(\pi )\subseteq range(\pi _{Q,\infty })$
. Let
$range(\pi )\subseteq range(\pi _{Q,\infty })$
. Let
![]() $\pi ' = \pi _{Q,\infty }^{-1} \circ \pi $
. Then
$\pi ' = \pi _{Q,\infty }^{-1} \circ \pi $
. Then
![]() $\pi ':M^{\mathcal {S}}_b \to Q$
and
$\pi ':M^{\mathcal {S}}_b \to Q$
and
![]() $\pi '(i^{\mathcal {S}}_b(\tau ^W_n)) = \tau ^Q_n$
. Then by Lemma 2.34,
$\pi '(i^{\mathcal {S}}_b(\tau ^W_n)) = \tau ^Q_n$
. Then by Lemma 2.34,
![]() $i^{\mathcal {S}}_b(\tau ^W_n) = \tau ^{M_b^{\mathcal {S}}}_n$
.
$i^{\mathcal {S}}_b(\tau ^W_n) = \tau ^{M_b^{\mathcal {S}}}_n$
.
From the subclaim and the last part of Lemma 2.44, we have that
![]() $(x,y)\in \Sigma $
.
$(x,y)\in \Sigma $
.
We can now characterize
![]() $\Sigma $
as the set of
$\Sigma $
as the set of
![]() $(x,y)\in \mathbb {R}\times \mathbb {R}$
such that:
$(x,y)\in \mathbb {R}\times \mathbb {R}$
such that:
-
1. x codes an iteration tree
 $\mathcal {S}$
on W of limit length,
$\mathcal {S}$
on W of limit length, -
2. y codes a cofinal, wellfounded branch through
 $\mathcal {S}$
,
$\mathcal {S}$
, -
3.
 $(x,y)\in \Sigma '$
, and
$(x,y)\in \Sigma '$
, and -
4. for any
 $(x_0,y_0) \leq _T x$
such that
$(x_0,y_0) \leq _T x$
such that
 $x_0$
codes a proper initial segment
$x_0$
codes a proper initial segment
 $\mathcal {S}_0$
of
$\mathcal {S}_0$
of
 $\mathcal {S}$
of limit length and
$\mathcal {S}$
of limit length and
 $y_0$
codes the branch through
$y_0$
codes the branch through
 $\mathcal {S}_0$
determined by
$\mathcal {S}_0$
determined by
 $\mathcal {S}$
,
$\mathcal {S}$
,
 $(x_0,y_0)\in \Sigma '$
.
$(x_0,y_0)\in \Sigma '$
.
Condition 4 is just to guarantee
![]() $\mathcal {S}$
is in the domain of
$\mathcal {S}$
is in the domain of
![]() $\Sigma $
. It does so because any proper initial segment
$\Sigma $
. It does so because any proper initial segment
![]() $\mathcal {S}_0$
of
$\mathcal {S}_0$
of
![]() $\mathcal {S}$
is coded by some real computable from x. From this, and the preceding paragraphs, it is clear these conditions characterize
$\mathcal {S}$
is coded by some real computable from x. From this, and the preceding paragraphs, it is clear these conditions characterize
![]() $\Sigma $
. Since
$\Sigma $
. Since
![]() $\Sigma '$
is
$\Sigma '$
is
![]() $\delta _{M_\infty }$
-Suslin, this characterization of
$\delta _{M_\infty }$
-Suslin, this characterization of
![]() $\Sigma $
makes plain that
$\Sigma $
makes plain that
![]() $\Sigma $
is also
$\Sigma $
is also
![]() $\delta _{M_\infty }$
-Suslin.
$\delta _{M_\infty }$
-Suslin.
Claim 3.5.
![]() $\boldsymbol {\Gamma } = S(\boldsymbol {\delta _\Gamma })$
.
$\boldsymbol {\Gamma } = S(\boldsymbol {\delta _\Gamma })$
.
Proof. First, let’s establish
![]() $\boldsymbol {\Gamma }$
is Suslin (we say a pointclass is Suslin if it equals
$\boldsymbol {\Gamma }$
is Suslin (we say a pointclass is Suslin if it equals
![]() $S(\lambda )$
for some cardinal
$S(\lambda )$
for some cardinal
![]() $\lambda $
). Let
$\lambda $
). Let
It follows from Theorem 2.7 that
![]() $\boldsymbol {\Gamma }$
is the minimal non-selfdual pointclass closed under projection which contains every pointclass in
$\boldsymbol {\Gamma }$
is the minimal non-selfdual pointclass closed under projection which contains every pointclass in
![]() $\Omega $
. Let
$\Omega $
. Let
By Theorem 2.8,
![]() $\Psi $
is cofinal in
$\Psi $
is cofinal in
![]() $\Omega $
. But the minimal Suslin pointclass larger than any element of
$\Omega $
. But the minimal Suslin pointclass larger than any element of
![]() $\Psi $
is just the minimal non-selfdual pointclass closed under projection which contains every pointclass in
$\Psi $
is just the minimal non-selfdual pointclass closed under projection which contains every pointclass in
![]() $\Omega $
(by part 3 of Theorem 2.8). Since
$\Omega $
(by part 3 of Theorem 2.8). Since
![]() $\Psi $
is cofinal in
$\Psi $
is cofinal in
![]() $\Omega $
, this is
$\Omega $
, this is
![]() $\boldsymbol {\Gamma }$
.
$\boldsymbol {\Gamma }$
.
So
![]() $\boldsymbol {\Gamma } = S(\lambda )$
for some cardinal
$\boldsymbol {\Gamma } = S(\lambda )$
for some cardinal
![]() $\lambda $
. By the Kunen–Martin Theorem, there is a prewellordering of length
$\lambda $
. By the Kunen–Martin Theorem, there is a prewellordering of length
![]() $\lambda $
in
$\lambda $
in
![]() $\boldsymbol {\Gamma }$
but no prewellordering of length
$\boldsymbol {\Gamma }$
but no prewellordering of length
![]() $\lambda ^+$
. The latter implies that
$\lambda ^+$
. The latter implies that
![]() $\lambda \geq \boldsymbol {\delta _\Gamma }$
, since
$\lambda \geq \boldsymbol {\delta _\Gamma }$
, since
![]() $\boldsymbol {\delta _\Gamma }$
is a limit cardinal,Footnote
8
and since there are prewellorderings of length
$\boldsymbol {\delta _\Gamma }$
is a limit cardinal,Footnote
8
and since there are prewellorderings of length
![]() $\alpha $
in
$\alpha $
in
![]() $\boldsymbol {\Gamma }$
for all
$\boldsymbol {\Gamma }$
for all
![]() $\alpha <\boldsymbol {\delta _\Gamma }$
. The former implies that
$\alpha <\boldsymbol {\delta _\Gamma }$
. The former implies that
![]() $\lambda \leq \boldsymbol {\delta _\Gamma }$
, since there is no prewellordering of length
$\lambda \leq \boldsymbol {\delta _\Gamma }$
, since there is no prewellordering of length
![]() $\boldsymbol {\delta _\Gamma ^+}$
in
$\boldsymbol {\delta _\Gamma ^+}$
in
![]() $\boldsymbol {\Gamma .}$
(Otherwise a proper initial segment of this prewellordering would be of length
$\boldsymbol {\Gamma .}$
(Otherwise a proper initial segment of this prewellordering would be of length
![]() $\boldsymbol {\delta _\Gamma }$
, giving a prewellordering of length
$\boldsymbol {\delta _\Gamma }$
, giving a prewellordering of length
![]() $\boldsymbol {\delta _\Gamma }$
in
$\boldsymbol {\delta _\Gamma }$
in
![]() $\boldsymbol {\Delta .}$
) So
$\boldsymbol {\Delta .}$
) So
![]() $\boldsymbol {\delta _\Gamma }=\lambda $
.
$\boldsymbol {\delta _\Gamma }=\lambda $
.
By the previous two claims,
![]() $\Sigma \in S(\delta _{M_\infty }) \backslash S(\boldsymbol {\delta _\Gamma })$
. In particular,
$\Sigma \in S(\delta _{M_\infty }) \backslash S(\boldsymbol {\delta _\Gamma })$
. In particular,
![]() $\delta _{M_\infty } \geq \lambda '$
where
$\delta _{M_\infty } \geq \lambda '$
where
![]() $\lambda '$
is the next Suslin cardinal after
$\lambda '$
is the next Suslin cardinal after
![]() $\boldsymbol {\delta _\Gamma }$
.Footnote
9
But
$\boldsymbol {\delta _\Gamma }$
.Footnote
9
But
![]() $cof(\lambda ') = \omega $
by part 3 of Theorem 2.8, so
$cof(\lambda ') = \omega $
by part 3 of Theorem 2.8, so
![]() $\delta _{M_\infty } \geq \lambda '> \boldsymbol {\delta ^+_\Gamma }$
.
$\delta _{M_\infty } \geq \lambda '> \boldsymbol {\delta ^+_\Gamma }$
.
Lemma 3.6. Suppose
![]() $\mu < \delta _{M_\infty }$
is a regular cardinal of
$\mu < \delta _{M_\infty }$
is a regular cardinal of
![]() $M_\infty $
. Then
$M_\infty $
. Then
![]() $\mu $
is not measurable in
$\mu $
is not measurable in
![]() $M_\infty $
if and only if
$M_\infty $
if and only if
![]() $\mu $
has cofinality
$\mu $
has cofinality
![]() $\omega $
in
$\omega $
in
![]() $L(\mathbb {R})$
.
$L(\mathbb {R})$
.
Proof. Suppose
![]() $\mu $
is not measurable in
$\mu $
is not measurable in
![]() $M_\infty $
. Fix
$M_\infty $
. Fix
![]() $M \in \mathcal {I}$
and
$M \in \mathcal {I}$
and
![]() $\bar {\mu }$
such that
$\bar {\mu }$
such that
![]() $\pi _{M,\infty }(\bar {\mu }) = \mu $
. Then
$\pi _{M,\infty }(\bar {\mu }) = \mu $
. Then
![]() $\bar {\mu }$
is regular but not measurable in M. Since M is countable, there is a sequence of ordinals
$\bar {\mu }$
is regular but not measurable in M. Since M is countable, there is a sequence of ordinals
![]() $\langle \bar {\xi }_n: n < \omega \rangle $
cofinal in
$\langle \bar {\xi }_n: n < \omega \rangle $
cofinal in
![]() $\bar {\mu }$
. Let
$\bar {\mu }$
. Let
![]() $\xi _n = \pi _{M,\infty }(\bar {\xi }_n)$
. Since
$\xi _n = \pi _{M,\infty }(\bar {\xi }_n)$
. Since
![]() $\bar {\mu }$
is regular and not measurable in M,
$\bar {\mu }$
is regular and not measurable in M,
![]() $\pi _{M,\infty }$
is continuous at
$\pi _{M,\infty }$
is continuous at
![]() $\bar {\mu .}$
(This is because
$\bar {\mu .}$
(This is because
![]() $\pi _{M,\infty }$
is essentially an iteration embedding—in fact it is an iteration embedding in
$\pi _{M,\infty }$
is essentially an iteration embedding—in fact it is an iteration embedding in
![]() $V^{Col(\omega ,\mathbb {R})}$
. And any iteration embedding is continuous at a cardinal which is regular but not measurable, since ultrapower embeddings are continuous at such cardinals.) So
$V^{Col(\omega ,\mathbb {R})}$
. And any iteration embedding is continuous at a cardinal which is regular but not measurable, since ultrapower embeddings are continuous at such cardinals.) So
![]() $\langle \xi _n : n < \omega \rangle $
is cofinal in
$\langle \xi _n : n < \omega \rangle $
is cofinal in
![]() $\mu $
.
$\mu $
.
Now suppose
![]() $\mu $
has cofinality
$\mu $
has cofinality
![]() $\omega $
in
$\omega $
in
![]() $L(\mathbb {R})$
. Let
$L(\mathbb {R})$
. Let
![]() $\langle \xi _n: n <\omega \rangle $
be cofinal in
$\langle \xi _n: n <\omega \rangle $
be cofinal in
![]() $\mu $
. Fix
$\mu $
. Fix
![]() $M \in \mathcal {I}$
such that there is
$M \in \mathcal {I}$
such that there is
![]() $\bar {\mu }\in M$
and
$\bar {\mu }\in M$
and
![]() $\langle \bar {\xi }_n : n < \omega \rangle \subset M$
with
$\langle \bar {\xi }_n : n < \omega \rangle \subset M$
with
![]() $\pi _{M,\infty }(\bar {\mu }) = \mu $
and
$\pi _{M,\infty }(\bar {\mu }) = \mu $
and
![]() $\pi _{M,\infty }(\bar {\xi }_n) = \xi _n$
. If
$\pi _{M,\infty }(\bar {\xi }_n) = \xi _n$
. If
![]() $\mu $
is measurable in
$\mu $
is measurable in
![]() $M_\infty $
, then there is a total extender F on the fine extender sequence of M with critical point
$M_\infty $
, then there is a total extender F on the fine extender sequence of M with critical point
![]() $\bar {\mu }$
. Let
$\bar {\mu }$
. Let
![]() $M'$
be the ultrapower of M by F and
$M'$
be the ultrapower of M by F and
![]() $j:M \to M'$
the embedding induced by F. Then for any
$j:M \to M'$
the embedding induced by F. Then for any
![]() $n<\omega $
,
$n<\omega $
,
 $$ \begin{align*} \xi_n &= \pi_{M,\infty}(\bar{\xi}_n)\\ &= \pi_{M',\infty}\circ j(\bar{\xi}_n)\\ &= \pi_{M',\infty}(\bar{\xi}_n)\\ &< \pi_{M',\infty}(\bar{\mu})\\ &< \pi_{M',\infty}\circ j(\bar{\mu})\\ &= \mu. \end{align*} $$
$$ \begin{align*} \xi_n &= \pi_{M,\infty}(\bar{\xi}_n)\\ &= \pi_{M',\infty}\circ j(\bar{\xi}_n)\\ &= \pi_{M',\infty}(\bar{\xi}_n)\\ &< \pi_{M',\infty}(\bar{\mu})\\ &< \pi_{M',\infty}\circ j(\bar{\mu})\\ &= \mu. \end{align*} $$
So
![]() $\pi _{M',\infty }(\bar {\mu })$
is an upper bound for
$\pi _{M',\infty }(\bar {\mu })$
is an upper bound for
![]() $\bar {\xi }_n$
below
$\bar {\xi }_n$
below
![]() $\mu $
, a contradiction.
$\mu $
, a contradiction.
3.2 Definability in suitable mice
Lemma 3.7. Suppose N is a premouse satisfying enough of
![]() $ZFC$
,
$ZFC$
,
![]() $\nu $
is a cardinal of N,
$\nu $
is a cardinal of N,
![]() $Lp^\Gamma (a) \subset N$
for each
$Lp^\Gamma (a) \subset N$
for each
![]() $a\in N|\nu $
, and
$a\in N|\nu $
, and
![]() $\tau \in N^{Col(\omega ,\nu )}$
weakly captures
$\tau \in N^{Col(\omega ,\nu )}$
weakly captures
![]() $G_0$
. Then the map with domain
$G_0$
. Then the map with domain
![]() $N|\nu $
defined by
$N|\nu $
defined by
![]() $a \mapsto Lp^\Gamma (a)$
is definable in N from
$a \mapsto Lp^\Gamma (a)$
is definable in N from
![]() $\tau $
.
$\tau $
.
Proof. Recall
 $$ \begin{align*} G_0 = \{(x,y):\, & x \text{ codes some transitive set } a \text{ and } y \text{ codes an } \omega\text{-sound } \\ & a\text{-premouse } R \text{ such that } R \text{ projects to } a \text{ and } R \text{ has an } \\ & \omega_1\text{-iteration strategy in } \boldsymbol{\Delta}\}. \end{align*} $$
$$ \begin{align*} G_0 = \{(x,y):\, & x \text{ codes some transitive set } a \text{ and } y \text{ codes an } \omega\text{-sound } \\ & a\text{-premouse } R \text{ such that } R \text{ projects to } a \text{ and } R \text{ has an } \\ & \omega_1\text{-iteration strategy in } \boldsymbol{\Delta}\}. \end{align*} $$
Fix
![]() $a\in N|\nu $
. If R is any set in
$a\in N|\nu $
. If R is any set in
![]() $N|\nu $
and g is any
$N|\nu $
and g is any
![]() $Col(\omega ,\nu )$
-generic over N, then there are reals x and y in
$Col(\omega ,\nu )$
-generic over N, then there are reals x and y in
![]() $N[g]$
coding a and R, respectively. It is easy to see from this that
$N[g]$
coding a and R, respectively. It is easy to see from this that
![]() $Lp^\Gamma (a)$
is
$Lp^\Gamma (a)$
is
Corollary 3.8. If P is
![]() $\Gamma $
-ss, then the map with domain
$\Gamma $
-ss, then the map with domain
![]() $P|\nu _P$
defined by
$P|\nu _P$
defined by
![]() $a \mapsto Lp^\Gamma (a)$
is definable in P from
$a \mapsto Lp^\Gamma (a)$
is definable in P from
![]() $\tau ^P_{0,\nu _P}$
.
$\tau ^P_{0,\nu _P}$
.
Proof. It is clear from Remark 2.18 and Corollary 2.35 that P and
![]() $\tau ^P_{0,\nu _P}$
satisfy the conditions of Lemma 3.7.
$\tau ^P_{0,\nu _P}$
satisfy the conditions of Lemma 3.7.
Lemma 3.9. Suppose P is
![]() $\Gamma $
-ss and
$\Gamma $
-ss and
![]() $N \in P|\nu _P$
is
$N \in P|\nu _P$
is
![]() $\Gamma $
-suitable. Then
$\Gamma $
-suitable. Then
![]() $\{\tau ^N_{n,\mu }: \mu \text { is an uncountable cardinal of } N \}$
is definable in P from N and
$\{\tau ^N_{n,\mu }: \mu \text { is an uncountable cardinal of } N \}$
is definable in P from N and
![]() $\tau ^P_{n,\nu _P}$
(uniformly in P and N).
$\tau ^P_{n,\nu _P}$
(uniformly in P and N).
Proof. Let
![]() $\mu $
be an uncountable cardinal of N.
$\mu $
be an uncountable cardinal of N.
Note that if g is
![]() $Col(\omega ,\nu _P)$
-generic over P and
$Col(\omega ,\nu _P)$
-generic over P and
![]() $f\in P$
is a surjection of
$f\in P$
is a surjection of
![]() $\nu _P$
onto
$\nu _P$
onto
![]() $\mu $
, then
$\mu $
, then
![]() $f\circ g$
is P-generic for
$f\circ g$
is P-generic for
![]() $Col(\omega ,\mu )$
. In particular,
$Col(\omega ,\mu )$
. In particular,
![]() $f \circ g$
is N-generic for
$f \circ g$
is N-generic for
![]() $Col(\omega ,\mu )$
. Fix such an f which is minimal in the constructibility order of P. Let
$Col(\omega ,\mu )$
. Fix such an f which is minimal in the constructibility order of P. Let
 $$ \begin{align*} \tau_{n,\mu} = \,&\{(\sigma,p): \sigma \text{ is a } Col(\omega,\mu) \text{-standard term for a real}, p\in Col(\omega,\mu),\\ &\text{ and } \emptyset \Vdash^P_{Col(\omega,\nu_P)} (\check{p}\in \check{f}\circ \dot{g} \rightarrow \check{\sigma}[\check{f} \circ \dot{g}] \in \tau^P_{n,\nu_P})\}. \end{align*} $$
$$ \begin{align*} \tau_{n,\mu} = \,&\{(\sigma,p): \sigma \text{ is a } Col(\omega,\mu) \text{-standard term for a real}, p\in Col(\omega,\mu),\\ &\text{ and } \emptyset \Vdash^P_{Col(\omega,\nu_P)} (\check{p}\in \check{f}\circ \dot{g} \rightarrow \check{\sigma}[\check{f} \circ \dot{g}] \in \tau^P_{n,\nu_P})\}. \end{align*} $$
It is clear that
![]() $\tau _{n,\mu }$
is definable in P from N,
$\tau _{n,\mu }$
is definable in P from N,
![]() $\mu $
, and
$\mu $
, and
![]() $\tau ^P_{n,\nu _P}$
. It suffices to show
$\tau ^P_{n,\nu _P}$
. It suffices to show
![]() $\tau _{n,\mu } = \tau ^N_{n,\mu }$
.
$\tau _{n,\mu } = \tau ^N_{n,\mu }$
.
![]() $\tau _{n,\mu } \subseteq \tau ^N_{n,\mu }$
by Definition 2.32 and that comeager many
$\tau _{n,\mu } \subseteq \tau ^N_{n,\mu }$
by Definition 2.32 and that comeager many
![]() $h\subset Col(\omega ,\mu )$
which are generic over N are of the form
$h\subset Col(\omega ,\mu )$
which are generic over N are of the form
![]() $f \circ g$
for some g which is
$f \circ g$
for some g which is
![]() $Col(\omega ,\nu _P)$
-generic over P.
$Col(\omega ,\nu _P)$
-generic over P.
On the other hand, suppose
![]() $(\sigma ,p) \in \tau ^N_{n,\mu }$
. By Corollary 2.35,
$(\sigma ,p) \in \tau ^N_{n,\mu }$
. By Corollary 2.35,
![]() $\sigma [h]\in G_n$
for any h which is
$\sigma [h]\in G_n$
for any h which is
![]() $Col(\omega ,\mu )$
-generic over N such that
$Col(\omega ,\mu )$
-generic over N such that
![]() $p\in h$
. In particular,
$p\in h$
. In particular,
![]() $\sigma [f \circ g] \in \tau ^P_{n,\nu _P}[g]$
for any g which is
$\sigma [f \circ g] \in \tau ^P_{n,\nu _P}[g]$
for any g which is
![]() $Col(\omega ,\nu _P)$
-generic over P such that
$Col(\omega ,\nu _P)$
-generic over P such that
![]() $p\in f\circ g$
. Thus
$p\in f\circ g$
. Thus
![]() $(\sigma ,p) \in \tau _{n,\mu }$
.
$(\sigma ,p) \in \tau _{n,\mu }$
.
We will also need versions of Corollary 3.8 and Lemma 3.9 in generic extensions of
![]() $\Gamma $
-ss mice.
$\Gamma $
-ss mice.
Lemma 3.10. Suppose
![]() $B\subseteq \mathbb {R}$
, P is a premouse,
$B\subseteq \mathbb {R}$
, P is a premouse,
![]() $\delta $
is Woodin in P,
$\delta $
is Woodin in P,
![]() $\mu \geq \delta $
,
$\mu \geq \delta $
,
![]() $\tau \in P^{Col(\omega ,\mu )}$
weakly captures B over P, and y is
$\tau \in P^{Col(\omega ,\mu )}$
weakly captures B over P, and y is
![]() $Ea_P$
-generic over P. Then there is
$Ea_P$
-generic over P. Then there is
![]() $\tau '\in P[y]^{Col(\omega ,\mu )}$
which weakly captures B over
$\tau '\in P[y]^{Col(\omega ,\mu )}$
which weakly captures B over
![]() $P[y]$
. Moreover,
$P[y]$
. Moreover,
![]() $\tau '$
is definable in
$\tau '$
is definable in
![]() $P[y]$
from
$P[y]$
from
![]() $\tau $
and y (uniformly).
$\tau $
and y (uniformly).
Proof.
![]() $Col(\omega ,\mu )$
is universal for pointclasses of size
$Col(\omega ,\mu )$
is universal for pointclasses of size
![]() $\mu $
. So there is a complete embedding
$\mu $
. So there is a complete embedding
![]() $\Phi : Ea_p \times Col(\omega ,\mu ) \to Col(\omega ,\mu )$
.Footnote
10
If g is
$\Phi : Ea_p \times Col(\omega ,\mu ) \to Col(\omega ,\mu )$
.Footnote
10
If g is
![]() $Col(\omega ,\mu )$
-generic over P, let
$Col(\omega ,\mu )$
-generic over P, let
![]() $(y_g,f_g)$
be the
$(y_g,f_g)$
be the
![]() $Ea_P \times Col(\omega ,\mu )$
-generic consisting of all conditions
$Ea_P \times Col(\omega ,\mu )$
-generic consisting of all conditions
![]() $(p,q)\in Ea_P \times Col(\omega ,\mu )$
such that
$(p,q)\in Ea_P \times Col(\omega ,\mu )$
such that
![]() $\Phi ((p,q))\in g$
(see Chapter 7, Theorem 7.5 of [Reference Kunen6]). Let
$\Phi ((p,q))\in g$
(see Chapter 7, Theorem 7.5 of [Reference Kunen6]). Let
 $$ \begin{align*} \tau^* = \{(\sigma,(p,q)): & \,\sigma \text{ is an } Ea_P\text{-term for a } Col(\omega,\mu)\text{-standard term }\\ & \text{for a real, } (p,q)\in Ea_P\times Col(\omega,\mu), \text{ and }\\ & \Phi((p,q)) \Vdash^P_{Col(\omega,\mu)} \sigma[y_g][f_g] \in \tau[g]\}. \end{align*} $$
$$ \begin{align*} \tau^* = \{(\sigma,(p,q)): & \,\sigma \text{ is an } Ea_P\text{-term for a } Col(\omega,\mu)\text{-standard term }\\ & \text{for a real, } (p,q)\in Ea_P\times Col(\omega,\mu), \text{ and }\\ & \Phi((p,q)) \Vdash^P_{Col(\omega,\mu)} \sigma[y_g][f_g] \in \tau[g]\}. \end{align*} $$
Claim 3.11. For any
![]() $(y,f)$
which is
$(y,f)$
which is
![]() $Ea_P\times Col(\omega ,\mu )$
-generic over P,
$Ea_P\times Col(\omega ,\mu )$
-generic over P,
![]() $\tau ^*[y][f] = B \cap P[y][f]$
.
$\tau ^*[y][f] = B \cap P[y][f]$
.
Proof. Suppose
![]() $x\in \tau ^*[y][f]$
.
$x\in \tau ^*[y][f]$
.
![]() $x = \sigma [y][f]$
for some
$x = \sigma [y][f]$
for some
![]() $(\sigma ,(p,q))\in \tau ^*$
such that
$(\sigma ,(p,q))\in \tau ^*$
such that
![]() $p\in y$
and
$p\in y$
and
![]() $q\in f$
. Let g be
$q\in f$
. Let g be
![]() $Col(\omega ,\mu )$
-generic such that
$Col(\omega ,\mu )$
-generic such that
![]() $y_g = y$
and
$y_g = y$
and
![]() $f_g = f$
. In particular,
$f_g = f$
. In particular,
![]() $\Phi ((p,q))\in g$
. Then
$\Phi ((p,q))\in g$
. Then
![]() $P[g]\models \sigma [y_g][f_g]\in \tau [g]$
. Since
$P[g]\models \sigma [y_g][f_g]\in \tau [g]$
. Since
![]() $x= \sigma [y_g][f_g]$
and
$x= \sigma [y_g][f_g]$
and
![]() $\tau [g]= B \cap P[g]$
,
$\tau [g]= B \cap P[g]$
,
![]() $x\in B \cap P[g]$
.
$x\in B \cap P[g]$
.
Now suppose
![]() $x\in B\cap P[y][f]$
. Let
$x\in B\cap P[y][f]$
. Let
![]() $\sigma $
be an
$\sigma $
be an
![]() $Ea_P$
-term for a
$Ea_P$
-term for a
![]() $Col(\omega ,\mu )$
-standard term for a real such that
$Col(\omega ,\mu )$
-standard term for a real such that
![]() $x= \sigma [y][f]$
.
$x= \sigma [y][f]$
.
![]() $\bigcup \Phi "\{(p,q):(p,q)\in y\times g\}$
is a function
$\bigcup \Phi "\{(p,q):(p,q)\in y\times g\}$
is a function
![]() $g_1:S\to \mu $
for some
$g_1:S\to \mu $
for some
![]() $S\subseteq \omega $
. Let
$S\subseteq \omega $
. Let
(
![]() $\mathbb {Q}$
is the quotient of
$\mathbb {Q}$
is the quotient of
![]() $Col(\omega ,\mu )$
by
$Col(\omega ,\mu )$
by
![]() $g_1$
). Let
$g_1$
). Let
![]() $g_2$
be
$g_2$
be
![]() $\mathbb {Q}$
-generic over
$\mathbb {Q}$
-generic over
![]() $P[g_1]$
. Then
$P[g_1]$
. Then
![]() $g = g_1 \cup g_2$
is
$g = g_1 \cup g_2$
is
![]() $Col(\omega ,\mu )$
-generic over P.
$Col(\omega ,\mu )$
-generic over P.
We have
![]() $x\in \tau [g]$
. Pick
$x\in \tau [g]$
. Pick
![]() $s\in g$
such that
$s\in g$
such that
![]() $s \Vdash ^P_{Col(\omega ,\mu )} \sigma [y_g][f_g]\in \tau [g]$
.
$s \Vdash ^P_{Col(\omega ,\mu )} \sigma [y_g][f_g]\in \tau [g]$
.
![]() $s = r_1 \cup r_2$
for some
$s = r_1 \cup r_2$
for some
![]() $r_1\in g_1$
and
$r_1\in g_1$
and
![]() $r_2\in g_2$
.
$r_2\in g_2$
.
Subclaim 3.12.
![]() $r_1 \Vdash ^P_{Col(\omega ,\mu )} \sigma [y_g][f_g]\in \tau $
.
$r_1 \Vdash ^P_{Col(\omega ,\mu )} \sigma [y_g][f_g]\in \tau $
.
Proof. Suppose not. Then there is
![]() $g^{\prime }_2$
which is
$g^{\prime }_2$
which is
![]() $\mathbb {Q}$
-generic over
$\mathbb {Q}$
-generic over
![]() $P[g_1]$
such that, letting
$P[g_1]$
such that, letting
![]() $g' = g_1 \cup g^{\prime }_2$
,
$g' = g_1 \cup g^{\prime }_2$
,
![]() $\sigma [y_{g'}][f_{g'}]\notin \tau [g']$
.
$\sigma [y_{g'}][f_{g'}]\notin \tau [g']$
.
![]() $\sigma [y_{g'}][f_{g'}] = x$
, since
$\sigma [y_{g'}][f_{g'}] = x$
, since
![]() $y_g$
and
$y_g$
and
![]() $f_g$
depend only on
$f_g$
depend only on
![]() $g\upharpoonright S$
. But then
$g\upharpoonright S$
. But then
![]() $x\in (B \cap P[g'])\backslash \tau [g']$
, contradicting that
$x\in (B \cap P[g'])\backslash \tau [g']$
, contradicting that
![]() $\tau $
weakly captures B.
$\tau $
weakly captures B.
Pick
![]() $p\in y$
and
$p\in y$
and
![]() $q\in f$
such that
$q\in f$
such that
![]() $\Phi ((p,q))$
extends
$\Phi ((p,q))$
extends
![]() $r_1$
. Then
$r_1$
. Then
![]() $(\sigma ,(p,q))\in \tau ^*$
. So
$(\sigma ,(p,q))\in \tau ^*$
. So
![]() $x\in \tau ^*[y][f]$
.
$x\in \tau ^*[y][f]$
.
Let
![]() $\tau '$
is definable in
$\tau '$
is definable in
![]() $P[y]$
from
$P[y]$
from
![]() $\tau $
and y. It is clear from Claim 3.11 that
$\tau $
and y. It is clear from Claim 3.11 that
![]() $\tau '$
weakly captures B over
$\tau '$
weakly captures B over
![]() $P[y]$
.
$P[y]$
.
Lemma 3.13. Let P be
![]() $\Gamma $
-ss and y be
$\Gamma $
-ss and y be
![]() $Ea_P$
-generic over P. Then for any
$Ea_P$
-generic over P. Then for any
![]() $a\in P[y]$
,
$a\in P[y]$
,
![]() $Lp^\Gamma (a)\subset P[y]$
.
$Lp^\Gamma (a)\subset P[y]$
.
Proof. Let N be a
![]() $\Gamma $
-suitable mouse built over P. N has a Woodin cardinal
$\Gamma $
-suitable mouse built over P. N has a Woodin cardinal
![]() $\delta _N$
above
$\delta _N$
above
![]() $\delta _P$
. The iteration strategy for any proper initial segment of
$\delta _P$
. The iteration strategy for any proper initial segment of
![]() $N|\delta _N$
restricted to trees above
$N|\delta _N$
restricted to trees above
![]() $\delta _P$
is in
$\delta _P$
is in
![]() $\boldsymbol {\Delta }$
. And no initial segment of N above
$\boldsymbol {\Delta }$
. And no initial segment of N above
![]() $\delta _N$
projects strictly below
$\delta _N$
projects strictly below
![]() $\delta _N$
. It follows that any cardinal of P remains a cardinal in N. In particular,
$\delta _N$
. It follows that any cardinal of P remains a cardinal in N. In particular,
![]() $\delta _P$
remains Woodin in N and y is also
$\delta _P$
remains Woodin in N and y is also
![]() $Ea_P$
-generic over N.
$Ea_P$
-generic over N.
Suppose R is an
![]() $\omega $
-sound a-premouse with an
$\omega $
-sound a-premouse with an
![]() $\omega _1$
-iteration strategy in
$\omega _1$
-iteration strategy in
![]() $\boldsymbol {\Delta }$
such that R projects to a. It suffices to show
$\boldsymbol {\Delta }$
such that R projects to a. It suffices to show
![]() $R\in P[y]$
.
$R\in P[y]$
.
Let
![]() $\alpha $
be the height of R. Iterating N above R if necessary, we may assume there is a real g which is
$\alpha $
be the height of R. Iterating N above R if necessary, we may assume there is a real g which is
![]() $Col(\omega ,\delta _N)$
-generic over N such that some real in
$Col(\omega ,\delta _N)$
-generic over N such that some real in
![]() $N[y][g]$
codes R. By Lemma 3.10, there is a
$N[y][g]$
codes R. By Lemma 3.10, there is a
![]() $Col(\omega ,\delta _N)$
-term
$Col(\omega ,\delta _N)$
-term
![]() $\tau $
in
$\tau $
in
![]() $N[y]$
which weakly captures
$N[y]$
which weakly captures
![]() $G_0$
. Then R is the unique premouse in
$G_0$
. Then R is the unique premouse in
![]() $N[y][g]$
of height
$N[y][g]$
of height
![]() $\alpha $
such that if
$\alpha $
such that if
![]() $x_a$
codes a and
$x_a$
codes a and
![]() $x_R$
codes R, then
$x_R$
codes R, then
![]() $(x_a,x_R)\in \tau [g]$
. By homogeneity of the forcing, for any
$(x_a,x_R)\in \tau [g]$
. By homogeneity of the forcing, for any
![]() $g'$
which is
$g'$
which is
![]() $Col(\omega ,\delta _N)$
-generic over N, there is a premouse
$Col(\omega ,\delta _N)$
-generic over N, there is a premouse
![]() $R'\in N[y][g']$
of height
$R'\in N[y][g']$
of height
![]() $\alpha $
and reals
$\alpha $
and reals
![]() $x_a$
and
$x_a$
and
![]() $x_{R'}$
in
$x_{R'}$
in
![]() $N[y][g']$
coding a and
$N[y][g']$
coding a and
![]() $R'$
, respectively, such that
$R'$
, respectively, such that
![]() $(x_a,x_{R'})\in \tau [g']$
. The uniqueness of R implies
$(x_a,x_{R'})\in \tau [g']$
. The uniqueness of R implies
![]() $R\in N[y]$
. Since R is coded by a subset of a,
$R\in N[y]$
. Since R is coded by a subset of a,
![]() $R\in P[y]$
.
$R\in P[y]$
.
Corollary 3.14. If P is
![]() $\Gamma $
-ss and y is
$\Gamma $
-ss and y is
![]() $Ea_P$
-generic over P, then the map with domain
$Ea_P$
-generic over P, then the map with domain
![]() $P[y]|\nu _P$
defined by
$P[y]|\nu _P$
defined by
![]() $a \mapsto Lp^\Gamma (a)$
is definable in
$a \mapsto Lp^\Gamma (a)$
is definable in
![]() $P[y]$
from
$P[y]$
from
![]() $\tau ^P_{0,\nu _P}$
and y (uniformly in P and y).
$\tau ^P_{0,\nu _P}$
and y (uniformly in P and y).
Proof.
![]() $P[y]$
is
$P[y]$
is
![]() $Lp^\Gamma $
-closed by Lemma 3.13. Then by Lemma 3.7, the map
$Lp^\Gamma $
-closed by Lemma 3.13. Then by Lemma 3.7, the map
![]() $a\to Lp^\Gamma (a)$
with domain
$a\to Lp^\Gamma (a)$
with domain
![]() $P[y]|\nu _P$
is definable from any term
$P[y]|\nu _P$
is definable from any term
![]() $\tau \in P[y]^{Col(\omega ,\nu _P)}$
which weakly captures
$\tau \in P[y]^{Col(\omega ,\nu _P)}$
which weakly captures
![]() $G_0$
over
$G_0$
over
![]() $P[y]$
.
$P[y]$
.
Lemma 3.10 shows that there is a term
![]() $\tau \in P[y]^{Col(\omega ,\nu _P)}$
which weakly captures
$\tau \in P[y]^{Col(\omega ,\nu _P)}$
which weakly captures
![]() $G_0$
over
$G_0$
over
![]() $P[y]$
and is definable from
$P[y]$
and is definable from
![]() $\tau ^P_{0,\nu _P}$
and y in
$\tau ^P_{0,\nu _P}$
and y in
![]() $P[y]$
.
$P[y]$
.
Corollary 3.15. Suppose P is
![]() $\Gamma $
-ss, y is
$\Gamma $
-ss, y is
![]() $Ea_P$
-generic over P, and
$Ea_P$
-generic over P, and
![]() $N\in P[y]|\nu _P$
is
$N\in P[y]|\nu _P$
is
![]() $\Gamma $
-suitable. Then
$\Gamma $
-suitable. Then
![]() $\{\tau ^N_{n,\mu }: \mu \text { is an uncountable cardinal of } N \}$
is definable in
$\{\tau ^N_{n,\mu }: \mu \text { is an uncountable cardinal of } N \}$
is definable in
![]() $P[y]$
from N, y, and
$P[y]$
from N, y, and
![]() $\tau ^P_{n,\nu _P}$
(uniformly in P, y, and N).
$\tau ^P_{n,\nu _P}$
(uniformly in P, y, and N).
3.3 Internalizing the direct limit
Let
![]() $x_0\in \mathbb {R}$
be any real which is Turing above some real coding W and consider some M which is a countable, complete iterate of
$x_0\in \mathbb {R}$
be any real which is Turing above some real coding W and consider some M which is a countable, complete iterate of
![]() $M_{x_0}$
. For elements of
$M_{x_0}$
. For elements of
![]() $M|\nu _M$
, being a
$M|\nu _M$
, being a
![]() $\Gamma $
-suitable premouse, a
$\Gamma $
-suitable premouse, a
![]() $\Gamma $
-short iteration tree, or a
$\Gamma $
-short iteration tree, or a
![]() $\Gamma $
-maximal iteration tree is definable over M from
$\Gamma $
-maximal iteration tree is definable over M from
![]() $\tau ^M_{0,\nu _M}$
. (This follows easily from Corollary 3.8.) Let
$\tau ^M_{0,\nu _M}$
. (This follows easily from Corollary 3.8.) Let
Lemma 3.16. Let
![]() $\mathcal {T} \in M|\nu _M$
be a
$\mathcal {T} \in M|\nu _M$
be a
![]() $\Gamma $
-short tree on some
$\Gamma $
-short tree on some
![]() $\Gamma $
-suitable
$\Gamma $
-suitable
![]() $P\in M$
. Then the branch b picked by the iteration strategy for P is in M and b is definable in M from
$P\in M$
. Then the branch b picked by the iteration strategy for P is in M and b is definable in M from
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\tau ^M_{0,\nu _M}$
(uniformly). In particular,
$\tau ^M_{0,\nu _M}$
(uniformly). In particular,
![]() $M_b^{\mathcal {T}}$
and the iteration map
$M_b^{\mathcal {T}}$
and the iteration map
![]() $i_b^{\mathcal {T}}:P\to M_b^{\mathcal {T}}$
are definable in M from
$i_b^{\mathcal {T}}:P\to M_b^{\mathcal {T}}$
are definable in M from
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\tau ^M_{0,\nu _M}$
.
$\tau ^M_{0,\nu _M}$
.
Proof. Let g be
![]() $Col(\omega ,\nu _M)$
-generic over M. Note that b is the unique branch through
$Col(\omega ,\nu _M)$
-generic over M. Note that b is the unique branch through
![]() $\mathcal {T}$
which absorbs
$\mathcal {T}$
which absorbs
![]() $\mathcal {Q}(\mathcal {T})$
. So by Shoenfield absoluteness,
$\mathcal {Q}(\mathcal {T})$
. So by Shoenfield absoluteness,
![]() $b \in M[g]$
(in
$b \in M[g]$
(in
![]() $M[g]$
the existence of such a branch is a
$M[g]$
the existence of such a branch is a
![]() $\Sigma ^1_2$
statement about reals). But b is independent of the generic g, so
$\Sigma ^1_2$
statement about reals). But b is independent of the generic g, so
![]() $b\in M$
.
$b\in M$
.
It then follows from Corollary 3.8 that b, and therefore also
![]() $M_b^{\mathcal {T}}$
and
$M_b^{\mathcal {T}}$
and
![]() $i^{\mathcal {T}}_b$
, are definable in M from
$i^{\mathcal {T}}_b$
, are definable in M from
![]() $\tau ^M_{0,\nu _M}$
.
$\tau ^M_{0,\nu _M}$
.
Corollary 3.17. Suppose
![]() $P \in \mathcal {I}^M$
and
$P \in \mathcal {I}^M$
and
![]() $\Sigma $
is the iteration strategy for P. Suppose also
$\Sigma $
is the iteration strategy for P. Suppose also
![]() $\mathcal {T} \in M|\nu _M$
is an iteration tree on P below
$\mathcal {T} \in M|\nu _M$
is an iteration tree on P below
![]() $\delta _P$
of limit length. Whether
$\delta _P$
of limit length. Whether
![]() $\mathcal {T}$
is according to
$\mathcal {T}$
is according to
![]() $\Sigma $
is definable in M from parameter
$\Sigma $
is definable in M from parameter
![]() $\tau ^M_{0,\nu _M}$
by a formula independent of
$\tau ^M_{0,\nu _M}$
by a formula independent of
![]() $\mathcal {T}$
and the choice of
$\mathcal {T}$
and the choice of
![]() $\Gamma $
-ss mouse M.
$\Gamma $
-ss mouse M.
Lemma 3.18. Suppose
![]() $P,Q\in \mathcal {I}^M$
. Then there is
$P,Q\in \mathcal {I}^M$
. Then there is
![]() $R \in \mathcal {I}^M$
and normal iteration trees
$R \in \mathcal {I}^M$
and normal iteration trees
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
on P and Q, respectively, such that:
$\mathcal {U}$
on P and Q, respectively, such that:
-
1.
 $\mathcal {T}$
realizes R is a complete iterate of P,
$\mathcal {T}$
realizes R is a complete iterate of P, -
2.
 $\mathcal {U}$
realizes R is a complete iterate of Q,
$\mathcal {U}$
realizes R is a complete iterate of Q, -
3.
 $\mathcal {T}\upharpoonright lh(\mathcal {T}) \in M|\nu _M$
,
$\mathcal {T}\upharpoonright lh(\mathcal {T}) \in M|\nu _M$
, -
4.
 $\mathcal {U}\upharpoonright lh(\mathcal {U}) \in M|\nu _M$
, and
$\mathcal {U}\upharpoonright lh(\mathcal {U}) \in M|\nu _M$
, and -
5. R is definable in M from P, Q, and
 $\tau ^M_{0,\nu _M}$
(uniformly).
$\tau ^M_{0,\nu _M}$
(uniformly).
Proof. We perform a coiteration of P and Q inside M. Suppose so far from the coiteration we have obtained iteration trees
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
on P and Q, respectively.
$\mathcal {U}$
on P and Q, respectively.
Suppose
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
have successor length. Let
$\mathcal {U}$
have successor length. Let
![]() $P'$
and
$P'$
and
![]() $Q'$
be the last models of
$Q'$
be the last models of
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
, respectively. First consider the case
$\mathcal {U}$
, respectively. First consider the case
![]() $P' \trianglelefteq Q'$
or
$P' \trianglelefteq Q'$
or
![]() $P' \trianglelefteq Q'$
. If either is a proper initial segment of the other, or there are any drops on the branches to
$P' \trianglelefteq Q'$
. If either is a proper initial segment of the other, or there are any drops on the branches to
![]() $P'$
or
$P'$
or
![]() $Q'$
, we have violated the Dodd–Jensen property. So
$Q'$
, we have violated the Dodd–Jensen property. So
![]() $P'=Q'$
and
$P'=Q'$
and
![]() $P'$
is a common, complete iterate of P and Q. Otherwise, we continue the coiteration as usual by applying the extender at the least point of disagreement between the last models of
$P'$
is a common, complete iterate of P and Q. Otherwise, we continue the coiteration as usual by applying the extender at the least point of disagreement between the last models of
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
, respectively.
$\mathcal {U}$
, respectively.
Now suppose
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
are of limit length. In this case
$\mathcal {U}$
are of limit length. In this case
![]() $\mathcal {M}(\mathcal {T}) = \mathcal {M}(\mathcal {U})$
. If
$\mathcal {M}(\mathcal {T}) = \mathcal {M}(\mathcal {U})$
. If
![]() $\mathcal {T}$
is
$\mathcal {T}$
is
![]() $\Gamma $
-short, so is
$\Gamma $
-short, so is
![]() $\mathcal {U}$
, and by Lemma 3.16, M can identify the branches that the iteration strategies for P and Q pick through
$\mathcal {U}$
, and by Lemma 3.16, M can identify the branches that the iteration strategies for P and Q pick through
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
, respectively. So the coiteration can be continued inside M. Otherwise,
$\mathcal {U}$
, respectively. So the coiteration can be continued inside M. Otherwise,
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
are
$\mathcal {U}$
are
![]() $\Gamma $
-maximal. In this case let R be the unique
$\Gamma $
-maximal. In this case let R be the unique
![]() $\Gamma $
-suitable mouse extending
$\Gamma $
-suitable mouse extending
![]() $\mathcal {M}(\mathcal {T})$
. R is just the result of applying
$\mathcal {M}(\mathcal {T})$
. R is just the result of applying
![]() $Lp^\Gamma $
to
$Lp^\Gamma $
to
![]() $\mathcal {M}(\mathcal {T}) \omega $
times, so M can identify R by Lemma 3.7. Then R is a complete iterate of P and Q.
$\mathcal {M}(\mathcal {T}) \omega $
times, so M can identify R by Lemma 3.7. Then R is a complete iterate of P and Q.
The proof of the Comparison Lemma gives the coiteration terminates in fewer than
![]() $\nu _M$
steps. Then the argument above implies the trees from this coiteration, without their last branches, are in
$\nu _M$
steps. Then the argument above implies the trees from this coiteration, without their last branches, are in
![]() $M|\nu _M$
and definable in M.
$M|\nu _M$
and definable in M.
The lemma implies that
![]() $\mathcal {I}^M$
is a directed system.
$\mathcal {I}^M$
is a directed system.
![]() $\mathcal {I}^M$
is countable and contained in
$\mathcal {I}^M$
is countable and contained in
![]() $\mathcal {I}$
, so we may define the direct limit
$\mathcal {I}$
, so we may define the direct limit
![]() $\mathcal {H}^M$
of
$\mathcal {H}^M$
of
![]() $\mathcal {I}^M$
, and
$\mathcal {I}^M$
, and
![]() $\mathcal {H}^M \in \mathcal {I}$
. Let
$\mathcal {H}^M \in \mathcal {I}$
. Let
 $$ \begin{align*} \tilde{\mathcal{I}}^M =\, \{P \in \mathcal{I}^M : &\text{ there is a normal iteration tree } \mathcal{T} \text{ such that } \mathcal{T} \text{ realizes } \\ & P \text{ is a complete iterate of } W \text{ and } \mathcal{T}\upharpoonright lh(\mathcal{T}) \in M|\nu_M\}. \end{align*} $$
$$ \begin{align*} \tilde{\mathcal{I}}^M =\, \{P \in \mathcal{I}^M : &\text{ there is a normal iteration tree } \mathcal{T} \text{ such that } \mathcal{T} \text{ realizes } \\ & P \text{ is a complete iterate of } W \text{ and } \mathcal{T}\upharpoonright lh(\mathcal{T}) \in M|\nu_M\}. \end{align*} $$
![]() $\tilde {\mathcal {I}}^M$
is definable in M by Corollary 3.17.
$\tilde {\mathcal {I}}^M$
is definable in M by Corollary 3.17.
Lemma 3.19.
![]() $\tilde {\mathcal {I}}^M$
is cofinal in
$\tilde {\mathcal {I}}^M$
is cofinal in
![]() $\mathcal {I}^M$
. In particular, the direct limit of
$\mathcal {I}^M$
. In particular, the direct limit of
![]() $\tilde {\mathcal {I}}^M$
is
$\tilde {\mathcal {I}}^M$
is
![]() $\mathcal {H}^M$
.
$\mathcal {H}^M$
.
Proof. Suppose
![]() $P\in \mathcal {I}^M$
. By Lemma 3.18, there is
$P\in \mathcal {I}^M$
. By Lemma 3.18, there is
![]() $R \in \mathcal {I}^M$
which is a common, complete, normal iterate of both P and W by trees which are in M (modulo their final branches). Then R is below P in
$R \in \mathcal {I}^M$
which is a common, complete, normal iterate of both P and W by trees which are in M (modulo their final branches). Then R is below P in
![]() $\mathcal {I}^M$
and
$\mathcal {I}^M$
and
![]() $R\in \tilde {\mathcal {I}}^M$
.
$R\in \tilde {\mathcal {I}}^M$
.
Lemma 3.20. Suppose
![]() $P\in \mathcal {I}^M$
. Let
$P\in \mathcal {I}^M$
. Let
![]() $\Sigma $
be the (unique) iteration strategy for P. Suppose
$\Sigma $
be the (unique) iteration strategy for P. Suppose
![]() $\mathcal {T}\in M|\nu _M$
is an iteration tree on P according to
$\mathcal {T}\in M|\nu _M$
is an iteration tree on P according to
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $b = \Sigma (\mathcal {T})$
and let
$b = \Sigma (\mathcal {T})$
and let
![]() $Q = M^{\mathcal {T}}_b$
. Then Q is definable in M from
$Q = M^{\mathcal {T}}_b$
. Then Q is definable in M from
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\tau ^M_{0,\nu _M}$
. And
$\tau ^M_{0,\nu _M}$
. And
![]() $\pi _{P,Q}\upharpoonright \gamma ^P_n$
is definable in M from
$\pi _{P,Q}\upharpoonright \gamma ^P_n$
is definable in M from
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\langle \tau ^M_{k,\nu _M}: k < n \rangle $
(uniformly).
$\langle \tau ^M_{k,\nu _M}: k < n \rangle $
(uniformly).
Proof. If
![]() $\mathcal {T}$
is
$\mathcal {T}$
is
![]() $\Gamma $
-short, then this is by Lemma 3.16.
$\Gamma $
-short, then this is by Lemma 3.16.
Suppose
![]() $\mathcal {T}$
is
$\mathcal {T}$
is
![]() $\Gamma $
-maximal. Then
$\Gamma $
-maximal. Then
![]() $Q = \bigcup _{i < \omega } Q_i$
, where
$Q = \bigcup _{i < \omega } Q_i$
, where
![]() $Q_0 = \mathcal {M}(\mathcal {T})$
and
$Q_0 = \mathcal {M}(\mathcal {T})$
and
![]() $Q_{i+1} = Lp^\Gamma (Q_i)$
. So Q is definable from
$Q_{i+1} = Lp^\Gamma (Q_i)$
. So Q is definable from
![]() $\mathcal {M}(\mathcal {T})$
and
$\mathcal {M}(\mathcal {T})$
and
![]() $\tau ^M_{0,\nu _M}$
by Corollary 3.8. And
$\tau ^M_{0,\nu _M}$
by Corollary 3.8. And
![]() $\pi _{P,Q}\upharpoonright \gamma ^P_n = \pi _c\upharpoonright \gamma ^P_n$
, where c is any branch through
$\pi _{P,Q}\upharpoonright \gamma ^P_n = \pi _c\upharpoonright \gamma ^P_n$
, where c is any branch through
![]() $\mathcal {T}$
respecting
$\mathcal {T}$
respecting
![]() $\vec {G}_n$
. The argument of Lemma 3.16 shows that there is a branch c in M respecting
$\vec {G}_n$
. The argument of Lemma 3.16 shows that there is a branch c in M respecting
![]() $\vec {G}_n$
. Then
$\vec {G}_n$
. Then
![]() $\pi _{P,Q}\upharpoonright \gamma ^P_n = \pi _c\upharpoonright \gamma ^P_n$
for any wellfounded branch
$\pi _{P,Q}\upharpoonright \gamma ^P_n = \pi _c\upharpoonright \gamma ^P_n$
for any wellfounded branch
![]() $c\in M$
through
$c\in M$
through
![]() $\mathcal {T}$
such that
$\mathcal {T}$
such that
![]() $\pi _c(\langle \tau ^P_k: k < n \rangle ) = \langle \tau ^Q_k: k < n \rangle $
.
$\pi _c(\langle \tau ^P_k: k < n \rangle ) = \langle \tau ^Q_k: k < n \rangle $
.
![]() $\langle \tau ^P_k: k < n \rangle $
and
$\langle \tau ^P_k: k < n \rangle $
and
![]() $\langle \tau ^Q_k: k < n \rangle $
are definable in M from P, Q, and
$\langle \tau ^Q_k: k < n \rangle $
are definable in M from P, Q, and
![]() $\langle \tau ^M_{k,\nu _M}: k < n \rangle $
by Lemma 3.9. So
$\langle \tau ^M_{k,\nu _M}: k < n \rangle $
by Lemma 3.9. So
![]() $\pi _{P,Q}\upharpoonright \gamma _n^P$
is definable in M from
$\pi _{P,Q}\upharpoonright \gamma _n^P$
is definable in M from
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\langle \tau ^M_{k,\nu _M}: k < n \rangle $
.
$\langle \tau ^M_{k,\nu _M}: k < n \rangle $
.
It follows from the previous lemmas that for any
![]() $P\in \mathcal {I}^M$
,
$P\in \mathcal {I}^M$
,
![]() $\pi _{P,\mathcal {H}^M}\upharpoonright \gamma ^P_n$
is definable in M from P and
$\pi _{P,\mathcal {H}^M}\upharpoonright \gamma ^P_n$
is definable in M from P and
![]() $\langle \tau ^M_{k,\nu _M}: k < n \rangle $
(uniformly in M). The same lemmas hold in
$\langle \tau ^M_{k,\nu _M}: k < n \rangle $
(uniformly in M). The same lemmas hold in
![]() $M[y]$
for
$M[y]$
for
![]() $y\ Ea_M$
-generic over M. In particular, we have the following lemma.
$y\ Ea_M$
-generic over M. In particular, we have the following lemma.
Lemma 3.21. Suppose y is
![]() $Ea_M$
-generic over M and
$Ea_M$
-generic over M and
![]() $P \in \mathcal {I} \cap M[y]|\nu _M$
. Let
$P \in \mathcal {I} \cap M[y]|\nu _M$
. Let
![]() $\Sigma $
be the (unique) iteration strategy for P. Suppose
$\Sigma $
be the (unique) iteration strategy for P. Suppose
![]() $\mathcal {T}\in M[y]|\nu _M$
is an iteration tree on P according to
$\mathcal {T}\in M[y]|\nu _M$
is an iteration tree on P according to
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $b = \Sigma (\mathcal {T})$
and let
$b = \Sigma (\mathcal {T})$
and let
![]() $Q = M^{\mathcal {T}}_b$
. Then Q is definable in
$Q = M^{\mathcal {T}}_b$
. Then Q is definable in
![]() $M[y]$
from
$M[y]$
from
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\tau ^M_{0,\nu _M}$
. And
$\tau ^M_{0,\nu _M}$
. And
![]() $\pi _{P,Q}\upharpoonright \gamma ^P_n$
is definable in
$\pi _{P,Q}\upharpoonright \gamma ^P_n$
is definable in
![]() $M[y]$
from
$M[y]$
from
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\langle \tau ^M_{k,\nu _M}: k < n\rangle $
(uniformly). Moreover, the definition is independent not just of the choice of
$\langle \tau ^M_{k,\nu _M}: k < n\rangle $
(uniformly). Moreover, the definition is independent not just of the choice of
![]() $\Gamma $
-ss mouse M, but also of the generic y.
$\Gamma $
-ss mouse M, but also of the generic y.
Lemma 3.22. Suppose
![]() $p\in Ea_M$
and
$p\in Ea_M$
and
![]() $\dot {S}$
is an
$\dot {S}$
is an
![]() $Ea_M$
-name in
$Ea_M$
-name in
![]() $M|\nu _M$
such that
$M|\nu _M$
such that
![]() $p \Vdash _{Ea_M}$
“
$p \Vdash _{Ea_M}$
“
![]() $\dot {S}$
is a complete iterate of W.” Then there is
$\dot {S}$
is a complete iterate of W.” Then there is
![]() $R\in \tilde {I}^M$
such that R is a complete iterate of
$R\in \tilde {I}^M$
such that R is a complete iterate of
![]() $S[y]$
for every
$S[y]$
for every
![]() $y \in \mathbb {R}$
which is
$y \in \mathbb {R}$
which is
![]() $Ea_M$
-generic over M. Moreover, we can pick R such that R is (uniformly) definable in M from parameters
$Ea_M$
-generic over M. Moreover, we can pick R such that R is (uniformly) definable in M from parameters
![]() $\dot {S}$
and p.
$\dot {S}$
and p.
Proof. Let
![]() $\mathbb {P}$
be the finite support product
$\mathbb {P}$
be the finite support product
![]() $\Pi _{j<\omega } \mathbb {P}_j$
, where each
$\Pi _{j<\omega } \mathbb {P}_j$
, where each
![]() $\mathbb {P}_j$
is a copy of the part of
$\mathbb {P}_j$
is a copy of the part of
![]() $Ea_M$
below p. Let H be
$Ea_M$
below p. Let H be
![]() $\mathbb {P}$
-generic over M. We can represent H as
$\mathbb {P}$
-generic over M. We can represent H as
![]() $\Pi _{j<\omega } H_j$
, where
$\Pi _{j<\omega } H_j$
, where
![]() $H_j$
is
$H_j$
is
![]() $\mathbb {P}_j$
-generic over M. Let
$\mathbb {P}_j$
-generic over M. Let
![]() $\dot {S}_j$
be a
$\dot {S}_j$
be a
![]() $\mathbb {P}$
-name for
$\mathbb {P}$
-name for
![]() $\dot {S}[H_j]$
. Let
$\dot {S}[H_j]$
. Let
![]() $S_j = \dot {S}_j[H]$
for
$S_j = \dot {S}_j[H]$
for
![]() $j\in \omega $
and
$j\in \omega $
and
![]() $S_{-1} = W$
.
$S_{-1} = W$
.
Lemma 3.21 tells us that
![]() $M[H]$
can perform the simultaneous coiteration of all of the
$M[H]$
can perform the simultaneous coiteration of all of the
![]() $S_j$
for
$S_j$
for
![]() $j\in [-1,\omega )$
(except possibly finding the last branches). The proof of the Comparison Lemma gives that this coiteration terminates after fewer than
$j\in [-1,\omega )$
(except possibly finding the last branches). The proof of the Comparison Lemma gives that this coiteration terminates after fewer than
![]() $\nu _M$
steps. Let
$\nu _M$
steps. Let
![]() $R_j$
be the last model of the iteration tree on
$R_j$
be the last model of the iteration tree on
![]() $S_j$
produced by the coiteration. Since each
$S_j$
produced by the coiteration. Since each
![]() $S_j$
is a complete iterate of W, the Dodd–Jensen property implies that there are no drops on the branches from
$S_j$
is a complete iterate of W, the Dodd–Jensen property implies that there are no drops on the branches from
![]() $S_j$
to
$S_j$
to
![]() $R_j$
and
$R_j$
and
![]() $R_j = R_i$
for all
$R_j = R_i$
for all
![]() $i,j\in [-1,\omega )$
. Let
$i,j\in [-1,\omega )$
. Let
![]() $R = R_j$
for some (equivalently all)
$R = R_j$
for some (equivalently all)
![]() $j\in [-1,\omega )$
. Then R is a complete iterate of M and R is a complete iterate of
$j\in [-1,\omega )$
. Then R is a complete iterate of M and R is a complete iterate of
![]() $S_j$
for each
$S_j$
for each
![]() $j\in \omega $
. Let
$j\in \omega $
. Let
![]() $\mathcal {U}$
be the iteration tree on W from the coiteration.
$\mathcal {U}$
be the iteration tree on W from the coiteration.
Claim 3.23. R is independent of the choice of generic H.
Proof. Code R by a set of ordinals X contained in
![]() $\nu _M$
. Let
$\nu _M$
. Let
![]() $\dot {X}$
be a name for X. If R is not independent of H, then there is
$\dot {X}$
be a name for X. If R is not independent of H, then there is
![]() $\alpha < \nu _M$
and
$\alpha < \nu _M$
and
![]() $q_1,q_2\in \mathbb {P}$
such that
$q_1,q_2\in \mathbb {P}$
such that
![]() $q_1 \Vdash \check {\alpha }\in \dot {X}$
and
$q_1 \Vdash \check {\alpha }\in \dot {X}$
and
![]() $q_2 \Vdash \check {\alpha }\notin \dot {X}$
.
$q_2 \Vdash \check {\alpha }\notin \dot {X}$
.
Let
![]() $N> max(support(q_2))$
. Let
$N> max(support(q_2))$
. Let
![]() $\bar {q}_1$
be the condition
$\bar {q}_1$
be the condition
![]() $q_1$
shifted over by N—that is,
$q_1$
shifted over by N—that is,
![]() $support(\bar {q}_1) = \{j\in [N,\omega ) :\, j-N \in support(q_1)\}$
and for
$support(\bar {q}_1) = \{j\in [N,\omega ) :\, j-N \in support(q_1)\}$
and for
![]() $j\in support(\bar {q}_1)$
,
$j\in support(\bar {q}_1)$
,
![]() $\bar {q_1}(j) = q_1(j-N)$
. So
$\bar {q_1}(j) = q_1(j-N)$
. So
![]() $\bar {q}_1$
is compatible with
$\bar {q}_1$
is compatible with
![]() $q_2$
and by symmetry,
$q_2$
and by symmetry,
![]() $\bar {q}_1 \Vdash \check {\alpha }\in \dot {X}$
. But then there is
$\bar {q}_1 \Vdash \check {\alpha }\in \dot {X}$
. But then there is
![]() $r \leq q_2,\bar {q}_1$
which forces both
$r \leq q_2,\bar {q}_1$
which forces both
![]() $\check {\alpha }\in \dot {X}$
and
$\check {\alpha }\in \dot {X}$
and
![]() $\check {\alpha }\notin \dot {X}$
.
$\check {\alpha }\notin \dot {X}$
.
Claim 3.24.
![]() $\mathcal {U} \upharpoonright lh(\mathcal {U})$
is independent of the choice of generic H.
$\mathcal {U} \upharpoonright lh(\mathcal {U})$
is independent of the choice of generic H.
Proof. The same proof as in Claim 3.23 works.
Claim 3.23 implies
![]() $R\in M|\nu _M$
and R is a complete iterate of
$R\in M|\nu _M$
and R is a complete iterate of
![]() $S[y]$
for any y which is
$S[y]$
for any y which is
![]() $Ea_M$
-generic over M. Claim 3.24 gives that
$Ea_M$
-generic over M. Claim 3.24 gives that
![]() $\mathcal {U} \upharpoonright lh(\mathcal {U}) \in M|\nu _M$
and thus
$\mathcal {U} \upharpoonright lh(\mathcal {U}) \in M|\nu _M$
and thus
![]() $R\in \tilde {\mathcal {I}}^M$
.
$R\in \tilde {\mathcal {I}}^M$
.
3.4 The StrLe construction
Recall the mouse operator
![]() $x \to M_x$
defined in Section 2.5. In the following lemmas let
$x \to M_x$
defined in Section 2.5. In the following lemmas let
![]() $z,x \in \mathbb {R}$
be such that
$z,x \in \mathbb {R}$
be such that
![]() $z\in M_x$
and let
$z\in M_x$
and let
![]() $M= M_x$
.
$M= M_x$
.
Lemma 3.25. Suppose
![]() $P = StrLe[M,z]$
. Then P is
$P = StrLe[M,z]$
. Then P is
![]() $\Gamma $
-ss and
$\Gamma $
-ss and
![]() $\delta _P = \delta _M$
.
$\delta _P = \delta _M$
.
Proof. Let
![]() $\delta = \delta _M$
. By Lemma 2.24, the cardinals of P above
$\delta = \delta _M$
. By Lemma 2.24, the cardinals of P above
![]() $\delta $
are the same as the cardinals of M and
$\delta $
are the same as the cardinals of M and
![]() $\nu _M$
is inaccessible in P. Any inaccessible of P above
$\nu _M$
is inaccessible in P. Any inaccessible of P above
![]() $\delta $
is inaccessible in M, since M is a generic extension of P by a
$\delta $
is inaccessible in M, since M is a generic extension of P by a
![]() $\delta $
-c.c. forcing. In particular,
$\delta $
-c.c. forcing. In particular,
![]() $\nu _M$
is the unique inaccessible of P above
$\nu _M$
is the unique inaccessible of P above
![]() $\delta $
. Then it suffices to show the following claim.
$\delta $
. Then it suffices to show the following claim.
Claim 3.26.
-
(a) If
 $\eta < \delta $
, then
$\eta < \delta $
, then
 $Lp^\Gamma (P|\eta ) \triangleleft P$
.
$Lp^\Gamma (P|\eta ) \triangleleft P$
. -
(b)
 $\delta $
is a
$\delta $
is a
 $\Gamma $
-Woodin of P. That is,
$\Gamma $
-Woodin of P. That is,
 $\delta $
is Woodin in
$\delta $
is Woodin in
 $Lp^\Gamma (P|\delta )$
.
$Lp^\Gamma (P|\delta )$
. -
(c) If
 $\eta \in P$
and
$\eta \in P$
and
 $\eta \geq \delta $
, then
$\eta \geq \delta $
, then
 $P|(\eta ^+)^P \trianglelefteq Lp^\Gamma (P|\eta )$
.
$P|(\eta ^+)^P \trianglelefteq Lp^\Gamma (P|\eta )$
. -
(d)
 $P\models \delta $
is Woodin.
$P\models \delta $
is Woodin. -
(e) If
 $\eta < \delta $
,
$\eta < \delta $
,
 $\eta $
is not Woodin in
$\eta $
is not Woodin in
 $Lp^\Gamma (P|\eta )$
.
$Lp^\Gamma (P|\eta )$
. -
(f) If
 $\eta \in P$
and
$\eta \in P$
and
 $\delta \leq \eta $
, then
$\delta \leq \eta $
, then
 $Lp^\Gamma (P|\eta ) \subseteq P$
.
$Lp^\Gamma (P|\eta ) \subseteq P$
.
Proof. To prove (a), it suffices to show if
![]() $\eta < \delta $
,
$\eta < \delta $
,
![]() $R\triangleleft Lp^\Gamma (P|\eta )$
, and
$R\triangleleft Lp^\Gamma (P|\eta )$
, and
![]() ${\rho _\omega (R) = \eta }$
, then
${\rho _\omega (R) = \eta }$
, then
![]() $R\triangleleft P$
. Coiterate R against
$R\triangleleft P$
. Coiterate R against
![]() $Le[M,z]$
. Suppose
$Le[M,z]$
. Suppose
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
are the iteration trees on R and
$\mathcal {U}$
are the iteration trees on R and
![]() $Le[M,z]$
, respectively, from the coiteration.
$Le[M,z]$
, respectively, from the coiteration.
![]() $\mathcal {T}$
is above
$\mathcal {T}$
is above
![]() $\eta $
because
$\eta $
because
![]() ${Le[M,z]|\eta = R|\eta }$
and
${Le[M,z]|\eta = R|\eta }$
and
![]() $\eta $
is a cutpoint of R. Let
$\eta $
is a cutpoint of R. Let
![]() $\lambda < lh(\mathcal {T})$
be a limit ordinal and
$\lambda < lh(\mathcal {T})$
be a limit ordinal and
![]() ${Q= \mathcal {Q}(\mathcal {T}) = \mathcal {Q}(\mathcal {U})}$
. Since
${Q= \mathcal {Q}(\mathcal {T}) = \mathcal {Q}(\mathcal {U})}$
. Since
![]() $R \in Lp^\Gamma (P|\eta )$
and
$R \in Lp^\Gamma (P|\eta )$
and
![]() $\mathcal {T}$
is above
$\mathcal {T}$
is above
![]() $\eta $
,
$\eta $
,
![]() $Q \in Lp^\Gamma (\mathcal {M}(\mathcal {T}))$
.
$Q \in Lp^\Gamma (\mathcal {M}(\mathcal {T}))$
.
![]() $[0,\lambda ]_T$
and
$[0,\lambda ]_T$
and
![]() $[0,\lambda ]_U$
are the unique branches through
$[0,\lambda ]_U$
are the unique branches through
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
, respectively, which absorb Q. By Corollary 3.8, these branches can be identified in M. In particular, the coiteration of R and
$\mathcal {U}$
, respectively, which absorb Q. By Corollary 3.8, these branches can be identified in M. In particular, the coiteration of R and
![]() $Le[M,z]$
can be performed in M. Theorem 2.21 gives that R cannot outiterate
$Le[M,z]$
can be performed in M. Theorem 2.21 gives that R cannot outiterate
![]() $Le[M,z]$
. Then since R is
$Le[M,z]$
. Then since R is
![]() $\omega $
-sound, R projects to
$\omega $
-sound, R projects to
![]() $\eta $
, and
$\eta $
, and
![]() $Le[M,z]$
does not project to
$Le[M,z]$
does not project to
![]() $\eta $
, R is a proper initial segment of
$\eta $
, R is a proper initial segment of
![]() $Le[M,z]|(\eta ^+)^{Le[M,z]}$
.
$Le[M,z]|(\eta ^+)^{Le[M,z]}$
.
![]() $Le[M,z]$
agrees with P up to
$Le[M,z]$
agrees with P up to
![]() $\delta $
, so
$\delta $
, so
![]() $R\triangleleft P$
.
$R\triangleleft P$
.
(b) is by the proof of Theorem 11.3 of [Reference Mitchell and Steel7]. For (c), the iteration strategies for initial segments of
![]() $P|(\eta ^+)^P$
restricted to iteration trees above
$P|(\eta ^+)^P$
restricted to iteration trees above
![]() $\delta $
are in
$\delta $
are in
![]() $\boldsymbol {\Delta }$
by Fact 2.25. (d) is immediate from (b) and (c). See Sublemma 7.4 of [Reference Steel, Woodin, Kechris, Löwe and Steel21] for a proof of (e).
$\boldsymbol {\Delta }$
by Fact 2.25. (d) is immediate from (b) and (c). See Sublemma 7.4 of [Reference Steel, Woodin, Kechris, Löwe and Steel21] for a proof of (e).
Towards (f), let
![]() $Q = Lp^\Gamma (P|\eta )$
. Let
$Q = Lp^\Gamma (P|\eta )$
. Let
![]() $\mathbb {P}$
be the extender algebra in P at
$\mathbb {P}$
be the extender algebra in P at
![]() $\delta $
with
$\delta $
with
![]() $\delta $
generators.
$\delta $
generators.
![]() $M|\delta $
is
$M|\delta $
is
![]() $\mathbb {P}$
-generic over P. Note that
$\mathbb {P}$
-generic over P. Note that
![]() $\delta $
is Woodin in Q by (b). In particular,
$\delta $
is Woodin in Q by (b). In particular,
![]() $\mathbb {P}$
is also
$\mathbb {P}$
is also
![]() $\delta $
-c.c. in Q, so any antichain of
$\delta $
-c.c. in Q, so any antichain of
![]() $\mathbb {P}$
in Q is also in P and
$\mathbb {P}$
in Q is also in P and
![]() $M|\delta $
is also
$M|\delta $
is also
![]() $\mathbb {P}$
-generic over Q.
$\mathbb {P}$
-generic over Q.
Let
![]() $B \in Lp^\Gamma (P|\eta )$
. B is in
$B \in Lp^\Gamma (P|\eta )$
. B is in
![]() $M = P[M|\delta ]$
since
$M = P[M|\delta ]$
since
![]() $P|\eta $
is in M and M is closed under
$P|\eta $
is in M and M is closed under
![]() $Lp^\Gamma $
. So let
$Lp^\Gamma $
. So let
![]() $\dot {B}$
be a
$\dot {B}$
be a
![]() $\mathbb {P}$
-name in P such that
$\mathbb {P}$
-name in P such that
![]() $\dot {B}[M|\delta ] = B$
.
$\dot {B}[M|\delta ] = B$
.
Choose
![]() $p\in \mathbb {P}$
such that
$p\in \mathbb {P}$
such that
![]() $p \Vdash ^Q_{\mathbb {P}} \dot {B} = \check {B}$
.
$p \Vdash ^Q_{\mathbb {P}} \dot {B} = \check {B}$
.
Any G which is
![]() $\mathbb {P}$
-generic over P is also
$\mathbb {P}$
-generic over P is also
![]() $\mathbb {P}$
-generic over Q. So for any G which is
$\mathbb {P}$
-generic over Q. So for any G which is
![]() $\mathbb {P}$
-generic over P such that
$\mathbb {P}$
-generic over P such that
![]() $p\in G$
,
$p\in G$
,
![]() $\dot {B}[G] = B$
. But then B is in P, since
$\dot {B}[G] = B$
. But then B is in P, since
![]() $B = \{\xi < \delta : p \Vdash ^P_{\mathbb {P}} \check {\xi } \in \dot {B}\}$
.Footnote
11
$B = \{\xi < \delta : p \Vdash ^P_{\mathbb {P}} \check {\xi } \in \dot {B}\}$
.Footnote
11
Lemma 3.27. Suppose
![]() $P = StrLe[M,z]$
. Let
$P = StrLe[M,z]$
. Let
![]() $\mu \geq \delta _P$
be a cardinal of P.
$\mu \geq \delta _P$
be a cardinal of P.
![]() $\tau ^P_{n,\mu }$
is definable in M from
$\tau ^P_{n,\mu }$
is definable in M from
![]() $\tau ^M_{n,\mu }$
and z.
$\tau ^M_{n,\mu }$
and z.
Proof. Let
 $$ \begin{align*} \tau = \, \{(\sigma,p)\in P : \, \sigma \text{ is a } Col(\omega,\mu) \text{-standard term for a real}, p\in Col(\omega,\mu), \\ \text{ and } p \Vdash^M_{Col(\omega,\mu)} \sigma \in P[\dot{g}] \cap \tau^M_{n,\mu}\}. \end{align*} $$
$$ \begin{align*} \tau = \, \{(\sigma,p)\in P : \, \sigma \text{ is a } Col(\omega,\mu) \text{-standard term for a real}, p\in Col(\omega,\mu), \\ \text{ and } p \Vdash^M_{Col(\omega,\mu)} \sigma \in P[\dot{g}] \cap \tau^M_{n,\mu}\}. \end{align*} $$
Since
![]() $\tau ^M_{n,\mu }\in M$
and P is definable over M from z,
$\tau ^M_{n,\mu }\in M$
and P is definable over M from z,
![]() $\tau \in M$
and is definable from
$\tau \in M$
and is definable from
![]() $\tau ^M_{n,\mu }$
and z. Then it suffices to show the following claim.
$\tau ^M_{n,\mu }$
and z. Then it suffices to show the following claim.
Claim 3.28.
![]() $\tau = \tau ^P_{n,\mu }$
$\tau = \tau ^P_{n,\mu }$
Proof. Clearly
![]() $\tau \subseteq \tau ^P_{n,\mu }$
.
$\tau \subseteq \tau ^P_{n,\mu }$
.
Suppose
![]() $(\sigma ,p)\in \tau $
. Let
$(\sigma ,p)\in \tau $
. Let
![]() $\mathcal {C}$
be the set of g which are
$\mathcal {C}$
be the set of g which are
![]() $Col(\omega ,\mu )$
-generic over M such that
$Col(\omega ,\mu )$
-generic over M such that
![]() $p\in g$
. For any
$p\in g$
. For any
![]() $g\in \mathcal {C}$
,
$g\in \mathcal {C}$
,
![]() $\sigma [g] \in \tau ^M_{n,\mu }[g]$
. In particular,
$\sigma [g] \in \tau ^M_{n,\mu }[g]$
. In particular,
![]() $\sigma [g]\in G_n$
. Since
$\sigma [g]\in G_n$
. Since
![]() $\mathcal {C}$
is comeager in the set of
$\mathcal {C}$
is comeager in the set of
![]() $Col(\omega ,\mu )$
-generics over P which extend p,
$Col(\omega ,\mu )$
-generics over P which extend p,
![]() $\sigma \in \tau ^P_{n,\mu }$
.
$\sigma \in \tau ^P_{n,\mu }$
.
Lemma 3.29. Suppose
![]() $P = StrLe[M,z]$
. The iteration strategy for P is fullness-preserving and guided by
$P = StrLe[M,z]$
. The iteration strategy for P is fullness-preserving and guided by
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Proof. Let
![]() $\Sigma $
be the (unique) iteration strategy for P. The proof of Theorem 2.22 gives that
$\Sigma $
be the (unique) iteration strategy for P. The proof of Theorem 2.22 gives that
![]() $\Sigma $
is determined by lifting an iteration on P to one on M. More precisely, if
$\Sigma $
is determined by lifting an iteration on P to one on M. More precisely, if
![]() $\mathcal {T}$
is a non-droppingFootnote
12
iteration tree on
$\mathcal {T}$
is a non-droppingFootnote
12
iteration tree on
![]() $P_0 = P$
with
$P_0 = P$
with
![]() $\langle P_\alpha \rangle $
the models of the iteration and
$\langle P_\alpha \rangle $
the models of the iteration and
![]() $i_{\beta ,\alpha }$
the associated iteration maps for
$i_{\beta ,\alpha }$
the associated iteration maps for
![]() $\beta <_T \alpha $
, then we maintain an iteration tree
$\beta <_T \alpha $
, then we maintain an iteration tree
![]() $\mathcal {T}^*$
on
$\mathcal {T}^*$
on
![]() $M_0 = M$
with models
$M_0 = M$
with models
![]() $\langle M_\alpha \rangle $
and associated iteration embeddings
$\langle M_\alpha \rangle $
and associated iteration embeddings
![]() $i^*_{\beta ,\alpha }$
. We also maintain embeddings
$i^*_{\beta ,\alpha }$
. We also maintain embeddings
![]() $\pi _\alpha : P_\alpha \to StrLe[M_\alpha ,z]$
such that
$\pi _\alpha : P_\alpha \to StrLe[M_\alpha ,z]$
such that
![]() $\pi _\alpha \circ i_{\beta ,\alpha } = i^*_{\beta ,\alpha } \circ \pi _\beta $
and
$\pi _\alpha \circ i_{\beta ,\alpha } = i^*_{\beta ,\alpha } \circ \pi _\beta $
and
![]() $\pi _0 = id$
. In particular,
$\pi _0 = id$
. In particular,
![]() $\pi _\alpha \circ i_{0,\alpha } = i^*_{0,\alpha }$
.
$\pi _\alpha \circ i_{0,\alpha } = i^*_{0,\alpha }$
.
Suppose
![]() $\mu $
is a cardinal of P and
$\mu $
is a cardinal of P and
![]() $\mu> \delta _P$
. By Lemma 3.27,
$\mu> \delta _P$
. By Lemma 3.27,
![]() $i^*_{0,\alpha }(\tau ^P_{n,\mu }) = \tau ^{StrLe[M_\alpha ,z]}_{n,\mu }$
for each
$i^*_{0,\alpha }(\tau ^P_{n,\mu }) = \tau ^{StrLe[M_\alpha ,z]}_{n,\mu }$
for each
![]() $n<\omega $
. Then
$n<\omega $
. Then
![]() $\pi _\alpha \circ i_{0,\alpha }(\tau ^P_{n,\mu }) = \tau ^{StrLe[M_\alpha ,z]}_{n,\mu }$
. Then by Lemma 2.34,
$\pi _\alpha \circ i_{0,\alpha }(\tau ^P_{n,\mu }) = \tau ^{StrLe[M_\alpha ,z]}_{n,\mu }$
. Then by Lemma 2.34,
![]() $P_\alpha $
is
$P_\alpha $
is
![]() $\Gamma $
-ss and
$\Gamma $
-ss and
![]() $\pi _\alpha (\tau ^{P_\alpha }_{n,\mu }) = \tau ^{StrLe[M_\alpha ,z]}_{n,\mu }$
. This gives
$\pi _\alpha (\tau ^{P_\alpha }_{n,\mu }) = \tau ^{StrLe[M_\alpha ,z]}_{n,\mu }$
. This gives
![]() $\Sigma $
is fullness-preserving. A second application of Lemma 2.34 gives
$\Sigma $
is fullness-preserving. A second application of Lemma 2.34 gives
![]() $i_{0,\alpha }(\tau ^P_{n,\mu }) = \tau ^{P_\alpha }_{n,\mu }$
. So
$i_{0,\alpha }(\tau ^P_{n,\mu }) = \tau ^{P_\alpha }_{n,\mu }$
. So
![]() $\Sigma $
is guided by
$\Sigma $
is guided by
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Corollary 3.30. Suppose
![]() $P = StrLe[M,z]$
. Then the
$P = StrLe[M,z]$
. Then the
![]() $\omega _1$
-iteration strategy for P is not in
$\omega _1$
-iteration strategy for P is not in
![]() $\boldsymbol {\Gamma }$
.
$\boldsymbol {\Gamma }$
.
Lemma 3.31. Suppose
![]() $x,z\in \mathbb {R}$
and x codes a mouse N which is a complete iterate of
$x,z\in \mathbb {R}$
and x codes a mouse N which is a complete iterate of
![]() $M_z$
. Let
$M_z$
. Let
![]() $P = StrLe[M_x,z]$
. Then P is a complete iterate of N below
$P = StrLe[M_x,z]$
. Then P is a complete iterate of N below
![]() $\delta _N$
.
$\delta _N$
.
Proof. Coiterate N and P. Let
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
be the iteration trees on N and P, respectively, from the coiteration. Let
$\mathcal {U}$
be the iteration trees on N and P, respectively, from the coiteration. Let
![]() $N^*$
and
$N^*$
and
![]() $P^*$
be the last models of
$P^*$
be the last models of
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
, respectively.
$\mathcal {U}$
, respectively.
Suppose P outiterates N. One possibility is that there is a drop on the branch of
![]() $\mathcal {T}$
from P to
$\mathcal {T}$
from P to
![]() $P^*$
. Since the iteration strategy for P is fullness-preserving by Lemma 3.29,
$P^*$
. Since the iteration strategy for P is fullness-preserving by Lemma 3.29,
![]() $P^*$
has an
$P^*$
has an
![]() $\omega _1$
-iteration strategy in
$\omega _1$
-iteration strategy in
![]() $\boldsymbol {\Delta }$
. But the strategy for N is fullness-preserving and guided by
$\boldsymbol {\Delta }$
. But the strategy for N is fullness-preserving and guided by
![]() $\mathcal {G}$
. So
$\mathcal {G}$
. So
![]() $N^*$
cannot have an iteration strategy in
$N^*$
cannot have an iteration strategy in
![]() $\boldsymbol {\Delta }$
, contradicting that
$\boldsymbol {\Delta }$
, contradicting that
![]() $N^* \trianglelefteq P^*$
.
$N^* \trianglelefteq P^*$
.
If there is no drop between P and
![]() $P^*$
, then
$P^*$
, then
![]() $N^* \triangleleft P$
. Since neither side of the coiteration drops,
$N^* \triangleleft P$
. Since neither side of the coiteration drops,
![]() $N^*$
and
$N^*$
and
![]() $P^*$
are both
$P^*$
are both
![]() $\Gamma $
-ss. But no
$\Gamma $
-ss. But no
![]() $\Gamma $
-ss mouse can have a proper initial segment which is
$\Gamma $
-ss mouse can have a proper initial segment which is
![]() $\Gamma $
-ss.
$\Gamma $
-ss.
An identical argument shows that N cannot outiterate P. Thus
![]() $N^* = P^*$
and
$N^* = P^*$
and
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {U}$
realize that
$\mathcal {U}$
realize that
![]() $N^*$
and
$N^*$
and
![]() $P^*$
are complete iterates of N and P, respectively. Since there are no total extenders on N above
$P^*$
are complete iterates of N and P, respectively. Since there are no total extenders on N above
![]() $\delta _N$
,
$\delta _N$
,
![]() $\mathcal {T}$
is below
$\mathcal {T}$
is below
![]() $\delta _N$
. Similarly,
$\delta _N$
. Similarly,
![]() $\mathcal {U}$
is below
$\mathcal {U}$
is below
![]() $\delta _P$
. Then stationarity of the Mitchell–Steel constructionFootnote
13
implies that
$\delta _P$
. Then stationarity of the Mitchell–Steel constructionFootnote
13
implies that
![]() $P^* = P$
. So
$P^* = P$
. So
![]() $\mathcal {T}$
realizes that P is a complete iterate of N.
$\mathcal {T}$
realizes that P is a complete iterate of N.
3.5 A reflection lemma
In this section we prove a lemma that any
![]() $\Sigma _1$
statement true in
$\Sigma _1$
statement true in
![]() $M_x$
also holds in some
$M_x$
also holds in some
![]() $N \triangleleft M_x|\kappa _{M_x}$
with the property that
$N \triangleleft M_x|\kappa _{M_x}$
with the property that
![]() $StrLe[N] \triangleleft StrLe[M]$
. A thorough reader not already familiar with the fully-backgrounded Mitchell–Steel construction may wish to review Section 2.3 before proceeding. A lazy one may read the statement of Lemma 3.35 and skip to Section 3.6.
$StrLe[N] \triangleleft StrLe[M]$
. A thorough reader not already familiar with the fully-backgrounded Mitchell–Steel construction may wish to review Section 2.3 before proceeding. A lazy one may read the statement of Lemma 3.35 and skip to Section 3.6.
First, we need to show that
![]() $M_x$
can compute the iteration strategies of its own initial segments below its Woodin cardinal. More precisely, we have the following lemma.
$M_x$
can compute the iteration strategies of its own initial segments below its Woodin cardinal. More precisely, we have the following lemma.
Lemma 3.32. Let
![]() $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
![]() $N \triangleleft M_x|\delta _{M_x}$
, and
$N \triangleleft M_x|\delta _{M_x}$
, and
![]() $\mathcal {T}\in M_x$
be an iteration tree on N of limit length
$\mathcal {T}\in M_x$
be an iteration tree on N of limit length
![]() $< \delta _{M_x}$
, according to the (unique) iteration strategy for N. The cofinal branch b through
$< \delta _{M_x}$
, according to the (unique) iteration strategy for N. The cofinal branch b through
![]() $\mathcal {T}$
determined by the iteration strategy for N is definable in
$\mathcal {T}$
determined by the iteration strategy for N is definable in
![]() $M_x$
(uniformly in N and
$M_x$
(uniformly in N and
![]() $\mathcal {T}$
, from the parameter
$\mathcal {T}$
, from the parameter
![]() $\tau ^{M_x}_{0,\nu _{M_x}}$
).
$\tau ^{M_x}_{0,\nu _{M_x}}$
).
Proof. Let
![]() $M = M_x$
. By Corollary 3.8, the function
$M = M_x$
. By Corollary 3.8, the function
![]() $a\mapsto Lp^\Gamma (a)$
with domain
$a\mapsto Lp^\Gamma (a)$
with domain
![]() $M|\delta _M$
is definable in M from the parameter
$M|\delta _M$
is definable in M from the parameter
![]() $\tau ^M_{0,\nu _M}$
.
$\tau ^M_{0,\nu _M}$
.
Let N and
![]() $\mathcal {T}$
be as in the statement of the lemma. Let
$\mathcal {T}$
be as in the statement of the lemma. Let
![]() $S = \mathcal {M}(\mathcal {T})$
. Clearly S is definable from
$S = \mathcal {M}(\mathcal {T})$
. Clearly S is definable from
![]() $\mathcal {T}$
. Let
$\mathcal {T}$
. Let
![]() $Q = \mathcal {Q}(\mathcal {T})$
. Q is an initial segment of
$Q = \mathcal {Q}(\mathcal {T})$
. Q is an initial segment of
![]() $Lp^\Gamma (S)$
. The previous paragraph implies that Q is definable in M from S and
$Lp^\Gamma (S)$
. The previous paragraph implies that Q is definable in M from S and
![]() $\tau ^M_{0,\nu _M}$
. The branch b through
$\tau ^M_{0,\nu _M}$
. The branch b through
![]() $\mathcal {T}$
chosen by the iteration strategy for N is the unique branch which absorbs Q.
$\mathcal {T}$
chosen by the iteration strategy for N is the unique branch which absorbs Q.
It remains to show that b is in M. Iterate M to
![]() $M'$
well above where
$M'$
well above where
![]() $\mathcal {T}$
is constructed to make some g generic over
$\mathcal {T}$
is constructed to make some g generic over
![]() $Ea^{M'}_{\delta _{M'}}$
so that g codes b.
$Ea^{M'}_{\delta _{M'}}$
so that g codes b.
![]() $M'[g]$
satisfies that b is the unique branch which absorbs Q. Since b is in fact the unique such branch in V, symmetry of the forcing gives b is in
$M'[g]$
satisfies that b is the unique branch which absorbs Q. Since b is in fact the unique such branch in V, symmetry of the forcing gives b is in
![]() $M'$
. But the iteration from M to
$M'$
. But the iteration from M to
![]() $M'$
does not add any subsets of
$M'$
does not add any subsets of
![]() $lh(\mathcal {T})$
, so in fact b is in M.
$lh(\mathcal {T})$
, so in fact b is in M.
We need to put down a few more properties of the Mitchell–Steel construction before proving the main lemma of this section.
Lemma 3.33. Suppose N is a mouse with a Woodin cardinal
![]() $\delta _N$
. Let
$\delta _N$
. Let
![]() $z\in N\cap \mathbb {R}$
. There is a club C of
$z\in N\cap \mathbb {R}$
. There is a club C of
![]() $\tau < \delta _N$
such that
$\tau < \delta _N$
such that
![]() $Le[N|\delta _N,z]|\tau = \mathcal {M}_\tau $
, where
$Le[N|\delta _N,z]|\tau = \mathcal {M}_\tau $
, where
![]() $\mathcal {M}_\tau $
is the Mitchell–Steel construction of length
$\mathcal {M}_\tau $
is the Mitchell–Steel construction of length
![]() $\tau $
in
$\tau $
in
![]() $N|\delta _N$
. Moreover, we can take C to be definable in N.
$N|\delta _N$
. Moreover, we can take C to be definable in N.
Proof. Let
![]() $\langle \mathcal {M}_\xi : \xi <\delta _N\rangle $
be the models from the Mitchell–Steel construction of length
$\langle \mathcal {M}_\xi : \xi <\delta _N\rangle $
be the models from the Mitchell–Steel construction of length
![]() $\delta _N$
over z, done inside
$\delta _N$
over z, done inside
![]() $N|\delta _N$
. Let
$N|\delta _N$
. Let
![]() $C'\subset \delta _N$
be the set of
$C'\subset \delta _N$
be the set of
![]() $\tau <\delta _N$
such that
$\tau <\delta _N$
such that
![]() $\mathcal {M}_\tau $
has height
$\mathcal {M}_\tau $
has height
![]() $\tau $
and
$\tau $
and
![]() $\rho _\omega (\mathcal {M}_\xi ) \geq \tau $
whenever
$\rho _\omega (\mathcal {M}_\xi ) \geq \tau $
whenever
![]() $\xi $
is between
$\xi $
is between
![]() $\tau $
and the height of N. It is not hard to see from the material in Section 2.3 that C is a club and if
$\tau $
and the height of N. It is not hard to see from the material in Section 2.3 that C is a club and if
![]() $\tau \in C$
, then
$\tau \in C$
, then
![]() $\mathcal {M}_\tau = Le[N|\delta _N,z]|\tau $
.
$\mathcal {M}_\tau = Le[N|\delta _N,z]|\tau $
.
Corollary 3.34. Let N, z, and C be as in Lemma 3.33. Let S be the set of inaccessibles of N below
![]() $\delta _N$
. Then
$\delta _N$
. Then
![]() $Le[N|\delta _N,z] = \bigcup _{\tau \in C\cap S} Le[N|\tau ,z]$
.
$Le[N|\delta _N,z] = \bigcup _{\tau \in C\cap S} Le[N|\tau ,z]$
.
Proof. Since
![]() $\delta _N$
is Woodin in N,
$\delta _N$
is Woodin in N,
![]() $N\models $
“S is stationary.” And C is definable in N, so
$N\models $
“S is stationary.” And C is definable in N, so
![]() $C\cap S$
is cofinal in
$C\cap S$
is cofinal in
![]() $\delta _N$
. Since
$\delta _N$
. Since
![]() $Le[N|\delta _N,z]$
has height
$Le[N|\delta _N,z]$
has height
![]() $\delta _N$
,
$\delta _N$
,
![]() $Le[N|\delta _N,z] = \bigcup _{\tau \in C\cap S} Le[N|\delta _N,z]|\tau $
. So it suffices to show that if
$Le[N|\delta _N,z] = \bigcup _{\tau \in C\cap S} Le[N|\delta _N,z]|\tau $
. So it suffices to show that if
![]() $\tau \in C \cap S$
, then
$\tau \in C \cap S$
, then
![]() $Le[N,z]|\tau = Le[N|\tau ,z]$
.
$Le[N,z]|\tau = Le[N|\tau ,z]$
.
Let
![]() $\langle \mathcal {M}_\xi : \xi <\delta _N\rangle $
be the models from the Mitchell–Steel construction of length
$\langle \mathcal {M}_\xi : \xi <\delta _N\rangle $
be the models from the Mitchell–Steel construction of length
![]() $\delta _N$
over z, done inside N.
$\delta _N$
over z, done inside N.
![]() $\tau \in C$
guarantees
$\tau \in C$
guarantees
![]() $Le[N,z]|\tau = \mathcal {M}_\tau $
. And by Remark 2.23,
$Le[N,z]|\tau = \mathcal {M}_\tau $
. And by Remark 2.23,
![]() $\tau \in S$
gives
$\tau \in S$
gives
![]() $\mathcal {M}_\tau = Le[N|\tau ,z]$
. So
$\mathcal {M}_\tau = Le[N|\tau ,z]$
. So
![]() $Le[N,z]|\tau = Le[N|\tau ,z]$
for
$Le[N,z]|\tau = Le[N|\tau ,z]$
for
![]() $\tau \in C \cap S$
.
$\tau \in C \cap S$
.
Lemma 3.35. Suppose
![]() $M_x\models \phi [\vec {a}, \delta _{M_x}]$
for some
$M_x\models \phi [\vec {a}, \delta _{M_x}]$
for some
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\phi $
,
$\phi $
,
![]() $z\in \mathbb {R} \cap M_x$
, and
$z\in \mathbb {R} \cap M_x$
, and
![]() $\vec {a}\in \mathbb {R}^{|\vec {a}|}\cap M_x$
. Then there exists
$\vec {a}\in \mathbb {R}^{|\vec {a}|}\cap M_x$
. Then there exists
![]() $N\triangleleft M_x|\kappa _{M_x}$
such that:
$N\triangleleft M_x|\kappa _{M_x}$
such that:
-
(a) N has one Woodin cardinal,
-
(b)
 $\delta _N$
is an inaccessible cardinal of
$\delta _N$
is an inaccessible cardinal of
 $M_x$
,
$M_x$
, -
(c)
 $N\models \phi [\vec {a}, \delta _N]$
, and
$N\models \phi [\vec {a}, \delta _N]$
, and -
(d)
 $StrLe[N,z] \triangleleft StrLe[M_x,z]$
.
$StrLe[N,z] \triangleleft StrLe[M_x,z]$
.
Proof. Denote
![]() $M_x$
by M. For ease of notation we will assume
$M_x$
by M. For ease of notation we will assume
![]() $z=0$
. Let
$z=0$
. Let
![]() $\mu $
be a cardinal of M above
$\mu $
be a cardinal of M above
![]() $\delta _M$
such that
$\delta _M$
such that
![]() $M|\mu \models \phi [\vec {a}]$
.
$M|\mu \models \phi [\vec {a}]$
.
Claim 3.36. There is a stationary set of
![]() $\tau <\delta _M$
such that
$\tau <\delta _M$
such that
![]() $\tau $
is inaccessible in M and if
$\tau $
is inaccessible in M and if
![]() $\tau \leq \zeta <\delta _M$
, then
$\tau \leq \zeta <\delta _M$
, then
![]() $\zeta $
is not definable in
$\zeta $
is not definable in
![]() $M|\mu $
from parameters below
$M|\mu $
from parameters below
![]() $\tau $
.
$\tau $
.
Proof. Work in M. Let S be the set of inaccessible cardinals below
![]() $\delta _M$
. Since
$\delta _M$
. Since
![]() $\delta _M$
is Woodin, S is stationary. Define
$\delta _M$
is Woodin, S is stationary. Define
![]() $f:S\to \delta _M$
by setting
$f:S\to \delta _M$
by setting
![]() $f(\zeta )$
to be the least
$f(\zeta )$
to be the least
![]() $\eta $
such that there is
$\eta $
such that there is
![]() $\zeta \leq \iota <\delta _M$
definable in
$\zeta \leq \iota <\delta _M$
definable in
![]() $M|\mu $
from parameters in
$M|\mu $
from parameters in
![]() $\eta $
. If the claim is false, then f is regressive on a stationary set. Then by Fodor’s Lemma, there is a stationary set
$\eta $
. If the claim is false, then f is regressive on a stationary set. Then by Fodor’s Lemma, there is a stationary set
![]() $S_0$
and
$S_0$
and
![]() $\eta <\delta _M$
such that
$\eta <\delta _M$
such that
![]() $f"S_0=\{\eta \}$
. But
$f"S_0=\{\eta \}$
. But
![]() $cof(\delta _M)>|\eta ^{<\omega }|\times \aleph _0$
, so we cannot have cofinally many elements of
$cof(\delta _M)>|\eta ^{<\omega }|\times \aleph _0$
, so we cannot have cofinally many elements of
![]() $\delta _M$
defined by some formula and parameters from
$\delta _M$
defined by some formula and parameters from
![]() $\eta $
.
$\eta $
.
Fix
![]() $\tau $
as in Lemma 3.33 and Claim 3.36. Let
$\tau $
as in Lemma 3.33 and Claim 3.36. Let
![]() $H = Hull^{M|\mu }(\tau )$
. Let N be the transitive collapse of H and
$H = Hull^{M|\mu }(\tau )$
. Let N be the transitive collapse of H and
![]() $\pi :N\to M|\mu $
the anti-collapse map.
$\pi :N\to M|\mu $
the anti-collapse map.
By condensation,
![]() $N\triangleleft M|\mu $
.Footnote
14
Clearly
$N\triangleleft M|\mu $
.Footnote
14
Clearly
![]() $N\triangleleft M|\delta _M$
,
$N\triangleleft M|\delta _M$
,
![]() $N\models \phi [\vec {a},\delta _N]$
,
$N\models \phi [\vec {a},\delta _N]$
,
![]() $\tau $
is the unique Woodin of N,
$\tau $
is the unique Woodin of N,
![]() $\tau $
is inaccessible in M, and
$\tau $
is inaccessible in M, and
![]() $\rho _\omega (N) = \tau $
.
$\rho _\omega (N) = \tau $
.
Claim 3.37.
![]() $Le[N|\tau ] \triangleleft Le[M|\delta _M].$
$Le[N|\tau ] \triangleleft Le[M|\delta _M].$
Proof. For
![]() $\zeta <\tau $
,
$\zeta <\tau $
,
![]() $Le[N|\zeta ] \triangleleft Le[N|\tau ] \iff Le[M|\zeta ] \triangleleft Le[M|\delta _M]$
by elementarity. But
$Le[N|\zeta ] \triangleleft Le[N|\tau ] \iff Le[M|\zeta ] \triangleleft Le[M|\delta _M]$
by elementarity. But
![]() $Le[N|\zeta ] = Le[M|\zeta ]$
for
$Le[N|\zeta ] = Le[M|\zeta ]$
for
![]() $\zeta < \tau $
. So if
$\zeta < \tau $
. So if
![]() $Le[N|\zeta ]$
is an initial segment of
$Le[N|\zeta ]$
is an initial segment of
![]() $Le[N|\tau ]$
, then it is also an initial segment of
$Le[N|\tau ]$
, then it is also an initial segment of
![]() $Le[M|\delta _M]$
. But this implies
$Le[M|\delta _M]$
. But this implies
![]() $Le[N|\tau ]\triangleleft Le[M|\delta _M]$
, since by Corollary 3.34,
$Le[N|\tau ]\triangleleft Le[M|\delta _M]$
, since by Corollary 3.34,
![]() $Le[N|\tau ]$
is a union of mice of the form
$Le[N|\tau ]$
is a union of mice of the form
![]() $Le[N|\zeta ]$
for
$Le[N|\zeta ]$
for
![]() $\zeta <\tau $
.
$\zeta <\tau $
.
We have found
![]() $N \triangleleft M|\delta _M$
satisfying a–c,
$N \triangleleft M|\delta _M$
satisfying a–c,
![]() $\rho _\omega (N) = \delta _N$
, and
$\rho _\omega (N) = \delta _N$
, and
![]() $Le[N|\delta _N]\triangleleft Le[M|\delta _M]$
(since
$Le[N|\delta _N]\triangleleft Le[M|\delta _M]$
(since
![]() $\delta _N = \tau )$
. Our next step is to reflect this below
$\delta _N = \tau )$
. Our next step is to reflect this below
![]() $\kappa _M$
. Let F be a total extender in M such that the strength of F is greater than
$\kappa _M$
. Let F be a total extender in M such that the strength of F is greater than
![]() $On \cap N$
. In particular, we have
$On \cap N$
. In particular, we have
![]() $N\triangleleft Ult(M|\delta _M,F)$
.
$N\triangleleft Ult(M|\delta _M,F)$
.
Claim 3.38.
![]() $Le[N|\tau ] \triangleleft Le[Ult(M|\delta _M,F)]$
.
$Le[N|\tau ] \triangleleft Le[Ult(M|\delta _M,F)]$
.
Proof.
![]() $\tau $
is inaccessible in
$\tau $
is inaccessible in
![]() $Ult(M|\delta _M,F)$
. So by Remark 2.23,
$Ult(M|\delta _M,F)$
. So by Remark 2.23,
![]() $Le[N|\tau ]$
equals the Mitchell–Steel construction of length
$Le[N|\tau ]$
equals the Mitchell–Steel construction of length
![]() $\tau $
in
$\tau $
in
![]() $Ult(M|\delta _M,F)$
.
$Ult(M|\delta _M,F)$
.
Suppose the claim fails. Then there is a mouse Q built during the Mitchell–Steel construction in
![]() $Ult(M|\delta _M,F)$
after
$Ult(M|\delta _M,F)$
after
![]() $Le[N|\tau ]$
is constructed, such that Q projects to some
$Le[N|\tau ]$
is constructed, such that Q projects to some
![]() $\beta < \tau $
. Pick such a Q which minimizes
$\beta < \tau $
. Pick such a Q which minimizes
![]() $\beta $
. By Lemma 3.32, any initial segment of M below
$\beta $
. By Lemma 3.32, any initial segment of M below
![]() $\delta _M$
is iterable in M. Then M has iteration strategies for
$\delta _M$
is iterable in M. Then M has iteration strategies for
![]() $Ult(P,F)$
for any
$Ult(P,F)$
for any
![]() $P\triangleleft M|\delta _M$
. Q is a mouse built during the Mitchell–Steel construction in
$P\triangleleft M|\delta _M$
. Q is a mouse built during the Mitchell–Steel construction in
![]() $Ult(P,F)$
for some
$Ult(P,F)$
for some
![]() $P\triangleleft M|\delta _M$
, so Q is also iterable in M. Let
$P\triangleleft M|\delta _M$
, so Q is also iterable in M. Let
![]() $Q' = \mathcal {C}_\omega (Q)$
. Then
$Q' = \mathcal {C}_\omega (Q)$
. Then
![]() $Q'$
is an
$Q'$
is an
![]() $\omega $
-sound mouse over
$\omega $
-sound mouse over
![]() $Le[N|\tau ]|\beta $
projecting to
$Le[N|\tau ]|\beta $
projecting to
![]() $\beta $
which is iterable in M. It follows from Theorem 2.21 that
$\beta $
which is iterable in M. It follows from Theorem 2.21 that
![]() $Le[M|\delta _M]$
outiterates
$Le[M|\delta _M]$
outiterates
![]() $Q'$
. Since both extend
$Q'$
. Since both extend
![]() $Le[N|\tau ]|\beta $
, and
$Le[N|\tau ]|\beta $
, and
![]() $Q'$
is
$Q'$
is
![]() $\omega $
-sound and projects to
$\omega $
-sound and projects to
![]() $\beta $
,
$\beta $
,
![]() $Q'\triangleleft Le[M|\delta _M]$
. But then since
$Q'\triangleleft Le[M|\delta _M]$
. But then since
![]() $\tau $
is inaccessible in M,
$\tau $
is inaccessible in M,
![]() $Le[M|\tau ]$
has height
$Le[M|\tau ]$
has height
![]() $\tau $
, and
$\tau $
, and
![]() $Le[M|\tau ]\triangleleft Le[M|\delta _M]$
,
$Le[M|\tau ]\triangleleft Le[M|\delta _M]$
,
![]() $Q'$
is in
$Q'$
is in
![]() $Le[M|\tau ]$
. This is a contradiction, since a subset of
$Le[M|\tau ]$
. This is a contradiction, since a subset of
![]() $\beta $
which is not in
$\beta $
which is not in
![]() $Le[M|\tau ]$
is definable over
$Le[M|\tau ]$
is definable over
![]() $Q'$
.
$Q'$
.
By elementarity of the ultrapower embedding induced by F, there exists
![]() $N\triangleleft M|\kappa _M$
satisfying a–c,
$N\triangleleft M|\kappa _M$
satisfying a–c,
![]() $\rho _\omega (N) = \delta _N$
, and
$\rho _\omega (N) = \delta _N$
, and
![]() $Le[N|\delta _N]\triangleleft Le[M|\delta _M]$
. It remains to prove the following claim.
$Le[N|\delta _N]\triangleleft Le[M|\delta _M]$
. It remains to prove the following claim.
Claim 3.39.
![]() $StrLe[N] \triangleleft StrLe[M]$
.
$StrLe[N] \triangleleft StrLe[M]$
.
Proof. Since N projects to
![]() $\delta _N$
, so does
$\delta _N$
, so does
![]() $StrLe[N]$
(by Lemma 2.24). And
$StrLe[N]$
(by Lemma 2.24). And
![]() $StrLe[N]$
agrees with
$StrLe[N]$
agrees with
![]() $StrLe[M]$
up to
$StrLe[M]$
up to
![]() $\delta _N$
since
$\delta _N$
since
![]() $Le[N|\delta _N] \triangleleft Le[M|\delta _M]$
. So it suffices to show
$Le[N|\delta _N] \triangleleft Le[M|\delta _M]$
. So it suffices to show
![]() $StrLe[M]$
outiterates
$StrLe[M]$
outiterates
![]() $StrLe[N]$
. But
$StrLe[N]$
. But
![]() $StrLe[N]$
has an iteration strategy in
$StrLe[N]$
has an iteration strategy in
![]() $\boldsymbol {\Gamma }$
, and
$\boldsymbol {\Gamma }$
, and
![]() $StrLe[M]$
cannot by Lemma 3.30.
$StrLe[M]$
cannot by Lemma 3.30.
3.6 Main theorem
We are ready to prove Theorem 1.12. Suppose for contradiction
![]() $\langle A_\alpha |\alpha < \boldsymbol {\delta _\Gamma ^+} \rangle $
is a sequence of distinct
$\langle A_\alpha |\alpha < \boldsymbol {\delta _\Gamma ^+} \rangle $
is a sequence of distinct
![]() $\boldsymbol {\Gamma }$
sets. Let
$\boldsymbol {\Gamma }$
sets. Let
![]() $U\subset \mathbb {R} \times \mathbb {R}$
be a universal
$U\subset \mathbb {R} \times \mathbb {R}$
be a universal
![]() $\boldsymbol {\Gamma }$
set.
$\boldsymbol {\Gamma }$
set.
Recall in Section 3.1 we defined
![]() $\mathcal {I}$
as the direct limit of all countable, complete iterates of the
$\mathcal {I}$
as the direct limit of all countable, complete iterates of the
![]() $\Gamma $
-suitable mouse W. Let
$\Gamma $
-suitable mouse W. Let
![]() $\mathcal {J} = \{(P,\xi ) : P \in \mathcal {I} \wedge \xi < \delta _P$
}. Say
$\mathcal {J} = \{(P,\xi ) : P \in \mathcal {I} \wedge \xi < \delta _P$
}. Say
![]() $(P,\xi )\leq _*(Q,\zeta )$
if
$(P,\xi )\leq _*(Q,\zeta )$
if
![]() $(P,\xi ),(Q,\zeta ) \in \mathcal {J}$
and whenever S is a complete iterate of both P and Q,
$(P,\xi ),(Q,\zeta ) \in \mathcal {J}$
and whenever S is a complete iterate of both P and Q,
![]() $\pi _{P,S}(\xi ) \leq \pi _{Q,S}(\zeta )$
. By Lemma 3.2, the relation
$\pi _{P,S}(\xi ) \leq \pi _{Q,S}(\zeta )$
. By Lemma 3.2, the relation
![]() $\leq _*$
has length
$\leq _*$
has length
![]() $> \boldsymbol {\delta _\Gamma ^+}$
. Fix n such that for some (equivalently any)
$> \boldsymbol {\delta _\Gamma ^+}$
. Fix n such that for some (equivalently any)
![]() $P\in \mathcal {I}$
,
$P\in \mathcal {I}$
,
![]() $\pi _{P,\infty }(\gamma ^P_n)> \boldsymbol {\delta _\Gamma ^+}$
. Let
$\pi _{P,\infty }(\gamma ^P_n)> \boldsymbol {\delta _\Gamma ^+}$
. Let
![]() $\leq ^{\prime }_*$
be
$\leq ^{\prime }_*$
be
![]() $\leq _*$
restricted to pairs
$\leq _*$
restricted to pairs
![]() $(P,\xi )$
such that
$(P,\xi )$
such that
![]() $\xi < \gamma ^P_n$
. Then
$\xi < \gamma ^P_n$
. Then
![]() $\leq ^{\prime }_*$
has length
$\leq ^{\prime }_*$
has length
![]() $\geq \boldsymbol {\delta _\Gamma ^+}$
and
$\geq \boldsymbol {\delta _\Gamma ^+}$
and
![]() $\leq ^{\prime }_*$
is in
$\leq ^{\prime }_*$
is in
![]() $J_{\beta '}(\mathbb {R})$
.Footnote
15
Let
$J_{\beta '}(\mathbb {R})$
.Footnote
15
Let
![]() $B_\alpha = \{y : U_y = A_\alpha \}$
. By the Coding Lemma there is a set D in
$B_\alpha = \{y : U_y = A_\alpha \}$
. By the Coding Lemma there is a set D in
![]() $J_{\beta '}(\mathbb {R})$
such that
$J_{\beta '}(\mathbb {R})$
such that
![]() $(x,y)\in D$
implies x codes a pair in the domain of
$(x,y)\in D$
implies x codes a pair in the domain of
![]() $\leq ^{\prime }_*$
and
$\leq ^{\prime }_*$
and
![]() $y\in B_{|x|_{\leq ^{\prime }_*}}$
, and
$y\in B_{|x|_{\leq ^{\prime }_*}}$
, and
![]() $D_x$
is nonempty for all x in the domain of
$D_x$
is nonempty for all x in the domain of
![]() $\leq ^{\prime }_*$
.
$\leq ^{\prime }_*$
.
Let
![]() $z_0\in \mathbb {R}$
be such that
$z_0\in \mathbb {R}$
be such that
![]() $z_0$
codes W and
$z_0$
codes W and
![]() $D\in OD^{<\beta '}(z_0)$
. Let
$D\in OD^{<\beta '}(z_0)$
. Let
![]() $\mathcal {I}'$
be the directed system of all countable, complete iterates of
$\mathcal {I}'$
be the directed system of all countable, complete iterates of
![]() $M_{z_0}$
. Let
$M_{z_0}$
. Let
![]() $M^{\prime }_\infty $
be the direct limit of
$M^{\prime }_\infty $
be the direct limit of
![]() $\mathcal {I}'$
. For
$\mathcal {I}'$
. For
![]() $M,N\in \mathcal {I}'$
and N an iterate of M, let
$M,N\in \mathcal {I}'$
and N an iterate of M, let
![]() $\pi _{M,N}: M \to N$
be the iteration map and
$\pi _{M,N}: M \to N$
be the iteration map and
![]() $\pi _{M,\infty }: M \to M^{\prime }_\infty $
the direct limit map. (We also used
$\pi _{M,\infty }: M \to M^{\prime }_\infty $
the direct limit map. (We also used
![]() $\pi _{M,N}$
and
$\pi _{M,N}$
and
![]() $\pi _{M,\infty }$
for
$\pi _{M,\infty }$
for
![]() $M,N\in \mathcal {I}$
, but this should not cause any confusion.)
$M,N\in \mathcal {I}$
, but this should not cause any confusion.)
For
![]() $M\in \mathcal {I}'$
, let
$M\in \mathcal {I}'$
, let
![]() $\tau ^M = \tau ^M_{D,\delta _M}$
. There is a slight issue in that our current definitions do not obviously guarantee that
$\tau ^M = \tau ^M_{D,\delta _M}$
. There is a slight issue in that our current definitions do not obviously guarantee that
![]() $\tau ^M$
is moved correctly. That is, we might have a complete iterate N of M such that
$\tau ^M$
is moved correctly. That is, we might have a complete iterate N of M such that
![]() $\pi _{M,N}(\tau ^M) \neq \tau ^N$
. This can happen because we defined the operator
$\pi _{M,N}(\tau ^M) \neq \tau ^N$
. This can happen because we defined the operator
![]() $x \mapsto M_x$
so that
$x \mapsto M_x$
so that
![]() $M_x$
is guided by
$M_x$
is guided by
![]() $\mathcal {G}$
, but it is possible
$\mathcal {G}$
, but it is possible
![]() $D\notin \mathcal {G}$
. There is no real issue here, since we can expand
$D\notin \mathcal {G}$
. There is no real issue here, since we can expand
![]() $\mathcal {G}$
to a larger self-justifying system
$\mathcal {G}$
to a larger self-justifying system
![]() $\mathcal {G}'$
such that
$\mathcal {G}'$
such that
![]() $D\in \mathcal {G}'$
and require
$D\in \mathcal {G}'$
and require
![]() $M_x$
be guided by
$M_x$
be guided by
![]() $\mathcal {G}'$
. However, we should leave the operator
$\mathcal {G}'$
. However, we should leave the operator
![]() $x \to W_x$
as is, otherwise we risk altering our construction of D. This raises another minor complication, because in Sections 3.2 and 3.3 we assumed our
$x \to W_x$
as is, otherwise we risk altering our construction of D. This raises another minor complication, because in Sections 3.2 and 3.3 we assumed our
![]() $\Gamma $
-ss mouse M was guided by the same self-justifying system as our
$\Gamma $
-ss mouse M was guided by the same self-justifying system as our
![]() $\Gamma $
-suitable mouse W. Fortunately, the results of those sections remain true so long as
$\Gamma $
-suitable mouse W. Fortunately, the results of those sections remain true so long as
![]() $\mathcal {G} \subseteq \mathcal {G}'$
, modulo increasing the number of terms required as parameters in some of the lemmas. For simplicity, in what follows we will just assume
$\mathcal {G} \subseteq \mathcal {G}'$
, modulo increasing the number of terms required as parameters in some of the lemmas. For simplicity, in what follows we will just assume
![]() $\tau ^M$
is moved correctly.
$\tau ^M$
is moved correctly.
Definition 3.40. Say
![]() $M \in \mathcal {I}'$
is locally
$M \in \mathcal {I}'$
is locally
![]() $\alpha $
-stable if there is
$\alpha $
-stable if there is
![]() $\xi \in M$
such that
$\xi \in M$
such that
![]() $\pi _{\mathcal {H}^M,\infty }(\xi )=\alpha $
. Write
$\pi _{\mathcal {H}^M,\infty }(\xi )=\alpha $
. Write
![]() $\alpha _M$
for this ordinal
$\alpha _M$
for this ordinal
![]() $\xi $
.
$\xi $
.
Definition 3.41. Say
![]() $M\in \mathcal {I}'$
is
$M\in \mathcal {I}'$
is
![]() $\alpha $
-stable if M is locally
$\alpha $
-stable if M is locally
![]() $\alpha $
-stable and whenever
$\alpha $
-stable and whenever
![]() $N\in \mathcal {I}'$
is a complete iterate of M,
$N\in \mathcal {I}'$
is a complete iterate of M,
![]() $\pi _{M,N}(\alpha _M) = \alpha _N$
.
$\pi _{M,N}(\alpha _M) = \alpha _N$
.
Lemma 3.42. For any
![]() $\alpha < \boldsymbol {\delta _\Gamma ^+}$
, there is an
$\alpha < \boldsymbol {\delta _\Gamma ^+}$
, there is an
![]() $\alpha $
-stable
$\alpha $
-stable
![]() $M\in \mathcal {I}'$
.
$M\in \mathcal {I}'$
.
Proof. This is essentially the same as the proof of the analogous lemma in [Reference Sargsyan11]. We will show for any
![]() $P\in \mathcal {I}'$
, there is an iterate of P which is
$P\in \mathcal {I}'$
, there is an iterate of P which is
![]() $\alpha $
-stable.
$\alpha $
-stable.
Claim 3.43. For any
![]() $P\in \mathcal {I}'$
, there is a countable, complete iterate R of P which is locally
$P\in \mathcal {I}'$
, there is a countable, complete iterate R of P which is locally
![]() $\alpha $
-stable.
$\alpha $
-stable.
Proof. Fix
![]() $S\in \mathcal {I}$
and
$S\in \mathcal {I}$
and
![]() $\zeta \in S$
such that
$\zeta \in S$
such that
![]() $\pi _{S,\infty }(\zeta ) = \alpha $
. Let R be a countable, complete iterate of P such that S is
$\pi _{S,\infty }(\zeta ) = \alpha $
. Let R be a countable, complete iterate of P such that S is
![]() $Ea_R$
-generic over R.
$Ea_R$
-generic over R.
Let
![]() $\dot {S}$
be an
$\dot {S}$
be an
![]() $Ea_R$
-name for S such that
$Ea_R$
-name for S such that
![]() $\emptyset \Vdash ^R_{Ea_R}$
“
$\emptyset \Vdash ^R_{Ea_R}$
“
![]() $\dot {S}$
is a complete iterate of W.” Applying Lemma 3.22 yields
$\dot {S}$
is a complete iterate of W.” Applying Lemma 3.22 yields
![]() $S'\in \mathcal {I}^R$
which is a complete iterate of S. Then
$S'\in \mathcal {I}^R$
which is a complete iterate of S. Then
In particular,
![]() $\alpha \in range(\pi _{\mathcal {H}^R,\infty })$
.
$\alpha \in range(\pi _{\mathcal {H}^R,\infty })$
.
Now suppose no
![]() $M \in \mathcal {I}'$
is
$M \in \mathcal {I}'$
is
![]() $\alpha $
-stable. Let
$\alpha $
-stable. Let
![]() $\langle R_j : j < \omega \rangle $
be a sequence in
$\langle R_j : j < \omega \rangle $
be a sequence in
![]() $\mathcal {I}'$
such that for all j,
$\mathcal {I}'$
such that for all j,
![]() $R_j$
is locally
$R_j$
is locally
![]() $\alpha $
-stable and
$\alpha $
-stable and
![]() $R_{j+1}$
is an iterate of
$R_{j+1}$
is an iterate of
![]() $R_j$
, but
$R_j$
, but
![]() $\pi _{R_j,R_{j+1}}(\alpha _{R_j}) \neq \alpha _{R_{j+1}}$
.
$\pi _{R_j,R_{j+1}}(\alpha _{R_j}) \neq \alpha _{R_{j+1}}$
.
Claim 3.44.
![]() $\pi _{R_j,R_{j+1}}(\alpha _{R_j}) \geq \alpha _{R_{j+1}}$
.
$\pi _{R_j,R_{j+1}}(\alpha _{R_j}) \geq \alpha _{R_{j+1}}$
.
Proof. By elementarity,
![]() $\pi _{R_j,R_{j+1}}\upharpoonright \mathcal {H}^{R_j}$
is an embedding of
$\pi _{R_j,R_{j+1}}\upharpoonright \mathcal {H}^{R_j}$
is an embedding of
![]() $\mathcal {H}^{R_j}$
into
$\mathcal {H}^{R_j}$
into
![]() $\mathcal {H}^{R_{j+1}}$
. Then the Dodd–Jensen property implies that for any common, complete iterate Q of
$\mathcal {H}^{R_{j+1}}$
. Then the Dodd–Jensen property implies that for any common, complete iterate Q of
![]() $\mathcal {H}^{R_j}$
and
$\mathcal {H}^{R_j}$
and
![]() $\mathcal {H}^{R_{j+1}}$
,
$\mathcal {H}^{R_{j+1}}$
,
Then
 $$ \begin{align*} \pi_{\mathcal{H}^{R_{j+1}},\infty} \circ \pi_{R_j,R_{j+1}}(\alpha_{R_j}) &\geq \pi_{\mathcal{H}^{R_j},\infty} (\alpha_{R_j}) \\ &= \alpha \\ &= \pi_{\mathcal{H}^{R_{j+1}},\infty}(\alpha_{R_{j+1}}). \end{align*} $$
$$ \begin{align*} \pi_{\mathcal{H}^{R_{j+1}},\infty} \circ \pi_{R_j,R_{j+1}}(\alpha_{R_j}) &\geq \pi_{\mathcal{H}^{R_j},\infty} (\alpha_{R_j}) \\ &= \alpha \\ &= \pi_{\mathcal{H}^{R_{j+1}},\infty}(\alpha_{R_{j+1}}). \end{align*} $$
So
![]() $\pi _{R_j,R_{j+1}}(\alpha _{R_j}) \geq \alpha _{R_{j+1}}$
.
$\pi _{R_j,R_{j+1}}(\alpha _{R_j}) \geq \alpha _{R_{j+1}}$
.
Let
![]() $R_\omega $
be the direct limit of the sequence
$R_\omega $
be the direct limit of the sequence
![]() $\langle R_j: j<\omega \rangle $
. Let
$\langle R_j: j<\omega \rangle $
. Let
![]() $\alpha _j = \pi _{R_j,R_\omega }(\alpha _{R_j})$
. Claim 3.44 implies
$\alpha _j = \pi _{R_j,R_\omega }(\alpha _{R_j})$
. Claim 3.44 implies
![]() $\alpha _{j+1} < \alpha _j$
for all j, contradicting the wellfoundedness of
$\alpha _{j+1} < \alpha _j$
for all j, contradicting the wellfoundedness of
![]() $R_\omega $
.
$R_\omega $
.
Let A be a maximal antichain in
![]() $Ea_M$
such that
$Ea_M$
such that
![]() $p\in A$
implies p forces the generic
$p\in A$
implies p forces the generic
![]() $ea$
is a pair
$ea$
is a pair
![]() $(ea^1,ea^2)$
, where
$(ea^1,ea^2)$
, where
![]() $ea^1$
codes a pair
$ea^1$
codes a pair
![]() $(R_{ea^1},\xi _{ea^1})$
such that there exists an iteration tree on W (according to the strategy for W) with last model
$(R_{ea^1},\xi _{ea^1})$
such that there exists an iteration tree on W (according to the strategy for W) with last model
![]() $R_{ea^1}$
and
$R_{ea^1}$
and
![]() $\xi _{ea^1} < \delta _{R_{ea^1}}$
.Footnote
16
Since
$\xi _{ea^1} < \delta _{R_{ea^1}}$
.Footnote
16
Since
![]() $Ea_M$
is
$Ea_M$
is
![]() $\delta _M$
-c.c.,
$\delta _M$
-c.c.,
![]() $|A|^M < \delta _M$
. Then the disjunction of conditions in A is also a condition in
$|A|^M < \delta _M$
. Then the disjunction of conditions in A is also a condition in
![]() $Ea_M$
. Pick
$Ea_M$
. Pick
![]() $p^M\in Ea_M$
to be the least condition in the constructability order of M which is the disjunction of conditions in some A as above, to ensure
$p^M\in Ea_M$
to be the least condition in the constructability order of M which is the disjunction of conditions in some A as above, to ensure
![]() $p^M$
is definable in M.
$p^M$
is definable in M.
![]() $p^M$
is a maximal condition forcing the property above, in that any condition
$p^M$
is a maximal condition forcing the property above, in that any condition
![]() $p'\in Ea_M$
which forces the same property is compatible with
$p'\in Ea_M$
which forces the same property is compatible with
![]() $p^M$
.
$p^M$
.
Lemma 3.45. There is
![]() $Q^M\in \mathcal {I}^M$
such that
$Q^M\in \mathcal {I}^M$
such that
![]() $p^M$
forces
$p^M$
forces
![]() $Q^M$
is a complete iterate of
$Q^M$
is a complete iterate of
![]() $R_{ea^1}$
. Moreover,
$R_{ea^1}$
. Moreover,
![]() $Q^M$
is definable in M from parameter
$Q^M$
is definable in M from parameter
![]() $p^M$
(uniformly in M).
$p^M$
(uniformly in M).
Proof. Apply Lemma 3.22 to the condition
![]() $p^M$
and a name for
$p^M$
and a name for
![]() $R_{ea^1}$
.
$R_{ea^1}$
.
Definition 3.46. For
![]() $\alpha $
-stable
$\alpha $
-stable
![]() $M\in \mathcal {I}'$
, say
$M\in \mathcal {I}'$
, say
![]() $p\in Ea_M$
is
$p\in Ea_M$
is
![]() $\alpha $
-good if p extends
$\alpha $
-good if p extends
![]() $p^M$
and p forces:
$p^M$
and p forces:
1.
![]() $\pi _{\check {Q}^M,\mathcal {H}^M} \circ \pi _{R_{ea^1},\check {Q}^M}(\xi _{ea^1}) = \alpha _M$
and
$\pi _{\check {Q}^M,\mathcal {H}^M} \circ \pi _{R_{ea^1},\check {Q}^M}(\xi _{ea^1}) = \alpha _M$
and
2.
![]() $(ea^1,ea^2)\in \tau ^M$
.
$(ea^1,ea^2)\in \tau ^M$
.
Remark 3.47. If
![]() $\alpha < \boldsymbol {\delta _\Gamma ^+}$
, being
$\alpha < \boldsymbol {\delta _\Gamma ^+}$
, being
![]() $\alpha $
-good is definable over
$\alpha $
-good is definable over
![]() $\alpha $
-stable
$\alpha $
-stable
![]() $M\in \mathcal {I}'$
from
$M\in \mathcal {I}'$
from
![]() $\alpha _M$
,
$\alpha _M$
,
![]() $\tau ^M$
, and
$\tau ^M$
, and
![]() $\langle \tau ^M_{k,\nu _M}: k < n \rangle $
(uniformly in M). This follows from Lemmas 3.20 and 3.21.
$\langle \tau ^M_{k,\nu _M}: k < n \rangle $
(uniformly in M). This follows from Lemmas 3.20 and 3.21.
Let
![]() $p^M_\alpha $
be the maximal
$p^M_\alpha $
be the maximal
![]() $\alpha $
-good condition in M which is least in the construction of M. Note that if M is
$\alpha $
-good condition in M which is least in the construction of M. Note that if M is
![]() $\alpha $
-stable and N is a complete iterate of M, then
$\alpha $
-stable and N is a complete iterate of M, then
![]() $\pi _{M,N}(p^M_\alpha ) = p^N_\alpha $
.
$\pi _{M,N}(p^M_\alpha ) = p^N_\alpha $
.
For
![]() $w\in \mathbb {R} \cap M$
and a
$w\in \mathbb {R} \cap M$
and a
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\psi (w)$
, write
$\psi (w)$
, write
![]() $M \models [\psi (w)]$
to mean whenever g is
$M \models [\psi (w)]$
to mean whenever g is
![]() $Col(\omega ,\delta _M)$
-generic over M, there is a proper initial segment of
$Col(\omega ,\delta _M)$
-generic over M, there is a proper initial segment of
![]() $M[g]$
which is a
$M[g]$
which is a
![]() $\langle \psi ',g\rangle $
-witness, where
$\langle \psi ',g\rangle $
-witness, where
![]() $\psi '(x)$
is a formula expressing “
$\psi '(x)$
is a formula expressing “
![]() $\psi (f(x))$
” for some computable function f such that
$\psi (f(x))$
” for some computable function f such that
![]() $f(g) = w$
. Note that “
$f(g) = w$
. Note that “
![]() $M\models [\psi (w)]$
” is
$M\models [\psi (w)]$
” is
![]() $\Sigma _1$
over M if M is iterable.
$\Sigma _1$
over M if M is iterable.
For
![]() $\alpha $
-stable
$\alpha $
-stable
![]() $M\in \mathcal {I}'$
, let
$M\in \mathcal {I}'$
, let
![]() $S^M_\alpha $
be the set of conditions q such that there exist
$S^M_\alpha $
be the set of conditions q such that there exist
![]() $N,r\in M$
satisfying:
$N,r\in M$
satisfying:
-
(a)
 $N\triangleleft M|\kappa _M$
,
$N\triangleleft M|\kappa _M$
, -
(b) N has one Woodin,
-
(c)
 $\delta _N$
is a cardinal of M,
$\delta _N$
is a cardinal of M, -
(d)
 $q,r\in Ea_N$
and
$q,r\in Ea_N$
and
 $(q,r) \Vdash ^N_{Ea_N \times Ea_N} [U(ea_l,ea_r^2)],$
Footnote
17
and
$(q,r) \Vdash ^N_{Ea_N \times Ea_N} [U(ea_l,ea_r^2)],$
Footnote
17
and -
(e) r is compatible with
 $p^M_\alpha $
.
$p^M_\alpha $
.
Let
![]() $S_\alpha = \pi _{M,\infty }(S^M_\alpha )$
for some (equivalently any)
$S_\alpha = \pi _{M,\infty }(S^M_\alpha )$
for some (equivalently any)
![]() $\alpha $
-stable
$\alpha $
-stable
![]() $M\in \mathcal {I}'$
.
$M\in \mathcal {I}'$
.
![]() $S_\alpha $
can be viewed as an element of
$S_\alpha $
can be viewed as an element of
![]() $P(\kappa _{M^{\prime }_\infty })^{M^{\prime }_\infty }$
.
$P(\kappa _{M^{\prime }_\infty })^{M^{\prime }_\infty }$
.
Let
![]() $A^{\prime }_\alpha $
be the set of reals x such that for any
$A^{\prime }_\alpha $
be the set of reals x such that for any
![]() $\alpha $
-stable
$\alpha $
-stable
![]() $\bar {M}\in \mathcal {I}'$
there is a countable, complete iterate M of
$\bar {M}\in \mathcal {I}'$
there is a countable, complete iterate M of
![]() $\bar {M}$
and
$\bar {M}$
and
![]() $q\in M$
satisfying:
$q\in M$
satisfying:
-
1.
 $q\in S_\alpha ^M$
,
$q\in S_\alpha ^M$
, -
2.
 $x\models q$
, and
$x\models q$
, and -
3. x is
 $Ea_M$
-generic over M.
$Ea_M$
-generic over M.
Lemma 3.48.
![]() $A^{\prime }_\alpha = A_\alpha $
.
$A^{\prime }_\alpha = A_\alpha $
.
Corollary 3.49.
![]() $\alpha \neq \beta \implies S_\alpha \neq S_\beta $
.
$\alpha \neq \beta \implies S_\alpha \neq S_\beta $
.
Proof. Suppose
![]() $S_\alpha = S_\beta $
. Let
$S_\alpha = S_\beta $
. Let
![]() $x\in A_\alpha $
. Let
$x\in A_\alpha $
. Let
![]() $\bar {M}\in \mathcal {I}'$
be
$\bar {M}\in \mathcal {I}'$
be
![]() $\beta $
-stable. There is a countable, complete iterate
$\beta $
-stable. There is a countable, complete iterate
![]() $\hat {M}$
of
$\hat {M}$
of
![]() $\bar {M}$
which is also
$\bar {M}$
which is also
![]() $\alpha $
-stable. By Lemma 3.48,
$\alpha $
-stable. By Lemma 3.48,
![]() $x\in A^{\prime }_\alpha $
, so there is a countable, complete iterate M of
$x\in A^{\prime }_\alpha $
, so there is a countable, complete iterate M of
![]() $\hat {M}$
such that
$\hat {M}$
such that
![]() $q\in S_\alpha ^M$
,
$q\in S_\alpha ^M$
,
![]() $x\models q$
, and x is
$x\models q$
, and x is
![]() $Ea_M$
-generic over M. M is also a complete iterate of
$Ea_M$
-generic over M. M is also a complete iterate of
![]() $\bar {M}$
, so we have shown
$\bar {M}$
, so we have shown
![]() $x\in A^{\prime }_\beta $
. Applying Lemma 3.48 again,
$x\in A^{\prime }_\beta $
. Applying Lemma 3.48 again,
![]() $x\in A_\beta $
. Similarly,
$x\in A_\beta $
. Similarly,
![]() $x\in A_\beta \implies x\in A_\alpha $
, so
$x\in A_\beta \implies x\in A_\alpha $
, so
![]() $A_\alpha = A_\beta $
and thus
$A_\alpha = A_\beta $
and thus
![]() $\alpha = \beta $
.
$\alpha = \beta $
.
It suffices to show Lemma 3.48. By the same proof as for
![]() $M_\infty $
given in Lemma 3.1,
$M_\infty $
given in Lemma 3.1,
![]() $\kappa _{M^{\prime }_\infty } \leq \boldsymbol {\delta _\Gamma }$
. Then by Corollary 3.49, we have
$\kappa _{M^{\prime }_\infty } \leq \boldsymbol {\delta _\Gamma }$
. Then by Corollary 3.49, we have
![]() $\boldsymbol {\delta _\Gamma ^+}$
distinct subsets of
$\boldsymbol {\delta _\Gamma ^+}$
distinct subsets of
![]() $\boldsymbol {\delta _\Gamma }$
in
$\boldsymbol {\delta _\Gamma }$
in
![]() $M^{\prime }_\infty $
. Then the successor of
$M^{\prime }_\infty $
. Then the successor of
![]() $\boldsymbol {\delta _\Gamma }$
in
$\boldsymbol {\delta _\Gamma }$
in
![]() $M^{\prime }_\infty $
is the successor of
$M^{\prime }_\infty $
is the successor of
![]() $\boldsymbol {\delta _\Gamma }$
in
$\boldsymbol {\delta _\Gamma }$
in
![]() $L(\mathbb {R})$
, contradicting the following claim.
$L(\mathbb {R})$
, contradicting the following claim.
Claim 3.50. Let
![]() $\eta = \boldsymbol {\delta _\Gamma }$
. Then
$\eta = \boldsymbol {\delta _\Gamma }$
. Then
![]() $(\eta ^+)^{M^{\prime }_\infty } < (\eta ^+)^{L(\mathbb {R})}$
.
$(\eta ^+)^{M^{\prime }_\infty } < (\eta ^+)^{L(\mathbb {R})}$
.
Proof. Let
![]() $\lambda = (\eta ^+)^{M^{\prime }_\infty }$
. Since
$\lambda = (\eta ^+)^{M^{\prime }_\infty }$
. Since
![]() $\lambda $
is regular in
$\lambda $
is regular in
![]() $M^{\prime }_\infty $
but not measurable, Lemma 3.6 implies that
$M^{\prime }_\infty $
but not measurable, Lemma 3.6 implies that
![]() $\lambda $
has cofinality
$\lambda $
has cofinality
![]() $\omega $
in
$\omega $
in
![]() $L(\mathbb {R})$
.
$L(\mathbb {R})$
.
Let
![]() $f\in L(\mathbb {R})$
be a cofinal function from
$f\in L(\mathbb {R})$
be a cofinal function from
![]() $\omega $
to
$\omega $
to
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $\langle g_\xi : \xi < \lambda \rangle $
be a sequence of functions in
$\langle g_\xi : \xi < \lambda \rangle $
be a sequence of functions in
![]() $M^{\prime }_\infty $
such that
$M^{\prime }_\infty $
such that
![]() $g_\xi :\eta \to \xi $
is a surjection. Such a sequence exists because
$g_\xi :\eta \to \xi $
is a surjection. Such a sequence exists because
![]() $M^{\prime }_\infty $
satisfies
$M^{\prime }_\infty $
satisfies
![]() $AC$
. Then in
$AC$
. Then in
![]() $L(\mathbb {R})$
we can construct from f and
$L(\mathbb {R})$
we can construct from f and
![]() $\langle g_\xi \rangle $
a surjection from
$\langle g_\xi \rangle $
a surjection from
![]() $\eta $
onto
$\eta $
onto
![]() $\lambda $
.
$\lambda $
.
Proof of Lemma 3.48.
First suppose
![]() $x\in A_\alpha $
. Let
$x\in A_\alpha $
. Let
![]() $\bar {M}\in \mathcal {I}'$
be
$\bar {M}\in \mathcal {I}'$
be
![]() $\alpha $
-stable. Pick
$\alpha $
-stable. Pick
![]() $y\in \mathbb {R}$
such that
$y\in \mathbb {R}$
such that
![]() $y = (y^1,y^2)$
,
$y = (y^1,y^2)$
,
![]() $D(y^1,y^2)$
holds, and
$D(y^1,y^2)$
holds, and
![]() $|y^1|_{\leq _*} = \alpha $
. Let z be a real coding
$|y^1|_{\leq _*} = \alpha $
. Let z be a real coding
![]() $\bar {M}$
and let
$\bar {M}$
and let
![]() $P=M_{\langle x,y,z \rangle }$
. Let
$P=M_{\langle x,y,z \rangle }$
. Let
![]() $S = StrLe[P,z_0]$
.
$S = StrLe[P,z_0]$
.
Claim 3.51.
x and y are
![]() $Ea_S$
-generic over S.Footnote
18
$Ea_S$
-generic over S.Footnote
18
Claim 3.52.
S is a complete iterate of
![]() $\bar {M}$
by an iteration below
$\bar {M}$
by an iteration below
![]() $\delta _{\bar {M}}$
.
$\delta _{\bar {M}}$
.
Proof. See Lemma 3.31.
Claim 3.53. There is
![]() $r\in Ea_S$
such that r is
$r\in Ea_S$
such that r is
![]() $\alpha $
-good and
$\alpha $
-good and
![]() $y\models r$
.
$y\models r$
.
Proof. Note that by choice of y,
![]() $y^1$
codes a pair
$y^1$
codes a pair
![]() $(R,\xi )$
such that R is a complete iterate of W,
$(R,\xi )$
such that R is a complete iterate of W,
![]() $\pi _{R,\mathcal {H}^S}(\xi ) = \alpha _S$
, and
$\pi _{R,\mathcal {H}^S}(\xi ) = \alpha _S$
, and
![]() $D(y^1,y^2)$
holds. Then there is
$D(y^1,y^2)$
holds. Then there is
![]() $r \in Ea_S$
such that
$r \in Ea_S$
such that
![]() $y\models r$
, r forces
$y\models r$
, r forces
![]() $\pi _{\check {Q}^S,\mathcal {H}^S} \circ \pi _{R_{ea^1},\check {Q}^S}(\xi _{ea^1}) = \alpha _S$
, and
$\pi _{\check {Q}^S,\mathcal {H}^S} \circ \pi _{R_{ea^1},\check {Q}^S}(\xi _{ea^1}) = \alpha _S$
, and
![]() $(ea^1,ea^2)\in \tau ^S$
.
$(ea^1,ea^2)\in \tau ^S$
.
Claim 3.54. There exist conditions
![]() $q,r\in Ea_S$
such that
$q,r\in Ea_S$
such that
![]() $x\models q$
,
$x\models q$
,
![]() $y\models r$
, and
$y\models r$
, and
![]() $(q,r) \Vdash ^S_{Ea_S \times Ea_S} [U(ea_l,ea_r^2)]$
.
$(q,r) \Vdash ^S_{Ea_S \times Ea_S} [U(ea_l,ea_r^2)]$
.
Proof. By Claim 3.53, y satisfies some
![]() $\alpha $
-good condition r. Let
$\alpha $
-good condition r. Let
![]() $y_0$
be
$y_0$
be
![]() $S[x]$
-generic such that
$S[x]$
-generic such that
![]() $y_0 \models r$
. Then by the definition of
$y_0 \models r$
. Then by the definition of
![]() $\alpha $
-good,
$\alpha $
-good,
![]() $y_0 = (y_0^1,y_0^2),$
where
$y_0 = (y_0^1,y_0^2),$
where
![]() $(y_0^1,y_0^2) \in D$
and
$(y_0^1,y_0^2) \in D$
and
![]() $|y_0^1|_{\leq _*} = \alpha $
. It follows that
$|y_0^1|_{\leq _*} = \alpha $
. It follows that
![]() $U_{y_0^2} = A_\alpha $
. So
$U_{y_0^2} = A_\alpha $
. So
![]() $x\in U_{y_0^2}$
.
$x\in U_{y_0^2}$
.
Subclaim 3.55.
![]() $S[x][y_0] \models [U(x,y_0^2)]$
.
$S[x][y_0] \models [U(x,y_0^2)]$
.
Proof. Let g be
![]() $Col(\omega , \delta _S)$
-generic over
$Col(\omega , \delta _S)$
-generic over
![]() $S[x][y_0]$
. Note that
$S[x][y_0]$
. Note that
![]() $S[x][y_0][g] = S[g]$
is a g-mouse. By the proof of Lemma 3.13,
$S[x][y_0][g] = S[g]$
is a g-mouse. By the proof of Lemma 3.13,
![]() $Lp^\Gamma (g)$
is contained in
$Lp^\Gamma (g)$
is contained in
![]() $S[g]$
. Let f be a computable function such that
$S[g]$
. Let f be a computable function such that
![]() $f(g) = (x,y_0^2)$
and let
$f(g) = (x,y_0^2)$
and let
![]() $U'(v)$
be a formula expressing
$U'(v)$
be a formula expressing
![]() $U(f(v))$
holds. By Lemma 2.48, there is a
$U(f(v))$
holds. By Lemma 2.48, there is a
![]() $\langle U', g\rangle $
-witness which is sound, projects to
$\langle U', g\rangle $
-witness which is sound, projects to
![]() $\omega $
, and has an iteration strategy in
$\omega $
, and has an iteration strategy in
![]() $\boldsymbol {\Delta }$
. Since
$\boldsymbol {\Delta }$
. Since
![]() $Lp^\Gamma (g)\subseteq S[g]$
, this witness is an initial segment of
$Lp^\Gamma (g)\subseteq S[g]$
, this witness is an initial segment of
![]() $S[g]$
.
$S[g]$
.
We have shown
![]() $S[x][y_0] \models [U(x,y_0^2)]$
for any
$S[x][y_0] \models [U(x,y_0^2)]$
for any
![]() $y_0$
which satisfies r and is
$y_0$
which satisfies r and is
![]() $S[x]$
-generic. Thus there is
$S[x]$
-generic. Thus there is
![]() $q\in Ea_S$
such that x satisfies q and
$q\in Ea_S$
such that x satisfies q and
![]() $(q,r) \Vdash [U(ea_l,ea_r^2)]$
.
$(q,r) \Vdash [U(ea_l,ea_r^2)]$
.
We next would like to find some
![]() $N\triangleleft S|\kappa _S$
with the properties of S we obtained above. Note Claims 3.51 and 3.54 are not first order over S, since x and y are not in S. So a straightforward reflection argument inside S will not suffice. The point of introducing P and obtaining S as a construction inside P is that these claims are first order in P. The next claim demonstrates that we can perform a reflection in P to obtain the desired initial segment of S.
$N\triangleleft S|\kappa _S$
with the properties of S we obtained above. Note Claims 3.51 and 3.54 are not first order over S, since x and y are not in S. So a straightforward reflection argument inside S will not suffice. The point of introducing P and obtaining S as a construction inside P is that these claims are first order in P. The next claim demonstrates that we can perform a reflection in P to obtain the desired initial segment of S.
Claim 3.56. There is
![]() $N\triangleleft S|\kappa _S$
such that N has one Woodin,
$N\triangleleft S|\kappa _S$
such that N has one Woodin,
![]() $\delta _N$
is an inaccessible cardinal of S, x and y are generic for
$\delta _N$
is an inaccessible cardinal of S, x and y are generic for
![]() $Ea_N$
, and there exist
$Ea_N$
, and there exist
![]() $q,r\in Ea_N \times Ea_N$
such that
$q,r\in Ea_N \times Ea_N$
such that
![]() $x\models q$
,
$x\models q$
,
![]() $y\models r$
, and
$y\models r$
, and
![]() $(q,r) \Vdash [U(ea_l,ea_r^2)]$
.
$(q,r) \Vdash [U(ea_l,ea_r^2)]$
.
Proof. By Claims 3.51 and 3.54, P satisfies:
-
1. x and y are
 $Ea_{StrLe[P,z_0]}$
-generic over
$Ea_{StrLe[P,z_0]}$
-generic over
 $StrLe[P,z_0]$
and
$StrLe[P,z_0]$
and -
2. there exist conditions
 $q,r\in StrLe[P,z_0]$
such that
$q,r\in StrLe[P,z_0]$
such that
 $x\models q$
,
$x\models q$
,
 $y\models r$
, and
$y\models r$
, and
 $(q,r) \Vdash ^{StrLe[P,z_0]}_{Ea_{StrLe[P,z_0]} \times Ea_{StrLe[P,z_0]}} [U(ea_l,ea^2_r)]$
.
$(q,r) \Vdash ^{StrLe[P,z_0]}_{Ea_{StrLe[P,z_0]} \times Ea_{StrLe[P,z_0]}} [U(ea_l,ea^2_r)]$
.
Both properties are
![]() $\Sigma _1$
over P in parameters x, y,
$\Sigma _1$
over P in parameters x, y,
![]() $z_0$
, and
$z_0$
, and
![]() $\delta _P$
. Then we may apply Lemma 3.35 to obtain
$\delta _P$
. Then we may apply Lemma 3.35 to obtain
![]() $P' \triangleleft P|\kappa _P$
such that
$P' \triangleleft P|\kappa _P$
such that
![]() $P'$
has one Woodin cardinal,
$P'$
has one Woodin cardinal,
![]() $\delta _{P'}$
is an inaccessible cardinal of P,
$\delta _{P'}$
is an inaccessible cardinal of P,
![]() $StrLe[P',z_0]\triangleleft S$
, and
$StrLe[P',z_0]\triangleleft S$
, and
![]() $P'$
satisfies properties 1 and 2.
$P'$
satisfies properties 1 and 2.
Let
![]() $N = StrLe[P',z_0]$
. Note that
$N = StrLe[P',z_0]$
. Note that
![]() $\delta _N = \delta _{P'}$
is an inaccessible cardinal of S. Then all the properties we required of N are apparent except that
$\delta _N = \delta _{P'}$
is an inaccessible cardinal of S. Then all the properties we required of N are apparent except that
![]() $N\triangleleft S|\kappa _S$
. Standard properties of the Mitchell–Steel construction imply that
$N\triangleleft S|\kappa _S$
. Standard properties of the Mitchell–Steel construction imply that
![]() $\kappa _S \geq \kappa _P$
.Footnote
19
Then N has cardinality less than
$\kappa _S \geq \kappa _P$
.Footnote
19
Then N has cardinality less than
![]() $\kappa _S$
in P, since N is contained in
$\kappa _S$
in P, since N is contained in
![]() $P'$
. Since also
$P'$
. Since also
![]() $N\triangleleft S$
, we have
$N\triangleleft S$
, we have
![]() $N\triangleleft S|\kappa _S$
.
$N\triangleleft S|\kappa _S$
.
To get
![]() $x\in A^{\prime }_\alpha $
, it remains to show the following claim.
$x\in A^{\prime }_\alpha $
, it remains to show the following claim.
Claim 3.57.
r is compatible with
![]() $p_\alpha ^S$
.
$p_\alpha ^S$
.
Proof. By Claim 3.53, y satisfies some
![]() $\alpha $
-good condition p. We may assume p extends r. p is
$\alpha $
-good condition p. We may assume p extends r. p is
![]() $\alpha $
-good, so by maximality p is compatible with
$\alpha $
-good, so by maximality p is compatible with
![]() $p^S_\alpha $
. Then r is compatible with
$p^S_\alpha $
. Then r is compatible with
![]() $p^S_\alpha $
as well.
$p^S_\alpha $
as well.
Now suppose
![]() $x\in A^{\prime }_\alpha $
. Let
$x\in A^{\prime }_\alpha $
. Let
![]() $M,q$
realize this (for whichever
$M,q$
realize this (for whichever
![]() $\bar {M}\in \mathcal {I}'$
you please) and let
$\bar {M}\in \mathcal {I}'$
you please) and let
![]() $N,r$
realize
$N,r$
realize
![]() $q\in S^M_\alpha $
. Let y be
$q\in S^M_\alpha $
. Let y be
![]() $M[x]$
-generic for
$M[x]$
-generic for
![]() $Ea_M$
such that
$Ea_M$
such that
![]() $y \models r \wedge p^M_\alpha $
. Since
$y \models r \wedge p^M_\alpha $
. Since
![]() $y \models p^M_\alpha $
,
$y \models p^M_\alpha $
,
![]() $y = (y^1,y^2),$
where
$y = (y^1,y^2),$
where
![]() $U_{y^2} = A_\alpha $
. Since
$U_{y^2} = A_\alpha $
. Since
![]() $(x,y)\models (q,r)$
,
$(x,y)\models (q,r)$
,
![]() $M[x][y] \models [U(x,y^2)]$
. Let
$M[x][y] \models [U(x,y^2)]$
. Let
![]() $g\subset Col(\omega ,\delta _M)$
be
$g\subset Col(\omega ,\delta _M)$
be
![]() $M[x][y]$
-generic. Then
$M[x][y]$
-generic. Then
![]() $M[x][y][g] = M[g]$
has an initial segment R witnessing
$M[x][y][g] = M[g]$
has an initial segment R witnessing
![]() $U(x,y^2)$
. By taking the least such R, we may assume R projects to
$U(x,y^2)$
. By taking the least such R, we may assume R projects to
![]() $\omega $
and hence
$\omega $
and hence
![]() $R \in Lp^\Gamma (g)$
. It follows that
$R \in Lp^\Gamma (g)$
. It follows that
![]() $x\in U_{y^2} = A_\alpha $
.
$x\in U_{y^2} = A_\alpha $
.
4 Remarks on some projective-like cases
Here we provide a few brief comments on the problem of unreachability for projective-like cases. Section 4.1 covers the projective pointclasses. In Section 4.2, we discuss what appears to be the main obstacle to proving the rest of the following conjecture.
Conjecture 4.1. Assume
![]() $ZF + AD + DC + V=L(\mathbb {R})$
. Suppose
$ZF + AD + DC + V=L(\mathbb {R})$
. Suppose
![]() $\kappa \leq \boldsymbol {\delta ^2_1}$
is a Suslin cardinal and
$\kappa \leq \boldsymbol {\delta ^2_1}$
is a Suslin cardinal and
![]() $\kappa $
is either a successor cardinal or a regular limit cardinal. Then
$\kappa $
is either a successor cardinal or a regular limit cardinal. Then
![]() $\kappa ^+$
is
$\kappa ^+$
is
![]() $S(\kappa )$
-unreachable.
$S(\kappa )$
-unreachable.
4.1 The projective cases
In the introduction, we discussed a theorem of Sargsysan solving the problem of unreachability for the projective pointclasses.
Theorem 4.2 (Sargsyan).
Assume
![]() $ZF + AD + DC$
. Then
$ZF + AD + DC$
. Then
![]() $\boldsymbol {\delta ^1_{2n+2}}$
is
$\boldsymbol {\delta ^1_{2n+2}}$
is
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
-unreachable.
$\boldsymbol {\Sigma ^1_{2n+2}}$
-unreachable.
Our technique for proving Theorem 1.12 gives another proof of Sargsyan’s theorem, which we outline below. We will assume
![]() $ZF + AD + DC$
for the rest of this section.
$ZF + AD + DC$
for the rest of this section.
Let
![]() $W = M_{2n+1}^\#$
. Let
$W = M_{2n+1}^\#$
. Let
![]() $\mathcal {I}$
be the directed system of countable, complete iterates of W and let
$\mathcal {I}$
be the directed system of countable, complete iterates of W and let
![]() $M_\infty $
be the direct limit of
$M_\infty $
be the direct limit of
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Fact 4.3.
![]() $\kappa _{M_\infty } < \boldsymbol {\delta ^1_{2n+2}}$
and
$\kappa _{M_\infty } < \boldsymbol {\delta ^1_{2n+2}}$
and
![]() $\delta _{M_\infty }> (\boldsymbol {\delta ^1_{2n+2}})^+$
.
$\delta _{M_\infty }> (\boldsymbol {\delta ^1_{2n+2}})^+$
.
The iteration strategy
![]() $\Sigma $
for W is guided by indiscernibles, analogously to how the iteration strategies for
$\Sigma $
for W is guided by indiscernibles, analogously to how the iteration strategies for
![]() $\Gamma $
-suitable mice are guided by terms for sets in a sjs.Footnote
20
[Reference Sargsyan10] covers this analysis of the iteration strategy for W in detail. Also analogously to Sections 3.2 and 3.3, inside an iterate M of
$\Gamma $
-suitable mice are guided by terms for sets in a sjs.Footnote
20
[Reference Sargsyan10] covers this analysis of the iteration strategy for W in detail. Also analogously to Sections 3.2 and 3.3, inside an iterate M of
![]() $M^\#_{2n+1}(x_0)$
for some
$M^\#_{2n+1}(x_0)$
for some
![]() $x_0\in \mathbb {R}$
coding W, we can form the direct limit
$x_0\in \mathbb {R}$
coding W, we can form the direct limit
![]() $\mathcal {H}^M$
of countable iterates of W in M and approximate the iteration maps from W to
$\mathcal {H}^M$
of countable iterates of W in M and approximate the iteration maps from W to
![]() $\mathcal {H}^M$
. This internalization is covered in [Reference Sargsyan11].
$\mathcal {H}^M$
. This internalization is covered in [Reference Sargsyan11].
The following fact gives us an analogue of the notion of a
![]() $\langle \phi ,z\rangle $
-witness.
$\langle \phi ,z\rangle $
-witness.
Fact 4.4. There is a computable function which sends a
![]() $\Sigma ^1_{2n+2}$
-formula
$\Sigma ^1_{2n+2}$
-formula
![]() $\phi $
to a formula
$\phi $
to a formula
![]() $\phi ^* = \phi ^*(u_0,\ldots ,u_{2n-1},v)$
in the language of mice such that the following hold:
$\phi ^* = \phi ^*(u_0,\ldots ,u_{2n-1},v)$
in the language of mice such that the following hold:
-
1. If
 $x\in \mathbb {R}$
, M is a countable,
$x\in \mathbb {R}$
, M is a countable,
 $\omega _1+1$
-iterable x-premouse,
$\omega _1+1$
-iterable x-premouse,
 $M\models ZFC$
, M has
$M\models ZFC$
, M has
 $2n$
Woodin cardinals
$2n$
Woodin cardinals
 $\delta _0,\ldots ,\delta _{2n-1}$
,
$\delta _0,\ldots ,\delta _{2n-1}$
,
 $\phi $
is a
$\phi $
is a
 $\Sigma ^1_{2n+2}$
formula, and
$\Sigma ^1_{2n+2}$
formula, and
 $M\models \phi ^*[\delta _0,\ldots ,\delta _{2n-1},x]$
, then
$M\models \phi ^*[\delta _0,\ldots ,\delta _{2n-1},x]$
, then
 $\phi (x)$
holds.
$\phi (x)$
holds. -
2. If
 $x\in \mathbb {R}$
,
$x\in \mathbb {R}$
,
 $\delta _0,\ldots ,\delta _{2n-1}$
are the Woodin cardinals of
$\delta _0,\ldots ,\delta _{2n-1}$
are the Woodin cardinals of
 $M^\#_{2n}(x)$
,
$M^\#_{2n}(x)$
,
 $\phi $
is a
$\phi $
is a
 $\Sigma ^1_{2n+2}$
formula, and
$\Sigma ^1_{2n+2}$
formula, and
 $\phi (x)$
holds, then a proper initial segment of M above
$\phi (x)$
holds, then a proper initial segment of M above
 $\delta _{2n-1}$
satisfies
$\delta _{2n-1}$
satisfies
 $ZFC$
and
$ZFC$
and
 $\phi ^*[\delta _0,\ldots ,\delta _{2n-1},x]$
.
$\phi ^*[\delta _0,\ldots ,\delta _{2n-1},x]$
.
With these tools it is not difficult to adapt our proof of Theorem 1.12 into a proof of Theorem 4.2.
Here is a brief overview of the proof of Theorem 4.2 in [Reference Sargsyan11]. The basis of this proof is also studying the directed system
![]() $\mathcal {I}'$
of countable iterates of
$\mathcal {I}'$
of countable iterates of
![]() $M^\#_{2n+1}(z_0)$
for some
$M^\#_{2n+1}(z_0)$
for some
![]() $z_0\in \mathbb {R}$
. Suppose
$z_0\in \mathbb {R}$
. Suppose
![]() $\langle A_\alpha : \alpha < \boldsymbol {\delta ^1_{2n+2}}\rangle $
is a sequence of distinct
$\langle A_\alpha : \alpha < \boldsymbol {\delta ^1_{2n+2}}\rangle $
is a sequence of distinct
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
sets. Fix a
$\boldsymbol {\Sigma ^1_{2n+2}}$
sets. Fix a
![]() $\Pi ^1_{2n+3}\backslash \Sigma ^1_{2n+3}$
set
$\Pi ^1_{2n+3}\backslash \Sigma ^1_{2n+3}$
set
![]() $A \subset \omega $
. If
$A \subset \omega $
. If
![]() $n\in A$
, this is witnessed in a proper initial segment of any
$n\in A$
, this is witnessed in a proper initial segment of any
![]() $M_{2n+1}$
-like
$M_{2n+1}$
-like
![]() $\Pi ^1_{2n+2}$
-iterable premouse M. Then there is a
$\Pi ^1_{2n+2}$
-iterable premouse M. Then there is a
![]() $\Sigma ^1_{2n+3}$
set
$\Sigma ^1_{2n+3}$
set
![]() $A' \subset A$
consisting of, roughly speaking, all
$A' \subset A$
consisting of, roughly speaking, all
![]() $n\in \omega $
which are witnessed in such an M before some
$n\in \omega $
which are witnessed in such an M before some
![]() $x\in A_\alpha $
is witnessed. There is
$x\in A_\alpha $
is witnessed. There is
![]() $n_0\in A'\backslash A$
. This is witnessed in some proper initial segment
$n_0\in A'\backslash A$
. This is witnessed in some proper initial segment
![]() $\bar {N}_M$
of
$\bar {N}_M$
of
![]() $M|\kappa _M$
for any
$M|\kappa _M$
for any
![]() $M\in \mathcal {I}'$
. A coding set
$M\in \mathcal {I}'$
. A coding set
![]() $S^M$
is defined analogously to our coding sets in the proof of Theorem 1.12, but with the additional requirement that the conditions appear below
$S^M$
is defined analogously to our coding sets in the proof of Theorem 1.12, but with the additional requirement that the conditions appear below
![]() $\bar {N}_M$
. The coding sets are used to show a
$\bar {N}_M$
. The coding sets are used to show a
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
code for
$\boldsymbol {\Sigma ^1_{2n+2}}$
code for
![]() $A_\alpha $
is small generic over M. The contradiction is obtained from this.
$A_\alpha $
is small generic over M. The contradiction is obtained from this.
The technique described in the previous paragraph is a stronger argument than the one we used for Theorem 1.12, since it gives coding sets which are uniformly bounded below the least strong cardinal. It is not clear whether a similar argument could work for inductive-like pointclasses. There is no obvious analogue of the
![]() $\Pi ^1_{2n+3}\backslash \Sigma ^1_{2n+3}$
set A for an inductive-like pointclass
$\Pi ^1_{2n+3}\backslash \Sigma ^1_{2n+3}$
set A for an inductive-like pointclass
![]() $\Gamma $
, since there is no universal
$\Gamma $
, since there is no universal
![]() $\Gamma \backslash \Gamma ^c$
set of integers. So the proof from [Reference Sargsyan11] is not applicable to inductive-like pointclasses. On the other hand, the techniques of Section 3 are applicable to the projective pointclasses. And this yields a substantially simpler proof of Theorem 4.2, since it eliminates the need for a uniform bound on our coding sets.
$\Gamma \backslash \Gamma ^c$
set of integers. So the proof from [Reference Sargsyan11] is not applicable to inductive-like pointclasses. On the other hand, the techniques of Section 3 are applicable to the projective pointclasses. And this yields a substantially simpler proof of Theorem 4.2, since it eliminates the need for a uniform bound on our coding sets.
4.2 Mouse sets and open problems
In this section we discuss the relationship between the problem of unreachability and well-known conjectures on mouse sets. We will assume
![]() $ZF + AD + DC + V=L(\mathbb {R})$
, although this is overkill for some of the results stated below.
$ZF + AD + DC + V=L(\mathbb {R})$
, although this is overkill for some of the results stated below.
Definition 4.5.
![]() $X \subset \mathbb {R}$
is a mouse set if there is an
$X \subset \mathbb {R}$
is a mouse set if there is an
![]() $\omega _1+1$
-iterable premouse M such that
$\omega _1+1$
-iterable premouse M such that
![]() $X = M \cap \mathbb {R}$
.
$X = M \cap \mathbb {R}$
.
Theorem 4.6 (Steel).
Suppose
![]() $\Gamma = \Sigma ^1_{n+2}$
for some
$\Gamma = \Sigma ^1_{n+2}$
for some
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $C_\Gamma $
is a mouse set.
$C_\Gamma $
is a mouse set.
Theorem 4.7 (Woodin).
Suppose
![]() $\lambda $
is a limit ordinal and let
$\lambda $
is a limit ordinal and let
![]() $\Gamma = \{ A \subseteq \mathbb {R} :\, A \text { is definable in } J_\beta (\mathbb {R}) \text { for some } \beta <\lambda \}$
. Then
$\Gamma = \{ A \subseteq \mathbb {R} :\, A \text { is definable in } J_\beta (\mathbb {R}) \text { for some } \beta <\lambda \}$
. Then
![]() $C_\Gamma $
is a mouse set.
$C_\Gamma $
is a mouse set.
See [Reference Steel16, Reference Steel, Kechris, Löwe and Steel20] for proofs of Theorems 4.6 and 4.7, respectively. Steel [Reference Steel, Kechris, Löwe and Steel20] also gives the following conjecture.
Conjecture 4.8 (Steel).
Suppose
![]() $\Gamma $
is a level of the (lightface) Levy hierarchy.Footnote
21
Then
$\Gamma $
is a level of the (lightface) Levy hierarchy.Footnote
21
Then
![]() $C_\Gamma $
is a mouse set.
$C_\Gamma $
is a mouse set.
Conjecture 4.8 is a way of asking if there is a mouse corresponding exactly to the pointclass
![]() $\Gamma $
. For each
$\Gamma $
. For each
![]() $\Gamma $
in the Levy hierarchy, the core model induction constructs a mouse which contains
$\Gamma $
in the Levy hierarchy, the core model induction constructs a mouse which contains
![]() $C_\Gamma $
, but in some cases the mouse constructed is too large. For example, let J be the mouse operator
$C_\Gamma $
, but in some cases the mouse constructed is too large. For example, let J be the mouse operator
![]() $J(x) = \bigcup _{n<\omega } M^\#_n(x)$
. If
$J(x) = \bigcup _{n<\omega } M^\#_n(x)$
. If
![]() $\Gamma = \Sigma _{n+2}(J_2(\mathbb {R}))$
, then
$\Gamma = \Sigma _{n+2}(J_2(\mathbb {R}))$
, then
There are many similar cases in which the mice constructed in [Reference Schindler and Steel13] skip the (hypothesized) mouse realizing Conjecture 4.8. Recent progress has been made towards Conjecture 4.8 in [Reference Rudominer9], which resolves the case
![]() $\Gamma = \Sigma _2(J_2(\mathbb {R}))$
.
$\Gamma = \Sigma _2(J_2(\mathbb {R}))$
.
The problem of unreachability is connected to a boldface version of Conjecture 4.8.
Conjecture 4.9. Suppose
![]() $\alpha \in ON$
and
$\alpha \in ON$
and
![]() $n \in \omega $
. For
$n \in \omega $
. For
![]() $x\in \mathbb {R}$
, let
$x\in \mathbb {R}$
, let
![]() $\Gamma _x$
consist of all pointsets A for which there is a
$\Gamma _x$
consist of all pointsets A for which there is a
![]() $\Sigma _n$
formula
$\Sigma _n$
formula
![]() $\phi $
with parameter x such that
$\phi $
with parameter x such that
![]() $A = \{y : J_\alpha (\mathbb {R})\models \phi [y]\}$
. Then for any
$A = \{y : J_\alpha (\mathbb {R})\models \phi [y]\}$
. Then for any
![]() $y\in \mathbb {R}$
, there is
$y\in \mathbb {R}$
, there is
![]() $x\in \mathbb {R}$
such that
$x\in \mathbb {R}$
such that
![]() $y \leq _T x$
and
$y \leq _T x$
and
![]() $C_{\Gamma _x}$
is a mouse set.
$C_{\Gamma _x}$
is a mouse set.
Presumably a proof of Conjecture 4.8 would relativize, so a proof of Conjecture 4.8 would also resolve Conjecture 4.9.
The mouse operator
![]() $x \mapsto M^\#_{2k}(x)$
realizes Conjecture 4.9 holds for
$x \mapsto M^\#_{2k}(x)$
realizes Conjecture 4.9 holds for
![]() $\alpha =1$
and
$\alpha =1$
and
![]() $n = 2k+2$
. To prove
$n = 2k+2$
. To prove
![]() $\boldsymbol {\delta ^1_{2n+2}}$
is
$\boldsymbol {\delta ^1_{2n+2}}$
is
![]() $\boldsymbol {\Sigma ^1_{2n+2}}$
-unreachable, we studied the direct limit of
$\boldsymbol {\Sigma ^1_{2n+2}}$
-unreachable, we studied the direct limit of
![]() $M = M^\#_{2n+1}(x_0)$
for some
$M = M^\#_{2n+1}(x_0)$
for some
![]() $x_0\in \mathbb {R}$
. Note that if g is
$x_0\in \mathbb {R}$
. Note that if g is
![]() $Col(\omega ,\delta _M)$
-generic over M, then
$Col(\omega ,\delta _M)$
-generic over M, then
![]() $M[g] = M^\#_{2n}(g)$
.
$M[g] = M^\#_{2n}(g)$
.
For
![]() $\alpha $
admissible, the mouse operator
$\alpha $
admissible, the mouse operator
![]() $x\mapsto M_x$
of Theorem 2.42 realizes Conjecture 4.9 holds in the case
$x\mapsto M_x$
of Theorem 2.42 realizes Conjecture 4.9 holds in the case
![]() $n=1$
. Note that if g is
$n=1$
. Note that if g is
![]() $Col(\omega ,\delta _{M_x})$
-generic over
$Col(\omega ,\delta _{M_x})$
-generic over
![]() $M_x$
, then
$M_x$
, then
![]() $M_x[g] \cap \mathbb {R} = Lp^\Gamma (g) \cap \mathbb {R} = C_{\Gamma }(g)$
. So in the inductive-like case as well we studied the direct limit of a mouse such that collapsing its least Woodin yields a mouse realizing one case of Conjecture 4.9.
$M_x[g] \cap \mathbb {R} = Lp^\Gamma (g) \cap \mathbb {R} = C_{\Gamma }(g)$
. So in the inductive-like case as well we studied the direct limit of a mouse such that collapsing its least Woodin yields a mouse realizing one case of Conjecture 4.9.
Thus for each pointclass
![]() $\boldsymbol {\Sigma _n}(J_\alpha (\mathbb {R}))$
for which we have proven Conjecture 1.10 holds, we used a mouse operator realizing Conjecture 4.9 holds for
$\boldsymbol {\Sigma _n}(J_\alpha (\mathbb {R}))$
for which we have proven Conjecture 1.10 holds, we used a mouse operator realizing Conjecture 4.9 holds for
![]() $\alpha $
and n. It seems likely a proof of Conjecture 4.1 would involve proving Conjecture 4.9 for each
$\alpha $
and n. It seems likely a proof of Conjecture 4.1 would involve proving Conjecture 4.9 for each
![]() $\alpha $
and n such that
$\alpha $
and n such that
![]() $\boldsymbol {\Sigma _n}(J_\alpha (\mathbb {R})) = S(\kappa )$
for some Suslin cardinal
$\boldsymbol {\Sigma _n}(J_\alpha (\mathbb {R})) = S(\kappa )$
for some Suslin cardinal
![]() $\kappa $
which is a successor cardinal or a regular limit cardinal.
$\kappa $
which is a successor cardinal or a regular limit cardinal.
Funding
The first two authors were supported by the National Science Foundation under Grant No. DMS-1764029. The third author gratefully acknowledges the support of the NCN Grant WEAVE-UNISONO, Id: 567137.