 $\mathfrak{M}_H(G)$-property
$\mathfrak{M}_H(G)$-property
 $\tau $-component in the Iwasawa main conjecture
$\tau $-component in the Iwasawa main conjecture
 ${\mathbb{Z}}_p$-towers
${\mathbb{Z}}_p$-towers
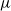 $\mu$-invariant of two-variable
$\mu$-invariant of two-variable  $2$-adic
$2$-adic  $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
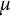 $\mu $-invariants of supersingular elliptic curves
$\mu $-invariants of supersingular elliptic curves