FirstView articles
Contents
Research Article
THE CLASS OF THE PRYM-BRILL-NOETHER DIVISOR
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2026, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HÖLDER CONTINUITY AND LAMINARITY OF THE GREEN CURRENTS FOR HÉNON-LIKE MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2026, pp. 1-30
-
- Article
- Export citation
ON THE GROWTH OF TORSION IN THE COHOMOLOGY OF SOME ARITHMETIC GROUPS OF
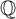 $\mathbb {Q}$-RANK ONE
$\mathbb {Q}$-RANK ONE
-
- Published online by Cambridge University Press:
- 30 January 2026, pp. 1-52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HOMOLOGICAL STRATIFICATION AND DESCENT
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2026, pp. 1-45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON RESIDUES OF INTERTWINING OPERATORS FOR HEISENBERG PARABOLIC SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-214
-
- Article
- Export citation
BEAUVILLE–LASZLO GLUING OF ALGEBRAIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 21 January 2026, pp. 1-43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRISMATIC COHOMOLOGY OF RIGID ANALYTIC SPACES OVER DE RHAM PERIOD RING
- Part of:
-
- Published online by Cambridge University Press:
- 20 January 2026, pp. 1-65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE LOCAL/LOGARITHMIC CORRESPONDENCE AND THE DEGENERATION FORMULA FOR QUASIMAPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2026, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SELF-DUAL AND EVEN POINCARÉ-EINSTEIN METRICS IN DIMENSION FOUR
-
- Published online by Cambridge University Press:
- 05 January 2026, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COHOMOLOGY OF THE BASIC UNRAMIFIED PEL UNITARY RAPOPORT-ZINK SPACE OF SIGNATURE
 $(1,n-1)$
$(1,n-1)$
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2025, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DETECTING IDEALS IN REDUCED CROSSED PRODUCT C*-ALGEBRAS OF TOPOLOGICAL DYNAMICAL SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 16 December 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
TWISTED BLANCHFIELD PAIRINGS AND TWISTED SIGNATURES II: RELATION TO CASSON-GORDON INVARIANTS – ERRATUM
-
- Published online by Cambridge University Press:
- 15 December 2025, p. 1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
J-INVARIANT OF LINEAR ALGEBRAIC GROUPS OF OUTER TYPE
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-28
-
- Article
- Export citation
2-CARTESIAN FIBRATIONS II: A GROTHENDIECK CONSTRUCTION FOR
 $\infty $-BICATEGORIES
$\infty $-BICATEGORIES
-
- Published online by Cambridge University Press:
- 02 December 2025, pp. 1-85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DYNAMIQUE ANALYTIQUE SUR Z. I: MESURES D’ÉQUILIBRE SUR UNE DROITE PROJECTIVE RELATIVE
- Part of:
-
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-43
-
- Article
- Export citation
PROPERTY (T) AND STRONG 1-BOUNDEDNESS FOR VON NEUMANN ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-34
-
- Article
- Export citation
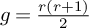
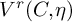
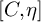
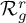
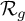
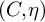
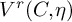
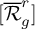
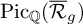
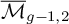
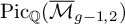
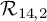





























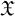
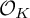
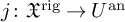
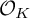
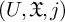
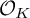
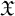
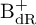










 -groupoid algebras to the general twisted setting.
-groupoid algebras to the general twisted setting.



 with values in the
with values in the 
