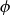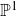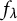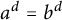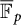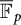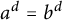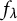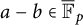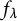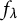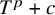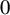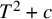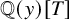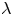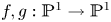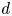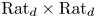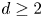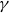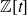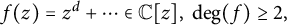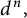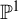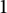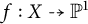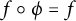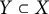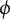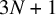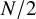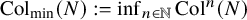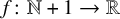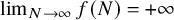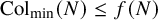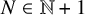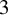Refine listing
Actions for selected content:
54 results in 37Pxx
Shared dynamically small points for polynomials on average
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-44
-
- Article
- Export citation
Iterating additive polynomials over finite fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 25 March 2025, pp. 795-810
-
- Article
- Export citation
Canonical heights for abelian group actions of maximal dynamical rank
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 28 January 2025, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entire maps with rational preperiodic points and multipliers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 15 January 2025, pp. 2636-2658
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniformity of quasi-integral points of bounded degree in higher-dimensional orbits
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 15-29
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Simultaneously preperiodic points for a family of polynomials in positive characteristic
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 December 2024, pp. 1-23
-
- Article
- Export citation
Counting points by height in semigroup orbits
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A MORDELL–LANG-TYPE PROBLEM FOR
 $\mathrm{GL}_{m}$
$\mathrm{GL}_{m}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 433-444
- Print publication:
- June 2025
-
- Article
- Export citation
Lower Bounds for the Canonical Height of a Unicritical Polynomial and Capacity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
There are at most finitely many singular moduli that are S-units
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 732-770
- Print publication:
- April 2024
-
- Article
- Export citation
Dynamics on ℙ1: preperiodic points and pairwise stability
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 356-387
- Print publication:
- February 2024
-
- Article
- Export citation
Finite orbits for large groups of automorphisms of projective surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 120-175
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Galois groups and prime divisors in random quadratic sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 07 September 2023, pp. 95-122
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mahler measure of polynomial iterates
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 January 2023, pp. 881-885
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic dynamics of the pentagram map
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 3460-3505
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-adelic measures and equidistribution on
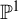 ${\mathbb P}^1$
${\mathbb P}^1$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 2732-2779
- Print publication:
- August 2023
-
- Article
- Export citation
Automorphism groups of endomorphisms of
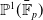 $\mathbb{P}^1 (\bar{\mathbb{F}}_p)$
$\mathbb{P}^1 (\bar{\mathbb{F}}_p)$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 222-255
- Print publication:
- January 2023
-
- Article
- Export citation
A conjecture strengthening the Zariski dense orbit problem for birational maps of dynamical degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 07 July 2022, pp. 477-491
- Print publication:
- June 2023
-
- Article
- Export citation
Almost all orbits of the Collatz map attain almost bounded values
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 May 2022, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform perfectness of the Berkovich Julia sets in non-archimedean dynamics
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 21 December 2021, pp. 573-590
- Print publication:
- November 2022
-
- Article
- Export citation