1 Introduction
Tensor triangular geometry, classically construed, studies the global and local geometry of a small tensor-triangulated category
![]() $\mathscr {K}$
through its spectrum
$\mathscr {K}$
through its spectrum
![]() $\operatorname {\mathrm {Spc}}(\mathscr {K})$
. This topological space, introduced by Balmer [Reference BalmerBal05], comes equipped with the universal theory of support for the objects of
$\operatorname {\mathrm {Spc}}(\mathscr {K})$
. This topological space, introduced by Balmer [Reference BalmerBal05], comes equipped with the universal theory of support for the objects of
![]() $\mathscr {K}$
, and yields a classification of the thick ideals of
$\mathscr {K}$
, and yields a classification of the thick ideals of
![]() $\mathscr {K}$
in terms of certain subsets of
$\mathscr {K}$
in terms of certain subsets of
![]() $\operatorname {\mathrm {Spc}}(\mathscr {K})$
, the so-called Thomason subsets. An important direction in recent years has been to extend this theory to the context of ‘big’Footnote 1 tensor-triangulated categories
$\operatorname {\mathrm {Spc}}(\mathscr {K})$
, the so-called Thomason subsets. An important direction in recent years has been to extend this theory to the context of ‘big’Footnote 1 tensor-triangulated categories
![]() $\mathscr {T}$
; here,
$\mathscr {T}$
; here,
![]() $\mathscr {K}$
arises as the full subcategory
$\mathscr {K}$
arises as the full subcategory
![]() $\mathscr {T}^c$
of compact-dualizable objects in
$\mathscr {T}^c$
of compact-dualizable objects in
![]() $\mathscr {T}$
.
$\mathscr {T}$
.
En route to the computation of the spectrum of the compact-dualizable objects in the derived category
![]() $\operatorname {\mathrm {D}}(R)$
of a noetherian commutative ring R, Neeman [Reference NeemanNee92] also classifies the localizing ideals of
$\operatorname {\mathrm {D}}(R)$
of a noetherian commutative ring R, Neeman [Reference NeemanNee92] also classifies the localizing ideals of
![]() $\operatorname {\mathrm {D}}(R)$
by showing that they correspond to arbitrary subsets of
$\operatorname {\mathrm {D}}(R)$
by showing that they correspond to arbitrary subsets of
![]() $\operatorname {\mathrm {Spec}}(R)$
. A systematic approach to such classification results for big tensor-triangulated categories was then introduced by Hovey, Palmieri and Strickland [Reference Hovey, Palmieri and StricklandHPS97] and further developed by Benson, Iyengar and Krause [Reference Benson, Iyengar and KrauseBIK08, Reference Benson, Iyengar and KrauseBIK11b]. The resulting notion of cohomological stratification for a big tensor-triangulated category
$\operatorname {\mathrm {Spec}}(R)$
. A systematic approach to such classification results for big tensor-triangulated categories was then introduced by Hovey, Palmieri and Strickland [Reference Hovey, Palmieri and StricklandHPS97] and further developed by Benson, Iyengar and Krause [Reference Benson, Iyengar and KrauseBIK08, Reference Benson, Iyengar and KrauseBIK11b]. The resulting notion of cohomological stratification for a big tensor-triangulated category
![]() $\mathscr {T}$
relies on the action of a noetherian ring R on
$\mathscr {T}$
relies on the action of a noetherian ring R on
![]() $\mathscr {T}$
in order to construct a suitable support theory. Cohomological stratification then asserts that this support theory induces a bijection
$\mathscr {T}$
in order to construct a suitable support theory. Cohomological stratification then asserts that this support theory induces a bijection
In practice, R is often taken to be the (graded) endomorphism ring ![]() of the unit in
of the unit in
![]() $\mathscr {T}$
.Footnote 2 A prominent application of this theory is the stratification of the stable module category of a finite group in modular characteristic due to Benson, Iyengar and Krause [Reference Benson, Iyengar and KrauseBIK11a]. Key to their proof is a descent result for cohomological stratification that provides a reduction from finite groups to elementary abelian groups, which can then be tackled via Neeman’s theorem.
$\mathscr {T}$
.Footnote 2 A prominent application of this theory is the stratification of the stable module category of a finite group in modular characteristic due to Benson, Iyengar and Krause [Reference Benson, Iyengar and KrauseBIK11a]. Key to their proof is a descent result for cohomological stratification that provides a reduction from finite groups to elementary abelian groups, which can then be tackled via Neeman’s theorem.
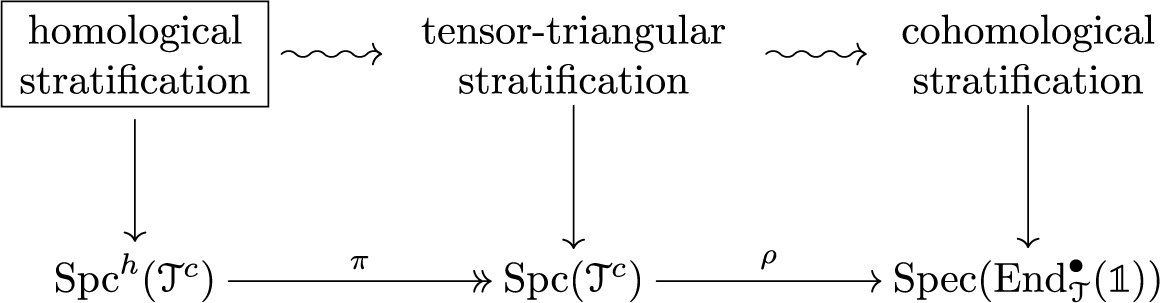
A significant drawback of cohomological stratification is that it can only apply in situations where the parametrizing object is affine and noetherian. Addressing both issues simultaneously, in [Reference Barthel, Heard and SandersBHS23b] the three first-named authors introduced a notion of tensor-triangular stratification which is instead based on the Balmer–Favi notion of support [Reference Balmer and FaviBF11]. The latter takes values in
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
and tensor-triangular stratification asserts that it provides a bijection
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
and tensor-triangular stratification asserts that it provides a bijection
The resulting theory has both theoretical and practical advantages, relates to cohomological stratification through Balmer’s comparison map
and applies to numerous new examples. However, two serious issues remain: Firstly, it still requires a topological assumption on the spectrum, namely the hypothesis of being ‘weakly noetherian’. Secondly, while the permanence of stratification has been established via many instances of descent (e.g., Zariski descent, finite étale descent, nil descent, etc.; see [Reference Barthel, Heard and SandersBHS23b, Reference Barthel, Castellana, Heard and SandersBCHS23, Reference Barthel, Castellana, Heard, Naumann, Pol and SandersBCH+24]), a general descent statement remains elusive.
In this paper, we introduce a theory of stratification based on the ‘homological’ support theory
![]() $\operatorname {\mathrm {Supp}}^h$
introduced in [Reference BalmerBal20a] which takes values in the homological spectrum
$\operatorname {\mathrm {Supp}}^h$
introduced in [Reference BalmerBal20a] which takes values in the homological spectrum
![]() $\smash {\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)}$
. This is a variant of the usual spectrum (also introduced by Balmer [Reference BalmerBal20b]) whose points correspond to the homological residue fields of
$\smash {\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)}$
. This is a variant of the usual spectrum (also introduced by Balmer [Reference BalmerBal20b]) whose points correspond to the homological residue fields of
![]() $\mathscr {T}^c$
. The key features of our theory of homological stratification may be summarized informally as follows:
$\mathscr {T}^c$
. The key features of our theory of homological stratification may be summarized informally as follows:
-
• (Generality) Homological stratification works without any point-set topological restrictions on the spectrum, thus avoiding the (weakly) noetherian assumptions required for tensor-triangular and cohomological stratification.
-
• (Descendability) Homological stratification satisfies a very general form of descent. This recovers, unifies and extends all known descent results for stratification in the literature.
-
• (Refinement) Homological stratification in general refines the notion of tensor-triangular stratification and coincides with it in cases where Balmer’s Nerves of Steel conjecture holds.
The last point requires some explanation. There is a canonical continuous and surjective map
and the Nerves of Steel conjecture states that
![]() $\pi $
is a bijection [Reference BalmerBal20b]. It is known to hold in numerous examples. When this is the case, the homological theory of stratification coincides with its tensor-triangular counterpart. On the other hand, any counterexample to the Nerves of Steel conjecture would have the property that the homological spectrum contains more points than the usual one, so homological stratification would have access to more refined information about
$\pi $
is a bijection [Reference BalmerBal20b]. It is known to hold in numerous examples. When this is the case, the homological theory of stratification coincides with its tensor-triangular counterpart. On the other hand, any counterexample to the Nerves of Steel conjecture would have the property that the homological spectrum contains more points than the usual one, so homological stratification would have access to more refined information about
![]() $\mathscr {T}$
.
$\mathscr {T}$
.

Figure 1 Schematic overview of the relations between the various notions of stratification.
The rich interplay between the notions of homological and tensor-triangular stratification is one of the themes of this paper. Each theory has certain advantages over the other; up to the Nerves of Steel conjecture, we can combine both features. Collecting several of our results, we can characterize when tensor-triangular stratification descends along a jointly conservative geometric family of functors, under the assumption that the Nerves of Steel conjecture holds:
Theorem A. Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a family of geometric functors that jointly detect when an object of
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a family of geometric functors that jointly detect when an object of
![]() $\mathscr {T}$
is zero. Suppose that
$\mathscr {T}$
is zero. Suppose that
![]() $\mathscr {S}_i$
is tt-stratified for all
$\mathscr {S}_i$
is tt-stratified for all
![]() $i \in I$
. If
$i \in I$
. If
![]() $\mathscr {T}$
satisfies the Nerves of Steel conjecture and has a weakly noetherian spectrum, then the following conditions are equivalent:
$\mathscr {T}$
satisfies the Nerves of Steel conjecture and has a weakly noetherian spectrum, then the following conditions are equivalent:
(a)
 $\mathscr {T}$
is tt-stratified;
$\mathscr {T}$
is tt-stratified;(b)
 $\mathscr {T}$
is h-stratified;
$\mathscr {T}$
is h-stratified;(c)
 $\mathscr {T}$
is generated by the images of the right adjoints
$\mathscr {T}$
is generated by the images of the right adjoints
 $(f_i)_*$
for all
$(f_i)_*$
for all
 $i \in I$
.
$i \in I$
.
In other words, this result provides one answer to the question:
Its proof is assembled at the end of Section 9. In addition, as we will demonstrate, it encompasses all known descent results for stratification and also gives rise to new ones.
Main results
We now give a more detailed overview of the main results of the paper. Throughout, ![]() denotes a rigidly-compactly generated tensor-triangulated category, that is, a tensor-triangulated (‘tt’) category that is compactly generated as a triangulated category and has the property that the compact objects and the dualizable objects in
denotes a rigidly-compactly generated tensor-triangulated category, that is, a tensor-triangulated (‘tt’) category that is compactly generated as a triangulated category and has the property that the compact objects and the dualizable objects in
![]() $\mathscr {T}$
coincide:
$\mathscr {T}$
coincide:
![]() $\mathscr {T}^c=\mathscr {T}^d$
. A geometric functor
$\mathscr {T}^c=\mathscr {T}^d$
. A geometric functor
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
between such categories is an exact and symmetric monoidal functor that preserves arbitrary set-indexed coproducts. In particular,
$f^*\colon \mathscr {T} \to \mathscr {S}$
between such categories is an exact and symmetric monoidal functor that preserves arbitrary set-indexed coproducts. In particular,
![]() $f^*$
admits a right adjoint
$f^*$
admits a right adjoint
![]() $f_*$
which itself admits a right adjoint
$f_*$
which itself admits a right adjoint
![]() $f^!$
.
$f^!$
.
We say that
![]() $\mathscr {T}$
is homologically stratified (or h-stratified, for short) if homological support induces a bijection
$\mathscr {T}$
is homologically stratified (or h-stratified, for short) if homological support induces a bijection
We emphasize that we are making no point-set topological assumptions on the homological spectrum; see Definition 4.2. Our first result provides a concrete criterion for homological stratification:
Theorem B (Theorem 4.1 and Theorem 5.6).
For a rigidly-compactly generated tt-category
![]() $\mathscr {T}$
, the following are equivalent:
$\mathscr {T}$
, the following are equivalent:
(a)
 $\mathscr {T}$
is homologically stratified;
$\mathscr {T}$
is homologically stratified;(b)
 $\mathscr {T}$
satisfies the following two conditions:
$\mathscr {T}$
satisfies the following two conditions:(i) the homological local-to-global principle holds, that is,
 $$\begin{align*}\operatorname{\mathrm{Locid}}\langle t \rangle = \operatorname{\mathrm{Locid}}\langle t \otimes E_{\mathscr{B}} \mid \mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t) \rangle \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Locid}}\langle t \rangle = \operatorname{\mathrm{Locid}}\langle t \otimes E_{\mathscr{B}} \mid \mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t) \rangle \end{align*}$$
for all
 $t \in \mathscr {T}$
;
$t \in \mathscr {T}$
;(ii)
 $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is a minimal localizing ideal for all
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is a minimal localizing ideal for all
 $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
;
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
;
(c)
 $\mathsf {hom}(t_1,t_2) = 0$
if and only if
$\mathsf {hom}(t_1,t_2) = 0$
if and only if
 $\operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2) = \varnothing $
for all
$\operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2) = \varnothing $
for all
 $t_1,t_2 \in \mathscr {T}$
.
$t_1,t_2 \in \mathscr {T}$
.
Here
![]() $E_{\mathscr {B}}$
is a pure-injective object in
$E_{\mathscr {B}}$
is a pure-injective object in
![]() $\mathscr {T}$
associated to each
$\mathscr {T}$
associated to each
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
; see Remark 2.1. The equivalence of the first two conditions is completely analogous to the characterization of cohomological stratification and tt-stratification established in [Reference Benson, Iyengar and KrauseBIK11b, Theorem 4.2] and [Reference Barthel, Heard and SandersBHS23b, Theorem 4.1], respectively. The third characterization is new and involves a notion of homological cosupport
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
; see Remark 2.1. The equivalence of the first two conditions is completely analogous to the characterization of cohomological stratification and tt-stratification established in [Reference Benson, Iyengar and KrauseBIK11b, Theorem 4.2] and [Reference Barthel, Heard and SandersBHS23b, Theorem 4.1], respectively. The third characterization is new and involves a notion of homological cosupport
![]() $\operatorname {\mathrm {Cosupp}}^h$
which we introduce and study in this paper, motivated by its tt-theoretic counterpart studied in [Reference Barthel, Castellana, Heard and SandersBCHS23].
$\operatorname {\mathrm {Cosupp}}^h$
which we introduce and study in this paper, motivated by its tt-theoretic counterpart studied in [Reference Barthel, Castellana, Heard and SandersBCHS23].
When establishing that a given category is tt-stratified by checking the conditions analogous to part (b) of the above theorem, the bulk of the work goes into establishing minimality. In fact, for cohomological stratification — where the Zariski spectrum is noetherian — stratification is equivalent to minimality. In sharp contrast, the homological minimality condition should — heuristically speaking — be detected in the residue fields of
![]() $\mathscr {T}$
and thereby be much easier to verify in practice. This is the underlying reason why the theory of homological stratification tends to be better behaved under descent than its cousins.
$\mathscr {T}$
and thereby be much easier to verify in practice. This is the underlying reason why the theory of homological stratification tends to be better behaved under descent than its cousins.
For instance, in favourable situations, the points of
![]() $\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
are detected not only by homological residue fields, but by tt-residue fields of
$\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
are detected not only by homological residue fields, but by tt-residue fields of
![]() $\mathscr {T}$
, i.e., for each
$\mathscr {T}$
, i.e., for each
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T})$
there exists a geometric functor
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T})$
there exists a geometric functor
![]() $\mathscr {T} \to \mathscr {F}$
to a tt-field which detects
$\mathscr {T} \to \mathscr {F}$
to a tt-field which detects
![]() $\mathscr {B}$
. If this is the case, we say that
$\mathscr {B}$
. If this is the case, we say that
![]() $\mathscr {T}$
admits enough tt-fields (Definition 2.13). As demonstrated in [Reference Balmer and CameronBC21], examples abound. Under the assumption that
$\mathscr {T}$
admits enough tt-fields (Definition 2.13). As demonstrated in [Reference Balmer and CameronBC21], examples abound. Under the assumption that
![]() $\mathscr {T}$
admits enough residue fields, homological stratification reduces to the homological local-to-global principle:
$\mathscr {T}$
admits enough residue fields, homological stratification reduces to the homological local-to-global principle:
Theorem C (Corollary 4.9 and Proposition 8.21).
Suppose that
![]() $\mathscr {T}$
admits enough tt-fields
$\mathscr {T}$
admits enough tt-fields
![]() $(f_{\mathscr {B}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {B}})$
. Then the following are equivalent:
$(f_{\mathscr {B}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {B}})$
. Then the following are equivalent:
(a)
 $\mathscr {T}$
is h-stratified;
$\mathscr {T}$
is h-stratified;(b)
 $\mathscr {T}$
satisfies the homological local-to-global principle;
$\mathscr {T}$
satisfies the homological local-to-global principle;(c)
 $\mathscr {T}$
is generated as a localizing ideal by the
$\mathscr {T}$
is generated as a localizing ideal by the
 $(f_{\mathscr {B}})_*(\mathscr {F}_{\mathscr {B}})$
.
$(f_{\mathscr {B}})_*(\mathscr {F}_{\mathscr {B}})$
.
The last condition says that the homological local-to-global principle holds in
![]() $\mathscr {T}$
whenever its tt-residue fields cover the entire category. It is possible to substantially generalize this to a relative context. To this end, we isolate a very general descent condition: A collection of geometric functors
$\mathscr {T}$
whenever its tt-residue fields cover the entire category. It is possible to substantially generalize this to a relative context. To this end, we isolate a very general descent condition: A collection of geometric functors
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i\in I}$
is said to be weakly descendable (Definition 8.2) if the essential images of the corresponding right adjoints
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i\in I}$
is said to be weakly descendable (Definition 8.2) if the essential images of the corresponding right adjoints
![]() $(f_i)_*$
generate
$(f_i)_*$
generate
![]() $\mathscr {T}$
as a localizing ideal:
$\mathscr {T}$
as a localizing ideal:
Note that we do not require any smallness conditions on ![]() . This notion of weak descendability covers all examples of descent previously considered in the tt-literature, and is arguably the most general setting in which one could expect descent to hold (Remark 8.15). With this in mind, the following result establishes that h-stratification essentially always satisfies descent.
. This notion of weak descendability covers all examples of descent previously considered in the tt-literature, and is arguably the most general setting in which one could expect descent to hold (Remark 8.15). With this in mind, the following result establishes that h-stratification essentially always satisfies descent.
Theorem D (Theorem 8.24).
Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable family of geometric functors. If
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable family of geometric functors. If
![]() $\mathscr {S}_i$
is h-stratified for all
$\mathscr {S}_i$
is h-stratified for all
![]() $i \in I$
, then
$i \in I$
, then
![]() $\mathscr {T}$
is h-stratified.
$\mathscr {T}$
is h-stratified.
This is in marked contrast to tt-stratification, where one has so far only been able to prove a patchwork of different descent theorems. With a satisfactory descent theorem for homological stratification in hand, one may then ask for a comparison with tt-stratification:
Theorem E (Theorem 9.6).
If
![]() $\mathscr {T}$
is a rigidly-compactly generated tt-category with
$\mathscr {T}$
is a rigidly-compactly generated tt-category with
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
weakly noetherian, then the following are equivalent:
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
weakly noetherian, then the following are equivalent:
(a)
 $\mathscr {T}$
is tt-stratified;
$\mathscr {T}$
is tt-stratified;(b)
 $\mathscr {T}$
is h-stratified and the Nerves of Steel conjecture holds for
$\mathscr {T}$
is h-stratified and the Nerves of Steel conjecture holds for
 $\mathscr {T}$
.
$\mathscr {T}$
.
Thus, whenever the Nerves of Steel conjecture is known or can be established through different methods, it suffices to consider the theory of homological stratification. This enables us to deduce strong novel descent results for tt-stratification itself. For instance, we prove:
Theorem F (Proposition 11.1
 $(c)$
and Remark 11.2).
$(c)$
and Remark 11.2).
Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family with each
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family with each
![]() $\mathscr {S}_i$
tt-stratified. Assume additionally that I is finite, that each right adjoint
$\mathscr {S}_i$
tt-stratified. Assume additionally that I is finite, that each right adjoint
![]() $(f_i)_*$
preserves compact objects, and that each
$(f_i)_*$
preserves compact objects, and that each
![]() $\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c)$
is noetherian. Then
$\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c)$
is noetherian. Then
![]() $\mathscr {T}$
is tt-stratified.
$\mathscr {T}$
is tt-stratified.
This result generalizes the étale descent theorem from [Reference Barthel, Heard and SandersBHS23b, Theorem 6.4] and [Reference BarthelBar22, Section 2.2.2] by removing the separability condition present there. As a special case, we obtain the following result, which generalizes the descent theorem of [Reference Barthel, Castellana, Heard, Naumann, Pol and SandersBCH+24, Example 12.18]:
Theorem G (Corollary 11.3).
Let
![]() $\mathscr {C}$
be a rigidly-compactly generated symmetric monoidal stable
$\mathscr {C}$
be a rigidly-compactly generated symmetric monoidal stable
![]() $\infty $
-category and let
$\infty $
-category and let
![]() $A \in \operatorname {\mathrm {CAlg}}(\mathscr {C}^c)$
be a descendable dualizable commutative algebra in
$A \in \operatorname {\mathrm {CAlg}}(\mathscr {C}^c)$
be a descendable dualizable commutative algebra in
![]() $\mathscr {C}$
. If
$\mathscr {C}$
. If
![]() $\operatorname {\mathrm {Mod}}_{\mathscr {C}}(A)$
is tt-stratified and has a noetherian spectrum, then
$\operatorname {\mathrm {Mod}}_{\mathscr {C}}(A)$
is tt-stratified and has a noetherian spectrum, then
![]() $\mathscr {C}$
is also tt-stratified and also has a noetherian spectrum.
$\mathscr {C}$
is also tt-stratified and also has a noetherian spectrum.
We also generalize nil-descent and quasi-finite descent established in [Reference Barthel, Castellana, Heard and SandersBCHS23] to families of geometric functors:
Theorem H (Proposition 11.1
 $(a)(b)$
).
$(a)(b)$
).
Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable family of geometric functors with
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable family of geometric functors with
![]() $\mathscr {S}_i$
tt-stratified for all
$\mathscr {S}_i$
tt-stratified for all
![]() $i \in I$
and let
$i \in I$
and let
be the induced map on tt-spectra. Assume that
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. Then:
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. Then:
(a) (Nil-descent) If
 $\varphi $
is injective then
$\varphi $
is injective then
 $\mathscr {T}$
is tt-stratified.
$\mathscr {T}$
is tt-stratified.(b) (Quasi-finite descent) If each right adjoint
 $(f_i)_*$
preserves compact objects and
$(f_i)_*$
preserves compact objects and
 $\varphi $
has discrete fibres then
$\varphi $
has discrete fibres then
 $\mathscr {T}$
is tt-stratified.
$\mathscr {T}$
is tt-stratified.
As a novel application of our results, we prove the following:
Theorem I (Theorem 12.13).
Let G be a compact Lie group and write
![]() $R_G$
for the inflation of a commutative ring spectrum
$R_G$
for the inflation of a commutative ring spectrum
![]() $R\in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}})$
. If
$R\in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}})$
. If
![]() $\operatorname {\mathrm {Mod}}(R)$
is h-stratified and satisfies the Nerves of Steel conjecture, then
$\operatorname {\mathrm {Mod}}(R)$
is h-stratified and satisfies the Nerves of Steel conjecture, then
![]() $\pi \circ \operatorname {\mathrm {Supp}}^h$
induces a bijection
$\pi \circ \operatorname {\mathrm {Supp}}^h$
induces a bijection
 $$\begin{align*}\begin{Bmatrix} \text{localizing ideals} \\ of \operatorname{\mathrm{Mod}}_G(R_G) \end{Bmatrix} \xrightarrow{\sim} \begin{Bmatrix} \text{subsets of } \\ \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}(R)^c) \end{Bmatrix}. \end{align*}$$
$$\begin{align*}\begin{Bmatrix} \text{localizing ideals} \\ of \operatorname{\mathrm{Mod}}_G(R_G) \end{Bmatrix} \xrightarrow{\sim} \begin{Bmatrix} \text{subsets of } \\ \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}(R)^c) \end{Bmatrix}. \end{align*}$$
This extends [Reference Barthel, Heard and SandersBHS23b, Theorem 15.1] from finite groups to compact Lie groups. Indeed, there we proved the finite analog of Theorem I under the assumption that
![]() $\operatorname {\mathrm {Mod}}(R)$
was tt-stratified, which implies both the Nerves of Steel conjecture and h-stratification by Theorem E.
$\operatorname {\mathrm {Mod}}(R)$
was tt-stratified, which implies both the Nerves of Steel conjecture and h-stratification by Theorem E.
Outline of the document.
In Section 2, we recall the definition and basic features of homological support and introduce the homological detection property. We also discuss the ‘naive’ definition of homological support and establish situations in which it coincides with the homological support. Finally, we introduce homological cosupport and the homological codetection property. In Section 3, we introduce the homological local-to-global principle and discuss its relationship with the h-codetection property. This leads to the definition of h-stratification in Section 4 and the fundamental characterization of h-stratification in terms of the homological local-to-global principle and homological minimality. We discuss examples and counterexamples arising in commutative algebra and explain that h-stratification is equivalent to the homological local-to-global principle when there are enough tt-fields (Corollary 4.9). We also show that a classification of Bousfield classes is implied by (and almost equivalent to) the h-detection property (Proposition 4.18). This surprising result has no tt-analogue. Finally, in Section 5, we provide a further characterization of h-stratification in terms of h-cosupport (Theorem 5.6).
We compare the homological support with the Balmer–Favi support in Section 6 and establish several base change results for the homological support in Section 7. Of particular note is Corollary 7.5, which establishes that the homological support satisfies the Avrunin–Scott identity whenever the h-detection property holds. In Section 8, we introduce the notion of a weakly descendable family of functors and argue that this is the appropriate context in which to study descent. This culminates in Theorem 8.24. We then turn to the comparison between h-stratification and tt-stratification in Section 9 yielding Theorem 9.6 and its corollaries. Then in Section 10 we turn to the task of descending the Nerves of Steel conjecture, yielding Proposition 10.2 and Proposition 10.4. We also show that the Nerves of Steel conjecture is equivalent to a purely support-theoretic statement (Proposition 10.6). Our descent results are then applied in Section 11 to obtain several specific descent results for tt-stratification, including Corollary 11.3 among others. Applications to equivariant spectra are then given in Section 12, including Theorem 12.13. Finally, we conclude the paper in Section 13 with a list of open problems.
Notation and conventions.
Throughout
![]() $\mathscr {T}$
and
$\mathscr {T}$
and
![]() $\mathscr {S}$
will denote rigidly-compactly generated tt-categories and
$\mathscr {S}$
will denote rigidly-compactly generated tt-categories and
![]() $f^*\colon \mathscr {T}\to \mathscr {S}$
will denote a geometric functor.
$f^*\colon \mathscr {T}\to \mathscr {S}$
will denote a geometric functor.
-
• We write
 $\varphi \colon \operatorname {\mathrm {Spc}}(\mathscr {S}^c)\to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
for the induced map on tt-spectra and write
$\varphi \colon \operatorname {\mathrm {Spc}}(\mathscr {S}^c)\to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
for the induced map on tt-spectra and write
 $\varphi ^h\colon \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c) \to \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
for the induced map on homological spectra.
$\varphi ^h\colon \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c) \to \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
for the induced map on homological spectra. -
• We write
 $\pi _{\mathscr {T}}\colon \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c) \to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
for the map between the two spectra.
$\pi _{\mathscr {T}}\colon \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c) \to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
for the map between the two spectra. -
• We thus have a commutative diagram

-
• We denote the right adjoint of
 $f^*$
by
$f^*$
by
 $f_*$
and the right adjoint of
$f_*$
and the right adjoint of
 $f_*$
by
$f_*$
by
 $f^!$
; in symbols,
$f^!$
; in symbols,
 $f^* \dashv f_* \dashv f^!$
. We will use the standard isomorphisms relating these functors established in [Reference Balmer, Dell’Ambrogio and SandersBDS16] without further comment.
$f^* \dashv f_* \dashv f^!$
. We will use the standard isomorphisms relating these functors established in [Reference Balmer, Dell’Ambrogio and SandersBDS16] without further comment. -
• We write
 $\operatorname {\mathrm {Locid}}\langle \mathscr {E} \rangle $
and
$\operatorname {\mathrm {Locid}}\langle \mathscr {E} \rangle $
and
 $\operatorname {\mathrm {Colocid}}\langle \mathscr {E} \rangle $
for the localizing ideal and the colocalizing coideal generated by a collection of objects
$\operatorname {\mathrm {Colocid}}\langle \mathscr {E} \rangle $
for the localizing ideal and the colocalizing coideal generated by a collection of objects
 $\mathscr {E} \subseteq \mathscr {T}$
, respectively.
$\mathscr {E} \subseteq \mathscr {T}$
, respectively. -
• Although not necessary to understand the logic of the results, some familiarity with the tt-theory of stratification and costratification developed in [Reference Barthel, Heard and SandersBHS23b] and [Reference Barthel, Castellana, Heard and SandersBCHS23] and the descent results of [Reference Barthel, Castellana, Heard, Naumann, Pol and SandersBCH+24] will be helpful to contextualize the results of this paper.
-
• We also take for granted some familiarity with the homological spectrum; see [Reference BalmerBal20b, Reference BalmerBal20a].
2 Homological support and cosupport
We begin with a discussion on the various notions of homological (co)support considered in this paper.
Remark 2.1. Recall from [Reference BalmerBal20a, Construction 2.11] that there is a pure-injective object
![]() $E_{\mathscr {B}} \in \mathscr {T}$
associated to each homological prime
$E_{\mathscr {B}} \in \mathscr {T}$
associated to each homological prime
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
and that
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
and that
![]() $E_{\mathscr {B}}$
has the structure of a weak ring in
$E_{\mathscr {B}}$
has the structure of a weak ring in
![]() $\mathscr {T}$
. For each object
$\mathscr {T}$
. For each object
![]() $t \in \mathscr {T}$
, we define
$t \in \mathscr {T}$
, we define
-
• The naive homological support

-
• The (genuine) homological support

-
• The homological cosupport

The homological cosupport does not appear to have been previously studied in this level of generality, but it will play its own role in the story, as in [Reference Barthel, Castellana, Heard and SandersBCHS23].
Example 2.2. For each
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T})$
, we have
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T})$
, we have
by [Reference BalmerBal20a, Example 4.8 and Corollary 4.9].
Remark 2.3. The homological support was introduced by Balmer [Reference BalmerBal20a] and in that paper he establishes a number of significant properties for it. For example, [Reference BalmerBal20a, Theorem 4.5] shows that the (genuine) homological support satisfies the tensor product property:
for all
![]() $t_1,t_2\in \mathscr {T}$
. He also proves the following:
$t_1,t_2\in \mathscr {T}$
. He also proves the following:
Proposition 2.5. For any
![]() $t \in \mathscr {T}$
, we have
$t \in \mathscr {T}$
, we have
Proof. As pointed out in [Reference BalmerBal20a], this follows from the tensor product property and the fact that
![]() $\operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}})=\{\mathscr {B}\}$
. On the other hand, part
$\operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}})=\{\mathscr {B}\}$
. On the other hand, part
![]() $(b)$
of Lemma 2.6 below (applied to the weak ring
$(b)$
of Lemma 2.6 below (applied to the weak ring
![]() $E_{\mathscr {B}}$
) provides a more ‘formal’ proof of the result.
$E_{\mathscr {B}}$
) provides a more ‘formal’ proof of the result.
Lemma 2.6. The following hold:
(a) If C is a weak coring then
 $$\begin{align*}C \otimes t = 0 \Longrightarrow \mathsf{hom}(C,t) = 0. \end{align*}$$
$$\begin{align*}C \otimes t = 0 \Longrightarrow \mathsf{hom}(C,t) = 0. \end{align*}$$
(b) If R is a weak ring then
 $$\begin{align*}t \otimes R = 0 \Longrightarrow \mathsf{hom}(t,R) = 0. \end{align*}$$
$$\begin{align*}t \otimes R = 0 \Longrightarrow \mathsf{hom}(t,R) = 0. \end{align*}$$
Proof.
![]() $(a)$
: Let
$(a)$
: Let ![]() be the counit of the weak coring structure and let
be the counit of the weak coring structure and let
![]() $\Delta \colon C \to C\otimes C$
be a choice of ‘comultiplication’, that is, a section of the map
$\Delta \colon C \to C\otimes C$
be a choice of ‘comultiplication’, that is, a section of the map
![]() $1\otimes \epsilon \colon {C \otimes C \to C}$
. One can check using dinaturality of coevaluation (with respect to
$1\otimes \epsilon \colon {C \otimes C \to C}$
. One can check using dinaturality of coevaluation (with respect to
![]() $\Delta $
) that the composite
$\Delta $
) that the composite
is the identity.
![]() $(b)$
: Let
$(b)$
: Let ![]() be the unit of the weak ring structure and let
be the unit of the weak ring structure and let
![]() $\mu :R\otimes R \to R$
be a choice of ‘multiplication’, that is, a retraction of the map
$\mu :R\otimes R \to R$
be a choice of ‘multiplication’, that is, a retraction of the map
![]() $1\otimes \eta \colon R \to R \otimes R$
. One can check using dinaturality of coevaluation (with respect to
$1\otimes \eta \colon R \to R \otimes R$
. One can check using dinaturality of coevaluation (with respect to
![]() $1\otimes \eta \colon t \to t\otimes R$
) that the composite
$1\otimes \eta \colon t \to t\otimes R$
) that the composite
is the identity.
Lemma 2.7. If C is a weak coring then
Proof. Let ![]() be the counit. One can readily check using dinaturality of evaluation (with respect to
be the counit. One can readily check using dinaturality of evaluation (with respect to
![]() $\epsilon $
) that the composite
$\epsilon $
) that the composite
is ![]() . Thus,
. Thus,
![]() $\mathsf {hom}(C,t)=0$
implies
$\mathsf {hom}(C,t)=0$
implies
![]() $t \otimes \epsilon = 0$
. Since the identity of
$t \otimes \epsilon = 0$
. Since the identity of
![]() $t\otimes C$
factors through
$t\otimes C$
factors through
![]() $t \otimes C \otimes C \xrightarrow {1 \otimes \epsilon \otimes 1} t \otimes C$
, we conclude that
$t \otimes C \otimes C \xrightarrow {1 \otimes \epsilon \otimes 1} t \otimes C$
, we conclude that
![]() $t\otimes C=0$
.
$t\otimes C=0$
.
Proposition 2.8. We have the equality
whenever t is a weak ring or a weak coring.
Proof. The case when t is a weak ring is [Reference BalmerBal20a, Theorem 4.7] while the case when t is a weak coring follows from Lemma 2.7 and part
![]() $(a)$
of Lemma 2.6.
$(a)$
of Lemma 2.6.
Remark 2.9. Balmer also establishes that if
![]() $t \in \mathscr {T}$
is a weak ring then
$t \in \mathscr {T}$
is a weak ring then
![]() ${\operatorname {\mathrm {Supp}}^h(t)=\varnothing }$
implies
${\operatorname {\mathrm {Supp}}^h(t)=\varnothing }$
implies
![]() $t=0$
. However, since
$t=0$
. However, since
![]() $\operatorname {\mathrm {Supp}}^h$
satisfies the tensor product property, the existence of categories which have nonzero tensor-nilpotent objects shows that in general it is possible for
$\operatorname {\mathrm {Supp}}^h$
satisfies the tensor product property, the existence of categories which have nonzero tensor-nilpotent objects shows that in general it is possible for
![]() $\operatorname {\mathrm {Supp}}^h(t) = \varnothing $
even with
$\operatorname {\mathrm {Supp}}^h(t) = \varnothing $
even with
![]() $t \neq 0$
. This leads to:
$t \neq 0$
. This leads to:
Definition 2.10. Let
![]() $\mathscr {T}$
be a rigidly-compactly generated tt-category.
$\mathscr {T}$
be a rigidly-compactly generated tt-category.
(a) We say that the h-detection property holds for
 $\mathscr {T}$
(short for homological detection property) if
$\mathscr {T}$
(short for homological detection property) if
 $\operatorname {\mathrm {Supp}}^h(t) = \varnothing $
implies
$\operatorname {\mathrm {Supp}}^h(t) = \varnothing $
implies
 $t=0$
.
$t=0$
.(b) We say that the h-codetection property holds for
 $\mathscr {T}$
(short for homological codetection property) if
$\mathscr {T}$
(short for homological codetection property) if
 $\operatorname {\mathrm {Cosupp}}^h(t) = \varnothing $
implies
$\operatorname {\mathrm {Cosupp}}^h(t) = \varnothing $
implies
 $t=0$
.
$t=0$
.
Lemma 2.11. If
![]() $\mathscr {T}$
has the h-detection property then
$\mathscr {T}$
has the h-detection property then
![]() $\operatorname {\mathrm {Supp}}^h(t) = \operatorname {\mathrm {Supp}}^n(t)$
for all
$\operatorname {\mathrm {Supp}}^h(t) = \operatorname {\mathrm {Supp}}^n(t)$
for all
![]() $t \in \mathscr {T}$
.
$t \in \mathscr {T}$
.
Proof. We always have the
![]() $\subseteq $
inclusion by Proposition 2.5. On the other hand, if
$\subseteq $
inclusion by Proposition 2.5. On the other hand, if
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(t)$
then
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(t)$
then
![]() $E_{\mathscr {B}} \otimes t \neq 0$
by definition. Hence the h-detection property implies that
$E_{\mathscr {B}} \otimes t \neq 0$
by definition. Hence the h-detection property implies that
![]() $\operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}} \otimes t) \neq \varnothing $
. By the tensor product property this implies
$\operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}} \otimes t) \neq \varnothing $
. By the tensor product property this implies
![]() $\varnothing \neq \operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}}) \cap \operatorname {\mathrm {Supp}}^h(t) = \{\mathscr {B}\} \cap \operatorname {\mathrm {Supp}}^h(t)$
so that
$\varnothing \neq \operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}}) \cap \operatorname {\mathrm {Supp}}^h(t) = \{\mathscr {B}\} \cap \operatorname {\mathrm {Supp}}^h(t)$
so that
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t)$
.
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t)$
.
Remark 2.12. As previously mentioned, the h-detection property does not always hold (Remark 2.9). Nevertheless, we can prove that the two notions of homological support coincide for many additional examples of interest, as follows.
Definition 2.13. A rigidly-compactly generated tt-category
![]() $\mathscr {T}$
admits enough tt-fields if for each
$\mathscr {T}$
admits enough tt-fields if for each
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
there exists a geometric functor
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
there exists a geometric functor
![]() $\mathscr {T} \to \mathscr {F}$
to a tt-field, in the sense of [Reference Balmer, Krause and StevensonBKS19, Definition 1.1], which maps the unique point in
$\mathscr {T} \to \mathscr {F}$
to a tt-field, in the sense of [Reference Balmer, Krause and StevensonBKS19, Definition 1.1], which maps the unique point in
![]() $\operatorname {\mathrm {Spc}}^h(\mathscr {F}^c)$
to
$\operatorname {\mathrm {Spc}}^h(\mathscr {F}^c)$
to
![]() $\mathscr {B}$
. Note that
$\mathscr {B}$
. Note that
![]() $\operatorname {\mathrm {Spc}}^h(\mathscr {F}^c)$
consists of a single point by [Reference Balmer, Krause and StevensonBKS19, Theorem 5.17(a)].
$\operatorname {\mathrm {Spc}}^h(\mathscr {F}^c)$
consists of a single point by [Reference Balmer, Krause and StevensonBKS19, Theorem 5.17(a)].
Example 2.14. The derived category
![]() $\operatorname {\mathrm {D}}(R)$
of a commutative ring R admits enough tt-fields. Indeed,
$\operatorname {\mathrm {D}}(R)$
of a commutative ring R admits enough tt-fields. Indeed,
![]() $\operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {D}}(R)^c) \cong \operatorname {\mathrm {Spec}}(R)$
and tt-fields are provided by the usual residue fields
$\operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {D}}(R)^c) \cong \operatorname {\mathrm {Spec}}(R)$
and tt-fields are provided by the usual residue fields
![]() $\operatorname {\mathrm {D}}(R) \to \operatorname {\mathrm {D}}(\kappa (\mathfrak p))$
. For the homological prime
$\operatorname {\mathrm {D}}(R) \to \operatorname {\mathrm {D}}(\kappa (\mathfrak p))$
. For the homological prime
![]() $\mathscr {B}\in \operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {D}}(R)^c)$
corresponding to
$\mathscr {B}\in \operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {D}}(R)^c)$
corresponding to
![]() $\mathfrak p \in \operatorname {\mathrm {Spec}}(R)$
, we have
$\mathfrak p \in \operatorname {\mathrm {Spec}}(R)$
, we have
![]() $E_{\mathscr {B}} \simeq \kappa (\mathfrak p)$
, considered as a complex concentrated in degree 0; see [Reference Balmer and CameronBC21, Corollary 3.3].
$E_{\mathscr {B}} \simeq \kappa (\mathfrak p)$
, considered as a complex concentrated in degree 0; see [Reference Balmer and CameronBC21, Corollary 3.3].
Lemma 2.15. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {F}$
be a geometric functor to a tt-field
$f^*\colon \mathscr {T} \to \mathscr {F}$
be a geometric functor to a tt-field
![]() $\mathscr {F}$
. Let
$\mathscr {F}$
. Let
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
be the image of the unique point in
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
be the image of the unique point in
![]() $\operatorname {\mathrm {Spc}}^h(\mathscr {F}^c)$
. Then
$\operatorname {\mathrm {Spc}}^h(\mathscr {F}^c)$
. Then
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(t)$
if and only if
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(t)$
if and only if
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t)$
.
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t)$
.
Proof. The inclusion
![]() $\operatorname {\mathrm {Supp}}^h(t) \subseteq \operatorname {\mathrm {Supp}}^n(t)$
is Proposition 2.5, so it remains to prove the ‘only if’ direction. First we claim that
$\operatorname {\mathrm {Supp}}^h(t) \subseteq \operatorname {\mathrm {Supp}}^n(t)$
is Proposition 2.5, so it remains to prove the ‘only if’ direction. First we claim that
![]() $f^! E_{\mathscr {B}} \neq 0$
. Otherwise, we would have
$f^! E_{\mathscr {B}} \neq 0$
. Otherwise, we would have ![]() . But
. But
![]() $E_{\mathscr {B}}$
is a direct summand of
$E_{\mathscr {B}}$
is a direct summand of ![]() by [Reference Balmer and CameronBC21, Theorem 3.1]. Thus we would have
by [Reference Balmer and CameronBC21, Theorem 3.1]. Thus we would have
![]() $\mathsf {hom}(E_{\mathscr {B}},E_{\mathscr {B}}) =0$
which contradicts
$\mathsf {hom}(E_{\mathscr {B}},E_{\mathscr {B}}) =0$
which contradicts
![]() $E_{\mathscr {B}} \neq 0$
.
$E_{\mathscr {B}} \neq 0$
.
If
![]() $\mathsf {hom}(t,E_{\mathscr {B}}) = 0$
, then
$\mathsf {hom}(t,E_{\mathscr {B}}) = 0$
, then
![]() $\mathsf {hom}(f^* t,f^! E_{\mathscr {B}}) = f^!\mathsf {hom}(t,E_{\mathscr {B}}) =0$
. Since
$\mathsf {hom}(f^* t,f^! E_{\mathscr {B}}) = f^!\mathsf {hom}(t,E_{\mathscr {B}}) =0$
. Since
![]() $\mathscr {F}$
is a tt-field, it follows that
$\mathscr {F}$
is a tt-field, it follows that
![]() $f^* t = 0$
by [Reference Balmer, Krause and StevensonBKS19, Theorem 5.21]. Hence
$f^* t = 0$
by [Reference Balmer, Krause and StevensonBKS19, Theorem 5.21]. Hence ![]() by the projection formula. Therefore
by the projection formula. Therefore
![]() $E_{\mathscr {B}} \otimes t = 0$
since
$E_{\mathscr {B}} \otimes t = 0$
since
![]() $E_{\mathscr {B}}$
is a direct summand of
$E_{\mathscr {B}}$
is a direct summand of ![]() .
.
Proposition 2.16. Suppose
![]() $\mathscr {T}$
admits enough tt-fields (Definition 2.13). Then
$\mathscr {T}$
admits enough tt-fields (Definition 2.13). Then
for all
![]() $t \in \mathscr {T}$
.
$t \in \mathscr {T}$
.
Proof. This follows immediately from Lemma 2.15.
2.17. We conclude this section with one further result concerning the relationship between the naive and genuine notions of homological support.
Lemma 2.18. Let
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
and suppose
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
and suppose
![]() $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is a minimal localizing ideal in
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is a minimal localizing ideal in
![]() $\mathscr {T}$
. Then
$\mathscr {T}$
. Then
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(t)$
if and only if
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(t)$
if and only if
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t)$
.
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t)$
.
Proof. The
![]() $(\Rightarrow )$
direction holds unconditionally by Proposition 2.5, so it suffices to prove the
$(\Rightarrow )$
direction holds unconditionally by Proposition 2.5, so it suffices to prove the
![]() $(\Leftarrow )$
implication. Let
$(\Leftarrow )$
implication. Let
![]() $t \in \mathscr {T}$
with
$t \in \mathscr {T}$
with
![]() $t \otimes E_{\mathscr {B}} \neq 0$
. By our minimality assumption, this implies that
$t \otimes E_{\mathscr {B}} \neq 0$
. By our minimality assumption, this implies that
![]() $E_{\mathscr {B}} \in \operatorname {\mathrm {Locid}}\langle t \otimes E_{\mathscr {B}} \rangle $
. If we had
$E_{\mathscr {B}} \in \operatorname {\mathrm {Locid}}\langle t \otimes E_{\mathscr {B}} \rangle $
. If we had
![]() $\mathsf {hom}(t \otimes E_{\mathscr {B}}, E_{\mathscr {B}}) = 0$
, then
$\mathsf {hom}(t \otimes E_{\mathscr {B}}, E_{\mathscr {B}}) = 0$
, then
![]() $\mathsf {hom}(E_{\mathscr {B}}, E_{\mathscr {B}}) = 0$
which contradicts
$\mathsf {hom}(E_{\mathscr {B}}, E_{\mathscr {B}}) = 0$
which contradicts
![]() $E_{\mathscr {B}} \neq 0$
. Therefore, we see
$E_{\mathscr {B}} \neq 0$
. Therefore, we see
In particular, this implies that
![]() $\mathsf {hom}(t,E_{\mathscr {B}}) \neq 0$
.
$\mathsf {hom}(t,E_{\mathscr {B}}) \neq 0$
.
3 The homological local-to-global principle
Definition 3.1. We say that
![]() $\mathscr {T}$
satisfies the homological local-to-global principle (or the h-LGP, for short) if we have the equality
$\mathscr {T}$
satisfies the homological local-to-global principle (or the h-LGP, for short) if we have the equality
for all
![]() $t \in \mathscr {T}$
.
$t \in \mathscr {T}$
.
Proposition 3.2. The following are equivalent:
(a)
 ;
;(b)
 $t \in \operatorname {\mathrm {Locid}}\langle t\otimes E_{\mathscr {B}} \mid \mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c) \rangle $
for all
$t \in \operatorname {\mathrm {Locid}}\langle t\otimes E_{\mathscr {B}} \mid \mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c) \rangle $
for all
 $t \in \mathscr {T}$
;
$t \in \mathscr {T}$
;(c)
 $t \in \operatorname {\mathrm {Locid}}\langle t\otimes E_{\mathscr {B}} \mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^n(t) \rangle $
for all
$t \in \operatorname {\mathrm {Locid}}\langle t\otimes E_{\mathscr {B}} \mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^n(t) \rangle $
for all
 $t \in \mathscr {T}$
;
$t \in \mathscr {T}$
;(d) The h-codetection property holds:
 $\operatorname {\mathrm {Cosupp}}^h(t) = \varnothing $
implies
$\operatorname {\mathrm {Cosupp}}^h(t) = \varnothing $
implies
 $t=0$
.
$t=0$
.
Proof. The equivalence of
![]() $(a)$
and
$(a)$
and
![]() $(d)$
follows verbatim from the argument in [Reference Barthel, Castellana, Heard and SandersBCHS23, Theorem 6.4] which establishes the equivalence of the classical LGP property and the classical codetection property. On the other hand, part
$(d)$
follows verbatim from the argument in [Reference Barthel, Castellana, Heard and SandersBCHS23, Theorem 6.4] which establishes the equivalence of the classical LGP property and the classical codetection property. On the other hand, part
![]() $(a)$
is equivalent to part
$(a)$
is equivalent to part
![]() $(b)$
by [Reference Barthel, Castellana, Heard and SandersBCHS23, (2.6)]. Finally, the equivalence of
$(b)$
by [Reference Barthel, Castellana, Heard and SandersBCHS23, (2.6)]. Finally, the equivalence of
![]() $(b)$
and
$(b)$
and
![]() $(c)$
is immediate from the definition of the naive h-support.
$(c)$
is immediate from the definition of the naive h-support.
Remark 3.3. The h-LGP property of Definition 3.1 implies the equivalent conditions of Proposition 3.2. However, a priori the latter conditions are weaker since we do not know whether
![]() $\operatorname {\mathrm {Supp}}^h(t)=\operatorname {\mathrm {Supp}}^n(t)$
in general. In particular, it is not immediate from the above whether the h-codetection property implies the h-detection property. This is in contrast to the situation in [Reference Barthel, Castellana, Heard and SandersBCHS23]. However, we have the following conditional result:
$\operatorname {\mathrm {Supp}}^h(t)=\operatorname {\mathrm {Supp}}^n(t)$
in general. In particular, it is not immediate from the above whether the h-codetection property implies the h-detection property. This is in contrast to the situation in [Reference Barthel, Castellana, Heard and SandersBCHS23]. However, we have the following conditional result:
Corollary 3.4. Suppose that
![]() $\mathscr {T}$
has the h-codetection property. Then the following are equivalent:
$\mathscr {T}$
has the h-codetection property. Then the following are equivalent:
(a)
 $\mathscr {T}$
satisfies the h-LGP;
$\mathscr {T}$
satisfies the h-LGP;(b)
 $\operatorname {\mathrm {Supp}}^h(t)=\operatorname {\mathrm {Supp}}^n(t)$
for all
$\operatorname {\mathrm {Supp}}^h(t)=\operatorname {\mathrm {Supp}}^n(t)$
for all
 $t \in \mathscr {T}$
.
$t \in \mathscr {T}$
.
Proof. Suppose that
![]() $(a)$
holds, so that in particular h-detection holds. Indeed,
$(a)$
holds, so that in particular h-detection holds. Indeed,
![]() ${\operatorname {\mathrm {Supp}}^h(t) = \varnothing }$
implies
${\operatorname {\mathrm {Supp}}^h(t) = \varnothing }$
implies
![]() $\operatorname {\mathrm {Locid}}\langle t \rangle = 0$
by the h-LGP, hence
$\operatorname {\mathrm {Locid}}\langle t \rangle = 0$
by the h-LGP, hence
![]() $t = 0$
. It then follows from Lemma 2.11 that
$t = 0$
. It then follows from Lemma 2.11 that
![]() $(b)$
holds. Conversely, the equality in
$(b)$
holds. Conversely, the equality in
![]() $(b)$
implies that
$(b)$
implies that
so the h-LGP follows from h-codetection by Proposition 3.2.
Example 3.5. In light of Example 2.14 and Proposition 2.16, we see that for the derived category
![]() $\operatorname {\mathrm {D}}(R)$
of a commutative ring R, the naive and genuine notions of homological support coincide. The previous corollary together with Remark 3.3 then imply that
$\operatorname {\mathrm {D}}(R)$
of a commutative ring R, the naive and genuine notions of homological support coincide. The previous corollary together with Remark 3.3 then imply that
![]() $\operatorname {\mathrm {D}}(R)$
satisfies the h-LGP if and only if it has the h-codetection property if and only if
$\operatorname {\mathrm {D}}(R)$
satisfies the h-LGP if and only if it has the h-codetection property if and only if
![]() $R \in \operatorname {\mathrm {Locid}}\langle \kappa (\mathfrak p)\mid \mathfrak p \in \operatorname {\mathrm {Spec}}(R) \rangle $
.
$R \in \operatorname {\mathrm {Locid}}\langle \kappa (\mathfrak p)\mid \mathfrak p \in \operatorname {\mathrm {Spec}}(R) \rangle $
.
Remark 3.6. We remind the reader that the homological local-to-global principle implies the homological detection property (Definition 2.10). The following example shows that the converse does not hold.
Example 3.7. Let
![]() $\operatorname {\mathrm {D}}(R)$
be the derived category of an absolutely flat ring R. It follows from [Reference StevensonSte14, Lemma 4.1] and Proposition 2.16 that the h-detection property holds. However, [Reference StevensonSte14, Theorem 4.8] and [Reference StevensonSte17, Theorem 6.3] establish that the h-LGP holds if and only if R is semi-artinian, in light of Example 3.5.
$\operatorname {\mathrm {D}}(R)$
be the derived category of an absolutely flat ring R. It follows from [Reference StevensonSte14, Lemma 4.1] and Proposition 2.16 that the h-detection property holds. However, [Reference StevensonSte14, Theorem 4.8] and [Reference StevensonSte17, Theorem 6.3] establish that the h-LGP holds if and only if R is semi-artinian, in light of Example 3.5.
4 Homological stratification
We now introduce homological stratification and establish its basic properties. We begin with the following homological variant of [Reference Barthel, Heard and SandersBHS23b, Theorem 4.1].
Theorem 4.1. Let
![]() $\mathscr {T}$
be a rigidly-compactly generated tt-category. The following conditions are equivalent:
$\mathscr {T}$
be a rigidly-compactly generated tt-category. The following conditions are equivalent:
(a) the homological local-to-global principle holds for
 $\mathscr {T}$
and
$\mathscr {T}$
and
 $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is a minimal localizing ideal for all
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is a minimal localizing ideal for all
 $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
;
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
;(b) for any
 $t \in \mathscr {T}$
, we have
$t \in \mathscr {T}$
, we have
 $\operatorname {\mathrm {Locid}}\langle t \rangle = \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t) \rangle $
;
$\operatorname {\mathrm {Locid}}\langle t \rangle = \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t) \rangle $
;(c) homological support induces a bijection
 $$\begin{align*}\operatorname{\mathrm{Supp}}^h\colon \big\{ \text{localizing ideals of }\mathscr{T} \big\} \xrightarrow{\cong} \big\{ \text{subsets of }\operatorname{\mathrm{Spc}}^h(\mathscr{T}^c)\big\}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Supp}}^h\colon \big\{ \text{localizing ideals of }\mathscr{T} \big\} \xrightarrow{\cong} \big\{ \text{subsets of }\operatorname{\mathrm{Spc}}^h(\mathscr{T}^c)\big\}. \end{align*}$$
Proof.
![]() $(a) \Rightarrow (b)$
: Consider
$(a) \Rightarrow (b)$
: Consider
![]() $t \in \mathscr {T}$
. The homological local-to-global principle implies
$t \in \mathscr {T}$
. The homological local-to-global principle implies
 $$ \begin{align*} \operatorname{\mathrm{Locid}}\langle t \rangle & = \operatorname{\mathrm{Locid}}\langle t \otimes E_{\mathscr{B}} \mid\mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t) \rangle \\ & \subseteq \operatorname{\mathrm{Locid}}\langle E_{\mathscr{B}} \mid\mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t) \rangle. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Locid}}\langle t \rangle & = \operatorname{\mathrm{Locid}}\langle t \otimes E_{\mathscr{B}} \mid\mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t) \rangle \\ & \subseteq \operatorname{\mathrm{Locid}}\langle E_{\mathscr{B}} \mid\mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t) \rangle. \end{align*} $$
On the other hand, minimality implies
![]() $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle = \operatorname {\mathrm {Locid}}\langle t\otimes E_{\mathscr {B}} \rangle $
for all
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle = \operatorname {\mathrm {Locid}}\langle t\otimes E_{\mathscr {B}} \rangle $
for all
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t)$
, which establishes the reverse inclusion.
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t)$
, which establishes the reverse inclusion.
![]() $(b) \Rightarrow (c)$
: On the one hand, since
$(b) \Rightarrow (c)$
: On the one hand, since
![]() $\operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}}) = \{\mathscr {B}\}$
for any
$\operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}}) = \{\mathscr {B}\}$
for any
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
, the map is always surjective. On the other hand, injectivity of the map is equivalent to the following statement:
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
, the map is always surjective. On the other hand, injectivity of the map is equivalent to the following statement:
This is a direct consequence of
![]() $(b)$
.
$(b)$
.
![]() $(c) \Rightarrow (a)$
: We first check the minimality condition. To this end, let
$(c) \Rightarrow (a)$
: We first check the minimality condition. To this end, let
![]() $\mathscr {B}$
be some homological prime and consider a nonzero
$\mathscr {B}$
be some homological prime and consider a nonzero
![]() $\mathscr {L} \subseteq \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
. It follows that
$\mathscr {L} \subseteq \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
. It follows that
![]() $\varnothing \subseteq \operatorname {\mathrm {Supp}}^h(\mathscr {L}) \subseteq \operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}})$
. Injectivity of the map in
$\varnothing \subseteq \operatorname {\mathrm {Supp}}^h(\mathscr {L}) \subseteq \operatorname {\mathrm {Supp}}^h(E_{\mathscr {B}})$
. Injectivity of the map in
![]() $(c)$
guarantees that
$(c)$
guarantees that
![]() $\operatorname {\mathrm {Supp}}^h(\mathscr {L})$
is non-empty, for otherwise
$\operatorname {\mathrm {Supp}}^h(\mathscr {L})$
is non-empty, for otherwise
![]() $\mathscr {L} = (0)$
. Therefore,
$\mathscr {L} = (0)$
. Therefore,
![]() $\operatorname {\mathrm {Supp}}^h(\mathscr {L}) = \{\mathscr {B}\}$
, so applying
$\operatorname {\mathrm {Supp}}^h(\mathscr {L}) = \{\mathscr {B}\}$
, so applying
![]() $(c)$
again gives
$(c)$
again gives
![]() $\mathscr {L} = \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
. To prove the homological local-to-global principle, we compute
$\mathscr {L} = \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
. To prove the homological local-to-global principle, we compute
 $$ \begin{align*} \operatorname{\mathrm{Supp}}^h(\operatorname{\mathrm{Locid}}\langle t \otimes E_{\mathscr{B}}\mid \mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t) \rangle) & = \bigcup_{\mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t)}\operatorname{\mathrm{Supp}}^h(t) \cap \operatorname{\mathrm{Supp}}^h(E_{\mathscr{B}}) \\ & = \operatorname{\mathrm{Supp}}^h(t) \\ & = \operatorname{\mathrm{Supp}}^h(\operatorname{\mathrm{Locid}}\langle t \rangle). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Supp}}^h(\operatorname{\mathrm{Locid}}\langle t \otimes E_{\mathscr{B}}\mid \mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t) \rangle) & = \bigcup_{\mathscr{B} \in \operatorname{\mathrm{Supp}}^h(t)}\operatorname{\mathrm{Supp}}^h(t) \cap \operatorname{\mathrm{Supp}}^h(E_{\mathscr{B}}) \\ & = \operatorname{\mathrm{Supp}}^h(t) \\ & = \operatorname{\mathrm{Supp}}^h(\operatorname{\mathrm{Locid}}\langle t \rangle). \end{align*} $$
Using the injectivity in
![]() $(c)$
once more, we see that
$(c)$
once more, we see that
![]() $\operatorname {\mathrm {Locid}}\langle t \otimes E_{\mathscr {B}}\mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t) \rangle = \operatorname {\mathrm {Locid}}\langle t \rangle $
, as desired.
$\operatorname {\mathrm {Locid}}\langle t \otimes E_{\mathscr {B}}\mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t) \rangle = \operatorname {\mathrm {Locid}}\langle t \rangle $
, as desired.
Definition 4.2. A rigidly-compactly generated tt-category
![]() $\mathscr {T}$
is said to be homologically stratified (or h-stratified, for short) if it satisfies the equivalent conditions of Theorem 4.1.
$\mathscr {T}$
is said to be homologically stratified (or h-stratified, for short) if it satisfies the equivalent conditions of Theorem 4.1.
Remark 4.3. It follows from Lemma 2.18 that
![]() $\operatorname {\mathrm {Supp}}^h=\operatorname {\mathrm {Supp}}^n$
when h-minimality holds at all homological primes
$\operatorname {\mathrm {Supp}}^h=\operatorname {\mathrm {Supp}}^n$
when h-minimality holds at all homological primes
![]() $\mathscr {B}$
. Thus, in part
$\mathscr {B}$
. Thus, in part
![]() $(a)$
of Theorem 4.1, the homological local-to-global principle could be replaced with the h-codetection property; see Proposition 3.2 and Remark 3.3.
$(a)$
of Theorem 4.1, the homological local-to-global principle could be replaced with the h-codetection property; see Proposition 3.2 and Remark 3.3.
Example 4.4. Any tt-field
![]() $\mathscr {F}$
is h-stratified. Indeed, first note that
$\mathscr {F}$
is h-stratified. Indeed, first note that
![]() $\mathscr {F}$
admits a unique homological prime by [Reference Balmer, Krause and StevensonBKS19, Theorem 5.17(a)]. It then suffices to show that the only localizing ideals of
$\mathscr {F}$
admits a unique homological prime by [Reference Balmer, Krause and StevensonBKS19, Theorem 5.17(a)]. It then suffices to show that the only localizing ideals of
![]() $\mathscr {F}$
are the zero ideal and
$\mathscr {F}$
are the zero ideal and
![]() $\mathscr {F}$
itself, that is,
$\mathscr {F}$
itself, that is, ![]() for any nonzero
for any nonzero
![]() $t\in \mathscr {F}$
. By the definition of tt-field, any nonzero object t admits a nonzero rigid-compact object c as a retract, hence
$t\in \mathscr {F}$
. By the definition of tt-field, any nonzero object t admits a nonzero rigid-compact object c as a retract, hence
![]() $\operatorname {\mathrm {Locid}}\langle c \rangle \subseteq \operatorname {\mathrm {Locid}}\langle t \rangle $
. Moreover,
$\operatorname {\mathrm {Locid}}\langle c \rangle \subseteq \operatorname {\mathrm {Locid}}\langle t \rangle $
. Moreover, ![]() since
since
![]() $\operatorname {\mathrm {Spc}}(\mathscr {F}^c)$
is a singleton by [Reference Balmer, Krause and StevensonBKS19, Proposition 5.15]. Therefore,
$\operatorname {\mathrm {Spc}}(\mathscr {F}^c)$
is a singleton by [Reference Balmer, Krause and StevensonBKS19, Proposition 5.15]. Therefore, ![]() .
.
Proposition 4.5. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {F}$
be a geometric functor to a tt-field and let
$f^*\colon \mathscr {T} \to \mathscr {F}$
be a geometric functor to a tt-field and let
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
be the unique point in the image of
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
be the unique point in the image of
![]() $\varphi ^h$
. Assume that
$\varphi ^h$
. Assume that
![]() $\mathscr {T}$
has no nontrivial tensor-nilpotent objects. Then
$\mathscr {T}$
has no nontrivial tensor-nilpotent objects. Then ![]() is a minimal localizing ideal.
is a minimal localizing ideal.
Proof. Balmer and Cameron [Reference Balmer and CameronBC21, Theorem 3.1] establish that
![]() $E_{\mathscr {B}}$
is a direct summand of
$E_{\mathscr {B}}$
is a direct summand of ![]() . Thus it suffices to prove that
. Thus it suffices to prove that ![]() is a minimal localizing ideal. Consider
is a minimal localizing ideal. Consider ![]() . If
. If
![]() $f^*(t) = 0$
then
$f^*(t) = 0$
then ![]() so that
so that
![]() ${t \otimes t = 0}$
. This contradicts
${t \otimes t = 0}$
. This contradicts
![]() $t \neq 0$
since we have assumed that there are no tensor-nilpotent objects in
$t \neq 0$
since we have assumed that there are no tensor-nilpotent objects in
![]() $\mathscr {T}$
. Thus,
$\mathscr {T}$
. Thus,
![]() $f^*(t) \neq 0$
and therefore
$f^*(t) \neq 0$
and therefore ![]() by Example 4.4. Hence
by Example 4.4. Hence
by [Reference Barthel, Castellana, Heard and SandersBCHS23, (13.4)]. This proves that ![]() is minimal.
is minimal.
Corollary 4.6. If
![]() $\mathscr {T}$
has no nontrivial tensor-nilpotent objects and admits enough tt-fields, then it has h-minimality at all homological primes.
$\mathscr {T}$
has no nontrivial tensor-nilpotent objects and admits enough tt-fields, then it has h-minimality at all homological primes.
Example 4.7. The corollary applies whenever
![]() $\mathscr {T}$
has the h-detection property and admits enough tt-fields.
$\mathscr {T}$
has the h-detection property and admits enough tt-fields.
Remark 4.8. Note that if
![]() $f^*\colon \mathscr {T} \to \mathscr {F}$
is a geometric functor to a tt-field then
$f^*\colon \mathscr {T} \to \mathscr {F}$
is a geometric functor to a tt-field then
![]() $f^*(t)=0$
for any tensor-nilpotent object
$f^*(t)=0$
for any tensor-nilpotent object
![]() $t \in \mathscr {T}$
. Hence, the argument in the proof of Proposition 4.5 shows that if
$t \in \mathscr {T}$
. Hence, the argument in the proof of Proposition 4.5 shows that if ![]() is tensor-nilpotent then
is tensor-nilpotent then
![]() $t^{\otimes 2} = 0$
. In other words, this localizing ideal can only contain tensor-nilpotent objects of order at most 2.
$t^{\otimes 2} = 0$
. In other words, this localizing ideal can only contain tensor-nilpotent objects of order at most 2.
Corollary 4.9. If
![]() $\mathscr {T}$
admits enough tt-fields then the following are equivalent:
$\mathscr {T}$
admits enough tt-fields then the following are equivalent:
(a)
 $\mathscr {T}$
has the h-LGP property;
$\mathscr {T}$
has the h-LGP property;(b)
 $\mathscr {T}$
is h-stratified.
$\mathscr {T}$
is h-stratified.
Proof. Certainly
![]() $(b)$
implies
$(b)$
implies
![]() $(a)$
by Theorem 4.1. Conversely, h-LGP implies the h-detection property so, since we have enough tt-fields by assumption, we automatically get h-minimality by Corollary 4.6.
$(a)$
by Theorem 4.1. Conversely, h-LGP implies the h-detection property so, since we have enough tt-fields by assumption, we automatically get h-minimality by Corollary 4.6.
Example 4.10. The corollary applies to the derived category
![]() $\mathscr {T}=\operatorname {\mathrm {D}}(R)$
of any commutative ring since it admits enough tt-fields (Example 2.14). Therefore,
$\mathscr {T}=\operatorname {\mathrm {D}}(R)$
of any commutative ring since it admits enough tt-fields (Example 2.14). Therefore,
![]() $\operatorname {\mathrm {D}}(R)$
is h-stratified if and only if
$\operatorname {\mathrm {D}}(R)$
is h-stratified if and only if
![]() $R \in \operatorname {\mathrm {Locid}}\langle \kappa (\mathfrak p)\mid \mathfrak p \in \operatorname {\mathrm {Spec}}(R) \rangle $
, in light of Example 3.5.
$R \in \operatorname {\mathrm {Locid}}\langle \kappa (\mathfrak p)\mid \mathfrak p \in \operatorname {\mathrm {Spec}}(R) \rangle $
, in light of Example 3.5.
Example 4.11. In particular, for R an absolutely flat ring,
![]() $\operatorname {\mathrm {D}}(R)$
is h-stratified if and only if R is semi-artinian (Example 3.7).
$\operatorname {\mathrm {D}}(R)$
is h-stratified if and only if R is semi-artinian (Example 3.7).
4.12. We give two examples where homological minimality fails:
Example 4.13. Let
![]() $\mathscr {T} = \operatorname {\mathrm {SH}}$
be the stable homotopy category. By [Reference BalmerBal20b, Corollary 5.10], which relies on the nilpotence theorem of Devinatz–Hopkins–Smith [Reference Devinatz, Hopkins and SmithDHS88], the canonical map
$\mathscr {T} = \operatorname {\mathrm {SH}}$
be the stable homotopy category. By [Reference BalmerBal20b, Corollary 5.10], which relies on the nilpotence theorem of Devinatz–Hopkins–Smith [Reference Devinatz, Hopkins and SmithDHS88], the canonical map
![]() $\operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {SH}}^c)\to \operatorname {\mathrm {Spc}}(\operatorname {\mathrm {SH}}^c)$
is a bijection; cf. Definition 9.1 below. In particular, for a given prime number p, there is a homological prime
$\operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {SH}}^c)\to \operatorname {\mathrm {Spc}}(\operatorname {\mathrm {SH}}^c)$
is a bijection; cf. Definition 9.1 below. In particular, for a given prime number p, there is a homological prime
![]() $\mathscr {B}_{p,\infty }$
corresponding to the tt-prime of all finite p-torsion spectra. The associated weak ring identifies with the mod p Eilenberg–Mac Lane spectrum
$\mathscr {B}_{p,\infty }$
corresponding to the tt-prime of all finite p-torsion spectra. The associated weak ring identifies with the mod p Eilenberg–Mac Lane spectrum
![]() $H{\mathbb {F}_{\hspace {-0.1em}p}}$
, i.e.,
$H{\mathbb {F}_{\hspace {-0.1em}p}}$
, i.e.,
![]() $E_{\mathscr {B}_{p,\infty }} = H{\mathbb {F}_{\hspace {-0.1em}p}}$
; see [Reference Balmer and CameronBC21, Corollary 3.6]. However, it follows from Ravenel’s work [Reference RavenelRav84] that there are strict inclusions
$E_{\mathscr {B}_{p,\infty }} = H{\mathbb {F}_{\hspace {-0.1em}p}}$
; see [Reference Balmer and CameronBC21, Corollary 3.6]. However, it follows from Ravenel’s work [Reference RavenelRav84] that there are strict inclusions
where I denotes the p-local Brown–Comenetz dual of the sphere spectrum. Indeed, on the one hand, we have
![]() $I \in \operatorname {\mathrm {Locid}}\langle H{\mathbb {F}_{\hspace {-0.1em}p}} \rangle $
because the homotopy groups of I are p-torsion and concentrated in non-negative degrees. On the other hand, we have
$I \in \operatorname {\mathrm {Locid}}\langle H{\mathbb {F}_{\hspace {-0.1em}p}} \rangle $
because the homotopy groups of I are p-torsion and concentrated in non-negative degrees. On the other hand, we have
![]() $H{\mathbb {F}_{\hspace {-0.1em}p}} \not \in \operatorname {\mathrm {Locid}}\langle I \rangle $
because
$H{\mathbb {F}_{\hspace {-0.1em}p}} \not \in \operatorname {\mathrm {Locid}}\langle I \rangle $
because
![]() $H{\mathbb {F}_{\hspace {-0.1em}p}} \otimes H{\mathbb {F}_{\hspace {-0.1em}p}} \neq 0$
while
$H{\mathbb {F}_{\hspace {-0.1em}p}} \otimes H{\mathbb {F}_{\hspace {-0.1em}p}} \neq 0$
while
![]() $H{\mathbb {F}_{\hspace {-0.1em}p}} \otimes I = 0$
.
$H{\mathbb {F}_{\hspace {-0.1em}p}} \otimes I = 0$
.
Example 4.14. Let A be the truncated polynomial ring over a field k considered by [Reference NeemanNee00]. We grade A as in [Reference Dwyer and PalmieriDP08]. The derived category
![]() $\operatorname {\mathrm {D}}(A)$
admits a unique tt-field
$\operatorname {\mathrm {D}}(A)$
admits a unique tt-field
![]() $\operatorname {\mathrm {D}}(A) \to \operatorname {\mathrm {D}}(k)$
, induced by the quotient
$\operatorname {\mathrm {D}}(A) \to \operatorname {\mathrm {D}}(k)$
, induced by the quotient
![]() $A\to k$
by the unique prime ideal of A. The pure-injective object
$A\to k$
by the unique prime ideal of A. The pure-injective object
![]() $E_{\mathscr {B}}$
associated to the unique homological prime
$E_{\mathscr {B}}$
associated to the unique homological prime
![]() $\mathscr {B}$
is just the ordinary residue field k. Let
$\mathscr {B}$
is just the ordinary residue field k. Let
![]() $I=\operatorname {\mathrm {Hom}}_k^*(A,k)$
be the graded k-dual of A, concentrated in non-positive degrees. We claim that
$I=\operatorname {\mathrm {Hom}}_k^*(A,k)$
be the graded k-dual of A, concentrated in non-positive degrees. We claim that
![]() $\operatorname {\mathrm {Locid}}\langle I \rangle $
is strictly contained in
$\operatorname {\mathrm {Locid}}\langle I \rangle $
is strictly contained in
![]() $\operatorname {\mathrm {Locid}}\langle k \rangle $
. Indeed, we have
$\operatorname {\mathrm {Locid}}\langle k \rangle $
. Indeed, we have
![]() $I\in \operatorname {\mathrm {Locid}}\langle k \rangle $
by [Reference Dwyer and PalmieriDP08, Lemma 4.9]. On the other hand,
$I\in \operatorname {\mathrm {Locid}}\langle k \rangle $
by [Reference Dwyer and PalmieriDP08, Lemma 4.9]. On the other hand,
![]() $k \not \in \operatorname {\mathrm {Locid}}\langle I \rangle $
since
$k \not \in \operatorname {\mathrm {Locid}}\langle I \rangle $
since
![]() $I\otimes k=0$
by [Reference Dwyer and PalmieriDP08, Proposition 4.11] while
$I\otimes k=0$
by [Reference Dwyer and PalmieriDP08, Proposition 4.11] while
![]() $k\otimes k\neq 0$
.
$k\otimes k\neq 0$
.
Remark 4.15. Recall from Corollary 4.9 that the homological local-to-global principle implies h-minimality in the presence of enough tt-fields. Hence the homological local-to-global principle fails in the previous two examples. Indeed, we have
![]() ${\operatorname {\mathrm {Supp}}^h(I)=\varnothing }$
in both examples above.
${\operatorname {\mathrm {Supp}}^h(I)=\varnothing }$
in both examples above.
Remark 4.16. The spectrum in Example 4.14 is a single point, which shows that there is no obvious condition on the space
![]() $\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
that ensures that the homological local-to-global principle holds. This should be contrasted with the classical local-to-global principle, which holds whenever
$\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
that ensures that the homological local-to-global principle holds. This should be contrasted with the classical local-to-global principle, which holds whenever
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c$
) is noetherian [Reference Barthel, Heard and SandersBHS23b, Theorem 3.22].
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c$
) is noetherian [Reference Barthel, Heard and SandersBHS23b, Theorem 3.22].
Remark 4.17. Recall that the Bousfield class
![]() $A(t)$
of an object
$A(t)$
of an object
![]() $t \in \mathscr {T}$
is the localizing ideal
$t \in \mathscr {T}$
is the localizing ideal ![]() and that the Bousfield lattice of
and that the Bousfield lattice of
![]() $\mathscr {T}$
is the lattice of Bousfield classes ordered by reverse inclusion; see [Reference Barthel, Heard and SandersBHS23b, Section 8]. Surprisingly, the following proposition shows that the classification of Bousfield classes is equivalent to the h-detection property whenever the homological support agrees with the naive homological support. Indeed, it is immediate from the definition of naive homological support that
$\mathscr {T}$
is the lattice of Bousfield classes ordered by reverse inclusion; see [Reference Barthel, Heard and SandersBHS23b, Section 8]. Surprisingly, the following proposition shows that the classification of Bousfield classes is equivalent to the h-detection property whenever the homological support agrees with the naive homological support. Indeed, it is immediate from the definition of naive homological support that
![]() $\operatorname {\mathrm {Supp}}^n(t)\subseteq \operatorname {\mathrm {Supp}}^n(s)$
whenever
$\operatorname {\mathrm {Supp}}^n(t)\subseteq \operatorname {\mathrm {Supp}}^n(s)$
whenever
![]() $A(t)\le A(s)$
. Therefore, there is a well-defined order-preserving map
$A(t)\le A(s)$
. Therefore, there is a well-defined order-preserving map
sending
![]() $A(t)$
to
$A(t)$
to
![]() $\operatorname {\mathrm {Supp}}^n(t)$
.
$\operatorname {\mathrm {Supp}}^n(t)$
.
Proposition 4.18. The following are equivalent:
(a) The h-detection property holds for
 $\mathscr {T}$
.
$\mathscr {T}$
.(b)
 $\operatorname {\mathrm {Supp}}^h(t)=\operatorname {\mathrm {Supp}}^n(t)$
for all
$\operatorname {\mathrm {Supp}}^h(t)=\operatorname {\mathrm {Supp}}^n(t)$
for all
 $t \in \mathscr {T}$
and the Bousfield lattice of
$t \in \mathscr {T}$
and the Bousfield lattice of
 $\mathscr {T}$
is isomorphic to the lattice of subsets of
$\mathscr {T}$
is isomorphic to the lattice of subsets of
 $\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
via the map sending
$\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
via the map sending
 $A(t)$
to
$A(t)$
to
 $\operatorname {\mathrm {Supp}}^h(t)$
.
$\operatorname {\mathrm {Supp}}^h(t)$
.
Proof.
![]() $(a) \Rightarrow (b)$
: The first statement follows from Lemma 2.11. For the second, note that the well-defined order-preserving map
$(a) \Rightarrow (b)$
: The first statement follows from Lemma 2.11. For the second, note that the well-defined order-preserving map
![]() $A(t)\mapsto \operatorname {\mathrm {Supp}}^n(t)=\operatorname {\mathrm {Supp}}^h(t)$
is a surjection since every subset S of
$A(t)\mapsto \operatorname {\mathrm {Supp}}^n(t)=\operatorname {\mathrm {Supp}}^h(t)$
is a surjection since every subset S of
![]() $\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
can be realized as the h-support of some object, say
$\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
can be realized as the h-support of some object, say
![]() $\bigsqcup _{\mathscr {B} \in S}E_{\mathscr {B}}$
, thanks to [Reference BalmerBal20a, Proposition 4.3(b)] and Example 2.2. We claim that
$\bigsqcup _{\mathscr {B} \in S}E_{\mathscr {B}}$
, thanks to [Reference BalmerBal20a, Proposition 4.3(b)] and Example 2.2. We claim that
Given the claim, the map sending
![]() $A(t)$
to
$A(t)$
to
![]() $\operatorname {\mathrm {Supp}}^h(t)$
is an order-preserving bijection with order-preserving inverse
$\operatorname {\mathrm {Supp}}^h(t)$
is an order-preserving bijection with order-preserving inverse
![]() $\operatorname {\mathrm {Supp}}^h(t)\mapsto A(t)$
and therefore an isomorphism of lattices. To prove the claim, it suffices to show that
$\operatorname {\mathrm {Supp}}^h(t)\mapsto A(t)$
and therefore an isomorphism of lattices. To prove the claim, it suffices to show that
This follows immediately from the equality
which holds by h-detection and the tensor product formula.
![]() $(b) \Rightarrow (a)$
: If
$(b) \Rightarrow (a)$
: If
![]() $\operatorname {\mathrm {Supp}}^h(t)=\varnothing $
then
$\operatorname {\mathrm {Supp}}^h(t)=\varnothing $
then
![]() $A(t)=A(0)$
and hence
$A(t)=A(0)$
and hence
![]() $t=0$
.
$t=0$
.
Remark 4.19. For any
![]() $\mathscr {T}$
satisfying the h-detection property, we obtain a description of the meet operation on its Bousfield lattice:
$\mathscr {T}$
satisfying the h-detection property, we obtain a description of the meet operation on its Bousfield lattice:
![]() $A(s)\wedge A(t)=A(s\otimes t)$
; cf. [Reference Barthel, Heard and SandersBHS23b, Theorem 8.8].
$A(s)\wedge A(t)=A(s\otimes t)$
; cf. [Reference Barthel, Heard and SandersBHS23b, Theorem 8.8].
Remark 4.20. If
![]() $\mathscr {T}$
is h-stratified then every localizing ideal is a Bousfield class and the lattice of localizing ideals of
$\mathscr {T}$
is h-stratified then every localizing ideal is a Bousfield class and the lattice of localizing ideals of
![]() $\mathscr {T}$
is isomorphic to the Bousfield lattice of
$\mathscr {T}$
is isomorphic to the Bousfield lattice of
![]() $\mathscr {T}$
; cf. [Reference Barthel, Heard and SandersBHS23b, Theorem 8.8].
$\mathscr {T}$
; cf. [Reference Barthel, Heard and SandersBHS23b, Theorem 8.8].
Example 4.21. Let R be an absolutely flat ring which is not semi-artinian. Then
![]() $\operatorname {\mathrm {D}}(R)$
is not h-stratified (Example 4.11), so the localizing subcategories of
$\operatorname {\mathrm {D}}(R)$
is not h-stratified (Example 4.11), so the localizing subcategories of
![]() $\operatorname {\mathrm {D}}(R)$
are not classified by the subsets of
$\operatorname {\mathrm {D}}(R)$
are not classified by the subsets of
![]() $\operatorname {\mathrm {Spec}}(R)$
via homological support. However, the h-detection property holds and hence the Bousfield lattice of
$\operatorname {\mathrm {Spec}}(R)$
via homological support. However, the h-detection property holds and hence the Bousfield lattice of
![]() $\operatorname {\mathrm {D}}(R)$
is isomorphic to the lattice of subsets of
$\operatorname {\mathrm {D}}(R)$
is isomorphic to the lattice of subsets of
![]() $\operatorname {\mathrm {Spec}}(R)$
.
$\operatorname {\mathrm {Spec}}(R)$
.
5 Homological stratification via cosupport
We now establish characterizations of homological stratification in terms of the behaviour of homological cosupport. The proof of the next proposition closely follows its tensor-triangular counterpart ([Reference Barthel, Castellana, Heard and SandersBCHS23, Theorem 7.15]):
Proposition 5.1. Consider the following statements for a rigidly-compactly generated tt-category
![]() $\mathscr {T}$
:
$\mathscr {T}$
:
(a)
 $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is a minimal localizing ideal for all
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is a minimal localizing ideal for all
 $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
;
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
;(b)
 $\operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2)) = \operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2)$
for all
$\operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2)) = \operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2)$
for all
 $t_1,t_2 \in \mathscr {T}$
;
$t_1,t_2 \in \mathscr {T}$
;(c)
 $\mathsf {hom}(t_1,t_2) = 0$
implies
$\mathsf {hom}(t_1,t_2) = 0$
implies
 $\operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2) = \varnothing $
for all
$\operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2) = \varnothing $
for all
 $t_1,t_2 \in \mathscr {T}$
.
$t_1,t_2 \in \mathscr {T}$
.
Then
![]() $(a) \Rightarrow (b) \Rightarrow (c)$
. If
$(a) \Rightarrow (b) \Rightarrow (c)$
. If
![]() $\mathscr {T}$
has the h-detection property, then
$\mathscr {T}$
has the h-detection property, then
![]() $(c) \Rightarrow (a)$
, so all conditions are equivalent in this case.
$(c) \Rightarrow (a)$
, so all conditions are equivalent in this case.
Proof.
![]() $(a) \Rightarrow (b)$
: The inclusion
$(a) \Rightarrow (b)$
: The inclusion
![]() $\operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2)) \subseteq \operatorname {\mathrm {Supp}}^n(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2)$
holds unconditionally. Since
$\operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2)) \subseteq \operatorname {\mathrm {Supp}}^n(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2)$
holds unconditionally. Since
![]() $(a)$
guarantees
$(a)$
guarantees
![]() $\operatorname {\mathrm {Supp}}^h(t_1) = \operatorname {\mathrm {Supp}}^n(t_1)$
by Lemma 2.18, we obtain
$\operatorname {\mathrm {Supp}}^h(t_1) = \operatorname {\mathrm {Supp}}^n(t_1)$
by Lemma 2.18, we obtain
![]() $\operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2)) \subseteq \operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2)$
and it remains to verify the reverse inclusion. Consider some
$\operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2)) \subseteq \operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2)$
and it remains to verify the reverse inclusion. Consider some
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2)$
. In particular,
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2)$
. In particular,
![]() $E_{\mathscr {B}} \otimes t_1 \neq 0$
, hence
$E_{\mathscr {B}} \otimes t_1 \neq 0$
, hence
![]() $E_{\mathscr {B}} \in \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}}\otimes t_1 \rangle $
since
$E_{\mathscr {B}} \in \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}}\otimes t_1 \rangle $
since
![]() $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is minimal by assumption. Since
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is minimal by assumption. Since
![]() $\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(t_2)$
, we have
$\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(t_2)$
, we have
By adjunction, we get
![]() $0 \neq \mathsf {hom}(E_{\mathscr {B}}, \mathsf {hom}(t_1,t_2))$
, so
$0 \neq \mathsf {hom}(E_{\mathscr {B}}, \mathsf {hom}(t_1,t_2))$
, so
![]() $\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2))$
.
$\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2))$
.
![]() $(b) \Rightarrow (c)$
: This is a direct consequence of
$(b) \Rightarrow (c)$
: This is a direct consequence of
![]() $\operatorname {\mathrm {Cosupp}}^h(0) = \varnothing $
.
$\operatorname {\mathrm {Cosupp}}^h(0) = \varnothing $
.
![]() $(c) \Rightarrow (a)$
: Consider two non-zero
$(c) \Rightarrow (a)$
: Consider two non-zero
![]() $t_1,t_2 \in \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
. We first claim that
$t_1,t_2 \in \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
. We first claim that
![]() $\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(t_2)$
. Indeed, if
$\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(t_2)$
. Indeed, if
![]() $\mathscr {B} \notin \operatorname {\mathrm {Cosupp}}^h(t_2)$
then
$\mathscr {B} \notin \operatorname {\mathrm {Cosupp}}^h(t_2)$
then
![]() $\mathsf {hom}(E_{\mathscr {B}},t_2)=0$
, which would imply
$\mathsf {hom}(E_{\mathscr {B}},t_2)=0$
, which would imply
![]() $\mathsf {hom}(t_2,t_2)=0$
, i.e.,
$\mathsf {hom}(t_2,t_2)=0$
, i.e.,
![]() $t_2 = 0$
, giving the desired contradiction. Moreover,
$t_2 = 0$
, giving the desired contradiction. Moreover,
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t_1)$
by the h-detection property. It then follows that
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t_1)$
by the h-detection property. It then follows that
so
![]() $\mathsf {hom}(t_1,t_2) \neq 0$
by
$\mathsf {hom}(t_1,t_2) \neq 0$
by
![]() $(c)$
. The minimality criterion [Reference Barthel, Castellana, Heard and SandersBCHS23, Lemma 7.12] then shows that
$(c)$
. The minimality criterion [Reference Barthel, Castellana, Heard and SandersBCHS23, Lemma 7.12] then shows that
![]() $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is minimal.
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
is minimal.
Corollary 5.2. A rigidly-compactly generated tt-category
![]() $\mathscr {T}$
is h-stratified if and only if the h-LGP holds for
$\mathscr {T}$
is h-stratified if and only if the h-LGP holds for
![]() $\mathscr {T}$
and
$\mathscr {T}$
and
for all
![]() $t_1,t_2 \in \mathscr {T}$
.
$t_1,t_2 \in \mathscr {T}$
.
Proof. The h-LGP implies the h-detection property (Remark 3.6), so the equivalence follows from Theorem 4.1 and Proposition 5.1.
Remark 5.3. Corollary 5.2 is a homological analogue of the characterization of stratification in terms of cosupport [Reference Barthel, Castellana, Heard and SandersBCHS23, Theorem 7.15]. The goal of the rest of this section is to establish a variant of this result formulated purely in terms of support and cosupport.
Remark 5.4. The proof of the next theorem makes use of Brown–Comenetz duality. Recall from [Reference Barthel, Castellana, Heard and SandersBCHS23, Definition 9.4] that the Brown–Comenetz dual
![]() $I_c$
of a compact object
$I_c$
of a compact object
![]() $c \in \mathscr {T}$
is characterized by the formula
$c \in \mathscr {T}$
is characterized by the formula
for all
![]() $t \in \mathscr {T}$
. Following the proof of [Reference Barthel, Castellana, Heard and SandersBCHS23, Proposition 12.9], we compute
$t \in \mathscr {T}$
. Following the proof of [Reference Barthel, Castellana, Heard and SandersBCHS23, Proposition 12.9], we compute
for any
![]() $c \in \mathscr {T}^c$
, where the last equality comes from [Reference BalmerBal20a, Proposition 4.4].
$c \in \mathscr {T}^c$
, where the last equality comes from [Reference BalmerBal20a, Proposition 4.4].
Theorem 5.6. For a rigidly-compactly generated tt-category
![]() $\mathscr {T}$
, the following are equivalent:
$\mathscr {T}$
, the following are equivalent:
(a)
 $\mathscr {T}$
is homologically stratified;
$\mathscr {T}$
is homologically stratified;(b)
 $\mathscr {T}$
satisfies the h-codetection property and, for all
$\mathscr {T}$
satisfies the h-codetection property and, for all
 $t_1,t_2 \in \mathscr {T}$
, we have (5.7)
$t_1,t_2 \in \mathscr {T}$
, we have (5.7) $$ \begin{align} \operatorname{\mathrm{Cosupp}}^h(\mathsf{hom}(t_1,t_2)) = \operatorname{\mathrm{Supp}}^h(t_1) \cap \operatorname{\mathrm{Cosupp}}^h(t_2); \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Cosupp}}^h(\mathsf{hom}(t_1,t_2)) = \operatorname{\mathrm{Supp}}^h(t_1) \cap \operatorname{\mathrm{Cosupp}}^h(t_2); \end{align} $$
(c)
 $\mathsf {hom}(t_1,t_2) = 0$
if and only if
$\mathsf {hom}(t_1,t_2) = 0$
if and only if
 $\operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2) = \varnothing $
for all
$\operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2) = \varnothing $
for all
 $t_1,t_2 \in \mathscr {T}$
.
$t_1,t_2 \in \mathscr {T}$
.
Proof. Throughout this proof, we will refer to (5.7) as the cosupport formula.
![]() $(a) \Rightarrow (b)$
: By Corollary 5.2, h-stratification implies the h-LGP for
$(a) \Rightarrow (b)$
: By Corollary 5.2, h-stratification implies the h-LGP for
![]() $\mathscr {T}$
as well as the cosupport formula. But the h-LGP implies the h-codetection property for
$\mathscr {T}$
as well as the cosupport formula. But the h-LGP implies the h-codetection property for
![]() $\mathscr {T}$
(see Proposition 3.2 and Remark 3.3), so we get the statement of
$\mathscr {T}$
(see Proposition 3.2 and Remark 3.3), so we get the statement of
![]() $(b)$
.
$(b)$
.
![]() $(b) \Rightarrow (c)$
: The only if direction in
$(b) \Rightarrow (c)$
: The only if direction in
![]() $(c)$
follows directly from the cosupport formula. For the converse, suppose that
$(c)$
follows directly from the cosupport formula. For the converse, suppose that
![]() $\operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2) = \varnothing $
. The cosupport formula then shows that
$\operatorname {\mathrm {Supp}}^h(t_1) \cap \operatorname {\mathrm {Cosupp}}^h(t_2) = \varnothing $
. The cosupport formula then shows that
![]() $\operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2)) = \varnothing $
, so h-codetection gives
$\operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(t_1,t_2)) = \varnothing $
, so h-codetection gives
![]() $\mathsf {hom}(t_1,t_2) = 0$
.
$\mathsf {hom}(t_1,t_2) = 0$
.
![]() $(c) \Rightarrow (a)$
: Taking
$(c) \Rightarrow (a)$
: Taking ![]() in
in
![]() $(c)$
and using Remark 5.4, we have
$(c)$
and using Remark 5.4, we have ![]() if and only if
if and only if
![]() $\operatorname {\mathrm {Supp}}^h(t_1)=\varnothing $
. Since
$\operatorname {\mathrm {Supp}}^h(t_1)=\varnothing $
. Since
![]() $t_1 = 0$
if and only if
$t_1 = 0$
if and only if ![]() , this establishes h-detection for
, this establishes h-detection for
![]() $\mathscr {T}$
. We may thus appeal to the implication
$\mathscr {T}$
. We may thus appeal to the implication
![]() $(c) \Rightarrow (a)$
in Proposition 5.1 to deduce the minimality of
$(c) \Rightarrow (a)$
in Proposition 5.1 to deduce the minimality of
![]() $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
for all
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle $
for all
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
.
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
.
Specializing
![]() $(c)$
to
$(c)$
to ![]() instead and using that
instead and using that ![]() , we get the h-codetection property for
, we get the h-codetection property for
![]() $\mathscr {T}$
. Lemma 2.18 together with Corollary 3.4 then imply that
$\mathscr {T}$
. Lemma 2.18 together with Corollary 3.4 then imply that
![]() $\mathscr {T}$
has the h-LGP. Finally, the characterization of h-stratification in Theorem 4.1 shows that
$\mathscr {T}$
has the h-LGP. Finally, the characterization of h-stratification in Theorem 4.1 shows that
![]() $\mathscr {T}$
is h-stratified.
$\mathscr {T}$
is h-stratified.
6 Comparison with the Balmer–Favi support
In this section we will compare the homological support with the Balmer–Favi support and, in particular, relate the h-detection and h-LGP properties with the usual detection and LGP properties. We assume some familiarity with [Reference Barthel, Heard and SandersBHS23b].
Notation 6.1. We will write
![]() $\pi \colon \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c) \to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
for the surjective comparison map between the two spectra.
$\pi \colon \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c) \to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
for the surjective comparison map between the two spectra.
Remark 6.2. For any compact object
![]() $x \in \mathscr {T}^c$
, we have
$x \in \mathscr {T}^c$
, we have
by [Reference BalmerBal20a, Proposition 4.4] where
![]() $\operatorname {\mathrm {supp}}$
denotes the universal support theory for
$\operatorname {\mathrm {supp}}$
denotes the universal support theory for
![]() $\mathscr {T}^c$
.
$\mathscr {T}^c$
.
Remark 6.3. A subset
![]() $W \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly visible if it can be written as the intersection of a Thomason subset and the complement of a Thomason subset:
$W \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly visible if it can be written as the intersection of a Thomason subset and the complement of a Thomason subset:
![]() $W= Y_1 \cap Y_2^c$
. In this case, the object
$W= Y_1 \cap Y_2^c$
. In this case, the object ![]() only depends on W up to isomorphism. A point
only depends on W up to isomorphism. A point
![]() $\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is said to be weakly visible if the singleton subset
$\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is said to be weakly visible if the singleton subset
![]() $\{\mathscr {P}\}$
is weakly visible, and in this case we write
$\{\mathscr {P}\}$
is weakly visible, and in this case we write ![]() . Finally, the space
. Finally, the space
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian if every point is weakly visible. See [Reference Barthel, Castellana, Heard and SandersBCHS23, Section 4] for further details.
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian if every point is weakly visible. See [Reference Barthel, Castellana, Heard and SandersBCHS23, Section 4] for further details.
Lemma 6.4. For any weakly visible subset
![]() $W \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, we have
$W \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, we have
Proof. For any Thomason subset
![]() $Y\subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, [Reference Barthel, Heard and SandersBHS23a, Lemmma 3.8] establishes that
$Y\subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, [Reference Barthel, Heard and SandersBHS23a, Lemmma 3.8] establishes that
![]() $\operatorname {\mathrm {Supp}}^h(e_Y)=\pi ^{-1}(Y)$
and
$\operatorname {\mathrm {Supp}}^h(e_Y)=\pi ^{-1}(Y)$
and
![]() $\operatorname {\mathrm {Supp}}^h(f_Y)=\pi ^{-1}(Y^c)$
. Moreover, we have
$\operatorname {\mathrm {Supp}}^h(f_Y)=\pi ^{-1}(Y^c)$
. Moreover, we have
![]() $\operatorname {\mathrm {Supp}}^h(e_Y)=\operatorname {\mathrm {Supp}}^n(e_Y)$
and
$\operatorname {\mathrm {Supp}}^h(e_Y)=\operatorname {\mathrm {Supp}}^n(e_Y)$
and
![]() $\operatorname {\mathrm {Supp}}^h(f_Y)=\operatorname {\mathrm {Supp}}^n(f_Y)$
since
$\operatorname {\mathrm {Supp}}^h(f_Y)=\operatorname {\mathrm {Supp}}^n(f_Y)$
since
![]() $e_Y$
is a (weak) coring and
$e_Y$
is a (weak) coring and
![]() $f_Y$
is a (weak) ring (Proposition 2.8). Finally, we claim that if
$f_Y$
is a (weak) ring (Proposition 2.8). Finally, we claim that if
![]() $a,b \in \mathscr {T}$
both have the property that their naive and genuine h-supports coincide, then so does their tensor product
$a,b \in \mathscr {T}$
both have the property that their naive and genuine h-supports coincide, then so does their tensor product
![]() $a \otimes b$
. Indeed,
$a \otimes b$
. Indeed,
while the reverse inclusion holds unconditionally. It follows that naive and genuine h-support coincide for
![]() $g_W$
for any weakly visible subset W.
$g_W$
for any weakly visible subset W.
Example 6.5. For any weakly visible point
![]() $\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, we have
$\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, we have
Lemma 6.6. We have an equality
whenever the object a is compact or
![]() $a=g_W$
for a weakly visible subset
$a=g_W$
for a weakly visible subset
![]() $W \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
.
$W \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
.
Proof. We always have the inclusion
For the objects a under consideration, the naive and genuine h-support coincide by Remark 6.2 and Lemma 6.4, so we actually have
Now suppose a is compact and let
![]() $\mathscr {B}$
be in the right-hand side. We claim
$\mathscr {B}$
be in the right-hand side. We claim
Otherwise,
![]() $\mathsf {hom}(a,\mathsf {hom}(E_{\mathscr {B}},t)) = 0$
so that
$\mathsf {hom}(a,\mathsf {hom}(E_{\mathscr {B}},t)) = 0$
so that
![]() $\mathsf {hom}(e_{\operatorname {\mathrm {supp}}(a)},\mathsf {hom}(E_{\mathscr {B}},t)) = 0$
. Hence
$\mathsf {hom}(e_{\operatorname {\mathrm {supp}}(a)},\mathsf {hom}(E_{\mathscr {B}},t)) = 0$
. Hence
![]() $\mathsf {hom}(E_{\mathscr {B}},t) \simeq \mathsf {hom}(f_{\operatorname {\mathrm {supp}}(a)},\mathsf {hom}(E_{\mathscr {B}},t))$
. But
$\mathsf {hom}(E_{\mathscr {B}},t) \simeq \mathsf {hom}(f_{\operatorname {\mathrm {supp}}(a)},\mathsf {hom}(E_{\mathscr {B}},t))$
. But
![]() $\mathsf {hom}(E_{\mathscr {B}},t) \neq 0$
by hypothesis. It follows that
$\mathsf {hom}(E_{\mathscr {B}},t) \neq 0$
by hypothesis. It follows that
![]() $E_{\mathscr {B}}\otimes f_{\operatorname {\mathrm {supp}}(a)}\neq 0$
. That is,
$E_{\mathscr {B}}\otimes f_{\operatorname {\mathrm {supp}}(a)}\neq 0$
. That is,
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(f_{\operatorname {\mathrm {supp}}(a)}) = \pi ^{-1}(\operatorname {\mathrm {supp}}(a)^c) = \pi ^{-1}(\operatorname {\mathrm {supp}}(a))^c = \operatorname {\mathrm {Supp}}^h(a)^c$
by Lemma 6.4, which contradicts the hypothesis. This proves the claim when a is compact.
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(f_{\operatorname {\mathrm {supp}}(a)}) = \pi ^{-1}(\operatorname {\mathrm {supp}}(a)^c) = \pi ^{-1}(\operatorname {\mathrm {supp}}(a))^c = \operatorname {\mathrm {Supp}}^h(a)^c$
by Lemma 6.4, which contradicts the hypothesis. This proves the claim when a is compact.
Now suppose
![]() $a=e_Y$
. Again, consider
$a=e_Y$
. Again, consider
![]() $\mathscr {B}$
in the right-hand side of (6.7). If it is not contained in the left-hand side then
$\mathscr {B}$
in the right-hand side of (6.7). If it is not contained in the left-hand side then
![]() $\mathsf {hom}(e_Y,\mathsf {hom}(E_{\mathscr {B}},t)) =0$
so that
$\mathsf {hom}(e_Y,\mathsf {hom}(E_{\mathscr {B}},t)) =0$
so that
![]() ${\mathsf {hom}(x,\mathsf {hom}(E_{\mathscr {B}},t)) = 0}$
for all compact x with
${\mathsf {hom}(x,\mathsf {hom}(E_{\mathscr {B}},t)) = 0}$
for all compact x with
![]() $\operatorname {\mathrm {supp}}(x) \subseteq Y$
. That is,
$\operatorname {\mathrm {supp}}(x) \subseteq Y$
. That is,
![]() $\mathscr {B} \not \in \operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(x,t))$
so that
$\mathscr {B} \not \in \operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(x,t))$
so that
![]() $\mathscr {B} \not \in \operatorname {\mathrm {Supp}}^h(x)$
. Hence
$\mathscr {B} \not \in \operatorname {\mathrm {Supp}}^h(x)$
. Hence
 $$\begin{align*}\mathscr{B} \not\in \bigcup_{x \in \mathscr{T}^c_Y} \operatorname{\mathrm{Supp}}^h(x) = \pi^{-1}(\bigcup_{x \in \mathscr{T}^c_Y} \operatorname{\mathrm{supp}}(x)) = \pi^{-1}(Y) = \operatorname{\mathrm{Supp}}^h(e_Y) \end{align*}$$
$$\begin{align*}\mathscr{B} \not\in \bigcup_{x \in \mathscr{T}^c_Y} \operatorname{\mathrm{Supp}}^h(x) = \pi^{-1}(\bigcup_{x \in \mathscr{T}^c_Y} \operatorname{\mathrm{supp}}(x)) = \pi^{-1}(Y) = \operatorname{\mathrm{Supp}}^h(e_Y) \end{align*}$$
which contradicts the hypothesis.
Now suppose
![]() $a=f_Y$
. Consider any
$a=f_Y$
. Consider any
![]() $\mathscr {B}$
contained in the right-hand side of (6.7). Note that
$\mathscr {B}$
contained in the right-hand side of (6.7). Note that
![]() $\mathscr {B} \not \in \operatorname {\mathrm {Supp}}^h(e_Y)$
since the latter is the complement of
$\mathscr {B} \not \in \operatorname {\mathrm {Supp}}^h(e_Y)$
since the latter is the complement of
![]() $\operatorname {\mathrm {Supp}}^h(f_Y)$
. Hence
$\operatorname {\mathrm {Supp}}^h(f_Y)$
. Hence
![]() $\mathscr {B} \not \in \operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(e_Y,t))$
. That is,
$\mathscr {B} \not \in \operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(e_Y,t))$
. That is,
![]() $\mathsf {hom}(E_{\mathscr {B}},\mathsf {hom}(e_Y,t)) = 0$
. Therefore,
$\mathsf {hom}(E_{\mathscr {B}},\mathsf {hom}(e_Y,t)) = 0$
. Therefore,
Hence
![]() $\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(f_Y,t))$
.
$\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(\mathsf {hom}(f_Y,t))$
.
It follows that we have the equality for a tensor product like
![]() $g_W = e_{Y_1} \otimes f_{Y_2}$
.
$g_W = e_{Y_1} \otimes f_{Y_2}$
.
Proposition 6.8. Assume that
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. Then
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. Then
(a)
 $\pi (\operatorname {\mathrm {Supp}}^h(t)) \subseteq \operatorname {\mathrm {Supp}}(t)$
for all
$\pi (\operatorname {\mathrm {Supp}}^h(t)) \subseteq \operatorname {\mathrm {Supp}}(t)$
for all
 $t \in \mathscr {T}$
with equality when h-detection holds.
$t \in \mathscr {T}$
with equality when h-detection holds.(b)
 $\pi (\operatorname {\mathrm {Cosupp}}^h(t)) \subseteq \operatorname {\mathrm {Cosupp}}(t)$
for all
$\pi (\operatorname {\mathrm {Cosupp}}^h(t)) \subseteq \operatorname {\mathrm {Cosupp}}(t)$
for all
 $t \in \mathscr {T}$
with equality when h-codetection holds.
$t \in \mathscr {T}$
with equality when h-codetection holds.
Proof. We proved in [Reference Barthel, Heard and SandersBHS23a, Proposition 3.10] that the inclusion
![]() $\pi (\operatorname {\mathrm {Supp}}^h(t)) \subseteq \operatorname {\mathrm {Supp}}(t)$
always holds. On the other hand, consider the purported inclusion
$\pi (\operatorname {\mathrm {Supp}}^h(t)) \subseteq \operatorname {\mathrm {Supp}}(t)$
always holds. On the other hand, consider the purported inclusion
If
![]() $\mathscr {P}$
is not contained in the right-hand side, that is,
$\mathscr {P}$
is not contained in the right-hand side, that is,
![]() $\mathsf {hom}(g_{\mathscr {P}},t) = 0$
, then
$\mathsf {hom}(g_{\mathscr {P}},t) = 0$
, then
by Lemma 6.6 and Lemma 6.4. Thus,
![]() $\mathscr {P} \not \in \pi (\operatorname {\mathrm {Cosupp}}^h(t))$
.
$\mathscr {P} \not \in \pi (\operatorname {\mathrm {Cosupp}}^h(t))$
.
Now for the equality in
![]() $(a)$
: If
$(a)$
: If
![]() $\mathscr {P} \in \operatorname {\mathrm {Supp}}(t)$
then
$\mathscr {P} \in \operatorname {\mathrm {Supp}}(t)$
then
![]() $g_{\mathscr {P}} \otimes t \neq 0$
. Hence, the h-detection property implies
$g_{\mathscr {P}} \otimes t \neq 0$
. Hence, the h-detection property implies
so that
![]() $\mathscr {P} \in \pi (\operatorname {\mathrm {Supp}}^h(t))$
.
$\mathscr {P} \in \pi (\operatorname {\mathrm {Supp}}^h(t))$
.
For the equality in
![]() $(b)$
: If
$(b)$
: If
![]() $\mathscr {P} \in \operatorname {\mathrm {Cosupp}}(t)$
then
$\mathscr {P} \in \operatorname {\mathrm {Cosupp}}(t)$
then
![]() $\mathsf {hom}(g_{\mathscr {P}},t) \neq 0$
. Hence, the h-codetection property implies
$\mathsf {hom}(g_{\mathscr {P}},t) \neq 0$
. Hence, the h-codetection property implies
by Lemma 6.6 and Lemma 6.4 so that
![]() $\mathscr {P} \in \pi (\operatorname {\mathrm {Cosupp}}^h(t))$
.
$\mathscr {P} \in \pi (\operatorname {\mathrm {Cosupp}}^h(t))$
.
Corollary 6.9. Assume that
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. Then
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. Then
(a) h-detection implies detection.
(b) h-codetection implies codetection.
Proof. This immediately follows from Proposition 6.8.
Remark 6.10. The detection property does not in general imply the h-detection property and the codetection property does not in general imply the h-codetection property. Indeed, as explained in [Reference Barthel, Heard and SandersBHS23a, Example 5.5], Neeman [Reference NeemanNee00] provides an example of a non-noetherian commutative ring R whose spectrum
![]() $\operatorname {\mathrm {Spec}}(R)$
is a single point with the property that
$\operatorname {\mathrm {Spec}}(R)$
is a single point with the property that
![]() $\operatorname {\mathrm {D}}(R)$
contains a nontrivial tensor-nilpotent object
$\operatorname {\mathrm {D}}(R)$
contains a nontrivial tensor-nilpotent object
![]() $I\in \operatorname {\mathrm {D}}(R)$
; cf. Example 4.14. The tensor product property forces
$I\in \operatorname {\mathrm {D}}(R)$
; cf. Example 4.14. The tensor product property forces
![]() ${\operatorname {\mathrm {Supp}}^h(I) =\varnothing }$
. Thus
${\operatorname {\mathrm {Supp}}^h(I) =\varnothing }$
. Thus
![]() $\operatorname {\mathrm {D}}(R)$
does not have the h-detection property and hence it does not have the h-LGP property or h-codetection property (Example 3.5), either. However, by [Reference Barthel, Heard and SandersBHS23b, Theorem 3.22] it does have the LGP (which is equivalent to the codetection property by [Reference Barthel, Castellana, Heard and SandersBCHS23, Theorem 6.4]) since the spectrum
$\operatorname {\mathrm {D}}(R)$
does not have the h-detection property and hence it does not have the h-LGP property or h-codetection property (Example 3.5), either. However, by [Reference Barthel, Heard and SandersBHS23b, Theorem 3.22] it does have the LGP (which is equivalent to the codetection property by [Reference Barthel, Castellana, Heard and SandersBCHS23, Theorem 6.4]) since the spectrum
![]() $\operatorname {\mathrm {Spc}}(\operatorname {\mathrm {D}}(R)^c)=\operatorname {\mathrm {Spec}}(R)=*$
is a noetherian space.
$\operatorname {\mathrm {Spc}}(\operatorname {\mathrm {D}}(R)^c)=\operatorname {\mathrm {Spec}}(R)=*$
is a noetherian space.
6.11. For weak rings, it is possible to prove an unconditional comparison result between the homological and Balmer–Favi support:
Proposition 6.12. Assume that
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. For any weak ring
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. For any weak ring
![]() $w \in \mathscr {T}$
, we have
$w \in \mathscr {T}$
, we have
![]() $\pi (\operatorname {\mathrm {Supp}}^h(w)) = \operatorname {\mathrm {Supp}}(w)$
.
$\pi (\operatorname {\mathrm {Supp}}^h(w)) = \operatorname {\mathrm {Supp}}(w)$
.
Proof. The
![]() $\subseteq $
inclusion always holds (Proposition 6.8), so it suffices to establish
$\subseteq $
inclusion always holds (Proposition 6.8), so it suffices to establish
![]() $\pi (\operatorname {\mathrm {Supp}}^h(w)) \supseteq \operatorname {\mathrm {Supp}}(w)$
. Let
$\pi (\operatorname {\mathrm {Supp}}^h(w)) \supseteq \operatorname {\mathrm {Supp}}(w)$
. Let
![]() $\mathscr {P} \in \operatorname {\mathrm {Supp}}(w)$
. We have
$\mathscr {P} \in \operatorname {\mathrm {Supp}}(w)$
. We have
![]() $\{\mathscr {P}\} = \operatorname {\mathrm {supp}}(x) \cap \operatorname {\mathrm {gen}}(\mathscr {P})$
for some
$\{\mathscr {P}\} = \operatorname {\mathrm {supp}}(x) \cap \operatorname {\mathrm {gen}}(\mathscr {P})$
for some
![]() $x \in \mathscr {T}^c$
by [Reference Barthel, Heard and SandersBHS23b, Remark 2.8]. Moreover, replacing x by
$x \in \mathscr {T}^c$
by [Reference Barthel, Heard and SandersBHS23b, Remark 2.8]. Moreover, replacing x by
![]() $x \otimes x^{\vee }$
we may assume that x is a (weak) ring. Then
$x \otimes x^{\vee }$
we may assume that x is a (weak) ring. Then
![]() $w \otimes g_{\mathscr {P}} \neq 0$
implies that
$w \otimes g_{\mathscr {P}} \neq 0$
implies that
![]() $w \otimes x \otimes f_{\operatorname {\mathrm {gen}}(\mathscr {P})^c} \neq 0$
is a nonzero weak ring. The homological support has the detection property for weak rings by [Reference BalmerBal20a, Theorem 4.7]. Hence
$w \otimes x \otimes f_{\operatorname {\mathrm {gen}}(\mathscr {P})^c} \neq 0$
is a nonzero weak ring. The homological support has the detection property for weak rings by [Reference BalmerBal20a, Theorem 4.7]. Hence
 $$ \begin{align*} \varnothing \neq \operatorname{\mathrm{Supp}}^h(w \otimes x \otimes f_{\operatorname{\mathrm{gen}}(\mathscr{P})^c}) &= \operatorname{\mathrm{Supp}}^h(w)\cap \operatorname{\mathrm{Supp}}^h(x) \cap \operatorname{\mathrm{Supp}}^h(f_{\operatorname{\mathrm{gen}}(\mathscr{P})^c}) \\ &= \operatorname{\mathrm{Supp}}^h(w) \cap \pi^{-1}(\{\mathscr{P}\}) \end{align*} $$
$$ \begin{align*} \varnothing \neq \operatorname{\mathrm{Supp}}^h(w \otimes x \otimes f_{\operatorname{\mathrm{gen}}(\mathscr{P})^c}) &= \operatorname{\mathrm{Supp}}^h(w)\cap \operatorname{\mathrm{Supp}}^h(x) \cap \operatorname{\mathrm{Supp}}^h(f_{\operatorname{\mathrm{gen}}(\mathscr{P})^c}) \\ &= \operatorname{\mathrm{Supp}}^h(w) \cap \pi^{-1}(\{\mathscr{P}\}) \end{align*} $$
by the tensor product property (2.4), Remark 6.2 and Lemma 6.4. Therefore
![]() $\mathscr {P} \in \pi (\operatorname {\mathrm {Supp}}^h(w))$
, as desired.
$\mathscr {P} \in \pi (\operatorname {\mathrm {Supp}}^h(w))$
, as desired.
7 Base change for homological support
We now turn to studying the behaviour of the homological (co)support in a relative situation. Here we discover some surprises, as the behavior of the homological support deviates strongly from that of the Balmer–Favi support.
7.1. The following result, due to Balmer, is crucial:
Lemma 7.2. Let
![]() $f^*:\mathscr {T} \to \mathscr {S}$
be a geometric functor. For any homological prime
$f^*:\mathscr {T} \to \mathscr {S}$
be a geometric functor. For any homological prime
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
,
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
,
![]() $E_{\varphi ^h(\mathscr {B})} \in \mathscr {T}$
is a direct summand of
$E_{\varphi ^h(\mathscr {B})} \in \mathscr {T}$
is a direct summand of
![]() ${f_*(E_{\mathscr {B}})\in \mathscr {T}}$
.
${f_*(E_{\mathscr {B}})\in \mathscr {T}}$
.
Proof. This is established in [Reference BalmerBal20a, Lemma 5.6].
Proposition 7.3. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. For any
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. For any
![]() $t \in \mathscr {T}$
, we have
$t \in \mathscr {T}$
, we have
Proof. Let
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
be such that
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
be such that
![]() $\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Supp}}^h(t)$
. By definition, this means
$\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Supp}}^h(t)$
. By definition, this means
![]() $\mathsf {hom}(t,E_{\varphi ^h(\mathscr {B})}) \neq 0$
. Hence
$\mathsf {hom}(t,E_{\varphi ^h(\mathscr {B})}) \neq 0$
. Hence
![]() $\mathsf {hom}(t,f_*E_{\mathscr {B}}) \neq 0$
by Lemma 7.2. That is,
$\mathsf {hom}(t,f_*E_{\mathscr {B}}) \neq 0$
by Lemma 7.2. That is,
![]() $f_*\mathsf {hom}(f^*(t),E_{\mathscr {B}}) \neq 0$
. Therefore,
$f_*\mathsf {hom}(f^*(t),E_{\mathscr {B}}) \neq 0$
. Therefore,
![]() $\mathsf {hom}(f^*(t),E_{\mathscr {B}}) \neq 0$
, i.e.,
$\mathsf {hom}(f^*(t),E_{\mathscr {B}}) \neq 0$
, i.e.,
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*(t))$
. This establishes the first inequality.
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*(t))$
. This establishes the first inequality.
Now suppose
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*(t))$
. Then by the first inequality applied to
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*(t))$
. Then by the first inequality applied to
![]() $E_{\varphi ^h(\mathscr {B})}$
, we have
$E_{\varphi ^h(\mathscr {B})}$
, we have
and thus
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*(t)) \cap \operatorname {\mathrm {Supp}}^h(f^*(E_{\varphi ^h(\mathscr {B})}))=\operatorname {\mathrm {Supp}}^h(f^*(t \otimes E_{\varphi ^h(\mathscr {B})}))$
. Therefore,
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*(t)) \cap \operatorname {\mathrm {Supp}}^h(f^*(E_{\varphi ^h(\mathscr {B})}))=\operatorname {\mathrm {Supp}}^h(f^*(t \otimes E_{\varphi ^h(\mathscr {B})}))$
. Therefore,
![]() $f^*(t \otimes E_{\varphi ^h(\mathscr {B})}) \neq 0$
. Hence,
$f^*(t \otimes E_{\varphi ^h(\mathscr {B})}) \neq 0$
. Hence,
![]() $t \otimes E_{\varphi ^h(\mathscr {B})} \neq 0$
. That is,
$t \otimes E_{\varphi ^h(\mathscr {B})} \neq 0$
. That is,
![]() $\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Supp}}^n(t)$
. This establishes the second inequality.
$\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Supp}}^n(t)$
. This establishes the second inequality.
Finally, suppose
![]() $\mathscr {B} \in (\varphi ^h)^{-1}(\operatorname {\mathrm {Supp}}^n(t))$
. That is,
$\mathscr {B} \in (\varphi ^h)^{-1}(\operatorname {\mathrm {Supp}}^n(t))$
. That is,
![]() $E_{\varphi ^h(\mathscr {B})}\otimes t \neq 0$
. Lemma 7.2 then implies
$E_{\varphi ^h(\mathscr {B})}\otimes t \neq 0$
. Lemma 7.2 then implies
![]() $f_*(E_{\mathscr {B}}) \otimes t \neq 0$
. By the projection formula, this means
$f_*(E_{\mathscr {B}}) \otimes t \neq 0$
. By the projection formula, this means
![]() $f_*(E_{\mathscr {B}} \otimes f^*(t)) \neq 0$
so
$f_*(E_{\mathscr {B}} \otimes f^*(t)) \neq 0$
so
![]() $E_{\mathscr {B}} \otimes f^*(t) \neq 0$
. Hence
$E_{\mathscr {B}} \otimes f^*(t) \neq 0$
. Hence
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(f^*(t))$
. This establishes the third inequality.
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^n(f^*(t))$
. This establishes the third inequality.
Corollary 7.5. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. The Avrunin–Scott identity
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. The Avrunin–Scott identity
holds
(a) for all weak rings
 $t \in \mathscr {T}$
; and
$t \in \mathscr {T}$
; and(b) for all weak corings
 $t \in \mathscr {T}$
; and
$t \in \mathscr {T}$
; and(c) for all objects
 $t \in \mathscr {T}$
if
$t \in \mathscr {T}$
if
 $\mathscr {T}$
has the h-detection property.
$\mathscr {T}$
has the h-detection property.
Proof. In cases
![]() $(a)$
,
$(a)$
,
![]() $(b)$
and
$(b)$
and
![]() $(c)$
, we have
$(c)$
, we have
![]() $\operatorname {\mathrm {Supp}}^h(t)=\operatorname {\mathrm {Supp}}^n(t)$
by Proposition 2.8 and Lemma 2.11, hence the result follows from Proposition 7.3.
$\operatorname {\mathrm {Supp}}^h(t)=\operatorname {\mathrm {Supp}}^n(t)$
by Proposition 2.8 and Lemma 2.11, hence the result follows from Proposition 7.3.
Example 7.6. We always have
![]() $(\varphi ^h)^{-1}(\{\mathscr {B}\}) = \operatorname {\mathrm {Supp}}^h(f^*(E_{\mathscr {B}}))$
.
$(\varphi ^h)^{-1}(\{\mathscr {B}\}) = \operatorname {\mathrm {Supp}}^h(f^*(E_{\mathscr {B}}))$
.
Remark 7.7. The above corollary (Corollary 7.5) shows that the Avrunin–Scott identity holds unconditionally whenever
![]() $\mathscr {T}$
has the h-detection property. This contrasts significantly with the situation for the Balmer–Favi support; cf. [Reference Barthel, Castellana, Heard and SandersBCHS23, Corollary 14.19] and [Reference Barthel, Castellana, Heard, Naumann, Pol and SandersBCH+24, Corollary 12.8].
$\mathscr {T}$
has the h-detection property. This contrasts significantly with the situation for the Balmer–Favi support; cf. [Reference Barthel, Castellana, Heard and SandersBCHS23, Corollary 14.19] and [Reference Barthel, Castellana, Heard, Naumann, Pol and SandersBCH+24, Corollary 12.8].
Corollary 7.8. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. If
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. If
![]() $\mathscr {T}$
has the h-detection property, then the following are equivalent:
$\mathscr {T}$
has the h-detection property, then the following are equivalent:
(a)
 $f^*$
is conservative;
$f^*$
is conservative;(b)
 $f^*$
is nil-conservative, i.e.,
$f^*$
is nil-conservative, i.e.,
 $f^*$
is conservative on weak rings;
$f^*$
is conservative on weak rings;(c)
 $\varphi ^h$
is surjective.
$\varphi ^h$
is surjective.
Proof. The equivalence of
![]() $(b)$
and
$(b)$
and
![]() $(c)$
is [Reference Barthel, Castellana, Heard and SandersBCHS24, Theorem 1.8] and
$(c)$
is [Reference Barthel, Castellana, Heard and SandersBCHS24, Theorem 1.8] and
![]() $(a)$
certainly implies
$(a)$
certainly implies
![]() $(b)$
. The implication
$(b)$
. The implication
![]() $(c) \Rightarrow (a)$
follows from Corollary 7.5.
$(c) \Rightarrow (a)$
follows from Corollary 7.5.
Proposition 7.9. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. Suppose
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. Suppose
![]() $\mathscr {S}$
satisfies h-minimality for all homological primes. Then
$\mathscr {S}$
satisfies h-minimality for all homological primes. Then
for all
![]() $t \in \mathscr {T}$
.
$t \in \mathscr {T}$
.
Proof. Let
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
be such that
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
be such that
![]() $\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Supp}}^h(t)$
, i.e.,
$\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Supp}}^h(t)$
, i.e.,
![]() $0 \neq \mathsf {hom}(t,E_{\varphi ^h(\mathscr {B})})$
. By adjunction and using Lemma 7.2, this implies
$0 \neq \mathsf {hom}(t,E_{\varphi ^h(\mathscr {B})})$
. By adjunction and using Lemma 7.2, this implies
In particular, we see that
![]() $0\neq \mathsf {hom}(f^*t, E_{\mathscr {B}})$
, that is
$0\neq \mathsf {hom}(f^*t, E_{\mathscr {B}})$
, that is
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*t)$
.
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*t)$
.
For the reverse inclusion, take
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*t)$
. We first claim that
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f^*t)$
. We first claim that
![]() $\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h (f^!E_{\varphi ^h(\mathscr {B})})$
. Indeed, since
$\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h (f^!E_{\varphi ^h(\mathscr {B})})$
. Indeed, since
![]() $\mathsf {hom}(E_{\varphi ^h(\mathscr {B})},E_{\varphi ^h(\mathscr {B})})\neq 0$
, Lemma 7.2 gives
$\mathsf {hom}(E_{\varphi ^h(\mathscr {B})},E_{\varphi ^h(\mathscr {B})})\neq 0$
, Lemma 7.2 gives
so in particular
![]() $\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(f^!E_{\varphi ^h(\mathscr {B})})$
. By assumption,
$\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(f^!E_{\varphi ^h(\mathscr {B})})$
. By assumption,
![]() $\mathscr {S}$
satisfies h-minimality at
$\mathscr {S}$
satisfies h-minimality at
![]() $\mathscr {B}$
, so Proposition 5.1 implies
$\mathscr {B}$
, so Proposition 5.1 implies
Hence
![]() $0 \neq \mathsf {hom}(f^*t,f^!E_{\varphi ^h(\mathscr {B})}) \simeq f^!\mathsf {hom}(t,E_{\varphi ^h(\mathscr {B})})$
, so
$0 \neq \mathsf {hom}(f^*t,f^!E_{\varphi ^h(\mathscr {B})}) \simeq f^!\mathsf {hom}(t,E_{\varphi ^h(\mathscr {B})})$
, so
![]() $\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Supp}}^h(t)$
.
$\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Supp}}^h(t)$
.
Corollary 7.10. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a conservative geometric functor. Suppose
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a conservative geometric functor. Suppose
![]() $\mathscr {S}$
is h-stratified. Then
$\mathscr {S}$
is h-stratified. Then
![]() $\mathscr {T}$
has the h-detection property.
$\mathscr {T}$
has the h-detection property.
Proof. If
![]() $\operatorname {\mathrm {Supp}}^h(t)=\varnothing $
then
$\operatorname {\mathrm {Supp}}^h(t)=\varnothing $
then
![]() $\operatorname {\mathrm {Supp}}^h(f^*(t))=\varnothing $
by Proposition 7.9 and hence
$\operatorname {\mathrm {Supp}}^h(f^*(t))=\varnothing $
by Proposition 7.9 and hence
![]() $f^*(t)=0$
since h-stratified categories have the h-detection property. Since
$f^*(t)=0$
since h-stratified categories have the h-detection property. Since
![]() $f^*$
is conservative, we conclude that
$f^*$
is conservative, we conclude that
![]() $t=0$
.
$t=0$
.
7.11. While this paper does not systematically develop the theory of homological cosupport, we do include the following cosupport-version of Proposition 7.9, which will be useful in Section 8 below.
Proposition 7.12. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. Suppose
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. Suppose
![]() $\mathscr {S}$
satisfies h-minimality for all homological primes. Then
$\mathscr {S}$
satisfies h-minimality for all homological primes. Then
for all
![]() $t \in \mathscr {T}$
.
$t \in \mathscr {T}$
.
Proof. The proof is similar to the one of Proposition 7.9. Let
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
be such that
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
be such that
![]() $\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Cosupp}}^h(t)$
, i.e.,
$\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Cosupp}}^h(t)$
, i.e.,
![]() $0 \neq \mathsf {hom}(E_{\varphi ^h(\mathscr {B})},t)$
. By adjunction and using Lemma 7.2, this implies
$0 \neq \mathsf {hom}(E_{\varphi ^h(\mathscr {B})},t)$
. By adjunction and using Lemma 7.2, this implies
In particular, we see that
![]() $0\neq \mathsf {hom}(E_{\mathscr {B}},f^!t)$
, that is
$0\neq \mathsf {hom}(E_{\mathscr {B}},f^!t)$
, that is
![]() $\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(f^!t)$
.
$\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(f^!t)$
.
To prove the reverse inclusion, consider some
![]() $\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(f^!t)$
. Since
$\mathscr {B} \in \operatorname {\mathrm {Cosupp}}^h(f^!t)$
. Since
![]() $\mathscr {S}$
satisfies h-minimality at
$\mathscr {S}$
satisfies h-minimality at
![]() $\mathscr {B}$
, (7.4) and Proposition 5.1 give
$\mathscr {B}$
, (7.4) and Proposition 5.1 give
Hence
![]() $0 \neq \mathsf {hom}(f^*E_{\varphi ^h(\mathscr {B})},f^!t) \simeq f^!\mathsf {hom}(E_{\varphi ^h(\mathscr {B})}, t)$
, so
$0 \neq \mathsf {hom}(f^*E_{\varphi ^h(\mathscr {B})},f^!t) \simeq f^!\mathsf {hom}(E_{\varphi ^h(\mathscr {B})}, t)$
, so
![]() $\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Cosupp}}^h(t)$
.
$\varphi ^h(\mathscr {B}) \in \operatorname {\mathrm {Cosupp}}^h(t)$
.
Proposition 7.13. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. Then
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor. Then
(a)
 $\varphi ^h(\operatorname {\mathrm {Supp}}^h(R)) = \operatorname {\mathrm {Supp}}^h(f_*(R))$
for any weak ring
$\varphi ^h(\operatorname {\mathrm {Supp}}^h(R)) = \operatorname {\mathrm {Supp}}^h(f_*(R))$
for any weak ring
 $R \in \mathscr {S}$
.
$R \in \mathscr {S}$
.(b) If
 $\mathscr {S}$
has the h-detection property then
$\mathscr {S}$
has the h-detection property then
 $\operatorname {\mathrm {Supp}}^h(f_*(s)) \subseteq \varphi ^h(\operatorname {\mathrm {Supp}}^h(s))$
for all
$\operatorname {\mathrm {Supp}}^h(f_*(s)) \subseteq \varphi ^h(\operatorname {\mathrm {Supp}}^h(s))$
for all
 $s\in \mathscr {S}$
.
$s\in \mathscr {S}$
.
Proof. For the first statement, observe that
 $$\begin{align*}\mathscr{B} \in \varphi^h(\operatorname{\mathrm{Supp}}^h(R)) &\Longleftrightarrow (\varphi^h)^{-1}(\{\mathscr{B}\}) \cap \operatorname{\mathrm{Supp}}^h(R) \neq \varnothing \\ &\Longleftrightarrow \operatorname{\mathrm{Supp}}^h(f^*(E_{\mathscr{B}})\otimes R) \neq \varnothing &&(\textrm{{{C}orollary~7.5}})\\ &\Longleftrightarrow f^*(E_{\mathscr{B}}) \otimes R \neq 0 &&(\textrm{{{R}emark~2.9}}) \\ &\Longleftrightarrow f_*(f^*(E_{\mathscr{B}}) \otimes R)\neq 0 &&([\mathrm{BCHS23},\ \textrm{Remark~13.12}])\\ &\Longleftrightarrow E_{\mathscr{B}}\otimes f_*(R) \neq 0 \\ &\Longleftrightarrow \mathscr{B} \in \operatorname{\mathrm{Supp}}^h(f_*(R)). \end{align*}$$
$$\begin{align*}\mathscr{B} \in \varphi^h(\operatorname{\mathrm{Supp}}^h(R)) &\Longleftrightarrow (\varphi^h)^{-1}(\{\mathscr{B}\}) \cap \operatorname{\mathrm{Supp}}^h(R) \neq \varnothing \\ &\Longleftrightarrow \operatorname{\mathrm{Supp}}^h(f^*(E_{\mathscr{B}})\otimes R) \neq \varnothing &&(\textrm{{{C}orollary~7.5}})\\ &\Longleftrightarrow f^*(E_{\mathscr{B}}) \otimes R \neq 0 &&(\textrm{{{R}emark~2.9}}) \\ &\Longleftrightarrow f_*(f^*(E_{\mathscr{B}}) \otimes R)\neq 0 &&([\mathrm{BCHS23},\ \textrm{Remark~13.12}])\\ &\Longleftrightarrow E_{\mathscr{B}}\otimes f_*(R) \neq 0 \\ &\Longleftrightarrow \mathscr{B} \in \operatorname{\mathrm{Supp}}^h(f_*(R)). \end{align*}$$
For the second statement, suppose
![]() $\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f_*(s))$
. This implies
$\mathscr {B} \in \operatorname {\mathrm {Supp}}^h(f_*(s))$
. This implies
![]() $E_{\mathscr {B}} \otimes f_*(s) \neq 0$
. That is,
$E_{\mathscr {B}} \otimes f_*(s) \neq 0$
. That is,
![]() $f_*(f^*(E_{\mathscr {B}})\otimes t)\neq 0$
. Hence
$f_*(f^*(E_{\mathscr {B}})\otimes t)\neq 0$
. Hence
![]() $f^*(E_{\mathscr {B}}) \otimes s\neq 0$
. The h-detection property for
$f^*(E_{\mathscr {B}}) \otimes s\neq 0$
. The h-detection property for
![]() $\mathscr {S}$
then implies
$\mathscr {S}$
then implies
![]() $\operatorname {\mathrm {Supp}}^h(f^*(E_{\mathscr {B}})\otimes s) \neq \varnothing $
. It then follows that
$\operatorname {\mathrm {Supp}}^h(f^*(E_{\mathscr {B}})\otimes s) \neq \varnothing $
. It then follows that
![]() $(\varphi ^h)^{-1}(\{\mathscr {B}\}) \cap \operatorname {\mathrm {Supp}}^h(s) \neq \varnothing $
by using Example 7.6. Hence
$(\varphi ^h)^{-1}(\{\mathscr {B}\}) \cap \operatorname {\mathrm {Supp}}^h(s) \neq \varnothing $
by using Example 7.6. Hence
![]() $\mathscr {B} \in \varphi ^h(\operatorname {\mathrm {Supp}}^h(s))$
.
$\mathscr {B} \in \varphi ^h(\operatorname {\mathrm {Supp}}^h(s))$
.
Proposition 7.14. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a finite localization. The induced map on homological spectra
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a finite localization. The induced map on homological spectra
![]() $\varphi ^h\colon \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c) \to \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
is an embedding with image
$\varphi ^h\colon \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c) \to \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
is an embedding with image
![]() $\operatorname {\mathrm {im}}(\varphi ^h) = \pi ^{-1}(\operatorname {\mathrm {im}}(\varphi ))$
.
$\operatorname {\mathrm {im}}(\varphi ^h) = \pi ^{-1}(\operatorname {\mathrm {im}}(\varphi ))$
.
Proof. First we establish injectivity. Let
![]() $\mathscr {C}_1, \mathscr {C}_2 \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
and suppose
$\mathscr {C}_1, \mathscr {C}_2 \in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
and suppose
![]() $\varphi ^h(\mathscr {C}_1) = \varphi ^h(\mathscr {C}_2)$
. Then
$\varphi ^h(\mathscr {C}_1) = \varphi ^h(\mathscr {C}_2)$
. Then
![]() $E_{\varphi ^h(\mathscr {C}_1)} \otimes E_{\varphi ^h(\mathscr {C}_2)} \neq 0$
. Hence
$E_{\varphi ^h(\mathscr {C}_1)} \otimes E_{\varphi ^h(\mathscr {C}_2)} \neq 0$
. Hence
![]() $f_*(E_{\mathscr {C}_1}) \otimes f_*(E_{\mathscr {C}_2}) \neq 0$
by Lemma 7.2. Moreover, since
$f_*(E_{\mathscr {C}_1}) \otimes f_*(E_{\mathscr {C}_2}) \neq 0$
by Lemma 7.2. Moreover, since
![]() $f^*$
is a finite localization, it is smashing, so
$f^*$
is a finite localization, it is smashing, so
![]() $f_*$
preserves the tensor product (but not necessarily the unit). Therefore,
$f_*$
preserves the tensor product (but not necessarily the unit). Therefore,
![]() $f_*(E_{\mathscr {C}_1}) \otimes f_*(E_{\mathscr {C}_2}) \simeq f_*(E_{\mathscr {C}_1} \otimes E_{\mathscr {C}_2})$
and hence we conclude that
$f_*(E_{\mathscr {C}_1}) \otimes f_*(E_{\mathscr {C}_2}) \simeq f_*(E_{\mathscr {C}_1} \otimes E_{\mathscr {C}_2})$
and hence we conclude that
![]() $E_{\mathscr {C}_1} \otimes E_{\mathscr {C}_2} \neq 0$
. Thus
$E_{\mathscr {C}_1} \otimes E_{\mathscr {C}_2} \neq 0$
. Thus
![]() $\mathscr {C}_1 = \mathscr {C}_2$
.
$\mathscr {C}_1 = \mathscr {C}_2$
.
Recall from [Reference BalmerBal20b, Remark 3.4] and [Reference Barthel, Heard and SandersBHS23a, Example 2.8] that a basis of closed sets for the topology on
![]() $\operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
is given by the
$\operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
is given by the
![]() $\operatorname {\mathrm {Supp}}^h(x)$
for
$\operatorname {\mathrm {Supp}}^h(x)$
for
![]() $x \in \mathscr {S}^c$
. Since
$x \in \mathscr {S}^c$
. Since
![]() $f^*$
is a finite localization,
$f^*$
is a finite localization,
![]() $x\oplus \Sigma x = f^*(c)$
for some compact
$x\oplus \Sigma x = f^*(c)$
for some compact
![]() $c \in \mathscr {T}^c$
and (replacing c with
$c \in \mathscr {T}^c$
and (replacing c with
![]() $c \otimes c^\vee $
) we can assume c is a (weak) ring. Then by Corollary 7.5 we have
$c \otimes c^\vee $
) we can assume c is a (weak) ring. Then by Corollary 7.5 we have
Moreover since
![]() $\varphi ^h$
is injective, it preserves intersections. It follows that for an arbitrary closed subset
$\varphi ^h$
is injective, it preserves intersections. It follows that for an arbitrary closed subset
![]() $Z \subseteq \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
, we similarly have
$Z \subseteq \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
, we similarly have
![]() $\varphi ^h(Z) = Z' \cap \operatorname {\mathrm {im}}(\varphi ^h)$
for some closed subset
$\varphi ^h(Z) = Z' \cap \operatorname {\mathrm {im}}(\varphi ^h)$
for some closed subset
![]() $Z' \subseteq \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
. This establishes that
$Z' \subseteq \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
. This establishes that
![]() $\varphi ^h$
is an embedding.
$\varphi ^h$
is an embedding.
To describe the image of
![]() $\varphi ^h$
, note that the object
$\varphi ^h$
, note that the object ![]() is the right idempotent of the finite localization so
is the right idempotent of the finite localization so ![]() by Lemma 6.4 and
by Lemma 6.4 and ![]() by [Reference BalmerBal20a, Theorem 5.12].
by [Reference BalmerBal20a, Theorem 5.12].
Corollary 7.15. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a finite localization. Then the induced diagram
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a finite localization. Then the induced diagram

is cartesian.
Proof. Let
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
. We claim that
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
. We claim that
![]() $\mathscr {B}$
is in the image of
$\mathscr {B}$
is in the image of
![]() $\varphi ^h$
if and only if
$\varphi ^h$
if and only if
![]() $\pi (\mathscr {B})$
is in the image of
$\pi (\mathscr {B})$
is in the image of
![]() $\varphi $
, but this is precisely what
$\varphi $
, but this is precisely what
![]() $\operatorname {\mathrm {im}}(\varphi ^h)=\pi ^{-1}(\operatorname {\mathrm {im}}(\varphi ))$
says.
$\operatorname {\mathrm {im}}(\varphi ^h)=\pi ^{-1}(\operatorname {\mathrm {im}}(\varphi ))$
says.
Corollary 7.16. Let
![]() $f^*\colon \mathscr {T}\to \mathscr {S}$
be a geometric functor and let
$f^*\colon \mathscr {T}\to \mathscr {S}$
be a geometric functor and let
![]() $V \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
be the complement of a Thomason subset. The induced diagram
$V \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
be the complement of a Thomason subset. The induced diagram

is cartesian.
Proof. This follows from Proposition 7.14 and the definitions.
8 Weakly descendable functors and descent
Terminology 8.1. Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a family of geometric functors between rigidly-compactly generated tt-categories, indexed on a (not necessarily finite) set I. We refer to
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a family of geometric functors between rigidly-compactly generated tt-categories, indexed on a (not necessarily finite) set I. We refer to
![]() $(f_i^*)_{i \in I}$
as a geometric family.
$(f_i^*)_{i \in I}$
as a geometric family.
Definition 8.2. The geometric family
![]() $(f_i^*)_{i \in I}$
is said to be weakly descendable if
$(f_i^*)_{i \in I}$
is said to be weakly descendable if
in
![]() $\mathscr {T}$
.
$\mathscr {T}$
.
Remark 8.4. The terminology of Definition 8.2 is inspired by the notion of a descendable algebra, introduced by [Reference MathewMat16]. More generally, we say that a geometric family
![]() $(f_i^*)_{i \in I}$
is descendable if
$(f_i^*)_{i \in I}$
is descendable if
in
![]() $\mathscr {T}$
. The situation studied in loc. cit. is the special case when I is a singleton and
$\mathscr {T}$
. The situation studied in loc. cit. is the special case when I is a singleton and
![]() $f^*$
is given by base-change along a commutative algebra.
$f^*$
is given by base-change along a commutative algebra.
Example 8.6. Base-change along
![]() $\mathbb {Z}_{(p)} \to \mathbb {Q} \times \mathbb {Z}/p$
provides a geometric functor on derived categories which is weakly descendable but not descendable.
$\mathbb {Z}_{(p)} \to \mathbb {Q} \times \mathbb {Z}/p$
provides a geometric functor on derived categories which is weakly descendable but not descendable.
Lemma 8.7. For a geometric family
![]() $(f_i^*)_{i \in I}$
, the following are equivalent:
$(f_i^*)_{i \in I}$
, the following are equivalent:
(a)
 $(f_i^*)_{i \in I}$
is weakly descendable;
$(f_i^*)_{i \in I}$
is weakly descendable;(b)
 $(f_i^!)_{i \in I}$
is jointly conservative;
$(f_i^!)_{i \in I}$
is jointly conservative;(c) for any
 $t_1,t_2 \in \mathscr {T}$
, we have
$t_1,t_2 \in \mathscr {T}$
, we have  $$\begin{align*}t_1 \in \operatorname{\mathrm{Locid}}\langle t_2 \rangle \iff \forall i \in I\colon f_i^*(t_1) \in \operatorname{\mathrm{Locid}}\langle f_i^*(t_2) \rangle. \end{align*}$$
$$\begin{align*}t_1 \in \operatorname{\mathrm{Locid}}\langle t_2 \rangle \iff \forall i \in I\colon f_i^*(t_1) \in \operatorname{\mathrm{Locid}}\langle f_i^*(t_2) \rangle. \end{align*}$$
Proof. We first prove
![]() $(a) \Leftrightarrow (b)$
. Write
$(a) \Leftrightarrow (b)$
. Write ![]() and consider its right orthogonal
and consider its right orthogonal
![]() $\mathscr {L}^{\perp }$
in
$\mathscr {L}^{\perp }$
in
![]() $\mathscr {T}$
. Note that
$\mathscr {T}$
. Note that

The first equivalence follows from [Reference Barthel, Castellana, Heard and SandersBCHS23, Definition 2.9], the second equivalence follows from the internal adjunction [Reference Balmer, Dell’Ambrogio and SandersBDS16, (2.18)], and the final equivalence follows from the observation that a left adjoint is conservative on the essential image of its right adjoint, by the unit-counit identity.
![]() $(a) \Rightarrow (c)$
: If
$(a) \Rightarrow (c)$
: If
![]() $t_1 \in \operatorname {\mathrm {Locid}}\langle t_2 \rangle $
then
$t_1 \in \operatorname {\mathrm {Locid}}\langle t_2 \rangle $
then
![]() $f_i^*(t_1) \in \operatorname {\mathrm {Locid}}\langle f_i^*(t_2) \rangle $
for all
$f_i^*(t_1) \in \operatorname {\mathrm {Locid}}\langle f_i^*(t_2) \rangle $
for all
![]() $i \in I$
, since
$i \in I$
, since
![]() $f_i^*$
are tt-functors, so it remains to prove the reverse implication in
$f_i^*$
are tt-functors, so it remains to prove the reverse implication in
![]() $(c)$
. Tensoring (8.3) with
$(c)$
. Tensoring (8.3) with
![]() $t_1$
and using the projection formula gives
$t_1$
and using the projection formula gives
Assuming
![]() $f_i^*(t_1) \in \operatorname {\mathrm {Locid}}\langle f_i^*(t_2) \rangle $
and using the projection formula again, we deduce
$f_i^*(t_1) \in \operatorname {\mathrm {Locid}}\langle f_i^*(t_2) \rangle $
and using the projection formula again, we deduce
![]() $(f_i)_*f_i^*(t_1) \in \operatorname {\mathrm {Locid}}\langle (f_i)_*f_i^*(t_2) \rangle $
. Now varying over
$(f_i)_*f_i^*(t_1) \in \operatorname {\mathrm {Locid}}\langle (f_i)_*f_i^*(t_2) \rangle $
. Now varying over
![]() $i \in I$
yields
$i \in I$
yields

as claimed.
![]() $(c) \Rightarrow (a)$
: By the triangle identity for the
$(c) \Rightarrow (a)$
: By the triangle identity for the
![]() $f_i^* \dashv (f_i)_*$
adjunction,
$f_i^* \dashv (f_i)_*$
adjunction, ![]() is a retract of
is a retract of ![]() , hence
, hence ![]() for all
for all
![]() $i \in I$
. Therefore, condition
$i \in I$
. Therefore, condition
![]() $(c)$
implies
$(c)$
implies ![]() , so
, so
![]() $(f_i^*)_{i \in I}$
is weakly descendable.
$(f_i^*)_{i \in I}$
is weakly descendable.
Example 8.8. A geometric functor
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
is weakly descendable if and only if its double-right adjoint
$f^*\colon \mathscr {T} \to \mathscr {S}$
is weakly descendable if and only if its double-right adjoint
![]() $f^!\colon \mathscr {T}\to \mathscr {S}$
is conservative.
$f^!\colon \mathscr {T}\to \mathscr {S}$
is conservative.
Remark 8.9. Condition
![]() $(c)$
of Lemma 8.7 has been used in [Reference Barthel, Benson, Iyengar, Krause and PevtsovaBBI+23] to establish a fibrewise criterion for stratification. Its tt-geometric incarnation is studied further in work of Juan Omar Gómez [Reference GómezGóm25].
$(c)$
of Lemma 8.7 has been used in [Reference Barthel, Benson, Iyengar, Krause and PevtsovaBBI+23] to establish a fibrewise criterion for stratification. Its tt-geometric incarnation is studied further in work of Juan Omar Gómez [Reference GómezGóm25].
Definition 8.10. A geometric family
![]() $(f_i^*)_{i \in I}$
is said to be weakly closed if
$(f_i^*)_{i \in I}$
is said to be weakly closed if ![]() is compact for all
is compact for all
![]() $i\in I$
. It is said to be strongly closed if
$i\in I$
. It is said to be strongly closed if
![]() $(f_i)_*:\mathscr {S}_i \to \mathscr {T}$
preserves compact objects for all
$(f_i)_*:\mathscr {S}_i \to \mathscr {T}$
preserves compact objects for all
![]() $i\in I$
.
$i\in I$
.
Proposition 8.11. Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i\in I}$
be a geometric family. Consider the following statements:
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i\in I}$
be a geometric family. Consider the following statements:
(a)
 $(f_i^*)_{i\in I}$
is weakly descendable;
$(f_i^*)_{i\in I}$
is weakly descendable;(b)
 $(f_i^*)_{i \in I}$
is jointly conservative;
$(f_i^*)_{i \in I}$
is jointly conservative;(c)
 $(f_i^*)_{i \in I}$
is jointly nil-conservative;
$(f_i^*)_{i \in I}$
is jointly nil-conservative;(d) the induced map on homological spectra
 $$\begin{align*}\varphi^h = \sqcup \varphi_i^h\colon \bigsqcup_{i \in I}\operatorname{\mathrm{Spc}}^h(\mathscr{S}_i^c) \to \operatorname{\mathrm{Spc}}^h(\mathscr{T}^c) \end{align*}$$
$$\begin{align*}\varphi^h = \sqcup \varphi_i^h\colon \bigsqcup_{i \in I}\operatorname{\mathrm{Spc}}^h(\mathscr{S}_i^c) \to \operatorname{\mathrm{Spc}}^h(\mathscr{T}^c) \end{align*}$$
is surjective;
(e) the induced map on tt-spectra
 $$\begin{align*}\varphi = \sqcup \varphi_i\colon \bigsqcup_{i \in I}\operatorname{\mathrm{Spc}}(\mathscr{S}_i^c) \to \operatorname{\mathrm{Spc}}(\mathscr{T}^c) \end{align*}$$
$$\begin{align*}\varphi = \sqcup \varphi_i\colon \bigsqcup_{i \in I}\operatorname{\mathrm{Spc}}(\mathscr{S}_i^c) \to \operatorname{\mathrm{Spc}}(\mathscr{T}^c) \end{align*}$$
is surjective.
Then
![]() $(a) \Rightarrow (b) \Rightarrow (c) \Leftrightarrow (d) \Rightarrow (e)$
. Moreover, if
$(a) \Rightarrow (b) \Rightarrow (c) \Leftrightarrow (d) \Rightarrow (e)$
. Moreover, if
![]() $(f_i^*)_{i \in I}$
is weakly closed then
$(f_i^*)_{i \in I}$
is weakly closed then
![]() $(e) \Rightarrow (a)$
and hence all the statements are equivalent.
$(e) \Rightarrow (a)$
and hence all the statements are equivalent.
Proof.
![]() $(a)\Rightarrow (b)$
: This follows from Lemma 8.7 and the proof of [Reference Barthel, Castellana, Heard and SandersBCHS23, Proposition 13.21].
$(a)\Rightarrow (b)$
: This follows from Lemma 8.7 and the proof of [Reference Barthel, Castellana, Heard and SandersBCHS23, Proposition 13.21].
![]() $(b)\Rightarrow (c)$
: This is immediate from the definitions.
$(b)\Rightarrow (c)$
: This is immediate from the definitions.
![]() $(c)\Leftrightarrow (d)$
: This is [Reference Barthel, Castellana, Heard and SandersBCHS24, Theorem 1.8].
$(c)\Leftrightarrow (d)$
: This is [Reference Barthel, Castellana, Heard and SandersBCHS24, Theorem 1.8].
![]() $(d) \Rightarrow (e)$
: This holds because
$(d) \Rightarrow (e)$
: This holds because
![]() $\pi $
is surjective.
$\pi $
is surjective.
![]() $(e)\Rightarrow (a)$
: Since
$(e)\Rightarrow (a)$
: Since
![]() $\varphi $
is surjective, we have
$\varphi $
is surjective, we have
If the
![]() $f_i^*$
are weakly closed then, by definition, each
$f_i^*$
are weakly closed then, by definition, each ![]() is compact. We then have
is compact. We then have ![]() by the argument given at the beginning of the proof of [Reference BalmerBal18, Theorem 1.7]. Hence
by the argument given at the beginning of the proof of [Reference BalmerBal18, Theorem 1.7]. Hence
so that ![]() by the classification of thick ideals.
by the classification of thick ideals.
Remark 8.12. In general,
![]() $(f_i^*)_{i \in I}$
being jointly conservative does not imply that the family is weakly descendable. Indeed, let k be a field and I an infinite set. By [Reference StevensonSte14], the projection functors
$(f_i^*)_{i \in I}$
being jointly conservative does not imply that the family is weakly descendable. Indeed, let k be a field and I an infinite set. By [Reference StevensonSte14], the projection functors
are jointly conservative. However, the localizing ideal
![]() $\operatorname {\mathrm {Locid}}\langle (\pi _i)_*k \rangle $
is a proper subcategory of
$\operatorname {\mathrm {Locid}}\langle (\pi _i)_*k \rangle $
is a proper subcategory of
![]() $\operatorname {\mathrm {D}}(\prod _{i \in I}k)$
since
$\operatorname {\mathrm {D}}(\prod _{i \in I}k)$
since
![]() $\prod _{i \in I}k$
is not semi-artinian (Example 3.7).
$\prod _{i \in I}k$
is not semi-artinian (Example 3.7).
Remark 8.13. The next result is a minor variation on Proposition 8.11 which improves on [Reference Barthel, Castellana, Heard and SandersBCHS23, Corollary 14.24] by extending the latter to families of geometric functors and weakening the tt-stratification assumption to h-stratification.
Corollary 8.14. Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i\in I}$
be a geometric family and assume that
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i\in I}$
be a geometric family and assume that
![]() $\mathscr {T}$
is h-stratified. Then the following are equivalent:
$\mathscr {T}$
is h-stratified. Then the following are equivalent:
(a)
 $(f_i^*)_{i\in I}$
is weakly descendable;
$(f_i^*)_{i\in I}$
is weakly descendable;(b)
 $(f_i^*)_{i \in I}$
is jointly conservative;
$(f_i^*)_{i \in I}$
is jointly conservative;(c)
 $(f_i^*)_{i \in I}$
is jointly nil-conservative;
$(f_i^*)_{i \in I}$
is jointly nil-conservative;(d) the induced map on homological spectra
 $$\begin{align*}\varphi^h = \sqcup \varphi_i^h\colon \bigsqcup_{i \in I}\operatorname{\mathrm{Spc}}^h(\mathscr{S}_i^c) \to \operatorname{\mathrm{Spc}}^h(\mathscr{T}^c) \end{align*}$$
$$\begin{align*}\varphi^h = \sqcup \varphi_i^h\colon \bigsqcup_{i \in I}\operatorname{\mathrm{Spc}}^h(\mathscr{S}_i^c) \to \operatorname{\mathrm{Spc}}^h(\mathscr{T}^c) \end{align*}$$
is surjective.
Proof. The implications
![]() $(a) \Rightarrow (b) \Rightarrow (c) \Rightarrow (d)$
are part of Proposition 8.11, so it remains to show
$(a) \Rightarrow (b) \Rightarrow (c) \Rightarrow (d)$
are part of Proposition 8.11, so it remains to show
![]() $(d) \Rightarrow (a)$
. Indeed, if
$(d) \Rightarrow (a)$
. Indeed, if
![]() $\varphi ^h$
is surjective, then
$\varphi ^h$
is surjective, then
where the second equality uses [Reference BalmerBal20a, Theorem 5.12]. Since
![]() $\mathscr {T}$
is h-stratified, this implies that
$\mathscr {T}$
is h-stratified, this implies that ![]() , so
, so
![]() $(f_i^*)_{i\in I}$
is weakly descendable.
$(f_i^*)_{i\in I}$
is weakly descendable.
Remark 8.15. In light of the above corollary and its analogue [Reference Barthel, Castellana, Heard and SandersBCHS23, Corollary 14.24], we regard weak descendability as the appropriate condition for studying descent properties in rigidly-compactly generated tt-geometry.
Example 8.16. Let
![]() $\mathscr {T}$
be a rigidly-compactly generated tt-category. By definition, the family of localizations
$\mathscr {T}$
be a rigidly-compactly generated tt-category. By definition, the family of localizations
![]() $\{ f_{\mathscr {P}}^*\colon \mathscr {T} \to \mathscr {T}_{\mathscr {P}}\}_{\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)}$
is weakly descendable if and only if
$\{ f_{\mathscr {P}}^*\colon \mathscr {T} \to \mathscr {T}_{\mathscr {P}}\}_{\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)}$
is weakly descendable if and only if
The following example demonstrates that this need not always be the case:
Example 8.17. Let
![]() $\mathscr {T}=\operatorname {\mathrm {D}}(R)$
be the derived category of an absolutely flat ring R. Then the local categories are precisely the derived categories of the residue fields and
$\mathscr {T}=\operatorname {\mathrm {D}}(R)$
be the derived category of an absolutely flat ring R. Then the local categories are precisely the derived categories of the residue fields and
![]() $f_{\operatorname {\mathrm {gen}}(\mathscr {P})^c} \simeq \kappa (\mathfrak p)$
for
$f_{\operatorname {\mathrm {gen}}(\mathscr {P})^c} \simeq \kappa (\mathfrak p)$
for
![]() $\mathscr {P}$
corresponding to
$\mathscr {P}$
corresponding to
![]() $\mathfrak p$
. Thus the family of localizations is weakly descendable if and only if
$\mathfrak p$
. Thus the family of localizations is weakly descendable if and only if
That is, if and only if
![]() $\operatorname {\mathrm {D}}(R)$
has the homological local-to-global principle (recall Example 3.5). This is the case if and only if R is semi-artinian; see Example 3.7.
$\operatorname {\mathrm {D}}(R)$
has the homological local-to-global principle (recall Example 3.5). This is the case if and only if R is semi-artinian; see Example 3.7.
Proposition 8.18. Let
![]() $\mathscr {T}$
be a rigidly-compactly generated tt-category. If the homological local-to-global principle holds then the family of localizations
$\mathscr {T}$
be a rigidly-compactly generated tt-category. If the homological local-to-global principle holds then the family of localizations
is weakly descendable.
Proof. By hypothesis and Remark 3.3, ![]() . Hence it suffices to prove that
. Hence it suffices to prove that ![]() for
for ![]() . This follows from the fact that
. This follows from the fact that ![]() ; see [Reference ZouZou25, Lemma 8.6].
; see [Reference ZouZou25, Lemma 8.6].
Remark 8.19. The converse of Proposition 8.18 does not hold. For example, the homological local-to-global principle does not hold for the derived category of the truncated polynomial ring in Example 4.14 (see Remark 4.15), but the family of localizations is weakly descendable for the trivial reason that the category is local.
Proposition 8.20. Let
![]() $\mathscr {T}$
be a rigidly-compactly generated tt-category whose spectrum is weakly noetherian. If the local-to-global principle holds then the family of localizations
$\mathscr {T}$
be a rigidly-compactly generated tt-category whose spectrum is weakly noetherian. If the local-to-global principle holds then the family of localizations
is weakly descendable.
Proof. Recall that
![]() $g_{\mathscr {P}} = e_{Y} \otimes f_{\operatorname {\mathrm {gen}}(\mathscr {P})^c}$
for some Thomason subset Y and
$g_{\mathscr {P}} = e_{Y} \otimes f_{\operatorname {\mathrm {gen}}(\mathscr {P})^c}$
for some Thomason subset Y and ![]() . Thus
. Thus
The local-to-global principle states that ![]() is contained in the left-hand side, while the family is weakly descendable if
is contained in the left-hand side, while the family is weakly descendable if ![]() is contained in the right-hand side.
is contained in the right-hand side.
Proposition 8.21. Suppose
![]() $\mathscr {T}$
admits enough tt-fields, say
$\mathscr {T}$
admits enough tt-fields, say
![]() $\{f_{\mathscr {B}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {B}}\}_{\mathscr {B}}$
. The following are equivalent:
$\{f_{\mathscr {B}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {B}}\}_{\mathscr {B}}$
. The following are equivalent:
(a) The family
 $\{f_{\mathscr {B}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {B}}\}$
is weakly descendable.
$\{f_{\mathscr {B}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {B}}\}$
is weakly descendable.(b) The homological local-to-global principle holds.
Proof. If
![]() $\mathscr {T}$
has the h-detection property then
$\mathscr {T}$
has the h-detection property then ![]() for every
for every
![]() $\mathscr {B}$
by Proposition 4.5, which implies the desired equivalence. Certainly h-LGP implies h-detection. To finish the proof, we claim that
$\mathscr {B}$
by Proposition 4.5, which implies the desired equivalence. Certainly h-LGP implies h-detection. To finish the proof, we claim that
![]() $(a)$
also implies h-detection. Indeed, since tt-fields are h-stratified (Example 4.4), we have
$(a)$
also implies h-detection. Indeed, since tt-fields are h-stratified (Example 4.4), we have
![]() $(\varphi ^h_{\mathscr {B}})^{-1}(\operatorname {\mathrm {Supp}}^h(t)) = \operatorname {\mathrm {Supp}}^h(f_{\mathscr {B}}^*(t))$
for every
$(\varphi ^h_{\mathscr {B}})^{-1}(\operatorname {\mathrm {Supp}}^h(t)) = \operatorname {\mathrm {Supp}}^h(f_{\mathscr {B}}^*(t))$
for every
![]() $\mathscr {B}$
and every object
$\mathscr {B}$
and every object
![]() $t \in \mathscr {T}$
by Proposition 7.9. Therefore, the h-detection property is equivalent to the family
$t \in \mathscr {T}$
by Proposition 7.9. Therefore, the h-detection property is equivalent to the family
![]() $\{f_{\mathscr {B}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {B}}\}_{\mathscr {B}}$
being jointly conservative. The claim thus follows from Proposition 8.11.
$\{f_{\mathscr {B}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {B}}\}_{\mathscr {B}}$
being jointly conservative. The claim thus follows from Proposition 8.11.
Example 8.22. The derived category
![]() $\operatorname {\mathrm {D}}(R)$
of a commutative ring R satisfies the h-LGP if and only if the family
$\operatorname {\mathrm {D}}(R)$
of a commutative ring R satisfies the h-LGP if and only if the family
![]() $\{\operatorname {\mathrm {D}}(R) \to \operatorname {\mathrm {D}}(\kappa (\mathfrak p))\}_{\mathfrak p\in \operatorname {\mathrm {Spec}}(R)}$
of residue fields is weakly descendable.
$\{\operatorname {\mathrm {D}}(R) \to \operatorname {\mathrm {D}}(\kappa (\mathfrak p))\}_{\mathfrak p\in \operatorname {\mathrm {Spec}}(R)}$
of residue fields is weakly descendable.
Remark 8.23. The following theorem shows that h-stratification always descends along a weakly descendable family of geometric functors. Although the proof is not difficult given our preparation, it is one of the key insights of the paper and will have various consequences below.
Theorem 8.24. Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family. Assume that
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family. Assume that
![]() $\mathscr {S}_i$
is h-stratified for each
$\mathscr {S}_i$
is h-stratified for each
![]() $i \in I$
. Then
$i \in I$
. Then
![]() $\mathscr {T}$
is h-stratified.
$\mathscr {T}$
is h-stratified.
Proof. We will verify condition
![]() $(b)$
of Theorem 4.1. To this end, let
$(b)$
of Theorem 4.1. To this end, let
![]() $t \in \mathscr {T}$
and first fix some
$t \in \mathscr {T}$
and first fix some
![]() $i \in I$
. Using Proposition 7.9 twice, we obtain equalities
$i \in I$
. Using Proposition 7.9 twice, we obtain equalities
Theorem 4.1
![]() $(b)$
applied to
$(b)$
applied to
![]() $\mathscr {S}_i$
then shows that
$\mathscr {S}_i$
then shows that
Keeping in mind that (8.3) holds by assumption, Lemma 8.7 implies that
![]() $\operatorname {\mathrm {Locid}}\langle t \rangle = \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}}\mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t) \rangle $
, as desired.
$\operatorname {\mathrm {Locid}}\langle t \rangle = \operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}}\mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t) \rangle $
, as desired.
8.25. We also include an alternative proof of Theorem 8.24 based on cosupport.
Proof Alternative proof of Theorem 8.24
We will verify condition (c) of Theorem 5.6. Note that the collection of maps
![]() $(\varphi _i^h)$
is jointly surjective by Proposition 8.11. Since
$(\varphi _i^h)$
is jointly surjective by Proposition 8.11. Since
![]() $(f_i^*)$
is weakly descendable and
$(f_i^*)$
is weakly descendable and
![]() $\mathscr {S}_i$
is h-stratified for all i, for any objects
$\mathscr {S}_i$
is h-stratified for all i, for any objects
![]() $t_1,t_2 \in \mathscr {T}$
we have equivalences:
$t_1,t_2 \in \mathscr {T}$
we have equivalences:
 $$ \begin{align*} 0 = \mathsf{hom}(t_1,t_2) & \iff \forall i \in I\colon 0 = f_i^!\mathsf{hom}(t_1,t_2) \simeq \mathsf{hom}(f_i^*t_1,f_i^!t_2) & & (8.7) \\ & \iff \forall i \in I\colon \varnothing = \operatorname{\mathrm{Supp}}^h(f_i^*t_1) \cap \operatorname{\mathrm{Cosupp}}^h(f_i^!t_2) & & (5.6) \\ & \iff \varnothing = \bigcup_{i \in I} (\varphi_i^h)^{-1}(\operatorname{\mathrm{Supp}}^h(t_1) \cap \operatorname{\mathrm{Cosupp}}^h(t_2)) && (7.9,7.12) \\ & \iff \varnothing = \operatorname{\mathrm{Supp}}^h(t_1) \cap \operatorname{\mathrm{Cosupp}}^h(t_2) & & (8.11), \end{align*} $$
$$ \begin{align*} 0 = \mathsf{hom}(t_1,t_2) & \iff \forall i \in I\colon 0 = f_i^!\mathsf{hom}(t_1,t_2) \simeq \mathsf{hom}(f_i^*t_1,f_i^!t_2) & & (8.7) \\ & \iff \forall i \in I\colon \varnothing = \operatorname{\mathrm{Supp}}^h(f_i^*t_1) \cap \operatorname{\mathrm{Cosupp}}^h(f_i^!t_2) & & (5.6) \\ & \iff \varnothing = \bigcup_{i \in I} (\varphi_i^h)^{-1}(\operatorname{\mathrm{Supp}}^h(t_1) \cap \operatorname{\mathrm{Cosupp}}^h(t_2)) && (7.9,7.12) \\ & \iff \varnothing = \operatorname{\mathrm{Supp}}^h(t_1) \cap \operatorname{\mathrm{Cosupp}}^h(t_2) & & (8.11), \end{align*} $$
as desired.
9 Comparison between h-stratification and tt-stratification
A theory of stratification for tt-categories is developed in [Reference Barthel, Heard and SandersBHS23b] under the assumption that the Balmer spectrum is weakly noetherian. Our next goal is to relate this notion of stratification (based on the Balmer spectrum and the Balmer–Favi support) with the homological stratification developed in this paper (based on the homological spectrum and the homological support).
Definition 9.1. We will say that a rigidly-compactly generated tt-category
![]() $\mathscr {T}$
satisfies the Nerves of Steel conjecture ([Reference BalmerBal20b, Remark 5.15]) if the surjective comparison map
$\mathscr {T}$
satisfies the Nerves of Steel conjecture ([Reference BalmerBal20b, Remark 5.15]) if the surjective comparison map
is a bijection.
Remark 9.2. The question of whether every rigidly-compactly generated tt-category satisfies the Nerves of Steel conjecture is an open problem, but it is known to be true in many examples of interest; see [Reference BalmerBal20b, Section 5], for example. For the state of the art, see [Reference HyslopHys24].
Proposition 9.3. Suppose
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)=\bigcup _{i\in I}V_i$
is a cover by complements
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)=\bigcup _{i\in I}V_i$
is a cover by complements
![]() $V_i$
of Thomason subsets. Then the Nerves of Steel conjecture holds for
$V_i$
of Thomason subsets. Then the Nerves of Steel conjecture holds for
![]() $\mathscr {T}$
if and only if it holds for each
$\mathscr {T}$
if and only if it holds for each
![]() $\mathscr {T}(V_i)$
.
$\mathscr {T}(V_i)$
.
Proof. The only if part follows immediately from the diagram in Corollary 7.15. Now suppose each
![]() $\mathscr {T}(V_i)$
satisfies the Nerves of Steel conjecture. For any
$\mathscr {T}(V_i)$
satisfies the Nerves of Steel conjecture. For any
![]() $\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
there exists some
$\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
there exists some
![]() $V_i$
containing
$V_i$
containing
![]() $\mathscr {P}$
. Applying Proposition 7.14 to the finite localization
$\mathscr {P}$
. Applying Proposition 7.14 to the finite localization
![]() $\mathscr {T} \to \mathscr {T}(V_i)$
we obtain the commutative diagram
$\mathscr {T} \to \mathscr {T}(V_i)$
we obtain the commutative diagram

which implies that
![]() $\pi ^{-1}(\{\mathscr {P}\})$
consists of exactly one point.
$\pi ^{-1}(\{\mathscr {P}\})$
consists of exactly one point.
Remark 9.4. In particular,
![]() $\mathscr {T}$
satisfies the Nerves of Steel conjecture if and only if each local category
$\mathscr {T}$
satisfies the Nerves of Steel conjecture if and only if each local category
![]() $\mathscr {T}_{\mathscr {P}}$
does.
$\mathscr {T}_{\mathscr {P}}$
does.
Definition 9.5. We will say that a rigidly-compactly generated tt-category whose spectrum
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian is tt-stratified if it is stratified in the sense of [Reference Barthel, Heard and SandersBHS23b].
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian is tt-stratified if it is stratified in the sense of [Reference Barthel, Heard and SandersBHS23b].
Theorem 9.6. Let
![]() $\mathscr {T}$
be a rigidly-compactly generated tt-category with
$\mathscr {T}$
be a rigidly-compactly generated tt-category with
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
weakly noetherian. The following are equivalent:
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
weakly noetherian. The following are equivalent:
(a)
 $\mathscr {T}$
is tt-stratified;
$\mathscr {T}$
is tt-stratified;(b)
 $\mathscr {T}$
is h-stratified and the Nerves of Steel conjecture holds for
$\mathscr {T}$
is h-stratified and the Nerves of Steel conjecture holds for
 $\mathscr {T}$
.
$\mathscr {T}$
.
Proof.
![]() $(a)\Rightarrow (b)$
: By [Reference Barthel, Heard and SandersBHS23a, Theorem 4.7] if
$(a)\Rightarrow (b)$
: By [Reference Barthel, Heard and SandersBHS23a, Theorem 4.7] if
![]() $\mathscr {T}$
is tt-stratified, then the Nerves of Steel conjecture holds for
$\mathscr {T}$
is tt-stratified, then the Nerves of Steel conjecture holds for
![]() $\mathscr {T}$
, so it remains to show that
$\mathscr {T}$
, so it remains to show that
![]() $\mathscr {T}$
is h-stratified. It was proved in [Reference Barthel, Heard and SandersBHS23a, Lemma 3.7] that
$\mathscr {T}$
is h-stratified. It was proved in [Reference Barthel, Heard and SandersBHS23a, Lemma 3.7] that
![]() $\operatorname {\mathrm {Supp}}(E_{\mathscr {B}})=\{ \pi (\mathscr {B})\}$
for any
$\operatorname {\mathrm {Supp}}(E_{\mathscr {B}})=\{ \pi (\mathscr {B})\}$
for any
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
. Hence
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
. Hence
![]() $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle = \operatorname {\mathrm {Locid}}\langle g_{\pi (\mathscr {B})} \rangle $
when
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \rangle = \operatorname {\mathrm {Locid}}\langle g_{\pi (\mathscr {B})} \rangle $
when
![]() $\mathscr {T}$
is tt-stratified. Therefore,
$\mathscr {T}$
is tt-stratified. Therefore,
for any
![]() $t \in \mathscr {T}$
. This coincides with
$t \in \mathscr {T}$
. This coincides with
![]() $\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t) \rangle $
since [Reference Barthel, Heard and SandersBHS23a, Theorem 4.7] establishes that
$\operatorname {\mathrm {Locid}}\langle E_{\mathscr {B}} \mid \mathscr {B} \in \operatorname {\mathrm {Supp}}^h(t) \rangle $
since [Reference Barthel, Heard and SandersBHS23a, Theorem 4.7] establishes that
![]() $\pi ^{-1}(\operatorname {\mathrm {Supp}}(t))=\operatorname {\mathrm {Supp}}^h(t)$
when
$\pi ^{-1}(\operatorname {\mathrm {Supp}}(t))=\operatorname {\mathrm {Supp}}^h(t)$
when
![]() $\mathscr {T}$
is tt-stratified. This establishes that
$\mathscr {T}$
is tt-stratified. This establishes that
![]() $\mathscr {T}$
is h-stratified by Theorem 4.1.
$\mathscr {T}$
is h-stratified by Theorem 4.1.
![]() $(b)\Rightarrow (a)$
: If
$(b)\Rightarrow (a)$
: If
![]() $\mathscr {T}$
is h-stratified then the h-detection property holds. Thus, Proposition 6.8 implies that
$\mathscr {T}$
is h-stratified then the h-detection property holds. Thus, Proposition 6.8 implies that
![]() $\pi (\operatorname {\mathrm {Supp}}^h(t))=\operatorname {\mathrm {Supp}}(t))$
for each
$\pi (\operatorname {\mathrm {Supp}}^h(t))=\operatorname {\mathrm {Supp}}(t))$
for each
![]() $t \in \mathscr {T}$
. It follows that the diagram
$t \in \mathscr {T}$
. It follows that the diagram

commutes. By hypothesis, the horizontal and vertical maps are injective (and thus bijective), hence so is the diagonal map; that is,
![]() $\mathscr {T}$
is tt-stratified.
$\mathscr {T}$
is tt-stratified.
Corollary 9.8. If the Nerves of Steel conjecture holds for
![]() $\mathscr {T}$
and
$\mathscr {T}$
and
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian then
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian then
![]() $\mathscr {T}$
is tt-stratified if and only if it is h-stratified.
$\mathscr {T}$
is tt-stratified if and only if it is h-stratified.
Proof. This immediately follows from Theorem 9.6.
Corollary 9.9. Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family. Assume that
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family. Assume that
![]() $\mathscr {S}_i$
is tt-stratified for each
$\mathscr {S}_i$
is tt-stratified for each
![]() $i \in I$
and that
$i \in I$
and that
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. If the Nerves of Steel conjecture holds for
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. If the Nerves of Steel conjecture holds for
![]() $\mathscr {T}$
then
$\mathscr {T}$
then
![]() $\mathscr {T}$
is tt-stratified.
$\mathscr {T}$
is tt-stratified.
Proof. For each
![]() $i \in I$
, the tt-category
$i \in I$
, the tt-category
![]() $\mathscr {S}_i$
is tt-stratified by assumption, hence h-stratified by Theorem 9.6. Descent for h-stratification as established in Theorem 8.24 then implies that
$\mathscr {S}_i$
is tt-stratified by assumption, hence h-stratified by Theorem 9.6. Descent for h-stratification as established in Theorem 8.24 then implies that
![]() $\mathscr {T}$
is h-stratified. Therefore, Theorem 9.6 implies that
$\mathscr {T}$
is h-stratified. Therefore, Theorem 9.6 implies that
![]() $\mathscr {T}$
is tt-stratified, due to our assumption that
$\mathscr {T}$
is tt-stratified, due to our assumption that
![]() $\mathscr {T}$
satisfies Nerves of Steel.
$\mathscr {T}$
satisfies Nerves of Steel.
9.10. We conclude this section with a proof of Theorem A from the introduction.
10 Descent for the Nerves of Steel conjecture
In order to apply Corollary 9.9 to descend tt-stratification, we desire methods for establishing the Nerves of Steel conjecture. This is the topic of the present section.
Lemma 10.1. Let
![]() $f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor and let
$f^*\colon \mathscr {T} \to \mathscr {S}$
be a geometric functor and let
![]() $V \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
be the complement of a Thomason subset. If
$V \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
be the complement of a Thomason subset. If
![]() $f^*$
is strongly closed, then the canonical corestriction functor
$f^*$
is strongly closed, then the canonical corestriction functor
![]() $\mathscr {T}(V) \to \mathscr {S}(\varphi ^{-1}(V))$
is also strongly closed.
$\mathscr {T}(V) \to \mathscr {S}(\varphi ^{-1}(V))$
is also strongly closed.
Proof. Let ![]() and consider the commutative square
and consider the commutative square

where the vertical arrows are the finite localizations and the bottom arrow is the induced functor. This diagram satisfies the Beck–Chevalley condition
![]() $h^* f_* \simeq g_* k^*$
; cf. [Reference SandersSan22, Lemma 5.5]. Indeed, this may be checked after applying the conservative
$h^* f_* \simeq g_* k^*$
; cf. [Reference SandersSan22, Lemma 5.5]. Indeed, this may be checked after applying the conservative
![]() $h_*$
. For any
$h_*$
. For any
![]() $s \in \mathscr {S}$
, we have
$s \in \mathscr {S}$
, we have ![]() where we have invoked [Reference Balmer and SandersBS17, Proposition 5.11]. With this in hand, consider a compact object
where we have invoked [Reference Balmer and SandersBS17, Proposition 5.11]. With this in hand, consider a compact object
![]() $x \in \mathscr {S}(\varphi ^{-1}(V))^c$
. Then
$x \in \mathscr {S}(\varphi ^{-1}(V))^c$
. Then
![]() $x \oplus \Sigma x = k^*(c)$
for some
$x \oplus \Sigma x = k^*(c)$
for some
![]() $c \in \mathscr {S}^c$
and it suffices to show that
$c \in \mathscr {S}^c$
and it suffices to show that
![]() $g_* k^*(c)$
is compact. This follows from our hypothesis, since
$g_* k^*(c)$
is compact. This follows from our hypothesis, since
![]() $g_* k^*(c) \simeq h^*f_*(c)$
.
$g_* k^*(c) \simeq h^*f_*(c)$
.
Proposition 10.2. Suppose
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
is a jointly nil-conservative family of geometric functors with
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
is a jointly nil-conservative family of geometric functors with
![]() $\mathscr {S}_i$
satisfying the Nerves of Steel conjecture for all
$\mathscr {S}_i$
satisfying the Nerves of Steel conjecture for all
![]() $i\in I$
. Assume additionally one of the following:
$i\in I$
. Assume additionally one of the following:
(a) the induced map
 $\varphi \colon \bigsqcup _{i \in I}\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c) \to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is injective; or
$\varphi \colon \bigsqcup _{i \in I}\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c) \to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is injective; or(b)
 $(f_i^*)_{i \in I}$
is strongly closed and
$(f_i^*)_{i \in I}$
is strongly closed and
 $\varphi _i$
has discrete fibres for all
$\varphi _i$
has discrete fibres for all
 $i \in I$
; or
$i \in I$
; or-
(c)
 $(f_i^*)_{i \in I}$
is strongly closed and
$(f_i^*)_{i \in I}$
is strongly closed and
 $\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c)$
is noetherian for all
$\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c)$
is noetherian for all
 $i \in I$
.
$i \in I$
.
Then
![]() $\mathscr {T}$
satisfies the Nerves of Steel conjecture.
$\mathscr {T}$
satisfies the Nerves of Steel conjecture.
Proof. Consider the commutative diagram

Recall from Proposition 8.11 that
![]() $(f_i^*)$
being jointly nil-conservative implies that
$(f_i^*)$
being jointly nil-conservative implies that
![]() $\varphi $
is also surjective. If
$\varphi $
is also surjective. If
![]() $\varphi $
is in addition injective as assumed in
$\varphi $
is in addition injective as assumed in
![]() $(a)$
, then it is bijective. Since
$(a)$
, then it is bijective. Since
![]() $\sqcup \pi _{\mathscr {S}_i}$
is bijective,
$\sqcup \pi _{\mathscr {S}_i}$
is bijective,
![]() $\varphi ^h$
is injective and hence bijective. Therefore
$\varphi ^h$
is injective and hence bijective. Therefore
![]() $\pi _{\mathscr {T}}$
is bijective.
$\pi _{\mathscr {T}}$
is bijective.
Now assume either condition
![]() $(b)$
or
$(b)$
or
![]() $(c)$
. By Corollary 7.15, the Nerves of Steel conjecture holds also for any finite localization of
$(c)$
. By Corollary 7.15, the Nerves of Steel conjecture holds also for any finite localization of
![]() $\mathscr {S}_i$
. Moreover, the property of being strongly closed is local in the target by Lemma 10.1, while the property of being nil-conservative is local in the target by Proposition 8.11[
$\mathscr {S}_i$
. Moreover, the property of being strongly closed is local in the target by Lemma 10.1, while the property of being nil-conservative is local in the target by Proposition 8.11[
![]() $(c) \Leftrightarrow (d)$
] and Corollary 7.16. Therefore, we can reduce to the case when
$(c) \Leftrightarrow (d)$
] and Corollary 7.16. Therefore, we can reduce to the case when
![]() $\mathscr {T}$
is local and check that the fibre of
$\mathscr {T}$
is local and check that the fibre of
![]() $\pi _{\mathscr {T}}\colon \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)\to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
over the unique closed point
$\pi _{\mathscr {T}}\colon \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)\to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
over the unique closed point
![]() $\mathfrak m \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is a singleton. Since
$\mathfrak m \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is a singleton. Since
![]() $\varphi $
is surjective, we may choose
$\varphi $
is surjective, we may choose
![]() $i \in I$
and a closed point
$i \in I$
and a closed point
![]() $\mathscr {M} \in \operatorname {\mathrm {Spc}}(\mathscr {S}_i^c)$
lying over
$\mathscr {M} \in \operatorname {\mathrm {Spc}}(\mathscr {S}_i^c)$
lying over
![]() $\mathfrak m$
. For the remainder of this proof, we set
$\mathfrak m$
. For the remainder of this proof, we set
![]() $\mathscr {S} = \mathscr {S}_i$
and simplify the notation accordingly.
$\mathscr {S} = \mathscr {S}_i$
and simplify the notation accordingly.
Observe that
![]() $\{\mathscr {M}\}$
is Thomason closed if
$\{\mathscr {M}\}$
is Thomason closed if
![]() $\operatorname {\mathrm {Spc}}(\mathscr {S}^c)$
is noetherian or
$\operatorname {\mathrm {Spc}}(\mathscr {S}^c)$
is noetherian or
![]() $\varphi $
has discrete fibres. In either case, by [Reference BalmerBal05, Proposition 2.14] there exists some compact object
$\varphi $
has discrete fibres. In either case, by [Reference BalmerBal05, Proposition 2.14] there exists some compact object
![]() $z \in \mathscr {S}^c$
with
$z \in \mathscr {S}^c$
with
![]() $\operatorname {\mathrm {supp}}(z)=\{\mathscr {M}\}$
. Replacing z by
$\operatorname {\mathrm {supp}}(z)=\{\mathscr {M}\}$
. Replacing z by
![]() $z \otimes z^{\vee }$
we may assume that z is a (weak) ring. Let
$z \otimes z^{\vee }$
we may assume that z is a (weak) ring. Let
![]() $\mathscr {A}\in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
be the unique homological prime such that
$\mathscr {A}\in \operatorname {\mathrm {Spc}}^h(\mathscr {S}^c)$
be the unique homological prime such that
![]() $\pi _{\mathscr {S}}(\mathscr {A}) = \mathscr {M}$
, so that
$\pi _{\mathscr {S}}(\mathscr {A}) = \mathscr {M}$
, so that
![]() $\operatorname {\mathrm {Supp}}^h(z) = \{\mathscr {A}\}$
.
$\operatorname {\mathrm {Supp}}^h(z) = \{\mathscr {A}\}$
.
Suppose for a contradiction that there exists a point
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
lying over
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
lying over
![]() $\mathfrak m$
such that
$\mathfrak m$
such that
![]() $\mathscr {B}\neq \varphi ^h(\mathscr {A})$
. Recall from Example 7.6 that
$\mathscr {B}\neq \varphi ^h(\mathscr {A})$
. Recall from Example 7.6 that
It follows that
and hence
![]() $f^*(E_{\mathscr {B}})\otimes z=0$
because homological support detects weak rings (Remark 2.9). Therefore,
$f^*(E_{\mathscr {B}})\otimes z=0$
because homological support detects weak rings (Remark 2.9). Therefore,
![]() $E_{\mathscr {B}} \otimes f_*(z)=0$
by the projection formula. That is
$E_{\mathscr {B}} \otimes f_*(z)=0$
by the projection formula. That is
![]() $\mathscr {B} \not \in \operatorname {\mathrm {Supp}}^h(f_*(z))$
. By the hypothesis that f is strongly closed,
$\mathscr {B} \not \in \operatorname {\mathrm {Supp}}^h(f_*(z))$
. By the hypothesis that f is strongly closed,
![]() $f_*(z)$
is compact and hence
$f_*(z)$
is compact and hence
![]() ${\operatorname {\mathrm {Supp}}^h(f_*(z)) = \pi _{\mathscr {T}}^{-1}(\operatorname {\mathrm {supp}}(f_*(z)))}$
by Remark 6.2. Therefore we have
${\operatorname {\mathrm {Supp}}^h(f_*(z)) = \pi _{\mathscr {T}}^{-1}(\operatorname {\mathrm {supp}}(f_*(z)))}$
by Remark 6.2. Therefore we have
![]() $\mathscr {B} \not \in \pi _{\mathscr {T}}^{-1}(\operatorname {\mathrm {supp}}(f_*(z)))$
so
$\mathscr {B} \not \in \pi _{\mathscr {T}}^{-1}(\operatorname {\mathrm {supp}}(f_*(z)))$
so
![]() $\mathfrak m = \pi _{\mathscr {T}}(\mathscr {B}) \not \in \operatorname {\mathrm {supp}}(f_*(z))=\varphi (\operatorname {\mathrm {supp}}(z))$
where the last equality is by [Reference Barthel, Castellana, Heard and SandersBCHS23, Theorem 13.13] since z is a compact weak ring. But
$\mathfrak m = \pi _{\mathscr {T}}(\mathscr {B}) \not \in \operatorname {\mathrm {supp}}(f_*(z))=\varphi (\operatorname {\mathrm {supp}}(z))$
where the last equality is by [Reference Barthel, Castellana, Heard and SandersBCHS23, Theorem 13.13] since z is a compact weak ring. But
![]() $\varphi (\operatorname {\mathrm {supp}}(z))$
contains
$\varphi (\operatorname {\mathrm {supp}}(z))$
contains
![]() $\varphi (\{\mathscr {M}\}) = \mathfrak m$
yielding the desired contradiction.
$\varphi (\{\mathscr {M}\}) = \mathfrak m$
yielding the desired contradiction.
Remark 10.3. The results of Proposition 10.2 are not entirely satisfying; variations on the theme are possible and we expect a more complete statement to exist. Nevertheless, using Proposition 10.2
![]() $(a)$
, we can provide a variant of the argument used in [Reference BalmerBal20b] to deduce the Nerves of Steel conjecture from nilpotence-type theorems in several examples of interest:
$(a)$
, we can provide a variant of the argument used in [Reference BalmerBal20b] to deduce the Nerves of Steel conjecture from nilpotence-type theorems in several examples of interest:
Proposition 10.4. Let
![]() $\mathscr {T}$
be a rigidly-compactly generated tt-category. Suppose there exists a tt-field
$\mathscr {T}$
be a rigidly-compactly generated tt-category. Suppose there exists a tt-field
![]() $f_{\mathscr {P}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {P}}$
detecting
$f_{\mathscr {P}}^*\colon \mathscr {T} \to \mathscr {F}_{\mathscr {P}}$
detecting
![]() $\mathscr {P}$
for each prime
$\mathscr {P}$
for each prime
![]() $\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, i.e.,
$\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, i.e.,
![]() $\mathscr {P}$
is in the image of
$\mathscr {P}$
is in the image of
![]() $\operatorname {\mathrm {Spc}}(f_{\mathscr {P}}^*)$
. The following are equivalent:
$\operatorname {\mathrm {Spc}}(f_{\mathscr {P}}^*)$
. The following are equivalent:
(a)
 $\mathscr {T}$
satisfies the Nerves of Steel conjecture.
$\mathscr {T}$
satisfies the Nerves of Steel conjecture.(b) The family
 $(f_{\mathscr {P}}^*)_{\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)}$
jointly detects
$(f_{\mathscr {P}}^*)_{\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)}$
jointly detects
 $\otimes $
-nilpotence of morphisms with dualizable source.
$\otimes $
-nilpotence of morphisms with dualizable source.(c) The family
 $(f_{\mathscr {P}}^*)_{\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)}$
is jointly nil-conservative.
$(f_{\mathscr {P}}^*)_{\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)}$
is jointly nil-conservative.
Proof. Recall from [Reference Balmer and CameronBC21, Lemma 2.2] that every tt-field induces a homological residue field. More precisely, for each
![]() $\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, there exists a homological prime
$\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, there exists a homological prime
![]() $\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
lying over
$\mathscr {B} \in \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
lying over
![]() $\mathscr {P}$
and a commutative diagram
$\mathscr {P}$
and a commutative diagram

where the functor
![]() $\overline {F}$
is faithful; see [Reference Balmer and CameronBC21, (2.3)]. It follows from this diagram and the fact that the tt-field
$\overline {F}$
is faithful; see [Reference Balmer and CameronBC21, (2.3)]. It follows from this diagram and the fact that the tt-field
![]() $\mathscr {F}_{\mathscr {P}}$
is phantomless that a morphism in
$\mathscr {F}_{\mathscr {P}}$
is phantomless that a morphism in
![]() $\mathscr {T}$
is killed by
$\mathscr {T}$
is killed by
![]() $f_{\mathscr {P}}^*$
if and only if it is killed by the homological residue field
$f_{\mathscr {P}}^*$
if and only if it is killed by the homological residue field ![]() . Thus, the family
. Thus, the family
![]() $(f_{\mathscr {P}}^*)_{\mathscr {P} \in \mathscr {\operatorname {\mathrm {Spc}}}(\mathscr {T}^c)}$
jointly detects
$(f_{\mathscr {P}}^*)_{\mathscr {P} \in \mathscr {\operatorname {\mathrm {Spc}}}(\mathscr {T}^c)}$
jointly detects
![]() $\otimes $
-nilpotence if and only if the corresponding family of homological residue fields (also indexed on
$\otimes $
-nilpotence if and only if the corresponding family of homological residue fields (also indexed on
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
) jointly detects
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
) jointly detects
![]() $\otimes $
-nilpotence. The latter is equivalent to the Nerves of Steel conjecture by [Reference BalmerBal20b, Corollary 4.7 and Theorem 5.4]. This establishes the equivalence of
$\otimes $
-nilpotence. The latter is equivalent to the Nerves of Steel conjecture by [Reference BalmerBal20b, Corollary 4.7 and Theorem 5.4]. This establishes the equivalence of
![]() $(a)$
and
$(a)$
and
![]() $(b)$
. On the other hand, contemplating the commutative diagram
$(b)$
. On the other hand, contemplating the commutative diagram

we see that
![]() $(a)$
implies that the map
$(a)$
implies that the map
![]() $\varphi ^h\colon \bigsqcup _{\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)} \operatorname {\mathrm {Spc}}^h(\mathscr {F}_{\mathscr {P}}^c)\to \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
is surjective. This is equivalent to the family being nil-conservative by [Reference Barthel, Castellana, Heard and SandersBCHS24, Theorem 1.9]. Thus
$\varphi ^h\colon \bigsqcup _{\mathscr {P} \in \operatorname {\mathrm {Spc}}(\mathscr {T}^c)} \operatorname {\mathrm {Spc}}^h(\mathscr {F}_{\mathscr {P}}^c)\to \operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
is surjective. This is equivalent to the family being nil-conservative by [Reference Barthel, Castellana, Heard and SandersBCHS24, Theorem 1.9]. Thus
![]() $(a)\Rightarrow (c)$
. Finally, the implication
$(a)\Rightarrow (c)$
. Finally, the implication
![]() $(c)\Rightarrow (a)$
follows from Proposition 10.2(a).
$(c)\Rightarrow (a)$
follows from Proposition 10.2(a).
Remark 10.5. The next result establishes an equivalent formulation for the Nerves of Steel conjecture entirely in terms of the tensor triangular support. It strengthens previous work [Reference Barthel, Heard and SandersBHS23a, Proposition 3.13] and could also be used to give an alternative deduction of Theorem 9.6.
Proposition 10.6. Suppose that
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. The Nerves of Steel conjecture holds for
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. The Nerves of Steel conjecture holds for
![]() $\mathscr {T}$
if and only if
$\mathscr {T}$
if and only if
![]() $\mathscr {T}$
satisfies the tensor product formula for all weak rings, i.e.,
$\mathscr {T}$
satisfies the tensor product formula for all weak rings, i.e.,
for any weak rings
![]() $w_1,w_2 \in \mathscr {T}$
.
$w_1,w_2 \in \mathscr {T}$
.
Proof. Assume first that the Nerves of Steel conjecture holds for
![]() $\mathscr {T}$
. Using Proposition 6.12 twice as well as the tensor product formula for homological support (2.4), we compute
$\mathscr {T}$
. Using Proposition 6.12 twice as well as the tensor product formula for homological support (2.4), we compute
 $$ \begin{align*} \operatorname{\mathrm{Supp}}(w_1 \otimes w_2) & = \pi \operatorname{\mathrm{Supp}}^h(w_1 \otimes w_2) \\ & = \pi(\operatorname{\mathrm{Supp}}^h(w_1) \cap \operatorname{\mathrm{Supp}}^h(w_2)) \\ & = \pi\operatorname{\mathrm{Supp}}^h(w_1) \cap \pi\operatorname{\mathrm{Supp}}^h(w_2) \\ & = \operatorname{\mathrm{Supp}}(w_1) \cap \operatorname{\mathrm{Supp}}(w_2), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Supp}}(w_1 \otimes w_2) & = \pi \operatorname{\mathrm{Supp}}^h(w_1 \otimes w_2) \\ & = \pi(\operatorname{\mathrm{Supp}}^h(w_1) \cap \operatorname{\mathrm{Supp}}^h(w_2)) \\ & = \pi\operatorname{\mathrm{Supp}}^h(w_1) \cap \pi\operatorname{\mathrm{Supp}}^h(w_2) \\ & = \operatorname{\mathrm{Supp}}(w_1) \cap \operatorname{\mathrm{Supp}}(w_2), \end{align*} $$
where the third equality uses the hypothesis that
![]() $\pi $
is a bijection.
$\pi $
is a bijection.
Conversely, suppose that the tensor product formula holds for all weak rings. The argument in the proof of [Reference Barthel, Heard and SandersBHS23a, Proposition 3.13] then implies the Nerves of Steel conjecture for
![]() $\mathscr {T}$
. Note that the result there assumed the full tensor product formula, but it is only used for the weak rings
$\mathscr {T}$
. Note that the result there assumed the full tensor product formula, but it is only used for the weak rings
![]() $E_{\mathscr {B}}$
.
$E_{\mathscr {B}}$
.
11 Applications to tt-stratification
We now state our main applications. We start with three descent results which extend those of [Reference Barthel, Castellana, Heard and SandersBCHS24, Section 17] and [Reference Barthel, Castellana, Heard, Naumann, Pol and SandersBCH+24, Section 12] to a family of functors.
Proposition 11.1. Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family with each
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family with each
![]() $\mathscr {S}_i$
tt-stratified. Suppose that
$\mathscr {S}_i$
tt-stratified. Suppose that
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. Assume additionally one of the following:
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian. Assume additionally one of the following:
(a) the induced map
 $\varphi \colon \bigsqcup _{i \in I}\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c) \to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is injective; or
$\varphi \colon \bigsqcup _{i \in I}\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c) \to \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is injective; or(b)
 $(f_i^*)_{i \in I}$
is strongly closed and
$(f_i^*)_{i \in I}$
is strongly closed and
 $\varphi _i$
has discrete fibres for all
$\varphi _i$
has discrete fibres for all
 $i \in I$
; or
$i \in I$
; or(c)
 $(f_i^*)_{i \in I}$
is strongly closed and
$(f_i^*)_{i \in I}$
is strongly closed and
 $\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c)$
is noetherian for all
$\operatorname {\mathrm {Spc}}(\mathscr {S}_i^c)$
is noetherian for all
 $i \in I$
.
$i \in I$
.
Then
![]() $\mathscr {T}$
is tt-stratified.
$\mathscr {T}$
is tt-stratified.
Proof. By Theorem 9.6 each
![]() $\mathscr {S}_i$
is h-stratified and satisfies the Nerves of Steel conjecture. The result then follows from Proposition 10.2 and Corollary 9.9 since
$\mathscr {S}_i$
is h-stratified and satisfies the Nerves of Steel conjecture. The result then follows from Proposition 10.2 and Corollary 9.9 since
![]() $(f_i^*)_{i \in I}$
is jointly nil-conservative by Proposition 8.11.
$(f_i^*)_{i \in I}$
is jointly nil-conservative by Proposition 8.11.
Remark 11.2. In the situation of Proposition 11.1
![]() $(c)$
, if the indexing set I is finite then
$(c)$
, if the indexing set I is finite then
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is automatically noetherian and hence the hypothesis that
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is automatically noetherian and hence the hypothesis that
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian is superfluous.
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian is superfluous.
Corollary 11.3. Let
![]() $\mathscr {C}$
be a rigidly-compactly generated symmetric monoidal stable
$\mathscr {C}$
be a rigidly-compactly generated symmetric monoidal stable
![]() $\infty $
-category and let
$\infty $
-category and let
![]() $A \in \operatorname {\mathrm {CAlg}}(\mathscr {C}^c)$
be a descendable dualizable commutative algebra in
$A \in \operatorname {\mathrm {CAlg}}(\mathscr {C}^c)$
be a descendable dualizable commutative algebra in
![]() $\mathscr {C}$
. If
$\mathscr {C}$
. If
![]() $\operatorname {\mathrm {Mod}}_{\mathscr {C}}(A)$
is tt-stratified and has a noetherian spectrum, then
$\operatorname {\mathrm {Mod}}_{\mathscr {C}}(A)$
is tt-stratified and has a noetherian spectrum, then
![]() $\mathscr {C}$
is also tt-stratified and also has a noetherian spectrum.
$\mathscr {C}$
is also tt-stratified and also has a noetherian spectrum.
Proof. Since A is descendable, the base-change functor
![]() $A\otimes -\colon \mathscr {C} \to \operatorname {\mathrm {Mod}}_{\mathscr {C}}(A)$
is conservative and hence induces a surjection
$A\otimes -\colon \mathscr {C} \to \operatorname {\mathrm {Mod}}_{\mathscr {C}}(A)$
is conservative and hence induces a surjection
![]() $\operatorname {\mathrm {Spc}}(\operatorname {\mathrm {Mod}}_{\mathscr {C}}(A)^c) \to \operatorname {\mathrm {Spc}}(\mathscr {C}^c)$
; see [Reference Barthel, Castellana, Heard and SandersBCHS24, Theorem 1.4] or [Reference Barthel, Castellana, Heard, Naumann, Pol and SandersBCH+24, Proposition 7.8]. Hence
$\operatorname {\mathrm {Spc}}(\operatorname {\mathrm {Mod}}_{\mathscr {C}}(A)^c) \to \operatorname {\mathrm {Spc}}(\mathscr {C}^c)$
; see [Reference Barthel, Castellana, Heard and SandersBCHS24, Theorem 1.4] or [Reference Barthel, Castellana, Heard, Naumann, Pol and SandersBCH+24, Proposition 7.8]. Hence
![]() $\operatorname {\mathrm {Spc}}(\mathscr {C}^c)$
is also noetherian. We may then invoke Proposition 11.1
$\operatorname {\mathrm {Spc}}(\mathscr {C}^c)$
is also noetherian. We may then invoke Proposition 11.1
![]() $(c)$
.
$(c)$
.
Remark 11.4. The previous corollary strengthens the results of [Reference Barthel, Castellana, Heard, Naumann, Pol and SandersBCH+24, Section 12] by removing the hypothesis that the descendable algebra A be separable of finite tt-degree.
11.5. We now turn to a cohomological criterion for stratification.
Definition 11.6. A rigidly-compactly generated tt-category with weakly noetherian spectrum is said to be cohomologically stratified if it is tt-stratified and the comparison map ([Reference BalmerBal10])
is a bijection.
Proposition 11.7. Let
![]() $(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family with
$(f_i^*\colon \mathscr {T} \to \mathscr {S}_i)_{i \in I}$
be a weakly descendable geometric family with
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
weakly noetherian. Assume that each
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
weakly noetherian. Assume that each
![]() $\mathscr {S}_i$
is cohomologically stratified and that
$\mathscr {S}_i$
is cohomologically stratified and that
is a bijection. Then
![]() $\mathscr {T}$
is cohomologically stratified.
$\mathscr {T}$
is cohomologically stratified.
Proof. The various comparison maps fit into a commutative diagram

in which the three indicated vertical maps are surjections. The top and middle horizontal maps are also surjections by Proposition 8.11. The bottom map is a bijection by assumption, hence
![]() $\rho _{\mathscr {T}}$
is surjective as well. Since the tt-categories
$\rho _{\mathscr {T}}$
is surjective as well. Since the tt-categories
![]() $\mathscr {S}_i$
are cohomologically stratified, the left vertical composite is a bijection, which then implies that all maps in this diagram are bijections. The result thus follows from Corollary 9.9.
$\mathscr {S}_i$
are cohomologically stratified, the left vertical composite is a bijection, which then implies that all maps in this diagram are bijections. The result thus follows from Corollary 9.9.
12 Equivariant applications
Throughout this section, G will denote a compact Lie group.
Remark 12.1. For foundational material on
![]() $\infty $
-categories of equivariant G-spectra, we refer the reader to [Reference Mathew, Naumann and NoelMNN17, Reference Barthel, Greenlees and HausmannBGH20, Reference Barthel, Castellana, Heard, Naumann and PolBCH+25], which are based on the more classical references [Reference Lewis, May and SteinbergerLMS86, Reference MayMay96, Reference Mandell and MayMM02]. We write
$\infty $
-categories of equivariant G-spectra, we refer the reader to [Reference Mathew, Naumann and NoelMNN17, Reference Barthel, Greenlees and HausmannBGH20, Reference Barthel, Castellana, Heard, Naumann and PolBCH+25], which are based on the more classical references [Reference Lewis, May and SteinbergerLMS86, Reference MayMay96, Reference Mandell and MayMM02]. We write
![]() $\operatorname {\mathrm {Sp}}_G$
for this category. Recall that this is a presentably symmetric monoidal stable
$\operatorname {\mathrm {Sp}}_G$
for this category. Recall that this is a presentably symmetric monoidal stable
![]() $\infty $
-category which is rigidly-compactly generated by the orbits
$\infty $
-category which is rigidly-compactly generated by the orbits
![]() $G/H_+$
associated to the (conjugacy classes) of closed subgroups
$G/H_+$
associated to the (conjugacy classes) of closed subgroups
![]() $H \le G$
. Here, we omit the suspension spectrum from our notation.
$H \le G$
. Here, we omit the suspension spectrum from our notation.
Remark 12.2. For any closed subgroup
![]() $H \le G$
, we have a geometric fixed point functor
$H \le G$
, we have a geometric fixed point functor
Importantly, these functors are jointly conservative [Reference SchwedeSch18, Proposition 3.3.10]. Moreover, for any commutative algebraFootnote 3
![]() $R \in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}}_G)$
, we write
$R \in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}}_G)$
, we write
![]() $\operatorname {\mathrm {Mod}}_G(R)$
for
$\operatorname {\mathrm {Mod}}_G(R)$
for
![]() $\operatorname {\mathrm {Mod}}_{\operatorname {\mathrm {Sp}}_G}(R)$
, and we have induced functors
$\operatorname {\mathrm {Mod}}_{\operatorname {\mathrm {Sp}}_G}(R)$
, and we have induced functors
which are still jointly conservative. In fact, the geometric fixed points functors only depend on the conjugacy class of H inside of G, and so it suffices to consider a single representative for each such conjugacy class.
Notation 12.3. We let
![]() $\operatorname {\mathrm {Sub}}(G)$
denote the set of closed subgroups of G and
$\operatorname {\mathrm {Sub}}(G)$
denote the set of closed subgroups of G and
![]() $\operatorname {\mathrm {Sub}}(G)/G$
the set of closed subgroups of G up to conjugation.
$\operatorname {\mathrm {Sub}}(G)/G$
the set of closed subgroups of G up to conjugation.
Recollection 12.4. We will use a number of facts about the equivariant homotopy category in the following result. In particular, recall that for
![]() $H \le G$
we have a restriction functor
$H \le G$
we have a restriction functor
![]() $\mathrm {res}^G_H \colon \operatorname {\mathrm {Sp}}_G \to \operatorname {\mathrm {Sp}}_H$
that admits left and right adjoints
$\mathrm {res}^G_H \colon \operatorname {\mathrm {Sp}}_G \to \operatorname {\mathrm {Sp}}_H$
that admits left and right adjoints
![]() $\operatorname {\mathrm {ind}}_H^G$
and
$\operatorname {\mathrm {ind}}_H^G$
and
![]() $\operatorname {\mathrm {coind}}_H^G$
, respectively. If G is finite, then these left and right adjoints are naturally isomorphic. This is not true in general, but rather there is a natural equivalence
$\operatorname {\mathrm {coind}}_H^G$
, respectively. If G is finite, then these left and right adjoints are naturally isomorphic. This is not true in general, but rather there is a natural equivalence
where L is the tangent H-representation of
![]() $G/H$
. Moreover, we have
$G/H$
. Moreover, we have
Finally, the projection formula holds in this context: there is a natural equivalence
Lemma 12.5. Let G be compact Lie group and let
![]() $R \in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}}_G)$
be a commutative equivariant ring spectrum. Then the collection of geometric fixed points
$R \in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}}_G)$
be a commutative equivariant ring spectrum. Then the collection of geometric fixed points
is weakly descendable.
Proof. Let us write
![]() $\Psi _G^H$
for the right adjoint of
$\Psi _G^H$
for the right adjoint of
![]() $\Phi _G^H$
(which sometimes goes by the name of geometric inflation). We denote the collection of conjugacy classes of proper closed subgroups of G by
$\Phi _G^H$
(which sometimes goes by the name of geometric inflation). We denote the collection of conjugacy classes of proper closed subgroups of G by
![]() $\mathcal {P}$
. We will establish that
$\mathcal {P}$
. We will establish that
Note that we can define an ordering on compact Lie groups by the pair
![]() $(\dim H,\pi _0H)$
ordered lexicographically. Specifically,
$(\dim H,\pi _0H)$
ordered lexicographically. Specifically,
![]() $H \le G$
if and only if
$H \le G$
if and only if
![]() $\dim (H) \leq \dim (G)$
or
$\dim (H) \leq \dim (G)$
or
![]() $\dim (H) = \dim (G)$
and the number of connected components of H is less than or equal to the number of connected components of G. We will prove (12.6) by induction, with the base case
$\dim (H) = \dim (G)$
and the number of connected components of H is less than or equal to the number of connected components of G. We will prove (12.6) by induction, with the base case
![]() $G = e$
being tautological. We then assume that (12.6) holds for all
$G = e$
being tautological. We then assume that (12.6) holds for all
![]() $H \lneq G$
, and let
$H \lneq G$
, and let
![]() $M \in \operatorname {\mathrm {Mod}}_G(R)$
.
$M \in \operatorname {\mathrm {Mod}}_G(R)$
.
If
![]() $G = H$
, then
$G = H$
, then
![]() $\Phi ^G_G$
is a finite localization away from
$\Phi ^G_G$
is a finite localization away from
![]() $\operatorname {\mathrm {Locid}}\langle G/H_+ \otimes R \mid H \in \mathcal {P} \rangle $
, factoring as
$\operatorname {\mathrm {Locid}}\langle G/H_+ \otimes R \mid H \in \mathcal {P} \rangle $
, factoring as
where the first map is base-change and the second map is the symmetric monoidal equivalence induced by taking categorical G-fixed points. This implies that
This also follows from [Reference HillHil12, Definition 4.1 and Proposition 4.4]. We claim that
It suffices to check this for the generators of
![]() $\operatorname {\mathrm {Mod}}_G(R)$
, i.e., for M of the form
$\operatorname {\mathrm {Mod}}_G(R)$
, i.e., for M of the form
![]() $G/K_+ \otimes R$
. The case
$G/K_+ \otimes R$
. The case
![]() $K=G$
is (12.7), while for
$K=G$
is (12.7), while for
![]() $K \lneq G$
the claim holds since
$K \lneq G$
the claim holds since
![]() $G/K_+ \otimes \tilde {E}\mathcal {P} = 0$
.
$G/K_+ \otimes \tilde {E}\mathcal {P} = 0$
.
Now let H be a proper closed subgroup of G and consider subgroups
![]() $K \le H$
. The corresponding geometric fixed-point functors then factor as
$K \le H$
. The corresponding geometric fixed-point functors then factor as
By the inductive hypothesis
in
![]() $\operatorname {\mathrm {Mod}}_H(R)$
. In particular,
$\operatorname {\mathrm {Mod}}_H(R)$
. In particular, ![]() , where L is the tangent H-representation of
, where L is the tangent H-representation of
![]() $G/H$
. Applying coinduction, we get
$G/H$
. Applying coinduction, we get
By Recollection 12.4 we have
 $$ \begin{align*} \operatorname{\mathrm{coind}}_H^G(\operatorname{\mathrm{res}}_H(M) \otimes S^L) & \simeq \operatorname{\mathrm{coind}}_H^G(S^L) \otimes M \\ & \simeq \operatorname{\mathrm{ind}}_H^G(S_H^0) \otimes M \\ & \simeq G/H_+ \otimes M. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{coind}}_H^G(\operatorname{\mathrm{res}}_H(M) \otimes S^L) & \simeq \operatorname{\mathrm{coind}}_H^G(S^L) \otimes M \\ & \simeq \operatorname{\mathrm{ind}}_H^G(S_H^0) \otimes M \\ & \simeq G/H_+ \otimes M. \end{align*} $$
Since
![]() $\operatorname {\mathrm {coind}}_H^G\Psi _H^K \simeq \Psi _G^K$
, this implies that
$\operatorname {\mathrm {coind}}_H^G\Psi _H^K \simeq \Psi _G^K$
, this implies that
The isotropy separation sequence takes the form
We claim that
![]() $M \otimes E\mathcal {P}_+ \in \operatorname {\mathrm {Loc}}\langle G/H_+\otimes M \mid H \in \mathcal {P} \rangle $
. Indeed, as a consequence of work of Illman [Reference IllmanIll83] on the existence of G-triangulations (see [Reference SandersSan19, Remark 3.6]), we have
$M \otimes E\mathcal {P}_+ \in \operatorname {\mathrm {Loc}}\langle G/H_+\otimes M \mid H \in \mathcal {P} \rangle $
. Indeed, as a consequence of work of Illman [Reference IllmanIll83] on the existence of G-triangulations (see [Reference SandersSan19, Remark 3.6]), we have
It follows that
as desired. Consequently, from isotropy separation and the previous claim we get
Substituting (12.8) and (12.9) thus gives
which finishes the proof.
Lemma 12.10. Let
![]() $R\in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}}_G)$
be a commutative equivariant ring spectrum. The spectra of
$R\in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}}_G)$
be a commutative equivariant ring spectrum. The spectra of
![]() $\operatorname {\mathrm {Mod}}_G(R)^c$
decompose set-theoretically as
$\operatorname {\mathrm {Mod}}_G(R)^c$
decompose set-theoretically as
 $$\begin{align*}\operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}_G(R)^c) = \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{im}} \varphi_H, \quad \operatorname{\mathrm{Spc}}^h(\operatorname{\mathrm{Mod}}_G(R)^c) = \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{im}} \varphi^h_H, \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}_G(R)^c) = \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{im}} \varphi_H, \quad \operatorname{\mathrm{Spc}}^h(\operatorname{\mathrm{Mod}}_G(R)^c) = \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{im}} \varphi^h_H, \end{align*}$$
where
![]() $\varphi _H = \operatorname {\mathrm {Spc}}(\Phi ^H)$
and
$\varphi _H = \operatorname {\mathrm {Spc}}(\Phi ^H)$
and
![]() $\varphi ^h_H = \operatorname {\mathrm {Spc}}^h(\Phi ^H)$
are the maps on spectra induced by H-geometric fixed points, respectively.
$\varphi ^h_H = \operatorname {\mathrm {Spc}}^h(\Phi ^H)$
are the maps on spectra induced by H-geometric fixed points, respectively.
Proof. First we show that the claim is true for
![]() $R=S_G^0$
. Indeed, by [Reference Barthel, Greenlees and HausmannBGH20, Theorem 3.14], the analogous result is true for the Balmer spectrum. Because the Nerves of Steel conjecture holds for
$R=S_G^0$
. Indeed, by [Reference Barthel, Greenlees and HausmannBGH20, Theorem 3.14], the analogous result is true for the Balmer spectrum. Because the Nerves of Steel conjecture holds for
![]() $\operatorname {\mathrm {Sp}}_G$
by [Reference BalmerBal20b, Corollary 5.10] (which in turn relies on [Reference Barthel, Greenlees and HausmannBGH20, Corollary 3.18]), the claim follows.
$\operatorname {\mathrm {Sp}}_G$
by [Reference BalmerBal20b, Corollary 5.10] (which in turn relies on [Reference Barthel, Greenlees and HausmannBGH20, Corollary 3.18]), the claim follows.
For the general case, consider the commutative diagram

induced by base-change
![]() $S_G^0\to R$
and the H-geometric fixed point functors for
$S_G^0\to R$
and the H-geometric fixed point functors for
![]() $\operatorname {\mathrm {Mod}}_G(R)$
and
$\operatorname {\mathrm {Mod}}_G(R)$
and
![]() $\operatorname {\mathrm {Sp}}_G$
. This diagram shows that the images of the maps
$\operatorname {\mathrm {Sp}}_G$
. This diagram shows that the images of the maps
![]() $\varphi ^h_H$
are disjoint in
$\varphi ^h_H$
are disjoint in
![]() $\operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {Mod}}_G(R)^c)$
for non-conjugate subgroups, since this is true for the
$\operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {Mod}}_G(R)^c)$
for non-conjugate subgroups, since this is true for the
![]() $R=S^0_G$
case just mentioned. As a consequence of Lemma 12.5 and Proposition 8.11, these images also cover the homological spectrum, which gives the desired decomposition of the homological spectrum. The analogous statement for the tt-spectrum is proved similarly.
$R=S^0_G$
case just mentioned. As a consequence of Lemma 12.5 and Proposition 8.11, these images also cover the homological spectrum, which gives the desired decomposition of the homological spectrum. The analogous statement for the tt-spectrum is proved similarly.
Proposition 12.11. Let G be a compact Lie group and
![]() $R \in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}}_G)$
a commutative equivariant ring spectrum. If
$R \in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}}_G)$
a commutative equivariant ring spectrum. If
![]() $\operatorname {\mathrm {Mod}}(\Phi ^HR)$
is h-stratified for every closed subgroup
$\operatorname {\mathrm {Mod}}(\Phi ^HR)$
is h-stratified for every closed subgroup
![]() $H \le G$
, then
$H \le G$
, then
![]() $\operatorname {\mathrm {Mod}}_G(R)$
is h-stratified. In this case, h-support and geometric fixed points induce a bijection
$\operatorname {\mathrm {Mod}}_G(R)$
is h-stratified. In this case, h-support and geometric fixed points induce a bijection
 $$\begin{align*}\big\{ \text{localizing ideals of }\operatorname{\mathrm{Mod}}_G(R) \big\} \xrightarrow{\cong} \big\{ \text{subsets of }\bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{im}} \varphi^h_H\big\}. \end{align*}$$
$$\begin{align*}\big\{ \text{localizing ideals of }\operatorname{\mathrm{Mod}}_G(R) \big\} \xrightarrow{\cong} \big\{ \text{subsets of }\bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{im}} \varphi^h_H\big\}. \end{align*}$$
Proof. The first part follows from Theorem 8.24, which applies due to Lemma 12.5. The claimed bijection is then Theorem 4.1 combined with Lemma 12.10.
Remark 12.12. We next make the previous proposition more explicit in the special case of commutative equivariant ring spectra with trivial action, i.e., those that arise via inflation from (non-equivariant) commutative ring spectra. This provides a generalization of [Reference Barthel, Heard and SandersBHS23b, Theorem 15.1], extending it from finite groups to compact Lie groups and removing any topological assumptions on the spectrum.
Theorem 12.13. Let G be a compact Lie group and write
![]() $R_G = \operatorname {\mathrm {infl}}_GR$
for the inflation of a commutative ring spectrum
$R_G = \operatorname {\mathrm {infl}}_GR$
for the inflation of a commutative ring spectrum
![]() $R\in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}})$
. If
$R\in \operatorname {\mathrm {CAlg}}(\operatorname {\mathrm {Sp}})$
. If
![]() $\operatorname {\mathrm {Mod}}(R)$
is h-stratified and satisfies the Nerves of Steel conjecture, then
$\operatorname {\mathrm {Mod}}(R)$
is h-stratified and satisfies the Nerves of Steel conjecture, then
![]() $\pi \circ \operatorname {\mathrm {Supp}}^h$
induces a bijection
$\pi \circ \operatorname {\mathrm {Supp}}^h$
induces a bijection
 $$\begin{align*}\begin{Bmatrix} \text{localizing ideals} \\ of \operatorname{\mathrm{Mod}}_G(R_G) \end{Bmatrix} \xrightarrow{\sim} \begin{Bmatrix} \text{subsets of } \\ \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}(R)^c) \end{Bmatrix}. \end{align*}$$
$$\begin{align*}\begin{Bmatrix} \text{localizing ideals} \\ of \operatorname{\mathrm{Mod}}_G(R_G) \end{Bmatrix} \xrightarrow{\sim} \begin{Bmatrix} \text{subsets of } \\ \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}(R)^c) \end{Bmatrix}. \end{align*}$$
Proof. Since the geometric fixed points for
![]() $R_G$
are split by inflation,
$R_G$
are split by inflation,
is a homeomorphism onto its image for any subgroup H in G. In particular, using Lemma 12.10, these maps induce a bijection
 $$\begin{align*}\operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}_G(R_G)^c) \simeq \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}(R)^c). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}_G(R_G)^c) \simeq \bigsqcup_{H \in \operatorname{\mathrm{Sub}}(G)/G} \operatorname{\mathrm{Spc}}(\operatorname{\mathrm{Mod}}(R)^c). \end{align*}$$
By Proposition 10.2(a), the Nerves of Steel conjecture descends to
![]() $\operatorname {\mathrm {Mod}}_G(R_G)$
, i.e.,
$\operatorname {\mathrm {Mod}}_G(R_G)$
, i.e.,
![]() $\pi \colon \operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {Mod}}_G(R_G)^c) \to \operatorname {\mathrm {Spc}}(\operatorname {\mathrm {Mod}}_G(R_G)^c)$
is a bijection. Proposition 12.11 then implies that
$\pi \colon \operatorname {\mathrm {Spc}}^h(\operatorname {\mathrm {Mod}}_G(R_G)^c) \to \operatorname {\mathrm {Spc}}(\operatorname {\mathrm {Mod}}_G(R_G)^c)$
is a bijection. Proposition 12.11 then implies that
![]() $\operatorname {\mathrm {Mod}}_G(R_G)$
is h-stratified, as well as the claimed parametrization of localizing ideals.
$\operatorname {\mathrm {Mod}}_G(R_G)$
is h-stratified, as well as the claimed parametrization of localizing ideals.
Remark 12.14. In fact, an elaboration on the proof of Lemma 12.5 can be used to show that
![]() $\operatorname {\mathrm {Spc}}(\operatorname {\mathrm {Mod}}_G(R_G)^c)$
is weakly noetherian if
$\operatorname {\mathrm {Spc}}(\operatorname {\mathrm {Mod}}_G(R_G)^c)$
is weakly noetherian if
![]() $\operatorname {\mathrm {Spc}}(\operatorname {\mathrm {Mod}}(R)^c)$
is. Moreover, in this case the function
$\operatorname {\mathrm {Spc}}(\operatorname {\mathrm {Mod}}(R)^c)$
is. Moreover, in this case the function
![]() $\pi \circ \operatorname {\mathrm {Supp}}^h$
identifies with the Balmer–Favi notion of support.
$\pi \circ \operatorname {\mathrm {Supp}}^h$
identifies with the Balmer–Favi notion of support.
13 Open questions
We end the paper with a few open questions.
Remark 13.1. We have defined h-stratification for any rigidly-compactly generated tt-category (Definition 4.2), but we only defined tt-stratification for those
![]() $\mathscr {T}$
whose spectrum
$\mathscr {T}$
whose spectrum
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian (Definition 9.5). This is because the latter topological condition is needed for the construction of the Balmer–Favi support. However, W. Sanders [Reference SandersSan17] has introduced a generalization of the Balmer–Favi support which does not require the spectrum to be weakly noetherian. The caveat is that the Balmer–Favi–Sanders support of an object (or localizing ideal) is always closed with respect to the so-called localizing topology on
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian (Definition 9.5). This is because the latter topological condition is needed for the construction of the Balmer–Favi support. However, W. Sanders [Reference SandersSan17] has introduced a generalization of the Balmer–Favi support which does not require the spectrum to be weakly noetherian. The caveat is that the Balmer–Favi–Sanders support of an object (or localizing ideal) is always closed with respect to the so-called localizing topology on
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
; see [Reference SandersSan17, Theorem 4.2].Footnote 4 Using this theory of support, one can extend the definition of tt-stratification to arbitrary rigidly-compactly generated tt-categories as in [Reference ZouZou25, Definition 8.1]. However, it turns out that if
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
; see [Reference SandersSan17, Theorem 4.2].Footnote 4 Using this theory of support, one can extend the definition of tt-stratification to arbitrary rigidly-compactly generated tt-categories as in [Reference ZouZou25, Definition 8.1]. However, it turns out that if
![]() $\mathscr {T}$
is tt-stratified in this a priori more general sense, then the spectrum
$\mathscr {T}$
is tt-stratified in this a priori more general sense, then the spectrum
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is necessarily weakly noetherian; see [Reference ZouZou25, Theorem 8.13]. Thus, using the Balmer–Favi–Sanders support does not provide a more general notion of tt-stratification. With this and Theorem 9.6 in mind, it is natural to ask:
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is necessarily weakly noetherian; see [Reference ZouZou25, Theorem 8.13]. Thus, using the Balmer–Favi–Sanders support does not provide a more general notion of tt-stratification. With this and Theorem 9.6 in mind, it is natural to ask:
Question 13.2. Suppose
![]() $\mathscr {T}$
is a rigidly-compactly generated tt-category. If
$\mathscr {T}$
is a rigidly-compactly generated tt-category. If
![]() $\mathscr {T}$
is h-stratified and satisfies the Nerves of Steel conjecture, does it follow that
$\mathscr {T}$
is h-stratified and satisfies the Nerves of Steel conjecture, does it follow that
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian?
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
is weakly noetherian?
Remark 13.3. We do not even know the answer for the derived category of a commutative ring
![]() $\operatorname {\mathrm {D}}(R)$
. Recall from Example 4.10 that in this case the Nerves of Steel conjecture always holds and h-stratification is equivalent to
$\operatorname {\mathrm {D}}(R)$
. Recall from Example 4.10 that in this case the Nerves of Steel conjecture always holds and h-stratification is equivalent to
Thus, a negative answer to the following question would also provide a negative answer to Question 13.2.
Question 13.5. If (∗) holds, does it follow that
![]() $\operatorname {\mathrm {Spec}}(R)$
is weakly noetherian?
$\operatorname {\mathrm {Spec}}(R)$
is weakly noetherian?
Example 13.6. For a field k, the spectrum of the ring
![]() $k[x_1,x_2,\ldots ]$
is not weakly noetherian; this follows, for example, from [Reference Barthel, Castellana, Heard and SandersBCHS23, Proposition 4.13]. Even for this relatively simple non-noetherian ring, we are unable to determine whether (∗) holds.
$k[x_1,x_2,\ldots ]$
is not weakly noetherian; this follows, for example, from [Reference Barthel, Castellana, Heard and SandersBCHS23, Proposition 4.13]. Even for this relatively simple non-noetherian ring, we are unable to determine whether (∗) holds.
Remark 13.7. As noted above, for an object
![]() $t \in \mathscr {T}$
, the Balmer–Favi–Sanders support
$t \in \mathscr {T}$
, the Balmer–Favi–Sanders support
![]() $\operatorname {\mathrm {Supp}}(t)$
is always closed in the localizing topology on
$\operatorname {\mathrm {Supp}}(t)$
is always closed in the localizing topology on
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
. On the other hand, since
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
. On the other hand, since
![]() $\operatorname {\mathrm {Supp}}^h(\coprod _{\mathscr {B} \in S} E_{\mathscr {B}}) = S$
for any subset
$\operatorname {\mathrm {Supp}}^h(\coprod _{\mathscr {B} \in S} E_{\mathscr {B}}) = S$
for any subset
![]() $S \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, the homological support
$S \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
, the homological support
![]() $\operatorname {\mathrm {Supp}}^h(t)$
takes values in arbitrary subsets of
$\operatorname {\mathrm {Supp}}^h(t)$
takes values in arbitrary subsets of
![]() $\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
. This complicates the relationship between
$\operatorname {\mathrm {Spc}}^h(\mathscr {T}^c)$
. This complicates the relationship between
![]() $\pi (\operatorname {\mathrm {Supp}}^h(t))$
and
$\pi (\operatorname {\mathrm {Supp}}^h(t))$
and
![]() $\operatorname {\mathrm {Supp}}(t)$
. Nonetheless, one has the following strengthening of Proposition 6.8; for unfamiliar terminology, we refer the reader to [Reference ZouZou25].
$\operatorname {\mathrm {Supp}}(t)$
. Nonetheless, one has the following strengthening of Proposition 6.8; for unfamiliar terminology, we refer the reader to [Reference ZouZou25].
Proposition 13.8. Suppose that h-detection holds. Then the following holds for any
![]() $t \in \mathscr {T}$
:
$t \in \mathscr {T}$
:
where the left-hand side denotes the closure of
![]() $\pi (\operatorname {\mathrm {Supp}}^h t)$
in the localizing topology on
$\pi (\operatorname {\mathrm {Supp}}^h t)$
in the localizing topology on
![]() $\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
.
$\operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
.
Proof. We always have
![]() $\pi (\operatorname {\mathrm {Supp}}^h(t)) \subseteq \operatorname {\mathrm {Supp}}(t)$
by [Reference ZouZou25, Lemma 8.5] and the latter is localizing closed, hence
$\pi (\operatorname {\mathrm {Supp}}^h(t)) \subseteq \operatorname {\mathrm {Supp}}(t)$
by [Reference ZouZou25, Lemma 8.5] and the latter is localizing closed, hence
![]() $ \overline {\pi (\operatorname {\mathrm {Supp}}^h(t))}^{\mathrm {loc}} \subseteq \operatorname {\mathrm {Supp}}(t)$
. For the reverse inclusion, recall that weakly visible subsets form a basis of open subsets for the localizing topology. If
$ \overline {\pi (\operatorname {\mathrm {Supp}}^h(t))}^{\mathrm {loc}} \subseteq \operatorname {\mathrm {Supp}}(t)$
. For the reverse inclusion, recall that weakly visible subsets form a basis of open subsets for the localizing topology. If
![]() ${\mathscr {P} \notin \overline {\pi (\operatorname {\mathrm {Supp}}^h(t))}^{\mathrm {loc}}}$
then there exists a weakly visible subset
${\mathscr {P} \notin \overline {\pi (\operatorname {\mathrm {Supp}}^h(t))}^{\mathrm {loc}}}$
then there exists a weakly visible subset
![]() $W \ni \mathscr {P}$
such that
$W \ni \mathscr {P}$
such that
![]() $\pi (\operatorname {\mathrm {Supp}}^h (t))\cap W = \varnothing $
and hence
$\pi (\operatorname {\mathrm {Supp}}^h (t))\cap W = \varnothing $
and hence
![]() $\pi ^{-1}(W) \cap \operatorname {\mathrm {Supp}}^h (t) = \varnothing $
. By the tensor product formula and Lemma 6.4, we obtain
$\pi ^{-1}(W) \cap \operatorname {\mathrm {Supp}}^h (t) = \varnothing $
. By the tensor product formula and Lemma 6.4, we obtain
![]() $\operatorname {\mathrm {Supp}}^h(t \otimes g_W) = \varnothing $
. It then follows from h-detection that
$\operatorname {\mathrm {Supp}}^h(t \otimes g_W) = \varnothing $
. It then follows from h-detection that
![]() $t \otimes g_W = 0$
. Therefore,
$t \otimes g_W = 0$
. Therefore,
![]() $\mathscr {P} \not \in \operatorname {\mathrm {Supp}}(t)$
by the definition of the Balmer–Favi–Sanders support; see [Reference ZouZou25, Definition 5.17].
$\mathscr {P} \not \in \operatorname {\mathrm {Supp}}(t)$
by the definition of the Balmer–Favi–Sanders support; see [Reference ZouZou25, Definition 5.17].
13.9. We also have the following strengthening of Proposition 6.12:
Proposition 13.10. For any weak ring
![]() $w \in \mathscr {T}$
, we have
$w \in \mathscr {T}$
, we have
Proof. The
![]() $\subseteq $
inclusion always holds, as explained in the proof of Proposition 13.8. Moreover, as before, if
$\subseteq $
inclusion always holds, as explained in the proof of Proposition 13.8. Moreover, as before, if
![]() $\mathscr {P} \not \in \overline {\pi (\operatorname {\mathrm {Supp}}^h(w))}^{\mathrm {loc}}$
then there exists a weakly visible subset
$\mathscr {P} \not \in \overline {\pi (\operatorname {\mathrm {Supp}}^h(w))}^{\mathrm {loc}}$
then there exists a weakly visible subset
![]() $W \ni \mathscr {P}$
such that
$W \ni \mathscr {P}$
such that
![]() $\pi ^{-1}(W) \cap \operatorname {\mathrm {Supp}}^h(w) = \varnothing $
and it suffices to establish that
$\pi ^{-1}(W) \cap \operatorname {\mathrm {Supp}}^h(w) = \varnothing $
and it suffices to establish that
![]() ${g_W \otimes w=0}$
. Write
${g_W \otimes w=0}$
. Write
![]() $W=Y_1 \cap Y_2^c$
. Since
$W=Y_1 \cap Y_2^c$
. Since
![]() $Y_1$
is a union of Thomason closed sets, we may assume without loss of generality that
$Y_1$
is a union of Thomason closed sets, we may assume without loss of generality that
![]() $Y_1$
is a Thomason closed set. Then
$Y_1$
is a Thomason closed set. Then
![]() $Y_1=\operatorname {\mathrm {supp}}(x)$
for some
$Y_1=\operatorname {\mathrm {supp}}(x)$
for some
![]() $x\in \mathscr {T}^c$
and replacing x by
$x\in \mathscr {T}^c$
and replacing x by
![]() $x \otimes x^{\vee }$
we may assume that x is a (weak) ring. Observe then that
$x \otimes x^{\vee }$
we may assume that x is a (weak) ring. Observe then that
by Remark 6.2 and Lemma 6.4. Hence
This implies that
![]() $x \otimes f_{Y_2} \otimes w=0$
since the homological support has the detection property for weak rings (Remark 2.9). We conclude that
$x \otimes f_{Y_2} \otimes w=0$
since the homological support has the detection property for weak rings (Remark 2.9). We conclude that
![]() $e_{\operatorname {\mathrm {supp}}(x)} \otimes f_{Y_2} \otimes w =0$
. That is,
$e_{\operatorname {\mathrm {supp}}(x)} \otimes f_{Y_2} \otimes w =0$
. That is,
![]() $g_W \otimes x =0$
, as desired.
$g_W \otimes x =0$
, as desired.
Remark 13.11. In general, we do not have a complete understanding of the relationship between the three notions of support considered in this paper (Remark 2.1). We recalled in Proposition 2.5 that the inclusion
always holds, and showed that it is actually an equality under suitable conditions (for example, h-detection). In Corollary 3.4 we showed moreover that, assuming h-codetection, the h-LGP is equivalent to the equality of the two notions of support. Given an unconditional equality between
![]() $\operatorname {\mathrm {Supp}}^h$
and
$\operatorname {\mathrm {Supp}}^h$
and
![]() $\operatorname {\mathrm {Supp}}^n$
, some portion of this paper would simplify; hence, we are led to ask the following:
$\operatorname {\mathrm {Supp}}^n$
, some portion of this paper would simplify; hence, we are led to ask the following:
Question 13.12. Is there always an equality
Example 13.13. By Proposition 2.16 this holds whenever
![]() $\mathscr {T}$
has enough tt-fields. For example, this holds in the derived category
$\mathscr {T}$
has enough tt-fields. For example, this holds in the derived category
![]() $\operatorname {\mathrm {D}}(R)$
of a commutative ring.
$\operatorname {\mathrm {D}}(R)$
of a commutative ring.
Remark 13.14. Note that we do not know whether
![]() $\operatorname {\mathrm {Supp}}^n(t)$
satisfies the tensor-product property, while the homological support always does, so in fact there is an inclusion
$\operatorname {\mathrm {Supp}}^n(t)$
satisfies the tensor-product property, while the homological support always does, so in fact there is an inclusion
One can therefore ask the following a priori weaker variant of Question 13.12:
Question 13.15. Is there always an equality
Remark 13.16. We have introduced a notion of homological cosupport and proved in Lemma 6.6 that
if
![]() $t_1$
is compact or
$t_1$
is compact or
![]() $t_1 = g_W$
for a weakly visible subset
$t_1 = g_W$
for a weakly visible subset
![]() $W \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
. Assuming that the h-LGP holds, asking that (13.17) holds for all
$W \subseteq \operatorname {\mathrm {Spc}}(\mathscr {T}^c)$
. Assuming that the h-LGP holds, asking that (13.17) holds for all
![]() $t_1,t_2 \in \mathscr {T}$
is equivalent to h-stratification; see Proposition 5.1. On the other hand, we always have
$t_1,t_2 \in \mathscr {T}$
is equivalent to h-stratification; see Proposition 5.1. On the other hand, we always have
for any
![]() $t_1,t_2 \in \mathscr {T}$
.
$t_1,t_2 \in \mathscr {T}$
.
Question 13.18. Is there a variant of homological cosupport which always satisfies
Acknowledgments
We thank Scott Balchin and Paul Balmer for helpful discussions, as well as Jordan Williamson and the anonymous referee for useful comments on an earlier version. TB is supported by the European Research Council (ERC) under Horizon Europe (grant No. 101042990) and would like to thank the Max Planck Institute for its hospitality. DH is supported by grant number TMS2020TMT02 from the Trond Mohn Foundation.
Competing interests
The authors declare none.