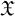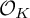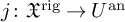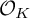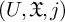1 Introduction
In this article we deal with the following basic problem. Let K be a non-archimedean field with valuation ring
$\mathcal {O}$
, and let U be a separated scheme locally of finite type over K. By a model of U over
$\mathcal {O}$
we shall mean a separated scheme of locally finite type X over
$\mathcal {O}$
with generic fibre
$X_K \simeq U$
. The question is:
$$ \begin{align*} \textit{How can we economically describe all models } X \textit{ of } U? \end{align*} $$
Our answer uses formal and rigid geometry, and is hinted at in multiple earlier works (e.g., [Reference Artin2], [Reference Ben-Bassat and Temkin4] and [Reference Bosch and Lütkebohmert8]). To illustrate the idea, let us consider a basic example from Bruhat–Tits theory.
Example 1.1 (Models of
$\mathrm {GL}_n$
.)
Let
$G = \mathrm {GL}(V)$
for a finite-dimensional vector space V over K. We aim to describe all smooth affine group schemes
$\mathcal {G}$
over
$\mathcal {O}$
with generic fibre G. There are many interesting examples of such
$\mathcal {G}$
:
-
• An
$\mathcal {O}$
-lattice
$\Lambda \subseteq V$
gives rise to the model
$\mathcal {G} = \mathrm {Aut}(\Lambda )$
of G over
$\mathcal {O}$
. -
• If K is discretely valued with uniformizer
$\pi $
, we have the Iwahori model
$\mathcal {I}$
with
$$\begin{align*}\mathcal{I}(\mathcal{O}) = \{(a_{ij})\in \mathrm{GL}_n(\mathcal{O})\,:\, a_{ij}\in (\pi) \text{ when }i<j\}. \end{align*}$$
A choice of
$\mathcal {G}$
gives rise to rigid-geometric data: the image of
$\mathcal {G}(\mathcal {O})$
in
$G(K)$
is the set of K-points of a rigid-analytic affinoid (i.e., ‘compact’) subgroup
$\mathsf {G}$
of
$G^{\mathrm {an}}$
. In the first example above, for
$V = K^n$
and
$\Lambda \simeq \mathcal {O}^n$
, we have
$$\begin{align*}\mathsf{G} = \{(a_{ij})\in \mathrm{GL}_n\,:\, |a_{ij}|\leqslant 1\}, \end{align*}$$
while for the Iwahori model we obtain the Iwahori subgroup of
$G(K)$
$$ \begin{align*} \mathsf{I}(K) = \{(a_{ij})\in \mathrm{GL}_n(K)\,:\, |a_{ij}|\leqslant 1\text{ and }|a_{ij}|\leqslant| \pi|\text{ when }i<j\}. \end{align*} $$
Furthermore,
$\mathcal {G}$
allows us to define a reduction map
$\mathsf {G}(K)=\mathcal {G}(\mathcal {O})\to \mathcal {G}(k)$
, where k is the residue field of K. One may think of
$\mathcal {G}$
as the result of ‘gluing’ G to
$\mathcal {G}_k$
along
$\mathsf {G}$
, with the ‘glue’ being provided by
$\mathsf {G}$
and the reduction map. In fact, all smooth affine models of G arise from such gluings (cf. [Reference Kaletha and Prasad20, Corollary 2.10.11], which implies that
$\mathsf {G}$
determines
$\mathcal {G}$
).
The procedure of Example 1.1 applies in general when appropriately formulated. To a scheme X locally of finite type over
$\mathcal {O}$
, one attaches a triple
$\mathcal {t}(X)=(X_K, \widehat {X}, j_X)$
consisting of
-
• its generic fibre
$X_K$
, -
• its
$\pi $
-adic formal completion
$\widehat {X}$
(where
$\pi $
is a pseudouniformizer of K), -
• the natural morphism of rigid analytic spaces over K (see Proposition 2.17)
where
$$\begin{align*}j_X \colon \widehat{X}^{\mathrm{rig}} \to X_K^{\mathrm{an}}, \end{align*}$$
$\widehat {X}^{\mathrm {rig}}$
is the rigid generic fibre of
$\widehat {X}$
and
$X_K^{\mathrm {an}}$
is the analytification of
$X_K$
.
We treat
$\mathcal {t}(X)$
as an object of the category of triples
$(U,\mathfrak {X},j)$
consisting of a K-scheme U, a formal scheme
$\mathfrak {X}$
over
$\mathcal {O}$
and a morphism of rigid spaces
$j\colon \mathfrak {X}^{\mathrm {rig}}\to U^{\mathrm {an}}$
. Intuitively, X should be described as the effect of gluing
$\widehat {X}$
to
$X_K$
along
$\widehat {X}^{\mathrm {rig}}$
. To connect this to Example 1.1, observe that
$\mathsf {G}=\widehat {\mathcal {G}}^{\mathrm {rig}}$
and the reduction map
$\mathsf {G}(K)\to \mathcal {G}(k)$
is obtained by passing to K-points from the specialization map
$\mathrm {sp}\colon \widehat {\mathcal {G}}^{\mathrm {rig}}\to \mathcal {G}_k$
of the formal scheme
$\widehat {\mathcal {G}}$
.
While the pushout
$X_K\sqcup _{\widehat {X}^{\mathrm {rig}}}\widehat {X}$
does not literally make sense, we can show the following result also previously observed (in lesser generality) in [Reference Bosch and Lütkebohmert8] and [Reference Imai, Kato and Youcis19].
Proposition 1.2 (see Corollary 5.4.)
The functor
$\mathcal {t}$
is fully faithful.
It is a natural question if, or to what extent, the functor t is an equivalence. Let us only consider separated schemes, and let the target category be that of triples
$(U, \mathfrak {X}, j)$
as above but with both U and
$\mathfrak {X}$
separated, and where the map j is an open embedding. In [Reference Matsumoto24, §5.2] one finds a smooth proper algebraic space X over
$\mathbb {Z}_p$
such that both
$X_{\mathbb {Q}_p}$
and
$X_{\mathbb {F}_p}$
are projective schemes (K3 surfaces), and which is not a scheme. One may deduce that the corresponding triple
$(X_{\mathbb {Q}_p}, \widehat {X}, j_X)$
is not in the essential image of
$\mathcal {t}$
. This example shows that the question is more naturally formulated in the realm of algebraic spaces. Somewhat surprisingly, it is always possible to ‘glue’ such triples into algebraic spaces.
To state our result, we require some setup. Let S be an excellent algebraic space and
$S_0\subseteq S$
a closed subspace (e.g.,
$(S,S_0)=(\operatorname {\mathrm {Spec}}(\mathcal {O}),V(\pi ))$
when K is discretely valued). Let
$\widehat {S}$
be the formal completion of S along
$S_0$
, and let 
. For an algebraic space X over S we write
$X^\circ = X\times _S S^\circ $
. Denote by
$\mathbf {AlgSp}^{\mathrm {sep}}_S$
the category of algebraic spaces X separated and locally of finite type over S. In §2.2 we introduce the category
$\mathbf {Trip}^{\mathrm {sep}}_{(S, S_0)}$
of separated gluing triples
$(U, \mathfrak {X}, j)$
over S, where:
-
• U is an algebraic space separated and locally of finite type over
$S^\circ $
, -
•
$\mathfrak {X}$
is a formal algebraic space separated and locally of finite type over
$\widehat {S}$
, -
•
$j\colon \mathfrak {X}^{\mathrm {rig}}\to U^{\mathrm {an}}$
is an open embedding of rigid algebraic spaces over
$\widehat {S}^{\mathrm {rig}}$
,Footnote 1
(see §2.1 for a recollection of these concepts in this generality). One might picture a gluing triple as in Figure 1 below.
Figure 1 A picture of the gluing triple
$(U,\mathfrak {X},j)$
.
The precise version of the claim that one can always uniquely glue a separated gluing triple
$(U,\mathfrak {X},j)$
together into some algebraic space X is the following.
Theorem 1.3 (Beauville–Laszlo Gluing of algebraic spaces, see Theorem 2.26)
The functor
$$\begin{align*}\mathcal{t} \colon \mathbf{AlgSp}^{\mathrm{sep}}_S \longrightarrow \mathbf{Trip}^{\mathrm{sep}}_{(S, S_0)}, \qquad \mathcal{t}(X) = (X^\circ, \widehat{X}, j_X) \end{align*}$$
is an equivalence of categories.
Theorem 1.3 is quite clarifying with respect to several well-known phenomena in arithmetic geometry. For example:
-
⋄ questions of good reduction over K vs.
$\widehat {K}$
(see Example 3.11 and Proposition 3.12), -
⋄ the construction and behaviour of Néron models (see Example 3.13 and Remark 3.15),
-
⋄ algebraizability of formal schemes (see Example 3.16 and Proposition 3.17),
-
⋄ questions related to the existence of a specialization morphism for the étale fundamental group beyond the proper case (see Proposition 3.27 and Remark 3.29).
In addition, the ideas surrounding it play a central role in [Reference Imai, Kato and Youcis18], and appear implicitly in Bruhat–Tits theory (see [Reference Kaletha and Prasad20, §2.10]).
Relationship to the classical Beauville–Laszlo theorem
To explain the terminology ‘Beauville–Laszlo gluing’, let us recall the statement of the Beauville–Laszlo theorem from [Reference Beauville and Laszlo3]. Let A be a ring with a non-zerodivisor
$\pi $
. Then, the theorem asserts that the functor from the category of
$\pi $
-torsionfree A-modules M, to the category of triples
$(F,G,\iota )$
where
-
(i) F is a
-module, -
(ii) G is a
$\pi $
-torsionfree
$\widehat {A}$
-module, -
(iii)
is an isomorphism of -modules,
-module,
is an isomorphism of 
-modules,given by sending M to 
(where
$\iota _M$
is the natural isomorphism) is an equivalence. One can extend this result to more general pairs
$(A,\pi )$
, and to the setting where M is replaced by an affine scheme
$\operatorname {\mathrm {Spec}}(R)$
over
$\operatorname {\mathrm {Spec}}(A)$
(e.g., see (30, Lemma 0F9Q)).Footnote 2
There is simplicity in the Beauville–Laszlo method as it avoids needing to explicitly think about formal geometry, using
$\operatorname {\mathrm {Spec}}(\widehat {R})$
instead of
$\operatorname {\mathrm {Spf}}(\widehat {R})$
. That said, this prevents one from being able to globalize such gluing procedures on a general scheme
$X=\bigcup \operatorname {\mathrm {Spec}}(R_i)$
over
$\operatorname {\mathrm {Spec}}(A)$
, as the correct gluing cannot happen between
$\operatorname {\mathrm {Spec}}(\widehat {R}_i)$
and
$\operatorname {\mathrm {Spec}}(\widehat {R}_j)$
, but only between
$\operatorname {\mathrm {Spf}}(\widehat {R}_i)$
and
$\operatorname {\mathrm {Spf}}(\widehat {R}_j)$
. Similar problems arise when trying to globalize the base
$\operatorname {\mathrm {Spec}}(A)$
. This forces the introduction of formal geometry and in turn the introduction of rigid geometry, as the analogue of the isomorphism in (iii) above must now take place over the locus
$\{\pi \ne 0\}$
in
$\operatorname {\mathrm {Spf}}(\widehat {A})$
which only exists in the world of rigid analytic geometry.
Despite this connection, we do emphasize that our gluing results differ from the classical version of Beauville–Laszlo gluing outside of the coherent situation, that is, when
$\operatorname {\mathrm {Spec}}(R)$
is not a finite scheme over
$\operatorname {\mathrm {Spec}}(A)$
. Indeed, while 
has a close connection to 
in the finite case (e.g., the latter is the analytification of the former), the difference becomes drastic even for finite type (but not finite) affine schemes over
$\operatorname {\mathrm {Spec}}(A)$
. For instance, 
but the
$\{\pi \ne 0\}$
locus in
$\operatorname {\mathrm {Spf}}(\mathcal {O}[x^{\pm 1}]^\wedge )$
is the circle group
$\{x\in \mathbb {G}_{m,K}^{\mathrm {an}}:|x|=1\}$
.
Idea of proof and conditions on S
Many of our results, including the fully faithfulness portion of Theorem 1.3 requires only that
$(S,S_0)$
is of type (N)/(V) (i.e., S is Noetherian or the spectrum of a complete rank one valuation ring). But, our proof of essential surjectivity uses
-
(a) the Artin contraction theorem (see Theorem 5.9) which (with some work) handles the case when the gluing triple is ‘proper-like’, and
-
(b) Nagata compactification for algebraic spaces (see [Reference Conrad, Lieblich and Olsson11]) to reduce to the ‘proper-like’ case.
Roughly, (a) explains our restriction to S excellent, and (b) explains our separation hypotheses. It would be worthwhile to try and relax either of these hypotheses (e.g., allowing
$S = \operatorname {\mathrm {Spec}}(\mathcal {O}_{\mathbb {C}_p})$
).
Outline of the article
In §2.1–2.2 we review the necessary background in rigid geometry to define the category of gluing triples in the generality we require. In §3 we discuss some illustrative examples of triples and give some applications of Theorem 1.3 to clarify them. In particular, in Proposition 3.6, we explain how to single out those gluing triples whose gluing is a scheme (as opposed to an algebraic space), generalizing results from [Reference Bosch and Lütkebohmert8]. In §4 we prove gluing for coherent sheaves: that for an algebraic space X, coherent sheaves on X and
$\mathcal {t}(X)$
are the same. In §5 we supply proofs of Theorem 1.3 and two other lengthier propositions.
Notation and conventions
-
• All (formal) algebraic spaces in this article are assumed quasi-separated.
-
• A non-archimedean field is a field which is complete with respect to a rank one valuation. We denote by
$\mathcal {O}_K$
or simply by
$\mathcal {O}$
the valuation ring of a non-archimedean field K. -
• For a Huber ring A, we shorten the notation
$\operatorname {\mathrm {Spa}}(A,A^\circ )$
to
$\operatorname {\mathrm {Spa}}(A)$
. -
• A locally spectral space is called coherent if it is quasi-compact and quasi-separated.
-
• For categories of schemes, formal schemes, algebraic spaces etc. over a fixed base, we shall use the following abbreviations (as superscripts) to denote properties specifying the corresponding full subcategories:
-
• We shall almost always use different types of letters/fonts to denote objects over different spaces. The letters
$X,Y,Z$
will denote algebraic spaces over some algebraic space S, the letters
$U,V,W$
will denote algebraic spaces over an open algebraic subspace
$S^\circ \subseteq S$
, the letters
$\mathfrak {X},\mathfrak {Y},\mathfrak {Z}$
will denote formal algebraic spaces over a completion
$\widehat {S}$
of S, and letters like
$\mathsf {X},\mathsf {Y},\mathsf {Z}$
will denote rigid algebraic spaces over the rigid locus
$\widehat {S}^{\mathrm {rig}}$
. If X is an algebraic space over S we shall usually denote
$X\times _S S^\circ $
by
$X^\circ $
.
2 Gluing triples
In this section, we formalize the notion of gluing triples over a general base S, define the ‘associated gluing triple’ of an algebraic space over S, and establish some basic properties of such objects. We then formulate the main result of this article: Beauville–Laszlo Gluing of algebraic spaces (see Theorem 2.26).
2.1 Formal and rigid algebraic spaces
In this subsection, we recall the definitions of the geometric objects appearing in the definition of a gluing triple.
Formal schemes and formal algebraic spaces
Our references for formal algebraic spaces are [Reference Fujiwara and Kato15] and (30, Chapter 0AHW). We refer the reader to these references for any undefined terms. But unlike in both of these references, in this article all formal schemes and formal algebraic spaces are quasi-separated and (Zariski or étale) locally of the form
$\mathrm {Spf}(A)$
for a ring A which is I-adically complete and separated for a finitely generated ideal
$I\subseteq A$
, endowed with the I-adic topology. Also, like [Reference Fujiwara and Kato15] (but unlike [30]) our initial definitions of algebraic spaces over a base S are as sheaves on the big étale site of S.
We further always assume our formal algebraic spaces
$\mathfrak {S}$
are locally universally rigid-Noetherian as in [Reference Fujiwara and Kato15, Chapter I, Definitions 2.1.7 and 6.5.1], that is, étale locally of the form
$\operatorname {\mathrm {Spf}}(A)$
as above such that the schemes 
are Noetherian for all
$n\geqslant 0$
. We shall often further assume
$\mathfrak {S}$
is either
-
⋄ of type (N): admits an étale cover
$\mathfrak {U}\to \mathfrak {S}$
where
$\mathfrak {U}$
is a locally Noetherian formal scheme, or -
⋄ of type (V): admits an étale cover
$\mathfrak {U}\to \mathfrak {S}$
where
$\mathfrak {U}$
is a formal scheme locally of finite type over a complete rank one valuation ring.
Note that every algebraic space of type (N)/(V) is locally universally rigid-Noetherian (see [Reference Fujiwara and Kato15, Chapter I, Example 2.1.4]).
Notation 2.1. Let 
be an ideal sheaf of definition (see [Reference Fujiwara and Kato15, Chapter I, Definitions 1.1.18 and 6.3.16]) of a coherent formal algebraic space
$\mathfrak {S}$
. We write
$\mathfrak {S}_n$
for 
, leaving 
implicit.
We next set our notation for categories of formal schemes over a fixed base
$\mathfrak {S}$
.
Notation 2.2. Denote the category of formal schemes (resp. formal algebraic spaces) over
$\mathfrak {S}$
by
$\mathbf {FSch}_{\mathfrak {S}}$
(resp.
$\mathbf {FAlgSp}_{\mathfrak {S}}$
). Let
$\mathbf {FSch}^\ast _{\mathfrak {S}}$
or
$\mathbf {FAlgSp}^\ast _{\mathfrak {S}}$
be the subcategories with the same objects but only adic morphisms (see [Reference Fujiwara and Kato15, Chapter I, Definitions 1.3.1 and 6.3.18]). If
$\mathfrak {S}$
is a scheme, let
$\mathbf {Sch}_{\mathfrak {S}}$
and
$\mathbf {AlgSp}_{\mathfrak {S}}$
be the category of schemes and algebraic spaces over
$\mathfrak {S}$
, respectively.
We next recall our notation for the underlying topological space of a formal algebraic space.
Definition 2.3. Let
$\mathfrak {S}$
be a formal algebraic space. We define the underlying space to have set
$$ \begin{align*} |\mathfrak{S}|= \left\{x\colon \operatorname{\mathrm{Spec}}(k_x)\to \mathfrak{S}: k_x\text{ is a field}\right\}/\sim, \end{align*} $$
where
$x\sim y$
if they can be dominated by a common
$z\colon \operatorname {\mathrm {Spec}}(k_z)\to \mathfrak {S}$
. As in (30, Lemma 03BX), we may uniquely, functorially topologize this set so that it agrees with the usual underlying space in the representable case.Footnote 3
Finally, we recall that for a closed algebraic subspace
$S_0$
of an algebraic space S, one may form the completion denoted
$\widehat {S}$
(leaving the role of
$S_0$
implicit) as in [Reference Fujiwara and Kato15, Chapter I, §6.3. (f)]). This defines a functor
$\widehat {(-)}\colon \mathbf {AlgSp}_S\to \mathbf {FAlgSp}^\ast _{\widehat {S}}$
, where we complete
$X\to S$
along
$X_0=X\times _S S_0$
.
Adic spaces and adic algebraic spaces
In this article we use the theory of adic spaces as our foundation for rigid geometry with our main reference being [Reference Huber17]. That said, we expand the category of adic spaces under consideration to include those adic spaces
$\mathsf {S}$
which are locally strongly rigid-Noetherian, that is, such that every point has an affinoid open neighbourhood
$\operatorname {\mathrm {Spa}}(A,A^+)\subseteq \mathsf {S}$
where A is strongly rigid-Noetherian in the sense of [Reference Zavyalov33, Definition 2.8].
To simplify terminology and notation, we refer to such locally strongly rigid-Noetherian adic spaces as just ‘adic spaces’. Also, for any category of adic spaces, an asterisk as a superscript refers to restricting to the wide subcategory consisting of adic morphisms (in the sense of [Reference Huber16, §3])
Definition 2.4. A point s of an adic space
$\mathsf {S}$
is analytic if the topological field
$k(s)$
is non-discrete. The set
$\mathsf {S}_{\mathrm {a}}\subseteq \mathsf {S}$
of analytic points of
$\mathsf {S}$
forms an open subset which we call the analytic locus, and we say that
$\mathsf {S}$
is analytic if
$\mathsf {S}=\mathsf {S}_{\mathrm {a}}$
. The analytic locus forms a functor
$$ \begin{align} (-)_{\mathrm{a}}\colon \left\{\begin{matrix}\text{Adic}\\ \text{spaces}\end{matrix}\right\}^\ast \to \left\{\begin{matrix}\text{Analytic adic}\\ \text{spaces}\end{matrix}\right\}, \end{align} $$
which is right adjoint to the inclusion of analytic adic spaces into the category of adic spaces with adic morphisms.
We come to our definition of algebraic spaces in the adic space world.
Definition 2.5. An adic algebraic space is a sheaf
$\mathsf {S}$
on the big étale site of adic spaces such that
-
(i) the diagonal map
$\Delta _{\mathsf {S}}\colon \mathsf {S}\to \mathsf {S}\times \mathsf {S}$
is representable by adic spaces and quasi-compact, -
(ii) there exists an étale cover
$\mathsf {U}\to \mathsf {S}$
where
$\mathsf {U}$
is an adic space.
We say an adic algebraic space
$\mathsf {S}$
is analytic if it admits an étale cover
$\mathsf {U}\to \mathsf {X}$
with
$\mathsf {U}$
analytic.
We often assume that our analytic algebraic space
$\mathsf {S}$
is of one of the following types:
-
⋄ type (N): admits an étale cover
$\mathsf {U}\to \mathsf {S}$
where
$\mathsf {U}$
is an adic space locally of the form
$\operatorname {\mathrm {Spa}}(A,A^+)$
where A has a Noetherian ring of definition, -
⋄ type (V): admits an étale cover
$\mathsf {U}\to \mathsf {S}$
where
$\mathsf {U}$
is an adic space locally of finite type over some non-archimedean field.
We will be particularly interested in certain categories of adic algebraic spaces, and so we give specific notation to them.
Notation 2.6. For an analytic algebraic space
$\mathsf {S}$
, denote by
$\mathbf {RigAlgSp}_{\mathsf {S}}$
the category of adic algebraic spaces locally of finite type over
$\mathsf {S}$
, whose objects are rigid algebraic spaces over
$\mathsf {S}$
.
Our definition of the underlying topological space is as in the case of formal algebraic space.
Definition 2.7. Let
$\mathsf {S}$
be an adic algebraic space. We define the underlying space to have set
$$ \begin{align*} |\mathsf{S}|= \left\{x\colon \operatorname{\mathrm{Spa}}(k_x,k_x^+)\to \mathsf{S}:(k_x,k_x^+)\text{ is an affinoid field}\right\} \end{align*} $$
where
$x\sim y$
if they can be dominated by a common
$z\colon \operatorname {\mathrm {Spa}}(k_z,k_z^+)\to \mathsf {S}$
. As in (30, Lemma 03BX), we may uniquely, functorially topologize this set so that it agrees with the usual underlying space in the representable case.
Finally, we extend Definition 2.4 to the case of adic algebraic spaces.
Definition 2.8. If
$\mathsf {S}$
is an adic algebraic space, a point of
$|\mathsf {S}|$
is analytic if it can be represented as
$x\colon \operatorname {\mathrm {Spa}}(k_x,k_x^+)\to \mathsf {S}$
such that
$k_x$
is not discrete. The subset
$|\mathsf {S}|_{\mathrm {a}}\subseteq |\mathsf {S}|$
of analytic points is open and so corresponds to a unique open embedding of adic algebraic spaces
$\mathsf {S}_{\mathrm {a}}\to \mathsf {S}$
. We call
$\mathsf {S}_{\mathrm {a}}$
the analytic locus of
$\mathsf {S}$
. This defines a functor
$$ \begin{align*} (-)_{\mathrm{a}}\colon \left\{\begin{matrix}\text{Adic algebraic}\\ \text{spaces}\end{matrix}\right\}^\ast \to \left\{\begin{matrix}\text{Analytic adic}\\ \text{algebraic spaces}\end{matrix}\right\}, \end{align*} $$
which is right adjoint to the inclusion of analytic adic algebraic spaces into the category of adic algebraic spaces with adic morphisms.
Rigid locus and a result of Raynaud and Fujiwara–Kato
To begin, we observe there is a functor (recalling our conventions for formal schemes)
$$ \begin{align*} (-)^{\mathrm{ad}}\colon \left\{\begin{matrix}\text{Formal}\\ \text{schemes}\end{matrix}\right\}\to\left\{\begin{matrix}\text{Adic}\\\text{spaces}\end{matrix}\right\}, \end{align*} $$
uniquely characterized by preserving open embeddings/coverings and such that there is a functorial identification
$\operatorname {\mathrm {Spf}}(A)^{\mathrm {ad}}=\operatorname {\mathrm {Spa}}(A)$
(e.g., combine [Reference Huber16, Propositions 4.1 and 4.2. (i)] with [Reference Zavyalov33]). We may compose the functors
$(-)^{\mathrm {ad}}$
and
$(-)_{\mathrm {a}}$
to obtain the rigid locus functor
$$ \begin{align*} (-)^{\mathrm{rig}} = (-)_{\mathrm{a}}\circ(-)^{\mathrm{ad}}\colon \left\{\begin{matrix}\text{Formal}\\ \text{schemes}\end{matrix}\right\}^\ast\to \left\{\begin{matrix}\text{Analytic}\\\text{adic spaces}\end{matrix}\right\}, \end{align*} $$
where again the asterisk means restricting only to adic morphisms. If
$\mathfrak {S}=\operatorname {\mathrm {Spf}}(A)$
where
$(\pi )\subseteq A$
is an ideal of definition, then 
(see [Reference Fujiwara and Kato15, Chapter II, §A.4. (b)–§A.4. (d)]).
The rigid locus functor extends to, and has quite pleasant properties on, the category of formal algebraic spaces locally of finite type over
$\mathfrak {S}$
. To state this precisely, first recall that a morphism
$\mathfrak {f}\colon \mathfrak {X}'\to \mathfrak {X}$
of formal schemes is an admissible blowup if there exists a quasi-coherent, locally finitely generated, open ideal sheaf 
such that
$\mathfrak {f}$
is final among adic and proper morphisms
$\mathfrak {g}\colon \mathfrak {Y}\to \mathfrak {X}$
with 
a Cartier divisor (see [Reference Fujiwara and Kato15, Chapter II, §1.1. (a)-1.1. (b)] for a more explicit description). We say that
$\mathfrak {f}$
is an admissible modification if it is adic and
$\mathfrak {f}^{\mathrm {rig}}$
is an isomorphism. If
$\mathfrak {X}'$
and
$\mathfrak {X}$
are coherent this condition is equivalent to the existence of a decomposition
$\mathfrak {f}\circ \pi _1=\pi _2$
for a diagram of admissible blowups
$$ \begin{align*} \mathfrak{X}'\xleftarrow{\pi_1}\mathfrak{Y}\xrightarrow{\pi_2}\mathfrak{X}. \end{align*} $$
(see [Reference Fujiwara and Kato15, Chapter II, Corollary 2.1.5]).
Definition 2.9. A morphism
$\mathfrak {f}\colon \mathfrak {X}'\to \mathfrak {X}$
of formal algebraic spaces is an admissible modification if
$\mathfrak {X}'\times _{\mathfrak {X}}\mathfrak {Y}\to \mathfrak {Y}$
is an admissible modification for any morphism
$\mathfrak {Y}\to \mathfrak {X}$
from a formal scheme
$\mathfrak {Y}$
.
Denote by W the class of admissible modifications of coherent formal algebraic spaces. This is left multiplicative (see (30, Section 04VB)) and so the localization
$(-)[W^{-1}]$
with respect to W is well-behaved.
Theorem 2.10 (Raynaud, Fujiwara–Kato)
There exists a unique functor
$$\begin{align*}(-)^{\mathrm{rig}} \colon \mathbf{FAlgSp} \to\left\{\begin{matrix}\mathit{Analytic adic}\\ \mathit{algebraic spaces}\end{matrix}\right\} \end{align*}$$
extending the rigid locus functor on formal schemes, and such that the natural map
$$ \begin{align*} \mathfrak{U}^{\mathrm{rig}}/\mathfrak{R}^{\mathrm{rig}}\to (\mathfrak{U}/\mathfrak{R})^{\mathrm{rig}} \end{align*} $$
is an isomorphism for every étale equivalence relation
$\mathfrak {U}\rightrightarrows \mathfrak {R}$
. This functor sends W to isomorphisms and for any coherent formal algebraic space
$\mathfrak {S}$
induces an equivalence of categories
The functor
$(-)^{\mathrm {rig}}$
commutes with fibre products.
Remark 2.11. The last equivalence in Theorem 2.10 is well-known to the experts, and will appear in the forthcoming follow up to [Reference Fujiwara and Kato15]. The proof is largely the same as in the case of formal schemes (i.e., the representable case), which is contained in the material developed in the main body of [Reference Fujiwara and Kato15, Chapter II], as well as [Reference Fujiwara and Kato15, Chapter II, Theorem A.5.2]. The argument for formal algebraic spaces extends largely to this case with one caveat which we briefly discuss here.
For a formal algebraic space
$\mathfrak {Y}$
locally of finite type over
$\mathfrak {S}$
, one wishes to define
$\mathfrak {Y}^{\mathrm {rig}}$
as the functor associating to a rigid
$\mathfrak {S}$
-space
$\mathsf {X}$
the set
$$ \begin{align*} \mathfrak{Y}^{\mathrm{rig}}(\mathsf{X})= \varinjlim_{\widehat{U}}\varinjlim_{\widehat{V}}\varinjlim_{\widehat{U}'} \operatorname{\mathrm{Hom}}(\widehat{U}',\widehat{V}), \end{align*} $$
where
$\widehat {U}$
and
$\widehat {V}$
travel over the coherent open subsets of
$\mathfrak {X}$
and
$\widehat {Y}$
respectively, and where
$\widehat {U}'$
travels over all admissible modifications of
$\widehat {U}$
. Here we are implicitly using the representable version of Theorem 2.10 as mentioned in the last paragraph to identify
$\mathsf {X}=\mathfrak {X}^{\mathrm {rig}}$
for some formal algebraic space locally of finite type over
$\mathfrak {S}$
(the choice is immaterial).
The issue with this definition is that it is not clear that
$\mathfrak {Y}^{\mathrm {rig}}$
is an étale sheaf. The operative issue is that, in general, one cannot find an étale formal model of an étale morphism of rigid spaces. Instead, one should prove the stronger statement that
$\mathfrak {Y}^{\mathrm {rig}}$
is a sheaf for the flat topology (appropriately defined) as one can always find flat models of flat morphisms by Theorem 2.14. The final key missing step is the observation that while
$\mathfrak {Y}$
is only assumed to be a sheaf for the étale topology, it is actually a sheaf for the (adic) flat topology as follows from [Reference Laumon and Moret-Bailly22, §A.4] by working modulo powers of the ideal sheaf of definition.
Warning 2.12. The finite-type hypotheses in the final statement of Theorem 2.10 are crucial. Let
$K\subseteq L$
be a finite extension of non-archimedean fields with
$\mathcal {O}_L$
not finite over
$\mathcal {O}_K$
(see [Reference Bosch, Güntzer and Remmert5, §6.4.1]). Write
$L=K[x_1,\ldots ,x_n]/(f_1,\ldots ,f_m)$
with
$f_i$
in
$\mathcal {O}_K[x_1,\ldots ,x_n]$
, and set A to be
$\mathcal {O}_K\langle x_1,\ldots ,x_n\rangle /(f_1,\ldots ,f_m)$
. Then,
$\operatorname {\mathrm {Spf}}(\mathcal {O}_L)$
is not of finite type over
$\operatorname {\mathrm {Spf}}(\mathcal {O}_K)$
and
$$ \begin{align*} \operatorname{\mathrm{Spf}}(\mathcal{O}_L)^{\mathrm{rig}}\simeq \operatorname{\mathrm{Spa}}(L)\simeq \operatorname{\mathrm{Spf}}(A)^{\mathrm{rig}}. \end{align*} $$
That said, there is no common admissible blowup of
$\operatorname {\mathrm {Spf}}(\mathcal {O}_L)$
and
$\operatorname {\mathrm {Spf}}(A)$
, and so they are not isomorphic in the localization of
$\mathbf {FSch}^{\mathrm {coh}}_{\mathcal {O}_K}$
with respect to admissible modifications.
We will often use the following terminology in the sequel.
Terminology 2.13. Let
$\mathsf {X}$
(resp.
$\mathsf {f}\colon \mathsf {X}'\to \mathsf {X}$
) be an object (resp. morphism) of
$\mathbf {RigAlgSp}_{\mathfrak {S}^{\mathrm {rig}}}$
.
-
• A model of
$\mathsf {X}$
is a formal algebraic space
$\mathfrak {X}$
locally of finite type over
$\mathfrak {S}$
together with an identification
$\mathfrak {X}^{\mathrm {rig}}\simeq \mathsf {X}$
, which we always leave implicit. -
• A model of
$\mathsf {f}$
is a morphism
$\mathfrak {f}\colon \mathfrak {X}'\to \mathfrak {X}$
of formal algebraic spaces locally of finite type over
$\mathfrak {S}$
together with an identification
$\mathsf {f}\simeq \mathfrak {f}^{\mathrm {rig}}$
, which we always leave implicit. -
• We say a model
$\mathfrak {X}$
(resp.
$\mathfrak {f}$
) of
$\mathsf {X}$
(resp.
$\mathsf {f}$
) is admissible or coherent if
$\mathfrak {X}$
(resp. the source and target of
$\mathfrak {f}$
are both) admissible or coherent, respectively.
Finally, we recall a well-known result saying that essentially all reasonable properties P of
$\mathfrak {f}$
are inherited by
$\mathfrak {f}^{\mathrm {rig}}$
, and in many cases
$\mathsf {f}$
satisfying P is equivalent to having a model
$\mathfrak {f}$
satisfying P.
Theorem 2.14 (Bosch–Lütkebohmert–Raynaud)
Let P be one of the following properties
If a morphism
$\mathfrak {f}\colon \mathfrak {X}\to \mathfrak {Y}$
locally of finite type between formal schemes of type (N)/(V) satisfies P, then the induced map
$\mathfrak {f}^{\mathrm {rig}}$
satisfies P (for cases (vii) and (viii) we assume the formal scheme is Jacobson). Moreover, except in case (ix), a finite type morphism
$\mathsf {f}\colon \mathsf {X}\to \mathsf {Y}$
between coherent analytic adic spaces of type (N)/(V) satisfies P, then it has a coherent admissible formal model
$\mathfrak {f}$
which satisfies P.
Proof. The claim in case i) follows from (Reference Fujiwara and Kato15, Chapter II, Proposition 7.1.1). The claim in case ii) is (Reference Fujiwara and Kato15, Chapter II, Proposition 3.1.3). The claim concerning iii) follows from (Reference Fujiwara and Kato15, Chapter II, Proposition 7.3.5). The claim concerning iv) follows from (Reference Fujiwara and Kato15, Chapter II, Proposition 7.2.4). The claim concerning v) follows from (Reference Fujiwara and Kato15, Chapter II, Theorem 7.5.6). The claim concerning vi) follows by combining (Reference Fujiwara and Kato15, Chapter II, Theorem 7.5.17) together with (Reference Huber17, Corollary 1.3.9).
To prove vii), we first observe that as the question is clearly unchanged by replacing
$\mathfrak {X}$
and
$\mathfrak {Y}$
by an open cover and/or an admissible blowup, we may assume without loss of generality that
$\mathfrak {X}=\operatorname {\mathrm {Spf}}(B)$
,
$\mathfrak {Y}=\operatorname {\mathrm {Spf}}(A)$
, and 
for some non-zerodivisor a of A. In this case,
$\mathfrak {f}^{\mathrm {rig}}$
is the map 
induced by the natural map
$A\to B$
.
Suppose first that
$\mathfrak {f}$
is flat, and that
$(S,S_0)$
is Jacobson. Then, by (Reference Fujiwara and Kato15, Chapter I, Proposition 4.8.1) the map
$A\to B$
is flat. Thus, so is the map 
. Let x be a classical point of 
in the sense of (Reference Fujiwara and Kato15, Chapter II, §8), then
$\mathfrak {f}^{\mathrm {rig}}(x)=y$
is a classical point of 
by (Reference Fujiwara and Kato15, Chapter II, Proposition 8.2.14). Moreover, by (Reference Fujiwara and Kato15, Chapter II, Proposition 8.3.1) there exists maximal ideals
$\mathfrak {m}$
and
$\mathfrak {n}$
of
$\operatorname {\mathrm {Spec}}(B)$
and
$\operatorname {\mathrm {Spec}}(A)$
, respectively, such that the map 
may be identified with the map 
. As all rings are Noetherian (see (Reference Fujiwara and Kato15, Chapter II, Theorem 8.3.6)) this implies by (30, Tag 0523) that 
is flat. This is sufficient to imply that 
is flat by applying (Reference Fujiwara and Kato15, Chapter II, Corollary 8.2.12).
Conversely, suppose that
$\mathfrak {f}^{\mathrm {rig}}$
is flat. By (Reference Zavyalov34, Lemma B.4.3.) the map 
is flat. Then,
$\operatorname {\mathrm {Spf}}(B)\to \operatorname {\mathrm {Spf}}(A)$
is rig-flat in the sense of Reference Bosch and Lütkebohmert9. So, by the main theorem of op. cit. (see (Reference Bosch and Lütkebohmert9, Theorem 5.2)) there exists an admissible blowup
$\mathfrak {Y}'\to \operatorname {\mathrm {Spf}}(A)$
such that
$\mathfrak {Y}'\times _{\operatorname {\mathrm {Spf}}(A)}\operatorname {\mathrm {Spf}}(B)\to \mathfrak {Y}'$
is flat and induces the morphism
$\mathfrak {f}^{\mathrm {rig}}$
on generic fibers, as desired.
To show viii), let us first assume that
$\mathfrak {f}$
is faithfully flat. The fact that
$\mathfrak {f}^{\mathrm {rig}}$
is flat follows from the claim about vii). To see that
$\mathfrak {f}^{\mathrm {rig}}$
is surjective, consider a rigid point
$\operatorname {\mathrm {Spf}}(V)\to \widehat {Y}$
in the sense of (Reference Fujiwara and Kato15, Chapter II, §3.3.). Then, by (Reference Fujiwara and Kato15, Chapter II, Proposition 3.3.6)) it suffices to find an adic faithfully flat cover
$\operatorname {\mathrm {Spf}}(W)\to \operatorname {\mathrm {Spf}}(V)$
such that
$\operatorname {\mathrm {Spf}}(W)\to \mathfrak {Y}$
lifts to
$\mathfrak {X}$
(e.g., see (Reference Fujiwara and Kato15, Chapter II, Proposition 3.3.6)). In the parlance of (Reference Česnavičius and Scholze31, §2.2.1) we must then show that
$\mathfrak {X}\to \mathfrak {Y}$
is a 
-complete arc cover. But, this follows from the 
-adic faithful flatness of
$\mathfrak {X}\to \mathfrak {Y}$
by the argument of (Reference Česnavičius and Scholze31, (2), p. 73). Conversely, if
$\mathsf {f}$
is faithfully flat, then by the argument for the claim about vii) we may find an admissible formal model
$\mathfrak {f}\colon \mathfrak {X}\to \mathfrak {Y}$
which is flat. This is automatically faithfully flat by the diagram
as the top arrow is surjective by assumption and the vertical arrows are surjective by part (2) of Proposition 2.15 below.
The proof of the claim about ix), is the same as (Reference Achinger, Lara and Youcis1, Proposition 2.10).
Specialization map
We now recall the existence of the specialization map, whose proof follows easily from bootstrapping the arguments in [Reference Fujiwara and Kato15, Chapter II, Theorems 3.1.2 and Proposition 3.1.5].
For a formal or adic algebraic space
$\mathscr {S}$
we let
$\mathscr {S}_{\mathrm {\acute {E}t}}$
denote the big étale topos. It is endowed with the usual structure sheaf given by the following formula
$$ \begin{align} \mathcal{O}_{\mathscr{S}}(\mathscr{T})= \varprojlim_{\mathscr{U}\to\mathscr{T}}\mathcal{O}_{\mathscr{U}}(\mathscr{U}) \end{align} $$
where
$\mathscr {U}\to \mathscr {T}$
ranges over morphisms to
$\mathscr {T}$
from representable objects. When
$\mathsf {S}$
is an adic algebraic space, one may similarly define the sheaf of rings
$\mathcal {O}_{\mathsf {S}}^+$
.
Proposition 2.15. Let
$\mathfrak {S}$
be a formal algebraic space.
-
(1) There exists a unique natural morphism
such that for
$$ \begin{align*} \mathrm{sp}_{\mathfrak{S}}\colon |\mathfrak{S}^{\mathrm{rig}}|\to |\mathfrak{S}|, \end{align*} $$
$\mathfrak {S}=\operatorname {\mathrm {Spf}}(A)$
with ideal of definition
$(\pi )\subseteq A$
, one has (2.1.3)The map
$\mathrm {sp}_{\mathfrak {S}}$
is quasi-compact and closed, and is surjective if
$\mathfrak {S}$
is admissible. -
(2) There exists a unique morphism of locally topologically ringed spaces
functorial in a formal scheme
$$ \begin{align*} \mathrm{sp}_{\mathfrak{S}}\colon (\mathfrak{S}^{\mathrm{rig}},\mathcal{O}_{\mathfrak{S}^{\mathrm{rig}}}^+)\to (\mathfrak{S},\mathcal{O}_{\mathfrak{S}}) \end{align*} $$
$\mathfrak {S}$
such that on global sections (2.1.3) is the map , and which recovers (1) on the underlying topological space.
-
(3) There exists a unique morphism of locally topologically ringed topoi
functorial in a formal algebraic space
$$ \begin{align*} \mathrm{sp}_{\mathfrak{S}}\colon (\mathfrak{S}^{\mathrm{rig}}_{\mathrm{\acute{E}t}},\mathcal{O}_{\mathfrak{S}^{\mathrm{rig}}}^+)\to (\mathfrak{S}_{\mathrm{\acute{E}t}},\mathcal{O}_{\mathfrak{S}}), \end{align*} $$
$\mathfrak {S}$
whose underlying morphism of sites associates sends
$\mathfrak {Y}\to \mathfrak {X}$
to
$\mathfrak {Y}^{\mathrm {rig}}\to \mathfrak {X}^{\mathrm {rig}}$
, and which recovers (1) and (2) in the obvious sense.
, and which recovers (1) on the underlying topological space.
In all cases we call
$\mathrm {sp}_{\mathfrak {S}}$
the specialization morphism associated to
$\mathfrak {S}$
.
2.2 Gluing triples and Beauville–Laszlo gluing of algebraic spaces
We now define the category of gluing triples in their natural generality and state our main theorem, Theorem 2.26.
Base setup
We begin by fixing the base for which the objects we study will live over. In the sequel we shall use all the following notation without comment.
Let S be a coherent algebraic space and let
$S_0$
be a finitely presented closed subspace of S, cut out by a quasi-coherent ideal sheaf 
. We set
-
•
, an open algebraic subspace of S, -
•
for
$n\geqslant 0$
, a finitely presented closed subspace of S, -
•
$\widehat {S}$
the completion of S along , a formal algebraic space.
, an open algebraic subspace of S,
for 
, a formal algebraic space.For an algebraic space X over S we shall consistently write
$X^\circ $
instead of
$X\times _S S^\circ $
.
We shall always assume that
$(S,S_0)$
is one of the following types:
-
• type (N): S is locally Noetherian,
-
• type (V):
$S = \operatorname {\mathrm {Spec}}(\mathcal {O})$
for a complete rank one valuation ring
$\mathcal {O}$
, and
$S_0 = V(\pi )$
for a pseudouniformizer
$\pi $
of
$\mathcal {O}$
.
Analytification
Suppose temporarily that S is a scheme. Consider the following sequence of maps of locally ringed spaces
$$ \begin{align} (\widehat{S}^{\mathrm{rig}},\mathcal{O}_{\widehat{S}^{\mathrm{rig}}})\xrightarrow{\mathrm{nat.}}(\widehat{S}^{\mathrm{rig}},\mathcal{O}^+_{\widehat{S}^{\mathrm{rig}}})\xrightarrow{\mathrm{sp}_{\widehat{S}}}(\widehat{S},\mathcal{O}_{\widehat{S}})\xrightarrow{\mathrm{nat.}} (S,\mathcal{O}_S), \end{align} $$
where each
$\mathrm {nat.}$
stands for the natural map. The composition of these maps then uniquely factorizes through the map
$(S^\circ ,\mathcal {O}_{S^\circ })\to (S,\mathcal {O}_S)$
as 
. When
$(S,S_0)=(\operatorname {\mathrm {Spec}}(A),V(\pi ))$
then the map
$(\widehat {S}^{\mathrm {rig}},\mathcal {O}_{\widehat {S}^{\mathrm {rig}}})\to (S^\circ ,\mathcal {O}_{S^\circ })$
corresponds to the natural map of rings 
.
Using this map of locally ringed spaces, we can define the first instance of analytification.
Definition 2.16. Suppose S is a scheme and U is a scheme locally of finite type over
$S^\circ $
. We define the analytification of U to be the adic space
$$ \begin{align*} U^{\mathrm{an}}= U\times_{S^\circ}\widehat{S}^{\mathrm{rig}}, \end{align*} $$
where this fibre product is taken in the sense of [Reference Huber16, Proposition 3.8].
The functor
$(-)^{\mathrm {an}}$
preserves products, sends closed embeddings to (Zariski) closed embeddings (i.e., sends
$V(I)$
to
$V(I\mathcal {O}_{U^{\mathrm {an}}})$
), and sends open covers to open covers. Moreover, suppose that
$(S,S_0)=(\operatorname {\mathrm {Spec}}(A),V(\pi ))$
, then
where the transition maps are open embeddings taking x to
$\pi x$
. These properties uniquely pin down
$(-)^{\mathrm {an}}$
when
$(S,S_0)$
, and the additional observation that admissible blowups of
$(S,S_0)$
(resp. open covers) map to isomorphisms (resp. open covers) pin down the construction in general.
In order to extend this construction to algebraic spaces, we proceed in two steps. First, suppose that S is a scheme, and let
$U = W/R$
be an étale presentation of U. Then
$R^{\mathrm {an}} \rightrightarrows W^{\mathrm {an}}$
is an étale equivalence relation in rigid spaces over
$\widehat {S}^{\mathrm {rig}}$
, and the quotient space
$$\begin{align*}U^{\mathrm{an}} = W^{\mathrm{an}} / R^{\mathrm{an}} \end{align*}$$
is independent of the chosen presentation (cf. [Reference Conrad and Temkin12, Lemma 2.2.1]). For S general, we note that both algebraic spaces over
$S^\circ $
and rigid algebraic spaces over
$\widehat {S}^{\mathrm {rig}}$
can be defined étale locally on S. In order to define
$U^{\mathrm {an}}$
in general, we pick an étale presentation
$S = S'/S"$
of the base algebraic space S. Then
$(U\times _S S')^{\mathrm {an}}$
as defined above comes equipped with a descent datum to S (or rather to
$\widehat {S}^{\mathrm {rig}}$
), producing the desired rigid algebraic space
$U^{\mathrm {an}}$
.
Analytification and rigid locus of completion
Let X be an algebraic space locally of finite type over S. One can construct a rigid algebraic space over
$\widehat {S}^{\mathrm {rig}}$
in two different ways: by taking the analytification
$(X^\circ )^{\mathrm {an}}$
of
$X^\circ = X\times _S S^\circ $
, and by taking the rigid locus
$\widehat {X}^{\mathrm {rig}}$
of its formal completion
$\widehat {X}$
along
$X_0 = X\times _S S_0$
. These constructions yield a diagram of categories
for which there exists a natural transformation (not an equivalence) between its compositions.
Proposition 2.17 (cf. [Reference Huber17, Proposition 1.9.6])
There is a unique map of rigid algebraic spaces
$j_{X}\colon \widehat {X}^{\mathrm {rig}} \to (X^\circ )^{\mathrm {an}}$
over
$\widehat {S}^{\mathrm {rig}}$
, functorial in X and such that the following diagram of locally ringed spaces commutes when X is a scheme
Moreover, the map
$j_X$
is étale. If
$X\to S$
is a separated, proper, or representable morphism then
$j_X$
is an open embedding, isomorphism, or locally open embedding, respectively.
Gluing triples
We now come to the category of gluing triples.
Definition 2.18. A gluing triple over
$(S,S_0)$
is a triple
$(U, \mathfrak {X}, j)$
where
-
• U is an algebraic space locally of finite type over
$S^\circ $
, -
•
$\mathfrak {X}$
is a formal algebraic space locally of finite type over
$\widehat {S}$
, -
•
$j\colon \mathfrak {X}^{\mathrm {rig}}\to U^{\mathrm {an}}$
is an étale morphism.
A morphism of gluing triples
$(U_1, \mathfrak {X}_1, j_1)\to (U, \mathfrak {X}, j)$
is a pair of morphisms
$\alpha \colon U_1\to U$
and
$\beta \colon \mathfrak {X}_1\to \mathfrak {X}$
of algebraic spaces over
$S^\circ $
and formal algebraic spaces over
$\widehat {S}$
, respectively, such that
$\alpha ^{\mathrm {an}}\circ j_1=j\circ \beta ^{\mathrm {rig}}$
. We denote the category of gluing triples over
$(S,S_0)$
by
$\mathbf {Trip}_{(S,S_0)}$
.
Informally, one can visualize a triple
$(U,\mathfrak {X},j)$
in the form of the following diagram (of ringed spaces/topoi), in which we interpret the leftmost and rightmost square as being ‘cartesian’
We will often use the following terminology concerning gluing triples.
Terminology 2.19. Let
$(U,\mathfrak {X},j)$
be a gluing triple over
$(S,S_0)$
.
-
• Let P be a property of morphisms of (formal) algebraic spaces. We say that a morphism
$(U_1,\mathfrak {X}_1,j_1)\to (U,\mathfrak {X},j)$
satisfies P if both
$U_1\to U$
and
$\mathfrak {X}_1\to \mathfrak {X}$
satisfy P. -
• A collection
$\{(U_i,\mathfrak {X}_i,j_{i})\to (U,\mathfrak {X},j)\}$
of open embeddings (resp. étale morphisms) is an open cover (resp. étale cover) if
$\{U_i\to U\}$
and
$\{\mathfrak {X}_i\to \mathfrak {X}\}$
are jointly surjective. -
• We say that
$(U,\mathfrak {X},j)$
is separated if
$U\to S^\circ $
and
$\mathfrak {X}\to \widehat {S}$
are separated maps and j is an open embedding. We write
$\mathbf {Trip}_{(S,S_0)}^{\mathrm {sep}}$
for the full subcategory of separated gluing triples.
Warning 2.20. We have defined the notion of separatedness for a triple in Terminology 2.19 in two different ways: implicitly in the first point with P being ‘separated’, and in the third point. These notions are not equivalent: if
$(U, \mathfrak {X}, j)$
is separated, then both U and
$\mathfrak {X}$
are separated, but not conversely. We shall always use the more restrictive notion.
The category
$\mathbf {Trip}_{(S,S_0)}$
has a final object given by the triple
$(S^\circ ,\widehat {S},\mathrm {id})$
. It furthermore admits all fibre products, computed in the obvious way:
$$ \begin{align*} (U_1,\mathfrak{X}_1,j_1)\times_{(U_2,\mathfrak{X}_2,j_2)}(U_3,\mathfrak{X}_3,j_3)=(U_1\times_{U_2}U_3,\mathfrak{X}_1\times_{\mathfrak{X}_2}\mathfrak{X}_3,j_1\times j_3). \end{align*} $$
Moreover, if
$(T,T_0)\to (S,S_0)$
is a morphism, with
$|T_0|=|T\times S_0|\subseteq |T|$
, then there is a natural base change functor
$\mathbf {Trip}_{(S,S_0)}\to \mathbf {Trip}_{(T,T_0)}$
computed in the same way. Both of these operations preserve the full subcategories of separated triples.
We now summarize the basic descent properties of the category of gluing triples below. Before we do so, let us establish the following terminology. By an étale gluing datum in
$\mathbf {Trip}_{(S,S_0)}$
we mean an index set
$\Sigma $
and collections of triples
$$ \begin{align*} \{T_\sigma=(U_\sigma,\mathfrak{X}_\sigma,j_ \sigma)\}_{\sigma\in\Sigma},\qquad \{T_{\sigma\tau}=(U_{\sigma\tau},\mathfrak{X}_{\sigma\tau},j_{\sigma\tau})\}_{\sigma,\tau\in\Sigma}, \end{align*} $$
with
$T_{\sigma \tau }=T_{\tau \sigma }$
, together with étale morphisms
$\phi ^\sigma _{\sigma \tau }\colon T_{\sigma \tau }\to T_{\sigma }$
. We say that an étale gluing datum is separated if for all
$\sigma ,\tau \in \Sigma $
the map
$$ \begin{align*} (\phi^\sigma_{\sigma\tau},\phi^\tau_{\sigma\tau})\colon T_{\sigma\tau}\to T_\sigma\times T_\tau \end{align*} $$
is a closed embedding. We say that an étale gluing datum is effective if the natural diagram in
$\mathbf {Trip}_{(S,S_0)}$
it forms admits a colimit. The following statement is obvious.
Proposition 2.21. Every étale gluing datum in
$\mathbf {Trip}_{(S,S_0)}$
is effective. Every separated étale gluing datum in
$\mathbf {Trip}_{(S,S_0)}^{\mathrm {sep}}$
is effective.
Corollary 2.22. For an étale map
$S'\to S$
, set
$S^{\prime}_0=S'\times _S S_0$
. Then, the associations of
$\mathbf {Trip}_{(S',S^{\prime}_0)}$
and
$\mathbf {Trip}_{(S',S^{\prime}_0)}^{\mathrm {sep}}$
to
$S'\to S$
are stacks for the étale topology.
Beauville–Laszlo Gluing of algebraic spaces
To state our main theorem we first observe that Proposition 2.17 allows us to realize algebraic spaces over S as gluing triples.
Definition 2.23. Let X be an algebraic space locally of finite type over S. The (gluing) triple associated to X is defined as follows:
$$ \begin{align*} \mathcal{t}(X)= (X^\circ,\widehat{X},j_X). \end{align*} $$
This association gives rise to functors
$$ \begin{align*} \mathcal{t} \colon \mathbf{AlgSp}^{\mathrm{lft}}_S \to \mathbf{Trip}_{(S, S_0)},\qquad \mathcal{t} \colon \mathbf{AlgSp}^{\mathrm{lft,sep}}_S \to \mathbf{Trip}^{\mathrm{sep}}_{(S, S_0)}. \end{align*} $$
Again, one can visualize the triple
$\mathcal {t}(X) = (X^\circ , \widehat {X}, j_X)$
in the form of a diagram, in which the diagram (2.2.2) features as the three back faces of the prism.
We come now to our main theorem, whose proof will occupy the entirety of §5. We preface this by saying that an algebraic space X locally of finite type over S is the gluing of a gluing triple
$(U,\mathfrak {X},j)$
if
$\mathcal {t}(X)\simeq (U,\mathfrak {X},j)$
. Informally, this means that the square below is a pushout
Beauville–Laszlo gluing of algebraic spaces says such a gluing always exists if S is a G-space.
Definition 2.24. An algebraic space S is called a G-space if for each finite type point s of S (see (30, Section 06EE)) there exists an étale morphism
$\varphi \colon S'\to S$
with
$S'$
a scheme, and a closed point
$s'$
of
$S'$
such that
$\varphi (s')=s$
and
$\mathcal {O}_{S',s'}$
is a G-ring in the sense of (30, Definition 07GH).
Example 2.25. If S is an algebraic space which admits an étale cover
$\bigsqcup _i \operatorname {\mathrm {Spec}}(A_i)\to S$
where each
$A_i$
is an excellent ring (in the sense of (30, Section 07QS)), then S is a G-space.
Theorem 2.26 (Beauville–Laszlo Gluing of algebraic spaces)
Let
$(S,S_0)$
be a pair of type (N)/(V). Then, the functor
$$ \begin{align*} \mathcal{t} \colon \mathbf{AlgSp}^{\mathrm{lft,sep}}_S \to \mathbf{Trip}^{\mathrm{sep}}_{(S, S_0)} \end{align*} $$
from Definition 2.23 is fully faithful. Furthermore, if S is a G-space then
$\mathcal {t}$
is an equivalence of categories with quasi-inverse
$$ \begin{align*} \mathcal{g}\colon \mathbf{Trip}^{\mathrm{sep}}_{(S,S_0)}\to \mathbf{AlgSp}_S^{\mathrm{lft},\mathrm{sep}},\quad (U,\mathfrak{X},j)\mapsto \left(Y\mapsto \operatorname{\mathrm{Hom}}_{\mathbf{Trip}_{(S,S_0)}}\left(\mathcal{t}(Y),(U,\mathfrak{X},j)\right)\right). \end{align*} $$
We sometimes call the functor
$\mathcal {g}$
the gluing functor.
Properties of triples and morphisms of triples
Finally we give an omnibus result that shows that the functor
$\mathcal {t}$
reflects and preserves most frequently-encountered properties of morphisms. We defer its proof to §5.4, as it relies on later material.
Proposition 2.27. Let
$f\colon Y\to X$
be a morphism of algebraic spaces separated and locally of finite type over S, and let P be one of the following properties:
Then, the map f has property P if and only if
$\mathcal {t}(f)$
does.
3 Examples and further results
In this section we illustrate Theorem 2.26 by giving several concrete examples of gluing. When applicable, we also remark on natural corollaries of Beauville–Laszlo Gluing of algebraic spaces that the example more generally suggests.
3.1 Gluing produces finite type outputs
We begin by showing how simple gluing triples can give rise to quite exotic-looking schemes.
Example 3.1 (Two formal disks glued to the affine line)
Consider the gluing triple
$$ \begin{align*}(\mathbb{A}^1_{\mathbb{Q}_p},\widehat{\mathbb{A}}^1_{\mathbb{Z}_p}\sqcup \widehat{\mathbb{A}}^1_{\mathbb{Z}_p},j), \end{align*} $$
where j is the natural embedding
In this case one may show that
$\mathcal {g}(\mathbb {A}^1_{\mathbb {Q}_p},\widehat {\mathbb {A}}^1_{\mathbb {Z}_p}\sqcup \widehat {\mathbb {A}}^1_{\mathbb {Z}_p},j)\simeq \operatorname {\mathrm {Spec}}(A)$
where
(we provide the details of this computation in Example 5.10). In particular, the special fibre of the resulting affine scheme
$X = \operatorname {\mathrm {Spec}}(A)$
is isomorphic to the disjoint union of two copies of
$\mathbb {A}^1_{\mathbb {F}_p}$
.
The reason this example is worth remarking on is that it is not even clear whether the ring A from (3.1.1) is a finitely generated
$\mathbb {Z}_p$
-algebra. That said, one may check by hand that it is generated by the elements
$$\begin{align*}\alpha = x(1-px)^2, \qquad \beta = px^2(1-px), \qquad \gamma = px \end{align*}$$
subject to the relations
$$\begin{align*}p\alpha = \gamma(1-\gamma)^2, \qquad p\beta = \gamma^2(1-\gamma), \qquad \gamma\alpha = (1-\gamma)\beta. \end{align*}$$
In fact, one has that such a gluing is finite type quite generally as the following result shows. We delay its proof until §5.5 due to its length.
Proposition 3.2. Let R be a Noetherian ring and
$(\pi )\subseteq R$
an ideal. We further let
-
• A be a finitely generated
-algebra, -
• B be a topologically finitely generated
$\widehat {R}$
-algebra, -
• and
be a map of -algebras with dense image and for which the induced map
$\operatorname {\mathrm {Spa}}(C) \to \operatorname {\mathrm {Spec}}(A)^{\mathrm {an}}$
is an open immersion.
-algebra,
be a map of 
-algebras with dense image and for which the induced map 
Then the R-algebra D defined as the pullback
is finitely generated, and satisfies 
and
$\widehat {D} = B$
.
3.2 Characterization of (affine) schematic gluing triples
It is natural to ask how to recognize the ‘(affine) schematic separated gluing triples’, that is, the essential image of separated (affine) schemes under the functor
$\mathcal {t}$
. One might guess the answer is that a separated gluing triple
$(U,\mathfrak {X},j)$
is (affine) schematic if U and
$\mathfrak {X}$
are (affine) formal schemes. The following example shows this is not right: one can glue two affine objects together to obtain a non-affine object.
Example 3.3. Let
$\mathbb {A}^1_{\mathbb {Z}_p}=\operatorname {\mathrm {Spec}}(\mathbb {Z}_p[x])$
. Then, 
satisfies
$\mathcal {t}(X)=(\mathbb {A}^1_{\mathbb {Z}_p},\widehat {\mathbb {G}}_{m,\mathbb {Z}_p},j)$
where j is the natural inclusion of the unit circle
$$ \begin{align*} \widehat {\mathbb {G}}_{m,\mathbb {Z}_p}^{\mathrm {rig}}\simeq \{x\in \mathbb {A}^{1,\mathrm {an}}_{\mathbb {Q}_p}:|x|=1\} \end{align*} $$
into
$\mathbb {A}^{1,\mathrm {an}}_{\mathbb {Q}_p}$
.
More seriously, it is not even true that the result of gluing a formal scheme to a scheme along a rigid analytic open is even a scheme as the following example shows.
Example 3.4 (Matsumoto)
Matsumoto [Reference Matsumoto24, §5.2] observed that a K3 surface over a discretely valued field might have good reduction as an algebraic space but not as a scheme. More precisely, for every prime
$p\geqslant 7$
he constructed a smooth and proper algebraic space X over
$\mathbb {Z}_p$
whose fibres
$X_{\mathbb {Q}_p}$
and
$X_{\mathbb {F}_p}$
are (projective) K3 surfaces, but such that
$X_{\mathbb {Q}_p}$
does not admit a smooth proper scheme model over
$\mathbb {Z}_p$
. Moreover, this property persists even after passing to
$\mathcal {O}_K$
for a finite extension K of
$\mathbb {Q}_p$
. The generic fibre
$X_{\mathbb {Q}_p}$
is a double cover of
$\mathbb {P}^2_{\mathbb {Q}_p}$
ramified along a sextic and has geometric Picard number one. What prevents X from being projective itself is that no extension of an ample line bundle on the generic fibre is ample on the special fibre, and no ample line bundle on the special fibre lifts to a line bundle on X.
The triple
$\mathcal {t}(X) = (X_{\mathbb {Q}_p},\widehat {X},j_X)$
is separated (
$j_X$
is even an isomorphism), the algebraic space
$X_{\mathbb {Q}_p}$
is a projective scheme, and the formal algebraic space
$\widehat {X}$
is a proper formal scheme. In fact, by a simple deformation theory argument (cf. (30, Tag 09MW)) one may see that
$\widehat {X}_n$
is projective for all
$n\geqslant 0$
, though
$\widehat {X}$
itself admits no line bundle whose restriction to
$\widehat {X}_0 = X_{\mathbb {F}_p}$
is ample. Matsumoto’s observations combined with Theorem 2.26 imply that there does not exist a scheme
$X'$
over
$\mathbb {Z}_p$
with
$\mathcal {t}(X') = \mathcal {t}(X)$
.
The missing hypothesis in these examples is one involving the topology of rings: for a ring A and element
$\pi $
, the natural map 
has dense image. This explains the phenomenon witnessed in Example 3.3 as
$j^\ast \colon \mathbb {Q}_p[x]\to \mathbb {Q}_p\langle x^{\pm 1 }\rangle $
does not have dense image.
Definition 3.5. Suppose
$(S,S_0)=(\operatorname {\mathrm {Spec}}(R),V(\pi ))$
where R is a Noetherian ring. A gluing triple
$(U,\mathfrak {X},j)$
over
$(S, S_0)$
is affine if the following conditions are satisfied:
-
(a)
$U = \operatorname {\mathrm {Spec}}(A)$
is affine, -
(b)
$\mathfrak {X} = \operatorname {\mathrm {Spf}}(\widehat {B})$
is affine, -
(c)
is an open immersion, -
(d) and
has (
$\pi $
-adically) dense image.
is an open immersion,
has (
Proposition 3.6. Suppose
$(S,S_0)=(\operatorname {\mathrm {Spec}}(R),V(\pi ))$
and R is Noetherian. The functor
$\mathcal {t}$
induces an equivalence between the category of finite type affine schemes over
$\operatorname {\mathrm {Spec}}(R)$
and that of affine gluing triples over
$(S,S_0)$
.
Proof. The full faithfulness of
$\mathcal {t}$
follows Theorem 2.26 (or more precisely Corollary 5.4 below), and the essential surjectivity follows from Proposition 3.2.
Definition 3.7. A gluing triple
$(U,\mathfrak {X},j)$
is schematic if it admits an open cover by affine gluing triples
$(U_i, \mathfrak {X}_i, j_i)$
.
Corollary 3.8. Let
$(S,S_0)$
be as in Proposition 3.6. Then
$\mathcal {t}$
induces an equivalence between the category of schemes locally of finite type over S and that of schematic gluing triples over
$(S,S_0)$
.
Remark 3.9. A characterization similar to that in Proposition 3.6 appears in [Reference Bosch and Lütkebohmert8, Remark 1.6] in the case of type (V) and with the restriction that the triples have reduced special fibre. This latter condition is quite restrictive and considerably simplifies the proof of the important Proposition 3.2 as, with notation in that proposition, D is then the elements of A with
$\pi $
-adic absolute value bounded by
$1$
.
Finally, we observe that Theorem 2.26 (together with ((30, Proposition 03XX)) gives a more practical criterion for proving that a separated gluing triple is schematic.
Proposition 3.10. If S is a G-space a separated gluing triple
$(U,\mathfrak {X},j)$
over
$(S,S_0)$
is schematic if it admits a separated and locally quasi-finite map to a separated schematic gluing triple.
3.3 Good reduction of algebraic spaces over K vs.
$\widehat {K}$
Examples similar to Example 3.4 arise naturally in simple questions regarding good reduction of a smooth proper
$\mathbb {Q}$
-scheme X:
If
$X_{\mathbb {Q}_p}$
has good reduction (i.e., admits a smooth proper model over
$\mathbb {Z}_p$
), does X have good reduction at p (i.e., admit a smooth proper model over
$\mathbb {Z}_{(p)}$
)?
The following example shows this question has a negative answer in general.
Example 3.11 (Poonen)
In [Reference Poonen26, Warning 3.5.79] there is constructed a smooth quartic surface
$X\subseteq \mathbb {P}^3_{\mathbb {Q}}$
which does not admit a smooth proper model over
$\mathbb {Z}_{(p)}$
, but such that
$X_{\mathbb {Q}_p}$
does admit a smooth proper model 
over
$\mathbb {Z}_p$
. In particular, 
is another (see Example 3.4) non-representable algebraic space with representable components.
As is implicit in Example 3.11 (see also [Reference Poonen26, Remark 3.5.80]), Theorem 2.26, or the earlier results of [Reference Artin2], shows that the answer to the above-posed question is no, but only because we insisted on having a model which is a scheme. More generally, Theorem 2.26 implies the following result (which is not directly deducible from [Reference Artin2] although can be deduced from (30, Tag 04UC)).
Proposition 3.12. Let K be a discrete valuation field with excellent valuation ring
$\mathcal {O}$
. Let
-
• X be an algebraic space separated and locally of finite type over K,
-
• and
be a separated and locally of finite type algebraic space model of
$X_{\widehat {K}}$
over
$\widehat {\mathcal {O}}$
.
be a separated and locally of finite type algebraic space model of 
Then, there exists a unique separated and locally of finite type algebraic space model 
over
$\mathcal {O}$
of X whose base change to
$\widehat {\mathcal {O}}$
is isomorphic to 
.
3.4 Néron models and triples
It was already observed in [Reference Bosch and Lütkebohmert8] that a theory like that of gluing triples is useful to understand Néron models of abelian varieties. This usefulness can also be seen to hold if one replaces abelian varieties by tori, as the following example illustrates.
Example 3.13. Let K be a discrete valuation field with valuation ring
$\mathcal {O}$
and uniformizer
$\pi $
. Set
$$ \begin{align*} U_K= \mathbb{G}_{m,K},\qquad \mathfrak{X}_{\mathcal{O}}= \bigsqcup_{n\in\mathbb{Z}}\widehat{\mathbb{G}}_{m,\widehat{\mathcal{O}}}\simeq \widehat{\mathbb{G}}_{m,\widehat{\mathcal{O}}}\times \underline{\mathbb{Z}}. \end{align*} $$
For an element
$\omega $
of
$\mathcal {O}$
, define the open embedding
$j_\omega \colon \mathfrak {X}_{\mathcal {O}}^{\mathrm {rig}}\hookrightarrow U_K^{\mathrm {an}}$
on the
$n^{\text {th}}$
component via
It is clear that
$(U_K,\mathfrak {X}_{\mathcal {O}},j_\omega )$
defines a group object in the category of separated gluing triples over
$(\operatorname {\mathrm {Spec}}(\mathcal {O}),V(\pi ))$
. Moreover, taking
$\omega $
to be
$\pi $
, its gluing gives the Néron model of
$\mathbb {G}_{m,K}$
over
$\mathcal {O}$
. Indeed, by design this gluing results in a model satisfying the Néron mapping property (e.g., as can easily be checked using [Reference Bosch, Lütkebohmert and Raynaud10, §10.1, Proposition 2]).
Example 3.13 nicely illustrates why Néron models do not commute with ramified base change. Namely, if
$\mathcal {O}\subseteq \mathcal {O}'$
is an extension then it is clear that the base change of the triple
$(U_K,\mathfrak {X}_{\mathcal {O}},j_\pi )$
along the map
$(\operatorname {\mathrm {Spec}}(\mathcal {O}'),V(\pi ))\to (\operatorname {\mathrm {Spec}}(\mathcal {O}),V(\pi ))$
is
$(U_{K'},\mathfrak {X}_{\mathcal {O}'},j_\pi )$
. But, the Néron model for
$\mathbb {G}_{m,K'}$
over
$\mathcal {O}'$
is
$(U_{K'},\mathfrak {X}_{\mathcal {O}'},j_{\pi '})$
where
$\pi '$
is a uniformizer of
$\mathcal {O}'$
. It is easy to check that
$$ \begin{align*} (U_{K'},\mathfrak{X}_{\mathcal{O}'},j_\pi)\simeq (U_{K'},\mathfrak{X}_{\mathcal{O}'},j_{\pi'})\,\,\Longleftrightarrow\,\, |\pi|=|\pi'|\,\,\Longleftrightarrow \,\,\mathcal{O}\subseteq\mathcal{O}'\text{ is unramified}, \end{align*} $$
as predicted by the behaviour of Néron models under base change.
We find it an interesting question whether one can extend Example 3.13 to arbitrary tori.
Question 3.14. Can one extend Example 3.13 to construct Néron models of all tori, and their finite-type and connected analogues as studied in Bruhat–Tits theory (see [Reference Kaletha and Prasad20, Appendix B])?
Remark 3.15. We lastly remark that Theorem 2.26 also conceptually simplifies the construction in [Reference Bosch and Lütkebohmert8]. In our terminology and with notation as in Example 3.13, in [Reference Bosch and Lütkebohmert8] they construct for an abelian variety A over K a gluing triple
$(A,\mathfrak {A},j)$
so that if 
for some group
$\mathcal {O}$
-scheme 
, then 
is the Néron model of A. Without Theorem 2.26, the construction of 
is quite involved. But, using Theorem 2.26,
$\mathcal {g}(A,\mathfrak {A},j)$
is a separated group algebraic
$\mathcal {O}$
-space which is automatically representable by [Reference Raynaud27, Theorem 3.3.1].
3.5 Algebraizability of a formal scheme is detected by its rigid locus
Finally, we point out that using Theorem 2.26 one can show that algebraizability of a formal scheme is detected by its rigid locus if one expands the notion of algebraizability to include algebraic spaces. The following example illustrates this idea.
Example 3.16 (Tate uniformization)
Let K be a non-archimedean field with residue field k. Let E an elliptic curve over K with split multiplicative reduction and let 
be its minimal Weierstrass model over
$\mathcal {O}$
(e.g., [Reference Silverman29, §VII.1]). If k is the residue field of K, then 
which admits a
$\mathbb {Z}$
-covering space 
by an infinite chain of copies of
$\mathbb {P}^1_k$
glued pole-to-pole. Let
$\mathfrak {X}\to \mathfrak {E}$
be the unique étale deformation of f. One has an isomorphism 
, and hence by Theorem 2.26 there exists an algebraic space 
locally of finite type over
$\mathcal {O}_K$
with generic fibre
$\mathbb {G}_{m,K}$
and formal completion
$\mathfrak {X}$
. Using Corollary 3.8 it is not hard to see that 
is in fact a scheme. Such a scheme has been explicitly described in [Reference Deligne and Rapoport14, §VII.1].
To explain the general application of Theorem 2.26, we first give some notation. Fix a separated locally of finite type formal algebraic space
$\mathfrak {X}$
over
$\widehat {S}$
. Set
-
•
to be the category of algebraizations of
$\mathfrak {X}$
, that is, pairs
$(X,\iota )$
where X is an algebraic space separated and locally of finite type over S and an isomorphism, -
•
to be the category of pairs
$(U,j)$
where U is an algebraic space separated and locally of finite type over
$S^\circ $
and
$j\colon \mathfrak {X}^{\mathrm {rig}}\to U^{\mathrm {an}}$
an open embedding.
to be the category of algebraizations of 
an isomorphism,
to be the category of pairs 
The following proposition is an immediate corollary of, and largely equivalent to, Theorem 2.26.
Proposition 3.17. Suppose S is a G-space. Then, if
$j_X$
is as in Proposition 2.17, the functor
is an equivalence with quasi-inverse given by sending
$(U,j)$
to
$\mathcal {g}(U,\mathfrak {X},j)$
.
Let us say that a separated rigid algebraic space
$\mathsf {X}$
over
$\widehat {S}^{\mathrm {rig}}$
is weakly algebraizable if there exists an algebraic space U separated and locally of finite type over
$S^\circ $
and an open embedding
$\mathsf {X}\hookrightarrow U^{\mathrm {an}}$
. This is a better-behaved notion than that of literal algebraizability, as
$\mathsf {X}$
can never be algebraizable if it is quasi-compact and not proper over
$\widehat {S}^{\mathrm {rig}}$
.
Corollary 3.18. Suppose that S is a G-space and
$\mathfrak {X}$
is a formal algebraic space separated and locally of finite type over
$\widehat {S}$
. Then,
$\mathfrak {X}$
is algebraizable if and only if
$\mathfrak {X}^{\mathrm {rig}}$
is weakly algebraizable.
3.6 Gluing torsors
Theorem 2.26 implies that one can always glue an H-torsor over
$\mathcal {t}(X)$
to one over X, in a way which we now make precise. Throughout this subsection let us fix H to be a separated, flat, and locally of finite type group algebraic space over S.
Let X be an algebraic space over S and
$\mathfrak {X}$
a formal algebraic space over
$\widehat {S}$
. Recall that:
-
• an H-torsor on X is a locally non-empty sheaf Q on the fppf site of X together with a simply transitive action
$H\times Q\to Q$
, -
• an
$\widehat {H}$
-torsor on
$\mathfrak {X}$
is a locally non-empty sheaf
$\mathfrak {Q}$
on the adic flat site of
$\mathfrak {X}$
together with a simply transitive action
$\widehat {H}\times \mathfrak {Q}\to \mathfrak {Q}$
.
Recall here that a sheaf
$\mathcal {F}$
on a site
$\mathscr {S}$
is locally non-empty if for every object T of
$\mathscr {S}$
there exists a cover
$\{T_i\to T\}$
such that
$\mathcal {F}(T_i)$
is non-empty for all i. If there is a group sheaf
$\mathcal {H}$
on
$\mathscr {S}$
, then an action
$\mathcal {H}\times \mathcal {F}\to \mathcal {F}$
is simply transitive if the induced map
$$ \begin{align*} \mathcal{H}\times\mathcal{F}\to\mathcal{F}\times\mathcal{F},\qquad (h,f)\mapsto (hf,f), \end{align*} $$
is an isomorphism. Finally, we recall that the adic flat site on
$\mathfrak {X}$
consists of all formal schemes over
$\mathfrak {X}$
endowed with the topology generated by Zariski open covers and adically faithfully flat maps
$\mathfrak {Y}'\to \mathfrak {Y}$
of affine formal schemes (see [Reference Fujiwara and Kato15, Chapter I, §4.8. (c)]).
We denote these categories of torsors by
$\mathbf {Tors}_H(X)$
and
$\mathbf {Tors}_{\widehat {H}}(\mathfrak {X})$
, respectively. Applying (30, Lemma 04SK) to the pullback to each scheme
$S_n$
and passing to the colimit, any object of
$\mathbf {Tors}_H(X)$
and
$\mathbf {Tors}_{\widehat {H}}(\mathfrak {X})$
is represented by a (formal) algebraic space separated and locally of finite type over X and
$\mathfrak {X}$
, respectively. Thus, we treat torsors implicitly as such algebraic spaces in the sequel.
Definition 3.19. Let
$(U,\mathfrak {X},j)$
be a gluing triple over S. We then define the category
$\mathbf {Tors}_{H}(U,\mathfrak {X},j)$
of
${H}$
-torsors over
$(U,\mathfrak {X},j)$
to consist of triples
$(\mathcal {Q},\mathfrak {Q},\iota )$
where
-
•
$\mathcal {Q}$
is an object of
$\mathbf {Tors}_{H}(U)$
, -
•
$\mathfrak {{Q}}$
is an object of
$\mathbf {Tors}_{\widehat {H}}(\mathfrak {X})$
, -
•
$\iota $
is an open embedding of analytic adic algebraic spaces
$\mathfrak {Q}^{\mathrm {rig}}\to \mathcal {Q}^{\mathrm {an}}\times _{U^{\mathrm {an}}}\mathfrak {X}^{\mathrm {rig}}$
equivariant for the map of group rigid algebraic spaces
${\widehat {H}}^{\mathrm {rig}}\to ({H}^\circ )^{\mathrm {an}}$
over
$\mathfrak {X}^{\mathrm {rig}}$
.
Here a morphism
$(\mathcal {Q},\mathfrak {Q},\iota )\to (\mathcal {Q}',\mathfrak {Q}',\iota ')$
consists of an H-equivariant morphism
$\alpha \colon \mathcal {Q}\to \mathcal {Q}'$
and an
$\widehat {H}$
-equivariant morphism
$\beta \colon \mathfrak {Q}\to \mathfrak {Q}'$
such that
$\alpha ^{\mathrm {an}}\circ \iota =\iota '\circ \beta ^{\mathrm {rig}}$
.
Suppose now that X is an algebraic space separated and locally of finite type over S. Then, there is a functor
$$ \begin{align*} \tau\colon \mathbf{Tors}_{H}(X)\to \mathbf{Tors}_{H}(\mathcal{t}(X)),\quad Q\mapsto \tau(Q)=(Q^\circ,\widehat{Q},\iota_Q), \end{align*} $$
which is well-defined as the natural open embedding
$\iota _Q\colon \widehat {Q}^{\mathrm {rig}}\to (Q^\circ )^{\mathrm {an}}\times _{(X^\circ )^{\mathrm {an}}}\widehat {X}^{\mathrm {rig}}$
is evidently equivariant for the map of group rigid-algebraic spaces
$\widehat {H}^{\mathrm {rig}}\to (H^\circ )^{\mathrm {an}}$
.
The following is an immediate consequence of Theorem 2.26.
Proposition 3.20. Suppose that S is a G-space and let X be an algebraic space separated and locally of finite type over S. Then,
$$ \begin{align*} \tau\colon \mathbf{Tors}_{H}(X)\to \mathbf{Tors}_{H}(\mathcal{t}(X)),\quad Q\mapsto \tau(Q)=(Q^\circ,\widehat{Q},\iota_Q). \end{align*} $$
is an equivalence of categories.
3.7 Gluing finite étale covers and an integral Riemann existence theorem
Finally, we use gluing triples to give a finer understanding of the finite étale covers of an algebraic space.
Definition 3.21. Let
$(U,\mathfrak {X},j)$
be a separated gluing triple over
$(S,S_0)$
. Then, we define the category
$\mathbf {F\acute {E}t}(U,\mathfrak {X},j)$
of finite étale covers of
$(U,\mathfrak {X},j)$
to be the category of finite étale morphisms
$(U_1,\mathfrak {X}_1,j_1)\to (U,\mathfrak {X},j)$
, with morphisms being morphisms of gluing triples over
$(U,\mathfrak {X},j)$
.
The following is an immediate corollary of Theorem 2.26 together with Proposition 2.27.
Proposition 3.22. Suppose that S is a G-space and let X be an algebraic space separated and locally of finite type over S. Then,
$$ \begin{align*} \mathcal{t}\colon \mathbf{F\acute{E}t}(X)\to \mathbf{F\acute{E}t}(\mathcal{t}(X)), \end{align*} $$
is an equivalence of categories.
Proposition 3.22 implies an integral analogue of the Riemann existence theorem in rigid geometry (see [Reference Lütkebohmert23]). Throughout the rest of this section, we fix the following data:
-
• K a complete discretely valued field of characteristic
$p\geqslant 0$
, -
•
$\mathcal {O}$
is the valuation ring of K, -
• k is the residue field of K,
-
•
$\pi $
a uniformizer of K, -
• X is a scheme separated and locally of finite type over
$\mathcal {O}$
.
We associate to X an adic space over
$\operatorname {\mathrm {Spa}}(\mathcal {O})$
built from the associated triple
$\mathcal {t}(X)$
in a natural way, and which differs in the special fibre from the normal ‘analytification’ of X
$$ \begin{align*} X^{\mathrm{ad}}= X\times_{\operatorname{\mathrm{Spec}}(\mathcal{O})}\operatorname{\mathrm{Spa}}(\mathcal{O}), \end{align*} $$
as in [Reference Huber16, Proposition 3.8].
Definition 3.23. We define the adic space
$X^{\backslash \mathrm {ad}}$
over
$\operatorname {\mathrm {Spa}}(\mathcal {O})$
by the following construction:
$$ \begin{align*} X^{\backslash\mathrm{ad}}= (X^\circ)^{\mathrm{an}}\sqcup_{j_X,\widehat{X}^{\mathrm{rig}},\text{incl.}}\widehat{X}^{\mathrm{ad}}, \end{align*} $$
which is well-defined as
$j_X$
and the natural inclusion
$\widehat {X}^{\mathrm {rig}}\to \widehat {X}^{\mathrm {ad}}$
are open embeddings.
Remark 3.24. Such spaces are closely related to recent work in the theory of Shimura varieties, for example, see [Reference Pappas and Rapoport25] as well as [Reference Imai, Kato and Youcis19] and [Reference Imai, Kato and Youcis18]. Indeed, if one considers the v-sheaf
$(X^{\backslash \mathrm {ad}})^\lozenge $
associated to
$X^{\backslash \mathrm {ad}}$
as in [Reference Scholze and Weinstein28, §18.1] this agrees with the v-sheaf
$X^{\lozenge /}$
from [Reference Pappas and Rapoport25, Definition 2.1.9].
Example 3.25. If
$X=\mathbb {A}^1_{\mathcal {O}}$
, then the pullback of
$X^{\backslash \mathrm {ad}}$
and
$X^{\mathrm {ad}}$
to
$\operatorname {\mathrm {Spa}}(k)$
is
$\operatorname {\mathrm {Spa}}(k[x],k[x])$
and
$\operatorname {\mathrm {Spa}}(k[x],k)$
, respectively.
Let C be an algebraically closed non-archimedean extension of K, and let
$x\colon \operatorname {\mathrm {Spec}}(\mathcal {O}_C)\to X$
be a morphism over
$\mathcal {O}_K$
. As
$\mathcal {O}_C$
has no finite étale covers, we have natural fibre functors
$$ \begin{align*} F_x\colon \mathbf{F\acute{E}t}(X)\to \mathbf{Set},\qquad F_{x^{\backslash\mathrm{ad}}}\colon \mathbf{F\acute{E}t}(X^{\backslash\mathrm{ad}})\to\mathbf{Set}. \end{align*} $$
These give rise to the fundamental groups
$$ \begin{align*} \pi_1^{\mathrm{\acute{e}t}}(X,x)=\mathrm{Aut}(F_x),\qquad \pi_1^{\mathrm{\acute{e}t}}(X^{\backslash\mathrm{ad}},x^{\backslash\mathrm{ad}})=\mathrm{Aut}(F_{x^{\backslash\mathrm{ad}}}), \end{align*} $$
respectively. The notation
$(-)^{\prime p}$
means we restrict to the subcategory of finite étale covers with prime-to-p order or the associated quotients of their fundamental groups.
Proposition 3.26. The morphism
$(-)^{\backslash \mathrm {ad}}\colon \mathbf {F\acute {E}t}(X)^{\prime p}\to \mathbf {F\acute {E}t}(X^{\backslash \mathrm {ad}})^{\prime p}$
is an equivalence. Thus, the induced morphism
$$ \begin{align*} \pi_1(X,x)^{\prime p}\to \pi_1^{\mathrm{\acute{e}t}}(X^{\backslash\mathrm{ad}},x^{\backslash\mathrm{ad}})^{\prime p} \end{align*} $$
is an isomorphism.
Proof. We claim that there is a commutative diagram
with the marked arrows being equivalences of categories. This implies the desired claim. The curved arrow is just the equivalence from Proposition 3.22, and so it suffices to explain the horizontal and vertical marked arrows.
Here
$\mathbf {F\acute {E}t}(X_K^{\mathrm {an}},\widehat {X}^{\mathrm {ad}},j_X)^{\prime p}$
means the category of triples
$(\mathsf {X},\mathsf {Y},j)$
consisting of
-
• a prime-to-p finite étale cover
$\mathsf {X}\to X_K^{\mathrm {an}}$
, -
• a prime-to-p finite étale cover
$\mathsf {Y}\to \widehat {X}^{\mathrm {ad}}$
, -
• and j an isomorphism of their pullbacks to
$\widehat {X}^{\mathrm {rig}}$
.
The horizontal marked arrow is then the obvious equivalence obtained from the fact that
$X^{\backslash \mathrm {ad}}$
is the gluing of
$X_K^{\mathrm {an}}$
and
$\widehat {X}^{\mathrm {ad}}$
along the open subset
$\widehat {X}^{\mathrm {rig}}$
.
The vertical map associates to
$(U_1,\mathfrak {X}_1,j_1)$
the triple
$(U_1^{\mathrm {an}},\mathfrak {X}_1^{\mathrm {ad}},j_1)$
. That this is an equivalence follows from applying [Reference Lütkebohmert23, Theorem 4.1] and the fact that the functor
$$ \begin{align*} (-)^{\mathrm{ad}}\colon \mathbf{F\acute{E}t}(\widehat{X})\to \mathbf{F\acute{E}t}(\widehat{X}^{\mathrm{ad}}) \end{align*} $$
is an equivalence. For this latter claim we may reduce to the case when
$X=\operatorname {\mathrm {Spf}}(A)$
. But,
$$ \begin{align*} \mathbf{F\acute{E}t}(\operatorname{\mathrm{Spf}}(A))\simeq \mathbf{F\acute{E}t}(\operatorname{\mathrm{Spec}}(A))\simeq \mathbf{F\acute{E}t}(\operatorname{\mathrm{Spa}}(A)), \end{align*} $$
explicitly sending
$\operatorname {\mathrm {Spec}}(B)\to \operatorname {\mathrm {Spec}}(A)$
to
$\operatorname {\mathrm {Spf}}(B)\to \operatorname {\mathrm {Spf}}(A)$
and
$\operatorname {\mathrm {Spa}}(B)\to \operatorname {\mathrm {Spa}}(A)$
(B receiving the
$\pi $
-adic topology), respectively. The latter being an equivalence follows as in [Reference Huber17, Example 1.6.6 ii)], and the former by combining [Reference Fujiwara and Kato15, Chapter I, Proposition 4.2.1] and [Reference Achinger, Lara and Youcis1, Lemma A.13].
Finally, as a corollary of the above discussion we see that one can detect the algebraizability of a finite étale cover on the generic fibre, similar to Proposition 3.17. Namely, fix a finite étale cover
$\mathfrak {Y}\to \widehat {X}$
. Set
-
•
to be the category of algebraizations of
$\mathfrak {Y}$
, that is, pairs
$(Y,\iota )$
where Y is an algebraic space finite and étale over X and an isomorphism over
$\widehat {X}$
, -
•
to be the category of pairs
$(U,j)$
where U is a finite étale cover of
$X_K$
and j is an isomorphism of
$\mathfrak {Y}^{\mathrm {rig}}$
onto
$U^{\mathrm {an}}|_{\mathfrak {X}^{\mathrm {rig}}}\subseteq U^{\mathrm {an}}$
over
$\mathfrak {X}^{\mathrm {rig}}$
.
to be the category of algebraizations of 
an isomorphism over 
to be the category of pairs 
The following proposition is an immediate corollary of Proposition 3.22.
Proposition 3.27. Suppose that S is a G-space and let X be an algebraic space separated and locally of finite type over S. Then, the functor
is an equivalence with quasi-inverse given by sending
$(U,j)$
to
$\mathcal {g}(U,\mathfrak {Y},j)$
.
Corollary 3.28. A prime-to-p finite étale cover
$\mathfrak {Y}\to \widehat {X}$
is algebraizable if and only if the finite étale cover
$\mathfrak {Y}^{\mathrm {rig}}\to \widehat {X}^{\mathrm {rig}}$
extends to a finite étale cover of
$X_K^{\mathrm {an}}$
.
Remark 3.29. Part of Grothendieck’s construction of a specialization morphism for the étale fundamental group is the following result. If X is a proper scheme over
$\mathcal {O}$
then every finite étale cover
$Y_k\to X_k$
deforms uniquely to a finite étale cover
$Y\to X$
. It is instructive to think about this result in two steps:
-
Step 1: a finite étale cover
$Y_k\to X_k$
deforms uniquely to a finite étale cover
$\mathfrak {Y}\to \widehat {X}$
, -
Step 2: a finite étale cover
$\mathfrak {Y}\to \widehat {X}$
is uniquely algebraizable to a finite étale cover
$Y\to X$
.
It is Step 2 that requires X to be proper over
$\mathcal {O}$
as it utilizes Grothendieck’s existence theorem, and Step 1 is true for any X. As
$\widehat {X}^{\mathrm {rig}}=(X^\circ )^{\mathrm {an}}$
when X is proper over
$\mathcal {O}$
, one may view Proposition 3.27 and Corollary 3.28 as precisely qualifying the failure for Step 2 to hold in the non-proper case, where generally
$\widehat {X}^{\mathrm {rig}}\subsetneq (X^\circ )^{\mathrm {an}}$
, and providing the precise extra information required to mend it.
4 Coherent sheaves and gluing triples
In this section we show an equivalence of categories between coherent sheaves on an algebraic space X and on its associated triple
$\mathcal {t}(X)$
, which is important in our proof of Theorem 2.26.
4.1 Gluing for modules over an affine triple
We first recall the gluing of results of Artin (see [Reference Artin2, Theorem 2.6]) in the Noetherian case and Beauville–Laszlo (see [Reference Beauville and Laszlo3]) in the principal case, which can be uniformly extended to the type (V) situation thanks to the methods in (30, Lemma 0BNI). This accounts roughly for our desired gluing of coherent sheaves in the affine case.
Throughout we fix an affine scheme
$X=\operatorname {\mathrm {Spec}}(A)$
of finite type over S, with
$(S,S_0)$
and 
fixed as in §2.2, and set
the first an ideal of definition of A and the latter two schemes over
$S^\circ $
.
The following lemma summarizes the ring-theoretic properties of A.
Lemma 4.1. If
$(S,S_0)$
is of type (N)/(V), then the following properties hold.
-
(1) The pair
$(A,I)$
is universally pseudo-adhesive, and the ring A is coherent,Footnote 4 -
(2) the map
$X^\circ \sqcup \operatorname {\mathrm {Spec}}(\widehat {A})\to X$
is faithfully flat, -
(3) for any finite A-module M the natural map
$M\otimes _A \widehat {A}\to \widehat {M}$
is an isomorphism, -
(4) for any finite A-module M, the natural map
$M[I^\infty ]\to \widehat {M}[I^\infty ]$
is a bijection.
Proof. For the pseudo-adhesiveness claim in (1) see [Reference Fujiwara and Kato15, Chapter 0, Example 8.5.13] for type (N), and [Reference Zavyalov33, Theorem 2.16] and/or [Reference Fujiwara and Kato15, Chapter 0, Theorem 9.2.1] for type (V), respectively. The coherence claim in (1) is clear in type (N), and follows from [Reference Fujiwara and Kato15, Chapter 0, Corollary 9.2.9] in case of type (V). Given (1), the claim in (3) follows from [Reference Fujiwara and Kato15, Chapter 0, Proposition 8.2.18], and in fact this reference also implies (2). Indeed, evidently
$X^\circ \sqcup \operatorname {\mathrm {Spec}}(\widehat {A})\to X$
is surjective and and
$X^\circ \to X$
is flat, so it suffices to explain why
$A\to \widehat {A}$
is flat, but this follows from loc. cit.
Finally, we prove (4). Observe that we have a short exact sequence
$$ \begin{align*} 0\to M[I^\infty]\to M\to Q\to 0, \end{align*} $$
where Q is a finitely generated and I-torsion free A-module. By work of Raynaud–Gruson (see [Reference Bosch6, §7.3, Theorem 4]) Q is then finitely presented, and so
$M[I^\infty ]$
is actually finitely generated (see (30, Lemma 0519)). As
$A\to \widehat {A}$
is flat and
$M\otimes _A \widehat {A}\simeq \widehat {M}$
, we obtain an exact sequence
$$ \begin{align*} 0\to M[I^\infty]\otimes_A\widehat{A}\to \widehat{M}\to Q\otimes_A\widehat{A}\to 0. \end{align*} $$
As
$M[I^\infty ]$
and Q are finitely generated A-modules, we have isomorphisms
$$ \begin{align} M[I^\infty]\otimes_A\widehat{A}\simeq {A[I^\infty]}^\wedge,\quad Q\otimes_A\widehat{A}\simeq \widehat{Q}, \end{align} $$
where all completions are I-adic. But
$M[I^\infty ]$
is bounded I-torsion and so
$M[I^\infty ]^\wedge =M[I^\infty ]$
. So, all in all, we have the exact sequence
$$ \begin{align*} 0\to M[I^\infty]\to \widehat{M}\to \widehat{Q}\to 0. \end{align*} $$
So, it suffices to observe that
$\widehat {Q}$
is I-torsion free. By (4.1.1) this follows as
$A\to \widehat {A}$
is flat.
In this affine setting, the category
$\mathbf {Coh}(\operatorname {\mathrm {Spec}}(A))$
of coherent sheaves on
$\operatorname {\mathrm {Spec}}(A)$
is replaced by the category
$\mathbf {Mod}^{\mathrm {fp}}(A)$
of finitely-presented A-modules. The analogue for the gluing triple
$\mathcal {t}(A)$
is given by the following.
Definition 4.2. Denote by
$\mathbf {Mod}^{\mathrm {fp}}(\mathcal {t}(A))$
the category of triples
$(\mathcal {F},N,\iota )$
where
-
(1)
$\mathcal {F}$
is a coherent sheaf on
$X^\circ $
, -
(2) N is a finitely presented
$\widehat {A}$
-module, -
(3)
is an isomorphism of coherent sheaves on
$\widehat {X}^\circ $
,
is an isomorphism of coherent sheaves on 
with a morphism
$(\mathcal {F}_1,N_1,\iota _1)\to (\mathcal {F},N,\iota )$
a pair
$\alpha \colon \mathcal {F}_1\to \mathcal {F}$
and
$\beta \colon N_1\to N$
of morphisms such that
$\iota \circ \alpha |_{\widehat {X}^\circ }=\widetilde {\beta }|_{\widehat {X}^\circ }\circ \iota _1$
.
We will often abuse notation concerning a triple
$(\mathcal {F},N,\iota )$
and let
$\widehat {\mathcal {F}}$
denote the common (via the identification
$\iota $
) coherent sheaf on
$\widehat {X}^\circ $
.
Proposition 4.3. The functor
$$ \begin{align*} \mathcal{t}\colon \mathbf{Mod}^{\mathrm{fp}}(A)\to \mathbf{Mod}^{\mathrm{fp}}(\mathcal{t}(A)),\qquad M\mapsto (\widetilde{M}|_{X^\circ},\widehat{M},\mathrm{can.}), \end{align*} $$
is an equivalence of A-linear abelian
$\otimes $
-categories, with quasi-inverse given by the gluing functor
$$ \begin{align*} \mathcal{g}\colon \mathbf{Mod}^{\mathrm{fp}}(\mathcal{t}(A))\to \mathbf{Mod}^{\mathrm{fp}}(A),\quad (\mathcal{F},N,\iota)\mapsto \mathcal{F}(X^\circ)\times_{\widehat{\mathcal{F}}(\widehat{X}^\circ)}N. \end{align*} $$
Proof. In type (N), this has been established by Artin in [Reference Artin2, Theorem 2.6]. In order to cover type (V) as well, we aim to employ the enhanced version of the Beauville–Laszlo theorem in (30, Theorem 0BP2). Type (N) already covered, we may assume that the ideal of definition I is principal, generated by an element
$\pi $
. Assertions (3) and (4) of Lemma 4.1 imply that every finitely generated A-module is glueable (as defined in (30, Section 0BNI)). It remains to show that an A-module M is finitely presented if both
$\widehat {M}$
and 
are. Since the map 
is faithfully flat by Lemma 4.1, we conclude by (30, Lemma 05B0).
Utilizing the equivalence of coherent modules on
$\widehat {X}^{\mathrm {rig}}$
and
$\widehat {X}^\circ $
as in [Reference Fujiwara and Kato15, Chapter II, Proposition 6.6.5], the following is an immediate corollary of Proposition 4.3.
Corollary 4.4. The natural map
$$ \begin{align} \mathcal{O}(X)\to \mathcal{O}(X^\circ)\times_{\mathcal{O}(\widehat{X}^{\mathrm{rig}})}\mathcal{O}(\widehat{X}), \end{align} $$
is an isomorphism of rings.
4.2 Coherent sheaves and triples
We now patch together the affine-local results of §4.1. This gives a globalization of the previously mentioned results of Artin and Beauville–Laszlo, which can only happen involving analytic geometry, and generalizes similar ideas in [Reference Ben-Bassat and Temkin4].
To set notation, we first recall the definition of coherent sheaves on algebraic spaces. In the following,
$(-)_{\mathrm {\acute {E}t}}$
and
$(-)_{\mathrm {top}}$
denotes the big sites with étale and topological open covers, respectively, and
$\mathcal {O}_{\mathscr {X}}$
is as in (2.1.2).
Definition 4.5. Let
$\mathscr {X}$
be a (formal) algebraic space or analytic adic algebraic space of type (N)/(V). The category
$\mathbf {Coh}(\mathscr {X})$
of coherent sheaves on
$\mathscr {X}$
is the full subcategory of
$\mathbf {Mod}(\mathscr {X}_{\mathrm {\acute {E}t}},\mathcal {O}_{\mathscr {X}})$
consisting of finitely presented
$\mathcal {O}_{\mathscr {X}}$
-modules (in the sense of (30, Definition 01BN)).
Defining
$\mathbf {Coh}^{\mathrm {top}}(\mathscr {X})$
using
$(-)_{\mathrm {top}}$
instead of
$(-)_{\mathrm {\acute {E}t}}$
, we have the following descent result
Proposition 4.6. Let
$\mathscr {U}\to \mathscr {X}$
be an étale surjection with
$\mathscr {U}$
representable. Then, the functor
$$ \begin{align*} \mathbf{Coh}(\mathscr{X})\to 2\text{-}\mathrm{Eq}\bigg(\mathbf{Coh}^{\mathrm{top}}(\mathscr{U})\mathrel{\substack{\textstyle\rightarrow\\[-0.6ex] \textstyle\rightarrow}} \mathbf{Coh}^{\mathrm{top}}(\mathscr{U}\times_{\mathscr{X}}\mathscr{U})\mathrel{\substack{\textstyle\rightarrow\\[-0.6ex] \textstyle\rightarrow \\[-0.6ex] \textstyle\rightarrow}} \mathbf{Coh}^{\mathrm{top}}(\mathscr{U}\times_{\mathscr{X}}\mathscr{U}\times_{\mathscr{X}}\mathscr{U})\bigg), \end{align*} $$
is a natural equivalence. Moreover, the global sections functors
$$ \begin{align*} \mathbf{Coh}(\operatorname{\mathrm{Spf}}(A))\to\mathbf{Mod}^{\mathrm{fp}}(A), \qquad \mathbf{Coh}(\operatorname{\mathrm{Spa}}(A,A^+))\to\mathbf{Mod}^{\mathrm{fp}}(A) \end{align*} $$
are natural equivalences of A-linear
$\otimes $
-categories.
Proof. The first claim follows from [Reference Fujiwara and Kato15, Chapter I, Proposition 6.1.11] and [Reference Bosch and Görtz7, Theorem 2.1] in the case of (formal) schemes and analytic adic space of type (N)/(V), respectively. The second pair of claimed equivalences follows, given the coherence of A from Lemma 4.1, from [Reference Fujiwara and Kato15, Chapter I, Theorem 3.2.8] and [Reference Kedlaya21, Theorem 1.4.18] for (formal) schemes and analytic adic spaces of type (N)/(V), respectively.
Reducing to the affine situation and applying Proposition 4.6, one deduces the following.
Lemma 4.7. For
$\mathscr {X}$
as in Definition 4.5,
$\mathbf {Coh}(\mathscr {X})$
is an
$\mathcal {O}_{\mathscr {X}}$
-linear abelian
$\otimes $
-category.
Observe that we have the following two natural functors.
-
(1) For a formal algebraic space
$\mathfrak {X}$
locally of finite type over
$\widehat {S}$
we have a functor
$$ \begin{align*} (-)^{\mathrm{rig}}\colon \mathbf{Coh}(\mathfrak{X})\to \mathbf{Coh}(\mathfrak{X}^{\mathrm{rig}}),\quad \mathfrak{F}\mapsto \mathfrak{F}^{\mathrm{rig}}=\mathrm{sp}_{\mathfrak{X}}^\ast(\mathfrak{F})\otimes_{\mathcal{O}_{\mathfrak{X}^{\mathrm{rig}}}^+}\mathcal{O}_{\mathfrak{X}^{\mathrm{rig}}}. \end{align*} $$
-
(2) If U is an algebraic space locally of finite type over
$S^\circ $
there is a map of ringed topoi
$$ \begin{align*} (-)^{\mathrm{an}}\colon (U^{\mathrm{an}}_{\mathrm{\acute{E}t}},\mathcal{O}_{U^{\mathrm{an}}})\to (U_{\mathrm{\acute{E}t}},\mathcal{O}_{U}), \end{align*} $$
which induces a natural functor
$$ \begin{align*} (-)^{\mathrm{an}}\colon \mathbf{Coh}(U)\to\mathbf{Coh}(U^{\mathrm{an}}). \end{align*} $$
We are now prepared to define coherent sheaves on gluing triples over
$(S,S_0)$
.
Definition 4.8. Let
$(U,\mathfrak {X},j)$
be a gluing triple over
$(S,S_0)$
. Then, we define the category
$\mathbf {Coh}(U,\mathfrak {X},j)$
of coherent sheaves to sit in the following
$2$
-cartesian diagram of categories:
that is, the category of triples
$(\mathcal {F},\mathfrak {F},\iota )$
where
$\mathcal {F}$
is a coherent
$\mathcal {O}_{U}$
-module,
$\mathfrak {F}$
is a coherent
$\mathcal {O}_{\mathfrak {X}}$
-module and 
is an isomorphism of coherent
$\mathcal {O}_{\mathfrak {X}^{\mathrm {rig}}}$
-modules.
If X is an algebraic space locally of finite type over S there is a natural functor
$$ \begin{align*} \mathcal{t}\colon \mathbf{Coh}(X)\to \mathbf{Coh}(\mathcal{t}(X)),\quad F\mapsto \mathcal{t}(F)=(F^\circ,\widehat{F},\iota_F). \end{align*} $$
Here we denote by
-
(i)
$(-)^\circ $
the pullback functor along the morphism of schemes
$X^\circ \to X$
, -
(ii)
$\widehat {(-)}$
the pullback functor along the morphism of ringed topoi
$\widehat {(-)}\colon (\widehat {X}_{\mathrm {\acute {E}t}},\mathcal {O}_{\widehat {X}})\to (X_{\mathrm {\acute {E}t}},\mathcal {O}_X)$
, -
(iii) and
is obtained as both are naturally the pullback of F along the morphism of ringed topoi
$(\widehat {X}^{\mathrm {rig}}_{\mathrm {\acute {E}t}},\mathcal {O}_{\widehat {X}^{\mathrm {rig}}})\to (X_{\mathrm {\acute {E}t}},\mathcal {O}_X)$
.
is obtained as both are naturally the pullback of F along the morphism of ringed topoi 
The functor
$\mathcal {t}$
is clearly
$2$
-functorial in X.
Proposition 4.9. Let X be an algebraic space separated and locally of finite type over S. Then,
$$ \begin{align*} \mathcal{t}\colon \mathbf{Coh}(X)\to \mathbf{Coh}(\mathcal{t}(X)), \end{align*} $$
is an
$\mathcal {O}_X$
-linear
$\otimes $
-equivalence of abelian
$\otimes $
-categories.
Proof. Observe that coherent sheaves on gluing triples satisfy étale descent as quickly follows from applying Proposition 4.6 component-wise. More precisely, the following holds.
Lemma 4.10. Suppose that
$(U_0,\mathfrak {X}_0,j_0)\to (U,\mathfrak {X},j)$
is an étale surjection of gluing triples over
$(S,S_0)$
. Write
$(U_1,\mathfrak {X}_1,j_1)$
and
$(U_2,\mathfrak {X}_2,j_2)$
for the self fibre product and self triple fibre product of
$(U_0,\mathfrak {X}_0,j_0)$
over
$(U,\mathfrak {X},j)$
, respectively. Then, the natural functor
$$ \begin{align*} \mathbf{Coh}(U,\mathfrak{X},j)\to 2\text{-}\mathrm{Eq}\left(\mathbf{Coh}(U_0,\mathfrak{X}_0,j_0)\mathrel{\substack{\textstyle\rightarrow\\[-0.6ex] \textstyle\rightarrow}} \mathbf{Coh}(U_1,\mathfrak{X}_1,j_1)\mathrel{\substack{\textstyle\rightarrow\\[-0.6ex] \textstyle\rightarrow \\[-0.6ex] \textstyle\rightarrow}} \mathbf{Coh}(U_2,\mathfrak{X}_2,j_2)\right), \end{align*} $$
is an equivalence of categories.
Applying this and the first part of Proposition 4.6 to an étale cover
$\{\operatorname {\mathrm {Spec}}(A_i)\to X\}$
quickly reduces us to the case when
$X=\operatorname {\mathrm {Spec}}(A)$
. Write 
, and recall from §4.1 that
$\widehat {X}^\circ $
is defined to be 
. There is a natural morphism of ringed spaces
$(\widehat {X}^{\mathrm {rig}},\mathcal {O}_{\widehat {X}^{\mathrm {rig}}})\to (\widehat {X}^\circ ,\mathcal {O}_{\widehat {X}^\circ })$
which induces a pullback
$\mathcal {O}_X$
-linear
$\otimes $
-equivalence of abelian categories of coherent sheaves (see [Reference Fujiwara and Kato15, Chapter II, Proposition 6.6.5]). Combining this and the second part of Proposition 4.6, we see that the claim for
$X=\operatorname {\mathrm {Spec}}(A)$
is reduced precisely to Proposition 4.3, from where the claim follows.
Corollary 4.11. Let X be an algebraic space separated and locally of finite type over S. Then,
$$ \begin{align*} \mathcal{t}\colon \mathbf{Vect}(X)\to \mathbf{Vect}(\mathcal{t}(X)), \end{align*} $$
is a Quillen-exact
$\mathcal {O}_X$
-linear
$\otimes $
-equivalence of
$\otimes $
-categories with Quillen-exact quasi-inverse.
Here we are denoting by
$\mathbf {Vect}(\mathcal {t}(X))$
the full subcategory of
$\mathbf {Coh}(\mathcal {t}(X))$
consisting of objects
$(\mathcal {F},\mathfrak {F},\iota )$
with
$\mathcal {F}$
and
$\mathfrak {F}$
both vector bundles. This forms an étale stack, as being a vector bundle is local for the étale topology.
Proof of Corollary 4.11
Given Proposition 4.9, it suffices to show that a coherent
$\mathcal {O}_X$
-module F is a vector bundle if and only if
$\mathcal {t}(F)$
is. But, we may quickly reduce to the case when
$X=\operatorname {\mathrm {Spec}}(A)$
is affine. Let us write
$M=F(X)$
. Note that
$\widehat {F}$
is a vector bundle if and only if
$\widehat {F}(\widehat {X})=\widehat {M}$
is a finite projective
$\widehat {A}$
-module (e.g., see the proof of [Reference Imai, Kato and Youcis19, Proposition A.13]). As
$\widehat {M}=M\otimes _A \widehat {A}$
by Lemma 4.1, we are thus reduced to the following claim: M is a finite projective A-module if and only if
$\widetilde {M}|_{X^\circ }$
and
$M\otimes _A \widehat {A}$
is a vector bundle on
$X^\circ $
and a finite projective
$\widehat {A}$
-module, respectively. But, given Lemma 4.1 this follows from (30, Theorem 05JZ).
5 Proofs
We now turn to the proof of Theorem 2.26. For ease of reading, we have broken this proof down into steps, comprising the first three subsections. In the remaining two subsections we provide the only remaining missing proofs, that of Propositions 2.27 and 3.2.
5.1 Explicit reconstruction in the schematic case
We first observe a more down-to-earth case of Theorem 2.26. Namely, we wish to show that if X is a scheme locally of finite type over S then one may explicitly reconstruct the ringed space
$(X,\mathcal {O}_X)$
from the triple
$\mathcal {t}(X)$
.
Definition 5.1. Let
$(S,S_0)$
be as in §2.2, and let
$(U,\mathfrak {X},j)$
be a gluing triple over
$(S,S_0)$
. The underlying topological space, denoted
$|(U,\mathfrak {X},j)|$
, has underlying set
$|U|\sqcup |\mathfrak {X}|$
, where a subset
$F = F_U\sqcup F_{\mathfrak {X}}$
is closed if and only if
$F_U = F\cap |U|$
is closed in
$|U|$
,
$F_{\mathfrak {X}} = F\cap |\mathfrak {X}|$
is closed in
$|\mathfrak {X}|$
, and
$$\begin{align*}F^{\mathrm{an}}_U\cap \mathfrak{X}^{\mathrm{rig}} \subseteq \mathrm{sp}_{\mathfrak{X}}^{-1}(F_{\mathfrak{X}}). \end{align*}$$
In other words, using Proposition 2.15, a set F is closed if and only if it is of the form
$C\sqcup \big (\mathrm {sp}_{\mathfrak {X}}(C^{\mathrm {an}}\cap \mathfrak {X}^{\mathrm {rig}})\cup D\big )$
, where C is a closed subset of U and D a closed subset of
$\mathfrak {X}$
. It is clear that the construction of the underlying topological space determines a functor
$$ \begin{align*} |\cdot|\colon \mathbf{Trip}_{(S,S_0)}\to \mathbf{Top}, \end{align*} $$
and that there is a natural map of topological spaces
$\alpha _X\colon |\mathcal {t}(X)|\to |X|$
.
Proposition 5.2. Let X be an algebraic space locally of finite type over S. Then, the map
$$ \begin{align*} \alpha_X\colon |\mathcal{t}(X)|\to |X| \end{align*} $$
is a homeomorphism.
Proof. As the map
$\alpha _X$
is continuous and bijective, it suffices to show this map is closed, that is, that if C is a closed subset of
$X^\circ $
, then
$C\sqcup \mathrm {sp}_{\widehat {X}}(C^{\mathrm {an}}\cap \widehat {X}^{\mathrm {rig}})$
is a closed subset of X.
We reduce to the case X affine and I principal invertible. In case (V), the ideal of definition I is invertible and principal. In case (N), we may assume
$X=S$
, and consider the blowup
$f\colon X'\to X$
along I. Then
$(X')^\circ = X^\circ $
,
$(\widehat {X}')^{\mathrm {rig}} = \widehat {X}^{\mathrm {rig}}$
and
$$\begin{align*}C\sqcup \mathrm{sp}_{\widehat{X}}(C^{\mathrm{an}}\cap \widehat{X}^{\mathrm{rig}}) = C\sqcup f(\mathrm{sp}_{\widehat{X}'}(C^{\mathrm{an}}\cap \widehat{X}^{\mathrm{rig}})). \end{align*}$$
Since the map
$f \colon |\widehat {X}'|\to |\widehat {X}|$
is closed, the assertion for X follows from that for
$X'$
, and we may assume I is invertible. Moreover, the assertion is étale local on X (since étale surjections induce quotient maps on topological spaces), and hence we may assume in addition that I is principal and
$X=\operatorname {\mathrm {Spec}}(A)$
is affine.
Suppose that
$C=V(J)$
for
$J\subseteq \mathcal {O}(X^\circ )$
an ideal. We claim that
$C\sqcup \mathrm {sp}_{\widehat {X}}(C^{\mathrm {an}}\cap \widehat {X}^{\mathrm {rig}})=V(J^c)$
where
$J^c$
is the pullback of J along the map
$A\to \mathcal {O}(X^\circ )$
. This reduces to showing that
$\mathrm {sp}_{\widehat {X}}(V(J)^{\mathrm {an}}\cap \widehat {X}^{\mathrm {rig}})=V(I,J^c)$
. Set
$B=A/J^c$
, then this is equivalent to the claim that
$\mathrm {sp}_{\widehat {X}}(\operatorname {\mathrm {Spf}}(\widehat {B})^{\mathrm {rig}})=\operatorname {\mathrm {Spec}}(B/IB)$
. By [Reference Fujiwara and Kato15, Chapter II, Proposition 3.1.5] it suffices to show that
$\widehat {B}$
is I-torsionfree. By Lemma 4.1,
$\operatorname {\mathrm {Spec}}(\widehat {B})\to \operatorname {\mathrm {Spec}}(B)$
is flat, and so it suffices to show that B is I-torsionfree. But,
$B=A/J^c$
injects into
$\mathcal {O}(X^\circ )/J$
which is I-torsionfree.
Define the full subcategory
$\mathscr {C}\subseteq \mathbf {Trip}_{(S,S_0)}$
to be the essential image under
$\mathcal {t}$
of representable objects, that is, those
$(U,\mathfrak {X},j)$
isomorphic to
$\mathcal {t}(X)$
for some scheme X. Let us observe that by Proposition 5.2 one has a canonical identification
$|(U,\mathfrak {X},j)|\simeq |X|$
. We now define a functor
$$ \begin{align*} \mathcal{g}\colon \mathscr{C}\to \mathbf{RS}_S,\quad \mathcal{g}(U,\mathfrak{X},j)=(|(U,\mathfrak{X},j)|,\mathcal{O}_{(U,\mathfrak{X},j)}). \end{align*} $$
Here
$\mathbf {RS}_S$
is the category of ringed spaces over S, and we define the sheaf
$\mathcal {O}_{(U,\mathfrak {X},j)}$
as follows:
$$ \begin{align*} \mathcal{O}_{(U,\mathfrak{X},j)}(|\mathcal{t}(X_1)|)= \mathcal{O}_U(X_1)\times_{\mathcal{O}(\widehat{X}_1^{\mathrm{rig}})}\mathcal{O}(\widehat{X}_1), \end{align*} $$
for any open subset
$X_1\subseteq X$
, which is clearly a well-defined sheaf on
$|(U,\mathfrak {X},j)|\simeq |X|$
(as all objects involved only require the knowledge of the underlying space of
$X_1$
), independent of choices, and that
$\mathcal {g}$
is a functor.
Proposition 5.3. For a scheme X locally of finite type over S, there is a natural isomorphism of ringed spaces over S
Proof. By Proposition 5.2,
$\alpha _X$
is a homeomorphism, so it suffices to show that the natural map
$\mathcal {O}_X\to (\alpha _X)_\ast \mathcal {O}_{\mathcal {t}(X)}$
is an isomorphism on affine open subsets. But, this is Corollary 4.4.
Corollary 5.4. The functor
$$ \begin{align*} \mathcal{t}\colon \mathbf{Sch}^{\mathrm{lft}}_S\to \mathbf{Trip}_{(S,S_0)} \end{align*} $$
is fully faithful.
5.2 Proof of Theorem 2.26: fully faithfulness
We now aim to show that for any algebraic spaces X and Y separated and locally of finite type over S, the natural map
$$ \begin{align} \operatorname{\mathrm{Hom}}(X,Y)\to \operatorname{\mathrm{Hom}}(\mathcal{t}(X),\mathcal{t}(Y)), \end{align} $$
is a bijection. We do this in three steps.
Step 0: when X and Y are both schemes
In this setting we see that the claim is a special case of Corollary 5.4.
Step 1: when X is a scheme
For injectivity, let
$Y'\to Y$
be an étale surjection from a scheme
$Y'$
separated and locally of finite type over S. If
$f_i\colon X\to Y$
(
$i=1,2$
) are morphisms with
$\mathcal {t}(f_1)=\mathcal {t}(f_2)$
then
$\mathcal {t}(f_1')=\mathcal {t}(f_2')$
, where
$f_i'\colon Y'\times _Y X\to Y'$
are the induced morphisms. But, as
$Y'\times _Y X$
is a scheme, this implies by Corollary 5.4 that
$f_1'=f_2'$
and, as
$Y'\times _X Y\to X$
is a surjection, that
$f_1=f_2$
.
For surjectivity, let
$f\colon \mathcal {t}(X)\to \mathcal {t}(Y)$
be a morphism. As X and Y are separated the graph morphisms
$\Gamma _{f^\circ }\colon X^\circ \to X^\circ \times _{S^\circ }Y^\circ $
and
$\Gamma _{\widehat {f}}\colon \widehat {X}\to \widehat {X}\times _{\widehat {S}}\widehat {Y}$
are closed embeddings, and so define ideal sheaves 
and 
. As
$f^\circ |_{\widehat {X}^{\mathrm {rig}}}=\widehat {f}^{\mathrm {rig}}$
it is clear that 
and 
induce the same ideal sheaf of
$\widehat {X}^{\mathrm {rig}}\times _{\widehat {S}^{\mathrm {rig}}}\widehat {Y}^{\mathrm {rig}}$
, so define an object 
in
$\mathbf {Coh}(\mathcal {t}(X\times _S Y))$
in the sense of Definition 4.8. By Proposition 4.9 this corresponds to a unique coherent sheaf 
(which is an ideal sheaf as an equivalence preserves subobjects) on
$X\times _S Y$
with 
.
Consider 
. The projection map furnishes a morphism 
which is separated (as each 
and X is) and quasi-finite (as this may be checked over
$X^\circ $
and
$\widehat {X}$
, where it is an isomorphism). Thus, 
is a scheme by (30, Proposition 03XX). Observe then that there is a natural isomorphism 
and thus by Corollary 5.4 there exists a unique isomorphism 
such that
$\mathcal {t}(i)=\iota $
. Composing i with the projection
$X\times _S Y\to Y$
produces a morphism
$g\colon X\to Y$
which, by construction, satisfies
$\mathcal {t}(g)=f$
, as desired.
Step 2: the general case
We may write
$X=U/R$
for an étale equivalence relation
$R\rightrightarrows U$
. In the diagram
the equalizers of the vertical parallel pairs in the bottom row are, by definition,
$\operatorname {\mathrm {Hom}}(\mathcal {t}(\bullet ), \mathcal {t}(Y))$
for
$\bullet =X,U$
, and R, respectively. Thus our goal is to show that the left column is an equalizer. Observe that by Step 1 that the middle and right columns are. But the rows of the diagram are also equalizers, as
$X^\circ =U^\circ /R^\circ $
,
$\widehat {X}=\widehat {U}/\widehat {R}$
, and
$\widehat {X}^{\mathrm {rig}} = \widehat {U}^{\mathrm {rig}}/\widehat {R}^{\mathrm {rig}}$
, and thus the assertion follows from a diagram chase.
5.3 Proof of the gluing theorem: essential surjectivity when S is a G-space
Our proof of essential surjectivity uses results relying on Artin approximation which requires excellence-like hypotheses. So, we now restrict to the case when S is a G-space (see Definition 2.24).
Artin’s contraction theorem
We begin by recalling the main theorem of [Reference Artin2], and the improvement in (30, Theorem 0GIB). Our exposition will follow that of (30, Section 0GH7).
Definition 5.5. A formal contraction problem over S is a quadruple of data
$(X',T',\mathfrak {X},\mathfrak {g})$
where
-
•
$X'$
is an algebraic space locally of finite over S, -
•
$T'$
is a closed subset of
$|X'|$
mapping into
$|S_0|$
in
$|S|$
, -
•
$\mathfrak {X}$
is a formal algebraic space locally of finite type over
$\widehat {S}$
, -
•
$\mathfrak {g}\colon \widehat {X}^{\prime}_{T'}\to \mathfrak {X}$
is a proper and rig-étale (see (30, Definition 0AQM)) morphism of formal algebraic spaces such that both
$\mathfrak {g}$
and its diagonal are rig-surjective (see (30, Definition 0AQQ)). Here
$\widehat {X}^{\prime}_{T'}$
denotes the formal completion of
$X'$
along
$T'$
.
We will only need the following very special case of a formal contraction problem.
Example 5.6. Let
$X'$
be an algebraic space locally of finite type over S, and let
$\mathfrak {g}\colon \widehat {X}'\to \mathfrak {X}$
be an admissible formal modification of formal algebraic spaces over
$\widehat {S}$
. Then,
$(X',|\widehat {X}'|,\mathfrak {X},\mathfrak {g})$
is a formal contraction problem. Indeed, it suffices to show that
$\mathfrak {g}$
is rig-étale and that
$\mathfrak {g}$
and its diagonal are rig-surjective. But, by assumption,
$\mathfrak {g}^{\mathrm {rig}}$
is an isomorphism, and thus so is its diagonal. It is easy to see this implies that
$\mathfrak {g}$
and its diagonal are rig-surjective (cf. [Reference Fujiwara and Kato15, Chapter II, Lemma 3.3.7]). To prove that
$\mathfrak {g}$
is rig-étale, we are reduced to the case of admissible blowups by combining [Reference Fujiwara and Kato15, Chapter II, Corollary 2.1.5] and part (4) of (30, Lemma 0GCZ), but this case is simple.
Remark 5.7. If S is Jacobson, then the converse holds: the conditions on the map
$\mathfrak {g}$
in Definition 5.5 are equivalent to saying that the induced map of rigid spaces
$\mathfrak {g}^{\mathrm {rig}}$
is an isomorphism. Indeed, this follows from Theorem 2.14 as the map
$\mathfrak {g}^{\mathrm {rig}}$
will then be a surjective étale monomorphism.
Definition 5.8. Let
$(X',T',\mathfrak {X},\mathfrak {g})$
be a formal contraction problem over S. Then, a potential solution to this formal contraction problem is a quadruple
$(X,T,g,\iota )$
where
-
• X is an algebraic space locally of finite type over S,
-
•
$g\colon X'\to X$
a proper morphism of algebraic spaces over S, -
•
$T\subseteq |X|$
a closed subset mapping into
$|S_0|\subseteq |S|$
, -
•
is an isomorphism of formal algebraic spaces over
$\widehat {S}$
.
is an isomorphism of formal algebraic spaces over 
We say a potential solution
$(X,T,g,\iota )$
is a solution if
-
•
$T'=g^{-1}(T)$
, -
•
is an isomorphism, -
• the completion of g recovers, via
$\iota $
, the map
$\mathfrak {g}$
.
is an isomorphism,
In [Reference Artin2] it is shown that every formal contraction problem has a solution when S is excellent. This result was strengthened in (30, Section 0GH7) to the case when S is a G-scheme.
Theorem 5.9 (Artin’s contraction theorem, see [Reference Artin2, Theorem 3.1] and [30, Theorem 0GIB])
Suppose that S is a G-scheme. Then, every formal contraction problem over S has a solution.
Essential surjectivity in the G-scheme case
Assume now that S is a G-space and let
$(U,\mathfrak {X},j)$
be a separated gluing triple over
$(S,S_0)$
. By Proposition 2.21 we may assume that S is a separated scheme.
Step 1: finite type case
Suppose first that
$U\to S^\circ $
and
$\mathfrak {X}\to \widehat {S}$
are finite type. By Nagata compactification for algebraic spaces (see [Reference Conrad, Lieblich and Olsson11, Theorem 1.2.1]), we may find a proper morphism of algebraic spaces
$\overline {X}\to S$
and a dense open embedding
$U\to \overline {X}^\circ $
. As
$\overline {X}\to S$
is proper, we know from Proposition 2.17 that
$j_{\overline {X}}$
is an isomorphism. In particular, we have an open embedding of rigid spaces obtained as the composition
$$ \begin{align} \mathfrak{X}^{\mathrm{rig}}\xrightarrow{j}U^{\mathrm{an}}\to (\overline{X}^\circ)^{\mathrm{an}}\xrightarrow{j_{\overline{X}}^{-1}}\widehat{\overline{X}}^{\mathrm{rig}}. \end{align} $$
Thus, by Theorem 2.10 and Theorem 2.14, there exist admissible modifications
$\mathfrak {g}\colon \mathfrak {Y}\to \mathfrak {X}$
and
$\mathfrak {Y}'\to \widehat {\overline {X}}$
and an open embedding
$\mathfrak {Y}\to \mathfrak {Y}'$
which recovers (5.3.1) on applying
$(-)^{\mathrm {rig}}$
.
By (30, Theorem 0GDU) there exists a unique U-modification
$Y'\to \overline {X}$
whose completion recovers
$\mathfrak {Y}'\to \widehat {\overline {X}}$
. Let
$|Y|\subseteq |Y'|$
be the union of
$$ \begin{align*} |U|\subseteq |\overline{X}^\circ|=|(Y')^\circ|,\quad\text{and}\quad |\mathfrak{Y}|\subseteq |\mathfrak{Y}'|=|\widehat{Y}'|\subseteq |Y'|. \end{align*} $$
Then using Proposition 5.2 one sees that
$|Y|$
is an open subset of
$|Y'|$
and so corresponds to an open algebraic subspace Y of
$Y'$
(see (30, Lemma 03BZ)).
The quadruple
$(Y,|\mathfrak {Y}|,\mathfrak {X}, \mathfrak {g})$
is then a formal contraction problem in the sense of Definition 5.5. As S is a G-scheme we see from Theorem 5.9 that this formal contraction problem has a solution in the sense of Definition 5.8. Write this solution as
$(X,T,g,\iota )$
. As T is the image of
$|\mathfrak {Y}|$
it is clear that
$T=|\mathfrak {X}|$
and so
$\mathcal {t}(X)=(U,\mathfrak {X},j)$
as desired.
Step 2: general case
Take coherent open covers 
and 
of U and
$\mathfrak {X}$
, respectively. For each k in 
one has that
$\mathfrak {X}_{k}^{\mathrm {rig}}$
is an open subset of
$U^{\mathrm {an}}=\bigcup _i U_i^{\mathrm {an}}$
, and so there exists some finite subset 
such that
$\mathfrak {X}_{k}^{\mathrm {rig}}\subseteq W_{i(k)}^{\mathrm {an}}$
where
$W_{i(k)}= \bigcup _{i\in S_{i(k)}}U_{i(k)}$
. Then, for each k in 
and each pair
$(k,k')$
in 
the triples
$(W_{i(k)}^\circ ,\mathfrak {X}_k,k)$
and
$(W_{i(k)}\cap W_{i(k')},\mathfrak {X}_k\cap \mathfrak {X}_{k'},j)$
is a separated open gluing datum with finite type constituents.
By Step 1, there exist algebraic spaces
$X_k$
and
$X_{k,k'}$
with
$$ \begin{align*} \mathcal{t}(X_k)=(W_{i(k)},\mathfrak{X}_k,k),\qquad \mathcal{t}(X_{k,k'})=(W_{i(k)}\cap W_{i(k')},\mathfrak{X}_k\cap \mathfrak{X}_{k'},j), \end{align*} $$
respectively. Moreover, combining the fully faithfulness argument from Step 2 of §5.2 and Proposition 2.27, we obtain a separated open gluing datum of algebraic spaces. Taking the gluing of this datum results in an algebraic space X separated and locally of finite type over S which, by construction, satisfies
$\mathcal {t}(X)=(U,\mathfrak {X},j)$
.
5.4 Proof of Proposition 2.27
We recall the statement below for convenience.
Proposition. Let
$f\colon Y\to X$
be a morphism of algebraic spaces separated and locally of finite type over S, and let P be one of the following properties:
Then, the map f has property P if and only if
$\mathcal {t}(f)$
does.
Proof. As all these properties are stable/local for the étale topology, by considering
$X'\times _X Y\to X'$
for an étale cover
$X'\to X$
where
$X'$
is a separated scheme locally of finite type over S, we may assume X and Y are representable.
For all of these properties P, it is evident if f satisfies P then
$f^\circ \colon Y^\circ \to X^\circ $
and
$f_n\colon Y_n\to X_n$
satisfies P for all n. Thus, to verify that
$\mathcal {t}(f)$
satisfies P it suffices to show that
$\widehat {f}\colon \widehat {Y}\to \widehat {X}$
satisfies P if and only if
$f_n$
satisfies P for all n. But, in all cases this is true as is seen from
where each reference is to a result in [Reference Fujiwara and Kato15, Chapter I].
So, suppose now that
$\mathcal {t}(f)$
is P. The fact that f is P is obvious for i), ii), v). Let us then observe that every other claim follows easily once we establish vii) and ix). Namely, x) and xi) easily follow once ix) is established from (30, Lemma 01V9). Moreover, once xi) is known, the case of iii) follows easily: if
$\mathcal {t}(f)$
is an open embedding, then f is étale, and so by (30, Lemma 02LC) it suffices to show that f is universally injective. But, by (30, Lemma 01S4) it suffices to show that
$\Delta _f$
is surjective, which can clearly be checked on the level of
$\mathcal {t}(f)$
. Then, from iii) and ii) we see that vi) follows as an isomorphism is a surjective open embedding. Now suppose that vii) is established. Then, to show iv) it suffices by (30, Lemma 03BB) that f is a monomorphism. But, this means showing that
$\Delta _f$
is an isomorphism, which follows easily from vi). Finally, to show viii) we must show that
$\Delta _f$
is a closed embedding, but this follows from iv).
To address case ix), we assume
$Y=\operatorname {\mathrm {Spec}}(B)$
and
$X=\operatorname {\mathrm {Spec}}(A)$
and show that
$A\to B$
is flat. By assumption, 
and
$\widehat {A}\to \widehat {B}$
are flat (see [Reference Fujiwara and Kato15, Chapter I, Proposition 4.8.1]). Suppose that
$\mathfrak {n}$
is a point of
$V(IB)$
and let
$\mathfrak {m}$
be its image in
$V(IA)$
. As
$A_{\mathfrak {m}}/I^nA_{\mathfrak {m}}\to B_{\mathfrak {n}}/I^nB_{\mathfrak {n}}$
is flat, it suffices to verify that the conditions of [Reference Fujiwara and Kato15, Chapter 0, Corollary 8.3.9] are satisfied. Evidently the pair
$(B_{\mathfrak {n}},I)$
is Zariskian, and so it suffices to verify that the pairs
$(A_{\mathfrak {m}},IA_{\mathfrak {m}})$
and
$(B_{\mathfrak {n}},IB_{\mathfrak {n}})$
are (APf) as in [Reference Fujiwara and Kato15, Chapter 0, §7. (c)]. For type (N) this follows from [Reference Fujiwara and Kato15, Chapter 0, Proposition 7.4.14]. For type (V), it suffices by [Reference Fujiwara and Kato15, Chapter 0, Corollary 8.2.17] to show that
$(B_{\mathfrak {n}},IB_{\mathfrak {n}})$
is pseudo-adhesive, but by [Reference Fujiwara and Kato15, Chapter 0, Proposition 8.5.7] it further suffices to show that
$(B,IB)$
is pseudo-adhesive. But,
$(\mathcal {O},(\varpi ))$
is universally pseudo-adhesive (see [Reference Zavyalov33, Theorem 2.16] and [Reference Fujiwara and Kato15, Chapter 0, Theorem 9.2.1]) from where the claim follows.
Finally, to show case vii), that is, finite, let us observe that we may write 
for a coherent
$\mathcal {O}_{X^\circ }$
-algebra 
, and similarly we may write 
for a coherent
$\mathcal {O}_{\widehat {X}}$
-algebra 
(see [Reference Fujiwara and Kato15, Chapter I, Proposition 4.2.6]). By setup the pullbacks of 
and
$\widehat {A}$
to
$\widehat {X}^{\mathrm {rig}}$
are isomorphic, and so by Proposition 4.9 we may find a coherent
$\mathcal {O}_X$
-algebra 
inducing 
and
$\widehat {A}$
. Then, 
is a finite morphism, and by construction 
is isomorphic to
$\mathcal {t}(Y)$
. By Corollary 5.4, 
is isomorphic to Y as an X-scheme, from where the claim follows.
5.5 Proof of Proposition 3.2
We recall the statement below for convenience.
Proposition. Let R be a Noetherian ring and
$(\pi )\subseteq R$
an ideal. We further let
-
• A be a finitely generated
-algebra, -
• B be a topologically finitely generated
$\widehat {R}$
-algebra, -
• and
be a map of -algebras with dense image and for which the induced map
$\operatorname {\mathrm {Spa}}(C) \to \operatorname {\mathrm {Spec}}(A)^{\mathrm {an}}$
is an open immersion.
-algebra,
be a map of 
-algebras with dense image and for which the induced map 
Then the R-algebra D defined as the pullback
is finitely generated, and satisfies 
and
$\widehat {D} = B$
.
Proof. We break the proof into four steps.
Step 1
We shall find elements
$x_1, \ldots , x_n$
in D satisfying the following properties:
-
(1) their images in A generate it as an
-algebra, -
(2) their images in B topologically generate it as an
$\widehat {R}$
-algebra, -
(3) the open subset
$\operatorname {\mathrm {Spa}}(C)$
of
$\operatorname {\mathrm {Spec}}(A)^{\mathrm {an}}$
is cut out by the inequalities
$|x_i|\leqslant 1$
(
$i=1, \ldots , n$
), -
(4) the
$\pi $
-torsion of B (which is the kernel of
$B\to C$
) is generated as an ideal by the image of a subset
$\{x_1, \ldots , x_r\}$
, and
$x_1, \ldots , x_r$
map to zero in A.
-algebra,
Let
$\{y^{\prime}_i\}$
be any finite set of generators for A over 
. Note that
$\{\pi ^N y_i'\}$
is also a set of generators and, as B has open image in C, have image in C lying in the image of B for
$N\gg 0$
. Choose such an N and let
$\{y_i\}$
be a subset of D mapping to
$\{\pi ^N y^{\prime}_i\}$
in A. Similarly, let
$\{\hat z_j\}$
be a finite set of topological generators for B over
$\widehat {R}$
. Then, for any other elements
$\widehat {z}^{\prime}_j$
the set
$\{\widehat {z}_j+\pi \widehat {z}^{\prime}_j\}$
topologically generates B, as
$j^*$
has dense image we can choose elements
$\widehat {z}^{\prime}_j$
such that the image of
$\{\widehat {z}_j+\pi \widehat {z}^{\prime}_j\}$
in C lies in the image of A. Choose such
$\{\widehat {z}^{\prime}_j\}$
and let
$\{z_j\}$
be a subset of D mapping to
$\{\widehat {z}_j+\pi \widehat {z}^{\prime}_j\}$
. Write
$\{u_1,\ldots ,u_m\}= \{y_i\}\cup \{z_j\}$
.
Observe that by construction the map 
with
$U_\alpha \mapsto u_\alpha $
is surjective. Let us write I for its kernel. Consider the natural map
$C'\to C$
where
which is surjective by construction. The space
$\operatorname {\mathrm {Spa}}(C')$
is a Weierstrass affinoid subdomain of
$\operatorname {\mathrm {Spec}}(A)^{\mathrm {an}}$
defined by
$|u_\alpha |_\pi \leqslant 1$
. Indeed,
$\operatorname {\mathrm {Spa}}(C')$
is the pullback of the Weierstrass domain 
along the Zariski closed embedding 
.
As
$\operatorname {\mathrm {Spa}}(C)\to \operatorname {\mathrm {Spec}}(A)^{\mathrm {an}}$
is also an open embedding, we deduce that the map
$\operatorname {\mathrm {Spa}}(C)\to \operatorname {\mathrm {Spa}}(C')$
induced by (5.5.1) is an open immersion. But since this morphism is also a closed immersion, we must have a decomposition
$C' = C\times C"$
where
$C'\to C$
is the first projection. Consider the element
$t' = (0, 1/\pi )\in C\times C"=C'$
. Since
$A\to C'$
has dense image by construction, we may find an element
$t_0$
in A whose image is close enough to
$t'$
so that
$t_0$
is power bounded on
$\operatorname {\mathrm {Spa}}(C)$
and
$t_0$
is not power bounded on
$\operatorname {\mathrm {Spa}}(C")$
. Observe that, in particular,
$j^\ast (t_0)$
lies in the image of
$B\to C$
, and so we may choose some t in D mapping to it.
Let
$\{w_1,\ldots ,w_k\}$
be generators of the
$\pi $
-torsion
$B[\pi ^\infty ]$
which is finitely generated as R is of type (N). Set
$\{x_1,\ldots ,x_n\}=\{u_1,\ldots ,u_m,t,w_1,\ldots ,w_k\}$
.
Step 2
We shall prove that
$\{x_1, \ldots , x_n\}$
in D as in Step 1 generate D as an R-algebra, assuming that B is
$\pi $
-torsionfree. Let x be shorthand for
$\{x_1,\ldots ,x_n\}$
and consider the commutative diagram
Our goal is to show that the top arrow
$\delta $
is surjective. Fix d in D and denote by
$a,b,c$
its images in
$A,B,C$
, and let
$U,V,W$
be their preimages in 
,
$R\langle x\rangle $
, 
. Since the left square is cartesian as well, we need to show that the images of U and V in W intersect. To this end, it is enough to show two assertions:
-
(i) The image of U in W is dense.
-
(ii) The image of V in W is open (and non-empty).
Let us denote by I, J, K the kernels of
$\alpha $
,
$\beta $
,
$\gamma $
. Thus
$$\begin{align*}U = \tilde\alpha + I, \qquad V = \tilde\beta + J, \qquad W = \tilde\gamma + K \end{align*}$$
for arbitrary lifts
$\tilde \alpha $
,
$\tilde \beta $
,
$\tilde \gamma $
of
$a,b,c$
. In particular, showing (i) and (ii) is equivalent to showing the density of the image of I in K and the openness of the image of J in K.
For the first assertion, we note first that condition (3) means that
This is equivalent to saying that 
. Thus the image of I is dense in K. For the second assertion, the assumed injectivity of
$B\to C$
implies that
$J = K\cap R\langle x\rangle $
. Since
$R\langle x\rangle $
is open in 
, J is open in K.
Step 3
We now show that D is a finitely generated R-algebra in general. Since B is Noetherian, there exists an
$N\geqslant 0$
such that
$B[\pi ^\infty ] = B[\pi ^N]$
. In this case, we have
$B \simeq B'\times _{B"'} B"$
, where
$$ \begin{align*} B'=B/B[\pi^\infty] = \mathrm{im}(B\to C), \qquad B"=B/\pi^N B, \qquad B"' = B'\otimes_B B" = B'/\pi^NB'. \end{align*} $$
Therefore, setting
$D' = A\times _C B'$
, we have
Now
$D'$
,
$B"$
and
$B"'$
are finitely generated R-algebras. Moreover, the maps
$B"\to B"'$
and
$D'\to B"'$
are surjective. Therefore by (30, Lemma 00IT), the ring D is finitely generated over R.
Step 4
It finally suffices to verify that 
and
$\widehat {D}=B$
. By the arguments in Step 1, both 
and
$\widehat {D}\to B$
are surjective, thus it suffices to verify both maps are injective. Suppose that
$d=(a,b)$
belongs to 
. Then, it is of the form
$d=(0,b)$
and so b is itself
$\pi $
-torsion. Thus, d is actually zero in 
as desired. To see that
$\widehat {D}\to \widehat {B}$
injective it suffices to show that
$D/\pi ^n\to B/\pi ^n$
is injective for all n. But, if
$d=(a,b)$
in D maps to zero in
$B/\pi ^n$
we can write
$b=\pi ^nb'$
and then
$d=\pi ^n d'$
where 
from where the injectivity of
$D/\pi ^n\to B/\pi ^n$
follows.
Example 5.10 (Continuation of Example 3.1)
We illustrate the proof of Proposition 3.2 in the case presented in Example 3.1. Let 
be the coordinate on the disk 
. The data
$(A,B,C,j^*)$
as in Proposition 3.2 are then
The proof asks us first to find generators of A whose images in C belong to B: here
$\gamma = px$
will do. Next, we find topological generators of B, for example,
$\alpha '=(x, 0)$
and
$\beta '=(0,y)$
, which we need to approximate with elements of B whose images in C belong to A. For this, we note that
$$ \begin{align*} u = j^*((1-px)^2) = ((1-px)^2, (py)^2),\qquad v = j^*((px)^2) = ((px)^2, (1+py)^2) \end{align*} $$
are equal to
$(1, 0)$
and
$(0,1)$
modulo p, respectively. Thus
$$ \begin{align*} \alpha = u x = x(1-px)^2,\qquad \beta = v y = px^2(1-px) \end{align*} $$
have the desired properties.
Since B has no p-torsion, the proof shows that the pullback algebra D is generated by
$\alpha $
,
$\beta $
and
$\gamma $
. These generators satisfy the stated relations
$$ \begin{align*} p\alpha = \gamma(1-\gamma)^2,\qquad p\beta = \gamma^2(1-\gamma),\qquad \gamma \alpha = (1-\gamma)\beta. \end{align*} $$
We claim that to show that the map
$$\begin{align*}\mathbb{Z}_p[\alpha, \beta,\gamma]/(p\alpha - \gamma(1-\gamma)^2, p\beta - \gamma^2(1-\gamma), \gamma \alpha - (1-\gamma)\beta) \to D \end{align*}$$
is an isomorphism it suffices to check isomorphy over both
$\mathbb {Q}_p$
and over
$\mathbb {F}_p$
, both of which are clear. Indeed, observe that as D is a subring of
$A\times B$
, it is evidently
$\mathbb {Z}_p$
-flat. The claim then follows from the fibrewise criterion for isomorphism.
Acknowledgements
The authors would like to thank Ofer Gabber, David Hansen, Aise Johan de Jong and Martin Olsson for helpful discussions.
The first author (PA) was supported by the project KAPIBARA funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 802787). Part of this work was conducted while the second author (AY) was visiting the Hausdorff Research Institute for Mathematics, funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2047/1 – 390685813. Part of this work was also carried out while the second author (AY) was supported by JSPS KAKENHI Grant Number 22F22323.
Competing interests
The authors have no competing interests to declare.
Data availability statement
Data availability is not applicable to this article as no data was created or analyzed.
is Noetherian, and for any finitely generated R-module M the module 
Open access
