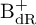1 Introduction
1.1 Background and main theorems
Let k be a complete discretely valued p-adic field that has a perfect residue field, and let K be its completed algebraic closure. In the seminal work of Bhatt and Scholze [Reference Bhatt and ScholzeBS22], they introduce the notion of prisms and prismatic cohomology for a p-adic smooth formal scheme X over
![]() $\mathcal {O}_k$
. A prism over X can be defined as a diagram of algebras
$\mathcal {O}_k$
. A prism over X can be defined as a diagram of algebras
where A is equipped with an additional structure of a lift of Frobenius operator, I is an invertible ideal in A and
![]() $\operatorname {\mathrm {Spf}}(R)$
is an open subset of X (c.f. [Reference Bhatt and ScholzeBS22, Section 3] for precise definition). The resulted cohomology theory, namely prismatic cohomology, turns out to specialize to many other important p-adic cohomology in the p-adic Hodge theory, and thus provides a powerful tool to study the relation of different cohomology associated to the given formal scheme X.
$\operatorname {\mathrm {Spf}}(R)$
is an open subset of X (c.f. [Reference Bhatt and ScholzeBS22, Section 3] for precise definition). The resulted cohomology theory, namely prismatic cohomology, turns out to specialize to many other important p-adic cohomology in the p-adic Hodge theory, and thus provides a powerful tool to study the relation of different cohomology associated to the given formal scheme X.
Let X now be a rigid space over K, and let
![]() $\xi $
be a fixed generator of the kernel ideal of the natural surjection
$\xi $
be a fixed generator of the kernel ideal of the natural surjection
![]() $\theta :{\mathrm {B_{dR}^+}} \rightarrow K$
, where
$\theta :{\mathrm {B_{dR}^+}} \rightarrow K$
, where
![]() ${\mathrm {B_{dR}^+}}$
is Fontaine’s de Rham period ring ([Reference FontaineFon94]). In this article, we study a rational analogue of prismatic cohomology for rigid spaces over K, with coefficients in
${\mathrm {B_{dR}^+}}$
is Fontaine’s de Rham period ring ([Reference FontaineFon94]). In this article, we study a rational analogue of prismatic cohomology for rigid spaces over K, with coefficients in
![]() ${\mathrm {B_{dR}^+}}$
. We start by defining the notion of a prism in our setting.
${\mathrm {B_{dR}^+}}$
. We start by defining the notion of a prism in our setting.
Definition 1.1.1. A
![]() ${\mathrm {B_{dR}^+}}$
-prism over X is a diagram of
${\mathrm {B_{dR}^+}}$
-prism over X is a diagram of
![]() ${\mathrm {B_{dR}^+}}$
-algebras
${\mathrm {B_{dR}^+}}$
-algebras
where
![]() $\mathrm {Spa}(R)$
is an affinoid open subset of X, and B is a
$\mathrm {Spa}(R)$
is an affinoid open subset of X, and B is a
![]() $\xi $
-adic complete,
$\xi $
-adic complete,
![]() $\xi $
-torsionfree algebra over
$\xi $
-torsionfree algebra over
![]() ${\mathrm {B_{dR}^+}}$
satisfying the finite type condition as in Definition 2.2.1 (i).
${\mathrm {B_{dR}^+}}$
satisfying the finite type condition as in Definition 2.2.1 (i).
The opposite category of
![]() ${\mathrm {B_{dR}^+}}$
-prisms over X is denoted as
${\mathrm {B_{dR}^+}}$
-prisms over X is denoted as ![]() .
.
An essential difference between our notion of prisms and that of Bhatt–Scholze in [Reference Bhatt and ScholzeBS22] is that there is no Frobenius structure in our definition. Nonetheless, as we shall see in our first main result below, the resulted cohomology theory over the opposite category of prisms still enjoys many good properties when X has mild singularities.
Theorem 1.1.2. There is a
![]() ${\mathrm {B_{dR}^+}}$
-linear cohomology theory on the category of K-rigid spaces
${\mathrm {B_{dR}^+}}$
-linear cohomology theory on the category of K-rigid spaces
such that for an affinoid rigid space X that has l.c.i. singularities, it satisfies the following property (as
![]() $\mathbb {E}_\infty $
-algebras over
$\mathbb {E}_\infty $
-algebras over
![]() ${\mathrm {B_{dR}^+}}$
):
${\mathrm {B_{dR}^+}}$
):
-
(i) (Pro-étale comparison) There is a natural map
(1.1.1)
where the right hand side is pro-étale cohomology of the de Rham period sheaf as in Scholze [Reference ScholzeSch13] and Brinon [Reference BrinonBri08]. The map is an isomorphism when X is smooth.
-
(ii) (Infinitesimal comparison) There is a natural map
(1.1.2)
which factors through the complex
 . Here the left hand side is infinitesimal cohomology of
. Here the left hand side is infinitesimal cohomology of
 $X/{\mathrm {B_{dR}^+}}$
as in [Reference GuoGuo24, Section 7] (see also Section 4.2).
$X/{\mathrm {B_{dR}^+}}$
as in [Reference GuoGuo24, Section 7] (see also Section 4.2).Moreover, if X is smooth, the above induces an isomorphism
 .
. -
(iii) (Hodge–Tate filtration) There is a natural
 $\mathbb {N}^{\mathrm {op}}$
-indexed increasing exhaustive filtration over the reduction
$\mathbb {N}^{\mathrm {op}}$
-indexed increasing exhaustive filtration over the reduction  , whose i-th graded piece is
, whose i-th graded piece is
 $R\Gamma (X,L\wedge ^i \mathbb {L}^{\mathrm {an}}_{X/K}(-i)[-i])$
.
$R\Gamma (X,L\wedge ^i \mathbb {L}^{\mathrm {an}}_{X/K}(-i)[-i])$
. -
(iv) (Galois invariant) Assume
 $X=Y_K$
for some affinoid rigid space Y over k. There is a natural
$X=Y_K$
for some affinoid rigid space Y over k. There is a natural
 $G_k$
-equivariant condensed algebra
$G_k$
-equivariant condensed algebra  underlying
underlying  , satisfying
, satisfying 
where
 $R\Gamma (G_k, -)$
is defined as the condensed group cohomology as in [Reference BoscoBos21, Appendix 2].
$R\Gamma (G_k, -)$
is defined as the condensed group cohomology as in [Reference BoscoBos21, Appendix 2].
We give several comments on the result above.
Remark 1.1.3 (Cohomology of
 ${\mathbb {B}^+_{\mathrm {dR}}}$
and the divided de Rham complex).
${\mathbb {B}^+_{\mathrm {dR}}}$
and the divided de Rham complex).
Let X be a smooth rigid space over K of dimension n. In this case, infinitesimal cohomology
![]() $R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})$
was first introduced in [Reference Bhatt, Morrow and ScholzeBMS, Section 13] (denoted there as
$R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})$
was first introduced in [Reference Bhatt, Morrow and ScholzeBMS, Section 13] (denoted there as
![]() $R\Gamma _{\mathrm {crys}}(X/{\mathrm {B_{dR}^+}})$
and is called crystalline cohomology). It is locally computed by the formal completion of the de Rham complex of a smooth ambient space with respect to a closed immersion ([Reference Bhatt, Morrow and ScholzeBMS, Section 13.1], [Reference GuoGuo24, Theorem 4.1.1]). Shown in [Reference Bhatt, Morrow and ScholzeBMS, Theorem 13.1], infinitesimal cohomology admits a map to pro-étale cohomology
$R\Gamma _{\mathrm {crys}}(X/{\mathrm {B_{dR}^+}})$
and is called crystalline cohomology). It is locally computed by the formal completion of the de Rham complex of a smooth ambient space with respect to a closed immersion ([Reference Bhatt, Morrow and ScholzeBMS, Section 13.1], [Reference GuoGuo24, Theorem 4.1.1]). Shown in [Reference Bhatt, Morrow and ScholzeBMS, Theorem 13.1], infinitesimal cohomology admits a map to pro-étale cohomology
![]() $R\Gamma _{\mathrm {pro\acute {e}t}}(X,{\mathbb {B}^+_{\mathrm {dR}}})$
, which is an isomorphism after tensoring with
$R\Gamma _{\mathrm {pro\acute {e}t}}(X,{\mathbb {B}^+_{\mathrm {dR}}})$
, which is an isomorphism after tensoring with
![]() $\mathrm {B_{dR}}$
. This in particular allows us to compute pro-étale cohomology of
$\mathrm {B_{dR}}$
. This in particular allows us to compute pro-étale cohomology of
![]() ${\mathbb {B}_{\mathrm {dR}}}={\mathbb {B}^+_{\mathrm {dR}}}[\frac {1}{\xi }]$
using the de Rham complex. It is then a natural question if one can also compute pro-étale cohomology of
${\mathbb {B}_{\mathrm {dR}}}={\mathbb {B}^+_{\mathrm {dR}}}[\frac {1}{\xi }]$
using the de Rham complex. It is then a natural question if one can also compute pro-étale cohomology of
![]() ${\mathbb {B}^+_{\mathrm {dR}}}$
using a de Rham-style cohomology and within the category of noetherian algebras.
${\mathbb {B}^+_{\mathrm {dR}}}$
using a de Rham-style cohomology and within the category of noetherian algebras.
Our Theorem 1.1.2.(i) gives an answer to the aforementioned question. Indeed, assume the rigid space
![]() $X=\mathrm {Spa}(R)$
is smooth of dimension n and there is a compatible system of smooth
$X=\mathrm {Spa}(R)$
is smooth of dimension n and there is a compatible system of smooth
![]() ${\mathrm {B_{dR}^+}}/\xi ^e$
-algebras
${\mathrm {B_{dR}^+}}/\xi ^e$
-algebras
![]() $\widetilde R_e$
that lift R (which always exists locally). We let
$\widetilde R_e$
that lift R (which always exists locally). We let
![]() $\widetilde R$
be the inverse limit of
$\widetilde R$
be the inverse limit of
![]() $\widetilde {R}_e$
. Then
$\widetilde {R}_e$
. Then ![]() is isomorphic to the following
is isomorphic to the following
![]() $\xi $
-divided de Rham complex
$\xi $
-divided de Rham complex
Here
![]() $\widetilde \Omega ^1 :=\varprojlim _e \Omega _{(\widetilde R/\xi ^e)/{\mathrm {B^+_{dR,e}}}}^1$
is the inverse limit of analytic differentials of affinoid algebras
$\widetilde \Omega ^1 :=\varprojlim _e \Omega _{(\widetilde R/\xi ^e)/{\mathrm {B^+_{dR,e}}}}^1$
is the inverse limit of analytic differentials of affinoid algebras
![]() $\widetilde R_e$
over
$\widetilde R_e$
over
![]() ${\mathrm {B^+_{dR,e}}}$
, and the map d is defined as the composition
${\mathrm {B^+_{dR,e}}}$
, and the map d is defined as the composition
 $$\begin{align*}\widetilde R \longrightarrow \widetilde\Omega^1 \longrightarrow \frac{\widetilde\Omega^1}{\xi}, \end{align*}$$
$$\begin{align*}\widetilde R \longrightarrow \widetilde\Omega^1 \longrightarrow \frac{\widetilde\Omega^1}{\xi}, \end{align*}$$
where the first map is the continuous differential over
![]() ${\mathrm {B_{dR}^+}}$
, and the second map is the natural inclusion.
${\mathrm {B_{dR}^+}}$
, and the second map is the natural inclusion.
Remark 1.1.4 (Relationship with Bhatt–Scholze’s prismatic cohomology).
As we mentioned above, despite a prism over
![]() ${\mathrm {B_{dR}^+}}$
appears to be similar to a prism in the sense of Bhatt–Scholze, a striking difference is that the former does not have any Frobenius structure. So one can ask if there is any deeper relationship between the two cohomology theory. Indeed, it is not hard to see that the same definition of a prism without Frobenius as in Definition 1.1.1 can be introduced in the p-complete integral setting, yielding an integral cohomology theory for p-adic formal schemes over
${\mathrm {B_{dR}^+}}$
appears to be similar to a prism in the sense of Bhatt–Scholze, a striking difference is that the former does not have any Frobenius structure. So one can ask if there is any deeper relationship between the two cohomology theory. Indeed, it is not hard to see that the same definition of a prism without Frobenius as in Definition 1.1.1 can be introduced in the p-complete integral setting, yielding an integral cohomology theory for p-adic formal schemes over
![]() ${\mathrm {A_{inf}}}$
. Then by using an integral analogue of the Hodge–Tate comparison, one can prove that for a smooth p-adic formal scheme X over
${\mathrm {A_{inf}}}$
. Then by using an integral analogue of the Hodge–Tate comparison, one can prove that for a smooth p-adic formal scheme X over
![]() ${\mathrm {A_{inf}}}$
, the aforementioned cohomology is naturally isomorphic to the relative prismatic cohomology for
${\mathrm {A_{inf}}}$
, the aforementioned cohomology is naturally isomorphic to the relative prismatic cohomology for ![]() in the sense of Bhatt–Scholze [Reference Bhatt and ScholzeBS22]. In particular, the underlying complex of the Bhatt–Scholze relative prismatic cohomology (forgetting its Frobenius structure) can be computed in a much simpler way.Footnote
1
in the sense of Bhatt–Scholze [Reference Bhatt and ScholzeBS22]. In particular, the underlying complex of the Bhatt–Scholze relative prismatic cohomology (forgetting its Frobenius structure) can be computed in a much simpler way.Footnote
1
Remark 1.1.5 (Globalization and the finiteness).
Theorem 1.1.2 naturally extends to proper rigid spaces that has l.c.i. singularities (with ![]() in Theorem 1.1.2 (ii) replaced by a sheafy version).
in Theorem 1.1.2 (ii) replaced by a sheafy version).
-
(i) When X is proper and smooth, using the Hodge–Tate filtration and the finiteness of coherent cohomology, we know that each
 is finite generated over
is finite generated over
 ${\mathrm {B_{dR}^+}}$
and lives in cohomological degree
${\mathrm {B_{dR}^+}}$
and lives in cohomological degree
 $0\leq i\leq 2\dim (X)$
. In fact, using the primitive comparison theorem ([Reference ScholzeSch12]) one can even show that each
$0\leq i\leq 2\dim (X)$
. In fact, using the primitive comparison theorem ([Reference ScholzeSch12]) one can even show that each  is finite free over
is finite free over
 ${\mathrm {B_{dR}^+}}$
.
${\mathrm {B_{dR}^+}}$
. -
(ii) When X is proper but not smooth, the Hodge–Tate filtration in Theorem 1.1.2.(iii) can have infinity many non-zero graded pieces. For example, in the special case when
 $X=Y_K$
for a proper rigid space Y over a discretely valued subfield k, the Hodge–Tate filtration splits into an infinite direct sum
$X=Y_K$
for a proper rigid space Y over a discretely valued subfield k, the Hodge–Tate filtration splits into an infinite direct sum  , which in general is infinite dimensional for proper rigid spaces that have l.c.i. singularities. Thus one loses the finiteness of
, which in general is infinite dimensional for proper rigid spaces that have l.c.i. singularities. Thus one loses the finiteness of  if we go beyond the proper and smooth assumption.
if we go beyond the proper and smooth assumption.
By combining Theorem 1.1.2 (i) and (ii), one obtains the following composition
It can be shown that the composition is an isomorphism after inverting
![]() $\xi $
([Reference GuoGuo24, Theoren 7.3.2]), and thus
$\xi $
([Reference GuoGuo24, Theoren 7.3.2]), and thus
![]() $R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})[\frac {1}{\xi }]$
is a direct summand of
$R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})[\frac {1}{\xi }]$
is a direct summand of ![]() , and contains all Galois invariants when
, and contains all Galois invariants when
![]() $X=Y_K$
is defined over k (notice the latter is finite when Y is proper). One can then ask if the complement of
$X=Y_K$
is defined over k (notice the latter is finite when Y is proper). One can then ask if the complement of
![]() $R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})$
in
$R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})$
in ![]() always has bounded
always has bounded
![]() $\xi $
-power torsion. We propose the following more general question, which would have an affirmative answer if the
$\xi $
-power torsion. We propose the following more general question, which would have an affirmative answer if the
![]() $\xi ^\infty $
-torsion of
$\xi ^\infty $
-torsion of ![]() is bounded.
is bounded.
Question 1.1.6 (Rational comparison maps).
Do the maps (1.1.1) and (1.1.2) in Theorem 1.1.2 induce isomorphisms after inverting
![]() $\xi $
?
$\xi $
?
In the case when
![]() $X=Y_K$
is defined over the discretely valued subfield k, it can be shown that the boundedness of
$X=Y_K$
is defined over the discretely valued subfield k, it can be shown that the boundedness of
![]() $\xi $
-power torsion in
$\xi $
-power torsion in ![]() follows from the following question on the analytic derived de Rham cohomology of
follows from the following question on the analytic derived de Rham cohomology of
![]() $Y/k$
.
$Y/k$
.
Question 1.1.7 (Transition morphism for the Hodge filtration).
Let Y be a rigid space over k that has l.c.i. singularities. Is there a positive integer N, such that the following map of cohomology is equivalent to the zero map for any
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $i\in \mathbb {Z}$
$i\in \mathbb {Z}$
Here
![]() ${\mathrm {Fil}}^{\bullet }$
is the Hodge filtration on the analytic derived de Rham complex.
${\mathrm {Fil}}^{\bullet }$
is the Hodge filtration on the analytic derived de Rham complex.
Remark 1.1.8. Question 1.1.7 has a more classical variant in the complex algebraic geometry. Namely for a complex algebraic variety Y that has l.c.i. singularities, can we find a positive integer N so that the following map is always zero
Here
![]() ${\mathrm {Fil}}^{\bullet }$
is the Hodge filtration on the Hodge-completed derived de Rham complex
${\mathrm {Fil}}^{\bullet }$
is the Hodge filtration on the Hodge-completed derived de Rham complex
![]() $\widehat {\mathrm {dR}}_{Y/\mathbb {C}}$
.
$\widehat {\mathrm {dR}}_{Y/\mathbb {C}}$
.
If Y is of dimension zero, one can show the above by hand, using explicit calculation for a closed immersion into
![]() $\mathbb {A}^1$
. On the other hand, it is shown in [Reference BhattBha12, Corollary 5.4] that the map of cohomology
$\mathbb {A}^1$
. On the other hand, it is shown in [Reference BhattBha12, Corollary 5.4] that the map of cohomology
![]() ${\mathrm {Fil}}^n\widehat {\mathrm {dR}}_{Y/\mathbb {C}} \rightarrow \widehat {\mathrm {dR}}_{Y/\mathbb {C}}$
is the zero map for
${\mathrm {Fil}}^n\widehat {\mathrm {dR}}_{Y/\mathbb {C}} \rightarrow \widehat {\mathrm {dR}}_{Y/\mathbb {C}}$
is the zero map for
![]() $n\gg 0$
.
$n\gg 0$
.
Remark 1.1.9 (Condensed mathematics).
In Theorem 1.1.2.(iv), the Galois invariant of prismatic cohomology is studied using the notion of condensed mathematics of Clausen–Scholze, which provides a natural derived categorical framework for topological groups and their cohomology. As byproducts, we also compute Galois invariant of infinitesimal cohomology, and give a condensed base extension formula of infinitesimal cohomology, as in Theorem 8.2.3 and Theorem 8.2.3 (see also the filtered versions as in Corollary 8.2.5 and Remark 8.2.6).
We now briefly discuss the proof in next two subsections.
1.2 Simpson’s functor over
 ${\mathrm {B_{dR}^+}}$
${\mathrm {B_{dR}^+}}$
Recall from [Reference SimpsonSimp] that Simpson introduced an equivalence between the category of
![]() $\mathbb {Z}^{\mathrm {op}}$
-filtered vector spaces over a field and the category of modules over
$\mathbb {Z}^{\mathrm {op}}$
-filtered vector spaces over a field and the category of modules over
![]() $\mathbb {A}^1/\mathbb {G}_m$
, using the Rees algebra construction. The functor is defined as follows
$\mathbb {A}^1/\mathbb {G}_m$
, using the Rees algebra construction. The functor is defined as follows

where t is the coordinate of
![]() $\mathbb {A}^1$
, and the image admits a natural action by
$\mathbb {A}^1$
, and the image admits a natural action by
![]() $\mathbb {G}_m$
. By identifying the countable direct sum appeared in (1.2.1) as a special type of colimit, we may rewrite the functor (1.2.1) as
$\mathbb {G}_m$
. By identifying the countable direct sum appeared in (1.2.1) as a special type of colimit, we may rewrite the functor (1.2.1) as
The functor can be extended to an equivalence in the derived level ([Reference MoulinousMou21]), and its pullback along
![]() $\{t=0\}\rightarrow \mathbb {A}^1$
is the direct sum of graded pieces for
$\{t=0\}\rightarrow \mathbb {A}^1$
is the direct sum of graded pieces for
![]() $(V,{\mathrm {Fil}}^{\bullet })$
.
$(V,{\mathrm {Fil}}^{\bullet })$
.
Inspired by the above construction, we introduce the following variant of the Simpson’s functor, sending a
![]() $\mathbb {N}^{\mathrm {op}}$
-filtered
$\mathbb {N}^{\mathrm {op}}$
-filtered
![]() ${\mathrm {B_{dR}^+}}$
-complex onto the
${\mathrm {B_{dR}^+}}$
-complex onto the
![]() ${\mathrm {B_{dR}^+}}$
-complex as below
${\mathrm {B_{dR}^+}}$
-complex as below
 $$\begin{align*}\Psi:(M, {\mathrm{Fil}}^{\bullet}) \longmapsto (\underset{i\in\mathbb{N}}{{\mathrm{colim}}} \frac{{\mathrm{Fil}}^iM}{\xi^i})^\wedge, \end{align*}$$
$$\begin{align*}\Psi:(M, {\mathrm{Fil}}^{\bullet}) \longmapsto (\underset{i\in\mathbb{N}}{{\mathrm{colim}}} \frac{{\mathrm{Fil}}^iM}{\xi^i})^\wedge, \end{align*}$$
where
![]() $(-)^\wedge $
is the derived
$(-)^\wedge $
is the derived
![]() $\xi $
-completion. It can be shown that the functor
$\xi $
-completion. It can be shown that the functor
![]() $\Psi $
is equivalent to the
$\Psi $
is equivalent to the
![]() $\xi $
-completed derived reduction of the Simpson’s Rees construction by the ideal
$\xi $
-completed derived reduction of the Simpson’s Rees construction by the ideal
![]() $(t-\xi )$
, where the degrees of the elements t and
$(t-\xi )$
, where the degrees of the elements t and
![]() $\xi $
are
$\xi $
are
![]() $(-1)$
and
$(-1)$
and
![]() $0$
respectively (see Remark 4.1.2 for details). One of our main observations is that prismatic cohomology over
$0$
respectively (see Remark 4.1.2 for details). One of our main observations is that prismatic cohomology over
![]() ${\mathrm {B_{dR}^+}}$
can be computed by applying Simpson’s functor at infinitesimal cohomology of
${\mathrm {B_{dR}^+}}$
can be computed by applying Simpson’s functor at infinitesimal cohomology of
![]() $X/{\mathrm {B_{dR}^+}}$
with a lifted infinitesimal filtration.
$X/{\mathrm {B_{dR}^+}}$
with a lifted infinitesimal filtration.
Theorem 1.2.1. Let X be an affinoid rigid space over K that has l.c.i. singularities. Then we have the following formula
Here
![]() $\widetilde {\mathrm {Fil}}^{\bullet }$
is a lift of the infinitesimal filtration of
$\widetilde {\mathrm {Fil}}^{\bullet }$
is a lift of the infinitesimal filtration of
![]() $X/K$
along
$X/K$
along
![]() ${\mathrm {B_{dR}^+}}\rightarrow K$
, and is not canonical in general (see discussion around Definition 4.3.9). We use the following two examples to illustrate what the formula looks like.
${\mathrm {B_{dR}^+}}\rightarrow K$
, and is not canonical in general (see discussion around Definition 4.3.9). We use the following two examples to illustrate what the formula looks like.
Example 1.2.2 (Affinoid case).
Assume
![]() $X=\mathrm {Spa}(R)$
is smooth affinoid and admits a compatible system of lifts
$X=\mathrm {Spa}(R)$
is smooth affinoid and admits a compatible system of lifts
![]() $\mathrm {Spa}(\widetilde R_e)$
as in Remark 1.1.3. Then
$\mathrm {Spa}(\widetilde R_e)$
as in Remark 1.1.3. Then
![]() $R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})$
is isomorphic to
$R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})$
is isomorphic to
![]() $\widetilde \Omega ^{\bullet }$
, and the lifted infinitesimal filtration is defined as the Hodge filtration
$\widetilde \Omega ^{\bullet }$
, and the lifted infinitesimal filtration is defined as the Hodge filtration
In particular, applying Simpson’s functor at this filtered object, we get
 $$\begin{align*}\Psi(R\Gamma_{\inf}(X/{\mathrm{B_{dR}^+}}), \widetilde{\mathrm{Fil}}^{\bullet}) = \widetilde \Omega^{\bullet} \cup \frac{\widetilde\Omega^{\geq 1}}{\xi} \cup \cdots \cup \frac{\widetilde\Omega^d}{\xi^d}, \end{align*}$$
$$\begin{align*}\Psi(R\Gamma_{\inf}(X/{\mathrm{B_{dR}^+}}), \widetilde{\mathrm{Fil}}^{\bullet}) = \widetilde \Omega^{\bullet} \cup \frac{\widetilde\Omega^{\geq 1}}{\xi} \cup \cdots \cup \frac{\widetilde\Omega^d}{\xi^d}, \end{align*}$$
which is exactly the
![]() $\xi $
-divided de Rham complex as in (1.1.3). Here the union is taken inside of
$\xi $
-divided de Rham complex as in (1.1.3). Here the union is taken inside of
![]() $\widetilde \Omega ^{\bullet }[\frac {1}{\xi }]$
.
$\widetilde \Omega ^{\bullet }[\frac {1}{\xi }]$
.
Example 1.2.3 (Arithmetic case).
Assume
![]() $X=Y_K$
for an affinoid rigid space Y over a discretely valued subfield k. Under the assumption, we can take the completed base extension of the infinitesimal filtration of
$X=Y_K$
for an affinoid rigid space Y over a discretely valued subfield k. Under the assumption, we can take the completed base extension of the infinitesimal filtration of
![]() $Y/k$
along a fixed embedding
$Y/k$
along a fixed embedding
![]() $k\rightarrow {\mathrm {B_{dR}^+}}$
$k\rightarrow {\mathrm {B_{dR}^+}}$
which in particular admits a
![]() $G_k$
-action. We warn the reader that this is not the same as the infinitesimal filtration for
$G_k$
-action. We warn the reader that this is not the same as the infinitesimal filtration for
![]() $R\Gamma _{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
.
$R\Gamma _{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
.
1.3 Simplicial resolution
Another ingredient of the proof is the simplicial resolution and the left Kan extension for affinoid algebras. Not as in the algebraic setting, where one can use polynomial rings of infinite variables to resolve any algebra; in the rigid geometry a typical algebraic object is topologically generated by finite variables. It is then natural to ask if we can resolve an affinoid algebra by convergent power series rings of finite variables, thus within the rigid geometry. We give a positive answer to this question, and show in Section 5.2 that an affinoid algebra admits a simplicial resolution of Tate algebras with finite variables. Moreover, we use this to show that the analytic cotangent complex
![]() $\mathbb {L}^{\mathrm {an}}$
and the analytic derived de Rham complex
$\mathbb {L}^{\mathrm {an}}$
and the analytic derived de Rham complex
![]() ${\widehat {\mathrm {dR}}^{\mathrm {an}}}$
for an affinoid algebra can be computed using the aforementioned resolution (Proposition 5.3.1).
${\widehat {\mathrm {dR}}^{\mathrm {an}}}$
for an affinoid algebra can be computed using the aforementioned resolution (Proposition 5.3.1).
With the help of the simplicial resolution, we can apply the left Kan extension at prismatic cohomology of smooth affinoid algebras. This allows us to define a notion of derived prismatic cohomology ![]() for an arbitrary affinoid algebra R over K (see Definition 5.3.4), analogous to [Reference Bhatt and ScholzeBS22, Section 7]. As expected, derived prismatic cohomology and usual prismatic cohomology coincide for l.c.i. singularities.
for an arbitrary affinoid algebra R over K (see Definition 5.3.4), analogous to [Reference Bhatt and ScholzeBS22, Section 7]. As expected, derived prismatic cohomology and usual prismatic cohomology coincide for l.c.i. singularities.
Theorem 1.3.1. Let X be a rigid space over K that has l.c.i. singularities. There is a natural isomorphism of
![]() ${\mathrm {B_{dR}^+}}$
-
${\mathrm {B_{dR}^+}}$
-
![]() $\mathbb {E}_\infty $
-algebras
$\mathbb {E}_\infty $
-algebras
This in particular allows us to define the Hodge–Tate filtration on reduced prismatic cohomology ![]() for rigid spaces with l.c.i. singularities, which is Theorem 1.1.2 (iii).
for rigid spaces with l.c.i. singularities, which is Theorem 1.1.2 (iii).
Remark 1.3.2. For our application, we consider a slightly more general situation. Namely we show the existence of the finite type resolutions for a pair
![]() $(B,I)$
, consisting of a topologically finite type algebra B over
$(B,I)$
, consisting of a topologically finite type algebra B over
![]() ${\mathrm {A_{inf}}}/\xi ^e$
(resp.
${\mathrm {A_{inf}}}/\xi ^e$
(resp.
![]() ${\mathrm {B_{dR}^+}}/\xi ^e$
, or
${\mathrm {B_{dR}^+}}/\xi ^e$
, or
![]() ${\mathrm {B_{dR}^+}}$
) together with an ideal I. This roughly means that any closed immersion of topologically finite type affine formal schemes (resp. affinoid rigid spaces) can be simplicially resolved by regular closed immersions. In the special case when I is the zero ideal, we get the aforementioned simplicial resolution for a topological algebra itself.
${\mathrm {B_{dR}^+}}$
) together with an ideal I. This roughly means that any closed immersion of topologically finite type affine formal schemes (resp. affinoid rigid spaces) can be simplicially resolved by regular closed immersions. In the special case when I is the zero ideal, we get the aforementioned simplicial resolution for a topological algebra itself.
Remark 1.3.3. As both derived prismatic cohomology and the usual prismatic cohomology are well-defined for general rigid spaces, it is a natural question if Theorem 1.3.1 holds without the assumption on X, or if the cone of the comparing map always has bounded
![]() $\xi $
-torsion. We hope to investigate the question in the future.
$\xi $
-torsion. We hope to investigate the question in the future.
1.4 Other comments
Remark 1.4.1. We want to mention that one can define an analogous notion of prismatic cohomology for complex algebraic varieties, replacing
![]() ${\mathrm {B_{dR}^+}}$
by
${\mathrm {B_{dR}^+}}$
by
![]() $\mathbb {C}[[t]]$
. In the smooth case, this was studied independently in an unpublished article by Nils Waßmuth ([Reference WaßmuthWaß19]), where he proved the de Rham comparison and the Hodge–Tate comparison for affine smooth varieties over
$\mathbb {C}[[t]]$
. In the smooth case, this was studied independently in an unpublished article by Nils Waßmuth ([Reference WaßmuthWaß19]), where he proved the de Rham comparison and the Hodge–Tate comparison for affine smooth varieties over
![]() $\mathbb {C}$
. In general, similar to what we do in this article, one can use Simpson’s equivalence to study prismatic cohomology for complex varieties that have l.c.i. singularities, using derived de Rham cohomology ([Reference IllusieIll71], [Reference BhattBha12]) and Hartshorne’s de Rham cohomology over
$\mathbb {C}$
. In general, similar to what we do in this article, one can use Simpson’s equivalence to study prismatic cohomology for complex varieties that have l.c.i. singularities, using derived de Rham cohomology ([Reference IllusieIll71], [Reference BhattBha12]) and Hartshorne’s de Rham cohomology over
![]() $\mathbb {C}$
([Reference HartshorneHar75]).
$\mathbb {C}$
([Reference HartshorneHar75]).
Remark 1.4.2 (Crystal).
As in [Reference Bhatt and ScholzeBS23], our prismatic site ![]() admits a natural notion of crystals over the structure sheaf
admits a natural notion of crystals over the structure sheaf ![]() , which we study in Section 3. Analogous to the crystal-connection translation in the crystalline theory, a prismatic crystal corresponds to a quasi-nilpotent integrable connections that have log poles at
, which we study in Section 3. Analogous to the crystal-connection translation in the crystalline theory, a prismatic crystal corresponds to a quasi-nilpotent integrable connections that have log poles at
![]() $\{\xi =0\}$
(Definition 3.0.3, Proposition 3.0.12). In fact, important resources of prismatic crystals are those coming from the infinitesimal site
$\{\xi =0\}$
(Definition 3.0.3, Proposition 3.0.12). In fact, important resources of prismatic crystals are those coming from the infinitesimal site
![]() $(X/{\mathrm {B_{dR}^+}})_{\inf }$
, whose associated log-connections are integral. Moreover, our Theorem 1.2.1 can be extended to prismatic crystals that come from the infinitesimal site. The notion of crystals over the reduced structure sheaf
$(X/{\mathrm {B_{dR}^+}})_{\inf }$
, whose associated log-connections are integral. Moreover, our Theorem 1.2.1 can be extended to prismatic crystals that come from the infinitesimal site. The notion of crystals over the reduced structure sheaf ![]() , on the other hand, naturally form a full subcategory of twisted Higgs fields, and is closely related to the p-adic Simpson correspondence.
, on the other hand, naturally form a full subcategory of twisted Higgs fields, and is closely related to the p-adic Simpson correspondence.
Remark 1.4.3 (Non-noetherian enlargement).
As mentioned in the beginning, our prismatic site (Definition 1.1.1) consists only of those
![]() ${\mathrm {B_{dR}^+}}$
-algebras that are noetherian. However, one can still ask if we could allow other interesting but non-noetherian rings. In fact, to compare prismatic cohomology with pro-étale cohomology as in Theorem 1.1.2 (i), we consider an enlarged version of the prismatic site (with the same indiscrete topology) in Section 7.2, adding algebras coming from perfectoid rings. There we prove that cohomology of the enlarged site coincides with the smaller one in Definition 1.1.1. Similarly, adding
${\mathrm {B_{dR}^+}}$
-algebras that are noetherian. However, one can still ask if we could allow other interesting but non-noetherian rings. In fact, to compare prismatic cohomology with pro-étale cohomology as in Theorem 1.1.2 (i), we consider an enlarged version of the prismatic site (with the same indiscrete topology) in Section 7.2, adding algebras coming from perfectoid rings. There we prove that cohomology of the enlarged site coincides with the smaller one in Definition 1.1.1. Similarly, adding
![]() ${\mathbb {B}^+_{\mathrm {dR}}}(R)$
for quasi-regular semiperfectoid rings R over
${\mathbb {B}^+_{\mathrm {dR}}}(R)$
for quasi-regular semiperfectoid rings R over
![]() $\mathcal {O}_K$
would not change the cohomology.
$\mathcal {O}_K$
would not change the cohomology.
Leitfaden of the paper
The article is structured as follows. We start with Section 2 about the basics on the prismatic site over
![]() ${\mathrm {B_{dR}^+}}$
. Then we study the notion of prismatic crystals in Section 3, where we relate it to log connections, and compute their cohomology using Čech-Alexander complex. In Section 4, we give a local calculation of cohomology for an affinoid rigid space that admits a regular immersion. Here we first introduce the
${\mathrm {B_{dR}^+}}$
. Then we study the notion of prismatic crystals in Section 3, where we relate it to log connections, and compute their cohomology using Čech-Alexander complex. In Section 4, we give a local calculation of cohomology for an affinoid rigid space that admits a regular immersion. Here we first introduce the
![]() ${\mathrm {B_{dR}^+}}$
-variant of Simpson’s functor in Section 4.1. Then in Section 4.2 we construct a natural functor from infinitesimal crystals to prismatic crystals. In Section 4.3 we compute prismatic cohomology using regular immersions and Simpson’s functor, and in particular prove Theorem 1.2.1 (in Theorem 4.3.12). Next in Section 5, we prove the Hodge–Tate filtration theorem (i.e. Theorem 1.1.2 (iii)) in Theorem 5.1.1 and Corollary 5.3.6. We start by proving the version for smooth rigid spaces in Theorem 5.1.1. Then we prove the existence of simplicial resolution for affinoid algebras paired with ideals in Section 5.2. With the help of the simplicial resolution, we are able to define the notion of derived prismatic cohomology and its Hodge–Tate filtration (Section 5.3.4). Finally we show derived prismatic cohomology and usual prismatic cohomology coincide for l.c.i. singularities (Section 5.3.5), thus finishes the proof of Section 1.2.1 (iii). In Section 6, we prove the infinitesimal comparison theorem (i.e. Section 1.1.2 (ii)) in Section 6.0.1. In Section 7, we prove the pro-étale comparison theorem (i.e. Section 1.1.2 (i)) in Section 7.2.1. As a byproduct we also give a Künneth formula for reduced prismatic cohomology in Section 7.1.2. Finally we prove the formula on Galois invariant (i.e. Theorem 1.1.2 (iv)) in Section 8. We start with a brief discussion in Section 8.1 recalling basic results we need from condensed mathematics. Then we calculate Galois invariant of infinitesimal cohomology and prismatic cohomology in Section 8.2.3, Corollary 8.2.5 and Section 8.2.9.
${\mathrm {B_{dR}^+}}$
-variant of Simpson’s functor in Section 4.1. Then in Section 4.2 we construct a natural functor from infinitesimal crystals to prismatic crystals. In Section 4.3 we compute prismatic cohomology using regular immersions and Simpson’s functor, and in particular prove Theorem 1.2.1 (in Theorem 4.3.12). Next in Section 5, we prove the Hodge–Tate filtration theorem (i.e. Theorem 1.1.2 (iii)) in Theorem 5.1.1 and Corollary 5.3.6. We start by proving the version for smooth rigid spaces in Theorem 5.1.1. Then we prove the existence of simplicial resolution for affinoid algebras paired with ideals in Section 5.2. With the help of the simplicial resolution, we are able to define the notion of derived prismatic cohomology and its Hodge–Tate filtration (Section 5.3.4). Finally we show derived prismatic cohomology and usual prismatic cohomology coincide for l.c.i. singularities (Section 5.3.5), thus finishes the proof of Section 1.2.1 (iii). In Section 6, we prove the infinitesimal comparison theorem (i.e. Section 1.1.2 (ii)) in Section 6.0.1. In Section 7, we prove the pro-étale comparison theorem (i.e. Section 1.1.2 (i)) in Section 7.2.1. As a byproduct we also give a Künneth formula for reduced prismatic cohomology in Section 7.1.2. Finally we prove the formula on Galois invariant (i.e. Theorem 1.1.2 (iv)) in Section 8. We start with a brief discussion in Section 8.1 recalling basic results we need from condensed mathematics. Then we calculate Galois invariant of infinitesimal cohomology and prismatic cohomology in Section 8.2.3, Corollary 8.2.5 and Section 8.2.9.
Conventions and notations
We fix a complete perfectoid field extension
![]() $K/\mathbb {Q}_p$
such that K contains all
$K/\mathbb {Q}_p$
such that K contains all
![]() $p^\infty $
roots of unity. We also fix a generator
$p^\infty $
roots of unity. We also fix a generator
![]() $\xi =\frac {[\epsilon ]-1}{\varphi ^{-1}[\epsilon ] -1}$
for the canonical surjection
$\xi =\frac {[\epsilon ]-1}{\varphi ^{-1}[\epsilon ] -1}$
for the canonical surjection
![]() $\theta :{\mathrm {B_{dR}^+}}\rightarrow K$
, following [Reference FontaineFon94]. For a non-negative integer e, we denote
$\theta :{\mathrm {B_{dR}^+}}\rightarrow K$
, following [Reference FontaineFon94]. For a non-negative integer e, we denote
![]() ${\mathrm {A_{inf,e}}}$
to be the quotient ring
${\mathrm {A_{inf,e}}}$
to be the quotient ring
![]() ${\mathrm {A_{inf}}}/\xi ^e$
, and
${\mathrm {A_{inf}}}/\xi ^e$
, and
![]() ${\mathrm {B^+_{dR,e}}}$
to be
${\mathrm {B^+_{dR,e}}}$
to be
![]() ${\mathrm {B_{dR}^+}}/\xi ^e$
with the p-adic rational topology. We assume the basics of quasi-compact quasi-separated topologically of finite type adic spaces over a p-adic field or
${\mathrm {B_{dR}^+}}/\xi ^e$
with the p-adic rational topology. We assume the basics of quasi-compact quasi-separated topologically of finite type adic spaces over a p-adic field or
![]() ${\mathrm {B^+_{dR,e}}}$
(which we call K-rigid space or
${\mathrm {B^+_{dR,e}}}$
(which we call K-rigid space or
![]() ${\mathrm {B^+_{dR,e}}}$
-rigid spaces separately), and refer the reader to [Reference HuberHu96] for a detailed foundational study. We also use the notation
${\mathrm {B^+_{dR,e}}}$
-rigid spaces separately), and refer the reader to [Reference HuberHu96] for a detailed foundational study. We also use the notation
![]() ${\mathrm {B_{dR}^+}}\langle T_i\rangle ={\mathrm {B_{dR}^+}}\langle T_1,\ldots , T_l\rangle $
throughout the article to denote the inverse limit of affinoid rings
${\mathrm {B_{dR}^+}}\langle T_i\rangle ={\mathrm {B_{dR}^+}}\langle T_1,\ldots , T_l\rangle $
throughout the article to denote the inverse limit of affinoid rings
![]() ${\mathrm {B^+_{dR,e}}}\langle T_1,\ldots , T_l\rangle $
with respect to e. For a
${\mathrm {B^+_{dR,e}}}\langle T_1,\ldots , T_l\rangle $
with respect to e. For a
![]() ${\mathrm {B_{dR}^+}}$
-module M, we use
${\mathrm {B_{dR}^+}}$
-module M, we use
![]() $M_{\mathrm {tf}}$
to denote its
$M_{\mathrm {tf}}$
to denote its
![]() $\xi $
-torsionfree quotient
$\xi $
-torsionfree quotient
![]() $M/(\xi ^\infty \text {-torsion})$
.
$M/(\xi ^\infty \text {-torsion})$
.
We use mildly the language of infinity category and
![]() $\mathbb {E}_\infty $
-algebras throughout the article, and refer the reader to [Reference LurieLu09] and [Reference LurieLu17] for the foundations.
$\mathbb {E}_\infty $
-algebras throughout the article, and refer the reader to [Reference LurieLu09] and [Reference LurieLu17] for the foundations.
2 Prismatic site over
 ${\mathrm {B_{dR}^+}}$
${\mathrm {B_{dR}^+}}$
In this section, we define the prismatic site over
![]() ${\mathrm {B_{dR}^+}}$
for an affinoid rigid space over K.
${\mathrm {B_{dR}^+}}$
for an affinoid rigid space over K.
2.1 Algebraic preliminary
We start with an algebraic preliminary on power-bounded functions of a finite type scheme over a rigid space. The result here will be used later to show the weak finality of the prismatic envelope (Proposition 2.2.11).
Proposition 2.1.1. Let R be a topologically finite type algebra over K, and let S be a finite type algebra over R. Assume there exists a K-linear homomorphism
![]() $\phi :K\langle T\rangle \rightarrow S$
. Then the image
$\phi :K\langle T\rangle \rightarrow S$
. Then the image
![]() $\phi (T)$
is finite over R.
$\phi (T)$
is finite over R.
When R is the p-adic field K, this is proved in [Reference Hansen and LiHL20, Lemma 5.5].
Proof.
-
Step 1 We first reduce to the case when S is normal. Let
 $S_{\mathrm {red}}$
be the reduced quotient of the noetherian ring S, and let
$S_{\mathrm {red}}$
be the reduced quotient of the noetherian ring S, and let
 $S_{\mathrm {nor}}$
be the normalization of
$S_{\mathrm {nor}}$
be the normalization of
 $S_{\mathrm {red}}$
. We then have the diagram
$S_{\mathrm {red}}$
. We then have the diagram 
Denote t,
 $t_1$
and
$t_1$
and
 $t_2$
to be the image of T in S,
$t_2$
to be the image of T in S,
 $S_{\mathrm {red}}$
and
$S_{\mathrm {red}}$
and
 $S_{\mathrm {nor}}$
separately. Assume there exists a monic polynomial
$S_{\mathrm {nor}}$
separately. Assume there exists a monic polynomial
 $g(X)\in R[X]$
over R such that
$g(X)\in R[X]$
over R such that
 $g(t_2)=0$
. As the ring
$g(t_2)=0$
. As the ring
 $S_{\mathrm {red}}$
is noetherian, the normalization
$S_{\mathrm {red}}$
is noetherian, the normalization
 $S_{\mathrm {red}} \rightarrow S_{\mathrm {nor}}$
is injective. In particular,
$S_{\mathrm {red}} \rightarrow S_{\mathrm {nor}}$
is injective. In particular,
 $g(t_2)=0$
implies
$g(t_2)=0$
implies
 $g(t_1)$
is zero, which then implies that
$g(t_1)$
is zero, which then implies that
 $g(t)$
is nilpotent in S. Thus by taking
$g(t)$
is nilpotent in S. Thus by taking
 $h(X):=g(X)^N\in R[X]$
for some large N, we can find a monic polynomial
$h(X):=g(X)^N\in R[X]$
for some large N, we can find a monic polynomial
 $h(X)$
over R with
$h(X)$
over R with
 $h(t)=0$
. So it suffices to show that by passing to the normalization of S, the image of
$h(t)=0$
. So it suffices to show that by passing to the normalization of S, the image of
 $T\in K\langle T\rangle $
is finite over R.
$T\in K\langle T\rangle $
is finite over R. -
Step 2 Denote by X the scheme
 $\operatorname {\mathrm {Spec}}(S)$
, and
$\operatorname {\mathrm {Spec}}(S)$
, and
 $X^{\mathrm {an}}$
the relative analytification of S over the affinoid ring R, as a rigid space over
$X^{\mathrm {an}}$
the relative analytification of S over the affinoid ring R, as a rigid space over
 $\mathrm {Spa}(R)$
(c.f [Reference ConradCon06]). Here we note that
$\mathrm {Spa}(R)$
(c.f [Reference ConradCon06]). Here we note that
 $X^{\mathrm {an}}$
is also a normal rigid space, as the normality is checked around each K-valued point of the scheme X ([Reference BerkovichBerk93, Theorem 2.2.1]). For each affinoid open subset
$X^{\mathrm {an}}$
is also a normal rigid space, as the normality is checked around each K-valued point of the scheme X ([Reference BerkovichBerk93, Theorem 2.2.1]). For each affinoid open subset
 $U=\mathrm {Spa}(A)$
of
$U=\mathrm {Spa}(A)$
of
 $X^{\mathrm {an}}$
, the composition of rings
$X^{\mathrm {an}}$
, the composition of rings
 $K\langle T\rangle \rightarrow S\rightarrow A$
is automatically continuous by [Reference Bosch, Güntzer and RemmertBGR, 6.1.3/1]. In particular, this induces a map of rigid spaces
$K\langle T\rangle \rightarrow S\rightarrow A$
is automatically continuous by [Reference Bosch, Güntzer and RemmertBGR, 6.1.3/1]. In particular, this induces a map of rigid spaces
 $X^{\mathrm {an}} \rightarrow \mathbb {B}^1$
, where
$X^{\mathrm {an}} \rightarrow \mathbb {B}^1$
, where
 $\mathbb {B}^1=\mathrm {Spa}(K\langle T\rangle )$
is the unit disc over K. Here we note that the ring S is contained in the global section
$\mathbb {B}^1=\mathrm {Spa}(K\langle T\rangle )$
is the unit disc over K. Here we note that the ring S is contained in the global section
 $\mathcal {O}_{X^{\mathrm {an}}}(X^{\mathrm {an}})$
of the structure sheaf. Moreover, to give a map from the rigid space
$\mathcal {O}_{X^{\mathrm {an}}}(X^{\mathrm {an}})$
of the structure sheaf. Moreover, to give a map from the rigid space
 $Y=X^{\mathrm {an}}$
to
$Y=X^{\mathrm {an}}$
to
 $\mathbb {B}^1$
is equivalent to give a power-bounded global analytic function over Y, i.e. an element in
$\mathbb {B}^1$
is equivalent to give a power-bounded global analytic function over Y, i.e. an element in
 $\mathcal {O}_Y^+(Y)$
.Footnote
2
So the image
$\mathcal {O}_Y^+(Y)$
.Footnote
2
So the image
 $t=\phi (T)$
is a power-bounded element in
$t=\phi (T)$
is a power-bounded element in
 $\mathcal {O}_{X^{\mathrm {an}}}(X^{\mathrm {an}})$
.
$\mathcal {O}_{X^{\mathrm {an}}}(X^{\mathrm {an}})$
. -
Step 3 As the affine scheme
 $X=\operatorname {\mathrm {Spec}}(S)$
is finite type over the noetherian scheme
$X=\operatorname {\mathrm {Spec}}(S)$
is finite type over the noetherian scheme
 $\operatorname {\mathrm {Spec}}(R)$
, by Nagata’s compactification theorem we could find a schematic open immersion
$\operatorname {\mathrm {Spec}}(R)$
, by Nagata’s compactification theorem we could find a schematic open immersion
 $X\rightarrow \overline X$
with dense image, where
$X\rightarrow \overline X$
with dense image, where
 $\overline X$
is a proper
$\overline X$
is a proper
 $\operatorname {\mathrm {Spec}}(R)$
-scheme. In particular, by taking the relative analytification
$\operatorname {\mathrm {Spec}}(R)$
-scheme. In particular, by taking the relative analytification
 $\overline X^{\mathrm {an}}$
of
$\overline X^{\mathrm {an}}$
of
 $\overline X$
, the induced morphism
$\overline X$
, the induced morphism
 $X^{\mathrm {an}} \rightarrow \overline X^{\mathrm {an}}$
is an open immersion of rigid spaces over
$X^{\mathrm {an}} \rightarrow \overline X^{\mathrm {an}}$
is an open immersion of rigid spaces over
 $\mathrm {Spa}(R)$
whose complement is Zariski closed of codimension
$\mathrm {Spa}(R)$
whose complement is Zariski closed of codimension
 $\geq 1$
in
$\geq 1$
in
 $\overline X$
. Moreover, notice that since
$\overline X$
. Moreover, notice that since
 $X^{\mathrm {an}}$
is normal, it is also an open dense subspace in the normalization of
$X^{\mathrm {an}}$
is normal, it is also an open dense subspace in the normalization of
 $\overline X^{\mathrm {an}}$
, so we can thus assume
$\overline X^{\mathrm {an}}$
, so we can thus assume
 $\overline X^{\mathrm {an}}$
is normal ([Reference ConradCon99, Theorem 2.1.2]). We apply the first Riemann extension theorem ([Reference BartenwerferBar76,
$\overline X^{\mathrm {an}}$
is normal ([Reference ConradCon99, Theorem 2.1.2]). We apply the first Riemann extension theorem ([Reference BartenwerferBar76,
 $\S$
3, Theorem]) for the open immersion
$\S$
3, Theorem]) for the open immersion
 $X^{\mathrm {an}} \rightarrow \overline X^{\mathrm {an}}$
into the proper normal rigid space, to get the isomorphism
$X^{\mathrm {an}} \rightarrow \overline X^{\mathrm {an}}$
into the proper normal rigid space, to get the isomorphism  $$\begin{align*}\mathcal{O}^+_{X^{\mathrm{an}}}(X^{\mathrm{an}})= \mathcal{O}^+_{\overline X^{\mathrm{an}}}(\overline X^{\mathrm{an}}). \end{align*}$$
$$\begin{align*}\mathcal{O}^+_{X^{\mathrm{an}}}(X^{\mathrm{an}})= \mathcal{O}^+_{\overline X^{\mathrm{an}}}(\overline X^{\mathrm{an}}). \end{align*}$$
But since
 $\overline X^{\mathrm {an}}$
is proper over
$\overline X^{\mathrm {an}}$
is proper over
 $\mathrm {Spa}(R)$
, the global section of the structure sheaf
$\mathrm {Spa}(R)$
, the global section of the structure sheaf
 $\mathcal {O}_{\overline X^{\mathrm {an}}}(\overline X^{\mathrm {an}})$
is a finite R-algebra. In this way, the element
$\mathcal {O}_{\overline X^{\mathrm {an}}}(\overline X^{\mathrm {an}})$
is a finite R-algebra. In this way, the element
 $t=\phi (T)\in \mathcal {O}^+_{X^{\mathrm {an}}}(X^{\mathrm {an}})= \mathcal {O}^+_{\overline X^{\mathrm {an}}}(\overline X^{\mathrm {an}})\subset \mathcal {O}_{\overline X^{\mathrm {an}}}(\overline X^{\mathrm {an}})$
is also finite over R, and we are done.
$t=\phi (T)\in \mathcal {O}^+_{X^{\mathrm {an}}}(X^{\mathrm {an}})= \mathcal {O}^+_{\overline X^{\mathrm {an}}}(\overline X^{\mathrm {an}})\subset \mathcal {O}_{\overline X^{\mathrm {an}}}(\overline X^{\mathrm {an}})$
is also finite over R, and we are done.
The proof above also shows the following result.
Corollary 2.1.2. Let Y be the relative analytification of a finite type scheme over an affinoid rigid space
![]() $\mathrm {Spa}(R)$
. Then any power-bounded function of Y is finite over R.
$\mathrm {Spa}(R)$
. Then any power-bounded function of Y is finite over R.
The analogous result of Proposition 2.1.1 holds for
![]() ${\mathrm {B^+_{dR,m}}}$
as well.
${\mathrm {B^+_{dR,m}}}$
as well.
Corollary 2.1.3. Let R be a topologically finite type algebra over
![]() ${\mathrm {B^+_{dR,m}}}$
, and let S be a finite type algebra over R. Assume there exists a K-linear homomorphism
${\mathrm {B^+_{dR,m}}}$
, and let S be a finite type algebra over R. Assume there exists a K-linear homomorphism
![]() $\phi :{\mathrm {B^+_{dR,m}}}\langle T\rangle \rightarrow S$
. Then the image
$\phi :{\mathrm {B^+_{dR,m}}}\langle T\rangle \rightarrow S$
. Then the image
![]() $\phi (T)$
is finite over R.
$\phi (T)$
is finite over R.
Proof. By Proposition 2.1.1, the image
![]() $\phi (T)$
mod
$\phi (T)$
mod
![]() $\xi $
is finite over
$\xi $
is finite over
![]() $R/\xi $
. In particular, there exists a polynomial
$R/\xi $
. In particular, there exists a polynomial
![]() $g(X)\in {\mathrm {B^+_{dR,m}}}[X]$
, such that
$g(X)\in {\mathrm {B^+_{dR,m}}}[X]$
, such that
![]() $g(\phi (T))=0$
mod
$g(\phi (T))=0$
mod
![]() $\xi $
. Thus by taking a power of
$\xi $
. Thus by taking a power of
![]() $g(X)$
we get the result.
$g(X)$
we get the result.
2.2 Prismatic site
In this subsection, we introduce the basics on the prismatic site over
![]() ${\mathrm {B_{dR}^+}}$
.
${\mathrm {B_{dR}^+}}$
.
We start by defining the prismatic site.
Definition 2.2.1. Let
![]() $X=\mathrm {Spa}(R)$
be an affinoid rigid space over K.
$X=\mathrm {Spa}(R)$
be an affinoid rigid space over K.
-
(i) A
 ${\mathrm {B_{dR}^+}}$
-prism (or in short a prism)
${\mathrm {B_{dR}^+}}$
-prism (or in short a prism)
 $(B,\xi B)$
over X is defined by the following diagram of maps
$(B,\xi B)$
over X is defined by the following diagram of maps 
where B is a noetherian
 ${\mathrm {B_{dR}^+}}$
-algebra satisfying the conditions below:
${\mathrm {B_{dR}^+}}$
-algebra satisfying the conditions below:-
• it is
 $\xi $
-torsion free and
$\xi $
-torsion free and
 $\xi $
-adic complete;
$\xi $
-adic complete; -
• each quotient
 $B/\xi ^m$
is a finite type algebra over some
$B/\xi ^m$
is a finite type algebra over some
 ${\mathrm {B^+_{dR,m}}}\langle T_i\rangle $
.
${\mathrm {B^+_{dR,m}}}\langle T_i\rangle $
.
The map
 $B\rightarrow B/\xi $
is the natural surjection, and
$B\rightarrow B/\xi $
is the natural surjection, and
 $f:R \rightarrow B/\xi $
is a map of K-algebras.
$f:R \rightarrow B/\xi $
is a map of K-algebras. -
-
(ii) A map of prisms
 $(B,\xi B)\rightarrow (B',\xi B')$
over R is defined as a commutative diagram between the data above.
$(B,\xi B)\rightarrow (B',\xi B')$
over R is defined as a commutative diagram between the data above. -
(iii) The prismatic site of
 $X=\mathrm {Spa}(R)$
over
$X=\mathrm {Spa}(R)$
over
 ${\mathrm {B_{dR}^+}}$
, denoted as
${\mathrm {B_{dR}^+}}$
, denoted as  , is defined on the opposite category of all
, is defined on the opposite category of all
 ${\mathrm {B_{dR}^+}}$
-prisms over X and is equipped with the indiscrete topology.
${\mathrm {B_{dR}^+}}$
-prisms over X and is equipped with the indiscrete topology.
Remark 2.2.2. By definition, given a prism
![]() $(B,\xi B)$
over R, the only covering of the prism
$(B,\xi B)$
over R, the only covering of the prism
![]() $(B,\xi B)$
is the identity map from itself.
$(B,\xi B)$
is the identity map from itself.
Remark 2.2.3. Except for everything in the rational level (namely over
![]() $\mathbb {Q}$
), the most obvious simplification from [Reference Bhatt and ScholzeBS22] is that a prism does not come with a delta structure defined integrally. Namely there is no Frobenius lift structure.
$\mathbb {Q}$
), the most obvious simplification from [Reference Bhatt and ScholzeBS22] is that a prism does not come with a delta structure defined integrally. Namely there is no Frobenius lift structure.
Remark 2.2.4. To save us from complicated notations, we will abbreviate notation of a prism
![]() $(B,\xi B)$
simply into B from time to time, when the meaning is clear.
$(B,\xi B)$
simply into B from time to time, when the meaning is clear.
Next we define the notion of the prismatic envelope.
Definition 2.2.5. Let
![]() $B\rightarrow B'$
be a surjection of complete noetherian
$B\rightarrow B'$
be a surjection of complete noetherian
![]() ${\mathrm {B_{dR}^+}}$
-algebras, and let I be the kernel ideal. The prismatic envelope of
${\mathrm {B_{dR}^+}}$
-algebras, and let I be the kernel ideal. The prismatic envelope of
![]() $B'$
in B, is defined as the
$B'$
in B, is defined as the
![]() ${\mathrm {B_{dR}^+}}$
-algebra
${\mathrm {B_{dR}^+}}$
-algebra
 $$\begin{align*}B\left[\frac{I}{\xi}\right]{\wedge_{\mathrm{tf}}}:= \left(B[x_1, \ldots, x_m]/(\xi x_i-f_i, 1\leq i\leq m)\right)^\wedge/(\xi^\infty\text{-}torsion), \end{align*}$$
$$\begin{align*}B\left[\frac{I}{\xi}\right]{\wedge_{\mathrm{tf}}}:= \left(B[x_1, \ldots, x_m]/(\xi x_i-f_i, 1\leq i\leq m)\right)^\wedge/(\xi^\infty\text{-}torsion), \end{align*}$$
where
![]() $(f_i)$
is a finite set of generators for the ideal I, and
$(f_i)$
is a finite set of generators for the ideal I, and
![]() $(-)^\wedge $
is the classical
$(-)^\wedge $
is the classical
![]() $\xi $
-adic completion.
$\xi $
-adic completion.
To make sense of the notation that is independent of the choice of generators, we have the following easy property.
Lemma 2.2.6. Let I be an ideal of a noetherian
![]() ${\mathrm {B_{dR}^+}}$
-algebra B, and let
${\mathrm {B_{dR}^+}}$
-algebra B, and let
![]() $(f_i)\subset (f_i,g)$
be two finite sets of generators of I. Then the natural map of rings below is an isomorphism
$(f_i)\subset (f_i,g)$
be two finite sets of generators of I. Then the natural map of rings below is an isomorphism
In particular, the ring
![]() $B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}/(\xi ^\infty \text {-}torsion)$
in Definition 2.2.5 is independent of the choice of generators of I.
$B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}/(\xi ^\infty \text {-}torsion)$
in Definition 2.2.5 is independent of the choice of generators of I.
Proof. As a finite type algebra over B is noetherian, its formal completion along
![]() $\xi =0$
identifies the
$\xi =0$
identifies the
![]() $\xi ^\infty $
-elements before and after the completion ([Sta, Tag 05E9]). In particular, we can switch the order of the
$\xi ^\infty $
-elements before and after the completion ([Sta, Tag 05E9]). In particular, we can switch the order of the
![]() $\xi $
-completion and the
$\xi $
-completion and the
![]() $\xi $
-torsionfree quotient, and it suffices to show the isomorphism of the map between incomplete algebras
$\xi $
-torsionfree quotient, and it suffices to show the isomorphism of the map between incomplete algebras
By assumption, since
![]() $(f_i)$
generates the ideal, we can write
$(f_i)$
generates the ideal, we can write
![]() $g=\sum a_jf_j$
. So we get the formula in the second ring above
$g=\sum a_jf_j$
. So we get the formula in the second ring above
Thus by the
![]() $\xi $
-torsion freeness of the target ring, the map above is surjective. Moreover, we can define a section of the above map by mapping y onto
$\xi $
-torsion freeness of the target ring, the map above is surjective. Moreover, we can define a section of the above map by mapping y onto
![]() $\sum a_jx_j$
, which is possible by the
$\sum a_jx_j$
, which is possible by the
![]() $\xi $
-torsion freeness of the quotient. Hence we get the isomorphism.
$\xi $
-torsion freeness of the quotient. Hence we get the isomorphism.
Remark 2.2.7. In the above setting, we note that as a B-algebra, the envelope is automatically complete I-adically, by the
![]() $\xi $
-adic completeness and the
$\xi $
-adic completeness and the
![]() $\xi $
-divisibility of the image of I in the envelope. In particular, the map
$\xi $
-divisibility of the image of I in the envelope. In particular, the map
![]() $B\rightarrow B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
factors through the I-adic completion of B. As a consequence, mod any power of
$B\rightarrow B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
factors through the I-adic completion of B. As a consequence, mod any power of
![]() $\xi $
, there is a natural isomorphism of B-algebras
$\xi $
, there is a natural isomorphism of B-algebras
 $$\begin{align*}B\left[\frac{I}{\xi}\right]^\wedge_{\mathrm{tf}}\cong D\left[\frac{I}{\xi}\right]^\wedge_{\mathrm{tf}}, \end{align*}$$
$$\begin{align*}B\left[\frac{I}{\xi}\right]^\wedge_{\mathrm{tf}}\cong D\left[\frac{I}{\xi}\right]^\wedge_{\mathrm{tf}}, \end{align*}$$
where D is the formal completion of B along the ideal I.
Remark 2.2.8. Let B and I be as in Definition 2.2.5, and let
![]() $R=B/(I,\xi )$
. As the image of
$R=B/(I,\xi )$
. As the image of
![]() $(I,\xi )$
under the composition
$(I,\xi )$
under the composition
 $$\begin{align*}B \rightarrow B\left[\frac{I}{\xi}\right]^\wedge_{\mathrm{tf}} \rightarrow B\left[\frac{I}{\xi}\right]^\wedge_{\mathrm{tf}}/\xi \end{align*}$$
$$\begin{align*}B \rightarrow B\left[\frac{I}{\xi}\right]^\wedge_{\mathrm{tf}} \rightarrow B\left[\frac{I}{\xi}\right]^\wedge_{\mathrm{tf}}/\xi \end{align*}$$
is zero, it naturally induces a continuous map
![]() $f:R=B/(I,\xi ) \rightarrow B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}/ \xi $
. This in particular produces a prism
$f:R=B/(I,\xi ) \rightarrow B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}/ \xi $
. This in particular produces a prism
![]() $B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
over R. Furthermore, for a prism
$B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
over R. Furthermore, for a prism
![]() $(B',\xi B')$
in
$(B',\xi B')$
in ![]() , to give a continuous
, to give a continuous
![]() ${\mathrm {B_{dR}^+}}$
-map from the complete
${\mathrm {B_{dR}^+}}$
-map from the complete
![]() ${\mathrm {B_{dR}^+}}$
-algebra B to
${\mathrm {B_{dR}^+}}$
-algebra B to
![]() $B'$
such that the composition with
$B'$
such that the composition with
![]() $B'\rightarrow B'/\xi $
factors through the surjection
$B'\rightarrow B'/\xi $
factors through the surjection
![]() $B\rightarrow R$
, it is equivalent to give a map of prisms from
$B\rightarrow R$
, it is equivalent to give a map of prisms from
![]() $(B\left[\frac {I}{\xi }\right]^\wedge_{\mathrm {tf}}), B\left[\frac {I}{\xi }\right]^\wedge _{\mathrm{tf}} / \xi)$
to
$(B\left[\frac {I}{\xi }\right]^\wedge_{\mathrm {tf}}), B\left[\frac {I}{\xi }\right]^\wedge _{\mathrm{tf}} / \xi)$
to
![]() $(B', \xi B')$
, by the
$(B', \xi B')$
, by the
![]() $\xi $
-torsion free assumption on
$\xi $
-torsion free assumption on
![]() $B'$
.
$B'$
.
Definition 2.2.9. We define the prism ![]() associated to the envelope for the surjection
associated to the envelope for the surjection
![]() $B\rightarrow I$
to be the one associated to the ring
$B\rightarrow I$
to be the one associated to the ring
![]() $B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
.
$B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
.
To simplify the notation, we also use the same symbol ![]() to denote the ring
to denote the ring
![]() $B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
itself.
$B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
itself.
Example 2.2.10. Let B be the limit ring
![]() ${\mathrm {B_{dR}^+}}\langle T,S\rangle = \varprojlim _n{\mathrm {B_{dR}^+}}/\xi ^n\langle T,S\rangle $
, and assume R is the quotient ring
${\mathrm {B_{dR}^+}}\langle T,S\rangle = \varprojlim _n{\mathrm {B_{dR}^+}}/\xi ^n\langle T,S\rangle $
, and assume R is the quotient ring
![]() $K\langle T\rangle $
of B. Then the envelope of the surjection
$K\langle T\rangle $
of B. Then the envelope of the surjection
![]() $B\rightarrow {\mathrm {B_{dR}^+}}\langle T\rangle $
is given by the following formula
$B\rightarrow {\mathrm {B_{dR}^+}}\langle T\rangle $
is given by the following formula
 $$\begin{align*}{\mathrm{B_{dR}^+}}\langle T\rangle[\frac{S}{\xi}]^\wedge=\varprojlim_n \left( {\mathrm{B^+_{dR,n}}}\langle T\rangle[\frac{S}{\xi}] \right). \end{align*}$$
$$\begin{align*}{\mathrm{B_{dR}^+}}\langle T\rangle[\frac{S}{\xi}]^\wedge=\varprojlim_n \left( {\mathrm{B^+_{dR,n}}}\langle T\rangle[\frac{S}{\xi}] \right). \end{align*}$$
Thanks to Proposition 2.1.1, the envelope of a
![]() ${\mathrm {B_{dR}^+}}$
-lift of R into a formally smooth topological algebra over
${\mathrm {B_{dR}^+}}$
-lift of R into a formally smooth topological algebra over
![]() ${\mathrm {B_{dR}^+}}$
covers the final object in the prismatic topos.
${\mathrm {B_{dR}^+}}$
covers the final object in the prismatic topos.
Proposition 2.2.11. Let P be the ring
![]() ${\mathrm {B_{dR}^+}}\langle T_i\rangle $
and I be an ideal of P, and
${\mathrm {B_{dR}^+}}\langle T_i\rangle $
and I be an ideal of P, and
![]() $f_0:P \rightarrow R:=P/(I,\xi )$
be the quotient. Then the prism
$f_0:P \rightarrow R:=P/(I,\xi )$
be the quotient. Then the prism ![]() associated to the envelope for
associated to the envelope for
![]() $P\rightarrow R$
covers the final object of the topos
$P\rightarrow R$
covers the final object of the topos ![]() .
.
Proof. Let
![]() $(B,\xi B)$
be a prism over R. We need to show that it admits a map from the prism associated to the envelope
$(B,\xi B)$
be a prism over R. We need to show that it admits a map from the prism associated to the envelope
![]() $P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
. We first notice the following commutative diagram
$P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
. We first notice the following commutative diagram

Then we show the diagram lifts to a homomorphism
![]() $P\rightarrow B$
over
$P\rightarrow B$
over
![]() ${\mathrm {B_{dR}^+}}$
. By the assumption of a prism in Definition 2.2.1 (ii), the ring
${\mathrm {B_{dR}^+}}$
. By the assumption of a prism in Definition 2.2.1 (ii), the ring
![]() $B/\xi ^m$
admits a surjection from
$B/\xi ^m$
admits a surjection from
![]() ${\mathrm {B^+_{dR,m}}}\langle a_{j_m}\rangle [b_{l_m}]$
for finite sets of
${\mathrm {B^+_{dR,m}}}\langle a_{j_m}\rangle [b_{l_m}]$
for finite sets of
![]() $j_m$
and
$j_m$
and
![]() $l_m$
, compatible with
$l_m$
, compatible with
![]() $m\in \mathbb {N}$
. Moreover, by enlarging the set of
$m\in \mathbb {N}$
. Moreover, by enlarging the set of
![]() $j_m$
and
$j_m$
and
![]() $l_m$
inductively for each m, we may assume a compatible system of surjections as below
$l_m$
inductively for each m, we may assume a compatible system of surjections as below

In particular, when
![]() $m=1$
, the quotient ring
$m=1$
, the quotient ring
![]() $B/\xi $
is a finite type algebra over an affinoid ring
$B/\xi $
is a finite type algebra over an affinoid ring
![]() $K\langle a_{j_1}\rangle $
, and it admits a map from
$K\langle a_{j_1}\rangle $
, and it admits a map from
![]() $P/\xi =K\langle T_i\rangle $
by the diagram above. Note that by Proposition 2.1.1 the image
$P/\xi =K\langle T_i\rangle $
by the diagram above. Note that by Proposition 2.1.1 the image
![]() $t_i$
of each
$t_i$
of each
![]() $T_i$
in
$T_i$
in
![]() $B/\xi $
is integral over
$B/\xi $
is integral over
![]() $K\langle a_{j_1}\rangle $
. Moreover, by Corollary 2.1.3 any lift
$K\langle a_{j_1}\rangle $
. Moreover, by Corollary 2.1.3 any lift
![]() $\widetilde t_i$
of
$\widetilde t_i$
of
![]() $t_i$
in
$t_i$
in
![]() $B/\xi ^m$
is integral over
$B/\xi ^m$
is integral over
![]() ${\mathrm {B^+_{dR,m}}}\langle a_{j_m}\rangle $
. So by choosing compatible lifts
${\mathrm {B^+_{dR,m}}}\langle a_{j_m}\rangle $
. So by choosing compatible lifts
![]() $\widetilde t_i$
of
$\widetilde t_i$
of
![]() $t_i$
in
$t_i$
in
![]() $B/\xi ^m$
for each
$B/\xi ^m$
for each
![]() $m\in \mathbb {N}$
, we could extend the map
$m\in \mathbb {N}$
, we could extend the map
![]() ${\mathrm {B^+_{dR,m}}}\langle a_{j_m}\rangle \rightarrow B/\xi $
to
${\mathrm {B^+_{dR,m}}}\langle a_{j_m}\rangle \rightarrow B/\xi $
to
![]() ${\mathrm {B^+_{dR,m}}}\langle a_{j_m}; c_i\rangle \rightarrow B/\xi ^m$
, where
${\mathrm {B^+_{dR,m}}}\langle a_{j_m}; c_i\rangle \rightarrow B/\xi ^m$
, where
![]() $c_i$
maps onto lifts
$c_i$
maps onto lifts
![]() $\widetilde t_i$
of
$\widetilde t_i$
of
![]() $t_i\in B/\xi $
. As a consequence, we can enlarge variables
$t_i\in B/\xi $
. As a consequence, we can enlarge variables
![]() $\{a_{j_m}\}$
into
$\{a_{j_m}\}$
into
![]() $\{a_{j_m}, c_i\}$
to get a surjection
$\{a_{j_m}, c_i\}$
to get a surjection
![]() ${\mathrm {B^+_{dR,m}}}\langle a_{j_m, c_i}\rangle [b_{l_m}]\rightarrow B/\xi ^m\rightarrow B/\xi $
. In particular, we may assume the map
${\mathrm {B^+_{dR,m}}}\langle a_{j_m, c_i}\rangle [b_{l_m}]\rightarrow B/\xi ^m\rightarrow B/\xi $
. In particular, we may assume the map
![]() $P={\mathrm {B_{dR}^+}}\langle T_i\rangle \rightarrow B/\xi $
above factors through the surjections as below:
$P={\mathrm {B_{dR}^+}}\langle T_i\rangle \rightarrow B/\xi $
above factors through the surjections as below:

which is compatible with
![]() $m\in \mathbb {N}$
. So by taking an inverse limit with respect to m, we get the commutative diagram
$m\in \mathbb {N}$
. So by taking an inverse limit with respect to m, we get the commutative diagram

At last, since the image of the ideal
![]() $I\subset P$
in B is killed by
$I\subset P$
in B is killed by
![]() $\xi $
and the ring B is
$\xi $
and the ring B is
![]() $\xi $
-torsion free, the homomorphism
$\xi $
-torsion free, the homomorphism
![]() $P\rightarrow B$
induces a natural commutative diagram as below
$P\rightarrow B$
induces a natural commutative diagram as below

where
![]() $P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
is the
$P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
is the
![]() $\xi $
-adic completion of the
$\xi $
-adic completion of the
![]() ${\mathrm {B_{dR}^+}}$
-algebra
${\mathrm {B_{dR}^+}}$
-algebra
![]() $P[\frac {I}{\xi }]$
. Hence the ring
$P[\frac {I}{\xi }]$
. Hence the ring
![]() $P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
together with the R-algebra structure of its quotient forms a prism
$P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
together with the R-algebra structure of its quotient forms a prism ![]() , and we get a map of prisms
, and we get a map of prisms ![]() .
.
3 Prismatic crystal and log connection
There are two natural structure sheaves over ![]() , defined as follows:
, defined as follows:

This allows us to define the notion of the crystal over the prismatic site, analogous to the infinitesimal story.
Definition 3.0.1. A (coherent) prismatic crystal over
![]() $X/{\mathrm {B_{dR}^+}}$
is defined as a sheaf
$X/{\mathrm {B_{dR}^+}}$
is defined as a sheaf
![]() $\mathcal {F}$
of
$\mathcal {F}$
of ![]() -modules over
-modules over ![]() , satisfying
, satisfying
-
(a) each
 $\mathcal {F}(B,\xi B)$
is a finite module over B, for every prism
$\mathcal {F}(B,\xi B)$
is a finite module over B, for every prism  ;
; -
(b) for every map of prisms
 $(B,\xi B)\rightarrow (B',\xi B')$
, the natural base change map below is an isomorphism of
$(B,\xi B)\rightarrow (B',\xi B')$
, the natural base change map below is an isomorphism of
 $B'$
-modules
$B'$
-modules  $$\begin{align*}\mathcal{F}(B,\xi B)\otimes_B B' \longrightarrow \mathcal{F}(B',\xi B'). \end{align*}$$
$$\begin{align*}\mathcal{F}(B,\xi B)\otimes_B B' \longrightarrow \mathcal{F}(B',\xi B'). \end{align*}$$
Notice that given any prismatic crystal
![]() $\mathcal {F}$
, there is a way to associate a reduction
$\mathcal {F}$
, there is a way to associate a reduction
![]() $\overline {\mathcal {F}}$
to it, by assigning
$\overline {\mathcal {F}}$
to it, by assigning
This in particular gives a prismatic crystal over the reduced structure sheaf ![]() .
.
Definition 3.0.2. A prismatic crystal
![]() $\mathcal {F}$
is called flat if each B-module
$\mathcal {F}$
is called flat if each B-module
![]() $\mathcal {F}(B,\xi B)$
is locally free over B. It is called reduced if each B-module
$\mathcal {F}(B,\xi B)$
is locally free over B. It is called reduced if each B-module
![]() $\mathcal {F}(B,\xi B)$
is locally free over
$\mathcal {F}(B,\xi B)$
is locally free over
![]() $B/\xi $
.
$B/\xi $
.
Analogous to the infinitesimal theory as in [Reference GuoGuo24, Theorem 3.3.1], a crystal can be described as an integrable log connection over the envelope.
To start, let
![]() $B=\varprojlim _m B_m$
be an inverse limit of flat noetherian
$B=\varprojlim _m B_m$
be an inverse limit of flat noetherian
![]() ${\mathrm {B^+_{dR,m}}}$
-algebras
${\mathrm {B^+_{dR,m}}}$
-algebras
![]() $B_m$
, such that the transition maps induce isomorphisms
$B_m$
, such that the transition maps induce isomorphisms
![]() $B_m\otimes _{{\mathrm {B^+_{dR,m}}}} \mathrm {B_{dR,m-1}^+} \rightarrow B_{m-1}$
, and
$B_m\otimes _{{\mathrm {B^+_{dR,m}}}} \mathrm {B_{dR,m-1}^+} \rightarrow B_{m-1}$
, and
![]() $B_1$
is isomorphic to a formal completion of some Tate algebra
$B_1$
is isomorphic to a formal completion of some Tate algebra
![]() $K\langle T_1,\ldots , T_l\rangle $
. Let I be an ideal of B. Denote
$K\langle T_1,\ldots , T_l\rangle $
. Let I be an ideal of B. Denote ![]() to be
to be
![]() $\xi $
-torsion free quotient of the classical
$\xi $
-torsion free quotient of the classical
![]() $\xi $
-completion of the noetherian ring
$\xi $
-completion of the noetherian ring
![]() $B[\frac {I}{\xi }]$
.
$B[\frac {I}{\xi }]$
.
Fix a map
![]() $P:={\mathrm {B_{dR}^+}}\langle T_i\rangle \rightarrow B$
lifting
$P:={\mathrm {B_{dR}^+}}\langle T_i\rangle \rightarrow B$
lifting
![]() $K\langle T_i\rangle \rightarrow B_1$
as above. We first notice that there is a natural diagram of
$K\langle T_i\rangle \rightarrow B_1$
as above. We first notice that there is a natural diagram of
![]() ${\mathrm {B_{dR}^+}}$
-linear continuous differentials
${\mathrm {B_{dR}^+}}$
-linear continuous differentials

Here
![]() $\Omega _{P/{\mathrm {B_{dR}^+}}}^1$
is the inverse limit of the p-adic continuous Kähler differential of
$\Omega _{P/{\mathrm {B_{dR}^+}}}^1$
is the inverse limit of the p-adic continuous Kähler differential of
![]() $P_m/{\mathrm {B^+_{dR,m}}}$
, and horizontal maps are continuous with respect to
$P_m/{\mathrm {B^+_{dR,m}}}$
, and horizontal maps are continuous with respect to
![]() $\xi $
-adic topology, such that their mod
$\xi $
-adic topology, such that their mod
![]() $\xi $
-reduction are continuous differentials with respect to
$\xi $
-reduction are continuous differentials with respect to
![]() $K \langle T_i\rangle $
and
$K \langle T_i\rangle $
and
![]() $B/\xi $
. On the other hand, the vertical maps are natural maps induced from the inclusions
$B/\xi $
. On the other hand, the vertical maps are natural maps induced from the inclusions
 $$\begin{align*}\Omega_{P/{\mathrm{B_{dR}^+}}}^1\subset \frac{\Omega_{P/{\mathrm{B_{dR}^+}}}^1}{\xi} \subset \Omega_{P/{\mathrm{B_{dR}^+}}}^1\otimes_{\mathrm{B_{dR}^+}} \mathrm{B_{dR}}. \end{align*}$$
$$\begin{align*}\Omega_{P/{\mathrm{B_{dR}^+}}}^1\subset \frac{\Omega_{P/{\mathrm{B_{dR}^+}}}^1}{\xi} \subset \Omega_{P/{\mathrm{B_{dR}^+}}}^1\otimes_{\mathrm{B_{dR}^+}} \mathrm{B_{dR}}. \end{align*}$$
In particular, for an element
![]() $\frac {f_1\cdots f_i}{\xi ^i}$
in
$\frac {f_1\cdots f_i}{\xi ^i}$
in ![]() with
with
![]() $f_1,\ldots , f_i\in I$
, we have
$f_1,\ldots , f_i\in I$
, we have

Now we can consider a generalization to the coefficient theory.
Definition 3.0.3. For a finite generated module M over ![]() , a log connection of M is defined as an
, a log connection of M is defined as an
![]() ${\mathrm {B_{dR}^+}}$
-linear morphism
${\mathrm {B_{dR}^+}}$
-linear morphism

such that for
![]() $x\in M$
and
$x\in M$
and ![]() we have
we have
where
![]() $df$
is the continuous relative differential of
$df$
is the continuous relative differential of ![]() over
over
![]() ${\mathrm {B_{dR}^+}}$
constructed above.
${\mathrm {B_{dR}^+}}$
constructed above.
The connection is called integrable if the induced composition below is zero

Here the map ![]() is given by the formula
is given by the formula
Remark 3.0.4. When B is the J-adic completion of
![]() $P={\mathrm {B_{dR}^+}}\langle T_i\rangle $
for some ideal J in P, and I is the zero ideal, the above definition extends the notion of connections in the infinitesimal theory defined in [Reference GuoGuo24, Definition 3.1.8], allowing a log pole at
$P={\mathrm {B_{dR}^+}}\langle T_i\rangle $
for some ideal J in P, and I is the zero ideal, the above definition extends the notion of connections in the infinitesimal theory defined in [Reference GuoGuo24, Definition 3.1.8], allowing a log pole at
![]() $\{\xi =0\}$
.
$\{\xi =0\}$
.
Remark 3.0.5. In the special case when ![]() factors through
factors through ![]() , we call the connection integral. We will see soon that log connections coming from the infinitesimal site are all integral.
, we call the connection integral. We will see soon that log connections coming from the infinitesimal site are all integral.
Different from the infinitesimal theory, not all of the integrable log connections come from crystal. This is more similar to the schematic theory in mixed characteristic, where quasi-nilpotence condition is needed in order to make the transition power series associated to a connection to be convergent (c.f. [Reference Berthelot and OgusBO78]). We now define the
![]() ${\mathrm {B_{dR}^+}}$
-analogue of the quasi-nilpotence as below.
${\mathrm {B_{dR}^+}}$
-analogue of the quasi-nilpotence as below.
Definition 3.0.6. Let
![]() $B, ~I, ~P={\mathrm {B_{dR}^+}}\langle T_1,\ldots ,T_l\rangle $
be as above, and
$B, ~I, ~P={\mathrm {B_{dR}^+}}\langle T_1,\ldots ,T_l\rangle $
be as above, and
![]() $(M,\nabla )$
be a log connection over
$(M,\nabla )$
be a log connection over ![]() . We say
. We say
![]() $(M,\nabla )$
is quasi-nilpotent if for any element
$(M,\nabla )$
is quasi-nilpotent if for any element
![]() $x\in M$
, the following power series are convergent in the module
$x\in M$
, the following power series are convergent in the module ![]()
 $$\begin{align*}\sum_{E=(e_i)} \prod_{i=1}^l \widetilde\nabla_i^{e_i}(x)\otimes \frac{\widetilde \delta_i^{e_i}}{e_i!}. \end{align*}$$
$$\begin{align*}\sum_{E=(e_i)} \prod_{i=1}^l \widetilde\nabla_i^{e_i}(x)\otimes \frac{\widetilde \delta_i^{e_i}}{e_i!}. \end{align*}$$
Here
![]() $\widetilde \nabla _i:M\rightarrow M$
is defined as the composition
$\widetilde \nabla _i:M\rightarrow M$
is defined as the composition

where j above is not equals to i.
Remark 3.0.7. As an exercise of Taylor expansion in calculus, it can be shown that in order to show the quasi-nilpotence, it is enough to check the convergence for a set of generators in Definition 3.0.6.
Remark 3.0.8. The map
![]() $\widetilde \nabla _i$
should be thought as the multiplication of
$\widetilde \nabla _i$
should be thought as the multiplication of
![]() $\xi $
with the classically defined map
$\xi $
with the classically defined map
![]() $\nabla _i$
, where the latter is the composition of
$\nabla _i$
, where the latter is the composition of
![]() $\nabla $
and the pairing with
$\nabla $
and the pairing with
![]() $\frac {\partial }{\partial T_i}$
. More explicitly the pairing map sends
$\frac {\partial }{\partial T_i}$
. More explicitly the pairing map sends
![]() $\Omega _{P/{\mathrm {B_{dR}^+}}}^1$
to P by the formula
$\Omega _{P/{\mathrm {B_{dR}^+}}}^1$
to P by the formula
This could be made precise either by inverting
![]() $\xi $
or when M has no
$\xi $
or when M has no
![]() $\xi $
-torsion.
$\xi $
-torsion.
Example 3.0.9. As a simple example of a quasi-nilpotent log connection, let
![]() $R=K \langle T\rangle , P={\mathrm {B_{dR}^+}} \langle T\rangle $
and
$R=K \langle T\rangle , P={\mathrm {B_{dR}^+}} \langle T\rangle $
and
![]() $I=(0)$
, so that
$I=(0)$
, so that ![]() . Let
. Let
![]() $(M,\nabla )=({\mathrm {B_{dR}^+}} \langle T\rangle ,d)$
be the natural continuous differential operator on the structure sheaf with
$(M,\nabla )=({\mathrm {B_{dR}^+}} \langle T\rangle ,d)$
be the natural continuous differential operator on the structure sheaf with
![]() $df(T)=f'(T)dT$
. Then for an element
$df(T)=f'(T)dT$
. Then for an element
![]() $f(T)\in {\mathrm {B_{dR}^+}} \langle T\rangle $
, the power series in Definition 3.0.6 is
$f(T)\in {\mathrm {B_{dR}^+}} \langle T\rangle $
, the power series in Definition 3.0.6 is
 $$\begin{align*}\sum_e f^{(e)}(T)\cdot \xi^e\otimes \frac{\widetilde\delta^e}{e!}=f(T+\xi\widetilde\delta), \end{align*}$$
$$\begin{align*}\sum_e f^{(e)}(T)\cdot \xi^e\otimes \frac{\widetilde\delta^e}{e!}=f(T+\xi\widetilde\delta), \end{align*}$$
which is convergent in the ring
![]() $P[{\widetilde \delta }]^\wedge ={\mathrm {B_{dR}^+}} \langle T\rangle [\widetilde \delta ]^\wedge $
, by checking mod
$P[{\widetilde \delta }]^\wedge ={\mathrm {B_{dR}^+}} \langle T\rangle [\widetilde \delta ]^\wedge $
, by checking mod
![]() $\xi ^n$
for every
$\xi ^n$
for every
![]() $n\in \mathbb {N}$
. Thus the canonical continuous differential on P is quasi-nilpotent.
$n\in \mathbb {N}$
. Thus the canonical continuous differential on P is quasi-nilpotent.
In fact, as we will see, this is the (log) connection corresponds to the prismatic structure sheaf ![]() over
over ![]() .
.
Example 3.0.10. If a log connection is integral, then it is quasi-nilpotent. To show this, it suffices to notice that by assumption in Remark 3.0.5 when
![]() $(M,\nabla )$
is integral, each
$(M,\nabla )$
is integral, each
![]() $\widetilde \nabla _i$
(x) is divisible by
$\widetilde \nabla _i$
(x) is divisible by
![]() $\xi $
.
$\xi $
.
Example 3.0.11. To give an example that is not quasi-nilpotent, still consider the special setting as above when
![]() $R=K \langle T \rangle $
,
$R=K \langle T \rangle $
,
![]() $P={\mathrm {B_{dR}^+}} \langle T \rangle $
and I is the zero ideal, in which case the envelope
$P={\mathrm {B_{dR}^+}} \langle T \rangle $
and I is the zero ideal, in which case the envelope ![]() is equal to the ring P. Let M be
is equal to the ring P. Let M be ![]() itself, and let
itself, and let
![]() $\nabla $
be the twisted differential map
$\nabla $
be the twisted differential map
Then this is an integrable log connection of M over ![]() but is not nilpotent. To see the latter, it suffices to notice that given
but is not nilpotent. To see the latter, it suffices to notice that given
![]() $f(T)\in {\mathrm {B_{dR}^+}} \langle T\rangle $
, the formal power series in Definition 3.0.6 is equal to
$f(T)\in {\mathrm {B_{dR}^+}} \langle T\rangle $
, the formal power series in Definition 3.0.6 is equal to
 $$\begin{align*}\sum_e f^{(e)}(T)\otimes \frac{\widetilde \delta^e}{e!}=f(T+\widetilde \delta), \end{align*}$$
$$\begin{align*}\sum_e f^{(e)}(T)\otimes \frac{\widetilde \delta^e}{e!}=f(T+\widetilde \delta), \end{align*}$$
which after mod
![]() $\xi $
is not convergent in
$\xi $
is not convergent in
![]() $K\langle T\rangle [\widetilde \delta ]$
whenever f mod
$K\langle T\rangle [\widetilde \delta ]$
whenever f mod
![]() $\xi $
is an infinite series.
$\xi $
is an infinite series.
Proposition 3.0.12. Let
![]() $P={\mathrm {B_{dR}^+}}\langle T_i\rangle $
, let I be an ideal of P, let R be the topologically finite type algebra
$P={\mathrm {B_{dR}^+}}\langle T_i\rangle $
, let I be an ideal of P, let R be the topologically finite type algebra
![]() $P/(I,\xi )$
and let
$P/(I,\xi )$
and let ![]() be the associated envelope. Then the following two categories are equivalent:
be the associated envelope. Then the following two categories are equivalent:

Proof. The proof is similar to that of [Reference GuoGuo24, Theorem 3.3.1]. We first notice that by Proposition 2.2.11 the prism ![]() associated to the prismatic envelope for the surjection
associated to the prismatic envelope for the surjection
![]() $P\rightarrow P/I$
covers the final object of the topos. Let
$P\rightarrow P/I$
covers the final object of the topos. Let
![]() $\mathcal {F}$
be a coherent prismatic crystal over R. By Taylor expansion, the formula in Definition 3.0.6 is exactly the transition isomorphism of the pullbacks along the two projections
$\mathcal {F}$
be a coherent prismatic crystal over R. By Taylor expansion, the formula in Definition 3.0.6 is exactly the transition isomorphism of the pullbacks along the two projections
where
![]() $\mathrm {pr}_i$
are two canonical maps of rings
$\mathrm {pr}_i$
are two canonical maps of rings ![]() induced by
induced by
![]() $P\langle \Delta (1)\rangle \leftleftarrows P$
. Here
$P\langle \Delta (1)\rangle \leftleftarrows P$
. Here
![]() $\Delta (1)$
is the kernel ideal of the diagonal surjection
$\Delta (1)$
is the kernel ideal of the diagonal surjection
![]() $P^{\widehat \otimes _{{\mathrm {B_{dR}^+}}} 2}\rightarrow P$
. To define the log connection on
$P^{\widehat \otimes _{{\mathrm {B_{dR}^+}}} 2}\rightarrow P$
. To define the log connection on ![]() , we note that the following map has the image in
, we note that the following map has the image in ![]() (which is isomorphic to
(which is isomorphic to ![]() )
)

This allows us to define the log connection as

Then as a consequence of the crystal condition, both ![]() are isomorphic to
are isomorphic to ![]() , and the existence of the isomorphism implies the convergence of the power series. Moreover, integrability for the log connection coming from the crystal follows from the crystal conditions again, and can be proved as in [Sta][07J6].
, and the existence of the isomorphism implies the convergence of the power series. Moreover, integrability for the log connection coming from the crystal follows from the crystal conditions again, and can be proved as in [Sta][07J6].
Conversely, given an integrable, quasi-nilpotent log connection
![]() $(M,\nabla )$
over an envelope, Proposition 2.2.11 allows us to define a finite module over any prism
$(M,\nabla )$
over an envelope, Proposition 2.2.11 allows us to define a finite module over any prism
![]() $(B,\xi B)$
via the pullback along a map
$(B,\xi B)$
via the pullback along a map ![]() . Then the rest is to show the independence of the choice of maps, which follows from the quasi-nilpotence and the integrability, and can be checked as in the proof of [Reference GuoGuo24, Theorem 3.3.1] (especially [Reference GuoGuo24, Claim 3.3.4]). Here we note that the quasi-nilpotence assumption is used to show the formal power series associated to the transition morphism converges, thus exists.
. Then the rest is to show the independence of the choice of maps, which follows from the quasi-nilpotence and the integrability, and can be checked as in the proof of [Reference GuoGuo24, Theorem 3.3.1] (especially [Reference GuoGuo24, Claim 3.3.4]). Here we note that the quasi-nilpotence assumption is used to show the formal power series associated to the transition morphism converges, thus exists.
We also compute the Čech-Alexander complex under the prismatic setting. As a preparation, we introduce the following notations. As before, let
![]() $P={\mathrm {B_{dR}^+}}\langle T_1,\ldots , T_m\rangle \rightarrow P/I \rightarrow R=P/(I,\xi )$
be surjections, and let
$P={\mathrm {B_{dR}^+}}\langle T_1,\ldots , T_m\rangle \rightarrow P/I \rightarrow R=P/(I,\xi )$
be surjections, and let ![]() be the associated envelope. Denote
be the associated envelope. Denote
![]() $P(l)$
to be the inverse limit
$P(l)$
to be the inverse limit
 $$\begin{align*}P(l):=\varprojlim_n \left( {\mathrm{B^+_{dR,n}}}\langle T_i\rangle^{\widehat\otimes_{{\mathrm{B^+_{dR,n}}}} (l+1)} \right)\cong \varprojlim_n {\mathrm{B^+_{dR,n}}} \langle T_i,\delta_{j,i} \rangle, \end{align*}$$
$$\begin{align*}P(l):=\varprojlim_n \left( {\mathrm{B^+_{dR,n}}}\langle T_i\rangle^{\widehat\otimes_{{\mathrm{B^+_{dR,n}}}} (l+1)} \right)\cong \varprojlim_n {\mathrm{B^+_{dR,n}}} \langle T_i,\delta_{j,i} \rangle, \end{align*}$$
where
![]() $\delta _{j,i}$
for
$\delta _{j,i}$
for
![]() $1\leq j\leq l,~1\leq i\leq m$
correspond to natural generators of the kernel ideal
$1\leq j\leq l,~1\leq i\leq m$
correspond to natural generators of the kernel ideal
![]() $\Delta (l)$
for the diagonal surjection
$\Delta (l)$
for the diagonal surjection
![]() $P(l) \rightarrow P$
, and the complete tensor product
$P(l) \rightarrow P$
, and the complete tensor product
![]() $\widehat \otimes _{{\mathrm {B^+_{dR,n}}}}$
above is defined as the integrally p-complete tensor product.
$\widehat \otimes _{{\mathrm {B^+_{dR,n}}}}$
above is defined as the integrally p-complete tensor product.
Proposition 3.0.13. Let
![]() $P, R$
and
$P, R$
and
![]() $P(l)$
be as above. The
$P(l)$
be as above. The
![]() $(l+1)$
-th self-fibre product of the prism
$(l+1)$
-th self-fibre product of the prism ![]() over the final object in the prismatic topos is representable by the prism associated to the prismatic envelope
over the final object in the prismatic topos is representable by the prism associated to the prismatic envelope ![]() for
for
![]() $P(l)\rightarrow P(l)/(\Delta (l),I)=P/I$
.
$P(l)\rightarrow P(l)/(\Delta (l),I)=P/I$
.
Proof. Let
![]() $(B,\xi B)$
be a prism over R. We first notice that by Remark 2.2.8, to give a map of prisms from
$(B,\xi B)$
be a prism over R. We first notice that by Remark 2.2.8, to give a map of prisms from ![]() to
to
![]() $(B,\xi B)$
, it is equivalent to give a continuous
$(B,\xi B)$
, it is equivalent to give a continuous
![]() ${\mathrm {B_{dR}^+}}$
-linear morphism
${\mathrm {B_{dR}^+}}$
-linear morphism
![]() $g:P={\mathrm {B_{dR}^+}}\langle T_i\rangle \rightarrow B$
, satisfying the following commutative diagram
$g:P={\mathrm {B_{dR}^+}}\langle T_i\rangle \rightarrow B$
, satisfying the following commutative diagram

This implies that a map from
![]() $(l+1)$
-th self product of the prism
$(l+1)$
-th self product of the prism ![]() to
to
![]() $(B,\xi B)$
is equivalent to
$(B,\xi B)$
is equivalent to
![]() $(l+1)$
continuous
$(l+1)$
continuous
![]() ${\mathrm {B_{dR}^+}}$
-linear morphisms
${\mathrm {B_{dR}^+}}$
-linear morphisms
![]() $g_0,\ldots , g_l:P \rightarrow B$
, such that the induced compositions
$g_0,\ldots , g_l:P \rightarrow B$
, such that the induced compositions
![]() $P \rightarrow B \rightarrow B/\xi $
all factor through the morphism
$P \rightarrow B \rightarrow B/\xi $
all factor through the morphism
![]() $f:R \rightarrow B/\xi $
.
$f:R \rightarrow B/\xi $
.
We then consider the integral level. To give
![]() $(l+1)$
continuous maps from P to B, it suffices to give a sequence of
$(l+1)$
continuous maps from P to B, it suffices to give a sequence of
![]() ${\mathrm {A_{inf,n}}}$
-linear (for
${\mathrm {A_{inf,n}}}$
-linear (for
![]() ${\mathrm {A_{inf,n}}}={\mathrm {A_{inf}}}/\xi ^n$
) continuous maps
${\mathrm {A_{inf,n}}}={\mathrm {A_{inf}}}/\xi ^n$
) continuous maps
![]() $g_{0,n},\ldots , g_{l,n}:{\mathrm {A_{inf,n}}}\langle T_i\rangle \rightarrow B/\xi ^n$
, compatible with
$g_{0,n},\ldots , g_{l,n}:{\mathrm {A_{inf,n}}}\langle T_i\rangle \rightarrow B/\xi ^n$
, compatible with
![]() $n\in \mathbb {N}$
via natural surjections, and with the commutative diagrams
$n\in \mathbb {N}$
via natural surjections, and with the commutative diagrams
![]() $(\ast )$
above (after inverting p). When
$(\ast )$
above (after inverting p). When
![]() $n=1$
, the maps
$n=1$
, the maps
![]() $g_{j,n}$
all factors through the same map
$g_{j,n}$
all factors through the same map
![]() $\mathcal {O}_K\langle T_i\rangle \rightarrow R_0 \rightarrow B/\xi $
, where
$\mathcal {O}_K\langle T_i\rangle \rightarrow R_0 \rightarrow B/\xi $
, where
![]() $R_0$
is a ring of definition of R and
$R_0$
is a ring of definition of R and
![]() $R_0\rightarrow B/\xi $
is induced from
$R_0\rightarrow B/\xi $
is induced from
![]() $f:R \rightarrow B/\xi $
. This is equivalent to give a map
$f:R \rightarrow B/\xi $
. This is equivalent to give a map
![]() $\mathcal {O}_K\langle T_i\rangle ^{\otimes _{\mathcal {O}_K} (l+1)} \rightarrow B/\xi $
that factors through the diagonal and the above surjection
$\mathcal {O}_K\langle T_i\rangle ^{\otimes _{\mathcal {O}_K} (l+1)} \rightarrow B/\xi $
that factors through the diagonal and the above surjection
![]() $\mathcal {O}_K\langle T_i\rangle \rightarrow R_0 \rightarrow B/\xi $
. Notice that the tensor product is a priori only the ordinary tensor product of
$\mathcal {O}_K\langle T_i\rangle \rightarrow R_0 \rightarrow B/\xi $
. Notice that the tensor product is a priori only the ordinary tensor product of
![]() $\mathcal {O}_K$
-rings, but since
$\mathcal {O}_K$
-rings, but since
![]() $R_0$
is p-complete, the above induces uniquely a continuous map
$R_0$
is p-complete, the above induces uniquely a continuous map
![]() $\mathcal {O}_K\langle T_i\rangle ^{\widehat \otimes _{\mathcal {O}_K} (l+1)} \rightarrow B/\xi $
for the p-adic completed tensor product. For general
$\mathcal {O}_K\langle T_i\rangle ^{\widehat \otimes _{\mathcal {O}_K} (l+1)} \rightarrow B/\xi $
for the p-adic completed tensor product. For general
![]() $n\in \mathbb {N}$
, the choice of
$n\in \mathbb {N}$
, the choice of
![]() $\{g_{0,n},\ldots , g_{l,n}\}$
amounts to give a map from
$\{g_{0,n},\ldots , g_{l,n}\}$
amounts to give a map from
![]() ${\mathrm {A_{inf,n}}}\langle T_i\rangle ^{\otimes _{{\mathrm {A_{inf,n}}}} (l+1)} \rightarrow B/\xi ^n$
, whose composition with
${\mathrm {A_{inf,n}}}\langle T_i\rangle ^{\otimes _{{\mathrm {A_{inf,n}}}} (l+1)} \rightarrow B/\xi ^n$
, whose composition with
![]() $B/\xi ^n\rightarrow B/\xi $
factors through the diagonal surjection of
$B/\xi ^n\rightarrow B/\xi $
factors through the diagonal surjection of
![]() ${\mathrm {A_{inf,n}}}\langle T_i\rangle ^{\otimes _{{\mathrm {A_{inf,n}}}} (l+1)}$
and
${\mathrm {A_{inf,n}}}\langle T_i\rangle ^{\otimes _{{\mathrm {A_{inf,n}}}} (l+1)}$
and
![]() ${\mathrm {A_{inf,n}}}\langle T_i\rangle \rightarrow R_0 \rightarrow B/\xi $
. Using Corollary 2.1.3, the images of incomplete tensor product in
${\mathrm {A_{inf,n}}}\langle T_i\rangle \rightarrow R_0 \rightarrow B/\xi $
. Using Corollary 2.1.3, the images of incomplete tensor product in
![]() $B/\xi ^n$
are within an affinoid algebra over
$B/\xi ^n$
are within an affinoid algebra over
![]() ${\mathrm {B^+_{dR,n}}}$
, so the map uniquely factors through a map
${\mathrm {B^+_{dR,n}}}$
, so the map uniquely factors through a map
![]() ${\mathrm {A_{inf,n}}}\langle T_i\rangle ^{\widehat \otimes _{{\mathrm {A_{inf,n}}}} (l+1)} \rightarrow B/\xi ^n$
, where the tensor product of the source is p-completed. In this way, by inverting p and taking the inverse limit with respect to n, we see to give
${\mathrm {A_{inf,n}}}\langle T_i\rangle ^{\widehat \otimes _{{\mathrm {A_{inf,n}}}} (l+1)} \rightarrow B/\xi ^n$
, where the tensor product of the source is p-completed. In this way, by inverting p and taking the inverse limit with respect to n, we see to give
![]() $(l+1)$
continuous
$(l+1)$
continuous
![]() ${\mathrm {B_{dR}^+}}$
-linear map from
${\mathrm {B_{dR}^+}}$
-linear map from
![]() $P \rightarrow B$
satisfying the diagram
$P \rightarrow B$
satisfying the diagram
![]() $(\ast )$
, it is the same as giving the following commutative diagram
$(\ast )$
, it is the same as giving the following commutative diagram

In this way, by the construction of the prismatic envelope in Definition 2.2.5 and Remark 2.2.8, we see this is equivalent to give a map of prisms from ![]() to
to
![]() $(B,\xi B)$
, where
$(B,\xi B)$
, where ![]() is the prismatic envelope.
is the prismatic envelope.
Corollary 3.0.14. Let
![]() $P={\mathrm {B_{dR}^+}}\langle T_i\rangle \rightarrow P/I\rightarrow R=P/(I,\xi )$
be surjections with R being topologically finite type over K. Let
$P={\mathrm {B_{dR}^+}}\langle T_i\rangle \rightarrow P/I\rightarrow R=P/(I,\xi )$
be surjections with R being topologically finite type over K. Let
![]() $\mathcal {F}$
be a sheaf over
$\mathcal {F}$
be a sheaf over ![]() , and let
, and let ![]() be the prismatic envelope as in Proposition 3.0.13. Then the following natural map from the homotopy limit over the simplicial diagram
be the prismatic envelope as in Proposition 3.0.13. Then the following natural map from the homotopy limit over the simplicial diagram
![]() $\Delta ^{\mathrm {op}}$
is a quasi-isomorphism
$\Delta ^{\mathrm {op}}$
is a quasi-isomorphism
Proof. This follows from the general category theory and Proposition 3.0.13, as the simplicial diagram of prisms ![]() in the prismatic site
in the prismatic site ![]() forms the Čech nerve of the covering map
forms the Čech nerve of the covering map ![]() (Proposition 2.2.11), where
(Proposition 2.2.11), where ![]() is the final object in the prismatic topos
is the final object in the prismatic topos ![]() .
.
As an application, we obtain a tensor product formula relating the cohomology of a crystal and its reduction.
Corollary 3.0.15. Let
![]() $\mathcal {F}$
be a flat prismatic crystal over X, and let
$\mathcal {F}$
be a flat prismatic crystal over X, and let
![]() $\overline {\mathcal {F}}=\mathcal {F}\otimes _{\mathrm {B_{dR}^+}} K$
be its reduction. Then the natural map below is an isomorphism
$\overline {\mathcal {F}}=\mathcal {F}\otimes _{\mathrm {B_{dR}^+}} K$
be its reduction. Then the natural map below is an isomorphism
Proof. First notice the map of cohomology above is induced by the reduction map of crystals
![]() $\mathcal {F}\rightarrow \overline {\mathcal {F}}$
. So it suffices to check that the map of cohomology is an isomorphism, assuming R admits a surjection as in Corollary 3.0.14. Then we notice that by the local freeness of each
$\mathcal {F}\rightarrow \overline {\mathcal {F}}$
. So it suffices to check that the map of cohomology is an isomorphism, assuming R admits a surjection as in Corollary 3.0.14. Then we notice that by the local freeness of each ![]() over
over
![]() $D(l)$
and the
$D(l)$
and the
![]() $\xi $
-torsion freeness of
$\xi $
-torsion freeness of
![]() $D(l)$
over
$D(l)$
over
![]() ${\mathrm {B_{dR}^+}}$
, the derived tensor product of the cosimplicial diagram
${\mathrm {B_{dR}^+}}$
, the derived tensor product of the cosimplicial diagram ![]() with K is equal to
with K is equal to
Thus the rest follows from Corollary 3.0.14.
4 From infinitesimal to prismatic
In this section, we show how to compute cohomology of a prismatic crystal locally by using infinitesimal cohomology, for rigid spaces that has l.c.i. singularity.
4.1 A variant of Simpson’s functor over
 ${\mathrm {B_{dR}^+}}$
${\mathrm {B_{dR}^+}}$
We start this subsection with introducing a variant of Simpson’s functor in [Reference SimpsonSimp, Lemma 19], from the (
![]() $\infty $
) category of filtered objects (rings, modules, or complexes) over a
$\infty $
) category of filtered objects (rings, modules, or complexes) over a
![]() ${\mathrm {B_{dR}^+}}$
-algebra. This will be used to connect the infinitesimal theory to the prismatic theory.
${\mathrm {B_{dR}^+}}$
-algebra. This will be used to connect the infinitesimal theory to the prismatic theory.
Construction 4.1.1. Let
![]() $(M,{\mathrm {Fil}}^{\bullet } M)$
be a
$(M,{\mathrm {Fil}}^{\bullet } M)$
be a
![]() $\mathbb {N}^{\mathrm {op}}$
-indexed descending filtered complex of
$\mathbb {N}^{\mathrm {op}}$
-indexed descending filtered complex of
![]() ${\mathrm {B_{dR}^+}}$
-modules. Namely
${\mathrm {B_{dR}^+}}$
-modules. Namely
![]() ${\mathrm {Fil}}^{\bullet } M$
is an object in
${\mathrm {Fil}}^{\bullet } M$
is an object in
![]() ${\mathscr {DF}}({\mathrm {Mod}}_{{\mathrm {B_{dR}^+}}})=\textrm {Fun}(\mathbb {N}^{\mathrm {op}}, {\mathrm {Mod}}_{{\mathrm {B_{dR}^+}}})$
as in the beginning of [Reference GuoGuo24, Section 5]. Then we define the functor
${\mathscr {DF}}({\mathrm {Mod}}_{{\mathrm {B_{dR}^+}}})=\textrm {Fun}(\mathbb {N}^{\mathrm {op}}, {\mathrm {Mod}}_{{\mathrm {B_{dR}^+}}})$
as in the beginning of [Reference GuoGuo24, Section 5]. Then we define the functor
![]() $\Psi (M,{\mathrm {Fil}}^{\bullet } M)$
(or
$\Psi (M,{\mathrm {Fil}}^{\bullet } M)$
(or
![]() $\Psi (M)$
in short if there is no confusion) as an object in
$\Psi (M)$
in short if there is no confusion) as an object in
![]() $\mathscr {D}({\mathrm {B_{dR}^+}})$
by the following formula
$\mathscr {D}({\mathrm {B_{dR}^+}})$
by the following formula

Here
![]() $(-)^\wedge $
above is the derived
$(-)^\wedge $
above is the derived
![]() $\xi $
-adic completion, and precisely the colimit is taken over the following diagram of
$\xi $
-adic completion, and precisely the colimit is taken over the following diagram of
![]() ${\mathrm {B_{dR}^+}}$
-complexes
${\mathrm {B_{dR}^+}}$
-complexes

where all horizontal arrows are defining morphisms of the filtration.
Remark 4.1.2 (Comparison with Simpson’s functor).
Let
![]() $(M,{\mathrm {Fil}}^{\bullet } M)$
be a filtered
$(M,{\mathrm {Fil}}^{\bullet } M)$
be a filtered
![]() ${\mathrm {B_{dR}^+}}$
-complexes as in Construction 4.1.1, and let
${\mathrm {B_{dR}^+}}$
-complexes as in Construction 4.1.1, and let ![]() be the associated Rees construction, regarded as a
be the associated Rees construction, regarded as a
![]() ${\mathrm {B_{dR}^+}}[t]$
-complex. It can be shown that the functor
${\mathrm {B_{dR}^+}}[t]$
-complex. It can be shown that the functor
![]() $\Psi (M,{\mathrm {Fil}}^{\bullet } M)$
is naturally isomorphic to the
$\Psi (M,{\mathrm {Fil}}^{\bullet } M)$
is naturally isomorphic to the
![]() $\xi $
-completed derived reduction
$\xi $
-completed derived reduction
To see this, we notice that by construction, the complex
![]() $\Psi '(M,{\mathrm {Fil}}^{\bullet } M)$
is the derived
$\Psi '(M,{\mathrm {Fil}}^{\bullet } M)$
is the derived
![]() $\xi $
-completion of the derived co-equalizer of the diagram
$\xi $
-completion of the derived co-equalizer of the diagram

Then it suffices to notice that, by putting all the direct summands of the source and the target of (4.1.2) together, and by assigning the multiplication by t as horizontal arrows, and assigning the multiplication by
![]() $\xi $
as the vertical arrows, we exactly obtain the diagram (4.1.1). Here the terms on the main-diagonal of (4.1.1) correspond to the direct summands from the target of (4.1.2), and the terms on the sup-diagonal of (4.1.1) correspond to the direct summands from the source of (4.1.2).
$\xi $
as the vertical arrows, we exactly obtain the diagram (4.1.1). Here the terms on the main-diagonal of (4.1.1) correspond to the direct summands from the target of (4.1.2), and the terms on the sup-diagonal of (4.1.1) correspond to the direct summands from the source of (4.1.2).
Remark 4.1.3. The idea of the diagram in Construction 4.1.1 is that we want to add the denominator
![]() $\xi ^i$
to the i-th filtration. To see this, we change the notation and denote
$\xi ^i$
to the i-th filtration. To see this, we change the notation and denote
![]() $\frac {{\mathrm {Fil}}^iM}{\xi ^i}$
to be the
$\frac {{\mathrm {Fil}}^iM}{\xi ^i}$
to be the
![]() ${\mathrm {B_{dR}^+}}$
-complex
${\mathrm {B_{dR}^+}}$
-complex
![]() ${\mathrm {Fil}}^i M$
but formally adjoining the denominator
${\mathrm {Fil}}^i M$
but formally adjoining the denominator
![]() $\frac {1}{\xi ^i}$
. Then the diagram in Construction 4.1.1 can be rewritten as the following
$\frac {1}{\xi ^i}$
. Then the diagram in Construction 4.1.1 can be rewritten as the following

where each vertical map identifies
![]() $\frac {Fil^i M}{\xi ^{i-1}}$
with
$\frac {Fil^i M}{\xi ^{i-1}}$
with
![]() $\xi \cdot \frac {Fil^i M}{\xi ^i}$
via the multiplication by
$\xi \cdot \frac {Fil^i M}{\xi ^i}$
via the multiplication by
![]() $\xi $
. Note that in the special case when each
$\xi $
. Note that in the special case when each
![]() ${\mathrm {Fil}}^iM$
is a complex of
${\mathrm {Fil}}^iM$
is a complex of
![]() $\xi $
-torsionfree
$\xi $
-torsionfree
![]() ${\mathrm {B_{dR}^+}}$
-modules, the vertical maps are all inclusion maps.
${\mathrm {B_{dR}^+}}$
-modules, the vertical maps are all inclusion maps.
Remark 4.1.4. When
![]() $(M,{\mathrm {Fil}}^{\bullet } M)=(A,I^\bullet )$
is a noetherian
$(M,{\mathrm {Fil}}^{\bullet } M)=(A,I^\bullet )$
is a noetherian
![]() $\xi $
-torsionfree
$\xi $
-torsionfree
![]() ${\mathrm {B_{dR}^+}}$
-algebra A together with a filtration given by a power of its ideal I, the module
${\mathrm {B_{dR}^+}}$
-algebra A together with a filtration given by a power of its ideal I, the module
![]() $\Psi (A,I^\bullet )$
is also equipped with a natural
$\Psi (A,I^\bullet )$
is also equipped with a natural
![]() ${\mathrm {B_{dR}^+}}$
-algebra structure, by
${\mathrm {B_{dR}^+}}$
-algebra structure, by
 $$\begin{align*}\frac{I^i}{\xi^i}\otimes \frac{I^j}{\xi^j} \longrightarrow \frac{I^{i+j}}{\xi^{i+j}}. \end{align*}$$
$$\begin{align*}\frac{I^i}{\xi^i}\otimes \frac{I^j}{\xi^j} \longrightarrow \frac{I^{i+j}}{\xi^{i+j}}. \end{align*}$$
More generally, under the Day convolution on
![]() ${\mathscr {DF}}({\mathrm {Mod}}_{{\mathrm {B_{dR}^+}}})$
(see for example [Reference Gwilliam and PavlovGP18]), the functor
${\mathscr {DF}}({\mathrm {Mod}}_{{\mathrm {B_{dR}^+}}})$
(see for example [Reference Gwilliam and PavlovGP18]), the functor
![]() $\Psi :{\mathscr {DF}}({\mathrm {Mod}}_{{\mathrm {B_{dR}^+}}}) \rightarrow \mathscr {D}({\mathrm {B_{dR}^+}})$
is lax-symmetric monoidal, thus inducing a functor on
$\Psi :{\mathscr {DF}}({\mathrm {Mod}}_{{\mathrm {B_{dR}^+}}}) \rightarrow \mathscr {D}({\mathrm {B_{dR}^+}})$
is lax-symmetric monoidal, thus inducing a functor on
![]() $\mathbb {E}_\infty $
:
$\mathbb {E}_\infty $
:
Intuitively, using the notation in the above remark, this is to say the following multiplicative structure in
![]() $\Psi (M,{\mathrm {Fil}}^{\bullet } M)$
$\Psi (M,{\mathrm {Fil}}^{\bullet } M)$
 $$\begin{align*}\frac{{\mathrm{Fil}}^i M}{\xi^i} \otimes \frac{{\mathrm{Fil}}^j M}{\xi^j} \longrightarrow \frac{{\mathrm{Fil}}^{i+j} M}{\xi^{i+j}}. \end{align*}$$
$$\begin{align*}\frac{{\mathrm{Fil}}^i M}{\xi^i} \otimes \frac{{\mathrm{Fil}}^j M}{\xi^j} \longrightarrow \frac{{\mathrm{Fil}}^{i+j} M}{\xi^{i+j}}. \end{align*}$$
Remark 4.1.5. Moreover, when
![]() $(M,{\mathrm {Fil}}^{\bullet } M)$
is a filtered complex of A-modules for a
$(M,{\mathrm {Fil}}^{\bullet } M)$
is a filtered complex of A-modules for a
![]() $\xi $
-adic complete
$\xi $
-adic complete
![]() ${\mathrm {B_{dR}^+}}$
-algebra A, as the arrows in the diagram of Construction 4.1.1 above are all A-linear, the object
${\mathrm {B_{dR}^+}}$
-algebra A, as the arrows in the diagram of Construction 4.1.1 above are all A-linear, the object
![]() $\Psi (M,{\mathrm {Fil}}^{\bullet } M)$
is also a complex of A-modules.
$\Psi (M,{\mathrm {Fil}}^{\bullet } M)$
is also a complex of A-modules.
In the following, for a K-module M, we denote
![]() $M\otimes _K \xi ^i/\xi ^{i+1}$
as
$M\otimes _K \xi ^i/\xi ^{i+1}$
as
![]() $M(i)$
, called the i-th Tate twist of M. This would not change the underlying K-module structure, but its Galois structure is replaced by the i-th Tate twist when M itself is equipped with one.
$M(i)$
, called the i-th Tate twist of M. This would not change the underlying K-module structure, but its Galois structure is replaced by the i-th Tate twist when M itself is equipped with one.
Remark 4.1.6. Given a filtered
![]() ${\mathrm {B_{dR}^+}}$
-complex
${\mathrm {B_{dR}^+}}$
-complex
![]() $(M,{\mathrm {Fil}}^{\bullet } M)$
such that
$(M,{\mathrm {Fil}}^{\bullet } M)$
such that
![]() ${\mathrm {Fil}}^{\bullet } M$
is uniformly bounded to the right, we note that the derived mod
${\mathrm {Fil}}^{\bullet } M$
is uniformly bounded to the right, we note that the derived mod
![]() $\xi $
reduction has the following formula
$\xi $
reduction has the following formula
where
![]() $M\otimes ^L_{\mathrm {B_{dR}^+}} K$
is the filtered complex of K-modules endowed with filtration
$M\otimes ^L_{\mathrm {B_{dR}^+}} K$
is the filtered complex of K-modules endowed with filtration
![]() ${\mathrm {Fil}}^iM\otimes ^L_{\mathrm {B_{dR}^+}} K$
. This follows from [Sta, Tag 0EEV], the commutativity of colimit and derived tensor product, and the diagram in Construction 4.1.1.
${\mathrm {Fil}}^iM\otimes ^L_{\mathrm {B_{dR}^+}} K$
. This follows from [Sta, Tag 0EEV], the commutativity of colimit and derived tensor product, and the diagram in Construction 4.1.1.
4.2 Prisms associated to infinitesimal thickenings
We now construct a functor from the infinitesimal site to the prismatic site, over the de Rham period ring
![]() ${\mathrm {B_{dR}^+}}$
.
${\mathrm {B_{dR}^+}}$
.
To start, we consider the following pro-version analogue of the infinitesimal site considered in [Reference GuoGuo24].
Definition 4.2.1. Let X be a rigid space over K. The pro-infinitesimal site of
![]() $X/{\mathrm {B_{dR}^+}}$
, denoted as
$X/{\mathrm {B_{dR}^+}}$
, denoted as
![]() $(X/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
, is defined as the category of
$(X/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
, is defined as the category of
![]() $(U,T_\ast ):=(U,T_e)$
for
$(U,T_\ast ):=(U,T_e)$
for
![]() $e\in \mathbb {N}$
, such that
$e\in \mathbb {N}$
, such that
-
• each
 $(U,T_e)$
is an infinitesimal thickening of affinoid rigid spaces over
$(U,T_e)$
is an infinitesimal thickening of affinoid rigid spaces over
 ${\mathrm {B^+_{dR,e}}}$
(in the sense of [Reference GuoGuo24, Section 2.1], with
${\mathrm {B^+_{dR,e}}}$
(in the sense of [Reference GuoGuo24, Section 2.1], with
 $T_e$
flat over
$T_e$
flat over
 ${\mathrm {B^+_{dR,e}}}$
and U an affinoid open subspace of X;
${\mathrm {B^+_{dR,e}}}$
and U an affinoid open subspace of X; -
• transition maps
 $T_e \rightarrow T_{e+1}$
are also infinitesimal thickenings that are compatible with maps from U, and there is a compatible system of closed immersions
$T_e \rightarrow T_{e+1}$
are also infinitesimal thickenings that are compatible with maps from U, and there is a compatible system of closed immersions
 $T_e\rightarrow \mathrm {Spa}({\mathrm {B^+_{dR,e}}} \langle x_1,\ldots , x_l\rangle )$
for some fixed
$T_e\rightarrow \mathrm {Spa}({\mathrm {B^+_{dR,e}}} \langle x_1,\ldots , x_l\rangle )$
for some fixed
 $l\in \mathbb {N}$
.
$l\in \mathbb {N}$
.
The category is equipped with indiscrete topology.
Remark 4.2.2. Let R be a topologically of finite type K-algebra, and let
![]() $P\rightarrow R$
be a surjection for a smooth
$P\rightarrow R$
be a surjection for a smooth
![]() ${\mathrm {B_{dR}^+}}$
-algebra P (in the sense that each
${\mathrm {B_{dR}^+}}$
-algebra P (in the sense that each
![]() $P/\xi ^e$
is smooth over
$P/\xi ^e$
is smooth over
![]() ${\mathrm {B^+_{dR,e}}}$
as an adic space). Then the induced pro-infinitesimal thickening
${\mathrm {B^+_{dR,e}}}$
as an adic space). Then the induced pro-infinitesimal thickening
![]() $(U=\mathrm {Spa}(R), T_e=\mathrm {Spa}(P/I^e))$
is weakly final over
$(U=\mathrm {Spa}(R), T_e=\mathrm {Spa}(P/I^e))$
is weakly final over
![]() $\mathrm {Spa}(R)/{\mathrm {B_{dR}^+}}_{\mathrm {inf}}$
, where
$\mathrm {Spa}(R)/{\mathrm {B_{dR}^+}}_{\mathrm {inf}}$
, where
![]() $I=\ker (P\rightarrow R)$
.
$I=\ker (P\rightarrow R)$
.
Remark 4.2.3. Analogously to the classical infinitesimal theory, we can define the infinitesimal structure sheaf
![]() $\mathcal {O}_{X/{\mathrm {B_{dR}^+}}}$
and the notion of crystals over
$\mathcal {O}_{X/{\mathrm {B_{dR}^+}}}$
and the notion of crystals over
![]() $(X/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
, as in [Reference GuoGuo24]. Here for a pro-infinitesimal thickening
$(X/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
, as in [Reference GuoGuo24]. Here for a pro-infinitesimal thickening
![]() $(U,T_e=\mathrm {Spa}(B_e))$
we have
$(U,T_e=\mathrm {Spa}(B_e))$
we have
Moreover, by [Reference GuoGuo24, Theorem 7.2.3, Theorem 3.3.1], the category of crystals over
![]() $X/{\mathrm {B_{dR}^+}}_{\mathrm {inf}}$
in the sense of [Reference GuoGuo24] is naturally equivalent to that over
$X/{\mathrm {B_{dR}^+}}_{\mathrm {inf}}$
in the sense of [Reference GuoGuo24] is naturally equivalent to that over
![]() $(X/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
, inducing natural isomorphisms between their cohomology.
$(X/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
, inducing natural isomorphisms between their cohomology.
Next we define a natural functor from the infinitesimal site to the prismatic site. Let R be a fixed topologically finite type algebra over K, and let
![]() $X=\mathrm {Spa}(R)$
.
$X=\mathrm {Spa}(R)$
.
Definition 4.2.4. Let
![]() $(U=\mathrm {Spa}(A),T_e=\mathrm {Spa}(B_e))\in (X/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
be a pro-infinitesimal thickening over the rigid space
$(U=\mathrm {Spa}(A),T_e=\mathrm {Spa}(B_e))\in (X/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
be a pro-infinitesimal thickening over the rigid space
![]() $X=\mathrm {Spa}(R)$
over K, and let
$X=\mathrm {Spa}(R)$
over K, and let
![]() $B=\varprojlim _e B_e$
, with the ideal
$B=\varprojlim _e B_e$
, with the ideal
![]() $I=\ker (B\rightarrow A)$
. The associated prism of
$I=\ker (B\rightarrow A)$
. The associated prism of
![]() $(U,T_e)$
is defined as
$(U,T_e)$
is defined as
where
![]() $B'=B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
, the symbol
$B'=B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
, the symbol
![]() $(-)^\wedge $
is the classical
$(-)^\wedge $
is the classical
![]() $\xi $
-adic completion and the arrow on the right is the natural composition
$\xi $
-adic completion and the arrow on the right is the natural composition
![]() $R\rightarrow A \rightarrow B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}/\xi $
.
$R\rightarrow A \rightarrow B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}/\xi $
.
Remark 4.2.5. When
![]() $(U,T_e)$
is a pro-infinitesimal thickening as in Remark 4.2.2, by the construction above together with Proposition 2.2.11, the associated prism covers the final object of the prismatic site.
$(U,T_e)$
is a pro-infinitesimal thickening as in Remark 4.2.2, by the construction above together with Proposition 2.2.11, the associated prism covers the final object of the prismatic site.
By construction, this defines a map of ringed sites
Moreover, by taking the coherent pullback, we can produce a prismatic crystal from an infinitesimal crystal.
Definition/Lemma 4.2.6. There is a natural functor between categories of crystals
such that for an infinitesimal thickening
![]() $(U=\mathrm {Spa}(A),T_e=\mathrm {Spa}(B_e))$
with
$(U=\mathrm {Spa}(A),T_e=\mathrm {Spa}(B_e))$
with
![]() $(B'\rightarrow B'/\xi \leftarrow R)$
being the associated prism as in Definition 4.2.4, we have
$(B'\rightarrow B'/\xi \leftarrow R)$
being the associated prism as in Definition 4.2.4, we have
Proof. For each
![]() $(U=\mathrm {Spa}(A), T_e=\mathrm {Spa}(B_e))$
, we construct a module over
$(U=\mathrm {Spa}(A), T_e=\mathrm {Spa}(B_e))$
, we construct a module over
![]() $B'=B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
by taking the tensor product as in the formula above. Then by the crystal condition of
$B'=B[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
by taking the tensor product as in the formula above. Then by the crystal condition of
![]() $\mathcal {F}\in \mathrm {Cry}_{X/{\mathrm {B_{dR}^+}}_{\mathrm {inf}}}$
, this satisfies the crystal condition with respect to prisms coming from infinitesimal thickenings. Then it suffices to notice that by Remark 4.2.5 the category of associated prisms covers the final objects of the prismatic topos.
$\mathcal {F}\in \mathrm {Cry}_{X/{\mathrm {B_{dR}^+}}_{\mathrm {inf}}}$
, this satisfies the crystal condition with respect to prisms coming from infinitesimal thickenings. Then it suffices to notice that by Remark 4.2.5 the category of associated prisms covers the final objects of the prismatic topos.
4.3 Local calculation for l.c.i. singularities
In this subsection, we give some concrete local formulae computing prismatic cohomology of crystals using Simpson’s functor, for affinoid rigid space that has l.c.i. singularities (in the sense of [Reference Guo and LiGL20, Appendix]). Precisely, we assume the following throughout the subsection.
Assumption 4.3.1. We let R be a fixed topologically finite type K-algebra, and let P be the ring
![]() ${\mathrm {B_{dR}^+}} \langle T_i\rangle $
. Assume I is a Koszul-regular ideal of P (in the sense of [Sta, Tag 07CU]), such that
${\mathrm {B_{dR}^+}} \langle T_i\rangle $
. Assume I is a Koszul-regular ideal of P (in the sense of [Sta, Tag 07CU]), such that
![]() $P/I$
is flat over
$P/I$
is flat over
![]() ${\mathrm {B_{dR}^+}}$
, and
${\mathrm {B_{dR}^+}}$
, and
![]() $P/(I,\xi )$
is isomorphic to R.
$P/(I,\xi )$
is isomorphic to R.
Slightly abuse the language, we call any such surjection
![]() $P \rightarrow P/I$
as above a regular closed immersion.
$P \rightarrow P/I$
as above a regular closed immersion.
Example 4.3.2. Assume R is a topologically finite type algebra over K that has l.c.i. singularities. By definition in [Reference Guo and LiGL20, Proposition 5.3], the kernel ideal
![]() $\overline I$
of any surjection from
$\overline I$
of any surjection from
![]() $K \langle T_i\rangle $
onto R is a Koszul-regular ideal in
$K \langle T_i\rangle $
onto R is a Koszul-regular ideal in
![]() $K\langle T_i\rangle $
. In particular, by [Sta, Tag 0669], as the union of
$K\langle T_i\rangle $
. In particular, by [Sta, Tag 0669], as the union of
![]() $\xi $
with a lift of any (Zariski) local Koszul-regular sequence of
$\xi $
with a lift of any (Zariski) local Koszul-regular sequence of
![]() $\overline I$
is a Koszul-regular sequence, the ideal
$\overline I$
is a Koszul-regular sequence, the ideal
![]() $\ker (P\rightarrow R)$
is also a Koszul-regular ideal of P. So by taking any lift of Koszul-regular sequence of
$\ker (P\rightarrow R)$
is also a Koszul-regular ideal of P. So by taking any lift of Koszul-regular sequence of
![]() $\overline I$
, we see Zariski (thus analytic) locally the affinoid algebra R always admits a setup as in Assumption 4.3.1.
$\overline I$
, we see Zariski (thus analytic) locally the affinoid algebra R always admits a setup as in Assumption 4.3.1.
Remark 4.3.3. It is worth mentioning the category of (regular) closed immersions is sifted. This is because given any two surjections
![]() $P_i \rightarrow P_i/I_i \rightarrow R$
for
$P_i \rightarrow P_i/I_i \rightarrow R$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $P_i$
being of the form
$P_i$
being of the form
![]() ${\mathrm {B_{dR}^+}} \langle T_j\rangle $
, we can form the product
${\mathrm {B_{dR}^+}} \langle T_j\rangle $
, we can form the product
which naturally admits a surjection to R together with maps from
![]() $P_i$
. Moreover, by taking the ideal
$P_i$
. Moreover, by taking the ideal
![]() $I\subset P$
generated by the image of
$I\subset P$
generated by the image of
![]() $I_1$
and
$I_1$
and
![]() $I_2$
, the quotient ring
$I_2$
, the quotient ring
![]() $P/I$
is a flat
$P/I$
is a flat
![]() ${\mathrm {B_{dR}^+}}$
-lift of R along
${\mathrm {B_{dR}^+}}$
-lift of R along
![]() ${\mathrm {B_{dR}^+}}\rightarrow K$
. At last, when both surjections
${\mathrm {B_{dR}^+}}\rightarrow K$
. At last, when both surjections
![]() $P_i \rightarrow R$
are locally complete intersection, we can use the analytic cotangent complex to check that
$P_i \rightarrow R$
are locally complete intersection, we can use the analytic cotangent complex to check that
![]() $P \rightarrow R$
is also regular ([Reference Guo and LiGL20, Appendix]).
$P \rightarrow R$
is also regular ([Reference Guo and LiGL20, Appendix]).
We start by computing the prismatic envelope using Simpson’s functor.
Lemma 4.3.4. Let P, I and R be as in Assumption 4.3.1. Then the prismatic envelope
![]() $P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
for
$P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
for
![]() $P\rightarrow P/I$
is naturally isomorphic to
$P\rightarrow P/I$
is naturally isomorphic to
![]() $\Psi (P,I^{\bullet })$
. In particular,
$\Psi (P,I^{\bullet })$
. In particular,
![]() $\Psi (P,I^{\bullet })$
lives in cohomological degree zero and is a
$\Psi (P,I^{\bullet })$
lives in cohomological degree zero and is a
![]() $\xi $
-adically complete,
$\xi $
-adically complete,
![]() $\xi $
-torsionfree noetherian algebra over P.
$\xi $
-torsionfree noetherian algebra over P.
Proof. We first assume that I admits a finite set of generators
![]() $(f_i)$
such that
$(f_i)$
such that
![]() $(\xi , f_i)$
is a Koszul-regular sequence, which is always true Zariski locally around
$(\xi , f_i)$
is a Koszul-regular sequence, which is always true Zariski locally around
![]() $\operatorname {\mathrm {Spec}}(R)$
in
$\operatorname {\mathrm {Spec}}(R)$
in
![]() $\operatorname {\mathrm {Spec}}(P)$
(c.f. Example 4.3.2). Then there exists a natural map from the polynomial algebra
$\operatorname {\mathrm {Spec}}(P)$
(c.f. Example 4.3.2). Then there exists a natural map from the polynomial algebra
![]() $P[x_i]$
to
$P[x_i]$
to
![]() $\Psi (P,I^{\bullet })$
, sending
$\Psi (P,I^{\bullet })$
, sending
![]() $x_i$
onto
$x_i$
onto
![]() $\frac {f_i}{\xi }\in \frac {I}{\xi }$
. This induces a natural homomorphism from the noetherian ring
$\frac {f_i}{\xi }\in \frac {I}{\xi }$
. This induces a natural homomorphism from the noetherian ring
![]() $P[\frac {f_i}{\xi }]=P[x_i]/(\xi \cdot x_i -f_i)$
to
$P[\frac {f_i}{\xi }]=P[x_i]/(\xi \cdot x_i -f_i)$
to
![]() $\Psi (P,I^{\bullet })$
, and factors through the derived
$\Psi (P,I^{\bullet })$
, and factors through the derived
![]() $\xi $
-completion of
$\xi $
-completion of
![]() $P[\frac {f_i}{\xi }]$
. Note by [Sta, Tag 0A06] the classical
$P[\frac {f_i}{\xi }]$
. Note by [Sta, Tag 0A06] the classical
![]() $\xi $
-completion and the derived
$\xi $
-completion and the derived
![]() $\xi $
-completion of a noetherian
$\xi $
-completion of a noetherian
![]() ${\mathrm {B_{dR}^+}}$
-algebra are the same. Thus the above leads to a natural map from the actual noetherian algebra
${\mathrm {B_{dR}^+}}$
-algebra are the same. Thus the above leads to a natural map from the actual noetherian algebra
![]() $P[\frac {f_i}{\xi }]^\wedge $
to
$P[\frac {f_i}{\xi }]^\wedge $
to
![]() $\Psi (P,I^{\bullet })$
, where the former is classically
$\Psi (P,I^{\bullet })$
, where the former is classically
![]() $\xi $
-completed. Moreover, as
$\xi $
-completed. Moreover, as
![]() $(\xi , f_i)$
forms a regular sequence of the ring P, the map of rings
$(\xi , f_i)$
forms a regular sequence of the ring P, the map of rings
![]() ${\mathrm {B_{dR}^+}}[y_i] \rightarrow P$
,
${\mathrm {B_{dR}^+}}[y_i] \rightarrow P$
,
![]() $y_i\mapsto f_i$
is flat after localizing at the ideal
$y_i\mapsto f_i$
is flat after localizing at the ideal
![]() $(\xi )$
(c.f. [Reference HartshorneHar66, Proposition 1]). As a consequence, the ring
$(\xi )$
(c.f. [Reference HartshorneHar66, Proposition 1]). As a consequence, the ring
![]() $P[\frac {f_i}{\xi }]$
has no
$P[\frac {f_i}{\xi }]$
has no
![]() $\xi $
-torsion, and we get a map from
$\xi $
-torsion, and we get a map from
![]() $P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
to
$P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
to
![]() $\Psi (P, I^{\bullet })$
.
$\Psi (P, I^{\bullet })$
.
To show the isomorphism, by the derived Nakayama lemma ([Sta, Tag 0G1U]) for
![]() ${\mathrm {B_{dR}^+}}$
, it suffices to check the above is an isomorphism after a derived tensor product with K. On the one hand, by Remark 4.1.6 we have
${\mathrm {B_{dR}^+}}$
, it suffices to check the above is an isomorphism after a derived tensor product with K. On the one hand, by Remark 4.1.6 we have
By the assumption of P, each
![]() $I^n/I^{n+1}$
is Tor-independent of K over
$I^n/I^{n+1}$
is Tor-independent of K over
![]() ${\mathrm {B_{dR}^+}}$
. So the above tensor product is equal to the discrete module as below
${\mathrm {B_{dR}^+}}$
. So the above tensor product is equal to the discrete module as below
where
![]() $\overline I$
is the tensor product
$\overline I$
is the tensor product
![]() $I\otimes _{\mathrm {B_{dR}^+}} K$
. On the other hand, the assumption of P and
$I\otimes _{\mathrm {B_{dR}^+}} K$
. On the other hand, the assumption of P and
![]() $I=(f_i)$
implies the ring
$I=(f_i)$
implies the ring
![]() $P[x_1, \ldots , x_m]/(\xi x_i-f_i, 1\leq i\leq m)$
is flat over
$P[x_1, \ldots , x_m]/(\xi x_i-f_i, 1\leq i\leq m)$
is flat over
![]() ${\mathrm {B_{dR}^+}}$
. In particular, we have
${\mathrm {B_{dR}^+}}$
. In particular, we have
 $$ \begin{align*} P[\frac{f_i}{\xi}]\otimes^L_{\mathrm{B_{dR}^+}} K & \cong P[\frac{f_i}{\xi}]\otimes_{\mathrm{B_{dR}^+}} K\\ &\cong P/(\xi ,f_i)[x_i], \end{align*} $$
$$ \begin{align*} P[\frac{f_i}{\xi}]\otimes^L_{\mathrm{B_{dR}^+}} K & \cong P[\frac{f_i}{\xi}]\otimes_{\mathrm{B_{dR}^+}} K\\ &\cong P/(\xi ,f_i)[x_i], \end{align*} $$
which by assumption is exactly the direct sum
![]() $\bigoplus _{n\in \mathbb {N}} (\overline I)^n/(\overline I)^{n+1}$
. In this way, as the above two reductions are abstractly isomorphic to each other, to finish the proof, it suffices to notice that the map we constructed identifies the generators of each direct summand.
$\bigoplus _{n\in \mathbb {N}} (\overline I)^n/(\overline I)^{n+1}$
. In this way, as the above two reductions are abstractly isomorphic to each other, to finish the proof, it suffices to notice that the map we constructed identifies the generators of each direct summand.
In general, one can still form the map from
![]() $P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
to
$P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}} $
to
![]() $\Psi (P,I^{\bullet })$
, replacing
$\Psi (P,I^{\bullet })$
, replacing
![]() $(f_i)$
above by any finite set of generators of I. As the ring P is noetherian, we can switch the order of the torsionfree quotient and the
$(f_i)$
above by any finite set of generators of I. As the ring P is noetherian, we can switch the order of the torsionfree quotient and the
![]() $\xi $
-completion to get
$\xi $
-completion to get
 $$\begin{align*}P[\frac{I}{\xi}]^\wedge_{\mathrm{tf}} = \left( P[\frac{f_i}{\xi}]/(\xi^\infty\text{-torsion}) \right)^\wedge. \end{align*}$$
$$\begin{align*}P[\frac{I}{\xi}]^\wedge_{\mathrm{tf}} = \left( P[\frac{f_i}{\xi}]/(\xi^\infty\text{-torsion}) \right)^\wedge. \end{align*}$$
So to show the isomorphism, it suffices to take the derived reduction mod
![]() $\xi $
and consider the following
$\xi $
and consider the following
 $$\begin{align*}\left( P[\frac{f_i}{\xi}]/(\xi^\infty\text{-torsion}) \right) \otimes^L_{\mathrm{B_{dR}^+}} K \rightarrow \Psi(P, I^{\bullet})\otimes^L_{\mathrm{B_{dR}^+}} K. \end{align*}$$
$$\begin{align*}\left( P[\frac{f_i}{\xi}]/(\xi^\infty\text{-torsion}) \right) \otimes^L_{\mathrm{B_{dR}^+}} K \rightarrow \Psi(P, I^{\bullet})\otimes^L_{\mathrm{B_{dR}^+}} K. \end{align*}$$
But notice that the map commutes with any Zariski localization of P, and for each
![]() $\mathfrak {p}\in \operatorname {\mathrm {Spec}}(R)$
there is a Zariski open neighborhood of
$\mathfrak {p}\in \operatorname {\mathrm {Spec}}(R)$
there is a Zariski open neighborhood of
![]() $\mathfrak {p}$
in
$\mathfrak {p}$
in
![]() $\operatorname {\mathrm {Spec}}(P)$
such that I admits a set of Koszul-regular generators and the above is an isomorphism. Thus a Čech complex argument for an open covering finishes the proof.
$\operatorname {\mathrm {Spec}}(P)$
such that I admits a set of Koszul-regular generators and the above is an isomorphism. Thus a Čech complex argument for an open covering finishes the proof.
From now on towards the end of the subsection, we use
![]() $D_{\inf }$
to denote the infinitesimal envelope
$D_{\inf }$
to denote the infinitesimal envelope
![]() $\varprojlim P/I^m$
for the surjection
$\varprojlim P/I^m$
for the surjection
![]() $P\rightarrow R$
(c.f. [Reference GuoGuo24, Section 2.2]), and use
$P\rightarrow R$
(c.f. [Reference GuoGuo24, Section 2.2]), and use ![]() for the prismatic envelope, which by Lemma 4.3.4 is isomorphic to
for the prismatic envelope, which by Lemma 4.3.4 is isomorphic to
![]() $\Psi (P,I^{\bullet })$
.
$\Psi (P,I^{\bullet })$
.
Next we use Simpson’s functor to relate a connection over
![]() $D_{\inf }$
to a log connection over
$D_{\inf }$
to a log connection over ![]() .
.
Theorem 4.3.5. Let
![]() $P,I, R$
and
$P,I, R$
and ![]() be as above, let
be as above, let
![]() $\mathcal {F}$
be a flat infinitesimal crystal over
$\mathcal {F}$
be a flat infinitesimal crystal over
![]() $(R/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
, and let
$(R/{\mathrm {B_{dR}^+}})_{{\mathrm {pinf}}}$
, and let
![]() $(M, \nabla )$
be the integrable connection of
$(M, \nabla )$
be the integrable connection of
![]() $\mathcal {F}$
at
$\mathcal {F}$
at
![]() $D_{\inf }$
(as in [Reference GuoGuo24, Section 3]). Then the log connection of
$D_{\inf }$
(as in [Reference GuoGuo24, Section 3]). Then the log connection of
![]() $\pi ^*\mathcal {F}$
at
$\pi ^*\mathcal {F}$
at ![]() is integral, integrable, and is naturally isomorphic to the unique extension of
is integral, integrable, and is naturally isomorphic to the unique extension of
![]() $\nabla $
on
$\nabla $
on ![]() by the Leibniz rule.
by the Leibniz rule.
By Definition/Lemma 4.2.6, we can denote the log connection as
![]() $(\pi ^*M, \nabla )$
, with
$(\pi ^*M, \nabla )$
, with ![]() . Note that by Example 3.0.10, the log connection
. Note that by Example 3.0.10, the log connection
![]() $(\pi ^*M, \nabla )$
is in particular quasi-nilpotent.
$(\pi ^*M, \nabla )$
is in particular quasi-nilpotent.
Proof. By proof of Proposition 3.0.12, to describe the log connection structure on ![]() (see Definition/Lemma 4.2.6), it suffices to consider the difference map
(see Definition/Lemma 4.2.6), it suffices to consider the difference map
where ![]() is the isomorphism of
is the isomorphism of ![]() -modules induced from the crystal condition. Here by Definition/Lemma 4.2.6, the isomorphism
-modules induced from the crystal condition. Here by Definition/Lemma 4.2.6, the isomorphism ![]() is naturally isomorphic to
is naturally isomorphic to ![]() , with
, with
On the other hand, notice that the isomorphism
![]() $\phi _{\inf }$
is filtered under the
$\phi _{\inf }$
is filtered under the
![]() $(I,\Delta (1))$
-adic filtration, and in particular by applying
$(I,\Delta (1))$
-adic filtration, and in particular by applying
![]() $\Psi (-, (I,\Delta (1))^{\bullet })$
and Lemma 4.3.4 we have
$\Psi (-, (I,\Delta (1))^{\bullet })$
and Lemma 4.3.4 we have
Thus by taking the difference between
![]() $\operatorname {\mathrm {id}}\otimes 1$
and
$\operatorname {\mathrm {id}}\otimes 1$
and ![]() and mod the ideal
and mod the ideal
![]() $(\frac {\Delta (1)}{\xi })^2$
, we get a natural log connection on
$(\frac {\Delta (1)}{\xi })^2$
, we get a natural log connection on ![]() .
.
Moreover, by the property of colimits, there is a natural commutative diagram sending the connection
![]() $(M,\nabla )$
to the log connection on
$(M,\nabla )$
to the log connection on
![]() $\pi ^*M$
, compatible with the natural structure map
$\pi ^*M$
, compatible with the natural structure map ![]() :
:

where the vertical maps are natural maps compatible with the inclusion
![]() $\Omega _{P/{\mathrm {B_{dR}^+}}}^1\rightarrow \frac {\Omega _{P/{\mathrm {B_{dR}^+}}}^1}{\xi }$
over the ring P. From the diagram, we see the log connection on
$\Omega _{P/{\mathrm {B_{dR}^+}}}^1\rightarrow \frac {\Omega _{P/{\mathrm {B_{dR}^+}}}^1}{\xi }$
over the ring P. From the diagram, we see the log connection on
![]() $\pi ^*M$
coincides with
$\pi ^*M$
coincides with
![]() $\nabla $
when restricted to M, and is uniquely extended by
$\nabla $
when restricted to M, and is uniquely extended by
![]() $\nabla $
using the Leibniz rule of the log connection.
$\nabla $
using the Leibniz rule of the log connection.
At last, the integrability and the quasi-nilpotence either follow from the general result in Proposition 3.0.12, or the above commutative diagram and Leibniz rule, as
![]() $\widetilde \nabla _i(x)$
is
$\widetilde \nabla _i(x)$
is
![]() $\xi $
-divisible for any i and
$\xi $
-divisible for any i and
![]() $x\in M$
, and thus by Definition 3.0.6 the connection
$x\in M$
, and thus by Definition 3.0.6 the connection
![]() $\Psi (\nabla )$
is integral and thus quasi-nilpotent.
$\Psi (\nabla )$
is integral and thus quasi-nilpotent.
The following lemma is useful when relating the log connection
![]() $\pi ^*M$
with the filtration.
$\pi ^*M$
with the filtration.
Lemma 4.3.6. Assume the same as in Theorem 4.3.5. Then
![]() $\pi ^*M$
is naturally isomorphic to
$\pi ^*M$
is naturally isomorphic to
![]() $\Psi (M,I^{\bullet } M)$
.
$\Psi (M,I^{\bullet } M)$
.
Proof. There is a natural map below
By the commutativity between the derived tensor product functor and the colimit, the above is an isomorphism before the derived
![]() $\xi $
-adic completion for
$\xi $
-adic completion for
![]() $\Psi (-,-)$
as in Construction 4.1.1. So thanks to the derived
$\Psi (-,-)$
as in Construction 4.1.1. So thanks to the derived
![]() $\xi $
-completeness of
$\xi $
-completeness of ![]() and the finiteness of M over
and the finiteness of M over
![]() $D_{\inf }$
, we see the left hand side above is automatically
$D_{\inf }$
, we see the left hand side above is automatically
![]() $\xi $
-complete, and hence isomorphic to the right.
$\xi $
-complete, and hence isomorphic to the right.
In the l.c.i. case, we also get the faithfulness of the functor from infinitesimal crystals to prismatic crystals.
Proposition 4.3.7. Let X be an affinoid rigid space over K that is a local complete intersection. The functor
![]() $\pi ^*$
in Definition/Lemma 4.2.6 from the category of flat infinitesimal crystals over
$\pi ^*$
in Definition/Lemma 4.2.6 from the category of flat infinitesimal crystals over
![]() $X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
to the category of flat prismatic crystals over
$X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
to the category of flat prismatic crystals over ![]() is faithful.
is faithful.
Proof. By the tensor product formula of
![]() $\pi ^*M$
and the compatiblility between connections and log connections, it suffices to show that under Assumption 4.3.1 for the ring
$\pi ^*M$
and the compatiblility between connections and log connections, it suffices to show that under Assumption 4.3.1 for the ring
![]() $P={\mathrm {B_{dR}^+}} \langle T_i\rangle $
, the ideal I and the ring
$P={\mathrm {B_{dR}^+}} \langle T_i\rangle $
, the ideal I and the ring
![]() $R=P/(I,\xi )$
, the natural map
$R=P/(I,\xi )$
, the natural map ![]() is an inclusion.
is an inclusion.
By definition and Lemma 4.3.4, we have
![]() $D_{\inf }$
is the I-adic completion of P, and
$D_{\inf }$
is the I-adic completion of P, and ![]() is the
is the
![]() $\xi $
-adic completion of
$\xi $
-adic completion of
![]() $P[\frac {I}{\xi }]_{\mathrm {tf}}$
. So thanks to the left exactness of the inverse limit, it suffices to show the injectivity for each
$P[\frac {I}{\xi }]_{\mathrm {tf}}$
. So thanks to the left exactness of the inverse limit, it suffices to show the injectivity for each
![]() $n\in \mathbb {N}$
below
$n\in \mathbb {N}$
below
where we use the equality
![]() $\varprojlim P/(I^n,\xi ^n) =\varprojlim P/I^n$
by the
$\varprojlim P/(I^n,\xi ^n) =\varprojlim P/I^n$
by the
![]() $\xi $
-adic completeness of P. This can be checked Zariski locally, where we can assume I admits a finite set of regular generators
$\xi $
-adic completeness of P. This can be checked Zariski locally, where we can assume I admits a finite set of regular generators
![]() $(f_1,\ldots ,f_l)$
. In this case, the natural map below is flat
$(f_1,\ldots ,f_l)$
. In this case, the natural map below is flat
Thus the injectivity of
![]() $(\ast )$
for each n follows from that of
$(\ast )$
for each n follows from that of
by base change along the flat map
![]() ${\mathrm {B_{dR}^+}}[y_j] \rightarrow P$
.
${\mathrm {B_{dR}^+}}[y_j] \rightarrow P$
.
Remark 4.3.8. From Theorem 4.3.5, the log connection associated to the image of
![]() $\pi ^*$
is integral and integrable. One might also be able to use the explicit formula of the connection to describe the essential image of the functor
$\pi ^*$
is integral and integrable. One might also be able to use the explicit formula of the connection to describe the essential image of the functor
![]() $\pi ^*$
.
$\pi ^*$
.
We then give a formula computing prismatic cohomology of a crystal that comes from the infinitesimal site, using Simpson’s functor over
![]() ${\mathrm {B_{dR}^+}}$
and the de Rham complex.
${\mathrm {B_{dR}^+}}$
and the de Rham complex.
Assume there is a system of affinoid rigid spaces
![]() $\{X_e\}$
, with each
$\{X_e\}$
, with each
![]() $X_e$
flat over
$X_e$
flat over
![]() ${\mathrm {B^+_{dR,e}}}$
, lifting a given K-rigid space X. Let
${\mathrm {B^+_{dR,e}}}$
, lifting a given K-rigid space X. Let
![]() $\mathcal {F}$
be a crystal over
$\mathcal {F}$
be a crystal over
![]() $X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
, and let
$X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
, and let
![]() $\mathcal {F}_e$
be its restriction to
$\mathcal {F}_e$
be its restriction to
![]() $X_e$
, as a crystal over the infinitesimal site
$X_e$
, as a crystal over the infinitesimal site
![]() $X_e/{\mathrm {B^+_{dR,e}}}_{\inf }$
(c.f. [Reference GuoGuo24, Section 2.4]). Following [Reference GuoGuo24, Section 2], the
$X_e/{\mathrm {B^+_{dR,e}}}_{\inf }$
(c.f. [Reference GuoGuo24, Section 2.4]). Following [Reference GuoGuo24, Section 2], the
![]() $I_{X_e/{\mathrm {B^+_{dR,e}}}}$
-adic filtration on an infinitesimal crystal
$I_{X_e/{\mathrm {B^+_{dR,e}}}}$
-adic filtration on an infinitesimal crystal
![]() $\mathcal {F}_e$
induces a natural filtration of
$\mathcal {F}_e$
induces a natural filtration of
![]() $R\Gamma (X_e/{\mathrm {B^+_{dR,e}}}_{\inf }, \mathcal {F}_e)$
, compatible with the closed immersion
$R\Gamma (X_e/{\mathrm {B^+_{dR,e}}}_{\inf }, \mathcal {F}_e)$
, compatible with the closed immersion
![]() $X_e/{\mathrm {B^+_{dR,e}}}_{\inf } \rightarrow X_{e+1}/\mathrm {B^+_{dR,e+1}}_{\inf }$
. In particular, by the limit formula
$X_e/{\mathrm {B^+_{dR,e}}}_{\inf } \rightarrow X_{e+1}/\mathrm {B^+_{dR,e+1}}_{\inf }$
. In particular, by the limit formula
![]() $R\Gamma (X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {F})=R\varprojlim _e R\Gamma (X_e/{\mathrm {B^+_{dR,e}}}_{\inf },\mathcal {F}_e)$
, the above defines a filtration on infinitesimal cohomology of
$R\Gamma (X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {F})=R\varprojlim _e R\Gamma (X_e/{\mathrm {B^+_{dR,e}}}_{\inf },\mathcal {F}_e)$
, the above defines a filtration on infinitesimal cohomology of
![]() $X/{\mathrm {B_{dR}^+}}$
as below
$X/{\mathrm {B_{dR}^+}}$
as below
Definition 4.3.9. Let X be a rigid space over K, and let
![]() $\{X_e\}$
be a compatible system of
$\{X_e\}$
be a compatible system of
![]() ${\mathrm {B^+_{dR,e}}}$
-flat lifts of X. For a crystal
${\mathrm {B^+_{dR,e}}}$
-flat lifts of X. For a crystal
![]() $\mathcal {F}$
over
$\mathcal {F}$
over
![]() $X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
, the i-th lifted (infinitesimal) filtration on its cohomology is
$X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
, the i-th lifted (infinitesimal) filtration on its cohomology is
Note that similar to [Reference GuoGuo24, Theorem 7.2.3 (iii)], the derived tensor product of the lifted filtration with
![]() ${\mathrm {B^+_{dR,e}}}$
over
${\mathrm {B^+_{dR,e}}}$
over
![]() ${\mathrm {B_{dR}^+}}$
is isomorphic to the filtration of
${\mathrm {B_{dR}^+}}$
is isomorphic to the filtration of
![]() $R\Gamma (X_e/{\mathrm {B^+_{dR,e}}}_{\inf },\mathcal {F}_e)$
.
$R\Gamma (X_e/{\mathrm {B^+_{dR,e}}}_{\inf },\mathcal {F}_e)$
.
Remark 4.3.10. When
![]() $P/I$
is smooth over
$P/I$
is smooth over
![]() ${\mathrm {B_{dR}^+}}$
(in the sense that each reduction mod
${\mathrm {B_{dR}^+}}$
(in the sense that each reduction mod
![]() $\xi ^e$
is a smooth affinoid algebra over
$\xi ^e$
is a smooth affinoid algebra over
![]() ${\mathrm {B^+_{dR,e}}}$
), the i-th lifted filtration coincides with the i-th Hodge filtration of the de Rham complex of
${\mathrm {B^+_{dR,e}}}$
), the i-th lifted filtration coincides with the i-th Hodge filtration of the de Rham complex of
![]() $\mathcal {F}$
over
$\mathcal {F}$
over
![]() $P/I$
. In particular, this is the
$P/I$
. In particular, this is the
![]() ${\mathrm {B_{dR}^+}}$
-linear lift of the i-th Hodge filtration of the de Rham complex of
${\mathrm {B_{dR}^+}}$
-linear lift of the i-th Hodge filtration of the de Rham complex of
![]() $\mathcal {F}(R)$
over K, hence the name.
$\mathcal {F}(R)$
over K, hence the name.
Remark 4.3.11. When X is a rigid space defined over a discretely valued subfield k, it admits a canonical (depending on a choice of embedding
![]() $k\rightarrow {\mathrm {B_{dR}^+}}$
)
$k\rightarrow {\mathrm {B_{dR}^+}}$
)
![]() $G_k$
-equivariant lifts
$G_k$
-equivariant lifts
![]() $\{X_e\}$
, where each
$\{X_e\}$
, where each
![]() $X_e$
is the complete base extension of the k-rigid space with
$X_e$
is the complete base extension of the k-rigid space with
![]() ${\mathrm {B^+_{dR,e}}}$
. In particular the lifted filtration admits a natural action by the Galois group.
${\mathrm {B^+_{dR,e}}}$
. In particular the lifted filtration admits a natural action by the Galois group.
Theorem 4.3.12. Let
![]() $P,I,R$
be as in Assumption 4.3.1 with
$P,I,R$
be as in Assumption 4.3.1 with
![]() $X=\mathrm {Spa}(R)$
, and let
$X=\mathrm {Spa}(R)$
, and let
![]() $\mathcal {F}$
be a flat infinitesimal crystal over
$\mathcal {F}$
be a flat infinitesimal crystal over
![]() $X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
. There is a natural isomorphism, functorial in
$X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
. There is a natural isomorphism, functorial in
![]() $\mathcal {F}$
and the surjection
$\mathcal {F}$
and the surjection
![]() $P\rightarrow P/I$
, computing cohomology of the prismatic crystal
$P\rightarrow P/I$
, computing cohomology of the prismatic crystal
![]() $\pi ^*\mathcal {F}$
$\pi ^*\mathcal {F}$
Proof. The idea is to compare Čech-Alexander complexes of two sides. Denote
![]() $D(n)_{\inf }$
to be the formal completion of the complete tensor product
$D(n)_{\inf }$
to be the formal completion of the complete tensor product
![]() $P(n)=P^{\widehat \otimes _{{\mathrm {B_{dR}^+}}} n+1}:= {\mathrm {B_{dR}^+}} \langle T_i, \delta _{i,j}; 1\leq i\leq l, 1\leq j\leq n \rangle $
along the surjection onto
$P(n)=P^{\widehat \otimes _{{\mathrm {B_{dR}^+}}} n+1}:= {\mathrm {B_{dR}^+}} \langle T_i, \delta _{i,j}; 1\leq i\leq l, 1\leq j\leq n \rangle $
along the surjection onto
![]() $P/I$
, and let
$P/I$
, and let
![]() $\Delta (n)$
be the ideal of
$\Delta (n)$
be the ideal of
![]() $D(n)_{\inf }$
defined by
$D(n)_{\inf }$
defined by
![]() $(\delta _{i,j})$
. Let
$(\delta _{i,j})$
. Let ![]() be the prismatic envelope of
be the prismatic envelope of
![]() $P/I$
inside of
$P/I$
inside of
![]() $P^{\widehat \otimes _{{\mathrm {B_{dR}^+}}} n+1}$
(Lemma 4.3.4). Note that by Remark 2.2.7, the ring
$P^{\widehat \otimes _{{\mathrm {B_{dR}^+}}} n+1}$
(Lemma 4.3.4). Note that by Remark 2.2.7, the ring ![]() is also naturally isomorphic to
is also naturally isomorphic to
![]() $D(n)_{\inf }[\frac {I,\Delta (n)}{\xi }]^\wedge _{\mathrm {tf}}$
.
$D(n)_{\inf }[\frac {I,\Delta (n)}{\xi }]^\wedge _{\mathrm {tf}}$
.
We then turn to the Čech-Alexander complexes of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\pi ^*\mathcal {F}$
. By [Reference GuoGuo24, Proposition 2.2.7] and its
$\pi ^*\mathcal {F}$
. By [Reference GuoGuo24, Proposition 2.2.7] and its
![]() ${\mathrm {B_{dR}^+}}$
-linear version [Reference GuoGuo24, Theorem 7.2.3], we have a natural filtered isomorphism
${\mathrm {B_{dR}^+}}$
-linear version [Reference GuoGuo24, Theorem 7.2.3], we have a natural filtered isomorphism
where the left side is endowed with the lifted filtration, and each term of the right side is equipped with the
![]() $(I,\Delta (n))$
-adic filtration (as
$(I,\Delta (n))$
-adic filtration (as
![]() $(I,\Delta (n))$
is the kernel ideal of the pro-infiniteisimal thickening
$(I,\Delta (n))$
is the kernel ideal of the pro-infiniteisimal thickening
![]() $D(n)_{\inf } \rightarrow P/I$
). On the other hand, by Corollary 3.0.14 we have the natural isomorphism
$D(n)_{\inf } \rightarrow P/I$
). On the other hand, by Corollary 3.0.14 we have the natural isomorphism
Moreover, by the construction of
![]() $\pi ^*\mathcal {F}$
in Theorem 4.3.5 and Lemma 4.3.6 the right hand side above is equal to
$\pi ^*\mathcal {F}$
in Theorem 4.3.5 and Lemma 4.3.6 the right hand side above is equal to
In this way, by applying
![]() $\Psi $
at the sequence (1) using the lifted filtration, and notice that homotopy limit along
$\Psi $
at the sequence (1) using the lifted filtration, and notice that homotopy limit along
![]() $\Delta ^{\mathrm {op}}$
commutes with
$\Delta ^{\mathrm {op}}$
commutes with
![]() $\Psi $
, we get
$\Psi $
, we get

As a corollary, we have the following explicit formula computing prismatic cohomology.
Corollary 4.3.13. Let P, I, R be as in Assumption 4.3.1. Let
![]() $\mathcal {F}$
be a flat infinitesimal crystal over
$\mathcal {F}$
be a flat infinitesimal crystal over
![]() $X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
, and let M be its section at the pro-infinitesimal thickening
$X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
, and let M be its section at the pro-infinitesimal thickening
![]() $D_{\inf }=\varprojlim _n P/I^n$
. Then there is an isomorphism, functorial in
$D_{\inf }=\varprojlim _n P/I^n$
. Then there is an isomorphism, functorial in
![]() $\mathcal {F}$
, as below
$\mathcal {F}$
, as below

where
![]() $\widetilde M=\pi ^*\mathcal {F}(P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}})\cong M\otimes _{D_{\inf }} P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
is the section of
$\widetilde M=\pi ^*\mathcal {F}(P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}})\cong M\otimes _{D_{\inf }} P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
is the section of
![]() $\pi ^*\mathcal {F}$
at the prismatic envelope
$\pi ^*\mathcal {F}$
at the prismatic envelope
![]() $P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
, and the right hand side is the de Rham complex associated to the log connection of
$P[\frac {I}{\xi }]^\wedge _{\mathrm {tf}}$
, and the right hand side is the de Rham complex associated to the log connection of
![]() $\widetilde M$
$\widetilde M$
Proof. Using Theorem 4.3.12, cohomology of
![]() $\pi ^*\mathcal {F}$
is isomorphic to
$\pi ^*\mathcal {F}$
is isomorphic to
![]() $\Psi (R\Gamma (X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {F}), \widetilde {\mathrm {Fil}}^{\bullet })$
. Then by taking an inverse limit of [Reference GuoGuo24, Theorem 4.1.1] with respect to
$\Psi (R\Gamma (X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {F}), \widetilde {\mathrm {Fil}}^{\bullet })$
. Then by taking an inverse limit of [Reference GuoGuo24, Theorem 4.1.1] with respect to
![]() $\mathrm {Spa}(P/(I,\xi ^e))$
over
$\mathrm {Spa}(P/(I,\xi ^e))$
over
![]() ${\mathrm {B^+_{dR,e}}}$
, we have
${\mathrm {B^+_{dR,e}}}$
, we have
where
![]() $\widetilde {\mathrm {Fil}}^{\bullet }$
is the lifted infinitesimal filtration on the de Rham complex. Thus by writing out the right hand side above explicitly, we get the conclusion.
$\widetilde {\mathrm {Fil}}^{\bullet }$
is the lifted infinitesimal filtration on the de Rham complex. Thus by writing out the right hand side above explicitly, we get the conclusion.
In the special case when R is smooth over K, we can obtain a simpler formula of cohomology of
![]() $\pi ^*\mathcal {F}$
using the de Rham complex.
$\pi ^*\mathcal {F}$
using the de Rham complex.
Corollary 4.3.14. Assume
![]() $X=\mathrm {Spa}(R)$
is smooth of dimension d over K, and
$X=\mathrm {Spa}(R)$
is smooth of dimension d over K, and
![]() $\widetilde R=\varprojlim _e \widetilde R/\xi ^e$
is a smooth lift over
$\widetilde R=\varprojlim _e \widetilde R/\xi ^e$
is a smooth lift over
![]() ${\mathrm {B_{dR}^+}}$
. Let
${\mathrm {B_{dR}^+}}$
. Let
![]() $\mathcal {F}$
be a flat infinitesimal crystal over
$\mathcal {F}$
be a flat infinitesimal crystal over
![]() $X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
, and let M be its section at the pro-infinitesimal thickening
$X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
, and let M be its section at the pro-infinitesimal thickening
![]() $\widetilde R \rightarrow R$
. Then we have
$\widetilde R \rightarrow R$
. Then we have

Proof. As a smooth lift
![]() $\widetilde R/\xi ^e$
itself is an infinitesimal envelope of R into a smooth rigid space over
$\widetilde R/\xi ^e$
itself is an infinitesimal envelope of R into a smooth rigid space over
![]() ${\mathrm {B^+_{dR,e}}}$
, we can apply Theorem 4.3.12 at the filtered isomorphism
${\mathrm {B^+_{dR,e}}}$
, we can apply Theorem 4.3.12 at the filtered isomorphism
![]() $R\Gamma (X/{\mathrm {B^+_{dR,e}}}_{\inf }, \mathcal {F})\cong (M/\xi ^e\otimes _{\widetilde R/\xi ^e} \Omega _{(\widetilde R/\xi ^e)/{\mathrm {B^+_{dR,e}}}}^{\bullet })$
in [Reference GuoGuo24, Theorem 4.1.1] to get the result.
$R\Gamma (X/{\mathrm {B^+_{dR,e}}}_{\inf }, \mathcal {F})\cong (M/\xi ^e\otimes _{\widetilde R/\xi ^e} \Omega _{(\widetilde R/\xi ^e)/{\mathrm {B^+_{dR,e}}}}^{\bullet })$
in [Reference GuoGuo24, Theorem 4.1.1] to get the result.
Another special case is when
![]() $\mathcal {F}$
is the infinitesimal structure sheaf, in which case
$\mathcal {F}$
is the infinitesimal structure sheaf, in which case
![]() $\pi ^*\mathcal {F}$
is the prismatic structure sheaf
$\pi ^*\mathcal {F}$
is the prismatic structure sheaf ![]() . In this case, we can compute prismatic cohomology using Simpson’s functor and the analytic derived de Rham complex.
. In this case, we can compute prismatic cohomology using Simpson’s functor and the analytic derived de Rham complex.
Corollary 4.3.15. Let P, I, R be as in Assumption 4.3.1. Then there is an isomorphism as below
Proof. Recall the analytic derived de Rham complex
![]() ${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{(P/I)/{\mathrm {B_{dR}^+}}}$
over
${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{(P/I)/{\mathrm {B_{dR}^+}}}$
over
![]() ${\mathrm {B_{dR}^+}}$
is defined as the filtered object
${\mathrm {B_{dR}^+}}$
is defined as the filtered object
where
![]() ${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{(P/(I,\xi ^e))/{\mathrm {B^+_{dR,e}}}}$
is constructed as in [Reference GuoGuo24, Section 5] for affinoid algebras over
${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{(P/(I,\xi ^e))/{\mathrm {B^+_{dR,e}}}}$
is constructed as in [Reference GuoGuo24, Section 5] for affinoid algebras over
![]() ${\mathrm {B^+_{dR,e}}}$
. By [Reference GuoGuo24, Corollary 5.5.2], assuming Assumption 4.3.1, the derived de Rham complex
${\mathrm {B^+_{dR,e}}}$
. By [Reference GuoGuo24, Corollary 5.5.2], assuming Assumption 4.3.1, the derived de Rham complex
![]() ${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{(P/(I,\xi ^e))/{\mathrm {B^+_{dR,e}}}}$
is filtered isomorphic to
${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{(P/(I,\xi ^e))/{\mathrm {B^+_{dR,e}}}}$
is filtered isomorphic to
![]() $R\Gamma (\mathrm {Spa}(P/(I,\xi ^e))/{\mathrm {B^+_{dR,e}}}_{\inf }, \mathcal {O}_{e \inf })$
. Thus the formula follows from Theorem 4.3.12.
$R\Gamma (\mathrm {Spa}(P/(I,\xi ^e))/{\mathrm {B^+_{dR,e}}}_{\inf }, \mathcal {O}_{e \inf })$
. Thus the formula follows from Theorem 4.3.12.
Corollary 4.3.16. Assume
![]() $X=\mathrm {Spa}(R)$
is smooth of dimension d over K, and
$X=\mathrm {Spa}(R)$
is smooth of dimension d over K, and
![]() $\widetilde R=\varprojlim _e \widetilde R/\xi ^e$
is a smooth lift over
$\widetilde R=\varprojlim _e \widetilde R/\xi ^e$
is a smooth lift over
![]() ${\mathrm {B_{dR}^+}}$
. Then we have
${\mathrm {B_{dR}^+}}$
. Then we have

To finish this section, we show that a choice of regular immersion induces a splitting of reduced prismatic cohomology.
Proposition 4.3.17. Let X be a rigid space over K, and let
![]() $\{Y_e\}_{e\in \mathbb {N}}$
be a system of smooth rigid spaces over
$\{Y_e\}_{e\in \mathbb {N}}$
be a system of smooth rigid spaces over
![]() ${\mathrm {B^+_{dR,e}}}$
with
${\mathrm {B^+_{dR,e}}}$
with
![]() $Y_{e+1}\times _{\mathrm {B_{dR,e+1}^+}} {\mathrm {B^+_{dR,e}}} \cong Y_e$
, and
$Y_{e+1}\times _{\mathrm {B_{dR,e+1}^+}} {\mathrm {B^+_{dR,e}}} \cong Y_e$
, and
![]() $X\rightarrow Y_0$
is a regular closed immersion. Let
$X\rightarrow Y_0$
is a regular closed immersion. Let
![]() $\mathcal {F}$
be a flat infinitesimal crystal over
$\mathcal {F}$
be a flat infinitesimal crystal over
![]() $X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
. Then the choice of
$X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
. Then the choice of
![]() $\{Y_e\}$
induces an isomorphism as below
$\{Y_e\}$
induces an isomorphism as below
where the latter is the direct sum of graded pieces for the infinitesimal filtration over cohomology of the crystal
![]() $\overline {\mathcal {F}}=\mathcal {F}/\xi $
over
$\overline {\mathcal {F}}=\mathcal {F}/\xi $
over
![]() $X/K_{\mathrm {pinf}}$
.
$X/K_{\mathrm {pinf}}$
.
Proof. By the global version of Theorem 4.3.12 and Corollary 3.0.15, the regular immersion induces an isomorphism between the left hand side above and the following
where
![]() $\widetilde {\mathrm {Fil}}^{\bullet }$
is the lifted infinitesimal filtration. By Remark 4.1.6 it is further equal to
$\widetilde {\mathrm {Fil}}^{\bullet }$
is the lifted infinitesimal filtration. By Remark 4.1.6 it is further equal to
Here the filtration is the infinitesimal filtration. At last, by [Reference GuoGuo24, Theorem 7.2.3], the base change
![]() $R\Gamma (X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {F})\otimes ^L_{\mathrm {B_{dR}^+}} K$
is isomorphic to infinitesimal cohomology
$R\Gamma (X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {F})\otimes ^L_{\mathrm {B_{dR}^+}} K$
is isomorphic to infinitesimal cohomology
![]() $R\Gamma (X/K_{\mathrm {inf}}, \overline {\mathcal {F}})$
with the canonical infinitesimal filtration.
$R\Gamma (X/K_{\mathrm {inf}}, \overline {\mathcal {F}})$
with the canonical infinitesimal filtration.
Note that in the special case when
![]() $\mathcal {F}=\mathcal {O}_{X/{\mathrm {B_{dR}^+}}}$
is the infinitesimal structure sheaf, the i-th graded piece above is isomorphic to
$\mathcal {F}=\mathcal {O}_{X/{\mathrm {B_{dR}^+}}}$
is the infinitesimal structure sheaf, the i-th graded piece above is isomorphic to
![]() $R\Gamma (X, L\wedge ^i\mathbb {L}^{\mathrm {an}}_{R/K})(-i)[-i]$
.
$R\Gamma (X, L\wedge ^i\mathbb {L}^{\mathrm {an}}_{R/K})(-i)[-i]$
.
5 Hodge–Tate filtration
Using the local computation from the last section and the simplicial resolutions, we are able to prove the Hodge–Tate filtration theorem.
5.1 Smooth case
In the smooth case, we first construct a natural map from Hodge–Tate cohomology to prismatic cohomology, using the Bockstein operator as in [Reference Bhatt and ScholzeBS22]. Let R be a topological finite type algebra over K. Consider the short exact sequence of
![]() ${\mathrm {B_{dR}^+}}$
-modules
${\mathrm {B_{dR}^+}}$
-modules
We take the derived tensor product of the sequence with ![]() over
over
![]() ${\mathrm {B_{dR}^+}}$
, then the connecting morphism induces the following
${\mathrm {B_{dR}^+}}$
, then the connecting morphism induces the following
By the reduction isomorphism in Corollary 3.0.15 we have
Thus we can rewrite the connecting morphism as below
As in [Reference Bhatt and ScholzeBS22, Section 4], by evaluating at the i-th cohomology group, the above induces a K-linear cdga over R
So by the universal property of the algebraic de Rham complex
![]() $\Omega _{R/K}^{\bullet , alg}$
of
$\Omega _{R/K}^{\bullet , alg}$
of
![]() $R/K$
, we get a natural map of cdga
$R/K$
, we get a natural map of cdga
The next result proves that the map induces an isomorphism of Hodge–Tate cohomology with the analytic differentials when R is smooth.
Theorem 5.1.1. Assume R is a smooth affinoid algebra over K. Then there is a natural isomorphism
where
![]() $\Omega _{R/K}^i$
is the sheaf of i-th analytic differentials.
$\Omega _{R/K}^i$
is the sheaf of i-th analytic differentials.
Assume the above case when R is smooth and affinoid, we call the Postnikov filtration of ![]() the Hodge–Tate filtration.
the Hodge–Tate filtration.
Proof. As we have constructed a natural map from algebraic de Rham complex of
![]() $R/K$
to the cdga
$R/K$
to the cdga ![]() , it suffices to show that the map factors through the analytic de Rham complex of
, it suffices to show that the map factors through the analytic de Rham complex of
![]() $R/K$
, and induces a termwise isomorphism with the target.
$R/K$
, and induces a termwise isomorphism with the target.
Let us assume R admits a surjection from
![]() $P={\mathrm {B_{dR}^+}} \langle T_i\rangle $
, together with an ideal
$P={\mathrm {B_{dR}^+}} \langle T_i\rangle $
, together with an ideal
![]() $I\in P$
satisfying Assumption 4.3.1. By Corollary 4.3.13, prismatic cohomology is isomorphic to
$I\in P$
satisfying Assumption 4.3.1. By Corollary 4.3.13, prismatic cohomology is isomorphic to
![]() $\xi $
-divided de Rham cohomology
$\xi $
-divided de Rham cohomology

where each differential map is the continuous differential with respect to
![]() $(\xi ,p)$
-adic topology. Denote its termwise reduction by
$(\xi ,p)$
-adic topology. Denote its termwise reduction by
![]() $\overline {C}_{P}$
, which by Theorem 4.3.12 and Remark 4.1.6 is isomorphic to
$\overline {C}_{P}$
, which by Theorem 4.3.12 and Remark 4.1.6 is isomorphic to
As R is smooth over K, each
![]() $L\wedge ^i\mathbb {L}_{R/K}$
is isomorphic to i-th analytic differential
$L\wedge ^i\mathbb {L}_{R/K}$
is isomorphic to i-th analytic differential
![]() $\Omega _{R/K}^i$
. So by applying the Bockstein operator
$\Omega _{R/K}^i$
. So by applying the Bockstein operator
![]() $\beta _\xi $
and its associated complex, we have
$\beta _\xi $
and its associated complex, we have
where d is the p-adic continuous differential. Thus the universal map from algebraic de Rham complex
![]() $(\Omega _{R/K}^{\bullet ,alg}, d)$
to
$(\Omega _{R/K}^{\bullet ,alg}, d)$
to
![]() $(\mathrm {H}^{\bullet }(\overline {C}_{P})(\bullet ), \beta _\xi )$
identifies its analytic quotient with the target. At last, notice that since the category of regular surjections
$(\mathrm {H}^{\bullet }(\overline {C}_{P})(\bullet ), \beta _\xi )$
identifies its analytic quotient with the target. At last, notice that since the category of regular surjections
![]() $P\rightarrow R$
is sifted as in Remark 4.3.3 (c.f. [Reference GuoGuo24, Lemma 5.5.4]), the isomorphism above is independent of the choice of
$P\rightarrow R$
is sifted as in Remark 4.3.3 (c.f. [Reference GuoGuo24, Lemma 5.5.4]), the isomorphism above is independent of the choice of
![]() $P\rightarrow R$
. So we are done.
$P\rightarrow R$
. So we are done.
5.2 Simplicial resolution for affinoid algebras
To extend the Hodge–Tate filtration to non-smooth rigid spaces, we will need the simplicial resolution of affinoid algebras by smooth ones. Here we mention that different from the algebraic setting, we cannot use the standard polynomial resolution where variables are infinite. To resolve topologically finite type algebras over a p-adic field, we will need a version of simplicial resolution such that each term satisfies the finite generatedness condition, thus within the category of topologically finite type affinoid algebras. The latter is achieved by applying a construction of Iyengar ([Reference IyengarIy07]) consecutively in the topologically context.
We start by recalling the following general construction resolving a given homology class of a given simplicial algebra using finite type polynomials. As a convention, for a simplicial abelian group
![]() $A=A_{\bullet }$
and a co-degeneracy map
$A=A_{\bullet }$
and a co-degeneracy map
![]() $s^j:[n+1]\rightarrow [n]$
, we use
$s^j:[n+1]\rightarrow [n]$
, we use
![]() $s_j$
to denote the corresponding map
$s_j$
to denote the corresponding map
![]() $A_n \rightarrow A_{n+1}$
for A. Similarly for (co-) face maps. Here
$A_n \rightarrow A_{n+1}$
for A. Similarly for (co-) face maps. Here
![]() $[n]\in \Delta $
is the finite set of integers
$[n]\in \Delta $
is the finite set of integers
![]() $\{0,1,\ldots , n\}$
.
$\{0,1,\ldots , n\}$
.
Construction 5.2.1. Let R be a commutative ring, and A be a simplicial R-algebra. Let
![]() $d\in \mathbb {N}$
be an integer, and let
$d\in \mathbb {N}$
be an integer, and let
![]() $\omega \in A_{d-1}$
be an element that represents a homology class
$\omega \in A_{d-1}$
be an element that represents a homology class
![]() $\bar {\omega }$
of degree
$\bar {\omega }$
of degree
![]() $d-1$
.
$d-1$
.
For each
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $X_n$
be the finite set of abstract variables
$X_n$
be the finite set of abstract variables
Then by [Reference IyengarIy07, 4.10], there is a free simplicial A-algebra B, denoted as
![]() $A[\{x\}|\partial x=\omega ]$
in loc. cit., defined such that
$A[\{x\}|\partial x=\omega ]$
in loc. cit., defined such that
![]() $B_n=A_n[X_n]$
.
$B_n=A_n[X_n]$
.
The lemma below describes the properties we need for the resolution
![]() $A[\{x\}|\partial x=\omega ]$
.
$A[\{x\}|\partial x=\omega ]$
.
Lemma 5.2.2. Let R be a ring, and A be a simplicial R-algebra. Then the simplicial A-algebra
![]() $B=A[\{x\}|\partial x=\omega ]$
satisfies the following:
$B=A[\{x\}|\partial x=\omega ]$
satisfies the following:
-
(i) For
 $n\leq d-1$
, we have
$n\leq d-1$
, we have
 $A_n=B_n$
.
$A_n=B_n$
. -
(ii) For each
 $n\in \mathbb {N}$
, the ring
$n\in \mathbb {N}$
, the ring
 $B_n$
is a polynomial of finite variables over
$B_n$
is a polynomial of finite variables over
 $A_n$
.
$A_n$
. -
(iii) The natural map
 $A\rightarrow B$
induces a short exact sequence
$A\rightarrow B$
induces a short exact sequence  $$\begin{align*}0\longrightarrow A_{d-1}\cdot \omega\longrightarrow \pi_{d-1}(A)\longrightarrow \pi_{d-1}(B)\longrightarrow 0. \end{align*}$$
$$\begin{align*}0\longrightarrow A_{d-1}\cdot \omega\longrightarrow \pi_{d-1}(A)\longrightarrow \pi_{d-1}(B)\longrightarrow 0. \end{align*}$$
In particular the homology class
![]() $\bar {\omega }\in \pi _{d-1}(A)$
is killed in B.
$\bar {\omega }\in \pi _{d-1}(A)$
is killed in B.
Now we apply the above construction to the p-adic setting, to show the existence of topologically finite type resolutions for an affinoid algebra.
Theorem 5.2.3. Let
![]() $(A,I)$
be a p-torsionfree topologically finitely presented algebra over
$(A,I)$
be a p-torsionfree topologically finitely presented algebra over
![]() ${\mathrm {A_{inf,e}}}$
with a finitely generated ideal. Then there exists a quasi-isomorphism from simplicial pairs of
${\mathrm {A_{inf,e}}}$
with a finitely generated ideal. Then there exists a quasi-isomorphism from simplicial pairs of
![]() ${\mathrm {A_{inf,e}}}$
-algebras with ideals,
${\mathrm {A_{inf,e}}}$
-algebras with ideals,
where both
![]() $X_i$
and
$X_i$
and
![]() $Y_i$
are finite for each
$Y_i$
are finite for each
![]() $i\in \mathbb {N}$
.
$i\in \mathbb {N}$
.
In the following, to simplify the notation, for a subset C in a given ring A, we use
![]() $(C)$
to denote the ideal of A generated by C.
$(C)$
to denote the ideal of A generated by C.
Proof. We proceed with the construction by induction as below.
-
Step 1 We first construct a constant simplicial pair, defined by a p-complete polynomial ring of finite variables over
 ${\mathrm {A_{inf,e}}}$
together with an ideal generated by a subset of variables, such that it maps surjectively onto the pair
${\mathrm {A_{inf,e}}}$
together with an ideal generated by a subset of variables, such that it maps surjectively onto the pair
 $(B,I)$
.
$(B,I)$
.More specifically, by the finiteness assumption, we may pick two finite sets X and Y that correspond to generators of A (over
 ${\mathrm {A_{inf,e}}}$
as a topological algebra) and I (over A as a module) separately, with surjections of pairs
${\mathrm {A_{inf,e}}}$
as a topological algebra) and I (over A as a module) separately, with surjections of pairs  $$\begin{align*}(f^{(0)},g^{(0)}):{\mathrm{A_{inf,e}}}\langle X, Y\rangle\rightarrow A, ~\text{and}~(Y)\rightarrow I. \end{align*}$$
$$\begin{align*}(f^{(0)},g^{(0)}):{\mathrm{A_{inf,e}}}\langle X, Y\rangle\rightarrow A, ~\text{and}~(Y)\rightarrow I. \end{align*}$$
We use the same notation
 $({\mathrm {A_{inf,e}}}\langle X, Y \rangle , (Y))$
to be the associated constant simplicial algebra with the ideal.
$({\mathrm {A_{inf,e}}}\langle X, Y \rangle , (Y))$
to be the associated constant simplicial algebra with the ideal. -
Step 2 In this step, building onto the simplicial p-complete polynomial rings constructed in Step 1, we add finitely many more variables on each simplicial term, such that the zeroth homotopy group of the new simplicial pair is isomorphic to
 $(A,I)$
. Our strategy is to use a p-completed version of Construction 5.2.1 to kill the difference between
$(A,I)$
. Our strategy is to use a p-completed version of Construction 5.2.1 to kill the difference between
 $(A,I)$
and
$(A,I)$
and
 ${\mathrm {A_{inf,e}}}\langle X, Y\rangle , (Y))$
.
${\mathrm {A_{inf,e}}}\langle X, Y\rangle , (Y))$
.We now give the construction of the simplicial pair
 $({\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet }, Y \rangle , (Y))$
together with a map
$({\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet }, Y \rangle , (Y))$
together with a map  $$\begin{align*}f^{(1)}:({\mathrm{A_{inf,e}}}\langle X,Y\rangle, (Y))\longrightarrow ({\mathrm{A_{inf,e}}}\langle X^{(1)}_{\bullet},Y\rangle, (Y)), \end{align*}$$
$$\begin{align*}f^{(1)}:({\mathrm{A_{inf,e}}}\langle X,Y\rangle, (Y))\longrightarrow ({\mathrm{A_{inf,e}}}\langle X^{(1)}_{\bullet},Y\rangle, (Y)), \end{align*}$$
such that the image of
 $(\ker (f^{(0)}),\ker (g^{(0)}))$
is killed. First, recall that the ideal
$(\ker (f^{(0)}),\ker (g^{(0)}))$
is killed. First, recall that the ideal
 $\ker (f^{(0)})$
of
$\ker (f^{(0)})$
of
 ${\mathrm {A_{inf,e}}}\langle X,Y\rangle $
(and hence
${\mathrm {A_{inf,e}}}\langle X,Y\rangle $
(and hence
 $\ker (g^{(0)})$
, which by definition is contained in
$\ker (g^{(0)})$
, which by definition is contained in
 $\ker (f^{(0)})$
) is a finitely presented
$\ker (f^{(0)})$
) is a finitely presented
 ${\mathrm {A_{inf,e}}}\langle X,Y \rangle $
-module ([Reference GuoGuo24, Corollary 5.1.3.(iii)]). So we can pick finite generators
${\mathrm {A_{inf,e}}}\langle X,Y \rangle $
-module ([Reference GuoGuo24, Corollary 5.1.3.(iii)]). So we can pick finite generators
 $v_1,\ldots ,v_s$
of
$v_1,\ldots ,v_s$
of
 $\ker (g^{(0)})$
, and additional finitely many elements
$\ker (g^{(0)})$
, and additional finitely many elements
 $u_1,\ldots ,u_r$
to generate
$u_1,\ldots ,u_r$
to generate
 $\ker (f^{(0)})$
. Using Construction 5.2.1 we then form a free simplicial algebra of finite variables
$\ker (f^{(0)})$
. Using Construction 5.2.1 we then form a free simplicial algebra of finite variables 
over
 ${\mathrm {A_{inf,e}}}\langle X, Y \rangle $
, such that the images of the following induced maps vanish (Lemma 5.2.2 (iii)):
${\mathrm {A_{inf,e}}}\langle X, Y \rangle $
, such that the images of the following induced maps vanish (Lemma 5.2.2 (iii)):  $$ \begin{align*} \ker(f^{(0)})&\longrightarrow \pi_0(S_{\bullet}),\\ \ker(g^{(0)})&\longrightarrow \pi_0(S_{\bullet}). \end{align*} $$
$$ \begin{align*} \ker(f^{(0)})&\longrightarrow \pi_0(S_{\bullet}),\\ \ker(g^{(0)})&\longrightarrow \pi_0(S_{\bullet}). \end{align*} $$
Now we take the term-wise p-adic completion at the simplicial ring
 $S_{\bullet }$
. Then by Lemma 5.2.2.(ii), we obtain a new simplicial pair over
$S_{\bullet }$
. Then by Lemma 5.2.2.(ii), we obtain a new simplicial pair over
 ${\mathrm {A_{inf,e}}}$
, denoted as
${\mathrm {A_{inf,e}}}$
, denoted as  $$\begin{align*}({\mathrm{A_{inf,e}}}\langle X^{(1)}_{\bullet}, Y \rangle, (Y)), \end{align*}$$
$$\begin{align*}({\mathrm{A_{inf,e}}}\langle X^{(1)}_{\bullet}, Y \rangle, (Y)), \end{align*}$$
where each
 $X^{(1)}_n$
is the finite set given by the union of X with the newly added variables from
$X^{(1)}_n$
is the finite set given by the union of X with the newly added variables from
 $[\partial U_i=u_i]$
and
$[\partial U_i=u_i]$
and
 $[\partial V_j=v_j]$
, following Construction 5.2.1. Moreover, the image of the pair of ideals
$[\partial V_j=v_j]$
, following Construction 5.2.1. Moreover, the image of the pair of ideals
 $(\ker (f^{(0)}),\ker (g^{(0)})$
in
$(\ker (f^{(0)}),\ker (g^{(0)})$
in
 $\pi _0\big ({\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet }, Y \rangle , (Y)\big )$
vanishes, thanks to the natural composition below
$\pi _0\big ({\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet }, Y \rangle , (Y)\big )$
vanishes, thanks to the natural composition below 
Note that by Lemma 5.2.2 (iii) the zeroth fundamental group of
 $({\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet },Y\rangle , (Y))$
is exactly isomorphic to
$({\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet },Y\rangle , (Y))$
is exactly isomorphic to
 $(A,I)$
.
$(A,I)$
. -
Step 3 As homotopy groups
 $\pi _i$
of
$\pi _i$
of
 $(A,I)$
are trivial for
$(A,I)$
are trivial for
 $i\geq 1$
, to finish the construction, it suffices to kill the higher homotopy classes of
$i\geq 1$
, to finish the construction, it suffices to kill the higher homotopy classes of
 $({\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet },Y \rangle , (Y))$
inductively, starting from
$({\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet },Y \rangle , (Y))$
inductively, starting from
 $\pi _1$
. By the long exact sequence of homotopy groups with respect to the maps
$\pi _1$
. By the long exact sequence of homotopy groups with respect to the maps  $$\begin{align*}(Y) \longrightarrow {\mathrm{A_{inf,e}}}\langle X^{(1)}_{\bullet}, Y \rangle \longrightarrow {\mathrm{A_{inf,e}}}\langle X^{(1)}_{\bullet}, Y \rangle/(Y), \end{align*}$$
$$\begin{align*}(Y) \longrightarrow {\mathrm{A_{inf,e}}}\langle X^{(1)}_{\bullet}, Y \rangle \longrightarrow {\mathrm{A_{inf,e}}}\langle X^{(1)}_{\bullet}, Y \rangle/(Y), \end{align*}$$
it is equivalent to kill the higher homotopy groups of
 $ {\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet }, Y \rangle $
and
$ {\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet }, Y \rangle $
and
 ${\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet }, Y \rangle /(Y)$
. We will use the similar argument as above.
${\mathrm {A_{inf,e}}}\langle X^{(1)}_{\bullet }, Y \rangle /(Y)$
. We will use the similar argument as above.Before the construction, we make the following observation on the finite generatedness:
Claim 5.2.4. Let
 $J=J_{\bullet }$
be a simplicial finitely generated ideal of a simplicial topologically finitely presented p-torsionfree
$J=J_{\bullet }$
be a simplicial finitely generated ideal of a simplicial topologically finitely presented p-torsionfree
 $\mathrm {A_{inf, e}}$
-algebra
$\mathrm {A_{inf, e}}$
-algebra
 $A_{\bullet }$
. Then for each
$A_{\bullet }$
. Then for each
 $n\in \mathbb {N}$
, the n-th fundamental group
$n\in \mathbb {N}$
, the n-th fundamental group
 $\pi _n(J_{\bullet })$
is a finitely generated
$\pi _n(J_{\bullet })$
is a finitely generated
 $A_n$
-module.
$A_n$
-module.Granting Claim 5.2.4, we can apply it at the unit ideals in the simplicial rings
 ${\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y \rangle /(Y)$
and
${\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y \rangle /(Y)$
and
 ${\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y \rangle $
respectively. Then similar to Step 2, by using Construction 5.2.1 and taking the term-wise p-adic completion, we can produce the simplicial pair
${\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y \rangle $
respectively. Then similar to Step 2, by using Construction 5.2.1 and taking the term-wise p-adic completion, we can produce the simplicial pair
 $({\mathrm {A_{inf,e}}}\langle X^{(n+1)}_{\bullet },Y \rangle , (Y))$
, so that
$({\mathrm {A_{inf,e}}}\langle X^{(n+1)}_{\bullet },Y \rangle , (Y))$
, so that
 $\pi _n$
of both
$\pi _n$
of both
 ${\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y\rangle /(Y)$
and
${\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y\rangle /(Y)$
and
 ${\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y\rangle $
are killed. Note that by Lemma 5.2.2.(ii), for each
${\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y\rangle $
are killed. Note that by Lemma 5.2.2.(ii), for each
 $i\leq n$
we have the identification of the finite sets
$i\leq n$
we have the identification of the finite sets  $$\begin{align*}X_i^{(n+1)} = X_i^{(n)}, \end{align*}$$
$$\begin{align*}X_i^{(n+1)} = X_i^{(n)}, \end{align*}$$
which in particular implies that
 $\pi _i({\mathrm {A_{inf,e}}}\langle X^{(n+1)}_{\bullet },Y\rangle , (Y)) = \pi _i({\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y\rangle , (Y))$
for each
$\pi _i({\mathrm {A_{inf,e}}}\langle X^{(n+1)}_{\bullet },Y\rangle , (Y)) = \pi _i({\mathrm {A_{inf,e}}}\langle X^{(n)}_{\bullet },Y\rangle , (Y))$
for each
 $i\leq n$
. Hence by taking the colimit with respect to n, we get a simplicial finitely presented
$i\leq n$
. Hence by taking the colimit with respect to n, we get a simplicial finitely presented
 ${\mathrm {A_{inf,e}}}$
-pair
${\mathrm {A_{inf,e}}}$
-pair  $$\begin{align*}({\mathrm{A_{inf,e}}}\langle X_{\bullet},Y \rangle, (Y)):=\underset{n\in \mathbb{N}}{{\mathrm{colim}}} ({\mathrm{A_{inf,e}}}\langle X^{(n)}_{\bullet},Y\rangle, (Y)). \end{align*}$$
$$\begin{align*}({\mathrm{A_{inf,e}}}\langle X_{\bullet},Y \rangle, (Y)):=\underset{n\in \mathbb{N}}{{\mathrm{colim}}} ({\mathrm{A_{inf,e}}}\langle X^{(n)}_{\bullet},Y\rangle, (Y)). \end{align*}$$
Note that by the construction, as
 $\pi _0({\mathrm {A_{inf,e}}}\langle X_{\bullet },Y \rangle , (Y))=\pi _0({\mathrm {A_{inf,e}}}\langle X_{\bullet },Y \rangle , (Y))=(A,I)$
, the natural map from
$\pi _0({\mathrm {A_{inf,e}}}\langle X_{\bullet },Y \rangle , (Y))=\pi _0({\mathrm {A_{inf,e}}}\langle X_{\bullet },Y \rangle , (Y))=(A,I)$
, the natural map from
 $ ({\mathrm {A_{inf,e}}}\langle X_{\bullet },Y \rangle , (Y))$
to its
$ ({\mathrm {A_{inf,e}}}\langle X_{\bullet },Y \rangle , (Y))$
to its
 $0$
-th fundamental group is a surjective quasi-isomorphism. This finishes the construction we need.
$0$
-th fundamental group is a surjective quasi-isomorphism. This finishes the construction we need.Proof of the Claim.
As in [Reference IyengarIy07, 3.4], to compute the i-th fundamental group, we can take the normalization of
 $J_{\bullet }$
by
$J_{\bullet }$
by  $$\begin{align*}N(J)_n=\cap_{i=1}^n \ker(d_i). \end{align*}$$
$$\begin{align*}N(J)_n=\cap_{i=1}^n \ker(d_i). \end{align*}$$
Under the notation, the homotopy group
 $\pi _n(J)$
is a quotient of the kernel ideal of the
$\pi _n(J)$
is a quotient of the kernel ideal of the
 $A_n$
-linear map
$A_n$
-linear map  $$\begin{align*}\ker(d_0|_{N(J)_n}:N(J)_n\rightarrow N(J)_{n-1}). \end{align*}$$
$$\begin{align*}\ker(d_0|_{N(J)_n}:N(J)_n\rightarrow N(J)_{n-1}). \end{align*}$$
We note that the group
 $N(J)_n$
can be written as the kernel of the
$N(J)_n$
can be written as the kernel of the
 $A_n$
-linear map
$A_n$
-linear map  $$\begin{align*}J_n\xrightarrow{\oplus_{i=1}^n d_i} \bigoplus_{i=1}^n J_{n-1}, \end{align*}$$
$$\begin{align*}J_n\xrightarrow{\oplus_{i=1}^n d_i} \bigoplus_{i=1}^n J_{n-1}, \end{align*}$$
where the
 $A_n$
-linear structure on each component of the right side is defined through the ring homomorphism
$A_n$
-linear structure on each component of the right side is defined through the ring homomorphism
 $d_i:A_n\rightarrow A_{n-1}$
. But since
$d_i:A_n\rightarrow A_{n-1}$
. But since
 $J_n$
is finitely generated, while
$J_n$
is finitely generated, while
 $J_{n-1}$
is p-torsion free, by [Sta, Tag 0519] and [Reference GuoGuo24, Corollary 5.1.3], the kernel of the map above is finitely generated over
$J_{n-1}$
is p-torsion free, by [Sta, Tag 0519] and [Reference GuoGuo24, Corollary 5.1.3], the kernel of the map above is finitely generated over
 $A_n$
. This implies that the p-torsion free
$A_n$
. This implies that the p-torsion free
 $A_n$
-module
$A_n$
-module
 $N(J)_n$
is finitely presented over
$N(J)_n$
is finitely presented over
 $A_n$
. As a consequence, the kernel of the
$A_n$
. As a consequence, the kernel of the
 $A_n$
-linear map
$A_n$
-linear map  $$\begin{align*}d_0:N(J)_n\longrightarrow N(J)_{n-1}, \end{align*}$$
$$\begin{align*}d_0:N(J)_n\longrightarrow N(J)_{n-1}, \end{align*}$$
with the source being finitely presented and the target being p-torsion free, is finitely generated over
 $A_n$
. Hence
$A_n$
. Hence
 $\pi _n(J_{\bullet })$
is finitely generated over
$\pi _n(J_{\bullet })$
is finitely generated over
 $A_n$
.
$A_n$
.
Moreover, the above allows us to establish a rational version as well.
Proposition 5.2.5. Let
![]() $(B,I)$
be a topologically finitely presented algebra over
$(B,I)$
be a topologically finitely presented algebra over
![]() ${\mathrm {B^+_{dR,e}}}$
with a finitely generated ideal. Then there exists a quasi-isomorphism from a simplicial pair of
${\mathrm {B^+_{dR,e}}}$
with a finitely generated ideal. Then there exists a quasi-isomorphism from a simplicial pair of
![]() ${\mathrm {B^+_{dR,e}}}$
-algebras with ideals
${\mathrm {B^+_{dR,e}}}$
-algebras with ideals
where both
![]() $X_i$
and
$X_i$
and
![]() $Y_i$
are finite for each
$Y_i$
are finite for each
![]() $i\in \mathbb {N}$
. Moreover, the same holds if we replace
$i\in \mathbb {N}$
. Moreover, the same holds if we replace
![]() ${\mathrm {B^+_{dR,e}}}$
by
${\mathrm {B^+_{dR,e}}}$
by
![]() ${\mathrm {B_{dR}^+}}$
.
${\mathrm {B_{dR}^+}}$
.
Proof. The case for
![]() ${\mathrm {B^+_{dR,e}}}$
follows from Theorem 5.2.3 by choosing an integral model of the pair
${\mathrm {B^+_{dR,e}}}$
follows from Theorem 5.2.3 by choosing an integral model of the pair
![]() $(B,I)$
over
$(B,I)$
over
![]() ${\mathrm {A_{inf,e}}}$
, since
${\mathrm {A_{inf,e}}}$
, since
![]() ${\mathrm {B^+_{dR,e}}}={\mathrm {A_{inf,e}}}[\frac {1}{p}]$
. To get the result for
${\mathrm {B^+_{dR,e}}}={\mathrm {A_{inf,e}}}[\frac {1}{p}]$
. To get the result for
![]() ${\mathrm {B_{dR}^+}}$
-pair
${\mathrm {B_{dR}^+}}$
-pair
![]() $(B,I)$
, we need to adjust the proof of Theorem 5.2.3, changing its base from
$(B,I)$
, we need to adjust the proof of Theorem 5.2.3, changing its base from
![]() ${\mathrm {A_{inf,e}}}$
to
${\mathrm {A_{inf,e}}}$
to
![]() ${\mathrm {B_{dR}^+}}$
. The Step 1 in Theorem 5.2.3 is identical. For Step 2, we need to find a map
${\mathrm {B_{dR}^+}}$
. The Step 1 in Theorem 5.2.3 is identical. For Step 2, we need to find a map
such that the image of
![]() $(\ker (f^{(0)}),\ker (g^{(0)}))$
vanishes. Notice that the latter are
$(\ker (f^{(0)}),\ker (g^{(0)}))$
vanishes. Notice that the latter are
![]() $\xi $
-complete modules. Let us choose a finite set of generators
$\xi $
-complete modules. Let us choose a finite set of generators
![]() $\{h_l\}$
of the kernel ideals so that their mod
$\{h_l\}$
of the kernel ideals so that their mod
![]() $\xi $
reduction are power bounded (i.e. inside of
$\xi $
reduction are power bounded (i.e. inside of
![]() $\mathcal {O}_K \langle X, Y \rangle $
), which exist by multiplying a sufficiently large power of p. Then imitating Step 2 in Theorem 5.2.3, we may choose a compatible set of maps
$\mathcal {O}_K \langle X, Y \rangle $
), which exist by multiplying a sufficiently large power of p. Then imitating Step 2 in Theorem 5.2.3, we may choose a compatible set of maps
such that the image of the mod
![]() $\xi ^e$
reduction of
$\xi ^e$
reduction of
![]() $\{h_l\}$
vanishes. Thus by taking the inverse limit with respect to e, we get Step 2.
$\{h_l\}$
vanishes. Thus by taking the inverse limit with respect to e, we get Step 2.
At last, to modify Step 3 of Theorem 5.2.3, we notice that the finiteness in Claim 5.2.4 holds automatically for
![]() ${\mathrm {B_{dR}^+}}$
-pairs the
${\mathrm {B_{dR}^+}}$
-pairs the
![]() $({\mathrm {B_{dR}^+}}\langle X^{(n)}_{\bullet },Y \rangle , (Y))$
over
$({\mathrm {B_{dR}^+}}\langle X^{(n)}_{\bullet },Y \rangle , (Y))$
over
![]() ${\mathrm {B_{dR}^+}}$
, as each
${\mathrm {B_{dR}^+}}$
, as each
![]() ${\mathrm {B_{dR}^+}}\langle X^{(n)}_i,Y\rangle $
is noetherian. For a given integer n, we fix finitely such many homotopy classes. Then similar to the above modification on Step 2, we can mod powers of
${\mathrm {B_{dR}^+}}\langle X^{(n)}_i,Y\rangle $
is noetherian. For a given integer n, we fix finitely such many homotopy classes. Then similar to the above modification on Step 2, we can mod powers of
![]() $\xi $
and kills the reduction of a fixed finite set of generators for
$\xi $
and kills the reduction of a fixed finite set of generators for
![]() $\pi _n({\mathrm {B_{dR}^+}}\langle X^{(n)}_{\bullet },Y \rangle /(Y))$
and
$\pi _n({\mathrm {B_{dR}^+}}\langle X^{(n)}_{\bullet },Y \rangle /(Y))$
and
![]() $\pi _n({\mathrm {B_{dR}^+}}\langle X^{(n)}_{\bullet },Y \rangle )$
. A further inverse limit of this compatible system of simplicial pairs finishes the proof.
$\pi _n({\mathrm {B_{dR}^+}}\langle X^{(n)}_{\bullet },Y \rangle )$
. A further inverse limit of this compatible system of simplicial pairs finishes the proof.
In the special case when I is the zero ideal, we get the resolution of the algebra itself.
Corollary 5.2.6. Assume R is either a p-torsionfree topologically finitely presented
![]() ${\mathrm {A_{inf,e}}}/{\mathrm {B^+_{dR,e}}}/{\mathrm {B_{dR}^+}}$
-algebra. There is a simplicial
${\mathrm {A_{inf,e}}}/{\mathrm {B^+_{dR,e}}}/{\mathrm {B_{dR}^+}}$
-algebra. There is a simplicial
![]() ${\mathrm {A_{inf,e}}}/{\mathrm {B^+_{dR,e}}}/{\mathrm {B_{dR}^+}}$
-algebra resolution
${\mathrm {A_{inf,e}}}/{\mathrm {B^+_{dR,e}}}/{\mathrm {B_{dR}^+}}$
-algebra resolution
![]() $A_{\bullet } \rightarrow R$
, such that each
$A_{\bullet } \rightarrow R$
, such that each
![]() $A_n$
is isomorphic to a Tate algebra of finite variables over
$A_n$
is isomorphic to a Tate algebra of finite variables over
![]() ${\mathrm {A_{inf,e}}}/{\mathrm {B^+_{dR,e}}}/{\mathrm {B_{dR}^+}}$
.
${\mathrm {A_{inf,e}}}/{\mathrm {B^+_{dR,e}}}/{\mathrm {B_{dR}^+}}$
.
5.3 Left Kan extension and Hodge–Tate filtration
Now we are able to extend the Hodge–Tate filtration to general l.c.i. rigid spaces, using simplicial resolution developed last subsection. The idea is similar to the left Kan extension used in the algebraic setting, but we do it over affinoid algebras.
We start by observing that the analytic cotangent complex and the analytic derived de Rham complex can be computed using simplicial resolutions. Before the statement, we refer the reader to [Reference GuoGuo24, Def. 5.2.10, Def. 5.3.6] for the detailed definitions and the constructions of the analytic cotangent complex (resp. the analytic derived de Rham complex) for a map of topologically finite type algebras
![]() $A\to B$
over
$A\to B$
over
![]() ${\mathrm {B^+_{dR,e}}}$
. As a quick recollection, the analytic cotangent complex can be defined by inverting the element p at the p-completed algebraic cotangent complex (resp. the p-completed derived de Rham complex) for a map of rings
${\mathrm {B^+_{dR,e}}}$
. As a quick recollection, the analytic cotangent complex can be defined by inverting the element p at the p-completed algebraic cotangent complex (resp. the p-completed derived de Rham complex) for a map of rings
![]() $A_0\to B_0$
, where the latter is a map of any compatible choices of the rings of integers of A and B (c.f. [Reference GuoGuo24, Prop. 5.2.13, Cor. 5.3.7]).
$A_0\to B_0$
, where the latter is a map of any compatible choices of the rings of integers of A and B (c.f. [Reference GuoGuo24, Prop. 5.2.13, Cor. 5.3.7]).
Proposition 5.3.1. Let R be a topologically finite type
![]() ${\mathrm {B^+_{dR,e}}}$
-algebra. Then for a given simplicial resolution
${\mathrm {B^+_{dR,e}}}$
-algebra. Then for a given simplicial resolution
![]() ${\mathrm {B^+_{dR,e}}} \langle X_{\bullet }\rangle \rightarrow R$
where each set of variables
${\mathrm {B^+_{dR,e}}} \langle X_{\bullet }\rangle \rightarrow R$
where each set of variables
![]() $X_n$
is finite, we have
$X_n$
is finite, we have
 $$ \begin{align*} &\underset{\Delta}{{\mathrm{colim}}} ~\mathbb{L}^{\mathrm{an}}_{{\mathrm{B^+_{dR,e}}} \langle X_{\bullet}\rangle/{\mathrm{B^+_{dR,e}}}} \cong \mathbb{L}^{\mathrm{an}}_{R/{\mathrm{B^+_{dR,e}}}}, \\ &\underset{\Delta}{{\mathrm{colim}}} ~{\widehat{\mathrm{dR}}^{\mathrm{an}}}_{{\mathrm{B^+_{dR,e}}} \langle X_{\bullet}\rangle/{\mathrm{B^+_{dR,e}}}}/{\mathrm{Fil}}^m \cong {\widehat{\mathrm{dR}}^{\mathrm{an}}}_{R/{\mathrm{B^+_{dR,e}}}}/{\mathrm{Fil}}^m, \\ &\text{filtered completion of }\left( \underset{\Delta}{{\mathrm{colim}}}~ {\widehat{\mathrm{dR}}^{\mathrm{an}}}_{{\mathrm{B^+_{dR,e}}} \langle X_{\bullet}\rangle/{\mathrm{B^+_{dR,e}}}}\right) \cong {\widehat{\mathrm{dR}}^{\mathrm{an}}}_{R/{\mathrm{B^+_{dR,e}}}}. \end{align*} $$
$$ \begin{align*} &\underset{\Delta}{{\mathrm{colim}}} ~\mathbb{L}^{\mathrm{an}}_{{\mathrm{B^+_{dR,e}}} \langle X_{\bullet}\rangle/{\mathrm{B^+_{dR,e}}}} \cong \mathbb{L}^{\mathrm{an}}_{R/{\mathrm{B^+_{dR,e}}}}, \\ &\underset{\Delta}{{\mathrm{colim}}} ~{\widehat{\mathrm{dR}}^{\mathrm{an}}}_{{\mathrm{B^+_{dR,e}}} \langle X_{\bullet}\rangle/{\mathrm{B^+_{dR,e}}}}/{\mathrm{Fil}}^m \cong {\widehat{\mathrm{dR}}^{\mathrm{an}}}_{R/{\mathrm{B^+_{dR,e}}}}/{\mathrm{Fil}}^m, \\ &\text{filtered completion of }\left( \underset{\Delta}{{\mathrm{colim}}}~ {\widehat{\mathrm{dR}}^{\mathrm{an}}}_{{\mathrm{B^+_{dR,e}}} \langle X_{\bullet}\rangle/{\mathrm{B^+_{dR,e}}}}\right) \cong {\widehat{\mathrm{dR}}^{\mathrm{an}}}_{R/{\mathrm{B^+_{dR,e}}}}. \end{align*} $$
Proof. We temporarily use the notation
![]() $(-)^\wedge _p$
to denote the derived p-completion. Let
$(-)^\wedge _p$
to denote the derived p-completion. Let
![]() $R_0$
be a ring of definition of R, which is topologically finite type over
$R_0$
be a ring of definition of R, which is topologically finite type over
![]() ${\mathrm {A_{inf,e}}}$
. By induction, we can find a simplicial topologically finite type
${\mathrm {A_{inf,e}}}$
. By induction, we can find a simplicial topologically finite type
![]() ${\mathrm {A_{inf,e}}}$
-algebras
${\mathrm {A_{inf,e}}}$
-algebras
![]() $A_{\bullet } \rightarrow R_0$
, such that each
$A_{\bullet } \rightarrow R_0$
, such that each
![]() $A_n$
is a ring of definition of
$A_n$
is a ring of definition of
![]() ${\mathrm {B^+_{dR,e}}} \langle X_n\rangle $
. The triple of rings
${\mathrm {B^+_{dR,e}}} \langle X_n\rangle $
. The triple of rings
![]() ${\mathrm {A_{inf,e}}} \rightarrow A_{\bullet } \rightarrow R_0$
then induces the natural triangle of algebraic cotangent complexes
${\mathrm {A_{inf,e}}} \rightarrow A_{\bullet } \rightarrow R_0$
then induces the natural triangle of algebraic cotangent complexes
where the final term is equal to the homotopy colimit
![]() $\underset {[n]\in \Delta }{{\mathrm {colim}}}~ \mathbb {L}_{R_0/A_n}$
. We then apply the derived p-completion at the triangle and then invert at p. By [Sta, Tag 091V], the derived completion commutes with colimits. In particular we get the equalities
$\underset {[n]\in \Delta }{{\mathrm {colim}}}~ \mathbb {L}_{R_0/A_n}$
. We then apply the derived p-completion at the triangle and then invert at p. By [Sta, Tag 091V], the derived completion commutes with colimits. In particular we get the equalities
 $$ \begin{align*} (\mathbb{L}_{R_0/A_{\bullet}})^\wedge_p\left[\frac{1}{p}\right] &= (\underset{[n]\in \Delta}{{\mathrm{colim}}} ~\mathbb{L}_{R_0/A_n})^\wedge_p \left[\frac{1}{p}\right] \\ &\cong \underset{[n]\in \Delta}{{\mathrm{colim}}}~ (\mathbb{L}_{R_0/A_n})^\wedge_p \left[\frac{1}{p}\right] \\ &= \underset{[n]\in \Delta}{{\mathrm{colim}}}~ \mathbb{L}^{\mathrm{an}}_{R/{\mathrm{B^+_{dR,e}}} \langle X_n\rangle}. \end{align*} $$
$$ \begin{align*} (\mathbb{L}_{R_0/A_{\bullet}})^\wedge_p\left[\frac{1}{p}\right] &= (\underset{[n]\in \Delta}{{\mathrm{colim}}} ~\mathbb{L}_{R_0/A_n})^\wedge_p \left[\frac{1}{p}\right] \\ &\cong \underset{[n]\in \Delta}{{\mathrm{colim}}}~ (\mathbb{L}_{R_0/A_n})^\wedge_p \left[\frac{1}{p}\right] \\ &= \underset{[n]\in \Delta}{{\mathrm{colim}}}~ \mathbb{L}^{\mathrm{an}}_{R/{\mathrm{B^+_{dR,e}}} \langle X_n\rangle}. \end{align*} $$
Note that by assumption the map
![]() ${\mathrm {B^+_{dR,e}}} \langle X_n\rangle \rightarrow R$
is a surjection. In particular, by [Reference GuoGuo24, Corollary 5.2.15] we have a natural isomorphism
${\mathrm {B^+_{dR,e}}} \langle X_n\rangle \rightarrow R$
is a surjection. In particular, by [Reference GuoGuo24, Corollary 5.2.15] we have a natural isomorphism
where the latter is the algebraic cotangent complex. So by taking the colimit, the equalities above together with the assumption that
![]() ${\mathrm {B^+_{dR,e}}} \langle X_{\bullet }\rangle $
resolves the ring R, imply the following
${\mathrm {B^+_{dR,e}}} \langle X_{\bullet }\rangle $
resolves the ring R, imply the following
 $$\begin{align*}(\mathbb{L}_{R_0/A_{\bullet}})^\wedge_p\left[\frac{1}{p}\right] \cong \underset{[n]\in \Delta}{{\mathrm{colim}}}~\mathbb{L}_{R/{\mathrm{B^+_{dR,e}}} \langle X_n\rangle} \cong 0. \end{align*}$$
$$\begin{align*}(\mathbb{L}_{R_0/A_{\bullet}})^\wedge_p\left[\frac{1}{p}\right] \cong \underset{[n]\in \Delta}{{\mathrm{colim}}}~\mathbb{L}_{R/{\mathrm{B^+_{dR,e}}} \langle X_n\rangle} \cong 0. \end{align*}$$
Thus the triangle at the begining leads to the isomorphism
 $$\begin{align*}\left(\mathbb{L}_{A_{\bullet}/{\mathrm{A_{inf,e}}}}\otimes_{A_{\bullet}}^L R_0\right)^\wedge_p\left[\frac{1}{p}\right] \cong (\mathbb{L}_{R_0/{\mathrm{A_{inf,e}}}})^\wedge_p\left[\frac{1}{p}\right], \end{align*}$$
$$\begin{align*}\left(\mathbb{L}_{A_{\bullet}/{\mathrm{A_{inf,e}}}}\otimes_{A_{\bullet}}^L R_0\right)^\wedge_p\left[\frac{1}{p}\right] \cong (\mathbb{L}_{R_0/{\mathrm{A_{inf,e}}}})^\wedge_p\left[\frac{1}{p}\right], \end{align*}$$
namely the first formula in the statement.
For the equality on
![]() ${\widehat {\mathrm {dR}}^{\mathrm {an}}}/{\mathrm {Fil}}^m$
and
${\widehat {\mathrm {dR}}^{\mathrm {an}}}/{\mathrm {Fil}}^m$
and
![]() ${\widehat {\mathrm {dR}}^{\mathrm {an}}}$
, it suffices to notice that each graded piece is functorially given by
${\widehat {\mathrm {dR}}^{\mathrm {an}}}$
, it suffices to notice that each graded piece is functorially given by
![]() $L\wedge ^i\mathbb {L}^{\mathrm {an}}[-i]$
. Thus the last two isomorphisms follows from the first one by applying derived wedge powers.
$L\wedge ^i\mathbb {L}^{\mathrm {an}}[-i]$
. Thus the last two isomorphisms follows from the first one by applying derived wedge powers.
Following the above result on analytic cotangent complexes, we can use the left Kan extension to give another construction of prismatic cohomology as below.
Proposition 5.3.2. Let
![]() $R_0$
be a topologically finite type algebra over
$R_0$
be a topologically finite type algebra over
![]() $\mathcal {O}_K$
, and let
$\mathcal {O}_K$
, and let
![]() $\epsilon :\mathcal {O}_K \langle X_{\bullet }\rangle \rightarrow R_0$
be a simplicial resolution such that each set of variables
$\epsilon :\mathcal {O}_K \langle X_{\bullet }\rangle \rightarrow R_0$
be a simplicial resolution such that each set of variables
![]() $X_n$
is finite.
$X_n$
is finite.
-
(i) The following colimits are independent of the choice of the resolution

where
 $(-)^\wedge $
is the derived
$(-)^\wedge $
is the derived
 $\xi $
-completion.
$\xi $
-completion. -
(ii) When
 $R=R_0[\frac {1}{p}]$
is smooth over K, the above are naturally isomorphic to
$R=R_0[\frac {1}{p}]$
is smooth over K, the above are naturally isomorphic to  and
and  separately.
separately.
Proof. Consider the category
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\mathcal {O}_K$
-linear maps
$\mathcal {O}_K$
-linear maps
![]() $(\mathcal {O_K} \langle E \rangle , \beta : \mathcal {O_K} \langle E \rangle \rightarrow R_0)$
for finite sets E, and equip its opposite category with the indiscrete topology. Then it suffices to show that any such resolution
$(\mathcal {O_K} \langle E \rangle , \beta : \mathcal {O_K} \langle E \rangle \rightarrow R_0)$
for finite sets E, and equip its opposite category with the indiscrete topology. Then it suffices to show that any such resolution
![]() $\mathcal {O}_K \langle X_{\bullet }\rangle \rightarrow R_0$
is equivalent to the final object of the associated topos. This is shown as in [Sta, 08PS], with the only difference being that we use the p-completeness of
$\mathcal {O}_K \langle X_{\bullet }\rangle \rightarrow R_0$
is equivalent to the final object of the associated topos. This is shown as in [Sta, 08PS], with the only difference being that we use the p-completeness of
![]() $\mathcal {O}_K \langle X_{\bullet }\rangle $
to get the equality
$\mathcal {O}_K \langle X_{\bullet }\rangle $
to get the equality
Now we consider the presheaf of complexes ![]() over
over
![]() $\mathcal {C}$
sending a given map
$\mathcal {C}$
sending a given map
![]() $\mathcal {O_K} \langle E \rangle \rightarrow R_0$
onto reduced prismatic cohomology
$\mathcal {O_K} \langle E \rangle \rightarrow R_0$
onto reduced prismatic cohomology ![]() together with its Hodge–Tate filtration as in Corollary 5.3.6. Then by the above argument, the global section of
together with its Hodge–Tate filtration as in Corollary 5.3.6. Then by the above argument, the global section of ![]() is isomorphic to
is isomorphic to
In particular, it is independent of the choice of the simplicial resolution
![]() $\mathcal {O}_K \langle X_{\bullet }\rangle \rightarrow R_0$
. Moreover, by Corollary 5.3.6 the i-th graded piece of the Hodge–Tate filtration is equal to the following colimit
$\mathcal {O}_K \langle X_{\bullet }\rangle \rightarrow R_0$
. Moreover, by Corollary 5.3.6 the i-th graded piece of the Hodge–Tate filtration is equal to the following colimit
which by Proposition 5.3.1 is naturally isomorphic to
![]() $L\wedge ^i\mathbb {L}^{\mathrm {an}}_{R/K}(-1)[-1]$
. In particular, when R is smooth over K, as the analytic cotangent complex coincides with its continuous differential over K, the graded pieces of the colimit of the Hodge–Tate filtrations in
$L\wedge ^i\mathbb {L}^{\mathrm {an}}_{R/K}(-1)[-1]$
. In particular, when R is smooth over K, as the analytic cotangent complex coincides with its continuous differential over K, the graded pieces of the colimit of the Hodge–Tate filtrations in
![]() $(\ast )$
is isomorphic to the Hodge–Tate filtration of
$(\ast )$
is isomorphic to the Hodge–Tate filtration of ![]() . So by taking colimits with respect to the exhaustive increasing filtrations of both, we finish the proof of (ii) for reduced prismatic cohomology. At last, the extension of the above to prismatic cohomology of
. So by taking colimits with respect to the exhaustive increasing filtrations of both, we finish the proof of (ii) for reduced prismatic cohomology. At last, the extension of the above to prismatic cohomology of ![]() follows from the derived Nakayama’s lemma by the reduction mod
follows from the derived Nakayama’s lemma by the reduction mod
![]() $\xi $
.
$\xi $
.
Remark 5.3.3. Here we notice that Proposition 5.3.2 starts with a simplicial resolution in the integral level, which is a priori different from the left Kan extension but in the rational level. In fact, using the Hodge–Tate resolution as in the second half of the proof and Proposition 5.3.1, one can show that the analogous statement of Proposition 5.3.2 holds true for a simplicial resolution
![]() $K \langle X_{\bullet }\rangle \rightarrow R$
over K, without assuming the resolution is defined integrally.
$K \langle X_{\bullet }\rangle \rightarrow R$
over K, without assuming the resolution is defined integrally.
Definition 5.3.4. Let R be a topologically finite type algebra over K, and let
![]() $K \langle X_{\bullet }\rangle \rightarrow R$
be any simplicial resolution such that each
$K \langle X_{\bullet }\rangle \rightarrow R$
be any simplicial resolution such that each
![]() $X_n$
is finite.
$X_n$
is finite.
-
(i) We define derived prismatic cohomology
 and its reduction
and its reduction  as below
as below 
where
 $(-)^\wedge $
is the derived
$(-)^\wedge $
is the derived
 $\xi $
-completion.
$\xi $
-completion. -
(ii) The i-th Hodge–Tate filtration on
 is defined as
is defined as 
Using the above notations, Proposition 5.3.2 shows that for a smooth rigid space X over K, its derived prismatic cohomology is isomorphic to prismatic cohomology ![]() , and its Hodge–Tate-filtered reduced derived prismatic cohomology is isomorphic to reduced prismatic cohomology
, and its Hodge–Tate-filtered reduced derived prismatic cohomology is isomorphic to reduced prismatic cohomology ![]() with its Postnikov filtration.
with its Postnikov filtration.
Finally, we are able to show that derived prismatic cohomology coincides with originally defined prismatic cohomology, for general l.c.i. rigid spaces.
Theorem 5.3.5. Let R be a topologically finite type algebra over K that has l.c.i. singularities. Then there are natural isomorphisms

Proof. By derived Nakayama’s lemma, it suffices to show the second isomorphism. As both reduced cohomologies are étale local, we may assume R admits a regular closed immersion as in Assumption 4.3.1. Namely, we assume that there are surjections
![]() $P={\mathrm {B_{dR}^+}} \langle T_i\rangle \rightarrow P/I \rightarrow P/(I,\xi )\cong R$
, where I is a Koszul-regular ideal of P with
$P={\mathrm {B_{dR}^+}} \langle T_i\rangle \rightarrow P/I \rightarrow P/(I,\xi )\cong R$
, where I is a Koszul-regular ideal of P with
![]() $P/I$
being flat over
$P/I$
being flat over
![]() ${\mathrm {B_{dR}^+}}$
. We then use Proposition 5.2.5 to find a simplicial resolution of pairs
${\mathrm {B_{dR}^+}}$
. We then use Proposition 5.2.5 to find a simplicial resolution of pairs
such that each of
![]() $X_n$
and
$X_n$
and
![]() $Y_n$
is a finite set. Note that the induced simplicial K-algebra
$Y_n$
is a finite set. Note that the induced simplicial K-algebra
![]() $K \langle X_{\bullet }\rangle $
resolves
$K \langle X_{\bullet }\rangle $
resolves
![]() $P/\xi =R$
under the quotient map.
$P/\xi =R$
under the quotient map.
To compare two prismatic cohomology, we apply Proposition 5.3.2 at the K-resolution
![]() $K \langle X_{\bullet }\rangle \rightarrow R$
to represent derived prismatic cohomology. It then suffices to show the following isomorphism
$K \langle X_{\bullet }\rangle \rightarrow R$
to represent derived prismatic cohomology. It then suffices to show the following isomorphism
Notice that the pairs
![]() $({\mathrm {B_{dR}^+}} \langle X_n, Y_n\rangle , (Y_n))$
and
$({\mathrm {B_{dR}^+}} \langle X_n, Y_n\rangle , (Y_n))$
and
![]() $(P,I)$
all satisfy Assumption 4.3.1. In particular, we can apply Simpson’s functor as in Theorem 4.3.12 (and in particular Corollary 4.3.16) at the pair
$(P,I)$
all satisfy Assumption 4.3.1. In particular, we can apply Simpson’s functor as in Theorem 4.3.12 (and in particular Corollary 4.3.16) at the pair
![]() $({\mathrm {B_{dR}^+}} \langle X_n, Y_n\rangle , (Y_n))$
to compute
$({\mathrm {B_{dR}^+}} \langle X_n, Y_n\rangle , (Y_n))$
to compute ![]() , which is functorial with respect to
, which is functorial with respect to
![]() $[n]\in \Delta $
. In particular, by taking the colimit at their reduced prismatic cohomology, we get the following graded morphism
$[n]\in \Delta $
. In particular, by taking the colimit at their reduced prismatic cohomology, we get the following graded morphism
In this way, thanks to the simplicial descent for the analytic cotangent complex in Proposition 5.3.1, we get the isomorphism for the graded pieces, thus the one for reduced prismatic cohomology.
As a consequence, we obtain a naturally defined Hodge–Tate filtration on reduced prismatic cohomology.
Corollary 5.3.6. Let X be a rigid space over K that is a locally complete intersection. There exists an ascending exhaustive
![]() $\mathbb {N}^{\mathrm {op}}$
-filtration
$\mathbb {N}^{\mathrm {op}}$
-filtration
![]() ${\mathrm {Fil}}^{\mathrm {HT}}_{\bullet }$
on
${\mathrm {Fil}}^{\mathrm {HT}}_{\bullet }$
on ![]() , and is multiplicative under the canonical
, and is multiplicative under the canonical
![]() $\mathbb {E}_\infty $
-ring structure. It satisfies the following:
$\mathbb {E}_\infty $
-ring structure. It satisfies the following:
-
(i) the i-th graded piece is naturally isomorphic to
 $R\Gamma (X, L\wedge ^i\mathbb {L}^{\mathrm {an}}_{R/K})(-i)[-i]$
;
$R\Gamma (X, L\wedge ^i\mathbb {L}^{\mathrm {an}}_{R/K})(-i)[-i]$
; -
(ii) when X is smooth and affinoid, it coincides with the Postnikov filtration as in Theorem 5.1.1.
Note that by assumption, the i-th graded piece of the Hodge–Tate filtration is also isomorphic to ![]() for the infinitesimal filtration on infinitesimal cohomology, which follows from the comparison between the infinitesimal cohomology and the derived de Rham cohomology as in [Reference GuoGuo24].
for the infinitesimal filtration on infinitesimal cohomology, which follows from the comparison between the infinitesimal cohomology and the derived de Rham cohomology as in [Reference GuoGuo24].
6 Infinitesimal comparison
In this section, we prove the infinitesimal comparison theorem, using the decalage functor
![]() $L_\eta $
.
$L_\eta $
.
Theorem 6.0.1. Let X be an affinoid rigid space over K that has l.c.i. singularities. There is a natural map of complexes as below
The map
![]() $\phi $
is an isomorphism when X is smooth and affinoid.
$\phi $
is an isomorphism when X is smooth and affinoid.
To simplify the notation, we use
![]() $R\Gamma _{\mathrm {inf}}(X/{\mathrm {B_{dR}^+}})$
and
$R\Gamma _{\mathrm {inf}}(X/{\mathrm {B_{dR}^+}})$
and ![]() to denote infinitesimal and prismatic cohomology.
to denote infinitesimal and prismatic cohomology.
Proof. To start, we first note that map from infinitesimal cohomology to prismatic cohomology can be constructed without the l.c.i. assumption on X. Recall there is a natural morphism of ringed sites in Definition 4.2.4,
sending a pro-infinitesimal thickening
![]() $(U=\mathrm {Spa}(A),T_e=\mathrm {Spa}(B_e))$
onto the prism
$(U=\mathrm {Spa}(A),T_e=\mathrm {Spa}(B_e))$
onto the prism
where I is the kernel of the surjection
![]() $\mathcal {O}_{X/{\mathrm {B_{dR}^+}}}(U,T_e)=B:=\varprojlim B_e \rightarrow A$
. Notice that there is a natural map of
$\mathcal {O}_{X/{\mathrm {B_{dR}^+}}}(U,T_e)=B:=\varprojlim B_e \rightarrow A$
. Notice that there is a natural map of
![]() ${\mathrm {B_{dR}^+}}$
-algebras
${\mathrm {B_{dR}^+}}$
-algebras
![]() $B\rightarrow B'$
by construction. Thus by taking the homotopy limit among all pro-infinitesimal thickenings in
$B\rightarrow B'$
by construction. Thus by taking the homotopy limit among all pro-infinitesimal thickenings in
![]() $X/{\mathrm {B_{dR}^+}}_{\mathrm {inf}}$
, we get a map of complexes
$X/{\mathrm {B_{dR}^+}}_{\mathrm {inf}}$
, we get a map of complexes
On the other hand, the decalage functor naturally induces a map ![]() . To see this, by [Reference Bhatt, Morrow and ScholzeBMS, Lemma 6.10], it suffices to show that under the assumption
. To see this, by [Reference Bhatt, Morrow and ScholzeBMS, Lemma 6.10], it suffices to show that under the assumption ![]() has no
has no
![]() $\xi $
-torsion. In this case, we consider the natural triangle induced by multiplication by
$\xi $
-torsion. In this case, we consider the natural triangle induced by multiplication by
![]() $\xi $
on
$\xi $
on ![]() , and get
, and get
Notice that everything above has no negative cohomology. So by taking the long exact sequence and looking at
![]() $\mathrm {H}^0$
, we get the
$\mathrm {H}^0$
, we get the
![]() $\xi $
-torsion freeness of
$\xi $
-torsion freeness of ![]() .
.
To see the map
![]() $\phi $
from infinitesimal cohomology to
$\phi $
from infinitesimal cohomology to ![]() , we assume
, we assume
![]() $X=\mathrm {Spa}(R)$
admits a regular closed immersion into
$X=\mathrm {Spa}(R)$
admits a regular closed immersion into
![]() $P={\mathrm {B_{dR}^+}} \langle T_i\rangle $
as in Assumption 4.3.1. In this case, by translating both cohomology into forms involving de Rham complexes ([Reference GuoGuo24, Theorem 4.1.1] for infinitesimal cohomology, and Corollary 4.3.13 for prismatic cohomology), the natural map
$P={\mathrm {B_{dR}^+}} \langle T_i\rangle $
as in Assumption 4.3.1. In this case, by translating both cohomology into forms involving de Rham complexes ([Reference GuoGuo24, Theorem 4.1.1] for infinitesimal cohomology, and Corollary 4.3.13 for prismatic cohomology), the natural map
![]() $\psi $
can be rewritten as
$\psi $
can be rewritten as

where ![]() . Notice that the image of each
. Notice that the image of each
![]() $D_{\inf }\otimes _P \Omega _P^i$
in
$D_{\inf }\otimes _P \Omega _P^i$
in ![]() is contained in the submodule
is contained in the submodule ![]() . In particular, by the explicit construction of the
. In particular, by the explicit construction of the
![]() $\eta _\xi $
functor in [Reference Bhatt, Morrow and ScholzeBMS, Section 6], as
$\eta _\xi $
functor in [Reference Bhatt, Morrow and ScholzeBMS, Section 6], as
![]() $\psi ^i(\omega ^i)$
(for
$\psi ^i(\omega ^i)$
(for
![]() $\omega ^i\in D_{\inf }\otimes _P \Omega _P^i$
) is contained in
$\omega ^i\in D_{\inf }\otimes _P \Omega _P^i$
) is contained in ![]() , we see
, we see

Thus the map from infinitesimal cohomology to prismatic cohomology naturally factors through the map
![]() $\psi $
.
$\psi $
.
At last, let us further assume X is smooth. By the derived
![]() $\xi $
-completeness of
$\xi $
-completeness of ![]() ([Reference Bhatt, Morrow and ScholzeBMS, Lemma 6.19]) and that of infinitesimal cohomology
([Reference Bhatt, Morrow and ScholzeBMS, Lemma 6.19]) and that of infinitesimal cohomology
![]() $R\Gamma _{\mathrm {inf}}(X/{\mathrm {B_{dR}^+}})$
, it suffices to check the isomorphism after reducing
$R\Gamma _{\mathrm {inf}}(X/{\mathrm {B_{dR}^+}})$
, it suffices to check the isomorphism after reducing
![]() $\phi $
mod
$\phi $
mod
![]() $\xi $
. Notice infinitesimal cohomology satisfies the formula
$\xi $
. Notice infinitesimal cohomology satisfies the formula
On the other hand, by the Hodge–Tate comparison (Theorem 5.1.1) and [Reference Bhatt, Morrow and ScholzeBMS, Proposition 6.12], we have
where Bockstein operator is exactly the continuous differential operator in this form. So both the source and the target are abstractly isomorphic to each other. Finally, to see the map
![]() $\phi $
is indeed an isomorphism, it suffices to do this locally, assuming R admits a smooth lift
$\phi $
is indeed an isomorphism, it suffices to do this locally, assuming R admits a smooth lift
![]() $\widetilde R$
over
$\widetilde R$
over
![]() ${\mathrm {B_{dR}^+}}$
, where we use the
${\mathrm {B_{dR}^+}}$
, where we use the
![]() $\xi $
-divided de Rham complex in Corollary 4.3.14 to identify termwise generators.
$\xi $
-divided de Rham complex in Corollary 4.3.14 to identify termwise generators.
It is well-known to experts that the decalage functor does not commute with taking derived global sections (c.f. [Reference Bhatt, Morrow and ScholzeBMS, discussion above Theorem 1.17]). We give a simple example illustrating the discrepancy.
Example 6.0.2. Let X be a projective curve over K, defined over a discretely valued subfield k that has a perfect residue field. By [Reference Bhatt, Morrow and ScholzeBMS, Proposition 6.12] and the Hodge–Tate comparison Theorem 5.1.1, the mod
![]() $\xi $
-reduction
$\xi $
-reduction
![]() $(L\eta _\xi C)\otimes _{\mathrm {B_{dR}^+}}^L K$
for
$(L\eta _\xi C)\otimes _{\mathrm {B_{dR}^+}}^L K$
for ![]() is isomorphic to the following explicit complex
is isomorphic to the following explicit complex
By the Galois equivariance, the complex is isomorphic to the derived sum of
![]() $\left ( \mathrm {H}^0(X,\mathcal {O}_X) \rightarrow \mathrm {H}^0(X,\Omega _X^1)\right )$
and
$\left ( \mathrm {H}^0(X,\mathcal {O}_X) \rightarrow \mathrm {H}^0(X,\Omega _X^1)\right )$
and
![]() $\left ( \mathrm {H}^1(X,\mathcal {O}_X) \rightarrow \mathrm {H}^1(X,\Omega _X^1) \right )(1)$
, where each map is induced from the differential
$\left ( \mathrm {H}^1(X,\mathcal {O}_X) \rightarrow \mathrm {H}^1(X,\Omega _X^1) \right )(1)$
, where each map is induced from the differential
![]() $\mathcal {O}_X\rightarrow \Omega _X^1$
, and is zero by the degeneration of the Hodge-de Rham spectral sequence. In particular
$\mathcal {O}_X\rightarrow \Omega _X^1$
, and is zero by the degeneration of the Hodge-de Rham spectral sequence. In particular
![]() $(L\eta _\xi C)\otimes _{\mathrm {B_{dR}^+}}^L K$
has nonzero direct summands of Hodge–Tate weight
$(L\eta _\xi C)\otimes _{\mathrm {B_{dR}^+}}^L K$
has nonzero direct summands of Hodge–Tate weight
![]() $(-1)$
. On the other hand, the reduction
$(-1)$
. On the other hand, the reduction
![]() $R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})\otimes _{\mathrm {B_{dR}^+}} K\cong R\Gamma _{\mathrm {dR}}(X/K)$
only has weight
$R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})\otimes _{\mathrm {B_{dR}^+}} K\cong R\Gamma _{\mathrm {dR}}(X/K)$
only has weight
![]() $0$
cohomology. Thus it is impossible to have a natural isomorphism between
$0$
cohomology. Thus it is impossible to have a natural isomorphism between
![]() $R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})$
and
$R\Gamma _{\inf }(X/{\mathrm {B_{dR}^+}})$
and ![]() in general.
in general.
Remark 6.0.3. The above example indicates that certain components of infinitesimal cohomology and decalaged-prismatic cohomology still coincide. In fact, for smooth rigid spaces in general, one may form a map between them, but in the other direction. To see this, let X be a smooth rigid space and let
![]() $\{U_j\rightarrow X\}$
be an affinoid open covering. Then we have
$\{U_j\rightarrow X\}$
be an affinoid open covering. Then we have

where we use the natural isomorphism in Theorem 6.0.1 for smooth affinoid
![]() $U_j$
in the second isomorphism above. When X is smooth and proper, the above identifies the first row of Hodge–Tate spectral sequence with the weight
$U_j$
in the second isomorphism above. When X is smooth and proper, the above identifies the first row of Hodge–Tate spectral sequence with the weight
![]() $0$
part of the decalaged-prismatic cohomology after mod
$0$
part of the decalaged-prismatic cohomology after mod
![]() $\xi $
.
$\xi $
.
We also give an example illustrating the discrepancy for l.c.i. rigid spaces that are not smooth.
Example 6.0.4. Let
![]() $X=\mathrm {Spa}(R)$
be an affinoid rigid space that has l.c.i. singularities and is defined over a discretely valued subfield k. Assume its embedded dimension into polydiscs
$X=\mathrm {Spa}(R)$
be an affinoid rigid space that has l.c.i. singularities and is defined over a discretely valued subfield k. Assume its embedded dimension into polydiscs
![]() $K\langle T_i\rangle $
is N ([Reference Guo and LiGL20, Appendix 5.6]). By [Reference Bhatt, Morrow and ScholzeBMS, Proposition 6.12] again, we can write
$K\langle T_i\rangle $
is N ([Reference Guo and LiGL20, Appendix 5.6]). By [Reference Bhatt, Morrow and ScholzeBMS, Proposition 6.12] again, we can write
![]() $(L\eta _\xi C)\otimes _{\mathrm {B_{dR}^+}}^L K$
for
$(L\eta _\xi C)\otimes _{\mathrm {B_{dR}^+}}^L K$
for ![]() into the following direct sum of complexes
into the following direct sum of complexes

Note that the weight zero part is the cohomology of the usual continuous de Rham complex
![]() $\Omega _{R/K}^{\bullet }$
. On the other hand, the mod
$\Omega _{R/K}^{\bullet }$
. On the other hand, the mod
![]() $\xi $
reduction
$\xi $
reduction
![]() $R\Gamma _{\inf }(R/K)=R\Gamma _{\inf }(R/{\mathrm {B_{dR}^+}})\otimes _{\mathrm {B_{dR}^+}}^L K$
is computed as the cohomology of the analytic derived de Rham complex
$R\Gamma _{\inf }(R/K)=R\Gamma _{\inf }(R/{\mathrm {B_{dR}^+}})\otimes _{\mathrm {B_{dR}^+}}^L K$
is computed as the cohomology of the analytic derived de Rham complex
![]() ${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{R/K}$
. It is known that in this case the latter cohomology is a direct summand of the former one ([Reference GuoGuo24, Remark 6.2.3], see also [Reference BhattBha12, Section 5] for algebraic case), and different in general (see [Reference Arapura and KangAK11, Example 4.4] for an example of affine variety that has different cohomology). So by choosing an affinoid open subset around the singularity for the example in loc. cit., we see those two cohomologies are different in general.
${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{R/K}$
. It is known that in this case the latter cohomology is a direct summand of the former one ([Reference GuoGuo24, Remark 6.2.3], see also [Reference BhattBha12, Section 5] for algebraic case), and different in general (see [Reference Arapura and KangAK11, Example 4.4] for an example of affine variety that has different cohomology). So by choosing an affinoid open subset around the singularity for the example in loc. cit., we see those two cohomologies are different in general.
Remark 6.0.5. To globalize Theorem 6.0.1, one can consider a (pre)sheaf of complexes ![]() over a general rigid space X, sending each affinoid open subset
over a general rigid space X, sending each affinoid open subset
![]() $\mathrm {Spa}(R)$
to its prismatic cohomology complex
$\mathrm {Spa}(R)$
to its prismatic cohomology complex ![]() . In this case, similar to [Reference Bhatt, Morrow and ScholzeBMS], one can show that for a smooth rigid space X we have a natural isomorphism
. In this case, similar to [Reference Bhatt, Morrow and ScholzeBMS], one can show that for a smooth rigid space X we have a natural isomorphism
where
![]() $Ru_{X/{\mathrm {B_{dR}^+}} *} \mathcal {O}_{X/{\mathrm {B_{dR}^+}}}$
is the infinitesimal cohomology sheaf as in [Reference GuoGuo24, Section 7].
$Ru_{X/{\mathrm {B_{dR}^+}} *} \mathcal {O}_{X/{\mathrm {B_{dR}^+}}}$
is the infinitesimal cohomology sheaf as in [Reference GuoGuo24, Section 7].
7 Pro-étale comparison
In this section, we prove the comparison theorem between prismatic cohomology over
![]() ${\mathrm {B_{dR}^+}}$
and pro-étale cohomology of
${\mathrm {B_{dR}^+}}$
and pro-étale cohomology of
![]() ${\mathbb {B}^+_{\mathrm {dR}}}$
, studied in [Reference ScholzeSch13] and [Reference Bhatt, Morrow and ScholzeBMS, Section 13].
${\mathbb {B}^+_{\mathrm {dR}}}$
, studied in [Reference ScholzeSch13] and [Reference Bhatt, Morrow and ScholzeBMS, Section 13].
7.1 Künneth formula and étale localization
As a preparation for the pro-étale comparison, we first prove the Künneth formula and the étale localization for reduced prismatic cohomology.
We start by observing that the analytic cotangent complex admits a natural product formula.
Lemma 7.1.1. Let
![]() $R_1$
and
$R_1$
and
![]() $R_2$
be two topologically finite type K-algebras, and let
$R_2$
be two topologically finite type K-algebras, and let
![]() $p_i$
be the two natural maps from
$p_i$
be the two natural maps from
![]() $R_i$
to
$R_i$
to
![]() $R_1\widehat {\otimes }_K R_2$
. Then the following natural map is an isomorphism after an integral derived p-completion.
$R_1\widehat {\otimes }_K R_2$
. Then the following natural map is an isomorphism after an integral derived p-completion.
Proof. Let
![]() $R_{1,0}$
and
$R_{1,0}$
and
![]() $R_{2,0}$
be two topologically finite type
$R_{2,0}$
be two topologically finite type
![]() $\mathcal {O}_K$
-algebras whose generic fibres are
$\mathcal {O}_K$
-algebras whose generic fibres are
![]() $R_1$
and
$R_1$
and
![]() $R_2$
separately. By [Reference Gabber and RameroGR, Remark 7.2.45], the analytic cotangent complex
$R_2$
separately. By [Reference Gabber and RameroGR, Remark 7.2.45], the analytic cotangent complex
![]() $\mathbb {L}^{\mathrm {an}}_{R/K}$
is obtained by inverting p at the derived p-completion of the algebraic cotangent complex
$\mathbb {L}^{\mathrm {an}}_{R/K}$
is obtained by inverting p at the derived p-completion of the algebraic cotangent complex
![]() $\mathbb {L}_{R_0/\mathcal {O}_K}$
, where R is any of
$\mathbb {L}_{R_0/\mathcal {O}_K}$
, where R is any of
![]() $R_1, R_2$
or
$R_1, R_2$
or
![]() $R_1\widehat {\otimes }_K R_2$
(respectively for
$R_1\widehat {\otimes }_K R_2$
(respectively for
![]() $R_0$
). Denote by
$R_0$
). Denote by
![]() $\mathbb {L}^{\mathrm {an}}_{R_0/\mathcal {O}_K}$
the derived p-completion of the algebraic cotangent complex
$\mathbb {L}^{\mathrm {an}}_{R_0/\mathcal {O}_K}$
the derived p-completion of the algebraic cotangent complex
![]() $\mathbb {L}_{R_0/\mathcal {O}_K}$
. Then we notice that by [Reference Gabber and RameroGR, Proposition 7.1.31], each of
$\mathbb {L}_{R_0/\mathcal {O}_K}$
. Then we notice that by [Reference Gabber and RameroGR, Proposition 7.1.31], each of
![]() $\mathbb {L}^{\mathrm {an}}_{R_0/\mathcal {O}_K}$
for
$\mathbb {L}^{\mathrm {an}}_{R_0/\mathcal {O}_K}$
for
![]() $R_0=R_{1,0}, R_{2,0}$
or
$R_0=R_{1,0}, R_{2,0}$
or
![]() $R_{1,0}\widehat {\otimes } R_{2,0}$
is pseudo-coherent. On the other hand, recall the natural isomorphism for the algebraic cotangent complex ([Sta, Tag 09DL]) as below
$R_{1,0}\widehat {\otimes } R_{2,0}$
is pseudo-coherent. On the other hand, recall the natural isomorphism for the algebraic cotangent complex ([Sta, Tag 09DL]) as below
In this way, by applying the derived p-completion and using [Reference Gabber and RameroGR, Lemma 7.1.25], we get a natural isomorphism
Thus the result follows after inverting p.
In the following, to simplify the notation we denote ![]() to be reduced prismatic cohomology
to be reduced prismatic cohomology ![]() .
.
Theorem 7.1.2. Let
![]() $R_1$
and
$R_1$
and
![]() $R_2$
be two topologically finite type algebras over K that have l.c.i. singularities, and let
$R_2$
be two topologically finite type algebras over K that have l.c.i. singularities, and let
![]() $p_i$
be the two natural maps
$p_i$
be the two natural maps
![]() $R_i \rightarrow R_1\widehat {\otimes }_K R_2$
. There is a natural isomorphism of
$R_i \rightarrow R_1\widehat {\otimes }_K R_2$
. There is a natural isomorphism of
![]() $\mathbb {E}_\infty $
-rings over
$\mathbb {E}_\infty $
-rings over
![]() $R_1\widehat {\otimes }_K R_2$
:
$R_1\widehat {\otimes }_K R_2$
:
Proof. Let R be a topologically finite type algebra over K that has l.c.i. singularities. Recall the Hodge–Tate filtration from Corollary 5.3.6 that there is an ascending exhaustive
![]() $\mathbb {N}^{\mathrm {op}}$
-filtration
$\mathbb {N}^{\mathrm {op}}$
-filtration
![]() ${\mathrm {Fil}}^{\mathrm {HT}}_{\bullet }$
on
${\mathrm {Fil}}^{\mathrm {HT}}_{\bullet }$
on ![]() , such that the i-th graded piece is equal to
, such that the i-th graded piece is equal to
Moreover, it is compatible with the
![]() $\mathbb {E}_\infty $
-ring structure on
$\mathbb {E}_\infty $
-ring structure on ![]() , and is induced from the infinitesimal filtration on the derived de Rham cohomology
, and is induced from the infinitesimal filtration on the derived de Rham cohomology
![]() ${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{R/K}$
. In particular, this implies that the graded algebra
${\widehat {\mathrm {dR}}^{\mathrm {an}}}_{R/K}$
. In particular, this implies that the graded algebra ![]() obtained by taking the graded pieces of the Hodge–Tate filtration on
obtained by taking the graded pieces of the Hodge–Tate filtration on ![]() is generated by the first graded pieces
is generated by the first graded pieces
![]() $\mathbb {L}^{\mathrm {an}}_{R/K}(-1)[-1]$
. Namely, we have
$\mathbb {L}^{\mathrm {an}}_{R/K}(-1)[-1]$
. Namely, we have
Back to the Künneth formula. By the functoriality and lax-monoidal structure, the maps
![]() $p_i:R_i \rightarrow R_1\widehat {\otimes } R_2$
induces a natural map of
$p_i:R_i \rightarrow R_1\widehat {\otimes } R_2$
induces a natural map of
![]() $\mathbb {E}_\infty $
-algebras
$\mathbb {E}_\infty $
-algebras
By the
![]() $R_1\widehat {\otimes }R_2$
-linearity of the target, we can improve the above to an
$R_1\widehat {\otimes }R_2$
-linearity of the target, we can improve the above to an
![]() $R_1\widehat {\otimes }R_2$
-linear homomorphism
$R_1\widehat {\otimes }R_2$
-linear homomorphism
Notice that the Hodge–Tate filtration on both sides are compatible under the map. Moreover, by applying the Day convolution ([Reference Gwilliam and PavlovGP18]) on the Hodge–Tate filtration of ![]() , we can define a product filtration on the left side. As the colimit commutes with the tensor product, the product filtration is again ascending and exhaustive. The product filtration is further compatible with the Hodge–Tate filtration on
, we can define a product filtration on the left side. As the colimit commutes with the tensor product, the product filtration is again ascending and exhaustive. The product filtration is further compatible with the Hodge–Tate filtration on ![]() under the map above. Thus to show the Künneth formula, it amounts to check the isomorphism after applying the graded pieces.
under the map above. Thus to show the Künneth formula, it amounts to check the isomorphism after applying the graded pieces.
Now by the observation on the Hodge-Tate graded algebra, the induced map of graded algebras looks like

Moreover, taking the pullback functors inside of the symmetric functor, the left hand side above can be rewritten as
Thus by the compatibility of the Hodge–Tate filtration and the infinitesimal filtration, the isomorphism follows from Lemma 7.1.1. So we are done.
Remark 7.1.3. The above uses crucially the pseudo-coherence of the analytic cotangent complex to free us from a p-adic completion ‘rational’. Using the condensed mathematics, one might ask if the above can be improved to a Künneth formula of non-reduced prismatic cohomology, namely an isomorphism of solid
![]() $\mathbb {E}_\infty $
-algebras over
$\mathbb {E}_\infty $
-algebras over
![]() ${\mathrm {B_{dR}^+}}$
as below
${\mathrm {B_{dR}^+}}$
as below
Notice that the above is taking the tensor product over
![]() ${\mathrm {B_{dR}^+}}$
directly in the solid category, while a tensor product in the usual derived category would lose the topological completion.
${\mathrm {B_{dR}^+}}$
directly in the solid category, while a tensor product in the usual derived category would lose the topological completion.
Reduced prismatic cohomology also enjoys the étale localization formula.
Proposition 7.1.4. Let
![]() $R_1 \rightarrow R_2$
be an étale morphism of topologically finite type K-algebras that have l.c.i. singularities. Then the natural map of
$R_1 \rightarrow R_2$
be an étale morphism of topologically finite type K-algebras that have l.c.i. singularities. Then the natural map of
![]() $\mathbb {E}_\infty $
-algebras below is an isomorphism
$\mathbb {E}_\infty $
-algebras below is an isomorphism
Proof. We first notice that the analytic cotangent complex satisfies the following natural isomorphism by [Reference Gabber and RameroGR, Proposition 7.2.39, Theorem 7.2.42]
By taking derived wedge powers of the isomorphism and the commutativity of
![]() $L\wedge ^i$
and derived tensor product
$L\wedge ^i$
and derived tensor product
![]() $R_2\otimes _{R_1}^L (-)$
, the above tensor product formula extends to all of
$R_2\otimes _{R_1}^L (-)$
, the above tensor product formula extends to all of
![]() $L\wedge ^i\mathbb {L}^{\mathrm {an}}_{R/K}$
. On the other hand, notice that the map in the statement is equivariant under the Hodge–Tate filtration on
$L\wedge ^i\mathbb {L}^{\mathrm {an}}_{R/K}$
. On the other hand, notice that the map in the statement is equivariant under the Hodge–Tate filtration on ![]() and
and ![]() . Moreover, by construction of the Hodge–Tate filtration as in Corollary 5.3.6, the induced map of graded pieces is isomorphic to the map of wedge powers of analytic cotangent complexes, up to Tate twists and cohomological shifts. In particular, the induced map of graded algebras for the Hodge–Tate filtration is an isomorphism, namely
. Moreover, by construction of the Hodge–Tate filtration as in Corollary 5.3.6, the induced map of graded pieces is isomorphic to the map of wedge powers of analytic cotangent complexes, up to Tate twists and cohomological shifts. In particular, the induced map of graded algebras for the Hodge–Tate filtration is an isomorphism, namely
In this way, by the exhaustiveness of the Hodge–Tate filtration, the isomorphism of graded pieces above implies the isomorphism of ![]() as in the statement.
as in the statement.
7.2 Pro-étale comparison
Now we can prove the proétale comparison.
Theorem 7.2.1. Let X be a smooth rigid space over K. There is a natural isomorphism of
![]() ${\mathrm {B_{dR}^+}}$
-
${\mathrm {B_{dR}^+}}$
-
![]() $\mathbb {E}_\infty $
-algebras as below
$\mathbb {E}_\infty $
-algebras as below
Our strategy is to first build a canonical morphism, and reduce the question to showing that it is an isomorphism. To achieve the latter, we may assume X is one dimensional using the Künneth formula, where we show that both the source and the target can be compared naturally with the cotangent complex (c.f. Proposition 7.2.5).
We start by constructing a natural map. Recall from [Reference ScholzeSch13] that given a rigid space X over K, its pro-étale site
![]() $X_{\mathrm {pro\acute {e}t}}$
has a basis consisting of affinoid perfectoid objects U, associated with a complete adic space
$X_{\mathrm {pro\acute {e}t}}$
has a basis consisting of affinoid perfectoid objects U, associated with a complete adic space
![]() $\hat U=\mathrm {Spa}(A,A+)$
, where
$\hat U=\mathrm {Spa}(A,A+)$
, where
![]() $(A,A+)$
is a perfectoid affinoid algebra over K. There is a de Rham sheaf
$(A,A+)$
is a perfectoid affinoid algebra over K. There is a de Rham sheaf
![]() ${\mathbb {B}^+_{\mathrm {dR}}}$
over
${\mathbb {B}^+_{\mathrm {dR}}}$
over
![]() $X_{\mathrm {pro\acute {e}t}}$
, sending an affinoid perfectoid object U to the following
$X_{\mathrm {pro\acute {e}t}}$
, sending an affinoid perfectoid object U to the following
where
![]() $(-)^\wedge $
is the
$(-)^\wedge $
is the
![]() $\xi $
-adic completion. Here
$\xi $
-adic completion. Here
![]() ${\mathbb {B}^+_{\mathrm {dR}}}(U)$
is a complete topological
${\mathbb {B}^+_{\mathrm {dR}}}(U)$
is a complete topological
![]() ${\mathrm {B_{dR}^+}}$
-algebra with
${\mathrm {B_{dR}^+}}$
-algebra with
![]() ${\mathbb {B}^+_{\mathrm {dR}}}(U)/\xi =A$
. To simplify the notation, we use
${\mathbb {B}^+_{\mathrm {dR}}}(U)/\xi =A$
. To simplify the notation, we use
![]() ${\mathbb {B}^+_{\mathrm {dR}}}(A)$
to denote
${\mathbb {B}^+_{\mathrm {dR}}}(A)$
to denote
![]() ${\mathbb {B}^+_{\mathrm {dR}}}(U)$
, where U is an affinoid perfectoid object in
${\mathbb {B}^+_{\mathrm {dR}}}(U)$
, where U is an affinoid perfectoid object in
![]() $X_{\mathrm {pro\acute {e}t}}$
associated with the perfectoid space
$X_{\mathrm {pro\acute {e}t}}$
associated with the perfectoid space
![]() $\hat U=\mathrm {Spa}(A,A^+)$
.
$\hat U=\mathrm {Spa}(A,A^+)$
.
We then define an enlarged category ![]() of prisms over
of prisms over
![]() $X=\mathrm {Spa}(R)$
, whose object is the union of
$X=\mathrm {Spa}(R)$
, whose object is the union of ![]() and the collection of triples
and the collection of triples
where
![]() $A=(A,A^+)$
is an affinoid perfectoid object in
$A=(A,A^+)$
is an affinoid perfectoid object in
![]() $X_{\mathrm {\acute {e}t}}$
. A morphism is a commutative diagram of triples that are continuous under the
$X_{\mathrm {\acute {e}t}}$
. A morphism is a commutative diagram of triples that are continuous under the
![]() $(p,\xi )$
-adic topology, and we equip the category with the indiscrete topology. Similar to the discussions in the previous sections, we can define the structure sheaves and their cohomology. The following lemma tells us that this enlargement would not change the cohomology.
$(p,\xi )$
-adic topology, and we equip the category with the indiscrete topology. Similar to the discussions in the previous sections, we can define the structure sheaves and their cohomology. The following lemma tells us that this enlargement would not change the cohomology.
Lemma 7.2.2. Let R be a topologically finite type K-algebra, and let
![]() $P={\mathrm {B_{dR}^+}} \langle T_i\rangle $
admit surjections
$P={\mathrm {B_{dR}^+}} \langle T_i\rangle $
admit surjections
![]() $P\rightarrow P/I\rightarrow R$
. Then the prism associated to the envelope
$P\rightarrow P/I\rightarrow R$
. Then the prism associated to the envelope ![]() covers the final object of
covers the final object of ![]() .
.
Proof. By Proposition 2.2.11, the prism associated to the envelope ![]() is weakly initial when restricted to the subcategory
is weakly initial when restricted to the subcategory ![]() . So it suffices to show that any prism
. So it suffices to show that any prism
![]() $({\mathbb {B}^+_{\mathrm {dR}}}(A) \rightarrow A \leftarrow R)$
for a perfectoid algebra
$({\mathbb {B}^+_{\mathrm {dR}}}(A) \rightarrow A \leftarrow R)$
for a perfectoid algebra
![]() $(A,A^+)$
over R admits a map from
$(A,A^+)$
over R admits a map from ![]() . Let
. Let
![]() $R_0$
be a ring of definition of R that is topologically finite type over
$R_0$
be a ring of definition of R that is topologically finite type over
![]() $\mathcal {O}_K$
, such that the image of
$\mathcal {O}_K$
, such that the image of
![]() $R_0$
in A is inside of
$R_0$
in A is inside of
![]() $A^+$
. By lifting generators of I into
$A^+$
. By lifting generators of I into
![]() ${\mathrm {A_{inf}}} \langle T_i\rangle $
, we choose surjection
${\mathrm {A_{inf}}} \langle T_i\rangle $
, we choose surjection
![]() ${\mathrm {A_{inf}}} \langle T_i\rangle \rightarrow R_0$
compatible with
${\mathrm {A_{inf}}} \langle T_i\rangle \rightarrow R_0$
compatible with
![]() $P \rightarrow R$
. Then by lifting the image of
$P \rightarrow R$
. Then by lifting the image of
![]() $T_i$
to
$T_i$
to
![]() $W(A^{+\flat })$
, we can form the following commutative diagram
$W(A^{+\flat })$
, we can form the following commutative diagram

Next we invert p and take the
![]() $\xi $
-adic completion, we get the following commutative diagram
$\xi $
-adic completion, we get the following commutative diagram

Note that from the diagram, the image of
![]() $I\subset P$
is inside of
$I\subset P$
is inside of
![]() $\xi \cdot {\mathbb {B}^+_{\mathrm {dR}}}(A)$
. At last, as
$\xi \cdot {\mathbb {B}^+_{\mathrm {dR}}}(A)$
. At last, as
![]() $\xi $
is a nonzero divisor in
$\xi $
is a nonzero divisor in
![]() ${\mathbb {B}^+_{\mathrm {dR}}}(A)$
([Reference ScholzeSch13, Theorem 6.5]), we thus get a map of prisms by the
${\mathbb {B}^+_{\mathrm {dR}}}(A)$
([Reference ScholzeSch13, Theorem 6.5]), we thus get a map of prisms by the
![]() $\xi $
-torsion freeness of
$\xi $
-torsion freeness of
![]() ${\mathbb {B}^+_{\mathrm {dR}}}(A)$
${\mathbb {B}^+_{\mathrm {dR}}}(A)$

The inclusion functor naturally defines a map of indiscrete ringed sites
The above lemma then leads to the following simple comparison.
Corollary 7.2.3. The natural map of cohomology of the structure sheaf of ![]() and
and ![]() is an isomorphism. The same holds for the reduced structure sheaf
is an isomorphism. The same holds for the reduced structure sheaf ![]() .
.
Proof. Using the same proof of Proposition 3.0.13, the Čech nerve for the map from ![]() to the final object of
to the final object of ![]() is the same as the one for
is the same as the one for ![]() . So by taking the Čech-Alexander complex as in Corollary 3.0.14, we get the result.
. So by taking the Čech-Alexander complex as in Corollary 3.0.14, we get the result.
Remark 7.2.4. The above in particular shows that for any map of sheaves
![]() $\iota ^{-1} \mathcal {F}_1 \rightarrow \mathcal {F}_2$
over
$\iota ^{-1} \mathcal {F}_1 \rightarrow \mathcal {F}_2$
over ![]() that induces an isomorphism when restricted to
that induces an isomorphism when restricted to ![]() , we have a natural isomorphism
, we have a natural isomorphism
Now we can build the natural map of cohomology. By construction, each affinoid perfectoid object
![]() $U\in X_{\mathrm {pro\acute {e}t}}$
for
$U\in X_{\mathrm {pro\acute {e}t}}$
for
![]() $\hat U=\mathrm {Spa}(A,A^+)$
over some affinoid open subset
$\hat U=\mathrm {Spa}(A,A^+)$
over some affinoid open subset
![]() $\mathrm {Spa}(R)\subset X$
naturally determines a unique prism
$\mathrm {Spa}(R)\subset X$
naturally determines a unique prism
![]() $({\mathbb {B}^+_{\mathrm {dR}}}(A) \rightarrow A \leftarrow R)$
. In particular, as the collection of such affinoid perfectoid objects forms a basis of
$({\mathbb {B}^+_{\mathrm {dR}}}(A) \rightarrow A \leftarrow R)$
. In particular, as the collection of such affinoid perfectoid objects forms a basis of
![]() $X_{\mathrm {pro\acute {e}t}}$
, by taking the derived limit over all such U and R, we get
$X_{\mathrm {pro\acute {e}t}}$
, by taking the derived limit over all such U and R, we get
Thus by composing with the isomorphism as in Corollary 7.2.3, we get
Proof of Theorem 7.2.1.
By taking derived limits on an affinoid open covering, it suffices to assume
![]() $X=\mathrm {Spa}(R)$
is affinoid. Moreover, as both sides are derived complete
$X=\mathrm {Spa}(R)$
is affinoid. Moreover, as both sides are derived complete
![]() $\xi $
-adically, by the derived Nakayama [Sta, Tag 0G1U], it suffices to show the isomorphism after mod
$\xi $
-adically, by the derived Nakayama [Sta, Tag 0G1U], it suffices to show the isomorphism after mod
![]() $\xi $
. Namely the following map of
$\xi $
. Namely the following map of
![]() $\mathbb {E}_\infty $
-algebras over K
$\mathbb {E}_\infty $
-algebras over K
where
![]() $\widehat {\mathcal {O}}_X$
is the complete structure sheaf over the pro-étale site, as in [Reference ScholzeSch13]. Here we notice that the map is also R-linear.
$\widehat {\mathcal {O}}_X$
is the complete structure sheaf over the pro-étale site, as in [Reference ScholzeSch13]. Here we notice that the map is also R-linear.
To proceed, we notice that a truncation of the R-complexes above can be computed using the analytic cotangent complex.
Proposition 7.2.5. Let R be a smooth affinoid algebra over K. There is a natural commutative diagram as below, compatible with the map in Theorem 7.2.1, such that every arrow becomes an isomorphism after a cohomological truncation at degree
![]() $\leq 0$
:
$\leq 0$
:

We grant this claim at the moment. By the Hodge–Tate comparison as in Theorem 5.1.1, the above shows that the pro-étale comparison map in Theorem 7.2.1 is an isomorphism when X is a smooth curve. On the other hand, as the étale localization holds on both sides of
![]() $(\ast )$
and everything is R-linear (Proposition 7.1.4 for reduced prismatic cohomology and [Reference ScholzeSch13] for pro-étale cohomology of
$(\ast )$
and everything is R-linear (Proposition 7.1.4 for reduced prismatic cohomology and [Reference ScholzeSch13] for pro-étale cohomology of
![]() $\widehat {\mathcal {O}}_X$
), we may assume X is equal to the n-dimensional closed disc
$\widehat {\mathcal {O}}_X$
), we may assume X is equal to the n-dimensional closed disc
![]() $\mathbb {D}^n$
. At last, notice that both sides of
$\mathbb {D}^n$
. At last, notice that both sides of
![]() $(\ast )$
satisfy the Künneth formula (Theorem 7.1.2 for reduced prismatic cohomology and [Reference Bhatt, Morrow and ScholzeBMS, Proposition 8.14] for the integral version of pro-étale cohomology). Thus we can reduce the isomorphism to the case when
$(\ast )$
satisfy the Künneth formula (Theorem 7.1.2 for reduced prismatic cohomology and [Reference Bhatt, Morrow and ScholzeBMS, Proposition 8.14] for the integral version of pro-étale cohomology). Thus we can reduce the isomorphism to the case when
![]() $n=1$
and X is a curve, which finishes the proof.
$n=1$
and X is a curve, which finishes the proof.
Proof of Proposition 7.2.5.
As we shall see below, after constructing the natural maps we want, the essential work is to show that the canonical map between the cotangent complex and the reduced prismatic cohomology induces an isomorphism. The idea is then to translate both into a natural map between two cosimplicial objects associated to the same cosimplicial topological polynomial ring, and reduce the task to explicit calculations.
We first notice that for any prism
![]() $(B \rightarrow B/\xi \leftarrow R)$
, there is a natural map of analytic cotangent complex
$(B \rightarrow B/\xi \leftarrow R)$
, there is a natural map of analytic cotangent complex
where the isomorphism on the right hand side is because
![]() $\xi $
is a nonzerodivisor in B. This in particular includes the case when
$\xi $
is a nonzerodivisor in B. This in particular includes the case when
![]() $B={\mathbb {B}^+_{\mathrm {dR}}}(A)$
for a perfectoid R-algebra
$B={\mathbb {B}^+_{\mathrm {dR}}}(A)$
for a perfectoid R-algebra
![]() $(A,A^+)$
. So by applying the derived limit over all prisms in
$(A,A^+)$
. So by applying the derived limit over all prisms in ![]() , in
, in ![]() , and over all prisms coming from affinoid perfectoid objects in
, and over all prisms coming from affinoid perfectoid objects in
![]() $X_{\mathrm {pro\acute {e}t}}$
separately, we get three maps from the cotangent complex in the following diagram
$X_{\mathrm {pro\acute {e}t}}$
separately, we get three maps from the cotangent complex in the following diagram

where the left horizontal arrow is an isomorphism by Corollary 7.2.3.
To show the isomorphism after the truncation, we first notice that by applying the distinguished triangle at the triple
![]() ${\mathrm {B_{dR}^+}} \rightarrow K \rightarrow R$
and the smoothness of R over K, we see
${\mathrm {B_{dR}^+}} \rightarrow K \rightarrow R$
and the smoothness of R over K, we see
![]() $\mathbb {L}^{\mathrm {an}}_{R/{\mathrm {B_{dR}^+}}}$
lives in degree
$\mathbb {L}^{\mathrm {an}}_{R/{\mathrm {B_{dR}^+}}}$
lives in degree
![]() $[-1,0]$
and fits in the triangle
$[-1,0]$
and fits in the triangle
Moreover, it is shown in [Reference GuoGuo23, Theorem 7.2.3] that the map below towards pro-étale cohomology is an isomorphism
So it is left to show the isomorphism of
![]() $\mathbb {L}^{\mathrm {an}}_{R/{\mathrm {B_{dR}^+}}}$
with the truncated prismatic cohomology.
$\mathbb {L}^{\mathrm {an}}_{R/{\mathrm {B_{dR}^+}}}$
with the truncated prismatic cohomology.
Using the étale localization of both sides, we may assume
![]() $R=K\langle T_i\rangle $
. As in the proof of [Reference GuoGuo24, Theorem 5.5.1], by the distinguished triangle of the analytic cotangent complex for
$R=K\langle T_i\rangle $
. As in the proof of [Reference GuoGuo24, Theorem 5.5.1], by the distinguished triangle of the analytic cotangent complex for
![]() ${\mathrm {B_{dR}^+}} \rightarrow P^{\widehat \otimes _{\mathrm {B_{dR}^+}} \bullet +1} \rightarrow R$
, there is a cosimplicial diagram computing
${\mathrm {B_{dR}^+}} \rightarrow P^{\widehat \otimes _{\mathrm {B_{dR}^+}} \bullet +1} \rightarrow R$
, there is a cosimplicial diagram computing
![]() $\mathbb {L}^{\mathrm {an}}_{R/{\mathrm {B_{dR}^+}}}$
as follows
$\mathbb {L}^{\mathrm {an}}_{R/{\mathrm {B_{dR}^+}}}$
as follows
where
![]() $P^{\widehat \otimes n+1}=P\langle \Delta (n) \rangle $
is the inverse limit (with respect to e) of the
$P^{\widehat \otimes n+1}=P\langle \Delta (n) \rangle $
is the inverse limit (with respect to e) of the
![]() $(n+1)$
-th complete self product of
$(n+1)$
-th complete self product of
![]() ${\mathrm {B^+_{dR,e}}} \langle T_i\rangle $
. As each surjection
${\mathrm {B^+_{dR,e}}} \langle T_i\rangle $
. As each surjection
![]() $P\langle \Delta (n) \rangle \rightarrow R$
is regular, the above cosimplicial diagram is isomorphic to
$P\langle \Delta (n) \rangle \rightarrow R$
is regular, the above cosimplicial diagram is isomorphic to
On the other hand, by Proposition 3.0.13 the above induces the Čech nerve for the weakly final prism
![]() $(P \rightarrow P/\xi \leftarrow R)$
, and we can form the Čech-Alexander complex for reduced prismatic cohomology in Corollary 3.0.14 as the following
$(P \rightarrow P/\xi \leftarrow R)$
, and we can form the Čech-Alexander complex for reduced prismatic cohomology in Corollary 3.0.14 as the following
 $$\begin{align*}\varprojlim_{[n]\in \Delta^{\mathrm{op}}} P[\frac{\Delta(n)}{\xi}]^\wedge_{\mathrm{tf}}/\xi=\varprojlim_{[n]\in \Delta^{\mathrm{op}}} R[\frac{\Delta(n)}{\xi}]. \end{align*}$$
$$\begin{align*}\varprojlim_{[n]\in \Delta^{\mathrm{op}}} P[\frac{\Delta(n)}{\xi}]^\wedge_{\mathrm{tf}}/\xi=\varprojlim_{[n]\in \Delta^{\mathrm{op}}} R[\frac{\Delta(n)}{\xi}]. \end{align*}$$
So the map ![]() is equivalent to the following map of homotopy limits
is equivalent to the following map of homotopy limits
 $$\begin{align*}\left( \varprojlim_{[n]\in \Delta^{\mathrm{op}}} (\xi, \Delta(n))/(\xi,\Delta(n))^2 [1] \right) \longrightarrow \left( \varprojlim_{[n]\in \Delta^{\mathrm{op}}} R[\frac{\Delta(n)}{\xi}](1)[1]\right). \end{align*}$$
$$\begin{align*}\left( \varprojlim_{[n]\in \Delta^{\mathrm{op}}} (\xi, \Delta(n))/(\xi,\Delta(n))^2 [1] \right) \longrightarrow \left( \varprojlim_{[n]\in \Delta^{\mathrm{op}}} R[\frac{\Delta(n)}{\xi}](1)[1]\right). \end{align*}$$
Namely we reduce the question to show that the following map of cosimplicial diagrams induces an isomorphism of
![]() $\mathrm {H}^{\leq 1}$
$\mathrm {H}^{\leq 1}$

Finally, to finish the calculation, it suffices to notice that the maps above are all compatible with the original construction of the cosimplicial diagram
![]() $P^{\widehat {\otimes }_{\mathrm {B_{dR}^+}} \bullet +1}$
. So by simply tracking the generators
$P^{\widehat {\otimes }_{\mathrm {B_{dR}^+}} \bullet +1}$
. So by simply tracking the generators
![]() $T_i\in R=K \langle T_i\rangle $
and
$T_i\in R=K \langle T_i\rangle $
and
![]() $\delta _i=1\otimes T_i -T_i \otimes 1 \in \Delta (1)$
for the first two degrees, we get the isomorphism of
$\delta _i=1\otimes T_i -T_i \otimes 1 \in \Delta (1)$
for the first two degrees, we get the isomorphism of
![]() $\mathrm {H}^{\leq 1}$
.
$\mathrm {H}^{\leq 1}$
.
Corollary 7.2.6. Let X be a smooth rigid space over K. Then there is a natural isomorphism for complexes of
![]() $\mathbb {E}_\infty $
-
$\mathbb {E}_\infty $
-
![]() $\mathrm {B_{dR}}$
-algebras
$\mathrm {B_{dR}}$
-algebras
Proof. This follows from [Reference Bhatt, Morrow and ScholzeBMS, Theorem 13.1].
8 Galois invariant
In this section, we show that Galois invariant of prismatic cohomology is isomorphic to infinitesimal cohomology, when the rigid space is defined over a discretely valued subfield. We will use the condensed mathematics developed by Clausen–Scholze. Our references are the lecture notes [Reference ScholzeSch19] by Scholze and the recent preprint [Reference BoscoBos21] by Bosco.
Throughout the section, we fix a discretely valued subfield k of K that has perfect residue field. We denote by
![]() $G_k$
the Galois group for the extension
$G_k$
the Galois group for the extension
![]() $K/k$
. We also fix an embedding
$K/k$
. We also fix an embedding
![]() $k\rightarrow {\mathrm {B_{dR}^+}}$
compatible with the surjection
$k\rightarrow {\mathrm {B_{dR}^+}}$
compatible with the surjection
![]() ${\mathrm {B_{dR}^+}}\rightarrow K$
.
${\mathrm {B_{dR}^+}}\rightarrow K$
.
8.1 Condensed mathematics and condensed group cohomology
We recall the basics about condensed mathematics and condensed group cohomology, following [Reference ScholzeSch19], [Reference BoscoBos21, Appendix] and [Reference Bhatt and ScholzeBS15, Section 4.3].
Convention 8.1.1. As in [Reference ScholzeSch19], we fix an uncountable strong limit cardinality
![]() $\kappa $
throughout the section. Every construction is defined to be
$\kappa $
throughout the section. Every construction is defined to be
![]() $\kappa $
-small unless otherwise specified.
$\kappa $
-small unless otherwise specified.
Definition 8.1.2. The category of condensed sets/groups/rings, is defined as a sheaf of sets/groups/rings over the pro-étale site of a point
![]() $\ast _{\mathrm {pro\acute {e}t}}$
.
$\ast _{\mathrm {pro\acute {e}t}}$
.
To relate to the usual notion of the topological structure, we have the following results.
Theorem 8.1.3 [Reference ScholzeSch19, Example 1.5, Proposition 1.7, Theorem 2.16].
There is a natural functor from the category of topological spaces/groups/rings to the category of condensed sets/groups/rings, denoted as
![]() $M\mapsto \underline M$
, where the latter sends a profinite set
$M\mapsto \underline M$
, where the latter sends a profinite set
![]() $S\in \ast _{\mathrm {pro\acute {e}t}}$
to the set of continuous maps from S to M. The functor satisfies the following:
$S\in \ast _{\mathrm {pro\acute {e}t}}$
to the set of continuous maps from S to M. The functor satisfies the following:
-
(i) the functor is faithful, and is fully faithful when restricted to those T whose underlying topological space is
 $\kappa $
-compactly generated;
$\kappa $
-compactly generated; -
(ii) it induces an equivalence between compact Hausdorff spaces X and qcqs condensed sets;
-
(iii) it admits a left adjoint
 $X\mapsto X(\ast )_{\mathrm {top}}$
, such that for a topological space T, the composition
$X\mapsto X(\ast )_{\mathrm {top}}$
, such that for a topological space T, the composition
 $\underline T(\ast )_{\mathrm {top}}$
is the same set but with the compactly generated topology.
$\underline T(\ast )_{\mathrm {top}}$
is the same set but with the compactly generated topology.
For a set/group/ring M, we say a condensed set/group/ring A underlies M if we have
![]() $A(\ast )\cong M$
.
$A(\ast )\cong M$
.
Denote
![]() $\mathrm {LCA}$
to be the category of locally compact abelian groups, and
$\mathrm {LCA}$
to be the category of locally compact abelian groups, and
![]() ${\mathrm {Cond(Ab)}}$
to be the category of condensed abelian group. For two condensed abelian groups M and N, we let the condensed group
${\mathrm {Cond(Ab)}}$
to be the category of condensed abelian group. For two condensed abelian groups M and N, we let the condensed group
![]() $\underline {\mathrm {Hom}}_{\mathrm {Cond(Ab)}}(M,N)\in {\mathrm {Cond(Ab)}}$
be the internal group of homomorphisms between them ([Reference ScholzeSch19, Section 2]).
$\underline {\mathrm {Hom}}_{\mathrm {Cond(Ab)}}(M,N)\in {\mathrm {Cond(Ab)}}$
be the internal group of homomorphisms between them ([Reference ScholzeSch19, Section 2]).
When restricted to abelian groups, the functor
![]() $M \mapsto \underline M$
induces a fully faithful embedding from
$M \mapsto \underline M$
induces a fully faithful embedding from
![]() $\mathrm {LCA}$
.
$\mathrm {LCA}$
.
Theorem 8.1.4 [Reference ScholzeSch19, Proposition 4.2, Corollary 4.9].
The natural functor
![]() $M \mapsto \underline M$
induces a fully faithful embedding
$M \mapsto \underline M$
induces a fully faithful embedding
such that
On the other hand, the category of condensed abelian groups behave exactly like the category of abelian groups.
Theorem 8.1.5 [Reference ScholzeSch19, Theorem 2.2].
The category
![]() ${\mathrm {Cond(Ab)}}$
is an abelian category, satisfying Grothendieck’s axioms (AB3), (AB4), (AB5), (AB3*), (AB4*) and (AB6). Moreover, it is generated by compact projective objects
${\mathrm {Cond(Ab)}}$
is an abelian category, satisfying Grothendieck’s axioms (AB3), (AB4), (AB5), (AB3*), (AB4*) and (AB6). Moreover, it is generated by compact projective objects
![]() $\mathbb {Z}[S]$
, for
$\mathbb {Z}[S]$
, for
![]() $S\in \ast _{\mathrm {pro\acute {e}t}}$
being an extremally disconnected set.
$S\in \ast _{\mathrm {pro\acute {e}t}}$
being an extremally disconnected set.
Inside of the category
![]() ${\mathrm {Cond(Ab)}}$
, there is abelian subcategory called
${\mathrm {Cond(Ab)}}$
, there is abelian subcategory called
![]() ${\mathrm {Solid}}$
. We recall its definition as below.
${\mathrm {Solid}}$
. We recall its definition as below.
Definition 8.1.6 [Reference ScholzeSch19, Definition 5.1].
-
(1) For a profinite set S, we define the condensed abelian group
 $\mathbb {Z}[S]^\blacksquare :=\varprojlim _i \mathbb {Z}[S_i]$
, where each
$\mathbb {Z}[S]^\blacksquare :=\varprojlim _i \mathbb {Z}[S_i]$
, where each
 $S_i$
is finite and
$S_i$
is finite and
 $S=\varprojlim _i S_i$
;
$S=\varprojlim _i S_i$
; -
(2) A condensed group A is called solid if the natural map below is an isomorphism
 $$\begin{align*}{\mathrm{Hom}}_{\mathrm{Cond(Ab)}}(\mathbb{Z}[S], A) \longrightarrow {\mathrm{Hom}}_{\mathrm{Cond(Ab)}}(\mathbb{Z}[S]^\blacksquare, A). \end{align*}$$
$$\begin{align*}{\mathrm{Hom}}_{\mathrm{Cond(Ab)}}(\mathbb{Z}[S], A) \longrightarrow {\mathrm{Hom}}_{\mathrm{Cond(Ab)}}(\mathbb{Z}[S]^\blacksquare, A). \end{align*}$$
Similarly one can define a complex
![]() $C\in D({\mathrm {Cond(Ab)}})$
to be solid by replacing
$C\in D({\mathrm {Cond(Ab)}})$
to be solid by replacing
![]() $ {\mathrm {Hom}}$
by
$ {\mathrm {Hom}}$
by
![]() $R {\mathrm {Hom}}$
, and it can be shown that those two notions are compatible ([Reference ScholzeSch19, Theorem 5.8]). We list the important properties of
$R {\mathrm {Hom}}$
, and it can be shown that those two notions are compatible ([Reference ScholzeSch19, Theorem 5.8]). We list the important properties of
![]() ${\mathrm {Solid}}$
below.
${\mathrm {Solid}}$
below.
Theorem 8.1.7 [Reference ScholzeSch19, Theorem 5.8, Corollary 5.5].
-
(i) The category
 ${\mathrm {Solid}}$
is an abelian subcategory of
${\mathrm {Solid}}$
is an abelian subcategory of
 ${\mathrm {Cond(Ab)}}$
that is stable under limits, colimits and extensions.
${\mathrm {Cond(Ab)}}$
that is stable under limits, colimits and extensions. -
(ii) The objects
 $\prod _I \mathbb {Z}\in {\mathrm {Solid}}$
for any set of I forms a family of compact projective generators of
$\prod _I \mathbb {Z}\in {\mathrm {Solid}}$
for any set of I forms a family of compact projective generators of
 ${\mathrm {Solid}}$
. In particular
${\mathrm {Solid}}$
. In particular
 $\mathbb {Z}[S]^\blacksquare $
is solid for any profinite set S.
$\mathbb {Z}[S]^\blacksquare $
is solid for any profinite set S. -
(iii) The functor
 $D({\mathrm {Solid}})\subset D({\mathrm {Cond(Ab)}})$
is fully faithful whose essential image is solid complexes, and a complex is solid if and only if each of its cohomology is solid.
$D({\mathrm {Solid}})\subset D({\mathrm {Cond(Ab)}})$
is fully faithful whose essential image is solid complexes, and a complex is solid if and only if each of its cohomology is solid. -
(iv) The inclusion
 ${\mathrm {Solid}}\subset {\mathrm {Cond(Ab)}}$
admits a left adjoint
${\mathrm {Solid}}\subset {\mathrm {Cond(Ab)}}$
admits a left adjoint
 $A\mapsto A^\blacksquare $
, which is the unique colimit preserving functor extending
$A\mapsto A^\blacksquare $
, which is the unique colimit preserving functor extending
 $\mathbb {Z}[S] \mapsto \mathbb {Z}[S]^\blacksquare $
. The left derived functor associated to
$\mathbb {Z}[S] \mapsto \mathbb {Z}[S]^\blacksquare $
. The left derived functor associated to
 $A\mapsto A^\blacksquare $
is also the left adjoint to the inclusion
$A\mapsto A^\blacksquare $
is also the left adjoint to the inclusion
 $D({\mathrm {Solid}})\subset D({\mathrm {Cond(Ab)}})$
.
$D({\mathrm {Solid}})\subset D({\mathrm {Cond(Ab)}})$
.
We then turn to the notion of condensed group cohomology. We first recall its definition as in [Reference BoscoBos21, Appendix B.1].
Definition 8.1.8. Let G be a condensed group, and let A be a G-module in
![]() ${\mathrm {Cond(Ab)}}$
. The i-th condensed group cohomology of G in A, as an object in
${\mathrm {Cond(Ab)}}$
. The i-th condensed group cohomology of G in A, as an object in
![]() ${\mathrm {Cond(Ab)}}$
, is
${\mathrm {Cond(Ab)}}$
, is
We use the notation
![]() $R\Gamma (G,-)$
for the composition functor
$R\Gamma (G,-)$
for the composition functor
![]() $R {\mathrm {Hom}}_{\mathbb {Z}[G]}(\mathbb {Z}, -)=R\Gamma (\ast , R\underline {\mathrm {Hom}}_{\mathbb {Z}[G]}(\mathbb {Z}, -))$
, evaluating at condensed G-modules.
$R {\mathrm {Hom}}_{\mathbb {Z}[G]}(\mathbb {Z}, -)=R\Gamma (\ast , R\underline {\mathrm {Hom}}_{\mathbb {Z}[G]}(\mathbb {Z}, -))$
, evaluating at condensed G-modules.
The following useful proposition says condensed group cohomology recovers the usual notion of continuous group cohomology in many cases.
Proposition 8.1.9 [Reference BoscoBos21, Appendix B.2].
Let G be a profinite group, and let A be a solid
![]() $\underline G$
-module.
$\underline G$
-module.
-
(1) The complex
 $R\underline {\mathrm {Hom}}_{\mathbb {Z}[\underline G]}(\mathbb {Z}, A)$
is isomorphic to the complex of solid abelian groups
$R\underline {\mathrm {Hom}}_{\mathbb {Z}[\underline G]}(\mathbb {Z}, A)$
is isomorphic to the complex of solid abelian groups  $$\begin{align*}A \longrightarrow \underline{\mathrm{Hom}}_{\mathbb{Z}}(\mathbb{Z}[\underline G], A) \longrightarrow \underline{\mathrm{Hom}}_{\mathbb{Z}}(\mathbb{Z}[\underline G \times \underline G], A) \longrightarrow \cdots. \end{align*}$$
$$\begin{align*}A \longrightarrow \underline{\mathrm{Hom}}_{\mathbb{Z}}(\mathbb{Z}[\underline G], A) \longrightarrow \underline{\mathrm{Hom}}_{\mathbb{Z}}(\mathbb{Z}[\underline G \times \underline G], A) \longrightarrow \cdots. \end{align*}$$
-
(2) If
 $A=\underline M$
for some
$A=\underline M$
for some
 $T_1$
topological G-module M, then the global section functor induces a natural isomorphism below
$T_1$
topological G-module M, then the global section functor induces a natural isomorphism below  $$\begin{align*}{\mathrm{Ext}}_{\mathbb{Z}[\underline G]}^i (\mathbb{Z}, \underline M) \longrightarrow \mathrm{H}^i_{\mathrm{cont}}(G,M). \end{align*}$$
$$\begin{align*}{\mathrm{Ext}}_{\mathbb{Z}[\underline G]}^i (\mathbb{Z}, \underline M) \longrightarrow \mathrm{H}^i_{\mathrm{cont}}(G,M). \end{align*}$$
Proof. Here we note that though the item (i) is slightly different from the statement in [Reference BoscoBos21, Appendix B.2. (i)] where A is assumed to be
![]() $\underline M$
already, the proof applies to the more general case.
$\underline M$
already, the proof applies to the more general case.
Remark 8.1.10. The condensed group cohomology functor
![]() $R\underline {\mathrm {Hom}}_{\mathbb {Z}[G]}(\mathbb {Z}, -)$
for a condensed group G is the right derived functor of
$R\underline {\mathrm {Hom}}_{\mathbb {Z}[G]}(\mathbb {Z}, -)$
for a condensed group G is the right derived functor of
![]() $\underline {\mathrm {Hom}}_{\mathbb {Z}[G]}(\mathbb {Z}, -)$
. In particular, since the latter is lax-symmetric monoidal, it naturally induces a functor from
$\underline {\mathrm {Hom}}_{\mathbb {Z}[G]}(\mathbb {Z}, -)$
. In particular, since the latter is lax-symmetric monoidal, it naturally induces a functor from
![]() $\mathbb {E}_\infty $
-algebras in
$\mathbb {E}_\infty $
-algebras in
![]() ${\mathrm {Cond(Ab)}}$
(resp.
${\mathrm {Cond(Ab)}}$
(resp.
![]() ${\mathrm {Solid}}$
) that admits a G-action to
${\mathrm {Solid}}$
) that admits a G-action to
![]() $\mathbb {E}_\infty $
-algebras in
$\mathbb {E}_\infty $
-algebras in
![]() ${\mathrm {Cond(Ab)}}$
(resp.
${\mathrm {Cond(Ab)}}$
(resp.
![]() ${\mathrm {Solid}}$
).
${\mathrm {Solid}}$
).
We finish this subsection by collecting some results on affinoid algebras and its associated condensed rings. We refer the reader to [Reference BoscoBos21, Appendix A] for a discussion of solid k-modules, together with the symmetric tensor product
![]() $-\otimes _k^{\blacksquare } -$
.
$-\otimes _k^{\blacksquare } -$
.
Lemma 8.1.11. Let
![]() $R_0=k \langle T_i\rangle / I_0$
be a topologically finite type k-algebra, let
$R_0=k \langle T_i\rangle / I_0$
be a topologically finite type k-algebra, let
![]() $R=R_0\widehat \otimes _k K\cong K\langle T_i\rangle / I_0$
, let
$R=R_0\widehat \otimes _k K\cong K\langle T_i\rangle / I_0$
, let
![]() $R_e= {\mathrm {B^+_{dR,e}}} \langle T_i\rangle /I_0$
and let
$R_e= {\mathrm {B^+_{dR,e}}} \langle T_i\rangle /I_0$
and let
![]() $\widetilde R={\mathrm {B_{dR}^+}} \langle T_i\rangle /I_0=\varprojlim R_e$
. Then each of
$\widetilde R={\mathrm {B_{dR}^+}} \langle T_i\rangle /I_0=\varprojlim R_e$
. Then each of
![]() $\underline R_0, \underline R, \underline R_e, \underline {\widetilde R}$
is solid, and satisfies the formulae
$\underline R_0, \underline R, \underline R_e, \underline {\widetilde R}$
is solid, and satisfies the formulae
To save us from complicated notations, we use k, K,
![]() ${\mathrm {B^+_{dR,e}}}$
, and
${\mathrm {B^+_{dR,e}}}$
, and
![]() ${\mathrm {B_{dR}^+}}$
instead of
${\mathrm {B_{dR}^+}}$
instead of
![]() $\underline k$
,
$\underline k$
,
![]() $\underline K$
,
$\underline K$
,
![]() $\underline {\mathrm {B^+_{dR,e}}}$
or
$\underline {\mathrm {B^+_{dR,e}}}$
or
![]() $\underline {\mathrm {B_{dR}^+}}$
to denote their associated solid rings.
$\underline {\mathrm {B_{dR}^+}}$
to denote their associated solid rings.
Proof. For the solidity of the rings above, this can be checked using the definition of the functor
![]() $M\mapsto \underline M$
in Theorem 8.1.3, and the fact that solid modules are preserved under limits and colimits as in Theorem 8.1.7. For example the ring R is computed as
$M\mapsto \underline M$
in Theorem 8.1.3, and the fact that solid modules are preserved under limits and colimits as in Theorem 8.1.7. For example the ring R is computed as
 $$\begin{align*}R\cong {\mathrm{colim}}_{n\in\mathbb{N}} \left(\varprojlim_{m\in\mathbb{N}} p^{-n}(R'/p^mR') \right), \end{align*}$$
$$\begin{align*}R\cong {\mathrm{colim}}_{n\in\mathbb{N}} \left(\varprojlim_{m\in\mathbb{N}} p^{-n}(R'/p^mR') \right), \end{align*}$$
where
![]() $R'$
is a ring of definition of R, and thus each
$R'$
is a ring of definition of R, and thus each
![]() $R'/p^mR'$
is a discrete abelian group. By Theorem 8.1.3, it then suffices to notice that a continuous map from a profinite set S to R can be written as a limit of continuous maps from S to
$R'/p^mR'$
is a discrete abelian group. By Theorem 8.1.3, it then suffices to notice that a continuous map from a profinite set S to R can be written as a limit of continuous maps from S to
![]() $p^{-n}(R'/p^mR')$
, for some
$p^{-n}(R'/p^mR')$
, for some
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
For the tensor product formulae, the first two with
![]() $\underline K$
and
$\underline K$
and
![]() ${\mathrm {B^+_{dR,n}}}$
follows from the observation that the functor taking the associated condensed group commutes with the complete tensor product, over the category of Banach k-algebras ([Reference BoscoBos21, Appendix A.26]). For the last one, we apply the limit-tensor formula in [Reference BoscoBos21, Appendix A.24. (i)] at
${\mathrm {B^+_{dR,n}}}$
follows from the observation that the functor taking the associated condensed group commutes with the complete tensor product, over the category of Banach k-algebras ([Reference BoscoBos21, Appendix A.26]). For the last one, we apply the limit-tensor formula in [Reference BoscoBos21, Appendix A.24. (i)] at
![]() $V_n={\mathrm {B^+_{dR,n}}}$
and
$V_n={\mathrm {B^+_{dR,n}}}$
and
![]() $W=\underline R_0$
, to get
$W=\underline R_0$
, to get
where the last formula follows from [Reference BoscoBos21, Appendix A.26] (recall from [Reference FontaineFon94] that
![]() ${\mathrm {B_{dR}^+}}$
is a k-Fréchet algebra). To finish the proof, we notice that by definition of the functor
${\mathrm {B_{dR}^+}}$
is a k-Fréchet algebra). To finish the proof, we notice that by definition of the functor
![]() $M\mapsto \underline M$
in Theorem 8.1.3 we have
$M\mapsto \underline M$
in Theorem 8.1.3 we have
![]() $\varprojlim _n (\underline {{\mathrm {B^+_{dR,n}}} \langle T_i\rangle /I_0})=\underline {{\mathrm {B_{dR}^+}} \langle T_i\rangle /I_0}=\underline {\widetilde R}.$
$\varprojlim _n (\underline {{\mathrm {B^+_{dR,n}}} \langle T_i\rangle /I_0})=\underline {{\mathrm {B_{dR}^+}} \langle T_i\rangle /I_0}=\underline {\widetilde R}.$
8.2 Galois invariant of cohomology
We now compute Galois invariants of cohomology.
We recall the following fact computing continuous Galois cohomology of
![]() ${\mathrm {B_{dR}^+}}$
-modules.
${\mathrm {B_{dR}^+}}$
-modules.
Lemma 8.2.1. We have the following equalities:
 $$\begin{align*}\mathrm{H}_{\mathrm{cont}}^n(G_k, K(i))= \begin{cases} k,~n=i=0;\\ k\cup \log\chi,~n=1,~i=0;\\ 0,~n\geq 2,~or~i\neq 0. \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{H}_{\mathrm{cont}}^n(G_k, K(i))= \begin{cases} k,~n=i=0;\\ k\cup \log\chi,~n=1,~i=0;\\ 0,~n\geq 2,~or~i\neq 0. \end{cases} \end{align*}$$
The same results hold if we replace
![]() $K(0)$
by
$K(0)$
by
![]() ${\mathrm {B_{dR}^+}}$
. Here
${\mathrm {B_{dR}^+}}$
. Here
![]() $\log \chi \in \mathrm {H^1}_{\mathrm {cont}}(G_k, \mathbb {Q}_p)=\mathrm {Hom_{cont}}(G_k,\mathbb {Q}_p)$
is the logarithm of the cyclotomic character.
$\log \chi \in \mathrm {H^1}_{\mathrm {cont}}(G_k, \mathbb {Q}_p)=\mathrm {Hom_{cont}}(G_k,\mathbb {Q}_p)$
is the logarithm of the cyclotomic character.
Proof. The calculation of Galois cohomology for
![]() $K(i)=\xi ^i{\mathrm {B_{dR}^+}}/\xi ^{i+1}{\mathrm {B_{dR}^+}}$
can be found in [[Reference TateTat67]]. For
$K(i)=\xi ^i{\mathrm {B_{dR}^+}}/\xi ^{i+1}{\mathrm {B_{dR}^+}}$
can be found in [[Reference TateTat67]]. For
![]() ${\mathrm {B_{dR}^+}}$
this follows from an induction and an inverse limit process.
${\mathrm {B_{dR}^+}}$
this follows from an induction and an inverse limit process.
Lemma 8.2.2. Let P be the
![]() ${\mathrm {B_{dR}^+}}$
-algebra
${\mathrm {B_{dR}^+}}$
-algebra
![]() ${\mathrm {B_{dR}^+}} \langle T_j\rangle $
, and let
${\mathrm {B_{dR}^+}} \langle T_j\rangle $
, and let
![]() $\Omega _{P/{\mathrm {B_{dR}^+}}}^i=\varprojlim \Omega _{{\mathrm {B^+_{dR,e}}} \langle T_j\rangle /{\mathrm {B^+_{dR,e}}}}^i$
be the inverse limit of p-adic continuous differentials. Let
$\Omega _{P/{\mathrm {B_{dR}^+}}}^i=\varprojlim \Omega _{{\mathrm {B^+_{dR,e}}} \langle T_j\rangle /{\mathrm {B^+_{dR,e}}}}^i$
be the inverse limit of p-adic continuous differentials. Let
![]() $P_0=k \langle T_j\rangle $
be the affinoid k-subalgebra inside of P, let
$P_0=k \langle T_j\rangle $
be the affinoid k-subalgebra inside of P, let
![]() $I_0$
be an ideal in
$I_0$
be an ideal in
![]() $P_0$
and let
$P_0$
and let
![]() $I=I_0\otimes _{P_0} P$
be the ideal in P. Then for
$I=I_0\otimes _{P_0} P$
be the ideal in P. Then for
![]() $n,i \in \mathbb {N}$
we have
$n,i \in \mathbb {N}$
we have
 $$\begin{align*}\mathrm{H}_{\mathrm{cont}}^n(G_k, \Omega_{P/{\mathrm{B_{dR}^+}}}^i\otimes_P I)= \begin{cases} \Omega_{P_0/k}^i\otimes_{P_0} I_0,~n=0;\\ \Omega_{P_0/k}^i\otimes_{P_0} I_0\cup \log\chi,~n=1;\\ 0,~n\geq 2, \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{H}_{\mathrm{cont}}^n(G_k, \Omega_{P/{\mathrm{B_{dR}^+}}}^i\otimes_P I)= \begin{cases} \Omega_{P_0/k}^i\otimes_{P_0} I_0,~n=0;\\ \Omega_{P_0/k}^i\otimes_{P_0} I_0\cup \log\chi,~n=1;\\ 0,~n\geq 2, \end{cases} \end{align*}$$
where
![]() $\Omega _{P_0/k}^i$
is the i-th continuous differential of
$\Omega _{P_0/k}^i$
is the i-th continuous differential of
![]() $P_0$
over k. The same holds if we replace P by
$P_0$
over k. The same holds if we replace P by
![]() $K \langle T_i\rangle $
or
$K \langle T_i\rangle $
or
![]() ${\mathrm {B^+_{dR,e}}} \langle T_i\rangle $
.
${\mathrm {B^+_{dR,e}}} \langle T_i\rangle $
.
Proof. Similarly to Lemma 8.2.1, by a limit argument and the induction, one can reduce to the calculation of continuous group cohomology for
![]() $P/\xi (i)=K \langle T_i\rangle (i)$
, which follows from Tate-Sen formalism (see [Reference Liu and ZhuLZ17, Lemma 3.10] for example).
$P/\xi (i)=K \langle T_i\rangle (i)$
, which follows from Tate-Sen formalism (see [Reference Liu and ZhuLZ17, Lemma 3.10] for example).
Now we compute Galois invariant of infinitesimal cohomology.
Theorem 8.2.3. Let Y be a rigid space over k, and let
![]() $Y_K$
be its complete base extension to K.
$Y_K$
be its complete base extension to K.
-
(i) There is a natural complex of condensed abelian groups
 $\underline {R\Gamma }_{\inf }(Y/k)$
and a complex of
$\underline {R\Gamma }_{\inf }(Y/k)$
and a complex of
 $\underline G_k$
-condensed modules
$\underline G_k$
-condensed modules
 $\underline {R\Gamma }_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
underlying infinitesimal cohomology
$\underline {R\Gamma }_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
underlying infinitesimal cohomology
 $R\Gamma (Y/k_{\inf }, \mathcal {O}_{Y/k})$
and
$R\Gamma (Y/k_{\inf }, \mathcal {O}_{Y/k})$
and
 $R\Gamma (Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {O}_{Y_K/{\mathrm {B_{dR}^+}}})$
separately;
$R\Gamma (Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {O}_{Y_K/{\mathrm {B_{dR}^+}}})$
separately; -
(ii) the above complexes satisfy a solid base change formula
 $$\begin{align*}\underline{R\Gamma}_{\inf}(Y/k) \otimes_k^{L{\blacksquare}} {\mathrm{B_{dR}^+}} \cong \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}}); \end{align*}$$
$$\begin{align*}\underline{R\Gamma}_{\inf}(Y/k) \otimes_k^{L{\blacksquare}} {\mathrm{B_{dR}^+}} \cong \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}}); \end{align*}$$
-
(iii) the
 $\underline G_k$
-action induces the equality
$\underline G_k$
-action induces the equality  $$\begin{align*}R\Gamma(\underline G_k, {\mathrm{B_{dR}^+}})\otimes_k R\Gamma(Y/k_{\inf}, \mathcal{O}_{Y/k}) \longrightarrow R\Gamma(\underline G_k, \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}})). \end{align*}$$
$$\begin{align*}R\Gamma(\underline G_k, {\mathrm{B_{dR}^+}})\otimes_k R\Gamma(Y/k_{\inf}, \mathcal{O}_{Y/k}) \longrightarrow R\Gamma(\underline G_k, \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}})). \end{align*}$$
Remark 8.2.4. Before we jump to the proof, one might attempt to ask if we can replace the condensed infinitesimal cohomology
![]() $\underline {R\Gamma }_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
in (iii) by the actual infinitesimal cohomology
$\underline {R\Gamma }_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
in (iii) by the actual infinitesimal cohomology
![]() $R\Gamma (Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {O}_{Y_K/{\mathrm {B_{dR}^+}}})$
and compute continuous group cohomology in the classical sense. However, even though each object in
$R\Gamma (Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {O}_{Y_K/{\mathrm {B_{dR}^+}}})$
and compute continuous group cohomology in the classical sense. However, even though each object in
![]() $Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
admits a natural k-Fréchet structure, one cannot conclude that
$Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
admits a natural k-Fréchet structure, one cannot conclude that
![]() $R\Gamma (Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {O}_{Y_K/{\mathrm {B_{dR}^+}}})$
is also topological. This is due to the lack of the notion of a derived/homotopy limit for topological groups.
$R\Gamma (Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {O}_{Y_K/{\mathrm {B_{dR}^+}}})$
is also topological. This is due to the lack of the notion of a derived/homotopy limit for topological groups.
Proof. We first give the definition of condensed infinitesimal cohomology as in part (i). The idea is to consider the natural condensed enhancement for each topological algebra that appears in the Čech–Alexander complex of the infinitesimal cohomology.
We define the condensed structure sheaf
![]() $\underline {\mathcal {O}}_{\inf }$
over
$\underline {\mathcal {O}}_{\inf }$
over
![]() $Y/k_{\inf }$
, by sending an affinoid infinitesimal thickening
$Y/k_{\inf }$
, by sending an affinoid infinitesimal thickening
![]() $(R_0, S_0)$
onto the condensed ring
$(R_0, S_0)$
onto the condensed ring
![]() $\underline S_0$
. Here recall that both
$\underline S_0$
. Here recall that both
![]() $R_0$
and
$R_0$
and
![]() $S_0$
are topologically finite type algebras over k, and
$S_0$
are topologically finite type algebras over k, and
![]() $S_0\rightarrow R_0$
is a surjection with the kernel being nilpotent. On the other hand, recall for a pro-infinitesimal thickening
$S_0\rightarrow R_0$
is a surjection with the kernel being nilpotent. On the other hand, recall for a pro-infinitesimal thickening
![]() $(\mathrm {Spa}(R), \mathrm {Spa}(B_e))\in Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
with
$(\mathrm {Spa}(R), \mathrm {Spa}(B_e))\in Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
with
![]() $B_e$
being a topologically finite type algebra over
$B_e$
being a topologically finite type algebra over
![]() ${\mathrm {B^+_{dR,e}}}$
, we can consider the induced condensed ring
${\mathrm {B^+_{dR,e}}}$
, we can consider the induced condensed ring
![]() $\underline B=\varprojlim \underline B_e$
. This allows us to define the condensed structure sheaf
$\underline B=\varprojlim \underline B_e$
. This allows us to define the condensed structure sheaf
![]() $\underline {\mathcal {O}}_{Y_K/{\mathrm {B_{dR}^+}}}$
over
$\underline {\mathcal {O}}_{Y_K/{\mathrm {B_{dR}^+}}}$
over
![]() $Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
separately, sending any such pro-infinitesimal thickening onto
$Y_K/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}$
separately, sending any such pro-infinitesimal thickening onto
![]() $\underline B$
.Footnote
3
Our condensed infinitesimal cohomology is then defined as infinitesimal cohomology of condensed structure sheaves, as objects in
$\underline B$
.Footnote
3
Our condensed infinitesimal cohomology is then defined as infinitesimal cohomology of condensed structure sheaves, as objects in
![]() $D({\mathrm {Cond(Ab)}})$
$D({\mathrm {Cond(Ab)}})$
 $$ \begin{align*} \underline{R\Gamma}_{\inf}(Y/k) & := R\Gamma(Y/k_{\inf}, \underline{\mathcal{O}}_{Y/k});\\ \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}}) & := R\Gamma(Y_K/{\mathrm{B_{dR}^+}}_{\mathrm{pinf}}, \underline{\mathcal{O}}_{Y_K/{\mathrm{B_{dR}^+}}}). \end{align*} $$
$$ \begin{align*} \underline{R\Gamma}_{\inf}(Y/k) & := R\Gamma(Y/k_{\inf}, \underline{\mathcal{O}}_{Y/k});\\ \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}}) & := R\Gamma(Y_K/{\mathrm{B_{dR}^+}}_{\mathrm{pinf}}, \underline{\mathcal{O}}_{Y_K/{\mathrm{B_{dR}^+}}}). \end{align*} $$
We now temporarily let
![]() $Y=\mathrm {Spa}(R_0)$
for a topological finite type algebra R over k, and let
$Y=\mathrm {Spa}(R_0)$
for a topological finite type algebra R over k, and let
![]() $R=R_0\widehat \otimes _k K$
be its complete field extension. Suppose we have a surjection of affinoid k-algebras
$R=R_0\widehat \otimes _k K$
be its complete field extension. Suppose we have a surjection of affinoid k-algebras
![]() $P_0=k \langle T_i \rangle \rightarrow R$
with
$P_0=k \langle T_i \rangle \rightarrow R$
with
![]() $R=P_0/I_0$
for an ideal
$R=P_0/I_0$
for an ideal
![]() $I_0\subset P_0$
, and let P be the
$I_0\subset P_0$
, and let P be the
![]() ${\mathrm {B_{dR}^+}}$
-algebra
${\mathrm {B_{dR}^+}}$
-algebra
![]() ${\mathrm {B_{dR}^+}} \langle T_i\rangle $
. We then obtain a
${\mathrm {B_{dR}^+}} \langle T_i\rangle $
. We then obtain a
![]() $\underline G_k$
-condensed algebra underlying the infinitesimal envelope
$\underline G_k$
-condensed algebra underlying the infinitesimal envelope
![]() $D_{\inf }=\varprojlim {\mathrm {B^+_{dR,e}}} \langle T_i\rangle /I_0^e$
of the pro-infinitesimal thickening
$D_{\inf }=\varprojlim {\mathrm {B^+_{dR,e}}} \langle T_i\rangle /I_0^e$
of the pro-infinitesimal thickening
![]() $(Y,\mathrm {Spa}(P/(\xi ^e,I_0^e)))$
as below
$(Y,\mathrm {Spa}(P/(\xi ^e,I_0^e)))$
as below
Here we note that by rewriting this limit, the above is also equal to
![]() $\varprojlim \underline {{\mathrm {B_{dR}^+}} \langle T_i\rangle /I_0^e}$
, where by Lemma 8.1.11 each
$\varprojlim \underline {{\mathrm {B_{dR}^+}} \langle T_i\rangle /I_0^e}$
, where by Lemma 8.1.11 each
![]() $\underline {{\mathrm {B_{dR}^+}} \langle T_i\rangle /I_0^e}$
is isomorphic to the solid tensor product
$\underline {{\mathrm {B_{dR}^+}} \langle T_i\rangle /I_0^e}$
is isomorphic to the solid tensor product
![]() ${\mathrm {B_{dR}^+}} \otimes ^{\blacksquare }_k \underline {P_0/I_0^e}$
. So thanks to the limit-tensor product formula [Reference BoscoBos21, Appendix A.24], since
${\mathrm {B_{dR}^+}} \otimes ^{\blacksquare }_k \underline {P_0/I_0^e}$
. So thanks to the limit-tensor product formula [Reference BoscoBos21, Appendix A.24], since
![]() $\{P_0/I_0\}$
is an inverse system of K-Banach algebras, we get
$\{P_0/I_0\}$
is an inverse system of K-Banach algebras, we get
where
![]() $D_{0,{\inf }}$
is the infinitesimal envelope of
$D_{0,{\inf }}$
is the infinitesimal envelope of
![]() $R_0$
inside of
$R_0$
inside of
![]() $P_0$
, as a pro-infinitesimal thickening in
$P_0$
, as a pro-infinitesimal thickening in
![]() $R_0/k_{\inf }$
, and
$R_0/k_{\inf }$
, and
![]() $\underline {D}_{0,{\inf }}$
is the section of
$\underline {D}_{0,{\inf }}$
is the section of
![]() $\underline {\mathcal {O}}_{Y/k}$
at it.
$\underline {\mathcal {O}}_{Y/k}$
at it.
Now we apply the above computation to the Čech-Alexander complex for the infinitesimal sites. Recall from [Reference GuoGuo24, Proposition 2.2.7] that infinitesimal cohomology for
![]() $Y/k_{\inf }$
and
$Y/k_{\inf }$
and
![]() $Y_K/{\mathrm {B_{dR}^+}}_{\inf }$
are computed by the cosimplicial complexes
$Y_K/{\mathrm {B_{dR}^+}}_{\inf }$
are computed by the cosimplicial complexes
![]() $D_{0,{\inf }}(\bullet )$
and
$D_{0,{\inf }}(\bullet )$
and
![]() $D_{\inf }(\bullet )$
, where
$D_{\inf }(\bullet )$
, where
![]() $D_{0,{\inf }}(n)$
and
$D_{0,{\inf }}(n)$
and
![]() $D_{\inf }(n)$
are formal completion for the surjections
$D_{\inf }(n)$
are formal completion for the surjections
![]() $P_0(n):=P_0^{\widehat \otimes _k n+1} \rightarrow R_0$
and
$P_0(n):=P_0^{\widehat \otimes _k n+1} \rightarrow R_0$
and
![]() $P(n):=P^{\widehat \otimes _{\mathrm {B_{dR}^+}} n+1} \rightarrow R$
separately. We apply these to the condensed structure sheaves to get the cosimplicial condensed algebras
$P(n):=P^{\widehat \otimes _{\mathrm {B_{dR}^+}} n+1} \rightarrow R$
separately. We apply these to the condensed structure sheaves to get the cosimplicial condensed algebras
 $$ \begin{align*} \underline{R\Gamma}_{\inf}(Y/k) &\cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} \underline{D}_{0,{\inf}}(n) ;\\ \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}}) & \cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} \underline{D}_{{\inf}}(n). \end{align*} $$
$$ \begin{align*} \underline{R\Gamma}_{\inf}(Y/k) &\cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} \underline{D}_{0,{\inf}}(n) ;\\ \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}}) & \cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} \underline{D}_{{\inf}}(n). \end{align*} $$
Here we note that since a condensed group is a sheaf over the pro-étale site
![]() $\ast _{\mathrm {pro\acute {e}t}}$
, by applying the derived global section functor
$\ast _{\mathrm {pro\acute {e}t}}$
, by applying the derived global section functor
![]() $R\Gamma (\ast ,-)$
, we see from below that the complex of condensed groups
$R\Gamma (\ast ,-)$
, we see from below that the complex of condensed groups
![]() $\underline {R\Gamma }_{\inf }(Y/k)$
underlies the corresponding usual infinitesimal cohomology
$\underline {R\Gamma }_{\inf }(Y/k)$
underlies the corresponding usual infinitesimal cohomology
 $$ \begin{align*} R\Gamma(\ast, \underline{R\Gamma}_{\inf}(Y/k)) &\cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} R\Gamma(\ast, \underline{D}_{0,{\inf}}(n)) \\ &\cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} D_{0,{\inf}}(n) \\ &\cong R\Gamma_{\inf}(Y/k_{\inf}, \mathcal{O}_{Y/k}). \end{align*} $$
$$ \begin{align*} R\Gamma(\ast, \underline{R\Gamma}_{\inf}(Y/k)) &\cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} R\Gamma(\ast, \underline{D}_{0,{\inf}}(n)) \\ &\cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} D_{0,{\inf}}(n) \\ &\cong R\Gamma_{\inf}(Y/k_{\inf}, \mathcal{O}_{Y/k}). \end{align*} $$
Similarly for
![]() $\underline {R\Gamma }_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
. Here we use Theorem 8.1.3 together with the exactness of
$\underline {R\Gamma }_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
. Here we use Theorem 8.1.3 together with the exactness of
![]() $R\Gamma (\ast , -)$
, as each profinite set admits a map from
$R\Gamma (\ast , -)$
, as each profinite set admits a map from
![]() $\ast $
.
$\ast $
.
Moreover, notice that each
![]() $\underline {D}_{{\inf }}(n)$
satisfies the solid tensor product formula
$\underline {D}_{{\inf }}(n)$
satisfies the solid tensor product formula
So combining with the flatness of
![]() $\underline {{\mathrm {B_{dR}^+}}}$
over
$\underline {{\mathrm {B_{dR}^+}}}$
over
![]() $\underline k$
as in [Reference BoscoBos21, Appendix A.6, A.10, A.12], we get the solid tensor product formula for condensed infinitesimal cohomology as in item (ii)
$\underline k$
as in [Reference BoscoBos21, Appendix A.6, A.10, A.12], we get the solid tensor product formula for condensed infinitesimal cohomology as in item (ii)
To compute Galois cohomology, we notice the following formula at each
![]() $[n]\in \Delta ^{\mathrm {op}}$
Footnote
4
$[n]\in \Delta ^{\mathrm {op}}$
Footnote
4
 $$ \begin{align*} R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, \underline{D}_{{\inf}}(n)) & = R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}\left(\mathbb{Z}, \varprojlim_m \underline{P(n)/(I_0, \Delta(n))^mP(n)}\right), \end{align*} $$
$$ \begin{align*} R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, \underline{D}_{{\inf}}(n)) & = R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}\left(\mathbb{Z}, \varprojlim_m \underline{P(n)/(I_0, \Delta(n))^mP(n)}\right), \end{align*} $$
where
![]() $(I_0, \Delta (n))P(n)$
is the ideal of
$(I_0, \Delta (n))P(n)$
is the ideal of
![]() $P(n)$
generated by the ideal
$P(n)$
generated by the ideal
![]() $(I_0,\Delta (n))\subset P_0(n)$
. By commuting the order of limit and Galois cohomology, the above is further equal to
$(I_0,\Delta (n))\subset P_0(n)$
. By commuting the order of limit and Galois cohomology, the above is further equal to
Here we use explicitly the equality
![]() $\varprojlim _m \underline {P(n)/(I_0, \Delta (n))^mP(n)} \cong R\varprojlim _m \underline {P(n)/(I_0, \Delta (n))^mP(n)}$
, by the repleteness of
$\varprojlim _m \underline {P(n)/(I_0, \Delta (n))^mP(n)} \cong R\varprojlim _m \underline {P(n)/(I_0, \Delta (n))^mP(n)}$
, by the repleteness of
![]() $\mathrm {Sh}(\ast _{\mathrm {pro\acute {e}t}})$
([Reference Bhatt and ScholzeBS15, 3.1.10, 3.2.3, 4.2.8]) together with the surjectivity of condensed groups
$\mathrm {Sh}(\ast _{\mathrm {pro\acute {e}t}})$
([Reference Bhatt and ScholzeBS15, 3.1.10, 3.2.3, 4.2.8]) together with the surjectivity of condensed groups
![]() $\underline {P(n)/(I_0, \Delta (n))^{m+1}P(n)}\rightarrow \underline {P(n)/(I_0, \Delta (n))^mP(n)}$
([Reference BoscoBos21, Appenxid A.15]). Notice that by Lemma 8.2.2 and Proposition 8.1.9, applying
$\underline {P(n)/(I_0, \Delta (n))^{m+1}P(n)}\rightarrow \underline {P(n)/(I_0, \Delta (n))^mP(n)}$
([Reference BoscoBos21, Appenxid A.15]). Notice that by Lemma 8.2.2 and Proposition 8.1.9, applying
![]() $R {\mathrm {Hom}}_{\mathbb {Z}[\underline G_k]}(\mathbb {Z}, - )$
at the short exact sequence
$R {\mathrm {Hom}}_{\mathbb {Z}[\underline G_k]}(\mathbb {Z}, - )$
at the short exact sequence
we get
 $$\begin{align*}R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}\left(\mathbb{Z}, \underline{P(n)/(I_0, \Delta(n))^mP(n)}\right)& \cong R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, {\mathrm{B_{dR}^+}})\\& \quad\otimes_k \left( P_0(n)/(I_0, \Delta(n))^mP(n) \right). \end{align*}$$
$$\begin{align*}R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}\left(\mathbb{Z}, \underline{P(n)/(I_0, \Delta(n))^mP(n)}\right)& \cong R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, {\mathrm{B_{dR}^+}})\\& \quad\otimes_k \left( P_0(n)/(I_0, \Delta(n))^mP(n) \right). \end{align*}$$
After a further inverse limit with respect to m, and with the help of the finiteness of Galois cohomology of
![]() ${\mathrm {B_{dR}^+}}$
as in Lemma 8.2.1, we have
${\mathrm {B_{dR}^+}}$
as in Lemma 8.2.1, we have
In this way, applying the above formula at the cosimplicial diagram, we get
 $$ \begin{align*} R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}})) & \cong R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} \underline{D}_{{\inf}}(n)) \\ & \cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, \underline{D}_{{\inf}}(n)) \\ & \cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} \left( R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, {\mathrm{B_{dR}^+}})\otimes_k D_{0,{\inf}}(n) \right)\\ & \cong R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, {\mathrm{B_{dR}^+}}) \otimes_k \left( R\varprojlim_{[n]\in \Delta^{\mathrm{op}}}D_{0,{\inf}}(n) \right)\\ & \cong R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, {\mathrm{B_{dR}^+}}) \otimes_k R\Gamma_{\inf}(Y/k, \mathcal{O}_{Y/k}). \end{align*} $$
$$ \begin{align*} R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, \underline{R\Gamma}_{\inf}(Y_K/{\mathrm{B_{dR}^+}})) & \cong R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} \underline{D}_{{\inf}}(n)) \\ & \cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, \underline{D}_{{\inf}}(n)) \\ & \cong R\varprojlim_{[n]\in \Delta^{\mathrm{op}}} \left( R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, {\mathrm{B_{dR}^+}})\otimes_k D_{0,{\inf}}(n) \right)\\ & \cong R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, {\mathrm{B_{dR}^+}}) \otimes_k \left( R\varprojlim_{[n]\in \Delta^{\mathrm{op}}}D_{0,{\inf}}(n) \right)\\ & \cong R{\mathrm{Hom}}_{\mathbb{Z}[\underline G_k]}(\mathbb{Z}, {\mathrm{B_{dR}^+}}) \otimes_k R\Gamma_{\inf}(Y/k, \mathcal{O}_{Y/k}). \end{align*} $$
Here the second to the last isomorphism again follows from the finiteness of Galois cohomology of
![]() ${\mathrm {B_{dR}^+}}$
in Lemma 8.2.1.
${\mathrm {B_{dR}^+}}$
in Lemma 8.2.1.
At last, to get the result for general rigid spaces Y (which are assumed to be qcqs), we can form a homotopy limit over a finite affinoid Čech covering, and apply the equalities above. Here we use the finiteness of
![]() $R {\mathrm {Hom}}_{\mathbb {Z}[\underline G_k]}(\mathbb {Z}, {\mathrm {B_{dR}^+}})$
and the flatness of
$R {\mathrm {Hom}}_{\mathbb {Z}[\underline G_k]}(\mathbb {Z}, {\mathrm {B_{dR}^+}})$
and the flatness of
![]() $\underline {\mathrm {B_{dR}^+}}$
over
$\underline {\mathrm {B_{dR}^+}}$
over
![]() $\underline k$
again to guarantee that the homotopy limits commute with the tensor products.
$\underline k$
again to guarantee that the homotopy limits commute with the tensor products.
Here we notice that using the same method, we can improve the above into a filtered version as below.
Corollary 8.2.5. Let Y be a rigid space over k, and let
![]() $Y_K$
be its complete base extension to K.
$Y_K$
be its complete base extension to K.
-
(i) There is a natural complex of condensed abelian groups
 $\underline {{\mathrm {Fil}}}^i_{\inf }(Y/k)$
and a complex of
$\underline {{\mathrm {Fil}}}^i_{\inf }(Y/k)$
and a complex of
 $\underline G_k$
-condensed modules
$\underline G_k$
-condensed modules
 $\underline {{\mathrm {Fil}}}^i_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
underlying the i-th infinitesimal filtration
$\underline {{\mathrm {Fil}}}^i_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
underlying the i-th infinitesimal filtration
 $R\Gamma (Y/k_{\inf }, \mathcal {I}^i_{Y/k})$
and the i-th lifted filtration
$R\Gamma (Y/k_{\inf }, \mathcal {I}^i_{Y/k})$
and the i-th lifted filtration
 $\widetilde {\mathrm {Fil}}^iR\Gamma (X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {O}_{X/{\mathrm {B_{dR}^+}}})$
associated to
$\widetilde {\mathrm {Fil}}^iR\Gamma (X/{\mathrm {B_{dR}^+}}_{\mathrm {pinf}}, \mathcal {O}_{X/{\mathrm {B_{dR}^+}}})$
associated to
 $\{Y_{{\mathrm {B^+_{dR,e}}}}\}$
(c.f. Definition 4.3.9) separately;
$\{Y_{{\mathrm {B^+_{dR,e}}}}\}$
(c.f. Definition 4.3.9) separately; -
(ii) the above complexes satisfy a solid base change formula
 $$\begin{align*}\underline{{\mathrm{Fil}}}^i_{\inf}(Y/k) \otimes_k^{L{\blacksquare}} {\mathrm{B_{dR}^+}} \cong \underline{{\mathrm{Fil}}}^i_{\inf}(Y_K/{\mathrm{B_{dR}^+}}); \end{align*}$$
$$\begin{align*}\underline{{\mathrm{Fil}}}^i_{\inf}(Y/k) \otimes_k^{L{\blacksquare}} {\mathrm{B_{dR}^+}} \cong \underline{{\mathrm{Fil}}}^i_{\inf}(Y_K/{\mathrm{B_{dR}^+}}); \end{align*}$$
-
(iii) the
 $\underline G_k$
-action induces the equality
$\underline G_k$
-action induces the equality  $$\begin{align*}R\Gamma(\underline G_k, {\mathrm{B_{dR}^+}})\otimes_k R\Gamma(Y/k_{\inf}, \mathcal{I}^i_{Y/k}) \longrightarrow R\Gamma(\underline G_k, \underline{{\mathrm{Fil}}}^i_{\inf}(Y_K/{\mathrm{B_{dR}^+}})). \end{align*}$$
$$\begin{align*}R\Gamma(\underline G_k, {\mathrm{B_{dR}^+}})\otimes_k R\Gamma(Y/k_{\inf}, \mathcal{I}^i_{Y/k}) \longrightarrow R\Gamma(\underline G_k, \underline{{\mathrm{Fil}}}^i_{\inf}(Y_K/{\mathrm{B_{dR}^+}})). \end{align*}$$
The same holds if we replace
![]() ${\mathrm {B_{dR}^+}}$
by
${\mathrm {B_{dR}^+}}$
by
![]() ${\mathrm {B^+_{dR,e}}}$
.
${\mathrm {B^+_{dR,e}}}$
.
Remark 8.2.6. It is worth mentioning that 8.2.5 (ii) is not the same as the filtered tensor product formula considered in the usual sense; instead we endow
![]() ${\mathrm {B_{dR}^+}}$
here with the trivial filtration at the degree
${\mathrm {B_{dR}^+}}$
here with the trivial filtration at the degree
![]() $0$
. To get the usual filtered tensor product formula for infinitesimal cohomology, we may regard
$0$
. To get the usual filtered tensor product formula for infinitesimal cohomology, we may regard
![]() ${\mathrm {B_{dR}^+}}$
as a filtered solid algebra with
${\mathrm {B_{dR}^+}}$
as a filtered solid algebra with
![]() ${\mathrm {Fil}}^i{\mathrm {B_{dR}^+}}= \xi ^i{\mathrm {B_{dR}^+}}$
. In this way, using a similar idea of proof as in Theorem 8.2.3 (with the difference that we take the filtered completion of the filtered tensor product
${\mathrm {Fil}}^i{\mathrm {B_{dR}^+}}= \xi ^i{\mathrm {B_{dR}^+}}$
. In this way, using a similar idea of proof as in Theorem 8.2.3 (with the difference that we take the filtered completion of the filtered tensor product
![]() $\underline D_{0, {\inf }}(n)\otimes _k^{\blacksquare } {\mathrm {B_{dR}^+}}$
as
$\underline D_{0, {\inf }}(n)\otimes _k^{\blacksquare } {\mathrm {B_{dR}^+}}$
as
![]() $\underline D_{\inf }(n)$
), one can also prove the following tensor product formula in the filtered derived category
$\underline D_{\inf }(n)$
), one can also prove the following tensor product formula in the filtered derived category
![]() ${\mathscr {DF}}(k)$
:
${\mathscr {DF}}(k)$
:
where the right hand side is equipped with the usual infinitesimal filtration for
![]() $Y_K/{\mathrm {B_{dR}^+}}_{\inf }$
(instead of the lifted filtration), and
$Y_K/{\mathrm {B_{dR}^+}}_{\inf }$
(instead of the lifted filtration), and
![]() $(-)^\wedge $
is the filtered completion.
$(-)^\wedge $
is the filtered completion.
Notice that the proof of Theorem 8.2.3 above also implies the following formula of Galois invariant.
Corollary 8.2.7. Let Y be a rigid space over k, and let
![]() $Y_K$
be its complete base extension to K. Then we have an isomorphism of k-vector spaces
$Y_K$
be its complete base extension to K. Then we have an isomorphism of k-vector spaces
Proof. Thanks to Lemma 8.2.1 and Lemma 8.2, we have
and vanishes for other i. Thus the statement follows by inductively applying the equality at the cosimplicial diagram
![]() $\underline D_{\inf }(n)$
and Mayer-Vietoris sequences for Čech covering by affinoid open subsets.
$\underline D_{\inf }(n)$
and Mayer-Vietoris sequences for Čech covering by affinoid open subsets.
Remark 8.2.8. When Y is affinoid, by choosing a closed immersion into a polydisc
![]() $k\langle T_i\rangle $
, one can compute its infinitesimal cohomology using the completed de Rham complex of
$k\langle T_i\rangle $
, one can compute its infinitesimal cohomology using the completed de Rham complex of
![]() $k\langle T_i\rangle ^\wedge _{I_0}$
over k, where
$k\langle T_i\rangle ^\wedge _{I_0}$
over k, where
![]() $I_0$
is the defining ideal of Y. In the special case when Y is smooth, we can even use the continuous de Rham complex of
$I_0$
is the defining ideal of Y. In the special case when Y is smooth, we can even use the continuous de Rham complex of
![]() $Y/k$
. Pointed out as in [Reference BoscoBos21, Remark 5.14, 5.22], the underlying topological structures of the condensed infinitesimal cohomology and the usual infinitesimal cohomology are not the same. Thus the underlying topological group of condensed Galois invariant in Theorem 8.2.3 is different from the usual continuous Galois invariant of infinitesimal cohomology. However, one may still use criteria in [Reference Bhatt and ScholzeBS15, Lemma 4.3.9] to check that the underlying group structures, forgetting their topology, would coincide.
$Y/k$
. Pointed out as in [Reference BoscoBos21, Remark 5.14, 5.22], the underlying topological structures of the condensed infinitesimal cohomology and the usual infinitesimal cohomology are not the same. Thus the underlying topological group of condensed Galois invariant in Theorem 8.2.3 is different from the usual continuous Galois invariant of infinitesimal cohomology. However, one may still use criteria in [Reference Bhatt and ScholzeBS15, Lemma 4.3.9] to check that the underlying group structures, forgetting their topology, would coincide.
We are now ready to compute Galois invariant of prismatic cohomology.
Theorem 8.2.9. Let Y be a rigid space over k that has l.c.i. singularities, and let
![]() $Y_K$
be its complete field extension to K.
$Y_K$
be its complete field extension to K.
-
(i) There is a natural complex of condensed groups
 underlying prismatic cohomology
underlying prismatic cohomology  ;
; -
(ii) Galois invariant of prismatic cohomology is equal to infinitesimal cohomology of
 $Y/k_{\inf }$
, namely
$Y/k_{\inf }$
, namely 
Proof. Similar to Theorem 4.3.12, we apply Simpson’s functor at the condensed complex
![]() $\underline {R\Gamma }_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
and its lifted filtration (associated to the canonical lifts
$\underline {R\Gamma }_{\inf }(Y_K/{\mathrm {B_{dR}^+}})$
and its lifted filtration (associated to the canonical lifts
![]() $\{Y_{\mathrm {B^+_{dR,e}}}\}$
). Namely, we consider the condensed complex below
$\{Y_{\mathrm {B^+_{dR,e}}}\}$
). Namely, we consider the condensed complex below

where
![]() $(-)^\wedge $
is the condensed version of derived
$(-)^\wedge $
is the condensed version of derived
![]() $\xi $
-adic completion, i.e. the functor
$\xi $
-adic completion, i.e. the functor
![]() $R\varprojlim _e (-\otimes _{\mathrm {B_{dR}^+}}^{L{\blacksquare } }{\mathrm {B^+_{dR,e}}})$
. Then to see
$R\varprojlim _e (-\otimes _{\mathrm {B_{dR}^+}}^{L{\blacksquare } }{\mathrm {B^+_{dR,e}}})$
. Then to see ![]() underlies the usual prismatic cohomology, we apply
underlies the usual prismatic cohomology, we apply
![]() $R\Gamma (\ast , -)$
at
$R\Gamma (\ast , -)$
at ![]() , and use a global version of Theorem 4.3.12 and Corollary 8.2.5. Here we notice that thanks to the compactness of the final object
, and use a global version of Theorem 4.3.12 and Corollary 8.2.5. Here we notice that thanks to the compactness of the final object
![]() $\ast $
, the functor
$\ast $
, the functor
![]() $R\Gamma (\ast , -)$
commutes with the colimit in the formula above.
$R\Gamma (\ast , -)$
commutes with the colimit in the formula above.
For (ii), we first consider Galois cohomology of the complex
 $$\begin{align*}C_e:=\left( \underset{n\in \mathbb{N}}{{\mathrm{colim}}} ~ \xi^{-n}\cdot\underline{{\mathrm{Fil}}}^n_{\inf}(Y_K/{\mathrm{B_{dR}^+}}) \right) \otimes_{\mathrm{B_{dR}^+}}^{\blacksquare} {\mathrm{B^+_{dR,e}}}. \end{align*}$$
$$\begin{align*}C_e:=\left( \underset{n\in \mathbb{N}}{{\mathrm{colim}}} ~ \xi^{-n}\cdot\underline{{\mathrm{Fil}}}^n_{\inf}(Y_K/{\mathrm{B_{dR}^+}}) \right) \otimes_{\mathrm{B_{dR}^+}}^{\blacksquare} {\mathrm{B^+_{dR,e}}}. \end{align*}$$
By Corollary 8.2.5, applying
![]() $R {\mathrm {Hom}}_{\mathbb {Z}[\underline G_k]}(\mathbb {Z}, -)$
at this colimit diagram, we get the following derived tensor product
$R {\mathrm {Hom}}_{\mathbb {Z}[\underline G_k]}(\mathbb {Z}, -)$
at this colimit diagram, we get the following derived tensor product
![]() $R\Gamma (\underline G_k, {\mathrm {B_{dR}^+}})\otimes _k C'$
, where
$R\Gamma (\underline G_k, {\mathrm {B_{dR}^+}})\otimes _k C'$
, where
![]() $C'$
is the following colimit
$C'$
is the following colimit

Notice that from the diagram it is clear that
![]() $C'\cong R\Gamma (Y/k_{\inf }, \mathcal {O}_{Y/k})$
, so we have
$C'\cong R\Gamma (Y/k_{\inf }, \mathcal {O}_{Y/k})$
, so we have
At last, by construction the condensed complex ![]() is equal to
is equal to
![]() $R\varprojlim _e C_e$
. Thus by switching the order of right derived functors, we get Galois invariant of condensed prismatic cohomology as below
$R\varprojlim _e C_e$
. Thus by switching the order of right derived functors, we get Galois invariant of condensed prismatic cohomology as below

Corollary 8.2.10. Let Y be a proper rigid space over k that has l.c.i. singularities. Then Galois invariant of condensed prismatic cohomology ![]() is finite dimensional over k.
is finite dimensional over k.
Proof. This follows from Corollary 8.2.7, the finiteness of
![]() $R\Gamma (\underline G_k, {\mathrm {B_{dR}^+}})$
in Lemma 8.2.1, and finiteness of infinitesimal cohomology
$R\Gamma (\underline G_k, {\mathrm {B_{dR}^+}})$
in Lemma 8.2.1, and finiteness of infinitesimal cohomology
![]() $R\Gamma (Y/k_{\inf }, \mathcal {O}_{Y/k})$
for proper rigid space as in [Reference GuoGuo24].
$R\Gamma (Y/k_{\inf }, \mathcal {O}_{Y/k})$
for proper rigid space as in [Reference GuoGuo24].
Acknowledgements
The project was initiated during a conversation with Arthur-César Le Bras. I thank Le Bras heartily for encouraging me to work on this topic at the very beginning. It is obvious that the article is heavily influenced by the foundational work of Bhatt–Scholze [Reference Bhatt and ScholzeBS22]. I am grateful for various helpful discussions with Bhargav Bhatt on construction of prismatic sites. Many thanks go to Sebastian Bartling and Shizhang Li for communications in the early stage of the work, and to Peter Scholze for explaining condensed group cohomology. I also thank Dmitry Kubrak and Emanuel Reinecke for asking questions in an informal seminar, which motivates me to consider the left Kan extension for rigid spaces; and thank Guido Bosco for useful comments on the draft. Finally, I am thankful to the anonymous referee for reading carefully my article and for offering valuable insights on potential improvements.
During the writing process I was funded by National Science Foundation FRG grant no. DMS-1952399 and by Max Planck Institute for Mathematics. During the revision, I was supported by the University of Chicago.
Competing interests
The author declares none.
Data availability statement
Not applicable.