1 Introduction
A pseudofinite structure is an
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
such that every
$\mathcal {M}$
such that every
![]() $\mathcal {L}$
-sentence that holds in
$\mathcal {L}$
-sentence that holds in
![]() $\mathcal {M}$
has finite models, or equivalently, an
$\mathcal {M}$
has finite models, or equivalently, an
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {M}$
that is elementarily equivalent to an ultraproduct of finite
$\mathcal {M}$
that is elementarily equivalent to an ultraproduct of finite
![]() $\mathcal {L}$
-structures. Some notable algebraic examples include the vector spaces over the finite field
$\mathcal {L}$
-structures. Some notable algebraic examples include the vector spaces over the finite field
![]() $\mathbb {F}_p$
, the group
$\mathbb {F}_p$
, the group
![]() $(\mathbb {R},+)$
(which is isomorphic to any non-principal ultraproduct of groups in the class
$(\mathbb {R},+)$
(which is isomorphic to any non-principal ultraproduct of groups in the class
![]() $\mathcal {C}=\{(\mathbb {Z}/p\mathbb {Z},+):p\ \text {prime}\}$
), or the pseudofinite fields characterized by Ax as those infinite fields that are perfect, quasifinite (have a unique algebraic extension of degree n for every
$\mathcal {C}=\{(\mathbb {Z}/p\mathbb {Z},+):p\ \text {prime}\}$
), or the pseudofinite fields characterized by Ax as those infinite fields that are perfect, quasifinite (have a unique algebraic extension of degree n for every
![]() $n\geq 1$
), and pseudo-algebraically closed (see [Reference Ax3]).
$n\geq 1$
), and pseudo-algebraically closed (see [Reference Ax3]).
For combinatorial structures, some notable examples of pseudofinite structures are the random graph (see [Reference Marker15, Section 2.4]), any discrete linear order with end points, and the generic limit
![]() $\mathcal {M}_\alpha $
of the class of graphs
$\mathcal {M}_\alpha $
of the class of graphs
![]() $\mathcal {C}_\alpha $
of finite graphs G such that
$\mathcal {C}_\alpha $
of finite graphs G such that
![]() $\delta _\alpha (A)=|V(A)|-\alpha |E(A)|\geq 0$
for every finite subset A of G. In this setting, perhaps the most important open questions include whether the generic triangle-free graph or the Urysohn sphere are pseudofinite [Reference Cherlin4].
$\delta _\alpha (A)=|V(A)|-\alpha |E(A)|\geq 0$
for every finite subset A of G. In this setting, perhaps the most important open questions include whether the generic triangle-free graph or the Urysohn sphere are pseudofinite [Reference Cherlin4].
One of the main features that appear when working with ultraproducts of finite structures is the analysis of non-standard cardinalities of definable sets. If
![]() $\mathcal {M}$
is an infinite ultraproduct of finite structures in a class
$\mathcal {M}$
is an infinite ultraproduct of finite structures in a class
![]() $\mathcal {C}=\{M_n:n\in \mathbb {N}\}$
with respect to an ultrafilter
$\mathcal {C}=\{M_n:n\in \mathbb {N}\}$
with respect to an ultrafilter
![]() $\mathcal {U}$
, then for every definable set
$\mathcal {U}$
, then for every definable set
![]() $X=[X_n]_{\mathcal {U}}$
there is a non-standard real number
$X=[X_n]_{\mathcal {U}}$
there is a non-standard real number
![]() $\alpha =|X|\in \mathbb {R}^{\mathcal {U}}$
that acts as the non-standard cardinality of X and satisfies the same combinatorial properties that hold for
$\alpha =|X|\in \mathbb {R}^{\mathcal {U}}$
that acts as the non-standard cardinality of X and satisfies the same combinatorial properties that hold for
![]() $\mathcal {U}$
-almost all finite cardinalities
$\mathcal {U}$
-almost all finite cardinalities
![]() $\alpha _n:=|X_n|$
. This allows the use of combinatorial methods in the analysis of properties in the ultraproduct
$\alpha _n:=|X_n|$
. This allows the use of combinatorial methods in the analysis of properties in the ultraproduct
![]() $\mathcal {M}$
, essentially because the counting measure in the class
$\mathcal {M}$
, essentially because the counting measure in the class
![]() $\mathcal {C}$
of finite structures can be lifted using Łoś’ theorem to provide notions of dimension and measure on the ultraproduct
$\mathcal {C}$
of finite structures can be lifted using Łoś’ theorem to provide notions of dimension and measure on the ultraproduct
![]() $\mathcal {M}$
. This provides access to ideas from measure theory and geometric model theory in the context of pseudofinite structures, and can be used to prove results in finite combinatorics (of graphs, groups, fields, etc.) by studying the corresponding properties in the ultraproducts. For some examples of these phenomena, see [Reference Goldbring and Towsner10, Reference Hrushovski12, Reference Di Nasso, Goldbring and Lupini6, Reference Tao17].
$\mathcal {M}$
. This provides access to ideas from measure theory and geometric model theory in the context of pseudofinite structures, and can be used to prove results in finite combinatorics (of graphs, groups, fields, etc.) by studying the corresponding properties in the ultraproducts. For some examples of these phenomena, see [Reference Goldbring and Towsner10, Reference Hrushovski12, Reference Di Nasso, Goldbring and Lupini6, Reference Tao17].
In the general case, very little can be said about the possible non-standard cardinalities of definable sets, even for a fixed class of finite structures. However, under certain tameness conditions on the ultraproducts, or in the case of ultraproducts of asymptotic classes, it is possible to give a precise description of the possible sizes of definable sets.
In this direction, a remarkable result of A. Pillay [Reference Pillay16] states that, if
![]() $\mathcal {M}$
is an ultraproduct of finite
$\mathcal {M}$
is an ultraproduct of finite
![]() $\mathcal {L}$
-structures that is strongly minimal, then for every
$\mathcal {L}$
-structures that is strongly minimal, then for every
![]() $\mathcal {L}$
-definable set X there is a polynomial
$\mathcal {L}$
-definable set X there is a polynomial
![]() $p_X(t)$
with integer coefficients such that
$p_X(t)$
with integer coefficients such that
![]() $|X|=p_X(\alpha )$
, where
$|X|=p_X(\alpha )$
, where
![]() $\alpha =|M|$
is the non-standard cardinality of the whole structure. Moreover, Pillay showed that for every
$\alpha =|M|$
is the non-standard cardinality of the whole structure. Moreover, Pillay showed that for every
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\varphi (\overline {x},\overline {y})$
there are finitely many polynomials
$\varphi (\overline {x},\overline {y})$
there are finitely many polynomials
![]() $p_1(t),\ldots ,p_k(t)\in \mathbb {Z}[t]$
and
$p_1(t),\ldots ,p_k(t)\in \mathbb {Z}[t]$
and
![]() $\mathcal {L}$
-formulas
$\mathcal {L}$
-formulas
![]() $\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
forming a partition of
$\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
forming a partition of
![]() $M^{|\overline {y}|}$
such that for every
$M^{|\overline {y}|}$
such that for every
![]() $\overline {a}$
,
$\overline {a}$
,
![]() $\mathcal {M}\models \psi _i(\overline {a})$
if and only if the
$\mathcal {M}\models \psi _i(\overline {a})$
if and only if the
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\varphi (\overline {x},\overline {a})$
defines a set with non-standard cardinality
$\varphi (\overline {x},\overline {a})$
defines a set with non-standard cardinality
![]() $p_i(\alpha )$
. In other words, for a strongly minimal ultraproduct of finite structures
$p_i(\alpha )$
. In other words, for a strongly minimal ultraproduct of finite structures
![]() $\mathcal {M}$
, the non-standard cardinalities of definable sets are definable within its theory
$\mathcal {M}$
, the non-standard cardinalities of definable sets are definable within its theory
![]() $\operatorname {Th}_{\mathcal {L}}(\mathcal {M})$
.
$\operatorname {Th}_{\mathcal {L}}(\mathcal {M})$
.
The concept of asymptotic classes was defined in [Reference Macpherson and Steinhorn14] by Macpherson and Steinhorn. These are classes of finite structures that satisfy strong conditions on the possible cardinalities of definable sets. The most notable examples are the class of finite fields, the class of cyclic groups, or the class of Paley graphs. The infinite ultraproducts of asymptotic classes are all supersimple of finite SU-rank, but recent generalizations of this concept (known as multidimensional asymptotic classes, or m.a.c.) are more flexible and allow the presence of ultraproducts whose SU-rank is possibly infinite.
This article deals with the pseudofiniteness and measurability of certain acyclic graphs (trees). Note first that not every countable acyclic graphs is pseudofinite. For instance, consider the 3-branching tree ![]() given by the following picture:
given by the following picture:

We have that ![]() satisfies the sentence
satisfies the sentence
If there were a finite graph G with n vertices such that
![]() $G\models \sigma $
, then by the handshaking lemma we would have
$G\models \sigma $
, then by the handshaking lemma we would have
which is a contradiction because the right-hand side of the equality is an odd number.
Two of the most important examples of acyclic graphs studied in model theory are the r-regular infinite tree
![]() $\Gamma _r$
in which each vertex has degree r and the infinite branching tree
$\Gamma _r$
in which each vertex has degree r and the infinite branching tree
![]() $\Gamma _\infty $
, in which every vertex has infinite degree. The theory
$\Gamma _\infty $
, in which every vertex has infinite degree. The theory
![]() $\mathcal {T}_r:=\operatorname {Th}(\Gamma _r)$
is a well-known example of a strongly minimal theory with a trivial pregeometry, while
$\mathcal {T}_r:=\operatorname {Th}(\Gamma _r)$
is a well-known example of a strongly minimal theory with a trivial pregeometry, while
![]() $\mathcal {T}_\infty :=\operatorname {Th}(\Gamma _\infty )$
is an
$\mathcal {T}_\infty :=\operatorname {Th}(\Gamma _\infty )$
is an
![]() $\omega $
-stable theory of Morley rank
$\omega $
-stable theory of Morley rank
![]() $\omega $
that is CM-trivial.
$\omega $
that is CM-trivial.
The main purpose of this aticle is to show that both theories
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
are pseudofinite, and to analyze the possible non-standard cardinalities of their definable sets. In Section 3 we show that the theory
$\mathcal {T}_\infty $
are pseudofinite, and to analyze the possible non-standard cardinalities of their definable sets. In Section 3 we show that the theory
![]() $\mathcal {T}_r$
corresponds to the theory of infinite ultraproducts of some classes of finite r-regular graphs
$\mathcal {T}_r$
corresponds to the theory of infinite ultraproducts of some classes of finite r-regular graphs
![]() $\mathcal {C}_{r,g}=\{G_n:n<\omega \}$
where g is a function defined as
$\mathcal {C}_{r,g}=\{G_n:n<\omega \}$
where g is a function defined as
![]() $g(n)=\operatorname {girth}(G_n)$
—the length of the minimal cycle in
$g(n)=\operatorname {girth}(G_n)$
—the length of the minimal cycle in
![]() $G_n$
—, and it tends to infinity. In contrast,
$G_n$
—, and it tends to infinity. In contrast,
![]() $\mathcal {T}_\infty $
corresponds to the theory of infinite ultraproducts of classes of regular graphs
$\mathcal {T}_\infty $
corresponds to the theory of infinite ultraproducts of classes of regular graphs
![]() $\mathcal {C}_{d,g}=\{H_n:n<\omega \}$
where g is as above, and d is a function such that
$\mathcal {C}_{d,g}=\{H_n:n<\omega \}$
where g is as above, and d is a function such that
![]() $d(n)$
is the degree of regularity of
$d(n)$
is the degree of regularity of
![]() $H_n$
, and it tends to infinity as well. We also provide an analysis of the possible cardinalities of formulas in one-variable defined in uniform models of
$H_n$
, and it tends to infinity as well. We also provide an analysis of the possible cardinalities of formulas in one-variable defined in uniform models of
![]() $\mathcal {T}_\infty $
. Namely, for every definable set
$\mathcal {T}_\infty $
. Namely, for every definable set
![]() $X\subseteq \mathcal {M}^1$
there is a polynomial
$X\subseteq \mathcal {M}^1$
there is a polynomial
![]() $p_X(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
such that
$p_X(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
such that
![]() $|X|=p_X(\alpha ,\beta )$
, where
$|X|=p_X(\alpha ,\beta )$
, where
![]() $\alpha =|\mathcal {M}|$
and
$\alpha =|\mathcal {M}|$
and
![]() $\beta =[d(n)]_{\mathcal {U}}$
, which corresponds to the non-standard size of some (every) ball of radius 1 in
$\beta =[d(n)]_{\mathcal {U}}$
, which corresponds to the non-standard size of some (every) ball of radius 1 in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
In Section 4 we recall the main definitions and properties of multidimensional asymptotic classes from [Reference Anscombe, Macpherson, Steinhorn and Wolf2]. We also show that the classes
![]() $\mathcal {C}_{r,g}$
are 1-dimensional asymptotic classes, while the classes
$\mathcal {C}_{r,g}$
are 1-dimensional asymptotic classes, while the classes
![]() $\mathcal {C}_{d,g}$
are polynomial exact classes, even though they are not N-asymptotic classes for any
$\mathcal {C}_{d,g}$
are polynomial exact classes, even though they are not N-asymptotic classes for any
![]() $N\in \mathbb {N}$
. This result allows us to extend the characterization of cardinalities for formulas in several variables, and it is the key ingredient used in Section 5 to show that the Morley rank of a definable set X can be computed in terms of the degrees of the polynomial
$N\in \mathbb {N}$
. This result allows us to extend the characterization of cardinalities for formulas in several variables, and it is the key ingredient used in Section 5 to show that the Morley rank of a definable set X can be computed in terms of the degrees of the polynomial
![]() $p_X(t_1,t_2)$
. Furthermore, these results solve partially Problem 7.0.1 and answer negatively Question 7.0.9 of [Reference Anscombe, Macpherson, Steinhorn and Wolf2], as the classes of finite graphs
$p_X(t_1,t_2)$
. Furthermore, these results solve partially Problem 7.0.1 and answer negatively Question 7.0.9 of [Reference Anscombe, Macpherson, Steinhorn and Wolf2], as the classes of finite graphs
![]() $\mathcal {C}_{d,g}$
provide examples of multidimensional exact classes whose ultraproducts are models of
$\mathcal {C}_{d,g}$
provide examples of multidimensional exact classes whose ultraproducts are models of
![]() $\mathcal {T}_\infty $
, and so they are stable and CM-trivial, but not one-based.
$\mathcal {T}_\infty $
, and so they are stable and CM-trivial, but not one-based.
2 Basic notation and results on acyclic graphs
We start by stating some basic notation and results from graph theory that will be used throughout this article.
Definition 2.1.
-
(1) A (simple) graph is a set G with a binary relation R that is irreflexive and symmetric.
-
(2) A graph G is called acyclic if there are no distinct vertices
 $a_1,\ldots ,a_k$
(with
$a_1,\ldots ,a_k$
(with
 $k\geq 3$
) such that
$k\geq 3$
) such that
 $G\models a_1 R a_2 \wedge \cdots \wedge a_{k-1}R a_k\wedge a_k Ra_1$
.
$G\models a_1 R a_2 \wedge \cdots \wedge a_{k-1}R a_k\wedge a_k Ra_1$
. -
(3) Given two vertices
 $a,b$
in a graph G, a path from a and b is a finite sequence of distinct vertices
$a,b$
in a graph G, a path from a and b is a finite sequence of distinct vertices
 $c_0,\ldots ,c_k$
such that
$c_0,\ldots ,c_k$
such that
 $a=c_0, b=c_k$
, and
$a=c_0, b=c_k$
, and
 $G\models c_iRc_{i+1}$
for
$G\models c_iRc_{i+1}$
for
 $i=0,\ldots ,k-1$
. In this case, we say that
$i=0,\ldots ,k-1$
. In this case, we say that
 $a=c_0,c_1,\ldots ,c_k=b$
is a path of length k from a to b.
$a=c_0,c_1,\ldots ,c_k=b$
is a path of length k from a to b. -
(4) Given two elements
 $a,b\in G$
, we say that the distance between a and b is k (and write
$a,b\in G$
, we say that the distance between a and b is k (and write
 $\operatorname {dist}(a,b)=k$
) if k is the minimal integer such that there is a path from a to b of length k. If no such path exists, we write
$\operatorname {dist}(a,b)=k$
) if k is the minimal integer such that there is a path from a to b of length k. If no such path exists, we write
 $\operatorname {dist}(a,b)=\infty $
.
$\operatorname {dist}(a,b)=\infty $
. -
(5) If
 $A\subseteq G$
and b is a vertex of G, we define
$A\subseteq G$
and b is a vertex of G, we define  $$\begin{align*}\operatorname{dist}(b,A):=\min\{\operatorname{dist}(b,a):a\in A\}.\end{align*}$$
$$\begin{align*}\operatorname{dist}(b,A):=\min\{\operatorname{dist}(b,a):a\in A\}.\end{align*}$$
Remark 2.2. In this article we will deal only with acyclic graphs. Hence, we will use repeatedly the fact that paths are unique: given
![]() $a,b\in G$
such that
$a,b\in G$
such that
![]() $\operatorname {dist}(a,b)=k<\infty $
, there is a unique sequence of vertices
$\operatorname {dist}(a,b)=k<\infty $
, there is a unique sequence of vertices
![]() $c_0=a,c_1,\ldots ,c_k=b$
that forms a path from a to b. In this case, we will denote by
$c_0=a,c_1,\ldots ,c_k=b$
that forms a path from a to b. In this case, we will denote by
![]() $P(a,b)$
the set
$P(a,b)$
the set
![]() $\{c_0=a,c_1,\ldots ,c_k=b\}$
. Note that in this case we have that
$\{c_0=a,c_1,\ldots ,c_k=b\}$
. Note that in this case we have that
![]() $\operatorname {dist}(a,b)=|P(a,b)|-1$
.
$\operatorname {dist}(a,b)=|P(a,b)|-1$
.
Definition 2.3. Let G be an acyclic graph and
![]() $A\subseteq G$
.
$A\subseteq G$
.
-
(1) We define the connected closure of A as the set of all elements at finite distance from A,
 $$\begin{align*}\operatorname{conn}(A)=\{b\in G: \operatorname{dist}(b,A)=k \text{ for some}\ k<\omega\}.\end{align*}$$
$$\begin{align*}\operatorname{conn}(A)=\{b\in G: \operatorname{dist}(b,A)=k \text{ for some}\ k<\omega\}.\end{align*}$$
-
(2) The convex closure of A is defined as the collection of all vertices that lie in the paths between elements of A. Namely,
 $$\begin{align*}\operatorname{conv}(A)=A\cup \bigcup\{P(a,a'): a,a'\in A \text{ and }\operatorname{dist}(a,a')<\infty\}.\end{align*}$$
$$\begin{align*}\operatorname{conv}(A)=A\cup \bigcup\{P(a,a'): a,a'\in A \text{ and }\operatorname{dist}(a,a')<\infty\}.\end{align*}$$
-
(3) If A is finite and c is an element in
 $\operatorname {conv}(A)$
, we define the degree of c in A as the number of neighbors of c in G that belong to
$\operatorname {conv}(A)$
, we define the degree of c in A as the number of neighbors of c in G that belong to
 $\operatorname {conv}(A)$
, namely
$\operatorname {conv}(A)$
, namely  $$\begin{align*}\operatorname{deg}_A(c)=|\{b\in\operatorname{conv}(A):b\ \text{is adjacent to}\ c\}|.\end{align*}$$
$$\begin{align*}\operatorname{deg}_A(c)=|\{b\in\operatorname{conv}(A):b\ \text{is adjacent to}\ c\}|.\end{align*}$$
The following is a stronger version of Remark 2.2.
Proposition 2.4. Let G be an acyclic graph and let A be a subset of G such that
![]() $\operatorname {conv}(A)=A$
. Then, for every vertex
$\operatorname {conv}(A)=A$
. Then, for every vertex
![]() $b\in G$
such that
$b\in G$
such that
![]() $\operatorname {dist}(b,A)<\infty $
there is a unique
$\operatorname {dist}(b,A)<\infty $
there is a unique
![]() $c\in A$
such that
$c\in A$
such that
![]() $\operatorname {dist}(b,A)=\operatorname {dist}(b,c)$
.
$\operatorname {dist}(b,A)=\operatorname {dist}(b,c)$
.
Proof. First notice that, since
![]() $\operatorname {dist}(b,A)=\min \{\operatorname {dist}(b,a):a\in A\}$
, there must be an element
$\operatorname {dist}(b,A)=\min \{\operatorname {dist}(b,a):a\in A\}$
, there must be an element
![]() $c\in A$
such that
$c\in A$
such that
![]() $\operatorname {dist}(b,A)=\operatorname {dist}(b,c)$
. If there are two elements
$\operatorname {dist}(b,A)=\operatorname {dist}(b,c)$
. If there are two elements
![]() $c_1$
and
$c_1$
and
![]() $c_2$
in A such that
$c_2$
in A such that
![]() $\operatorname {dist}(b,c_1)=\operatorname {dist}(b,c_2)=\operatorname {dist}(b,A)<\infty $
, then we would have
$\operatorname {dist}(b,c_1)=\operatorname {dist}(b,c_2)=\operatorname {dist}(b,A)<\infty $
, then we would have
![]() $b\in P(c_1,c_2)$
. Hence, since
$b\in P(c_1,c_2)$
. Hence, since
![]() $A=\operatorname {conv}(A)$
, we have
$A=\operatorname {conv}(A)$
, we have
![]() $b\in A$
. Therefore,
$b\in A$
. Therefore,
![]() $\operatorname {dist}(b,A)=0$
, and so
$\operatorname {dist}(b,A)=0$
, and so
![]() $c_1=c_2=b$
.
$c_1=c_2=b$
.
Definition 2.5. When dealing with acyclic graphs, it would be useful to use the first-order language
![]() $\mathcal {L}'=\{D_k(x,y):k<\omega \}$
where each
$\mathcal {L}'=\{D_k(x,y):k<\omega \}$
where each
![]() $D_k$
is a binary relation interpreted in an acyclic graph
$D_k$
is a binary relation interpreted in an acyclic graph
![]() $(G,R)$
as follows:
$(G,R)$
as follows:
 $$ \begin{align*} G\models D_k(a,b)&\Leftrightarrow \operatorname{dist}_G(a,b)=k\\ &\Leftrightarrow \exists z_0,\ldots,z_k\left(a=z_0 \wedge b=z_k \wedge \bigwedge_{0\leq i<j\leq k}z_i\neq z_j \wedge \bigwedge_{i=0}^{k-1} z_iRz_{i+1}\right). \end{align*} $$
$$ \begin{align*} G\models D_k(a,b)&\Leftrightarrow \operatorname{dist}_G(a,b)=k\\ &\Leftrightarrow \exists z_0,\ldots,z_k\left(a=z_0 \wedge b=z_k \wedge \bigwedge_{0\leq i<j\leq k}z_i\neq z_j \wedge \bigwedge_{i=0}^{k-1} z_iRz_{i+1}\right). \end{align*} $$
In Appendix A we show that the theories
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
have quantifier elimination in the language
$\mathcal {T}_\infty $
have quantifier elimination in the language
![]() $\mathcal {L}'$
, but for the moment let us show a couple of results that provide a characterization of certain
$\mathcal {L}'$
, but for the moment let us show a couple of results that provide a characterization of certain
![]() $\mathcal {L}'$
-definable sets that works for arbitrary acyclic graphs.
$\mathcal {L}'$
-definable sets that works for arbitrary acyclic graphs.
Lemma 2.6. Let G be an acyclic graph and let
![]() $a_1$
and
$a_1$
and
![]() $a_2$
be vertices in G such that
$a_2$
be vertices in G such that
![]() $\operatorname {dist}(a_1,a_2)=d$
.
$\operatorname {dist}(a_1,a_2)=d$
.
-
(1) If there is an element
 $b\in G$
such that
$b\in G$
such that
 $G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
, then
$G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
, then
 $d\leq k_1+k_2$
and
$d\leq k_1+k_2$
and
 $\operatorname {dist}(b,P(a_1,a_2)) =\frac {1}{2}(k_1+k_2-d)$
.
$\operatorname {dist}(b,P(a_1,a_2)) =\frac {1}{2}(k_1+k_2-d)$
. -
(2) Conversely, whenever
 $k_1$
and
$k_1$
and
 $k_2$
are non-negative integers such that
$k_2$
are non-negative integers such that
 $k_1\leq k_2+d$
and
$k_1\leq k_2+d$
and
 $\ell =\frac {1}{2}(k_1+k_2-d)$
is a non-negative integer, there exists a unique
$\ell =\frac {1}{2}(k_1+k_2-d)$
is a non-negative integer, there exists a unique
 $c\in P(a_1,a_2)$
such that for every
$c\in P(a_1,a_2)$
such that for every
 $b\in G$
,
$b\in G$
,
 $G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
if and only if
$G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
if and only if
 $\operatorname {dist}(b,c)=\ell $
and
$\operatorname {dist}(b,c)=\ell $
and
 $P(b,c)\cap P(a_1,a_2)=\{c\}.$
$P(b,c)\cap P(a_1,a_2)=\{c\}.$
Proof. For part (1), let c be the unique element in
![]() $P(a_1,a_2)$
such that
$P(a_1,a_2)$
such that
![]() $\operatorname {dist}(b,c)=\operatorname {dist}(b,P(a_1,a_2))$
. By the triangle inequality,
$\operatorname {dist}(b,c)=\operatorname {dist}(b,P(a_1,a_2))$
. By the triangle inequality,
![]() $d=\operatorname {dist}(a_1,a_2)\leq \operatorname {dist}(b,a_1)+\operatorname {dist}(b,a_2)=k_1+k_2$
. Also, by uniqueness of paths in G we have
$d=\operatorname {dist}(a_1,a_2)\leq \operatorname {dist}(b,a_1)+\operatorname {dist}(b,a_2)=k_1+k_2$
. Also, by uniqueness of paths in G we have
![]() $P(b,a_1)=P(b,c)\cup P(c,a_1)$
and
$P(b,a_1)=P(b,c)\cup P(c,a_1)$
and
![]() $P(b,a_2)=P(b,c)\cup P(c,a_2)$
, so
$P(b,a_2)=P(b,c)\cup P(c,a_2)$
, so
![]() $\operatorname {dist}(b,a_1)+\operatorname {dist}(b,a_2)=2\operatorname {dist}(b,c)+d$
, from which it follows that the distance from b to the path
$\operatorname {dist}(b,a_1)+\operatorname {dist}(b,a_2)=2\operatorname {dist}(b,c)+d$
, from which it follows that the distance from b to the path
![]() $P(a_1,a_2)$
satisfies
$P(a_1,a_2)$
satisfies
![]() $\operatorname {dist}(b,P(a_1,a_2))=\frac {1}{2}(k_1+k_2-d)$
.
$\operatorname {dist}(b,P(a_1,a_2))=\frac {1}{2}(k_1+k_2-d)$
.
We now proceed to prove part (2). Since
![]() $k_1\leq k_2+d$
, we have that
$k_1\leq k_2+d$
, we have that
![]() $k_1-\ell \leq d.$
Hence, there is a unique element c in
$k_1-\ell \leq d.$
Hence, there is a unique element c in
![]() $P(a_1,a_2)$
which is at distance
$P(a_1,a_2)$
which is at distance
![]() $k_1-\ell $
from
$k_1-\ell $
from
![]() $a_1$
. Note that the distance from c to
$a_1$
. Note that the distance from c to
![]() $a_2$
is equal to
$a_2$
is equal to
Let b be an arbitrary vertex in G. If
![]() $\operatorname {dist}(b,c)=\ell $
and
$\operatorname {dist}(b,c)=\ell $
and
![]() $P(b,c)\cap P(a_1,a_2)=\{c\}$
, then we have
$P(b,c)\cap P(a_1,a_2)=\{c\}$
, then we have
![]() $P(b,a_1)=P(b,c)\cup P(c,a_1)$
and
$P(b,a_1)=P(b,c)\cup P(c,a_1)$
and
![]() $P(b,a_2)=P(b,c)\cup P(c,a_2)$
, which implies that
$P(b,a_2)=P(b,c)\cup P(c,a_2)$
, which implies that
![]() $\operatorname {dist}(b,a_1)=k_1.$
Similarly, we have
$\operatorname {dist}(b,a_1)=k_1.$
Similarly, we have
![]() $\operatorname {dist}(b,a_2)=k_2$
, so
$\operatorname {dist}(b,a_2)=k_2$
, so
![]() $G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
.
$G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
.
Now, suppose that
![]() $\operatorname {dist}(b,a_1)=k_1$
and
$\operatorname {dist}(b,a_1)=k_1$
and
![]() $\operatorname {dist}(b,a_2)=k_2$
. Hence, we can pick
$\operatorname {dist}(b,a_2)=k_2$
. Hence, we can pick
![]() $c'$
to be an element in
$c'$
to be an element in
![]() $P(a_1,a_2)$
such that
$P(a_1,a_2)$
such that
![]() $\operatorname {dist}(b,c')=\ell '$
is minimal. Then we have
$\operatorname {dist}(b,c')=\ell '$
is minimal. Then we have
![]() $P(b,c')\cap P(a_1,a_2)=\{c'\}$
, because if there were another element in
$P(b,c')\cap P(a_1,a_2)=\{c'\}$
, because if there were another element in
![]() $P(b,c')$
that lies in
$P(b,c')$
that lies in
![]() $P(a_1,a_2)$
it would contradict the minimality of
$P(a_1,a_2)$
it would contradict the minimality of
![]() $\operatorname {dist}(b,c')$
. Since paths are unique, we have that
$\operatorname {dist}(b,c')$
. Since paths are unique, we have that
![]() $P(b,a_1)=P(b,c')\cup P(c',a_1)$
and
$P(b,a_1)=P(b,c')\cup P(c',a_1)$
and
![]() $P(b,a_2)=P(b,c')\cup P(c',a_2)$
, so
$P(b,a_2)=P(b,c')\cup P(c',a_2)$
, so
![]() $\operatorname {dist}(a_1,c')=k_1-\ell '$
and
$\operatorname {dist}(a_1,c')=k_1-\ell '$
and
![]() $\operatorname {dist}(c',a_2)=k_2-\ell '$
. Hence,
$\operatorname {dist}(c',a_2)=k_2-\ell '$
. Hence,
and so we obtain
![]() $\ell '=\ell $
, and since
$\ell '=\ell $
, and since
![]() $c'$
is an element in
$c'$
is an element in
![]() $P(a_1,a_2)$
at distance
$P(a_1,a_2)$
at distance
![]() $k_1-\ell $
from
$k_1-\ell $
from
![]() $a_1$
and
$a_1$
and
![]() $k_2-\ell $
from
$k_2-\ell $
from
![]() $a_2$
, we can conclude that
$a_2$
, we can conclude that
![]() $c=c'$
.
$c=c'$
.
Proposition 2.7. Let
![]() $A=\{a_1,\ldots ,a_n\}$
be a finite set of vertices in G such that
$A=\{a_1,\ldots ,a_n\}$
be a finite set of vertices in G such that
![]() $\operatorname {dist}(a_i,a_j)=d_{ij}<\infty $
for every
$\operatorname {dist}(a_i,a_j)=d_{ij}<\infty $
for every
![]() $1\leq i<j\leq n$
. Let
$1\leq i<j\leq n$
. Let
![]() $k_1,\ldots ,k_n$
be non-negative integers such that
$k_1,\ldots ,k_n$
be non-negative integers such that
![]() $\ell _{ij}=\frac {1}{2}(k_i+k_j-d_{ij})$
are all integers, and put
$\ell _{ij}=\frac {1}{2}(k_i+k_j-d_{ij})$
are all integers, and put
![]() $\ell =\min \{\ell _{ij}:1\leq i<j\leq n\}$
. Without loss of generality, let us assume that
$\ell =\min \{\ell _{ij}:1\leq i<j\leq n\}$
. Without loss of generality, let us assume that
![]() $\ell =\ell _{12}$
. Furthermore, assume that:
$\ell =\ell _{12}$
. Furthermore, assume that:
-
(i) For every
 $1\leq i<j\leq n$
,
$1\leq i<j\leq n$
,
 $k_i\leq k_j+d_{ij}$
.
$k_i\leq k_j+d_{ij}$
. -
(ii) For every
 $i=1,\ldots ,n$
, exactly one of the following conditions holds:
$i=1,\ldots ,n$
, exactly one of the following conditions holds:-
(a)
 $d_{1i}+k_2<k_1+d_{2i}$
and
$d_{1i}+k_2<k_1+d_{2i}$
and
 $k_i+d_{12}=k_1+d_{2i}$
,
$k_i+d_{12}=k_1+d_{2i}$
, -
(b)
 $d_{1i}+k_2\geq k_1+d_{2i}$
and
$d_{1i}+k_2\geq k_1+d_{2i}$
and
 $k_i+d_{12}=k_2+d_{1i}$
.
$k_i+d_{12}=k_2+d_{1i}$
.
-
Then, there is a unique
![]() $c\in \operatorname {conv}(A)$
such that for every
$c\in \operatorname {conv}(A)$
such that for every
![]() $b\in G$
we have
$b\in G$
we have
 $$\begin{align*}G\models \bigwedge_{i=1}^n D_{k_i}(b,a_i)\text{\ if and only if\ }\operatorname{dist}(b,c)=\ell \text{\ and\ }P(b,c)\cap \operatorname{conv}(A)=\{c\}.\end{align*}$$
$$\begin{align*}G\models \bigwedge_{i=1}^n D_{k_i}(b,a_i)\text{\ if and only if\ }\operatorname{dist}(b,c)=\ell \text{\ and\ }P(b,c)\cap \operatorname{conv}(A)=\{c\}.\end{align*}$$
Proof. As in the proof of Lemma 2.6, we have that
![]() $k_1-\ell \leq d_{12}$
, so we can take c to be the unique element in the path
$k_1-\ell \leq d_{12}$
, so we can take c to be the unique element in the path
![]() $P(a_1,a_2)\subseteq \operatorname {conv}(A)$
at distance
$P(a_1,a_2)\subseteq \operatorname {conv}(A)$
at distance
![]() $k_1-\ell $
from
$k_1-\ell $
from
![]() $a_1$
. We will now show that the equivalence holds.
$a_1$
. We will now show that the equivalence holds.
First, suppose that
![]() $b\in G$
satisfies
$b\in G$
satisfies
![]() $G\models \bigwedge _{i=1}^n D_{k_i}(b,a_i)$
. In particular,
$G\models \bigwedge _{i=1}^n D_{k_i}(b,a_i)$
. In particular,
![]() $G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
, so by Lemma 2.6 we have that
$G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
, so by Lemma 2.6 we have that
![]() $\operatorname {dist}(b,c)=\ell $
and
$\operatorname {dist}(b,c)=\ell $
and
![]() $P(b,c)\cap P(a_1,a_2)=\{c\}$
. Suppose now that d is the unique element in
$P(b,c)\cap P(a_1,a_2)=\{c\}$
. Suppose now that d is the unique element in
![]() $\operatorname {conv}(A)$
satisfying
$\operatorname {conv}(A)$
satisfying
![]() $\operatorname {dist}(b,d)=\operatorname {dist}(b,\operatorname {conv}(A))$
. Since d belongs to the convex closure of A,
$\operatorname {dist}(b,d)=\operatorname {dist}(b,\operatorname {conv}(A))$
. Since d belongs to the convex closure of A,
![]() $d\in P(a_i,a_j)$
for some
$d\in P(a_i,a_j)$
for some
![]() $a_i,a_j\in A$
. Therefore, by Lemma 2.6, we have that
$a_i,a_j\in A$
. Therefore, by Lemma 2.6, we have that
![]() $\operatorname {dist}(b,d)=\frac {1}{2}(k_i+k_j-d_{ij})=\ell _{ij}\leq \ell $
. By the minimality of
$\operatorname {dist}(b,d)=\frac {1}{2}(k_i+k_j-d_{ij})=\ell _{ij}\leq \ell $
. By the minimality of
![]() $\ell $
, we conclude that
$\ell $
, we conclude that
![]() $\ell =\ell _{12}=\ell _{ij}$
, so
$\ell =\ell _{12}=\ell _{ij}$
, so
![]() $c=d$
and
$c=d$
and
![]() $P(b,c)\cap \operatorname {conv}(A)=\{c\}$
.
$P(b,c)\cap \operatorname {conv}(A)=\{c\}$
.
Conversely, suppose that
![]() $\operatorname {dist}(b,c)=\ell $
and
$\operatorname {dist}(b,c)=\ell $
and
![]() $P(b,c)\cap \operatorname {conv}(A)=\{c\}$
. These conditions imply that
$P(b,c)\cap \operatorname {conv}(A)=\{c\}$
. These conditions imply that
![]() $\operatorname {dist}(b,\operatorname {conv}(A))=\ell $
and c is the closest element in
$\operatorname {dist}(b,\operatorname {conv}(A))=\ell $
and c is the closest element in
![]() $\operatorname {conv}(A)$
to b. By Lemma 2.6, since
$\operatorname {conv}(A)$
to b. By Lemma 2.6, since
![]() $k_1\leq k_2+d_{12}$
and
$k_1\leq k_2+d_{12}$
and
![]() $\ell =\ell _{12}=\frac {1}{2}(k_1+k_2-d_{12})$
, we already have that
$\ell =\ell _{12}=\frac {1}{2}(k_1+k_2-d_{12})$
, we already have that
![]() $G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
. For
$G\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_2)$
. For
![]() $i\geq 3$
, since
$i\geq 3$
, since
![]() $G\models D_{d_{1i}}(a_i,a_1)\wedge D_{d_{2i}}(a_i,a_2)$
, we know by Lemma 2.6 that there is a unique element
$G\models D_{d_{1i}}(a_i,a_1)\wedge D_{d_{2i}}(a_i,a_2)$
, we know by Lemma 2.6 that there is a unique element
![]() $e_i$
be the unique element in
$e_i$
be the unique element in
![]() $P(a_1,a_2)$
such that
$P(a_1,a_2)$
such that
![]() $\operatorname {dist}(a_i,e_i)=\operatorname {dist}(a_i,P(a_1,a_2))=\frac {1}{2}(d_{1i}+d_{2i}-d_{12})$
. We have either
$\operatorname {dist}(a_i,e_i)=\operatorname {dist}(a_i,P(a_1,a_2))=\frac {1}{2}(d_{1i}+d_{2i}-d_{12})$
. We have either
![]() $e_i\in P(a_1,c)\setminus \{c\}$
or
$e_i\in P(a_1,c)\setminus \{c\}$
or
![]() $e_i\in P(c,a_2)$
, and we will consider these two cases separately.
$e_i\in P(c,a_2)$
, and we will consider these two cases separately.
If
![]() $e_i\in P(a_1,c)\setminus \{c\}$
, then
$e_i\in P(a_1,c)\setminus \{c\}$
, then
![]() $\operatorname {dist}(a_1,e_i)<\operatorname {dist}(a_1,c)$
, from which we have
$\operatorname {dist}(a_1,e_i)<\operatorname {dist}(a_1,c)$
, from which we have
 $$ \begin{align*} d_{1i}-\frac{1}{2}(d_{1i}+d_{2i}-d_{12})&<k_1-\ell=k_1-\frac{1}{2}(k_1+k_2-d_{12}),\\ d_{1i}-d_{2i}+d_{12}&<k_1-k_2+d_{12},\\ d_{1i}+k_2&<k_1+d_{2i}. \end{align*} $$
$$ \begin{align*} d_{1i}-\frac{1}{2}(d_{1i}+d_{2i}-d_{12})&<k_1-\ell=k_1-\frac{1}{2}(k_1+k_2-d_{12}),\\ d_{1i}-d_{2i}+d_{12}&<k_1-k_2+d_{12},\\ d_{1i}+k_2&<k_1+d_{2i}. \end{align*} $$

So, condition ii(a) holds and since the path from b and
![]() $a_i$
is given by
$a_i$
is given by
we have
 $$ \begin{align*} \operatorname{dist}(b,a_i)&=\operatorname{dist}(b,c)+\operatorname{dist}(c,e_i)+\operatorname{dist}(e_i,a_i)\\ &=\operatorname{dist}(b,c)+[\operatorname{dist}(a_1,c)-\operatorname{dist}(a_1,e_i)]+\operatorname{dist}(e_i,a_i)\\ &=\operatorname{dist}(b,c)+[\operatorname{dist}(a_1,c)-(\operatorname{dist}(a_1,a_i)-\operatorname{dist}(a_i,e_i))]+\operatorname{dist}(e_i,a_i)\\ &=\operatorname{dist}(b,c)+\operatorname{dist}(a_1,c)-\operatorname{dist}(a_1,a_i)+2\operatorname{dist}(a_i,e_i)\\ &=\ell+(k_1-\ell)-d_{1i}+(d_{1i}+d_{2i}-d_{12})\\ &=k_1+d_{2i}-d_{12}=k_i. \end{align*} $$
$$ \begin{align*} \operatorname{dist}(b,a_i)&=\operatorname{dist}(b,c)+\operatorname{dist}(c,e_i)+\operatorname{dist}(e_i,a_i)\\ &=\operatorname{dist}(b,c)+[\operatorname{dist}(a_1,c)-\operatorname{dist}(a_1,e_i)]+\operatorname{dist}(e_i,a_i)\\ &=\operatorname{dist}(b,c)+[\operatorname{dist}(a_1,c)-(\operatorname{dist}(a_1,a_i)-\operatorname{dist}(a_i,e_i))]+\operatorname{dist}(e_i,a_i)\\ &=\operatorname{dist}(b,c)+\operatorname{dist}(a_1,c)-\operatorname{dist}(a_1,a_i)+2\operatorname{dist}(a_i,e_i)\\ &=\ell+(k_1-\ell)-d_{1i}+(d_{1i}+d_{2i}-d_{12})\\ &=k_1+d_{2i}-d_{12}=k_i. \end{align*} $$
If
![]() $e_i\in P(c,a_2)$
, by a symmetric argument we obtain
$e_i\in P(c,a_2)$
, by a symmetric argument we obtain
![]() $k_1 + d_{2i} \leq k_2 + d_{1i}$
and
$k_1 + d_{2i} \leq k_2 + d_{1i}$
and
![]() $\operatorname {dist}(b,a_i) = k_i$
.
$\operatorname {dist}(b,a_i) = k_i$
.

Therefore, we conclude that
![]() $G\models D_{k_i}(b,a_i)$
for every
$G\models D_{k_i}(b,a_i)$
for every
![]() $i=1,2,\ldots ,n$
, which finishes the proof.
$i=1,2,\ldots ,n$
, which finishes the proof.
Remark 2.8. Notice that Proposition 2.7 has the following converse: if there is b such that
![]() $G\models \bigwedge _{i=1}^n D_{k_i}(b,a_i)$
, then
$G\models \bigwedge _{i=1}^n D_{k_i}(b,a_i)$
, then
-
(a) The distances
 $\operatorname {dist}(a_i,a_j)=d_{ij}$
are all finite for every
$\operatorname {dist}(a_i,a_j)=d_{ij}$
are all finite for every
 $i,j\leq n$
,
$i,j\leq n$
, -
(b) The numbers
 $\ell _{ij}=\frac {1}{2}(k_i+k_j-d_{ij})$
are all non-negative integers,
$\ell _{ij}=\frac {1}{2}(k_i+k_j-d_{ij})$
are all non-negative integers, -
(c) Conditions (i) and (ii) in the hypothesis of Proposition 2.7 hold.
Proposition 2.9. Let
![]() $A=\{a_1,\ldots ,a_n\}$
be a finite set of vertices of an acyclic graph G, and let b be a vertex in G such that
$A=\{a_1,\ldots ,a_n\}$
be a finite set of vertices of an acyclic graph G, and let b be a vertex in G such that
![]() $G\models \bigwedge _{i=1}^n D_{k_i}(b,a_i)$
. Let c be the element in
$G\models \bigwedge _{i=1}^n D_{k_i}(b,a_i)$
. Let c be the element in
![]() $\operatorname {conv}(A)$
that is closest to b, and let us define the numbers
$\operatorname {conv}(A)$
that is closest to b, and let us define the numbers
![]() $d_{ij}=\operatorname {dist}(a_i,a_j), \ell _{i,j}=\frac {1}{2}(k_i+k_j-d_{ij}),$
and
$d_{ij}=\operatorname {dist}(a_i,a_j), \ell _{i,j}=\frac {1}{2}(k_i+k_j-d_{ij}),$
and
If
![]() $\operatorname {deg}_{\operatorname {conv}(A)}(c)=m\geq 2$
, there are indices
$\operatorname {deg}_{\operatorname {conv}(A)}(c)=m\geq 2$
, there are indices
![]() $s_1,\ldots ,s_m$
such that:
$s_1,\ldots ,s_m$
such that:
-
(i)
 $\ell _{s_i,s_j}=\ell $
whenever
$\ell _{s_i,s_j}=\ell $
whenever
 $1\leq i<j\leq m$
.
$1\leq i<j\leq m$
. -
(ii) For every
 $t\neq s_1,\ldots ,s_m$
such that
$t\neq s_1,\ldots ,s_m$
such that
 $a_t\neq c$
, there are
$a_t\neq c$
, there are
 $s_1^t,s_2^t$
such that either
$s_1^t,s_2^t$
such that either
 $\ell _{t,s_1^t}=\ell $
or
$\ell _{t,s_1^t}=\ell $
or
 $\ell _{t,s_2^t}=\ell $
, but not both.
$\ell _{t,s_2^t}=\ell $
, but not both.
Proof. Since
![]() $\deg _{\operatorname {conv}(A)}(c)=m$
, there are by definition different elements
$\deg _{\operatorname {conv}(A)}(c)=m$
, there are by definition different elements
![]() $e_1,\ldots ,e_m\in \operatorname {conv}(A)$
all adjacent to c, and so we can pick elements
$e_1,\ldots ,e_m\in \operatorname {conv}(A)$
all adjacent to c, and so we can pick elements
![]() $a_{s_1},\ldots ,a_{s_m}\in A$
such that
$a_{s_1},\ldots ,a_{s_m}\in A$
such that
![]() $e_i\in P(c,a_{s_i})$
.
$e_i\in P(c,a_{s_i})$
.

By Lemma 2.6, we have
![]() $c\in P(a_{s_1},a_{s_2})$
and
$c\in P(a_{s_1},a_{s_2})$
and
![]() $\ell =\ell _{s_1,s_2}$
. Moreover, by Remark 2.8 we know that condition (ii) of Proposition 2.7 holds, and it guarantees that for every
$\ell =\ell _{s_1,s_2}$
. Moreover, by Remark 2.8 we know that condition (ii) of Proposition 2.7 holds, and it guarantees that for every
![]() ${i\leq m}$
we have either
${i\leq m}$
we have either
![]() $\ell _{s_i,s_1}=\ell $
or
$\ell _{s_i,s_1}=\ell $
or
![]() $\ell _{s_i,s_2}=\ell $
. Since
$\ell _{s_i,s_2}=\ell $
. Since
![]() $c\in P(a_{s_i},a_{s_1})\cap P(a_{s_i},a_{s_2})$
, we have
$c\in P(a_{s_i},a_{s_1})\cap P(a_{s_i},a_{s_2})$
, we have
![]() $\operatorname {dist}(c,a_{s_1})+\operatorname {dist}(c,a_{s_i})=d_{s_1,s_i}$
and
$\operatorname {dist}(c,a_{s_1})+\operatorname {dist}(c,a_{s_i})=d_{s_1,s_i}$
and
![]() $\operatorname {dist}(c,a_{s_2})+\operatorname {dist}(c,a_{s_i})=d_{s_2,s_i}$
. Therefore, we have the equalities
$\operatorname {dist}(c,a_{s_2})+\operatorname {dist}(c,a_{s_i})=d_{s_2,s_i}$
. Therefore, we have the equalities
![]() $k_{s_1}-\ell +k_{s_i}-\ell =d_{s_1,s_i}$
and
$k_{s_1}-\ell +k_{s_i}-\ell =d_{s_1,s_i}$
and
![]() $k_{s_2}-\ell +k_{s_i}-\ell =d_{s_2,s_i}$
, which implies by definition that
$k_{s_2}-\ell +k_{s_i}-\ell =d_{s_2,s_i}$
, which implies by definition that
![]() $\ell =\ell _{s_1,s_i}=\ell _{s_2,s_i}$
. This proves part (i) of the Proposition.
$\ell =\ell _{s_1,s_i}=\ell _{s_2,s_i}$
. This proves part (i) of the Proposition.
For part (ii), suppose that
![]() $t\neq s_1,\ldots ,s_m$
and
$t\neq s_1,\ldots ,s_m$
and
![]() $a_t\neq c$
. Since
$a_t\neq c$
. Since
![]() $G\models D_{k_t}(b,a_t)$
, the distance between c and
$G\models D_{k_t}(b,a_t)$
, the distance between c and
![]() $a_t$
is finite and so the path
$a_t$
is finite and so the path
![]() $P(a_t,c)$
includes an element
$P(a_t,c)$
includes an element
![]() $e_i$
. If we choose
$e_i$
. If we choose
![]() $s_2^t$
to be
$s_2^t$
to be
![]() $s_i$
and let
$s_i$
and let
![]() $s_1^t$
be an arbitrary in
$s_1^t$
be an arbitrary in
![]() $\{s_1,\ldots ,s_m\}$
different from
$\{s_1,\ldots ,s_m\}$
different from
![]() $s_i$
, we will have by Lemma 2.6 that
$s_i$
, we will have by Lemma 2.6 that
![]() $\ell _{t,s_1^t}=\operatorname {dist}(b,P(a_{s_1^t},a_t))=\ell $
and
$\ell _{t,s_1^t}=\operatorname {dist}(b,P(a_{s_1^t},a_t))=\ell $
and
![]() $\ell _{t,s_2^t}=\operatorname {dist}(b,P(a_{s_2^t},a_t))\geq \operatorname {dist}(b,e_i)=\ell +1$
. This finishes the proof.
$\ell _{t,s_2^t}=\operatorname {dist}(b,P(a_{s_2^t},a_t))\geq \operatorname {dist}(b,e_i)=\ell +1$
. This finishes the proof.
3 Pseudofiniteness and cardinalities of definable sets in
 $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
 $\mathcal {T}_\infty $
$\mathcal {T}_\infty $
In this section we will show that the theory of the r-regular infinite tree (
![]() $\mathcal {T}_r$
) and the theory of the infinite-branching tree (
$\mathcal {T}_r$
) and the theory of the infinite-branching tree (
![]() $\mathcal {T}_\infty $
) are both pseudofinite and we will give an explicit description of the possible cardinalities of the definable sets in one variable.
$\mathcal {T}_\infty $
) are both pseudofinite and we will give an explicit description of the possible cardinalities of the definable sets in one variable.
From here, and throughout the rest of the article we will use several known results about the model theory of
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
. These results are all considered folklore, but given the difficulty in finding a complete reference we included the proofs as an Appendix in the present article.
$\mathcal {T}_\infty $
. These results are all considered folklore, but given the difficulty in finding a complete reference we included the proofs as an Appendix in the present article.
Definition 3.1. The theory of the infinite branching tree (also known as the everywhere infinite forest) is the theory
![]() $\mathcal {T}_{\infty }$
in the language of graphs
$\mathcal {T}_{\infty }$
in the language of graphs
![]() $L=\{R\}$
given by the following collection of sentences:
$L=\{R\}$
given by the following collection of sentences:
-
(1) Each vertex in G has infinite degree:
 $$\begin{align*}\left\{\sigma_n:=\forall x\exists y_1,\ldots,y_n\left(\bigwedge_{1\leq i<j\leq n}y_i\neq y_j \wedge \bigwedge_{i=1}^n xRy_i\right):n<\omega\right\}.\end{align*}$$
$$\begin{align*}\left\{\sigma_n:=\forall x\exists y_1,\ldots,y_n\left(\bigwedge_{1\leq i<j\leq n}y_i\neq y_j \wedge \bigwedge_{i=1}^n xRy_i\right):n<\omega\right\}.\end{align*}$$
-
(2) G is an acyclic graph:
 $$\begin{align*}\left\{\tau_n:=\forall y_1,\ldots,y_n\, \neg \left(\bigwedge_{1\leq i<j\leq n}y_i\neq y_j \wedge \bigwedge_{i=1}^{n-1}y_iRy_{i+1} \wedge y_n R y_1\right):n<\omega\right\}.\end{align*}$$
$$\begin{align*}\left\{\tau_n:=\forall y_1,\ldots,y_n\, \neg \left(\bigwedge_{1\leq i<j\leq n}y_i\neq y_j \wedge \bigwedge_{i=1}^{n-1}y_iRy_{i+1} \wedge y_n R y_1\right):n<\omega\right\}.\end{align*}$$
Definition 3.2. Similarly, for a fixed
![]() $r\in \mathbb {N}$
, we define the theory of the r-regular infinite tree as the theory
$r\in \mathbb {N}$
, we define the theory of the r-regular infinite tree as the theory
![]() $\mathcal {T}_r$
given by:
$\mathcal {T}_r$
given by:
-
(1) Each vertex in G has degree r:
 $$\begin{align*}\forall x \,\exists y_1,\ldots,y_r\,\left(\bigwedge_{1\leq i<j\leq r}y_i\neq y_j \wedge \bigwedge_{i=1}^r xRy_i\wedge \forall z\left(xRz\to \bigvee_{i=1}^r z=y_i\right)\right).\end{align*}$$
$$\begin{align*}\forall x \,\exists y_1,\ldots,y_r\,\left(\bigwedge_{1\leq i<j\leq r}y_i\neq y_j \wedge \bigwedge_{i=1}^r xRy_i\wedge \forall z\left(xRz\to \bigvee_{i=1}^r z=y_i\right)\right).\end{align*}$$
-
(2) G is an acyclic graph:
 $\{\tau _n:n<\omega \}$
, as in part (2) of Definition 3.1.
$\{\tau _n:n<\omega \}$
, as in part (2) of Definition 3.1.
In Corollary A.2 we show that the theories
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
are complete. So, to show that these theories are pseudofinite, we will show that there are infinite ultraproducts of finite graphs that satisfy the sentences described in Definitions 3.1 and 3.2. However, notice that every finite acyclic graph contains vertices of degree 1, and so there is no model of
$\mathcal {T}_\infty $
are complete. So, to show that these theories are pseudofinite, we will show that there are infinite ultraproducts of finite graphs that satisfy the sentences described in Definitions 3.1 and 3.2. However, notice that every finite acyclic graph contains vertices of degree 1, and so there is no model of
![]() $\mathcal {T}_\infty $
that is elementarily equivalent to an ultraproduct of finite acyclic graphs.
$\mathcal {T}_\infty $
that is elementarily equivalent to an ultraproduct of finite acyclic graphs.
We start with the following combinatorial construction.
Definition 3.3. Let
![]() $G=(V,E)$
be a finite graph. We define the lift of G as the graph
$G=(V,E)$
be a finite graph. We define the lift of G as the graph
![]() $L[G]$
whose vertex set is
$L[G]$
whose vertex set is
![]() $V(G)\times \{0,1\}^{E(G)}$
, and whose edge relation is given by
$V(G)\times \{0,1\}^{E(G)}$
, and whose edge relation is given by
![]() $(u,f)R(v,g)$
if and only if
$(u,f)R(v,g)$
if and only if
![]() $e=\{u,v\}\in E(G), f(e)\neq g(e)$
, and
$e=\{u,v\}\in E(G), f(e)\neq g(e)$
, and
![]() $f(e')=g(e')$
for every edge
$f(e')=g(e')$
for every edge
![]() $e'\neq e.$
$e'\neq e.$
Proposition 3.4. Let
![]() $G=(V,E)$
be a finite k-regular graph, and suppose that the minimal cycle of G has length n. Then:
$G=(V,E)$
be a finite k-regular graph, and suppose that the minimal cycle of G has length n. Then:
-
(1)
 $L[G]$
is a k-regular graph.
$L[G]$
is a k-regular graph. -
(2) The minimal cycle of
 $L[G]$
has length
$L[G]$
has length
 $2n$
.
$2n$
.
Proof. First, suppose that every vertex in G has degree k. For fixed vertices
![]() $(u,f),(v,g)\in L[G]$
, and in order to have
$(u,f),(v,g)\in L[G]$
, and in order to have
![]() $(u,f)R(v,g)$
, it is necessary that
$(u,f)R(v,g)$
, it is necessary that
![]() $uEv$
, and once this occurs there is only one possibility for g, namely being the same function as f but changing its value exactly in the edge
$uEv$
, and once this occurs there is only one possibility for g, namely being the same function as f but changing its value exactly in the edge
![]() $e=\{u,v\}$
. Therefore, any
$e=\{u,v\}$
. Therefore, any
![]() $(u,f)\in L[G]$
is connected precisely with k other vertices of the form
$(u,f)\in L[G]$
is connected precisely with k other vertices of the form
![]() $(v,g)$
in
$(v,g)$
in
![]() $L[G]$
.
$L[G]$
.
Now, suppose that
![]() $x_1=(v_1,f_1),\ldots ,x_m=(v_m,f_m)$
are pairwise distinct vertices in
$x_1=(v_1,f_1),\ldots ,x_m=(v_m,f_m)$
are pairwise distinct vertices in
![]() $L[G]$
that form a cycle, and put
$L[G]$
that form a cycle, and put
![]() $x_{m+1}=(v_{m+1},f_{m+1})=(v_1,f_1)$
. Let
$x_{m+1}=(v_{m+1},f_{m+1})=(v_1,f_1)$
. Let
![]() $s<t$
in
$s<t$
in
![]() $\{1,\ldots ,m+1\}$
such that
$\{1,\ldots ,m+1\}$
such that
![]() $v_s=v_t$
, and
$v_s=v_t$
, and
![]() $t-s$
is minimal. Note that
$t-s$
is minimal. Note that
![]() $t-s\geq 3$
as
$t-s\geq 3$
as
![]() ${t=s+1}$
would imply an edge between a vertex and itself in G, and
${t=s+1}$
would imply an edge between a vertex and itself in G, and
![]() $t=s+2$
would correspond to a path in
$t=s+2$
would correspond to a path in
![]() $L[G]$
of the form
$L[G]$
of the form
![]() $x_sRx_{s+1}Rx_s$
, which is not possible in a cycle. Hence,
$x_sRx_{s+1}Rx_s$
, which is not possible in a cycle. Hence,
![]() $t\geq s+3$
, and we may suppose without loss of generality that
$t\geq s+3$
, and we may suppose without loss of generality that
![]() $x_s=x_1$
. Putting
$x_s=x_1$
. Putting
![]() $\ell =t-s$
, we then have a cycle
$\ell =t-s$
, we then have a cycle
![]() $v_1, v_2, \ldots , v_\ell , v_{\ell +1}=v_1$
in G, so
$v_1, v_2, \ldots , v_\ell , v_{\ell +1}=v_1$
in G, so
![]() $\ell \geq n$
.
$\ell \geq n$
.
On the other hand, considering the functions
![]() $f_1,\ldots ,f_m$
, notice that
$f_1,\ldots ,f_m$
, notice that
![]() $f_{i+1}$
is obtained from
$f_{i+1}$
is obtained from
![]() $f_i$
by changing exactly one of the values. So,
$f_i$
by changing exactly one of the values. So,
![]() $f_{\ell +1}$
is obtained from
$f_{\ell +1}$
is obtained from
![]() $f_1$
by performing changes in
$f_1$
by performing changes in
![]() $\ell $
different entries, and to complete the cycle in
$\ell $
different entries, and to complete the cycle in
![]() $L[G]$
the function
$L[G]$
the function
![]() $f_{\ell +1}$
would need to be restored to
$f_{\ell +1}$
would need to be restored to
![]() $f_1$
. That is, it would be necessary to change at least change these
$f_1$
. That is, it would be necessary to change at least change these
![]() $\ell $
different entries back to their original value. Therefore,
$\ell $
different entries back to their original value. Therefore,
![]() $m\geq 2n$
, that is, the length of the minimal cycle in
$m\geq 2n$
, that is, the length of the minimal cycle in
![]() $L[G]$
is at least
$L[G]$
is at least
![]() $2n$
.
$2n$
.
To show that the length of the minimal cycle is exactly
![]() $2n$
, we can first consider a cycle given by
$2n$
, we can first consider a cycle given by
![]() $v_1,\ldots ,v_n,v_{n+1}=v_1$
in G. Let us enumerate the edges
$v_1,\ldots ,v_n,v_{n+1}=v_1$
in G. Let us enumerate the edges
![]() $e_i=\{v_i,v_{i+1}\}$
for
$e_i=\{v_i,v_{i+1}\}$
for
![]() $i=1,\ldots ,n$
. This produces the following cycle in
$i=1,\ldots ,n$
. This produces the following cycle in
![]() $L[G]$
of length exactly
$L[G]$
of length exactly
![]() $2n$
:
$2n$
:

The next result is not connected with other results in the article. However, it is worth noticing that the lifting of a graph increases the number of vertices exponentially.
Proposition 3.5. Let G be a k-regular graph. Then
![]() $|L[G]|=|G|\cdot (2^{k/2})^{|G|}$
, where
$|L[G]|=|G|\cdot (2^{k/2})^{|G|}$
, where
![]() $|G|$
denotes the number of vertices in G.
$|G|$
denotes the number of vertices in G.
Proof. Given that the vertex set of
![]() $L[G]$
is
$L[G]$
is
![]() $V(G)\times \{0,1\}^{|E(G)|}$
, it is clear that
$V(G)\times \{0,1\}^{|E(G)|}$
, it is clear that
![]() $|L[G]|=|G|\cdot 2^{|E(G)|}$
. On the other hand, by the Hand-shaking lemma, we have that
$|L[G]|=|G|\cdot 2^{|E(G)|}$
. On the other hand, by the Hand-shaking lemma, we have that
so
![]() $|E(G)|=|V(G)|\cdot \frac {k}{2}$
, and the result follows.
$|E(G)|=|V(G)|\cdot \frac {k}{2}$
, and the result follows.
Proposition 3.6. Let
![]() $d,g:\mathbb {N}\to \mathbb {N}$
be two arbitrary functions. There is a family
$d,g:\mathbb {N}\to \mathbb {N}$
be two arbitrary functions. There is a family
![]() $\mathcal {C}_{d,g}=\{H_k:1\leq k<\omega \}$
of finite graphs satisfying the following:
$\mathcal {C}_{d,g}=\{H_k:1\leq k<\omega \}$
of finite graphs satisfying the following:
-
(1)
 $\displaystyle {\lim _{k\to \infty } |H_k|=\infty }$
.
$\displaystyle {\lim _{k\to \infty } |H_k|=\infty }$
. -
(2) Every
 $H_k$
is
$H_k$
is
 $d(k)$
-regular, for all
$d(k)$
-regular, for all
 $k\geq 3$
.
$k\geq 3$
. -
(3) The minimal cycle in
 $H_k$
has length at least
$H_k$
has length at least
 $3\cdot g(k)$
, for all
$3\cdot g(k)$
, for all
 $k\geq 3$
.
$k\geq 3$
.
Proof. For
![]() $1\leq k<\omega $
, let us put
$1\leq k<\omega $
, let us put
![]() $\ell _k=\lceil \log _2(g(k))\rceil $
and define the graphs
$\ell _k=\lceil \log _2(g(k))\rceil $
and define the graphs
![]() $H_{k,0}',\ldots ,H_{k,\ell _k}'=H_k$
recursively. First, let
$H_{k,0}',\ldots ,H_{k,\ell _k}'=H_k$
recursively. First, let
![]() $H_{k,0}$
be the complete graph
$H_{k,0}$
be the complete graph
![]() $K_{d(k)+1}$
, which is a
$K_{d(k)+1}$
, which is a
![]() $d(k)$
-regular graph whose minimal cycle has length
$d(k)$
-regular graph whose minimal cycle has length
![]() $3$
. Now, supposing
$3$
. Now, supposing
![]() $H_{k,j}'$
has been given and
$H_{k,j}'$
has been given and
![]() $j<\ell _k$
, we take
$j<\ell _k$
, we take
![]() $H_{k,j+1}'=L[H_{k,j}']$
. Finally, we put
$H_{k,j+1}'=L[H_{k,j}']$
. Finally, we put
![]() $H_k:=H^{\prime }_{k,\ell _k}$
, and we have the following:
$H_k:=H^{\prime }_{k,\ell _k}$
, and we have the following:
-
(1)
 $|H_k|\geq |K_{k+1}|=k+1$
, so
$|H_k|\geq |K_{k+1}|=k+1$
, so
 $\displaystyle {\lim _{k\to \infty } |H_k|=\infty }$
.
$\displaystyle {\lim _{k\to \infty } |H_k|=\infty }$
. -
(2) Since
 $H_{k,0}'$
is a
$H_{k,0}'$
is a
 $d(k)$
-regular graph, we have by Proposition 3.4 that its
$d(k)$
-regular graph, we have by Proposition 3.4 that its
 $\ell _k$
-th lift
$\ell _k$
-th lift
 $H_k=H^{\prime }_{k,\ell _k}$
is also
$H_k=H^{\prime }_{k,\ell _k}$
is also
 $d(k)$
-regular.
$d(k)$
-regular. -
(3) Since the minimal cycle in
 $H_{k,0}'$
has length 3, again by Proposition 3.4 we have that the minimal cycle in
$H_{k,0}'$
has length 3, again by Proposition 3.4 we have that the minimal cycle in
 $H_k$
has length
$H_k$
has length
 $3\cdot 2^{\ell _k} \geq 3\cdot g(k)$
.
$3\cdot 2^{\ell _k} \geq 3\cdot g(k)$
.
Thus, the family of graphs
![]() $\{H_k:1\leq k<\omega \}$
satisfies the required conditions.
$\{H_k:1\leq k<\omega \}$
satisfies the required conditions.
Theorem 3.7. The theories
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
are pseudofinite.
$\mathcal {T}_\infty $
are pseudofinite.
Proof. Let us consider the functions
![]() $d_1,d_2,g:\mathbb {N}\to \mathbb {N}$
defined by
$d_1,d_2,g:\mathbb {N}\to \mathbb {N}$
defined by
![]() $d_1(k)=r$
and
$d_1(k)=r$
and
![]() $d_2(k)=g(k)=k$
for every
$d_2(k)=g(k)=k$
for every
![]() $k\in \mathbb {N}$
. Let
$k\in \mathbb {N}$
. Let
![]() $\mathcal {C}_{d_1,g}=\{G_k:k<\omega \}$
and
$\mathcal {C}_{d_1,g}=\{G_k:k<\omega \}$
and
![]() ${\mathcal {C}_{d_2,g}=\{H_k:k<\omega \}}$
be families of finite graphs satisfying the conditions provided by Proposition 3.6, and consider the ultraproducts
${\mathcal {C}_{d_2,g}=\{H_k:k<\omega \}}$
be families of finite graphs satisfying the conditions provided by Proposition 3.6, and consider the ultraproducts
![]() $G=\prod _{\mathcal {U}}G_k$
and
$G=\prod _{\mathcal {U}}G_k$
and
![]() $H=\prod _{\mathcal {U}}H_k$
with respect to a non-principal ultrafilter
$H=\prod _{\mathcal {U}}H_k$
with respect to a non-principal ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\omega $
. We will now show that
$\omega $
. We will now show that
![]() $G\models \mathcal {T}_r$
, and
$G\models \mathcal {T}_r$
, and
![]() $H\models \mathcal {T}_\infty $
.
$H\models \mathcal {T}_\infty $
.
Property (1) in Proposition 3.6 implies that the vertex sets of
![]() $G, H$
are infinite, and property (3) implies that neither
$G, H$
are infinite, and property (3) implies that neither
![]() $G_k$
nor
$G_k$
nor
![]() $H_k$
contain cycles of length
$H_k$
contain cycles of length
![]() $n<g(k)=k$
. So, the collection of indices
$n<g(k)=k$
. So, the collection of indices
![]() $\{k<\omega :G_k,H_k\models \tau _n\}$
contains
$\{k<\omega :G_k,H_k\models \tau _n\}$
contains
![]() $\mathbb {N}^{\geq n}$
and so belongs to the ultrafilter
$\mathbb {N}^{\geq n}$
and so belongs to the ultrafilter
![]() $\mathcal {U}$
. Therefore, by Łoś’ theorem, both G and H are acyclic graphs. Finally, note that every graph
$\mathcal {U}$
. Therefore, by Łoś’ theorem, both G and H are acyclic graphs. Finally, note that every graph
![]() $G_k$
is r-regular and so G is r-regular, and since every graph
$G_k$
is r-regular and so G is r-regular, and since every graph
![]() $H_k$
is k-regular, we have that for any fixed
$H_k$
is k-regular, we have that for any fixed
![]() $n<\omega H_k\models \sigma _n$
whenever
$n<\omega H_k\models \sigma _n$
whenever
![]() $n\leq k$
. Thus, by Łoś Theorem, every vertex of H has infinite degree.
$n\leq k$
. Thus, by Łoś Theorem, every vertex of H has infinite degree.
Remark 3.8. We have given an explicit example of an ultraproduct of finite graphs that satisfies the theory
![]() $\mathcal {T}_\infty $
, but there is great flexibility in the construction. For instance, whenever
$\mathcal {T}_\infty $
, but there is great flexibility in the construction. For instance, whenever
![]() $d,g:\mathbb {N}\to \mathbb {N}$
are non-decreasing functions that tend to infinity and
$d,g:\mathbb {N}\to \mathbb {N}$
are non-decreasing functions that tend to infinity and
![]() $\mathcal {C}_{d,g}$
is a class of graphs satisfying the hypotheses of Proposition 3.6, every ultraproduct of the graphs in
$\mathcal {C}_{d,g}$
is a class of graphs satisfying the hypotheses of Proposition 3.6, every ultraproduct of the graphs in
![]() $\mathcal {C}_{d,g}$
with respect to a non-principal ultrafilter will be a model of
$\mathcal {C}_{d,g}$
with respect to a non-principal ultrafilter will be a model of
![]() $\mathcal {T}_\infty $
. These classes of graphs will be better explored in Section 4, where we show that they are examples of multidimensional exact classes.
$\mathcal {T}_\infty $
. These classes of graphs will be better explored in Section 4, where we show that they are examples of multidimensional exact classes.
We will now turn our attention to the study of possible non-standard cardinalities of definable sets in ultraproducts of finite graphs that are models of
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
. Suppose that
$\mathcal {T}_\infty $
. Suppose that
![]() $\mathcal {M}=\prod _{\mathcal {U}} G_k$
is an ultraproduct of finite graphs that models
$\mathcal {M}=\prod _{\mathcal {U}} G_k$
is an ultraproduct of finite graphs that models
![]() $\mathcal {T}_r$
. Since
$\mathcal {T}_r$
. Since
![]() $\mathcal {T}_r$
is strongly minimal, we have by Theorem 1.1(i) of [Reference Pillay16] that for every definable set
$\mathcal {T}_r$
is strongly minimal, we have by Theorem 1.1(i) of [Reference Pillay16] that for every definable set
![]() ${E\subseteq M^n}$
there is a polynomial
${E\subseteq M^n}$
there is a polynomial
![]() $p_E(t)$
with integer coefficients such that
$p_E(t)$
with integer coefficients such that
![]() $|E|=p_X(|E|)$
, and in fact the Morley rank of E corresponds to the degree of the polynomial
$|E|=p_X(|E|)$
, and in fact the Morley rank of E corresponds to the degree of the polynomial
![]() $p_E$
.
$p_E$
.
In the rest of this section we will obtain a similar result for models of
![]() $\mathcal {T}_\infty $
, and in Section 5 we will deal with the characterization of the Morley rank in terms of degrees of polynomials.
$\mathcal {T}_\infty $
, and in Section 5 we will deal with the characterization of the Morley rank in terms of degrees of polynomials.
Definition 3.9. Let us consider an infinite ultraproduct
![]() $\mathcal {M}=\prod _{\mathcal {U}} H_k$
of a class of graphs
$\mathcal {M}=\prod _{\mathcal {U}} H_k$
of a class of graphs
![]() $\mathcal {C}=\{H_k:k<\omega \}$
such that each
$\mathcal {C}=\{H_k:k<\omega \}$
such that each
![]() $H_k$
is a
$H_k$
is a
![]() $d(k)$
-regular graph, and both functions
$d(k)$
-regular graph, and both functions
![]() $d(k),\operatorname {girth}(H_k)\to \infty $
as k increases. Finally, let us fix the non-standard natural numbers
$d(k),\operatorname {girth}(H_k)\to \infty $
as k increases. Finally, let us fix the non-standard natural numbers
![]() $\alpha =|\mathcal {M}|=[\,\,|H_k|\,\,]_{\mathcal {U}}$
and
$\alpha =|\mathcal {M}|=[\,\,|H_k|\,\,]_{\mathcal {U}}$
and
![]() $\beta =[d(k)]_{\mathcal {U}}$
in
$\beta =[d(k)]_{\mathcal {U}}$
in
![]() $\mathbb {R}^*:=\mathbb {R}^{\mathcal {U}}$
.
$\mathbb {R}^*:=\mathbb {R}^{\mathcal {U}}$
.
Remark 3.10. Notice that the acyclic graph
![]() $\mathcal {M}$
is regular in a very strong form: for every element
$\mathcal {M}$
is regular in a very strong form: for every element
![]() $a\in \mathcal {M}$
, the set
$a\in \mathcal {M}$
, the set
![]() $D_1(\mathcal {M},a)$
of neighbours of a has non-standard cardinality
$D_1(\mathcal {M},a)$
of neighbours of a has non-standard cardinality
![]() $\beta $
. This follows from Łoś’ theorem when applied to a natural extension
$\beta $
. This follows from Łoś’ theorem when applied to a natural extension
![]() $\mathcal {L}^+$
of the language
$\mathcal {L}^+$
of the language
![]() $\mathcal {L}'$
that includes certain counting functions, and on which the condition
$\mathcal {L}'$
that includes certain counting functions, and on which the condition
![]() $\Theta (y,t):="\,\,|D_1(\mathcal{M},y)|=t\,\,$
” is definable. For more details, see [Reference García, Macpherson and Steinhorn9, Section 2] or the proof of Theorem 4.6.
$\Theta (y,t):="\,\,|D_1(\mathcal{M},y)|=t\,\,$
” is definable. For more details, see [Reference García, Macpherson and Steinhorn9, Section 2] or the proof of Theorem 4.6.
Theorem 3.11. Let
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
![]() $\alpha $
, and
$\alpha $
, and
![]() $\beta $
as in Definition 3.9. If
$\beta $
as in Definition 3.9. If
![]() $X=\varphi (\mathcal {M},\overline {a})$
is a definable set of
$X=\varphi (\mathcal {M},\overline {a})$
is a definable set of
![]() $\mathcal {M}^1$
, then there exists a polynomial
$\mathcal {M}^1$
, then there exists a polynomial
![]() $p_X(t_1,t_2)$
in two variables with integer coefficients such that
$p_X(t_1,t_2)$
in two variables with integer coefficients such that
![]() $|X| = p_X(\alpha ,\beta ).$
$|X| = p_X(\alpha ,\beta ).$
Proof. Since
![]() $\mathcal {T}_\infty $
has quantifier elimination, every definable set
$\mathcal {T}_\infty $
has quantifier elimination, every definable set
![]() $X \subseteq M^1$
is determined by a formula
$X \subseteq M^1$
is determined by a formula
![]() $\varphi (x,\overline {a})$
that is equivalent to a disjunction of formulas
$\varphi (x,\overline {a})$
that is equivalent to a disjunction of formulas
![]() $\tau _j(x,\overline {a})$
, where each
$\tau _j(x,\overline {a})$
, where each
![]() $\tau _j(x,\overline {a})$
is a conjunction of basic formulas. By increasing the number of conjunctions if necessary, we can assume that the sets defined by the formulas
$\tau _j(x,\overline {a})$
is a conjunction of basic formulas. By increasing the number of conjunctions if necessary, we can assume that the sets defined by the formulas
![]() $\tau _i(x,\overline {a})$
are all disjoint. Consequently, we have
$\tau _i(x,\overline {a})$
are all disjoint. Consequently, we have
![]() $|X|=\sum _{i=1}^{k}|\tau _i(\mathcal {M},\overline {a})|$
and thus it suffices to prove the statement for sets defined by a single conjunction of basic formulas.
$|X|=\sum _{i=1}^{k}|\tau _i(\mathcal {M},\overline {a})|$
and thus it suffices to prove the statement for sets defined by a single conjunction of basic formulas.
We will first show the result for a set X defined by a formula of the form
![]() $\varphi (x, \overline {a}) \equiv \bigwedge _{j = 1}^{n} D_{k_i}(x,a_i)$
. If the definable set X is empty, then we can take
$\varphi (x, \overline {a}) \equiv \bigwedge _{j = 1}^{n} D_{k_i}(x,a_i)$
. If the definable set X is empty, then we can take
![]() $p_X(t_1,t_2)=0$
. So, we can assume that
$p_X(t_1,t_2)=0$
. So, we can assume that
![]() $X\neq \emptyset $
, which implies that the set
$X\neq \emptyset $
, which implies that the set
![]() $\displaystyle {A=\operatorname {conv}(\{a_1,\ldots ,a_n\})}$
is finite. By Proposition 2.7, there is a non-negative integer
$\displaystyle {A=\operatorname {conv}(\{a_1,\ldots ,a_n\})}$
is finite. By Proposition 2.7, there is a non-negative integer
![]() $\ell $
and a unique element
$\ell $
and a unique element
![]() $c\in A$
such that for every
$c\in A$
such that for every
![]() $b\in \mathcal {M}$
,
$b\in \mathcal {M}$
,
![]() $b\in E$
if and only if
$b\in E$
if and only if
![]() $\operatorname {dist}(b,c)=\ell $
and
$\operatorname {dist}(b,c)=\ell $
and
![]() $P(b,c)\cap A=\{c\}$
. Hence, since c has precisely
$P(b,c)\cap A=\{c\}$
. Hence, since c has precisely
![]() $\beta -\operatorname {deg}_A(c)$
neighbours that do not belong to A and each of these neighbours adds
$\beta -\operatorname {deg}_A(c)$
neighbours that do not belong to A and each of these neighbours adds
![]() $(\beta -1)^{\ell -1}$
new elements at distance
$(\beta -1)^{\ell -1}$
new elements at distance
![]() $\ell $
from c, we have
$\ell $
from c, we have
![]() $|X|=(\beta -\deg _A(c))(\beta -1)^{\ell -1}$
. Therefore, we can choose
$|X|=(\beta -\deg _A(c))(\beta -1)^{\ell -1}$
. Therefore, we can choose
Next, we will analyze the case when X is defined by a formula of the form
 $$\begin{align*}\varphi(x,\overline{a}) \equiv \bigwedge_{i=1}^{n_1} D_{k_i}(x,a_i) \wedge \bigwedge_{j=1}^{n_2} \neg D_{t_j}(x,a_j'). \end{align*}$$
$$\begin{align*}\varphi(x,\overline{a}) \equiv \bigwedge_{i=1}^{n_1} D_{k_i}(x,a_i) \wedge \bigwedge_{j=1}^{n_2} \neg D_{t_j}(x,a_j'). \end{align*}$$
Let us fix the formula
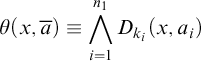 $\displaystyle {\theta (x,\overline {a})\equiv \bigwedge _{i=1}^{n_1}D_{k_i}(x,a_i)}$
. By the previous case, for every subset
$\displaystyle {\theta (x,\overline {a})\equiv \bigwedge _{i=1}^{n_1}D_{k_i}(x,a_i)}$
. By the previous case, for every subset
![]() $S\subseteq \{1,\ldots ,n_2\}$
there is a polynomial
$S\subseteq \{1,\ldots ,n_2\}$
there is a polynomial
![]() $q_S(t_1,t_2)$
such that
$q_S(t_1,t_2)$
such that
 $$\begin{align*}\left|\theta(\mathcal{M},\overline{a})\wedge \bigwedge_{j\in S}D_{t_j}(x,a_j')\right|=q_S(\alpha,\beta).\end{align*}$$
$$\begin{align*}\left|\theta(\mathcal{M},\overline{a})\wedge \bigwedge_{j\in S}D_{t_j}(x,a_j')\right|=q_S(\alpha,\beta).\end{align*}$$
Therefore, by the inclusion–exclusion principle, we have that
 $$ \begin{align*} |\varphi(\mathcal{M},\overline{a})|&=\bigg|\theta(\mathcal{M},\overline{a}) \bigg| - \bigg| \theta(\mathcal{M},\overline{a}) \wedge \bigvee_{j=1}^{n_2} D_{t_j}(x,a_j') \bigg|\\ &=\bigg|\theta(\mathcal{M},\overline{a}) \bigg| - \bigg| \bigvee_{j=1}^{n_2}[\,\,\theta(\mathcal{M},\overline{a}) \wedge D_{t_j}(x,a_j)\,\,] \bigg|\\ &=\bigg|\theta(\mathcal{M},\overline{a}) \bigg| - \left(\sum_{r=1}^{n_2}(-1)^r\cdot \sum_{S\subseteq \{1,\ldots,n_2\}, |S|=r}\bigg|\theta(\mathcal{M},\overline{a})\wedge \bigwedge_{j\in S}D_{t_j}(x,a_j')\bigg|\right)\\ &=q_{\emptyset}(\alpha,\beta)-\sum_{r=1}^{n_2}(-1)^r\cdot \left( \sum_{S\subseteq \{1,\ldots,n_2\}, |S|=r}q_S(\alpha,\beta)\right), \end{align*} $$
$$ \begin{align*} |\varphi(\mathcal{M},\overline{a})|&=\bigg|\theta(\mathcal{M},\overline{a}) \bigg| - \bigg| \theta(\mathcal{M},\overline{a}) \wedge \bigvee_{j=1}^{n_2} D_{t_j}(x,a_j') \bigg|\\ &=\bigg|\theta(\mathcal{M},\overline{a}) \bigg| - \bigg| \bigvee_{j=1}^{n_2}[\,\,\theta(\mathcal{M},\overline{a}) \wedge D_{t_j}(x,a_j)\,\,] \bigg|\\ &=\bigg|\theta(\mathcal{M},\overline{a}) \bigg| - \left(\sum_{r=1}^{n_2}(-1)^r\cdot \sum_{S\subseteq \{1,\ldots,n_2\}, |S|=r}\bigg|\theta(\mathcal{M},\overline{a})\wedge \bigwedge_{j\in S}D_{t_j}(x,a_j')\bigg|\right)\\ &=q_{\emptyset}(\alpha,\beta)-\sum_{r=1}^{n_2}(-1)^r\cdot \left( \sum_{S\subseteq \{1,\ldots,n_2\}, |S|=r}q_S(\alpha,\beta)\right), \end{align*} $$
obtaining the polynomial
 $$\begin{align*}p_X(t_1,t_2)=q_{\emptyset}(t_1,t_2)-\sum_{r=1}^{n_2}(-1)^r\cdot \left(\sum_{S\subseteq \{1,\ldots,n_2\}, |S|=r}q_S(t_1,t_2)\right).\end{align*}$$
$$\begin{align*}p_X(t_1,t_2)=q_{\emptyset}(t_1,t_2)-\sum_{r=1}^{n_2}(-1)^r\cdot \left(\sum_{S\subseteq \{1,\ldots,n_2\}, |S|=r}q_S(t_1,t_2)\right).\end{align*}$$
Finally, for a formula of the form
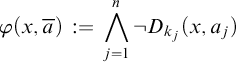 $\varphi (x,\overline {a})\,:=\, \displaystyle {\bigwedge _{j=1}^n \neg D_{k_j}(x,a_j)}$
, we can apply the same argument replacing the formula
$\varphi (x,\overline {a})\,:=\, \displaystyle {\bigwedge _{j=1}^n \neg D_{k_j}(x,a_j)}$
, we can apply the same argument replacing the formula
![]() $\theta (x,\overline {a})$
by
$\theta (x,\overline {a})$
by
![]() $x=x$
. Hence, we have
$x=x$
. Hence, we have
 $$\begin{align*}|\varphi(\mathcal{M},\overline{a})|=\left|\mathcal{M}\setminus \bigcup_{j=1}^n D_{k_j}(x,a_j)\right|=\alpha-\sum_{r=0}^n(-1)^r\cdot \left(\sum_{S\subseteq \{1,\ldots,n\}, |S|=r}q_S(\alpha,\beta)\right),\end{align*}$$
$$\begin{align*}|\varphi(\mathcal{M},\overline{a})|=\left|\mathcal{M}\setminus \bigcup_{j=1}^n D_{k_j}(x,a_j)\right|=\alpha-\sum_{r=0}^n(-1)^r\cdot \left(\sum_{S\subseteq \{1,\ldots,n\}, |S|=r}q_S(\alpha,\beta)\right),\end{align*}$$
thus obtaining the polynomial
 $$\begin{align*}p_X(t_1,t_2)=t_1-\sum_{r=0}^n(-1)^r\cdot \left(\sum_{S\subseteq \{1,\ldots,n\}, |S|=r}q_S(t_1,t_2)\right).\end{align*}$$
$$\begin{align*}p_X(t_1,t_2)=t_1-\sum_{r=0}^n(-1)^r\cdot \left(\sum_{S\subseteq \{1,\ldots,n\}, |S|=r}q_S(t_1,t_2)\right).\end{align*}$$
This completes the proof.
The following results proves definability in the choice of the polynomial
![]() $p_X(t_1,t_2)$
, depending on the formula
$p_X(t_1,t_2)$
, depending on the formula
![]() $\varphi (x,\overline {y})$
used to define X and the choice of parameters.
$\varphi (x,\overline {y})$
used to define X and the choice of parameters.
Theorem 3.12. For every formula
![]() $\varphi (x,\overline {y})$
with one object-variable in the extended language
$\varphi (x,\overline {y})$
with one object-variable in the extended language
![]() $\mathcal {L}'$
there are finitely many polynomials
$\mathcal {L}'$
there are finitely many polynomials
![]() $p_{1}^\varphi (t_1,t_2), p_{2}^\varphi (t_1,t_2), \ldots , p_{k_\varphi }^\varphi (t_1,t_2) \in \mathbb {Z}[t_1,t_2]$
and formulas
$p_{1}^\varphi (t_1,t_2), p_{2}^\varphi (t_1,t_2), \ldots , p_{k_\varphi }^\varphi (t_1,t_2) \in \mathbb {Z}[t_1,t_2]$
and formulas
![]() $\psi _1(\overline {y}), \psi _2(\overline {y}), \dots , \psi _{k_\varphi }(\overline {y})$
such that whenever
$\psi _1(\overline {y}), \psi _2(\overline {y}), \dots , \psi _{k_\varphi }(\overline {y})$
such that whenever
![]() $\mathcal {M},\alpha ,$
and
$\mathcal {M},\alpha ,$
and
![]() $\beta $
are as in Definition 3.9 we have:
$\beta $
are as in Definition 3.9 we have:
-
(1) The family
 $\{\psi _i(\overline {y})\}_{i=1}^{k_\varphi }$
defines a partition of
$\{\psi _i(\overline {y})\}_{i=1}^{k_\varphi }$
defines a partition of
 $\mathcal {M}^{|\overline {y}|}$
.
$\mathcal {M}^{|\overline {y}|}$
. -
(2) For every
 $\overline {a}\in \mathcal {M}^{|\overline {y}|}$
,
$\overline {a}\in \mathcal {M}^{|\overline {y}|}$
,
 $\mathcal {M} \models \psi _i(\overline {a}) \iff |\varphi (\mathcal {M},\overline {a})| = p_i(\alpha , \beta ).$
$\mathcal {M} \models \psi _i(\overline {a}) \iff |\varphi (\mathcal {M},\overline {a})| = p_i(\alpha , \beta ).$
Proof. We will first show the result for a formula
![]() $\varphi (x,\overline {y})\,:=\, \bigwedge _{i = 1}^n D_{k_i} (x,y_i)$
. If we take an arbitrary tuple
$\varphi (x,\overline {y})\,:=\, \bigwedge _{i = 1}^n D_{k_i} (x,y_i)$
. If we take an arbitrary tuple
![]() $\overline {a} \in M^{|\overline {y}|}$
we know by Lemma 2.6 that, if
$\overline {a} \in M^{|\overline {y}|}$
we know by Lemma 2.6 that, if
![]() $\operatorname {dist}(a_{j_1},a_{j_2})> k_{j_1} + k_{j_2}$
for any
$\operatorname {dist}(a_{j_1},a_{j_2})> k_{j_1} + k_{j_2}$
for any
![]() $1 \leq j_1 < j_2 \leq n$
, then
$1 \leq j_1 < j_2 \leq n$
, then
![]() $\varphi (\mathcal {M},\overline {a}) = \emptyset $
. Therefore, if
$\varphi (\mathcal {M},\overline {a}) = \emptyset $
. Therefore, if
![]() $\varphi (\mathcal {M},\overline {a}) \neq \emptyset $
then the configuration of distances
$\varphi (\mathcal {M},\overline {a}) \neq \emptyset $
then the configuration of distances
![]() $\overline {d}=\langle d_{ij}:=\operatorname {dist}(a_i,a_j)\rangle _{i,j} $
must satisfy
$\overline {d}=\langle d_{ij}:=\operatorname {dist}(a_i,a_j)\rangle _{i,j} $
must satisfy
![]() $d_{ij} \leq k_i+k_j$
for every
$d_{ij} \leq k_i+k_j$
for every
![]() $i,j$
. This guarantees that the possible configurations for which
$i,j$
. This guarantees that the possible configurations for which
![]() $\varphi (x,\overline {a})$
defines a non-empty set are finite. In fact, the number of this configurations is bounded by the product
$\varphi (x,\overline {a})$
defines a non-empty set are finite. In fact, the number of this configurations is bounded by the product
![]() $\displaystyle {\prod _{1\leq i < j \leq n} (k_i+k_j+1).}$
$\displaystyle {\prod _{1\leq i < j \leq n} (k_i+k_j+1).}$
Moreover, Proposition 2.7 and Remark 2.8 establish conditions under which, given a configuration of finite distances
![]() $\overline {d}$
and non-negative integers
$\overline {d}$
and non-negative integers
![]() $k_1,k_2,\dots , k_n$
, the set defined by
$k_1,k_2,\dots , k_n$
, the set defined by
![]() $\bigwedge _{i = 1}^n D_{k_i} (x,a_i)$
is empty, and furthermore, these conditions are first-order definable. So, given integers
$\bigwedge _{i = 1}^n D_{k_i} (x,a_i)$
is empty, and furthermore, these conditions are first-order definable. So, given integers
![]() $k_1,\ldots ,k_n$
, we can denote by J the set of possible configurations of distances of the form
$k_1,\ldots ,k_n$
, we can denote by J the set of possible configurations of distances of the form
![]() $\overline {d}=(d_{ij})_{ij}$
that satisfy the conditions (i),(ii) described in Proposition 2.7. Notice that J is a finite set, and consider the formula
$\overline {d}=(d_{ij})_{ij}$
that satisfy the conditions (i),(ii) described in Proposition 2.7. Notice that J is a finite set, and consider the formula
 $$ \begin{align*}\theta(\overline{y}) \equiv \bigvee_{\overline{d}=(d_{ij})_{ij} \in J} \ \bigwedge_{i < j \leq n} D_{d_{ij}}(y_i,y_j).\end{align*} $$
$$ \begin{align*}\theta(\overline{y}) \equiv \bigvee_{\overline{d}=(d_{ij})_{ij} \in J} \ \bigwedge_{i < j \leq n} D_{d_{ij}}(y_i,y_j).\end{align*} $$
Hence, a tuple
![]() $\overline {a}$
satisfies
$\overline {a}$
satisfies
![]() $\theta (\overline {y})$
if and only if the set defined by
$\theta (\overline {y})$
if and only if the set defined by
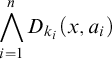 $\displaystyle {\bigwedge _{i=1}^n D_{k_i}(x,a_i)}$
is not empty.
$\displaystyle {\bigwedge _{i=1}^n D_{k_i}(x,a_i)}$
is not empty.
In Theorem 3.11 we showed that for each tuple
![]() $\overline {a} \in M^{|\overline {y}|}$
, the polynomials depend both on the distance
$\overline {a} \in M^{|\overline {y}|}$
, the polynomials depend both on the distance
![]() $\ell $
from the vertex
$\ell $
from the vertex
![]() $c\in A=\operatorname {conv}(a_1,\ldots ,a_n)$
to each element on
$c\in A=\operatorname {conv}(a_1,\ldots ,a_n)$
to each element on
![]() $ \varphi (\mathcal {M},\overline {a})$
and the degree
$ \varphi (\mathcal {M},\overline {a})$
and the degree
![]() $\operatorname {deg}_A(c)$
. As in the previous case, there are only finitely many possible values for
$\operatorname {deg}_A(c)$
. As in the previous case, there are only finitely many possible values for
![]() $\ell $
and
$\ell $
and
![]() $\operatorname {deg}_A(c)$
. In fact,
$\operatorname {deg}_A(c)$
. In fact,
![]() $\ell \leq \min \{k_1,\dots ,k_n\}$
and
$\ell \leq \min \{k_1,\dots ,k_n\}$
and
![]() $\operatorname {deg}_A(c) \leq n$
.
$\operatorname {deg}_A(c) \leq n$
.
Let us fix a tuple
![]() $\overline {a} \in M^n$
and suppose that
$\overline {a} \in M^n$
and suppose that
![]() $\ell = 0$
. This means that the set defined by
$\ell = 0$
. This means that the set defined by
![]() $\varphi (x,\overline {a})$
contains only one element in A. By Proposition 2.7 it also implies that there are indices
$\varphi (x,\overline {a})$
contains only one element in A. By Proposition 2.7 it also implies that there are indices
![]() $i,j\leq n$
such that
$i,j\leq n$
such that
![]() $\ell _{ij} = 0$
. Hence, we can define the formula and the corresponding polynomial for this case as
$\ell _{ij} = 0$
. Hence, we can define the formula and the corresponding polynomial for this case as
Now suppose that
![]() $\ell> 0$
and
$\ell> 0$
and
![]() $\operatorname {deg}_A(c) = 1$
. In this case
$\operatorname {deg}_A(c) = 1$
. In this case
![]() $c=a_s$
for some s,
$c=a_s$
for some s,
![]() $k_s = \min \{k_1, \dots , k_n\}$
and for every
$k_s = \min \{k_1, \dots , k_n\}$
and for every
![]() $i\leq n$
,
$i\leq n$
,
![]() $\operatorname {dist}(a_i,a_s) = k_i - k_s $
. In this way, we can define the formula and the respective polynomial as
$\operatorname {dist}(a_i,a_s) = k_i - k_s $
. In this way, we can define the formula and the respective polynomial as
For the general case when
![]() $\ell> 0$
and
$\ell> 0$
and
![]() $\operatorname {deg}(c) = m> 1$
, we have to define a formula that stating that
$\operatorname {deg}(c) = m> 1$
, we have to define a formula that stating that
![]() $\operatorname {deg}(c) = m> 1$
. In this case, there are m vertices
$\operatorname {deg}(c) = m> 1$
. In this case, there are m vertices
![]() $a_{s_1}, a_{s_2}, \dots a_{s_m}$
such that
$a_{s_1}, a_{s_2}, \dots a_{s_m}$
such that
![]() $\ell _{s_i,s_j}$
is equal to
$\ell _{s_i,s_j}$
is equal to
![]() $\ell $
for every
$\ell $
for every
![]() $i,j \leq m$
. Proposition 2.9 guarantees that the vertices
$i,j \leq m$
. Proposition 2.9 guarantees that the vertices
![]() $a_f$
with
$a_f$
with
![]() $f \notin \{s_1,\dots ,s_m\}$
there exists a pair of vertices
$f \notin \{s_1,\dots ,s_m\}$
there exists a pair of vertices
![]() $a_{s_1^t}$
and
$a_{s_1^t}$
and
![]() $a_{s_2^t}$
such that either
$a_{s_2^t}$
such that either
![]() $\ell = \ell _{f,s_i}$
or
$\ell = \ell _{f,s_i}$
or
![]() $\ell = \ell _{f,s_j}$
but not both, since otherwise
$\ell = \ell _{f,s_j}$
but not both, since otherwise
![]() $\operatorname {deg}(c)$
would be grater than m. Therefore, we can take the defining formula to be
$\operatorname {deg}(c)$
would be grater than m. Therefore, we can take the defining formula to be
 $$ \begin{align*} &\psi_{\ell,m}(\overline{y})\,:=\, \theta(\overline{y}) \wedge \bigvee_{s_1 < \dots < s_m} \left( \bigwedge_{s_i<s_j} D_{k_{s_i}+k_{s_j}-2\ell}(y_i,y_j) \wedge \right. \\ &\bigwedge_{i \neq s_1,\dots,s_m} \left( \bigvee_{s_i < s_j}(D_{k_i+k_{s_i}-2\ell} (y_i,y_{k_1}) \vee D_{k_i+k_{s_j}-2\ell}(y_i,y_{k_2}) )\right. \\ &\left.\left.\vphantom{\bigwedge_{i \neq s_1,\dots,s_m}}\wedge \lnot (D_{k_i+k_{d_i}-2\ell} (y_i,y_{s_i}) \wedge D_{k_i+k_{s_j}-2\ell}(y_i,y_{s_j}) ) \right) \right), \end{align*} $$
$$ \begin{align*} &\psi_{\ell,m}(\overline{y})\,:=\, \theta(\overline{y}) \wedge \bigvee_{s_1 < \dots < s_m} \left( \bigwedge_{s_i<s_j} D_{k_{s_i}+k_{s_j}-2\ell}(y_i,y_j) \wedge \right. \\ &\bigwedge_{i \neq s_1,\dots,s_m} \left( \bigvee_{s_i < s_j}(D_{k_i+k_{s_i}-2\ell} (y_i,y_{k_1}) \vee D_{k_i+k_{s_j}-2\ell}(y_i,y_{k_2}) )\right. \\ &\left.\left.\vphantom{\bigwedge_{i \neq s_1,\dots,s_m}}\wedge \lnot (D_{k_i+k_{d_i}-2\ell} (y_i,y_{s_i}) \wedge D_{k_i+k_{s_j}-2\ell}(y_i,y_{s_j}) ) \right) \right), \end{align*} $$
and the respective polynomial is
![]() $p_{\ell ,m}(t_1,t_2) = (t_2-m)(t_2-1)^{\ell -1}$
.
$p_{\ell ,m}(t_1,t_2) = (t_2-m)(t_2-1)^{\ell -1}$
.
The only case that is left to analyze occurs when
![]() $\varphi (x,\overline {a})$
defines an empty set. By the construction of the formula
$\varphi (x,\overline {a})$
defines an empty set. By the construction of the formula
![]() $\theta (\overline {y})$
, we can take
$\theta (\overline {y})$
, we can take
![]() $\psi (\overline {y})$
as
$\psi (\overline {y})$
as
![]() $\lnot \theta (\overline {y})$
and the respective polynomial as
$\lnot \theta (\overline {y})$
and the respective polynomial as
![]() $p_0(t_1,t_2) = 0$
. As we saw in Theorem 3.11, this concludes the case when
$p_0(t_1,t_2) = 0$
. As we saw in Theorem 3.11, this concludes the case when
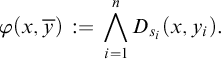 $\displaystyle {\varphi (x,\overline {y})\,:=\, \bigwedge _{i = 1}^n D_{s_i} (x,y_i).}$
$\displaystyle {\varphi (x,\overline {y})\,:=\, \bigwedge _{i = 1}^n D_{s_i} (x,y_i).}$
On the other hand, if
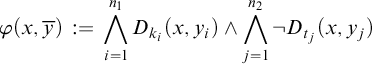 $\displaystyle {\varphi (x,\overline {y}) \,:=\, \bigwedge _{i=1}^{n_1} D_{k_i}(x,y_i) \wedge \bigwedge _{j=1}^{n_2} \lnot D_{t_j}(x,y_j)}$
with
$\displaystyle {\varphi (x,\overline {y}) \,:=\, \bigwedge _{i=1}^{n_1} D_{k_i}(x,y_i) \wedge \bigwedge _{j=1}^{n_2} \lnot D_{t_j}(x,y_j)}$
with
![]() $n_2> 0$
, recall that the proof of Theorem 3.11 provides us an explicit construction of the polynomials that we are looking for in function of polynomials in the previous case. By this construction, the maximum number of polynomials can be bounded above by the product
$n_2> 0$
, recall that the proof of Theorem 3.11 provides us an explicit construction of the polynomials that we are looking for in function of polynomials in the previous case. By this construction, the maximum number of polynomials can be bounded above by the product
 $$ \begin{align*} &\prod_{1\leq i < j \leq n_1} (k_i+k_j+1) \cdot \prod_{r = 1}^{n_2} \left(\prod_{1\leq i < j \leq n_1} (k_i+k_j+1) \cdot \prod_{i=1}^{n_1} (k_i+t_r+1)\right) \cdot\\ & \prod_{1 \leq r_1 < r_2 \leq n_2} \left( \prod_{1\leq i < j \leq n_1} (k_i+k_j+1) \cdot \prod_{i=1}^{n_1} (k_i+t_{r_1}+1) \cdot \prod_{i=1}^{n_1} (k_i+t_{r_2}+1)\right) \cdots \\ & \prod_{1\leq i < j \leq n_1} (k_i+k_j+1) \cdot \prod_{r=1}^{n_2} \left( \prod_{i=1}^{n_1} (k_i+t_{r}+1)\right) < \infty.\\[-44pt] \end{align*} $$
$$ \begin{align*} &\prod_{1\leq i < j \leq n_1} (k_i+k_j+1) \cdot \prod_{r = 1}^{n_2} \left(\prod_{1\leq i < j \leq n_1} (k_i+k_j+1) \cdot \prod_{i=1}^{n_1} (k_i+t_r+1)\right) \cdot\\ & \prod_{1 \leq r_1 < r_2 \leq n_2} \left( \prod_{1\leq i < j \leq n_1} (k_i+k_j+1) \cdot \prod_{i=1}^{n_1} (k_i+t_{r_1}+1) \cdot \prod_{i=1}^{n_1} (k_i+t_{r_2}+1)\right) \cdots \\ & \prod_{1\leq i < j \leq n_1} (k_i+k_j+1) \cdot \prod_{r=1}^{n_2} \left( \prod_{i=1}^{n_1} (k_i+t_{r}+1)\right) < \infty.\\[-44pt] \end{align*} $$
Remark 3.13. In order to show some more examples, we explicitly list below some formulas and respective polynomials for the case
![]() $n=2$
,
$n=2$
,
 $$ \begin{align*} \varphi_1(y_1,y_2) &\equiv D_{k_1+k_2}(y_1,y_2) & p^{\varphi_1}(t_1,t_2) &= 1\\ \varphi_2(y_1,y_2) &\equiv D_{\max\{k_1,k_2\}-\min\{k_1,k_2\}}(y_1,y_2) & p^{\varphi_2}(t_1,t_2) &= (t_1-1)^{\min\{k_1,k_2\}}\\ \varphi_{3,\ell}(y_1,y_2) &\equiv D_{k_1+k_2-2\ell}(y_1,y_2) & p^{\varphi_3}(t_1,t_2) &= (t_1-2)(t_1-1)^{\ell - 1}\\ \varphi_{4}(y_1,y_2) &\equiv \lnot \varphi_1(y_1,y_2) & p^{\varphi_4}(t_1,t_2) &= 0.\\\wedge \lnot \varphi_2(y_1,y_2) &\wedge \bigwedge_{\ell \leq \min\{k_1,k_2\}}\lnot \varphi_{3,\ell}(y_1,y_2) \end{align*} $$
$$ \begin{align*} \varphi_1(y_1,y_2) &\equiv D_{k_1+k_2}(y_1,y_2) & p^{\varphi_1}(t_1,t_2) &= 1\\ \varphi_2(y_1,y_2) &\equiv D_{\max\{k_1,k_2\}-\min\{k_1,k_2\}}(y_1,y_2) & p^{\varphi_2}(t_1,t_2) &= (t_1-1)^{\min\{k_1,k_2\}}\\ \varphi_{3,\ell}(y_1,y_2) &\equiv D_{k_1+k_2-2\ell}(y_1,y_2) & p^{\varphi_3}(t_1,t_2) &= (t_1-2)(t_1-1)^{\ell - 1}\\ \varphi_{4}(y_1,y_2) &\equiv \lnot \varphi_1(y_1,y_2) & p^{\varphi_4}(t_1,t_2) &= 0.\\\wedge \lnot \varphi_2(y_1,y_2) &\wedge \bigwedge_{\ell \leq \min\{k_1,k_2\}}\lnot \varphi_{3,\ell}(y_1,y_2) \end{align*} $$
Remark 3.14. Notice that in Theorem 3.12 we have proved that for every formula
![]() $\varphi (x,\overline {y})$
in one object variable there is finite collection of formulas
$\varphi (x,\overline {y})$
in one object variable there is finite collection of formulas
![]() $\{\psi _i(\overline {y}):i\leq k\}$
that partition the space
$\{\psi _i(\overline {y}):i\leq k\}$
that partition the space
![]() $\mathcal {M}^{|\overline {y}|}$
and define the possible cardinalities of definable sets of the form
$\mathcal {M}^{|\overline {y}|}$
and define the possible cardinalities of definable sets of the form
![]() $\varphi (\mathcal {M},\overline {a})$
as
$\varphi (\mathcal {M},\overline {a})$
as
![]() $p_i(\alpha ,\beta )$
, where
$p_i(\alpha ,\beta )$
, where
![]() $p_i(t_1,t_2)$
is a polynomial in
$p_i(t_1,t_2)$
is a polynomial in
![]() $\mathbb {Z}[t_1,t_2]$
. It is possible to extend this to formulas with several object variables using induction on formulas, but we will use instead the results in the next section together with the so-called Projection Lemma (see [Reference Wolf18, Lemma 2.3.1]) to give a simplified proof of this stronger result.
$\mathbb {Z}[t_1,t_2]$
. It is possible to extend this to formulas with several object variables using induction on formulas, but we will use instead the results in the next section together with the so-called Projection Lemma (see [Reference Wolf18, Lemma 2.3.1]) to give a simplified proof of this stronger result.
4 Measurability of the everywhere infinite forest
In this section we will study the classes of the graphs
![]() $\mathcal {C}_{d,g}$
whose infinite ultraproducts provide models of
$\mathcal {C}_{d,g}$
whose infinite ultraproducts provide models of
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
. We showed in Section 3 that these are classes that induce strong properties on the cardinalities of definable sets in their ultraproducts, so it is natural to ask if they correspond to examples of asymptotic classes of finite graphs.
$\mathcal {T}_\infty $
. We showed in Section 3 that these are classes that induce strong properties on the cardinalities of definable sets in their ultraproducts, so it is natural to ask if they correspond to examples of asymptotic classes of finite graphs.
Note that if
![]() $d:\mathbb {N}\to \mathbb {N}$
is a bounded function (i.e., there is
$d:\mathbb {N}\to \mathbb {N}$
is a bounded function (i.e., there is
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
![]() $d(k)\leq N$
for every
$d(k)\leq N$
for every
![]() $k\in \mathbb {N}$
), then every infinite ultraproduct of graphs in the class
$k\in \mathbb {N}$
), then every infinite ultraproduct of graphs in the class
![]() $\mathcal {C}_{d,g}$
would be a model of
$\mathcal {C}_{d,g}$
would be a model of
![]() $\mathcal {T}_r$
for some
$\mathcal {T}_r$
for some
![]() $r<\omega $
, and so it is strongly minimal. By Lemma 2.5 in [Reference Macpherson and Steinhorn14], this implies that
$r<\omega $
, and so it is strongly minimal. By Lemma 2.5 in [Reference Macpherson and Steinhorn14], this implies that
![]() $\mathcal {C}_{d,g}$
is a 1-dimensional asymptotic class. In contrast, if
$\mathcal {C}_{d,g}$
is a 1-dimensional asymptotic class. In contrast, if
![]() $d:\mathbb {N}\to \mathbb {N}$
is a strictly increasing function, then the infinite ultraproducts of the graphs in the class
$d:\mathbb {N}\to \mathbb {N}$
is a strictly increasing function, then the infinite ultraproducts of the graphs in the class
![]() $\mathcal {C}_{d,g}$
are models of
$\mathcal {C}_{d,g}$
are models of
![]() $\mathcal {T}_\infty $
. Since
$\mathcal {T}_\infty $
. Since
![]() $\mathcal {T}_\infty $
has infinite
$\mathcal {T}_\infty $
has infinite
![]() $\operatorname {SU}$
-rank and every infinite ultraproduct of N-dimensional asymptotic classes has finite
$\operatorname {SU}$
-rank and every infinite ultraproduct of N-dimensional asymptotic classes has finite
![]() $\operatorname {SU}$
-rank (see [Reference Elwes7, Corollary 2.8]), we conclude that
$\operatorname {SU}$
-rank (see [Reference Elwes7, Corollary 2.8]), we conclude that
![]() $\mathcal {C}_{d,g}$
is not an N-dimensional asymptotic class for any
$\mathcal {C}_{d,g}$
is not an N-dimensional asymptotic class for any
![]() $N\in \mathbb {N}$
.
$N\in \mathbb {N}$
.
There is however a notion of multidimensional asymptotic classes (due to S. Anscombe, D. Macpherson, C. Steinhorn, and D. Wolf [Reference Anscombe, Macpherson, Steinhorn and Wolf2]), which generalizes the definition of asymptotic classes allowing certain classes of finite structures whose ultraproducts may have infinite rank. Let us recall some definitions and basic results from [Reference Wolf18].
Definition 4.1. Let
![]() $\mathcal {L}$
be a finitary first-order language and let
$\mathcal {L}$
be a finitary first-order language and let
![]() $\mathcal {C}$
be a class of
$\mathcal {C}$
be a class of
![]() $\mathcal {L}$
-structures. For
$\mathcal {L}$
-structures. For
![]() $m\in \mathbb {N}^+$
, define
$m\in \mathbb {N}^+$
, define
Definition 4.2 (Definable partition).
Let
![]() $\Phi $
be a partition of
$\Phi $
be a partition of
![]() $\mathcal {C}(m)$
. An element
$\mathcal {C}(m)$
. An element
![]() $\pi \in \Phi $
is definable if there exists a parameter-free
$\pi \in \Phi $
is definable if there exists a parameter-free
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\psi (\overline {y})$
with
$\psi (\overline {y})$
with
![]() $|\overline {y}|=m$
such that for every
$|\overline {y}|=m$
such that for every
![]() $(\mathcal {M},\overline {a})\in \mathcal {C}(m)$
we have
$(\mathcal {M},\overline {a})\in \mathcal {C}(m)$
we have
![]() $(\mathcal {M},\overline {a})\in \pi $
if and only if
$(\mathcal {M},\overline {a})\in \pi $
if and only if
![]() $\mathcal {M}\models \psi (\overline {a})$
. The partition
$\mathcal {M}\models \psi (\overline {a})$
. The partition
![]() $\Phi $
is definable if
$\Phi $
is definable if
![]() $\pi $
is definable for every
$\pi $
is definable for every
![]() $\pi \in \Phi $
.
$\pi \in \Phi $
.
Definition 4.3 (
 $\mathcal {R}$
-mec).
$\mathcal {R}$
-mec).
Let
![]() $\mathcal {C}$
be a class of finite
$\mathcal {C}$
be a class of finite
![]() $\mathcal {L}$
-structures and let
$\mathcal {L}$
-structures and let
![]() $\mathcal {R}$
be a set of functions from
$\mathcal {R}$
be a set of functions from
![]() $\mathcal {C}$
to
$\mathcal {C}$
to
![]() $\mathbb {N}$
. Then
$\mathbb {N}$
. Then
![]() $\mathcal {C}$
is a multidimensional exact class for
$\mathcal {C}$
is a multidimensional exact class for
![]() $\mathcal {R}$
in
$\mathcal {R}$
in
![]() $\mathcal {L}$
(or
$\mathcal {L}$
(or
![]() $\mathcal {R}$
-mec in
$\mathcal {R}$
-mec in
![]() $\mathcal {L}$
for short) if for every parameter-free
$\mathcal {L}$
for short) if for every parameter-free
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\varphi (\overline {x},\overline {y})$
with
$\varphi (\overline {x},\overline {y})$
with
![]() $m=|\overline {y}|$
and
$m=|\overline {y}|$
and
![]() $n=|\overline {x}|$
there exists a finite definable partition
$n=|\overline {x}|$
there exists a finite definable partition
![]() $\Phi $
of
$\Phi $
of
![]() $\mathcal {C}(m)$
such that for each
$\mathcal {C}(m)$
such that for each
![]() $\pi \in \Phi $
there is a function
$\pi \in \Phi $
there is a function
![]() $h_\pi \in \mathcal {R}$
such that
$h_\pi \in \mathcal {R}$
such that
for all
![]() $(\mathcal {M},\overline {a})\in \pi $
.
$(\mathcal {M},\overline {a})\in \pi $
.
Definitions 5.1–5.3 given so far correspond exactly to the definitions given in [Reference Wolf18]. However, we give here an equivalent definition of multidimensional exact classes, that suits better the presentation and the results given in this article.
Definition 4.4 (
 $\mathcal {R}$
-mec, alternative definition).
$\mathcal {R}$
-mec, alternative definition).
Let
![]() $\mathcal {C}$
be a class of finite
$\mathcal {C}$
be a class of finite
![]() $\mathcal {L}$
-structures, and let
$\mathcal {L}$
-structures, and let
![]() $\mathcal {R}$
be a set of functions from
$\mathcal {R}$
be a set of functions from
![]() $\mathcal {C}$
to
$\mathcal {C}$
to
![]() $\mathbb {N}$
. We say that
$\mathbb {N}$
. We say that
![]() $\mathcal {C}$
is a multidimensional exact class for
$\mathcal {C}$
is a multidimensional exact class for
![]() $\mathcal {R}$
in
$\mathcal {R}$
in
![]() $\mathcal {L}$
(or
$\mathcal {L}$
(or
![]() $\mathcal {R}$
-mec in
$\mathcal {R}$
-mec in
![]() $\mathcal {L}$
for short) if for every parameter-free
$\mathcal {L}$
for short) if for every parameter-free
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\varphi (\overline {x},\overline {y})$
with
$\varphi (\overline {x},\overline {y})$
with
![]() $m=|\overline {y}|$
and
$m=|\overline {y}|$
and
![]() $n=|\overline {x}|$
there exists finitely many functions
$n=|\overline {x}|$
there exists finitely many functions
![]() $h_1,\ldots ,h_k\in \mathcal {R}$
and formulas
$h_1,\ldots ,h_k\in \mathcal {R}$
and formulas
![]() $\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
such that the following hold:
$\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
such that the following hold:
-
(1) For every
 $\mathcal {M}\in \mathcal {C}$
, the formulas
$\mathcal {M}\in \mathcal {C}$
, the formulas
 $\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
provide a definable partition of
$\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
provide a definable partition of
 $\mathcal {M}^m$
.
$\mathcal {M}^m$
. -
(2) For every structure
 $\mathcal {M}$
in
$\mathcal {M}$
in
 $\mathcal {C}$
and every tuple
$\mathcal {C}$
and every tuple
 $\overline {a}$
from
$\overline {a}$
from
 $\mathcal {M}^m$
, we have
$\mathcal {M}^m$
, we have  $$\begin{align*}|\varphi(\mathcal{M};\overline{a})|=h_i(\mathcal{M}) \text{\ if and only if\ }\mathcal{M}\models \psi_i(\overline{a}).\end{align*}$$
$$\begin{align*}|\varphi(\mathcal{M};\overline{a})|=h_i(\mathcal{M}) \text{\ if and only if\ }\mathcal{M}\models \psi_i(\overline{a}).\end{align*}$$
Also, we say that
![]() $\mathcal {C}$
is an R-polynomial exact class if the set of functions
$\mathcal {C}$
is an R-polynomial exact class if the set of functions
![]() $\mathcal {R}$
is the collection of polynomials with coefficients in some ring R, possibly with several variables. In the case where
$\mathcal {R}$
is the collection of polynomials with coefficients in some ring R, possibly with several variables. In the case where
![]() $R=\mathbb {Q}$
, we simply call them polynomial exact classes.
$R=\mathbb {Q}$
, we simply call them polynomial exact classes.
By the results of A. Pillay in [Reference Pillay16] we know that if
![]() $\mathcal {C}$
is a class of finite
$\mathcal {C}$
is a class of finite
![]() $\mathcal {L}$
-structures and all infinite ultraproducts of structures in
$\mathcal {L}$
-structures and all infinite ultraproducts of structures in
![]() $\mathcal {C}$
are strongly minimal, then
$\mathcal {C}$
are strongly minimal, then
![]() $\mathcal {C}$
is a polynomial exact class and the functions h correspond to polynomials in one variable and integer coefficients. This includes the classes
$\mathcal {C}$
is a polynomial exact class and the functions h correspond to polynomials in one variable and integer coefficients. This includes the classes
![]() $\mathcal {C}_{r,g}$
defined in Section 3, with
$\mathcal {C}_{r,g}$
defined in Section 3, with
![]() $r\geq 1$
fixed. Pillay’s results were generalized by A. van Abel in [Reference Van Abel1] to classes whose infinite ultraproducts are uncountably categorical, and in this case the polynomials may have rational coefficients. Some other examples of polynomial exact classes include the class of abelian groups and the class
$r\geq 1$
fixed. Pillay’s results were generalized by A. van Abel in [Reference Van Abel1] to classes whose infinite ultraproducts are uncountably categorical, and in this case the polynomials may have rational coefficients. Some other examples of polynomial exact classes include the class of abelian groups and the class
![]() $\mathcal {C}(d,\mathcal {L})$
of all finite
$\mathcal {C}(d,\mathcal {L})$
of all finite
![]() $\mathcal {L}$
-structures with at most d 4-types (see [Reference Wolf18, Theorem 4.6.4]).
$\mathcal {L}$
-structures with at most d 4-types (see [Reference Wolf18, Theorem 4.6.4]).
The following result shows that in order to verify that a class
![]() $\mathcal {C}$
is a multidimensional exact class, it is enough to verify the conditions for formulas
$\mathcal {C}$
is a multidimensional exact class, it is enough to verify the conditions for formulas
![]() $\varphi (x;\overline {y})$
in one object-variable x.
$\varphi (x;\overline {y})$
in one object-variable x.
Fact 4.5 (Projection Lemma, Lemma 2.3.1 in [Reference Wolf18]).
Let
![]() $\mathcal {C}$
be a class of
$\mathcal {C}$
be a class of
![]() $\mathcal {L}$
-structures such that the definition of an R-mec holds in
$\mathcal {L}$
-structures such that the definition of an R-mec holds in
![]() $\mathcal {C}$
for all formulas
$\mathcal {C}$
for all formulas
![]() $\varphi (x,\overline {y})$
with a single object variable x. Then
$\varphi (x,\overline {y})$
with a single object variable x. Then
![]() $\mathcal {C}$
is an
$\mathcal {C}$
is an
![]() $R'$
-mec in
$R'$
-mec in
![]() $\mathcal {L}$
, where
$\mathcal {L}$
, where
![]() $R'$
is generated under addition and multiplication by the functions in R.
$R'$
is generated under addition and multiplication by the functions in R.
Theorem 4.6. Let
![]() $d,g:\mathbb {N}\to \mathbb {N}$
be two non-decreasing unbounded functions, and let
$d,g:\mathbb {N}\to \mathbb {N}$
be two non-decreasing unbounded functions, and let
![]() $\mathcal {C}_{d,g}=\{H_k:k\in \mathbb {N}\}$
be a collection of finite graphs such that for every
$\mathcal {C}_{d,g}=\{H_k:k\in \mathbb {N}\}$
be a collection of finite graphs such that for every
![]() $k\in \mathbb {N}$
the graph
$k\in \mathbb {N}$
the graph
![]() $H_k$
is
$H_k$
is
![]() $d(k)$
-regular of girth at least
$d(k)$
-regular of girth at least
![]() $g(k)$
. Then, for every formula
$g(k)$
. Then, for every formula
![]() $\varphi (x,\overline {y})$
in the language of graphs, there is a finite set of polynomials
$\varphi (x,\overline {y})$
in the language of graphs, there is a finite set of polynomials
![]() $E_\varphi =\{p_1(t_1,t_2),\ldots ,p_n(t_1,t_2)\}\subseteq \mathbb {Z}[t_1,t_2]$
and finitely many formulas
$E_\varphi =\{p_1(t_1,t_2),\ldots ,p_n(t_1,t_2)\}\subseteq \mathbb {Z}[t_1,t_2]$
and finitely many formulas
![]() $\{\psi _1(\overline {y}),\ldots , \psi _n(\overline {y})\}$
such that:
$\{\psi _1(\overline {y}),\ldots , \psi _n(\overline {y})\}$
such that:
-
(1) For every graph
 $H_k$
in the class
$H_k$
in the class
 $\mathcal {C}_{d,g}$
, the collection of sets
$\mathcal {C}_{d,g}$
, the collection of sets
 $\{\psi _1(H_k^{|\overline {y}|}),\ldots , \psi _n(H_k^{|\overline {y}|})\}$
is a partition of
$\{\psi _1(H_k^{|\overline {y}|}),\ldots , \psi _n(H_k^{|\overline {y}|})\}$
is a partition of
 $H_k^{|\overline {y}|}$
.
$H_k^{|\overline {y}|}$
. -
(2) For every
 $H_k\in \mathcal {C}_{d,g}$
and every tuple
$H_k\in \mathcal {C}_{d,g}$
and every tuple
 $\overline {a}$
from
$\overline {a}$
from
 $H_k^{|\overline {y}|}$
,
$H_k^{|\overline {y}|}$
,  $$\begin{align*}|\varphi(H_k,\overline{a})|=p_i(|H_k|,d(k)) \text{ if and only if }H_k\models \psi_i(\overline{a}).\end{align*}$$
$$\begin{align*}|\varphi(H_k,\overline{a})|=p_i(|H_k|,d(k)) \text{ if and only if }H_k\models \psi_i(\overline{a}).\end{align*}$$
Proof. For a given formula
![]() $\varphi (x,\overline {y})$
, consider the finite set of polynomials
$\varphi (x,\overline {y})$
, consider the finite set of polynomials
and the formulas
![]() $\psi _1(\overline {y}),\ldots ,\psi _{k_\varphi }(\overline {y})$
given by Theorem 3.12. By quantifier elimination in
$\psi _1(\overline {y}),\ldots ,\psi _{k_\varphi }(\overline {y})$
given by Theorem 3.12. By quantifier elimination in
![]() $\mathcal {T}_\infty $
(Proposition A.1), there is a quantifier-free
$\mathcal {T}_\infty $
(Proposition A.1), there is a quantifier-free
![]() $\mathcal {L}'$
-formula
$\mathcal {L}'$
-formula
![]() $\theta (x,\overline {y})$
such that
$\theta (x,\overline {y})$
such that
![]() $\mathcal {T}_\infty \models \forall x,\overline {y}\left (\varphi (x,\overline {y})\leftrightarrow \theta (x,\overline {y})\right ).$
Moreover, since
$\mathcal {T}_\infty \models \forall x,\overline {y}\left (\varphi (x,\overline {y})\leftrightarrow \theta (x,\overline {y})\right ).$
Moreover, since
![]() $\mathcal {T}_\infty $
is axiomatized by the collection of sentences
$\mathcal {T}_\infty $
is axiomatized by the collection of sentences
![]() $\{\sigma _n,\tau _n:n<\omega \}$
, by compactness there is some
$\{\sigma _n,\tau _n:n<\omega \}$
, by compactness there is some
![]() $k_0\in \mathbb {N}$
such that
$k_0\in \mathbb {N}$
such that
![]() $\{\sigma _n,\tau _n:n\leq k_0\}\models \forall x,\overline {y}\left (\varphi (x,\overline {y})\leftrightarrow \theta (x,\overline {y})\right ).$
$\{\sigma _n,\tau _n:n\leq k_0\}\models \forall x,\overline {y}\left (\varphi (x,\overline {y})\leftrightarrow \theta (x,\overline {y})\right ).$
We will consider now a further expansion of the language
![]() $\mathcal {L}'$
to a two-sorted language
$\mathcal {L}'$
to a two-sorted language
![]() $\mathcal {L}^+$
defined as follows:
$\mathcal {L}^+$
defined as follows:
-
• In
 $\mathcal {L}^+$
there are two sorts: one sort
$\mathcal {L}^+$
there are two sorts: one sort
 $\mathbb {K}$
with the language
$\mathbb {K}$
with the language
 $\mathcal {L}'$
, and another sort
$\mathcal {L}'$
, and another sort
 $\mathbb {D}$
carrying the language of ordered rings
$\mathbb {D}$
carrying the language of ordered rings
 $\mathcal {L}_{or}=\{+,-,\cdot ,<\}$
together with two constant symbols,
$\mathcal {L}_{or}=\{+,-,\cdot ,<\}$
together with two constant symbols,
 $\{A,B\}$
.
$\{A,B\}$
. -
• For every formula
 $\varphi (\overline {x},\overline {y})$
in the language
$\varphi (\overline {x},\overline {y})$
in the language
 $\mathcal {L}^{\prime }_g$
, we add a function symbol
$\mathcal {L}^{\prime }_g$
, we add a function symbol
 $f_\varphi :\mathbb {K}^{|\overline {y}|}\to \mathbb {D}$
.
$f_\varphi :\mathbb {K}^{|\overline {y}|}\to \mathbb {D}$
.
Every finite structure
![]() $H_k$
in
$H_k$
in
![]() $\mathcal {C}_{d,g}$
induces an
$\mathcal {C}_{d,g}$
induces an
![]() $\mathcal {L}^+$
-structure
$\mathcal {L}^+$
-structure
![]() $H_k^+$
in a canonical way. Namely, we can consider the pair
$H_k^+$
in a canonical way. Namely, we can consider the pair
![]() $(H_k,\mathbb {R})$
with the usual interpretation of the languages
$(H_k,\mathbb {R})$
with the usual interpretation of the languages
![]() $\mathcal {L}'$
and
$\mathcal {L}'$
and
![]() $\mathcal {L}_{or}$
in each sort, together with the interpretations
$\mathcal {L}_{or}$
in each sort, together with the interpretations
![]() $A^{H_k}:=|H_k|$
and
$A^{H_k}:=|H_k|$
and
![]() $B^{H_k}:=d(k)$
, the degree of regularity of the graph
$B^{H_k}:=d(k)$
, the degree of regularity of the graph
![]() $H_k$
. Also, we can interpret the functions
$H_k$
. Also, we can interpret the functions
![]() $f_{\varphi (\overline {x},\overline {y})}: H_k^{|\overline {y}|}\to \mathbb {R}$
as
$f_{\varphi (\overline {x},\overline {y})}: H_k^{|\overline {y}|}\to \mathbb {R}$
as
![]() $f_\varphi (\overline {a}):=|\varphi (H_k^{|\overline {x}|},\overline {a})|$
.
$f_\varphi (\overline {a}):=|\varphi (H_k^{|\overline {x}|},\overline {a})|$
.
Therefore, in the language
![]() $\mathcal {L}^+$
, the statement saying that the collection of polynomials
$\mathcal {L}^+$
, the statement saying that the collection of polynomials
![]() $p_1(t_1,t_2)$
,
$p_1(t_1,t_2)$
,
![]() $p_2(t_1,t_2),\ldots ,p_k(t_1,t_2)$
, together with the formulas
$p_2(t_1,t_2),\ldots ,p_k(t_1,t_2)$
, together with the formulas
![]() $\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
satisfy the conclusion of Theorem 4.6 for the formula
$\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
satisfy the conclusion of Theorem 4.6 for the formula
![]() $\varphi (x,\overline {y})$
can be written in a first-order fashion using the following
$\varphi (x,\overline {y})$
can be written in a first-order fashion using the following
![]() $\mathcal {L}^+$
-sentence:
$\mathcal {L}^+$
-sentence:
 $$ \begin{align*} &\Phi(\varphi,p_1,\ldots,p_k,\psi_1,\ldots,\psi_k):\\ &\forall \overline{y}\left(\bigvee_{i=1}^k \psi_i(\overline{y})\right)\wedge \forall \overline{y}\left(\bigwedge_{1\leq i<j\leq k}\neg\left(\psi_i(\overline{y})\wedge \psi_j(\overline{y})\right)\right)\\&\quad\wedge\forall \overline{y}\left(\bigwedge_{1\leq i\leq k}[f_\varphi(\overline{y})=p_i(A,B)\leftrightarrow \psi_i(\overline{y})]\right). \end{align*} $$
$$ \begin{align*} &\Phi(\varphi,p_1,\ldots,p_k,\psi_1,\ldots,\psi_k):\\ &\forall \overline{y}\left(\bigvee_{i=1}^k \psi_i(\overline{y})\right)\wedge \forall \overline{y}\left(\bigwedge_{1\leq i<j\leq k}\neg\left(\psi_i(\overline{y})\wedge \psi_j(\overline{y})\right)\right)\\&\quad\wedge\forall \overline{y}\left(\bigwedge_{1\leq i\leq k}[f_\varphi(\overline{y})=p_i(A,B)\leftrightarrow \psi_i(\overline{y})]\right). \end{align*} $$
Note that there must be an integer N such that for every
![]() $k\geq N$
we have
$k\geq N$
we have
since otherwise there would be a subsequence of graphs of graphs
![]() $\{H_{k_i}:i<\omega \}\subseteq \mathcal {C}_{d,g}$
such that
$\{H_{k_i}:i<\omega \}\subseteq \mathcal {C}_{d,g}$
such that
![]() $H_{k_i}^+\models \neg \Phi (\varphi ,p_1,\ldots ,p_k,\psi _1,\ldots ,\psi _k)$
, and every ultraproduct with respect to an ultrafilter
$H_{k_i}^+\models \neg \Phi (\varphi ,p_1,\ldots ,p_k,\psi _1,\ldots ,\psi _k)$
, and every ultraproduct with respect to an ultrafilter
![]() $\mathcal {U}$
containing the set
$\mathcal {U}$
containing the set
![]() $\{k_i:i<\omega \}$
would contradict Theorem 3.12.
$\{k_i:i<\omega \}$
would contradict Theorem 3.12.
So, by taking
![]() $C=\max \{|H_k|:k\leq N\}$
, completing the collection of possible polynomials with
$C=\max \{|H_k|:k\leq N\}$
, completing the collection of possible polynomials with
![]() $j=0,1,\ldots ,C$
and using the formulas
$j=0,1,\ldots ,C$
and using the formulas
![]() $\psi _j'\,:=\, \exists ^{=j}x\varphi (x,\overline {y})$
, we obtained the desired result.
$\psi _j'\,:=\, \exists ^{=j}x\varphi (x,\overline {y})$
, we obtained the desired result.
Theorem 4.7. Let
![]() $d,g:\mathbb {N}\to \mathbb {N}$
be two non-decreasing unbounded functions. If
$d,g:\mathbb {N}\to \mathbb {N}$
be two non-decreasing unbounded functions. If
![]() $\mathcal {C}_{d,g}=\{H_k:k\in \mathbb {N}\}$
is a collection of finite graphs such that for every
$\mathcal {C}_{d,g}=\{H_k:k\in \mathbb {N}\}$
is a collection of finite graphs such that for every
![]() $k\in \mathbb {N}$
the graph
$k\in \mathbb {N}$
the graph
![]() $H_k$
is
$H_k$
is
![]() $d(k)$
-regular of girth at least
$d(k)$
-regular of girth at least
![]() $g(k)$
then
$g(k)$
then
![]() $\mathcal {C}_{d,g}$
is a polynomial exact class.
$\mathcal {C}_{d,g}$
is a polynomial exact class.
Proof. Note that Theorem 4.6 establishes precisely the polynomial exact conditions for formulas in one object variable
![]() $\varphi (x,\overline {y})$
. This, together with the Projection Lemma, yields the desired result.
$\varphi (x,\overline {y})$
. This, together with the Projection Lemma, yields the desired result.
A direct consequence of Theorem 4.7 is precisely the desired characterization of cardinalities of definable sets in pseudofinite models of
![]() $\mathcal {T}_\infty $
, for formulas in several object variables.
$\mathcal {T}_\infty $
, for formulas in several object variables.
Corollary 4.8. Let
![]() $d,g:\mathbb {N}\to \mathbb {N}$
be two non-decreasing unbounded functions, and let
$d,g:\mathbb {N}\to \mathbb {N}$
be two non-decreasing unbounded functions, and let
![]() $\mathcal {C}_{d,g}=\{H_k:k\in \mathbb {N}\}$
be a collection of finite graphs such that for every
$\mathcal {C}_{d,g}=\{H_k:k\in \mathbb {N}\}$
be a collection of finite graphs such that for every
![]() $k\in \mathbb {N}$
the graph
$k\in \mathbb {N}$
the graph
![]() $H_k$
is
$H_k$
is
![]() $d(k)$
-regular of girth at least
$d(k)$
-regular of girth at least
![]() $g(k)$
. Consider the ultraproduct
$g(k)$
. Consider the ultraproduct
![]() $M=\prod _{\mathcal {U}}H_k$
of the graphs in
$M=\prod _{\mathcal {U}}H_k$
of the graphs in
![]() $\mathcal {C}_{d,g}$
with respect to a non-principal ultrafilter
$\mathcal {C}_{d,g}$
with respect to a non-principal ultrafilter
![]() $\mathcal {U}$
. Then, for every formula
$\mathcal {U}$
. Then, for every formula
![]() $\varphi (\overline {x},\overline {y})$
there exists finitely many polynomials
$\varphi (\overline {x},\overline {y})$
there exists finitely many polynomials
![]() $p_1(t_1,t_2),\ldots ,p_{k_\varphi }(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
and finitely many formulas
$p_1(t_1,t_2),\ldots ,p_{k_\varphi }(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
and finitely many formulas
![]() $\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
in the language of graphs such that:
$\psi _1(\overline {y}),\ldots ,\psi _k(\overline {y})$
in the language of graphs such that:
-
(1)
 $\{\psi _1(M^{|\overline {y}|}),\ldots ,\psi _{k}(\overline {M}^{|\overline {y}|})\}$
forms a partition of
$\{\psi _1(M^{|\overline {y}|}),\ldots ,\psi _{k}(\overline {M}^{|\overline {y}|})\}$
forms a partition of
 $M^{|\overline {y}|}$
.
$M^{|\overline {y}|}$
. -
(2) For every
 $\overline {a}\in M^{|\overline {y}|}$
we have
$\overline {a}\in M^{|\overline {y}|}$
we have
 $|\varphi (M^{|\overline {x}|},\overline {a})|=p_i(\alpha ,\beta )$
if and only if
$|\varphi (M^{|\overline {x}|},\overline {a})|=p_i(\alpha ,\beta )$
if and only if
 $M\models \psi _i(\overline {a})$
, where
$M\models \psi _i(\overline {a})$
, where
 $\alpha =|M|$
and
$\alpha =|M|$
and
 $\beta =|\{x\in M: xRb\}|=[d(k)]_{\mathcal {U}}$
where b is an arbitrary vertex in M.
$\beta =|\{x\in M: xRb\}|=[d(k)]_{\mathcal {U}}$
where b is an arbitrary vertex in M.
Remark 4.9. In [Reference Elwes and Macpherson8] it is proved that every ultraproduct of an N-dimensional asymptotic class that is stable must be one-based. The previous corollary shows that this result does not extend to multidimensional asymptotic classes—even in the polynomial exact case, and assuming
![]() $\omega $
-stability—because the theory
$\omega $
-stability—because the theory
![]() $\mathcal {T}_\infty $
of the everywhere infinite forest is
$\mathcal {T}_\infty $
of the everywhere infinite forest is
![]() $\omega $
-stable but not one-based.
$\omega $
-stable but not one-based.
Remark 4.10. In [Reference Dahan5], X. Dahan shows that there are families of
![]() $(d+1)$
-regular graphs which have girth
$(d+1)$
-regular graphs which have girth
![]() $\geq \log _d |G_n|$
. These are Caley graphs on
$\geq \log _d |G_n|$
. These are Caley graphs on
![]() $PGL(\mathbb {F}_q)$
, and are inspired on the Ramanujan graphs of Lubotzky–Phillips–Sarnak and Margulis [Reference Lubotzky, Phillips and Sarnak13].
$PGL(\mathbb {F}_q)$
, and are inspired on the Ramanujan graphs of Lubotzky–Phillips–Sarnak and Margulis [Reference Lubotzky, Phillips and Sarnak13].
Ramanujan graphs have been proposed as a theoretical basis for elliptic curve cryptography, especially for the study of percolation in large networks. Given the properties of large regularity degree and large girth, the infinite ultraproducts of these classes of Ramanujan graphs are models of
![]() $\mathcal {T}_\infty $
due to Proposition 3.6 and Theorem 3.7, and they form examples of polynomial exact classes of graphs by Theorem 4.7
$\mathcal {T}_\infty $
due to Proposition 3.6 and Theorem 3.7, and they form examples of polynomial exact classes of graphs by Theorem 4.7
5 Pseudofinite dimensions and Morley rank in
 $\mathcal {T}_\infty $
$\mathcal {T}_\infty $
In this section we show that for the pseudofinite models of
![]() $\mathcal {T}_\infty $
described in Section 3 it is possible to calculate the SU-rank (equal to the Morley rank in this context) for definable sets
$\mathcal {T}_\infty $
described in Section 3 it is possible to calculate the SU-rank (equal to the Morley rank in this context) for definable sets
![]() $X\subseteq \mathcal {M}^k$
using the counting polynomial
$X\subseteq \mathcal {M}^k$
using the counting polynomial
![]() $p_X(t_1,t_2)$
provided by Corollary 4.8. In models of
$p_X(t_1,t_2)$
provided by Corollary 4.8. In models of
![]() $\mathcal {T}_\infty $
, we can define the ordinal distance between a vertex b and a set A as
$\mathcal {T}_\infty $
, we can define the ordinal distance between a vertex b and a set A as
![]() $D(b/A)=\operatorname {dist}(b,\operatorname {conv}(A))$
if there a finite path between b and A, or
$D(b/A)=\operatorname {dist}(b,\operatorname {conv}(A))$
if there a finite path between b and A, or
![]() $\omega $
otherwise. This combinatorially defined quantity turns out to be the key to understand the Morley rank in models of
$\omega $
otherwise. This combinatorially defined quantity turns out to be the key to understand the Morley rank in models of
![]() $\mathcal {T}_\infty $
.
$\mathcal {T}_\infty $
.
Theorem 5.1. Let
![]() $\mathcal {M}\models \mathcal {T}_\infty $
and let
$\mathcal {M}\models \mathcal {T}_\infty $
and let
![]() $A\subseteq M$
be a small subset of parameters. Then, for every tuple
$A\subseteq M$
be a small subset of parameters. Then, for every tuple
![]() $\overline {b}=(b_1,\ldots ,b_n)\in M^n$
we have
$\overline {b}=(b_1,\ldots ,b_n)\in M^n$
we have
 $$\begin{align*}\operatorname{SU}(\overline{b}/A)=\operatorname{RM}(\overline{b}/A)=\bigoplus_{i=1}^n D(b_i/A\overline{b}_{<i}),\end{align*}$$
$$\begin{align*}\operatorname{SU}(\overline{b}/A)=\operatorname{RM}(\overline{b}/A)=\bigoplus_{i=1}^n D(b_i/A\overline{b}_{<i}),\end{align*}$$
where for two countable ordinals in Cantor normal form
![]() $\alpha =\sum _{i=1}^k\omega ^{\gamma _i}\cdot n_i$
and
$\alpha =\sum _{i=1}^k\omega ^{\gamma _i}\cdot n_i$
and
![]() $\beta =\sum _{i=1}^k\omega ^{\gamma _i}\cdot m_i$
, we define the sum
$\beta =\sum _{i=1}^k\omega ^{\gamma _i}\cdot m_i$
, we define the sum
![]() $\alpha \oplus \beta =\sum _{i=1}^k \omega ^{\gamma _i}\cdot (n_i+m_i)$
.
$\alpha \oplus \beta =\sum _{i=1}^k \omega ^{\gamma _i}\cdot (n_i+m_i)$
.
Throughout this section, we will suppose that
![]() $\mathcal {M}$
is an infinite ultraproduct of structures in a class
$\mathcal {M}$
is an infinite ultraproduct of structures in a class
![]() $\mathcal {C}_{d,g}=\{H_n:n\in \mathbb {N}\}$
of finite graphs such that for every
$\mathcal {C}_{d,g}=\{H_n:n\in \mathbb {N}\}$
of finite graphs such that for every
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $H_n$
is a
$H_n$
is a
![]() $d(n)$
-regular and has girth
$d(n)$
-regular and has girth
![]() $g(n)$
, for some increasing functions
$g(n)$
, for some increasing functions
![]() $d,g:\mathbb {N}\to \mathbb {N}$
. By Theorem 3.7,
$d,g:\mathbb {N}\to \mathbb {N}$
. By Theorem 3.7,
![]() $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
![]() $\mathcal {T}_\infty $
.
$\mathcal {T}_\infty $
.
As in Section 3, let us denote by
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
the non-standard cardinalities
$\beta $
the non-standard cardinalities
![]() $\alpha =[|G_n|]_{\mathcal {U}}$
and
$\alpha =[|G_n|]_{\mathcal {U}}$
and
![]() $\beta =[d(n)]_{\mathcal {U}}$
, respectively. By Theorem 3.11 and Corollary 4.8, we know already that for every definable set X there is a polynomial
$\beta =[d(n)]_{\mathcal {U}}$
, respectively. By Theorem 3.11 and Corollary 4.8, we know already that for every definable set X there is a polynomial
![]() $p_X(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
such that the non-standard cardinality of X is precisely
$p_X(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
such that the non-standard cardinality of X is precisely
![]() $p_X(\alpha ,\beta )$
.
$p_X(\alpha ,\beta )$
.
Definition 5.2. For a monomial
![]() $At_1^mt_2^n\in \mathbb {Z}[t_1,t_2]$
, we define its pair-degree as the pair
$At_1^mt_2^n\in \mathbb {Z}[t_1,t_2]$
, we define its pair-degree as the pair
![]() $(m,n)\in \mathbb {N}\times \mathbb {N}$
. Also, for a polynomial
$(m,n)\in \mathbb {N}\times \mathbb {N}$
. Also, for a polynomial
![]() $p(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
, we define its leading-degree as the maximum of the pair-degrees of its monomials with respect to the lexicographical order, or equivalently, as the pair-degree of the monomial in
$p(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
, we define its leading-degree as the maximum of the pair-degrees of its monomials with respect to the lexicographical order, or equivalently, as the pair-degree of the monomial in
![]() $p(t_1,t_2)$
that has the highest degree in the variable
$p(t_1,t_2)$
that has the highest degree in the variable
![]() $t_1$
.
$t_1$
.
Finally, we will define the leading monomial of a polynomial
![]() $p(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
to be the monomial whose pair-degree is precisely the leading-degree of
$p(t_1,t_2)\in \mathbb {Z}[t_1,t_2]$
to be the monomial whose pair-degree is precisely the leading-degree of
![]() $p(t_1,t_2)$
.
$p(t_1,t_2)$
.
Theorem 5.3. Suppose that X is a non-empty definable subset of
![]() $\mathcal {M}^k$
, and let
$\mathcal {M}^k$
, and let
![]() $p_X(t_1,t_2)$
be the polynomial satisfying
$p_X(t_1,t_2)$
be the polynomial satisfying
![]() $|X|=p_X(\alpha ,\beta )$
. If the leading monomial of
$|X|=p_X(\alpha ,\beta )$
. If the leading monomial of
![]() $P_X(t_1,t_2)$
is
$P_X(t_1,t_2)$
is
![]() $At_1^mt_2^n$
then the Morley rank of X is precisely
$At_1^mt_2^n$
then the Morley rank of X is precisely
![]() $(\omega \cdot m)\oplus n$
.
$(\omega \cdot m)\oplus n$
.
Proof. We will prove this result by induction on k. For
![]() $k=1$
, suppose that
$k=1$
, suppose that
![]() $\varphi (x;\overline {a})$
is a formula defining a non-empty set
$\varphi (x;\overline {a})$
is a formula defining a non-empty set
![]() $X\subseteq \mathcal {M}^1$
, with
$X\subseteq \mathcal {M}^1$
, with
![]() $\overline {a}=a_1,\ldots ,a_s$
. Using quantifier elimination and normal prenex form, we may assume that
$\overline {a}=a_1,\ldots ,a_s$
. Using quantifier elimination and normal prenex form, we may assume that
![]() $\varphi (x;\overline {a})$
is equivalent to a disjunction of conjunctions of basic formulas. Moreover, by adding formulas in the conjunctions we may assume without loss of generality that the disjunctives are pairwise inconsistent.
$\varphi (x;\overline {a})$
is equivalent to a disjunction of conjunctions of basic formulas. Moreover, by adding formulas in the conjunctions we may assume without loss of generality that the disjunctives are pairwise inconsistent.
Since the Morley rank of a finite union of definable sets is equal to the maximum of the Morley ranks of its parts, we may assume that
![]() $\varphi (x;\overline {a})$
is equivalent to a formula of the form
$\varphi (x;\overline {a})$
is equivalent to a formula of the form
for some sets
![]() $I,J\subseteq \{1,\ldots ,s\}$
and non-negative integers
$I,J\subseteq \{1,\ldots ,s\}$
and non-negative integers
![]() $\{k_i:i\in I\}$
and
$\{k_i:i\in I\}$
and
![]() $\{\ell _j:j\in J\}$
. Let b be a generic element in X, that is, an element
$\{\ell _j:j\in J\}$
. Let b be a generic element in X, that is, an element
![]() $b\in X$
such that
$b\in X$
such that
![]() $\operatorname {RM}(X)=\operatorname {RM}(b/\overline {a})$
.
$\operatorname {RM}(X)=\operatorname {RM}(b/\overline {a})$
.
If
![]() $I\neq \emptyset $
, we know by Proposition 2.7 that there is an element
$I\neq \emptyset $
, we know by Proposition 2.7 that there is an element
![]() $c\in \operatorname {conv}(\{a_i:i\in I\})$
and
$c\in \operatorname {conv}(\{a_i:i\in I\})$
and
![]() $\ell \in \mathbb {N}$
such that for any element
$\ell \in \mathbb {N}$
such that for any element
![]() $b'$
,
$b'$
,
![]() $\mathcal {M}\models \bigwedge _{i\in I}D_{k_i}(b',a_i)$
if and only if
$\mathcal {M}\models \bigwedge _{i\in I}D_{k_i}(b',a_i)$
if and only if
![]() $\operatorname {dist}(b',c)=\ell $
and
$\operatorname {dist}(b',c)=\ell $
and
![]() $P(b',c)\cap \operatorname {conv}(\{a_i:i\in I\})=\{c\}$
. By Theorem 5.1 we obtain the equalities
$P(b',c)\cap \operatorname {conv}(\{a_i:i\in I\})=\{c\}$
. By Theorem 5.1 we obtain the equalities
and calculating the size of X we obtain
![]() $|X|=(\beta -\operatorname {deg}_{\operatorname {conv}(\overline {a})}(c))\cdot (\beta -1)^{\ell -1}=p_X(\alpha ,\beta )$
, showing that the leading monomial of
$|X|=(\beta -\operatorname {deg}_{\operatorname {conv}(\overline {a})}(c))\cdot (\beta -1)^{\ell -1}=p_X(\alpha ,\beta )$
, showing that the leading monomial of
![]() $p_X(t_1,t_2)$
is
$p_X(t_1,t_2)$
is
![]() $t_2^{\ell }$
, as desired.
$t_2^{\ell }$
, as desired.
Suppose now that
![]() $I=\emptyset $
. Hence
$I=\emptyset $
. Hence
![]() $\varphi (x;\overline {a})$
is equivalent to a conjunction of the form
$\varphi (x;\overline {a})$
is equivalent to a conjunction of the form
![]() $\displaystyle {\bigwedge _{j\in J}\neg D_{\ell _j}(x,a_j)}$
, which defines the set
$\displaystyle {\bigwedge _{j\in J}\neg D_{\ell _j}(x,a_j)}$
, which defines the set
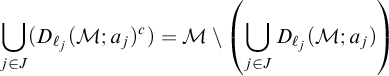 $\displaystyle {\bigcup _{j\in J}(D_{\ell _j}(\mathcal {M};a_j)^c)=\mathcal {M}\setminus \left (\bigcup _{j\in J}D_{\ell _j}(\mathcal {M};a_j)\right )}$
. Using inclusion–exclusion, we obtain that the size
$\displaystyle {\bigcup _{j\in J}(D_{\ell _j}(\mathcal {M};a_j)^c)=\mathcal {M}\setminus \left (\bigcup _{j\in J}D_{\ell _j}(\mathcal {M};a_j)\right )}$
. Using inclusion–exclusion, we obtain that the size
![]() $|X|$
has the form
$|X|$
has the form
![]() $\alpha -q(\beta )$
for some polynomial
$\alpha -q(\beta )$
for some polynomial
![]() $q(t_2)\in \mathbb {Z}[t_2]$
, showing that the leading monomial of
$q(t_2)\in \mathbb {Z}[t_2]$
, showing that the leading monomial of
![]() $p_X(t_1,t_2)$
is
$p_X(t_1,t_2)$
is
![]() $t_1^1$
. On the other hand, since
$t_1^1$
. On the other hand, since
![]() $\operatorname {RM}\left (\bigwedge _{j\in J}D_{\ell _j}(x;a_j)\right )$
is finite, we have
$\operatorname {RM}\left (\bigwedge _{j\in J}D_{\ell _j}(x;a_j)\right )$
is finite, we have
![]() $\operatorname {RM}(X)=\operatorname {RM}(\mathcal {M})=\omega =(\omega \cdot 1)\oplus 0$
. This completes the proof of the case
$\operatorname {RM}(X)=\operatorname {RM}(\mathcal {M})=\omega =(\omega \cdot 1)\oplus 0$
. This completes the proof of the case
![]() $k=1$
.
$k=1$
.
Suppose now the result holds for every definable subset of
![]() $\mathcal {M}^k$
. Let X be a non-empty definable subset of
$\mathcal {M}^k$
. Let X be a non-empty definable subset of
![]() $\mathcal {M}^{k+1}$
defined by a formula of the form
$\mathcal {M}^{k+1}$
defined by a formula of the form
![]() $\varphi (\overline {x},z;\overline {a})$
with
$\varphi (\overline {x},z;\overline {a})$
with
![]() $|\overline {x}|=k$
. Applying Theorem 3.12 to the formula with one object-variable defined by
$|\overline {x}|=k$
. Applying Theorem 3.12 to the formula with one object-variable defined by
![]() $\theta (z;\overline {x},\overline {a}):=\varphi (\overline {x},z;\overline {a})$
, we know that there are finitely many formulas
$\theta (z;\overline {x},\overline {a}):=\varphi (\overline {x},z;\overline {a})$
, we know that there are finitely many formulas
![]() $\psi _1(\overline {x};\overline {a}),\ldots ,\psi _r(\overline {x};\overline {a})$
forming a partition of
$\psi _1(\overline {x};\overline {a}),\ldots ,\psi _r(\overline {x};\overline {a})$
forming a partition of
![]() $\mathcal {M}^k$
and finitely many polynomials
$\mathcal {M}^k$
and finitely many polynomials
![]() $q_1,\ldots ,q_r\in \mathbb {Z}[t_1,t_2]$
such that for every
$q_1,\ldots ,q_r\in \mathbb {Z}[t_1,t_2]$
such that for every
![]() $\overline {b}'\in \mathcal {M}^k$
and
$\overline {b}'\in \mathcal {M}^k$
and
![]() $i\leq r$
,
$i\leq r$
,
![]() $\mathcal {M}\models \psi _i(\overline {b}',\overline {a})$
if and only if
$\mathcal {M}\models \psi _i(\overline {b}',\overline {a})$
if and only if
![]() $|\varphi (\mathcal {M};\overline {b}',\overline {a})|=q_i(\alpha ,\beta )$
.
$|\varphi (\mathcal {M};\overline {b}',\overline {a})|=q_i(\alpha ,\beta )$
.
For
![]() $i=1,\ldots ,r$
, let us define the set
$i=1,\ldots ,r$
, let us define the set
![]() $Z_i$
by the formula
$Z_i$
by the formula
![]() $\varphi (\overline {x},z;\overline {a})\wedge \psi _i(\overline {x};\overline {a})$
, and the set
$\varphi (\overline {x},z;\overline {a})\wedge \psi _i(\overline {x};\overline {a})$
, and the set
![]() $Y_i\subseteq \mathcal {M}^k$
by
$Y_i\subseteq \mathcal {M}^k$
by
![]() $\psi _i(\overline {x};\overline {a})$
. Hence, we have
$\psi _i(\overline {x};\overline {a})$
. Hence, we have
 $$\begin{align*}|X|=\displaystyle{\sum_{i=1}^r|Z_i|=\sum_{i=1}^r q_i(\alpha,\beta)\cdot |Y_i|=\sum_{i=1}^r q_i(\alpha,\beta)\cdot p_{Y_i}(\alpha,\beta)},\end{align*}$$
$$\begin{align*}|X|=\displaystyle{\sum_{i=1}^r|Z_i|=\sum_{i=1}^r q_i(\alpha,\beta)\cdot |Y_i|=\sum_{i=1}^r q_i(\alpha,\beta)\cdot p_{Y_i}(\alpha,\beta)},\end{align*}$$
and so the leading-degree of
![]() $p_X(t_1,t_2)$
is equal to the maximum of the leading-degrees of the products
$p_X(t_1,t_2)$
is equal to the maximum of the leading-degrees of the products
![]() $q_i(\alpha ,\beta )\cdot p_{Y_i}(\alpha ,\beta )=p_{Z_i}(\alpha ,\beta )$
. Suppose now that
$q_i(\alpha ,\beta )\cdot p_{Y_i}(\alpha ,\beta )=p_{Z_i}(\alpha ,\beta )$
. Suppose now that
![]() $(\overline {b}_i,c_i)$
be a generic element for the set
$(\overline {b}_i,c_i)$
be a generic element for the set
![]() $Z_i$
, which in particular implies that
$Z_i$
, which in particular implies that
![]() $\overline {b}_i$
satisfies
$\overline {b}_i$
satisfies
![]() $\psi _i(\overline {x};\overline {a})$
.
$\psi _i(\overline {x};\overline {a})$
.
By induction hypothesis we know that, for each
![]() $i\leq r$
,
$i\leq r$
,
![]() $\operatorname {RM}(Y_i)=(\omega \cdot m_i)\oplus n_i$
if and only if the leading monomial of
$\operatorname {RM}(Y_i)=(\omega \cdot m_i)\oplus n_i$
if and only if the leading monomial of
![]() $p_{Y_i}(t_1,t_2)$
has the form
$p_{Y_i}(t_1,t_2)$
has the form
![]() $A_it_1^{m_i}t_2^{n_i}$
. By the case
$A_it_1^{m_i}t_2^{n_i}$
. By the case
![]() $k=1$
, we have two cases for
$k=1$
, we have two cases for
![]() $q_i(t_1,t_2)$
:
$q_i(t_1,t_2)$
:
-
• If
 $\operatorname {dist}(c_i/\operatorname {conv}(\overline {a}\overline {b}_i))=\infty $
, the leading monomial of
$\operatorname {dist}(c_i/\operatorname {conv}(\overline {a}\overline {b}_i))=\infty $
, the leading monomial of
 $q_i(t_1,t_2)$
has the form
$q_i(t_1,t_2)$
has the form
 $B_it_1$
, and so the leading monomial of
$B_it_1$
, and so the leading monomial of
 $p_{Z_i}(t_1,t_2)$
would have the form
$p_{Z_i}(t_1,t_2)$
would have the form
 $A_it_1^{m_i}t_2^{n_i}\cdot B_it_1=A_iB_i\cdot t_1^{m_i+1}t_2^{n_i}$
. Also, by induction hypothesis and Theorem 5.1, the Morley rank of
$A_it_1^{m_i}t_2^{n_i}\cdot B_it_1=A_iB_i\cdot t_1^{m_i+1}t_2^{n_i}$
. Also, by induction hypothesis and Theorem 5.1, the Morley rank of
 $Z_i$
is given by
$Z_i$
is given by  $$ \begin{align*} \operatorname{RM}(Z_i)&=\operatorname{RM}(\overline{b}_i,c_i/\overline{a})=\operatorname{RM}(\overline{b}_i/\overline{a})\oplus d(c_i/\overline{b}_i\overline{a})\\ &=(\omega\cdot m_i)\oplus n_i \oplus \omega=(\omega\cdot (m_i+1))\oplus n_i. \end{align*} $$
$$ \begin{align*} \operatorname{RM}(Z_i)&=\operatorname{RM}(\overline{b}_i,c_i/\overline{a})=\operatorname{RM}(\overline{b}_i/\overline{a})\oplus d(c_i/\overline{b}_i\overline{a})\\ &=(\omega\cdot m_i)\oplus n_i \oplus \omega=(\omega\cdot (m_i+1))\oplus n_i. \end{align*} $$
-
• If
 $\operatorname {dist}(c_i/\operatorname {conv}(\overline {a}\overline {b}_i))=\ell <\infty $
, the leading monomial of
$\operatorname {dist}(c_i/\operatorname {conv}(\overline {a}\overline {b}_i))=\ell <\infty $
, the leading monomial of
 $q_i(t_1,t_2)$
has the form
$q_i(t_1,t_2)$
has the form
 $C_it_2^{\ell }$
, and so the leading monomial of
$C_it_2^{\ell }$
, and so the leading monomial of
 $p_{Z_i}(t_1,t_2)$
is
$p_{Z_i}(t_1,t_2)$
is
 $A_it_1^{m_i}t_2^{n_i}\cdot C_it_2^{\ell }=A_iC_i\cdot t_1^{m_i}t_2^{n_i+\ell }$
. Again, by induction hypothesis and Theorem 5.1, the Morley rank of
$A_it_1^{m_i}t_2^{n_i}\cdot C_it_2^{\ell }=A_iC_i\cdot t_1^{m_i}t_2^{n_i+\ell }$
. Again, by induction hypothesis and Theorem 5.1, the Morley rank of
 $Z_i$
is given by
$Z_i$
is given by  $$ \begin{align*} \operatorname{RM}(Z_i)&=\operatorname{RM}(\overline{b}_i,c_i/\overline{a})=\operatorname{RM}(\overline{b}_i/\overline{a})\oplus d(c_i/\overline{b}_i\overline{a})\\ &=(\omega\cdot m_i)\oplus n_i \oplus \ell=(\omega\cdot m_i)\oplus (n_i\oplus \ell). \end{align*} $$
$$ \begin{align*} \operatorname{RM}(Z_i)&=\operatorname{RM}(\overline{b}_i,c_i/\overline{a})=\operatorname{RM}(\overline{b}_i/\overline{a})\oplus d(c_i/\overline{b}_i\overline{a})\\ &=(\omega\cdot m_i)\oplus n_i \oplus \ell=(\omega\cdot m_i)\oplus (n_i\oplus \ell). \end{align*} $$
Therefore, each set
![]() $Z_i$
satisfies the conclusion of the theorem, and since
$Z_i$
satisfies the conclusion of the theorem, and since
![]() $\operatorname {RM}(X)$
is the maximum of
$\operatorname {RM}(X)$
is the maximum of
![]() $\{\operatorname {RM}(Z_1),\ldots ,\operatorname {RM}(Z_r)\}$
and the leading degree of
$\{\operatorname {RM}(Z_1),\ldots ,\operatorname {RM}(Z_r)\}$
and the leading degree of
![]() $p_X(t_1,t_2)$
corresponds to the maximum (in the lexicographical order) of the leading degrees of the polynomials
$p_X(t_1,t_2)$
corresponds to the maximum (in the lexicographical order) of the leading degrees of the polynomials
![]() $p_{Z_1}(t_1,t_2),\ldots ,p_{Z_r}(t_1,t_2)$
the conclusion also holds for the set X.
$p_{Z_1}(t_1,t_2),\ldots ,p_{Z_r}(t_1,t_2)$
the conclusion also holds for the set X.
A Model-theoretic properties of
 $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
 $\mathcal {T}_\infty $
$\mathcal {T}_\infty $
In this Appendix we recall several known results about the model theory of the r-regular infinite tree
![]() $\mathcal {T}_r$
and the infinite-branching tree
$\mathcal {T}_r$
and the infinite-branching tree
![]() $\mathcal {T}_\infty $
, which were used in Sections 3 and 5. These results are all considered folklore, but given the difficulty in finding a complete reference we include the proofs here for the sake of completeness.
$\mathcal {T}_\infty $
, which were used in Sections 3 and 5. These results are all considered folklore, but given the difficulty in finding a complete reference we include the proofs here for the sake of completeness.
We will show that these theories have elimination of quantifiers in the language
![]() $\mathcal {L}'=\{D_k(x,y):k<\omega \}$
described in Definition 2.5.
$\mathcal {L}'=\{D_k(x,y):k<\omega \}$
described in Definition 2.5.
Proposition A.1. The theories
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
have quantifier elimination in the language
$\mathcal {T}_\infty $
have quantifier elimination in the language
![]() $\mathcal {L}'=\{D_k(x,y):k<\omega \}$
.
$\mathcal {L}'=\{D_k(x,y):k<\omega \}$
.
Proof. Let
![]() $\mathcal {M},\mathcal {N}$
be
$\mathcal {M},\mathcal {N}$
be
![]() $\mathcal {L}'$
-structures that are both models of
$\mathcal {L}'$
-structures that are both models of
![]() $\mathcal {T}_\infty $
(resp.
$\mathcal {T}_\infty $
(resp.
![]() $\mathcal {T}_r$
) and let
$\mathcal {T}_r$
) and let
![]() $\mathcal {A}$
be a finitely generated common
$\mathcal {A}$
be a finitely generated common
![]() $\mathcal {L}'$
-substructure. Since
$\mathcal {L}'$
-substructure. Since
![]() $\mathcal {L}'$
is a relational language,
$\mathcal {L}'$
is a relational language,
![]() $\mathcal {A}$
is finite. By Theorem 8.4.1 in [Reference Hodges11], it suffices to show that for every
$\mathcal {A}$
is finite. By Theorem 8.4.1 in [Reference Hodges11], it suffices to show that for every
![]() $b\in \mathcal {M}$
there is an elementary extension
$b\in \mathcal {M}$
there is an elementary extension
![]() $\mathcal {N}'$
of
$\mathcal {N}'$
of
![]() $\mathcal {N}$
and a partial
$\mathcal {N}$
and a partial
![]() $\mathcal {L}'$
-embedding
$\mathcal {L}'$
-embedding
![]() $f:\mathcal {A}\cup \{b\} \to \mathcal {N}'$
such that
$f:\mathcal {A}\cup \{b\} \to \mathcal {N}'$
such that
![]() $f\upharpoonright _{\mathcal {A}}=\operatorname {id}_{\mathcal {A}}$
. There are three cases to consider:
$f\upharpoonright _{\mathcal {A}}=\operatorname {id}_{\mathcal {A}}$
. There are three cases to consider:
-
(1) Suppose that
 $b\in \operatorname {conv}_{\mathcal {M}}(\mathcal {A})$
. Then b lies in a path between two elements
$b\in \operatorname {conv}_{\mathcal {M}}(\mathcal {A})$
. Then b lies in a path between two elements
 $a_1,a_2$
of
$a_1,a_2$
of
 $\mathcal {A}$
, then there are integers
$\mathcal {A}$
, then there are integers
 $k_1,k_2<\omega $
such that
$k_1,k_2<\omega $
such that
 $\mathcal {M}\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_{2})\wedge D_{k_1+k_2}(a_1,a_2)$
. Since
$\mathcal {M}\models D_{k_1}(b,a_1)\wedge D_{k_2}(b,a_{2})\wedge D_{k_1+k_2}(a_1,a_2)$
. Since
 $\mathcal {A}$
is an
$\mathcal {A}$
is an
 $\mathcal {L}'$
-substructure of both
$\mathcal {L}'$
-substructure of both
 $\mathcal {M}, \mathcal {N}$
, we must have
$\mathcal {M}, \mathcal {N}$
, we must have
 $N\models D_{k_1+k_2}(a_1,a_2)$
and there is a unique element
$N\models D_{k_1+k_2}(a_1,a_2)$
and there is a unique element
 $b'$
in the path
$b'$
in the path
 $P(a_1,a_2)$
at distance
$P(a_1,a_2)$
at distance
 $k_1$
from
$k_1$
from
 $a_1$
and
$a_1$
and
 $k_2$
from
$k_2$
from
 $a_2$
. Thus, we can take
$a_2$
. Thus, we can take
 $f=\operatorname {id}_{\mathcal {A}}\cup \{(b,b')\}$
. In this case, for an arbitrary
$f=\operatorname {id}_{\mathcal {A}}\cup \{(b,b')\}$
. In this case, for an arbitrary
 $a\in \mathcal {A}$
we have and so f is a partial
$a\in \mathcal {A}$
we have and so f is a partial $$\begin{align*}\mathcal{M}\models D_\ell(b,a)\Leftrightarrow \mathcal{A}\models D_{k_1+\ell}(a_1,a)\vee D_{k_2+\ell}(a_2,a) \Leftrightarrow \mathcal{N}\models D_{k_1+\ell}(b',a),\end{align*}$$
$$\begin{align*}\mathcal{M}\models D_\ell(b,a)\Leftrightarrow \mathcal{A}\models D_{k_1+\ell}(a_1,a)\vee D_{k_2+\ell}(a_2,a) \Leftrightarrow \mathcal{N}\models D_{k_1+\ell}(b',a),\end{align*}$$
 $\mathcal {L}'$
-embedding.
$\mathcal {L}'$
-embedding.
-
(2) Suppose
 $b\not \in \operatorname {conv}_{\mathcal {M}}(\mathcal {A})$
and
$b\not \in \operatorname {conv}_{\mathcal {M}}(\mathcal {A})$
and
 $\operatorname {dist}(b,\mathcal {A})$
is finite. Since
$\operatorname {dist}(b,\mathcal {A})$
is finite. Since
 $\operatorname {conv}(\mathcal {A})\setminus \mathcal {A}$
is finite, we have by case (1) that there is an
$\operatorname {conv}(\mathcal {A})\setminus \mathcal {A}$
is finite, we have by case (1) that there is an
 $\mathcal {L}'$
-embedding
$\mathcal {L}'$
-embedding
 $f_1:\operatorname {conv}_{\mathcal {M}}(\mathcal {A})\to \mathcal {N}$
extending
$f_1:\operatorname {conv}_{\mathcal {M}}(\mathcal {A})\to \mathcal {N}$
extending
 $\operatorname {id}_{\mathcal {A}}$
. Now, since
$\operatorname {id}_{\mathcal {A}}$
. Now, since
 $\operatorname {dist}(b,\mathcal {A})$
is finite, there is an element
$\operatorname {dist}(b,\mathcal {A})$
is finite, there is an element
 $c\in \operatorname {conv}(\mathcal {A})$
such that
$c\in \operatorname {conv}(\mathcal {A})$
such that
 $\ell =\operatorname {dist}(b,c)=\operatorname {dist}(b,\operatorname {conv}(\mathcal {A}))$
. This implies in particular that for every
$\ell =\operatorname {dist}(b,c)=\operatorname {dist}(b,\operatorname {conv}(\mathcal {A}))$
. This implies in particular that for every
 $a\in \mathcal {A}$
, we have
$a\in \mathcal {A}$
, we have
 $\operatorname {dist}(a,b)=\operatorname {dist}_{\mathcal {M}}(a,c)+\ell $
. Note also that the only neighbour of c in the path
$\operatorname {dist}(a,b)=\operatorname {dist}_{\mathcal {M}}(a,c)+\ell $
. Note also that the only neighbour of c in the path
 $P(c,b)$
does not belong to
$P(c,b)$
does not belong to
 $\operatorname {conv}_{\mathcal {M}}(\mathcal {A})$
.
$\operatorname {conv}_{\mathcal {M}}(\mathcal {A})$
.Since both
 $\mathcal {M}$
and
$\mathcal {M}$
and
 $\mathcal {N}$
are models of
$\mathcal {N}$
are models of
 $\mathcal {T}_\infty $
(resp. of
$\mathcal {T}_\infty $
(resp. of
 $\mathcal {T}_r$
), there is a neighbour
$\mathcal {T}_r$
), there is a neighbour
 $d'\in \mathcal {N}$
of
$d'\in \mathcal {N}$
of
 $f(c)$
which does not belong to
$f(c)$
which does not belong to
 $f(\operatorname {conv}(\mathcal {A}))$
. Let
$f(\operatorname {conv}(\mathcal {A}))$
. Let
 $b'$
be an element in
$b'$
be an element in
 $\mathcal {N}$
such that
$\mathcal {N}$
such that
 $\operatorname {dist}_{\mathcal {N}}(b',f_1(c))=\ell $
and
$\operatorname {dist}_{\mathcal {N}}(b',f_1(c))=\ell $
and
 $\operatorname {dist}_{\mathcal {N}}(b',d')=\ell -1$
. Thus, since
$\operatorname {dist}_{\mathcal {N}}(b',d')=\ell -1$
. Thus, since
 $f_1$
is an
$f_1$
is an
 $\mathcal {L}'$
-embedding, we have for every
$\mathcal {L}'$
-embedding, we have for every
 $a\in \mathcal {A}$
that
$a\in \mathcal {A}$
that
 $\operatorname {dist}_{\mathcal {N}}(b',a)=\operatorname {dist}_{\mathcal {N}}(a,f_1(c))+\ell =\operatorname {dist}_{\mathcal {M}}(a,c)+\ell =\operatorname {dist}_{\mathcal {M}}(b,a)$
. Therefore, the map
$\operatorname {dist}_{\mathcal {N}}(b',a)=\operatorname {dist}_{\mathcal {N}}(a,f_1(c))+\ell =\operatorname {dist}_{\mathcal {M}}(a,c)+\ell =\operatorname {dist}_{\mathcal {M}}(b,a)$
. Therefore, the map
 $f=f_1\cup \{(b,b')\}$
is an
$f=f_1\cup \{(b,b')\}$
is an
 $\mathcal {L}'$
-embedding from
$\mathcal {L}'$
-embedding from
 $\operatorname {conv}(\mathcal {A})\cup \{b\}$
to
$\operatorname {conv}(\mathcal {A})\cup \{b\}$
to
 $\mathcal {N}$
.
$\mathcal {N}$
. -
(3) Suppose now that b is not at finite distance from any element in
 $\mathcal {A}$
, and consider the type
$\mathcal {A}$
, and consider the type  $$\begin{align*}q(x)=\{\neg D_k(x,a):k<\omega,\ a\in\mathcal{A}\}.\end{align*}$$
$$\begin{align*}q(x)=\{\neg D_k(x,a):k<\omega,\ a\in\mathcal{A}\}.\end{align*}$$
Since
 $\mathcal {A}$
is finite and
$\mathcal {A}$
is finite and
 $\mathcal {N}$
is a model of
$\mathcal {N}$
is a model of
 $\mathcal {T}_\infty $
(resp.
$\mathcal {T}_\infty $
(resp.
 $\mathcal {T}_r$
), this type is finitely satisfiable in
$\mathcal {T}_r$
), this type is finitely satisfiable in
 $\mathcal {N}$
, and so there is an elementary extension
$\mathcal {N}$
, and so there is an elementary extension
 $\mathcal {N}'$
of
$\mathcal {N}'$
of
 $\mathcal {N}$
with an element
$\mathcal {N}$
with an element
 $b'$
realizing
$b'$
realizing
 $q(x)$
. Thus, by putting
$q(x)$
. Thus, by putting
 $f(b)=b'$
, we obtain a partial
$f(b)=b'$
, we obtain a partial
 $\mathcal {L}'$
-embedding
$\mathcal {L}'$
-embedding
 $f=\operatorname {id}_{\mathcal {A}}\cup \{(b,c)\}:A\cup \{b\}\to \mathcal {N}'$
.
$f=\operatorname {id}_{\mathcal {A}}\cup \{(b,c)\}:A\cup \{b\}\to \mathcal {N}'$
.
Thus, we conclude that
![]() $\mathcal {T}_\infty $
has quantifier elimination in the language
$\mathcal {T}_\infty $
has quantifier elimination in the language
![]() $\mathcal {L}'=\{D_k:k<\omega \}$
. The same proof also shows that the theory
$\mathcal {L}'=\{D_k:k<\omega \}$
. The same proof also shows that the theory
![]() $\mathcal {T}_r$
eliminates quantifiers in the language
$\mathcal {T}_r$
eliminates quantifiers in the language
![]() $\mathcal {L}'$
.
$\mathcal {L}'$
.
Note that both theories
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
have prime models given by the corresponding connected r-regular tree and infinite branching tree, respectively. This property, together with quantifier elimination, suffices to conclude the following result.
$\mathcal {T}_\infty $
have prime models given by the corresponding connected r-regular tree and infinite branching tree, respectively. This property, together with quantifier elimination, suffices to conclude the following result.
Corollary A.2. The theories
![]() $\mathcal {T}_r$
and
$\mathcal {T}_r$
and
![]() $\mathcal {T}_\infty $
are complete.
$\mathcal {T}_\infty $
are complete.
Proposition A.3. The theory
![]() $\mathcal {T}_r$
is strongly minimal and for every
$\mathcal {T}_r$
is strongly minimal and for every
![]() $\mathcal {M}\models \mathcal {T}_r$
and
$\mathcal {M}\models \mathcal {T}_r$
and
![]() $a\in M$
we have
$a\in M$
we have
![]() $\displaystyle {\operatorname {acl}_M(a)=\{b\in M: \operatorname {dist}(a,b)=k \text {\ for some }k<\omega \}.}$
Moreover, the pregeometry in every model of
$\displaystyle {\operatorname {acl}_M(a)=\{b\in M: \operatorname {dist}(a,b)=k \text {\ for some }k<\omega \}.}$
Moreover, the pregeometry in every model of
![]() $\mathcal {T}_r$
is trivial, and for every
$\mathcal {T}_r$
is trivial, and for every
![]() $A\subseteq M$
we have
$A\subseteq M$
we have
![]() $\operatorname {acl}(A)=\operatorname {conn}(A)$
.
$\operatorname {acl}(A)=\operatorname {conn}(A)$
.
Proof. Note that for any
![]() $\mathcal {M}\models \mathcal {T}_r$
and
$\mathcal {M}\models \mathcal {T}_r$
and
![]() $a\in M$
, the formula
$a\in M$
, the formula
![]() $D_k(x,a)$
defines a set of size
$D_k(x,a)$
defines a set of size
![]() $r(r-1)^{k-1}$
, so it is finite. By quantifier elimination in
$r(r-1)^{k-1}$
, so it is finite. By quantifier elimination in
![]() $\mathcal {L}'$
, this is enough to show that
$\mathcal {L}'$
, this is enough to show that
![]() $\mathcal {T}_r$
is strongly minimal. This also shows that the unique generic type over a set A is completely determined by the partial type
$\mathcal {T}_r$
is strongly minimal. This also shows that the unique generic type over a set A is completely determined by the partial type
![]() $\pi (x)=\{\neg D_k(x,a):a\in A, k<\omega \}.$
$\pi (x)=\{\neg D_k(x,a):a\in A, k<\omega \}.$
Suppose now that A is an arbitrary subset of a model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {T}_r$
that is
$\mathcal {T}_r$
that is
![]() $|A|$
-saturated, and let
$|A|$
-saturated, and let
![]() $b\in M$
an arbitrary element. We have two options:
$b\in M$
an arbitrary element. We have two options:
-
• If
 $\mathcal {M}\models D_k(b,a)$
for some
$\mathcal {M}\models D_k(b,a)$
for some
 $k<\omega $
and
$k<\omega $
and
 $a\in A$
, then
$a\in A$
, then
 $b\in \operatorname {acl}(a)\subseteq \operatorname {acl}(A)$
because b lies in the set defined by the formula
$b\in \operatorname {acl}(a)\subseteq \operatorname {acl}(A)$
because b lies in the set defined by the formula
 $D_k(x,a)$
which has
$D_k(x,a)$
which has
 $r(r-1)^{k-1}$
elements.
$r(r-1)^{k-1}$
elements. -
• If
 $\mathcal {M}\models \neg D_k(b,a)$
for every
$\mathcal {M}\models \neg D_k(b,a)$
for every
 $k<\omega $
and
$k<\omega $
and
 $a\in A$
, then
$a\in A$
, then
 $b\models \pi (x)$
, and so
$b\models \pi (x)$
, and so
 $b\not \in \operatorname {acl}(A)$
.
$b\not \in \operatorname {acl}(A)$
.
Therefore, we have shown that
![]() $\operatorname {acl}_M(a)=\{b\in M: M\models D_k(b,a) \text {for some} k<\omega \}$
and that
$\operatorname {acl}_M(a)=\{b\in M: M\models D_k(b,a) \text {for some} k<\omega \}$
and that
![]() $\operatorname {acl}(A)=\bigcup _{a\in A}\operatorname {acl}(a)$
. This implies that the pregeometry in models of
$\operatorname {acl}(A)=\bigcup _{a\in A}\operatorname {acl}(a)$
. This implies that the pregeometry in models of
![]() $\mathcal {T}_r$
is trivial.
$\mathcal {T}_r$
is trivial.
Proposition A.4. The theory
![]() $\mathcal {T}_\infty $
is
$\mathcal {T}_\infty $
is
![]() $\omega $
-stable. Moreover, for every
$\omega $
-stable. Moreover, for every
![]() $\mathcal {M}\models \mathcal {T}_\infty $
and
$\mathcal {M}\models \mathcal {T}_\infty $
and
![]() $A\subseteq M$
, the algebraic closure
$A\subseteq M$
, the algebraic closure
![]() $\operatorname {acl}(A)$
coincides with the convex closure
$\operatorname {acl}(A)$
coincides with the convex closure
![]() $\operatorname {conv}(A)$
.
$\operatorname {conv}(A)$
.
Proof. Let
![]() $A=\{a_n:n<\omega \}$
be an enumeration of a countable subset of
$A=\{a_n:n<\omega \}$
be an enumeration of a countable subset of
![]() $M\models \mathcal {T}_\infty $
. By quantifier elimination, every type
$M\models \mathcal {T}_\infty $
. By quantifier elimination, every type
![]() $q(x)\in S_1(A)$
is completely determined by the formulas of the form
$q(x)\in S_1(A)$
is completely determined by the formulas of the form
![]() $D_k(x,a_n)$
that belong to
$D_k(x,a_n)$
that belong to
![]() $q(x)$
, with
$q(x)$
, with
![]() $k,n<\omega $
. We have three cases to consider for the type
$k,n<\omega $
. We have three cases to consider for the type
![]() $q(x)$
:
$q(x)$
:
-
(1) There are two elements
 $a_{m_1},a_{m_2}$
such that
$a_{m_1},a_{m_2}$
such that
 $D_{k_1}(x,a_{m_1}),D_{k_2}(x,a_{m_2})\in q(x)$
and also
$D_{k_1}(x,a_{m_1}),D_{k_2}(x,a_{m_2})\in q(x)$
and also
 $\mathcal {M}\models D_{k_1+k_2}(a_{m_1},a_{m_2})$
. In this case, there is a unique realization b of
$\mathcal {M}\models D_{k_1+k_2}(a_{m_1},a_{m_2})$
. In this case, there is a unique realization b of
 $q(x)$
that lies in the path between
$q(x)$
that lies in the path between
 $a_{m_1}$
and
$a_{m_1}$
and
 $a_{m_2}$
, and so
$a_{m_2}$
, and so
 $q(x)$
is completely determined by the tuple
$q(x)$
is completely determined by the tuple
 $(m_1,m_2,\operatorname {dist}(a_{m_1},a_{m_2}))\in \mathbb {N}^3$
. There are at most
$(m_1,m_2,\operatorname {dist}(a_{m_1},a_{m_2}))\in \mathbb {N}^3$
. There are at most
 $\aleph _0$
such types.
$\aleph _0$
such types. -
(2) There is an element
 $a_{m_1}\in A$
such that
$a_{m_1}\in A$
such that
 $D_\ell (x,a_{m_1})\in \operatorname {tp}(b/A)$
and
$D_\ell (x,a_{m_1})\in \operatorname {tp}(b/A)$
and
 $\operatorname {dist}(b,a_{m_1})\leq \operatorname {dist}(b,a_n)$
for every
$\operatorname {dist}(b,a_{m_1})\leq \operatorname {dist}(b,a_n)$
for every
 $n<\omega $
. In this case, the formulas
$n<\omega $
. In this case, the formulas
 $D_k(x,a_n)$
that belong to
$D_k(x,a_n)$
that belong to
 $q(x)$
are precisely those corresponding to the pairs
$q(x)$
are precisely those corresponding to the pairs
 $(k,n)$
where
$(k,n)$
where
 $k=\operatorname {dist}(a_{m_1},a_n)+\ell $
. So, the type
$k=\operatorname {dist}(a_{m_1},a_n)+\ell $
. So, the type
 $q(x)$
is completely determined by the pair
$q(x)$
is completely determined by the pair
 $(\ell ,m_1)$
. There are at most
$(\ell ,m_1)$
. There are at most
 $\aleph _0$
such types.
$\aleph _0$
such types. -
(3) If there is no pair
 $(k,n)\in \mathbb {N}^2$
such that
$(k,n)\in \mathbb {N}^2$
such that
 $D_k(x,a_n)\in q(x)$
, then
$D_k(x,a_n)\in q(x)$
, then
 $q(x)$
is determined by the partial type
$q(x)$
is determined by the partial type
 $\pi (x)=\{\neg D_k(x,a_n): n,k<\omega \}$
. There is only one type with this condition.
$\pi (x)=\{\neg D_k(x,a_n): n,k<\omega \}$
. There is only one type with this condition.
This shows that
![]() $|S_1(A)|\leq \aleph _0+\aleph _0+1=\aleph _0$
, and since A is an arbitrary countable set we conclude that
$|S_1(A)|\leq \aleph _0+\aleph _0+1=\aleph _0$
, and since A is an arbitrary countable set we conclude that
![]() $\mathcal {T}_\infty $
is
$\mathcal {T}_\infty $
is
![]() $\omega $
-stable. Moreover, since each vertex in
$\omega $
-stable. Moreover, since each vertex in
![]() $\mathcal {M}$
has infinite degree, the only algebraic type is given by case (1), and so every algebraic element lies in the unique path between two elements from A. This shows that
$\mathcal {M}$
has infinite degree, the only algebraic type is given by case (1), and so every algebraic element lies in the unique path between two elements from A. This shows that
![]() $\operatorname {acl}(A)=\operatorname {conv}(A)$
.
$\operatorname {acl}(A)=\operatorname {conv}(A)$
.
We will see now that the SU-rank and the Morley rank coincide for definable sets in models of
![]() $\mathcal {T}_\infty $
, even though these notions of rank do not coincide in general in
$\mathcal {T}_\infty $
, even though these notions of rank do not coincide in general in
![]() $\omega $
-stable theories. Let us first recall the definition of SU-rank.
$\omega $
-stable theories. Let us first recall the definition of SU-rank.
Definition A.5. Let T be a simple theory. We define the relation
![]() $\operatorname {SU}(p(\overline {x}))\geq \alpha $
for a type
$\operatorname {SU}(p(\overline {x}))\geq \alpha $
for a type
![]() $p(\overline {x})$
by recursion on
$p(\overline {x})$
by recursion on
![]() $\alpha $
:
$\alpha $
:
-
•
 $\operatorname {SU}(p(\overline {x}))\geq 0$
for every (consistent) type
$\operatorname {SU}(p(\overline {x}))\geq 0$
for every (consistent) type
 $p(\overline {x})$
.
$p(\overline {x})$
. -
• For a limit ordinal
 $\lambda $
,
$\lambda $
,
 $\operatorname {SU}(p(\overline {x}))\geq \lambda $
if and only if
$\operatorname {SU}(p(\overline {x}))\geq \lambda $
if and only if
 $\operatorname {SU}(p(\overline {x}))\geq \beta $
for all
$\operatorname {SU}(p(\overline {x}))\geq \beta $
for all
 $\beta <\lambda $
.
$\beta <\lambda $
. -
• For a successor ordinal
 $\alpha =\beta +1$
,
$\alpha =\beta +1$
,
 $\operatorname {SU}(\alpha )$
if and only if
$\operatorname {SU}(\alpha )$
if and only if
 $p(\overline {x})$
has a forking (dividing) extension
$p(\overline {x})$
has a forking (dividing) extension
 $q(\overline {x})$
such that
$q(\overline {x})$
such that
 $\operatorname {SU}(q(\overline {x}))\geq \beta $
.
$\operatorname {SU}(q(\overline {x}))\geq \beta $
.
Fact A.6. Let
![]() $p(\overline {x})$
be a complete type with parameters over A. Then
$p(\overline {x})$
be a complete type with parameters over A. Then
![]() $\operatorname {SU}(p(\overline {x})\leq \operatorname {RM}(p(\overline {x}))$
.
$\operatorname {SU}(p(\overline {x})\leq \operatorname {RM}(p(\overline {x}))$
.
Definition A.7. Let
![]() $\mathcal {M}$
be a model of
$\mathcal {M}$
be a model of
![]() $\mathcal {T}_\infty $
,
$\mathcal {T}_\infty $
,
![]() $A\subseteq \mathcal {M}$
. Given an element
$A\subseteq \mathcal {M}$
. Given an element
![]() $b\in \mathcal {M}$
, we define its ordinal distance to A as follows:
$b\in \mathcal {M}$
, we define its ordinal distance to A as follows:
 $$\begin{align*}D(b/A):= \begin{cases} \operatorname{dist}(b,\operatorname{conv}(A)) &\text{if }\operatorname{dist}(b,\operatorname{conv}(A))<\infty,\\ \ \ \omega &\text{if }\operatorname{dist}(b,\operatorname{conv}(A))=\infty. \end{cases} \end{align*}$$
$$\begin{align*}D(b/A):= \begin{cases} \operatorname{dist}(b,\operatorname{conv}(A)) &\text{if }\operatorname{dist}(b,\operatorname{conv}(A))<\infty,\\ \ \ \omega &\text{if }\operatorname{dist}(b,\operatorname{conv}(A))=\infty. \end{cases} \end{align*}$$
Proposition A.8. The theory
![]() $\mathcal {T}_\infty $
has Morley rank
$\mathcal {T}_\infty $
has Morley rank
![]() $\omega $
. Moreover, given a model
$\omega $
. Moreover, given a model
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {T}_\infty $
, an
$\mathcal {T}_\infty $
, an
![]() $\operatorname {acl}$
-closed finite subset
$\operatorname {acl}$
-closed finite subset
![]() $A\subseteq M$
and an element
$A\subseteq M$
and an element
![]() $b\in M$
, we have
$b\in M$
, we have
Proof. By quantifier elimination,
![]() $\operatorname {tp}(b/A)$
is completely determined by the formulas of the form
$\operatorname {tp}(b/A)$
is completely determined by the formulas of the form
![]() $D_k(x,a)$
that hold for b, and so the Morley rank of
$D_k(x,a)$
that hold for b, and so the Morley rank of
![]() $\operatorname {tp}(b/A)$
is equal to the Morley rank of a formula of the form
$\operatorname {tp}(b/A)$
is equal to the Morley rank of a formula of the form
 $$\begin{align*}\theta(x)=\bigwedge_{i=1}^m D_{k_i}(x,a_i)\wedge \bigwedge_{j=1}^n \neg D_{\ell_j}(x,a^{\prime}_j)\in\operatorname{tp}(b/A)\end{align*}$$
$$\begin{align*}\theta(x)=\bigwedge_{i=1}^m D_{k_i}(x,a_i)\wedge \bigwedge_{j=1}^n \neg D_{\ell_j}(x,a^{\prime}_j)\in\operatorname{tp}(b/A)\end{align*}$$
for some elements
![]() $a_1,\ldots ,a_m,a_1',\ldots ,a_n'\in A$
.
$a_1,\ldots ,a_m,a_1',\ldots ,a_n'\in A$
.
It follows by induction that the formula
![]() $D_k(x,a)$
has SU-rank at least k, which also implies that
$D_k(x,a)$
has SU-rank at least k, which also implies that
![]() $\operatorname {SU}(\neg D_k(x,a)) \geq \omega $
. Now we will show that the formula
$\operatorname {SU}(\neg D_k(x,a)) \geq \omega $
. Now we will show that the formula
![]() $D_k(x,a)$
has Morley rank at most k. For a contradiction, let m be minimal such that
$D_k(x,a)$
has Morley rank at most k. For a contradiction, let m be minimal such that
![]() $RM(D_m(x,a)) \geq m+1$
and let S be a definable subset of
$RM(D_m(x,a)) \geq m+1$
and let S be a definable subset of
![]() $D_m(x,a)$
with parameters
$D_m(x,a)$
with parameters
![]() $a,a_1,\ldots ,a_n$
such that
$a,a_1,\ldots ,a_n$
such that
![]() $\operatorname {RM}(S)=m$
. Let
$\operatorname {RM}(S)=m$
. Let
![]() $A=\operatorname {conv}(a,a_1,\ldots ,a_n)$
, and let
$A=\operatorname {conv}(a,a_1,\ldots ,a_n)$
, and let
![]() $b\in S$
such that
$b\in S$
such that
![]() $\operatorname {RM}(S)=\operatorname {RM}(\operatorname {tp}(b/A))=m$
. By Proposition 2.7, we know that there is a unique element
$\operatorname {RM}(S)=\operatorname {RM}(\operatorname {tp}(b/A))=m$
. By Proposition 2.7, we know that there is a unique element
![]() $c\in A$
and an integer
$c\in A$
and an integer
![]() $\ell $
such that
$\ell $
such that
![]() $\operatorname {dist}(b,A)=\operatorname {dist}(b,c)=\ell $
and
$\operatorname {dist}(b,A)=\operatorname {dist}(b,c)=\ell $
and
![]() $P(b,c)\cap A=\{c\}$
. By construction we have
$P(b,c)\cap A=\{c\}$
. By construction we have
![]() $\ell \leq m$
, and given that c is definable over
$\ell \leq m$
, and given that c is definable over
![]() $a,a_1,\ldots ,a_m$
and the formula
$a,a_1,\ldots ,a_m$
and the formula
![]() $D_\ell (x,c)$
belongs to
$D_\ell (x,c)$
belongs to
![]() $\operatorname {tp}(b/A)$
, we have by minimality of m that
$\operatorname {tp}(b/A)$
, we have by minimality of m that
![]() $m\leq \ell $
. From this we conclude that
$m\leq \ell $
. From this we conclude that
![]() $c=a$
, and so the definable set S is contained in the set defined by a formula of the form
$c=a$
, and so the definable set S is contained in the set defined by a formula of the form
where
![]() $\mathcal {N}(a)$
is the set of vertices in M that are adjacent to a. With these conditions, we will have that
$\mathcal {N}(a)$
is the set of vertices in M that are adjacent to a. With these conditions, we will have that
 $$ \begin{align*} m+1&=\operatorname{RM}(D_m(x,a))=\max\{\operatorname{RM}(S),\operatorname{RM}(D_m(x,a)\wedge \neg S)\}\\ &=\max\left\{\operatorname{RM}(S),\max_{d\in\mathcal{N}(a)\cap A}\{\operatorname{RM}\left(D_m(x,a)\wedge D_{m-1}(x,d)\right)\}\right\}\leq m, \end{align*} $$
$$ \begin{align*} m+1&=\operatorname{RM}(D_m(x,a))=\max\{\operatorname{RM}(S),\operatorname{RM}(D_m(x,a)\wedge \neg S)\}\\ &=\max\left\{\operatorname{RM}(S),\max_{d\in\mathcal{N}(a)\cap A}\{\operatorname{RM}\left(D_m(x,a)\wedge D_{m-1}(x,d)\right)\}\right\}\leq m, \end{align*} $$
thus obtaining a contradiction.
Let now b be an element in M and let A be a finite algebraically closed subset of M. By Fact A.6 we already have
![]() $\operatorname {SU}(b/A)\leq \operatorname {RM}(b/A)$
, so it suffices to show that either
$\operatorname {SU}(b/A)\leq \operatorname {RM}(b/A)$
, so it suffices to show that either
![]() $\operatorname {dist}(b,A)=k< \omega $
and we have
$\operatorname {dist}(b,A)=k< \omega $
and we have
![]() $\operatorname {RM}(b/A)\leq k\leq \operatorname {SU}(b/A)$
, or
$\operatorname {RM}(b/A)\leq k\leq \operatorname {SU}(b/A)$
, or
![]() $\operatorname {dist}(b,A)=\infty $
and
$\operatorname {dist}(b,A)=\infty $
and
![]() $\operatorname {RM}(b/A)\leq \omega \leq \operatorname {SU}(b/A)$
. If
$\operatorname {RM}(b/A)\leq \omega \leq \operatorname {SU}(b/A)$
. If
![]() $\operatorname {dist}(b,A)=\infty $
, then
$\operatorname {dist}(b,A)=\infty $
, then
![]() $\operatorname {tp}(b/A)=\{\neg D_k(x,a):a\in A, k<\omega \}$
, which implies that
$\operatorname {tp}(b/A)=\{\neg D_k(x,a):a\in A, k<\omega \}$
, which implies that
![]() $\operatorname {SU}(b/A)\geq \omega $
because each finite conjunction of these formulas has SU-rank at least
$\operatorname {SU}(b/A)\geq \omega $
because each finite conjunction of these formulas has SU-rank at least
![]() $\omega $
. So we obtain
$\omega $
. So we obtain
On the other hand, if
![]() $\operatorname {dist}(b/A)=k<\omega $
, we have
$\operatorname {dist}(b/A)=k<\omega $
, we have
![]() $\operatorname {RM}(b/A)\leq \operatorname {RM}(D_k(x,a))\leq k\leq \operatorname {SU}(b/A).$
$\operatorname {RM}(b/A)\leq \operatorname {RM}(D_k(x,a))\leq k\leq \operatorname {SU}(b/A).$
We will now provide a characterization of the SU-rank and the Morley rank for types in several variables. For this, let us recall the following operation between ordinals.
Definition A.9 (Cantor addition).
Let
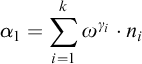 $\alpha _1 =\displaystyle {\sum _{i=1}^k \omega ^{\gamma _i}\cdot n_i}$
and
$\alpha _1 =\displaystyle {\sum _{i=1}^k \omega ^{\gamma _i}\cdot n_i}$
and
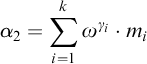 $\alpha _2 = \displaystyle {\sum _{i=1}^k \omega ^{\gamma _i}\cdot m_i}$
be two ordinals written in Cantor’s normal form (i.e.,
$\alpha _2 = \displaystyle {\sum _{i=1}^k \omega ^{\gamma _i}\cdot m_i}$
be two ordinals written in Cantor’s normal form (i.e.,
![]() $\gamma _1>\gamma _2>\cdots >\gamma _k$
). The Cantor addition is defined as
$\gamma _1>\gamma _2>\cdots >\gamma _k$
). The Cantor addition is defined as
 $$\begin{align*}\alpha_1 \oplus \alpha_2 = \sum_{i=1}^k \omega^{\gamma_i} n_i \oplus \sum_{i=1}^k \omega^{\gamma_i} m_i = \sum_{i=1}^k \omega^{\gamma_i} (n_i + m_i).\end{align*}$$
$$\begin{align*}\alpha_1 \oplus \alpha_2 = \sum_{i=1}^k \omega^{\gamma_i} n_i \oplus \sum_{i=1}^k \omega^{\gamma_i} m_i = \sum_{i=1}^k \omega^{\gamma_i} (n_i + m_i).\end{align*}$$
Lemma A.10. Let
![]() $\mathcal {M}\models \mathcal {T}_\infty $
and let
$\mathcal {M}\models \mathcal {T}_\infty $
and let
![]() $A\subseteq M$
be a small set of parameters. If
$A\subseteq M$
be a small set of parameters. If
![]() $\overline {b}=(b_1,\ldots ,b_n)\in M^n$
and
$\overline {b}=(b_1,\ldots ,b_n)\in M^n$
and
![]() $D(c/A\overline {b})=1$
then
$D(c/A\overline {b})=1$
then
![]() $\operatorname {RM}(\overline {b},c/A)=\operatorname {RM}(\overline {b}/A)\oplus 1$
.
$\operatorname {RM}(\overline {b},c/A)=\operatorname {RM}(\overline {b}/A)\oplus 1$
.
Proof. First, notice that
![]() $c\not \in \operatorname {conv}(A\overline {b})=\operatorname {acl}(A\overline {b})$
, so we must have
$c\not \in \operatorname {conv}(A\overline {b})=\operatorname {acl}(A\overline {b})$
, so we must have
![]() $\operatorname {RM}(\overline {b},c/A)>\operatorname {RM}(\overline {b}/A)$
, so
$\operatorname {RM}(\overline {b},c/A)>\operatorname {RM}(\overline {b}/A)$
, so
![]() $\operatorname {RM}(\overline {b},c/A)\geq \alpha \oplus 1$
.
$\operatorname {RM}(\overline {b},c/A)\geq \alpha \oplus 1$
.
Suppose now that
![]() $\varphi (\overline {x})$
is a minimal formula for
$\varphi (\overline {x})$
is a minimal formula for
![]() $\operatorname {tp}(\overline {b}/A)$
, that is, a formula with parameters from A such that
$\operatorname {tp}(\overline {b}/A)$
, that is, a formula with parameters from A such that
![]() $\operatorname {RM}(\overline {b}/A)=\operatorname {RM}(\varphi (\overline {x}))=\alpha $
. Since
$\operatorname {RM}(\overline {b}/A)=\operatorname {RM}(\varphi (\overline {x}))=\alpha $
. Since
![]() $\varphi (\overline {x})$
is a formula with parameters in a finite subset
$\varphi (\overline {x})$
is a formula with parameters in a finite subset
![]() $A_0\subseteq A$
, we may assume that
$A_0\subseteq A$
, we may assume that
![]() $\varphi (\overline {x})$
implies all the formulas of the form
$\varphi (\overline {x})$
implies all the formulas of the form
![]() $D_r(x_i,x_j)$
or
$D_r(x_i,x_j)$
or
![]() $D_s(x_i,a)$
(with
$D_s(x_i,a)$
(with
![]() $a\in A_0$
) that belong to
$a\in A_0$
) that belong to
![]() $\operatorname {tp}(b_1,\ldots ,b_n/A_0)$
.
$\operatorname {tp}(b_1,\ldots ,b_n/A_0)$
.
Since
![]() $D(c/A\overline {b})=1$
, there is an element
$D(c/A\overline {b})=1$
, there is an element
![]() $e\in \operatorname {conv}(A\overline {b})$
such that
$e\in \operatorname {conv}(A\overline {b})$
such that
![]() $\operatorname {dist}(e,c)=1$
. Moreover, since the convex closure is the union of the paths between vertices at finite distance, we may assume that there are elements
$\operatorname {dist}(e,c)=1$
. Moreover, since the convex closure is the union of the paths between vertices at finite distance, we may assume that there are elements
![]() $e_1,e_2$
from
$e_1,e_2$
from
![]() $A\overline {b}$
such that
$A\overline {b}$
such that
![]() $e\in P(e_1,e_2)$
. Without loss of generality, we may suppose that
$e\in P(e_1,e_2)$
. Without loss of generality, we may suppose that
![]() $e_1=b_1$
and
$e_1=b_1$
and
![]() $e_2=a\in A$
as all the other cases can be analyzed in a similar fashion. Finally, let us fix the distances
$e_2=a\in A$
as all the other cases can be analyzed in a similar fashion. Finally, let us fix the distances
![]() $\operatorname {dist}(b_1,e)=k_1$
and
$\operatorname {dist}(b_1,e)=k_1$
and
![]() $\operatorname {dist}(e,a)=k_2$
.
$\operatorname {dist}(e,a)=k_2$
.
Consider the formula
![]() $\zeta (\overline {x},y):=\varphi (\overline {x})\wedge D_{k_1+1}(y,x_1)\wedge D_{k_2+1}(y,a)$
. Note that
$\zeta (\overline {x},y):=\varphi (\overline {x})\wedge D_{k_1+1}(y,x_1)\wedge D_{k_2+1}(y,a)$
. Note that
![]() $\mathcal {M}\models \zeta (\overline {b},c)$
, so to prove
$\mathcal {M}\models \zeta (\overline {b},c)$
, so to prove
![]() $\operatorname {RM}(\overline {b},c/A)\leq \alpha \oplus 1$
it is enough to show that
$\operatorname {RM}(\overline {b},c/A)\leq \alpha \oplus 1$
it is enough to show that
![]() $\operatorname {RM}(\zeta (\overline {x},y))\leq \alpha \oplus 1$
.
$\operatorname {RM}(\zeta (\overline {x},y))\leq \alpha \oplus 1$
.
For a contradiction, suppose that
![]() $\operatorname {RM}(\zeta (\overline {x},y))\geq \alpha \oplus 2$
. By definition of the Morley rank, there is an A-definable set
$\operatorname {RM}(\zeta (\overline {x},y))\geq \alpha \oplus 2$
. By definition of the Morley rank, there is an A-definable set
![]() $S(\overline {x},y)$
implying
$S(\overline {x},y)$
implying
![]() $\zeta (\overline {x},y)$
such that
$\zeta (\overline {x},y)$
such that
![]() $\operatorname {RM}(S(\overline {x},y))=\alpha \oplus 1$
. Let
$\operatorname {RM}(S(\overline {x},y))=\alpha \oplus 1$
. Let
![]() $\overline {b}',c'$
be a realization of
$\overline {b}',c'$
be a realization of
![]() $S(\overline {x},y)$
such that
$S(\overline {x},y)$
such that
![]() $\operatorname {RM}(\overline {b}',c')=\alpha \oplus 1$
.
$\operatorname {RM}(\overline {b}',c')=\alpha \oplus 1$
.
By quantifier elimination and the fact that the Morley rank of a finite disjunction is equal to the maximum of the Morley rank of its disjunctives, we may assume that
![]() $S(\overline {x},y)$
is equivalent to the conjunction of
$S(\overline {x},y)$
is equivalent to the conjunction of
![]() $\zeta (\overline {x},y)$
with formulas of the form
$\zeta (\overline {x},y)$
with formulas of the form
![]() $D_{r_i}(y,x_i), D_{s_i}(y,a_i), \neg D_{p_j}(y,x_{j})$
or
$D_{r_i}(y,x_i), D_{s_i}(y,a_i), \neg D_{p_j}(y,x_{j})$
or
![]() $\neg D_{q_j}(y,a_j)$
for some non-negative integers
$\neg D_{q_j}(y,a_j)$
for some non-negative integers
![]() $r_i,s_i,p_j,q_j$
and vertices
$r_i,s_i,p_j,q_j$
and vertices
![]() $a_i,a_j$
from A.
$a_i,a_j$
from A.
Let
![]() $e'$
be the unique element in
$e'$
be the unique element in
![]() $P(b_1',a)$
at distance
$P(b_1',a)$
at distance
![]() $1$
from
$1$
from
![]() $c'$
. If
$c'$
. If
![]() $\overline {b}',c'\models D_{r_i}(y,x_i)$
, then
$\overline {b}',c'\models D_{r_i}(y,x_i)$
, then
![]() $\operatorname {dist}(c',b_i')=r_i$
and we have either
$\operatorname {dist}(c',b_i')=r_i$
and we have either
![]() $\operatorname {dist}(e',b_i')=r_i+1$
or
$\operatorname {dist}(e',b_i')=r_i+1$
or
![]() $\operatorname {dist}(e',b_i')=r_i-1$
. However,
$\operatorname {dist}(e',b_i')=r_i-1$
. However,
![]() $\operatorname {dist}(e',b_i')=r_i+1$
would imply that
$\operatorname {dist}(e',b_i')=r_i+1$
would imply that
![]() $c'\in P(e',b_i')\subseteq P(b_1',b_i')$
, which is impossible because that would imply
$c'\in P(e',b_i')\subseteq P(b_1',b_i')$
, which is impossible because that would imply
![]() $c'\in \operatorname {acl}(A\overline {b}')$
and
$c'\in \operatorname {acl}(A\overline {b}')$
and
![]() $\operatorname {RM}(\overline {b}',c'/A)=\operatorname {RM}(\overline {b}'/A)=\alpha $
. Hence,
$\operatorname {RM}(\overline {b}',c'/A)=\operatorname {RM}(\overline {b}'/A)=\alpha $
. Hence,
![]() $D_{r_i-1}(e',b_i')$
holds, and there is a path with length less than
$D_{r_i-1}(e',b_i')$
holds, and there is a path with length less than
![]() $r_i$
connecting
$r_i$
connecting
![]() $b_i'$
with
$b_i'$
with
![]() $P(b_1',a)$
.
$P(b_1',a)$
.
Let
![]() $h'$
be the element in
$h'$
be the element in
![]() $P(b_1',a)$
that is closest to
$P(b_1',a)$
that is closest to
![]() $b_i'$
and put
$b_i'$
and put
![]() $t=\operatorname {dist}(b_i',P(b_1',a))=\operatorname {dist}(b_i',h')$
,
$t=\operatorname {dist}(b_i',P(b_1',a))=\operatorname {dist}(b_i',h')$
,
![]() $r=\operatorname {dist}(h',e')$
. Notice that
$r=\operatorname {dist}(h',e')$
. Notice that
![]() $r+t=\operatorname {dist}(b_i',e')=r_i-1$
, and we have two cases:
$r+t=\operatorname {dist}(b_i',e')=r_i-1$
, and we have two cases:
-
• If
 $h'\in P(b_1',e')$
, we have
$h'\in P(b_1',e')$
, we have
 $\operatorname {dist}(b_1',b_i')=t+k_1-r$
and
$\operatorname {dist}(b_1',b_i')=t+k_1-r$
and
 $\operatorname {dist}(b_i',a)=t+k_2+r$
.
$\operatorname {dist}(b_i',a)=t+k_2+r$
. -
• If
 $h'\in P(e',a)$
, we have
$h'\in P(e',a)$
, we have
 $\operatorname {dist}(b_i',b_1')=t+k_1+r$
and
$\operatorname {dist}(b_i',b_1')=t+k_1+r$
and
 $\operatorname {dist}(b_i',a)=t+k_2-r$
.
$\operatorname {dist}(b_i',a)=t+k_2-r$
.

Therefore, by checking all the
![]() $k_1+k_2=\operatorname {dist}(b_1,a)$
possibilities we have that
$k_1+k_2=\operatorname {dist}(b_1,a)$
possibilities we have that
![]() $D_{r_i}(y,x_j)$
is implied by the disjunction
$D_{r_i}(y,x_j)$
is implied by the disjunction
which itself is implied by the formula
![]() $\zeta (\overline {x},y)$
. So,
$\zeta (\overline {x},y)$
. So,
![]() $\overline {b},c\models D_{r_i}(y,x_i)$
. A similar case occurs if
$\overline {b},c\models D_{r_i}(y,x_i)$
. A similar case occurs if
![]() $\overline {b}',c'$
satisfies a formula of the form
$\overline {b}',c'$
satisfies a formula of the form
![]() $D_{s_i}(y,a)$
for some
$D_{s_i}(y,a)$
for some
![]() $a\in A_0$
.
$a\in A_0$
.
Suppose now that
![]() $\overline {b}',c'\models \neg D_{p_j}(y,x_j)$
. If
$\overline {b}',c'\models \neg D_{p_j}(y,x_j)$
. If
![]() $\overline {b},c\models D_{p_j}(y,x_j)$
then
$\overline {b},c\models D_{p_j}(y,x_j)$
then
![]() $\operatorname {dist}(c,b_j)=p_j$
, and as in the previous paragraph this implies that either
$\operatorname {dist}(c,b_j)=p_j$
, and as in the previous paragraph this implies that either
![]() $c\in P(b_1,b_j)$
(which is not possible since
$c\in P(b_1,b_j)$
(which is not possible since
![]() $c\not \in \operatorname {acl}(A\overline {b})$
) or the formula
$c\not \in \operatorname {acl}(A\overline {b})$
) or the formula
![]() $D_{p_j}(y,x_j)$
is implied by
$D_{p_j}(y,x_j)$
is implied by
![]() $\zeta (\overline {x},y)$
, which is clearly a contradiction because
$\zeta (\overline {x},y)$
, which is clearly a contradiction because
![]() $\overline {b}',c'\models \zeta (\overline {x},y)$
. Therefore,
$\overline {b}',c'\models \zeta (\overline {x},y)$
. Therefore,
![]() $\overline {b},c$
also satisfies the formula
$\overline {b},c$
also satisfies the formula
![]() $\neg D_{p_j}(y,x_j)$
. A similar situation will occur for a formula of the form
$\neg D_{p_j}(y,x_j)$
. A similar situation will occur for a formula of the form
![]() $\neg D_{q_j}(y,a_j)$
for some element
$\neg D_{q_j}(y,a_j)$
for some element
![]() $q_j\in A_0$
.
$q_j\in A_0$
.
We have shown that
![]() $\zeta (\overline {x},y)$
implies each of the formulas in the conjunction defining
$\zeta (\overline {x},y)$
implies each of the formulas in the conjunction defining
![]() $S(\overline {x},y)$
, so
$S(\overline {x},y)$
, so
![]() $\zeta (\mathcal {M}^{n+1})=S(\mathcal {M}^{n+1})$
, which is a contradiction because
$\zeta (\mathcal {M}^{n+1})=S(\mathcal {M}^{n+1})$
, which is a contradiction because
![]() $\operatorname {RM}(\zeta (\overline {x},y))\geq \alpha \oplus 2$
and
$\operatorname {RM}(\zeta (\overline {x},y))\geq \alpha \oplus 2$
and
![]() $\operatorname {RM}(S(\overline {x},y)=\alpha \oplus 1$
. This contradiction shows that
$\operatorname {RM}(S(\overline {x},y)=\alpha \oplus 1$
. This contradiction shows that
![]() $\operatorname {RM}(\zeta (\overline {x},y))\leq \alpha \oplus 1$
and so,
$\operatorname {RM}(\zeta (\overline {x},y))\leq \alpha \oplus 1$
and so,
![]() $\operatorname {RM}(\overline {b},c)\leq \alpha \oplus 1$
.
$\operatorname {RM}(\overline {b},c)\leq \alpha \oplus 1$
.
Theorem A.11. Let
![]() $\mathcal {M}\models \mathcal {T}_\infty $
and let
$\mathcal {M}\models \mathcal {T}_\infty $
and let
![]() $A\subseteq M$
be a small set of parameters. Then for every tuple
$A\subseteq M$
be a small set of parameters. Then for every tuple
![]() $\overline {b}=(b_1,\ldots ,b_n)\in M^n$
we have
$\overline {b}=(b_1,\ldots ,b_n)\in M^n$
we have
 $$\begin{align*}\operatorname{SU}(\overline{b}/A)=\operatorname{RM}(\overline{b}/A)=\bigoplus_{i=1}^n D(b_i/A\overline{b}_{<i}).\end{align*}$$
$$\begin{align*}\operatorname{SU}(\overline{b}/A)=\operatorname{RM}(\overline{b}/A)=\bigoplus_{i=1}^n D(b_i/A\overline{b}_{<i}).\end{align*}$$
Proof. We will show the result by induction on n, and notice that the case
![]() $n=1$
is precisely Proposition A.8. Suppose the result holds for every tuple
$n=1$
is precisely Proposition A.8. Suppose the result holds for every tuple
![]() $\overline {b}$
of length n, and so there is an ordinal
$\overline {b}$
of length n, and so there is an ordinal
![]() $\alpha $
such that
$\alpha $
such that
 $$\begin{align*}\alpha=\operatorname{SU}(\overline{b}/A)=\operatorname{RM}(\overline{b}/A)=\bigoplus_{i=1}^n D(b_i/A\overline{b}_{<i}).\end{align*}$$
$$\begin{align*}\alpha=\operatorname{SU}(\overline{b}/A)=\operatorname{RM}(\overline{b}/A)=\bigoplus_{i=1}^n D(b_i/A\overline{b}_{<i}).\end{align*}$$
For the inductive step, it suffices to show that given an arbitrary element
![]() $c\in M$
we have
$c\in M$
we have
![]() $\operatorname {SU}(\overline {b},c/A)=\operatorname {RM}(\overline {b},c/A)=\alpha \oplus D(c/A\overline {b}).$
By Fact A.6 we know already that
$\operatorname {SU}(\overline {b},c/A)=\operatorname {RM}(\overline {b},c/A)=\alpha \oplus D(c/A\overline {b}).$
By Fact A.6 we know already that
![]() $\operatorname {SU}(\overline {b},c/A)\leq \operatorname {RM}(\overline {b},c/A)$
.
$\operatorname {SU}(\overline {b},c/A)\leq \operatorname {RM}(\overline {b},c/A)$
.
Suppose now that
![]() $D(c/A\overline {b})=m$
for some
$D(c/A\overline {b})=m$
for some
![]() $m\in \mathbb {N}$
. Hence, there is an element
$m\in \mathbb {N}$
. Hence, there is an element
![]() ${e\in \operatorname {conv}(A\overline {b})}$
and elements
${e\in \operatorname {conv}(A\overline {b})}$
and elements
![]() $c_0=e,c_1,\ldots ,c_m=c$
that form a path from e to c of length m. Note that for every
$c_0=e,c_1,\ldots ,c_m=c$
that form a path from e to c of length m. Note that for every
![]() $i=1,\ldots ,m$
we have
$i=1,\ldots ,m$
we have
![]() $c_{i-1}\in \operatorname {acl}(A,\overline {b},c_i)$
and
$c_{i-1}\in \operatorname {acl}(A,\overline {b},c_i)$
and
![]() $D(c_i/A\overline {b}c_{<i})=1$
. So, by Lemma A.10, we obtain
$D(c_i/A\overline {b}c_{<i})=1$
. So, by Lemma A.10, we obtain
 $$ \begin{align*} \operatorname{RM}(\overline{b},c/A)&=\operatorname{RM}(\overline{b},c_1,\ldots,c_{m-1},c/A)=\operatorname{RM}(\overline{b},c_1,\ldots,c_{m-1}/A)\oplus 1\\ &=\operatorname{RM}(\overline{b},c_1,\ldots,c_{m-2}/A)\oplus 2=\cdots = \operatorname{RM}(\overline{b},c_1/A)\oplus (m-1)\\ &=\operatorname{RM}(\overline{b}/A)\oplus m=\alpha\oplus m=\alpha\oplus D(c/A\overline{b}). \end{align*} $$
$$ \begin{align*} \operatorname{RM}(\overline{b},c/A)&=\operatorname{RM}(\overline{b},c_1,\ldots,c_{m-1},c/A)=\operatorname{RM}(\overline{b},c_1,\ldots,c_{m-1}/A)\oplus 1\\ &=\operatorname{RM}(\overline{b},c_1,\ldots,c_{m-2}/A)\oplus 2=\cdots = \operatorname{RM}(\overline{b},c_1/A)\oplus (m-1)\\ &=\operatorname{RM}(\overline{b}/A)\oplus m=\alpha\oplus m=\alpha\oplus D(c/A\overline{b}). \end{align*} $$
Suppose now that
![]() $D(c/A\overline {b})=\omega $
. By quantifier elimination
$D(c/A\overline {b})=\omega $
. By quantifier elimination
![]() $\operatorname {tp}(\overline {b},c/A)$
is completely characterized by
$\operatorname {tp}(\overline {b},c/A)$
is completely characterized by
![]() $\operatorname {tp}(\overline {b}/A)\cup \{\neg D_k(y,x_i)\wedge \neg D_\ell (y,a): a\in A; k,\ell <\omega , 1\leq i\leq n\}$
. Let
$\operatorname {tp}(\overline {b}/A)\cup \{\neg D_k(y,x_i)\wedge \neg D_\ell (y,a): a\in A; k,\ell <\omega , 1\leq i\leq n\}$
. Let
![]() $\varphi (\overline {x})$
be a minimal formula for
$\varphi (\overline {x})$
be a minimal formula for
![]() $\operatorname {tp}(\overline {b}/A)$
defined over a finite set of parameters
$\operatorname {tp}(\overline {b}/A)$
defined over a finite set of parameters
![]() $A_0\subseteq A$
, and assume that the formula is a conjunction including all instances of possible distances between elements in the tuple
$A_0\subseteq A$
, and assume that the formula is a conjunction including all instances of possible distances between elements in the tuple
![]() $\overline {b}$
and elements in
$\overline {b}$
and elements in
![]() $A_0$
, when they are finite.
$A_0$
, when they are finite.
Towards a contradiction, assume that
![]() $\operatorname {RM}(\overline {b},c/A)\geq \alpha \oplus (\omega +1)$
. Note that the formula
$\operatorname {RM}(\overline {b},c/A)\geq \alpha \oplus (\omega +1)$
. Note that the formula
![]() $\theta (\overline {x},y):=\varphi (\overline {x})$
in
$\theta (\overline {x},y):=\varphi (\overline {x})$
in
![]() $\operatorname {tp}(\overline {b},c/A)$
must have Morley rank at least
$\operatorname {tp}(\overline {b},c/A)$
must have Morley rank at least
![]() $\alpha \oplus (\omega +1)$
. By definition of Morley rank, there must be a formula
$\alpha \oplus (\omega +1)$
. By definition of Morley rank, there must be a formula
![]() $S(\overline {x},y)$
implying
$S(\overline {x},y)$
implying
![]() $\varphi (\overline {x})$
that has Morley rank
$\varphi (\overline {x})$
that has Morley rank
![]() $\alpha \oplus \omega $
. Hence
$\alpha \oplus \omega $
. Hence
![]() $S(\overline {x},y)\not \in \operatorname {tp}(\overline {b},c/A)$
, and so it must imply a formula of the form
$S(\overline {x},y)\not \in \operatorname {tp}(\overline {b},c/A)$
, and so it must imply a formula of the form
![]() $\varphi (\overline {x})\wedge D_k(y,x_i)$
or
$\varphi (\overline {x})\wedge D_k(y,x_i)$
or
![]() $\varphi (\overline {x})\wedge D_\ell (y,a)$
. In either case, if
$\varphi (\overline {x})\wedge D_\ell (y,a)$
. In either case, if
![]() $\overline {b}',c'$
is a generic tuple for
$\overline {b}',c'$
is a generic tuple for
![]() $S(\overline {x},y)$
,
$S(\overline {x},y)$
,
![]() $\operatorname {RM}(\overline {b}'/A)\leq \operatorname {RM}(\varphi (\overline {x}))=\alpha $
and
$\operatorname {RM}(\overline {b}'/A)\leq \operatorname {RM}(\varphi (\overline {x}))=\alpha $
and
![]() $D(c'/A\overline {b}')$
would be finite. So, by the previous case,
$D(c'/A\overline {b}')$
would be finite. So, by the previous case,
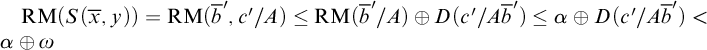 $\operatorname {RM}(S(\overline {x},y))=\operatorname {RM}(\overline {b}',c'/A)\leq \operatorname {RM}(\overline {b}'/A)\oplus D(c'/A\overline {b}')\leq \alpha \oplus D(c'/A\overline {b}')<\alpha \oplus \omega $
, which is a contradiction. This proves that when
$\operatorname {RM}(S(\overline {x},y))=\operatorname {RM}(\overline {b}',c'/A)\leq \operatorname {RM}(\overline {b}'/A)\oplus D(c'/A\overline {b}')\leq \alpha \oplus D(c'/A\overline {b}')<\alpha \oplus \omega $
, which is a contradiction. This proves that when
![]() $D(c/A\overline {b})=\omega $
we have
$D(c/A\overline {b})=\omega $
we have
![]() $\operatorname {RM}(\overline {b},c/A)\leq \alpha \oplus \omega $
.
$\operatorname {RM}(\overline {b},c/A)\leq \alpha \oplus \omega $
.
Proposition A.12. If
![]() $\mathcal {M}$
is a model of
$\mathcal {M}$
is a model of
![]() $\mathcal {T}_\infty $
and
$\mathcal {T}_\infty $
and
![]() $A,B,C\subseteq M$
are
$A,B,C\subseteq M$
are
![]() $\operatorname {acl}$
-closed subsets of M, then
$\operatorname {acl}$
-closed subsets of M, then ![]() if and only if every path between vertices of A and vertices of B passes through a vertex in C.
if and only if every path between vertices of A and vertices of B passes through a vertex in C.
Proof. Suppose first that there is a path between two elements
![]() $a\in A$
and
$a\in A$
and
![]() $b\in B$
that does not pass through any vertex in C. In particular,
$b\in B$
that does not pass through any vertex in C. In particular,
![]() $a\not \in C$
. If
$a\not \in C$
. If
![]() ${1\leq \operatorname {dist}(a,C)<\infty }$
, then there is an element
${1\leq \operatorname {dist}(a,C)<\infty }$
, then there is an element
![]() $e\in P(a,b)\setminus C$
that lies in the unique path between an element
$e\in P(a,b)\setminus C$
that lies in the unique path between an element
![]() $c\in C$
and b. Thus,
$c\in C$
and b. Thus,
![]() $\operatorname {RM}(a/BC)=\operatorname {dist}(a,e)<\operatorname {dist}(a,C)=\operatorname {RM}(a/C)$
. On the other hand, if
$\operatorname {RM}(a/BC)=\operatorname {dist}(a,e)<\operatorname {dist}(a,C)=\operatorname {RM}(a/C)$
. On the other hand, if
![]() $\operatorname {dist}(a,C)=\infty $
, then
$\operatorname {dist}(a,C)=\infty $
, then
![]() $\operatorname {RM}(a/BC)\leq \operatorname {dist}(a,b)<\omega =\operatorname {RM}(a/C)$
. In any case, we conclude that
$\operatorname {RM}(a/BC)\leq \operatorname {dist}(a,b)<\omega =\operatorname {RM}(a/C)$
. In any case, we conclude that ![]() , which implies
, which implies ![]() .
.
Now, suppose that every path between a vertex in A and a vertex in B passes through C. By finite character, to conclude that ![]() it suffices to show that whenever
it suffices to show that whenever
![]() $a_1,\ldots ,a_n$
is a finite tuple of elements in A, then
$a_1,\ldots ,a_n$
is a finite tuple of elements in A, then ![]() . We prove this by induction on n. For
. We prove this by induction on n. For
![]() $n=1$
, given an arbitrary element
$n=1$
, given an arbitrary element
![]() $a_1\in A$
, we know by the assumption that the distance between
$a_1\in A$
, we know by the assumption that the distance between
![]() $a_1$
and
$a_1$
and
![]() $BC$
is equal to the distance between
$BC$
is equal to the distance between
![]() $a_1$
and C. By Theorem A.11, this implies
$a_1$
and C. By Theorem A.11, this implies
![]() $\operatorname {RM}(a_1/BC)=\operatorname {RM}(a_1/C)$
, and so
$\operatorname {RM}(a_1/BC)=\operatorname {RM}(a_1/C)$
, and so ![]() for every element
for every element
![]() $a_1\in A$
.
$a_1\in A$
.
Suppose now that
![]() $a_1,\ldots ,a_n,a_{n+1}\in A$
. By induction hypothesis we have that
$a_1,\ldots ,a_n,a_{n+1}\in A$
. By induction hypothesis we have that ![]() , and by symmetry this implies
, and by symmetry this implies ![]() . Since every path between
. Since every path between
![]() $a_{n+1}$
and B passes through
$a_{n+1}$
and B passes through
![]() $Ca_1,\ldots ,a_n$
(because it passes through C), we have by the base case that
$Ca_1,\ldots ,a_n$
(because it passes through C), we have by the base case that ![]() , and by symmetry,
, and by symmetry, ![]() . Transitivity implies
. Transitivity implies ![]() , and symmetry again yields
, and symmetry again yields ![]() , as desired.
, as desired.
Acknowledgments
We would like to thank Alexander Berenstein and Tristram Bogart for their valuable comments and suggestions in the previous versions of this article.












