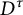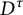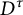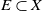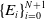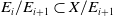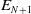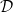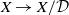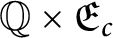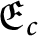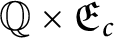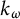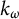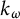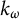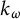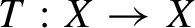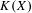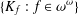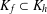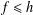Refine listing
Actions for selected content:
37 results in 54Bxx
SOME RESULTS ON FINITELY SPLITTING SUBTREES OF ARONSZAJN TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-31
-
- Article
- Export citation
Relative cell complexes in closure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-9
-
- Article
- Export citation
DUALITY FOR COALGEBRAS FOR VIETORIS AND MONADICITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1022-1055
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear homeomorphisms of function spaces and the position of a space in its compactification
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2151-2172
- Print publication:
- December 2024
-
- Article
- Export citation
The tamely ramified geometric quantitative minimal ramification problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 November 2023, pp. 21-51
- Print publication:
- January 2024
-
- Article
- Export citation
ON SEPARATE CONTINUITY AND SEPARATE CONVEXITY: A SYNTHETIC TREATMENT FOR FUNCTIONS AND SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 541-551
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On homogeneity of Cantor cubes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 1084-1090
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Null, recursively starlike-equivalent decompositions shrink
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 28 October 2022, pp. 328-336
- Print publication:
- May 2023
-
- Article
- Export citation
The equivalence between rational G-sheaves and rational G-Mackey functors for profinite G
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 345-368
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The spectrum of a localic semiring
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 28 February 2022, pp. 647-668
- Print publication:
- November 2022
-
- Article
- Export citation
A characterization of the product of the rational numbers and complete Erdős space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 27 January 2022, pp. 87-102
- Print publication:
- March 2023
-
- Article
- Export citation
Pure quotients and Morita’s theorem for
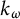 $k_{\omega }$-spaces
$k_{\omega }$-spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 July 2021, pp. 582-597
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 161-170
- Print publication:
- February 2022
-
- Article
- Export citation
Uniformly positive entropy of induced transformations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 9-18
- Print publication:
- January 2022
-
- Article
- Export citation
GAMES AND HEREDITARY BAIRENESS IN HYPERSPACES AND SPACES OF PROBABILITY MEASURES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 15 June 2020, pp. 851-868
- Print publication:
- May 2022
-
- Article
- Export citation
RECOVERING THE BOUNDARY PATH SPACE OF A TOPOLOGICAL GRAPH USING POINTLESS TOPOLOGY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 232-248
- Print publication:
- October 2021
-
- Article
- Export citation
A UNIFIED APPROACH TO CONTINUOUS, MEASURABLE SELECTIONS, AND SELECTIONS FOR HYPERSPACES
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 21 May 2018, pp. 607-627
- Print publication:
- 2018
-
- Article
- Export citation
A TOPOLOGICAL VARIATION OF THE RECONSTRUCTION CONJECTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 221-235
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
LIPSCHITZ RETRACTION OF FINITE SUBSETS OF HILBERT SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 146-151
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
DOMINATION CONDITIONS UNDER WHICH A COMPACT SPACE IS METRISABLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 11 February 2015, pp. 502-507
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation