1. Introduction
The classification of rational Mackey functors for finite groups is well known and highly useful. An algebraic version of this result is given by Thévenaz and Webb [ Reference Thévenaz and WebbTW95 ]. A version more suited to algebraic topology can be found in work of Greenlees and May [ Reference Greenlees and MayGM95 , appendix A]. In this case the classification is given as an equivalence of categories
where the product runs over G-conjugacy classes of subgroups of G. Greenlees and May proved this result in order to classify rational G-spectra (for finite G) in terms of an algebraic model. A gentle introduction to classifying rational G-spectra (and similar results) can be found in work of the first author and Kędziorek [ Reference Barnes and KędziorekBK20 ].
Profinite groups (compact Hausdorff totally-disconnected topological groups) are an important class of topological groups that contain all finite groups. Examples of where profinite groups occur include the automorphism groups of Galois extensions of fields, the étale fundamental groups of algebraic geometry and the Morava stabiliser group
![]() $\mathbb{S}_n$
from chromatic homotopy theory. The standard example is the p-adic integers
$\mathbb{S}_n$
from chromatic homotopy theory. The standard example is the p-adic integers
![]() ${\mathbb{Z}_{p}^{\wedge}}$
for p a prime.
${\mathbb{Z}_{p}^{\wedge}}$
for p a prime.
The main result of this paper is an extension of the classification of rational Mackey functors to profinite groups.
Theorem A. For G a profinite group, there is an exact equivalence
Here
![]() $\mathcal{S} G$
denotes the space of closed subgroups of G, see Definition 2·8 for the topology. A Weyl-G-sheaf over
$\mathcal{S} G$
denotes the space of closed subgroups of G, see Definition 2·8 for the topology. A Weyl-G-sheaf over
![]() $\mathcal{S} G$
is a G-equivariant sheaf over
$\mathcal{S} G$
is a G-equivariant sheaf over
![]() $\mathcal{S} G$
such that the stalk at a closed subgroup
$\mathcal{S} G$
such that the stalk at a closed subgroup
![]() $K \leqslant G$
is K-fixed. Hence, the stalk at K has an action of the Weyl group
$K \leqslant G$
is K-fixed. Hence, the stalk at K has an action of the Weyl group
![]() $W_G K$
. This result appears as Theorem 4·8 in the main body.
$W_G K$
. This result appears as Theorem 4·8 in the main body.
The reason why Mackey functors for finite groups have a simpler description is that
![]() $\mathcal{S} G$
is a discrete space when G is finite. In which case, a Weyl-G-sheaf over
$\mathcal{S} G$
is a discrete space when G is finite. In which case, a Weyl-G-sheaf over
![]() $\mathcal{S} G$
is a product of
$\mathcal{S} G$
is a product of
![]() $\mathbb{Q}$
-modules with actions of the Weyl groups. Choosing representatives for conjugacy classes gives the description (1·1) above. Furthermore, the rational Burnside ring for a profinite group is isomorphic to the ring of continuous functions from
$\mathbb{Q}$
-modules with actions of the Weyl groups. Choosing representatives for conjugacy classes gives the description (1·1) above. Furthermore, the rational Burnside ring for a profinite group is isomorphic to the ring of continuous functions from
![]() $\mathcal{S} G /G$
to
$\mathcal{S} G /G$
to
![]() $\mathbb{Q}$
. Hence, when G is finite, the rational Burnside ring is simply a product of copies of
$\mathbb{Q}$
. Hence, when G is finite, the rational Burnside ring is simply a product of copies of
![]() $\mathbb{Q}$
, indexed over the set of conjugacy classes of subgroups of G.
$\mathbb{Q}$
, indexed over the set of conjugacy classes of subgroups of G.
Our next result, see Lemma 2·17, extends a vital identity on rational G-Mackey functors from the finite case to the profinite case. In the finite setting, the restriction map induces an isomorphism
where
![]() $e^H_K$
is the idempotent in the rational Burnside ring of H corresponding to the conjugacy class of
$e^H_K$
is the idempotent in the rational Burnside ring of H corresponding to the conjugacy class of
![]() $K \leqslant H$
. To extend this to the profinite case, we use the idempotents
$K \leqslant H$
. To extend this to the profinite case, we use the idempotents
![]() ${e^{H}_{{N},{K}}}$
and
${e^{H}_{{N},{K}}}$
and
![]() ${e^{{K}}_{{N},{K}}}$
of Definition 2·13, which are analogous to
${e^{{K}}_{{N},{K}}}$
of Definition 2·13, which are analogous to
![]() $e^H_K$
and
$e^H_K$
and
![]() $e^K_K$
.
$e^K_K$
.
Lemma B. Let
![]() $K \leqslant H$
be open subgroups of G and N an open normal subgroup of K. Restriction from H to K induces an isomorphism
$K \leqslant H$
be open subgroups of G and N an open normal subgroup of K. Restriction from H to K induces an isomorphism
The following is Proposition 2·21 and relates the equivariance of the stalks to that of representing sections. This proposition and the preceding lemma are key to proving the equivalence of categories of Theorem A.
Proposition C. Let E be a Weyl-G-sheaf over
![]() $\mathcal{S} G$
and K a closed subgroup of G. A germ over K can be represented by an NK-equivariant section over a neighbourhood of K, for some open normal subgroup N of G.
$\mathcal{S} G$
and K a closed subgroup of G. A germ over K can be represented by an NK-equivariant section over a neighbourhood of K, for some open normal subgroup N of G.
This work is part of the second author’s PhD thesis, [
Reference SugrueSug19
], completed under the supervision of the first author. That thesis applies the main result of this paper to obtain a classification of rational G-spectra for profinite G in terms of chain complexes of Weyl-G-sheaves over
![]() $\mathcal{S} G$
, see [
Reference SugrueSug19
, chapters 3 and 6]. This extends the work of the first author on the case where G is the p-adic integers, [
Reference BarnesBar11
]. A further application of the classification of rational G-Mackey functors in terms of sheaves is a calculation of the injective dimension of these categories in terms of the Cantor–Bendixson rank of the space
$\mathcal{S} G$
, see [
Reference SugrueSug19
, chapters 3 and 6]. This extends the work of the first author on the case where G is the p-adic integers, [
Reference BarnesBar11
]. A further application of the classification of rational G-Mackey functors in terms of sheaves is a calculation of the injective dimension of these categories in terms of the Cantor–Bendixson rank of the space
![]() $\mathcal{S} G$
, see [
Reference SugrueSug19
, chapter 8].
$\mathcal{S} G$
, see [
Reference SugrueSug19
, chapter 8].
1·1. Organisation
We define the categories involved in Section 2 and construct the two functors of the classification in Section 3. We prove directly that the functors give an equivalence in Section 4. We end the paper with some examples and the relation between G-sheaves over
![]() $\mathcal{S} G$
and Weyl-G-sheaves over
$\mathcal{S} G$
and Weyl-G-sheaves over
![]() $\mathcal{S} G$
, see Section 5.
$\mathcal{S} G$
, see Section 5.
2. Mackey functors and sheaves
We introduce the definitions and categories that are used in the paper.
2·1. Basic facts on profinite groups
We give a few reminders of useful facts on profinite groups. More details can be found in Wilson [ Reference WilsonWil98 ] or Ribes and Zalesskii [ Reference Ribes and ZalesskiiRZ00 ].
A profinite group is a compact, Hausdorff, totally disconnected topological group. A profinite group G is homeomorphic to the inverse limit of its finite quotients:
The limit has the canonical topology which can either be described as the subspace topology on the product or as the topology generated by the pre-images of the open sets in
![]() $G/N$
under the projection map
$G/N$
under the projection map
![]() $G \to G/N$
, as N runs over the open normal subgroups of G.
$G \to G/N$
, as N runs over the open normal subgroups of G.
Closed subgroups and quotients by closed subgroups of profinite groups are also profinite. A subgroup of a profinite group is open if and only if it is finite index and closed. The trivial subgroup
![]() $\{ e\}$
is open if and only if the group is finite. The intersection of all open normal subgroups is
$\{ e\}$
is open if and only if the group is finite. The intersection of all open normal subgroups is
![]() $\{ e \}$
. Any open subgroup H contains an open normal subgroup, the core of H in G, defined as the following intersection. Note that as H has finite index in G, this intersection has only finitely many distinct terms.
$\{ e \}$
. Any open subgroup H contains an open normal subgroup, the core of H in G, defined as the following intersection. Note that as H has finite index in G, this intersection has only finitely many distinct terms.
We can also define a profinite topological space to be a Hausdorff, compact and totally disconnected topological space. As with profinite groups, such a space is homeomorphic to the inverse limit of a filtered diagram of finite spaces. Moreover, a profinite topological space has a closed-open basis.
2·2. Mackey functors for profinite groups
There are many equivalent definitions of Mackey functors for a finite group G. Our preferred version is a collection of abelian groups indexed over the subgroups of G with induction (transfer), restriction and conjugation maps satisfying a list of axioms. In turn, there are several (inequivalent) extensions to profinite groups. Since we have in mind applications to algebraic topology and the work of Fausk [ Reference FauskFau08 ], we choose a generalisation that emphasises the role of the open subgroups.
The following definition can be found in Bley and Boltje [ Reference Bley and BoltjeBB04 , definition 2·1 and examples 2·2] as the “finite natural Mackey system” and in Thiel [ Reference ThielThi11 , definition 2·2·12]. In the case of a finite group, it restricts to the usual definition.
Definition 2·1. Let G be a profinite group, then a rational G-Mackey functor M is:
-
(i) a collection of
 $\mathbb{Q}$
-modules M(H) for each open subgroup
$\mathbb{Q}$
-modules M(H) for each open subgroup
 $H \leqslant G$
;
$H \leqslant G$
; -
(ii) for open subgroups
 $K,H \leqslant G$
with
$K,H \leqslant G$
with
 $K\leqslant H$
and any
$K\leqslant H$
and any
 $g \in G$
we have a restriction map, an induction map and a conjugation map
$g \in G$
we have a restriction map, an induction map and a conjugation map  \[R^H_K \colon M(H)\Longrightarrow M(K), \quad I^H_K \colon M(K)\Longrightarrow M(H) \quad \text{ and } \quad C_g \colon M(H)\Longrightarrow M(gHg^{-1}).\]
\[R^H_K \colon M(H)\Longrightarrow M(K), \quad I^H_K \colon M(K)\Longrightarrow M(H) \quad \text{ and } \quad C_g \colon M(H)\Longrightarrow M(gHg^{-1}).\]
These maps satisfy the following conditions.
-
(i) For all open subgroups H of G and all
 $h\in H$
the structure maps are unital
$h\in H$
the structure maps are unital  \[R^H_H=\textrm{Id}_{M(H)}=I^H_H \quad \text{ and } \quad C_h=\textrm{Id}_{M(H)}.\]
\[R^H_H=\textrm{Id}_{M(H)}=I^H_H \quad \text{ and } \quad C_h=\textrm{Id}_{M(H)}.\]
-
(ii) For
 $L\leqslant K\leqslant H$
open subgroups of G and
$L\leqslant K\leqslant H$
open subgroups of G and
 $g,h\in G$
, there are composition rules The first two are transitivity of induction and restriction. The last is associativity of conjugation.
$g,h\in G$
, there are composition rules The first two are transitivity of induction and restriction. The last is associativity of conjugation. \[I^H_L=I^H_K\circ I^K_L, \qquad R^H_L=R^K_L\circ R^H_K, \quad \text{ and } \quad C_{gh}=C_g\circ C_h.\]
\[I^H_L=I^H_K\circ I^K_L, \qquad R^H_L=R^K_L\circ R^H_K, \quad \text{ and } \quad C_{gh}=C_g\circ C_h.\]
-
(iii) For
 $g\in G$
and
$g\in G$
and
 $K\leqslant H$
open subgroups of G, there are composition rules This is the equivariance of restriction and induction.
$K\leqslant H$
open subgroups of G, there are composition rules This is the equivariance of restriction and induction. \[R^{gHg^{-1}}_{gKg^{-1}}\circ C_g=C_g\circ R^H_K \quad \text{ and } \quad I^{gHg^{-1}}_{gKg^{-1}}\circ C_g=C_g\circ I^H_K.\]
\[R^{gHg^{-1}}_{gKg^{-1}}\circ C_g=C_g\circ R^H_K \quad \text{ and } \quad I^{gHg^{-1}}_{gKg^{-1}}\circ C_g=C_g\circ I^H_K.\]
-
(iv) For open subgroups
 $K,L\leqslant H$
of G This condition is known as the Mackey axiom.
$K,L\leqslant H$
of G This condition is known as the Mackey axiom. \[R^H_K\circ I^H_L=\sum_{x\in\left[ K \backslash H / L \right]} I^K_{K\cap xLx^{-1}}\circ C_x\circ R^L_{L\cap x^{-1}Kx}.\]
\[R^H_K\circ I^H_L=\sum_{x\in\left[ K \backslash H / L \right]} I^K_{K\cap xLx^{-1}}\circ C_x\circ R^L_{L\cap x^{-1}Kx}.\]
A map of Mackey functors
![]() $f \colon M \to N$
is a collection of
$f \colon M \to N$
is a collection of
![]() $\mathbb{Q}$
-module maps
$\mathbb{Q}$
-module maps
for each open subgroup
![]() $H \leqslant G$
, which commute with the induction, restriction and conjugation maps. We use
$H \leqslant G$
, which commute with the induction, restriction and conjugation maps. We use
![]() ${\textrm{Mackey}_{\mathbb{Q}}({G})}$
to denote this category.
${\textrm{Mackey}_{\mathbb{Q}}({G})}$
to denote this category.
See Thévenaz and Webb [ Reference Thévenaz and WebbTW95 ] for an introduction into Mackey functors for finite groups. The case of rational Mackey functors is also discussed in work of the first author with Kędziorek [ Reference Barnes and KędziorekBK20 ]. Alternative definitions of Mackey functors in a general setting are discussed in Lindner [ Reference LindnerLin76 , definition 1].
We have some standard examples similar to those for finite groups.
Example 2·2. Consider the profinite group given by the p-adic integers,
![]() ${\mathbb{Z}_{p}^{\wedge}}$
. The open subgroups in this case are of the form
${\mathbb{Z}_{p}^{\wedge}}$
. The open subgroups in this case are of the form
![]() $p^k{\mathbb{Z}_{p}^{\wedge}}$
for
$p^k{\mathbb{Z}_{p}^{\wedge}}$
for
![]() $k\geqslant 0$
. We define a constant Mackey functor by sending each open subgroup to
$k\geqslant 0$
. We define a constant Mackey functor by sending each open subgroup to
![]() $\mathbb{Q}$
with all restriction and conjugation maps taken to be the identity. The subgroup
$\mathbb{Q}$
with all restriction and conjugation maps taken to be the identity. The subgroup
![]() $p^l{\mathbb{Z}_{p}^{\wedge}}$
is contained inside
$p^l{\mathbb{Z}_{p}^{\wedge}}$
is contained inside
![]() $p^k{\mathbb{Z}_{p}^{\wedge}}$
if and only if
$p^k{\mathbb{Z}_{p}^{\wedge}}$
if and only if
![]() $l\geqslant k$
. The Mackey axiom forces the induction maps to be
$l\geqslant k$
. The Mackey axiom forces the induction maps to be
In general, there is a constant Mackey functor for any profinite group G, which takes value
![]() $\mathbb{Q}$
at every open subgroup H of G. The conjugation and restriction maps are identity maps and induction from K to H is multiplication by the index of K in H.
$\mathbb{Q}$
at every open subgroup H of G. The conjugation and restriction maps are identity maps and induction from K to H is multiplication by the index of K in H.
Example 2·3. Let R(G) denote the ring of finite dimensional complex representations of the profinite group G. We define a rational Mackey functor
![]() $M_R$
by
$M_R$
by
![]() $M_R(H) = R(H) \otimes \mathbb{Q}$
, with induction and restriction induced by induction and restriction of representations. Conjugation is induced from precomposition with the conjugation homomorphism of groups.
$M_R(H) = R(H) \otimes \mathbb{Q}$
, with induction and restriction induced by induction and restriction of representations. Conjugation is induced from precomposition with the conjugation homomorphism of groups.
In the case of finite groups, another common example is the fixed point Mackey functor. A profinite analogue exists, but one needs to be more careful over the action of G on a
![]() $\mathbb{Q}$
-module.
$\mathbb{Q}$
-module.
Definition 2·4. A rational discrete G-module M is a
![]() $\mathbb{Q}$
-module such that
$\mathbb{Q}$
-module such that
The definition is equivalent to the statement that any
![]() $m \in M$
is stabilised by an open subgroup of G. If we give a rational G-module M the discrete topology, then the action of G on M is continuous if and only if M is discrete in the preceding sense.
$m \in M$
is stabilised by an open subgroup of G. If we give a rational G-module M the discrete topology, then the action of G on M is continuous if and only if M is discrete in the preceding sense.
Example 2·5. Given M a discrete G-module, there is a Mackey functor which at an open subgroup
![]() $H \leqslant G$
takes value
$H \leqslant G$
takes value
![]() $M^H$
. The restriction maps are inclusion of fixed points and the conjugation maps are given by left multiplication. The induction map from K to H is given by summing over the action of a left transversal of K in H (which is finite as the subgroups are open).
$M^H$
. The restriction maps are inclusion of fixed points and the conjugation maps are given by left multiplication. The induction map from K to H is given by summing over the action of a left transversal of K in H (which is finite as the subgroups are open).
Example 2·6. The rational Burnside ring
![]() ${\textbf{A}_\mathbb{Q}}(G)$
of a profinite group G defines a rational Mackey functor. For H an open subgroup of G, the ring
${\textbf{A}_\mathbb{Q}}(G)$
of a profinite group G defines a rational Mackey functor. For H an open subgroup of G, the ring
![]() ${\textbf{A}_\mathbb{Q}}(H)$
is the rational Grothendieck ring of finite H-sets (that is, finite discrete topological spaces with a continuous action of H). The multiplication is given by the product of H-sets.
${\textbf{A}_\mathbb{Q}}(H)$
is the rational Grothendieck ring of finite H-sets (that is, finite discrete topological spaces with a continuous action of H). The multiplication is given by the product of H-sets.
Restriction and induction between
![]() ${\textbf{A}_\mathbb{Q}}(H)$
and
${\textbf{A}_\mathbb{Q}}(H)$
and
![]() ${\textbf{A}_\mathbb{Q}}(K)$
are given by the usual restriction and induction of sets with group actions. Moreover, the restriction maps are maps of rings. Conjugation is induced from precomposition with the conjugation homomorphism of groups.
${\textbf{A}_\mathbb{Q}}(K)$
are given by the usual restriction and induction of sets with group actions. Moreover, the restriction maps are maps of rings. Conjugation is induced from precomposition with the conjugation homomorphism of groups.
Given a G-Mackey functor M, we can define an action of the Burnside ring
![]() ${\textbf{A}_\mathbb{Q}}(H)$
on the abelian group M(H) by
${\textbf{A}_\mathbb{Q}}(H)$
on the abelian group M(H) by
and extending linearly from the additive basis for
![]() ${\textbf{A}_\mathbb{Q}}(H)$
given by
${\textbf{A}_\mathbb{Q}}(H)$
given by
![]() $H/K$
for open subgroups K of H. The Mackey axiom implies that this action is compatible with the multiplication of
$H/K$
for open subgroups K of H. The Mackey axiom implies that this action is compatible with the multiplication of
![]() ${\textbf{A}_\mathbb{Q}}(H)$
, so that M(H) is a module over
${\textbf{A}_\mathbb{Q}}(H)$
, so that M(H) is a module over
![]() ${\textbf{A}_\mathbb{Q}}(H)$
. Moreover, the following square commutes
${\textbf{A}_\mathbb{Q}}(H)$
. Moreover, the following square commutes

We also have the relation, known as Frobenius reciprocity, between induction and the action of Burnside rings. Let
![]() $\alpha \in {\textbf{A}_\mathbb{Q}}(H)$
,
$\alpha \in {\textbf{A}_\mathbb{Q}}(H)$
,
![]() $\beta \in {\textbf{A}_\mathbb{Q}}(K)$
,
$\beta \in {\textbf{A}_\mathbb{Q}}(K)$
,
![]() $m \in M(K)$
and
$m \in M(K)$
and
![]() $n \in M(H)$
, then
$n \in M(H)$
, then
See Yoshida [ Reference YoshidaYos80 , definition 2·3 and example 2·11]. We summarise this discussion in the following proposition.
Proposition 2·7. If M is a Mackey functor for a profinite group G and H is an open subgroup of G, then each M(H) has an
![]() ${\textbf{A}_\mathbb{Q}}(H)$
-module structure. Moreover, the restriction map
${\textbf{A}_\mathbb{Q}}(H)$
-module structure. Moreover, the restriction map
![]() $M(H) \to M(K)$
is a map of modules over the restriction map
$M(H) \to M(K)$
is a map of modules over the restriction map
![]() ${\textbf{A}_\mathbb{Q}}(H) \to {\textbf{A}_\mathbb{Q}}(K)$
, which is compatible with the conjugation maps. The Burnside ring actions satisfy Frobenius reciprocity with respect to the induction maps.
${\textbf{A}_\mathbb{Q}}(H) \to {\textbf{A}_\mathbb{Q}}(K)$
, which is compatible with the conjugation maps. The Burnside ring actions satisfy Frobenius reciprocity with respect to the induction maps.
2·3. Burnside ring idempotents
As with finite groups, there is a description of the rational Burnside ring in terms of continuous maps out of the space of subgroups of G. We will use this structure repeatedly, so we examine the result in detail and use it to describe idempotents of the Burnside ring.
Definition 2·8. For G a profinite group, the space of closed subgroups of G,
![]() $\mathcal{S} G$
, is the topological space
$\mathcal{S} G$
, is the topological space
where
![]() $\mathcal{S} (G/N)$
is a finite space with the discrete topology. For
$\mathcal{S} (G/N)$
is a finite space with the discrete topology. For
![]() $N \leqslant N'$
, the corresponding map of the limit diagram is
$N \leqslant N'$
, the corresponding map of the limit diagram is
The limit is topologised as either the subspace of the product or as the coarsest topology so that the projection maps
are continuous. The group G acts continuously on
![]() $\mathcal{S} G$
by conjugation,
$\mathcal{S} G$
by conjugation,
![]() $g \in G$
sends a closed subgroup K to
$g \in G$
sends a closed subgroup K to
![]() $gK g^{-1} = ^{g}{}{K}$
.
$gK g^{-1} = ^{g}{}{K}$
.
Following Gartside and Smith [ Reference Gartside and SmithGS10 , lemma 2·14], we can give a compact-open basis for this topology.
Lemma 2·9. An explicit basis for
![]() $\mathcal{S} G$
is the collection of closed and open sets
$\mathcal{S} G$
is the collection of closed and open sets
such that N is an open normal subgroup of G, and J is an open subgroup of G (that contains N).
Proof. The set
![]() $O_G(N, J)$
is the pre-image of the set
$O_G(N, J)$
is the pre-image of the set
![]() $\{ J/N \} \in \mathcal{S} (G/N)$
under
$\{ J/N \} \in \mathcal{S} (G/N)$
under
![]() $p_N$
, hence it is open and closed. To see this is a basis, let
$p_N$
, hence it is open and closed. To see this is a basis, let
![]() $A \in O_G(N, J) \cap O_G(N', J')$
and set
$A \in O_G(N, J) \cap O_G(N', J')$
and set
![]() $N''=N \cap N'$
, then
$N''=N \cap N'$
, then
These sets are compatible with the G-action:
Since any open subgroup of G has form N K for N some open normal subgroup of G and K a closed subgroup of G, we can rewrite the basis to consist of the sets
If we fix K and allow N to vary, these sets give a neighbourhood basis for
![]() $K \in \mathcal{S} G$
. We further define
$K \in \mathcal{S} G$
. We further define
the quotient under the conjugation action. This set is open in
![]() $\mathcal{S} G/G$
as the quotient map is open. It is closed as
$\mathcal{S} G/G$
as the quotient map is open. It is closed as
![]() $O_G(N,K)$
is compact. We will also make use of the equality
$O_G(N,K)$
is compact. We will also make use of the equality
Theorem 2·10. For G a profinite group, there is an isomorphism of commutative rings
Proof. This is Dress [
Reference DressDre71
, theorem B·2·3(a)]. As with finite groups, the isomorphism maps
![]() $[G/H]$
to the function which sends a conjugacy class of closed subgroup K to
$[G/H]$
to the function which sends a conjugacy class of closed subgroup K to
![]() $| (G/H)^K |$
.
$| (G/H)^K |$
.
Lemma 2·11. For G a profinite group, there is a natural isomorphism of commutative rings
Proof. Since any
![]() $G/N$
-set is a G-set by precomposing with the quotient
$G/N$
-set is a G-set by precomposing with the quotient
![]() $G \to G/N$
, we have the given map of rings, which is injective. Surjectivity follows as a continuous action of G on a finite set factors through some finite quotient of G.
$G \to G/N$
, we have the given map of rings, which is injective. Surjectivity follows as a continuous action of G on a finite set factors through some finite quotient of G.
Remark 2·12. Similar to Pontryagin duality, the previous lemma and theorem imply that the canonical map
induced by the surjections
![]() $\mathcal{S} G/G \to \mathcal{S} (G/N)/(G/N)$
is an isomorphism.
$\mathcal{S} G/G \to \mathcal{S} (G/N)/(G/N)$
is an isomorphism.
This type of isomorphism holds for any profinite space X. The difficult step is proving surjectivity. This comes from the fact that any map
![]() $X \to \mathbb{Q}$
must have finite image and hence factor through some finite quotient of X. See Ribes and Zalesskii [
Reference Ribes and ZalesskiiRZ00
, proposition 1·1·16 (a) and lemma 5·6·3].
$X \to \mathbb{Q}$
must have finite image and hence factor through some finite quotient of X. See Ribes and Zalesskii [
Reference Ribes and ZalesskiiRZ00
, proposition 1·1·16 (a) and lemma 5·6·3].
An idempotent of
![]() ${\textbf{A}_\mathbb{Q}}(H)=C(\mathcal{S} H/H,\mathbb{Q})$
corresponds to an open and closed subset of
${\textbf{A}_\mathbb{Q}}(H)=C(\mathcal{S} H/H,\mathbb{Q})$
corresponds to an open and closed subset of
![]() $\mathcal{S} H/H$
. The projection map
$\mathcal{S} H/H$
. The projection map
![]() $p_H \colon \mathcal{S} H \to \mathcal{S} H/H$
is open and both domain and codomain are compact, hence an open and closed subset of
$p_H \colon \mathcal{S} H \to \mathcal{S} H/H$
is open and both domain and codomain are compact, hence an open and closed subset of
![]() $\mathcal{S} H$
defines an idempotent of
$\mathcal{S} H$
defines an idempotent of
![]() ${\textbf{A}_\mathbb{Q}}(H)$
. Indeed, the set of idempotents of
${\textbf{A}_\mathbb{Q}}(H)$
. Indeed, the set of idempotents of
![]() ${\textbf{A}_\mathbb{Q}}(H)$
is in bijection with the set of open, closed and H-invariant subsets of
${\textbf{A}_\mathbb{Q}}(H)$
is in bijection with the set of open, closed and H-invariant subsets of
![]() $\mathcal{S} H$
.
$\mathcal{S} H$
.
Definition 2·13. For U an open and closed subset of
![]() $\mathcal{S} H/H$
, there is an idempotent
$\mathcal{S} H/H$
, there is an idempotent
![]() ${e^{H}_{U}}$
, the characteristic function of U.
${e^{H}_{U}}$
, the characteristic function of U.
An open and closed subset V of
![]() $\mathcal{S} H$
(that is not necessarily H-invariant) defines an idempotent
$\mathcal{S} H$
(that is not necessarily H-invariant) defines an idempotent
![]() ${e^{H}_{V}} := {e^{H}_{p_H(V)}}$
of
${e^{H}_{V}} := {e^{H}_{p_H(V)}}$
of
![]() ${\textbf{A}_\mathbb{Q}}(H)$
, the characteristic function of
${\textbf{A}_\mathbb{Q}}(H)$
, the characteristic function of
![]() $V/H$
. In turn, we define
$V/H$
. In turn, we define
the characteristic function for
![]() $\overline{O}_H(N,J)=O_H(N,J)/H$
, for J an open subgroup of H.
$\overline{O}_H(N,J)=O_H(N,J)/H$
, for J an open subgroup of H.
We relate our closed-open basis for
![]() $\mathcal{S} G$
to idempotents of
$\mathcal{S} G$
to idempotents of
![]() $C(\mathcal{S} G/G,\mathbb{Q})$
and the additive basis of that ring. For the formula we will use the Moebius function
$C(\mathcal{S} G/G,\mathbb{Q})$
and the additive basis of that ring. For the formula we will use the Moebius function
![]() $\mu$
for pairs of subgroups
$\mu$
for pairs of subgroups
![]() $D\leqslant K$
$D\leqslant K$
where
![]() $c_i$
is the number of strictly increasing chains from D to K of length i. Note that a chain of the form
$c_i$
is the number of strictly increasing chains from D to K of length i. Note that a chain of the form
![]() $D < K$
has length 1 and, by convention,
$D < K$
has length 1 and, by convention,
![]() $\mu(K,K)=1$
.
$\mu(K,K)=1$
.
Proposition 2·14. For G a profinite group, with open normal subgroup N and closed subgroup K
Proof. The sum is finite as we range over open subgroups of G that contain N.
The method is to reduce the calculation to the case of finite groups, and use the formula for idempotents of the rational Burnside ring of the finite group
![]() $G/N$
from Gluck [
Reference GluckGlu81
, section 2]. The reduction comes from the following commuting diagrams, where
$G/N$
from Gluck [
Reference GluckGlu81
, section 2]. The reduction comes from the following commuting diagrams, where
![]() $p_N \colon \mathcal{S} G \to \mathcal{S} (G/N)$
sends H to
$p_N \colon \mathcal{S} G \to \mathcal{S} (G/N)$
sends H to
![]() $HN/N$
. The second diagram uses the homeomorphism of G-spaces:
$HN/N$
. The second diagram uses the homeomorphism of G-spaces:

If we replace
![]() $p_N$
by
$p_N$
by
![]() $\overline{p}_N \colon \mathcal{S} G/G \to \mathcal{S} (G/N)/(G/N)$
the two diagrams above remain commutative.
$\overline{p}_N \colon \mathcal{S} G/G \to \mathcal{S} (G/N)/(G/N)$
the two diagrams above remain commutative.
The first diagram and the formula for idempotents gives
The second diagram completes the proof.
The coefficients are constant under certain conjugations. More precisely, for
![]() $K\leqslant J\leqslant G$
open subgroups of G and
$K\leqslant J\leqslant G$
open subgroups of G and
![]() $a \in N_G(J)$
, if we define
$a \in N_G(J)$
, if we define
A simple observation shows that for a rational G-Mackey functor M, each component M(H) is a sheaf over the profinite space
![]() $\mathcal{S} H / H$
. This holds as M(H) is a module over
$\mathcal{S} H / H$
. This holds as M(H) is a module over
![]() ${\textbf{A}_\mathbb{Q}}(H) = C(\mathcal{S} H/H, \mathbb{Q})$
.
${\textbf{A}_\mathbb{Q}}(H) = C(\mathcal{S} H/H, \mathbb{Q})$
.
Proposition 2·15. Suppose X is a profinite space and M is a
![]() $C(X,\mathbb{Q})$
-module, then M determines a sheaf of
$C(X,\mathbb{Q})$
-module, then M determines a sheaf of
![]() $\mathbb{Q}$
-modules over X.
$\mathbb{Q}$
-modules over X.
Proof. Let
![]() $\mathfrak{B}$
be an open-closed basis for X. Given a module M, we define a sheaf F by giving its values on
$\mathfrak{B}$
be an open-closed basis for X. Given a module M, we define a sheaf F by giving its values on
![]() $\mathfrak{B}$
. Let
$\mathfrak{B}$
. Let
![]() $U \in \mathfrak{B}$
and define the characteristic function of U to be the map which sends elements of U to 1 and the rest of X to 0. This map, which is denoted
$U \in \mathfrak{B}$
and define the characteristic function of U to be the map which sends elements of U to 1 and the rest of X to 0. This map, which is denoted
![]() $e_U \in C(X,\mathbb{Q})$
, is continuous as U is both open and closed. We define
$e_U \in C(X,\mathbb{Q})$
, is continuous as U is both open and closed. We define
![]() $F(U) = e_U M$
. For
$F(U) = e_U M$
. For
![]() $V \subseteq U$
in
$V \subseteq U$
in
![]() $\mathfrak{B}$
, we define the restriction map to be the projection (where
$\mathfrak{B}$
, we define the restriction map to be the projection (where
![]() $V^c$
is the complement of V in X)
$V^c$
is the complement of V in X)
which is equivalent to multiplying by
![]() $e_V$
.
$e_V$
.
The sheaf condition follows as we have a closed-open basis of a compact space and hence can write any open cover of a basis element as a finite partition of basis elements.
Corollary 2·16. If M is a Mackey functor over a profinite group G, then for each open subgroup H of G, the
![]() $\mathbb{Q}$
-module M(H) defines a sheaf over
$\mathbb{Q}$
-module M(H) defines a sheaf over
![]() $\mathcal{S} H/H$
, the space of H-conjugacy classes of closed subgroups of H.
$\mathcal{S} H/H$
, the space of H-conjugacy classes of closed subgroups of H.
Paraphrasing the corollary, we see that a G-Mackey functor is a collection of sheaves, one for each open subgroup of G. The rough idea of the equivalence is to patch parts of these sheaves together to construct a G-equivariant sheaf. It will take some time to make this rigorous, but we can give a useful relation between the various sheaves M(H). This relation is an extension of a result for finite groups, as referenced in the proof, see also Equation (1·2) of the introduction.
Lemma 2·17. Let
![]() $K \leqslant H$
be open subgroups of G and N an open normal subgroup of K. Restriction from H to K gives an isomorphism
$K \leqslant H$
be open subgroups of G and N an open normal subgroup of K. Restriction from H to K gives an isomorphism
Proof. The method is to reduce the problem to the case of finite groups. Similarly to Greenlees and May [
Reference Greenlees and MayGM92
, definition 3] or Thévenaz and Webb [
Reference Thévenaz and WebbTW95
], we may define a
![]() $G/N$
-Mackey functor
$G/N$
-Mackey functor
![]() $\overline{M}$
by
$\overline{M}$
by
Proposition 2·14 implies that when
![]() $J \geqslant N$
,
$J \geqslant N$
,
Now that we have Mackey functors for finite groups, we may use [ Reference GreenleesGre98 , example 5C(i) and corollary 5·3] to see that restriction induces an isomorphism
Alternative proofs of that result occur in [
Reference SugrueSug19
, lemma 6·1·9] and [
Reference Barnes and KędziorekBK20
]. Combining these isomorphisms and the fact
![]() $N_{H/N}(K/N)\cong N_H(K)/N$
, we obtain
$N_{H/N}(K/N)\cong N_H(K)/N$
, we obtain
 \begin{align*}{e^{K}_{{N},{K}}} M(K)^{N_H(K)}&={e^{K}_{{N},{K}}} M(K)^{N_H(K)/N}\\[5pt]&=e_{K/N}^{K/N} \overline{M} ( K/N )^{N_{H/N}(K/N)} \\[5pt]&=e_{K/N}^{H/N} \overline{M} ( H/N ) \\[5pt]&={e^{H}_{{N},{K}}} M(H).\end{align*}
\begin{align*}{e^{K}_{{N},{K}}} M(K)^{N_H(K)}&={e^{K}_{{N},{K}}} M(K)^{N_H(K)/N}\\[5pt]&=e_{K/N}^{K/N} \overline{M} ( K/N )^{N_{H/N}(K/N)} \\[5pt]&=e_{K/N}^{H/N} \overline{M} ( H/N ) \\[5pt]&={e^{H}_{{N},{K}}} M(H).\end{align*}
2·4. Equivariant sheaves
We begin with the definition of a G-equivariant sheaf over a profinite G-space X where G is a profinite group. The second author gives two equivalent definitions in [ Reference SugrueSug19 ], see also [ Reference Barnes and SugrueBS20 ]. We work with just one for brevity.
Definition 2·18. A
G-equivariant sheaf of
![]() $\mathbb{Q}$
-modules over X is a map of topological spaces
$\mathbb{Q}$
-modules over X is a map of topological spaces
![]() $p \colon E \to X$
such that:
$p \colon E \to X$
such that:
-
(i) p is a G-equivariant map
 $p\;:\;E\rightarrow X$
of spaces with continuous G-actions,
$p\;:\;E\rightarrow X$
of spaces with continuous G-actions, -
(ii) (E, p) is a sheaf space (étale space) of
 $\mathbb{Q}$
-modules,
$\mathbb{Q}$
-modules,
(iii) each map
![]() $g \colon p^{-1} (x) \rightarrow p^{-1} (g x)$
is a map of
$g \colon p^{-1} (x) \rightarrow p^{-1} (g x)$
is a map of
![]() $\mathbb{Q}$
-modules for every
$\mathbb{Q}$
-modules for every
![]() $x\in X,g\in G$
.
$x\in X,g\in G$
.
We will write this as either the pair (E, p) or simply as E. We call E the total space, X the base space and p the structure map.
We call
![]() $p^{-1}(x)$
the stalk of E at x and denote it
$p^{-1}(x)$
the stalk of E at x and denote it
![]() $E_x$
. An element of a stalk is called a germ.
$E_x$
. An element of a stalk is called a germ.
Note that points (i) and (ii) give a map of sets for point (iii), but they do not imply that it is a map of
![]() $\mathbb{Q}$
-modules. Given a G-equivariant sheaf (E, p) over X and
$\mathbb{Q}$
-modules. Given a G-equivariant sheaf (E, p) over X and
![]() $x \in X$
, the stalk
$x \in X$
, the stalk
![]() $E_x$
(equipped with the discrete topology) has a continuous action of
$E_x$
(equipped with the discrete topology) has a continuous action of
![]() $\textrm{stab}_G(x)$
.
$\textrm{stab}_G(x)$
.
As in the non-equivariant case, given an open subset
![]() $U \subseteq X$
the space of (continuous) sections
$U \subseteq X$
the space of (continuous) sections
has an addition operation (defined stalk-wise). The sections are not required to be G-equivariant. Allowing U to vary defines a functor from the set of open subsets of X to
![]() $\mathbb{Q}$
-modules. Moreover, one can show that
$\mathbb{Q}$
-modules. Moreover, one can show that
as in the non-equivariant setting.
Given a section
![]() $s \colon U \to E$
and
$s \colon U \to E$
and
![]() $g \in G$
, we can define
$g \in G$
, we can define
which sends
![]() $v=gu$
to
$v=gu$
to
![]() $gs(u) = gs(g^{-1} v)$
. Hence, if U is invariant under the action of a subgroup H (that is,
$gs(u) = gs(g^{-1} v)$
. Hence, if U is invariant under the action of a subgroup H (that is,
![]() $h U = U$
for all
$h U = U$
for all
![]() $h \in H$
), the space of sections
$h \in H$
), the space of sections
![]() $\Gamma(U,E)$
has an H-action. The fixed points of this space are those sections which commute with the action of H, which we call
H
-equivariant sections.
$\Gamma(U,E)$
has an H-action. The fixed points of this space are those sections which commute with the action of H, which we call
H
-equivariant sections.
Definition 2·19. A Weyl-G-sheaf of
![]() $\mathbb{Q}$
-modules over
$\mathbb{Q}$
-modules over
![]() $\mathcal{S} G$
is a G-sheaf of
$\mathcal{S} G$
is a G-sheaf of
![]() $\mathbb{Q}$
-modules over
$\mathbb{Q}$
-modules over
![]() $\mathcal{S} G$
such that action of H on
$\mathcal{S} G$
such that action of H on
![]() $E_H$
is trivial. Hence
$E_H$
is trivial. Hence
![]() $E_H$
has an action of the Weyl group
$E_H$
has an action of the Weyl group
![]() $W_G H$
of H in G. We use
$W_G H$
of H in G. We use
![]() ${\textrm{Weyl}\hbox{-}{G}\hbox{-}\textrm{sheaf}_{\mathbb{Q}}(\mathcal{S} {G})}$
to denote this category.
${\textrm{Weyl}\hbox{-}{G}\hbox{-}\textrm{sheaf}_{\mathbb{Q}}(\mathcal{S} {G})}$
to denote this category.
The idea of the classification result is to construct a Mackey functor M from a Weyl-G-sheaf E by setting
![]() $M(H) = E(\mathcal{S} H)^H$
. For this we need
$M(H) = E(\mathcal{S} H)^H$
. For this we need
![]() $\mathcal{S} H$
to be an open subset of
$\mathcal{S} H$
to be an open subset of
![]() $\mathcal{S} G$
when H is open in G.
$\mathcal{S} G$
when H is open in G.
Lemma 2·20. For H a closed subgroup of G,
![]() $\mathcal{S} H$
is closed in
$\mathcal{S} H$
is closed in
![]() $\mathcal{S} G$
. This subspace is also open when H is open.
$\mathcal{S} G$
. This subspace is also open when H is open.
Proof. The open statement follows from noting that
For the closed statement we see that H is the limit of finite groups of the form
![]() $H/(H \cap N) = HN/N$
for N an open normal subgroup of G. Since
$H/(H \cap N) = HN/N$
for N an open normal subgroup of G. Since
![]() $\mathcal{S} (HN/N)$
is a closed subset of
$\mathcal{S} (HN/N)$
is a closed subset of
![]() $\mathcal{S} (G/N)$
, the result follows by taking limits.
$\mathcal{S} (G/N)$
, the result follows by taking limits.
We also need a result which can be described as saying that a section of a G-equivariant sheaf over a profinite G-space is “locally sub-equivariant”. See [ Reference SugrueSug19 , section 4·3] for related results.
Proposition 2·21. If E is a Weyl-G-sheaf over
![]() $\mathcal{S} G$
and K a closed subgroup of G, then any
$\mathcal{S} G$
and K a closed subgroup of G, then any
![]() $s_K\in E_K$
can be represented by an NK-equivariant section
$s_K\in E_K$
can be represented by an NK-equivariant section
for N some open normal subgroup of G.
Proof. Let
![]() $s \colon O_{M K}(M ,M K)=U \to E$
be a section representing
$s \colon O_{M K}(M ,M K)=U \to E$
be a section representing
![]() $s_K$
. The set s(U) is not necessarily closed under the action of G, but if
$s_K$
. The set s(U) is not necessarily closed under the action of G, but if
![]() $gu \in U$
and
$gu \in U$
and
![]() $gs(u) \in s(U)$
for some
$gs(u) \in s(U)$
for some
![]() $g \in G$
and
$g \in G$
and
![]() $u \in U$
, then
$u \in U$
, then
as p is G-equivariant. Since p is injective when restricted to s(U), we see that
![]() $s(gu)=g(s(u))$
. The method of the proof is to restrict the domain and codomain so that they are closed under the action of NK, for N some open normal subgroup of G.
$s(gu)=g(s(u))$
. The method of the proof is to restrict the domain and codomain so that they are closed under the action of NK, for N some open normal subgroup of G.
The set s(U) is open (by definition of the topology on a sheaf space) and is the image of compact set. Hence, there is an open normal subgroup M ′ of G such that
![]() $M' s(U)=s(U)$
by [
Reference Barnes and SugrueBS20
, lemma A·1]. Let
$M' s(U)=s(U)$
by [
Reference Barnes and SugrueBS20
, lemma A·1]. Let
which consists of only finally many distinct terms as
![]() $M' \cap K$
has finite index in K. Moreover,
$M' \cap K$
has finite index in K. Moreover,
![]() $s_K=s(K) \in V$
as s(K) is K-fixed, so V is a non-empty compact open subset of E which is invariant under M ′′
K for some open normal subgroup M ′′ of G.
$s_K=s(K) \in V$
as s(K) is K-fixed, so V is a non-empty compact open subset of E which is invariant under M ′′
K for some open normal subgroup M ′′ of G.
The set p(V) is open and contains K, hence we can find a basic open set containing K of the form
for some
![]() $N \leqslant M \cap M''$
. The section
$N \leqslant M \cap M''$
. The section
![]() $s_{\mid W}$
is NK-equivariant by our earlier argument as
$s_{\mid W}$
is NK-equivariant by our earlier argument as
![]() $gw \in W$
and
$gw \in W$
and
![]() $gs(w) \in V \subseteq s(U)$
for all
$gs(w) \in V \subseteq s(U)$
for all
![]() $g \in NK$
and
$g \in NK$
and
![]() $w \in W$
.
$w \in W$
.
3. The functors
In this chapter we will construct a correspondence between rational G-Mackey functors and Weyl-G-sheaves over
![]() $\mathcal{S} G$
. We shall explicitly construct functors between the categories, see Theorems 3·5 and 3·13. In Theorem 4·8 we will see that these functors are equivalences of categories.
$\mathcal{S} G$
. We shall explicitly construct functors between the categories, see Theorems 3·5 and 3·13. In Theorem 4·8 we will see that these functors are equivalences of categories.
3·1. Weyl-G-sheaves determine Mackey functors
We define a functor:
We will not need the input sheaf to be a Weyl-G-sheaf, a detail we return to in Subsection 5·2.
Construction 3·1. Let (E,p) be a G-sheaf over
![]() $\mathcal{S} G$
, we define a Mackey functor
$\mathcal{S} G$
, we define a Mackey functor
![]() $\textrm{Mackey}(E)$
as follows.
$\textrm{Mackey}(E)$
as follows.
For
![]() $H\leqslant G$
an open subgroup define
$H\leqslant G$
an open subgroup define
the set of H-equivariant sections on
![]() $\mathcal{S} H$
. The conjugation maps
$\mathcal{S} H$
. The conjugation maps
![]() $C_g$
are given by the G-action on the sheaf E.
$C_g$
are given by the G-action on the sheaf E.
For
![]() $K \leqslant H$
another open subgroup, the restriction map
$K \leqslant H$
another open subgroup, the restriction map
is given by restriction of a section to the subspace
![]() $\mathcal{S} K$
.
$\mathcal{S} K$
.
Let
![]() $T \subset H$
be a left transversal of K in H. For
$T \subset H$
be a left transversal of K in H. For
![]() $\beta$
a section of
$\beta$
a section of
![]() $\mathcal{S} K$
, let
$\mathcal{S} K$
, let
![]() $\overline{\beta}$
be the extension by zero to
$\overline{\beta}$
be the extension by zero to
![]() $\mathcal{S} H$
. We define the induction map by
$\mathcal{S} H$
. We define the induction map by
We prove that the induction functor is well defined in Lemma 3·2. The structure maps compose and interact appropriately by Lemma 3·3. Lemma 3·4 proves that the Mackey axiom holds.
Lemma 3·2. The induction map given in Construction 3·1 is well defined.
Proof. Let
![]() $hK=h'K$
be two representatives for the same coset. Since the section
$hK=h'K$
be two representatives for the same coset. Since the section
![]() $\beta$
is K-fixed,
$\beta$
is K-fixed,
as h and h ′ differ by an element of K. It follows that
![]() $I^H_K $
is independent of the choice of T.
$I^H_K $
is independent of the choice of T.
The sum of
![]() $h \ast \overline{\beta}$
over
$h \ast \overline{\beta}$
over
![]() $h \in T$
is H-equivariant as T is a transversal.
$h \in T$
is H-equivariant as T is a transversal.
Lemma 3·3. The structure maps of Mackey
![]() $(E)$
are unital, associative, transitive and equivariant.
$(E)$
are unital, associative, transitive and equivariant.
Proof. The part of most interest is that the induction maps are transitive and equivariant. The first follows from the fact that given open subgroups
![]() $J \leqslant K \leqslant H$
, one can combine a transversal of J in K with a transversal of K in H to get a transversal of J in H. This gives the transitivity. For equivariance, the result follows as one can conjugate a transversal to get a transversal of the conjugate.
$J \leqslant K \leqslant H$
, one can combine a transversal of J in K with a transversal of K in H to get a transversal of J in H. This gives the transitivity. For equivariance, the result follows as one can conjugate a transversal to get a transversal of the conjugate.
We note that
![]() $\mathcal{S} H$
is invariant under the action of
$\mathcal{S} H$
is invariant under the action of
![]() $N_G H \leqslant G$
, so
$N_G H \leqslant G$
, so
![]() $E( \mathcal{S} H)$
has a continuous action of
$E( \mathcal{S} H)$
has a continuous action of
![]() $N_G H$
.
$N_G H$
.
It remains to show the Mackey axiom, which is a direct calculation.
Lemma 3·4. The construction Mackey
![]() $(E)$
satisfies the Mackey axiom.
$(E)$
satisfies the Mackey axiom.
Proof. We start with
![]() $J,L\leqslant H$
where
$J,L\leqslant H$
where
![]() $H,J,L\leqslant G$
are open. We can decompose H into double cosets.
$H,J,L\leqslant G$
are open. We can decompose H into double cosets.
 \[H=\underset{hL\in H/L}{\coprod} hL=\underset{x\in\left[J\backslash H/ L\right]}{\coprod}JxL=\underset{x\in \left[J\backslash H/ L\right]}{\coprod}\,\,\,\underset{j\in J}{\bigcup} jxL=\underset{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}{\coprod} j_x xL. \]
\[H=\underset{hL\in H/L}{\coprod} hL=\underset{x\in\left[J\backslash H/ L\right]}{\coprod}JxL=\underset{x\in \left[J\backslash H/ L\right]}{\coprod}\,\,\,\underset{j\in J}{\bigcup} jxL=\underset{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}{\coprod} j_x xL. \]
Given a transversal T for L in H we have
 \[R^H_JI^H_L(\beta)=\left(\underset{h \in T}{\sum} h \ast \overline{\beta}\right)\Big|_{\mathcal{S} J}=\Big( \sum_{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}j_x x \ast \overline{\beta}\Big) {\Big|}_{\mathcal{S} J}=\sum_{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}\left(j_x x\overline{\beta|_{\mathcal{S} \left(x^{-1}Jx\cap L\right)}}\right), \]
\[R^H_JI^H_L(\beta)=\left(\underset{h \in T}{\sum} h \ast \overline{\beta}\right)\Big|_{\mathcal{S} J}=\Big( \sum_{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}j_x x \ast \overline{\beta}\Big) {\Big|}_{\mathcal{S} J}=\sum_{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}\left(j_x x\overline{\beta|_{\mathcal{S} \left(x^{-1}Jx\cap L\right)}}\right), \]
where the extension by zero in the third term is with respect to H and in the in the fourth term it is with respect to J. If we start from the other direction we have:
 \begin{align*}\underset{x\in \left[J\backslash H/ L\right]}{\sum}I^J_{J\cap xLx^{-1}} \circ C_x \circ R^L_{x^{-1}Jx\cap L}(\beta)&=\sum_{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}j_x x \ast \left(\overline{\beta|_{S\left(L\cap x^{-1}Jx\right)}}\right)\\[5pt]&=\sum_{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}\left(j_x x\overline{\beta|_{S\left(L\cap x^{-1}Jx\right)}}\right)\end{align*}
\begin{align*}\underset{x\in \left[J\backslash H/ L\right]}{\sum}I^J_{J\cap xLx^{-1}} \circ C_x \circ R^L_{x^{-1}Jx\cap L}(\beta)&=\sum_{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}j_x x \ast \left(\overline{\beta|_{S\left(L\cap x^{-1}Jx\right)}}\right)\\[5pt]&=\sum_{\substack{x\in\left[J\backslash H/ L\right] \\[1pt] j_x \in J/J\cap xLx^{-1}}}\left(j_x x\overline{\beta|_{S\left(L\cap x^{-1}Jx\right)}}\right)\end{align*}
proving that the two sides coincide.
Similar arguments to the above show that a map of sheaves
![]() $E \to E'$
induces a map of G-Mackey functors
$E \to E'$
induces a map of G-Mackey functors
![]() $\textrm{Mackey}(E) \to \textrm{Mackey}(E')$
. We summarise this section in the following theorem.
$\textrm{Mackey}(E) \to \textrm{Mackey}(E')$
. We summarise this section in the following theorem.
Theorem 3·5. Let G be a profinite group. If E is a G-sheaf of
![]() $\mathbb{Q}$
-modules over
$\mathbb{Q}$
-modules over
![]() $\mathcal{S} G$
, then Mackey
$\mathcal{S} G$
, then Mackey
![]() $(E)$
from Construction 3·1 is a Mackey functor and the assignment is functorial. Hence, there is a functor
$(E)$
from Construction 3·1 is a Mackey functor and the assignment is functorial. Hence, there is a functor
3·2 Mackey functors determine Weyl-G-sheaves
We construct a functor in the opposite direction, from rational G-Mackey functors to Weyl-G-sheaves of
![]() $\mathbb{Q}$
-modules over
$\mathbb{Q}$
-modules over
![]() $\mathcal{S} G$
. We start by constructing the stalks of the Weyl-G-sheaf.
$\mathcal{S} G$
. We start by constructing the stalks of the Weyl-G-sheaf.
Definition 3·6. For M a rational G-Mackey functor and K a closed subgroup of G, we define a
![]() $\mathbb{Q}$
-module
$\mathbb{Q}$
-module
The maps in the colimits are induced by the restriction maps of M and applying idempotents. The notation
![]() $M(J)_{(K)}$
refers to the stalk of the
$M(J)_{(K)}$
refers to the stalk of the
![]() $\mathcal{S} J/J$
-sheaf M(J) at the J-conjugacy class of K, for J an open subgroup of G containing K.
$\mathcal{S} J/J$
-sheaf M(J) at the J-conjugacy class of K, for J an open subgroup of G containing K.
The restriction maps are compatible with taking stalks since
![]() ${e^{H}_{{N},{NK}}} \in {\textbf{A}_\mathbb{Q}}(H)$
restricts to an idempotent
${e^{H}_{{N},{NK}}} \in {\textbf{A}_\mathbb{Q}}(H)$
restricts to an idempotent
![]() $f \in {\textbf{A}_\mathbb{Q}}(J)$
for
$f \in {\textbf{A}_\mathbb{Q}}(J)$
for
![]() $K \leqslant J \leqslant H$
, where the support of f is those subgroups of J (up to J-conjugacy) which are H-conjugate to an element of
$K \leqslant J \leqslant H$
, where the support of f is those subgroups of J (up to J-conjugacy) which are H-conjugate to an element of
![]() $O_H(N, NK)$
. This support contains
$O_H(N, NK)$
. This support contains
We begin our construction of a rational G-equivariant sheaf (E, p) over
![]() $\mathcal{S} G$
from a Mackey functor M. We first define E and p.
$\mathcal{S} G$
from a Mackey functor M. We first define E and p.
Construction 3·7. If M is a rational G-Mackey functor, we define the underlying set of the sheaf space
The projection map
![]() $p \colon \textrm{Sheaf}(M) \to \mathcal{S} G$
sends all of
$p \colon \textrm{Sheaf}(M) \to \mathcal{S} G$
sends all of
![]() $\textrm{Sheaf}(M)_K$
to K. The conjugation maps of M induces maps
$\textrm{Sheaf}(M)_K$
to K. The conjugation maps of M induces maps
for each
![]() $g \in G$
. Thus
$g \in G$
. Thus
![]() $\textrm{Sheaf}(M)$
has a G-action and p is G-equivariant.
$\textrm{Sheaf}(M)$
has a G-action and p is G-equivariant.
We construct a set of sections that will give a basis for a topology on
![]() $\textrm{Sheaf}(M)$
. For H an open subgroup of G, define a map
$\textrm{Sheaf}(M)$
. For H an open subgroup of G, define a map
where
![]() $\theta_H(m)$
sends
$\theta_H(m)$
sends
![]() $K \leqslant H$
to
$K \leqslant H$
to
![]() $m_K$
, the image of
$m_K$
, the image of
![]() $m \in M(H)$
in
$m \in M(H)$
in
![]() $\textrm{Sheaf}(M)_K$
. We must check that
$\textrm{Sheaf}(M)_K$
. We must check that
![]() $\theta_H(m)$
defines an H-equivariant map. As restriction and applying idempotents are equivariant, the square below commutes:
$\theta_H(m)$
defines an H-equivariant map. As restriction and applying idempotents are equivariant, the square below commutes:
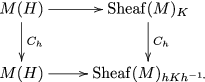
Since
![]() $C_h= \textrm{Id}_{M(H)}$
, we have the desired equivariance. We also see that
$C_h= \textrm{Id}_{M(H)}$
, we have the desired equivariance. We also see that
![]() $m_K$
is fixed by
$m_K$
is fixed by
![]() $N_H(K)$
.
$N_H(K)$
.
We can restrict a section
![]() $s =\theta_{NK} (m)$
coming from
$s =\theta_{NK} (m)$
coming from
![]() $m \in {e^{NK}_{{N},{NK}}} M(NK)$
to a section over
$m \in {e^{NK}_{{N},{NK}}} M(NK)$
to a section over
The sets
![]() $s(O_G(N,NK))$
for varying open and normal N, closed K, and
$s(O_G(N,NK))$
for varying open and normal N, closed K, and
![]() $s=\theta_{NK}(m)$
for m in
$s=\theta_{NK}(m)$
for m in
![]() ${e^{NK}_{{N},{NK}}} M(NK)$
, define a topology on
${e^{NK}_{{N},{NK}}} M(NK)$
, define a topology on
![]() $\textrm{Sheaf}(M)$
by Lemma 3·8.
$\textrm{Sheaf}(M)$
by Lemma 3·8.
The G-action is continuous by Lemma 3·9 and the projection map p is a G-equivariant local homeomorphism by Proposition 3·10.
Lemma 3·11 shows that
![]() $(\textrm{Sheaf}(M),p)$
is a sheaf of
$(\textrm{Sheaf}(M),p)$
is a sheaf of
![]() $\mathbb{Q}$
-modules. Lemma 3·12 completes the construction by showing that we have a Weyl-G-sheaf.
$\mathbb{Q}$
-modules. Lemma 3·12 completes the construction by showing that we have a Weyl-G-sheaf.
Lemma 3·8. The sets
![]() $s(O_G(N,NL))$
constructed above form a basis for a topology on
$s(O_G(N,NL))$
constructed above form a basis for a topology on
Proof. Given
![]() $a \in \textrm{Sheaf}(M)_L$
, we can find a representative
$a \in \textrm{Sheaf}(M)_L$
, we can find a representative
![]() $m \in {e^{NL}_{{N},{NL}}} M(NL)$
. We then take the composite
$m \in {e^{NL}_{{N},{NL}}} M(NL)$
. We then take the composite
We see that
![]() $m_L =\theta_{NL}(m)(L)= a$
and so each germ is in the image of one of our chosen sections. It follows that the open sets
$m_L =\theta_{NL}(m)(L)= a$
and so each germ is in the image of one of our chosen sections. It follows that the open sets
![]() $s(O_G(N,NK))$
cover
$s(O_G(N,NK))$
cover
![]() $\textrm{Sheaf}(M)$
.
$\textrm{Sheaf}(M)$
.
Now we show that the intersection of two basis sets is a union of basis elements. Take sections
![]() $t_1=\theta_{N_1 K_1} (m_1)$
and
$t_1=\theta_{N_1 K_1} (m_1)$
and
![]() $t_2=\theta_{N_2 K_2} (m_2)$
and let
$t_2=\theta_{N_2 K_2} (m_2)$
and let
We construct a
![]() $t(O_G(N,NK))$
satisfying
$t(O_G(N,NK))$
satisfying
Given such an x, we let
![]() $L=p(x)$
, which is a closed subgroup of G. We see that
$L=p(x)$
, which is a closed subgroup of G. We see that
and
![]() ${t_1}(L)={t_2}(L)$
in
${t_1}(L)={t_2}(L)$
in
![]() $\textrm{Sheaf}(M)_L$
. Hence, there is an open normal subgroup
$\textrm{Sheaf}(M)_L$
. Hence, there is an open normal subgroup
![]() $N \leqslant N_1 \cap N_2$
of G such that
$N \leqslant N_1 \cap N_2$
of G such that
![]() $m_1$
and
$m_1$
and
![]() $m_2$
restricted to
$m_2$
restricted to
![]() ${e^{NL}_{{N},{NL}}} M(NL)$
agree. It follows that
${e^{NL}_{{N},{NL}}} M(NL)$
agree. It follows that
![]() $t_1$
and
$t_1$
and
![]() $t_2$
agree when restricted to
$t_2$
agree when restricted to
![]() $O_{NL}(N,NL) = O_G(N,NL)$
. We define t to be this common refinement and see
$O_{NL}(N,NL) = O_G(N,NL)$
. We define t to be this common refinement and see
Lemma 3·9. The G-action on the space
![]() ${Sheaf}(M)$
from Construction 3·7 is continuous.
${Sheaf}(M)$
from Construction 3·7 is continuous.
Proof. Take a basic open set
![]() $s(O_G(N,NK))$
for
$s(O_G(N,NK))$
for
![]() $s=\theta_{NK}(m)$
with
$s=\theta_{NK}(m)$
with
![]() $m \in M(NK)$
. Take any point
$m \in M(NK)$
. Take any point
![]() $(g,t_L)$
in the pre-image of
$(g,t_L)$
in the pre-image of
![]() $s(O_G(N,NK))$
under the group action map. Then
$s(O_G(N,NK))$
under the group action map. Then
We can therefore find an open normal subgroup N and representatives such that
These sections have N-invariant domains and are obtained from an N-fixed module M(NL). We can conclude that the open set:
is contained in pre-image of
![]() $s(O_G(N,NK))$
under the group action map.
$s(O_G(N,NK))$
under the group action map.
Proposition 3·10. The projection map in Construction 3·7 is a continuous G-map and a local homeomorphism.
Proof. We first prove that p is continuous. Given a basic open subset of
![]() $\mathcal{S} G$
of the form
$\mathcal{S} G$
of the form
![]() $O_G(N,NK)$
, we have that
$O_G(N,NK)$
, we have that
Take
![]() $s \in \textrm{Sheaf}(M)_L$
and a section
$s \in \textrm{Sheaf}(M)_L$
and a section
with
![]() $t(L) =s$
and
$t(L) =s$
and
![]() $N' \leqslant N$
. Then
$N' \leqslant N$
. Then
![]() $t(O_G(N',N' L)) \subseteq p^{-1}(O_G(N,NK))$
and is open.
$t(O_G(N',N' L)) \subseteq p^{-1}(O_G(N,NK))$
and is open.
We now show that p is a local homeomorphism. A point s in
![]() $\textrm{Sheaf}(M)_L$
has a neighbourhood of the form
$\textrm{Sheaf}(M)_L$
has a neighbourhood of the form
![]() $t(O_G(N,NK))$
as seen previously. Let
$t(O_G(N,NK))$
as seen previously. Let
![]() $f=p_{|t(O_G(N,NK))}$
, we claim that
$f=p_{|t(O_G(N,NK))}$
, we claim that
is a homeomorphism. Since f is bijective and continuous, we need only show that it is open.
A basic open set of
![]() $t(O_G(N,NK))$
is a set of the form
$t(O_G(N,NK))$
is a set of the form
![]() $t'(O_G(N',N'K')) \leqslant t(O_G(N,NK))$
for
$t'(O_G(N',N'K')) \leqslant t(O_G(N,NK))$
for
![]() $O_G(N',N'K') \subseteq O_G(N,NK)$
. The map f sends
$O_G(N',N'K') \subseteq O_G(N,NK)$
. The map f sends
![]() $t'(O_G(N',N'K'))$
to
$t'(O_G(N',N'K'))$
to
![]() $O_G(N',N'K')$
, which is open in
$O_G(N',N'K')$
, which is open in
![]() $O_G(N,NK)$
.
$O_G(N,NK)$
.
Lemma 3·11. If U is any open subset of
![]() $\mathcal{S} G$
, then the set of sections of p over U from Construction 3·7 is a
$\mathcal{S} G$
, then the set of sections of p over U from Construction 3·7 is a
![]() $\mathbb{Q}$
-module. Hence
$\mathbb{Q}$
-module. Hence
![]() $({Sheaf}(M),p)$
is a sheaf of
$({Sheaf}(M),p)$
is a sheaf of
![]() $\mathbb{Q}$
-modules.
$\mathbb{Q}$
-modules.
Proof. Given two sections s and t of p we can restrict ourselves to neighbourhoods of
![]() $\mathcal{S} G$
and E such that p is a local homeomorphism. From the construction of the topology on E it follows that on this region, s and t come from elements of some M(NK), where N is an open normal subgroup and K is a closed subgroup of G. The addition of M(NK) defines a section
$\mathcal{S} G$
and E such that p is a local homeomorphism. From the construction of the topology on E it follows that on this region, s and t come from elements of some M(NK), where N is an open normal subgroup and K is a closed subgroup of G. The addition of M(NK) defines a section
![]() $s+t$
. Similarly, the
$s+t$
. Similarly, the
![]() $\mathbb{Q}$
-action on M(NK) defines
$\mathbb{Q}$
-action on M(NK) defines
![]() $q \cdot t$
for
$q \cdot t$
for
![]() $q \in \mathbb{Q}$
.
$q \in \mathbb{Q}$
.
Lemma 3·12. The G-sheaf of
![]() $\mathbb{Q}$
-modules
$\mathbb{Q}$
-modules
![]() $({Sheaf}(M),p)$
defined in Construction 3·7 is a Weyl-G-sheaf. That is,
$({Sheaf}(M),p)$
defined in Construction 3·7 is a Weyl-G-sheaf. That is,
![]() $g \in G$
gives maps of
$g \in G$
gives maps of
![]() $\mathbb{Q}$
-modules
$\mathbb{Q}$
-modules
and
![]() ${Sheaf}(M)_K$
is K-fixed for each
${Sheaf}(M)_K$
is K-fixed for each
![]() $K \in \mathcal{S} G$
.
$K \in \mathcal{S} G$
.
Proof. If
![]() $K\in \mathcal{S} G$
, then
$K\in \mathcal{S} G$
, then
with J running over all of the open subgroups containing K. An element
![]() $g \in G$
induces maps
$g \in G$
induces maps
by acting as
![]() $C_g$
on the terms
$C_g$
on the terms
![]() $ M(J)_{(K)}$
. This action is a map of
$ M(J)_{(K)}$
. This action is a map of
![]() $\mathbb{Q}$
-modules and hence gives a
$\mathbb{Q}$
-modules and hence gives a
![]() $\mathbb{Q}$
-module map on the stalks.
$\mathbb{Q}$
-module map on the stalks.
The
![]() $\mathbb{Q}$
-module M(J) is J-fixed and the idempotents defining the stalk
$\mathbb{Q}$
-module M(J) is J-fixed and the idempotents defining the stalk
![]() $M(J)_{(K)}$
are J-fixed and hence K-fixed. Thus
$M(J)_{(K)}$
are J-fixed and hence K-fixed. Thus
![]() $(\textrm{Sheaf}(M),p)$
is a Weyl-G-sheaf.
$(\textrm{Sheaf}(M),p)$
is a Weyl-G-sheaf.
We summarise this work in the following theorem. The additional statement here is that the construction is functorial. This follows from the fact that maps of Mackey functors commute with actions of Burnside rings.
Theorem 3·13. For G a profinite group, there is a functor
which sends a Mackey functor M over G to a Weyl-G-sheaf denoted
![]() ${Sheaf}(M)$
, as defined in Construction 3·7.
${Sheaf}(M)$
, as defined in Construction 3·7.
We end this subsection by noting that the maps
![]() $\theta_H$
from Construction 3·7 are injective.
$\theta_H$
from Construction 3·7 are injective.
Lemma 3·14. Let
![]() $m \in M(H)$
. If
$m \in M(H)$
. If
![]() $\theta_H(m)(L) =m_L =0$
for all
$\theta_H(m)(L) =m_L =0$
for all
![]() $L \leqslant H$
, then
$L \leqslant H$
, then
![]() $m=0$
in M(H).
$m=0$
in M(H).
Proof. For
![]() $L \leqslant H$
, there is an open normal subgroup N such that the image of m in
$L \leqslant H$
, there is an open normal subgroup N such that the image of m in
![]() ${e^{NL}_{{N},{NL}}} M(NL)$
is zero. As m is H-fixed, the image of m is
${e^{NL}_{{N},{NL}}} M(NL)$
is zero. As m is H-fixed, the image of m is
![]() $N_H(NL)$
-fixed. By Lemma 2·17, restriction and applying idempotents gives an isomorphism
$N_H(NL)$
-fixed. By Lemma 2·17, restriction and applying idempotents gives an isomorphism
Hence, we see that
![]() ${e^{H}_{{N},{NL}}} m$
is zero in
${e^{H}_{{N},{NL}}} m$
is zero in
![]() ${e^{H}_{{N},{NL}}} M(H)$
. As the sets
${e^{H}_{{N},{NL}}} M(H)$
. As the sets
![]() $\overline{O}_H(N,NL)$
are an open cover of the compact space
$\overline{O}_H(N,NL)$
are an open cover of the compact space
![]() $\mathcal{S} H/H$
, we see that m must be zero in M(H).
$\mathcal{S} H/H$
, we see that m must be zero in M(H).
4. The equivalence
In this section we prove that the two functors Mackey and Sheaf are inverse equivalences, see Theorem 4·8.
4·1. The equivalence on sheaves
We prove that for a Weyl-G-sheaf of
![]() $\mathbb{Q}$
-modules F, we have an isomorphism of equivariant sheaves of
$\mathbb{Q}$
-modules F, we have an isomorphism of equivariant sheaves of
![]() $\mathbb{Q}$
-modules
$\mathbb{Q}$
-modules
The first part is to show that we have an isomorphism on each stalk. For that, we need to know how the action of the Burnside ring on Mackey functors translates to sheaves.
Lemma 4·1. Let F be G-sheaf of
![]() $\mathbb{Q}$
-modules on
$\mathbb{Q}$
-modules on
![]() $\mathcal{S} G$
and
$\mathcal{S} G$
and
![]() $K \leqslant H$
open subgroups of G. The Mackey functor
$K \leqslant H$
open subgroups of G. The Mackey functor
![]() $M=\textrm{Mackey}\;{F}$
satisfies
$M=\textrm{Mackey}\;{F}$
satisfies
for all
![]() $L \in \mathcal{S} H$
and
$L \in \mathcal{S} H$
and
![]() $s \in M(H) = F(\mathcal{S} H)^H$
.
$s \in M(H) = F(\mathcal{S} H)^H$
.
Proof. The element
![]() $[H/K] \in {\textbf{A}_\mathbb{Q}}(H)$
acts on M(H) by the formula
$[H/K] \in {\textbf{A}_\mathbb{Q}}(H)$
acts on M(H) by the formula
As
![]() $s \in M(H)$
is H-fixed, the section
$s \in M(H)$
is H-fixed, the section
![]() $t=C_h\overline{s_{|_{\mathcal{S} K}}}$
satisfies
$t=C_h\overline{s_{|_{\mathcal{S} K}}}$
satisfies
![]() $t(hJh^{-1})= s(hJh^{-1})$
for
$t(hJh^{-1})= s(hJh^{-1})$
for
![]() $J \in \mathcal{S} K$
. It is zero outside of
$J \in \mathcal{S} K$
. It is zero outside of
![]() $\mathcal{S} (hKh^{-1})$
. Hence, for
$\mathcal{S} (hKh^{-1})$
. Hence, for
![]() $L \in \mathcal{S} H$
, t(L) is non-zero exactly when
$L \in \mathcal{S} H$
, t(L) is non-zero exactly when
![]() $L \in \mathcal{S} (hKh^{-1})$
. This is equivalent to the condition
$L \in \mathcal{S} (hKh^{-1})$
. This is equivalent to the condition
![]() $h NA \in (H/K)^L$
. We see that
$h NA \in (H/K)^L$
. We see that
We can now see that a idempotent of
![]() ${\textbf{A}_\mathbb{Q}}(H)$
acts by restricting a section and then extending the result by zero.
${\textbf{A}_\mathbb{Q}}(H)$
acts by restricting a section and then extending the result by zero.
Proposition 4·2. For H an open subgroup of G, let U be an H-invariant open and closed subset of
![]() $\mathcal{S} H$
. If F is a G-sheaf then
$\mathcal{S} H$
. If F is a G-sheaf then
![]() $e_U^H{Mackey}(F)(H)$
is equal to the set of H-equivariant sections of
$e_U^H{Mackey}(F)(H)$
is equal to the set of H-equivariant sections of
![]() $\mathcal{S} H$
which are zero outside U. Hence,
$\mathcal{S} H$
which are zero outside U. Hence,
![]() $e_U^H{Mackey}(F)(H) \cong F(U)^H$
.
$e_U^H{Mackey}(F)(H) \cong F(U)^H$
.
Proof. The definition of
![]() $\textrm{Mackey}(F)$
gives:
$\textrm{Mackey}(F)$
gives:
Since the sets of the form
![]() $O_H(N,NK)$
form a basis for
$O_H(N,NK)$
form a basis for
![]() $\mathcal{S} H$
where N is open and normal in H, we can assume that
$\mathcal{S} H$
where N is open and normal in H, we can assume that
![]() $U=O_H(N,NK)$
. By Proposition 2·14 (and using the notation
$U=O_H(N,NK)$
. By Proposition 2·14 (and using the notation
![]() $\alpha_{NA,NK}$
from the proof of that proposition), we have the first equality below for
$\alpha_{NA,NK}$
from the proof of that proposition), we have the first equality below for
![]() $s \in F(\mathcal{S} H)^H$
.
$s \in F(\mathcal{S} H)^H$
.
 \begin{align*}{e^{H}_{{N},{NK}}} s(L)&=\underset{N \leqslant NA\leqslant NK}{\sum}\left(\alpha_{NA,NK} [G/NA] (s)\right)(L) \\[5pt]&=\Big(\underset{N \leqslant NA\leqslant NK}{\sum}\alpha_{NA,NK} |(G/NA)^L| \Big)s(L) \\[5pt]&={e^{H}_{{N},{NK}}}(L) s(L).\end{align*}
\begin{align*}{e^{H}_{{N},{NK}}} s(L)&=\underset{N \leqslant NA\leqslant NK}{\sum}\left(\alpha_{NA,NK} [G/NA] (s)\right)(L) \\[5pt]&=\Big(\underset{N \leqslant NA\leqslant NK}{\sum}\alpha_{NA,NK} |(G/NA)^L| \Big)s(L) \\[5pt]&={e^{H}_{{N},{NK}}}(L) s(L).\end{align*}
The second is Lemma 4·1. The last is an instance of how
![]() $[G/NA] \in {\textbf{A}_\mathbb{Q}}(H)$
defines a function from
$[G/NA] \in {\textbf{A}_\mathbb{Q}}(H)$
defines a function from
![]() $\mathcal{S} H/H$
to
$\mathcal{S} H/H$
to
![]() $\mathbb{Q}$
, see Theorem 2·10.
$\mathbb{Q}$
, see Theorem 2·10.
Proposition 4·3. If F is a Weyl-G-Sheaf over
![]() $\mathcal{S} G$
, then for each
$\mathcal{S} G$
, then for each
![]() $K\in \mathcal{S} G$
we have an isomorphism of
$K\in \mathcal{S} G$
we have an isomorphism of
![]() $\mathbb{Q}$
-modules
$\mathbb{Q}$
-modules
Proof. The left-hand side can be expanded to
 \begin{align*}\underset{N {\underset{\textrm{open}}{\leqslant}} G}{{\mathop{\textrm{colim}}}}\; {e^{NK}_{{N},{NK}}} \textrm{Mackey}(F)(NK)&=\underset{N {\underset{\textrm{open}}{\leqslant}} G}{{\mathop{\textrm{colim}}}}\; {e^{NK}_{{N},{NK}}} F(\mathcal{S} (NK))^{NK} \\[5pt]& \cong\underset{N {\underset{\textrm{open}}{\leqslant}} G}{{\mathop{\textrm{colim}}}}\; F(O_{NK}(N, NK))^{NK}\end{align*}
\begin{align*}\underset{N {\underset{\textrm{open}}{\leqslant}} G}{{\mathop{\textrm{colim}}}}\; {e^{NK}_{{N},{NK}}} \textrm{Mackey}(F)(NK)&=\underset{N {\underset{\textrm{open}}{\leqslant}} G}{{\mathop{\textrm{colim}}}}\; {e^{NK}_{{N},{NK}}} F(\mathcal{S} (NK))^{NK} \\[5pt]& \cong\underset{N {\underset{\textrm{open}}{\leqslant}} G}{{\mathop{\textrm{colim}}}}\; F(O_{NK}(N, NK))^{NK}\end{align*}
using Proposition 4·2 for the last term. The right-hand side is
The inclusions
![]() $F(O_{NK}(N, NK)^{NK} \to F(O_{NK}(N, NK)$
induce the desired map
$F(O_{NK}(N, NK)^{NK} \to F(O_{NK}(N, NK)$
induce the desired map
![]() $\psi_K$
. It is an isomorphism as any germ can be represented by a section that is locally sub-equivariant by Proposition 2·21
$\psi_K$
. It is an isomorphism as any germ can be represented by a section that is locally sub-equivariant by Proposition 2·21
The proof requires F to be a Weyl-G-sheaf as we need the local sub-equivariance property.
We now check that the preceding isomorphism is compatible with the group actions.
Lemma 4·4. Let F be a Weyl-G-sheaf of
![]() $\mathbb{Q}$
-modules. If
$\mathbb{Q}$
-modules. If
![]() $K\in \mathcal{S} G$
and
$K\in \mathcal{S} G$
and
![]() $g\in G$
, then the following square commutes
$g\in G$
, then the following square commutes

where
![]() $\psi_K$
is the map defined in the proof of Proposition 4·3.
$\psi_K$
is the map defined in the proof of Proposition 4·3.
Proof. A germ
![]() $s_K\in \textrm{Sheaf} \circ\textrm{Mackey}(F)_K$
can be represented by an NK-equivariant section
$s_K\in \textrm{Sheaf} \circ\textrm{Mackey}(F)_K$
can be represented by an NK-equivariant section
This section is also a representative for
![]() $\psi_K(s_K)$
, from which the commutativity of the square follows.
$\psi_K(s_K)$
, from which the commutativity of the square follows.
Theorem 4·5. If F is any Weyl-G-sheaf of
![]() $\mathbb{Q}$
-modules, then the maps
$\mathbb{Q}$
-modules, then the maps
![]() $\psi_K$
induce an isomorphism
$\psi_K$
induce an isomorphism
in the category of Weyl-G-Sheaves.
Proof. By Proposition 4·3 and Lemma 4·4, we see that they are isomorphic as G-sets. To prove that they are topologically equivalent, we need to show that they have the same sections. As both objects are sheaves, it suffices to do so locally, which amounts to considering sections that represent stalks. By Proposition 4·3, a germ over
![]() $K \in \mathcal{S} G$
of
$K \in \mathcal{S} G$
of
![]() $\textrm{Sheaf} \circ \textrm{Mackey}(F)$
is represented by some element of
$\textrm{Sheaf} \circ \textrm{Mackey}(F)$
is represented by some element of
![]() $F(O_{NK}(N, NK) )^{NK}$
. By the local sub-equivariance property of Proposition 2·21 the same is true for a stalk of F.
$F(O_{NK}(N, NK) )^{NK}$
. By the local sub-equivariance property of Proposition 2·21 the same is true for a stalk of F.
4·2. The equivalence on Mackey functors
The starting point is to give a levelwise isomorphism of
![]() $\mathbb{Q}$
-modules.
$\mathbb{Q}$
-modules.
Proposition 4·6. If H is an open subgroup of a profinite group G and M a Mackey functor for G, then there is an isomorphism of
![]() $\mathbb{Q}$
-modules (constructed in the proof)
$\mathbb{Q}$
-modules (constructed in the proof)
Proof. Recall from Constructions 3·1 and 3·7 that the stalks of
![]() $\textrm{Sheaf}(M)$
are given by
$\textrm{Sheaf}(M)$
are given by
Recall the map
![]() $\theta_H$
from Construction 3·7
$\theta_H$
from Construction 3·7
where
![]() $\theta_H(m)(K) = m_K$
, the image of m in
$\theta_H(m)(K) = m_K$
, the image of m in
![]() $\textrm{Sheaf}(M)_K$
. The topology on
$\textrm{Sheaf}(M)_K$
. The topology on
![]() $\textrm{Sheaf}(M)$
is defined in terms of
$\textrm{Sheaf}(M)$
is defined in terms of
![]() $\theta_H(m)$
for varying H and m.
$\theta_H(m)$
for varying H and m.
The composite of the two functors at H is
 \begin{align*}\textrm{Mackey} \circ \textrm{Sheaf}(M)(H) &=\textrm{Sheaf}(M)(\mathcal{S} H)^H \\[5pt]&=\Big\lbrace s \colon \mathcal{S} H\longrightarrow \coprod_{K \in \mathcal{S} H} \textrm{Sheaf}(M)_K \Bigm| \textrm{\textit{s} continuous},\,p\circ s=\textrm{Id} \Big\rbrace^H.\end{align*}
\begin{align*}\textrm{Mackey} \circ \textrm{Sheaf}(M)(H) &=\textrm{Sheaf}(M)(\mathcal{S} H)^H \\[5pt]&=\Big\lbrace s \colon \mathcal{S} H\longrightarrow \coprod_{K \in \mathcal{S} H} \textrm{Sheaf}(M)_K \Bigm| \textrm{\textit{s} continuous},\,p\circ s=\textrm{Id} \Big\rbrace^H.\end{align*}
Since the topology was defined using the images of
![]() $\theta_H$
, it follows that
$\theta_H$
, it follows that
![]() $\theta_H(m)$
is a continuous section. Thus
$\theta_H(m)$
is a continuous section. Thus
![]() $\theta_H$
defines a map as in the statement. Moreover, it is additive and surjective, injectivity follows from Lemma 3·14.
$\theta_H$
defines a map as in the statement. Moreover, it is additive and surjective, injectivity follows from Lemma 3·14.
Theorem 4·7. The maps
![]() $\theta_H$
induce a natural isomorphism of Mackey functors
$\theta_H$
induce a natural isomorphism of Mackey functors
Proof. We need to show that the correspondence between M and
![]() $\textrm{Mackey} \circ\textrm{Sheaf}(M)$
commutes with the three maps; restriction, induction and conjugation.
$\textrm{Mackey} \circ\textrm{Sheaf}(M)$
commutes with the three maps; restriction, induction and conjugation.
For conjugation and restriction one can calculate the effect directly on a stalk of some
![]() $m \in M(H)$
, for H an open subgroup of G. One will see that the map
$m \in M(H)$
, for H an open subgroup of G. One will see that the map
![]() $\theta$
is compatible with conjugation as the restriction maps of a Mackey functor are equivariant and the action of the Burnside ring is compatible with conjugation. Similarly, since
$\theta$
is compatible with conjugation as the restriction maps of a Mackey functor are equivariant and the action of the Burnside ring is compatible with conjugation. Similarly, since
![]() $\theta$
is defined via the restriction maps of Mackey functors and the restriction of
$\theta$
is defined via the restriction maps of Mackey functors and the restriction of
![]() $\textrm{Mackey} \circ\textrm{Sheaf}(M)$
is defined by restricting a section to a smaller domain,
$\textrm{Mackey} \circ\textrm{Sheaf}(M)$
is defined by restricting a section to a smaller domain,
![]() $\theta$
is compatible with restrictions.
$\theta$
is compatible with restrictions.
Induction requires more work. Suppose
![]() $K\leqslant H$
are open and
$K\leqslant H$
are open and
![]() $s\in M(K)$
. We must show that the square
$s\in M(K)$
. We must show that the square

commutes, where
![]() $\overline{I^H_K}$
is the induction map for
$\overline{I^H_K}$
is the induction map for
![]() $\textrm{Mackey} \circ \textrm{Sheaf}(M)$
.
$\textrm{Mackey} \circ \textrm{Sheaf}(M)$
.
Chasing through the definitions gives
 \begin{align*}\left( \overline{I^H_K} \theta_K(m) \right)_L=\Big(\underset{h \in H/K}{\sum} h\ast \overline{ \theta_K(m) }\Big)_L=\sum_{\substack{h \in H/K \\[1pt] h^{-1} L h \leqslant K}} (h \ast \theta_K(m))_L.\end{align*}
\begin{align*}\left( \overline{I^H_K} \theta_K(m) \right)_L=\Big(\underset{h \in H/K}{\sum} h\ast \overline{ \theta_K(m) }\Big)_L=\sum_{\substack{h \in H/K \\[1pt] h^{-1} L h \leqslant K}} (h \ast \theta_K(m))_L.\end{align*}
In the final equality we replace the extension by zero by an explicit condition on the subgroups.
Conversely, we use the Mackey axiom to rewrite
![]() $(\theta_H I^H_K(m))_L \in \textrm{Sheaf}(M)_L$
. We may choose a representative
$(\theta_H I^H_K(m))_L \in \textrm{Sheaf}(M)_L$
. We may choose a representative
![]() $a \in {e^{NL}_{{N},{NL}}} M(NL)$
for this germ, with
$a \in {e^{NL}_{{N},{NL}}} M(NL)$
for this germ, with
![]() $N \leqslant K$
an open normal subgroup of G. Then
$N \leqslant K$
an open normal subgroup of G. Then
 \begin{align*}a& ={e^{NL}_{{N},{NL}}} R^H_{NL} I^H_K(m) \\[5pt]& ={e^{NL}_{{N},{NL}}} \underset{\left[ NL \backslash H/ K \right]}{\sum}I^{NL}_{NL\cap xKx^{-1}} \circ C_x \circ R^K_{K\cap x^{-1}NLx} (m) \\[5pt]&={e^{NL}_{{N},{NL}}} \underset{\left[ NL\backslash H/ K \right]}{\sum}I^{NL}_{NL\cap xKx^{-1}}\circ R^{xKx^{-1}}_{NL \cap xKx^{-1}}\circ C_x (m). \\[5pt]&=\underset{\left[ NL\backslash H/ K \right]}{\sum}I^{NL}_{NL\cap xKx^{-1}} \Big(R^{NL}_{NL \cap xKx^{-1}} \big( {e^{NL}_{{N},{NL}}} \big) \cdot R^{xKx^{-1}}_{NL \cap xKx^{-1}} C_x (m) \Big).\end{align*}
\begin{align*}a& ={e^{NL}_{{N},{NL}}} R^H_{NL} I^H_K(m) \\[5pt]& ={e^{NL}_{{N},{NL}}} \underset{\left[ NL \backslash H/ K \right]}{\sum}I^{NL}_{NL\cap xKx^{-1}} \circ C_x \circ R^K_{K\cap x^{-1}NLx} (m) \\[5pt]&={e^{NL}_{{N},{NL}}} \underset{\left[ NL\backslash H/ K \right]}{\sum}I^{NL}_{NL\cap xKx^{-1}}\circ R^{xKx^{-1}}_{NL \cap xKx^{-1}}\circ C_x (m). \\[5pt]&=\underset{\left[ NL\backslash H/ K \right]}{\sum}I^{NL}_{NL\cap xKx^{-1}} \Big(R^{NL}_{NL \cap xKx^{-1}} \big( {e^{NL}_{{N},{NL}}} \big) \cdot R^{xKx^{-1}}_{NL \cap xKx^{-1}} C_x (m) \Big).\end{align*}
Consider the term
![]() $R^{NL}_{NL \cap xKx^{-1}} {e^{NL}_{{N},{NL}}}$
. If this is non-zero, there is a subgroup J of
$R^{NL}_{NL \cap xKx^{-1}} {e^{NL}_{{N},{NL}}}$
. If this is non-zero, there is a subgroup J of
![]() $NL \cap xKx^{-1}$
in the support of the idempotent. Hence,
$NL \cap xKx^{-1}$
in the support of the idempotent. Hence,
If
![]() $x \in \left[ NL\backslash H/ K \right] = \left[ L\backslash H/ K \right]$
is such that
$x \in \left[ NL\backslash H/ K \right] = \left[ L\backslash H/ K \right]$
is such that
![]() $L\leqslant xKx^{-1}$
, then
$L\leqslant xKx^{-1}$
, then
![]() $NL \cap xKx^{-1} =NL$
. The corresponding summand is
$NL \cap xKx^{-1} =NL$
. The corresponding summand is
which is sent to
![]() $C_x (m)_L$
in the L-stalk.
$C_x (m)_L$
in the L-stalk.
The collection of
![]() $x \in \left[ L\backslash H/ K \right]$
such that
$x \in \left[ L\backslash H/ K \right]$
such that
![]() $L\leqslant xKx^{-1}$
, is exactly the set
$L\leqslant xKx^{-1}$
, is exactly the set
![]() $hK \in H/K$
such that
$hK \in H/K$
such that
![]() $h^{-1} L h \leqslant K$
(the canonical isomorphism sends LxK to xK). Hence,
$h^{-1} L h \leqslant K$
(the canonical isomorphism sends LxK to xK). Hence,
 \[(\theta_H I^H_K(m))_L=\sum_{\substack{h \in H/K \\[1pt] h^{-1} L h \leqslant K}} (\theta_{hKh^{-1}} C_h(m))_L=\sum_{\substack{h \in H/K \\[1pt] h^{-1} L h \leqslant K}} (h \ast \theta_{K} (m))_L.\]
\[(\theta_H I^H_K(m))_L=\sum_{\substack{h \in H/K \\[1pt] h^{-1} L h \leqslant K}} (\theta_{hKh^{-1}} C_h(m))_L=\sum_{\substack{h \in H/K \\[1pt] h^{-1} L h \leqslant K}} (h \ast \theta_{K} (m))_L.\]
We combine Theorems 4·5 and 4·7 and note that our constructions are compatible with maps in the two categories to obtain the main result.
Theorem 4·8. If G is a profinite group then the category of rational G-Mackey functors is equivalent to the category of Weyl-G-sheaves over
![]() $\mathcal{S} G$
. Furthermore, this is an exact equivalence.
$\mathcal{S} G$
. Furthermore, this is an exact equivalence.
5. Consequences
5·1. Examples
Just as non-equivariantly, one can make constant sheaves and skyscraper sheaves. We leave the details to the second author’s thesis [
Reference SugrueSug19
] and the forthcoming paper by the authors [
Reference Barnes and SugrueBS20
]. The stalks of the constant sheaf at a
![]() $\mathbb{Q}$
-module B are all isomorphic to B. The sections are as for the non-equivariant constant sheaf.
$\mathbb{Q}$
-module B are all isomorphic to B. The sections are as for the non-equivariant constant sheaf.
Example 5·1. The Burnside ring Mackey functor corresponds to the constant Weyl-G-Sheaf at
![]() $\mathbb{Q}$
. The constant sheaf at a
$\mathbb{Q}$
. The constant sheaf at a
![]() $\mathbb{Q}$
-module B corresponds to the Mackey functor
$\mathbb{Q}$
-module B corresponds to the Mackey functor
![]() ${\textbf{A}_\mathbb{Q}} \otimes B$
.
${\textbf{A}_\mathbb{Q}} \otimes B$
.
For an equivariant skyscraper sheaf, one picks a closed subgroup K of G and a discrete
![]() $W_G K$
-module C. The stalk at K is C, for
$W_G K$
-module C. The stalk at K is C, for
![]() $g \in G$
, the stalk at
$g \in G$
, the stalk at
![]() $gKg^{-1}$
is gC (with the expected
$gKg^{-1}$
is gC (with the expected
![]() $gKg^{-1}$
-action), all other stalks are zero. The sections of this sheaf over U are given by a direct sum of copies of gB, with one copy for each
$gKg^{-1}$
-action), all other stalks are zero. The sections of this sheaf over U are given by a direct sum of copies of gB, with one copy for each
![]() $gKg^{-1} \in U$
, where the sums runs over
$gKg^{-1} \in U$
, where the sums runs over
![]() $G/K$
.
$G/K$
.
Example 5·2. For K a closed subgroup of G, we can describe the Mackey functor M that corresponds to the skyscraper sheaf
![]() $\textrm{Sky}_K(C)$
built from a discrete
$\textrm{Sky}_K(C)$
built from a discrete
![]() $W_G K$
-module C. At an open subgroup H, M(H) is the H-fixed points of
$W_G K$
-module C. At an open subgroup H, M(H) is the H-fixed points of
![]() $\textrm{Sky}_K(C)(\mathcal{S} H)$
. When K is open, there are only finitely many distinct conjugates of K, hence we can express M(H) as a finite direct sum indexed by the distinct conjugates
$\textrm{Sky}_K(C)(\mathcal{S} H)$
. When K is open, there are only finitely many distinct conjugates of K, hence we can express M(H) as a finite direct sum indexed by the distinct conjugates
![]() $gKg^{-1}$
of K that are subgroups of H
$gKg^{-1}$
of K that are subgroups of H
 \[M(H)=\textrm{Sky}_K(C)(\mathcal{S} H)^H = \Big( \bigoplus_{ \{gKg^{-1} \leqslant H\} } gC \Big)^H.\]
\[M(H)=\textrm{Sky}_K(C)(\mathcal{S} H)^H = \Big( \bigoplus_{ \{gKg^{-1} \leqslant H\} } gC \Big)^H.\]
If K is the trivial group, then the Mackey functor
![]() $M_C$
corresponding to
$M_C$
corresponding to
![]() $\textrm{Sky}_{\{ e\}}(C)$
is the fixed point Mackey functor, see Example 2·5, of the discrete G-module C.
$\textrm{Sky}_{\{ e\}}(C)$
is the fixed point Mackey functor, see Example 2·5, of the discrete G-module C.
It can be illuminating to perform the reverse calculation. The fixed point Mackey functor
![]() $M_C$
is cohomological, that is, restriction followed by induction is multiplication by the subgroup index
$M_C$
is cohomological, that is, restriction followed by induction is multiplication by the subgroup index
See Thévenaz and Webb [ Reference Thévenaz and WebbTW95 , section 16] for further details of cohomological Mackey functors.
This equation simplifies the behaviour of idempotents, particularly when we calculate the stalk of
![]() $\textrm{Sheaf}(M_C)$
at some closed subgroup K. As a self-map of
$\textrm{Sheaf}(M_C)$
at some closed subgroup K. As a self-map of
![]() $M_C(NK)$
,
$M_C(NK)$
,
 \begin{align*}{e^{NK}_{{N},{NK}}}& =\sum_{N \leqslant NA\leqslant NK}\frac{|NA|}{|N_{NK}(NK)|}\mu(NA,NK) [NK\;:\;NA] \\[5pt]& =\sum_{N \leqslant NA\leqslant NK}\frac{|NA|}{|NK|}\mu(NA,NK) [NK\;:\;NA] \\[5pt]& =\sum_{N \leqslant NA\leqslant NK} \mu(NA,NK)\end{align*}
\begin{align*}{e^{NK}_{{N},{NK}}}& =\sum_{N \leqslant NA\leqslant NK}\frac{|NA|}{|N_{NK}(NK)|}\mu(NA,NK) [NK\;:\;NA] \\[5pt]& =\sum_{N \leqslant NA\leqslant NK}\frac{|NA|}{|NK|}\mu(NA,NK) [NK\;:\;NA] \\[5pt]& =\sum_{N \leqslant NA\leqslant NK} \mu(NA,NK)\end{align*}
which is zero for non-trivial K and the identity map for K the trivial group. Hence, the stalks at non-trivial subgroups are zero. We then use the fact that C is discrete to complete the calculation
5·2. Weyl Sheaves from equivariant sheaves
As mentioned, Construction 3·1 does not require the input G-sheaf to be a Weyl-G-sheaf. Hence, given a sheaf F,
![]() $\textrm{Sheaf} \circ \textrm{Mackey} (F)$
is a Weyl-G-sheaf. We can construct this operation explicitly.
$\textrm{Sheaf} \circ \textrm{Mackey} (F)$
is a Weyl-G-sheaf. We can construct this operation explicitly.
Proposition 5·3. If F is a G-sheaf then the underlying set of
![]() ${Sheaf} \circ {Mackey} (F)$
is
${Sheaf} \circ {Mackey} (F)$
is
Furthermore, the map
![]() $F \to {Sheaf} \circ {Mackey} (F)$
is induced from the stalkwise inclusions of fixed points.
$F \to {Sheaf} \circ {Mackey} (F)$
is induced from the stalkwise inclusions of fixed points.
Proof. The stalks are given by
One can prove directly that the stalks
![]() $F_K^K$
form a Weyl-G-sheaf, as Proposition 2·21 implies that a K-fixed germ can be represented by a section that is N K-equivariant for some open normal subgroup N. One can also prove that a map from a Weyl-G-sheaf E to F will factor through the composite
$F_K^K$
form a Weyl-G-sheaf, as Proposition 2·21 implies that a K-fixed germ can be represented by a section that is N K-equivariant for some open normal subgroup N. One can also prove that a map from a Weyl-G-sheaf E to F will factor through the composite
![]() $\textrm{Sheaf} \circ \textrm{Mackey} (F)$
. See [
Reference Barnes and SugrueBS20
, section 10] for further such results.
$\textrm{Sheaf} \circ \textrm{Mackey} (F)$
. See [
Reference Barnes and SugrueBS20
, section 10] for further such results.

