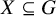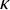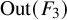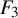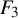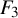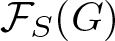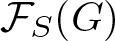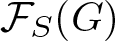Refine listing
Actions for selected content:
339 results in 20Exx
Type invariants for non-abelian odometers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On finite groups with bounded conjugacy classes of commutators
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-6
-
- Article
- Export citation
On congruence subgroups generated by two parabolic rational matrices
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-20
-
- Article
- Export citation
On closure operations in the space of subgroups and applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 05 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the quasi-transitivity degree of branch groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 04 August 2025, pp. 1-21
-
- Article
- Export citation
GROUPS WITH DENSE TRANSITIVELY NORMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-7
-
- Article
- Export citation
On derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 23 June 2025, e98
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Thompson groups for Ważewski dendrites
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 189-231
- Print publication:
- July 2025
-
- Article
- Export citation
Strongly reversible classes in
 $\mathrm{SL}(n,\mathbb{C})$
$\mathrm{SL}(n,\mathbb{C})$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 30 April 2025, pp. 1-32
-
- Article
- Export citation
A hyperbolic free-by-cyclic group determined by its finite quotients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 500-502
- Print publication:
- September 2025
-
- Article
- Export citation
Tree-like graphings, wallings, and median graphings of equivalence relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 March 2025, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Shelah group in ZFC
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linearity of compact R-analytic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 787-794
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The conjugacy problem for
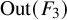 $\operatorname {Out}(F_3)$
$\operatorname {Out}(F_3)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal linear sofic approximations of countable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 24 January 2025, pp. 245-268
- Print publication:
- May 2025
-
- Article
- Export citation
Conditions for the supersolvability of
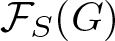 $\mathcal{F}_{S}(G)$
$\mathcal{F}_{S}(G)$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 23 January 2025, pp. 566-572
-
- Article
- Export citation
A characterization of virtually free groups among hyperbolic groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 477-483
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Presentation of an Iwasawa algebra: The pro-p Iwahori of simple, simply connected, split groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 377-394
- Print publication:
- June 2025
-
- Article
- Export citation
Product of two involutions in quaternionic special linear group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 421-439
- Print publication:
- June 2025
-
- Article
- Export citation
Order-automorphism groups of Archimedean ordered groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 628-633
- Print publication:
- June 2025
-
- Article
- Export citation