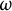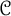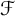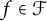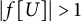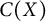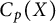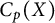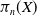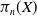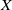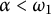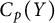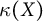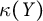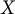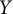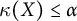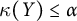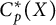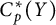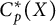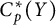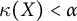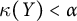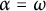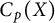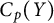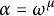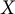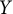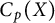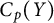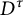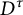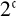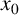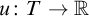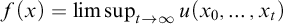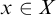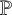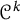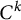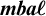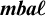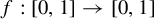Refine listing
Actions for selected content:
95 results in 54Cxx
Transitive mappings on the Cantor fan
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2601-2635
- Print publication:
- September 2025
-
- Article
- Export citation
ORDER-PRESERVING EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 17 December 2024, pp. 91-107
- Print publication:
- February 2025
-
- Article
- Export citation
Infinite dimensional sequential compactness: Sequential compactness based on barriers
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 December 2024, pp. 1-28
-
- Article
- Export citation
Sufficient conditions for non-zero entropy of closed relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 3091-3119
- Print publication:
- November 2024
-
- Article
- Export citation
Nowhere constant families of maps and resolvability
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 February 2024, pp. 701-705
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extension of monotone operators and Lipschitz maps invariant for a group of isometries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 December 2023, pp. 149-186
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear homeomorphisms of function spaces and the position of a space in its compactification
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 2151-2172
- Print publication:
- December 2024
-
- Article
- Export citation
A natural pseudometric on homotopy groups of metric spaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 162-174
- Print publication:
- January 2024
-
- Article
- Export citation
Universal spaces for asymptotic dimension via factorization
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 391-402
- Print publication:
- June 2024
-
- Article
- Export citation
Linear equivalence of scattered metric spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 29 May 2023, pp. 1354-1367
- Print publication:
- December 2023
-
- Article
- Export citation
On homogeneity of Cantor cubes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 1084-1090
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ERDŐS PROPERTIES OF SUBSETS OF THE MAHLER SET S
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 27 February 2023, pp. 504-510
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUASICONTINUITY, NONATTRACTING POINTS, DISTRIBUTIVE CHAOS AND RESISTANCE TO DISRUPTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 102-111
- Print publication:
- February 2023
-
- Article
- Export citation
GAMES CHARACTERIZING LIMSUP FUNCTIONS AND BAIRE CLASS 1 FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 1459-1473
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A CONTINUOUS HOMOMORPHISM OF A THIN SET ONTO A FAT SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 01 April 2022, pp. 500-503
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New Directions in Duality Theory for Modal Logic
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 February 2022, p. 527
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
A
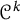 $\mathcal {C}^k$-seeley-extension-theorem for Bastiani’s differential calculus
$\mathcal {C}^k$-seeley-extension-theorem for Bastiani’s differential calculus
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 20 October 2021, pp. 170-201
- Print publication:
- February 2023
-
- Article
- Export citation
MODAL OPERATORS ON RINGS OF CONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 08 October 2021, pp. 1322-1348
- Print publication:
- December 2022
-
- Article
- Export citation
A characterization of a map whose inverse limit is an arc
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2533-2549
- Print publication:
- August 2022
-
- Article
- Export citation
Homotopy of gauge groups over high-dimensional manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 February 2021, pp. 182-208
- Print publication:
- February 2022
-
- Article
- Export citation