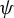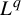Refine listing
Actions for selected content:
144 results in 37Exx
High-order persistence of resonant caustics in perturbed circular billiards
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 23 October 2025, pp. 1-29
-
- Article
- Export citation
Pensive Billiards, Point Vortices, And The Silver Ratio
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 October 2025, e171
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Entropy stability and Milnor–Thurston invariants for Bowen–Series-like maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CLASSIFICATION OF PERIODIC ORBITS FOR SQUARE AND RECTANGULAR BILLIARDS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost sure convergence of cover times for
 $\psi $-mixing systems
$\psi $-mixing systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quenched decay of correlations for random contracting Lorenz maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-58
-
- Article
- Export citation
Non-leading eigenvalues of the Perron–Frobenius operators for beta-maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-29
-
- Article
- Export citation
High-order homoclinic tangencies of corank 2
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-45
-
- Article
- Export citation
On
 $C^r$-generic twist maps of
$C^r$-generic twist maps of  $\mathrm {T^2}$
$\mathrm {T^2}$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-31
-
- Article
- Export citation
A trichotomy for hitting times and escape rates for a class of unimodal maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
log-Hölder continuity of the rotation number
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 08 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Real Teapot
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 21 April 2025, pp. 2945-2975
- Print publication:
- October 2025
-
- Article
- Export citation
Periodic points of rational area-preserving homeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 2890-2907
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
All, most, some? On diffeomorphisms of the interval that are distorted and/or conjugate to powers of themselves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 909-944
-
- Article
- Export citation
Characterization of the tree cycles with minimum positive entropy for any period
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 31 March 2025, pp. 3148-3191
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Renormalization of circle maps and smoothness of Arnold tongues
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2845-2889
- Print publication:
- September 2025
-
- Article
- Export citation
Existence of non-trivial embeddings of interval exchange transformations into piecewise isometries
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 2194-2232
- Print publication:
- July 2025
-
- Article
- Export citation
Erratum to ‘From Curves to Currents’
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 29 January 2025, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hölder continuity of measures for heavy tail potentials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 22 January 2025, pp. 2476-2513
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New classes of quasigeodesic Anosov flows in
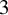 $3$-manifolds
$3$-manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 2095-2131
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation