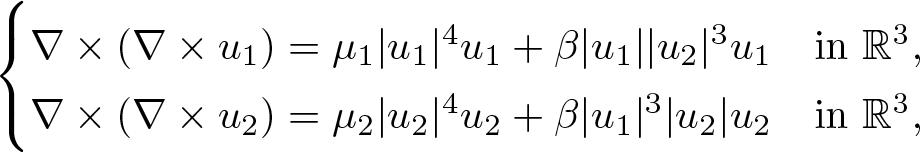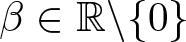Refine listing
Actions for selected content:
356 results in 35Qxx
Pensive Billiards, Point Vortices, And The Silver Ratio
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 October 2025, e171
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantitative quasi-invariance of Gaussian measures below the energy level for the 1D generalized nonlinear Schrödinger equation and application to global well-posedness
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 October 2025, pp. 1-33
-
- Article
- Export citation
Global smooth solutions and singularity formation for the relativistic Euler equations with radial symmetry
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-32
-
- Article
- Export citation
An extension theorem for weak solutions of the 3d incompressible Euler equations and applications to singular flows
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 29 September 2025, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Travelling breather solutions in waveguides for cubic nonlinear Maxwell equations with retarded material laws
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 18 September 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimization of the principal eigenvalue of the Neumann Laplacian with indefinite weight and monotonicity of minimizers in cylinders
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Well-posedness and averaging principle for non-Gaussian McKean–Vlasov stochastic differential equations with locally Lipschitz coefficients
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-44
-
- Article
-
- You have access
- HTML
- Export citation
Ill-posedness issue on the Oldroyd-B model in the critical Besov spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-20
-
- Article
- Export citation
Well-posedness of Naiver–Stokes equations in logarithmic Q spaces covering
 $BMO^{-1}$ and its fractional counterpart
$BMO^{-1}$ and its fractional counterpart
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The inverse scattering theory of Kadomtsev–Petviashvili II equations
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Keller–Segel type approximation for nonlocal Fokker–Planck equations in one-dimensional bounded domain
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ground state solution for weakly coupled time-harmonic Maxwell’s equations with critical exponent
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 July 2025, pp. 1-31
-
- Article
- Export citation
Local well-posedness and blow-up in the energy space for the 2D NLS with point interaction
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 July 2025, pp. 1-20
-
- Article
- Export citation
Regular solutions to the dissipative Aw–Rascle system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 July 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derivation of the Gross-Pitaevskii dynamics through renormalized excitation number operators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 July 2025, e107
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global boundedness and stabilization of solutions for a chemotaxis system with acceleration and logistic source
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-30
-
- Article
- Export citation
Regularity criteria for the 3D Navier–Stokes and MHD equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 26 June 2025, pp. 1262-1296
-
- Article
- Export citation
A multiscale model for espresso brewing: Asymptotic analysis and numerical simulation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cahn–Hilliard equations with singular potential, reaction term and pure phase initial datum
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the long-time asymptotics of the modified Camassa–Holm equation with step-like initial data
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 23 April 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation