1. Introduction
We show existence and regularity of spatially localized, real-valued and time-periodic solutions (called breathers) to Maxwell’s equations
 \begin{align}
\begin{aligned}
&\nabla \cdot \mathbf{D} = 0,
&&\nabla \times \mathbf{E} = - \mathbf{B}_t,
\\
&\nabla \cdot \mathbf{B} = 0,
&&\nabla \times \mathbf{H} = \mathbf{D}_t,
\end{aligned}
\end{align}
\begin{align}
\begin{aligned}
&\nabla \cdot \mathbf{D} = 0,
&&\nabla \times \mathbf{E} = - \mathbf{B}_t,
\\
&\nabla \cdot \mathbf{B} = 0,
&&\nabla \times \mathbf{H} = \mathbf{D}_t,
\end{aligned}
\end{align} without charges and currents. (1) is posed on all of ![]() $\mathbb{R}^3$ with an underlying material that is either a slab waveguide or a cylindrically symmetric waveguide. We look for solutions that are travelling parallel to the direction of the waveguide, and which are transverse-electric, i.e. the electric field E is orthogonal to the direction of travel. We assume that the material satisfies the constitutive relations
$\mathbb{R}^3$ with an underlying material that is either a slab waveguide or a cylindrically symmetric waveguide. We look for solutions that are travelling parallel to the direction of the waveguide, and which are transverse-electric, i.e. the electric field E is orthogonal to the direction of travel. We assume that the material satisfies the constitutive relations
where ![]() $\mu_0, \varepsilon_0 \in (0, \infty)$ are the vacuum permeability and permittivity, respectively. This means that the material is magnetically inactive. However, the displacement field D depends nonlinearly on the electric field E through the polarization field
$\mu_0, \varepsilon_0 \in (0, \infty)$ are the vacuum permeability and permittivity, respectively. This means that the material is magnetically inactive. However, the displacement field D depends nonlinearly on the electric field E through the polarization field ![]() $\mathbf{P}(\mathbf{E})$, which is modelled as a sum of a linear and a cubic function of E. Both parts are local in space but nonlocal in time (cf. [Reference Agrawal1] for a physical motivation) and are given by
$\mathbf{P}(\mathbf{E})$, which is modelled as a sum of a linear and a cubic function of E. Both parts are local in space but nonlocal in time (cf. [Reference Agrawal1] for a physical motivation) and are given by
 \begin{align}
\mathbf{P}(\mathbf{E})(x,t) &=\epsilon_0 \int_0^\infty \chi^{(1)}(\mathbf{x}, \tau)[\mathbf{E}(\mathbf{x}, t - \tau)] \mathrm{d}{\tau} \nonumber\\
&\quad +\epsilon_0 \int_0^\infty \int_0^\infty \int_0^\infty \chi^{(3)}(\mathbf{x}, \tau_1, \tau_2, \tau_3)[\mathbf{E}(\mathbf{x}, t - \tau_1),\mathbf{E}(\mathbf{x}, t - \tau_2),\mathbf{E}(\mathbf{x}, t - \tau_3)] \mathrm{d}{\tau_1}\mathrm{d}{\tau_2}\mathrm{d}{\tau_3}.
\end{align}
\begin{align}
\mathbf{P}(\mathbf{E})(x,t) &=\epsilon_0 \int_0^\infty \chi^{(1)}(\mathbf{x}, \tau)[\mathbf{E}(\mathbf{x}, t - \tau)] \mathrm{d}{\tau} \nonumber\\
&\quad +\epsilon_0 \int_0^\infty \int_0^\infty \int_0^\infty \chi^{(3)}(\mathbf{x}, \tau_1, \tau_2, \tau_3)[\mathbf{E}(\mathbf{x}, t - \tau_1),\mathbf{E}(\mathbf{x}, t - \tau_2),\mathbf{E}(\mathbf{x}, t - \tau_3)] \mathrm{d}{\tau_1}\mathrm{d}{\tau_2}\mathrm{d}{\tau_3}.
\end{align} Here ![]() $\mathbf{x} = (x,y,z)$ denotes the spatial variable, the susceptibility tensor
$\mathbf{x} = (x,y,z)$ denotes the spatial variable, the susceptibility tensor ![]() $\chi^{(1)}(\mathbf{x}, \tau) \colon \mathbb{R}^3 \to \mathbb{R}^3$ is linear and
$\chi^{(1)}(\mathbf{x}, \tau) \colon \mathbb{R}^3 \to \mathbb{R}^3$ is linear and ![]() $\chi^{(3)}(\mathbf{x}, \tau_1, \tau_2, \tau_3) \colon \mathbb{R}^3 \times \mathbb{R}^3 \times \mathbb{R}^3 \to \mathbb{R}^3$ is trilinear. Higher order terms
$\chi^{(3)}(\mathbf{x}, \tau_1, \tau_2, \tau_3) \colon \mathbb{R}^3 \times \mathbb{R}^3 \times \mathbb{R}^3 \to \mathbb{R}^3$ is trilinear. Higher order terms ![]() $\chi^{(2k+1)}$ which are
$\chi^{(2k+1)}$ which are ![]() $2k+1$-linear in E can in principle also occur. Even order terms vanish for materials (e.g. silica glasses) which have the inversion symmetry that
$2k+1$-linear in E can in principle also occur. Even order terms vanish for materials (e.g. silica glasses) which have the inversion symmetry that ![]() $\chi^{(l)}(-\mathbf{x},\ldots)=\chi^{(l)}(\mathbf{x},\ldots)$ and that
$\chi^{(l)}(-\mathbf{x},\ldots)=\chi^{(l)}(\mathbf{x},\ldots)$ and that ![]() $-\mathbf{E}(-\mathbf{x},t)$ solves the problem whenever
$-\mathbf{E}(-\mathbf{x},t)$ solves the problem whenever ![]() $\mathbf{E}(\mathbf{x},t)$ does so. In this paper we only consider the trilinear term and discuss two scenarios of its possible shape below. Comments on other scenarios are given below (before the literature section).
$\mathbf{E}(\mathbf{x},t)$ does so. In this paper we only consider the trilinear term and discuss two scenarios of its possible shape below. Comments on other scenarios are given below (before the literature section).
By taking the curl of Faraday’s law ![]() $\nabla \times \mathbf{E} = -\mathbf{B}_t$, we obtain from (1), (2) the second order form of Maxwell’s equations
$\nabla \times \mathbf{E} = -\mathbf{B}_t$, we obtain from (1), (2) the second order form of Maxwell’s equations
While (4) is an equation only for E, the other electromagnetic fields can be recovered if (4) holds: B is obtained from ![]() $\nabla \times \mathbf{E} = - \mathbf{B}_t$ by time-integration, and
$\nabla \times \mathbf{E} = - \mathbf{B}_t$ by time-integration, and ![]() $\mathbf{H}, \mathbf{D}$ are then determined by the material laws (2). Next, B is divergence-free if it is divergence-free at time 0 since
$\mathbf{H}, \mathbf{D}$ are then determined by the material laws (2). Next, B is divergence-free if it is divergence-free at time 0 since ![]() $\partial_t \nabla \cdot \mathbf{B} = -\nabla \cdot(\nabla \times \mathbf{E}) = 0$. Lastly,
$\partial_t \nabla \cdot \mathbf{B} = -\nabla \cdot(\nabla \times \mathbf{E}) = 0$. Lastly, ![]() $\mathbf{D} = \varepsilon_0 \mathbf{E} + \mathbf{P}(\mathbf{E})$ will be divergence-free because of the choices of
$\mathbf{D} = \varepsilon_0 \mathbf{E} + \mathbf{P}(\mathbf{E})$ will be divergence-free because of the choices of ![]() $\mathbf{E}, \mathbf{P}$ made later.
$\mathbf{E}, \mathbf{P}$ made later.
We assume that the material is either a slab waveguide or a cylindrical waveguide. In the first case, the susceptibility tensors ![]() $\chi^{(j)}$ remain constant as x moves parallel to the slab. Assuming that the slab is given by
$\chi^{(j)}$ remain constant as x moves parallel to the slab. Assuming that the slab is given by ![]() $\left\{ x = 0 \right\}$, this means that
$\left\{ x = 0 \right\}$, this means that
If instead the underlying material has a cylindrical waveguide geometry, we assume that the susceptibility tensors ![]() $\chi^{(j)}$ depend only on the distance from x to the cylinder core which we assume to be given by
$\chi^{(j)}$ depend only on the distance from x to the cylinder core which we assume to be given by ![]() $\left\{ x = y = 0 \right\}$, so that
$\left\{ x = y = 0 \right\}$, so that
where  $r = \sqrt{x^2 + y^2}$. The restriction to waveguide geometries allows us to choose ansatz functions for the electric field E which are divergence-free, cf. (7.1), (7.2). This not only satisfies the requirement of a divergence-free displacement field D but it is also advantageous since it simplifies the curl-curl operator in (4) to
$r = \sqrt{x^2 + y^2}$. The restriction to waveguide geometries allows us to choose ansatz functions for the electric field E which are divergence-free, cf. (7.1), (7.2). This not only satisfies the requirement of a divergence-free displacement field D but it is also advantageous since it simplifies the curl-curl operator in (4) to ![]() $-\Delta$ and thus drastically reduces its kernel. Waveguide geometries with more general cross-sections will make it necessary to deal with specific difficulties of the curl-curl operator and require a greatly enlarged technical effort, e.g., by Helmholtz decomposition, cf. [Reference Mederski21]. It is an open problem if these difficulties can be mastered in the context of polychromatic breathers.
$-\Delta$ and thus drastically reduces its kernel. Waveguide geometries with more general cross-sections will make it necessary to deal with specific difficulties of the curl-curl operator and require a greatly enlarged technical effort, e.g., by Helmholtz decomposition, cf. [Reference Mederski21]. It is an open problem if these difficulties can be mastered in the context of polychromatic breathers.
With I we denote the ![]() $3\times3$ identity matrix. We assume that the materials are isotropic, i.e.
$3\times3$ identity matrix. We assume that the materials are isotropic, i.e.
holds for ![]() $O \in \mathrm{SO}(3)$. This means that
$O \in \mathrm{SO}(3)$. This means that ![]() $\chi^{(1)}(\mathbf{x}, \tau) \in \mathbb{R} I$. For
$\chi^{(1)}(\mathbf{x}, \tau) \in \mathbb{R} I$. For ![]() $\chi^{(3)}$ a variety of isotropic scenarios are possible, but in this paper we only consider two kinds of nonlinear material responses: either
$\chi^{(3)}$ a variety of isotropic scenarios are possible, but in this paper we only consider two kinds of nonlinear material responses: either
or
where δ denotes the Dirac measure at 0, ![]() $\left\langle \,\cdot\, , \,\cdot\, \right\rangle$ is the standard inner product on
$\left\langle \,\cdot\, , \,\cdot\, \right\rangle$ is the standard inner product on ![]() $\mathbb{R}^3$, and
$\mathbb{R}^3$, and ![]() $h, \nu$ are given real-valued functions.
$h, \nu$ are given real-valued functions.
For these material laws, we will see that (4) can be viewed as a variational problem, and we will use a simple mountain-pass method in order to construct breather solutions to (1), (2). We deal with the kernel of the curl operator in (4) by looking for breather solutions in special divergence-free ansatz spaces that we discuss next. For the slab geometry (5.1) we make the TE-polarized traveling wave ansatz
 \begin{align}
\mathbf{E}(\mathbf{x}, t) = w(x, t - \tfrac{1}{c} z) \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}
\end{align}
\begin{align}
\mathbf{E}(\mathbf{x}, t) = w(x, t - \tfrac{1}{c} z) \cdot \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}
\end{align} where ![]() $w \colon \mathbb{R} \times \mathbb{R} \to \mathbb{R}$ is periodic in the second variable, which we again denote by t. For the cylindrical geometry (5.2) we instead consider the circular TE-polarized traveling wave ansatz
$w \colon \mathbb{R} \times \mathbb{R} \to \mathbb{R}$ is periodic in the second variable, which we again denote by t. For the cylindrical geometry (5.2) we instead consider the circular TE-polarized traveling wave ansatz
 \begin{align}
\mathbf{E}(\mathbf{x}, t) = w(r, t - \tfrac{1}{c} z) \cdot \begin{pmatrix} - y/r \\ x/r \\ 0 \end{pmatrix}
\end{align}
\begin{align}
\mathbf{E}(\mathbf{x}, t) = w(r, t - \tfrac{1}{c} z) \cdot \begin{pmatrix} - y/r \\ x/r \\ 0 \end{pmatrix}
\end{align} with  $r = \sqrt{x^2 + y^2}$ and
$r = \sqrt{x^2 + y^2}$ and ![]() $w \colon (0, \infty) \times \mathbb{R} \to \mathbb{R}$ being periodic in t. Both ansatzes for the electric field are divergence-free, so that
$w \colon (0, \infty) \times \mathbb{R} \to \mathbb{R}$ being periodic in t. Both ansatzes for the electric field are divergence-free, so that ![]() $\nabla\times\nabla\times \mathbf{E} = -\Delta \mathbf{E}$ holds, and are of a simple, essentially two-dimensional form, which greatly simplifies the discussion. More specifically, for the slab ansatz (7.1) problem (4) reduces to
$\nabla\times\nabla\times \mathbf{E} = -\Delta \mathbf{E}$ holds, and are of a simple, essentially two-dimensional form, which greatly simplifies the discussion. More specifically, for the slab ansatz (7.1) problem (4) reduces to
 \begin{align}
(- \partial_x^2 - \tfrac{1}{c^2} \partial_t^2) w + \epsilon_0 \mu_0 \partial_t^2 w + \mu_0 \partial_t^2 P(w)
= 0
\end{align}
\begin{align}
(- \partial_x^2 - \tfrac{1}{c^2} \partial_t^2) w + \epsilon_0 \mu_0 \partial_t^2 w + \mu_0 \partial_t^2 P(w)
= 0
\end{align}and for the cylindrical ansatz (7.2) to
 \begin{align}
(- \partial_r^2 - \tfrac{1}{r} \partial_r + \tfrac{1}{r^2} - \tfrac{1}{c^2} \partial_t^2) w + \epsilon_0 \mu_0 \partial_t^2 w + \mu_0 \partial_t^2 P(w)
= 0.
\end{align}
\begin{align}
(- \partial_r^2 - \tfrac{1}{r} \partial_r + \tfrac{1}{r^2} - \tfrac{1}{c^2} \partial_t^2) w + \epsilon_0 \mu_0 \partial_t^2 w + \mu_0 \partial_t^2 P(w)
= 0.
\end{align}Here, depending on the choice of the nonlinear susceptibility tensor, the scalar polarization P is given either by
 \begin{align}
P(w)(\mathbf{x}, t) &= \epsilon_0\int_0^\infty \chi^{(1)}(\mathbf{x}, \tau) w(\mathbf{x}, t - \tau) \mathrm{d}{\tau}
+ \epsilon_0 h(\mathbf{x}) \int_0^\infty w(\mathbf{x}, t - \tau)^3 \nu(\tau)\mathrm{d}{\tau}
\end{align}
\begin{align}
P(w)(\mathbf{x}, t) &= \epsilon_0\int_0^\infty \chi^{(1)}(\mathbf{x}, \tau) w(\mathbf{x}, t - \tau) \mathrm{d}{\tau}
+ \epsilon_0 h(\mathbf{x}) \int_0^\infty w(\mathbf{x}, t - \tau)^3 \nu(\tau)\mathrm{d}{\tau}
\end{align}or by
 \begin{align}
P(w)(\mathbf{x}, t) &= \epsilon_0\int_0^\infty \chi^{(1)}(\mathbf{x}, \tau) w(\mathbf{x}, t - \tau) \mathrm{d}{\tau}
+ \epsilon_0 h(\mathbf{x}) \left(\int_0^\infty w(\mathbf{x}, t - \tau) \nu(\tau)\mathrm{d}{\tau}\right)^3
\end{align}
\begin{align}
P(w)(\mathbf{x}, t) &= \epsilon_0\int_0^\infty \chi^{(1)}(\mathbf{x}, \tau) w(\mathbf{x}, t - \tau) \mathrm{d}{\tau}
+ \epsilon_0 h(\mathbf{x}) \left(\int_0^\infty w(\mathbf{x}, t - \tau) \nu(\tau)\mathrm{d}{\tau}\right)^3
\end{align} for susceptibilities (6.i) and (6.ii), respectively. The simple form of the nonlinearity in P(w), especially that the variables x and τ appear separated, are needed in order to obtain a variational problem. We denote by ![]() $\ast$ the convolution in time and normalize the speed of light to
$\ast$ the convolution in time and normalize the speed of light to  $c_0^2 = (\epsilon_0 \mu_0)^{-1} = 1$. Then problem (8.1) with polarization (9.i), which we discuss as an example, becomes
$c_0^2 = (\epsilon_0 \mu_0)^{-1} = 1$. Then problem (8.1) with polarization (9.i), which we discuss as an example, becomes
 \begin{align*}
\left(-\partial_x^2 + \left( 1 - \tfrac{1}{c^2} + \chi^{(1)} \ast \right) \partial_t^2\right) w + h(\mathbf{x}) (\nu \ast \partial_t^2) w^3
= 0.
\end{align*}
\begin{align*}
\left(-\partial_x^2 + \left( 1 - \tfrac{1}{c^2} + \chi^{(1)} \ast \right) \partial_t^2\right) w + h(\mathbf{x}) (\nu \ast \partial_t^2) w^3
= 0.
\end{align*} Inverting the convolution operator ![]() $\nu\ast\partial_t^2$ formallyFootnote 1, we then obtain
$\nu\ast\partial_t^2$ formallyFootnote 1, we then obtain
 \begin{align}
\left(\nu\ast\partial_t^2 \right)^{-1}\left(-\partial_x^2 + \left( 1 - \tfrac{1}{c^2} + \chi^{(1)} \ast\right) \partial_t^2\right) w + h(\mathbf{x}) w^3
= 0.
\end{align}
\begin{align}
\left(\nu\ast\partial_t^2 \right)^{-1}\left(-\partial_x^2 + \left( 1 - \tfrac{1}{c^2} + \chi^{(1)} \ast\right) \partial_t^2\right) w + h(\mathbf{x}) w^3
= 0.
\end{align}Given our assumptions, we can ensure that the linear operator is symmetric when restricted to suitable spaces of time-periodic functions. Hence solutions formally are critical points of the functional
 \begin{align}
J(w) = \int \left(\tfrac12 w \cdot \left(\nu\ast\partial_t^2\right)^{-1}\left(-\partial_x^2 + \left( 1 - \tfrac{1}{c^2} + \chi^{(1)} \ast \right) \partial_t^2\right) w + \tfrac1{4} h(\mathbf{x}) w^4\right) \mathrm{d}{(\mathbf{x}, t)}.
\end{align}
\begin{align}
J(w) = \int \left(\tfrac12 w \cdot \left(\nu\ast\partial_t^2\right)^{-1}\left(-\partial_x^2 + \left( 1 - \tfrac{1}{c^2} + \chi^{(1)} \ast \right) \partial_t^2\right) w + \tfrac1{4} h(\mathbf{x}) w^4\right) \mathrm{d}{(\mathbf{x}, t)}.
\end{align} Using the mountain-pass method, we will find critical points and then show that they are breather solutions to Maxwell’s equations (1), (2). Using a different but equivalent variational method also opens the door for numerical treatment of breather solutions. We comment on this at the end of Section 3. We also mention that the cubic nonlinearity in (10) can be replaced by any odd nonlinearity of power larger than 1 without any changes in our method. A replacement of the cubic nonlinearity ![]() $h(\mathbf{x}) w^3$ by any other odd Carathéodory-type nonlinearity
$h(\mathbf{x}) w^3$ by any other odd Carathéodory-type nonlinearity ![]() $f(\mathbf{x},w)$ cannot be achieved without substantial reworking of our arguments. We suspect that a condition of the type
$f(\mathbf{x},w)$ cannot be achieved without substantial reworking of our arguments. We suspect that a condition of the type ![]() $|f(\mathbf{x},w)| \leq C(1+|w|^p)$ for some p > 1 together with
$|f(\mathbf{x},w)| \leq C(1+|w|^p)$ for some p > 1 together with ![]() $f(\mathbf{x},w)=o(1)$ as w → 0 and an Ambrosetti-Rabinowitz condition
$f(\mathbf{x},w)=o(1)$ as w → 0 and an Ambrosetti-Rabinowitz condition ![]() $0 \lt (p+1)F(\mathbf{x},w)\leq f(\mathbf{x},w)w$ for
$0 \lt (p+1)F(\mathbf{x},w)\leq f(\mathbf{x},w)w$ for ![]() $w\not =0$ and all
$w\not =0$ and all ![]() $x\in \mathbb{R}$ where
$x\in \mathbb{R}$ where  $F(\mathbf{x},w)=\int_0^w f(\mathbf{x},z)\mathrm{d}z$ might be necessary. In view of our comments on the model at the beginning of this introduction, where we argue that the cubic nonlinearity is of most importance, this question is more of mathematical than of practical interest.
$F(\mathbf{x},w)=\int_0^w f(\mathbf{x},z)\mathrm{d}z$ might be necessary. In view of our comments on the model at the beginning of this introduction, where we argue that the cubic nonlinearity is of most importance, this question is more of mathematical than of practical interest.
In the literature, there are several papers treating existence of breather solutions of (4). Many authors have considered monochromatic solutions, i.e. solutions of the form ![]() $\mathbf{E}(\mathbf{x}, t) = \mathcal{E}(\mathbf{x}) \mathrm{e}^{\mathrm{i} \omega t} + c.c.$, where the complex conjugate is necessary in order to make the E-field real valued. This is a viable approach if one ignores the higher-order harmonics
$\mathbf{E}(\mathbf{x}, t) = \mathcal{E}(\mathbf{x}) \mathrm{e}^{\mathrm{i} \omega t} + c.c.$, where the complex conjugate is necessary in order to make the E-field real valued. This is a viable approach if one ignores the higher-order harmonics ![]() $\mathrm{e}^{\pm 3 \mathrm{i} \omega t}$ coming from the nonlinear part of the polarization, or if one considers a nonlinear susceptibility tensor given by
$\mathrm{e}^{\pm 3 \mathrm{i} \omega t}$ coming from the nonlinear part of the polarization, or if one considers a nonlinear susceptibility tensor given by
 \begin{align}
\chi^{(3)}(\mathbf{x}, \tau_1, \tau_2, \tau_3)[\mathbf{u}, \mathbf{v}, \mathbf{w}]
= \tfrac{1}{2T} h(\mathbf{x}) \mathbb{1}_{[0, T]}(\tau_1) \delta(\tau_2 - \tau_1) \delta(\tau_3) \left\langle \mathbf{u} , \mathbf{v} \right\rangle \mathbf{w},
\end{align}
\begin{align}
\chi^{(3)}(\mathbf{x}, \tau_1, \tau_2, \tau_3)[\mathbf{u}, \mathbf{v}, \mathbf{w}]
= \tfrac{1}{2T} h(\mathbf{x}) \mathbb{1}_{[0, T]}(\tau_1) \delta(\tau_2 - \tau_1) \delta(\tau_3) \left\langle \mathbf{u} , \mathbf{v} \right\rangle \mathbf{w},
\end{align} where  $T = \frac{2 \pi}{\omega}$ is the period of the breather E. Both approaches lead to the nonlinear curl-curl problem
$T = \frac{2 \pi}{\omega}$ is the period of the breather E. Both approaches lead to the nonlinear curl-curl problem
which is variational provided  $g(\mathbf{x}) = \int_0^\infty \chi^{(1)}(\mathbf{x}, \tau) \mathrm{e}^{\mathrm{i} \omega \tau} \mathrm{d}{\tau}$ is real valued. Instead of the cubic nonlinearity
$g(\mathbf{x}) = \int_0^\infty \chi^{(1)}(\mathbf{x}, \tau) \mathrm{e}^{\mathrm{i} \omega \tau} \mathrm{d}{\tau}$ is real valued. Instead of the cubic nonlinearity ![]() $h(\mathbf{x}) \left\lvert \mathcal{E} \right\rvert^2 \mathcal{E}$, saturated nonlinearities
$h(\mathbf{x}) \left\lvert \mathcal{E} \right\rvert^2 \mathcal{E}$, saturated nonlinearities ![]() $h(\mathbf{x}, \left\lvert \mathcal{E} \right\rvert^2) \mathcal{E}$, which grow linearly as
$h(\mathbf{x}, \left\lvert \mathcal{E} \right\rvert^2) \mathcal{E}$, which grow linearly as ![]() $\left\lvert \mathcal{E} \right\rvert \to \infty$, are also of interest and were first investigated by Stuart et al. [Reference McLeod, Stuart and Troy20, Reference Stuart27–Reference Stuart and Zhou33]. In these papers divergence-free, traveling, TE- or TM-polarized ansatz functions similar to (7.2) were used to reduce the Maxwell problem to an elliptic one-dimensional problem and to solve it via variational methods. An extension of Stuart’s approach to more general wave-guide profiles was given in [Reference Mederski and Reichel22]. Standing monochromatic breathers composed of axisymmetric divergence-free ansatz functions were considered in [Reference Azzollini, Benci, D’Aprile and Fortunato2, Reference Bartsch, Dohnal, Plum and Reichel3, Reference Bényi, Oh and Zhao6]. The next step forward to overcome special divergence-free ansatz functions was accomplished by Mederski et al. [Reference Bartsch and Mederski4, Reference Mederski21, Reference Mederski and Schino23, Reference Mederski, Schino and Szulkin24] who considered the full curl-curl problem (13), also for more general nonlinearities
$\left\lvert \mathcal{E} \right\rvert \to \infty$, are also of interest and were first investigated by Stuart et al. [Reference McLeod, Stuart and Troy20, Reference Stuart27–Reference Stuart and Zhou33]. In these papers divergence-free, traveling, TE- or TM-polarized ansatz functions similar to (7.2) were used to reduce the Maxwell problem to an elliptic one-dimensional problem and to solve it via variational methods. An extension of Stuart’s approach to more general wave-guide profiles was given in [Reference Mederski and Reichel22]. Standing monochromatic breathers composed of axisymmetric divergence-free ansatz functions were considered in [Reference Azzollini, Benci, D’Aprile and Fortunato2, Reference Bartsch, Dohnal, Plum and Reichel3, Reference Bényi, Oh and Zhao6]. The next step forward to overcome special divergence-free ansatz functions was accomplished by Mederski et al. [Reference Bartsch and Mederski4, Reference Mederski21, Reference Mederski and Schino23, Reference Mederski, Schino and Szulkin24] who considered the full curl-curl problem (13), also for more general nonlinearities ![]() $\partial_\mathcal{E} h(\mathbf{x}, \mathcal{E})$. The difficulties arising from the infinite-dimensional kernel of
$\partial_\mathcal{E} h(\mathbf{x}, \mathcal{E})$. The difficulties arising from the infinite-dimensional kernel of ![]() $\nabla \times$ were overcome by a Helmholtz decomposition and suitable profile decompositions for Palais-Smale sequences. Alternative approaches used limiting absorption principles [Reference Mandel17], dual variational approaches [Reference Mandel18, Reference Mandel19], approximations near gap edges of photonic crystals [Reference Dohnal and Romani10], and monochromatic time-decaying solutions at interfaces of metals and dielectrics [Reference Dohnal and He8, Reference Dohnal and Romani9, Reference Dohnal and Romani11]. In the latter series of papers, also time-periodic solutions can be found if one additionally assumes
$\nabla \times$ were overcome by a Helmholtz decomposition and suitable profile decompositions for Palais-Smale sequences. Alternative approaches used limiting absorption principles [Reference Mandel17], dual variational approaches [Reference Mandel18, Reference Mandel19], approximations near gap edges of photonic crystals [Reference Dohnal and Romani10], and monochromatic time-decaying solutions at interfaces of metals and dielectrics [Reference Dohnal and He8, Reference Dohnal and Romani9, Reference Dohnal and Romani11]. In the latter series of papers, also time-periodic solutions can be found if one additionally assumes ![]() $\mathcal{PT}$-symmetry of the materials.
$\mathcal{PT}$-symmetry of the materials.
If one does not want to rely on very specific retardation kernels as in (12) or if one wants to take higher harmonics into account then one is naturally led to polychromatic breather solutions, i.e. time-periodic solutions which have multiple (typically infinitely many) supported frequencies in time-domain. In the context of instantaneous material laws they have recently received increasing attention. As a model problem consider
For this problem, rigorous existence result for travelling breathers in the slab geometry (5.1) where either g or h contains delta distributions are given in [Reference Kohler and Reichel15] by variational methods and in [Reference Brüll, Idzik and Reichel7] via bifurcation theory. Even earlier in [Reference Pelinovsky, Simpson and Weinstein26] the authors used a combination of local bifurcation theory and continuation methods in a partly analytical and partly numerical study on traveling wave solutions where the linear coefficient g is a periodic arrangement of delta potentials. Another rigorous existence result for breathers on finite but large time scales can be found in [Reference Dohnal, Schnaubelt and Tietz12] for a set-up of Kerr-nonlinear dielectrics occupying two different halfspaces. In our recent paper [Reference Ohrem and Reichel25] we proved the first (to the best of our knowledge) existence result for polychromatic breathers in the context of nonlinear Maxwell’s equations without presence of any delta-potentials. The ![]() $\chi^{(1)}$-part of the polarization was instantaneous and the
$\chi^{(1)}$-part of the polarization was instantaneous and the ![]() $\chi^{(3)}$-part was compactly supported in space and either instantaneous or retarded. Due to the compact support in space both variants of the nonlinearity could be treated with the same variational method. Beyond this result we are not aware of any rigorous treatment of polychromatic breathers in the context of nonlinear Maxwell’s equations with time retarded material laws.
$\chi^{(3)}$-part was compactly supported in space and either instantaneous or retarded. Due to the compact support in space both variants of the nonlinearity could be treated with the same variational method. Beyond this result we are not aware of any rigorous treatment of polychromatic breathers in the context of nonlinear Maxwell’s equations with time retarded material laws.
1.1. Examples
In two theorems below, we give examples of susceptibility tensors ![]() $\chi^{(1)}, \chi^{(3)}$ for which breather solutions of Maxwell’s equations (1), (2), (3) exist. For simplicity, we choose an instantaneous linear response while the nonlinear response has to be retarded. These examples are special cases of a general existence result given later in this chapter, cf. Theorem 1.3. Let us note that in contrast to some of the previously mentioned results, our breather solutions are generally polychromatic in nature and the potentials considered are bounded functions. Since our breathers lie in suitable Sobolev spaces they are sufficiently differentiable to solve Maxwell’s equations pointwise, and they decay at infinity in an Lp-sense. They may have higher-order space-derivatives depending on smoothness of the material coefficients in space. They are also infinitely differentiable in time because the material properties do not change over time.
$\chi^{(1)}, \chi^{(3)}$ for which breather solutions of Maxwell’s equations (1), (2), (3) exist. For simplicity, we choose an instantaneous linear response while the nonlinear response has to be retarded. These examples are special cases of a general existence result given later in this chapter, cf. Theorem 1.3. Let us note that in contrast to some of the previously mentioned results, our breather solutions are generally polychromatic in nature and the potentials considered are bounded functions. Since our breathers lie in suitable Sobolev spaces they are sufficiently differentiable to solve Maxwell’s equations pointwise, and they decay at infinity in an Lp-sense. They may have higher-order space-derivatives depending on smoothness of the material coefficients in space. They are also infinitely differentiable in time because the material properties do not change over time.
We begin with an exemplary result for the slab geometry (5.1).
Theorem 1.1 Let ![]() $T \gt 0$ denote the temporal period,
$T \gt 0$ denote the temporal period,  $\omega := \frac{2 \pi}{T}$ the associated frequency, and
$\omega := \frac{2 \pi}{T}$ the associated frequency, and ![]() $c \in (0, 1)$ the speed of travel of the breather solution. Assume that the linear susceptibility tensor is given by
$c \in (0, 1)$ the speed of travel of the breather solution. Assume that the linear susceptibility tensor is given by ![]() $\chi^{(1)}(\mathbf{x}, \tau) = g(x) \delta(\tau)I$, and the nonlinear susceptibility tensor
$\chi^{(1)}(\mathbf{x}, \tau) = g(x) \delta(\tau)I$, and the nonlinear susceptibility tensor ![]() $\chi^{(3)}$ is given by (6.i) or (6.ii) with
$\chi^{(3)}$ is given by (6.i) or (6.ii) with
Moreover, assume that the potentials ![]() $g, h \in L^\infty(\mathbb{R})$ have periodic backgrounds
$g, h \in L^\infty(\mathbb{R})$ have periodic backgrounds ![]() $g^\mathrm{per}, h^\mathrm{per} \in L^\infty(\mathbb{R})$ with a common period, i.e.
$g^\mathrm{per}, h^\mathrm{per} \in L^\infty(\mathbb{R})$ with a common period, i.e.
and that the inequalities
 \begin{align*}
g^\mathrm{per} \leq g,
\qquad
\operatorname{ess~sup}_\mathbb{R} g \lt \tfrac{1}{c^2} - 1,
\qquad
h^\mathrm{per} \leq h,
\qquad
h^\mathrm{per} \not \leq 0
\end{align*}
\begin{align*}
g^\mathrm{per} \leq g,
\qquad
\operatorname{ess~sup}_\mathbb{R} g \lt \tfrac{1}{c^2} - 1,
\qquad
h^\mathrm{per} \leq h,
\qquad
h^\mathrm{per} \not \leq 0
\end{align*} are satisfied. Then there exist nonzero time-periodic solutions ![]() $\mathbf{D}, \mathbf{E}, \mathbf{B}, \mathbf{H}$ of Maxwell’s equations (1), (2), (3) where E is of the form (7.1). They satisfy
$\mathbf{D}, \mathbf{E}, \mathbf{B}, \mathbf{H}$ of Maxwell’s equations (1), (2), (3) where E is of the form (7.1). They satisfy
for all ![]() $n \in \mathbb{N}_0$,
$n \in \mathbb{N}_0$, ![]() $p \in [2, \infty]$ and all domains
$p \in [2, \infty]$ and all domains ![]() $\Omega = \mathbb{R} \times [y, y+1] \times [z, z+1] \times [t, t+1]$, with norm bounds independent of
$\Omega = \mathbb{R} \times [y, y+1] \times [z, z+1] \times [t, t+1]$, with norm bounds independent of ![]() $y, z, t$.
$y, z, t$.
The potentials ![]() $g, h$ describe the spatial dependency of the polarization field. In the above theorem we have required them to be asymptotically periodic at
$g, h$ describe the spatial dependency of the polarization field. In the above theorem we have required them to be asymptotically periodic at ![]() $\pm \infty$. This periodic structure helps us to overcome noncompactness of embeddings on
$\pm \infty$. This periodic structure helps us to overcome noncompactness of embeddings on ![]() $\mathbb{R}$. The assumption on the ordering
$\mathbb{R}$. The assumption on the ordering ![]() $g \geq g^\mathrm{per}, h \geq h^\mathrm{per}$ is a standard tool to resolve noncompactness issues also for the nonperiodic problem. The upper bound
$g \geq g^\mathrm{per}, h \geq h^\mathrm{per}$ is a standard tool to resolve noncompactness issues also for the nonperiodic problem. The upper bound  $\tfrac{1}{c^2} - 1$ on g and the choice of ν ensure that (4) is elliptic. One aspect of the choice of ν is that its Fourier coefficients are positive. This aspect will become very important in the general result of Theorem 1.3. Ellipticity will ensure that the associated energy has a mountain-pass geometry, and a mountain-pass method will be used to construct breather solutions. Note also that breathers are localized in the x-direction (in the Lp-sense stated above), but not in
$\tfrac{1}{c^2} - 1$ on g and the choice of ν ensure that (4) is elliptic. One aspect of the choice of ν is that its Fourier coefficients are positive. This aspect will become very important in the general result of Theorem 1.3. Ellipticity will ensure that the associated energy has a mountain-pass geometry, and a mountain-pass method will be used to construct breather solutions. Note also that breathers are localized in the x-direction (in the Lp-sense stated above), but not in ![]() $y, z,$ or t, which is due to the ansatz (7.1), since all solutions satisfying this ansatz necessarily are independent of y and periodic in both z and t.
$y, z,$ or t, which is due to the ansatz (7.1), since all solutions satisfying this ansatz necessarily are independent of y and periodic in both z and t.
Similar to Theorem 1.1 for the slab geometry, below we give an exemplary result with cylindrical geometry (5.2).
Theorem 1.2 Let ![]() $T \gt 0$ be the period of the breather,
$T \gt 0$ be the period of the breather, ![]() $c \in (0, 1)$ be its speed, and
$c \in (0, 1)$ be its speed, and ![]() $g, h \in L^\infty([0, \infty))$ be material coefficients. Define the linear susceptibility by
$g, h \in L^\infty([0, \infty))$ be material coefficients. Define the linear susceptibility by ![]() $\chi^{(1)}(\mathbf{x}, \tau) := g(r)\delta(\tau) I$ and let the nonlinear susceptibility
$\chi^{(1)}(\mathbf{x}, \tau) := g(r)\delta(\tau) I$ and let the nonlinear susceptibility ![]() $\chi^{(3)}$ be given by (6.i) or (6.ii) with
$\chi^{(3)}$ be given by (6.i) or (6.ii) with ![]() $h(\mathbf{x}) = h(r), \nu(\tau) = (2 - \left\lvert \sin(\omega \tau) \right\rvert)\mathbb{1}_{[0, T]}(\tau)$ where
$h(\mathbf{x}) = h(r), \nu(\tau) = (2 - \left\lvert \sin(\omega \tau) \right\rvert)\mathbb{1}_{[0, T]}(\tau)$ where  $r := \sqrt{x^2 + y^2}$,
$r := \sqrt{x^2 + y^2}$,  $\omega := \frac{2 \pi}{T}$. Further let
$\omega := \frac{2 \pi}{T}$. Further let
 \begin{align*}
\operatorname{ess~sup}_\mathbb{R} g \lt \tfrac{1}{c^2} - 1,
\qquad
h\not\leq0.
\end{align*}
\begin{align*}
\operatorname{ess~sup}_\mathbb{R} g \lt \tfrac{1}{c^2} - 1,
\qquad
h\not\leq0.
\end{align*} Then there exist nonzero time-periodic solutions ![]() $\mathbf{D}, \mathbf{E}, \mathbf{B}, \mathbf{H}$ of Maxwell’s equations (1), (2), (3) where E is of the form (7.2). They satisfy
$\mathbf{D}, \mathbf{E}, \mathbf{B}, \mathbf{H}$ of Maxwell’s equations (1), (2), (3) where E is of the form (7.2). They satisfy
for all ![]() $n \in \mathbb{N}_0$,
$n \in \mathbb{N}_0$, ![]() $p \in [2, \infty]$ and all domains
$p \in [2, \infty]$ and all domains ![]() $\Omega = \mathbb{R}^2 \times [z, z+1] \times [t, t+1]$, with norm bounds independent of
$\Omega = \mathbb{R}^2 \times [z, z+1] \times [t, t+1]$, with norm bounds independent of ![]() $z, t$.
$z, t$.
In contrast to Theorem 1.1, in Theorem 1.2 we do not need any asymptotics for the potentials ![]() $g, h$. This is because the cylindrical setting itself comes with compactness, as we discuss in Section 5. To illustrate this, recall that the Sobolev embedding
$g, h$. This is because the cylindrical setting itself comes with compactness, as we discuss in Section 5. To illustrate this, recall that the Sobolev embedding ![]() $H^1(\mathbb{R}^2) \hookrightarrow L^p(\mathbb{R}^2)$ for
$H^1(\mathbb{R}^2) \hookrightarrow L^p(\mathbb{R}^2)$ for ![]() $p \in (2, \infty)$ becomes compact when restricted to radially symmetric functions. Lastly, the ansatz (7.2) is periodic in both z and t, so breather solutions in the cylindrical setting decay in the x and y directions orthogonal to the direction of propagation.
$p \in (2, \infty)$ becomes compact when restricted to radially symmetric functions. Lastly, the ansatz (7.2) is periodic in both z and t, so breather solutions in the cylindrical setting decay in the x and y directions orthogonal to the direction of propagation.
1.2. Main theorem
Before stating the main theorem, we fix some notation.
1.2.1. Measures on torus and real line, periodic reduction of a measure
Since breathers are time-periodic, the natural time domain is the torus ![]() $\mathbb{T} := \mathbb{R}/_{T \mathbb{Z}}$ with period T, and we denote the canonical projection by
$\mathbb{T} := \mathbb{R}/_{T \mathbb{Z}}$ with period T, and we denote the canonical projection by ![]() $P_\mathbb{T} \colon \mathbb{R} \to \mathbb{T}$. With
$P_\mathbb{T} \colon \mathbb{R} \to \mathbb{T}$. With ![]() $\mathcal{M}(\mathbb{T})$,
$\mathcal{M}(\mathbb{T})$, ![]() $\mathcal{M}(\mathbb{R})$ we denote the set of all
$\mathcal{M}(\mathbb{R})$ we denote the set of all ![]() $\mathbb{R}$-valued measures λ on the Borel σ-algebra of
$\mathbb{R}$-valued measures λ on the Borel σ-algebra of ![]() $\mathbb{T}$ and
$\mathbb{T}$ and ![]() $\mathbb{R}$, respectively, and we equip it with the total variation norm
$\mathbb{R}$, respectively, and we equip it with the total variation norm ![]() $\left\lVert \lambda \right\rVert=|\lambda|(\mathbb{T})$ or
$\left\lVert \lambda \right\rVert=|\lambda|(\mathbb{T})$ or ![]() $\left\lVert \lambda \right\rVert=|\lambda|(\mathbb{R})$. The push-forward map
$\left\lVert \lambda \right\rVert=|\lambda|(\mathbb{R})$. The push-forward map ![]() $P_\mathbb{T}^*: \mathcal{M}(\mathbb{R})\to \mathcal{M}(\mathbb{T})$ is defined as follows: for
$P_\mathbb{T}^*: \mathcal{M}(\mathbb{R})\to \mathcal{M}(\mathbb{T})$ is defined as follows: for ![]() $\lambda\in \mathcal{M}(\mathbb{R})$ we set
$\lambda\in \mathcal{M}(\mathbb{R})$ we set ![]() $P_\mathbb{T}^*(\lambda)\in \mathcal{M}(\mathbb{T})$ by
$P_\mathbb{T}^*(\lambda)\in \mathcal{M}(\mathbb{T})$ by  $P_\mathbb{T}^*(\lambda)(E) = \lambda(P_\mathbb{T}^{-1}(E))$ for any Borel subset
$P_\mathbb{T}^*(\lambda)(E) = \lambda(P_\mathbb{T}^{-1}(E))$ for any Borel subset ![]() $E\subseteq \mathbb{T}$. The new measure
$E\subseteq \mathbb{T}$. The new measure ![]() $P_\mathbb{T}^*(\lambda)\in\mathcal{M}(\mathbb{T})$ is called the periodic reduction of λ. In this way, the torus is equipped with the measure
$P_\mathbb{T}^*(\lambda)\in\mathcal{M}(\mathbb{T})$ is called the periodic reduction of λ. In this way, the torus is equipped with the measure  $\mathrm{d} t = \frac{1}{T}P_\mathbb{T}^*(\mathbb{1}_{[0,T]}\mathrm{d}{\tau})$, where
$\mathrm{d} t = \frac{1}{T}P_\mathbb{T}^*(\mathbb{1}_{[0,T]}\mathrm{d}{\tau})$, where ![]() $\mathrm{d}{\tau}$ denotes the Lebesgue measure on
$\mathrm{d}{\tau}$ denotes the Lebesgue measure on ![]() $\mathbb{R}$.
$\mathbb{R}$.
1.2.2. Instantaneous vs. retarded  $\chi^{(1)}$-contribution
$\chi^{(1)}$-contribution
While the nonlinear susceptibility tensor ![]() $\chi^{(3)}$ necessarily represents a retarded material response, cf. (6.i) or (6.ii), the
$\chi^{(3)}$ necessarily represents a retarded material response, cf. (6.i) or (6.ii), the ![]() $\chi^{(1)}$-contribution to the material response may be instantaneous or retarded. The first case is given by
$\chi^{(1)}$-contribution to the material response may be instantaneous or retarded. The first case is given by ![]() $\chi^{(1)}(\mathbf{x},\tau)=g(x)\delta(\tau)I$ or
$\chi^{(1)}(\mathbf{x},\tau)=g(x)\delta(\tau)I$ or ![]() $\chi^{(1)}(\mathbf{x},\tau)=g(r)\delta(\tau)I$ from Section 1.1. The second case may be written in the form
$\chi^{(1)}(\mathbf{x},\tau)=g(r)\delta(\tau)I$ from Section 1.1. The second case may be written in the form ![]() $\chi^{(1)}(\mathbf{x},\tau)\mathrm{d}{\tau} = \mathrm{d} G(\mathbf{x})(\tau) I$ where for fixed
$\chi^{(1)}(\mathbf{x},\tau)\mathrm{d}{\tau} = \mathrm{d} G(\mathbf{x})(\tau) I$ where for fixed ![]() $\mathbf{x}\in\mathbb{R}^3$ we have that
$\mathbf{x}\in\mathbb{R}^3$ we have that ![]() $G(\mathbf{x})\in \mathcal{M}(\mathbb{R})$ is an
$G(\mathbf{x})\in \mathcal{M}(\mathbb{R})$ is an ![]() $\mathbb{R}$-valued Borel measure. Mathematically, the second case comprises the first and hence in the following an instantaneous
$\mathbb{R}$-valued Borel measure. Mathematically, the second case comprises the first and hence in the following an instantaneous ![]() $\chi^{(1)}$-contribution is subsumed in the retarded case.
$\chi^{(1)}$-contribution is subsumed in the retarded case.
1.2.3. Fourier transform
Let us fix a convention for Fourier series and Fourier transform. For a time-periodic function ![]() $v \colon \mathbb{T} \to \mathbb{C}$ we define its Fourier coefficients by
$v \colon \mathbb{T} \to \mathbb{C}$ we define its Fourier coefficients by  $\hat v_k = \mathcal{F}_k[v] = \int_\mathbb{T} v \overline{e_k} \mathrm{d}t$ with
$\hat v_k = \mathcal{F}_k[v] = \int_\mathbb{T} v \overline{e_k} \mathrm{d}t$ with ![]() $e_k(t) := \mathrm{e}^{\mathrm{i} k \omega t}$,
$e_k(t) := \mathrm{e}^{\mathrm{i} k \omega t}$,  $\omega := \frac{2 \pi}{T}$. Thus the inverse is
$\omega := \frac{2 \pi}{T}$. Thus the inverse is ![]() $v(t) = \mathcal{F}^{-1}_t[\hat v_k] = \sum_{k \in \mathbb{Z}} \hat v_k e_k(t)$. For a function v depending on space and T-periodically on time,
$v(t) = \mathcal{F}^{-1}_t[\hat v_k] = \sum_{k \in \mathbb{Z}} \hat v_k e_k(t)$. For a function v depending on space and T-periodically on time, ![]() $\hat v$ will always denote the (discrete) Fourier transform in time. In the same way we define the discrete Fourier transform in time
$\hat v$ will always denote the (discrete) Fourier transform in time. In the same way we define the discrete Fourier transform in time ![]() $\hat\lambda$ of a measure
$\hat\lambda$ of a measure ![]() $\lambda\in \mathcal{M}(\mathbb{T})$. Finally, a function
$\lambda\in \mathcal{M}(\mathbb{T})$. Finally, a function ![]() $v:\mathbb{T}\to\mathbb{R}$ or a measure
$v:\mathbb{T}\to\mathbb{R}$ or a measure ![]() $\lambda\in\mathcal{M}(\mathbb{T})$ is called positive semidefinite if the sequence
$\lambda\in\mathcal{M}(\mathbb{T})$ is called positive semidefinite if the sequence ![]() $\hat v=(\hat v_k)_{k\in\mathbb{Z}}$ or
$\hat v=(\hat v_k)_{k\in\mathbb{Z}}$ or ![]() $\hat\lambda=(\hat \lambda_k)_{k\in\mathbb{Z}}$, respectively, consists of nonnegative entries.
$\hat\lambda=(\hat \lambda_k)_{k\in\mathbb{Z}}$, respectively, consists of nonnegative entries.
Similarly we fix the notion of the spatial (continuous) Fourier transform of a space-dependent function ![]() $v \colon \mathbb{R}^d \to \mathbb{C}$, writing
$v \colon \mathbb{R}^d \to \mathbb{C}$, writing  $\mathcal{F}_\xi[v] = \int_{\mathbb{R}^d} v(x) \overline{\mathrm{e}^{\mathrm{i} x \cdot \xi}} \frac{\mathrm{d} x}{(2 \pi)^{{d}/{2}}}$ with inverse
$\mathcal{F}_\xi[v] = \int_{\mathbb{R}^d} v(x) \overline{\mathrm{e}^{\mathrm{i} x \cdot \xi}} \frac{\mathrm{d} x}{(2 \pi)^{{d}/{2}}}$ with inverse  $\mathcal{F}^{-1}_x[v] = \int_{\mathbb{R}^d} v(\xi) \mathrm{e}^{\mathrm{i} x \cdot \xi} \frac{\mathrm{d} \xi}{(2 \pi)^{{d}/{2}}}$
. The spatial (continuous) Fourier transform of a function depending on both space and time is defined analogously, and we omit indices of
$\mathcal{F}^{-1}_x[v] = \int_{\mathbb{R}^d} v(\xi) \mathrm{e}^{\mathrm{i} x \cdot \xi} \frac{\mathrm{d} \xi}{(2 \pi)^{{d}/{2}}}$
. The spatial (continuous) Fourier transform of a function depending on both space and time is defined analogously, and we omit indices of ![]() $\mathcal{F}, \mathcal{F}^{-1}$ when they are clear from the context.
$\mathcal{F}, \mathcal{F}^{-1}$ when they are clear from the context.
1.2.4. Cylindrical and slab geometry
We say that a map ![]() $A:\mathbb{R}^3\to Y$ possesses cylindrical symmetry if
$A:\mathbb{R}^3\to Y$ possesses cylindrical symmetry if ![]() $A(\mathbf{x})=A(\tilde{\mathbf{x}})$ for all
$A(\mathbf{x})=A(\tilde{\mathbf{x}})$ for all ![]() $\mathbf{x}=(x,y,z), \tilde{\mathbf{x}}=(\tilde x,\tilde y,\tilde z)\in\mathbb{R}^3$ with
$\mathbf{x}=(x,y,z), \tilde{\mathbf{x}}=(\tilde x,\tilde y,\tilde z)\in\mathbb{R}^3$ with ![]() $x^2+y^2={\tilde x}^2+{\tilde y}^2$. In this case we write
$x^2+y^2={\tilde x}^2+{\tilde y}^2$. In this case we write ![]() $A(\mathbf{x})=A(r)$ with
$A(\mathbf{x})=A(r)$ with  $r=\sqrt{x^2+y^2}$. Likewise we say that a map
$r=\sqrt{x^2+y^2}$. Likewise we say that a map ![]() $A:\mathbb{R}^3\to Y$ possesses slab symmetry if
$A:\mathbb{R}^3\to Y$ possesses slab symmetry if ![]() $A(\mathbf{x})=A(\tilde{\mathbf{x}})$ for all
$A(\mathbf{x})=A(\tilde{\mathbf{x}})$ for all ![]() $\mathbf{x}=(x,y,z), \tilde{\mathbf{x}}=(x,\tilde y,\tilde z)\in\mathbb{R}^3$ and write
$\mathbf{x}=(x,y,z), \tilde{\mathbf{x}}=(x,\tilde y,\tilde z)\in\mathbb{R}^3$ and write ![]() $A(\mathbf{x}) = A(x)$ in this case.
$A(\mathbf{x}) = A(x)$ in this case.
Having clarified our notation, we now present the main theorem of this paper.
Theorem 1.3 Let T > 0 denote the temporal period,  $\omega := \frac{2 \pi}{T}$ the associated frequency, and
$\omega := \frac{2 \pi}{T}$ the associated frequency, and ![]() $c \in (0, 1)$ the speed of travel of the breather solution. We make the following assumptions:
$c \in (0, 1)$ the speed of travel of the breather solution. We make the following assumptions:
(A1) The linear susceptibility tensor
 $\chi^{(1)}$ is given by
$\chi^{(1)}$ is given by  $\chi^{(1)}(\mathbf{x}, \tau)\mathrm{d}\tau = \mathrm{d}G(\mathbf{x})(\tau) I$ where
$\chi^{(1)}(\mathbf{x}, \tau)\mathrm{d}\tau = \mathrm{d}G(\mathbf{x})(\tau) I$ where  $G\colon \mathbb{R}^3 \to \mathcal{M}(\mathbb{R})$ is measurable. The nonlinear susceptibility tensor
$G\colon \mathbb{R}^3 \to \mathcal{M}(\mathbb{R})$ is measurable. The nonlinear susceptibility tensor  $\chi^{(3)}$ is given by (6.i) or (6.ii) where
$\chi^{(3)}$ is given by (6.i) or (6.ii) where  $h\in L^\infty(\mathbb{R}^3)$ and
$h\in L^\infty(\mathbb{R}^3)$ and  $\nu\in \mathcal{M}(\mathbb{R})$.
$\nu\in \mathcal{M}(\mathbb{R})$.(A2)
 $G$ and
$G$ and  $h$ both have either cylindrical or slab geometry.
$h$ both have either cylindrical or slab geometry.(A3)
 $\sup_{\mathbf{x} \in \mathbb{R}^3} \left\lVert G(\mathbf{x}) \right\rVert_{\mathcal{M}(\mathbb{R})} \lt \infty$ and
$\sup_{\mathbf{x} \in \mathbb{R}^3} \left\lVert G(\mathbf{x}) \right\rVert_{\mathcal{M}(\mathbb{R})} \lt \infty$ and  $h \not \leq 0$.
$h \not \leq 0$.(A4) The periodic reduction
 $\mathcal{G}(\mathbf{x})$ of
$\mathcal{G}(\mathbf{x})$ of  $G(\mathbf{x})$ is even in time for all
$G(\mathbf{x})$ is even in time for all  $\mathbf{x}\in \mathbb{R}^3$ and satisfies
$\mathbf{x}\in \mathbb{R}^3$ and satisfies  $\sup_{\substack{\mathbf{x} \in \mathbb{R}^3, k \in \mathbb{Z}}} \mathcal{F}_k[\mathcal{G}(\mathbf{x})] \lt \tfrac{1}{c^2} - 1$.
$\sup_{\substack{\mathbf{x} \in \mathbb{R}^3, k \in \mathbb{Z}}} \mathcal{F}_k[\mathcal{G}(\mathbf{x})] \lt \tfrac{1}{c^2} - 1$.(A5) The periodic reduction
 $\mathcal{N}$ of ν is even in time,
$\mathcal{N}$ of ν is even in time,  $\not =0$, and
$\not =0$, and  $\left\lvert k \right\rvert^{-\beta} \lesssim \mathcal{F}_k[\mathcal{N}] \lesssim \left\lvert k \right\rvert^{-\alpha}$ for all
$\left\lvert k \right\rvert^{-\beta} \lesssim \mathcal{F}_k[\mathcal{N}] \lesssim \left\lvert k \right\rvert^{-\alpha}$ for all  $k \in \mathbb{Z}\setminus\{0\}$ with
$k \in \mathbb{Z}\setminus\{0\}$ with  $\mathcal{F}_k[\mathcal{N}] \not =0$ and some
$\mathcal{F}_k[\mathcal{N}] \not =0$ and some  $\beta \geq \alpha \gt \alpha^\star$ where
$\beta \geq \alpha \gt \alpha^\star$ where  $\alpha^\star = 1$ in the slab geometry and
$\alpha^\star = 1$ in the slab geometry and  $\alpha^\star = \tfrac{3}{2}$ in the cylindrical geometry.
$\alpha^\star = \tfrac{3}{2}$ in the cylindrical geometry.(A6) In case of the slab geometry, one of the following holds in addition:
(A6a)
 $h(x) \to 0$ as
$h(x) \to 0$ as  $x \to \pm\infty$,
$x \to \pm\infty$,(A6b)
 $\mathcal{G}(x) = \mathcal{G}^\mathrm{per}(x) + \mathcal{G}^\mathrm{loc}(x)$ and
$\mathcal{G}(x) = \mathcal{G}^\mathrm{per}(x) + \mathcal{G}^\mathrm{loc}(x)$ and  $h(x) = h^\mathrm{per}(x) + h^\mathrm{loc}(x)$ where
$h(x) = h^\mathrm{per}(x) + h^\mathrm{loc}(x)$ where  $\mathcal{G}^\mathrm{per}(x), h(x)$ are periodic with common period, and we have
$\mathcal{G}^\mathrm{per}(x), h(x)$ are periodic with common period, and we have  $\left\lVert \mathcal{G}^\mathrm{loc}(x) \right\rVert_{\mathcal{M}(\mathbb{T})} \to 0$ and
$\left\lVert \mathcal{G}^\mathrm{loc}(x) \right\rVert_{\mathcal{M}(\mathbb{T})} \to 0$ and  $h^\mathrm{loc}(x) \to 0$ as
$h^\mathrm{loc}(x) \to 0$ as  $x \to \pm \infty$. Moreover,
$x \to \pm \infty$. Moreover,  $\mathcal{G}^\mathrm{loc}(x)$ is positive semidefinite for all
$\mathcal{G}^\mathrm{loc}(x)$ is positive semidefinite for all  $x \in \mathbb{R}$ and
$x \in \mathbb{R}$ and  $h^\mathrm{loc} \geq 0, h^\mathrm{per} \not\leq 0$ hold.
$h^\mathrm{loc} \geq 0, h^\mathrm{per} \not\leq 0$ hold.
Under these assumptions, there exists a nontrivial breather solution ![]() $\mathbf{D}, \mathbf{E}, \mathbf{B}, \mathbf{H}$ of Maxwell’s equations (1), (2). It satisfies
$\mathbf{D}, \mathbf{E}, \mathbf{B}, \mathbf{H}$ of Maxwell’s equations (1), (2). It satisfies
for all ![]() $n \in \mathbb{N}_0$,
$n \in \mathbb{N}_0$, ![]() $p \in [2, \infty]$ and all domains Ω that are of the form
$p \in [2, \infty]$ and all domains Ω that are of the form ![]() $\Omega = \mathbb{R} \times [y, y+1] \times [z, z+1] \times [t, t+1]$ in the slab case and
$\Omega = \mathbb{R} \times [y, y+1] \times [z, z+1] \times [t, t+1]$ in the slab case and ![]() $\Omega = \mathbb{R}^2 \times [z, z+1] \times [t, t+1]$ in the cylindrical case, with norm bounds independent of
$\Omega = \mathbb{R}^2 \times [z, z+1] \times [t, t+1]$ in the cylindrical case, with norm bounds independent of ![]() $y, z, t$.
$y, z, t$.
Remark 1.4. Let us comment on the assumptions (A1)–(A5) on the structure of the linear and nonlinear retardation kernels. They can be seen as a systematic attempt to find out what can be done in a variational setting. The main assumptions are expressed via the Fourier coefficients of ![]() $\mathcal{G}(\mathbf{x})$ and
$\mathcal{G}(\mathbf{x})$ and ![]() $\mathcal{N}$.
$\mathcal{N}$.
(a) The fact that both
 $\mathcal{G}(\mathbf{x})$ and
$\mathcal{G}(\mathbf{x})$ and  $\mathcal{N}$ have real Fourier coefficients stems from their evenness in time. This in turn implies that the operators
$\mathcal{N}$ have real Fourier coefficients stems from their evenness in time. This in turn implies that the operators  $\nu\ast$ and
$\nu\ast$ and  $\chi^{(1)}\ast$ are symmetric on time-periodic functions of period T which is necessary for the variational formulation of (10). Another way to interpret this fact is that along T-periodic solutions, Maxwell’s equations are invariant under time-inversion.
$\chi^{(1)}\ast$ are symmetric on time-periodic functions of period T which is necessary for the variational formulation of (10). Another way to interpret this fact is that along T-periodic solutions, Maxwell’s equations are invariant under time-inversion.(b) Assumption (A5) is on the smoothness of the nonlinear convolution kernel
 $\mathcal{N}$, which should be approximately between α- and β-times differentiable.
$\mathcal{N}$, which should be approximately between α- and β-times differentiable.(c) In assumption (A4) the upper bound on
 $\mathcal{F}_k[\mathcal{G}(\mathbf{x})]$ is effectively a smallness condition on the propagation speed c. It is exactly this assumption which makes the linear operator in (10) elliptic, and combined with positive definiteness of
$\mathcal{F}_k[\mathcal{G}(\mathbf{x})]$ is effectively a smallness condition on the propagation speed c. It is exactly this assumption which makes the linear operator in (10) elliptic, and combined with positive definiteness of  $\mathcal{N}$ it makes the quadratic part in (11) positive definite.
$\mathcal{N}$ it makes the quadratic part in (11) positive definite.(d) The condition
 $h \not \leq 0$ is necessary for breathers to exist with small speeds. Indeed, for
$h \not \leq 0$ is necessary for breathers to exist with small speeds. Indeed, for  $h \leq 0$ problem (10) only has the zero solution since both terms are negative.
$h \leq 0$ problem (10) only has the zero solution since both terms are negative.(e) The propagation speed c has been chosen between 0 and 1, so that the breather does not propagate faster than the speed of light. A choice
 $c\geq 1$ would be mathematically possible – but at the expense of the linear refractive indices
$c\geq 1$ would be mathematically possible – but at the expense of the linear refractive indices  $\mathcal{F}_k[\mathcal{G}]$, which must be negative everywhere.
$\mathcal{F}_k[\mathcal{G}]$, which must be negative everywhere.
Remark 1.5. If in the setting of Theorem 1.3 the set ![]() $\mathfrak{R} := \left\{ k \in \mathbb{Z}\setminus\left\{ 0 \right\} \colon \mathcal{F}_k[\mathcal{N}] \neq 0 \right\}$ is infinite then we moreover have existence of infinitely many nontrivial breathers with the stated properties.
$\mathfrak{R} := \left\{ k \in \mathbb{Z}\setminus\left\{ 0 \right\} \colon \mathcal{F}_k[\mathcal{N}] \neq 0 \right\}$ is infinite then we moreover have existence of infinitely many nontrivial breathers with the stated properties.
Remark 1.6. The sign assumptions on ![]() $\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}$ in (A6b) of Theorem 1.3 yield a strict relation between the mountain-pass energy level of the problem compared to the energy of the “periodic” problem, (i.e. with
$\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}$ in (A6b) of Theorem 1.3 yield a strict relation between the mountain-pass energy level of the problem compared to the energy of the “periodic” problem, (i.e. with ![]() $\mathcal{G}, h$ replaced by
$\mathcal{G}, h$ replaced by ![]() $\mathcal{G}^\mathrm{per}, h^\mathrm{per}$), see Lemma 3.7 for a precise formulation. This energy inequality gives us some compactness which is crucial for showing existence of breathers. For (A6a) the decay of the intensity h of the nonlinearity again generates some compactness.
$\mathcal{G}^\mathrm{per}, h^\mathrm{per}$), see Lemma 3.7 for a precise formulation. This energy inequality gives us some compactness which is crucial for showing existence of breathers. For (A6a) the decay of the intensity h of the nonlinearity again generates some compactness.
The exemplary Theorems 1.1 and 1.2 satisfy (A1)–(A6). For (A5) this is true because
 \begin{align*}
\mathcal{F}_k[\mathcal{N}] = \mathcal{F}_k[2 - \left\lvert \sin(\omega t) \right\rvert] = \begin{cases}
2 - \frac{2}{\pi}, & k = 0,
\\ 0, & k\,\text{odd},
\\ \frac{2}{\pi (k^2 - 1)}, & k \neq 0\,\text{even}.
\end{cases}
\end{align*}
\begin{align*}
\mathcal{F}_k[\mathcal{N}] = \mathcal{F}_k[2 - \left\lvert \sin(\omega t) \right\rvert] = \begin{cases}
2 - \frac{2}{\pi}, & k = 0,
\\ 0, & k\,\text{odd},
\\ \frac{2}{\pi (k^2 - 1)}, & k \neq 0\,\text{even}.
\end{cases}
\end{align*} Breather solutions are more regular when the material coefficients ![]() $\mathcal{G}, h$ have higher regularity. For
$\mathcal{G}, h$ have higher regularity. For ![]() $\Omega \subseteq \mathbb{R}^4$ we denote by
$\Omega \subseteq \mathbb{R}^4$ we denote by  $C_b^j(\Omega; \mathbb{R}^3)$ the space of j-times differentiable functions mapping into
$C_b^j(\Omega; \mathbb{R}^3)$ the space of j-times differentiable functions mapping into ![]() $\mathbb{R}^3$ with bounded derivatives, and abbreviate
$\mathbb{R}^3$ with bounded derivatives, and abbreviate  $\tilde C^j_b(\Omega; \mathbb{R}^3) := W^{j, 2}(\Omega; \mathbb{R}^3) \cap C^j_b(\Omega; \mathbb{R}^3)$.
$\tilde C^j_b(\Omega; \mathbb{R}^3) := W^{j, 2}(\Omega; \mathbb{R}^3) \cap C^j_b(\Omega; \mathbb{R}^3)$.
Corollary 1.7. If in the context of Theorem 1.3 we additionally have
(R)
 $g \in C_b^l(\mathbb{R}^3; \mathcal{M}(\mathbb{R})), h \in C_b^l(\mathbb{R}^3)$ for some
$g \in C_b^l(\mathbb{R}^3; \mathcal{M}(\mathbb{R})), h \in C_b^l(\mathbb{R}^3)$ for some  $l \in \mathbb{N}_0$,
$l \in \mathbb{N}_0$,
then the regularity improves to
 \begin{align*}
\partial_t^n \mathbf{E} \in \tilde C_b^{2+l}(\Omega; \mathbb{R}^3),
\quad
\partial_t^n \mathbf{B}, \partial_t^n \mathbf{H} \in \tilde C_b^{1+l}(\Omega; \mathbb{R}^3),
\quad
\partial_t^n \mathbf{D} \in \tilde C_b^{l}(\Omega; \mathbb{R}^3)
\end{align*}
\begin{align*}
\partial_t^n \mathbf{E} \in \tilde C_b^{2+l}(\Omega; \mathbb{R}^3),
\quad
\partial_t^n \mathbf{B}, \partial_t^n \mathbf{H} \in \tilde C_b^{1+l}(\Omega; \mathbb{R}^3),
\quad
\partial_t^n \mathbf{D} \in \tilde C_b^{l}(\Omega; \mathbb{R}^3)
\end{align*} with norm bounds independent of ![]() $y, z, t$.
$y, z, t$.
1.3. Outline of paper
We begin by investigating the slab geometry (5.1). In Section 2 we convert Maxwell’s equations into the Euler-Lagrange equation of a suitable Lagrangian functional, and show that this functional has mountain-pass geometry. Using the mountain-pass theorem, in Section 3 we show that the Euler-Lagrange equation admits a ground state solution. The convergence of Palais-Smale sequences approaching the ground state level is unclear in general because the spatial domain is unbounded, and thus our arguments depend on the particular form of the potentials in (A6). For (A6a), the nonlinearity is compact which makes this the easiest case. For (A6b) we first rely on translation arguments in space for the purely periodic case. Then we use comparison arguments for the perturbed periodic case. After having shown existence and multiplicity of breathers, we investigate their regularity in Section 4. Finally, Section 5 details the arguments for the cylindrical geometry (5.2) and highlights the differences to the slab geometry.
2. Variational problem
From now on, we always assume that the assumptions of Theorem 1.3 are satisfied. We transform (8.1) into a problem for a surrogate variable u, which we then treat using the mountain pass method. We only consider the slab problem (8.1) as the cylindrical problem (8.2) can be treated similarly. In Section 5 we discuss the differences between the slab and the cylindrical problem, and how to treat the latter.
Using the periodic reduction ![]() $\mathcal{G}(x), \mathcal{N}$ of
$\mathcal{G}(x), \mathcal{N}$ of ![]() $g(x), \nu$ we can rewrite the scalar polarization (9.i) as
$g(x), \nu$ we can rewrite the scalar polarization (9.i) as
 \begin{align*}
P(w)(x,t)
&= \epsilon_0 \int_0^\infty w(x, t - \tau) \mathrm{d}g(x)(\tau)
+ \epsilon_0 h(x) \int_0^\infty w(x, t - \tau)^3 \mathrm{d}\nu(\tau)
\\ &= \epsilon_0 \int_\mathbb{T} w(x, t - \tau) \mathrm{d}\mathcal{G}(x)(\tau)
+ \epsilon_0 h(x) \int_\mathbb{T} w(x, t - \tau)^3 \mathrm{d}\mathcal{N}(\tau)
\end{align*}
\begin{align*}
P(w)(x,t)
&= \epsilon_0 \int_0^\infty w(x, t - \tau) \mathrm{d}g(x)(\tau)
+ \epsilon_0 h(x) \int_0^\infty w(x, t - \tau)^3 \mathrm{d}\nu(\tau)
\\ &= \epsilon_0 \int_\mathbb{T} w(x, t - \tau) \mathrm{d}\mathcal{G}(x)(\tau)
+ \epsilon_0 h(x) \int_\mathbb{T} w(x, t - \tau)^3 \mathrm{d}\mathcal{N}(\tau)
\end{align*}since w is T-periodic in t. We abbreviate this by writing
where ![]() $\ast$ denotes convolution of a measure with a function on
$\ast$ denotes convolution of a measure with a function on ![]() $\mathbb{T}$. Similarly, the polarization (9.ii) can be written in the form
$\mathbb{T}$. Similarly, the polarization (9.ii) can be written in the form
Next we define the projection ![]() $P_\mathfrak{R}$ onto the set
$P_\mathfrak{R}$ onto the set ![]() $\mathfrak{R}:= \left\{ k \in \mathbb{Z}\setminus\left\{ 0 \right\} \colon \mathcal{F}_k[\mathcal{N}] \neq 0 \right\}$ of “regular” frequency indices by
$\mathfrak{R}:= \left\{ k \in \mathbb{Z}\setminus\left\{ 0 \right\} \colon \mathcal{F}_k[\mathcal{N}] \neq 0 \right\}$ of “regular” frequency indices by
 \begin{align*}
P_\mathfrak{R}[v] = \mathcal{F}^{-1}\bigl[\mathbb{1}_{k \in \mathfrak{R}} \mathcal{F}_k[v]\bigr],
\end{align*}
\begin{align*}
P_\mathfrak{R}[v] = \mathcal{F}^{-1}\bigl[\mathbb{1}_{k \in \mathfrak{R}} \mathcal{F}_k[v]\bigr],
\end{align*} as well as the projection onto the “singular” frequency indices ![]() $\mathfrak{S} := \mathbb{Z} \setminus \mathfrak{R}$ by
$\mathfrak{S} := \mathbb{Z} \setminus \mathfrak{R}$ by  $P_\mathfrak{S}[v] := \mathcal{F}^{-1}\bigl[\mathbb{1}_{k \in \mathfrak{S}} \mathcal{F}_k[v]\bigr] = (I - P_\mathfrak{R})[v]$. Note that
$P_\mathfrak{S}[v] := \mathcal{F}^{-1}\bigl[\mathbb{1}_{k \in \mathfrak{S}} \mathcal{F}_k[v]\bigr] = (I - P_\mathfrak{R})[v]$. Note that ![]() $\partial_t, \mathcal{G} \ast, P_\mathfrak{R}$, and
$\partial_t, \mathcal{G} \ast, P_\mathfrak{R}$, and ![]() $P_\mathfrak{S}$ mutually commute since they all act on t as Fourier multipliers. We apply both to (8.1) for time-periodic w to obtain the two problems
$P_\mathfrak{S}$ mutually commute since they all act on t as Fourier multipliers. We apply both to (8.1) for time-periodic w to obtain the two problems
 \begin{align*}
&\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)P_\mathfrak{R}[w]
+ h \partial_t^2 P_\mathfrak{R}[N(w)] = 0,
\\ &\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)P_\mathfrak{S}[w]
+ h \partial_t^2 P_\mathfrak{S}[N(w)] = 0,
\end{align*}
\begin{align*}
&\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)P_\mathfrak{R}[w]
+ h \partial_t^2 P_\mathfrak{R}[N(w)] = 0,
\\ &\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)P_\mathfrak{S}[w]
+ h \partial_t^2 P_\mathfrak{S}[N(w)] = 0,
\end{align*}where the cubic nonlinearity N(w) is given by
corresponding to (6.i) and (6.ii), respectively.
Let us first consider the nonlinearity ![]() $N(w) = \mathcal{N} \ast w^3$. Using
$N(w) = \mathcal{N} \ast w^3$. Using ![]() $P_\mathfrak{S} (\mathcal{N}\ast) = 0$ and that the linear operator
$P_\mathfrak{S} (\mathcal{N}\ast) = 0$ and that the linear operator  $\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)$ is injectiveFootnote 2, we can further simplify this to
$\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)$ is injectiveFootnote 2, we can further simplify this to
 \begin{align*}
\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right) w
+ h \partial_t^2 (\mathcal{N} \ast w^3) = 0,
\qquad
P_\mathfrak{S}[w] = 0.
\end{align*}
\begin{align*}
\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right) w
+ h \partial_t^2 (\mathcal{N} \ast w^3) = 0,
\qquad
P_\mathfrak{S}[w] = 0.
\end{align*} Observe that the convolution operator ![]() $\mathcal{N}\ast$ is formally invertible on
$\mathcal{N}\ast$ is formally invertible on ![]() $\ker P_\mathfrak{S}$ since
$\ker P_\mathfrak{S}$ since ![]() $\mathcal{F}_k[\mathcal{N}] \neq 0$ for
$\mathcal{F}_k[\mathcal{N}] \neq 0$ for ![]() $k \in \mathfrak{R}$. Therefore we may rephrase this problem as
$k \in \mathfrak{R}$. Therefore we may rephrase this problem as
 \begin{align}
(- \partial_t^2 \mathcal{N}\ast)^{-1}\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right) u
- h P_\mathfrak{R}[u^3] = 0,
\qquad
P_\mathfrak{S}[u] = 0
\end{align}
\begin{align}
(- \partial_t^2 \mathcal{N}\ast)^{-1}\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right) u
- h P_\mathfrak{R}[u^3] = 0,
\qquad
P_\mathfrak{S}[u] = 0
\end{align} with ![]() $u := w$.
$u := w$.
For the second nonlinearity ![]() $N(w) = (\mathcal{N} \ast w)^3$ we set
$N(w) = (\mathcal{N} \ast w)^3$ we set ![]() $u := \mathcal{N} \ast w$ and therefore get
$u := \mathcal{N} \ast w$ and therefore get
 \begin{align}
\begin{aligned}
&(-\partial_t^2 \mathcal{N}\ast)^{-1} \left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)u
- h P_\mathfrak{R}[u^3] = 0,
\qquad P_\mathfrak{S}[u] = 0,\\
&\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)P_\mathfrak{S}[w]
+ h \partial_t^2 P_\mathfrak{S}[u^3] = 0.
\end{aligned}
\end{align}
\begin{align}
\begin{aligned}
&(-\partial_t^2 \mathcal{N}\ast)^{-1} \left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)u
- h P_\mathfrak{R}[u^3] = 0,
\qquad P_\mathfrak{S}[u] = 0,\\
&\left( - \partial_x^2 + \partial_t^2 (1 - \tfrac{1}{c^2} + \mathcal{G}\ast) \right)P_\mathfrak{S}[w]
+ h \partial_t^2 P_\mathfrak{S}[u^3] = 0.
\end{aligned}
\end{align} Note that the first of the two equations above is (14). Hence, also for the second nonlinearity, it is sufficient to solve (14) for u and then use the second equation to determine the missing values of ![]() $\mathcal{F}_k[w]$ for
$\mathcal{F}_k[w]$ for ![]() $k\in\mathfrak{S}$.
$k\in\mathfrak{S}$.
We first focus our attention on investigating the “effective problem” (14), which using
 \begin{align*}
V(x) := \tfrac{1}{c^2} - 1 - \mathcal{G}\ast
\end{align*}
\begin{align*}
V(x) := \tfrac{1}{c^2} - 1 - \mathcal{G}\ast
\end{align*}we can write as
 \begin{align}
(- \partial_t^2 \mathcal{N}\ast)^{-1}\left( - \partial_x^2 - V(x)\partial_t^2 \right) u - h P_\mathfrak{R}[u^3] = 0,
\qquad P_\mathfrak{S}[u] = 0.
\end{align}
\begin{align}
(- \partial_t^2 \mathcal{N}\ast)^{-1}\left( - \partial_x^2 - V(x)\partial_t^2 \right) u - h P_\mathfrak{R}[u^3] = 0,
\qquad P_\mathfrak{S}[u] = 0.
\end{align} Since ![]() $\mathcal{G}, \mathcal{N}$ are even in time, the differential operator above is symmetric, and therefore solutions of (16) formally are critical points of the functional
$\mathcal{G}, \mathcal{N}$ are even in time, the differential operator above is symmetric, and therefore solutions of (16) formally are critical points of the functional
 \begin{align*}
J(u) = \int_{\mathbb{R} \times \mathbb{T}} \left(\tfrac12 u \cdot (- \partial_t^2 \mathcal{N}\ast)^{-1}\left( - \partial_x^2 - V(x)\partial_t^2 \right) u - \tfrac14 h(x) u^4 \right) \mathrm{d}(x, t),
\qquad P_\mathfrak{S}[u] = 0.
\end{align*}
\begin{align*}
J(u) = \int_{\mathbb{R} \times \mathbb{T}} \left(\tfrac12 u \cdot (- \partial_t^2 \mathcal{N}\ast)^{-1}\left( - \partial_x^2 - V(x)\partial_t^2 \right) u - \tfrac14 h(x) u^4 \right) \mathrm{d}(x, t),
\qquad P_\mathfrak{S}[u] = 0.
\end{align*} Next we properly define the domain H of the functional J sketched above, and we investigate embeddings ![]() $H \hookrightarrow L^p$.
$H \hookrightarrow L^p$.
Definition 2.1. We define the space
 \begin{align*}
H := \left\{ u \in L^2(\mathbb{R} \times \mathbb{T}) \colon \hat u_k \equiv 0\ \text{for } k \in \mathbb{Z} \setminus \mathfrak{R}, \left\lVert u \right\rVert_H^2 := \langle\!\langle u , u \rangle\!\rangle_{H} \lt \infty \right\}
\end{align*}
\begin{align*}
H := \left\{ u \in L^2(\mathbb{R} \times \mathbb{T}) \colon \hat u_k \equiv 0\ \text{for } k \in \mathbb{Z} \setminus \mathfrak{R}, \left\lVert u \right\rVert_H^2 := \langle\!\langle u , u \rangle\!\rangle_{H} \lt \infty \right\}
\end{align*}where
 \begin{align*}
\langle\!\langle u , v \rangle\!\rangle_H = \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}
\int_\mathbb{R} \left(\hat u_k' \overline{\hat v_k'} + \omega^2 k^2 \hat u_k \overline{\hat v_k} \right) \mathrm{d}x.
\end{align*}
\begin{align*}
\langle\!\langle u , v \rangle\!\rangle_H = \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}
\int_\mathbb{R} \left(\hat u_k' \overline{\hat v_k'} + \omega^2 k^2 \hat u_k \overline{\hat v_k} \right) \mathrm{d}x.
\end{align*} Note that  $V_k(x) := \tfrac{1}{c^2} - 1 - \mathcal{F}_k[\mathcal{G}(x)]$ is bounded and strictly positive by assumption (A4), so that
$V_k(x) := \tfrac{1}{c^2} - 1 - \mathcal{F}_k[\mathcal{G}(x)]$ is bounded and strictly positive by assumption (A4), so that
 \begin{align*}
\left\langle u , v \right\rangle_H := \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_\mathbb{R} \bigl(\hat u_k' \overline{\hat v_k'} + \omega^2 k^2 V_k(x) \hat u_k \overline{\hat v_k}\bigr) \mathrm{d}x
\end{align*}
\begin{align*}
\left\langle u , v \right\rangle_H := \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_\mathbb{R} \bigl(\hat u_k' \overline{\hat v_k'} + \omega^2 k^2 V_k(x) \hat u_k \overline{\hat v_k}\bigr) \mathrm{d}x
\end{align*}defines an equivalent inner product on H.
Assumption (A5) on the decay of the Fourier coefficients of ![]() $\mathcal{N}$ ensures that H continuously embeds into
$\mathcal{N}$ ensures that H continuously embeds into ![]() $L^p(\mathbb{R} \times \mathbb{T})$ for all
$L^p(\mathbb{R} \times \mathbb{T})$ for all ![]() $p \in [2, p^\star)$ where
$p \in [2, p^\star)$ where ![]() $p^\star \gt 4$, as we show below in Lemma 2.4. Boundedness of
$p^\star \gt 4$, as we show below in Lemma 2.4. Boundedness of ![]() $H\hookrightarrow L^2(\mathbb{R}\times\mathbb{T})$ helps to show that H is a Hilbert space. Indeed, if
$H\hookrightarrow L^2(\mathbb{R}\times\mathbb{T})$ helps to show that H is a Hilbert space. Indeed, if ![]() $(u^{(n)})$ is a Cauchy sequence in H, then from the embedding we have
$(u^{(n)})$ is a Cauchy sequence in H, then from the embedding we have ![]() $u^{(n)} \to u$ in
$u^{(n)} \to u$ in ![]() $L^2(\mathbb{R}\times\mathbb{T})$ and from the definition of H also
$L^2(\mathbb{R}\times\mathbb{T})$ and from the definition of H also ![]() $\mathcal{F}_k[u^{(n)}] \to v_k$ in
$\mathcal{F}_k[u^{(n)}] \to v_k$ in ![]() $H^1(\mathbb{R})$ for some
$H^1(\mathbb{R})$ for some ![]() $v_k \in H^1(\mathbb{R})$ and each
$v_k \in H^1(\mathbb{R})$ and each ![]() $k \in \mathfrak{R}$. Then
$k \in \mathfrak{R}$. Then ![]() $v_k = \hat u_k$ holds from which one finds
$v_k = \hat u_k$ holds from which one finds ![]() $u \in H$ and
$u \in H$ and ![]() $u^{(n)} \to u$ as
$u^{(n)} \to u$ as ![]() $n \to \infty$.
$n \to \infty$.
The Hilbert space H allows us to write
 \begin{align*}
J(u) = \tfrac12 \left\langle u , u \right\rangle_H - \tfrac14 \int_{\mathbb{R} \times \mathbb{T}} h(x) u^4 \mathrm{d}(x,t)
\quad\text{for}\quad
u \in H,
\end{align*}
\begin{align*}
J(u) = \tfrac12 \left\langle u , u \right\rangle_H - \tfrac14 \int_{\mathbb{R} \times \mathbb{T}} h(x) u^4 \mathrm{d}(x,t)
\quad\text{for}\quad
u \in H,
\end{align*} and to define solutions ![]() $u \in H$ of (14) in the following way.
$u \in H$ of (14) in the following way.
Definition 2.2. weak solution
A function ![]() $u \colon \mathbb{R} \times \mathbb{T} \to \mathbb{R}$ is called a weak solution to (14) if
$u \colon \mathbb{R} \times \mathbb{T} \to \mathbb{R}$ is called a weak solution to (14) if ![]() $u \in H$ and
$u \in H$ and
 \begin{align*}
\left\langle u , v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u^3 v \mathrm{d}(x,t) = 0
\end{align*}
\begin{align*}
\left\langle u , v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u^3 v \mathrm{d}(x,t) = 0
\end{align*} for all ![]() $v \in H$. This is equivalent to
$v \in H$. This is equivalent to ![]() $J'(u) = 0$.
$J'(u) = 0$.
It is standard to verify the validity of the following density result for H, which will prove very useful for some approximation arguments.
Lemma 2.3. The set  $\left\{ u \in C_c^\infty(\mathbb{R} \times \mathbb{T}) \colon \hat u_k \equiv 0\ \ \text{for almost all }\ k \in \mathbb{Z} \right\} \cap H$ is dense in
$\left\{ u \in C_c^\infty(\mathbb{R} \times \mathbb{T}) \colon \hat u_k \equiv 0\ \ \text{for almost all }\ k \in \mathbb{Z} \right\} \cap H$ is dense in ![]() $H$.
$H$.
Lemma 2.4. For any ![]() $p \in [2, p^\star)$ with
$p \in [2, p^\star)$ with  $p^\star := \frac{4}{2 - \alpha}$ (
$p^\star := \frac{4}{2 - \alpha}$ (![]() $p^\star = \infty$ if
$p^\star = \infty$ if ![]() $\alpha \geq 2$) and α > 1 from (A5), the embedding
$\alpha \geq 2$) and α > 1 from (A5), the embedding ![]() $H \hookrightarrow L^p(\mathbb{R} \times \mathbb{T})$ is continuous and the embedding
$H \hookrightarrow L^p(\mathbb{R} \times \mathbb{T})$ is continuous and the embedding  $H \hookrightarrow L^p_\mathrm{loc}(\mathbb{R} \times \mathbb{T})$ is compact.
$H \hookrightarrow L^p_\mathrm{loc}(\mathbb{R} \times \mathbb{T})$ is compact.
Proof. Let us first show continuity. For this, we calculate
 \begin{align*}
\left\lVert u \right\rVert_p
\lesssim \left\lVert \mathcal{F}_{\xi, k}[u] \right\rVert_{L^{p'}(\mathbb{R} \times \mathfrak{R})}
\lesssim \left\lVert \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\xi^2 + \omega^2 k^2}} \right\rVert_{L^r(\mathbb{R} \times \mathfrak{R})}
\cdot \left\lVert \sqrt{\frac{\xi^2 + \omega^2 k^2}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}} \mathcal{F}_{\xi, k}[u] \right\rVert_{L^2(\mathbb{R} \times \mathfrak{R})}
\lesssim \left\lVert u \right\rVert_H
\end{align*}
\begin{align*}
\left\lVert u \right\rVert_p
\lesssim \left\lVert \mathcal{F}_{\xi, k}[u] \right\rVert_{L^{p'}(\mathbb{R} \times \mathfrak{R})}
\lesssim \left\lVert \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\xi^2 + \omega^2 k^2}} \right\rVert_{L^r(\mathbb{R} \times \mathfrak{R})}
\cdot \left\lVert \sqrt{\frac{\xi^2 + \omega^2 k^2}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}} \mathcal{F}_{\xi, k}[u] \right\rVert_{L^2(\mathbb{R} \times \mathfrak{R})}
\lesssim \left\lVert u \right\rVert_H
\end{align*} where  $\frac{1}{r} = \frac{1}{2} - \frac{1}{p} \lt \frac{\alpha}{4}$ and the first factor is finite since by (A5) we have
$\frac{1}{r} = \frac{1}{2} - \frac{1}{p} \lt \frac{\alpha}{4}$ and the first factor is finite since by (A5) we have
 \begin{align*}
\left\lVert \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\xi^2 + \omega^2 k^2}} \right\rVert_{L^r(\mathbb{R} \times \mathfrak{R})}^r
&= \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \left( \frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\xi^2 + \omega^2 k^2} \right)^{ r/2} \mathrm{d}\xi
\\ &= \int_\mathbb{R} \left( \frac{1}{\xi^2 + 1} \right)^{ r/2} \mathrm{d}\xi \cdot \sum_{k \in \mathfrak{R}} \left\lvert \omega k \right\rvert \mathcal{F}_k[\mathcal{N}]^{{r}/{2}}
\lesssim \sum_{k \in \mathfrak{R}} \left\lvert k \right\rvert^{1 - \frac{\alpha r}{2}} \lt \infty.
\end{align*}
\begin{align*}
\left\lVert \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\xi^2 + \omega^2 k^2}} \right\rVert_{L^r(\mathbb{R} \times \mathfrak{R})}^r
&= \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \left( \frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\xi^2 + \omega^2 k^2} \right)^{ r/2} \mathrm{d}\xi
\\ &= \int_\mathbb{R} \left( \frac{1}{\xi^2 + 1} \right)^{ r/2} \mathrm{d}\xi \cdot \sum_{k \in \mathfrak{R}} \left\lvert \omega k \right\rvert \mathcal{F}_k[\mathcal{N}]^{{r}/{2}}
\lesssim \sum_{k \in \mathfrak{R}} \left\lvert k \right\rvert^{1 - \frac{\alpha r}{2}} \lt \infty.
\end{align*} In order to show compactness, define for ![]() $K \in \mathbb{N}_\mathrm{odd}$ the projection onto “small” frequencies
$K \in \mathbb{N}_\mathrm{odd}$ the projection onto “small” frequencies ![]() $P_K \colon H \to H$ by
$P_K \colon H \to H$ by  $P_K[u] = \mathcal{F}_t^{-1}\left[\mathbb{1}_{\left\lvert k \right\rvert \leq K} \mathcal{F}_k[u]\right]$. Then on
$P_K[u] = \mathcal{F}_t^{-1}\left[\mathbb{1}_{\left\lvert k \right\rvert \leq K} \mathcal{F}_k[u]\right]$. Then on ![]() $P_K H$ the norm
$P_K H$ the norm ![]() $\left\lVert u \right\rVert_H$ is equivalent to
$\left\lVert u \right\rVert_H$ is equivalent to
 \begin{align*}
\left\vert\left\vert\left\vert u\right\vert\right\vert\right\vert = \sum_{\substack{k \in \mathfrak{R} \\ \left\lvert k \right\rvert \leq K}} \left\lVert \hat u_k \right\rVert_{H^1(\mathbb{R})}.
\end{align*}
\begin{align*}
\left\vert\left\vert\left\vert u\right\vert\right\vert\right\vert = \sum_{\substack{k \in \mathfrak{R} \\ \left\lvert k \right\rvert \leq K}} \left\lVert \hat u_k \right\rVert_{H^1(\mathbb{R})}.
\end{align*} Since the embedding  $H^1(\mathbb{R}) \to L^p_\mathrm{loc}(\mathbb{R})$ is compact for any
$H^1(\mathbb{R}) \to L^p_\mathrm{loc}(\mathbb{R})$ is compact for any ![]() $p \in [2, \infty]$ and the sum above is finite, it follows that
$p \in [2, \infty]$ and the sum above is finite, it follows that  $P_K \colon H \to L^p_\mathrm{loc}(\mathbb{R} \times \mathbb{T})$ is compact. Next, the calculations above show for
$P_K \colon H \to L^p_\mathrm{loc}(\mathbb{R} \times \mathbb{T})$ is compact. Next, the calculations above show for ![]() $u \in H$ that
$u \in H$ that
 \begin{align*}
\left\lVert u - P_K[u] \right\rVert_p \leq C \sum_{\substack{k \in \mathfrak{R} \\ \left\lvert k \right\rvert \gt K}} \left\lvert k \right\rvert^{1 - \frac{\alpha r}{2}} \left\lVert u \right\rVert_H
\end{align*}
\begin{align*}
\left\lVert u - P_K[u] \right\rVert_p \leq C \sum_{\substack{k \in \mathfrak{R} \\ \left\lvert k \right\rvert \gt K}} \left\lvert k \right\rvert^{1 - \frac{\alpha r}{2}} \left\lVert u \right\rVert_H
\end{align*} for some C > 0 independent of K, so that ![]() $P_K \to I$ in
$P_K \to I$ in ![]() $\mathcal{B}(H; L^p(\mathbb{R} \times \mathbb{T}))$ as
$\mathcal{B}(H; L^p(\mathbb{R} \times \mathbb{T}))$ as ![]() $K\to\infty$. Thus H embeds compactly into
$K\to\infty$. Thus H embeds compactly into  $L^p_\mathrm{loc}(\mathbb{R} \times \mathbb{T})$.
$L^p_\mathrm{loc}(\mathbb{R} \times \mathbb{T})$.
We show that low-order (fractional) time-derivatives of u also lie in Lp in Corollary 2.6 as a generalization of the embedding of Lemma 2.4. This regularity gain will be used in Section 4 for a bootstrapping argument. We first give a definition of these derivatives.
Definition 2.5. For ![]() $s \in \mathbb{R}$ we define the fractional time-derivative
$s \in \mathbb{R}$ we define the fractional time-derivative ![]() $\left\lvert \partial_t \right\rvert^{s}$ as the Fourier multiplier
$\left\lvert \partial_t \right\rvert^{s}$ as the Fourier multiplier ![]() $\left\lvert \partial_t \right\rvert^{s} v(t) = \mathcal{F}_t^{-1}[\left\lvert \omega k \right\rvert^s \hat v_k]$.
$\left\lvert \partial_t \right\rvert^{s} v(t) = \mathcal{F}_t^{-1}[\left\lvert \omega k \right\rvert^s \hat v_k]$.
Corollary 2.6. As in the proof of Lemma 2.4 we see that for ![]() $p \in [2, p^\star)$ and ɛ > 0 sufficiently small (depending on
$p \in [2, p^\star)$ and ɛ > 0 sufficiently small (depending on ![]() $\alpha, p$), the map
$\alpha, p$), the map ![]() $\left\lvert \partial_t \right\rvert^{\varepsilon} \colon H \to L^p(\mathbb{R} \times \mathbb{T})$ is bounded and
$\left\lvert \partial_t \right\rvert^{\varepsilon} \colon H \to L^p(\mathbb{R} \times \mathbb{T})$ is bounded and  $\left\lvert \partial_t \right\rvert^{\varepsilon} \colon H \to L^p_\mathrm{loc}(\mathbb{R} \times \mathbb{T})$ is compact.
$\left\lvert \partial_t \right\rvert^{\varepsilon} \colon H \to L^p_\mathrm{loc}(\mathbb{R} \times \mathbb{T})$ is compact.
Let us recall the notion of a Palais-Smale sequence.
Definition 2.7. A sequence ![]() $(u_n)$ in
$(u_n)$ in ![]() $H$ is called a Palais-Smale sequence for
$H$ is called a Palais-Smale sequence for ![]() $J$ if
$J$ if ![]() $J'(u_n) \to 0$ in
$J'(u_n) \to 0$ in ![]() $H'$ and
$H'$ and ![]() $J(u_n)$ converges in
$J(u_n)$ converges in ![]() $\mathbb{R}$ as
$\mathbb{R}$ as ![]() $n\to\infty$. If
$n\to\infty$. If ![]() $\lim_{n\to\infty} J(u_n) = c$, we call
$\lim_{n\to\infty} J(u_n) = c$, we call ![]() $(u_n)$ a Palais-Smale sequence at level
$(u_n)$ a Palais-Smale sequence at level ![]() $c$.
$c$.
In the following lemma we show a variant of the concentration-compactness principle that will be a useful tool for extracting a nonzero limit from Palais-Smale sequences.
Lemma 2.8. Let ![]() $(u_n)$ be a bounded sequence in H, r > 0 and
$(u_n)$ be a bounded sequence in H, r > 0 and ![]() $\tilde p \in [2, p^\star)$ such that
$\tilde p \in [2, p^\star)$ such that
 \begin{align*}
\sup_{x \in \mathbb{R}} \left\lVert u_n \right\rVert_{L^{\tilde p}([x - r, x + r] \times \mathbb{T})} \to 0
\end{align*}
\begin{align*}
\sup_{x \in \mathbb{R}} \left\lVert u_n \right\rVert_{L^{\tilde p}([x - r, x + r] \times \mathbb{T})} \to 0
\end{align*} as ![]() $n \to \infty$. Then
$n \to \infty$. Then ![]() $u_n \to 0$ in
$u_n \to 0$ in ![]() $L^p(\mathbb{R} \times \mathbb{T})$ for all
$L^p(\mathbb{R} \times \mathbb{T})$ for all ![]() $p \in (2, p^\star)$.
$p \in (2, p^\star)$.
Proof. By Hölder’s inequality and Lemma 2.4 it suffices to show the result for ![]() $\tilde p = 2$ and one
$\tilde p = 2$ and one ![]() $p \in (2, p^\star)$, which we shall choose so close to 2 that
$p \in (2, p^\star)$, which we shall choose so close to 2 that  $2 \lt q := \frac{4}{4 - p} \lt p^\star$. Let
$2 \lt q := \frac{4}{4 - p} \lt p^\star$. Let ![]() $\phi_m \colon \mathbb{R} \to [0,1]$ be a smooth partition of unity with
$\phi_m \colon \mathbb{R} \to [0,1]$ be a smooth partition of unity with ![]() $\operatorname{supp} \phi_m \subseteq [(m-1)r, (m+1)r]$,
$\operatorname{supp} \phi_m \subseteq [(m-1)r, (m+1)r]$,  $\left\lVert \phi_m' \right\rVert_\infty \leq \frac{2}{r}$. Using that at any point of
$\left\lVert \phi_m' \right\rVert_\infty \leq \frac{2}{r}$. Using that at any point of ![]() $\mathbb{R}$ at most 2 of the ϕm are nonzero, we calculate
$\mathbb{R}$ at most 2 of the ϕm are nonzero, we calculate
 \begin{align*}
\left\lVert u_n \right\rVert_p^p
&= \int_{\mathbb{R} \times \mathbb{T}} \left\lvert \sum_{m \in \mathbb{Z}} \phi_m u_n \right\rvert^p \mathrm{d}(x, t)
\\ &\leq 2^{p-1} \int_{\mathbb{R} \times \mathbb{T}} \sum_{m \in \mathbb{Z}} \left\lvert \phi_m u_n \right\rvert^p \mathrm{d}(x, t)
\\ &= 2^{p-1} \sum_{m \in \mathbb{Z}} \left\lVert \phi_m u_n \right\rVert_p^p
\\ &\leq 2^{p-1} \sum_{m \in \mathbb{Z}} \left\lVert \phi_m u_n \right\rVert_{q}^2 \left\lVert \phi_m u_n \right\rVert_{2}^{p-2}
\\ &\lesssim \sup_{x \in \mathbb{R}} \left\lVert u_n \right\rVert_{L^2([x-r, x+r] \times \mathbb{T})}^{p-2} \sum_{m \in \mathbb{Z}} \left\lVert \phi_m u_n \right\rVert_H^2.
\end{align*}
\begin{align*}
\left\lVert u_n \right\rVert_p^p
&= \int_{\mathbb{R} \times \mathbb{T}} \left\lvert \sum_{m \in \mathbb{Z}} \phi_m u_n \right\rvert^p \mathrm{d}(x, t)
\\ &\leq 2^{p-1} \int_{\mathbb{R} \times \mathbb{T}} \sum_{m \in \mathbb{Z}} \left\lvert \phi_m u_n \right\rvert^p \mathrm{d}(x, t)
\\ &= 2^{p-1} \sum_{m \in \mathbb{Z}} \left\lVert \phi_m u_n \right\rVert_p^p
\\ &\leq 2^{p-1} \sum_{m \in \mathbb{Z}} \left\lVert \phi_m u_n \right\rVert_{q}^2 \left\lVert \phi_m u_n \right\rVert_{2}^{p-2}
\\ &\lesssim \sup_{x \in \mathbb{R}} \left\lVert u_n \right\rVert_{L^2([x-r, x+r] \times \mathbb{T})}^{p-2} \sum_{m \in \mathbb{Z}} \left\lVert \phi_m u_n \right\rVert_H^2.
\end{align*}Moreover, since
 \begin{align*}
\left\lVert \phi_m u_n \right\rVert_H^2
&= \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}
\int_\mathbb{R} \left(\left\lvert \phi_m' \hat u_k + \phi_m \hat u_k' \right\rvert^2 + \omega^2 k^2 \left\lvert \phi_m \hat u_k \right\rvert^2 \right) \mathrm{d}x
\\ &\leq C
\sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}
\int_{(m-1)r}^{(m+1)r} \left(\left\lvert \hat u_k' \right\rvert^2 + \omega^2 k^2 \left\lvert \hat u_k \right\rvert^2 \right) \mathrm{d}x,
\end{align*}
\begin{align*}
\left\lVert \phi_m u_n \right\rVert_H^2
&= \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}
\int_\mathbb{R} \left(\left\lvert \phi_m' \hat u_k + \phi_m \hat u_k' \right\rvert^2 + \omega^2 k^2 \left\lvert \phi_m \hat u_k \right\rvert^2 \right) \mathrm{d}x
\\ &\leq C
\sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}
\int_{(m-1)r}^{(m+1)r} \left(\left\lvert \hat u_k' \right\rvert^2 + \omega^2 k^2 \left\lvert \hat u_k \right\rvert^2 \right) \mathrm{d}x,
\end{align*} it follows that  $\sum_{m \in \mathbb{Z}} \left\lVert \phi_m u_n \right\rVert_H^2 \leq 2 C \left\lVert u \right\rVert_H^2$. Thus, from the assumptions we obtain
$\sum_{m \in \mathbb{Z}} \left\lVert \phi_m u_n \right\rVert_H^2 \leq 2 C \left\lVert u \right\rVert_H^2$. Thus, from the assumptions we obtain ![]() $\left\lVert u_n \right\rVert_p \to 0$ as
$\left\lVert u_n \right\rVert_p \to 0$ as ![]() $n \to \infty$.
$n \to \infty$.
3. Existence of ground states
In the following, let J be given by Definition 2.2. We call the energy level
 \begin{align*}
c_\mathrm{gs} := \inf_{\substack{u \in H \setminus \left\{ 0 \right\} \\ J'(u) = 0}} J(u)
\end{align*}
\begin{align*}
c_\mathrm{gs} := \inf_{\substack{u \in H \setminus \left\{ 0 \right\} \\ J'(u) = 0}} J(u)
\end{align*} the ground state energy level, and any solution ![]() $u \in H \setminus \left\{ 0 \right\}$ of
$u \in H \setminus \left\{ 0 \right\}$ of ![]() $J'(u) = 0$ with
$J'(u) = 0$ with ![]() $J(u) = c_\mathrm{gs}$ a ground state of J. Note that
$J(u) = c_\mathrm{gs}$ a ground state of J. Note that ![]() $c_\mathrm{gs}=+\infty$ if there are no nonzero critical points of
$c_\mathrm{gs}=+\infty$ if there are no nonzero critical points of ![]() $J$. Next we present the main result of this section. The rest of this section is dedicated to its proof.
$J$. Next we present the main result of this section. The rest of this section is dedicated to its proof.
Theorem 3.1 There exists a ground state of ![]() $J$.
$J$.
We first note that the following necessary condition for existence of ground states holds.
Lemma 3.2. ![]() $c_\mathrm{gs} \gt 0$.
$c_\mathrm{gs} \gt 0$.
Proof. By Lemma 2.4 with p = 4 we have  $J'(u)[u] = \left\langle u , u \right\rangle_H + \mathcal{O}(\left\lVert u \right\rVert_H^4)$ as
$J'(u)[u] = \left\langle u , u \right\rangle_H + \mathcal{O}(\left\lVert u \right\rVert_H^4)$ as ![]() $u_0$. In particular, for a critical point
$u_0$. In particular, for a critical point ![]() $u \in H$ of J we have
$u \in H$ of J we have  $0 = \left\lVert u \right\rVert_H^2 + \mathcal{O}(\left\lVert u \right\rVert_H^4)$, and therefore there exists c > 0 such that
$0 = \left\lVert u \right\rVert_H^2 + \mathcal{O}(\left\lVert u \right\rVert_H^4)$, and therefore there exists c > 0 such that ![]() $\left\lVert u \right\rVert_H \geq c$ for every critical point in
$\left\lVert u \right\rVert_H \geq c$ for every critical point in ![]() $H\setminus\{0\}$. The claim follows from this since every critical point u of J satisfies
$H\setminus\{0\}$. The claim follows from this since every critical point u of J satisfies  $J(u) = J(u) - \tfrac14 J'(u)[u] = \tfrac14 \left\langle u , u \right\rangle_H$.
$J(u) = J(u) - \tfrac14 J'(u)[u] = \tfrac14 \left\langle u , u \right\rangle_H$.
We will extract the ground state as a limit of a suitable Palais-Smale sequence. Next we use the mountain-pass theorem to obtain a particular Palais-Smale sequence.
Proposition 3.3. There exists ![]() $u_0 \in H$ with
$u_0 \in H$ with ![]() $J(u_0) \lt 0$. For such
$J(u_0) \lt 0$. For such ![]() $u_0$, the mountain-pass energy level
$u_0$, the mountain-pass energy level
 \begin{align*}
c_\mathrm{mp} :=
\inf_{\substack{\gamma \in C([0;1]; H) \\ \gamma(0) = 0, \gamma(1) = u_0}}
\sup_{s \in [0, 1]} J(\gamma(s))
\end{align*}
\begin{align*}
c_\mathrm{mp} :=
\inf_{\substack{\gamma \in C([0;1]; H) \\ \gamma(0) = 0, \gamma(1) = u_0}}
\sup_{s \in [0, 1]} J(\gamma(s))
\end{align*} is positive and there exists a Palais-Smale sequence for ![]() $J$ at level
$J$ at level ![]() $c_\mathrm{mp}$.
$c_\mathrm{mp}$.
Proof. For the construction of a suitable ![]() $u_0$ we choose
$u_0$ we choose ![]() $\varphi \in C_c^\infty(\mathbb{R})$ with
$\varphi \in C_c^\infty(\mathbb{R})$ with  $\int_\mathbb{R} h \varphi^4 \mathrm{d}x \gt 0$, which exists since
$\int_\mathbb{R} h \varphi^4 \mathrm{d}x \gt 0$, which exists since ![]() $h \not \leq 0$ and
$h \not \leq 0$ and ![]() $C_c^\infty(\mathbb{R})$ is dense in
$C_c^\infty(\mathbb{R})$ is dense in ![]() $L^4(\mathbb{R})$. We then choose
$L^4(\mathbb{R})$. We then choose ![]() $u_0(x,t) = r \operatorname{Re}[\varphi(x) e_{k_0}(t)]$ for some
$u_0(x,t) = r \operatorname{Re}[\varphi(x) e_{k_0}(t)]$ for some ![]() $k_0 \in \mathfrak{R}$ and r > 0. This implies that
$k_0 \in \mathfrak{R}$ and r > 0. This implies that
 \begin{align*}
J(u_0) = \tfrac{1}{2} r^2 \left\langle \operatorname{Re}[\varphi(x) e_{k_0}(t)] , \operatorname{Re}[\varphi(x) e_{k_0}(t)] \right\rangle_H - \tfrac{3}{32} r^4 \int_\mathbb{R} h \varphi^4 \mathrm{d}x
\end{align*}
\begin{align*}
J(u_0) = \tfrac{1}{2} r^2 \left\langle \operatorname{Re}[\varphi(x) e_{k_0}(t)] , \operatorname{Re}[\varphi(x) e_{k_0}(t)] \right\rangle_H - \tfrac{3}{32} r^4 \int_\mathbb{R} h \varphi^4 \mathrm{d}x
\end{align*} is negative, provided r has been chosen sufficiently large. By the embedding ![]() $H \hookrightarrow L^4$ we moreover have
$H \hookrightarrow L^4$ we moreover have
 \begin{align*}
J(u) = \tfrac12 \left\langle u , u \right\rangle_H - \mathcal{O}\left(\left\lVert u \right\rVert_H^4\right)
\end{align*}
\begin{align*}
J(u) = \tfrac12 \left\langle u , u \right\rangle_H - \mathcal{O}\left(\left\lVert u \right\rVert_H^4\right)
\end{align*} as ![]() $u_0$. Thus
$u_0$. Thus ![]() $c_\mathrm{mp} \gt 0$ and by the mountain pass theorem, cf. [Reference Willem35], there exists a Palais-Smale sequence
$c_\mathrm{mp} \gt 0$ and by the mountain pass theorem, cf. [Reference Willem35], there exists a Palais-Smale sequence ![]() $(u_n)$ at level
$(u_n)$ at level ![]() $c_\mathrm{mp}$.
$c_\mathrm{mp}$.
Lemma 3.4. Any Palais-Smale sequence for ![]() $J$ is bounded.
$J$ is bounded.
Proof. Let ![]() $(u_n)$ be a Palais-Smale sequence at level c. Then
$(u_n)$ be a Palais-Smale sequence at level c. Then
as ![]() $n \to \infty$, which shows that
$n \to \infty$, which shows that ![]() $(u_n)$ is bounded in H.
$(u_n)$ is bounded in H.
Next we show the following result on weakly convergent Palais-Smale sequences in our setting.
Lemma 3.5. Let ![]() $(u_n)$ be a Palais-Smale sequence for
$(u_n)$ be a Palais-Smale sequence for ![]() $J$ with
$J$ with ![]() $J(u_n) \to c$ and
$J(u_n) \to c$ and ![]() $u_n \rightharpoonup u$ in
$u_n \rightharpoonup u$ in ![]() $H$. Then
$H$. Then ![]() $u$ is a critical point of
$u$ is a critical point of ![]() $J$ and
$J$ and ![]() $J(u) \leq c$. Moreover, if
$J(u) \leq c$. Moreover, if ![]() $u_0$ and
$u_0$ and ![]() $c = c_\mathrm{gs}$ then
$c = c_\mathrm{gs}$ then ![]() $u$ is a ground state and
$u$ is a ground state and ![]() $u_n \to u$ in
$u_n \to u$ in ![]() $H$.
$H$.
Proof. By Lemmas 2.4 and 3.4 we have ![]() $u_n \to u$ in
$u_n \to u$ in  $L^4_\mathrm{loc}$. Thus for compactly supported
$L^4_\mathrm{loc}$. Thus for compactly supported ![]() $v \in H$ it follows that
$v \in H$ it follows that
 \begin{align*}
J'(u_n)[v] = \left\langle u_n , v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u_n^3 v \mathrm{d}(x, t)
\to \left\langle u , v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u^3 v \mathrm{d}(x, t)
= J'(u)[v]
\end{align*}
\begin{align*}
J'(u_n)[v] = \left\langle u_n , v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u_n^3 v \mathrm{d}(x, t)
\to \left\langle u , v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u^3 v \mathrm{d}(x, t)
= J'(u)[v]
\end{align*} so that ![]() $J'(u)[v] = 0$. By a density argument (cf. Lemma 2.3) it follows that u is a critical point of
$J'(u)[v] = 0$. By a density argument (cf. Lemma 2.3) it follows that u is a critical point of ![]() $J$. Next we calculate
$J$. Next we calculate
 \begin{align*}
J(u) = J(u) - \tfrac14 J'(u)[u] = \tfrac14 \left\langle u , u \right\rangle_H
\leq \tfrac14 \lim_{n \to \infty} \left\langle u_n , u_n \right\rangle_H = \lim_{n \to \infty} J(u_n) - \tfrac14 J'(u_n)[u_n] = c.
\end{align*}
\begin{align*}
J(u) = J(u) - \tfrac14 J'(u)[u] = \tfrac14 \left\langle u , u \right\rangle_H
\leq \tfrac14 \lim_{n \to \infty} \left\langle u_n , u_n \right\rangle_H = \lim_{n \to \infty} J(u_n) - \tfrac14 J'(u_n)[u_n] = c.
\end{align*} If ![]() $c = c_\mathrm{gs}$, then we have
$c = c_\mathrm{gs}$, then we have ![]() $J(u) \geq c_\mathrm{gs}$ since u ≠ 0 by assumption, and thus from the above inequality we find
$J(u) \geq c_\mathrm{gs}$ since u ≠ 0 by assumption, and thus from the above inequality we find ![]() $J(u) = c_\mathrm{gs}$ and in addition
$J(u) = c_\mathrm{gs}$ and in addition ![]() $\left\langle u_n , u_n \right\rangle_H \to \left\langle u , u \right\rangle_H$. Combined with
$\left\langle u_n , u_n \right\rangle_H \to \left\langle u , u \right\rangle_H$. Combined with ![]() $u_n \rightharpoonup u$ in H this shows
$u_n \rightharpoonup u$ in H this shows ![]() $u_n \to u$ in H.
$u_n \to u$ in H.
In many situations, e.g. in a translation-invariant setting, there are always Palais-Smale sequences converging weakly to 0. Therefore the main task in the following will be to find a Palais-Smale sequence with ![]() $u_n \rightharpoonup u \neq 0$. The arguments for this (and the proof of Theorem 3.1) differ between the types of nonlinearity, and are split into subsections accordingly.
$u_n \rightharpoonup u \neq 0$. The arguments for this (and the proof of Theorem 3.1) differ between the types of nonlinearity, and are split into subsections accordingly.
3.1. Proof of Theorem 3.1 for (A6a) and the purely periodic case of (A6b)
First we show how to extract a nonzero limit from a given Palais-Smale sequence.
Lemma 3.6. Assume (A6a) or (A6b) with ![]() $\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}\equiv 0$. Let
$\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}\equiv 0$. Let ![]() $(u_n)$ be a Palais-Smale sequence for
$(u_n)$ be a Palais-Smale sequence for ![]() $J$ at level c > 0. Then there exists a critical point
$J$ at level c > 0. Then there exists a critical point ![]() $u \in H \setminus\left\{ 0 \right\}$ of
$u \in H \setminus\left\{ 0 \right\}$ of ![]() $J$ with
$J$ with ![]() $J(u) \leq c$.
$J(u) \leq c$.
Proof. Part 1: We consider (A6a). Up to a subsequence we have ![]() $u_n \rightharpoonup u$ in H and
$u_n \rightharpoonup u$ in H and ![]() $u_n \to u$ in
$u_n \to u$ in  $L^4_\mathrm{loc}$ by Lemmas 2.4 and 3.4, where Lemma 3.5 guarantees that u is a critical point of
$L^4_\mathrm{loc}$ by Lemmas 2.4 and 3.4, where Lemma 3.5 guarantees that u is a critical point of ![]() $J$. Moreover, since h is bounded and
$J$. Moreover, since h is bounded and ![]() $h(x) \to 0$ as
$h(x) \to 0$ as ![]() $x \to \pm \infty$ by (A1) and (A6a), we have
$x \to \pm \infty$ by (A1) and (A6a), we have ![]() $h(x) u_n^3 \to h(x) u^3$ in
$h(x) u_n^3 \to h(x) u^3$ in ![]() $L^{4/3}(\mathbb{R} \times \mathbb{T})$. This implies for
$L^{4/3}(\mathbb{R} \times \mathbb{T})$. This implies for ![]() $v \in H$ that
$v \in H$ that
 \begin{align*}
\left\langle u_n - u , v \right\rangle_H
= J'(u_n)[v] - J'(u)[v] + \int_{\mathbb{R} \times \mathbb{T}} h(x) (u^3 - u_n^3) v \mathrm{d}(x, t)
= \hbox{o}(\left\lVert v \right\rVert_H)
\end{align*}
\begin{align*}
\left\langle u_n - u , v \right\rangle_H
= J'(u_n)[v] - J'(u)[v] + \int_{\mathbb{R} \times \mathbb{T}} h(x) (u^3 - u_n^3) v \mathrm{d}(x, t)
= \hbox{o}(\left\lVert v \right\rVert_H)
\end{align*} as ![]() $n \to \infty$. So
$n \to \infty$. So ![]() $u_n \to u$ in H, and in particular
$u_n \to u$ in H, and in particular ![]() $J(u) = c$ and u ≠ 0 hold.
$J(u) = c$ and u ≠ 0 hold.
Part 2: We now consider (A6b) with ![]() $\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}\equiv 0$. Since
$\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}\equiv 0$. Since
 \begin{align*}
\int_{\mathbb{R} \times \mathbb{T}} h(x) u_n^4 \mathrm{d}(x, t)
= 4 J(u_n) - 2 J'(u_n)[u_n] \to 4 c,
\end{align*}
\begin{align*}
\int_{\mathbb{R} \times \mathbb{T}} h(x) u_n^4 \mathrm{d}(x, t)
= 4 J(u_n) - 2 J'(u_n)[u_n] \to 4 c,
\end{align*} we have ![]() $u_n \not \to 0$ in
$u_n \not \to 0$ in ![]() $L^4(\mathbb{R} \times \mathbb{T})$. Let X > 0 denote the period of
$L^4(\mathbb{R} \times \mathbb{T})$. Let X > 0 denote the period of ![]() $\mathcal{G}$ and h. By Lemma 2.8 there exist
$\mathcal{G}$ and h. By Lemma 2.8 there exist ![]() $x_n \in \mathbb{R}$ with
$x_n \in \mathbb{R}$ with
 \begin{align}
\liminf_{n \to \infty} \left\lVert u_n \right\rVert_{L^4([x_n - X, x_n + X] \times \mathbb{T})} \gt 0
\end{align}
\begin{align}
\liminf_{n \to \infty} \left\lVert u_n \right\rVert_{L^4([x_n - X, x_n + X] \times \mathbb{T})} \gt 0
\end{align} and w.l.o.g. we may assume ![]() $x_n \in X \mathbb{Z}$. Let us define a new sequence
$x_n \in X \mathbb{Z}$. Let us define a new sequence ![]() $\tilde u_n$ by
$\tilde u_n$ by ![]() $\tilde u_n(x, t) = u_n(x - x_n, t)$, so that
$\tilde u_n(x, t) = u_n(x - x_n, t)$, so that ![]() $J(\tilde u_n) = J(u_n) \to c$ and
$J(\tilde u_n) = J(u_n) \to c$ and ![]() $J'(\tilde u_n) \to 0$. Up to a subsequence we have
$J'(\tilde u_n) \to 0$. Up to a subsequence we have ![]() $\tilde u_n \rightharpoonup u$ in H where u ≠ 0 by (17). The claim now follows from Lemma 3.5 applied to
$\tilde u_n \rightharpoonup u$ in H where u ≠ 0 by (17). The claim now follows from Lemma 3.5 applied to ![]() $(\tilde u_n)$.
$(\tilde u_n)$.
Proof of Lemma 3.1 for (A6a) and (A6b) with  $\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}\equiv 0$
$\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}\equiv 0$
Combining Proposition 3.3 and Lemma 3.6 we see that there exists a nonzero critical point of ![]() $J$. Thus
$J$. Thus ![]() $c_\mathrm{gs} \lt \infty$ and by definition of
$c_\mathrm{gs} \lt \infty$ and by definition of ![]() $c_\mathrm{gs}$ there exists a sequence
$c_\mathrm{gs}$ there exists a sequence ![]() $(u_n)$ of critical points of
$(u_n)$ of critical points of ![]() $J$ with
$J$ with ![]() $J(u_n) \to c_\mathrm{gs}$. Since
$J(u_n) \to c_\mathrm{gs}$. Since ![]() $c_\mathrm{gs} \gt 0$ by Lemma 3.2, applying Lemma 3.6 to
$c_\mathrm{gs} \gt 0$ by Lemma 3.2, applying Lemma 3.6 to ![]() $(u_n)$ we find a ground state of
$(u_n)$ we find a ground state of ![]() $J$.
$J$.
3.2. Proof of Theorem 3.1 for (A6b)
We call the problem with ![]() $\mathcal{G}, h$ replaced by
$\mathcal{G}, h$ replaced by ![]() $\mathcal{G}^\mathrm{per}, h^\mathrm{per}$ the periodic problem and denote it with the superscript “
$\mathcal{G}^\mathrm{per}, h^\mathrm{per}$ the periodic problem and denote it with the superscript “![]() $\mathrm{per}$”. The previous subsection guarantees the existence of a periodic ground state
$\mathrm{per}$”. The previous subsection guarantees the existence of a periodic ground state ![]() $u^\mathrm{per}$ of
$u^\mathrm{per}$ of ![]() $J^\mathrm{per}$.
$J^\mathrm{per}$.
Note that both ![]() $J$ and
$J$ and ![]() $J^\mathrm{per}$ are defined on the same Hilbert space H. The assumption (A6b) implies that
$J^\mathrm{per}$ are defined on the same Hilbert space H. The assumption (A6b) implies that ![]() $J \leq J^\mathrm{per}$ on H and, assuming
$J \leq J^\mathrm{per}$ on H and, assuming ![]() $(\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}) \neq 0$, the inequality is even strict on functions which do not have zero sets of positive measure. For our nonlocal problem (14) we do not know whether or not a unique continuation theorem holds, which is why we cannot rule out that a critical point of
$(\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}) \neq 0$, the inequality is even strict on functions which do not have zero sets of positive measure. For our nonlocal problem (14) we do not know whether or not a unique continuation theorem holds, which is why we cannot rule out that a critical point of ![]() $J$ or
$J$ or ![]() $J^\mathrm{per}$ could have a zero set of positive measure. Nevertheless, the subsequent arguments work without a unique continuation theorem and are based on the comparison of energy levels between our current and the periodic problem.
$J^\mathrm{per}$ could have a zero set of positive measure. Nevertheless, the subsequent arguments work without a unique continuation theorem and are based on the comparison of energy levels between our current and the periodic problem.
Lemma 3.7. Assume that no ground state of ![]() $J^\mathrm{per}$ is a critical point of
$J^\mathrm{per}$ is a critical point of ![]() $J$. Then there exists
$J$. Then there exists ![]() $u_0 \in H$ with
$u_0 \in H$ with ![]() $J(u_0) \lt 0$ such that the mountain-pass energy level
$J(u_0) \lt 0$ such that the mountain-pass energy level
 \begin{align*}
c_\mathrm{mp} :=
\inf_{\substack{\gamma \in C([0,1]; H) \\ \gamma(0) = 0, \gamma(1) = u_0}}
\sup_{s \in [0, 1]} J(\gamma(s))
\end{align*}
\begin{align*}
c_\mathrm{mp} :=
\inf_{\substack{\gamma \in C([0,1]; H) \\ \gamma(0) = 0, \gamma(1) = u_0}}
\sup_{s \in [0, 1]} J(\gamma(s))
\end{align*} satisfies  $0 \lt c_\mathrm{mp} \lt c_\mathrm{gs}^\mathrm{per}$.
$0 \lt c_\mathrm{mp} \lt c_\mathrm{gs}^\mathrm{per}$.
Proof. Let ![]() $u^\mathrm{per}$ be a ground state of
$u^\mathrm{per}$ be a ground state of ![]() $J^\mathrm{per}$. As
$J^\mathrm{per}$. As ![]() $u^\mathrm{per}$ is not a critical point of
$u^\mathrm{per}$ is not a critical point of ![]() $J$, we have
$J$, we have ![]() $\mathcal{G}^\mathrm{loc} \ast u^\mathrm{per} \neq 0$ or
$\mathcal{G}^\mathrm{loc} \ast u^\mathrm{per} \neq 0$ or ![]() $h^\mathrm{loc} (u^\mathrm{per})^3 \neq 0$. By the assumptions on the signs of
$h^\mathrm{loc} (u^\mathrm{per})^3 \neq 0$. By the assumptions on the signs of ![]() $\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}$ we moreover have
$\mathcal{G}^\mathrm{loc}, h^\mathrm{loc}$ we moreover have
 \begin{align*}
\left\langle u^\mathrm{per} , u^\mathrm{per} \right\rangle_H \leq \left\langle u^\mathrm{per} , u^\mathrm{per} \right\rangle_H^\mathrm{per}
\quad\text{and}\quad
\int_{\mathbb{R}\times\mathbb{T}} h(x) (u^\mathrm{per})^4 \mathrm{d}(x, t) \geq \int_{\mathbb{R}\times\mathbb{T}} h^\mathrm{per}(x) (u^\mathrm{per})^4 \mathrm{d}(x, t)
\end{align*}
\begin{align*}
\left\langle u^\mathrm{per} , u^\mathrm{per} \right\rangle_H \leq \left\langle u^\mathrm{per} , u^\mathrm{per} \right\rangle_H^\mathrm{per}
\quad\text{and}\quad
\int_{\mathbb{R}\times\mathbb{T}} h(x) (u^\mathrm{per})^4 \mathrm{d}(x, t) \geq \int_{\mathbb{R}\times\mathbb{T}} h^\mathrm{per}(x) (u^\mathrm{per})^4 \mathrm{d}(x, t)
\end{align*} where at least one inequality is strict. In particular, ![]() $J(s u^\mathrm{per}) \lt J^\mathrm{per}(s u^\mathrm{per})$ holds for s ≠ 0. Now set
$J(s u^\mathrm{per}) \lt J^\mathrm{per}(s u^\mathrm{per})$ holds for s ≠ 0. Now set ![]() $u_0 := \sqrt{2} u^\mathrm{per}$. Then
$u_0 := \sqrt{2} u^\mathrm{per}$. Then ![]() $J(u_0) \lt J^\mathrm{per}(u_0) = 0$ and
$J(u_0) \lt J^\mathrm{per}(u_0) = 0$ and
 \begin{align*}
c_\mathrm{mp} \leq \max_{s \in [0, 1]} J(s u_0) \lt \max_{s \in [0, 1]} J^\mathrm{per}(s u_0).
\end{align*}
\begin{align*}
c_\mathrm{mp} \leq \max_{s \in [0, 1]} J(s u_0) \lt \max_{s \in [0, 1]} J^\mathrm{per}(s u_0).
\end{align*} Moreover, the degree 4 polynomial ![]() $s \mapsto J^\mathrm{per}(s u^\mathrm{per})$ has the critical points
$s \mapsto J^\mathrm{per}(s u^\mathrm{per})$ has the critical points ![]() $0, 1, -1$ since
$0, 1, -1$ since ![]() $0, u^\mathrm{per}, -u^\mathrm{per}$ are critical points of
$0, u^\mathrm{per}, -u^\mathrm{per}$ are critical points of ![]() $J^\mathrm{per}$. Together with
$J^\mathrm{per}$. Together with ![]() $J(0) \lt J^\mathrm{per}(u^\mathrm{per}) = J^\mathrm{per}(-u^\mathrm{per})$ we see that the latter two points are the global maxima of the polynomial. Therefore
$J(0) \lt J^\mathrm{per}(u^\mathrm{per}) = J^\mathrm{per}(-u^\mathrm{per})$ we see that the latter two points are the global maxima of the polynomial. Therefore
 \begin{align*}
c_\mathrm{mp} \lt \max_{s \in [0, 1]} J^\mathrm{per}(s u_0)=J^\mathrm{per}(u^\mathrm{per}) = c_\mathrm{gs}^\mathrm{per}.
\end{align*}
\begin{align*}
c_\mathrm{mp} \lt \max_{s \in [0, 1]} J^\mathrm{per}(s u_0)=J^\mathrm{per}(u^\mathrm{per}) = c_\mathrm{gs}^\mathrm{per}.
\end{align*} Positivity of ![]() $c_\mathrm{mp}$ was already shown in Proposition 3.3.
$c_\mathrm{mp}$ was already shown in Proposition 3.3.
Similar to Lemma 3.6 of the previous subsection, we require a result on convergence of a given Palais-Smale sequence, which we present next.
Lemma 3.8. Assume (A6b). Let ![]() $u_n$ be a Palais-Smale sequence for
$u_n$ be a Palais-Smale sequence for ![]() $J$ at level
$J$ at level  $c \in (0, c_\mathrm{gs}^\mathrm{per})$. Then there also exists a critical point
$c \in (0, c_\mathrm{gs}^\mathrm{per})$. Then there also exists a critical point ![]() $u \in H \setminus\left\{ 0 \right\}$ of
$u \in H \setminus\left\{ 0 \right\}$ of ![]() $J$ with
$J$ with ![]() $J(u) \leq c$.
$J(u) \leq c$.
Proof. We denote by X the spatial period of ![]() $\mathcal{G}^\mathrm{per}, h^\mathrm{per}$. As in the proof of Lemma 3.6, Part 2, we have that
$\mathcal{G}^\mathrm{per}, h^\mathrm{per}$. As in the proof of Lemma 3.6, Part 2, we have that ![]() $u_n \not \to 0$ in
$u_n \not \to 0$ in ![]() $L^4(\mathbb{R} \times \mathbb{T})$ and that a sequence
$L^4(\mathbb{R} \times \mathbb{T})$ and that a sequence ![]() $x_n \in X \mathbb{Z}$ exists such that
$x_n \in X \mathbb{Z}$ exists such that
 \begin{align*}
\liminf_{n \to \infty} \left\lVert u_n \right\rVert_{L^4([x_n - X, x_n + X] \times \mathbb{T})} \gt 0.
\end{align*}
\begin{align*}
\liminf_{n \to \infty} \left\lVert u_n \right\rVert_{L^4([x_n - X, x_n + X] \times \mathbb{T})} \gt 0.
\end{align*} We claim that ![]() $u_n \not \to 0$ in
$u_n \not \to 0$ in  $L^4_\mathrm{loc}$ along any subsequence.
$L^4_\mathrm{loc}$ along any subsequence.
Assume for a contradiction that there exists a subsequence of ![]() $(u_n)$, which we again denote by
$(u_n)$, which we again denote by ![]() $(u_n)$, such that
$(u_n)$, such that ![]() $u_n \to 0$ in
$u_n \to 0$ in  $L^4_\mathrm{loc}$. Since
$L^4_\mathrm{loc}$. Since ![]() $u_n \not\to 0$ in L 4, we necessarily have
$u_n \not\to 0$ in L 4, we necessarily have ![]() $\left\lvert x_n \right\rvert \to \infty$. We define
$\left\lvert x_n \right\rvert \to \infty$. We define ![]() $\tilde u_n$ by
$\tilde u_n$ by ![]() $\tilde u_n(x, t) = u_n(x - x_n, t)$. Then up to a subsequence we have
$\tilde u_n(x, t) = u_n(x - x_n, t)$. Then up to a subsequence we have ![]() $\tilde u_n \rightharpoonup u$ in H and
$\tilde u_n \rightharpoonup u$ in H and ![]() $\tilde u_n \to u$ in
$\tilde u_n \to u$ in  $L^4_\mathrm{loc}$ for some
$L^4_\mathrm{loc}$ for some ![]() $u \in H \setminus\left\{ 0 \right\}$. For compactly supported
$u \in H \setminus\left\{ 0 \right\}$. For compactly supported ![]() $v \in H$ we set
$v \in H$ we set ![]() $v_n(x, t) = v(x + x_n, t)$ and calculate
$v_n(x, t) = v(x + x_n, t)$ and calculate
 \begin{align*}
J'(u_n)[v_n]
&= \left\langle u_n , v_n \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u_n^3 v_n \mathrm{d}(x, t)
\\ &= \left\langle u_n , v_n \right\rangle_H^\mathrm{per} - \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{per}(x) u_n^3 v_n \mathrm{d}(x, t)
\\ &\qquad- \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \frac{\mathcal{F}_k[\mathcal{G}^\mathrm{loc}(x)]}{\mathcal{F}_k[\mathcal{N}]} \bigl(\mathcal{F}_k[u_n] \overline{\mathcal{F}_k[v_n]}\bigr) \mathrm{d}x
- \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{loc}(x) u_n^3 v_n\ \mathrm{d}(x, t)
\\ &= \left\langle \tilde u_n , v \right\rangle_H^\mathrm{per} - \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{per}(x) {\tilde u_n}^3 v \ \mathrm{d}(x, t)
\\ &\qquad- \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \frac{\mathcal{F}_k[\mathcal{G}^\mathrm{loc}(x - x_n)]}{\mathcal{F}_k[\mathcal{N}]} \bigl(\mathcal{F}_k[\tilde u_n] \overline{\mathcal{F}_k[v]}\bigr) \mathrm{d}x
- \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{loc}(x - x_n) {\tilde u_n}^3 v \mathrm{d}(x, t)
\\ &\to \left\langle u , v \right\rangle_H^\mathrm{per} - \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{per}(x) u^3 v \mathrm{d}(x, t)
= (J^\mathrm{per})'(u)[v]
\end{align*}
\begin{align*}
J'(u_n)[v_n]
&= \left\langle u_n , v_n \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u_n^3 v_n \mathrm{d}(x, t)
\\ &= \left\langle u_n , v_n \right\rangle_H^\mathrm{per} - \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{per}(x) u_n^3 v_n \mathrm{d}(x, t)
\\ &\qquad- \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \frac{\mathcal{F}_k[\mathcal{G}^\mathrm{loc}(x)]}{\mathcal{F}_k[\mathcal{N}]} \bigl(\mathcal{F}_k[u_n] \overline{\mathcal{F}_k[v_n]}\bigr) \mathrm{d}x
- \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{loc}(x) u_n^3 v_n\ \mathrm{d}(x, t)
\\ &= \left\langle \tilde u_n , v \right\rangle_H^\mathrm{per} - \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{per}(x) {\tilde u_n}^3 v \ \mathrm{d}(x, t)
\\ &\qquad- \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \frac{\mathcal{F}_k[\mathcal{G}^\mathrm{loc}(x - x_n)]}{\mathcal{F}_k[\mathcal{N}]} \bigl(\mathcal{F}_k[\tilde u_n] \overline{\mathcal{F}_k[v]}\bigr) \mathrm{d}x
- \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{loc}(x - x_n) {\tilde u_n}^3 v \mathrm{d}(x, t)
\\ &\to \left\langle u , v \right\rangle_H^\mathrm{per} - \int_{\mathbb{R} \times \mathbb{T}} h^\mathrm{per}(x) u^3 v \mathrm{d}(x, t)
= (J^\mathrm{per})'(u)[v]
\end{align*} where we used ![]() $\left\lvert x_n \right\rvert \to \infty$ and
$\left\lvert x_n \right\rvert \to \infty$ and ![]() $\mathcal{G}^\mathrm{loc}(x) \to 0, h^\mathrm{loc}(x) \to 0$ as
$\mathcal{G}^\mathrm{loc}(x) \to 0, h^\mathrm{loc}(x) \to 0$ as ![]() $x \to \pm\infty$. This shows that u ≠ 0 is a critical point of
$x \to \pm\infty$. This shows that u ≠ 0 is a critical point of ![]() $J^\mathrm{per}$, and in particular
$J^\mathrm{per}$, and in particular  $J^\mathrm{per}(u) \geq c_\mathrm{gs}^\mathrm{per}$ holds. However, for fixed R > 0 we have
$J^\mathrm{per}(u) \geq c_\mathrm{gs}^\mathrm{per}$ holds. However, for fixed R > 0 we have
 \begin{align*}
&\sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_{-R}^R \bigl(\left\lvert \mathcal{F}_k[u]' \right\rvert^2 + \omega^2 k^2 V_k^\mathrm{per}(x) \left\lvert \mathcal{F}_k[u] \right\rvert^2\bigr) \mathrm{d}x
\\ &\leq \liminf_{n \to \infty} \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_{-R}^R \bigl(\left\lvert \mathcal{F}_k[\tilde u_n]' \right\rvert^2 + \omega^2 k^2 V_k^\mathrm{per}(x) \left\lvert \mathcal{F}_k[\tilde u_n] \right\rvert^2\bigr) \mathrm{d}x
\\ &= \liminf_{n \to \infty} \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_{x_n-R}^{x_n+R} \bigl(\left\lvert \mathcal{F}_k[u_n]' \right\rvert^2 + \omega^2 k^2 V_k^\mathrm{per}(x) \left\lvert \mathcal{F}_k[u_n] \right\rvert^2\bigr) \mathrm{d}x
\\ &= \liminf_{n \to \infty} \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_{x_n-R}^{x_n+R} \bigl(\left\lvert \mathcal{F}_k[u_n]' \right\rvert^2 + \omega^2 k^2 V_k(x) \left\lvert \mathcal{F}_k[u_n] \right\rvert^2\bigr) \mathrm{d}x
\\ &\leq \liminf_{n \to \infty} \left\langle u_n , u_n \right\rangle_H
\end{align*}
\begin{align*}
&\sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_{-R}^R \bigl(\left\lvert \mathcal{F}_k[u]' \right\rvert^2 + \omega^2 k^2 V_k^\mathrm{per}(x) \left\lvert \mathcal{F}_k[u] \right\rvert^2\bigr) \mathrm{d}x
\\ &\leq \liminf_{n \to \infty} \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_{-R}^R \bigl(\left\lvert \mathcal{F}_k[\tilde u_n]' \right\rvert^2 + \omega^2 k^2 V_k^\mathrm{per}(x) \left\lvert \mathcal{F}_k[\tilde u_n] \right\rvert^2\bigr) \mathrm{d}x
\\ &= \liminf_{n \to \infty} \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_{x_n-R}^{x_n+R} \bigl(\left\lvert \mathcal{F}_k[u_n]' \right\rvert^2 + \omega^2 k^2 V_k^\mathrm{per}(x) \left\lvert \mathcal{F}_k[u_n] \right\rvert^2\bigr) \mathrm{d}x
\\ &= \liminf_{n \to \infty} \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_{x_n-R}^{x_n+R} \bigl(\left\lvert \mathcal{F}_k[u_n]' \right\rvert^2 + \omega^2 k^2 V_k(x) \left\lvert \mathcal{F}_k[u_n] \right\rvert^2\bigr) \mathrm{d}x
\\ &\leq \liminf_{n \to \infty} \left\langle u_n , u_n \right\rangle_H
\end{align*} from which  $\left\langle u , u \right\rangle_H^\mathrm{per} \leq \liminf_{n\to\infty} \left\langle u_n , u_n \right\rangle_H$ follows in the limit
$\left\langle u , u \right\rangle_H^\mathrm{per} \leq \liminf_{n\to\infty} \left\langle u_n , u_n \right\rangle_H$ follows in the limit ![]() $R\to \infty$. This implies
$R\to \infty$. This implies
 \begin{align*}
c
& \lt c_\mathrm{gs}^\mathrm{per}
\leq J^\mathrm{per}(u)
= J^\mathrm{per}(u) - \tfrac14 (J^\mathrm{per})'(u)[u]
= \tfrac14 \left\langle u , u \right\rangle_H^\mathrm{per}
\\ &\leq \tfrac14 \liminf_{n\to\infty} \left\langle u_n , u_n \right\rangle_H
= \liminf_{n \to \infty} J(u_n) - \tfrac14 J'(u_n)[u_n] = c,
\end{align*}
\begin{align*}
c
& \lt c_\mathrm{gs}^\mathrm{per}
\leq J^\mathrm{per}(u)
= J^\mathrm{per}(u) - \tfrac14 (J^\mathrm{per})'(u)[u]
= \tfrac14 \left\langle u , u \right\rangle_H^\mathrm{per}
\\ &\leq \tfrac14 \liminf_{n\to\infty} \left\langle u_n , u_n \right\rangle_H
= \liminf_{n \to \infty} J(u_n) - \tfrac14 J'(u_n)[u_n] = c,
\end{align*}a contradiction.
Thus we have shown the claim. By Lemmas 2.4 and 3.4 up to a subsequence we have ![]() $u_n \rightharpoonup u$ in H and
$u_n \rightharpoonup u$ in H and ![]() $u_n \to u$ in
$u_n \to u$ in  $L^4_\mathrm{loc}$, where we now know u ≠ 0. Applying Lemma 3.5 completes the proof.
$L^4_\mathrm{loc}$, where we now know u ≠ 0. Applying Lemma 3.5 completes the proof.
Proof of Theorem 3.1 for (A6b)
Assume first that  $c_\mathrm{gs} \lt c_\mathrm{gs}^\mathrm{per}$ holds. Let un be a sequence of critical points of
$c_\mathrm{gs} \lt c_\mathrm{gs}^\mathrm{per}$ holds. Let un be a sequence of critical points of ![]() $J$ with
$J$ with ![]() $J(u_n) \to c_\mathrm{gs}$. From Lemmas 3.2 and 3.8 it follows that there exists a ground state of
$J(u_n) \to c_\mathrm{gs}$. From Lemmas 3.2 and 3.8 it follows that there exists a ground state of ![]() $J$. In the general situation, we distinguish between two cases.
$J$. In the general situation, we distinguish between two cases.
Case 1: If there exists a ground state ![]() $u^\mathrm{per}$ of
$u^\mathrm{per}$ of ![]() $J^\mathrm{per}$ which also is a critical point of
$J^\mathrm{per}$ which also is a critical point of ![]() $J$ then clearly
$J$ then clearly  $c_\mathrm{gs} \leq c_\mathrm{gs}^\mathrm{per}$ holds. If
$c_\mathrm{gs} \leq c_\mathrm{gs}^\mathrm{per}$ holds. If  $c_\mathrm{gs} \lt c_\mathrm{gs}^\mathrm{per}$ there is nothing left to show, and when
$c_\mathrm{gs} \lt c_\mathrm{gs}^\mathrm{per}$ there is nothing left to show, and when  $c_\mathrm{gs} = c_\mathrm{gs}^\mathrm{per}$ then
$c_\mathrm{gs} = c_\mathrm{gs}^\mathrm{per}$ then ![]() $u^\mathrm{per}$ is a ground state of
$u^\mathrm{per}$ is a ground state of ![]() $J$.
$J$.
Case 2: If no ground state of ![]() $J^\mathrm{per}$ solves
$J^\mathrm{per}$ solves ![]() $J'(u) = 0$, then by Lemma 3.7 there exists a Palais-Smale sequence un for
$J'(u) = 0$, then by Lemma 3.7 there exists a Palais-Smale sequence un for ![]() $J$ at some level
$J$ at some level  $c_\mathrm{mp} \in (0, c_\mathrm{gs}^\mathrm{per})$. Since
$c_\mathrm{mp} \in (0, c_\mathrm{gs}^\mathrm{per})$. Since ![]() $c_\mathrm{gs}\leq c_\mathrm{mp}$ by Lemma 3.8, this shows
$c_\mathrm{gs}\leq c_\mathrm{mp}$ by Lemma 3.8, this shows  $c_\mathrm{gs} \leq c_\mathrm{mp} \lt c_\mathrm{gs}^\mathrm{per}$.
$c_\mathrm{gs} \leq c_\mathrm{mp} \lt c_\mathrm{gs}^\mathrm{per}$.
We finish this section with an alternative formulation which may be useful for finding breathers numerically. Due to the simple structure of the functional ![]() $J$ an alternative characterization of the mountain pass level
$J$ an alternative characterization of the mountain pass level ![]() $c_\mathrm{mp}$ is given by
$c_\mathrm{mp}$ is given by
 \begin{equation*}
c_\mathrm{mp} = \min_{\|u\|_H=1} \max_{s \gt 0} J(su) = \frac{1}{2 \max_{\|u\|_H=1} \int_{\mathbb{R}\times\mathbb{T}} h(x) u^4 \mathrm{d}(x,t)}
\end{equation*}
\begin{equation*}
c_\mathrm{mp} = \min_{\|u\|_H=1} \max_{s \gt 0} J(su) = \frac{1}{2 \max_{\|u\|_H=1} \int_{\mathbb{R}\times\mathbb{T}} h(x) u^4 \mathrm{d}(x,t)}
\end{equation*} which means that is suffices to maximize  $\int_{\mathbb{R}\times\mathbb{T}} h(x) u^4\mathrm{d}(x,t)$ of the unit sphere in H. This can be done numerically by the method of constrained steepest increase. Further, one can relax the constraint to
$\int_{\mathbb{R}\times\mathbb{T}} h(x) u^4\mathrm{d}(x,t)$ of the unit sphere in H. This can be done numerically by the method of constrained steepest increase. Further, one can relax the constraint to ![]() $\|u\|\leq 1$ since all maximizers lie on the boundary of the norm-ball of radius 1. The numerical approximation of breathers is part of our ongoing work.
$\|u\|\leq 1$ since all maximizers lie on the boundary of the norm-ball of radius 1. The numerical approximation of breathers is part of our ongoing work.
4. Regularity
So far we have shown existence of a ground state to (14) in the slab geometry. In this section, we discuss its regularity properties. The necessary modifications for the cylindrical geometry are explained in Section 5.2.
We proceed in two steps. First, we show regularity for the solution u to (16): it is infinitely differentiable in time, twice differentiable in space, and derivatives lie in ![]() $L^2 \cap L^\infty$. We also show that if the material parameters are l times continuously differentiable, then u is l + 2 time differentiable in space and derivatives lie in
$L^2 \cap L^\infty$. We also show that if the material parameters are l times continuously differentiable, then u is l + 2 time differentiable in space and derivatives lie in ![]() $L^2 \cap C_b$.
$L^2 \cap C_b$.
Then we transfer this regularity from the function u to the electromagnetic fields ![]() $\mathbf{D}, \mathbf{E}, \mathbf{B}, \mathbf{H}$ since these can be expressed as functions of u.
$\mathbf{D}, \mathbf{E}, \mathbf{B}, \mathbf{H}$ since these can be expressed as functions of u.
We begin by showing infinite time differentiability in the space H, see Lemma 4.2, which we prepare with an auxiliary result.
Lemma 4.1. Let s > 0 and ![]() $u, \left\lvert \partial_t \right\rvert^{s} u \in L^p(\mathbb{R} \times \mathbb{T})$ where
$u, \left\lvert \partial_t \right\rvert^{s} u \in L^p(\mathbb{R} \times \mathbb{T})$ where ![]() $p \in [3, \infty]$. Then
$p \in [3, \infty]$. Then ![]() $\left\lvert \partial_t \right\rvert^{s}(u^3) \in L^{{p}/{3}}(\mathbb{R} \times \mathbb{T})$.
$\left\lvert \partial_t \right\rvert^{s}(u^3) \in L^{{p}/{3}}(\mathbb{R} \times \mathbb{T})$.
Proof. By [Reference Bényi, Oh and Zhao6, Proposition 1] the estimate
holds for all ![]() $r, p_j, q_j \in [1, \infty]$ with
$r, p_j, q_j \in [1, \infty]$ with  $\frac{1}{r} = \frac{1}{p_j} + \frac{1}{q_j}$ and
$\frac{1}{r} = \frac{1}{p_j} + \frac{1}{q_j}$ and ![]() $v \in C^\infty(\mathbb{T})$. By a density argument we obtain
$v \in C^\infty(\mathbb{T})$. By a density argument we obtain
 \begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} (u^3) \right\rVert_{L^{{p}/{3}}(\mathbb{R} \times \mathbb{T})}
&= \bigl\lVert \left\lVert \left\lvert \partial_t \right\rvert^{s} (u^3) \right\rVert_{L^{{p}/{3}}(\mathbb{T})} \bigr\rVert_{L^{{p}/{3}}(\mathbb{R})}
\\ &\lesssim \bigl\lVert
\left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_{L^p(\mathbb{T})}
\left\lVert u^2 \right\rVert_{L^{{p}/{2}}(\mathbb{T})}
+ \left\lVert u \right\rVert_{L^p(\mathbb{T})}
\left\lVert \left\lvert \partial_t \right\rvert^{s} (u^2) \right\rVert_{L^{{p}/{2}}(\mathbb{T})}
\bigr\rVert_{L^{{p}/{3}}(\mathbb{R})}
\\ &\lesssim \bigl\lVert
\left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_{L^p(\mathbb{T})}
\left\lVert u \right\rVert_{L^p(\mathbb{T})}^2
\bigr\rVert_{L^{{p}/{3}}(\mathbb{R})}
\\ &\leq \bigl\lVert \left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_{L^{p}(\mathbb{T})} \bigr\rVert_{L^{p}(\mathbb{R})} \bigl\lVert \left\lVert u \right\rVert_{L^{p}(\mathbb{T})} \bigr\rVert_{L^{p}(\mathbb{R})}^2.
\end{align*}
\begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} (u^3) \right\rVert_{L^{{p}/{3}}(\mathbb{R} \times \mathbb{T})}
&= \bigl\lVert \left\lVert \left\lvert \partial_t \right\rvert^{s} (u^3) \right\rVert_{L^{{p}/{3}}(\mathbb{T})} \bigr\rVert_{L^{{p}/{3}}(\mathbb{R})}
\\ &\lesssim \bigl\lVert
\left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_{L^p(\mathbb{T})}
\left\lVert u^2 \right\rVert_{L^{{p}/{2}}(\mathbb{T})}
+ \left\lVert u \right\rVert_{L^p(\mathbb{T})}
\left\lVert \left\lvert \partial_t \right\rvert^{s} (u^2) \right\rVert_{L^{{p}/{2}}(\mathbb{T})}
\bigr\rVert_{L^{{p}/{3}}(\mathbb{R})}
\\ &\lesssim \bigl\lVert
\left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_{L^p(\mathbb{T})}
\left\lVert u \right\rVert_{L^p(\mathbb{T})}^2
\bigr\rVert_{L^{{p}/{3}}(\mathbb{R})}
\\ &\leq \bigl\lVert \left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_{L^{p}(\mathbb{T})} \bigr\rVert_{L^{p}(\mathbb{R})} \bigl\lVert \left\lVert u \right\rVert_{L^{p}(\mathbb{T})} \bigr\rVert_{L^{p}(\mathbb{R})}^2.
\end{align*}Lemma 4.2. Let ![]() $u \in H$ be a critical point of
$u \in H$ be a critical point of ![]() $J$. Then
$J$. Then ![]() $\left\lvert \partial_t \right\rvert^{s} u \in H$ for all
$\left\lvert \partial_t \right\rvert^{s} u \in H$ for all ![]() $s \in \mathbb{R}$.
$s \in \mathbb{R}$.
Proof. Since ![]() $u \in H$,
$u \in H$, ![]() $\left\lvert \partial_t \right\rvert^{s} u \in H$ holds for
$\left\lvert \partial_t \right\rvert^{s} u \in H$ holds for ![]() $s \leq 0$. Moreover, if
$s \leq 0$. Moreover, if ![]() $\left\lvert \partial_t \right\rvert^{s} u \in H$ then
$\left\lvert \partial_t \right\rvert^{s} u \in H$ then ![]() $\left\lvert \partial_t \right\rvert^{\sigma} u \in H$ for all
$\left\lvert \partial_t \right\rvert^{\sigma} u \in H$ for all ![]() $\sigma\leq s$. By Corollary 2.6 there exists ɛ > 0 such that
$\sigma\leq s$. By Corollary 2.6 there exists ɛ > 0 such that ![]() $\left\lvert \partial_t \right\rvert^{\varepsilon} \colon H \to L^4(\mathbb{R} \times \mathbb{T})$ is bounded. We show by induction that
$\left\lvert \partial_t \right\rvert^{\varepsilon} \colon H \to L^4(\mathbb{R} \times \mathbb{T})$ is bounded. We show by induction that ![]() $\left\lvert \partial_t \right\rvert^{n \varepsilon} u \in H$ holds for
$\left\lvert \partial_t \right\rvert^{n \varepsilon} u \in H$ holds for ![]() $n \in \mathbb{N}_0$. So assume
$n \in \mathbb{N}_0$. So assume ![]() $\left\lvert \partial_t \right\rvert^{n \varepsilon} u \in H$ for fixed
$\left\lvert \partial_t \right\rvert^{n \varepsilon} u \in H$ for fixed ![]() $n \in \mathbb{N}_0$. Let
$n \in \mathbb{N}_0$. Let ![]() $v \in H$ with
$v \in H$ with ![]() $\left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} v \in H$. Then we have
$\left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} v \in H$. Then we have
 \begin{align*}
0 &= J'(u)[\left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} v]
\\ &= \left\langle u , \left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u^3 \cdot \left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} v\ \mathrm{d}(x, t)
\\ &= \left\langle \left\lvert \partial_t \right\rvert^{n\varepsilon}u , \left\lvert \partial_t \right\rvert^{\varepsilon} v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) \left\lvert \partial_t \right\rvert^{n \varepsilon}(u^3) \cdot \left\lvert \partial_t \right\rvert^{\varepsilon} v\ \mathrm{d}(x, t).
\end{align*}
\begin{align*}
0 &= J'(u)[\left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} v]
\\ &= \left\langle u , \left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) u^3 \cdot \left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} v\ \mathrm{d}(x, t)
\\ &= \left\langle \left\lvert \partial_t \right\rvert^{n\varepsilon}u , \left\lvert \partial_t \right\rvert^{\varepsilon} v \right\rangle_H - \int_{\mathbb{R} \times \mathbb{T}} h(x) \left\lvert \partial_t \right\rvert^{n \varepsilon}(u^3) \cdot \left\lvert \partial_t \right\rvert^{\varepsilon} v\ \mathrm{d}(x, t).
\end{align*} By Lemma 4.1 with ![]() $p=4$ and a density argument (cf. Lemma 2.3) we see that the map
$p=4$ and a density argument (cf. Lemma 2.3) we see that the map  $v \mapsto \int_{\mathbb{R} \times \mathbb{T}} h(x) \left\lvert \partial_t \right\rvert^{n \varepsilon}(u^3) \cdot \left\lvert \partial_t \right\rvert^{\varepsilon} v\ \mathrm{d}(x, t)$ extends to a bounded linear functional on H. Hence there exists
$v \mapsto \int_{\mathbb{R} \times \mathbb{T}} h(x) \left\lvert \partial_t \right\rvert^{n \varepsilon}(u^3) \cdot \left\lvert \partial_t \right\rvert^{\varepsilon} v\ \mathrm{d}(x, t)$ extends to a bounded linear functional on H. Hence there exists ![]() $w \in H$ with
$w \in H$ with
 \begin{align*}
\left\langle w , v \right\rangle_H
= \int_{\mathbb{R} \times \mathbb{T}} h(x) \left\lvert \partial_t \right\rvert^{n \varepsilon}(u^3) \cdot \left\lvert \partial_t \right\rvert^{\varepsilon} v\ \mathrm{d}(x, t)
= \left\langle \left\lvert \partial_t \right\rvert^{n\varepsilon}u , \left\lvert \partial_t \right\rvert^{\varepsilon} v \right\rangle_H
\end{align*}
\begin{align*}
\left\langle w , v \right\rangle_H
= \int_{\mathbb{R} \times \mathbb{T}} h(x) \left\lvert \partial_t \right\rvert^{n \varepsilon}(u^3) \cdot \left\lvert \partial_t \right\rvert^{\varepsilon} v\ \mathrm{d}(x, t)
= \left\langle \left\lvert \partial_t \right\rvert^{n\varepsilon}u , \left\lvert \partial_t \right\rvert^{\varepsilon} v \right\rangle_H
\end{align*} for ![]() $v \in H$ with
$v \in H$ with ![]() $\left\lvert \partial_t \right\rvert^{(n+1)\varepsilon}v \in H$. Again by density we get
$\left\lvert \partial_t \right\rvert^{(n+1)\varepsilon}v \in H$. Again by density we get ![]() $\left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} u = w$.
$\left\lvert \partial_t \right\rvert^{(n+1)\varepsilon} u = w$.
In order to proceed we need the following little result on the mapping properties of Fourier multiplier operators.
Lemma 4.3. Let ![]() $M v = \mathcal{F}^{-1}[m_k \hat v_k]$ be a Fourier multiplier with symbol
$M v = \mathcal{F}^{-1}[m_k \hat v_k]$ be a Fourier multiplier with symbol ![]() $\left\lvert m_k \right\rvert \lesssim \left\lvert k \right\rvert^\sigma$ of polynomial growth and let
$\left\lvert m_k \right\rvert \lesssim \left\lvert k \right\rvert^\sigma$ of polynomial growth and let ![]() $u$ be a function with
$u$ be a function with ![]() $\left\lvert \partial_t \right\rvert^{s} u \in H$ for all
$\left\lvert \partial_t \right\rvert^{s} u \in H$ for all ![]() $s \in \mathbb{R}$. Then
$s \in \mathbb{R}$. Then ![]() $\left\lvert \partial_t \right\rvert^{s} M u \in H$ for all
$\left\lvert \partial_t \right\rvert^{s} M u \in H$ for all ![]() $s \in \mathbb{R}$. The same holds for
$s \in \mathbb{R}$. The same holds for ![]() $H$ replaced by
$H$ replaced by ![]() $L^p(\mathbb{R} \times \mathbb{T})$ with
$L^p(\mathbb{R} \times \mathbb{T})$ with ![]() $p \in [1, \infty]$ if we require
$p \in [1, \infty]$ if we require ![]() $\hat u_0=0$.
$\hat u_0=0$.
Proof. In the Hilbert space setting we have
 \begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} M u \right\rVert_H \leq (\sup_{k \in \mathfrak{R}} \left\lvert m_k \right\rvert \left\lvert \omega k \right\rvert^{-\sigma}) \left\lVert \left\lvert \partial_t \right\rvert^{s + \sigma} u \right\rVert_H \lt \infty.
\end{align*}
\begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} M u \right\rVert_H \leq (\sup_{k \in \mathfrak{R}} \left\lvert m_k \right\rvert \left\lvert \omega k \right\rvert^{-\sigma}) \left\lVert \left\lvert \partial_t \right\rvert^{s + \sigma} u \right\rVert_H \lt \infty.
\end{align*} In the ![]() $L^p(\mathbb{R} \times \mathbb{T})$ case, the series
$L^p(\mathbb{R} \times \mathbb{T})$ case, the series 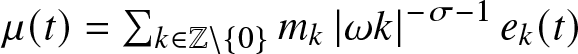 $\mu(t) = \sum_{k \in \mathbb{Z}\setminus\{0\}} m_k \left\lvert \omega k \right\rvert^{-\sigma-1} e_k(t)$ converges in
$\mu(t) = \sum_{k \in \mathbb{Z}\setminus\{0\}} m_k \left\lvert \omega k \right\rvert^{-\sigma-1} e_k(t)$ converges in ![]() $L^1(\mathbb{T})$. Hence
$L^1(\mathbb{T})$. Hence
 \begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} M u \right\rVert_p
= \left\lVert \mu \ast \left\lvert \partial_t \right\rvert^{s+\sigma+1} u \right\rVert_p
\leq \left\lVert \mu \right\rVert_1 \left\lVert \left\lvert \partial_t \right\rvert^{s+\sigma+1} u \right\rVert_p \lt \infty. &
\end{align*}
\begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} M u \right\rVert_p
= \left\lVert \mu \ast \left\lvert \partial_t \right\rvert^{s+\sigma+1} u \right\rVert_p
\leq \left\lVert \mu \right\rVert_1 \left\lVert \left\lvert \partial_t \right\rvert^{s+\sigma+1} u \right\rVert_p \lt \infty. &
\end{align*} Note that Lemma 4.3 applies to the multipliers ![]() $\mathcal{N} \ast, \mathcal{G}(x) \ast$ and by (A5) also to
$\mathcal{N} \ast, \mathcal{G}(x) \ast$ and by (A5) also to ![]() $(\mathcal{N}\ast)^{-1}$.
$(\mathcal{N}\ast)^{-1}$.
Continuing our regularity analysis we show that ![]() $u$ and its derivatives lie in
$u$ and its derivatives lie in ![]() $L^2 \cap L^\infty$. This also shows that
$L^2 \cap L^\infty$. This also shows that ![]() $u$ satisfies (14) strongly.
$u$ satisfies (14) strongly.
Proposition 4.4. Let ![]() $u \in H$ be a critical point of
$u \in H$ be a critical point of ![]() $J$. Then
$J$. Then ![]() $\left\lvert \partial_t \right\rvert^{s} u \in W^{2,p}(\mathbb{R} \times \mathbb{T})$ for all
$\left\lvert \partial_t \right\rvert^{s} u \in W^{2,p}(\mathbb{R} \times \mathbb{T})$ for all ![]() $s \in \mathbb{R}$ and
$s \in \mathbb{R}$ and ![]() $p \in [2, \infty]$, and it satisfies the equation
$p \in [2, \infty]$, and it satisfies the equation
 \begin{align}
- u_{xx} - V(x) \partial_t^2 u + h(x) \partial_t^2\left(\mathcal{N} \ast u^3\right) = 0.
\end{align}
\begin{align}
- u_{xx} - V(x) \partial_t^2 u + h(x) \partial_t^2\left(\mathcal{N} \ast u^3\right) = 0.
\end{align} If (R) holds, we moreover have  $\left\lvert \partial_t \right\rvert^{s} u \in W^{2+l,2}(\mathbb{R} \times \mathbb{T}) \cap C_b^{2+l}(\mathbb{R} \times \mathbb{T})$.
$\left\lvert \partial_t \right\rvert^{s} u \in W^{2+l,2}(\mathbb{R} \times \mathbb{T}) \cap C_b^{2+l}(\mathbb{R} \times \mathbb{T})$.
Proof. We remark that equation (18) formally follows by applying ![]() $-\partial_t^2 \mathcal{N} \ast$ to (14).
$-\partial_t^2 \mathcal{N} \ast$ to (14).
Part 1: We first show ![]() $\left\lvert \partial_t \right\rvert^{s} u \in L^p(\mathbb{R} \times \mathbb{T})$. Because of boundedness of the embedding
$\left\lvert \partial_t \right\rvert^{s} u \in L^p(\mathbb{R} \times \mathbb{T})$. Because of boundedness of the embedding ![]() $H \hookrightarrow L^2(\mathbb{R}\times\mathbb{T})$ and interpolation, it suffices to give the result for
$H \hookrightarrow L^2(\mathbb{R}\times\mathbb{T})$ and interpolation, it suffices to give the result for ![]() $p = \infty$. Similarly as in the proof of Lemma 2.4 we calculate
$p = \infty$. Similarly as in the proof of Lemma 2.4 we calculate
 \begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_{L^\infty(\mathbb{R} \times \mathbb{T})}
&\lesssim \left\lVert \left\lvert \omega k \right\rvert^s \mathcal{F}_{\xi,k}[u] \right\rVert_{L^1(\mathbb{R} \times \mathfrak{R})}
\\ &\leq \left\lVert \left\lvert \omega k \right\rvert^{-1/2} \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\xi^2 + \omega^2 k^2}} \right\rVert_{L^2(\mathbb{R} \times \mathfrak{R})}
\cdot \left\lVert \left\lvert \omega k \right\rvert^{s + 1/2} \sqrt{\frac{\xi^2 + \omega^2 k^2}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}} \mathcal{F}_{\xi, k}[u] \right\rVert_{L^2(\mathbb{R} \times \mathfrak{R})}
\end{align*}
\begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_{L^\infty(\mathbb{R} \times \mathbb{T})}
&\lesssim \left\lVert \left\lvert \omega k \right\rvert^s \mathcal{F}_{\xi,k}[u] \right\rVert_{L^1(\mathbb{R} \times \mathfrak{R})}
\\ &\leq \left\lVert \left\lvert \omega k \right\rvert^{-1/2} \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\xi^2 + \omega^2 k^2}} \right\rVert_{L^2(\mathbb{R} \times \mathfrak{R})}
\cdot \left\lVert \left\lvert \omega k \right\rvert^{s + 1/2} \sqrt{\frac{\xi^2 + \omega^2 k^2}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}} \mathcal{F}_{\xi, k}[u] \right\rVert_{L^2(\mathbb{R} \times \mathfrak{R})}
\end{align*} where the first factor is finite since ![]() $0 \leq \mathcal{F}_k[\mathcal{N}] \leq \left\lvert k \right\rvert^{-\alpha}$, α > 1, and the second factor is equivalent to
$0 \leq \mathcal{F}_k[\mathcal{N}] \leq \left\lvert k \right\rvert^{-\alpha}$, α > 1, and the second factor is equivalent to  $\left\lVert \left\lvert \partial_t \right\rvert^{s + 1/2} u \right\rVert_H$ and thus finite by Lemma 4.2.
$\left\lVert \left\lvert \partial_t \right\rvert^{s + 1/2} u \right\rVert_H$ and thus finite by Lemma 4.2.
Part 2: Next we show ![]() $\left\lvert \partial_t \right\rvert^{s} u_{x} \in L^2(\mathbb{R} \times \mathbb{T})$:
$\left\lvert \partial_t \right\rvert^{s} u_{x} \in L^2(\mathbb{R} \times \mathbb{T})$:
 \begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} u_x \right\rVert_{L^2(\mathbb{R} \times \mathbb{T})}^2
&= \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \left\lvert \omega k \right\rvert^{2s} \left\lvert \hat u_k' \right\rvert^2 \mathrm{d}x
\\ &\lesssim \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \frac{\left\lvert \omega k \right\rvert^{2s + 2 - \alpha}}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \left\lvert \hat u_k' \right\rvert^2 \mathrm{d}x
\leq \left\lVert \left\lvert \partial_t \right\rvert^{s + 1 - \frac{\alpha}{2}} u \right\rVert_H^2 \lt \infty.
\end{align*}
\begin{align*}
\left\lVert \left\lvert \partial_t \right\rvert^{s} u_x \right\rVert_{L^2(\mathbb{R} \times \mathbb{T})}^2
&= \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \left\lvert \omega k \right\rvert^{2s} \left\lvert \hat u_k' \right\rvert^2 \mathrm{d}x
\\ &\lesssim \sum_{k \in \mathfrak{R}} \int_\mathbb{R} \frac{\left\lvert \omega k \right\rvert^{2s + 2 - \alpha}}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \left\lvert \hat u_k' \right\rvert^2 \mathrm{d}x
\leq \left\lVert \left\lvert \partial_t \right\rvert^{s + 1 - \frac{\alpha}{2}} u \right\rVert_H^2 \lt \infty.
\end{align*} Now let ![]() $v \in H$ with
$v \in H$ with ![]() $\left\lvert \partial_t \right\rvert^{s+2} \mathcal{N} \ast v \in H$. As
$\left\lvert \partial_t \right\rvert^{s+2} \mathcal{N} \ast v \in H$. As ![]() $\mathcal{N}$ is even by (A5), we have
$\mathcal{N}$ is even by (A5), we have
 \begin{align*}
0
&= J'(u)[\left\lvert \partial_t \right\rvert^{s+2} \mathcal{N} \ast v]
\\ &= \sum_{k \in \mathfrak{R}} \left\lvert \omega k \right\rvert^s \int_\mathbb{R} \hat u_k' \overline{\hat v_k'} + \omega^2 k^2 V_k(x) \hat u_k \overline{\hat v_k} \mathrm{d}x
- \int_{\mathbb{R} \times \mathbb{T}} h(x) u^3 \cdot \left\lvert \partial_t \right\rvert^{s+2} \mathcal{N} \ast v\ \mathrm{d}(x, t)
\\ &= \int_{\mathbb{R} \times \mathbb{T}} \left\lvert \partial_t \right\rvert^{s} u_x \cdot v_x \mathrm{d}(x, t)
+ \int_{\mathbb{R} \times \mathbb{T}} \left\lvert \partial_t \right\rvert^{2+s}\left( V(x) u - h(x) \mathcal{N} \ast u^3 \right) \cdot v\ \mathrm{d}(x, t).
\end{align*}
\begin{align*}
0
&= J'(u)[\left\lvert \partial_t \right\rvert^{s+2} \mathcal{N} \ast v]
\\ &= \sum_{k \in \mathfrak{R}} \left\lvert \omega k \right\rvert^s \int_\mathbb{R} \hat u_k' \overline{\hat v_k'} + \omega^2 k^2 V_k(x) \hat u_k \overline{\hat v_k} \mathrm{d}x
- \int_{\mathbb{R} \times \mathbb{T}} h(x) u^3 \cdot \left\lvert \partial_t \right\rvert^{s+2} \mathcal{N} \ast v\ \mathrm{d}(x, t)
\\ &= \int_{\mathbb{R} \times \mathbb{T}} \left\lvert \partial_t \right\rvert^{s} u_x \cdot v_x \mathrm{d}(x, t)
+ \int_{\mathbb{R} \times \mathbb{T}} \left\lvert \partial_t \right\rvert^{2+s}\left( V(x) u - h(x) \mathcal{N} \ast u^3 \right) \cdot v\ \mathrm{d}(x, t).
\end{align*}Since v was arbitrary, by density it follows that
 \begin{align}
\left\lvert \partial_t \right\rvert^{s} u_{xx} = \left\lvert \partial_t \right\rvert^{2+s}\left( V(x) u - h(x) P_\mathfrak{R}[\mathcal{N} \ast u^3] \right)
\end{align}
\begin{align}
\left\lvert \partial_t \right\rvert^{s} u_{xx} = \left\lvert \partial_t \right\rvert^{2+s}\left( V(x) u - h(x) P_\mathfrak{R}[\mathcal{N} \ast u^3] \right)
\end{align} holds. The term on the right-hand side lies in ![]() $L^p(\mathbb{R} \times \mathbb{T})$ by Lemmas 4.1 and 4.3 and the first part of the proof. Thus,
$L^p(\mathbb{R} \times \mathbb{T})$ by Lemmas 4.1 and 4.3 and the first part of the proof. Thus, ![]() $\left\lvert \partial_t \right\rvert^{s} u_{xx} \in L^p(\mathbb{R} \times \mathbb{T})$ and
$\left\lvert \partial_t \right\rvert^{s} u_{xx} \in L^p(\mathbb{R} \times \mathbb{T})$ and ![]() $\left\lvert \partial_t \right\rvert^{s} u \in W^{2, p}(\mathbb{R} \times \mathbb{T})$.
$\left\lvert \partial_t \right\rvert^{s} u \in W^{2, p}(\mathbb{R} \times \mathbb{T})$.
Part 3: Assume (R), i.e.  $\mathcal{G} \in C_b^l(\mathbb{R}; \mathcal{M}(\mathbb{T}))$,
$\mathcal{G} \in C_b^l(\mathbb{R}; \mathcal{M}(\mathbb{T}))$,  $h \in C_b^l(\mathbb{R})$. First, we have
$h \in C_b^l(\mathbb{R})$. First, we have ![]() $\left\lvert \partial_t \right\rvert^{s} u \in C_b(\mathbb{R} \times \mathbb{T})$ by Part 1 and Sobolev’s embedding. Continuity of
$\left\lvert \partial_t \right\rvert^{s} u \in C_b(\mathbb{R} \times \mathbb{T})$ by Part 1 and Sobolev’s embedding. Continuity of ![]() $\mathcal{G}, h$ shows that the right-hand side of (19) is continuous, so
$\mathcal{G}, h$ shows that the right-hand side of (19) is continuous, so ![]() $\left\lvert \partial_t \right\rvert^{s} u_{xx} \in C_b(\mathbb{R} \times \mathbb{T})$ holds, and in particular
$\left\lvert \partial_t \right\rvert^{s} u_{xx} \in C_b(\mathbb{R} \times \mathbb{T})$ holds, and in particular  $\left\lvert \partial_t \right\rvert^{s} u \in C_b^2(\mathbb{R} \times \mathbb{T})$.
$\left\lvert \partial_t \right\rvert^{s} u \in C_b^2(\mathbb{R} \times \mathbb{T})$.
For l > 0 we argue by induction over ![]() $k=0,\ldots, l$. We use that by (19) we have
$k=0,\ldots, l$. We use that by (19) we have
 \begin{align*}
\partial_x^{k+2} \left\lvert \partial_t \right\rvert^{s} u = \partial_x^k \left\lvert \partial_t \right\rvert^{s+2} \left(V(x) u - h(x) \mathcal{N} \ast u^3\right)
\end{align*}
\begin{align*}
\partial_x^{k+2} \left\lvert \partial_t \right\rvert^{s} u = \partial_x^k \left\lvert \partial_t \right\rvert^{s+2} \left(V(x) u - h(x) \mathcal{N} \ast u^3\right)
\end{align*} where the right-hand side lies in ![]() $L^2(\mathbb{R} \times \mathbb{T}) \cap C_b(\mathbb{R} \times \mathbb{T})$ by the product rule and the induction hypothesis. This allows us to conclude
$L^2(\mathbb{R} \times \mathbb{T}) \cap C_b(\mathbb{R} \times \mathbb{T})$ by the product rule and the induction hypothesis. This allows us to conclude  $\left\lvert \partial_t \right\rvert^{s} u \in W^{2+k,2}(\mathbb{R} \times \mathbb{T}) \cap C_b^{k+2}(\mathbb{R} \times \mathbb{T})$.
$\left\lvert \partial_t \right\rvert^{s} u \in W^{2+k,2}(\mathbb{R} \times \mathbb{T}) \cap C_b^{k+2}(\mathbb{R} \times \mathbb{T})$.
Recall for the first type of nonlinearity (6.i) that the profile w of the electric field is given by ![]() $w=u$. For the second type of nonlinearity (6.ii), by (15) the profile satisfies
$w=u$. For the second type of nonlinearity (6.ii), by (15) the profile satisfies ![]() $P_\mathfrak{R}[w] = (\mathcal{N}\ast)^{-1} u$ where
$P_\mathfrak{R}[w] = (\mathcal{N}\ast)^{-1} u$ where ![]() $P_\mathfrak{S}[w]$ solves a differential equation. Therefore we need to discuss next the regularity of w for the second type of nonlinearity, which is done in the following analogue to Proposition 4.4.
$P_\mathfrak{S}[w]$ solves a differential equation. Therefore we need to discuss next the regularity of w for the second type of nonlinearity, which is done in the following analogue to Proposition 4.4.
Proposition 4.5. Let ![]() $u \in H$ be a critical point of
$u \in H$ be a critical point of ![]() $J$. Define
$J$. Define ![]() $w = w_1 + w_2$ where
$w = w_1 + w_2$ where
Then w satisfies ![]() $\left\lvert \partial_t \right\rvert^{s} w \in W^{2,p}(\mathbb{R} \times \mathbb{T})$ for all
$\left\lvert \partial_t \right\rvert^{s} w \in W^{2,p}(\mathbb{R} \times \mathbb{T})$ for all ![]() $s \in \mathbb{R}$,
$s \in \mathbb{R}$, ![]() $p \in [2, \infty]$ and solves
$p \in [2, \infty]$ and solves
If (R) holds, we moreover have  $\left\lvert \partial_t \right\rvert^{s} w \in W^{2+l,2}(\mathbb{R} \times \mathbb{T}) \cap C_b^{2+l}(\mathbb{R} \times \mathbb{T})$.
$\left\lvert \partial_t \right\rvert^{s} w \in W^{2+l,2}(\mathbb{R} \times \mathbb{T}) \cap C_b^{2+l}(\mathbb{R} \times \mathbb{T})$.
Proof. First, by Lemma 4.3 and Proposition 4.4 we see that the function  $w_1 := (\mathcal{N}\ast)^{-1} u := \sum_{k \in \mathfrak{R}} \frac{1}{\mathcal{F}_k[\mathcal{N}]} \hat u_k(x) e_k(t)$ satisfies
$w_1 := (\mathcal{N}\ast)^{-1} u := \sum_{k \in \mathfrak{R}} \frac{1}{\mathcal{F}_k[\mathcal{N}]} \hat u_k(x) e_k(t)$ satisfies ![]() $\left\lvert \partial_t \right\rvert^{s} w_1 \in W^{2,p}(\mathbb{R} \times \mathbb{T})$ for
$\left\lvert \partial_t \right\rvert^{s} w_1 \in W^{2,p}(\mathbb{R} \times \mathbb{T})$ for ![]() $s \in \mathbb{R}, p \in [2, \infty]$, with additional regularity if
$s \in \mathbb{R}, p \in [2, \infty]$, with additional regularity if ![]() $\mathcal{G}, h$ fulfills (R). Applying
$\mathcal{G}, h$ fulfills (R). Applying ![]() $(\mathcal{N}\ast)^{-1}$ to (18) we see that w 1 solves
$(\mathcal{N}\ast)^{-1}$ to (18) we see that w 1 solves
Let us now turn our attention to w 2 and define the space
 \begin{align*}
H_2 := \left\{ v \in H^1(\mathbb{R} \times \mathbb{T}) \colon \hat v_k \equiv 0\ \text{for }\ k \in \mathfrak{R} \cup \left\{ 0 \right\} \right\}.
\end{align*}
\begin{align*}
H_2 := \left\{ v \in H^1(\mathbb{R} \times \mathbb{T}) \colon \hat v_k \equiv 0\ \text{for }\ k \in \mathfrak{R} \cup \left\{ 0 \right\} \right\}.
\end{align*}
Since ![]() $V_k(x)$ is bounded and positive, the Riesz representation theorem provides
$V_k(x)$ is bounded and positive, the Riesz representation theorem provides ![]() $w_2 \in H_2$ with
$w_2 \in H_2$ with
 \begin{align}
\int_{\mathbb{R} \times \mathbb{T}} \partial_x w_2 \cdot \partial_x v + V(x) \partial_t w_2 \cdot \partial_t v\ \mathrm{d}(x, t)
= - \int_{\mathbb{R} \times \mathbb{T}} h(x) \partial_t^2 P_\mathfrak{S}[u^3] \cdot v\ \mathrm{d} (x, t)
\end{align}
\begin{align}
\int_{\mathbb{R} \times \mathbb{T}} \partial_x w_2 \cdot \partial_x v + V(x) \partial_t w_2 \cdot \partial_t v\ \mathrm{d}(x, t)
= - \int_{\mathbb{R} \times \mathbb{T}} h(x) \partial_t^2 P_\mathfrak{S}[u^3] \cdot v\ \mathrm{d} (x, t)
\end{align}
for all ![]() $v \in H_2$.
$v \in H_2$.
Similarly as for solutions u of ![]() $J'(u)[v] = 0$ for
$J'(u)[v] = 0$ for ![]() $v \in H$, we obtain regularity for the solution w 2 to (20). In contrast to
$v \in H$, we obtain regularity for the solution w 2 to (20). In contrast to ![]() $J$, where critical points satisfy a truly nonlinear equation, the right-hand side of (20) is independent of w 2 and its regularity properties have been established in Proposition 4.4. Let us sketch the arguments:
$J$, where critical points satisfy a truly nonlinear equation, the right-hand side of (20) is independent of w 2 and its regularity properties have been established in Proposition 4.4. Let us sketch the arguments:
As in Lemma 4.2 we find ![]() $\left\lvert \partial_t \right\rvert^{s} w_2 \in H_2$ for
$\left\lvert \partial_t \right\rvert^{s} w_2 \in H_2$ for ![]() $s \in \mathbb{R}$. Using that the 0-th Fourier mode of
$s \in \mathbb{R}$. Using that the 0-th Fourier mode of ![]() $h(x) \partial_t^2 P_\mathfrak{S}[u^3]$ vanishes, w 2 satisfies
$h(x) \partial_t^2 P_\mathfrak{S}[u^3]$ vanishes, w 2 satisfies
By the fractional Leibniz rule from Lemma 4.1, the regularity properties of u from Proposition 4.4 and the boundedness of the Fourier symbol of ![]() $P_\mathfrak{S}$ we find that the right-hand side of (21) lies in L 2. Therefore
$P_\mathfrak{S}$ we find that the right-hand side of (21) lies in L 2. Therefore ![]() $\left\lvert \partial_t \right\rvert^{s} w_2 \in W^{2,2}(\mathbb{R} \times \mathbb{T}) \subseteq L^\infty(\mathbb{R} \times \mathbb{T})$ holds for
$\left\lvert \partial_t \right\rvert^{s} w_2 \in W^{2,2}(\mathbb{R} \times \mathbb{T}) \subseteq L^\infty(\mathbb{R} \times \mathbb{T})$ holds for ![]() $s \in \mathbb{R}$ and (21) shows
$s \in \mathbb{R}$ and (21) shows ![]() $\left\lvert \partial_t \right\rvert^{s} w_2 \in W^{2,p}(\mathbb{R} \times \mathbb{T})$ for
$\left\lvert \partial_t \right\rvert^{s} w_2 \in W^{2,p}(\mathbb{R} \times \mathbb{T})$ for ![]() $s \in \mathbb{R}$,
$s \in \mathbb{R}$, ![]() $p \in [2, \infty]$. The additional regularity when
$p \in [2, \infty]$. The additional regularity when ![]() $\mathcal{G}, h$ satisfy (R) can then be shown as in Proposition 4.4 by iteratively applying space-derivatives to (21).
$\mathcal{G}, h$ satisfy (R) can then be shown as in Proposition 4.4 by iteratively applying space-derivatives to (21).
Lastly, we discuss the regularity of the corresponding electromagnetic fields.
Proof of Theorem 1.3 for slab geometries
Let u be a nontrivial critical point of ![]() $J$. If the nonlinearity is given by
$J$. If the nonlinearity is given by ![]() $N(w) = \mathcal{N} \ast w^3$ then we set
$N(w) = \mathcal{N} \ast w^3$ then we set ![]() $w:= u$. If otherwise
$w:= u$. If otherwise ![]() $N(w) = (\mathcal{N} \ast w)^3$ then let w be from Proposition 4.5. Then we define
$N(w) = (\mathcal{N} \ast w)^3$ then let w be from Proposition 4.5. Then we define ![]() $W := \partial_t^{-1} w$ and reconstruct the electromagnetic fields by
$W := \partial_t^{-1} w$ and reconstruct the electromagnetic fields by
 \begin{align*}
\mathbf{E}(\mathbf{x}, t) &= w(x, t - \tfrac{1}{c} z) \cdot \begin{pmatrix}
0 \\ 1 \\ 0
\end{pmatrix},
&\mathbf{B}(\mathbf{x}, t) &= - \begin{pmatrix}
\tfrac{1}{c} w(x, t - \tfrac{1}{c} z) \\ 0 \\ W_x(x, t - \tfrac{1}{c} z)
\end{pmatrix}
\\ \mathbf{D}(\mathbf{x}, t) &= \epsilon_0 \left( w + \mathcal{G} \ast w + h(x) N(w) \right) \cdot \begin{pmatrix}
0 \\ 1 \\ 0
\end{pmatrix},
&\mathbf{H}(\mathbf{x}, t) &= \tfrac{1}{\mu_0} \mathbf{B}(\mathbf{x}, t).
\end{align*}
\begin{align*}
\mathbf{E}(\mathbf{x}, t) &= w(x, t - \tfrac{1}{c} z) \cdot \begin{pmatrix}
0 \\ 1 \\ 0
\end{pmatrix},
&\mathbf{B}(\mathbf{x}, t) &= - \begin{pmatrix}
\tfrac{1}{c} w(x, t - \tfrac{1}{c} z) \\ 0 \\ W_x(x, t - \tfrac{1}{c} z)
\end{pmatrix}
\\ \mathbf{D}(\mathbf{x}, t) &= \epsilon_0 \left( w + \mathcal{G} \ast w + h(x) N(w) \right) \cdot \begin{pmatrix}
0 \\ 1 \\ 0
\end{pmatrix},
&\mathbf{H}(\mathbf{x}, t) &= \tfrac{1}{\mu_0} \mathbf{B}(\mathbf{x}, t).
\end{align*}Due to Propositions 4.4 and 4.5 we have the inclusions
and assuming (R) we moreover have
 \begin{align*}
\partial_t^n \mathbf{E} \in \tilde C_b^{2+l}(\Omega; \mathbb{R}^3),
\qquad
\partial_t^n \mathbf{B}, \partial_t^n \mathbf{H} \in \tilde C_b^{1+l}(\Omega; \mathbb{R}^3),
\qquad
\partial_t^n \mathbf{D} \in \tilde C_b^{l}(\Omega; \mathbb{R}^3)
\end{align*}
\begin{align*}
\partial_t^n \mathbf{E} \in \tilde C_b^{2+l}(\Omega; \mathbb{R}^3),
\qquad
\partial_t^n \mathbf{B}, \partial_t^n \mathbf{H} \in \tilde C_b^{1+l}(\Omega; \mathbb{R}^3),
\qquad
\partial_t^n \mathbf{D} \in \tilde C_b^{l}(\Omega; \mathbb{R}^3)
\end{align*} for any domain ![]() $\Omega = \mathbb{R} \times [y, y+1] \times [z, z + 1] \times [t, t+1]$ and all
$\Omega = \mathbb{R} \times [y, y+1] \times [z, z + 1] \times [t, t+1]$ and all ![]() $n \in \mathbb{N}$,
$n \in \mathbb{N}$, ![]() $p \in [2, \infty]$ with norm bounds independent of
$p \in [2, \infty]$ with norm bounds independent of ![]() $y, z, t$. By direct calculation one checks that the fields
$y, z, t$. By direct calculation one checks that the fields ![]() $\mathbf{E}, \mathbf{D}, \mathbf{B}, \mathbf{H}$ solve Maxwell’s equations (1), (2).
$\mathbf{E}, \mathbf{D}, \mathbf{B}, \mathbf{H}$ solve Maxwell’s equations (1), (2).
Proof of Remark 1.5.
To show that there exist infinitely many solutions, we search for breather solutions with time period ![]() $\frac{T}{n}$ instead of T. If we define the corresponding time-domain
$\frac{T}{n}$ instead of T. If we define the corresponding time-domain  $\mathbb{T}_n := \mathbb{R} /_{\frac{T}{n} \mathbb{Z}}$ then the k-th Fourier coefficient of a
$\mathbb{T}_n := \mathbb{R} /_{\frac{T}{n} \mathbb{Z}}$ then the k-th Fourier coefficient of a ![]() $\frac{T}{n}$-periodic function f, when understood as a
$\frac{T}{n}$-periodic function f, when understood as a ![]() $\mathbb{T}$-periodic function, satisfies
$\mathbb{T}$-periodic function, satisfies ![]() $\mathcal{F}_k[f \colon \mathbb{T}_n \to \mathbb{R}] = \mathcal{F}_{nk}[f \colon \mathbb{T} \to \mathbb{R}]$. Therefore, by the above arguments there exists a
$\mathcal{F}_k[f \colon \mathbb{T}_n \to \mathbb{R}] = \mathcal{F}_{nk}[f \colon \mathbb{T} \to \mathbb{R}]$. Therefore, by the above arguments there exists a ![]() $\frac{T}{n}$-periodic breather solution
$\frac{T}{n}$-periodic breather solution ![]() $(\mathbf{E}_n, \mathbf{D}_n, \mathbf{B}_n, \mathbf{H}_n)$ to (1), (2) with minimal period
$(\mathbf{E}_n, \mathbf{D}_n, \mathbf{B}_n, \mathbf{H}_n)$ to (1), (2) with minimal period ![]() $T_n \gt 0$ for all such
$T_n \gt 0$ for all such ![]() $n \in \mathbb{N}$ where
$n \in \mathbb{N}$ where ![]() $\mathfrak{R} \cap n \mathbb{Z} \neq \emptyset$. By assumption, the set
$\mathfrak{R} \cap n \mathbb{Z} \neq \emptyset$. By assumption, the set ![]() $\left\{ n \in \mathbb{N} \colon \mathfrak{R} \cap n \mathbb{Z} \neq \emptyset \right\}$ is infinite. Since Tn is a divisor of
$\left\{ n \in \mathbb{N} \colon \mathfrak{R} \cap n \mathbb{Z} \neq \emptyset \right\}$ is infinite. Since Tn is a divisor of ![]() $\frac{T}{n}$ the minimal period Tn goes to 0 for
$\frac{T}{n}$ the minimal period Tn goes to 0 for ![]() $n \to \infty$. Hence infinitely many among the breather solutions
$n \to \infty$. Hence infinitely many among the breather solutions ![]() $(\mathbf{E}_n, \mathbf{D}_n, \mathbf{B}_n, \mathbf{H}_n)$ must be mutually distinct.
$(\mathbf{E}_n, \mathbf{D}_n, \mathbf{B}_n, \mathbf{H}_n)$ must be mutually distinct.
5. Modifications for the cylindrical geometry
In this section, we discuss the cylindrical problem, that is, we consider equation (8.2) instead of (8.1). The only difference between the two problems is in the spatial differential operator, where we now work with  $-\partial_r^2 - \tfrac{1}{r} \partial_r + \tfrac{1}{r^2}$ on the domain
$-\partial_r^2 - \tfrac{1}{r} \partial_r + \tfrac{1}{r^2}$ on the domain ![]() $r \in [0, \infty)$ instead of
$r \in [0, \infty)$ instead of ![]() $-\partial_x^2$ for
$-\partial_x^2$ for ![]() $x \in \mathbb{R}$. The differential operator
$x \in \mathbb{R}$. The differential operator  $- \partial_r^2 - \tfrac{1}{r} \partial_r$ is the 2d Laplacian for radially symmetric functions, and
$- \partial_r^2 - \tfrac{1}{r} \partial_r$ is the 2d Laplacian for radially symmetric functions, and ![]() $\tfrac{1}{r^2}$ is an additional positive term. Hence it is natural to equip the domain
$\tfrac{1}{r^2}$ is an additional positive term. Hence it is natural to equip the domain ![]() $[0, \infty)$ with the measure
$[0, \infty)$ with the measure ![]() $r \mathrm{d} r$, and to identify functions on it with radially symmetric functions of the variables
$r \mathrm{d} r$, and to identify functions on it with radially symmetric functions of the variables ![]() $(x, y) \in \mathbb{R}^2$ via
$(x, y) \in \mathbb{R}^2$ via  $r = \sqrt{x^2 + y^2}$. We use the subscript “
$r = \sqrt{x^2 + y^2}$. We use the subscript “![]() $\mathrm{rad}$” to denote spaces of functions that are radially symmetric in (x, y). Since the term
$\mathrm{rad}$” to denote spaces of functions that are radially symmetric in (x, y). Since the term  $\int_0^\infty\frac{u^2}{r^2}\,r\mathrm d r$ cannot be controlled by the
$\int_0^\infty\frac{u^2}{r^2}\,r\mathrm d r$ cannot be controlled by the  $H^1_\mathrm{rad}$-Sobolev norm of u (recall that Hardy’s inequality fails in two dimensions) we need to add this term in the form domain of the differential operator.
$H^1_\mathrm{rad}$-Sobolev norm of u (recall that Hardy’s inequality fails in two dimensions) we need to add this term in the form domain of the differential operator.
We will discuss how the arguments from Sections 2 to 4 have to be adapted to treat the cylindrical problem. We use the same structure as in these sections. In order to not repeat the previous chapters, we discuss in detail only results that require new techniques to adapt them to the cylindrical geometry and roughly sketch the other results.
5.1. Modifications for Sections 2 and 3
In analogy to Definitions 2.1 and 2.2, we define the functional of interest ![]() ${\tilde J}$ and its domain
${\tilde J}$ and its domain ![]() ${\tilde H}$ (replacing
${\tilde H}$ (replacing ![]() $J$ and
$J$ and ![]() $H$).
$H$).
Definition 5.1. We define the space
 \begin{align*}
{\tilde H} := \left\{ u \in L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r, t)) \colon \hat u_k = 0\ \text{for } k \in \mathbb{Z}_\mathrm{even} \cup \mathfrak{S}, \left\lVert u \right\rVert_{\tilde H}^2 := \langle\!\langle u , u \rangle\!\rangle_{\tilde H} \lt \infty \right\}
\end{align*}
\begin{align*}
{\tilde H} := \left\{ u \in L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r, t)) \colon \hat u_k = 0\ \text{for } k \in \mathbb{Z}_\mathrm{even} \cup \mathfrak{S}, \left\lVert u \right\rVert_{\tilde H}^2 := \langle\!\langle u , u \rangle\!\rangle_{\tilde H} \lt \infty \right\}
\end{align*}with the two equivalent inner products
 \begin{align*}
\langle\!\langle u , v \rangle\!\rangle_{\tilde H} &:= \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}
\int_0^\infty \left(\hat u_k' \overline{\hat v_k'} + \bigl(\tfrac{1}{r^2} + \omega^2 k^2\bigr) \hat u_k \overline{\hat v_k} \right) \,r\mathrm{d}r
\\ \left\langle u , v \right\rangle_{\tilde H} &:= \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_0^\infty \bigl(\hat u_k' \overline{\hat v_k'} + \bigl(\tfrac{1}{r^2} + \omega^2 k^2 \tilde V_k(r)\bigr) \hat u_k \overline{\hat v_k}\bigr)\ r\mathrm{d}r
.\end{align*}
\begin{align*}
\langle\!\langle u , v \rangle\!\rangle_{\tilde H} &:= \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}
\int_0^\infty \left(\hat u_k' \overline{\hat v_k'} + \bigl(\tfrac{1}{r^2} + \omega^2 k^2\bigr) \hat u_k \overline{\hat v_k} \right) \,r\mathrm{d}r
\\ \left\langle u , v \right\rangle_{\tilde H} &:= \sum_{k \in \mathfrak{R}} \frac{1}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]} \int_0^\infty \bigl(\hat u_k' \overline{\hat v_k'} + \bigl(\tfrac{1}{r^2} + \omega^2 k^2 \tilde V_k(r)\bigr) \hat u_k \overline{\hat v_k}\bigr)\ r\mathrm{d}r
.\end{align*} where  $\tilde V_k(r) := \tfrac{1}{c^2} - 1 - \mathcal{F}_k[\mathcal{G}(r)]$. On
$\tilde V_k(r) := \tfrac{1}{c^2} - 1 - \mathcal{F}_k[\mathcal{G}(r)]$. On ![]() ${\tilde H}$, we define the functional
${\tilde H}$, we define the functional
 \begin{align*}
{\tilde J}(u) := \tfrac12\left\langle u , u \right\rangle_{\tilde H} - \tfrac14 \int_{[0, \infty) \times \mathbb{T}} h(x) u^4 \,r\mathrm{d}(r,t)
\quad\text{for}\quad
u \in {\tilde H}
\end{align*}
\begin{align*}
{\tilde J}(u) := \tfrac12\left\langle u , u \right\rangle_{\tilde H} - \tfrac14 \int_{[0, \infty) \times \mathbb{T}} h(x) u^4 \,r\mathrm{d}(r,t)
\quad\text{for}\quad
u \in {\tilde H}
\end{align*} so that its critical points ![]() $u \in {\tilde H}$ satisfy
$u \in {\tilde H}$ satisfy
 \begin{align*}
{\tilde J}'(u)[v]
= \left\langle u , v \right\rangle_{\tilde H} - \int_{[0, \infty) \times \mathbb{T}} h(x) u^3 v \,r\mathrm{d}(r,t) = 0
\quad\text{for}\quad
v \in {\tilde H}.
\end{align*}
\begin{align*}
{\tilde J}'(u)[v]
= \left\langle u , v \right\rangle_{\tilde H} - \int_{[0, \infty) \times \mathbb{T}} h(x) u^3 v \,r\mathrm{d}(r,t) = 0
\quad\text{for}\quad
v \in {\tilde H}.
\end{align*} As a first step, we discuss the embedding properties of ![]() ${\tilde H}$.
${\tilde H}$.
Lemma 5.2. For any ![]() $p \in (2, p^\star)$ with
$p \in (2, p^\star)$ with  $p^\star = \frac{6}{3 - \alpha}$ (
$p^\star = \frac{6}{3 - \alpha}$ (![]() $p^\star = \infty$ if
$p^\star = \infty$ if ![]() $\alpha \geq 3$), the embedding
$\alpha \geq 3$), the embedding ![]() ${\tilde H} \hookrightarrow L^p([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ is compact. Moreover,
${\tilde H} \hookrightarrow L^p([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ is compact. Moreover, ![]() ${\tilde H} \hookrightarrow L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ is continuous and
${\tilde H} \hookrightarrow L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ is continuous and  ${\tilde H} \hookrightarrow L^2_\mathrm{loc}([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ is compact.
${\tilde H} \hookrightarrow L^2_\mathrm{loc}([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ is compact.
Proof. We interpret a function ![]() $u \colon [0, \infty) \times \mathbb{T} \to \mathbb{R}$ as a function of the three variables
$u \colon [0, \infty) \times \mathbb{T} \to \mathbb{R}$ as a function of the three variables ![]() $(x,y,t)$ which is radially symmetric in (x, y) via
$(x,y,t)$ which is radially symmetric in (x, y) via  $r = \sqrt{x^2 + y^2}$. Let σρ be the surface measure of the sphere
$r = \sqrt{x^2 + y^2}$. Let σρ be the surface measure of the sphere ![]() $S_\rho \subseteq \mathbb{R}^2$ of radius ρ centered at 0, normalized such that
$S_\rho \subseteq \mathbb{R}^2$ of radius ρ centered at 0, normalized such that ![]() $\sigma_\rho(S_\rho) = 1$, and continued by 0 to a Borel measure on
$\sigma_\rho(S_\rho) = 1$, and continued by 0 to a Borel measure on ![]() $\mathbb{R}^2$. Using the Hansen-Bessel formula (cf. [Reference Temme34, equation 9.19]), we see that its Fourier transform is given by
$\mathbb{R}^2$. Using the Hansen-Bessel formula (cf. [Reference Temme34, equation 9.19]), we see that its Fourier transform is given by
 \begin{align*}
\mathcal{F}^{-1}_{(x,y)}(\sigma_\rho)
= \frac{1}{(2\pi)^2} \int_0^{2 \pi} \mathrm{e}^{- \mathrm{i} r \rho \sin(\varphi)} \mathrm{d} \varphi
= \frac{1}{2 \pi} J_0(r \rho)
\end{align*}
\begin{align*}
\mathcal{F}^{-1}_{(x,y)}(\sigma_\rho)
= \frac{1}{(2\pi)^2} \int_0^{2 \pi} \mathrm{e}^{- \mathrm{i} r \rho \sin(\varphi)} \mathrm{d} \varphi
= \frac{1}{2 \pi} J_0(r \rho)
\end{align*} where J 0 is the Bessel function of first kind. Using ![]() $\left\lvert J_0(s) \right\rvert \lesssim s^{-\theta}$ for
$\left\lvert J_0(s) \right\rvert \lesssim s^{-\theta}$ for  $\theta \in [0, \tfrac12]$ (cf. [Reference Gradštejn and Ryžik13]) we obtain
$\theta \in [0, \tfrac12]$ (cf. [Reference Gradštejn and Ryžik13]) we obtain
 \begin{align*}
\left\lVert r^\theta u \right\rVert_{L^\infty(\mathbb{R}^2 \times \mathbb{T})}
\lesssim \left\lVert \left\lvert \xi \right\rvert^{-\theta} \mathcal{F}_{\xi,k}[u] \right\rVert_{L^1(\mathbb{R}^2 \times \mathbb{Z})},
\end{align*}
\begin{align*}
\left\lVert r^\theta u \right\rVert_{L^\infty(\mathbb{R}^2 \times \mathbb{T})}
\lesssim \left\lVert \left\lvert \xi \right\rvert^{-\theta} \mathcal{F}_{\xi,k}[u] \right\rVert_{L^1(\mathbb{R}^2 \times \mathbb{Z})},
\end{align*} where we used that ![]() $\mathcal{F}_{\xi,k}[u]$ is radially symmetric in ξ. Note also that we have
$\mathcal{F}_{\xi,k}[u]$ is radially symmetric in ξ. Note also that we have  $\left\lVert u \right\rVert_{L^2(\mathbb{R}^2 \times \mathbb{T})} = \left\lVert \mathcal{F}_{\xi,k}[u] \right\rVert_{L^2(\mathbb{R}^2 \times \mathbb{Z})}$. This allows us to use the Riesz-Thorin interpolation theorem (cf. [Reference Lunardi16]) and get (with
$\left\lVert u \right\rVert_{L^2(\mathbb{R}^2 \times \mathbb{T})} = \left\lVert \mathcal{F}_{\xi,k}[u] \right\rVert_{L^2(\mathbb{R}^2 \times \mathbb{Z})}$. This allows us to use the Riesz-Thorin interpolation theorem (cf. [Reference Lunardi16]) and get (with ![]() $\mathrm{d}\#$ denoting the counting measure) that the map
$\mathrm{d}\#$ denoting the counting measure) that the map
 \begin{equation*}
T: \left\{\begin{array}{rcl}
L_\mathrm{rad}^{p'}(\mathbb{R}^2\times\mathbb{Z}; |\xi|^{-2\theta}\mathrm{d} \xi\otimes \mathrm{d}\#) & \to & L^p_\mathrm{rad}(\mathbb{R}^2\times\mathbb{T}; r^{-2\theta}\mathrm{d} (x,t)), \\
v & \mapsto & r^\theta \mathcal{F}^{-1}_{(x,y),t} (|\xi|^{-\theta} v)
\end{array} \right.
\end{equation*}
\begin{equation*}
T: \left\{\begin{array}{rcl}
L_\mathrm{rad}^{p'}(\mathbb{R}^2\times\mathbb{Z}; |\xi|^{-2\theta}\mathrm{d} \xi\otimes \mathrm{d}\#) & \to & L^p_\mathrm{rad}(\mathbb{R}^2\times\mathbb{T}; r^{-2\theta}\mathrm{d} (x,t)), \\
v & \mapsto & r^\theta \mathcal{F}^{-1}_{(x,y),t} (|\xi|^{-\theta} v)
\end{array} \right.
\end{equation*} is bounded for all ![]() $p\in [2,\infty]$. To see this note that with
$p\in [2,\infty]$. To see this note that with ![]() $v =|\xi|^{-\theta} \mathcal{F}_{\xi,k}[u]$ we have
$v =|\xi|^{-\theta} \mathcal{F}_{\xi,k}[u]$ we have
 \begin{align*}
\|v\|_{L^{p'}(\mathbb{R}^2\times\mathbb{Z}; |\xi|^{-2\theta}\mathrm{d} \xi\otimes\mathrm{d}\#)} &= \|\mathcal{F}_{\xi,k}[u] |\xi|^{-\theta_0}\|_{L^{p'}(\mathbb{R}^2\times\mathbb{Z}; \mathrm{d} \xi\otimes\mathrm{d}\#)} \\
\|Tv\|_{L^p(\mathbb{R}^2\times\mathbb{T}; r^{-2\theta}\mathrm{d} (x,t))} &= \|r^{\theta_0} u\|_{L^p(\mathbb{R}^2\times\mathbb{T}; \mathrm{d} (x,t))}
\end{align*}
\begin{align*}
\|v\|_{L^{p'}(\mathbb{R}^2\times\mathbb{Z}; |\xi|^{-2\theta}\mathrm{d} \xi\otimes\mathrm{d}\#)} &= \|\mathcal{F}_{\xi,k}[u] |\xi|^{-\theta_0}\|_{L^{p'}(\mathbb{R}^2\times\mathbb{Z}; \mathrm{d} \xi\otimes\mathrm{d}\#)} \\
\|Tv\|_{L^p(\mathbb{R}^2\times\mathbb{T}; r^{-2\theta}\mathrm{d} (x,t))} &= \|r^{\theta_0} u\|_{L^p(\mathbb{R}^2\times\mathbb{T}; \mathrm{d} (x,t))}
\end{align*} where  $\theta_0 = \theta \frac{(p-2)}{p}$ ranges through
$\theta_0 = \theta \frac{(p-2)}{p}$ ranges through  $[0,\tfrac12- \tfrac1p]$ as θ runs through
$[0,\tfrac12- \tfrac1p]$ as θ runs through  $[0,\tfrac12]$. Thus we have
$[0,\tfrac12]$. Thus we have
 \begin{align*}
\left\lVert r^{\theta_0} u \right\rVert_{L^p(\mathbb{R}^2 \times \mathbb{T})}
&\lesssim \left\lVert \left\lvert \xi \right\rvert^{-\theta_0} \mathcal{F}_{\xi, k}[u] \right\rVert_{L^{p'}(\mathbb{R}^2 \times \mathfrak{R})}
\\ &\leq \left\lVert \left\lvert \xi \right\rvert^{-\theta_0} \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\left\lvert \xi \right\rvert^2 + \omega^2 k^2}} \right\rVert_{L^r(\mathbb{R}^2 \times \mathfrak{R})}
\left\lVert \sqrt{\frac{\left\lvert \xi \right\rvert^2 + \omega^2 k^2}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}} \mathcal{F}_{\xi,k}[u] \right\rVert_{L^2(\mathbb{R}^2 \times \mathfrak{R})}
\end{align*}
\begin{align*}
\left\lVert r^{\theta_0} u \right\rVert_{L^p(\mathbb{R}^2 \times \mathbb{T})}
&\lesssim \left\lVert \left\lvert \xi \right\rvert^{-\theta_0} \mathcal{F}_{\xi, k}[u] \right\rVert_{L^{p'}(\mathbb{R}^2 \times \mathfrak{R})}
\\ &\leq \left\lVert \left\lvert \xi \right\rvert^{-\theta_0} \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\left\lvert \xi \right\rvert^2 + \omega^2 k^2}} \right\rVert_{L^r(\mathbb{R}^2 \times \mathfrak{R})}
\left\lVert \sqrt{\frac{\left\lvert \xi \right\rvert^2 + \omega^2 k^2}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}} \mathcal{F}_{\xi,k}[u] \right\rVert_{L^2(\mathbb{R}^2 \times \mathfrak{R})}
\end{align*} where  $\frac{1}{r} = \frac{1}{2} - \frac{1}{p} \lt \frac{\alpha}{6}$. By the choice of
$\frac{1}{r} = \frac{1}{2} - \frac{1}{p} \lt \frac{\alpha}{6}$. By the choice of ![]() $p^\star$ and assumption (A5), the Lr-norm is finite provided θ 0 is chosen sufficiently small, and the L 2-norm can be estimated against
$p^\star$ and assumption (A5), the Lr-norm is finite provided θ 0 is chosen sufficiently small, and the L 2-norm can be estimated against ![]() $\left\lVert u \right\rVert_{\tilde H}$.
$\left\lVert u \right\rVert_{\tilde H}$.
For the particular choice ![]() $\theta_0 = 0$, this shows that the embedding
$\theta_0 = 0$, this shows that the embedding  ${\tilde H} \hookrightarrow L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ is continuous. Moreover, we can argue similarly as in the proof of Lemma 2.4 to verify that the local embedding
${\tilde H} \hookrightarrow L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ is continuous. Moreover, we can argue similarly as in the proof of Lemma 2.4 to verify that the local embedding  ${\tilde H} \hookrightarrow L^p_{\mathrm{rad},\mathrm{loc}}(\mathbb{R}^2 \times \mathbb{T})$ is compact.
${\tilde H} \hookrightarrow L^p_{\mathrm{rad},\mathrm{loc}}(\mathbb{R}^2 \times \mathbb{T})$ is compact.
It remains to show that  ${\tilde H} \hookrightarrow L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ is compact for p ≠ 2. For R > 0 consider the compact map
${\tilde H} \hookrightarrow L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ is compact for p ≠ 2. For R > 0 consider the compact map  $E_R \colon {\tilde H} \to L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T}), u \mapsto u \mathbb{1}_{B_R(0) \times \mathbb{T}}$. Using the above inequality we have
$E_R \colon {\tilde H} \to L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T}), u \mapsto u \mathbb{1}_{B_R(0) \times \mathbb{T}}$. Using the above inequality we have
 \begin{align*}
\left\lVert E_R u - u \right\rVert_p
\leq \left\lVert \left(\tfrac{r}{R}\right)^{\theta_0} u \right\rVert_p
\lesssim R^{-\theta_0} \left\lVert u \right\rVert_{\tilde H}
\end{align*}
\begin{align*}
\left\lVert E_R u - u \right\rVert_p
\leq \left\lVert \left(\tfrac{r}{R}\right)^{\theta_0} u \right\rVert_p
\lesssim R^{-\theta_0} \left\lVert u \right\rVert_{\tilde H}
\end{align*} so by choosing any admissible ![]() $\theta_0 \gt 0$ and taking the limit
$\theta_0 \gt 0$ and taking the limit ![]() $R \to \infty$ we see that the embedding
$R \to \infty$ we see that the embedding  $I \colon {\tilde H} \to L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ is compact as the uniform limit of a sequence of compact operators.
$I \colon {\tilde H} \to L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ is compact as the uniform limit of a sequence of compact operators.
Notice that, unlike in the slab setting (cf. Lemma 2.4), the embedding of Lemma 5.2 is compact for p > 2. This is why we do not require additional assumptions (A6a) or (A6b) in the cylindrical setting. One can then show existence of ground states similar to the “compact” case (A6a) of Section 3. The only difference is that existence of a convergent subsequence of ![]() $h(r) u_n^3$ in
$h(r) u_n^3$ in  $L^{4/3}_\mathrm{rad}(\mathbb{R}^2\times\mathbb{T})$ is guaranteed by the compact embedding instead of decay properties of h.
$L^{4/3}_\mathrm{rad}(\mathbb{R}^2\times\mathbb{T})$ is guaranteed by the compact embedding instead of decay properties of h.
5.2. Modifications for Section 4
In the following, we show in Propositions 5.3 and 5.4 two regularity results that are the cylindrical counterparts to Propositions 4.4 and 4.5.
Here, arguments will get more difficult since the cylindrical geometry is effectively 2-dimensional in space (compared to 1d for the slab problem). For some arguments it will be advantageous to view the ![]() $\tfrac{1}{r^2}$ not as an additional order 0 term, but as part of the differential operator. From [Reference Bartsch, Dohnal, Plum and Reichel3] we use the identity
$\tfrac{1}{r^2}$ not as an additional order 0 term, but as part of the differential operator. From [Reference Bartsch, Dohnal, Plum and Reichel3] we use the identity
 \begin{align}
\partial_r^2 + \tfrac{1}{r} \partial_r - \tfrac{1}{r^2}
= \tfrac{1}{r^2} \partial_r r^3 \partial_r \tfrac{1}{r},
\end{align}
\begin{align}
\partial_r^2 + \tfrac{1}{r} \partial_r - \tfrac{1}{r^2}
= \tfrac{1}{r^2} \partial_r r^3 \partial_r \tfrac{1}{r},
\end{align} which means that up to the multiplicative factors  $r, \tfrac{1}{r}$ we are dealing with
$r, \tfrac{1}{r}$ we are dealing with  $\tfrac{1}{r^3} \partial_r r^3 \partial_r$, which is the Laplacian of a radially symmetric function in 4 dimensions.
$\tfrac{1}{r^3} \partial_r r^3 \partial_r$, which is the Laplacian of a radially symmetric function in 4 dimensions.
Similar to Proposition 4.4 we show that u and its derivatives lie in ![]() $L^2 \cap L^\infty$.
$L^2 \cap L^\infty$.
Proposition 5.3. Let ![]() $u \in {\tilde H}$ be a critical point of
$u \in {\tilde H}$ be a critical point of ![]() ${\tilde J}$. Then the terms
${\tilde J}$. Then the terms
 \begin{align*}
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} (\tfrac{u}{r}),
\qquad
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \partial_r (\tfrac{u}{r}),
\qquad
r \left\lvert \partial_t \right\rvert^{s} \partial_r^2 (\tfrac{u}{r})
\end{align*}
\begin{align*}
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} (\tfrac{u}{r}),
\qquad
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \partial_r (\tfrac{u}{r}),
\qquad
r \left\lvert \partial_t \right\rvert^{s} \partial_r^2 (\tfrac{u}{r})
\end{align*} lie in ![]() $L^{p}([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ for all
$L^{p}([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ for all ![]() $s \in \mathbb{R}$ and
$s \in \mathbb{R}$ and ![]() $p \in [2, \infty]$, and
$p \in [2, \infty]$, and ![]() $u$ solves pointwise
$u$ solves pointwise
 \begin{align*}
(-\partial_r^2 - \tfrac1r \partial_r + \tfrac{1}{r^2} - V(x) \partial_t^2) u + h(x) \partial_t^2 (\mathcal{N} \ast u^3) = 0.
\end{align*}
\begin{align*}
(-\partial_r^2 - \tfrac1r \partial_r + \tfrac{1}{r^2} - V(x) \partial_t^2) u + h(x) \partial_t^2 (\mathcal{N} \ast u^3) = 0.
\end{align*}If (R) holds, then the terms
 \begin{align*}
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \partial_r^n (\tfrac{u}{r})
\quad\text{for}\quad 0 \leq n \leq l+1
\qquad \text{as well as} \qquad
r \left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2} (\tfrac{u}{r})
\end{align*}
\begin{align*}
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \partial_r^n (\tfrac{u}{r})
\quad\text{for}\quad 0 \leq n \leq l+1
\qquad \text{as well as} \qquad
r \left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2} (\tfrac{u}{r})
\end{align*} lie in ![]() $L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t)) \cap C_b([0, \infty) \times \mathbb{T})$. Moreover, the second term vanishes at
$L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t)) \cap C_b([0, \infty) \times \mathbb{T})$. Moreover, the second term vanishes at ![]() $r=0$, and the same holds for the first term when
$r=0$, and the same holds for the first term when ![]() $n$ is odd.
$n$ is odd.
Proof. Part 1: First, following the proof of Lemma 4.2 we obtain ![]() $\left\lvert \partial_t \right\rvert^{s} u \in {\tilde H}$ for all
$\left\lvert \partial_t \right\rvert^{s} u \in {\tilde H}$ for all ![]() $s \in \mathbb{R}$.
$s \in \mathbb{R}$.
Next, for ![]() $p \in [2, \infty)$ we calculate
$p \in [2, \infty)$ we calculate
 \begin{align*}
&\left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_p
\lesssim \left\lVert \left\lvert \omega k \right\rvert^s \mathcal{F}_{\xi,k} \right\rVert_{L^{p'}(\mathbb{R}^2 \times \mathfrak{R})}
\\ &\leq \left\lVert \left\lvert \omega k \right\rvert^{-1} \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\left\lvert \xi \right\rvert^2 + \omega^2 k^2}} \right\rVert_{L^r(\mathbb{R}^2 \times \mathfrak{R})}
\left\lVert \left\lvert \omega k \right\rvert^{s + 1} \sqrt{\frac{\left\lvert \xi \right\rvert^2 + \omega^2 k^2}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}} \mathcal{F}_{\xi,k}[u] \right\rVert_{L^2(\mathbb{R}^2 \times \mathfrak{R})}
\lesssim \left\lVert \left\lvert \partial_t \right\rvert^{s + 1} u \right\rVert_{\tilde H}.
\end{align*}
\begin{align*}
&\left\lVert \left\lvert \partial_t \right\rvert^{s} u \right\rVert_p
\lesssim \left\lVert \left\lvert \omega k \right\rvert^s \mathcal{F}_{\xi,k} \right\rVert_{L^{p'}(\mathbb{R}^2 \times \mathfrak{R})}
\\ &\leq \left\lVert \left\lvert \omega k \right\rvert^{-1} \sqrt{\frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\left\lvert \xi \right\rvert^2 + \omega^2 k^2}} \right\rVert_{L^r(\mathbb{R}^2 \times \mathfrak{R})}
\left\lVert \left\lvert \omega k \right\rvert^{s + 1} \sqrt{\frac{\left\lvert \xi \right\rvert^2 + \omega^2 k^2}{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}} \mathcal{F}_{\xi,k}[u] \right\rVert_{L^2(\mathbb{R}^2 \times \mathfrak{R})}
\lesssim \left\lVert \left\lvert \partial_t \right\rvert^{s + 1} u \right\rVert_{\tilde H}.
\end{align*} Here  $1 - \frac{1}{p} = \frac{1}{p'} = \frac{1}{r} + \frac{1}{2}$, and the Lr-norm is finite since r > 2 and therefore
$1 - \frac{1}{p} = \frac{1}{p'} = \frac{1}{r} + \frac{1}{2}$, and the Lr-norm is finite since r > 2 and therefore
 \begin{align*}
\sum_{k \in \mathbb{R}} \left\lvert \omega k \right\rvert^{- r} \int_{\mathbb{R}^2} \left( \frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\left\lvert \xi \right\rvert^2 + \omega^2 k^2} \right)^{\frac r2} \mathrm{d}\xi = \int_{\mathbb{R}^2} \left(\frac{1}{\left\lvert \xi \right\rvert^2 + 1} \right)^{\frac{r}{2}} \mathrm{d}\xi \cdot \sum_{k \in \mathbb{R}} \left\lvert \omega k \right\rvert^{2-r} \mathcal{F}_k[\mathcal{N}]^{\frac r2}
\lesssim \sum_{k \in \mathfrak{R}} \left\lvert k \right\rvert^{2 - \frac74 r} \lt \infty.
\end{align*}
\begin{align*}
\sum_{k \in \mathbb{R}} \left\lvert \omega k \right\rvert^{- r} \int_{\mathbb{R}^2} \left( \frac{\omega^2 k^2 \mathcal{F}_k[\mathcal{N}]}{\left\lvert \xi \right\rvert^2 + \omega^2 k^2} \right)^{\frac r2} \mathrm{d}\xi = \int_{\mathbb{R}^2} \left(\frac{1}{\left\lvert \xi \right\rvert^2 + 1} \right)^{\frac{r}{2}} \mathrm{d}\xi \cdot \sum_{k \in \mathbb{R}} \left\lvert \omega k \right\rvert^{2-r} \mathcal{F}_k[\mathcal{N}]^{\frac r2}
\lesssim \sum_{k \in \mathfrak{R}} \left\lvert k \right\rvert^{2 - \frac74 r} \lt \infty.
\end{align*} Part 2: Arguing as in part 2 of the proof of Proposition 4.4 we have that  $\left\lvert \partial_t \right\rvert^{s} u_r, \tfrac{1}{r} \left\lvert \partial_t \right\rvert^{s} u \in L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ for
$\left\lvert \partial_t \right\rvert^{s} u_r, \tfrac{1}{r} \left\lvert \partial_t \right\rvert^{s} u \in L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ for ![]() $s \in \mathbb{R}$ and
$s \in \mathbb{R}$ and
 \begin{align}
\left\lvert \partial_t \right\rvert^{s} u_{rr} + \tfrac{1}{r} \left\lvert \partial_t \right\rvert^{s} u_r - \tfrac{1}{r^2} \left\lvert \partial_t \right\rvert^{s} u
= \left\lvert \partial_t \right\rvert^{s+2} \left(V(r)u - h(r) P_\mathfrak{R}[\mathcal{N} \ast u^3]\right)
\end{align}
\begin{align}
\left\lvert \partial_t \right\rvert^{s} u_{rr} + \tfrac{1}{r} \left\lvert \partial_t \right\rvert^{s} u_r - \tfrac{1}{r^2} \left\lvert \partial_t \right\rvert^{s} u
= \left\lvert \partial_t \right\rvert^{s+2} \left(V(r)u - h(r) P_\mathfrak{R}[\mathcal{N} \ast u^3]\right)
\end{align}holds pointwise. From now on arguments differ depending on if r is large or small, and we discuss these cases in part 3 and part 4, respectively.
Part 3a: Let ![]() $r \gt R_1$ for fixed
$r \gt R_1$ for fixed ![]() $R_1 \gt 0$. Then part 1 combined with (23) shows that
$R_1 \gt 0$. Then part 1 combined with (23) shows that  $\Delta_r \left\lvert \partial_t \right\rvert^{s} u := (\partial_r^2 + \tfrac{1}{r} \partial_r) \left\lvert \partial_t \right\rvert^{s} u \in L^p([R_1, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ for
$\Delta_r \left\lvert \partial_t \right\rvert^{s} u := (\partial_r^2 + \tfrac{1}{r} \partial_r) \left\lvert \partial_t \right\rvert^{s} u \in L^p([R_1, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$ for ![]() $p \in [2, \infty)$. Now choose a cutoff
$p \in [2, \infty)$. Now choose a cutoff ![]() $\psi_1 \in C^\infty([0, \infty))$ with
$\psi_1 \in C^\infty([0, \infty))$ with ![]() $\operatorname{supp} \psi_1 \subseteq (R_1, \infty)$ and
$\operatorname{supp} \psi_1 \subseteq (R_1, \infty)$ and ![]() $\psi_1 \equiv 1$ on
$\psi_1 \equiv 1$ on ![]() $[R_2, \infty)$ for
$[R_2, \infty)$ for ![]() $R_2 \gt R_1$. Then, interpreting
$R_2 \gt R_1$. Then, interpreting ![]() $v_1 := \psi_1(r) u$ as a function of the three variables
$v_1 := \psi_1(r) u$ as a function of the three variables ![]() $(x, y, t)$ via
$(x, y, t)$ via  $r = \sqrt{x^2 + y^2}$ and continuing by zero, we have
$r = \sqrt{x^2 + y^2}$ and continuing by zero, we have  $\left\lvert \partial_t \right\rvert^{s} v_1 \in L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ and
$\left\lvert \partial_t \right\rvert^{s} v_1 \in L^p_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ and
 \begin{align*}
\Delta_{(x,y)} \left\lvert \partial_t \right\rvert^{s} v_1 = \Delta_r \psi_1 \cdot \left\lvert \partial_t \right\rvert^{s} u + 2 \partial_r \psi_1 \cdot \partial_r \left\lvert \partial_t \right\rvert^{s} u + \psi_1 \cdot \Delta_r \left\lvert \partial_t \right\rvert^{s} u \in L^2(\mathbb{R}^2 \times \mathbb{T}).
\end{align*}
\begin{align*}
\Delta_{(x,y)} \left\lvert \partial_t \right\rvert^{s} v_1 = \Delta_r \psi_1 \cdot \left\lvert \partial_t \right\rvert^{s} u + 2 \partial_r \psi_1 \cdot \partial_r \left\lvert \partial_t \right\rvert^{s} u + \psi_1 \cdot \Delta_r \left\lvert \partial_t \right\rvert^{s} u \in L^2(\mathbb{R}^2 \times \mathbb{T}).
\end{align*} This shows  $\left\lvert \partial_t \right\rvert^{s} v_1 \in H^2_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$, and by Sobolev’s embedding we in particular have
$\left\lvert \partial_t \right\rvert^{s} v_1 \in H^2_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$, and by Sobolev’s embedding we in particular have ![]() $\left\lvert \partial_t \right\rvert^{s} u \in L^\infty([R_2, \infty) \times \mathbb{T})$,
$\left\lvert \partial_t \right\rvert^{s} u \in L^\infty([R_2, \infty) \times \mathbb{T})$, ![]() $\left\lvert \partial_t \right\rvert^{s} u_r \in L^6([R_2, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$.
$\left\lvert \partial_t \right\rvert^{s} u_r \in L^6([R_2, \infty) \times \mathbb{T}; r \mathrm{d} (r,t))$.
Similar to above, but now with a smooth cutoff ψ 2 such that ![]() $\operatorname{supp} \psi_2 \subseteq (R_2, \infty)$,
$\operatorname{supp} \psi_2 \subseteq (R_2, \infty)$, ![]() $\psi_2 \equiv 1$ on
$\psi_2 \equiv 1$ on ![]() $[R_3, \infty)$ for
$[R_3, \infty)$ for ![]() $R_3 \gt R_2$, we see that
$R_3 \gt R_2$, we see that ![]() $v_2 := \psi_2(r) u$ satisfies
$v_2 := \psi_2(r) u$ satisfies  $\Delta_{(x,y)} \left\lvert \partial_t \right\rvert^{s} v_2 \in L^6_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ where again (23) was used. Thus
$\Delta_{(x,y)} \left\lvert \partial_t \right\rvert^{s} v_2 \in L^6_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ where again (23) was used. Thus  $\left\lvert \partial_t \right\rvert^{s} v_2 \in W^{2,6}_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ by Lp-boundedness of the Riesz transform, cf. [Reference Grafakos14, Corollary 5.2.8]. By Sobolev’s embedding we have
$\left\lvert \partial_t \right\rvert^{s} v_2 \in W^{2,6}_\mathrm{rad}(\mathbb{R}^2 \times \mathbb{T})$ by Lp-boundedness of the Riesz transform, cf. [Reference Grafakos14, Corollary 5.2.8]. By Sobolev’s embedding we have ![]() $ \partial_r \left\lvert \partial_t \right\rvert^{s} u \in L^\infty([R_3, \infty) \times \mathbb{T})$, and then
$ \partial_r \left\lvert \partial_t \right\rvert^{s} u \in L^\infty([R_3, \infty) \times \mathbb{T})$, and then ![]() $\Delta_r \left\lvert \partial_t \right\rvert^{s} u \in L^\infty([R_3, \infty) \times \mathbb{T})$ by (23). So far we have shown
$\Delta_r \left\lvert \partial_t \right\rvert^{s} u \in L^\infty([R_3, \infty) \times \mathbb{T})$ by (23). So far we have shown
This shows the first part of Proposition 5.3 for ![]() $r \gt R_3$, where
$r \gt R_3$, where ![]() $R_3 \gt 0$ can be chosen arbitrarily.
$R_3 \gt 0$ can be chosen arbitrarily.
Part 3b: We assume (R), i.e.  $\mathcal{G}, h \in C_b^l$, and still consider large r. From Part 3a we obtain
$\mathcal{G}, h \in C_b^l$, and still consider large r. From Part 3a we obtain ![]() $\left\lvert \partial_t \right\rvert^{s} u, \left\lvert \partial_t \right\rvert^{s} u_r, \in C_b([R, \infty) \times \mathbb{T})$ from the high Sobolev regularity and therefore also
$\left\lvert \partial_t \right\rvert^{s} u, \left\lvert \partial_t \right\rvert^{s} u_r, \in C_b([R, \infty) \times \mathbb{T})$ from the high Sobolev regularity and therefore also ![]() $\left\lvert \partial_t \right\rvert^{s} u_{rr}\in C_b([R, \infty) \times \mathbb{T})$ by applying (23). Now
$\left\lvert \partial_t \right\rvert^{s} u_{rr}\in C_b([R, \infty) \times \mathbb{T})$ by applying (23). Now ![]() $\left\lvert \partial_t \right\rvert^{s} \partial_r^n u \in L^2([R, \infty) \times \mathbb{T}; r \mathrm{d} (r,t)) \cap C_b([R, \infty) \times \mathbb{T})$ for
$\left\lvert \partial_t \right\rvert^{s} \partial_r^n u \in L^2([R, \infty) \times \mathbb{T}; r \mathrm{d} (r,t)) \cap C_b([R, \infty) \times \mathbb{T})$ for ![]() $2 \lt n \leq l + 2$ can be shown iteratively by applying space-derivatives to (23) and using that all terms except the highest order space-derivative term lie in
$2 \lt n \leq l + 2$ can be shown iteratively by applying space-derivatives to (23) and using that all terms except the highest order space-derivative term lie in ![]() $L^2([R, \infty) \times \mathbb{T}; r \mathrm{d} (r,t)) \cap C_b([R, \infty) \times \mathbb{T})$ by the induction hypothesis.
$L^2([R, \infty) \times \mathbb{T}; r \mathrm{d} (r,t)) \cap C_b([R, \infty) \times \mathbb{T})$ by the induction hypothesis.
Part 4a: Let us now consider small r. We use the representation via the 4d Laplacian, i.e. we consider ![]() $U \colon \mathbb{R}^4 \times \mathbb{T} \to \mathbb{R}$,
$U \colon \mathbb{R}^4 \times \mathbb{T} \to \mathbb{R}$,  $U(X, t) = U(X_1, X_2, X_3, X_4, t) = \tfrac{1}{\left\lvert X \right\rvert} u(\left\lvert X \right\rvert, t)$. Notice that the L 2-norms are equivalent, i.e.
$U(X, t) = U(X_1, X_2, X_3, X_4, t) = \tfrac{1}{\left\lvert X \right\rvert} u(\left\lvert X \right\rvert, t)$. Notice that the L 2-norms are equivalent, i.e.
 \begin{align*}
\left\lVert \tfrac{1}{\left\lvert X \right\rvert} f(\left\lvert X \right\rvert, t) \right\rVert_{L^2(B_R \times \mathbb{T})} = \sqrt{2} \pi \left\lVert f \right\rVert_{L^2([0, R] \times \mathbb{T}; r \mathrm{d}(r,t))}
\end{align*}
\begin{align*}
\left\lVert \tfrac{1}{\left\lvert X \right\rvert} f(\left\lvert X \right\rvert, t) \right\rVert_{L^2(B_R \times \mathbb{T})} = \sqrt{2} \pi \left\lVert f \right\rVert_{L^2([0, R] \times \mathbb{T}; r \mathrm{d}(r,t))}
\end{align*} holds with ![]() $B_R \subseteq \mathbb{R}^4$ denoting the ball of radius R centered at 0. Multiplying (23) by
$B_R \subseteq \mathbb{R}^4$ denoting the ball of radius R centered at 0. Multiplying (23) by ![]() $\tfrac{1}{r}$, setting
$\tfrac{1}{r}$, setting ![]() $r = \left\lvert X \right\rvert$, and recalling (22) we have
$r = \left\lvert X \right\rvert$, and recalling (22) we have
 \begin{align}
\Delta_X \left\lvert \partial_t \right\rvert^{s} U = V(r) \left\lvert \partial_t \right\rvert^{s+2} U - \tfrac{h(r)}{r} \left\lvert \partial_t \right\rvert^{s+2} P_\mathfrak{R}[\mathcal{N} \ast u^3].
\end{align}
\begin{align}
\Delta_X \left\lvert \partial_t \right\rvert^{s} U = V(r) \left\lvert \partial_t \right\rvert^{s+2} U - \tfrac{h(r)}{r} \left\lvert \partial_t \right\rvert^{s+2} P_\mathfrak{R}[\mathcal{N} \ast u^3].
\end{align} By part 1 the right-hand side of (24) lies in ![]() $L^{2}(\mathbb{R}^4 \times \mathbb{T})$. Therefore
$L^{2}(\mathbb{R}^4 \times \mathbb{T})$. Therefore ![]() $\left\lvert \partial_t \right\rvert^{s} U \in H^2(\mathbb{R}^4 \times \mathbb{T})$, which by Sobolev’s embeddings shows
$\left\lvert \partial_t \right\rvert^{s} U \in H^2(\mathbb{R}^4 \times \mathbb{T})$, which by Sobolev’s embeddings shows  $\left\lvert \partial_t \right\rvert^{s} \partial_r U \in L^{\frac{10}{3}}(\mathbb{R}^4 \times \mathbb{T}), \left\lvert \partial_t \right\rvert^{s} U \in L^{10}(\mathbb{R}^4 \times \mathbb{T})$. Now let
$\left\lvert \partial_t \right\rvert^{s} \partial_r U \in L^{\frac{10}{3}}(\mathbb{R}^4 \times \mathbb{T}), \left\lvert \partial_t \right\rvert^{s} U \in L^{10}(\mathbb{R}^4 \times \mathbb{T})$. Now let ![]() $R_1 \gt 0$ and
$R_1 \gt 0$ and ![]() $\psi_1 \in C_c^\infty([0, R_1))$ be a smooth cutoff function with
$\psi_1 \in C_c^\infty([0, R_1))$ be a smooth cutoff function with ![]() $\psi_1 \equiv 1$ on
$\psi_1 \equiv 1$ on ![]() $[0, R_2]$ for some
$[0, R_2]$ for some ![]() $0 \lt R_2 \lt R_1$ and set
$0 \lt R_2 \lt R_1$ and set ![]() $v_1 := \psi_1(\left\lvert X \right\rvert) U$. Then, since
$v_1 := \psi_1(\left\lvert X \right\rvert) U$. Then, since
and since we may write (24) as
we have ![]() $\Delta_X \left\lvert \partial_t \right\rvert^{s} v_1 \in L^{{10}/{3}}(\mathbb{R}^4 \times \mathbb{T})$ which by Lp-boundedness of the Riesz transform implies
$\Delta_X \left\lvert \partial_t \right\rvert^{s} v_1 \in L^{{10}/{3}}(\mathbb{R}^4 \times \mathbb{T})$ which by Lp-boundedness of the Riesz transform implies ![]() $\left\lvert \partial_t \right\rvert^{s} v_1 \in W^{2,{10}/{3}}(\mathbb{R}^4 \times \mathbb{T})$. From Sobolev’s embedding we have
$\left\lvert \partial_t \right\rvert^{s} v_1 \in W^{2,{10}/{3}}(\mathbb{R}^4 \times \mathbb{T})$. From Sobolev’s embedding we have ![]() $\left\lvert \partial_t \right\rvert^{s} U \in L^\infty(B_{R_2} \times \mathbb{T})$,
$\left\lvert \partial_t \right\rvert^{s} U \in L^\infty(B_{R_2} \times \mathbb{T})$, ![]() $\nabla_X \left\lvert \partial_t \right\rvert^{s} U \in L^{10}(B_{R_2} \times \mathbb{T})$. Repeating this argument with
$\nabla_X \left\lvert \partial_t \right\rvert^{s} U \in L^{10}(B_{R_2} \times \mathbb{T})$. Repeating this argument with ![]() $0 \lt R_3 \lt R_2$ and a cutoff function
$0 \lt R_3 \lt R_2$ and a cutoff function ![]() $\psi_2 \in C_c^\infty([0, R_2))$,
$\psi_2 \in C_c^\infty([0, R_2))$, ![]() $\psi_j \equiv 1$ on
$\psi_j \equiv 1$ on ![]() $[0, R_3]$ shows
$[0, R_3]$ shows ![]() $\nabla_X \left\lvert \partial_t \right\rvert^{s} U \in L^\infty(B_{R_3} \times \mathbb{T})$. Using (25), regularity of the terms in the claim of Proposition 5.3 follows since
$\nabla_X \left\lvert \partial_t \right\rvert^{s} U \in L^\infty(B_{R_3} \times \mathbb{T})$. Using (25), regularity of the terms in the claim of Proposition 5.3 follows since
 \begin{align*}
\left\lvert \partial_t \right\rvert^{s} \tfrac{u}{r} = \left\lvert \partial_t \right\rvert^{s} U \in L^\infty,
\qquad
\left\lvert \partial_t \right\rvert^{s} \partial_r (\tfrac{u}{r}) = \tfrac{X}{r} \cdot \nabla_X \left\lvert \partial_t \right\rvert^{s} U \in L^\infty,
\\ r \left\lvert \partial_t \right\rvert^{s} \partial_r^2 (\tfrac{u}{r}) = r \Delta_X \left\lvert \partial_t \right\rvert^{s} U - 3 \tfrac{X}{r} \cdot \nabla_X \left\lvert \partial_t \right\rvert^{s} U \in L^\infty.
\end{align*}
\begin{align*}
\left\lvert \partial_t \right\rvert^{s} \tfrac{u}{r} = \left\lvert \partial_t \right\rvert^{s} U \in L^\infty,
\qquad
\left\lvert \partial_t \right\rvert^{s} \partial_r (\tfrac{u}{r}) = \tfrac{X}{r} \cdot \nabla_X \left\lvert \partial_t \right\rvert^{s} U \in L^\infty,
\\ r \left\lvert \partial_t \right\rvert^{s} \partial_r^2 (\tfrac{u}{r}) = r \Delta_X \left\lvert \partial_t \right\rvert^{s} U - 3 \tfrac{X}{r} \cdot \nabla_X \left\lvert \partial_t \right\rvert^{s} U \in L^\infty.
\end{align*} The Lp-estimates follow from these since ![]() $B_{R_3} \times \mathbb{T}$ has finite volume.
$B_{R_3} \times \mathbb{T}$ has finite volume.
Part 4b: Assume (R), and again consider small r. First, ![]() $\left\lvert \partial_t \right\rvert^{s} U, \nabla_X \left\lvert \partial_t \right\rvert^{s} U$ are continuous by Sobolev’s embedding, and continuity of
$\left\lvert \partial_t \right\rvert^{s} U, \nabla_X \left\lvert \partial_t \right\rvert^{s} U$ are continuous by Sobolev’s embedding, and continuity of ![]() $\Delta_X \left\lvert \partial_t \right\rvert^{s} U$ follows from this by (25). Existence and continuity of higher derivatives
$\Delta_X \left\lvert \partial_t \right\rvert^{s} U$ follows from this by (25). Existence and continuity of higher derivatives
 \begin{align*}
\nabla_X^n \Delta_X \left\lvert \partial_t \right\rvert^{s}\!\!U,
\qquad
\nabla_X^{n+1} \left\lvert \partial_t \right\rvert^{s}\!\!U,
\qquad
\nabla_X^n \left\lvert \partial_t \right\rvert^{s}\!\!U
\end{align*}
\begin{align*}
\nabla_X^n \Delta_X \left\lvert \partial_t \right\rvert^{s}\!\!U,
\qquad
\nabla_X^{n+1} \left\lvert \partial_t \right\rvert^{s}\!\!U,
\qquad
\nabla_X^n \left\lvert \partial_t \right\rvert^{s}\!\!U
\end{align*}
for ![]() $0 \lt n \leq l$ can again be shown using induction and repeatedly applying
$0 \lt n \leq l$ can again be shown using induction and repeatedly applying ![]() $\nabla_X$ to (25). This implies continuity of all terms except the highest order one in Proposition 5.3 since
$\nabla_X$ to (25). This implies continuity of all terms except the highest order one in Proposition 5.3 since  $\left\lvert \partial_t \right\rvert^{s} \partial_r^n (\tfrac{u}{r}) = (\nabla_X^n \left\lvert \partial_t \right\rvert^{s} U)[\tfrac{X}{r}, \dots, \tfrac{X}{r}]$. Moreover, odd r-derivatives of
$\left\lvert \partial_t \right\rvert^{s} \partial_r^n (\tfrac{u}{r}) = (\nabla_X^n \left\lvert \partial_t \right\rvert^{s} U)[\tfrac{X}{r}, \dots, \tfrac{X}{r}]$. Moreover, odd r-derivatives of ![]() $\frac{u}{r}$ vanish at r = 0 since U is radially symmetric. For the highest order term we have
$\frac{u}{r}$ vanish at r = 0 since U is radially symmetric. For the highest order term we have
 \begin{align*}
(\nabla_X^l \Delta_X \left\lvert \partial_t \right\rvert^{s} U)[\tfrac{X}{r}, \dots, \tfrac{X}{r}]
= \left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2}(\tfrac{u}{r})
+ \left\lvert \partial_t \right\rvert^{s} \partial_r^l (\tfrac{3}{r} \partial_r (\tfrac{u}{r})),
\end{align*}
\begin{align*}
(\nabla_X^l \Delta_X \left\lvert \partial_t \right\rvert^{s} U)[\tfrac{X}{r}, \dots, \tfrac{X}{r}]
= \left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2}(\tfrac{u}{r})
+ \left\lvert \partial_t \right\rvert^{s} \partial_r^l (\tfrac{3}{r} \partial_r (\tfrac{u}{r})),
\end{align*} which shows that  $\left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2}(\tfrac{u}{r})$ is continuous away from 0. To see the behaviour of the highest order term near r = 0 we use the differentiability properties of U and a Taylor expansion of
$\left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2}(\tfrac{u}{r})$ is continuous away from 0. To see the behaviour of the highest order term near r = 0 we use the differentiability properties of U and a Taylor expansion of ![]() $\left\lvert \partial_t \right\rvert^{s}(\tfrac{u}{r})$ about r = 0 as follows. Let
$\left\lvert \partial_t \right\rvert^{s}(\tfrac{u}{r})$ about r = 0 as follows. Let ![]() $\left\lvert \partial_t \right\rvert^{s}(\tfrac{u}{r}) = T_{l+1}(\left\lvert \partial_t \right\rvert^{s} (\tfrac{u}{r}); 0) + f$ be the Taylor expansion of
$\left\lvert \partial_t \right\rvert^{s}(\tfrac{u}{r}) = T_{l+1}(\left\lvert \partial_t \right\rvert^{s} (\tfrac{u}{r}); 0) + f$ be the Taylor expansion of ![]() $\left\lvert \partial_t \right\rvert^{s}(\frac{u}{r})$ of degree l + 1 about r = 0 with remainder f. Then we have
$\left\lvert \partial_t \right\rvert^{s}(\frac{u}{r})$ of degree l + 1 about r = 0 with remainder f. Then we have
 \begin{align*}
\left\lvert \partial_t \right\rvert^{s} \partial_r^l (\tfrac{3}{r} \partial_r (\tfrac{u}{r}))
= \partial_r^l \left(\tfrac{3}{r} \partial_r \left[T_{l+1}(\left\lvert \partial_t \right\rvert^{s} \tfrac{u}{r}; 0)\right]\right)
+ \partial_r^l \left(\tfrac{3}{r} \partial_r f\right)
= \frac{3 (-1)^l}{l!}\frac{\left\lvert \partial_t \right\rvert^{s}(\tfrac{u}{r})_r(0)}{r^{l+1}} + \hbox{o}(\tfrac{1}{r})
= \hbox{o}(\tfrac{1}{r}),
\end{align*}
\begin{align*}
\left\lvert \partial_t \right\rvert^{s} \partial_r^l (\tfrac{3}{r} \partial_r (\tfrac{u}{r}))
= \partial_r^l \left(\tfrac{3}{r} \partial_r \left[T_{l+1}(\left\lvert \partial_t \right\rvert^{s} \tfrac{u}{r}; 0)\right]\right)
+ \partial_r^l \left(\tfrac{3}{r} \partial_r f\right)
= \frac{3 (-1)^l}{l!}\frac{\left\lvert \partial_t \right\rvert^{s}(\tfrac{u}{r})_r(0)}{r^{l+1}} + \hbox{o}(\tfrac{1}{r})
= \hbox{o}(\tfrac{1}{r}),
\end{align*} as r → 0 since ![]() $\left\lvert \partial_t \right\rvert^{s}(\tfrac{u}{r})_r(0)=0$ by radial symmetry. This shows that
$\left\lvert \partial_t \right\rvert^{s}(\tfrac{u}{r})_r(0)=0$ by radial symmetry. This shows that  $r \left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2}(\tfrac{u}{r}) \to 0$ as r → 0.
$r \left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2}(\tfrac{u}{r}) \to 0$ as r → 0.
Next, in Proposition 5.4, similar to Proposition 4.5 we discuss the second nonlinearity (6.ii).
Proposition 5.4. Let ![]() $u \in {\tilde H}$ be a critical point of
$u \in {\tilde H}$ be a critical point of ![]() ${\tilde J}$ and let the nonlinearity be given by
${\tilde J}$ and let the nonlinearity be given by ![]() $N(w) = \mathcal{N} \ast w^3$. Define
$N(w) = \mathcal{N} \ast w^3$. Define ![]() $w = w_1 + w_2$ where
$w = w_1 + w_2$ where
 \begin{align*}
w_1 = P_\mathfrak{R}[w] = (\mathcal{N}\ast)^{-1} u,
\quad
w_2 = P_\mathfrak{S}[w] = (-\partial_r^2 - \tfrac{1}{r} \partial_r + \tfrac{1}{r^2} - V(x) \partial_t^2)^{-1} (h(x) \partial_t^2 P_\mathfrak{S}[u^3]).
\end{align*}
\begin{align*}
w_1 = P_\mathfrak{R}[w] = (\mathcal{N}\ast)^{-1} u,
\quad
w_2 = P_\mathfrak{S}[w] = (-\partial_r^2 - \tfrac{1}{r} \partial_r + \tfrac{1}{r^2} - V(x) \partial_t^2)^{-1} (h(x) \partial_t^2 P_\mathfrak{S}[u^3]).
\end{align*}Then the functions
 \begin{align*}
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \tfrac{w}{r},
\qquad
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \partial_r (\tfrac{w}{r}),
\qquad
r \left\lvert \partial_t \right\rvert^{s} \partial_r^2 (\tfrac{w}{r})
\end{align*}
\begin{align*}
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \tfrac{w}{r},
\qquad
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \partial_r (\tfrac{w}{r}),
\qquad
r \left\lvert \partial_t \right\rvert^{s} \partial_r^2 (\tfrac{w}{r})
\end{align*} lie in ![]() $L^{p}([0, \infty) \times \mathbb{T}; r \mathrm{d}(r,t))$ for all
$L^{p}([0, \infty) \times \mathbb{T}; r \mathrm{d}(r,t))$ for all ![]() $s \in \mathbb{R}$ and
$s \in \mathbb{R}$ and ![]() $p \in [2, \infty]$, and
$p \in [2, \infty]$, and ![]() $w$ solves
$w$ solves
 \begin{align*}
(-\partial_r^2 - \tfrac1r \partial_r + \tfrac{1}{r^2} - V(x) \partial_t^2) w + h(x) \partial_t^2 (\mathcal{N} \ast w)^3 = 0.
\end{align*}
\begin{align*}
(-\partial_r^2 - \tfrac1r \partial_r + \tfrac{1}{r^2} - V(x) \partial_t^2) w + h(x) \partial_t^2 (\mathcal{N} \ast w)^3 = 0.
\end{align*}If (R) holds, then the terms
 \begin{align*}
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \partial_r^n (\tfrac{w}{r})
\quad\text{for}\quad 0 \leq n \leq l+1
\qquad \text{as well as} \qquad
r \left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2} (\tfrac{w}{r})
\end{align*}
\begin{align*}
\max\left\{ r, 1 \right\} \left\lvert \partial_t \right\rvert^{s} \partial_r^n (\tfrac{w}{r})
\quad\text{for}\quad 0 \leq n \leq l+1
\qquad \text{as well as} \qquad
r \left\lvert \partial_t \right\rvert^{s} \partial_r^{l+2} (\tfrac{w}{r})
\end{align*} lie in ![]() $L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t)) \cap C_b([0, \infty) \times \mathbb{T})$. Moreover, the second term vanishes at
$L^2([0, \infty) \times \mathbb{T}; r \mathrm{d} (r,t)) \cap C_b([0, \infty) \times \mathbb{T})$. Moreover, the second term vanishes at ![]() $r=0$, and the same holds for the first term when
$r=0$, and the same holds for the first term when ![]() $n$ is odd.
$n$ is odd.
Proof. We follow Proposition 4.5, and define w 2 by
 \begin{align*}
w_2 \in {\tilde H}_2 :=
\left\{ v \in H^1([0, \infty) \times \mathbb{T}; \,r\mathrm{d}(r,t) \colon \tfrac{1}{r} v \in L^2([0, \infty) \times \mathbb{T}; r \mathrm{d}(r,t)), \hat v_k \equiv 0\ \text{for } k \in \mathfrak{R} \cup \left\{ 0 \right\} \right\}
\end{align*}
\begin{align*}
w_2 \in {\tilde H}_2 :=
\left\{ v \in H^1([0, \infty) \times \mathbb{T}; \,r\mathrm{d}(r,t) \colon \tfrac{1}{r} v \in L^2([0, \infty) \times \mathbb{T}; r \mathrm{d}(r,t)), \hat v_k \equiv 0\ \text{for } k \in \mathfrak{R} \cup \left\{ 0 \right\} \right\}
\end{align*}
and
 \begin{align*}
\int_{[0,\infty) \times \mathbb{T}} \left( \partial_r w_2 \cdot \partial_r v + \tfrac{1}{r^2} w_2 \cdot v + V(r) \partial_t w_2 \cdot \partial_t v \right) \,r\mathrm{d}(r,t)
= - \int_{[0, \infty) \times \mathbb{T}} \left(h(r) \partial_t^2 P_\mathfrak{S}[u^3] \cdot v\right) \,r\mathrm{d}(r,t)
\end{align*}
\begin{align*}
\int_{[0,\infty) \times \mathbb{T}} \left( \partial_r w_2 \cdot \partial_r v + \tfrac{1}{r^2} w_2 \cdot v + V(r) \partial_t w_2 \cdot \partial_t v \right) \,r\mathrm{d}(r,t)
= - \int_{[0, \infty) \times \mathbb{T}} \left(h(r) \partial_t^2 P_\mathfrak{S}[u^3] \cdot v\right) \,r\mathrm{d}(r,t)
\end{align*} for all ![]() $v \in {\tilde H}_2$. Regularity of w 1 follows from Proposition 5.3, and the arguments therein can also be used to show regularity of w 2.
$v \in {\tilde H}_2$. Regularity of w 1 follows from Proposition 5.3, and the arguments therein can also be used to show regularity of w 2.
As the last part of this chapter, we discuss regularity of the electromagnetic wave profiles.
Proof of Theorem 1.3 for cylindrical geometries
Part 1: Let ![]() $u \in {\tilde H}$ be a nontrivial critical point of
$u \in {\tilde H}$ be a nontrivial critical point of ![]() ${\tilde J}$. For the nonlinearity
${\tilde J}$. For the nonlinearity ![]() $N(w) = \mathcal{N} \ast w^3$ set
$N(w) = \mathcal{N} \ast w^3$ set ![]() $w := u$, else let w be from Proposition 5.4. Define
$w := u$, else let w be from Proposition 5.4. Define ![]() $W := \partial_t^{-1} w$ and the electromagnetic fields by
$W := \partial_t^{-1} w$ and the electromagnetic fields by
 \begin{align*}
\mathbf{D}(\mathbf{x}, t) &= \epsilon_0 \left( w + \mathcal{G} \ast w + h(r) N(w)\right) \cdot \begin{pmatrix}
- y/r \\ x/r \\ 0
\end{pmatrix},
& \mathbf{E}(\mathbf{x}, t) &= w(r, t - \tfrac{1}{c} z) \cdot \begin{pmatrix}
- y/r \\ x/r \\ 0
\end{pmatrix},
\\ \mathbf{B}(\mathbf{x}, t) &= - \tfrac{1}{c} w \cdot \begin{pmatrix}
x/r \\ y/r \\ 0
\end{pmatrix} - (\tfrac{1}{r} W + W_r) \cdot \begin{pmatrix}
0 \\ 0 \\ 1
\end{pmatrix},
& \mathbf{H}(\mathbf{x}, t) &= \tfrac{1}{\mu_0} \mathbf{B}(\mathbf{x}, t).
\end{align*}
\begin{align*}
\mathbf{D}(\mathbf{x}, t) &= \epsilon_0 \left( w + \mathcal{G} \ast w + h(r) N(w)\right) \cdot \begin{pmatrix}
- y/r \\ x/r \\ 0
\end{pmatrix},
& \mathbf{E}(\mathbf{x}, t) &= w(r, t - \tfrac{1}{c} z) \cdot \begin{pmatrix}
- y/r \\ x/r \\ 0
\end{pmatrix},
\\ \mathbf{B}(\mathbf{x}, t) &= - \tfrac{1}{c} w \cdot \begin{pmatrix}
x/r \\ y/r \\ 0
\end{pmatrix} - (\tfrac{1}{r} W + W_r) \cdot \begin{pmatrix}
0 \\ 0 \\ 1
\end{pmatrix},
& \mathbf{H}(\mathbf{x}, t) &= \tfrac{1}{\mu_0} \mathbf{B}(\mathbf{x}, t).
\end{align*} By a straightforward calculation one sees that ![]() $\mathbf{E}, \mathbf{D}, \mathbf{B}, \mathbf{H}$ solve Maxwell’s equations (1), (2), so it remains to show their regularity. For simplicity we only consider E and only discuss spatial derivatives. Abbreviating
$\mathbf{E}, \mathbf{D}, \mathbf{B}, \mathbf{H}$ solve Maxwell’s equations (1), (2), so it remains to show their regularity. For simplicity we only consider E and only discuss spatial derivatives. Abbreviating ![]() $p(\mathbf{x}) := (-y, x, 0)$, denoting the Euclidean scalar product in
$p(\mathbf{x}) := (-y, x, 0)$, denoting the Euclidean scalar product in ![]() $\mathbb{R}^3$ by
$\mathbb{R}^3$ by ![]() $\left\langle \,\cdot\, , \,\cdot\, \right\rangle$ and the space derivative by
$\left\langle \,\cdot\, , \,\cdot\, \right\rangle$ and the space derivative by ![]() $D_\mathbf{x}$, we have
$D_\mathbf{x}$, we have
 \begin{align*}
\mathbf{E}
&= \frac{w}{r} p
\\ &= r \frac{w}{r} \frac{p}{r},
\\ D_\mathbf{x} \mathbf{E}[h]
&= \frac{w}{r} D_\mathbf{x} p[h] + \tfrac{1}{r} \partial_r \left(\frac{w}{r}\right) \bigl\langle \mathbf{x} , h \bigr\rangle p
\\ &= \frac{w}{r} D_\mathbf{x} p[h] + r \partial_r \left(\frac{w}{r}\right) \bigl\langle \frac{\mathbf{x}}{r} , h \bigr\rangle \frac{p}{r}
\\ D_\mathbf{x}^2 \mathbf{E}[h_1, h_2]
&= \tfrac{1}{r} \partial_r \left(\frac{w}{r}\right) \left[\bigl\langle \mathbf{x} , h_1 \bigr\rangle D_\mathbf{x} p[h_2] + \bigl\langle \mathbf{x} , h_2 \bigr\rangle D_\mathbf{x} p[h_1] + \bigl\langle h_1 , h_2 \bigr\rangle p\right]
\\ &\qquad+ \left(\tfrac{1}{r}\partial_r\right)^2\left(\frac{w}{r}\right) \bigl\langle \mathbf{x} , h_1 \bigr\rangle \bigl\langle \mathbf{x} , h_2 \bigr\rangle p,
\\ &= \partial_r \left(\frac{w}{r}\right) \left[\bigl\langle \frac{\mathbf{x}}{r} , h_1 \bigr\rangle D_\mathbf{x} p[h_2] + \bigl\langle \frac{\mathbf{x}}{r} , h_2 \bigr\rangle D_\mathbf{x} p[h_1] + \bigl\langle h_1 , h_2 \bigr\rangle\frac{p}{r}\right]
\\ &\qquad+ \left[ r \partial_r^2 \left(\frac{w}{r}\right) - \partial_r \left(\frac{w}{r}\right) \right] \bigl\langle \frac{\mathbf{x}}{r} , h_1 \bigr\rangle \bigl\langle \frac{\mathbf{x}}{r} , h_2 \bigr\rangle \frac{p}{r},
\end{align*}
\begin{align*}
\mathbf{E}
&= \frac{w}{r} p
\\ &= r \frac{w}{r} \frac{p}{r},
\\ D_\mathbf{x} \mathbf{E}[h]
&= \frac{w}{r} D_\mathbf{x} p[h] + \tfrac{1}{r} \partial_r \left(\frac{w}{r}\right) \bigl\langle \mathbf{x} , h \bigr\rangle p
\\ &= \frac{w}{r} D_\mathbf{x} p[h] + r \partial_r \left(\frac{w}{r}\right) \bigl\langle \frac{\mathbf{x}}{r} , h \bigr\rangle \frac{p}{r}
\\ D_\mathbf{x}^2 \mathbf{E}[h_1, h_2]
&= \tfrac{1}{r} \partial_r \left(\frac{w}{r}\right) \left[\bigl\langle \mathbf{x} , h_1 \bigr\rangle D_\mathbf{x} p[h_2] + \bigl\langle \mathbf{x} , h_2 \bigr\rangle D_\mathbf{x} p[h_1] + \bigl\langle h_1 , h_2 \bigr\rangle p\right]
\\ &\qquad+ \left(\tfrac{1}{r}\partial_r\right)^2\left(\frac{w}{r}\right) \bigl\langle \mathbf{x} , h_1 \bigr\rangle \bigl\langle \mathbf{x} , h_2 \bigr\rangle p,
\\ &= \partial_r \left(\frac{w}{r}\right) \left[\bigl\langle \frac{\mathbf{x}}{r} , h_1 \bigr\rangle D_\mathbf{x} p[h_2] + \bigl\langle \frac{\mathbf{x}}{r} , h_2 \bigr\rangle D_\mathbf{x} p[h_1] + \bigl\langle h_1 , h_2 \bigr\rangle\frac{p}{r}\right]
\\ &\qquad+ \left[ r \partial_r^2 \left(\frac{w}{r}\right) - \partial_r \left(\frac{w}{r}\right) \right] \bigl\langle \frac{\mathbf{x}}{r} , h_1 \bigr\rangle \bigl\langle \frac{\mathbf{x}}{r} , h_2 \bigr\rangle \frac{p}{r},
\end{align*} so Propositions 5.3 and 5.4 show that these terms lie in Lp for ![]() $p \in [2, \infty]$.
$p \in [2, \infty]$.
Part 2: Let us now assume (R). We need to show that higher order derivatives exist, are continuous and square-integrable. Away from r = 0, this is clear by Propositions 5.3 and 5.4, so it remains to show continuity of derivatives in r = 0. First, by induction one can show that for ![]() $0 \leq n \leq l+2$ the derivative
$0 \leq n \leq l+2$ the derivative ![]() $D_\mathbf{x}^n \mathbf{E}$ can be written as a sum
$D_\mathbf{x}^n \mathbf{E}$ can be written as a sum
 \begin{align*}
D_\mathbf{x}^n \mathbf{E} =
\sum_{j=\left\lceil \frac{n-1}{2} \right\rceil}^{n}(\tfrac{1}{r}\partial_r)^{j} \left(\frac{w}{r}\right) \cdot p_{n,j},
\end{align*}
\begin{align*}
D_\mathbf{x}^n \mathbf{E} =
\sum_{j=\left\lceil \frac{n-1}{2} \right\rceil}^{n}(\tfrac{1}{r}\partial_r)^{j} \left(\frac{w}{r}\right) \cdot p_{n,j},
\end{align*} where ![]() $p_{n,j}(\mathbf{x}) \colon (\mathbb{R}^3)^n \to \mathbb{R}^3$ is symmetric, n-multilinear, and its coefficients are homogeneous polynomials of degree
$p_{n,j}(\mathbf{x}) \colon (\mathbb{R}^3)^n \to \mathbb{R}^3$ is symmetric, n-multilinear, and its coefficients are homogeneous polynomials of degree ![]() $2 j + 1 - n$ in x. We use Taylor approximation and write
$2 j + 1 - n$ in x. We use Taylor approximation and write ![]() $\tfrac{w}{r} = T_{n-1}(\tfrac{w}{r}; 0) + f$ with Taylor polynomial
$\tfrac{w}{r} = T_{n-1}(\tfrac{w}{r}; 0) + f$ with Taylor polynomial ![]() $T_{n-1}(\tfrac{w}{r}; 0)$ and remainder f.
$T_{n-1}(\tfrac{w}{r}; 0)$ and remainder f.
Let us next consider summands with j < n. Recall that all odd Taylor coefficients are zero, so  $q_{n,j} := (\tfrac{1}{r} \partial_r)^{j} T_{n-1}(\tfrac{w}{r}; 0)$ is an even polynomial. In addition, we can estimate the remainder via
$q_{n,j} := (\tfrac{1}{r} \partial_r)^{j} T_{n-1}(\tfrac{w}{r}; 0)$ is an even polynomial. In addition, we can estimate the remainder via  $(\tfrac{1}{r} \partial_r)^{j} f = \hbox{o}(r^{n - 1 - 2 j})$ as r → 0. Thus
$(\tfrac{1}{r} \partial_r)^{j} f = \hbox{o}(r^{n - 1 - 2 j})$ as r → 0. Thus
 \begin{align*}
(\tfrac{1}{r}\partial_r)^j \left(\frac{w}{r}\right) \cdot p_{n,j}
= (q_{n,j}(r) + \hbox{o}(r^{n-1-2j})) p_{n,j} \to q_{n,j}(0) p_{n,j}(0)
\end{align*}
\begin{align*}
(\tfrac{1}{r}\partial_r)^j \left(\frac{w}{r}\right) \cdot p_{n,j}
= (q_{n,j}(r) + \hbox{o}(r^{n-1-2j})) p_{n,j} \to q_{n,j}(0) p_{n,j}(0)
\end{align*}as r → 0. Now let j = n. Similar to the above arguments, one can show
 \begin{align*}
\left[(\tfrac{1}{r}\partial_r)^{n} - \frac{1}{r^n} \partial_r^n\right] \left(\frac{w}{r}\right)
= q_{n,n}(r) + \hbox{o}(r^{-n-1})
\end{align*}
\begin{align*}
\left[(\tfrac{1}{r}\partial_r)^{n} - \frac{1}{r^n} \partial_r^n\right] \left(\frac{w}{r}\right)
= q_{n,n}(r) + \hbox{o}(r^{-n-1})
\end{align*} as r → 0 for some polynomial ![]() $q_{n,n}$. Thus
$q_{n,n}$. Thus
 \begin{align*}
D_\mathbf{x}^n \mathbf{E}
= \frac{1}{r^n} \partial_r^n (\tfrac{w}{r}) \cdot p_{n, n} + \sum_{j=\left\lceil \frac{n-1}{2} \right\rceil}^{n} q_{n,j}(r) p_{n,j}(\mathbf{x}) + \hbox{o}(1)
\to \sum_{j=\left\lceil \frac{n-1}{2} \right\rceil}^{n} q_{n,j}(0) p_{n,j}(0)
\end{align*}
\begin{align*}
D_\mathbf{x}^n \mathbf{E}
= \frac{1}{r^n} \partial_r^n (\tfrac{w}{r}) \cdot p_{n, n} + \sum_{j=\left\lceil \frac{n-1}{2} \right\rceil}^{n} q_{n,j}(r) p_{n,j}(\mathbf{x}) + \hbox{o}(1)
\to \sum_{j=\left\lceil \frac{n-1}{2} \right\rceil}^{n} q_{n,j}(0) p_{n,j}(0)
\end{align*} as r → 0 by Propositions 5.3 and 5.4. Since the argument for existence of infinitely many solutions is the same as for slab geometries at the end of Section 4, this completes the proof. Observe that ![]() $p_{n,j}(0) = 0$ for
$p_{n,j}(0) = 0$ for  $j \neq \frac{n+1}{2}$, so in particular all even derivatives of E vanish at 0.
$j \neq \frac{n+1}{2}$, so in particular all even derivatives of E vanish at 0.
Data availability statement
No data was produced.
Author contributions
Both authors contributed to and approved the final submitted draft.
Funding statement
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 258734477 – SFB 1173.
Competing interests
None.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.









