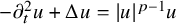Refine listing
Actions for selected content:
134 results in 35Cxx
A k-Hessian equation with a power nonlinearity source and self-similarity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-25
-
- Article
- Export citation
Impact of birth pulse and environment shift on population survival and propagation
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-27
-
- Article
- Export citation
Schwartz very weak solutions for Schrödinger type equations with distributional coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 29 September 2025, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tunable localisation in parity-time-symmetric resonator arrays with imaginary gauge potentials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 September 2025, e157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibrium and non-equilibrium diffusion approximation for the radiative transfer equation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Travelling breather solutions in waveguides for cubic nonlinear Maxwell equations with retarded material laws
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 18 September 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal boundary regularity of proper harmonic maps between asymptotically hyperbolic spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-38
-
- Article
- Export citation
Small-amplitude periodic travelling waves in dimer Fermi–Pasta–Ulam–Tsingou lattices without symmetry
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 15 August 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The inverse scattering theory of Kadomtsev–Petviashvili II equations
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functional separation solutions of the sinh-Gordon type equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 26 June 2025, pp. 1374-1388
- Print publication:
- December 2025
-
- Article
- Export citation
A multiscale model for espresso brewing: Asymptotic analysis and numerical simulation
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cahn–Hilliard equations with singular potential, reaction term and pure phase initial datum
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the long-time asymptotics of the modified Camassa–Holm equation with step-like initial data
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 23 April 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical solution of a PDE arising from prediction with expert advice
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 02 April 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spatio-temporal dynamics of a lattice prey–predator system with non-local diffusion in a periodic habitat
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 March 2025, pp. 1-43
-
- Article
- Export citation
On blow-up for the supercritical defocusing nonlinear wave equation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 31 March 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Harnack type estimates to non-linear elliptic systems in the plane
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 January 2025, pp. 1-14
-
- Article
- Export citation
Local regularity for nonlocal double phase equations in the Heisenberg group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-37
-
- Article
- Export citation
On Riemann–Hilbert problem and multiple high-order pole solutions to the cubic Camassa–Holm equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-51
-
- Article
- Export citation
Global existence of a weak solution for a reaction–diffusion system in a porous medium with membrane conditions and mass control
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 2006-2028
- Print publication:
- December 2025
-
- Article
- Export citation