This article is concerned with the following chemotaxis-growth system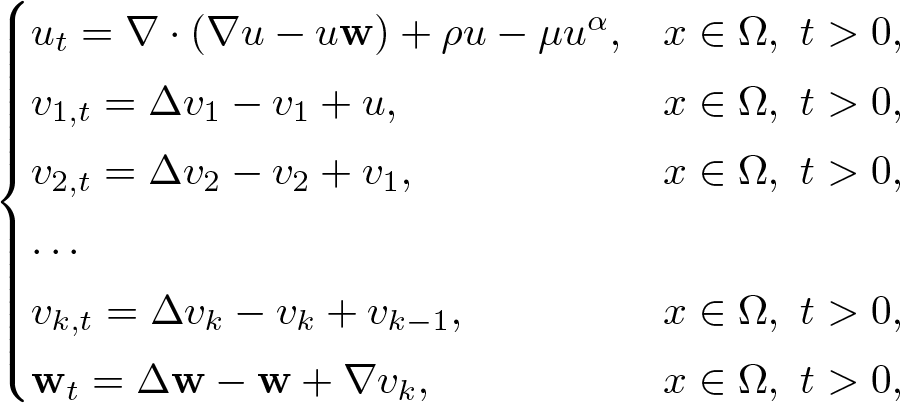

\begin{equation*}\begin{cases}u_t = \nabla\cdot \left(\nabla u - u\bf{w} \right) + \rho u - \mu u^\alpha ,&x \in \Omega ,\ t \gt 0,\\v_{1,t} = \Delta v_1 - v_1 + u,&x \in \Omega ,\ t \gt 0,\\v_{2,t} = \Delta v_2 - v_2 + v_1,&x \in \Omega ,\ t \gt 0,\\\ldots \\v_{k,t} = \Delta v_k - v_k + v_{k - 1},&x \in \Omega ,\ t \gt 0,\\{\bf{w}}_t = \Delta {\bf{w}} - {\bf{w}} + \nabla v_k,&x \in \Omega ,\ t \gt 0,\end{cases}\end{equation*}

under the homogeneous Neumann boundary condition for u, vi and the homogeneous Dirichlet boundary condition for 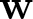$\bf{w}$ in a smooth bounded domain 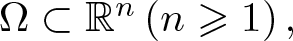$\Omega \subset {\mathbb{R}^n}\left( {n \geqslant 1} \right),$ where ρ > 0, µ > 0, α > 1 and 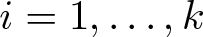$i=1,\ldots,k$. We reveal that when the index α, the spatial variable n, and the number of equations k satisfy certain relationships, the global solution of the system exists and converges to the constant equilibrium state in the form of exponential convergence.