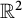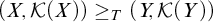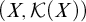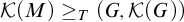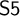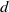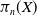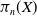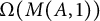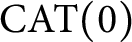Refine listing
Actions for selected content:
82 results in 54Exx
Generic properties of minimal surfaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 03 November 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
No product of two nontrivial countable-dimensional continua maps lightly into any of the factors
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-6
-
- Article
- Export citation
 $B_h$-sets of real and complex numbers
$B_h$-sets of real and complex numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 11 June 2025, pp. 1-5
-
- Article
- Export citation
Isometric rigidity of the Wasserstein space over the plane with the maximum metric
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Echeloned Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SHAPE OF COMPACT COVERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-15
-
- Article
- Export citation
THE BAIRE CLOSURE AND ITS LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 27-49
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLISH SPACES OF BANACH SPACES: COMPLEXITY OF ISOMETRY AND ISOMORPHISM CLASSES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1919-1957
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A natural pseudometric on homotopy groups of metric spaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 162-174
- Print publication:
- January 2024
-
- Article
- Export citation
A CLASSIFICATION OF THE WADGE HIERARCHIES ON ZERO-DIMENSIONAL POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 19 May 2023, pp. 887-917
- Print publication:
- June 2025
-
- Article
- Export citation
ON THE DOUBLING CONDITION IN THE INFINITE-DIMENSIONAL SETTING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 09 February 2023, pp. 480-491
- Print publication:
- December 2023
-
- Article
- Export citation
Polish spaces of Banach spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 May 2022, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compact and weakly compact Lipschitz operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 May 2022, pp. 1002-1020
- Print publication:
- June 2023
-
- Article
- Export citation
RETRACTED - Compact reduction in Lipschitz-free spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 08 December 2021, pp. 1683-1699
- Print publication:
- December 2021
-
- Article
- Export citation
Conditional mean dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 06 September 2021, pp. 3152-3166
- Print publication:
- October 2022
-
- Article
- Export citation
COUNTABLY PERFECTLY MEAGER SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 1214-1227
- Print publication:
- September 2021
-
- Article
- Export citation
NOTES ON ORTHOGONAL-COMPLETE METRIC SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 154-160
- Print publication:
- February 2022
-
- Article
- Export citation
On homotopy nilpotency of loop spaces of Moore spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 296-307
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on Mosco convergence in
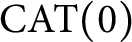 $\operatorname {\mathrm {CAT}}(0)$ spaces
$\operatorname {\mathrm {CAT}}(0)$ spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 17 January 2021, pp. 994-1003
- Print publication:
- December 2022
-
- Article
- Export citation
Proof of a conjecture of Galvin
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 21 December 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation