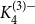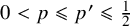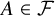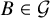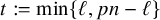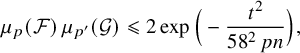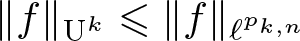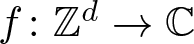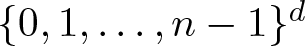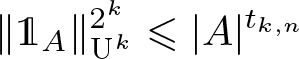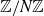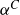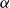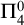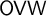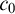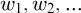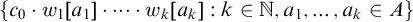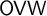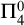Refine listing
Actions for selected content:
211 results in 05Dxx
Disperse hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 27 October 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random embeddings of bounded-degree trees with optimal spread
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Revisiting sums and products in countable and finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Beyond the broken tetrahedron
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 10 October 2025, pp. 1-12
-
- Article
- Export citation
On the existence of reflecting n-queens configurations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e169
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Forbidden induced subgraphs for graphs and signed graphs with eigenvalues bounded from below
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 October 2025, e163
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RAMSEY NUMBERS OF CYCLES VERSUS MULTIPLE ODD WHEELS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-9
-
- Article
- Export citation
Non-spherical sets versus lines in Euclidean Ramsey theory
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-5
-
- Article
- Export citation
Forbidden sparse intersections
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e99
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On off-diagonal Ramsey numbers for vector spaces over
 $\mathbb{F}_{2}$
$\mathbb{F}_{2}$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 25 June 2025, pp. 503-518
- Print publication:
- September 2025
-
- Article
- Export citation
Sharp estimates for Gowers norms on discrete cubes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-27
-
- Article
- Export citation
Echeloned Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniform sets with few progressions via colourings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 79-103
- Print publication:
- July 2025
-
- Article
- Export citation
On the Kohayakawa–Kreuter conjecture
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 293-320
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Ramsey–Turán density for cliques
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 April 2025, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite Hypergraph Families with Rich Extremal Turán Constructions via Mixing Patterns
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 06 March 2025, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved bounds for skew corner-free sets
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 177-192
- Print publication:
- March 2025
-
- Article
- Export citation
Common graphs with arbitrary chromatic number
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 03 July 2025, pp. 594-634
- Print publication:
- March 2025
-
- Article
- Export citation
Partition regularity of Pythagorean pairs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
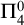 $\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM
$\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-16
-
- Article
- Export citation