Article contents
Beyond the broken tetrahedron
Published online by Cambridge University Press: 10 October 2025
Abstract
Here we consider the hypergraph Turán problem in uniformly dense hypergraphs as was suggested by Erdős and Sós. Given a  $3$-graph
$3$-graph  $F$, the uniform Turán density
$F$, the uniform Turán density  $\pi _{\boldsymbol{\therefore }}(F)$ of
$\pi _{\boldsymbol{\therefore }}(F)$ of  $F$ is defined as the supremum over all
$F$ is defined as the supremum over all  $d\in [0,1]$ for which there is an
$d\in [0,1]$ for which there is an  $F$-free uniformly
$F$-free uniformly  $d$-dense
$d$-dense  $3$-graph, where uniformly
$3$-graph, where uniformly  $d$-dense means that every linearly sized subhypergraph has density at least
$d$-dense means that every linearly sized subhypergraph has density at least  $d$. Recently, Glebov, Král’, and Volec and, independently, Reiher, Rödl, and Schacht proved that
$d$. Recently, Glebov, Král’, and Volec and, independently, Reiher, Rödl, and Schacht proved that  $\pi _{\boldsymbol{\therefore }}(K_4^{(3)-})=\frac {1}{4}$, solving a conjecture by Erdős and Sós. Despite substantial attention, the uniform Turán density is still only known for very few hypergraphs. In particular, the problem due to Erdős and Sós to determine
$\pi _{\boldsymbol{\therefore }}(K_4^{(3)-})=\frac {1}{4}$, solving a conjecture by Erdős and Sós. Despite substantial attention, the uniform Turán density is still only known for very few hypergraphs. In particular, the problem due to Erdős and Sós to determine  $\pi _{\boldsymbol{\therefore }}(K_4^{(3)})$ remains wide open.
$\pi _{\boldsymbol{\therefore }}(K_4^{(3)})$ remains wide open.
In this work, we determine the uniform Turán density of the  $3$-graph on five vertices that is obtained from
$3$-graph on five vertices that is obtained from  $K_4^{(3)-}$ by adding an additional vertex whose link forms a matching on the vertices of
$K_4^{(3)-}$ by adding an additional vertex whose link forms a matching on the vertices of 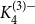 $K_4^{(3)-}$. Further, we point to two natural intermediate problems on the way to determining
$K_4^{(3)-}$. Further, we point to two natural intermediate problems on the way to determining  $\pi _{\boldsymbol{\therefore }}(K_4^{(3)})$, and solve the first of these.
$\pi _{\boldsymbol{\therefore }}(K_4^{(3)})$, and solve the first of these.
Keywords
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press
References
- 1
- Cited by


