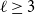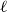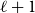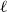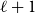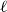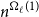1. Introduction
The Erdős-Hajnal conjecture [Reference Erdös and Hajnal6] is a fundamental problem in extremal graph theory, stating that for every fixed graph
![]() $H$
, every induced
$H$
, every induced
![]() $H$
-free
$H$
-free
![]() $n$
-vertex graph has a homogeneous set (i.e. a clique or independent set) of size at least
$n$
-vertex graph has a homogeneous set (i.e. a clique or independent set) of size at least
![]() $n^{c_H}$
, where
$n^{c_H}$
, where
![]() $c_H \gt 0$
is a constant depending only on
$c_H \gt 0$
is a constant depending only on
![]() $H$
. This is in sharp contrast to general graphs, which may only have homogeneous sets of size
$H$
. This is in sharp contrast to general graphs, which may only have homogeneous sets of size
![]() $O(\log n)$
. Despite significant recent progress (see, e.g. [Reference Bucić, Nguyen, Scott and Seymour4, Reference Nguyen, Scott and Seymour10, Reference Nguyen, Scott and Seymour11] and the references therein), the Erdős-Hajnal conjecture remains open in general.
$O(\log n)$
. Despite significant recent progress (see, e.g. [Reference Bucić, Nguyen, Scott and Seymour4, Reference Nguyen, Scott and Seymour10, Reference Nguyen, Scott and Seymour11] and the references therein), the Erdős-Hajnal conjecture remains open in general.
It is natural to ask for analogues of the Erdős-Hajnal conjecture for hypergraphs. We will use the term
![]() $\ell$
-graph as shorthand for
$\ell$
-graph as shorthand for
![]() $\ell$
-uniform hypergraph. Let
$\ell$
-uniform hypergraph. Let
![]() $\log _k(x)$
denote the
$\log _k(x)$
denote the
![]() $k$
-times iterated logarithm, that is,
$k$
-times iterated logarithm, that is,
![]() $\log _0(x) = x$
,
$\log _0(x) = x$
,
![]() $\log _1(x) = \log (x)$
, and
$\log _1(x) = \log (x)$
, and
![]() $\log _{k}(x) = \log (\log _{k-1}(x))$
. Let
$\log _{k}(x) = \log (\log _{k-1}(x))$
. Let
![]() $h_\ell (n)$
denote the maximum size of a homogeneous set guaranteed to exist in every
$h_\ell (n)$
denote the maximum size of a homogeneous set guaranteed to exist in every
![]() $\ell$
-vertex
$\ell$
-vertex
![]() $n$
-graph. It is well-known [Reference Erdos and Rado7] that
$n$
-graph. It is well-known [Reference Erdos and Rado7] that
![]() $h_{\ell }(n) \geq \left ( \log _{\ell -1}(n)\right )^{\Omega (1)}$
, and it is conjectured that the number
$h_{\ell }(n) \geq \left ( \log _{\ell -1}(n)\right )^{\Omega (1)}$
, and it is conjectured that the number
![]() $\ell -1$
of iterated logarithms is best possible, that is,
$\ell -1$
of iterated logarithms is best possible, that is,
![]() $h_{\ell }(n) \leq \left ( \log _{\ell -1}(n)\right )^{O(1)}$
. Thus, a natural analogue of the Erdős-Hajnal conjecture for
$h_{\ell }(n) \leq \left ( \log _{\ell -1}(n)\right )^{O(1)}$
. Thus, a natural analogue of the Erdős-Hajnal conjecture for
![]() $\ell$
-graphs would be that for every fixed
$\ell$
-graphs would be that for every fixed
![]() $\ell$
-graph
$\ell$
-graph
![]() $H$
, every induced
$H$
, every induced
![]() $H$
-free
$H$
-free
![]() $n$
-vertex
$n$
-vertex
![]() $\ell$
-graph has a homogeneous set of size
$\ell$
-graph has a homogeneous set of size
![]() $\left ( \log _{\ell -2}(n) \right )^{c_H}$
. However, there is some evidence that this might not be true for every
$\left ( \log _{\ell -2}(n) \right )^{c_H}$
. However, there is some evidence that this might not be true for every
![]() $H$
. Indeed, it is known that for uniformity
$H$
. Indeed, it is known that for uniformity
![]() $\ell \geq 4$
, the so-called stepping up construction gives a tight lower bound for Ramsey numbers in terms of the number of iterated logarithms (though this number is not known, as for the critical case
$\ell \geq 4$
, the so-called stepping up construction gives a tight lower bound for Ramsey numbers in terms of the number of iterated logarithms (though this number is not known, as for the critical case
![]() $\ell =3$
we only know that the number of logarithms is at least 1 and at most 2; this corresponds to at least
$\ell =3$
we only know that the number of logarithms is at least 1 and at most 2; this corresponds to at least
![]() $\ell -2$
and at most
$\ell -2$
and at most
![]() $\ell -1$
logarithms for uniformity
$\ell -1$
logarithms for uniformity
![]() $\ell$
). Conlon, Fox, and Sudakov [Reference Conlon, Fox and Sudakov5] showed that the stepping up construction avoids certain
$\ell$
). Conlon, Fox, and Sudakov [Reference Conlon, Fox and Sudakov5] showed that the stepping up construction avoids certain
![]() $H$
as induced subgraphs. Thus, for
$H$
as induced subgraphs. Thus, for
![]() $\ell \geq 4$
, there exist
$\ell \geq 4$
, there exist
![]() $\ell$
-graphs
$\ell$
-graphs
![]() $H$
such that induced
$H$
such that induced
![]() $H$
-free
$H$
-free
![]() $\ell$
-graphs do not have significantly larger homogeneous sets than general
$\ell$
-graphs do not have significantly larger homogeneous sets than general
![]() $\ell$
-graphs. Therefore, if
$\ell$
-graphs. Therefore, if
![]() $h_{\ell }(n) \leq \left ( \log _{\ell -1}(n)\right )^{O(1)}$
(as conjectured), then the above
$h_{\ell }(n) \leq \left ( \log _{\ell -1}(n)\right )^{O(1)}$
(as conjectured), then the above
![]() $\ell$
-uniform analogue of the Erdős-Hajnal conjecture fails. See also [Reference Amir, Shapira and Tyomkyn1, Reference Rödl and Schacht12] for additional Erdős-Hajnal-type results for hypergraphs.
$\ell$
-uniform analogue of the Erdős-Hajnal conjecture fails. See also [Reference Amir, Shapira and Tyomkyn1, Reference Rödl and Schacht12] for additional Erdős-Hajnal-type results for hypergraphs.
Recently, there has been some interest in variants of the Erdős-Hajnal problem where one forbids order-size pairs instead of induced subgraphs
![]() $H$
. To the best of our knowledge, this setting was first considered in [Reference Mubayi and Suk9]. Let us define the problem. For a set
$H$
. To the best of our knowledge, this setting was first considered in [Reference Mubayi and Suk9]. Let us define the problem. For a set
![]() $Q$
of pairs of integers, we say that an
$Q$
of pairs of integers, we say that an
![]() $\ell$
-graph
$\ell$
-graph
![]() $G$
is
$G$
is
![]() $Q$
-free if for every
$Q$
-free if for every
![]() $(m,f) \in Q$
, there is no set of
$(m,f) \in Q$
, there is no set of
![]() $m$
vertices in
$m$
vertices in
![]() $G$
which induces exactly
$G$
which induces exactly
![]() $f$
edges. What can we say about the size of homogeneous sets in
$f$
edges. What can we say about the size of homogeneous sets in
![]() $Q$
-free
$Q$
-free
![]() $\ell$
-graphs? It was recently shown by Arnold, the first author, and Sudakov [Reference Arnold, Gishboliner and Sudakov2] that this problem does in fact satisfy the natural hypergraph analogue of the Erdős-Hajnal conjecture, in the sense that for every
$\ell$
-graphs? It was recently shown by Arnold, the first author, and Sudakov [Reference Arnold, Gishboliner and Sudakov2] that this problem does in fact satisfy the natural hypergraph analogue of the Erdős-Hajnal conjecture, in the sense that for every
![]() $\ell \geq 2$
, all but a finite numberFootnote
1
of the sets
$\ell \geq 2$
, all but a finite numberFootnote
1
of the sets
![]() $Q \neq \emptyset$
satisfy that every
$Q \neq \emptyset$
satisfy that every
![]() $Q$
-free
$Q$
-free
![]() $\ell$
-graph on
$\ell$
-graph on
![]() $n$
vertices contains a homogeneous set of size at least
$n$
vertices contains a homogeneous set of size at least
![]() $\left ( \log _{\ell -2}(n) \right )^{c_Q}$
.
$\left ( \log _{\ell -2}(n) \right )^{c_Q}$
.
The papers [Reference Axenovich, Bradač, Gishboliner, Mubayi and Weber3, Reference Gishboliner and Tomon8] studied the special case where
![]() $\ell =3$
and
$\ell =3$
and
![]() $Q$
consists of pairs of the form
$Q$
consists of pairs of the form
![]() $(4,f)$
; that is, we forbid certain numbers of edges on vertex-sets of size four. The first author and Tomon [Reference Gishboliner and Tomon8] showed that if an
$(4,f)$
; that is, we forbid certain numbers of edges on vertex-sets of size four. The first author and Tomon [Reference Gishboliner and Tomon8] showed that if an
![]() $n$
-vertex 3-graph
$n$
-vertex 3-graph
![]() $G$
has no four vertices spanning exactly two edges, then
$G$
has no four vertices spanning exactly two edges, then
![]() $G$
has a homogeneous set of size
$G$
has a homogeneous set of size
![]() $n^c$
(where
$n^c$
(where
![]() $c \gt 0$
is an absolute constant). They also asked to show that this extends to
$c \gt 0$
is an absolute constant). They also asked to show that this extends to
![]() $\ell$
-graphs, in the following sense: If an
$\ell$
-graphs, in the following sense: If an
![]() $n$
-vertex
$n$
-vertex
![]() $\ell$
-graph
$\ell$
-graph
![]() $G$
, with
$G$
, with
![]() $\ell \geq 3$
, has no
$\ell \geq 3$
, has no
![]() $\ell +1$
vertices spanning
$\ell +1$
vertices spanning
![]() $2,3,4,\dots ,\ell -1$
edges, then
$2,3,4,\dots ,\ell -1$
edges, then
![]() $G$
has a homogeneous set of size
$G$
has a homogeneous set of size
![]() $n^{c_{\ell }}$
. Here we prove this conjecture. We call
$n^{c_{\ell }}$
. Here we prove this conjecture. We call
![]() $\ell$
-graphs with this property disperse.
$\ell$
-graphs with this property disperse.
Definition 1.1.
Let
![]() $G$
be an
$G$
be an
![]() $\ell$
-graph,
$\ell$
-graph,
![]() $\ell \geq 3$
. We say that
$\ell \geq 3$
. We say that
![]() $G$
is disperse if, for every
$G$
is disperse if, for every
![]() $(\ell + 1)$
-set
$(\ell + 1)$
-set
![]() $X = \{v_1, \dots , v_{\ell + 1}\} \subseteq V(G)$
, it holds that
$X = \{v_1, \dots , v_{\ell + 1}\} \subseteq V(G)$
, it holds that
![]() $e_G(X) \in \{0, 1, \ell , \ell + 1\}$
.
$e_G(X) \in \{0, 1, \ell , \ell + 1\}$
.
Note that if
![]() $G$
is disperse then so is its complement
$G$
is disperse then so is its complement
![]() $\overline {G}$
.
$\overline {G}$
.
Theorem 1.2.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph on
$\ell$
-graph on
![]() $n$
vertices. Then,
$n$
vertices. Then,
![]() $\max (\alpha (G), \omega (G)) \geq \Omega (n^{\frac {1}{3\ell - 1}})$
.
$\max (\alpha (G), \omega (G)) \geq \Omega (n^{\frac {1}{3\ell - 1}})$
.
The constant
![]() $\frac {1}{3\ell -1}$
in Theorem1.2 is best possible up to a factor of roughly
$\frac {1}{3\ell -1}$
in Theorem1.2 is best possible up to a factor of roughly
![]() $\frac {1}{3}$
. Indeed, note that if an
$\frac {1}{3}$
. Indeed, note that if an
![]() $\ell$
-graph
$\ell$
-graph
![]() $G$
has no two edges intersecting in
$G$
has no two edges intersecting in
![]() $\ell -1$
vertices, then
$\ell -1$
vertices, then
![]() $G$
is disperse (because every
$G$
is disperse (because every
![]() $(\ell +1)$
-set of vertices spans 0 or 1 edges). Such
$(\ell +1)$
-set of vertices spans 0 or 1 edges). Such
![]() $\ell$
-graphs are known aspartial
$\ell$
-graphs are known aspartial
![]() $(\ell ,\ell -1)$
-Steiner systems. It is known [Reference Rödl and Šinajová13] that there exist
$(\ell ,\ell -1)$
-Steiner systems. It is known [Reference Rödl and Šinajová13] that there exist
![]() $n$
-vertex partial
$n$
-vertex partial
![]() $(\ell ,\ell -1)$
-Steiner systems with independence number
$(\ell ,\ell -1)$
-Steiner systems with independence number
![]() $\tilde {O}(n^{\frac {1}{\ell -1}})$
. Hence, the constant in Theorem1.2 cannot be improved beyond
$\tilde {O}(n^{\frac {1}{\ell -1}})$
. Hence, the constant in Theorem1.2 cannot be improved beyond
![]() $\frac {1}{\ell -1}$
. It is also worth noting that in the case
$\frac {1}{\ell -1}$
. It is also worth noting that in the case
![]() $\ell =3$
, the constant
$\ell =3$
, the constant
![]() $\frac {1}{8}$
given by Theorem1.2 significantly improves the constant obtained in [Reference Gishboliner and Tomon8], which was much smaller and therefore not calculated explicitly. It would be interesting to determine the best possible constant in Theorem1.2. For
$\frac {1}{8}$
given by Theorem1.2 significantly improves the constant obtained in [Reference Gishboliner and Tomon8], which was much smaller and therefore not calculated explicitly. It would be interesting to determine the best possible constant in Theorem1.2. For
![]() $\ell =3$
, the best upper-bound on this constant comes from [Reference Axenovich, Bradač, Gishboliner, Mubayi and Weber3], which constructed a disperse
$\ell =3$
, the best upper-bound on this constant comes from [Reference Axenovich, Bradač, Gishboliner, Mubayi and Weber3], which constructed a disperse
![]() $n$
-vertex
$n$
-vertex
![]() $3$
-graph
$3$
-graph
![]() $G$
with
$G$
with
![]() $\max (\alpha (G), \omega (G)) \leq \tilde {O}(n^{1/3})$
.Footnote
2
$\max (\alpha (G), \omega (G)) \leq \tilde {O}(n^{1/3})$
.Footnote
2
As mentioned above, one example of disperse
![]() $\ell$
-graphs is partial
$\ell$
-graphs is partial
![]() $(\ell ,\ell -1)$
-Steiner systems. Let us now describe another important example. A hypergraph
$(\ell ,\ell -1)$
-Steiner systems. Let us now describe another important example. A hypergraph
![]() $G$
is called a cohypergraph if either
$G$
is called a cohypergraph if either
![]() $|V(G)| = 1$
, or there is a vertex partition
$|V(G)| = 1$
, or there is a vertex partition
![]() $V(G) = X \cup Y$
such that
$V(G) = X \cup Y$
such that
![]() $G[X],G[Y]$
are cohypergraphs and
$G[X],G[Y]$
are cohypergraphs and
![]() $E(G)$
contains all or none of the
$E(G)$
contains all or none of the
![]() $\ell$
-sets which intersect both
$\ell$
-sets which intersect both
![]() $X$
and
$X$
and
![]() $Y$
. It is easy to check (by induction) that every cohypergraph is disperse. Also, note that for
$Y$
. It is easy to check (by induction) that every cohypergraph is disperse. Also, note that for
![]() $\ell =2$
, this recovers the definition of cographs. Recall also that a graph is a cograph if and only if it is induced
$\ell =2$
, this recovers the definition of cographs. Recall also that a graph is a cograph if and only if it is induced
![]() $P_4$
-free, where
$P_4$
-free, where
![]() $P_4$
is the path with 4 vertices.
$P_4$
is the path with 4 vertices.
To prove Theorem1.2, we show (implicitly) that every disperse
![]() $\ell$
-graph is close to being a cohypergraph. To this end, we prove several structural properties of disperse hypergraphs. Let us now state the two key facts we will use, Theorems1.4 and 1.5. We first introduce the basic definitions related to tight connectivity.
$\ell$
-graph is close to being a cohypergraph. To this end, we prove several structural properties of disperse hypergraphs. Let us now state the two key facts we will use, Theorems1.4 and 1.5. We first introduce the basic definitions related to tight connectivity.
Definition 1.3.
Let
![]() $G$
be an
$G$
be an
![]() $\ell$
-graph. A tight walk is a sequence of edges
$\ell$
-graph. A tight walk is a sequence of edges
![]() $e_1, \dots , e_m \in E(G)$
such that
$e_1, \dots , e_m \in E(G)$
such that
![]() $|e_i \cap e_{i + 1}| \geq \ell - 1$
for all
$|e_i \cap e_{i + 1}| \geq \ell - 1$
for all
![]() $1 \leq i \leq m - 1$
. For
$1 \leq i \leq m - 1$
. For
![]() $A,B \in \binom {V(G)}{\ell -1}$
, we say that
$A,B \in \binom {V(G)}{\ell -1}$
, we say that
![]() $A,B$
are connected in
$A,B$
are connected in
![]() $G$
if there is a tight walk
$G$
if there is a tight walk
![]() $e_1,\dots ,e_m$
with
$e_1,\dots ,e_m$
with
![]() $A \subseteq e_1$
and
$A \subseteq e_1$
and
![]() $B \subseteq e_m$
. This is an equivalence relation.
Footnote
3
A tight component of
$B \subseteq e_m$
. This is an equivalence relation.
Footnote
3
A tight component of
![]() $G$
is an equivalence class in this relation. Thus, the tight components partition
$G$
is an equivalence class in this relation. Thus, the tight components partition
![]() $\binom {V(G)}{\ell -1}$
. We say that
$\binom {V(G)}{\ell -1}$
. We say that
![]() $G$
is tightly connected if there is a single tight component, namely
$G$
is tightly connected if there is a single tight component, namely
![]() $\binom {V(G)}{\ell -1}$
.
$\binom {V(G)}{\ell -1}$
.
In other words,
![]() $G$
is tightly connected if for every
$G$
is tightly connected if for every
![]() $A,B \in \binom {V(G)}{\ell -1}$
, there is a tight walk
$A,B \in \binom {V(G)}{\ell -1}$
, there is a tight walk
![]() $e_1,\dots ,e_m$
with
$e_1,\dots ,e_m$
with
![]() $A \subseteq e_1$
and
$A \subseteq e_1$
and
![]() $B \subseteq e_m$
. Note that in the case
$B \subseteq e_m$
. Note that in the case
![]() $\ell =2$
, this coincides with the usual notion of graph connectivity.
$\ell =2$
, this coincides with the usual notion of graph connectivity.
For a hypergraph
![]() $G$
, we use
$G$
, we use
![]() $\overline {G}$
to denote the complement of
$\overline {G}$
to denote the complement of
![]() $G$
. Our first theorem states that for a disperse
$G$
. Our first theorem states that for a disperse
![]() $G$
, either
$G$
, either
![]() $G$
or
$G$
or
![]() $\overline {G}$
is not tightly connected. Our second theorem states that in a disperse
$\overline {G}$
is not tightly connected. Our second theorem states that in a disperse
![]() $G$
, each tight component is a complete hypergraph, that is, it consists of all
$G$
, each tight component is a complete hypergraph, that is, it consists of all
![]() $(\ell -1)$
-tuples contained in some vertex set.
$(\ell -1)$
-tuples contained in some vertex set.
Theorem 1.4.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph. Then
$\ell$
-graph. Then
![]() $G$
or
$G$
or
![]() $\overline {G}$
is not tightly connected.
$\overline {G}$
is not tightly connected.
Theorem 1.5.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph. Then for every tight component
$\ell$
-graph. Then for every tight component
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $G$
, there is
$G$
, there is
![]() $U \subseteq V(G)$
such that
$U \subseteq V(G)$
such that
![]() $\mathcal{C} = \binom {U}{\ell -1}$
.
$\mathcal{C} = \binom {U}{\ell -1}$
.
Combining these two theorems, we conclude that for every disperse
![]() $\ell$
-graph
$\ell$
-graph
![]() $G$
, either in
$G$
, either in
![]() $G$
or in
$G$
or in
![]() $\overline {G}$
we can find a vertex set
$\overline {G}$
we can find a vertex set
![]() $\emptyset \neq X \subsetneq V(G)$
such that there is no edge having
$\emptyset \neq X \subsetneq V(G)$
such that there is no edge having
![]() $\ell -1$
vertices in
$\ell -1$
vertices in
![]() $X$
and one vertex in
$X$
and one vertex in
![]() $Y := V(G) \setminus X$
. Indeed, we simply take
$Y := V(G) \setminus X$
. Indeed, we simply take
![]() $X$
to be the vertex set corresponding to a tight component (via Theorem1.5). One can then show, using the fact that
$X$
to be the vertex set corresponding to a tight component (via Theorem1.5). One can then show, using the fact that
![]() $G$
is disperse, that there are only few edges intersecting both
$G$
is disperse, that there are only few edges intersecting both
![]() $X$
and
$X$
and
![]() $Y$
. Repeating this inside
$Y$
. Repeating this inside
![]() $X$
and
$X$
and
![]() $Y$
(with some technicalities omitted here), we can show that
$Y$
(with some technicalities omitted here), we can show that
![]() $G$
is close to a cohypergraph.
$G$
is close to a cohypergraph.
Theorems1.4 and 1.5 are proved in Section 2. We then prove Theorem1.2 in Section 3. Section 4 contains some further remarks and open problems. We mostly use standard graph-theoretic notation. For a vertex-set
![]() $X$
in a hypergraph
$X$
in a hypergraph
![]() $G$
, we use
$G$
, we use
![]() $e_G(X)$
to denote the number of edges of
$e_G(X)$
to denote the number of edges of
![]() $G$
contained in
$G$
contained in
![]() $X$
. Throughout the rest of the paper, we assume that the uniformity
$X$
. Throughout the rest of the paper, we assume that the uniformity
![]() $\ell$
is at least 3, unless explicitly stated otherwise.
$\ell$
is at least 3, unless explicitly stated otherwise.
2. Structural results
In this section we study the structure of disperse hypergraphs, and in particular prove Theorems1.4 and 1.5. Let us begin with some lemmas. For an
![]() $\ell$
-graph
$\ell$
-graph
![]() $G$
and
$G$
and
![]() $v \in V(G)$
, the link
$v \in V(G)$
, the link
![]() $L(v)$
is the
$L(v)$
is the
![]() $(\ell -1)$
-graph on
$(\ell -1)$
-graph on
![]() $V(G) \setminus \{v\}$
with edge set
$V(G) \setminus \{v\}$
with edge set
![]() $\{ e \in \binom {V(G) \setminus \{v\}}{\ell -1} : e \cup \{v\} \in E(G) \}$
. A useful fact is that the links of a disperse hypergraph are also disperse.
$\{ e \in \binom {V(G) \setminus \{v\}}{\ell -1} : e \cup \{v\} \in E(G) \}$
. A useful fact is that the links of a disperse hypergraph are also disperse.
Lemma 2.1.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph. Then for every
$\ell$
-graph. Then for every
![]() $v \in V(G)$
,
$v \in V(G)$
,
![]() $L(v)$
is disperse.
$L(v)$
is disperse.
Proof.
Suppose that there is
![]() $v \in G$
such that
$v \in G$
such that
![]() $L(v)$
is not disperse, and let
$L(v)$
is not disperse, and let
![]() $X = \{v_1, \dots , v_{\ell }\} \subseteq V \setminus \{v\}$
witness this, namely,
$X = \{v_1, \dots , v_{\ell }\} \subseteq V \setminus \{v\}$
witness this, namely,
![]() $2 \leq |e_{L(v)}(X)| \leq \ell - 2$
. Then
$2 \leq |e_{L(v)}(X)| \leq \ell - 2$
. Then
![]() $2 \leq e_G(X \cup \{v\}) \leq \ell -1$
, contradicting that
$2 \leq e_G(X \cup \{v\}) \leq \ell -1$
, contradicting that
![]() $G$
is disperse.
$G$
is disperse.
We will also use the following easy lemma.
Lemma 2.2.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph, let
$\ell$
-graph, let
![]() $f,g \in E(G)$
with
$f,g \in E(G)$
with
![]() $|f \cap g| \geq \ell -1$
, let
$|f \cap g| \geq \ell -1$
, let
![]() $v \in f$
and let
$v \in f$
and let
![]() $A,B \subseteq g \! \setminus \! \{v\}$
with
$A,B \subseteq g \! \setminus \! \{v\}$
with
![]() $|A| = |B| = \ell -2$
. Then
$|A| = |B| = \ell -2$
. Then
![]() $A,B$
are connected in
$A,B$
are connected in
![]() $L(v)$
.
$L(v)$
.
Proof.
If
![]() $v \in g$
then the assertion clearly holds, because
$v \in g$
then the assertion clearly holds, because
![]() $g \setminus \{v\}$
is a (one-edge) tight walk between
$g \setminus \{v\}$
is a (one-edge) tight walk between
![]() $A$
and
$A$
and
![]() $B$
in
$B$
in
![]() $L(v)$
. So suppose that
$L(v)$
. So suppose that
![]() $v \notin g$
. Then we can write
$v \notin g$
. Then we can write
![]() $f = \{v,v_1,\dots ,v_{\ell -1}\}, g = \{v_1,\dots ,v_{\ell -1},w\}$
with
$f = \{v,v_1,\dots ,v_{\ell -1}\}, g = \{v_1,\dots ,v_{\ell -1},w\}$
with
![]() $w \neq v$
. As
$w \neq v$
. As
![]() $G$
is disperse, the
$G$
is disperse, the
![]() $(\ell +1)$
-set
$(\ell +1)$
-set
![]() $f \cup g$
must miss at most one edge. This means that there are
$f \cup g$
must miss at most one edge. This means that there are
![]() $e_1,e_2 \in E(G)$
with
$e_1,e_2 \in E(G)$
with
![]() $\{v\} \cup A \subseteq e_1$
and
$\{v\} \cup A \subseteq e_1$
and
![]() $\{v\} \cup B \subseteq e_2$
. Now
$\{v\} \cup B \subseteq e_2$
. Now
![]() $e_1 \! \setminus \! \{v\},e_2 \! \setminus \! \{v\}$
is a tight walk between
$e_1 \! \setminus \! \{v\},e_2 \! \setminus \! \{v\}$
is a tight walk between
![]() $A$
and
$A$
and
![]() $B$
in
$B$
in
![]() $L(v)$
.
$L(v)$
.
The following is our main technical lemma. It shows that in a disperse hypergraph, if there is a tight walk of length 3 from a vertex
![]() $v$
to an
$v$
to an
![]() $(\ell -1)$
-set
$(\ell -1)$
-set
![]() $B$
, then there is also such a tight walk of length 2.
$B$
, then there is also such a tight walk of length 2.
Lemma 2.3.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph, let
$\ell$
-graph, let
![]() $e,f,g$
be a tight walk in
$e,f,g$
be a tight walk in
![]() $G$
, let
$G$
, let
![]() $v \in e$
, and let
$v \in e$
, and let
![]() $B \subseteq g$
with
$B \subseteq g$
with
![]() $|B| = \ell -1$
. Then there is a tight walk
$|B| = \ell -1$
. Then there is a tight walk
![]() $f',g'$
in
$f',g'$
in
![]() $G$
such that
$G$
such that
![]() $v \in f'$
and
$v \in f'$
and
![]() $B \subseteq g'$
.
$B \subseteq g'$
.
Proof.
We first consider some easy degenerate cases. If
![]() $v \in f$
or
$v \in f$
or
![]() $v \in g$
then we can take
$v \in g$
then we can take
![]() $(f',g') = (f,g)$
or
$(f',g') = (f,g)$
or
![]() $(f',g') = (g,g)$
, respectively. If
$(f',g') = (g,g)$
, respectively. If
![]() $B \subseteq f$
then take
$B \subseteq f$
then take
![]() $(f',g') = (e,f)$
, and if
$(f',g') = (e,f)$
, and if
![]() $|e \cap g| \geq \ell -1$
then take
$|e \cap g| \geq \ell -1$
then take
![]() $(f',g') = (e,g)$
. Assuming that none of the above holds, without loss of generality we may write
$(f',g') = (e,g)$
. Assuming that none of the above holds, without loss of generality we may write
![]() $e = \{v, w_1, \dots , w_{\ell - 1}\}, f = \{w_1, \dots , w_{\ell }\}$
and
$e = \{v, w_1, \dots , w_{\ell - 1}\}, f = \{w_1, \dots , w_{\ell }\}$
and
![]() $g = \{w_2, \dots , w_{\ell + 1}\}$
with the vertices
$g = \{w_2, \dots , w_{\ell + 1}\}$
with the vertices
![]() $v,w_1,\dots ,w_{\ell +1}$
being distinct, and
$v,w_1,\dots ,w_{\ell +1}$
being distinct, and
![]() $B = \{w_2, \dots , w_{\ell + 1}\} \backslash \{w_i\}$
for some
$B = \{w_2, \dots , w_{\ell + 1}\} \backslash \{w_i\}$
for some
![]() $i \neq \ell + 1$
. Note that
$i \neq \ell + 1$
. Note that
![]() $|f \cap B| = \ell -2$
.
$|f \cap B| = \ell -2$
.
Suppose, for the sake of contradiction, that there is no tight walk
![]() $f',g'$
as in the lemma. We proceed via a series of claims which will eventually give a contradiction.
$f',g'$
as in the lemma. We proceed via a series of claims which will eventually give a contradiction.
Claim 2.4.
For all
![]() $A \subseteq f \backslash \{w_1\}$
with
$A \subseteq f \backslash \{w_1\}$
with
![]() $|A| = \ell - 2$
, it holds that
$|A| = \ell - 2$
, it holds that
![]() $\{v, w_1\} \cup A \in E(G)$
.
$\{v, w_1\} \cup A \in E(G)$
.
Proof.
Consider the
![]() $(\ell +1)$
-set
$(\ell +1)$
-set
![]() $X = \{v, w_1, \ldots , w_{\ell }\}$
. As
$X = \{v, w_1, \ldots , w_{\ell }\}$
. As
![]() $e,f$
are both edges of
$e,f$
are both edges of
![]() $G$
contained in
$G$
contained in
![]() $X$
, and as
$X$
, and as
![]() $G$
is disperse,
$G$
is disperse,
![]() $G$
misses at most one edge on
$G$
misses at most one edge on
![]() $X$
. Note that
$X$
. Note that
![]() $h := \{v,w_2,\dots ,w_{\ell }\}$
is not an edge of
$h := \{v,w_2,\dots ,w_{\ell }\}$
is not an edge of
![]() $G$
, as otherwise
$G$
, as otherwise
![]() $f' = h$
and
$f' = h$
and
![]() $g' = g$
satisfy
$g' = g$
satisfy
![]() $v \in f'$
,
$v \in f'$
,
![]() $|f' \cap g'| = |\{w_2, \dots , w_{\ell }\}| = \ell - 1$
and
$|f' \cap g'| = |\{w_2, \dots , w_{\ell }\}| = \ell - 1$
and
![]() $B \subseteq g'$
. So,
$B \subseteq g'$
. So,
![]() $G$
contains all edges on
$G$
contains all edges on
![]() $X$
besides
$X$
besides
![]() $h$
; in particular,
$h$
; in particular,
![]() $G$
contains
$G$
contains
![]() $\{v, w_1\} \cup A$
for all
$\{v, w_1\} \cup A$
for all
![]() $A \subseteq f \backslash \{w_1\}$
of size
$A \subseteq f \backslash \{w_1\}$
of size
![]() $\ell - 2$
.
$\ell - 2$
.
Claim 2.5.
For all
![]() $A \subseteq g$
with
$A \subseteq g$
with
![]() $|A| = \ell - 1$
, it holds that
$|A| = \ell - 1$
, it holds that
![]() $\{v\} \cup A \not \in E(G)$
.
$\{v\} \cup A \not \in E(G)$
.
Proof.
Otherwise we can take
![]() $f' = \{v\} \cup A$
and
$f' = \{v\} \cup A$
and
![]() $g' = g$
, which satisfy
$g' = g$
, which satisfy
![]() $v \in f'$
,
$v \in f'$
,
![]() $|f' \cap g'| = |A| = \ell - 1$
and
$|f' \cap g'| = |A| = \ell - 1$
and
![]() $B \subseteq g'$
.
$B \subseteq g'$
.
Claim 2.6.
For all
![]() $A \subseteq g$
with
$A \subseteq g$
with
![]() $|A| = \ell - 1$
, it holds that
$|A| = \ell - 1$
, it holds that
![]() $\{w_1\} \cup A \in E(G)$
if and only if
$\{w_1\} \cup A \in E(G)$
if and only if
![]() $A \neq B$
.
$A \neq B$
.
Proof.
Let
![]() $X = \{w_1, \ldots , w_{\ell + 1}\}$
. Note that
$X = \{w_1, \ldots , w_{\ell + 1}\}$
. Note that
![]() $f, g$
are edges of
$f, g$
are edges of
![]() $G$
contained in
$G$
contained in
![]() $X$
, and thus,
$X$
, and thus,
![]() $G$
misses at most one edge on
$G$
misses at most one edge on
![]() $X$
. Moreover, if
$X$
. Moreover, if
![]() $\{w_1\} \cup B \in E(G)$
, then letting
$\{w_1\} \cup B \in E(G)$
, then letting
![]() $f' = \{v, w_1\} \cup (f \cap B)$
(which is an edge by Claim 2.4) and
$f' = \{v, w_1\} \cup (f \cap B)$
(which is an edge by Claim 2.4) and
![]() $g' = \{w_1\} \cup B$
gives the desired result. Thus,
$g' = \{w_1\} \cup B$
gives the desired result. Thus,
![]() $\{w_1\} \cup B \notin E(G)$
, implying that
$\{w_1\} \cup B \notin E(G)$
, implying that
![]() $G$
must contain all other edges on
$G$
must contain all other edges on
![]() $X$
– in particular, all edges of the form
$X$
– in particular, all edges of the form
![]() $\{w_1\} \cup A$
with
$\{w_1\} \cup A$
with
![]() $A \subseteq g$
,
$A \subseteq g$
,
![]() $|A| = \ell - 1$
and
$|A| = \ell - 1$
and
![]() $A \neq B$
.
$A \neq B$
.
Claim 2.7.
For all
![]() $A \subseteq B$
with
$A \subseteq B$
with
![]() $|A| = \ell - 2$
and
$|A| = \ell - 2$
and
![]() $A \neq f \cap B$
, it holds that
$A \neq f \cap B$
, it holds that
![]() $\{v, w_1\} \cup A \not \in E(G)$
.
$\{v, w_1\} \cup A \not \in E(G)$
.
Proof.
Let
![]() $X = \{v, w_1\} \cup B$
, so
$X = \{v, w_1\} \cup B$
, so
![]() $|X| = \ell +1$
. By Claim 2.5 we have
$|X| = \ell +1$
. By Claim 2.5 we have
![]() $\{v\} \cup B \not \in E(G)$
, and by Claim 2.6 we have
$\{v\} \cup B \not \in E(G)$
, and by Claim 2.6 we have
![]() $\{w_1\} \cup B \notin E(G)$
. Hence, as
$\{w_1\} \cup B \notin E(G)$
. Hence, as
![]() $G$
is disperse, it can contain at most one edge on
$G$
is disperse, it can contain at most one edge on
![]() $X$
, which must be the edge
$X$
, which must be the edge
![]() $\{v, w_1\} \cup (f \cap B)$
, as this is an edge by Claim 2.4. So,
$\{v, w_1\} \cup (f \cap B)$
, as this is an edge by Claim 2.4. So,
![]() $G$
cannot contain any edge of the form
$G$
cannot contain any edge of the form
![]() $\{v, w_1\} \cup A$
for
$\{v, w_1\} \cup A$
for
![]() $A \subseteq B$
with
$A \subseteq B$
with
![]() $|A| = \ell - 2$
and
$|A| = \ell - 2$
and
![]() $A \neq f \cap B$
.
$A \neq f \cap B$
.
Now, we use the above claims to derive a contradiction and hence prove Lemma 2.3. Fix an arbitrary
![]() $x \in f \cap B$
(this is possible because
$x \in f \cap B$
(this is possible because
![]() $|f \cap B| = \ell -2 \geq 1$
). Set
$|f \cap B| = \ell -2 \geq 1$
). Set
![]() $C = g \backslash \{x\}$
, and note that
$C = g \backslash \{x\}$
, and note that
![]() $|C| = \ell -1$
;
$|C| = \ell -1$
;
![]() $C \neq B$
and hence
$C \neq B$
and hence
![]() $|C \cap B| = \ell -2$
;
$|C \cap B| = \ell -2$
;
![]() $w_{\ell +1} \in C$
(as
$w_{\ell +1} \in C$
(as
![]() $w_{\ell +1} \notin f$
and so
$w_{\ell +1} \notin f$
and so
![]() $x \neq w_{\ell +1}$
); and
$x \neq w_{\ell +1}$
); and
![]() $C \cap B \neq f \cap B$
(as
$C \cap B \neq f \cap B$
(as
![]() $x \in f \cap B$
while
$x \in f \cap B$
while
![]() $x \notin C$
). Consider the set
$x \notin C$
). Consider the set
![]() $X = \{v, w_1\} \cup C$
, so
$X = \{v, w_1\} \cup C$
, so
![]() $|X| = \ell +1$
. We will show that there exist two edges and two non-edges on
$|X| = \ell +1$
. We will show that there exist two edges and two non-edges on
![]() $X$
. Indeed, by Claim 2.4,
$X$
. Indeed, by Claim 2.4,
![]() $\{v, w_1\} \cup (C \backslash \{w_{\ell + 1}\}) \in E(G)$
, and by Claim 2.6,
$\{v, w_1\} \cup (C \backslash \{w_{\ell + 1}\}) \in E(G)$
, and by Claim 2.6,
![]() $\{w_1\} \cup C \in E(G)$
. On the other hand, by Claim 2.5,
$\{w_1\} \cup C \in E(G)$
. On the other hand, by Claim 2.5,
![]() $\{v\} \cup C \not \in E(G)$
, and by Claim 2.7,
$\{v\} \cup C \not \in E(G)$
, and by Claim 2.7,
![]() $\{v, w_1\} \cup (C \cap B) \not \in E(G)$
. This contradicts the assumption that
$\{v, w_1\} \cup (C \cap B) \not \in E(G)$
. This contradicts the assumption that
![]() $G$
is disperse, as desired.
$G$
is disperse, as desired.
Lemma 2.3 easily implies the following.
Lemma 2.8.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph, let
$\ell$
-graph, let
![]() $e_1, \dots , e_m$
be a tight walk in
$e_1, \dots , e_m$
be a tight walk in
![]() $G$
, and let
$G$
, and let
![]() $v \in e_1$
. Then for all
$v \in e_1$
. Then for all
![]() $1 \leq i \leq m - 1$
, there exists a tight walk
$1 \leq i \leq m - 1$
, there exists a tight walk
![]() $f, g$
such that
$f, g$
such that
![]() $v \in f$
and
$v \in f$
and
![]() $e_i \cap e_{i + 1} \subseteq g$
.
$e_i \cap e_{i + 1} \subseteq g$
.
Proof.
We prove this by induction on
![]() $i$
. For
$i$
. For
![]() $i = 1$
the claim is trivial by letting
$i = 1$
the claim is trivial by letting
![]() $f = g = e_1$
. For the inductive step, let
$f = g = e_1$
. For the inductive step, let
![]() $f, g$
be a tight walk with
$f, g$
be a tight walk with
![]() $v \in f$
and
$v \in f$
and
![]() $e_{i - 1} \cap e_i \subseteq g$
. Note that
$e_{i - 1} \cap e_i \subseteq g$
. Note that
![]() $f, g, e_i$
is a tight walk as
$f, g, e_i$
is a tight walk as
![]() $f,g$
is a tight walk and
$f,g$
is a tight walk and
![]() $|g \cap e_i| \geq |e_{i - 1} \cap e_i| = \ell - 1$
. Moreover,
$|g \cap e_i| \geq |e_{i - 1} \cap e_i| = \ell - 1$
. Moreover,
![]() $v \in f$
and
$v \in f$
and
![]() $B := e_i \cap e_{i + 1} \subseteq e_i$
, so we may apply Lemma 2.3 to obtain a tight walk
$B := e_i \cap e_{i + 1} \subseteq e_i$
, so we may apply Lemma 2.3 to obtain a tight walk
![]() $f',g'$
with
$f',g'$
with
![]() $v \in f'$
and
$v \in f'$
and
![]() $e_i \cap e_{i + 1} \subseteq g'$
, as desired.
$e_i \cap e_{i + 1} \subseteq g'$
, as desired.
We now use this result to prove the following key lemma.
Lemma 2.9.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph, let
$\ell$
-graph, let
![]() $v \in V(G)$
and let
$v \in V(G)$
and let
![]() $A,B \subseteq V(G) \! \setminus \! \{v\}$
with
$A,B \subseteq V(G) \! \setminus \! \{v\}$
with
![]() $|A| = |B| = \ell -2$
. If
$|A| = |B| = \ell -2$
. If
![]() $A \cup \{v\}$
and
$A \cup \{v\}$
and
![]() $B \cup \{v\}$
are connected in
$B \cup \{v\}$
are connected in
![]() $G$
, then
$G$
, then
![]() $A$
and
$A$
and
![]() $B$
are connected in
$B$
are connected in
![]() $L(v)$
.
$L(v)$
.
Proof.
Let
![]() $e_1,\dots ,e_m$
be a tight walk in
$e_1,\dots ,e_m$
be a tight walk in
![]() $G$
between
$G$
between
![]() $A \cup \{v\}$
and
$A \cup \{v\}$
and
![]() $B \cup \{v\}$
. We will prove the lemma by induction on
$B \cup \{v\}$
. We will prove the lemma by induction on
![]() $m$
. For
$m$
. For
![]() $m \leq 2$
the lemma is trivial, by simply observing that
$m \leq 2$
the lemma is trivial, by simply observing that
![]() $e_1 \backslash \{v\}, e_m \backslash \{v\}$
is a tight walk between
$e_1 \backslash \{v\}, e_m \backslash \{v\}$
is a tight walk between
![]() $A$
and
$A$
and
![]() $B$
in
$B$
in
![]() $L(v)$
. So, suppose
$L(v)$
. So, suppose
![]() $m \geq 3$
. First, consider the case where
$m \geq 3$
. First, consider the case where
![]() $v \in e_i$
for some
$v \in e_i$
for some
![]() $1 \lt i \lt m$
. Fix any
$1 \lt i \lt m$
. Fix any
![]() $C \subseteq e_i \! \setminus \! \{v\}$
of size
$C \subseteq e_i \! \setminus \! \{v\}$
of size
![]() $\ell - 2$
. By the inductive hypothesis,
$\ell - 2$
. By the inductive hypothesis,
![]() $A$
and
$A$
and
![]() $C$
are connected in
$C$
are connected in
![]() $L(v)$
, because
$L(v)$
, because
![]() $e_1,\dots ,e_i$
is a tight walk between
$e_1,\dots ,e_i$
is a tight walk between
![]() $A \cup \{v\}$
and
$A \cup \{v\}$
and
![]() $C \cup \{v\}$
in
$C \cup \{v\}$
in
![]() $G$
. Similarly,
$G$
. Similarly,
![]() $C$
and
$C$
and
![]() $B$
are connected in
$B$
are connected in
![]() $L(v)$
, by applying the inductive hypothesis to
$L(v)$
, by applying the inductive hypothesis to
![]() $e_i,\dots ,e_m$
. By transitivity,
$e_i,\dots ,e_m$
. By transitivity,
![]() $A$
and
$A$
and
![]() $B$
are connected in
$B$
are connected in
![]() $L(v)$
.
$L(v)$
.
Now, suppose that
![]() $v \not \in e_i$
for every
$v \not \in e_i$
for every
![]() $1 \lt i \lt m$
. For
$1 \lt i \lt m$
. For
![]() $1 \leq i \leq m-2$
, let
$1 \leq i \leq m-2$
, let
![]() $C_i := e_i \cap e_{i+1} \cap e_{i+2}$
. Then
$C_i := e_i \cap e_{i+1} \cap e_{i+2}$
. Then
![]() $|C_i| \geq \ell -2$
and we may assume, by passing to a subset if necessary, that
$|C_i| \geq \ell -2$
and we may assume, by passing to a subset if necessary, that
![]() $|C_i| = \ell -2$
. Note that
$|C_i| = \ell -2$
. Note that
![]() $v \notin C_i$
for every
$v \notin C_i$
for every
![]() $1 \leq i \leq m-2$
. Set also
$1 \leq i \leq m-2$
. Set also
![]() $C_0 = A$
and
$C_0 = A$
and
![]() $C_{m-1} = B$
. It suffices to show that for every
$C_{m-1} = B$
. It suffices to show that for every
![]() $1 \leq i \leq m-1$
,
$1 \leq i \leq m-1$
,
![]() $C_{i-1},C_{i}$
are connected in
$C_{i-1},C_{i}$
are connected in
![]() $L(v)$
. Indeed, this would imply, by transitivity, that
$L(v)$
. Indeed, this would imply, by transitivity, that
![]() $A = C_0$
and
$A = C_0$
and
![]() $B = C_{m-1}$
are connected in
$B = C_{m-1}$
are connected in
![]() $L(v)$
. Observe that
$L(v)$
. Observe that
![]() $A$
and
$A$
and
![]() $C_1$
are connected in
$C_1$
are connected in
![]() $L(v)$
because
$L(v)$
because
![]() $e_1 \! \setminus \! \{v\}$
is an edge of
$e_1 \! \setminus \! \{v\}$
is an edge of
![]() $L(v)$
containing
$L(v)$
containing
![]() $A, C_1$
. Similarly,
$A, C_1$
. Similarly,
![]() $B$
and
$B$
and
![]() $C_{m-2}$
are connected in
$C_{m-2}$
are connected in
![]() $L(v)$
because
$L(v)$
because
![]() $v \in e_m$
and
$v \in e_m$
and
![]() $B,C_{m-2} \subseteq e_m \! \setminus \! \{v\}$
. Now let
$B,C_{m-2} \subseteq e_m \! \setminus \! \{v\}$
. Now let
![]() $2 \leq i \leq m-2$
. By Lemma 2.8, there is a tight walk
$2 \leq i \leq m-2$
. By Lemma 2.8, there is a tight walk
![]() $f, g$
with
$f, g$
with
![]() $v \in f$
and
$v \in f$
and
![]() $e_i \cap e_{i + 1} \subseteq g$
. By definition,
$e_i \cap e_{i + 1} \subseteq g$
. By definition,
![]() $C_i,C_{i-1} \subseteq e_i \cap e_{i+1}$
, and hence
$C_i,C_{i-1} \subseteq e_i \cap e_{i+1}$
, and hence
![]() $C_i,C_{i-1} \subseteq g$
. Now, by Lemma 2.2,
$C_i,C_{i-1} \subseteq g$
. Now, by Lemma 2.2,
![]() $C_i,C_{i-1}$
are connected in
$C_i,C_{i-1}$
are connected in
![]() $L(v)$
, as required.
$L(v)$
, as required.
Lemma 2.9 immediately implies the following.
Theorem 2.10.
Let
![]() $G$
be a tightly connected disperse
$G$
be a tightly connected disperse
![]() $\ell$
-graph. Then
$\ell$
-graph. Then
![]() $L(v)$
is tightly connected for all
$L(v)$
is tightly connected for all
![]() $v \in V(G)$
.
$v \in V(G)$
.
Proof.
Let
![]() $v \in V(G)$
. Fix any
$v \in V(G)$
. Fix any
![]() $A,B \subseteq V(G) \setminus \{v\}$
of size
$A,B \subseteq V(G) \setminus \{v\}$
of size
![]() $\ell -2$
. As
$\ell -2$
. As
![]() $G$
is tightly connected,
$G$
is tightly connected,
![]() $A \cup \{v\}$
and
$A \cup \{v\}$
and
![]() $B \cup \{v\}$
are connected in
$B \cup \{v\}$
are connected in
![]() $G$
. Hence, by Lemma 2.9,
$G$
. Hence, by Lemma 2.9,
![]() $A$
and
$A$
and
![]() $B$
are connected in
$B$
are connected in
![]() $L(v)$
. This shows that
$L(v)$
. This shows that
![]() $L(v)$
is tightly connected.
$L(v)$
is tightly connected.
Next, we need the following simple lemma proved by the first author and Tomon [Reference Gishboliner and Tomon8]. For completeness, we include the proof.
Lemma 2.11.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $3$
-graph. Then
$3$
-graph. Then
![]() $L(v)$
is a cograph for every
$L(v)$
is a cograph for every
![]() $v \in V(G)$
.
$v \in V(G)$
.
Proof.
Let
![]() $v \in V(G)$
, and suppose by contradiction that
$v \in V(G)$
, and suppose by contradiction that
![]() $a,b,c,d$
is an induced path in
$a,b,c,d$
is an induced path in
![]() $L(v)$
. In order for
$L(v)$
. In order for
![]() $v,a,b,c$
not to span two edges, we must have
$v,a,b,c$
not to span two edges, we must have
![]() $\{a,b,c\} \in E(G)$
. Similarly,
$\{a,b,c\} \in E(G)$
. Similarly,
![]() $\{b,c,d\} \in E(G)$
and
$\{b,c,d\} \in E(G)$
and
![]() $\{a,b,d\},\{a,c,d\} \notin E(G)$
. But now
$\{a,b,d\},\{a,c,d\} \notin E(G)$
. But now
![]() $a,b,c,d$
span two edges, a contradiction.
$a,b,c,d$
span two edges, a contradiction.
We now proceed to the proof of Theorem1.4.
Proof of Theorem 1.4. We use induction on
![]() $\ell$
. When
$\ell$
. When
![]() $\ell = 3$
, the link of each vertex is a cograph by Lemma 2.11, and every cograph
$\ell = 3$
, the link of each vertex is a cograph by Lemma 2.11, and every cograph
![]() $H$
satisfies that
$H$
satisfies that
![]() $H$
or
$H$
or
![]() $\overline {H}$
is not connected. In particular, by the contrapositive of Theorem2.10, this implies that
$\overline {H}$
is not connected. In particular, by the contrapositive of Theorem2.10, this implies that
![]() $G$
or
$G$
or
![]() $\overline {G}$
is not tightly connected. Now, suppose
$\overline {G}$
is not tightly connected. Now, suppose
![]() $\ell \gt 3$
. Fix any
$\ell \gt 3$
. Fix any
![]() $v \in V(G)$
. By Lemma 2.1,
$v \in V(G)$
. By Lemma 2.1,
![]() $L_G(v)$
is disperse. Hence, by the induction hypothesis,
$L_G(v)$
is disperse. Hence, by the induction hypothesis,
![]() $L_G(v)$
or
$L_G(v)$
or
![]() $\overline {L_G(v)} = L_{\overline {G}}(v)$
is not tightly connected. Thus,
$\overline {L_G(v)} = L_{\overline {G}}(v)$
is not tightly connected. Thus,
![]() $G$
or
$G$
or
![]() $\overline {G}$
is not tightly connected by the contrapositive of Theorem2.10, as desired.
$\overline {G}$
is not tightly connected by the contrapositive of Theorem2.10, as desired.
Next, we consider the structure of tight components in disperse hypergraphs, with the goal of proving Theorem1.5. We begin a sequence of lemmas.
Lemma 2.12.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph and let
$\ell$
-graph and let
![]() $A_1,A_2 \subseteq V(G)$
with
$A_1,A_2 \subseteq V(G)$
with
![]() $|A_1| = |A_2| = \ell -1$
and
$|A_1| = |A_2| = \ell -1$
and
![]() $|A_1 \cap A_2| = \ell -2$
. Suppose that
$|A_1 \cap A_2| = \ell -2$
. Suppose that
![]() $G$
has a tight walk between
$G$
has a tight walk between
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. Then there exists such a tight walk on two or less edges.
$A_2$
. Then there exists such a tight walk on two or less edges.
Proof.
We prove this claim by induction on the uniformity
![]() $\ell$
. First, suppose
$\ell$
. First, suppose
![]() $\ell = 3$
and write
$\ell = 3$
and write
![]() $A_1 = \{v,x\}$
,
$A_1 = \{v,x\}$
,
![]() $A_2 = \{v,y\}$
. By Lemma 2.9,
$A_2 = \{v,y\}$
. By Lemma 2.9,
![]() $x$
and
$x$
and
![]() $y$
are in the same component of
$y$
are in the same component of
![]() $L(v)$
. Since
$L(v)$
. Since
![]() $L(v)$
is a cograph by Lemma 2.11,
$L(v)$
is a cograph by Lemma 2.11,
![]() $L(v)$
is induced
$L(v)$
is induced
![]() $P_4$
-free, and so, the shortest path from
$P_4$
-free, and so, the shortest path from
![]() $x$
to
$x$
to
![]() $y$
in
$y$
in
![]() $L(v)$
has length at most 2. Thus,
$L(v)$
has length at most 2. Thus,
![]() $G$
contains a tight walk from
$G$
contains a tight walk from
![]() $\{v,x\}$
to
$\{v,x\}$
to
![]() $\{v,y\}$
of length at most 2, as required. Now, suppose
$\{v,y\}$
of length at most 2, as required. Now, suppose
![]() $\ell \geq 4$
. Let
$\ell \geq 4$
. Let
![]() $v \in A_1 \cap A_2$
be arbitrary. By Lemma 2.9, there is a tight walk from
$v \in A_1 \cap A_2$
be arbitrary. By Lemma 2.9, there is a tight walk from
![]() $A_1 \! \setminus \! \{v\}$
to
$A_1 \! \setminus \! \{v\}$
to
![]() $A_2 \! \setminus \! \{v\}$
in
$A_2 \! \setminus \! \{v\}$
in
![]() $L(v)$
. Hence, by the inductive hypothesis, there exists such a walk of length at most 2. Denote this walk by
$L(v)$
. Hence, by the inductive hypothesis, there exists such a walk of length at most 2. Denote this walk by
![]() $e_1, e_2$
(possibly
$e_1, e_2$
(possibly
![]() $e_1=e_2$
). Then,
$e_1=e_2$
). Then,
![]() $e_1 \cup \{v\}, e_2 \cup \{v\}$
is a tight walk of length at most 2 from
$e_1 \cup \{v\}, e_2 \cup \{v\}$
is a tight walk of length at most 2 from
![]() $A_1$
to
$A_1$
to
![]() $A_2$
in
$A_2$
in
![]() $G$
, as desired.
$G$
, as desired.
Lemma 2.13.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph, let
$\ell$
-graph, let
![]() $B \subseteq V(G)$
of size
$B \subseteq V(G)$
of size
![]() $\ell$
, and let
$\ell$
, and let
![]() $A_1,A_2 \subseteq B$
be distinct subsets of size
$A_1,A_2 \subseteq B$
be distinct subsets of size
![]() $\ell -1$
. If
$\ell -1$
. If
![]() $A_1,A_2$
belong to the same tight component
$A_1,A_2$
belong to the same tight component
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $G$
, then every
$G$
, then every
![]() $(\ell - 1)$
-subset of
$(\ell - 1)$
-subset of
![]() $B$
also belongs to
$B$
also belongs to
![]() $\mathcal{C}$
.
$\mathcal{C}$
.
Proof.
By assumption,
![]() $G$
has a tight walk between
$G$
has a tight walk between
![]() $A_1$
and
$A_1$
and
![]() $A_2$
. By Lemma 2.12, there exists such a tight walk
$A_2$
. By Lemma 2.12, there exists such a tight walk
![]() $W$
of length at most 2. If
$W$
of length at most 2. If
![]() $W$
has length 1 then it consists of the single edge
$W$
has length 1 then it consists of the single edge
![]() $e = A_1 \cup A_2 = B$
, and thus, any
$e = A_1 \cup A_2 = B$
, and thus, any
![]() $(\ell - 1)$
-subset of
$(\ell - 1)$
-subset of
![]() $B$
clearly belongs to
$B$
clearly belongs to
![]() $\mathcal{C}$
. So suppose that
$\mathcal{C}$
. So suppose that
![]() $W$
has length 2 and write
$W$
has length 2 and write
![]() $W = (e_1,e_2)$
, where
$W = (e_1,e_2)$
, where
![]() $A_1 \subseteq e_1$
,
$A_1 \subseteq e_1$
,
![]() $A_2 \subseteq e_2$
, and
$A_2 \subseteq e_2$
, and
![]() $e_1 \neq e_2$
. Since
$e_1 \neq e_2$
. Since
![]() $G$
is disperse,
$G$
is disperse,
![]() $G$
misses at most one edge on the
$G$
misses at most one edge on the
![]() $(\ell +1)$
-set
$(\ell +1)$
-set
![]() $C := e_1 \cup e_2$
. This implies that for every
$C := e_1 \cup e_2$
. This implies that for every
![]() $(\ell -1)$
-set
$(\ell -1)$
-set
![]() $A \subseteq C$
, there is an edge
$A \subseteq C$
, there is an edge
![]() $e \in E(G)$
with
$e \in E(G)$
with
![]() $A \subseteq e \subseteq C$
(indeed, otherwise
$A \subseteq e \subseteq C$
(indeed, otherwise
![]() $C$
misses at least two edges). As
$C$
misses at least two edges). As
![]() $|e \cap e_1| \geq \ell -1$
, we have a tight walk
$|e \cap e_1| \geq \ell -1$
, we have a tight walk
![]() $(e_1,e)$
between
$(e_1,e)$
between
![]() $A_1$
and
$A_1$
and
![]() $A$
. Hence,
$A$
. Hence,
![]() $A$
belongs to
$A$
belongs to
![]() $\mathcal{C}$
, as required.
$\mathcal{C}$
, as required.
Lemma 2.14.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph and let
$\ell$
-graph and let
![]() $e_1, \ldots , e_m$
be a tight walk in
$e_1, \ldots , e_m$
be a tight walk in
![]() $G$
. Then all
$G$
. Then all
![]() $(\ell - 1)$
-subsets of
$(\ell - 1)$
-subsets of
![]() $\bigcup _{i = 1}^me_i$
belong to the same tight component of
$\bigcup _{i = 1}^me_i$
belong to the same tight component of
![]() $G$
.
$G$
.
Proof.
We will prove this claim by induction on
![]() $m$
. The claim is trivial when
$m$
. The claim is trivial when
![]() $m = 1$
, as
$m = 1$
, as
![]() $e_1$
is a tight walk between any two
$e_1$
is a tight walk between any two
![]() $(\ell - 1)$
-subsets of
$(\ell - 1)$
-subsets of
![]() $e_1$
. Now assume
$e_1$
. Now assume
![]() $m \geq 2$
. By the induction hypothesis, there is a tight component
$m \geq 2$
. By the induction hypothesis, there is a tight component
![]() $\mathcal{C}$
containing all
$\mathcal{C}$
containing all
![]() $(\ell - 1)$
-subsets of
$(\ell - 1)$
-subsets of
![]() $W := \bigcup _{i = 1}^{m - 1}e_i$
. If
$W := \bigcup _{i = 1}^{m - 1}e_i$
. If
![]() $e_m \subseteq \bigcup _{i=1}^{m-1} e_i$
then there is nothing to prove, so suppose otherwise. Let
$e_m \subseteq \bigcup _{i=1}^{m-1} e_i$
then there is nothing to prove, so suppose otherwise. Let
![]() $x$
be the unique vertex in
$x$
be the unique vertex in
![]() $e_m \setminus e_{m-1}$
, and write
$e_m \setminus e_{m-1}$
, and write
![]() $e_m = \{v_1, v_2, \dots , v_{\ell - 1}, x\}$
. It suffices to show that for every
$e_m = \{v_1, v_2, \dots , v_{\ell - 1}, x\}$
. It suffices to show that for every
![]() $w_1,\dots ,w_{\ell -2} \in W$
, the
$w_1,\dots ,w_{\ell -2} \in W$
, the
![]() $(\ell - 1)$
-set
$(\ell - 1)$
-set
![]() $\{w_1, w_2, \ldots , w_{\ell - 2}, x\}$
belongs to
$\{w_1, w_2, \ldots , w_{\ell - 2}, x\}$
belongs to
![]() $\mathcal{C}$
. We now prove by induction on
$\mathcal{C}$
. We now prove by induction on
![]() $j$
that for every
$j$
that for every
![]() $0 \leq j \leq \ell -2$
,
$0 \leq j \leq \ell -2$
,
![]() $A_j := \{w_1, \ldots , w_j, v_{j + 1}, \ldots , v_{\ell - 2}, x\} \in \mathcal{C}$
. For the base case
$A_j := \{w_1, \ldots , w_j, v_{j + 1}, \ldots , v_{\ell - 2}, x\} \in \mathcal{C}$
. For the base case
![]() $j=0$
, note that
$j=0$
, note that
![]() $A_0 = \{v_1,\dots ,v_{\ell -2},x\}$
is in the same tight component as
$A_0 = \{v_1,\dots ,v_{\ell -2},x\}$
is in the same tight component as
![]() $\{v_1,\dots ,v_{\ell -1}\} \in \mathcal{C}$
, because both of these
$\{v_1,\dots ,v_{\ell -1}\} \in \mathcal{C}$
, because both of these
![]() $(\ell -1)$
-sets are contained in
$(\ell -1)$
-sets are contained in
![]() $e_m$
. For the induction step, let
$e_m$
. For the induction step, let
![]() $1 \leq j \leq \ell -2$
. By the inductive hypothesis,
$1 \leq j \leq \ell -2$
. By the inductive hypothesis,
![]() $A_{j-1} = \{w_1, \ldots , w_{j - 1}, v_j, v_{j + 1}, \ldots , v_{\ell - 2}, x\} \in \mathcal{C}$
. Also,
$A_{j-1} = \{w_1, \ldots , w_{j - 1}, v_j, v_{j + 1}, \ldots , v_{\ell - 2}, x\} \in \mathcal{C}$
. Also,
![]() $\{w_1, \ldots , w_j, v_j, v_{j + 1}, \ldots , v_{\ell - 2}\} \in \mathcal{C}$
because all vertices of this
$\{w_1, \ldots , w_j, v_j, v_{j + 1}, \ldots , v_{\ell - 2}\} \in \mathcal{C}$
because all vertices of this
![]() $(\ell -1)$
-set belong to
$(\ell -1)$
-set belong to
![]() $W$
. Hence, by Lemma 2.13 for the set
$W$
. Hence, by Lemma 2.13 for the set
![]() $B := \{w_1, \ldots , w_j, v_j, v_{j + 1}, \ldots , v_{\ell - 2}, x\}$
, every
$B := \{w_1, \ldots , w_j, v_j, v_{j + 1}, \ldots , v_{\ell - 2}, x\}$
, every
![]() $(\ell -1)$
-subset of
$(\ell -1)$
-subset of
![]() $B$
, and in particular
$B$
, and in particular
![]() $A_j$
, also belongs to
$A_j$
, also belongs to
![]() $\mathcal{C}$
. This completes the induction step. Taking
$\mathcal{C}$
. This completes the induction step. Taking
![]() $j = \ell -2$
, we get that
$j = \ell -2$
, we get that
![]() $A_{\ell -2} = \{w_1,\dots ,w_{\ell -2},x\} \in \mathcal{C}$
, as required.
$A_{\ell -2} = \{w_1,\dots ,w_{\ell -2},x\} \in \mathcal{C}$
, as required.
Using the above lemmas, we can now prove Theorem1.5.
Proof of Theorem 1.5. Let
![]() $\mathcal{C}$
be a tight component of
$\mathcal{C}$
be a tight component of
![]() $G$
. Let
$G$
. Let
![]() $U$
be the set of all
$U$
be the set of all
![]() $v \in V(G)$
such that
$v \in V(G)$
such that
![]() $v \in A$
for some
$v \in A$
for some
![]() $A \in \mathcal{C}$
. We want to show that
$A \in \mathcal{C}$
. We want to show that
![]() $\mathcal{C} = \binom {U}{\ell -1}$
. So suppose for the sake of contradiction that there exists some
$\mathcal{C} = \binom {U}{\ell -1}$
. So suppose for the sake of contradiction that there exists some
![]() $A \subseteq U$
of size
$A \subseteq U$
of size
![]() $\ell -1$
such that
$\ell -1$
such that
![]() $A \not \in \mathcal{C}$
. Let
$A \not \in \mathcal{C}$
. Let
![]() $A'$
be a largest subset of
$A'$
be a largest subset of
![]() $A$
such that
$A$
such that
![]() $A' \subseteq B$
for some
$A' \subseteq B$
for some
![]() $B \in \mathcal{C}$
. As
$B \in \mathcal{C}$
. As
![]() $A \notin \mathcal{C}$
, we have
$A \notin \mathcal{C}$
, we have
![]() $|A'| \lt |A|$
. So fix
$|A'| \lt |A|$
. So fix
![]() $x \in A \! \setminus \! A'$
. As
$x \in A \! \setminus \! A'$
. As
![]() $x \in U$
, there is some
$x \in U$
, there is some
![]() $C \in \mathcal{C}$
with
$C \in \mathcal{C}$
with
![]() $x \in C$
(by the definition of
$x \in C$
(by the definition of
![]() $U$
). As
$U$
). As
![]() $B,C \in \mathcal{C}$
, there is a tight walk
$B,C \in \mathcal{C}$
, there is a tight walk
![]() $e_1,\dots ,e_m$
in
$e_1,\dots ,e_m$
in
![]() $G$
between
$G$
between
![]() $B$
and
$B$
and
![]() $C$
. By Lemma 2.14, each
$C$
. By Lemma 2.14, each
![]() $(\ell -1)$
-tuple of vertices in
$(\ell -1)$
-tuple of vertices in
![]() $\bigcup _{i=1}^m e_i$
also belongs to
$\bigcup _{i=1}^m e_i$
also belongs to
![]() $\mathcal{C}$
. As
$\mathcal{C}$
. As
![]() $A' \cup \{x\} \subseteq B \cup C \subseteq \bigcup _{i=1}^m e_i$
, there is an
$A' \cup \{x\} \subseteq B \cup C \subseteq \bigcup _{i=1}^m e_i$
, there is an
![]() $(\ell -1)$
-tuple
$(\ell -1)$
-tuple
![]() $D \in \mathcal{C}$
with
$D \in \mathcal{C}$
with
![]() $A' \cup \{x\} \subseteq D$
. However, this contradicts the maximality of
$A' \cup \{x\} \subseteq D$
. However, this contradicts the maximality of
![]() $A'$
, completing the proof.
$A'$
, completing the proof.
3. Proof of Theorem1.2
The following is a standard bound on the independence number of hypergraphs, due to Spencer [Reference Spencer14].
Lemma 3.1.
Let
![]() $G$
be an
$G$
be an
![]() $\ell$
-graph with
$\ell$
-graph with
![]() $n$
vertices and average degree
$n$
vertices and average degree
![]() $d$
. Then
$d$
. Then
Proof.
If
![]() $d \lt 1$
then
$d \lt 1$
then
![]() $e(G) = \frac {nd}{\ell } \lt \frac {n}{\ell }$
, and deleting one vertex per edge gives an independent set of size at least
$e(G) = \frac {nd}{\ell } \lt \frac {n}{\ell }$
, and deleting one vertex per edge gives an independent set of size at least
![]() $\frac {\ell -1}{\ell }n$
. Suppose now that
$\frac {\ell -1}{\ell }n$
. Suppose now that
![]() $d \geq 1$
. Sample a random subset
$d \geq 1$
. Sample a random subset
![]() $U \subseteq V(G)$
with probability
$U \subseteq V(G)$
with probability
![]() $p := d^{-1/(\ell -1)} \leq 1$
. Deleting one vertex per edge in
$p := d^{-1/(\ell -1)} \leq 1$
. Deleting one vertex per edge in
![]() $U$
gives an independent set of size at least
$U$
gives an independent set of size at least
![]() $|U| - e(U)$
. By linearity of expectation, we have
$|U| - e(U)$
. By linearity of expectation, we have
![]() $\mathbb{E}[|U| - e(U)] = pn - p^{\ell } \frac {dn}{\ell } = pn(1 - \frac {p^{\ell -1}d}{\ell }) = \frac {\ell -1}{\ell }pn = \frac {\ell -1}{\ell }nd^{-1/(\ell -1)}$
.
$\mathbb{E}[|U| - e(U)] = pn - p^{\ell } \frac {dn}{\ell } = pn(1 - \frac {p^{\ell -1}d}{\ell }) = \frac {\ell -1}{\ell }pn = \frac {\ell -1}{\ell }nd^{-1/(\ell -1)}$
.
It is well-known that every
![]() $n$
-vertex cograph contains a homogeneous set of size at least
$n$
-vertex cograph contains a homogeneous set of size at least
![]() $n^{1/2}$
. The same proof applies to cohypergraphs, as follows.
$n^{1/2}$
. The same proof applies to cohypergraphs, as follows.
Lemma 3.2.
Every cohypergraph
![]() $G$
on
$G$
on
![]() $n$
vertices satisfies
$n$
vertices satisfies
![]() $\alpha (G) \cdot \omega (G) \geq n$
and hence
$\alpha (G) \cdot \omega (G) \geq n$
and hence
![]() $\max (\alpha (G), \omega (G)) \geq n^{\frac {1}{2}}$
.
$\max (\alpha (G), \omega (G)) \geq n^{\frac {1}{2}}$
.
Proof.
We prove this by induction on
![]() $n$
. The case
$n$
. The case
![]() $n=1$
is trivial, so suppose
$n=1$
is trivial, so suppose
![]() $n \geq 2$
. By definition, we can write
$n \geq 2$
. By definition, we can write
![]() $V(G) = V(H_1) \cup V(H_2)$
, where
$V(G) = V(H_1) \cup V(H_2)$
, where
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are vertex-disjoint cohypergraphs, and
$H_2$
are vertex-disjoint cohypergraphs, and
![]() $G$
has either all edges or no edges which intersect both
$G$
has either all edges or no edges which intersect both
![]() $V(H_1)$
and
$V(H_1)$
and
![]() $V(H_2)$
. By the inductive hypothesis,
$V(H_2)$
. By the inductive hypothesis,
![]() $\alpha (H_i) \cdot \omega (H_i) \geq |V(H_i)|$
for
$\alpha (H_i) \cdot \omega (H_i) \geq |V(H_i)|$
for
![]() $i=1,2$
. Let us assume that
$i=1,2$
. Let us assume that
![]() $G$
has all edges which intersect both
$G$
has all edges which intersect both
![]() $V(H_1)$
and
$V(H_1)$
and
![]() $V(H_2)$
; the other case is symmetrical (by switching to
$V(H_2)$
; the other case is symmetrical (by switching to
![]() $\overline {G}$
). Then
$\overline {G}$
). Then
![]() $\omega (G) = \omega (H_1) + \omega (H_2)$
and
$\omega (G) = \omega (H_1) + \omega (H_2)$
and
![]() $\alpha (G) = \max (\alpha (H_1), \alpha (H_2))$
, giving
$\alpha (G) = \max (\alpha (H_1), \alpha (H_2))$
, giving
 \begin{align*} \alpha (G) \cdot \omega (G) &= \max (\alpha (H_1), \alpha (H_2)) \cdot (\omega (H_1) + \omega (H_2)) \\ &\geq \alpha (H_1) \cdot \omega (H_1) + \alpha (H_2) \cdot \omega (H_2) \\ &\geq |V(H_1)| + |V(H_2)| \\ &= |V(G)| = n, \end{align*}
\begin{align*} \alpha (G) \cdot \omega (G) &= \max (\alpha (H_1), \alpha (H_2)) \cdot (\omega (H_1) + \omega (H_2)) \\ &\geq \alpha (H_1) \cdot \omega (H_1) + \alpha (H_2) \cdot \omega (H_2) \\ &\geq |V(H_1)| + |V(H_2)| \\ &= |V(G)| = n, \end{align*}
as desired.
For a tight component
![]() $\mathcal{C}$
of a disperse
$\mathcal{C}$
of a disperse
![]() $\ell$
-graph
$\ell$
-graph
![]() $G$
, we denote by
$G$
, we denote by
![]() $V(\mathcal{C})$
the vertex set
$V(\mathcal{C})$
the vertex set
![]() $U$
satisfying
$U$
satisfying
![]() $\mathcal{C} = \binom {U}{\ell -1}$
, using Theorem1.5. The following lemma shows that if all tight components of
$\mathcal{C} = \binom {U}{\ell -1}$
, using Theorem1.5. The following lemma shows that if all tight components of
![]() $G$
are small, then
$G$
are small, then
![]() $G$
has a large independent set.
$G$
has a large independent set.
Lemma 3.3.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph on
$\ell$
-graph on
![]() $n$
vertices, and suppose that for every tight component
$n$
vertices, and suppose that for every tight component
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $G$
it holds that
$G$
it holds that
![]() $|V(\mathcal{C})| \leq m$
. Then
$|V(\mathcal{C})| \leq m$
. Then
![]() $\alpha (G) \geq \frac {\ell -1}{\ell } \cdot (n/m)^{\frac {1}{\ell -1}}$
.
$\alpha (G) \geq \frac {\ell -1}{\ell } \cdot (n/m)^{\frac {1}{\ell -1}}$
.
Proof.
First, we will bound the number of edges of
![]() $G$
. Note that each edge of
$G$
. Note that each edge of
![]() $G$
is contained in
$G$
is contained in
![]() $V(\mathcal{C})$
for some tight component
$V(\mathcal{C})$
for some tight component
![]() $\mathcal{C}$
. Thus, by summing over all tight components, we obtain that
$\mathcal{C}$
. Thus, by summing over all tight components, we obtain that
 \begin{align*} e(G) &\leq \sum _{\mathcal{C}}\binom {|V(\mathcal{C})|}{\ell } \\ &\leq \frac {m}{\ell }\sum _{\mathcal{C}}\binom {|V(\mathcal{C})|}{\ell - 1} \\ &= \frac {m}{\ell }\binom {n}{\ell - 1}, \end{align*}
\begin{align*} e(G) &\leq \sum _{\mathcal{C}}\binom {|V(\mathcal{C})|}{\ell } \\ &\leq \frac {m}{\ell }\sum _{\mathcal{C}}\binom {|V(\mathcal{C})|}{\ell - 1} \\ &= \frac {m}{\ell }\binom {n}{\ell - 1}, \end{align*}
where the equality uses the fact that every
![]() $(\ell -1)$
-subset of
$(\ell -1)$
-subset of
![]() $V(G)$
is contained in
$V(G)$
is contained in
![]() $V(\mathcal{C})$
for exactly one tight component
$V(\mathcal{C})$
for exactly one tight component
![]() $\mathcal{C}$
, as the tight components partition
$\mathcal{C}$
, as the tight components partition
![]() $\binom {V(G)}{\ell -1}$
. Letting
$\binom {V(G)}{\ell -1}$
. Letting
![]() $d$
denote the average degree of
$d$
denote the average degree of
![]() $G$
, we get
$G$
, we get
Thus, by Lemma 3.1,
as desired.
For two disjoint vertex-sets
![]() $X,Y$
in an
$X,Y$
in an
![]() $\ell$
-graph
$\ell$
-graph
![]() $G$
and for
$G$
and for
![]() $1 \leq i \leq \ell -1$
, denote by
$1 \leq i \leq \ell -1$
, denote by
![]() $E_G(X^i,Y^{\ell -i})$
the set of edges of
$E_G(X^i,Y^{\ell -i})$
the set of edges of
![]() $G$
having
$G$
having
![]() $i$
vertices in
$i$
vertices in
![]() $X$
and
$X$
and
![]() $\ell -i$
vertices in
$\ell -i$
vertices in
![]() $Y$
, and let
$Y$
, and let
![]() $e_G(X^i,Y^{\ell -i})$
be the number of such edges. An edge in
$e_G(X^i,Y^{\ell -i})$
be the number of such edges. An edge in
![]() $\bigcup _{i=1}^{\ell -1} E_G(X^i,Y^{\ell -i})$
is said to cross
$\bigcup _{i=1}^{\ell -1} E_G(X^i,Y^{\ell -i})$
is said to cross
![]() $(X,Y)$
.
$(X,Y)$
.
Lemma 3.4.
Let
![]() $G$
be a disperse
$G$
be a disperse
![]() $\ell$
-graph, and let
$\ell$
-graph, and let
![]() $X,Y \subseteq V(G)$
be disjoint vertex-sets with
$X,Y \subseteq V(G)$
be disjoint vertex-sets with
![]() $e_G(X^{\ell -1},Y^1) = 0$
. Let
$e_G(X^{\ell -1},Y^1) = 0$
. Let
![]() $A = \{v_1, \dots , v_{\ell - 1}\} \subseteq X \cup Y$
, denote
$A = \{v_1, \dots , v_{\ell - 1}\} \subseteq X \cup Y$
, denote
![]() $i = |A \cap Y|$
and assume
$i = |A \cap Y|$
and assume
![]() $i \geq 1$
. Then there are less than
$i \geq 1$
. Then there are less than
![]() $2^{i - 1}$
edges in
$2^{i - 1}$
edges in
![]() $E_G(X^{\ell -i},Y^i)$
containing
$E_G(X^{\ell -i},Y^i)$
containing
![]() $A$
.
$A$
.
Proof.
We prove the claim by induction on
![]() $i$
. The base case
$i$
. The base case
![]() $i=1$
holds by assumption as
$i=1$
holds by assumption as
![]() $e_G(X^{\ell - 1}, Y^1) = 0$
. Now let
$e_G(X^{\ell - 1}, Y^1) = 0$
. Now let
![]() $2 \leq i \leq \ell -1$
and suppose that the result holds for
$2 \leq i \leq \ell -1$
and suppose that the result holds for
![]() $i-1$
. Without loss of generality, assume that
$i-1$
. Without loss of generality, assume that
![]() $v_1,v_{\ell -1} \in Y$
(note that
$v_1,v_{\ell -1} \in Y$
(note that
![]() $|A \cap Y| = i \geq 2$
). Suppose, for the sake of contradiction, that there are at least
$|A \cap Y| = i \geq 2$
). Suppose, for the sake of contradiction, that there are at least
![]() $2^{i - 1}$
edges in
$2^{i - 1}$
edges in
![]() $E_G(X^{\ell -i},Y^i)$
which contain
$E_G(X^{\ell -i},Y^i)$
which contain
![]() $A$
. As
$A$
. As
![]() $|A \cap Y| = i$
, each such edge consists of
$|A \cap Y| = i$
, each such edge consists of
![]() $A$
and a vertex from
$A$
and a vertex from
![]() $X$
. So let
$X$
. So let
![]() $X_A = \{x \in X \setminus A \, : \, \{x\} \cup A \in E(G)\}$
denote the set of vertices in
$X_A = \{x \in X \setminus A \, : \, \{x\} \cup A \in E(G)\}$
denote the set of vertices in
![]() $X$
such that
$X$
such that
![]() $\{x\} \cup A \in E_G(X^{\ell -i},Y^i)$
. Then
$\{x\} \cup A \in E_G(X^{\ell -i},Y^i)$
. Then
![]() $|X_A| \geq 2^{i - 1}$
. Observe that for any
$|X_A| \geq 2^{i - 1}$
. Observe that for any
![]() $x_1, x_2 \in X_A$
, the set of vertices
$x_1, x_2 \in X_A$
, the set of vertices
![]() $\{x_1, x_2\} \cup A$
contains at least two edges (namely, the edges
$\{x_1, x_2\} \cup A$
contains at least two edges (namely, the edges
![]() $\{x_j\} \cup A$
for
$\{x_j\} \cup A$
for
![]() $j=1,2$
), and thus, avoids at most one edge (as
$j=1,2$
), and thus, avoids at most one edge (as
![]() $G$
is disperse). Colour the pair
$G$
is disperse). Colour the pair
![]() $x_1x_2 \in \binom {X_A}{2}$
blue if
$x_1x_2 \in \binom {X_A}{2}$
blue if
![]() $\{x_1, x_2, v_2, \dots , v_{\ell -1}\} \in E(G)$
, and red otherwise. So, if
$\{x_1, x_2, v_2, \dots , v_{\ell -1}\} \in E(G)$
, and red otherwise. So, if
![]() $x_1x_2$
is coloured red, then
$x_1x_2$
is coloured red, then
![]() $\{x_1, x_2, v_1, \dots , v_{\ell - 2}\} \in E(G)$
. Fix any
$\{x_1, x_2, v_1, \dots , v_{\ell - 2}\} \in E(G)$
. Fix any
![]() $v \in X_A$
. By pigeonhole, at least
$v \in X_A$
. By pigeonhole, at least
![]() $\lceil \frac {|X_A|-1}{2} \rceil \geq 2^{i-2}$
of the edges touching
$\lceil \frac {|X_A|-1}{2} \rceil \geq 2^{i-2}$
of the edges touching
![]() $v$
have the same colour. Without loss of generality, suppose this colour is red. That is,
$v$
have the same colour. Without loss of generality, suppose this colour is red. That is,
![]() $\{v, x, v_1, \dots , v_{\ell - 2}\} \in E(G)$
for at least
$\{v, x, v_1, \dots , v_{\ell - 2}\} \in E(G)$
for at least
![]() $2^{i-2}$
vertices
$2^{i-2}$
vertices
![]() $x$
. Note that the set
$x$
. Note that the set
![]() $A' := \{v_1, \dots , v_{\ell - 2}, v\}$
satisfies
$A' := \{v_1, \dots , v_{\ell - 2}, v\}$
satisfies
![]() $|A' \cap Y| = i-1$
, because
$|A' \cap Y| = i-1$
, because
![]() $v_{\ell -1} \in Y$
and
$v_{\ell -1} \in Y$
and
![]() $v \in X$
. Hence, each edge
$v \in X$
. Hence, each edge
![]() $\{v, x, v_1, \dots , v_{\ell - 2}\}$
as above belongs to
$\{v, x, v_1, \dots , v_{\ell - 2}\}$
as above belongs to
![]() $E_G(X^{\ell - i + 1}, Y^{i - 1})$
. Therefore, the number of edges in
$E_G(X^{\ell - i + 1}, Y^{i - 1})$
. Therefore, the number of edges in
![]() $E_G(X^{\ell - i + 1}, Y^{i - 1})$
containing
$E_G(X^{\ell - i + 1}, Y^{i - 1})$
containing
![]() $A'$
is at least
$A'$
is at least
![]() $2^{i - 2}$
, a contradiction to the induction hypothesis.
$2^{i - 2}$
, a contradiction to the induction hypothesis.
Finally, we prove Theorem1.2.
Proof of Theorem 1.2. Set
![]() $\epsilon = \frac {\ell + 1}{3\ell - 1}, \gamma = \frac {2}{3\ell - 1}$
. We first define an algorithm to maintain a partition
$\epsilon = \frac {\ell + 1}{3\ell - 1}, \gamma = \frac {2}{3\ell - 1}$
. We first define an algorithm to maintain a partition
![]() $\mathcal{P}$
of
$\mathcal{P}$
of
![]() $V(G)$
and a set of
$V(G)$
and a set of
![]() $\ell$
-tuples
$\ell$
-tuples
![]() $\mathcal{B} \subseteq \binom {V(G)}{\ell }$
, as follows.
$\mathcal{B} \subseteq \binom {V(G)}{\ell }$
, as follows.
We first give the following claim, which will be used later.
Claim 3.5.
Let
![]() $U \subseteq V(G)$
. If
$U \subseteq V(G)$
. If
![]() $U$
contains no
$U$
contains no
![]() $\ell$
-tuple from
$\ell$
-tuple from
![]() $\mathcal{B}$
, then
$\mathcal{B}$
, then
![]() $G[U]$
is a cohypergraph.
$G[U]$
is a cohypergraph.
Proof.
Observe that at each step of the algorithm, the hypergraph
![]() $H$
(Line 3) has no edges which cross
$H$
(Line 3) has no edges which cross
![]() $(X \cap U, Y \cap U)$
(because all such edges are added to
$(X \cap U, Y \cap U)$
(because all such edges are added to
![]() $\mathcal{B}$
). This implies that
$\mathcal{B}$
). This implies that
![]() $G$
contains all or none of the edges crossing
$G$
contains all or none of the edges crossing
![]() $(X \cap U, Y \cap U)$
(by the choice of
$(X \cap U, Y \cap U)$
(by the choice of
![]() $H$
). Moreover,
$H$
). Moreover,
![]() $|U \cap W| \leq \ell -1$
for every
$|U \cap W| \leq \ell -1$
for every
![]() $W \in \mathcal{P}$
(here
$W \in \mathcal{P}$
(here
![]() $\mathcal{P}$
is the partition at the end of the algorithm), because
$\mathcal{P}$
is the partition at the end of the algorithm), because
![]() $U$
contains no
$U$
contains no
![]() $\ell$
-tuple from
$\ell$
-tuple from
![]() $\mathcal{B}$
, whereas
$\mathcal{B}$
, whereas
![]() $\binom {W}{\ell } \subseteq \mathcal{B}$
. It follows that
$\binom {W}{\ell } \subseteq \mathcal{B}$
. It follows that
![]() $G[U]$
is a cohypergraph obtained by starting with the empty hypergraphs
$G[U]$
is a cohypergraph obtained by starting with the empty hypergraphs
![]() $G[U \cap W]$
,
$G[U \cap W]$
,
![]() $W \in \mathcal{P}$
, and repeatedly joining two of the parts (by backtracking the algorithm).
$W \in \mathcal{P}$
, and repeatedly joining two of the parts (by backtracking the algorithm).
Algorithm 1: PARTITION-ALGORITHM

Note that in Line 9 of the algorithm, we have
![]() $E_H(X^{\ell -1},Y^1) = \emptyset$
, because
$E_H(X^{\ell -1},Y^1) = \emptyset$
, because
![]() $X$
is the vertex set of a tight component
$X$
is the vertex set of a tight component
![]() $\mathcal{C}$
of
$\mathcal{C}$
of
![]() $H$
. Indeed, if there were an edge
$H$
. Indeed, if there were an edge
![]() $\{x_1,\dots ,x_{\ell -1},y\} \in E_H(X^{\ell -1},Y^1)$
, then we would have
$\{x_1,\dots ,x_{\ell -1},y\} \in E_H(X^{\ell -1},Y^1)$
, then we would have
![]() $y \in V(\mathcal{C}) = X$
, a contradiction.
$y \in V(\mathcal{C}) = X$
, a contradiction.
If the algorithm terminates in the first condition (Lines 4-5), then there is some set
![]() $W \subseteq V(G)$
with
$W \subseteq V(G)$
with
![]() $|W| \geq n^{1 - \gamma }$
such that in either
$|W| \geq n^{1 - \gamma }$
such that in either
![]() $G[W]$
or
$G[W]$
or
![]() $\overline {G[W]}$
, all tight components have size at most
$\overline {G[W]}$
, all tight components have size at most
![]() $n^{1-\epsilon }$
. Thus, by Lemma 3.3 (with
$n^{1-\epsilon }$
. Thus, by Lemma 3.3 (with
![]() $m = n^{1-\epsilon }$
), we have
$m = n^{1-\epsilon }$
), we have
 \begin{align*} \max (\alpha (G), \omega (G)) &\geq \frac {\ell -1}{\ell } \cdot \left ( \frac {|W|}{m} \right )^{\frac {1}{\ell -1}} \\ &\geq 0.5 n^{\frac {\epsilon - \gamma }{\ell - 1}} \\ &= 0.5n^{\frac {1}{3\ell - 1}}, \end{align*}
\begin{align*} \max (\alpha (G), \omega (G)) &\geq \frac {\ell -1}{\ell } \cdot \left ( \frac {|W|}{m} \right )^{\frac {1}{\ell -1}} \\ &\geq 0.5 n^{\frac {\epsilon - \gamma }{\ell - 1}} \\ &= 0.5n^{\frac {1}{3\ell - 1}}, \end{align*}
using our choice of
![]() $\epsilon ,\gamma$
. Hence, we may assume from now on that the algorithm does not terminate on the first condition.
$\epsilon ,\gamma$
. Hence, we may assume from now on that the algorithm does not terminate on the first condition.
Thus, by Claim 3.5, our goal from now on is to find a large set
![]() $U \subseteq V(G)$
which is independent in the hypergraph with edge set
$U \subseteq V(G)$
which is independent in the hypergraph with edge set
![]() $\mathcal{B}$
. To this end, we upper-bound
$\mathcal{B}$
. To this end, we upper-bound
![]() $|\mathcal{B}|$
. Let
$|\mathcal{B}|$
. Let
![]() $\mathcal{B}_1$
(resp.
$\mathcal{B}_1$
(resp.
![]() $\mathcal{B}_2$
) be the set of
$\mathcal{B}_2$
) be the set of
![]() $\ell$
-tuples added to
$\ell$
-tuples added to
![]() $\mathcal{B}$
in Line 9 (resp. Line 13) of the algorithm.
$\mathcal{B}$
in Line 9 (resp. Line 13) of the algorithm.
Claim 3.6.
![]() $|\mathcal{B}_1| \leq 2^{\ell } n^{\ell - 1 + \epsilon }$
.
$|\mathcal{B}_1| \leq 2^{\ell } n^{\ell - 1 + \epsilon }$
.
Proof.
We will bound
![]() $|\mathcal{B}_1|$
as follows. For each pair of sets
$|\mathcal{B}_1|$
as follows. For each pair of sets
![]() $(X,Y)$
obtained in Line 7 of the algorithm, and each edge of
$(X,Y)$
obtained in Line 7 of the algorithm, and each edge of
![]() $H$
$H$
![]() $e$
which crosses
$e$
which crosses
![]() $(X,Y)$
, we assign to
$(X,Y)$
, we assign to
![]() $e$
an
$e$
an
![]() $(\ell -1)$
-subset
$(\ell -1)$
-subset
![]() $A \subseteq e$
with
$A \subseteq e$
with
![]() $A \cap Y = e \cap Y$
(if there are several such
$A \cap Y = e \cap Y$
(if there are several such
![]() $A$
, namely if
$A$
, namely if
![]() $|e \cap Y| \leq \ell -2$
, then choose one such
$|e \cap Y| \leq \ell -2$
, then choose one such
![]() $A$
arbitrarily). In other words, for any given
$A$
arbitrarily). In other words, for any given
![]() $(\ell -1$
)-set
$(\ell -1$
)-set
![]() $A$
, we will bound the number of edges
$A$
, we will bound the number of edges
![]() $e$
of
$e$
of
![]() $H$
crossing
$H$
crossing
![]() $(X,Y)$
, which contain
$(X,Y)$
, which contain
![]() $A$
and satisfy
$A$
and satisfy
![]() $A \cap Y = e \cap Y$
. Summing over all
$A \cap Y = e \cap Y$
. Summing over all
![]() $A \in \binom {V(G)}{\ell -1}$
and all choices for
$A \in \binom {V(G)}{\ell -1}$
and all choices for
![]() $(X,Y)$
will give us the desired bound on
$(X,Y)$
will give us the desired bound on
![]() $|\mathcal{B}_1|$
.
$|\mathcal{B}_1|$
.
So, let
![]() $A \subseteq V(G)$
be an arbitrary set of size
$A \subseteq V(G)$
be an arbitrary set of size
![]() $\ell -1$
. Let
$\ell -1$
. Let
![]() $(X_1, Y_1), \dots , (X_t, Y_t)$
be all pairs of sets
$(X_1, Y_1), \dots , (X_t, Y_t)$
be all pairs of sets
![]() $(X,Y)$
obtained in the course of the algorithm for which
$(X,Y)$
obtained in the course of the algorithm for which
![]() $A$
crosses
$A$
crosses
![]() $(X,Y)$
, ordered according to when the algorithm processed them. Since any two sets handled by the algorithm are disjoint or nested, and since all
$(X,Y)$
, ordered according to when the algorithm processed them. Since any two sets handled by the algorithm are disjoint or nested, and since all
![]() $Y_i$
intersect
$Y_i$
intersect
![]() $A$
, we must have
$A$
, we must have
![]() $Y_1 \supseteq Y_2 \supseteq \dots \supseteq Y_t$
. Also, since
$Y_1 \supseteq Y_2 \supseteq \dots \supseteq Y_t$
. Also, since
![]() $|X_i| \geq n^{1-\epsilon }$
for every
$|X_i| \geq n^{1-\epsilon }$
for every
![]() $i$
(see Line 7 of the algorithm), we have
$i$
(see Line 7 of the algorithm), we have
![]() $|Y_i| \leq |Y_{i - 1}| - n^{1 - \epsilon }$
for all
$|Y_i| \leq |Y_{i - 1}| - n^{1 - \epsilon }$
for all
![]() $2 \leq i \leq t$
, and thus,
$2 \leq i \leq t$
, and thus,
![]() $t \leq n^{\epsilon }$
. Now, fix any
$t \leq n^{\epsilon }$
. Now, fix any
![]() $1 \leq i \leq t$
. As
$1 \leq i \leq t$
. As
![]() $e_H(X_i^{\ell -1},Y_i^1) = 0$
, Lemma 3.4 implies that the number of edges
$e_H(X_i^{\ell -1},Y_i^1) = 0$
, Lemma 3.4 implies that the number of edges
![]() $e$
of
$e$
of
![]() $H$
crossing
$H$
crossing
![]() $(X_i,Y_i)$
and satisfying
$(X_i,Y_i)$
and satisfying
![]() $A \cap Y_i = e \cap Y_i$
is less than
$A \cap Y_i = e \cap Y_i$
is less than
![]() $\sum _{i=1}^{\ell -1} 2^{i - 1} = 2^{\ell - 1} - 1$
. Summing over all choices of
$\sum _{i=1}^{\ell -1} 2^{i - 1} = 2^{\ell - 1} - 1$
. Summing over all choices of
![]() $A \in \binom {V(G)}{\ell -1}$
and
$A \in \binom {V(G)}{\ell -1}$
and
![]() $i=1,\dots ,t$
, we get that
$i=1,\dots ,t$
, we get that
 \begin{align*} |\mathcal{B}_1| &\leq \binom {n}{\ell -1} \cdot n^{\epsilon } \cdot 2^{\ell } \\ &\leq 2^{\ell } n^{\ell - 1 + \epsilon }, \end{align*}
\begin{align*} |\mathcal{B}_1| &\leq \binom {n}{\ell -1} \cdot n^{\epsilon } \cdot 2^{\ell } \\ &\leq 2^{\ell } n^{\ell - 1 + \epsilon }, \end{align*}
as desired.
Claim 3.7.
![]() $|\mathcal{B}_2| \leq n^{\ell - (\ell - 1)\gamma }$
.
$|\mathcal{B}_2| \leq n^{\ell - (\ell - 1)\gamma }$
.
Proof.
By the definition of the algorithm, we have
![]() $|W| \leq n^{1-\gamma }$
for every
$|W| \leq n^{1-\gamma }$
for every
![]() $W \in \mathcal{P}$
(where
$W \in \mathcal{P}$
(where
![]() $\mathcal{P}$
denotes the partition at the end of the algorithm). Hence,
$\mathcal{P}$
denotes the partition at the end of the algorithm). Hence,
 \begin{align*} |\mathcal{B}_2| &\leq \sum _{W \in \mathcal{P}}\binom {|W|}{\ell } \\ &\leq (n^{1 - \gamma })^{\ell - 1} \cdot \sum _{W \in \mathcal{P}}|W| \\ &= n^{\ell - (\ell - 1)\gamma }, \end{align*}
\begin{align*} |\mathcal{B}_2| &\leq \sum _{W \in \mathcal{P}}\binom {|W|}{\ell } \\ &\leq (n^{1 - \gamma })^{\ell - 1} \cdot \sum _{W \in \mathcal{P}}|W| \\ &= n^{\ell - (\ell - 1)\gamma }, \end{align*}
as desired.
We now complete the proof of the theorem. Consider the auxiliary
![]() $\ell$
-graph on the vertex set
$\ell$
-graph on the vertex set
![]() $V(G)$
and edge set
$V(G)$
and edge set
![]() $\mathcal{B} = \mathcal{B}_1 \cup \mathcal{B}_2$
. Let us denote this hypergraph by
$\mathcal{B} = \mathcal{B}_1 \cup \mathcal{B}_2$
. Let us denote this hypergraph by
![]() $\mathcal{B}$
as well. By Claims 3.6 and 3.7,
$\mathcal{B}$
as well. By Claims 3.6 and 3.7,
 \begin{align*} |E(\mathcal{B})| &\leq 2^{\ell } n^{\ell - 1 + \epsilon } + n^{\ell - (\ell - 1)\gamma } \\ &= 2^{\ell } n^{\ell - 1 + \frac {\ell + 1}{3\ell - 1}} + n^{\ell - (\ell - 1) \cdot \frac {2}{3\ell - 1}} \\ &= 2^{\ell } n^{\frac {3\ell ^2 - 3\ell - \ell + 1 + \ell + 1}{3\ell - 1}} + n^{\frac {3\ell ^2 - \ell - 2\ell + 2}{3\ell - 1}} \\ &= (2^{\ell } + 1)n^{\frac {3\ell ^2 - 3\ell + 2}{3\ell - 1}}. \end{align*}
\begin{align*} |E(\mathcal{B})| &\leq 2^{\ell } n^{\ell - 1 + \epsilon } + n^{\ell - (\ell - 1)\gamma } \\ &= 2^{\ell } n^{\ell - 1 + \frac {\ell + 1}{3\ell - 1}} + n^{\ell - (\ell - 1) \cdot \frac {2}{3\ell - 1}} \\ &= 2^{\ell } n^{\frac {3\ell ^2 - 3\ell - \ell + 1 + \ell + 1}{3\ell - 1}} + n^{\frac {3\ell ^2 - \ell - 2\ell + 2}{3\ell - 1}} \\ &= (2^{\ell } + 1)n^{\frac {3\ell ^2 - 3\ell + 2}{3\ell - 1}}. \end{align*}
Hence, the average degree of
![]() $\mathcal{B}$
is at most
$\mathcal{B}$
is at most
Thus, by Lemma 3.1,
 \begin{align*} \alpha (\mathcal{B}) &\geq \Omega \Big ( n^{1 - \frac {3(\ell - 1)^2}{3\ell - 1} \cdot \frac {1}{\ell - 1}} \Big ) \\ &= \Omega \left(n^{1 - \frac {3\ell - 3}{3\ell - 1}}\right) \\ &= \Omega \left(n^{\frac {2}{3\ell - 1}}\right). \end{align*}
\begin{align*} \alpha (\mathcal{B}) &\geq \Omega \Big ( n^{1 - \frac {3(\ell - 1)^2}{3\ell - 1} \cdot \frac {1}{\ell - 1}} \Big ) \\ &= \Omega \left(n^{1 - \frac {3\ell - 3}{3\ell - 1}}\right) \\ &= \Omega \left(n^{\frac {2}{3\ell - 1}}\right). \end{align*}
Thus, by Claim 3.5,
![]() $G$
contains an induced cohypergraph of size
$G$
contains an induced cohypergraph of size
![]() $\Omega (n^{\frac {2}{3\ell - 1}})$
. By Lemma 3.2,
$\Omega (n^{\frac {2}{3\ell - 1}})$
. By Lemma 3.2,
as desired.
Note that the above proof in fact shows that every
![]() $n$
-vertex disperse
$n$
-vertex disperse
![]() $\ell$
-graph can be made into a cohypergraph by adding/deleting
$\ell$
-graph can be made into a cohypergraph by adding/deleting
![]() $O(n^{\frac {3\ell ^2-3\ell +2}{3\ell -1}}) = O(n^{\ell - \frac {2\ell -2}{3\ell -1}}) = o(n^{\ell })$
edges. Indeed, changing the
$O(n^{\frac {3\ell ^2-3\ell +2}{3\ell -1}}) = O(n^{\ell - \frac {2\ell -2}{3\ell -1}}) = o(n^{\ell })$
edges. Indeed, changing the
![]() $\ell$
-tuples in
$\ell$
-tuples in
![]() $\mathcal{B}$
in an appropriate way yields a cohypergraph.
$\mathcal{B}$
in an appropriate way yields a cohypergraph.
4. Concluding remarks
For a set
![]() $L \subseteq \{0,1,\dots ,\ell +1\}$
, let us call an
$L \subseteq \{0,1,\dots ,\ell +1\}$
, let us call an
![]() $\ell$
-graph
$\ell$
-graph
![]() $L$
-free if it contains no induced
$L$
-free if it contains no induced
![]() $(\ell +1)$
-vertex subgraph whose number of edges belongs to
$(\ell +1)$
-vertex subgraph whose number of edges belongs to
![]() $L$
. Thus, an
$L$
. Thus, an
![]() $\ell$
-graph is disperse if and only if it is
$\ell$
-graph is disperse if and only if it is
![]() $\{2,3,\dots ,\ell -1\}$
-free. Our main result is that disperse
$\{2,3,\dots ,\ell -1\}$
-free. Our main result is that disperse
![]() $\ell$
-graphs have polynomial-size homogeneous sets.
$\ell$
-graphs have polynomial-size homogeneous sets.
Problem 4.1.
Is there any proper subset
![]() $L \subsetneq \{2,3,\dots ,\ell -1\}$
for which
$L \subsetneq \{2,3,\dots ,\ell -1\}$
for which
![]() $L$
-free
$L$
-free
![]() $\ell$
-graphs have polynomial-size homogeneous sets?
$\ell$
-graphs have polynomial-size homogeneous sets?
This trivially fails for
![]() $\ell =3$
, and can also be shown to fail for
$\ell =3$
, and can also be shown to fail for
![]() $\ell =4$
; but such an
$\ell =4$
; but such an
![]() $L$
could exist for
$L$
could exist for
![]() $\ell \geq 5$
.
$\ell \geq 5$
.
By combining Lemmas 2.1 and 2.11, we get that in a disperse
![]() $\ell$
-graph
$\ell$
-graph
![]() $G$
, for every
$G$
, for every
![]() $\ell -2$
distinct vertices
$\ell -2$
distinct vertices
![]() $v_1,\dots ,v_{\ell -2}$
, the link graph
$v_1,\dots ,v_{\ell -2}$
, the link graph
![]() $L(v_1,\dots ,v_{\ell -2})$
is a cograph (this graph consists of all pairs
$L(v_1,\dots ,v_{\ell -2})$
is a cograph (this graph consists of all pairs
![]() $xy$
such that
$xy$
such that
![]() $\{v_1,\dots ,v_{\ell -2},x,y\} \in E(G)$
). Thus, the following would be a strengthening of Theorem1.2.
$\{v_1,\dots ,v_{\ell -2},x,y\} \in E(G)$
). Thus, the following would be a strengthening of Theorem1.2.
Problem 4.2.
Is there
![]() $c_{\ell } \gt 0$
such that if
$c_{\ell } \gt 0$
such that if
![]() $G$
is an
$G$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $\ell$
-graph in which all links
$\ell$
-graph in which all links
![]() $L(v_1,\dots ,v_{\ell -2})$
are cographs, then
$L(v_1,\dots ,v_{\ell -2})$
are cographs, then
![]() $G$
has a homogeneous set of size at least
$G$
has a homogeneous set of size at least
![]() $n^{c_{\ell }}\,?$
$n^{c_{\ell }}\,?$
Another well-studied graph class is that of split graphs. A graph is split if it has a vertex partition
![]() $X,Y$
such that
$X,Y$
such that
![]() $X$
is a clique and
$X$
is a clique and
![]() $Y$
is an independent set. One can ask for the size of homogeneous sets in
$Y$
is an independent set. One can ask for the size of homogeneous sets in
![]() $3$
-graphs in which every link is split. It turns out that such 3-graphs might only have homogeneous sets of logarithmic size, due to the following variant of a well-known construction. Take a random graph
$3$
-graphs in which every link is split. It turns out that such 3-graphs might only have homogeneous sets of logarithmic size, due to the following variant of a well-known construction. Take a random graph
![]() $F \sim G(n,\frac {1}{2})$
, and define a 3-graph
$F \sim G(n,\frac {1}{2})$
, and define a 3-graph
![]() $G$
on
$G$
on
![]() $V(F)$
in which
$V(F)$
in which
![]() $xyz$
is an edge if
$xyz$
is an edge if
![]() $e_F(\{x,y,z\}) \geq 2$
. It is easy to show, using standard arguments, that
$e_F(\{x,y,z\}) \geq 2$
. It is easy to show, using standard arguments, that
![]() $\omega (G),\alpha (G) = O(\log n)$
. Also, for every vertex
$\omega (G),\alpha (G) = O(\log n)$
. Also, for every vertex
![]() $v$
,
$v$
,
![]() $N_F(v)$
is a clique in the link of
$N_F(v)$
is a clique in the link of
![]() $v$
, and
$v$
, and
![]() $V(F) \! \setminus \! (N_F(v) \cup \{v\})$
is an independent set in the link of
$V(F) \! \setminus \! (N_F(v) \cup \{v\})$
is an independent set in the link of
![]() $v$
. Hence each link is split.
$v$
. Hence each link is split.
We can also show that the above construction is inevitable, in the sense that if
![]() $G$
is a 3-graph where all links are split, then
$G$
is a 3-graph where all links are split, then
![]() $G$
contains a large vertex-set which induces the above construction.
$G$
contains a large vertex-set which induces the above construction.
Proposition 4.3.
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex 3-graph in which every link is split. Then there is
$n$
-vertex 3-graph in which every link is split. Then there is
![]() $U \subseteq V(G)$
,
$U \subseteq V(G)$
,
![]() $|U| \geq n^{1/3}$
, and a graph
$|U| \geq n^{1/3}$
, and a graph
![]() $F$
on
$F$
on
![]() $U$
, such that for every distinct
$U$
, such that for every distinct
![]() $x,y,z \in U$
,
$x,y,z \in U$
,
![]() $xyz \in E(G)$
if and only if
$xyz \in E(G)$
if and only if
![]() $e_F(\{x,y,z\}) \geq 2$
.
$e_F(\{x,y,z\}) \geq 2$
.
Proof.
By assumption, for each
![]() $v \in V(G)$
, there is a partition
$v \in V(G)$
, there is a partition
![]() $V(G) \! \setminus \! \{v\} = A_v \cup B_v$
such that
$V(G) \! \setminus \! \{v\} = A_v \cup B_v$
such that
![]() $A_v$
is independent in the link of
$A_v$
is independent in the link of
![]() $v$
and
$v$
and
![]() $B_v$
is a clique in the link of
$B_v$
is a clique in the link of
![]() $v$
. Call a pair of vertices
$v$
. Call a pair of vertices
![]() $xy$
good if
$xy$
good if
![]() $x \in A_y \Longleftrightarrow y \in A_x$
(i.e.
$x \in A_y \Longleftrightarrow y \in A_x$
(i.e.
![]() $x \in A_y$
and
$x \in A_y$
and
![]() $y \in A_x$
, or
$y \in A_x$
, or
![]() $x \in B_y$
and
$x \in B_y$
and
![]() $y \in B_x$
). Otherwise, call
$y \in B_x$
). Otherwise, call
![]() $xy$
bad. We first claim that there is no
$xy$
bad. We first claim that there is no
![]() $K_4$
consisting of bad pairs. Suppose otherwise; let
$K_4$
consisting of bad pairs. Suppose otherwise; let
![]() $x_1,x_2,x_3,x_4$
such that
$x_1,x_2,x_3,x_4$
such that
![]() $x_ix_j$
is bad for every
$x_ix_j$
is bad for every
![]() $1 \leq i \lt j \leq 4$
. Orient the edges
$1 \leq i \lt j \leq 4$
. Orient the edges
![]() $x_ix_j$
by letting
$x_ix_j$
by letting
![]() $x_i \rightarrow x_j$
if
$x_i \rightarrow x_j$
if
![]() $x_j \in A_{x_i}$
(note that exactly one of
$x_j \in A_{x_i}$
(note that exactly one of
![]() $x_j \in A_{x_i}$
,
$x_j \in A_{x_i}$
,
![]() $x_i \in A_{x_j}$
holds). Every tournament on 4 vertices has a transitive tournament on 3 vertices. Hence, without loss of generality, we can assume that
$x_i \in A_{x_j}$
holds). Every tournament on 4 vertices has a transitive tournament on 3 vertices. Hence, without loss of generality, we can assume that
![]() $x_1 \rightarrow x_2,x_3$
and
$x_1 \rightarrow x_2,x_3$
and
![]() $x_2 \rightarrow x_3$
. It follows that
$x_2 \rightarrow x_3$
. It follows that
![]() $x_2,x_3 \in A_{x_1}$
, and hence
$x_2,x_3 \in A_{x_1}$
, and hence
![]() $x_1x_2x_3 \notin E(G)$
. On the other hand,
$x_1x_2x_3 \notin E(G)$
. On the other hand,
![]() $x_1,x_2 \in B_{x_3}$
, and hence
$x_1,x_2 \in B_{x_3}$
, and hence
![]() $x_1x_2x_3 \in E(G)$
, giving a contradiction.
$x_1x_2x_3 \in E(G)$
, giving a contradiction.
We showed that the graph of bad pairs has no
![]() $K_4$
. As
$K_4$
. As
![]() $R(K_4,K_m) \leq \binom {m+2}{3} \leq m^3$
, there is a set
$R(K_4,K_m) \leq \binom {m+2}{3} \leq m^3$
, there is a set
![]() $U \subseteq V(G)$
,
$U \subseteq V(G)$
,
![]() $|U| \geq n^{1/3}$
, such that
$|U| \geq n^{1/3}$
, such that
![]() $U$
contains no bad pairs. Now define a graph
$U$
contains no bad pairs. Now define a graph
![]() $F$
on
$F$
on
![]() $U$
by letting
$U$
by letting
![]() $xy$
be an edge of
$xy$
be an edge of
![]() $F$
if
$F$
if
![]() $x \in B_y$
and
$x \in B_y$
and
![]() $y \in B_x$
(so
$y \in B_x$
(so
![]() $xy$
is not an edge of
$xy$
is not an edge of
![]() $F$
if
$F$
if
![]() $x \in A_y$
and
$x \in A_y$
and
![]() $y \in A_x$
). Let
$y \in A_x$
). Let
![]() $x,y,z \in U$
be distinct. If
$x,y,z \in U$
be distinct. If
![]() $xy,xz \in E(F)$
, then
$xy,xz \in E(F)$
, then
![]() $y,z \in B_x$
, so
$y,z \in B_x$
, so
![]() $xyz \in E(G)$
. Similarly, if
$xyz \in E(G)$
. Similarly, if
![]() $xy,xz \notin E(F)$
, then
$xy,xz \notin E(F)$
, then
![]() $y,z \in A_x$
and so
$y,z \in A_x$
and so
![]() $xyz \notin E(F)$
. This proves the proposition.
$xyz \notin E(F)$
. This proves the proposition.
Financial support
Lior Gishboliner: Research supported by the NSERC Discovery Grant Problems in Extremal and Probabilistic Combinatorics.