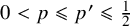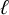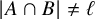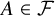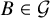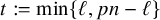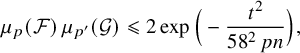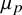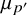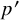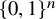1 Introduction
Extremal set theory can be traced back to the seminal workFootnote
1
of Erdős, Ko and Rado [Reference Erdős, Ko and RadoEKR61] who obtained sharp estimates of the cardinality of a family
![]() $\mathcal {A}\subseteq \binom {[n]}{k}$
that is intersecting; that is, it satisfies
$\mathcal {A}\subseteq \binom {[n]}{k}$
that is intersecting; that is, it satisfies
![]() $A\cap B\neq \emptyset $
for every
$A\cap B\neq \emptyset $
for every
![]() $A,B\in \mathcal {A}$
. (Here and in the rest of this paper,
$A,B\in \mathcal {A}$
. (Here and in the rest of this paper,
![]() $\binom {[n]}{k}$
denotes the set of all k-element subsets of the discrete interval
$\binom {[n]}{k}$
denotes the set of all k-element subsets of the discrete interval
![]() $[n]:= \{1,\dots ,n\}$
.) Since then, it is an active subfield of combinatorics; we refer the reader to [Reference EllisEl22, Reference Frankl and TokushigeFT18] for recent expositions of this theory and its applications.
$[n]:= \{1,\dots ,n\}$
.) Since then, it is an active subfield of combinatorics; we refer the reader to [Reference EllisEl22, Reference Frankl and TokushigeFT18] for recent expositions of this theory and its applications.
1.1 The Erdős–Sós problem and related results
A more challenging problem was posed in 1971 by Erdős and Sós (see [Reference ErdősErd75]); it asks to determine, for a given triple
![]() $\ell \leqslant k\leqslant n$
of positive integers, the cardinality of the largest family
$\ell \leqslant k\leqslant n$
of positive integers, the cardinality of the largest family
![]() $\mathcal {A}\subseteq \binom {[n]}{k}$
whose intersections forbid
$\mathcal {A}\subseteq \binom {[n]}{k}$
whose intersections forbid
![]() $\ell $
; that is, it satisfies
$\ell $
; that is, it satisfies
![]() $|A\cap B|\neq \ell $
for every
$|A\cap B|\neq \ell $
for every
![]() $A,B\in \mathcal {A}$
. Early significant progress on the Erdős–Sós problem was made by Frankl–Wilson [Reference Frankl and WilsonFW81] and Frankl–Füredi [Reference Frankl and FürediFF85]. Somewhat later, in 1987, a breakthrough was achieved by Frankl and Rödl, who obtained exponential estimates in the regime where
$A,B\in \mathcal {A}$
. Early significant progress on the Erdős–Sós problem was made by Frankl–Wilson [Reference Frankl and WilsonFW81] and Frankl–Füredi [Reference Frankl and FürediFF85]. Somewhat later, in 1987, a breakthrough was achieved by Frankl and Rödl, who obtained exponential estimates in the regime where
![]() $\ell $
is proportional to n. More precisely, it is shown in [Reference Frankl and RödlFR87, Theorem 1.5] that for every
$\ell $
is proportional to n. More precisely, it is shown in [Reference Frankl and RödlFR87, Theorem 1.5] that for every
![]() $0<\varepsilon <p\leqslant \frac 12$
, there exists a constant
$0<\varepsilon <p\leqslant \frac 12$
, there exists a constant
![]() $\gamma (\varepsilon ,p)>0$
such that for every pair of positive integers
$\gamma (\varepsilon ,p)>0$
such that for every pair of positive integers
![]() $\ell ,n$
with
$\ell ,n$
with
![]() $\varepsilon n\leqslant \ell \leqslant pn-\varepsilon n$
, and every pair of familiesFootnote
2
$\varepsilon n\leqslant \ell \leqslant pn-\varepsilon n$
, and every pair of familiesFootnote
2
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
whose cross intersections forbid
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
whose cross intersections forbid
![]() $\ell $
– that is, they satisfy
$\ell $
– that is, they satisfy
![]() $|A\cap B|\neq \ell $
for every
$|A\cap B|\neq \ell $
for every
![]() $A\in \mathcal {F}$
and every
$A\in \mathcal {F}$
and every
![]() $B\in \mathcal {G}$
– we have
$B\in \mathcal {G}$
– we have
where
![]() $\mu _p$
denotes the p-biased measure on
$\mu _p$
denotes the p-biased measure on
![]() $\{0,1\}^n$
– namely, the probability measure on
$\{0,1\}^n$
– namely, the probability measure on
![]() $\{0,1\}^n$
defined by setting for every
$\{0,1\}^n$
defined by setting for every
![]() $A\subseteq [n]$
,
$A\subseteq [n]$
,
(For the case
![]() $\mathcal {F}=\mathcal {G}$
, an alternative proof was given by Keevash and Long [Reference Keevash and LongKLo16]; see also [Reference Kupavskii, Sagdeev and ZakharovKSZ22].) The work of Frankl and Rödl has proven to be very influential, and it has found applications in a number of different areas such as discrete geometry [Reference Frankl and RödlFR90], communication complexity [Reference SgallS99] and quantum computing [Reference Buhrman, Cleve and WigdersonBCW99].
$\mathcal {F}=\mathcal {G}$
, an alternative proof was given by Keevash and Long [Reference Keevash and LongKLo16]; see also [Reference Kupavskii, Sagdeev and ZakharovKSZ22].) The work of Frankl and Rödl has proven to be very influential, and it has found applications in a number of different areas such as discrete geometry [Reference Frankl and RödlFR90], communication complexity [Reference SgallS99] and quantum computing [Reference Buhrman, Cleve and WigdersonBCW99].
Further progress on the Erdős–Sós problem was made by several authors, including the very recent works of Ellis–Keller–Lifshitz [Reference Ellis, Keller and LifshitzEKL24], Keller–Lifshitz [Reference Keller and LifshitzKLi21] and Kupavskii–Zaharov [Reference Kupavskii and ZaharovKZ24] (see, also, [Reference Keevash, Lifshitz, Long and MinzerKLLM23, Reference Keevash and LongKLo20] for closely related developments). Collectively, the papers [Reference Ellis, Keller and LifshitzEKL24, Reference Keller and LifshitzKLi21] obtain the sharp estimate
![]() $|\mathcal {A}|\leqslant \binom {n-(\ell +1)}{k-(\ell +1)}$
for every family
$|\mathcal {A}|\leqslant \binom {n-(\ell +1)}{k-(\ell +1)}$
for every family
![]() $\mathcal {A}\subseteq \binom {[n]}{k}$
whose intersections forbid
$\mathcal {A}\subseteq \binom {[n]}{k}$
whose intersections forbid
![]() $\ell $
in the regime
$\ell $
in the regime
![]() $2\ell < k\leqslant \big (\frac 12-\varepsilon \big )n$
with
$2\ell < k\leqslant \big (\frac 12-\varepsilon \big )n$
with
![]() $n\geqslant n_0(\ell ,\varepsilon )$
for some (unspecified) threshold function
$n\geqslant n_0(\ell ,\varepsilon )$
for some (unspecified) threshold function
![]() $n_0(\ell ,\varepsilon )$
. The more recent paper [Reference Kupavskii and ZaharovKZ24] extends this sharp estimate in the regime
$n_0(\ell ,\varepsilon )$
. The more recent paper [Reference Kupavskii and ZaharovKZ24] extends this sharp estimate in the regime
![]() $\ell =\lceil k^\beta \rceil $
and
$\ell =\lceil k^\beta \rceil $
and
![]() $n=\lceil k^\alpha \rceil $
, where
$n=\lceil k^\alpha \rceil $
, where
![]() $\alpha ,\beta>0$
are positive reals with
$\alpha ,\beta>0$
are positive reals with
![]() $\beta <\frac 12$
and
$\beta <\frac 12$
and
![]() $\alpha>1+2\beta $
and k is sufficiently large in terms of
$\alpha>1+2\beta $
and k is sufficiently large in terms of
![]() $\alpha ,\beta $
.
$\alpha ,\beta $
.
1.2 The main estimate
Our main result provides new estimates of the product of the biased measures of a pair of families with forbidden cross intersections, and in particular, it bridges the gap between the aforementioned results.
Theorem 1.1. Let n be a positive integer, let
![]() $0<p\leqslant p'\leqslant \frac 12$
, and let
$0<p\leqslant p'\leqslant \frac 12$
, and let
![]() $\ell \leqslant pn$
be a nonnegative integer. Also let
$\ell \leqslant pn$
be a nonnegative integer. Also let
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
be two families whose cross intersections forbid
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
be two families whose cross intersections forbid
![]() $\ell $
; that is,
$\ell $
; that is,
![]() $|A\cap B|\neq \ell $
for every
$|A\cap B|\neq \ell $
for every
![]() $A\in \mathcal {F}$
and
$A\in \mathcal {F}$
and
![]() $B\in \mathcal {G}$
. Then, setting
$B\in \mathcal {G}$
. Then, setting
![]() $t:=\min \{\ell ,pn-\ell \}$
, we have the subgaussian bound
$t:=\min \{\ell ,pn-\ell \}$
, we have the subgaussian bound
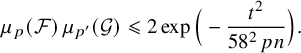 $$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) \leqslant 2\exp\Big( - \frac{t^2}{58^2\, pn}\Big). \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) \leqslant 2\exp\Big( - \frac{t^2}{58^2\, pn}\Big). \end{align} $$
Note that Theorem 1.1 extends the Frankl–Rödl theorem [Reference Frankl and RödlFR87, Theorem 1.5]; indeed, the bound (1.3) is nontrivial if
![]() $80\sqrt {pn}\leqslant \ell \leqslant pn-80\sqrt {pn}$
uniformly for
$80\sqrt {pn}\leqslant \ell \leqslant pn-80\sqrt {pn}$
uniformly for
![]() $p\geqslant \frac {160^2}{n}$
.
$p\geqslant \frac {160^2}{n}$
.
Remark 1.2. Theorem 1.1 can be extended to cover the case of all parameters
![]() $p,p'$
in the regime
$p,p'$
in the regime
![]() $0<p\leqslant p'\leqslant 1-p$
, and it also has a version for pairs of families
$0<p\leqslant p'\leqslant 1-p$
, and it also has a version for pairs of families
![]() $\mathcal {F},\mathcal {G}$
that are contained in two, possibly different, layers of the cube. We present these (standard) extensions in Section 7.
$\mathcal {F},\mathcal {G}$
that are contained in two, possibly different, layers of the cube. We present these (standard) extensions in Section 7.
Remark 1.3. The subgaussian bound (1.3) is actually optimal, modulo universal constants, for various choices of
![]() $p,p'$
and
$p,p'$
and
![]() $\ell $
. We discuss these issues in Section 8.
$\ell $
. We discuss these issues in Section 8.
Remark 1.4. Theorem 1.1 also has a supersaturation version, which is in the spirit of [Reference Frankl and RödlFR87, Theorem 1.14]; see Section 9 for details.
1.3 Outline of the proof of Theorem 1.1
The proof of Theorem 1.1 follows the general strategy invented by Frankl and Rödl [Reference Frankl and RödlFR87]. The idea is to gradually ‘deform’ the given families and eventually arrive at a pair of families whose cross intersections forbid an initial or a final interval; the measures of these final families can then be estimated by standard probabilistic tools. This ‘deformation’ is entirely algorithmic, and it is the heart of the proof.
The algorithm in [Reference Frankl and RödlFR87] takes as an input two families
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
whose cross intersections forbid an interval of
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
whose cross intersections forbid an interval of
![]() $[n]$
, and it starts by using a density increment argument in order to show that the two sections
$[n]$
, and it starts by using a density increment argument in order to show that the two sections
of
![]() $\mathcal {F}$
have roughly the same measure. Once this is done, the algorithm proceeds by comparing the measures of the union
$\mathcal {F}$
have roughly the same measure. Once this is done, the algorithm proceeds by comparing the measures of the union
![]() $\mathcal {G}_0\cup \mathcal {G}_1$
and the intersection
$\mathcal {G}_0\cup \mathcal {G}_1$
and the intersection
![]() $\mathcal {G}_0\cap \mathcal {G}_1$
of the sections of
$\mathcal {G}_0\cap \mathcal {G}_1$
of the sections of
![]() $\mathcal {G}$
. Again, a density increment argument is used to ensure that the measures of
$\mathcal {G}$
. Again, a density increment argument is used to ensure that the measures of
![]() $\mathcal {G}_0\cup \mathcal {G}_1$
and
$\mathcal {G}_0\cup \mathcal {G}_1$
and
![]() $\mathcal {G}_0\cap \mathcal {G}_1$
are roughly equal, which in turn implies that the two sections,
$\mathcal {G}_0\cap \mathcal {G}_1$
are roughly equal, which in turn implies that the two sections,
![]() $\mathcal {G}_0$
and
$\mathcal {G}_0$
and
![]() $\mathcal {G}_1$
, are almost equal. One can then use this structural information to produce a pair of families whose cross intersections forbid a larger interval, while at the same time, one keeps control of the product of their biased measures.
$\mathcal {G}_1$
, are almost equal. One can then use this structural information to produce a pair of families whose cross intersections forbid a larger interval, while at the same time, one keeps control of the product of their biased measures.
While the algorithm of Frankl and Rödl is elegant and efficient, unfortunately it leads to suboptimal results as p gets smaller, and it hits a barrierFootnote
3
at
![]() $p=o(1)$
. The reason is rather simple: if p is small, then having (or not having) density increment for the section
$p=o(1)$
. The reason is rather simple: if p is small, then having (or not having) density increment for the section
![]() $\mathcal {A}_1$
of a family
$\mathcal {A}_1$
of a family
![]() $\mathcal {A}\subseteq \{0,1\}^n$
has negligible effect on the measure of the other section
$\mathcal {A}\subseteq \{0,1\}^n$
has negligible effect on the measure of the other section
![]() $\mathcal {A}_0$
.
$\mathcal {A}_0$
.
We resolve this issue by introducing a new algorithm that also takes as an input two families
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
whose cross intersections forbid an interval of
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
whose cross intersections forbid an interval of
![]() $[n]$
, and it starts by seeking for a density increment for one of the pairs
$[n]$
, and it starts by seeking for a density increment for one of the pairs
![]() $(\mathcal {F}_1,\mathcal {G}_1)$
,
$(\mathcal {F}_1,\mathcal {G}_1)$
,
![]() $(\mathcal {F}_0, \mathcal {G}_0\cup \mathcal {G}_1)$
and
$(\mathcal {F}_0, \mathcal {G}_0\cup \mathcal {G}_1)$
and
![]() $(\mathcal {F}_0\cup \mathcal {F}_1, \mathcal {G}_0)$
. However, the density increment the algorithm is searching for is not uniform and depends on the specific pair it is looking at (as well as the parameter p). The particular choice of the density increments is justified analytically: if the algorithm does not succeed in this search, then this yields a strong lower bound for the product of the measures of
$(\mathcal {F}_0\cup \mathcal {F}_1, \mathcal {G}_0)$
. However, the density increment the algorithm is searching for is not uniform and depends on the specific pair it is looking at (as well as the parameter p). The particular choice of the density increments is justified analytically: if the algorithm does not succeed in this search, then this yields a strong lower bound for the product of the measures of
![]() $\mathcal {F}_1$
and
$\mathcal {F}_1$
and
![]() $\mathcal {G}_0\cap \mathcal {G}_1$
, or the product of the measures of
$\mathcal {G}_0\cap \mathcal {G}_1$
, or the product of the measures of
![]() $\mathcal {F}_0\cap \mathcal {F}_1$
and
$\mathcal {F}_0\cap \mathcal {F}_1$
and
![]() $\mathcal {G}_1$
. This is the content of Lemma 4.1 (the ‘widening lemma’) in Section 4. With this information at hand, we may proceed as in the algorithm of Frankl and Rödl. The main novelty (and technical difficulty) of the proof of Theorem 1.1 is thus to show that this rough outline is actually feasible by appropriately selecting the various parameters.
$\mathcal {G}_1$
. This is the content of Lemma 4.1 (the ‘widening lemma’) in Section 4. With this information at hand, we may proceed as in the algorithm of Frankl and Rödl. The main novelty (and technical difficulty) of the proof of Theorem 1.1 is thus to show that this rough outline is actually feasible by appropriately selecting the various parameters.
2 Background material
2.1 General notation
For every pair
![]() $a,b$
of integers with
$a,b$
of integers with
![]() $0\leqslant a\leqslant b$
by
$0\leqslant a\leqslant b$
by
![]() $[a,b]$
, we denote the discrete interval
$[a,b]$
, we denote the discrete interval
![]() $\{k\in \mathbb {Z}: a\leqslant k \leqslant b\}$
. Also recall that for every positive integer n and every nonnegative integer
$\{k\in \mathbb {Z}: a\leqslant k \leqslant b\}$
. Also recall that for every positive integer n and every nonnegative integer
![]() $k\leqslant n$
, we set
$k\leqslant n$
, we set
![]() $[n]:= \{1,\dots ,n\}$
and
$[n]:= \{1,\dots ,n\}$
and
![]() $\binom {[n]}{k}:=\{A\subseteq [n]: |A|=k\}$
; moreover, for every
$\binom {[n]}{k}:=\{A\subseteq [n]: |A|=k\}$
; moreover, for every
![]() $t\geqslant 0$
, we set
$t\geqslant 0$
, we set
![]() $[n]^{\leqslant t}:= \{A\subseteq [n]: |A|\leqslant t\}$
,
$[n]^{\leqslant t}:= \{A\subseteq [n]: |A|\leqslant t\}$
,
![]() $[n]^{<t}:= \{A\subseteq [n]: |A|<t\}$
,
$[n]^{<t}:= \{A\subseteq [n]: |A|<t\}$
,
![]() $[n]^{\geqslant t}:= \{A\subseteq [n]: |A|\geqslant t\}$
and
$[n]^{\geqslant t}:= \{A\subseteq [n]: |A|\geqslant t\}$
and
![]() $[n]^{>t}:= \{A\subseteq [n]: |A|>t\}$
.
$[n]^{>t}:= \{A\subseteq [n]: |A|>t\}$
.
2.2 Families of sets
Let n be a positive integer, and let
![]() $\mathcal {A}\subseteq \{0,1\}^n$
. We say that
$\mathcal {A}\subseteq \{0,1\}^n$
. We say that
![]() $\mathcal {A}$
is downwards closed if for every
$\mathcal {A}$
is downwards closed if for every
![]() $A\in \mathcal {A}$
and every
$A\in \mathcal {A}$
and every
![]() $B\subseteq A$
, we have that
$B\subseteq A$
, we have that
![]() $B\in \mathcal {A}$
; respectively, we say that
$B\in \mathcal {A}$
; respectively, we say that
![]() $\mathcal {A}$
is upwards closed if for every
$\mathcal {A}$
is upwards closed if for every
![]() $A\in \mathcal {A}$
and every
$A\in \mathcal {A}$
and every
![]() $B\supseteq A$
, we have that
$B\supseteq A$
, we have that
![]() $B\in \mathcal {A}$
. If, in addition,
$B\in \mathcal {A}$
. If, in addition,
![]() $n\geqslant 2$
, then we set
$n\geqslant 2$
, then we set
and we view both
![]() $\mathcal {A}_0$
and
$\mathcal {A}_0$
and
![]() $\mathcal {A}_1$
as subfamilies of
$\mathcal {A}_1$
as subfamilies of
![]() $\{0,1\}^{n-1}$
.
$\{0,1\}^{n-1}$
.
It is also convenient to introduce the following definition.
Definition 2.1 (Forbidden intersections).
Let n be a positive integer, let
![]() $L\subseteq [n]$
, and let
$L\subseteq [n]$
, and let
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
. We write
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
. We write
![]() $(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,L)$
to denote the fact that the cross intersections of
$(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,L)$
to denote the fact that the cross intersections of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
forbid L; that is,
$\mathcal {G}$
forbid L; that is,
![]() $|A\cap B|\notin L$
for every
$|A\cap B|\notin L$
for every
![]() $A\in \mathcal {F}$
and
$A\in \mathcal {F}$
and
![]() $B\in \mathcal {G}$
.
$B\in \mathcal {G}$
.
2.3 p-biased measures
Recall that for every positive integer n and every
![]() $0<p<1$
by
$0<p<1$
by
![]() $\mu _p$
, we denote the p-biased probability measure on
$\mu _p$
, we denote the p-biased probability measure on
![]() $\{0,1\}^n$
defined in (1.2). We record, for future use, the following elementary property of these measures.
$\{0,1\}^n$
defined in (1.2). We record, for future use, the following elementary property of these measures.
Fact 2.2. Let n be a positive integer, let
![]() $0<p\leqslant p'<1$
, and let
$0<p\leqslant p'<1$
, and let
![]() $\mathcal {A}\subseteq \{0,1\}^n$
. If
$\mathcal {A}\subseteq \{0,1\}^n$
. If
![]() $\mathcal {A}$
is upwards closed, then
$\mathcal {A}$
is upwards closed, then
![]() $\mu _p(\mathcal {A})\leqslant \mu _{p'}(\mathcal {A})$
; respectively, if
$\mu _p(\mathcal {A})\leqslant \mu _{p'}(\mathcal {A})$
; respectively, if
![]() $\mathcal {A}$
is downwards closed, then
$\mathcal {A}$
is downwards closed, then
![]() $\mu _p(\mathcal {A}) \geqslant \mu _{p'}(\mathcal {A})$
.
$\mu _p(\mathcal {A}) \geqslant \mu _{p'}(\mathcal {A})$
.
2.4 Chernoff bounds
We will need the following standard estimates of the biased measure of the tails of the binomial distribution (see, for example, [Reference Alon and SpencerAS16, Appendix A]).
Lemma 2.3. Let n be a positive integer, let t be a nonnegative real, and let
![]() $0<p<1$
.
$0<p<1$
.
-
(i) If
 $p\leqslant \frac 12 $
and
$p\leqslant \frac 12 $
and
 $pn\leqslant t\leqslant 2pn$
, then (2.2)
$pn\leqslant t\leqslant 2pn$
, then (2.2) $$ \begin{align} \mu_p\left([n]^{\geqslant t}\right) \leqslant \exp\left(-\frac{(t-pn)^2}{6p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_p\left([n]^{\geqslant t}\right) \leqslant \exp\left(-\frac{(t-pn)^2}{6p(1-p)n}\right). \end{align} $$
-
(ii) If
 $p\geqslant \frac 12 $
and
$p\geqslant \frac 12 $
and
 $t\geqslant pn$
, then (2.3)
$t\geqslant pn$
, then (2.3) $$ \begin{align} \mu_p\left([n]^{\geqslant t}\right) \leqslant \exp\left(-\frac{(t-pn)^2}{2p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_p\left([n]^{\geqslant t}\right) \leqslant \exp\left(-\frac{(t-pn)^2}{2p(1-p)n}\right). \end{align} $$
2.5 Estimates of binomial coefficients
We will also need the following basic estimates of binomial coefficients that follow from a non-asymptotic version of Stirling’s approximation—see, for example, [Reference RobbinsRo55]—and elementary computations.
Fact 2.4. Let
![]() $n\geqslant 2$
be an integer, and let
$n\geqslant 2$
be an integer, and let
![]() $k\in [n-1]$
. Then we have
$k\in [n-1]$
. Then we have
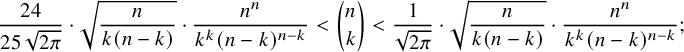 $$ \begin{align} \frac{24}{25 \, \sqrt{2\pi}} \cdot \sqrt{\frac{n}{k(n-k)}}\cdot \frac{n^n}{k^k(n-k)^{n-k}}< \binom{n}{k}< \frac{1}{\sqrt{2\pi}}\cdot \sqrt{\frac{n}{k(n-k)}}\cdot \frac{n^n}{k^k(n-k)^{n-k}}; \end{align} $$
$$ \begin{align} \frac{24}{25 \, \sqrt{2\pi}} \cdot \sqrt{\frac{n}{k(n-k)}}\cdot \frac{n^n}{k^k(n-k)^{n-k}}< \binom{n}{k}< \frac{1}{\sqrt{2\pi}}\cdot \sqrt{\frac{n}{k(n-k)}}\cdot \frac{n^n}{k^k(n-k)^{n-k}}; \end{align} $$
in particular, for every
![]() $\mathcal {F}\subseteq \binom {[n]}{k}$
we have
$\mathcal {F}\subseteq \binom {[n]}{k}$
we have
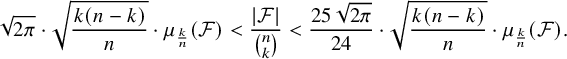 $$ \begin{align} \sqrt{2\pi}\cdot \sqrt{\frac{k(n-k)}{n}} \cdot \mu_{\frac{k}{n}}(\mathcal{F}) < \frac{|\mathcal{F}|}{\binom{n}{k}} < \frac{25 \, \sqrt{2\pi}}{24} \cdot \sqrt{\frac{k(n-k)}{n}}\cdot \mu_{\frac{k}{n}}(\mathcal{F}). \end{align} $$
$$ \begin{align} \sqrt{2\pi}\cdot \sqrt{\frac{k(n-k)}{n}} \cdot \mu_{\frac{k}{n}}(\mathcal{F}) < \frac{|\mathcal{F}|}{\binom{n}{k}} < \frac{25 \, \sqrt{2\pi}}{24} \cdot \sqrt{\frac{k(n-k)}{n}}\cdot \mu_{\frac{k}{n}}(\mathcal{F}). \end{align} $$
Moreover, if
![]() $H\colon [0,1]\to \mathbb {R}$
denotes the binary entropy functionFootnote
4
, then
$H\colon [0,1]\to \mathbb {R}$
denotes the binary entropy functionFootnote
4
, then
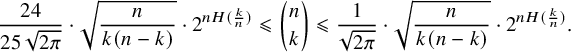 $$ \begin{align} \frac{24}{25 \, \sqrt{2\pi}} \cdot \sqrt{\frac{n}{k(n-k)}}\cdot 2^{nH(\frac{k}{n})} \leqslant \binom{n}{k} \leqslant \frac{1}{\sqrt{2\pi}}\cdot \sqrt{\frac{n}{k(n-k)}}\cdot 2^{nH(\frac{k}{n})}. \end{align} $$
$$ \begin{align} \frac{24}{25 \, \sqrt{2\pi}} \cdot \sqrt{\frac{n}{k(n-k)}}\cdot 2^{nH(\frac{k}{n})} \leqslant \binom{n}{k} \leqslant \frac{1}{\sqrt{2\pi}}\cdot \sqrt{\frac{n}{k(n-k)}}\cdot 2^{nH(\frac{k}{n})}. \end{align} $$
3 Forbidding initial or final intervals
Our goal in this section is to obtain estimates for the product of the biased measures of a pair of families
![]() $\mathcal {F}, \mathcal {G}\subseteq \{0,1\}^n$
whose cross intersections forbid an initial or a final subinterval of
$\mathcal {F}, \mathcal {G}\subseteq \{0,1\}^n$
whose cross intersections forbid an initial or a final subinterval of
![]() $[n]$
. This information is needed for the proof of Theorem 1.1.
$[n]$
. This information is needed for the proof of Theorem 1.1.
We note that closely related problems have been studied extensively in extremal combinatorics; see [Reference EllisEl22, Reference Frankl and TokushigeFT18] and the references therein. We shall obtain the desired estimates, however, from the following well-known concentration inequality for the biased measures. As usual, for a family
![]() $\mathcal {A}\subseteq \{0,1\}^n$
and a nonnegative real
$\mathcal {A}\subseteq \{0,1\}^n$
and a nonnegative real
![]() $t\leqslant n$
, we set
$t\leqslant n$
, we set
![]() $\mathcal {A}_t:= \{H\subseteq [n]: \exists A\in \mathcal {A} \text { such that } |H\bigtriangleup A|\leqslant t\}$
.
$\mathcal {A}_t:= \{H\subseteq [n]: \exists A\in \mathcal {A} \text { such that } |H\bigtriangleup A|\leqslant t\}$
.
Proposition 3.1. Let n be a positive integer, let
![]() $0<p<1$
, let
$0<p<1$
, let
![]() $t\leqslant pn$
be a nonnegative real, and let
$t\leqslant pn$
be a nonnegative real, and let
![]() $\mathcal {A}\subseteq \{0,1\}^n$
such that
$\mathcal {A}\subseteq \{0,1\}^n$
such that
![]() $\mu _{p}\left (\mathcal {A}\right )\geqslant \frac 12$
.
$\mu _{p}\left (\mathcal {A}\right )\geqslant \frac 12$
.
-
(i) If
 $0<p\leqslant \frac 12$
, then we have (3.1)
$0<p\leqslant \frac 12$
, then we have (3.1) $$ \begin{align} \mu_{p}\left(\mathcal{A}_t\right)\geqslant 1-\exp\left(-\frac{t^2}{6p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_{p}\left(\mathcal{A}_t\right)\geqslant 1-\exp\left(-\frac{t^2}{6p(1-p)n}\right). \end{align} $$
-
(ii) If
 $\frac 12<p<1$
, then we have (3.2)
$\frac 12<p<1$
, then we have (3.2) $$ \begin{align} \mu_{p}\left(\mathcal{A}_t\right)\geqslant 1-\exp\left(-\frac{t^2}{2p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_{p}\left(\mathcal{A}_t\right)\geqslant 1-\exp\left(-\frac{t^2}{2p(1-p)n}\right). \end{align} $$
Proposition 3.1 follows from the proof of [Reference Bobkov, Houdré and TetaliBHT06, Proposition 2.4] in the work of Bobkov, Choudré and Tetali, which in turn is based on results of Bollobás–Leader [Reference Bollobás and LeaderBL91], Jogdeo–Samuels [Reference Jogdeo and SamuelsJS68] and Talagrand [Reference TalagrandTa89]. Since Proposition 3.1 is not explicitly isolated in [Reference Bobkov, Houdré and TetaliBHT06], for the convenience of the reader, we briefly recall the argument.
Proof of Proposition 3.1.
As it is mentioned in [Reference Bobkov, Houdré and TetaliBHT06], it is enough to prove the result under the additional assumption that
![]() $\mathcal {A}$
is downwards closed. Indeed, Step 1 through Step 4 in the proof of [Reference TalagrandTa89, Theorem 7] carry out this reduction. So, suppose that
$\mathcal {A}$
is downwards closed. Indeed, Step 1 through Step 4 in the proof of [Reference TalagrandTa89, Theorem 7] carry out this reduction. So, suppose that
![]() $\mathcal {A}$
is downwards closed with
$\mathcal {A}$
is downwards closed with
![]() $\mu _{p}\left (\mathcal {A}\right )\geqslant \frac 12$
. By [Reference Jogdeo and SamuelsJS68, Theorem 3.2 and Corollary 3.1], we have
$\mu _{p}\left (\mathcal {A}\right )\geqslant \frac 12$
. By [Reference Jogdeo and SamuelsJS68, Theorem 3.2 and Corollary 3.1], we have
that is, the median of the binomial distribution
![]() $\mathrm {Bin}(n,p)$
is greater than or equal to
$\mathrm {Bin}(n,p)$
is greater than or equal to
![]() $\lfloor pn \rfloor $
. Moreover, since
$\lfloor pn \rfloor $
. Moreover, since
![]() $\mathcal {A}$
is downwards closed, by [Reference Bollobás and LeaderBL91, Corollary 5], we have
$\mathcal {A}$
is downwards closed, by [Reference Bollobás and LeaderBL91, Corollary 5], we have
which in turn implies that
Therefore, if
![]() $0<p\leqslant \frac 12$
, then (3.1) follows from (3.5) and (2.2), while if
$0<p\leqslant \frac 12$
, then (3.1) follows from (3.5) and (2.2), while if
![]() $\frac 12< p<1$
, then (3.2) follows from (3.5) and (2.3).
$\frac 12< p<1$
, then (3.2) follows from (3.5) and (2.3).
Proposition 3.1 will be used in the following form (the proof is straightforward, and it is left to the reader).
Corollary 3.2. Let n be a positive integer, let
![]() $0<p<1$
, let
$0<p<1$
, let
![]() $t\leqslant pn$
be a nonnegative real, and let
$t\leqslant pn$
be a nonnegative real, and let
![]() $\mathcal {A}\subseteq \{0,1\}^n$
.
$\mathcal {A}\subseteq \{0,1\}^n$
.
-
(i) If
 $0<p\leqslant \frac 12$
and
$0<p\leqslant \frac 12$
and
 $\mu _{p}\left (\mathcal {A}\right )>\exp \big (-\frac {t^2}{6p(1-p)n}\big )$
, then
$\mu _{p}\left (\mathcal {A}\right )>\exp \big (-\frac {t^2}{6p(1-p)n}\big )$
, then
 $\mu _{p}\left (\mathcal {A}_{2t}\right )>1-\exp \big (-\frac {t^2}{6p(1-p)n}\big )$
.
$\mu _{p}\left (\mathcal {A}_{2t}\right )>1-\exp \big (-\frac {t^2}{6p(1-p)n}\big )$
. -
(ii) If
 $\frac 12<p<1$
and
$\frac 12<p<1$
and
 $\mu _{p}\left (\mathcal {A}\right )>\exp \big (-\frac {t^2}{2p(1-p)n}\big )$
, then
$\mu _{p}\left (\mathcal {A}\right )>\exp \big (-\frac {t^2}{2p(1-p)n}\big )$
, then
 $\mu _{p}\left (\mathcal {A}_{2t}\right )>1-\exp \big (-\frac {t^2}{2p(1-p)n}\big )$
.
$\mu _{p}\left (\mathcal {A}_{2t}\right )>1-\exp \big (-\frac {t^2}{2p(1-p)n}\big )$
.
We are now ready to state the main result in this section.
Lemma 3.3. Let n be a positive integer, let
![]() $0<p\leqslant p'\leqslant 1-p$
with
$0<p\leqslant p'\leqslant 1-p$
with
![]() $p\leqslant \frac 12$
, and let
$p\leqslant \frac 12$
, and let
![]() $\alpha \leqslant pn$
be a positive integer. Also let
$\alpha \leqslant pn$
be a positive integer. Also let
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
.
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
.
-
(i) If
 $(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}\left (n,[0,\alpha ]\right )$
, then (3.6)
$(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}\left (n,[0,\alpha ]\right )$
, then (3.6) $$ \begin{align} \mu_p(\mathcal{F})\,\mu_{p'}(\mathcal{G})\leqslant\exp\left(-\frac{\alpha^2}{24p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F})\,\mu_{p'}(\mathcal{G})\leqslant\exp\left(-\frac{\alpha^2}{24p(1-p)n}\right). \end{align} $$
-
(ii) If
 $(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}\left (n,[pn-\alpha ,n]\right )$
, then (3.7)
$(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}\left (n,[pn-\alpha ,n]\right )$
, then (3.7) $$ \begin{align} \mu_{p}(\mathcal{F})\,\mu_{p'}(\mathcal{G})\leqslant 2\exp\left(-\frac{\alpha^2}{24p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_{p}(\mathcal{F})\,\mu_{p'}(\mathcal{G})\leqslant 2\exp\left(-\frac{\alpha^2}{24p(1-p)n}\right). \end{align} $$
Proof. We start with the proof of part (i). Clearly, we may assume that the pair
![]() $(\mathcal {F},\mathcal {G})$
is optimal, in the sense that it maximizes the quantity in the left-hand side of (3.6); consequently, we may assume that
$(\mathcal {F},\mathcal {G})$
is optimal, in the sense that it maximizes the quantity in the left-hand side of (3.6); consequently, we may assume that
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are both upwards closed. Next observe that if
$\mathcal {G}$
are both upwards closed. Next observe that if
![]() $\mu _{p}(\mathcal {F})\leqslant \exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
, then (3.6) is straightforward. Therefore, we may also assume that
$\mu _{p}(\mathcal {F})\leqslant \exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
, then (3.6) is straightforward. Therefore, we may also assume that
![]() $\mu _{p}(\mathcal {F})>\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
. By Corollary 3.2 applied for ‘
$\mu _{p}(\mathcal {F})>\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
. By Corollary 3.2 applied for ‘
![]() $t=\frac {\alpha }{2}$
’, we obtain that
$t=\frac {\alpha }{2}$
’, we obtain that
![]() $\mu _{p}(\mathcal {F}_{\alpha })>1-\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
, where
$\mu _{p}(\mathcal {F}_{\alpha })>1-\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
, where
![]() $\mathcal {F}_{\alpha }:= \{H\subseteq [n]: \exists A\in \mathcal {F} \text { with } |H\bigtriangleup A|\leqslant \alpha \}$
. Set
$\mathcal {F}_{\alpha }:= \{H\subseteq [n]: \exists A\in \mathcal {F} \text { with } |H\bigtriangleup A|\leqslant \alpha \}$
. Set
![]() $\overline {\mathcal {G}}:= \{[n]\setminus G:G\in \mathcal {G}\}$
, and note that for every
$\overline {\mathcal {G}}:= \{[n]\setminus G:G\in \mathcal {G}\}$
, and note that for every
![]() $F\in \mathcal {F}$
and every
$F\in \mathcal {F}$
and every
![]() $G\in \mathcal {G}$
, we have that
$G\in \mathcal {G}$
, we have that
![]() $|F\bigtriangleup ([n]\setminus G)|>\alpha $
. This yields that
$|F\bigtriangleup ([n]\setminus G)|>\alpha $
. This yields that
![]() $\overline {\mathcal {G}}\cap \mathcal {F}_{\alpha }=\emptyset $
, which in turn implies that
$\overline {\mathcal {G}}\cap \mathcal {F}_{\alpha }=\emptyset $
, which in turn implies that
![]() $\mu _{p}(\overline {\mathcal {G}})<\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
. Finally, since
$\mu _{p}(\overline {\mathcal {G}})<\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
. Finally, since
![]() $\mathcal {G}$
is upwards closed and
$\mathcal {G}$
is upwards closed and
![]() $p'\leqslant 1-p$
, by Fact 2.2, we conclude that
$p'\leqslant 1-p$
, by Fact 2.2, we conclude that
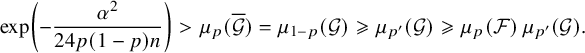 $$ \begin{align} \exp\left(-\frac{\alpha^2}{24p(1-p)n}\right)> \mu_{p}(\overline{\mathcal{G}})= \mu_{1-p}(\mathcal{G}) \geqslant \mu_{p'}(\mathcal{G}) \geqslant \mu_{p}(\mathcal{F})\, \mu_{p'}(\mathcal{G}). \end{align} $$
$$ \begin{align} \exp\left(-\frac{\alpha^2}{24p(1-p)n}\right)> \mu_{p}(\overline{\mathcal{G}})= \mu_{1-p}(\mathcal{G}) \geqslant \mu_{p'}(\mathcal{G}) \geqslant \mu_{p}(\mathcal{F})\, \mu_{p'}(\mathcal{G}). \end{align} $$
We proceed to the proof of part (ii). As before, we may assume that the pair
![]() $(\mathcal {F},\mathcal {G})$
is optimal and, hence, that
$(\mathcal {F},\mathcal {G})$
is optimal and, hence, that
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are both downwards closed. Consequently, by Fact 2.2, it is enough to show that
$\mathcal {G}$
are both downwards closed. Consequently, by Fact 2.2, it is enough to show that
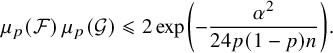 $$ \begin{align} \mu_{p}(\mathcal{F})\, \mu_{p}(\mathcal{G})\leqslant 2 \exp\left(-\frac{\alpha^2}{24p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_{p}(\mathcal{F})\, \mu_{p}(\mathcal{G})\leqslant 2 \exp\left(-\frac{\alpha^2}{24p(1-p)n}\right). \end{align} $$
Setting
-
•
 $\mathcal {F}^{\leqslant pn-\frac {\alpha }{2}}:= \{A\in \mathcal {F}: |A|\leqslant pn-\frac {\alpha }{2}\}$
,
$\mathcal {F}^{\leqslant pn-\frac {\alpha }{2}}:= \{A\in \mathcal {F}: |A|\leqslant pn-\frac {\alpha }{2}\}$
,
 $\mathcal {F}^{>pn-\frac {\alpha }{2}}:= \{A\in \mathcal {F} : |A|>pn-\frac {\alpha }{2}\}$
, and
$\mathcal {F}^{>pn-\frac {\alpha }{2}}:= \{A\in \mathcal {F} : |A|>pn-\frac {\alpha }{2}\}$
, and -
•
 $\mathcal {G}^{\leqslant pn-\frac {\alpha }{2}}:= \{B\in \mathcal {G} : |B|\leqslant pn-\frac {\alpha }{2}\}$
,
$\mathcal {G}^{\leqslant pn-\frac {\alpha }{2}}:= \{B\in \mathcal {G} : |B|\leqslant pn-\frac {\alpha }{2}\}$
,
 $\mathcal {G}^{>pn-\frac {\alpha }{2}}:= \{B\in \mathcal {G} : |B|>pn-\frac {\alpha }{2}\}$
,
$\mathcal {G}^{>pn-\frac {\alpha }{2}}:= \{B\in \mathcal {G} : |B|>pn-\frac {\alpha }{2}\}$
,
by part (ii) of Lemma 2.3 applied for
![]() $\mu _{1-p}$
, we see that
$\mu _{1-p}$
, we see that
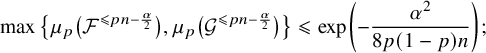 $$ \begin{align} \max\big\{ \mu_{p}\big(\mathcal{F}^{\leqslant pn-\frac{\alpha}{2}}\big), \mu_{p}\big(\mathcal{G}^{\leqslant pn-\frac{\alpha}{2}}\big)\big\} \leqslant \exp\left(-\frac{\alpha^2}{8p(1-p)n}\right); \end{align} $$
$$ \begin{align} \max\big\{ \mu_{p}\big(\mathcal{F}^{\leqslant pn-\frac{\alpha}{2}}\big), \mu_{p}\big(\mathcal{G}^{\leqslant pn-\frac{\alpha}{2}}\big)\big\} \leqslant \exp\left(-\frac{\alpha^2}{8p(1-p)n}\right); \end{align} $$
thus, if
![]() $\mu _{p}\big (\mathcal {F}^{> pn-\frac {\alpha }{2}}\big )<\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
, then the result follows from (3.10). So, suppose that
$\mu _{p}\big (\mathcal {F}^{> pn-\frac {\alpha }{2}}\big )<\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
, then the result follows from (3.10). So, suppose that
![]() $\mu _{p}\big (\mathcal {F}^{>pn-\frac {\alpha }{2}}\big )\geqslant \exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
. By Corollary 3.2 again applied for ‘
$\mu _{p}\big (\mathcal {F}^{>pn-\frac {\alpha }{2}}\big )\geqslant \exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
. By Corollary 3.2 again applied for ‘
![]() $t=\frac {\alpha }{2}$
’, we obtain that
$t=\frac {\alpha }{2}$
’, we obtain that
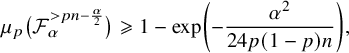 $$ \begin{align} \mu_{p}\big(\mathcal{F}^{>pn-\frac{\alpha}{2}}_\alpha\big)\geqslant 1-\exp\left(-\frac{\alpha^2}{24p(1-p)n}\right), \end{align} $$
$$ \begin{align} \mu_{p}\big(\mathcal{F}^{>pn-\frac{\alpha}{2}}_\alpha\big)\geqslant 1-\exp\left(-\frac{\alpha^2}{24p(1-p)n}\right), \end{align} $$
where
![]() $\mathcal {F}^{>pn-\frac {\alpha }{2}}_\alpha := \{H\subseteq [n]: \exists A\in \mathcal {F}^{>pn-\frac {\alpha }{2}} \text { with } |H\bigtriangleup A|\leqslant \alpha \}$
. Now note that, since
$\mathcal {F}^{>pn-\frac {\alpha }{2}}_\alpha := \{H\subseteq [n]: \exists A\in \mathcal {F}^{>pn-\frac {\alpha }{2}} \text { with } |H\bigtriangleup A|\leqslant \alpha \}$
. Now note that, since
![]() $(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}\left (n,[pn-\alpha ,n]\right )$
, for every
$(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}\left (n,[pn-\alpha ,n]\right )$
, for every
![]() $F\in \mathcal {F}^{> pn-\frac {\alpha }{2}}$
and every
$F\in \mathcal {F}^{> pn-\frac {\alpha }{2}}$
and every
![]() $G\in \mathcal {G}^{> pn-\frac {\alpha }{2}}$
, we have
$G\in \mathcal {G}^{> pn-\frac {\alpha }{2}}$
, we have
This observation yields that
![]() $\mathcal {G}^{> pn-\frac {\alpha }{2}}\cap \mathcal {F}^{> pn-\frac {\alpha }{2}}_\alpha =\emptyset $
, and therefore, by (3.11), we obtain that
$\mathcal {G}^{> pn-\frac {\alpha }{2}}\cap \mathcal {F}^{> pn-\frac {\alpha }{2}}_\alpha =\emptyset $
, and therefore, by (3.11), we obtain that
![]() $\mu _{p}\big (\mathcal {G}^{> pn-\frac {\alpha }{2}}\big )<\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
. Inequality (3.7) follows from this estimate and (3.10). The proof of Lemma 3.3 is thus completed.
$\mu _{p}\big (\mathcal {G}^{> pn-\frac {\alpha }{2}}\big )<\exp \big (-\frac {\alpha ^2}{24p(1-p)n}\big )$
. Inequality (3.7) follows from this estimate and (3.10). The proof of Lemma 3.3 is thus completed.
4 The widening lemma
The section is devoted to the proof of the following lemma. (Recall that for every family
![]() $\mathcal {A}\subseteq \{0,1\}^n$
(
$\mathcal {A}\subseteq \{0,1\}^n$
(
![]() $n\geqslant 2$
) by
$n\geqslant 2$
) by
![]() $\mathcal {A}_0$
and
$\mathcal {A}_0$
and
![]() $\mathcal {A}_1$
, we denote the sections of
$\mathcal {A}_1$
, we denote the sections of
![]() $\mathcal {A}$
defined in (2.1); we also recall that we view
$\mathcal {A}$
defined in (2.1); we also recall that we view
![]() $\mathcal {A}_0$
and
$\mathcal {A}_0$
and
![]() $\mathcal {A}_1$
as families in
$\mathcal {A}_1$
as families in
![]() $\{0,1\}^{n-1}$
.)
$\{0,1\}^{n-1}$
.)
Lemma 4.1 (Widening lemma).
Let
![]() $n\geqslant 2$
be an integer, let
$n\geqslant 2$
be an integer, let
![]() $0<p\leqslant p'\leqslant \frac 12$
, and let
$0<p\leqslant p'\leqslant \frac 12$
, and let
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
be nonempty. Also let
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
be nonempty. Also let
![]() $0<\delta <\frac {1}{10}$
, and assume that
$0<\delta <\frac {1}{10}$
, and assume that
and
Then we have
As we have noted in Subsection 1.3, Lemma 4.1 is a crucial ingredient of the proof of Theorem 1.1. That said, we advise the reader to skip its proof at first reading and return to this section once the basic steps of the proof of Theorem 1.1 have been properly understood.
We shall deduce Lemma 4.1 from the following, purely analytical, result.
Sublemma 4.2. Let
![]() $x,x',y,y',z,z',w,w',p,p',\delta \in [-1,1]$
be real numbers with
$x,x',y,y',z,z',w,w',p,p',\delta \in [-1,1]$
be real numbers with
![]() $y,w\geqslant 0$
,
$y,w\geqslant 0$
,
![]() $y',w'\leqslant 0$
,
$y',w'\leqslant 0$
,
![]() $\max \{x,x'\}\leqslant w$
,
$\max \{x,x'\}\leqslant w$
,
![]() $\max \{z,z'\}\leqslant y$
,
$\max \{z,z'\}\leqslant y$
,
![]() $0<p\leqslant p'\leqslant \frac {1}{2}$
and
$0<p\leqslant p'\leqslant \frac {1}{2}$
and
![]() $0<\delta <\frac {1}{10}$
. Assume that the following identities
$0<\delta <\frac {1}{10}$
. Assume that the following identities
as well as the following inequalities
are satisfied. Then at least one of the following inequalities
must also be satisfied.
We postpone the proof of Sublemma 4.2 to the end of this section. At this point, let us give the proof of Lemma 4.1.
Proof of Lemma 4.1.
Notice, first, that
Next, define the real numbers
![]() $x,x',y,y',z,z',w,w'$
by setting
$x,x',y,y',z,z',w,w'$
by setting
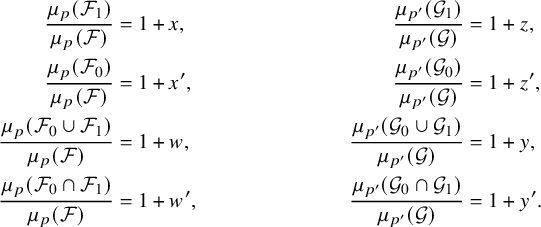 $$ \begin{align*} \frac{\mu_p(\mathcal{F}_1)}{\mu_p(\mathcal{F})}&=1+x, & \frac{\mu_{p'}(\mathcal{G}_1)}{\mu_{p'}(\mathcal{G})} & = 1+z,\\ \frac{\mu_p(\mathcal{F}_0)}{\mu_p(\mathcal{F})}&=1+x' ,& \frac{\mu_{p'}(\mathcal{G}_0)}{\mu_{p'}(\mathcal{G})} & =1+z',\\ \frac{\mu_p(\mathcal{F}_0\cup\mathcal{F}_1)}{\mu_p(\mathcal{F})}& = 1+w, & \frac{\mu_{p'}(\mathcal{G}_0\cup\mathcal{G}_1)}{\mu_{p'}(\mathcal{G})} & =1+y,\\ \frac{\mu_p(\mathcal{F}_0\cap\mathcal{F}_1)}{\mu_{p}\left(\mathcal{F}\right)}&=1+w', & \frac{\mu_{p'}(\mathcal{G}_0\cap\mathcal{G}_1)}{\mu_{p'}(\mathcal{G})} & =1+y'. \end{align*} $$
$$ \begin{align*} \frac{\mu_p(\mathcal{F}_1)}{\mu_p(\mathcal{F})}&=1+x, & \frac{\mu_{p'}(\mathcal{G}_1)}{\mu_{p'}(\mathcal{G})} & = 1+z,\\ \frac{\mu_p(\mathcal{F}_0)}{\mu_p(\mathcal{F})}&=1+x' ,& \frac{\mu_{p'}(\mathcal{G}_0)}{\mu_{p'}(\mathcal{G})} & =1+z',\\ \frac{\mu_p(\mathcal{F}_0\cup\mathcal{F}_1)}{\mu_p(\mathcal{F})}& = 1+w, & \frac{\mu_{p'}(\mathcal{G}_0\cup\mathcal{G}_1)}{\mu_{p'}(\mathcal{G})} & =1+y,\\ \frac{\mu_p(\mathcal{F}_0\cap\mathcal{F}_1)}{\mu_{p}\left(\mathcal{F}\right)}&=1+w', & \frac{\mu_{p'}(\mathcal{G}_0\cap\mathcal{G}_1)}{\mu_{p'}(\mathcal{G})} & =1+y'. \end{align*} $$
With these choices, the result follows from Sublemma 4.2 after taking into account the identities in (4.11).
4.1 Proof of Sublemma 4.2
First observe that, by (4.4) and (4.5), we have
that yields that
Combining these equalities with (4.7) and (4.8), we obtain that
and
Next, observe that since y and w are nonnegative, by (4.7) and (4.8), we have
that yields that
By (4.6), we have that either
-
(
 $\mathcal {A}1$
)
$\mathcal {A}1$
)
 $x<\frac {\delta }{2}$
, or
$x<\frac {\delta }{2}$
, or -
(
 $\mathcal {A}2$
)
$\mathcal {A}2$
)
 $z<\frac {\delta }{2}$
.
$z<\frac {\delta }{2}$
.
Claim 4.3. If
![]() $x<\frac {\delta }{2}$
, then
$x<\frac {\delta }{2}$
, then
However, if
![]() $z<\frac {\delta }{2}$
, then
$z<\frac {\delta }{2}$
, then
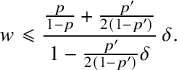 $$ \begin{align} w\leqslant \frac{\frac{p}{1-p}+\frac{p'}{2(1-p')}}{1-\frac{p'}{2(1-p')}\delta}\, \delta. \end{align} $$
$$ \begin{align} w\leqslant \frac{\frac{p}{1-p}+\frac{p'}{2(1-p')}}{1-\frac{p'}{2(1-p')}\delta}\, \delta. \end{align} $$
Proof of Claim 4.3.
First assume that
![]() $x<\frac {\delta }{2}$
. Then, by (4.7), we have
$x<\frac {\delta }{2}$
. Then, by (4.7), we have
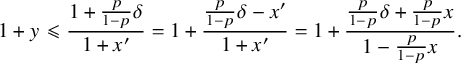 $$ \begin{align} 1+y\leqslant \frac{1+\frac{p}{1-p}\delta}{1+x'}= 1+\frac{\frac{p}{1-p}\delta-x'}{1+x'}= 1+\frac{\frac{p}{1-p}\delta+\frac{p}{1-p}x}{1-\frac{p}{1-p}x}. \end{align} $$
$$ \begin{align} 1+y\leqslant \frac{1+\frac{p}{1-p}\delta}{1+x'}= 1+\frac{\frac{p}{1-p}\delta-x'}{1+x'}= 1+\frac{\frac{p}{1-p}\delta+\frac{p}{1-p}x}{1-\frac{p}{1-p}x}. \end{align} $$
Since
![]() $-\frac {1}{10}<-\delta \leqslant x<\frac {\delta }{2}<\frac {1}{20}$
and the function
$-\frac {1}{10}<-\delta \leqslant x<\frac {\delta }{2}<\frac {1}{20}$
and the function
![]() $(-1,1)\ni x\mapsto \frac {\frac {p}{1-p}\delta +\frac {p}{1-p}x}{1-\frac {p}{1-p}x}$
is increasing, by (4.21), we see that (4.19) is satisfied.
$(-1,1)\ni x\mapsto \frac {\frac {p}{1-p}\delta +\frac {p}{1-p}x}{1-\frac {p}{1-p}x}$
is increasing, by (4.21), we see that (4.19) is satisfied.
Next assume that
![]() $z<\frac {\delta }{2}$
. By (4.8), we have
$z<\frac {\delta }{2}$
. By (4.8), we have
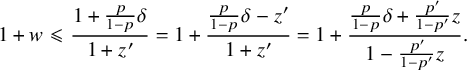 $$ \begin{align} 1+w \leqslant \frac{1+\frac{p}{1-p}\delta}{1+z'} = 1+\frac{\frac{p}{1-p}\delta-z'}{1+z'}= 1+\frac{\frac{p}{1-p}\delta+\frac{p'}{1-p'}z}{1-\frac{p'}{1-p'}z}. \end{align} $$
$$ \begin{align} 1+w \leqslant \frac{1+\frac{p}{1-p}\delta}{1+z'} = 1+\frac{\frac{p}{1-p}\delta-z'}{1+z'}= 1+\frac{\frac{p}{1-p}\delta+\frac{p'}{1-p'}z}{1-\frac{p'}{1-p'}z}. \end{align} $$
Thus, (4.20) follows from (4.22) using the fact that
![]() $-\frac {1}{10}<-\delta \leqslant z< \frac {\delta }{2}<\frac {1}{20}$
and the fact that the function
$-\frac {1}{10}<-\delta \leqslant z< \frac {\delta }{2}<\frac {1}{20}$
and the fact that the function
 $(-1,1)\ni z\mapsto \frac {\frac {p}{1-p}\delta +\frac {p'}{1-p'}z}{1-\frac {p'}{1-p'}z}$
is increasing.
$(-1,1)\ni z\mapsto \frac {\frac {p}{1-p}\delta +\frac {p'}{1-p'}z}{1-\frac {p'}{1-p'}z}$
is increasing.
We proceed by considering the following cases.
Case 1:
 $x\geqslant 0$
and
$x\geqslant 0$
and
 $z\geqslant 0$
.
$z\geqslant 0$
.
First assume that
![]() $x<\frac {\delta }{2}$
. Then, since
$x<\frac {\delta }{2}$
. Then, since
![]() $p\leqslant \frac {1}{2}$
, by (4.19), we see that
$p\leqslant \frac {1}{2}$
, by (4.19), we see that
![]() $\frac {xy}{1-p}< 2\frac {p}{1-p}\delta ^2$
. Moreover, since
$\frac {xy}{1-p}< 2\frac {p}{1-p}\delta ^2$
. Moreover, since
![]() $x,z\geqslant 0$
, we have
$x,z\geqslant 0$
, we have
![]() $\frac {1-2p}{1-p}x+\frac {1-2p'}{1-p'}z(1+x)\geqslant 0$
and so, by (4.15), we obtain that
$\frac {1-2p}{1-p}x+\frac {1-2p'}{1-p'}z(1+x)\geqslant 0$
and so, by (4.15), we obtain that
that is, (4.9) is satisfied.
However, if
![]() $z<\frac {\delta }{2}$
, then we consider the subcases ‘
$z<\frac {\delta }{2}$
, then we consider the subcases ‘
![]() $p\leqslant \frac 37$
’ and ‘
$p\leqslant \frac 37$
’ and ‘
![]() $\frac 37<p$
’. First observe that, by (4.20) and the fact that
$\frac 37<p$
’. First observe that, by (4.20) and the fact that
![]() $\delta <\frac {1}{10}$
, we have that
$\delta <\frac {1}{10}$
, we have that
![]() $w\leqslant 2\delta $
. If
$w\leqslant 2\delta $
. If
![]() $0<p\leqslant \frac {3}{7}$
then, since
$0<p\leqslant \frac {3}{7}$
then, since
![]() $w\geqslant 0$
, this yields that
$w\geqslant 0$
, this yields that
![]() $\frac {zw}{1-p'}<2\delta ^2<\frac {1-2p}{1-p}\delta $
. Using again our starting assumption that
$\frac {zw}{1-p'}<2\delta ^2<\frac {1-2p}{1-p}\delta $
. Using again our starting assumption that
![]() $x,z\geqslant 0$
, we see that
$x,z\geqslant 0$
, we see that
![]() $\frac {1-2p}{1-p}x(1+z)+\frac {1-2p'}{1-p'}z\geqslant 0$
. By (4.16) and the previous observations, we obtain that
$\frac {1-2p}{1-p}x(1+z)+\frac {1-2p'}{1-p'}z\geqslant 0$
. By (4.16) and the previous observations, we obtain that
in other words, in this subcase, (4.10) is satisfied. Finally, assume that
![]() $\frac 37<p\leqslant \frac 12$
. Then observe that
$\frac 37<p\leqslant \frac 12$
. Then observe that
![]() $\frac {p'}{2(1-p')}<\frac {2}{3}\frac {p}{1-p}$
, which in turn implies, by (4.20) and the fact that
$\frac {p'}{2(1-p')}<\frac {2}{3}\frac {p}{1-p}$
, which in turn implies, by (4.20) and the fact that
![]() $\delta <\frac {1}{10}$
, that
$\delta <\frac {1}{10}$
, that
![]() $w< 2\frac {p}{1-p}\delta $
. Therefore,
$w< 2\frac {p}{1-p}\delta $
. Therefore,
![]() $zw<\frac {p}{1-p}\delta ^2<2\frac {p}{1-p}\delta ^2$
. By the previous discussion, (4.16) and using once again the estimate
$zw<\frac {p}{1-p}\delta ^2<2\frac {p}{1-p}\delta ^2$
. By the previous discussion, (4.16) and using once again the estimate
![]() $\frac {1-2p}{1-p}x(1+z)+\frac {1-2p'}{1-p'}z\geqslant 0$
, we conclude that
$\frac {1-2p}{1-p}x(1+z)+\frac {1-2p'}{1-p'}z\geqslant 0$
, we conclude that
and so, in this subcase, (4.10) is satisfied.
Case 2:
 $x<0$
and
$x<0$
and
 $z\geqslant 0$
.
$z\geqslant 0$
.
Then we have
![]() $-\frac {xy}{1-p}\geqslant 0$
and
$-\frac {xy}{1-p}\geqslant 0$
and
![]() $\frac {1-2p}{1-p}x+\frac {1-2p'}{1-p'}z(1+x)\geqslant \frac {1-2p}{1-p}x$
, and so, by (4.15) and (4.18), we obtain that
$\frac {1-2p}{1-p}x+\frac {1-2p'}{1-p'}z(1+x)\geqslant \frac {1-2p}{1-p}x$
, and so, by (4.15) and (4.18), we obtain that
Thus, in this case, (4.9) is satisfied.
Case 3:
 $x\geqslant 0$
and
$x\geqslant 0$
and
 $z<0$
.
$z<0$
.
It is similar to Case 2. Indeed, observe that
![]() $-\frac {zw}{1-p}\geqslant 0$
and
$-\frac {zw}{1-p}\geqslant 0$
and
![]() $\frac {1-2p}{1-p}x(1+z)+\frac {1-2p'}{1-p'}z\geqslant \frac {1-2p'}{1-p'}z$
. Hence, by (4.16), (4.18) and the fact that
$\frac {1-2p}{1-p}x(1+z)+\frac {1-2p'}{1-p'}z\geqslant \frac {1-2p'}{1-p'}z$
. Hence, by (4.16), (4.18) and the fact that
![]() $\frac {1-2p}{1-p}\geqslant \frac {1-2p'}{1-p'}$
, we obtain that
$\frac {1-2p}{1-p}\geqslant \frac {1-2p'}{1-p'}$
, we obtain that
thus, in this case, (4.10) is satisfied.
Case 4:
 $x<0$
and
$x<0$
and
 $z<0$
.
$z<0$
.
First observe that
![]() $-\frac {xy}{1-p}>0$
. Moreover, since
$-\frac {xy}{1-p}>0$
. Moreover, since
![]() $z'\leqslant y$
, by (4.7),
$z'\leqslant y$
, by (4.7),
that implies that
![]() $x'+z'+x'z'\leqslant \frac {p}{1-p}\delta $
. Noticing that
$x'+z'+x'z'\leqslant \frac {p}{1-p}\delta $
. Noticing that
![]() $\frac {1-2p'}{p'}\leqslant \frac {1-2p}{p}$
, by (4.4) and (4.5),
$\frac {1-2p'}{p'}\leqslant \frac {1-2p}{p}$
, by (4.4) and (4.5),
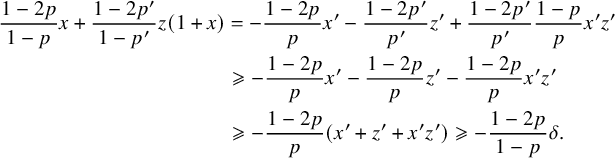 $$ \begin{align} \frac{1-2p}{1-p}x+\frac{1-2p'}{1-p'}z(1+x) & = -\frac{1-2p}{p}x'-\frac{1-2p'}{p'}z'+\frac{1-2p'}{p'}\frac{1-p}{p}x'z' \nonumber \\ & \geqslant -\frac{1-2p}{p}x'-\frac{1-2p}{p}z'-\frac{1-2p}{p}x'z' \nonumber \\ & \geqslant -\frac{1-2p}{p}(x'+z'+x'z')\geqslant -\frac{1-2p}{1-p}\delta. \end{align} $$
$$ \begin{align} \frac{1-2p}{1-p}x+\frac{1-2p'}{1-p'}z(1+x) & = -\frac{1-2p}{p}x'-\frac{1-2p'}{p'}z'+\frac{1-2p'}{p'}\frac{1-p}{p}x'z' \nonumber \\ & \geqslant -\frac{1-2p}{p}x'-\frac{1-2p}{p}z'-\frac{1-2p}{p}x'z' \nonumber \\ & \geqslant -\frac{1-2p}{p}(x'+z'+x'z')\geqslant -\frac{1-2p}{1-p}\delta. \end{align} $$
Hence, by (4.15) and (4.29), we conclude that
thus, in this case, (4.9) is satisfied.
The above cases are exhaustive, and so the proof of Sublemma 4.2 is completed.
5 The algorithm
In this section, we present the formal description and the basic properties of the algorithm that is used in the proof of Theorem 1.1; we shall also discuss in more loose terms its main features. (Again, we recall that for every family
![]() $\mathcal {A}\subseteq \{0,1\}^n$
(
$\mathcal {A}\subseteq \{0,1\}^n$
(
![]() $n\geqslant 2$
) by
$n\geqslant 2$
) by
![]() $\mathcal {A}_0,\mathcal {A}_1\subseteq \{0,1\}^{n-1}$
, we denote the sections of
$\mathcal {A}_0,\mathcal {A}_1\subseteq \{0,1\}^{n-1}$
, we denote the sections of
![]() $\mathcal {A}$
defined in (2.1).)
$\mathcal {A}$
defined in (2.1).)
For the analysis of the algorithm, we will need the following elementary, but crucial, fact that originates in the work of Frankl and Rödl [Reference Frankl and RödlFR87].
Fact 5.1. Let
![]() $n\geqslant 2$
be an integer, let
$n\geqslant 2$
be an integer, let
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
and let
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
and let
![]() $a,b\in [n]$
with
$a,b\in [n]$
with
![]() $a\leqslant b$
. Assume that
$a\leqslant b$
. Assume that
![]() $(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,[a,b])$
. Then we have
$(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,[a,b])$
. Then we have

The algorithm takes as an input
-
(I1) an integer
 $n\geqslant 2$
, two reals
$n\geqslant 2$
, two reals
 $0<p\leqslant p'\leqslant \frac 12$
and a positive integer
$0<p\leqslant p'\leqslant \frac 12$
and a positive integer
 $\ell < pn$
,
$\ell < pn$
, -
(I2) a real
 $0<\delta <\frac {1}{10}$
, and
$0<\delta <\frac {1}{10}$
, and -
(I3) two nonempty families
 $\mathcal {F}_{\mathrm {init}}, \mathcal {G}_{\mathrm {init}}\subseteq \{0,1\}^n$
whose cross intersections forbid
$\mathcal {F}_{\mathrm {init}}, \mathcal {G}_{\mathrm {init}}\subseteq \{0,1\}^n$
whose cross intersections forbid
 $\ell $
,
$\ell $
,
and outputs
-
(O1) three nonnegative integers
 $a^*\leqslant b^*\leqslant m^*$
with
$a^*\leqslant b^*\leqslant m^*$
with
 $m^*\geqslant 1$
, and
$m^*\geqslant 1$
, and -
(O2) two families
 $\mathcal {F}^*, \mathcal {G}^*\subseteq \{0,1\}^{m^*}$
such that (5.4)
$\mathcal {F}^*, \mathcal {G}^*\subseteq \{0,1\}^{m^*}$
such that (5.4) $$ \begin{align} (\mathcal{F}^*,\mathcal{G}^*)\in\mathrm{Forbid}\left(m^*,[0,b^*]\right) \ \ \text{ or } \ \ (\mathcal{F}^*,\mathcal{G}^*)\in \mathrm{Forbid}\left(m^*,[a^*,m^*]\right). \end{align} $$
$$ \begin{align} (\mathcal{F}^*,\mathcal{G}^*)\in\mathrm{Forbid}\left(m^*,[0,b^*]\right) \ \ \text{ or } \ \ (\mathcal{F}^*,\mathcal{G}^*)\in \mathrm{Forbid}\left(m^*,[a^*,m^*]\right). \end{align} $$
It also uses six counters
![]() $S_{d_1},S_{d_2},S_w,a,b,m$
that serve different purposes. The first three counters,
$S_{d_1},S_{d_2},S_w,a,b,m$
that serve different purposes. The first three counters,
![]() $S_{d_1},S_{d_2}$
and
$S_{d_1},S_{d_2}$
and
![]() $S_w$
, give us the total number of iterations, and they are used for bookkeeping the operations performed by the algorithm (we shall comment on these operations in due course). The counters
$S_w$
, give us the total number of iterations, and they are used for bookkeeping the operations performed by the algorithm (we shall comment on these operations in due course). The counters
![]() $a,b$
encode the interval that is forbidden for the families
$a,b$
encode the interval that is forbidden for the families
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
. Finally, the counter m keeps track of the dimension of
$\mathcal {G}$
. Finally, the counter m keeps track of the dimension of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
; in particular, m starts from n and drops by one at each iteration. Thus, we have
$\mathcal {G}$
; in particular, m starts from n and drops by one at each iteration. Thus, we have
Moreover, by Fact 5.1, at each iteration of ‘type’
![]() $S_{d_1}$
or
$S_{d_1}$
or
![]() $S_{w}$
(that is, at each iteration where one of the counters
$S_{w}$
(that is, at each iteration where one of the counters
![]() $S_{d_1}$
or
$S_{d_1}$
or
![]() $S_{w}$
is increased by one), the lower bound a of the forbidden interval
$S_{w}$
is increased by one), the lower bound a of the forbidden interval
![]() $[a,b]$
is reduced by one; since the algorithm starts with
$[a,b]$
is reduced by one; since the algorithm starts with
![]() $a=\ell $
, we obtain that
$a=\ell $
, we obtain that
Next, observe that
![]() $S_{d_1}$
and
$S_{d_1}$
and
![]() $S_{d_2}$
count the number of iterations where we have ‘density increment’. Note, however, that this increment is not uniform: at each iteration of ‘type’
$S_{d_2}$
count the number of iterations where we have ‘density increment’. Note, however, that this increment is not uniform: at each iteration of ‘type’
![]() $S_{d_1}$
, the product of the measures is increased by a factor
$S_{d_1}$
, the product of the measures is increased by a factor
![]() $(1+\delta )$
, while at each iteration of ‘type’
$(1+\delta )$
, while at each iteration of ‘type’
![]() $S_{d_2}$
, the product of the measures is increased by a factor
$S_{d_2}$
, the product of the measures is increased by a factor
![]() $(1+\frac {p}{1-p}\delta )$
. However, if at a certain iteration the algorithm reaches Step 6 and then moves to Step 1, then the product of the measures of the new families is comparable to the product of the measures of the previous families by a factor
$(1+\frac {p}{1-p}\delta )$
. However, if at a certain iteration the algorithm reaches Step 6 and then moves to Step 1, then the product of the measures of the new families is comparable to the product of the measures of the previous families by a factor
![]() $(1-\delta -2\frac {p}{1-p}\delta ^2)$
; in other words, the product of the measures may possibly drop, but not significantly. Finally, if at a certain iteration the algorithm reaches Step 7, then the widening lemma (Lemma 4.1) ensures that the product of the measures of the new families is also at least
$(1-\delta -2\frac {p}{1-p}\delta ^2)$
; in other words, the product of the measures may possibly drop, but not significantly. Finally, if at a certain iteration the algorithm reaches Step 7, then the widening lemma (Lemma 4.1) ensures that the product of the measures of the new families is also at least
![]() $(1-\delta -2\frac {p}{1-p}\delta ^2)$
times the product of the measures of the previous families.
$(1-\delta -2\frac {p}{1-p}\delta ^2)$
times the product of the measures of the previous families.
Summing up the previous observations, we arrive at the following basic estimate
that will be used in the analysis of the algorithm in the next section.
6 Proof of Theorem 1.1
Let
![]() $n,p,p',\ell ,\mathcal {F},\mathcal {G}$
be as in the statement of the theorem. Clearly, we may assume that
$n,p,p',\ell ,\mathcal {F},\mathcal {G}$
be as in the statement of the theorem. Clearly, we may assume that
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are nonempty. Notice that (1.3) is straightforward if
$\mathcal {G}$
are nonempty. Notice that (1.3) is straightforward if
![]() $\ell =0$
or
$\ell =0$
or
![]() $\ell =pn$
. Thus, we may also assume that
$\ell =pn$
. Thus, we may also assume that
![]() $\ell $
is a positive integer with
$\ell $
is a positive integer with
![]() $\ell <pn$
and, consequently,
$\ell <pn$
and, consequently,
![]() $n\geqslant 2$
; moreover, setting
$n\geqslant 2$
; moreover, setting
we have that
![]() $0<\delta <\frac {1}{10}$
. We will actually show the slightly stronger estimate
$0<\delta <\frac {1}{10}$
. We will actually show the slightly stronger estimate
Assume, towards a contradiction, that this is not the case; that is,
We run the algorithm described in Section 5 for
![]() $n,p,p',\ell ,\delta $
and the families
$n,p,p',\ell ,\delta $
and the families
![]() $\mathcal {F},\mathcal {G}$
. Let
$\mathcal {F},\mathcal {G}$
. Let
![]() $a^*,b^*,m^*,\mathcal {F}^*,\mathcal {G}^*$
denote the output of the algorithm. By (5.4), we see that either
$a^*,b^*,m^*,\mathcal {F}^*,\mathcal {G}^*$
denote the output of the algorithm. By (5.4), we see that either
-
(
 $\mathcal {A}1$
)
$\mathcal {A}1$
)
 $(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[0,b^*])$
, or
$(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[0,b^*])$
, or -
(
 $\mathcal {A}2$
)
$\mathcal {A}2$
)
 $(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[a^*,m^*])$
.
$(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[a^*,m^*])$
.
The contradiction will be derived by showing that none of these cases can occur.
To this end, we first observe that, by (5.7) and (6.3), we have
where
![]() $S_{d_1},S_{d_2},S_w$
are the counters used in the algorithm. We will need the following estimates for
$S_{d_1},S_{d_2},S_w$
are the counters used in the algorithm. We will need the following estimates for
![]() $S_{d_1},S_{d_2}$
and
$S_{d_1},S_{d_2}$
and
![]() $S_w$
.
$S_w$
.
Lemma 6.1. We have
In the proof of Lemma 6.1, as well as in the rest of this section, we will repeatedly use the following elementary observation, which we isolate for the convenience of the reader.
Observation 6.2. The following hold.
-
(i) We have
 $\frac {1}{1-x}=1+\frac {x}{1-x}$
for every
$\frac {1}{1-x}=1+\frac {x}{1-x}$
for every
 $x\neq 1$
.
$x\neq 1$
. -
(ii) We have
 $x-\frac {x^2}{2}\leqslant \ln (1+x)\leqslant x$
for every
$x-\frac {x^2}{2}\leqslant \ln (1+x)\leqslant x$
for every
 $x\geqslant 0$
.
$x\geqslant 0$
.
In particular, for every
![]() $0\leqslant x <1$
, we have
$0\leqslant x <1$
, we have
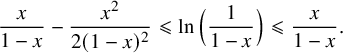 $$ \begin{align} \frac{x}{1-x} -\frac{x^2}{2(1-x)^2} \leqslant \ln\Big(\frac{1}{1-x}\Big) \leqslant \frac{x}{1-x}. \end{align} $$
$$ \begin{align} \frac{x}{1-x} -\frac{x^2}{2(1-x)^2} \leqslant \ln\Big(\frac{1}{1-x}\Big) \leqslant \frac{x}{1-x}. \end{align} $$
We are ready to proceed to the proof of Lemma 6.1.
Proof of Lemma 6.1.
We start with the proof of (6.5). Notice first that, by (6.4),
or, equivalently,
Since
![]() $(1+\delta )(1-\delta -2\frac {p}{1-p}\delta ^2)=1-\frac {1+p}{1-p}\delta ^2-2\frac {p}{1-p}\delta ^3$
, after taking logarithms and rearranging we find that
$(1+\delta )(1-\delta -2\frac {p}{1-p}\delta ^2)=1-\frac {1+p}{1-p}\delta ^2-2\frac {p}{1-p}\delta ^3$
, after taking logarithms and rearranging we find that
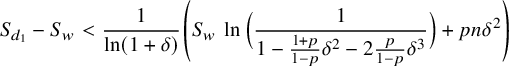 $$ \begin{align} S_{d_1}-S_w < \frac{1}{\ln(1+\delta)} \left(S_w\, \ln\Big(\frac{1}{1-\frac{1+p}{1-p}\delta^2-2\frac{p}{1-p}\delta^3}\Big)+pn\delta^2\right) \end{align} $$
$$ \begin{align} S_{d_1}-S_w < \frac{1}{\ln(1+\delta)} \left(S_w\, \ln\Big(\frac{1}{1-\frac{1+p}{1-p}\delta^2-2\frac{p}{1-p}\delta^3}\Big)+pn\delta^2\right) \end{align} $$
that implies, by Observation 6.2, that
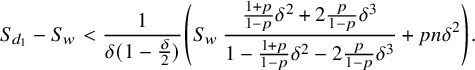 $$ \begin{align} S_{d_1}-S_w < \frac{1}{\delta(1-\frac{\delta}{2})} \left( S_w \, \frac{\frac{1+p}{1-p}\delta^2+2\frac{p}{1-p}\delta^3}{1-\frac{1+p}{1-p}\delta^2-2\frac{p}{1-p}\delta^3} +pn\delta^2\right). \end{align} $$
$$ \begin{align} S_{d_1}-S_w < \frac{1}{\delta(1-\frac{\delta}{2})} \left( S_w \, \frac{\frac{1+p}{1-p}\delta^2+2\frac{p}{1-p}\delta^3}{1-\frac{1+p}{1-p}\delta^2-2\frac{p}{1-p}\delta^3} +pn\delta^2\right). \end{align} $$
By (5.6), the fact that
![]() $\ell < pn$
and (6.11), we conclude that
$\ell < pn$
and (6.11), we conclude that
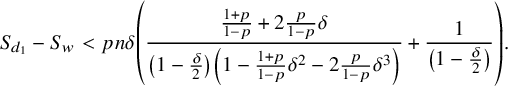 $$ \begin{align} S_{d_1}-S_w<pn\delta \left(\frac{\frac{1+p}{1-p}+2\frac{p}{1-p}\delta}{\left(1-\frac{\delta}{2}\right) \left(1-\frac{1+p}{1-p}\delta^2-2\frac{p}{1-p}\delta^3\right)}+\frac{1}{\left(1-\frac{\delta}{2}\right)}\right). \end{align} $$
$$ \begin{align} S_{d_1}-S_w<pn\delta \left(\frac{\frac{1+p}{1-p}+2\frac{p}{1-p}\delta}{\left(1-\frac{\delta}{2}\right) \left(1-\frac{1+p}{1-p}\delta^2-2\frac{p}{1-p}\delta^3\right)}+\frac{1}{\left(1-\frac{\delta}{2}\right)}\right). \end{align} $$
The desired estimate (6.5) follows from (6.12) and the fact that
![]() $0<\delta <\frac {1}{10}$
and
$0<\delta <\frac {1}{10}$
and
![]() $p\leqslant \frac 12$
.
$p\leqslant \frac 12$
.
We proceed to show that inequality (6.6) is also satisfied. As before, we first observe that (6.4) yields that
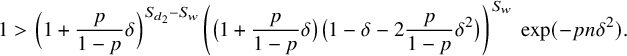 $$ \begin{align} 1> \Big(1+\frac{p}{1-p}\delta\Big)^{S_{d_2}-S_w} \left(\big(1+\frac{p}{1-p}\delta\big)\big(1-\delta-2\frac{p}{1-p}\delta^2\big)\right)^{S_w}\, \exp(-pn\delta^2). \end{align} $$
$$ \begin{align} 1> \Big(1+\frac{p}{1-p}\delta\Big)^{S_{d_2}-S_w} \left(\big(1+\frac{p}{1-p}\delta\big)\big(1-\delta-2\frac{p}{1-p}\delta^2\big)\right)^{S_w}\, \exp(-pn\delta^2). \end{align} $$
However, since
![]() $0<\delta <\frac {1}{10}$
, we have
$0<\delta <\frac {1}{10}$
, we have
that combined with (6.13) yields that
Now after taking logarithms and rearranging, we have
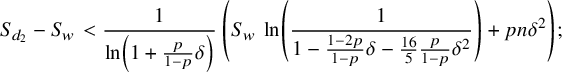 $$ \begin{align} S_{d_2}-S_w < \frac{1}{\ln\left(1+\frac{p}{1-p}\delta\right)} \, \left(S_w\, \ln\left(\frac{1}{1-\frac{1-2p}{1-p}\delta-\frac{16}{5}\frac{p}{1-p}\delta^2}\right)+pn\delta^2\right); \end{align} $$
$$ \begin{align} S_{d_2}-S_w < \frac{1}{\ln\left(1+\frac{p}{1-p}\delta\right)} \, \left(S_w\, \ln\left(\frac{1}{1-\frac{1-2p}{1-p}\delta-\frac{16}{5}\frac{p}{1-p}\delta^2}\right)+pn\delta^2\right); \end{align} $$
by Observation 6.2, this yields that
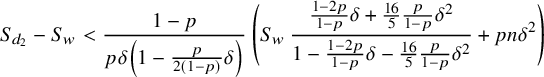 $$ \begin{align} S_{d_2}-S_w < \frac{1-p}{p\delta\left(1-\frac{p}{2(1-p)}\delta\right)} \, \left(S_w\, \frac{\frac{1-2p}{1-p}\delta+\frac{16}{5} \frac{p}{1-p}\delta^2}{1-\frac{1-2p}{1-p}\delta-\frac{16}{5}\frac{p}{1-p}\delta^2} + pn\delta^2\right) \end{align} $$
$$ \begin{align} S_{d_2}-S_w < \frac{1-p}{p\delta\left(1-\frac{p}{2(1-p)}\delta\right)} \, \left(S_w\, \frac{\frac{1-2p}{1-p}\delta+\frac{16}{5} \frac{p}{1-p}\delta^2}{1-\frac{1-2p}{1-p}\delta-\frac{16}{5}\frac{p}{1-p}\delta^2} + pn\delta^2\right) \end{align} $$
that can be further simplified to
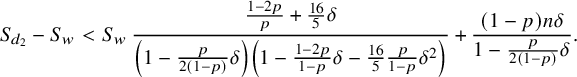 $$ \begin{align} S_{d_2}-S_w < S_w\, \frac{\frac{1-2p}{p}+\frac{16}{5}\delta}{\left(1-\frac{p}{2(1-p)}\delta\right) \left(1-\frac{1-2p}{1-p}\delta-\frac{16}{5}\frac{p}{1-p}\delta^2\right)}+ \frac{(1-p)n\delta}{1-\frac{p}{2(1-p)}\delta}. \end{align} $$
$$ \begin{align} S_{d_2}-S_w < S_w\, \frac{\frac{1-2p}{p}+\frac{16}{5}\delta}{\left(1-\frac{p}{2(1-p)}\delta\right) \left(1-\frac{1-2p}{1-p}\delta-\frac{16}{5}\frac{p}{1-p}\delta^2\right)}+ \frac{(1-p)n\delta}{1-\frac{p}{2(1-p)}\delta}. \end{align} $$
However, since
![]() $p\leqslant \frac 12$
, for every
$p\leqslant \frac 12$
, for every
![]() $0<\delta <\frac {1}{10}$
we have
$0<\delta <\frac {1}{10}$
we have
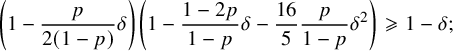 $$ \begin{align} \left(1-\frac{p}{2(1-p)}\delta\right) \left(1-\frac{1-2p}{1-p}\delta-\frac{16}{5}\frac{p}{1-p}\delta^2\right)\geqslant 1-\delta; \end{align} $$
$$ \begin{align} \left(1-\frac{p}{2(1-p)}\delta\right) \left(1-\frac{1-2p}{1-p}\delta-\frac{16}{5}\frac{p}{1-p}\delta^2\right)\geqslant 1-\delta; \end{align} $$
indeed, after noticing that
the desired estimate (6.19) follows from the elementary inequality
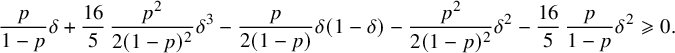 $$ \begin{align} \frac{p}{1-p}\delta + \frac{16}{5}\, \frac{p^2}{2(1-p)^2}\delta^3 - \frac{p}{2(1-p)}\delta(1-\delta) - \frac{p^2}{2(1-p)^2}\delta^2 - \frac{16}{5}\, \frac{p}{1-p}\delta^2 \geqslant 0. \end{align} $$
$$ \begin{align} \frac{p}{1-p}\delta + \frac{16}{5}\, \frac{p^2}{2(1-p)^2}\delta^3 - \frac{p}{2(1-p)}\delta(1-\delta) - \frac{p^2}{2(1-p)^2}\delta^2 - \frac{16}{5}\, \frac{p}{1-p}\delta^2 \geqslant 0. \end{align} $$
By (6.18) and (6.19), we obtain that
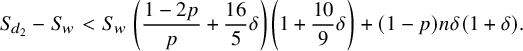 $$ \begin{align} S_{d_2}-S_w < S_w\, \left(\frac{1-2p}{p}+\frac{16}{5}\delta\right) \left(1+\frac{10}{9}\delta\right)+(1-p)n\delta\left(1+\delta\right). \end{align} $$
$$ \begin{align} S_{d_2}-S_w < S_w\, \left(\frac{1-2p}{p}+\frac{16}{5}\delta\right) \left(1+\frac{10}{9}\delta\right)+(1-p)n\delta\left(1+\delta\right). \end{align} $$
We then expand (6.22) to
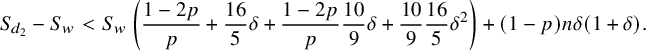 $$ \begin{align} S_{d_2}-S_w < S_w\, \left(\frac{1-2p}{p}+ \frac{16}{5}\delta+ \frac{1-2p}{p}\frac{10}{9}\delta +\frac{10}{9}\frac{16}{5}\delta^2\right)+(1-p)n\delta\left(1+\delta\right). \end{align} $$
$$ \begin{align} S_{d_2}-S_w < S_w\, \left(\frac{1-2p}{p}+ \frac{16}{5}\delta+ \frac{1-2p}{p}\frac{10}{9}\delta +\frac{10}{9}\frac{16}{5}\delta^2\right)+(1-p)n\delta\left(1+\delta\right). \end{align} $$
By (5.6), we see that
![]() $S_w\leqslant \ell < pn$
, and so (6.23) yields that
$S_w\leqslant \ell < pn$
, and so (6.23) yields that
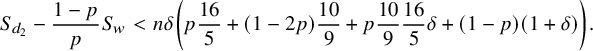 $$ \begin{align} S_{d_2}-\frac{1-p}{p}S_w < n\delta \left(p\frac{16}{5}+(1-2p)\frac{10}{9}+p\frac{10}{9}\frac{16}{5}\delta+(1-p)\left(1+\delta\right)\right). \end{align} $$
$$ \begin{align} S_{d_2}-\frac{1-p}{p}S_w < n\delta \left(p\frac{16}{5}+(1-2p)\frac{10}{9}+p\frac{10}{9}\frac{16}{5}\delta+(1-p)\left(1+\delta\right)\right). \end{align} $$
Inequality (6.6) follows from (6.24) and the fact that
![]() $0<\delta <\frac {1}{10}$
and
$0<\delta <\frac {1}{10}$
and
![]() $0<p\leqslant \frac {1}{2}$
.
$0<p\leqslant \frac {1}{2}$
.
After these preliminary steps, we are ready to consider cases.
Case 1:
 $(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[0,b^*])$
$(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[0,b^*])$
Note that, in this case, the cardinality of the final forbidden interval
![]() $[0,b^*]$
is
$[0,b^*]$
is
![]() $b^*+1$
; however, the forbidden interval for the initial families
$b^*+1$
; however, the forbidden interval for the initial families
![]() $\mathcal {F},\mathcal {G}$
was a singleton. By Fact 5.1, the cardinality of the forbidden interval increases by
$\mathcal {F},\mathcal {G}$
was a singleton. By Fact 5.1, the cardinality of the forbidden interval increases by
![]() $1$
if and only if the algorithm executes an iteration of ‘type’
$1$
if and only if the algorithm executes an iteration of ‘type’
![]() $S_w$
. Thus,
$S_w$
. Thus,
Next observe that the initial value of the lower bound a of the forbidden interval is equal to
![]() $\ell $
, and it is equal to
$\ell $
, and it is equal to
![]() $0$
when the algorithm terminates. Using Fact 5.1 again, we see that the counter a decreases by
$0$
when the algorithm terminates. Using Fact 5.1 again, we see that the counter a decreases by
![]() $1$
if and only if an iteration of ‘type’
$1$
if and only if an iteration of ‘type’
![]() $S_{d_1}$
or an iteration of ‘type’
$S_{d_1}$
or an iteration of ‘type’
![]() $S_w$
is executed. Therefore, we also have that
$S_w$
is executed. Therefore, we also have that
By (6.5) and (6.26), we obtain that
However, since
![]() $\left (\mathcal {F}^*,\mathcal {G}^*\right )\in \mathrm {Forbid}(m^*,[0,b^*])$
and
$\left (\mathcal {F}^*,\mathcal {G}^*\right )\in \mathrm {Forbid}(m^*,[0,b^*])$
and
![]() $b^*=S_w$
, by part (i) of Lemma 3.3, we have
$b^*=S_w$
, by part (i) of Lemma 3.3, we have
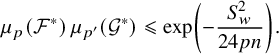 $$ \begin{align} \mu_p(\mathcal{F}^*)\,\mu_{p'}(\mathcal{G}^*)\leqslant \exp\left(-\frac{S_w^2}{24pn}\right). \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F}^*)\,\mu_{p'}(\mathcal{G}^*)\leqslant \exp\left(-\frac{S_w^2}{24pn}\right). \end{align} $$
Combining (5.7), (6.3), (6.26) and (6.28), we obtain in particular that
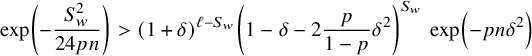 $$ \begin{align} \exp\left(-\frac{S_w^2}{24pn}\right)> (1+\delta)^{\ell-S_w} \left(1-\delta-2\frac{p}{1-p}\delta^2\right)^{S_w}\, \exp\left(-pn\delta^2\right) \end{align} $$
$$ \begin{align} \exp\left(-\frac{S_w^2}{24pn}\right)> (1+\delta)^{\ell-S_w} \left(1-\delta-2\frac{p}{1-p}\delta^2\right)^{S_w}\, \exp\left(-pn\delta^2\right) \end{align} $$
that implies, after taking logarithms and using Observation 6.2, that
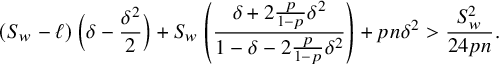 $$ \begin{align} (S_w-\ell)\, \Big(\delta-\frac{\delta^2}{2}\Big) + S_w\, \left(\frac{\delta+2\frac{p}{1-p}\delta^2}{1-\delta-2\frac{p}{1-p}\delta^2}\right)+pn\delta^2> \frac{S_w^2}{24pn}. \end{align} $$
$$ \begin{align} (S_w-\ell)\, \Big(\delta-\frac{\delta^2}{2}\Big) + S_w\, \left(\frac{\delta+2\frac{p}{1-p}\delta^2}{1-\delta-2\frac{p}{1-p}\delta^2}\right)+pn\delta^2> \frac{S_w^2}{24pn}. \end{align} $$
Moreover, since
![]() $0<\delta <\frac {1}{10}$
and
$0<\delta <\frac {1}{10}$
and
![]() $0<p\leqslant \frac 12$
, we have
$0<p\leqslant \frac 12$
, we have
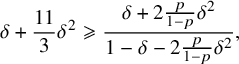 $$ \begin{align} \delta+\frac{11}{3}\delta^2 \geqslant \frac{\delta+2\frac{p}{1-p}\delta^2}{1-\delta-2\frac{p}{1-p}\delta^2}, \end{align} $$
$$ \begin{align} \delta+\frac{11}{3}\delta^2 \geqslant \frac{\delta+2\frac{p}{1-p}\delta^2}{1-\delta-2\frac{p}{1-p}\delta^2}, \end{align} $$
which, combined with (6.30), implies that
We now consider the following subcases.
Subcase 1.1:
 $S_w\leqslant \frac 23\ell $
$S_w\leqslant \frac 23\ell $
In this subcase, by (6.27) and the choice of
![]() $\delta $
in (6.1), we have
$\delta $
in (6.1), we have
indeed, by (6.27) and (6.1),
![]() $S_w\geqslant \frac {\ell }{2}-\frac 52 pn\delta \geqslant \ell \big (\frac 12- \frac {5}{116}\big ) \geqslant 58pn\delta \big (\frac 12- \frac {5}{116}\big )\geqslant \frac {53}{2}pn\delta $
. Hence, by (6.32), (6.33) and the fact that
$S_w\geqslant \frac {\ell }{2}-\frac 52 pn\delta \geqslant \ell \big (\frac 12- \frac {5}{116}\big ) \geqslant 58pn\delta \big (\frac 12- \frac {5}{116}\big )\geqslant \frac {53}{2}pn\delta $
. Hence, by (6.32), (6.33) and the fact that
![]() $\delta <\frac {1}{10}$
, we obtain that
$\delta <\frac {1}{10}$
, we obtain that
which is clearly a contradiction.
Subcase 1.2:
 $S_w>\frac 23\ell $
$S_w>\frac 23\ell $
Therefore, by (6.32) and (6.35), we get that
which leads, again, to a contradiction.
Case 2:
 $(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[a^*,m^*])$
$(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[a^*,m^*])$
The proof in this case is slightly more involved. We start by observing that the initial value of the upper bound b of the forbidden interval is equal to
![]() $\ell $
, and it is equal to
$\ell $
, and it is equal to
![]() $m^*$
when the algorithm terminates. Moreover, by Fact 5.1, the counter b decreases by
$m^*$
when the algorithm terminates. Moreover, by Fact 5.1, the counter b decreases by
![]() $1$
if and only if an iteration of ‘type’
$1$
if and only if an iteration of ‘type’
![]() $S_{d_1}$
is executed. Thus,
$S_{d_1}$
is executed. Thus,
Combining (5.5) and (6.37), we obtain that
This identity together with (6.6) yields that
![]() $S_w\geqslant pn-3pn\delta -p\ell $
that we rewrite as
$S_w\geqslant pn-3pn\delta -p\ell $
that we rewrite as
Moreover, as we have already noted in the previous case, the cardinality of the forbidden interval increases by
![]() $1$
if and only if the algorithm executes an iteration of ‘type’
$1$
if and only if the algorithm executes an iteration of ‘type’
![]() $S_w$
. Therefore, we also have that
$S_w$
. Therefore, we also have that
Next, we introduce the quantity
and we observe that, by (6.39), we have the lower bound
notice that
![]() $\alpha>0$
by the choice of
$\alpha>0$
by the choice of
![]() $\delta $
in (6.1). Also notice that, by (6.40) and (6.41),
$\delta $
in (6.1). Also notice that, by (6.40) and (6.41),
However, setting
by (6.43) and the fact that
![]() $(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[a^*,m^*])$
, we see that
$(\mathcal {F}^*,\mathcal {G}^*)\in \mathrm {Forbid}(m^*,[a^*,m^*])$
, we see that
-
(i)
 $\mu _p(\mathcal {F}^*)=\mu _p(\widehat {\mathcal {F}})$
and
$\mu _p(\mathcal {F}^*)=\mu _p(\widehat {\mathcal {F}})$
and
 $\mu _{p'}(\mathcal {G}^*)=\mu _{p'}(\widehat {\mathcal {G}})$
, and
$\mu _{p'}(\mathcal {G}^*)=\mu _{p'}(\widehat {\mathcal {G}})$
, and -
(ii)
 $(\widehat {\mathcal {F}},\widehat {\mathcal {G}})\in \mathrm {Forbid}(\ell ,[p\ell -\alpha ,\ell ])$
.
$(\widehat {\mathcal {F}},\widehat {\mathcal {G}})\in \mathrm {Forbid}(\ell ,[p\ell -\alpha ,\ell ])$
.
Hence, by part (ii) of Lemma 3.3, we obtain that
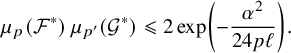 $$ \begin{align} \mu_p(\mathcal{F}^*)\, \mu_{p'}(\mathcal{G}^*)\leqslant 2\exp\left(-\frac{\alpha^2}{24p\ell}\right). \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F}^*)\, \mu_{p'}(\mathcal{G}^*)\leqslant 2\exp\left(-\frac{\alpha^2}{24p\ell}\right). \end{align} $$
In particular, by (5.7), (6.3) and (6.46), we have that
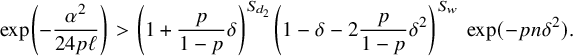 $$ \begin{align} \exp\left(-\frac{\alpha^2}{24p\ell}\right)> \left(1+\frac{p}{1-p}\delta\right)^{S_{d_2}} \left(1-\delta-2\frac{p}{1-p}\delta^2\right)^{S_w}\, \exp(-pn\delta^2). \end{align} $$
$$ \begin{align} \exp\left(-\frac{\alpha^2}{24p\ell}\right)> \left(1+\frac{p}{1-p}\delta\right)^{S_{d_2}} \left(1-\delta-2\frac{p}{1-p}\delta^2\right)^{S_w}\, \exp(-pn\delta^2). \end{align} $$
As in the previous case, we will show that (6.47) leads to a contradiction.
To this end, it is enough to show that, by the choice of
![]() $\delta $
in (6.1), we have
$\delta $
in (6.1), we have
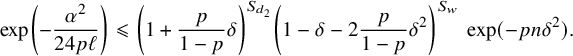 $$ \begin{align} \exp\left(-\frac{\alpha^2}{24p\ell}\right) \leqslant \left(1+\frac{p}{1-p}\delta\right)^{S_{d_2}} \left(1-\delta-2\frac{p}{1-p}\delta^2\right)^{S_w}\, \exp(-pn\delta^2). \end{align} $$
$$ \begin{align} \exp\left(-\frac{\alpha^2}{24p\ell}\right) \leqslant \left(1+\frac{p}{1-p}\delta\right)^{S_{d_2}} \left(1-\delta-2\frac{p}{1-p}\delta^2\right)^{S_w}\, \exp(-pn\delta^2). \end{align} $$
After taking logarithms and using Observation 6.2, it is enough to show that
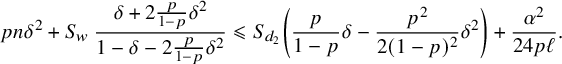 $$ \begin{align} pn\delta^2+S_w\, \frac{\delta+2\frac{p}{1-p}\delta^2}{1-\delta-2\frac{p}{1-p}\delta^2} \leqslant S_{d_2}\left(\frac{p}{1-p}\delta-\frac{p^2}{2(1-p)^2}\delta^2\right)+\frac{\alpha^2}{24p\ell}. \end{align} $$
$$ \begin{align} pn\delta^2+S_w\, \frac{\delta+2\frac{p}{1-p}\delta^2}{1-\delta-2\frac{p}{1-p}\delta^2} \leqslant S_{d_2}\left(\frac{p}{1-p}\delta-\frac{p^2}{2(1-p)^2}\delta^2\right)+\frac{\alpha^2}{24p\ell}. \end{align} $$
Since
![]() $0<\delta <\frac {1}{10}$
and
$0<\delta <\frac {1}{10}$
and
![]() $p\leqslant \frac 12$
, we have
$p\leqslant \frac 12$
, we have
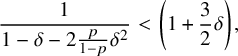 $$ \begin{align} & \ \ \ \ \ \ \, \frac{1}{1-\delta-2\frac{p}{1-p}\delta^2} < \left(1+\frac32\delta\right), \end{align} $$
$$ \begin{align} & \ \ \ \ \ \ \, \frac{1}{1-\delta-2\frac{p}{1-p}\delta^2} < \left(1+\frac32\delta\right), \end{align} $$
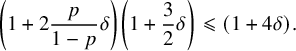 $$ \begin{align} & \left(1+2\frac{p}{1-p}\delta\right) \left(1+\frac32\delta\right)\leqslant (1+4\delta). \end{align} $$
$$ \begin{align} & \left(1+2\frac{p}{1-p}\delta\right) \left(1+\frac32\delta\right)\leqslant (1+4\delta). \end{align} $$
Thus, by (6.49)–(6.51), it is enough to show that
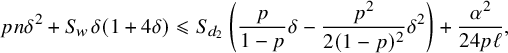 $$ \begin{align} pn\delta^2+S_w\delta(1+4\delta)\leqslant S_{d_2}\, \left(\frac{p}{1-p}\delta-\frac{p^2}{2(1-p)^2}\delta^2\right) +\frac{\alpha^2}{24p\ell}, \end{align} $$
$$ \begin{align} pn\delta^2+S_w\delta(1+4\delta)\leqslant S_{d_2}\, \left(\frac{p}{1-p}\delta-\frac{p^2}{2(1-p)^2}\delta^2\right) +\frac{\alpha^2}{24p\ell}, \end{align} $$
which is equivalent to saying, after rearranging, that
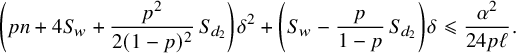 $$ \begin{align} \left(pn+4S_w+\frac{p^2}{2(1-p)^2}\, S_{d_2}\right)\delta^2+\left(S_w-\frac{p}{1-p}\,S_{d_2}\right)\delta \leqslant \frac{\alpha^2}{24p\ell}. \end{align} $$
$$ \begin{align} \left(pn+4S_w+\frac{p^2}{2(1-p)^2}\, S_{d_2}\right)\delta^2+\left(S_w-\frac{p}{1-p}\,S_{d_2}\right)\delta \leqslant \frac{\alpha^2}{24p\ell}. \end{align} $$
By (5.6), we have
![]() $S_w\leqslant \ell < pn$
and, clearly,
$S_w\leqslant \ell < pn$
and, clearly,
![]() $S_{d_2}\leqslant n$
. Hence, by (6.53) and the fact that
$S_{d_2}\leqslant n$
. Hence, by (6.53) and the fact that
![]() $0<p\leqslant \frac 12$
, it is enough to show that
$0<p\leqslant \frac 12$
, it is enough to show that
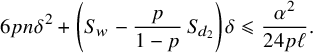 $$ \begin{align} 6pn\delta^2 +\left(S_w-\frac{p}{1-p}\,S_{d_2}\right)\delta \leqslant \frac{\alpha^2}{24p\ell}. \end{align} $$
$$ \begin{align} 6pn\delta^2 +\left(S_w-\frac{p}{1-p}\,S_{d_2}\right)\delta \leqslant \frac{\alpha^2}{24p\ell}. \end{align} $$
Observe that
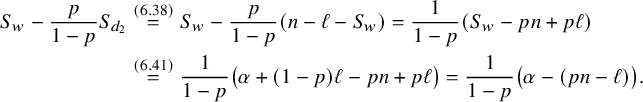 $$ \begin{align} S_w-\frac{p}{1-p}S_{d_2} & \stackrel{(6.38)}{=} S_w-\frac{p}{1-p}\left(n-\ell-S_w\right) =\frac{1}{1-p}(S_w-pn+p\ell) \nonumber \\ & \stackrel{(6.41)}{=} \frac{1}{1-p}\big(\alpha+(1-p)\ell-pn+p\ell\big) = \frac{1}{1-p}\big(\alpha-(pn-\ell)\big). \end{align} $$
$$ \begin{align} S_w-\frac{p}{1-p}S_{d_2} & \stackrel{(6.38)}{=} S_w-\frac{p}{1-p}\left(n-\ell-S_w\right) =\frac{1}{1-p}(S_w-pn+p\ell) \nonumber \\ & \stackrel{(6.41)}{=} \frac{1}{1-p}\big(\alpha+(1-p)\ell-pn+p\ell\big) = \frac{1}{1-p}\big(\alpha-(pn-\ell)\big). \end{align} $$
In order to verify (6.54), we consider the following subcases.
Subcase 2.1:
 $\alpha \leqslant pn-\ell $
$\alpha \leqslant pn-\ell $
By (6.55), we have
![]() $S_w-\frac {p}{1-p}S_{d_2}\leqslant 0$
, and so it is enough to show that
$S_w-\frac {p}{1-p}S_{d_2}\leqslant 0$
, and so it is enough to show that
Since
![]() $0<\delta <\frac {pn-\ell }{51pn}$
, by the choice of
$0<\delta <\frac {pn-\ell }{51pn}$
, by the choice of
![]() $\delta $
in (6.1), the estimate (6.56) – and, consequently, (6.54) – follows from (6.42).
$\delta $
in (6.1), the estimate (6.56) – and, consequently, (6.54) – follows from (6.42).
Subcase 2.2:
 $\alpha> pn-\ell $
$\alpha> pn-\ell $
In this subcase, by (6.55), we have
![]() $S_w-\frac {p}{1-p}S_{d_2}>0$
. Hence, using again the fact that
$S_w-\frac {p}{1-p}S_{d_2}>0$
. Hence, using again the fact that
![]() $0<\delta <\frac {pn-\ell }{51pn}$
, it is enough to show that
$0<\delta <\frac {pn-\ell }{51pn}$
, it is enough to show that
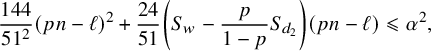 $$ \begin{align} \frac{144}{51^2}(pn-\ell)^2 + \frac{24}{51}\left(S_w-\frac{p}{1-p}S_{d_2}\right)(pn-\ell)\leqslant \alpha^2, \end{align} $$
$$ \begin{align} \frac{144}{51^2}(pn-\ell)^2 + \frac{24}{51}\left(S_w-\frac{p}{1-p}S_{d_2}\right)(pn-\ell)\leqslant \alpha^2, \end{align} $$
which is equivalent to saying, by (6.55), that
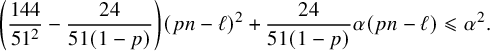 $$ \begin{align} \left(\frac{144}{51^2}-\frac{24}{51(1-p)}\right) (pn-\ell)^2 + \frac{24}{51(1-p)}\alpha (pn-\ell)\leqslant \alpha^2. \end{align} $$
$$ \begin{align} \left(\frac{144}{51^2}-\frac{24}{51(1-p)}\right) (pn-\ell)^2 + \frac{24}{51(1-p)}\alpha (pn-\ell)\leqslant \alpha^2. \end{align} $$
Since
![]() $0<p\leqslant \frac 12$
, it is enough to show that
$0<p\leqslant \frac 12$
, it is enough to show that
that follows from our starting assumption that
![]() $\alpha>pn-\ell $
.
$\alpha>pn-\ell $
.
Summing up, we conclude that (6.54) is satisfied, and as we have already indicated, this contradicts (6.47). This completes the proof that Case 2 cannot occur, and so the entire proof of Theorem 1.1 is completed.
7 Extensions of the main estimate
We start with the following proposition, which is the analogue of Theorem 1.1 for families of sets contained in layers of the cube.
Proposition 7.1. Let
![]() $\ell \leqslant k\leqslant m\leqslant n$
be positive integers, and let
$\ell \leqslant k\leqslant m\leqslant n$
be positive integers, and let
![]() $\mathcal {F}\subseteq \binom {[n]}{k}$
and
$\mathcal {F}\subseteq \binom {[n]}{k}$
and
![]() $\mathcal {G}\subseteq \binom {[n]}{m}$
with
$\mathcal {G}\subseteq \binom {[n]}{m}$
with
![]() $(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,\{\ell \})$
.
$(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,\{\ell \})$
.
-
(i) If
 $k\leqslant \frac {n}{2}$
and
$k\leqslant \frac {n}{2}$
and
 $m\leqslant n-k$
, then, setting
$m\leqslant n-k$
, then, setting
 $t:= \min \{\ell ,k-\ell \}$
, we have (7.1)
$t:= \min \{\ell ,k-\ell \}$
, we have (7.1) $$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} \leqslant 50\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \exp\Big(-\frac{t^2}{58^2\,k}\Big). \end{align} $$
$$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} \leqslant 50\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \exp\Big(-\frac{t^2}{58^2\,k}\Big). \end{align} $$
-
(ii) If
 $k\leqslant \frac {n}{2}\leqslant n-k< m\leqslant n-k+\ell $
, then, setting
$k\leqslant \frac {n}{2}\leqslant n-k< m\leqslant n-k+\ell $
, then, setting
 $\bar {t}:= \min \{k-\ell ,n-m-(k-\ell )\}$
, (7.2)
$\bar {t}:= \min \{k-\ell ,n-m-(k-\ell )\}$
, (7.2) $$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} \leqslant 50\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \exp\Big(-\frac{\bar{t}^{\,2}}{58^2\, (n-m)}\Big). \end{align} $$
$$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} \leqslant 50\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \exp\Big(-\frac{\bar{t}^{\,2}}{58^2\, (n-m)}\Big). \end{align} $$
Proof. We start with the proof of part (i). Assume, first, that
![]() $m\leqslant \frac {n}{2}$
. Then,
$m\leqslant \frac {n}{2}$
. Then,
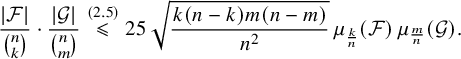 $$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} \stackrel{(2.5)}{\leqslant} 25\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \mu_{\frac{k}{n}}(\mathcal{F})\, \mu_{\frac{m}{n}}(\mathcal{G}). \end{align} $$
$$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} \stackrel{(2.5)}{\leqslant} 25\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \mu_{\frac{k}{n}}(\mathcal{F})\, \mu_{\frac{m}{n}}(\mathcal{G}). \end{align} $$
Thus, in this case, (7.1) follows from (7.3) and (1.3) applied for ‘
![]() $p=\frac {k}{n}$
’ and ‘
$p=\frac {k}{n}$
’ and ‘
![]() $p'=\frac {m}{n}$
’. Next, assume that
$p'=\frac {m}{n}$
’. Next, assume that
![]() $\frac {n}{2}\leqslant m\leqslant n-k$
and set
$\frac {n}{2}\leqslant m\leqslant n-k$
and set
![]() $\overline {\mathcal {G}}:= \{[n]\setminus G: G\in \mathcal {G}\} \subseteq \binom {[n]}{n-m}$
. Notice that
$\overline {\mathcal {G}}:= \{[n]\setminus G: G\in \mathcal {G}\} \subseteq \binom {[n]}{n-m}$
. Notice that
![]() $(\mathcal {F},\overline {\mathcal {G}})\in \mathrm {Forbid}(n,\{k-\ell \})$
and, moreover,
$(\mathcal {F},\overline {\mathcal {G}})\in \mathrm {Forbid}(n,\{k-\ell \})$
and, moreover,
![]() $k-\ell \leqslant k \leqslant n-m \leqslant \frac {n}{2}$
. Therefore, applying the estimate obtained in the first part of the proof to the pair
$k-\ell \leqslant k \leqslant n-m \leqslant \frac {n}{2}$
. Therefore, applying the estimate obtained in the first part of the proof to the pair
![]() $(\mathcal {F},\overline {\mathcal {G}})$
and invoking the choice of t, we obtain that
$(\mathcal {F},\overline {\mathcal {G}})$
and invoking the choice of t, we obtain that
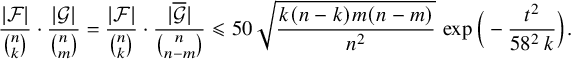 $$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} = \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\overline{\mathcal{G}}|}{\binom{n}{n-m}} \leqslant 50\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \exp\Big(-\frac{t^2}{58^2\, k}\Big). \end{align} $$
$$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} = \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\overline{\mathcal{G}}|}{\binom{n}{n-m}} \leqslant 50\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \exp\Big(-\frac{t^2}{58^2\, k}\Big). \end{align} $$
We proceed to the proof of part (ii). As before, we set
![]() $\overline {\mathcal {G}}:= \{[n]\setminus G:G\in \mathcal {G}\}\subseteq \binom {[n]}{n-m}$
, and we observe that
$\overline {\mathcal {G}}:= \{[n]\setminus G:G\in \mathcal {G}\}\subseteq \binom {[n]}{n-m}$
, and we observe that
![]() $(\mathcal {F},\overline {\mathcal {G}})\in \mathrm {Forbid}(n,\{k-\ell \})$
and
$(\mathcal {F},\overline {\mathcal {G}})\in \mathrm {Forbid}(n,\{k-\ell \})$
and
![]() $k-\ell \leqslant n-m < k\leqslant \frac {n}{2}$
. Thus, applying part (i) to the pair
$k-\ell \leqslant n-m < k\leqslant \frac {n}{2}$
. Thus, applying part (i) to the pair
![]() $(\mathcal {F},\overline {\mathcal {G}})$
and using the fact that
$(\mathcal {F},\overline {\mathcal {G}})$
and using the fact that
![]() $\bar {t}=\min \{k-\ell ,n-m-(k-\ell )\}$
, we conclude that
$\bar {t}=\min \{k-\ell ,n-m-(k-\ell )\}$
, we conclude that
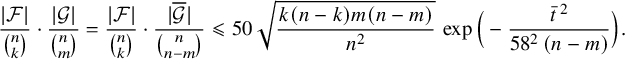 $$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} = \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\overline{\mathcal{G}}|}{\binom{n}{n-m}} \leqslant 50\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \exp\Big(-\frac{\bar{t}^{\, 2}}{58^2\,(n-m)}\Big). \end{align} $$
$$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\mathcal{G}|}{\binom{n}{m}} = \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot \frac{|\overline{\mathcal{G}}|}{\binom{n}{n-m}} \leqslant 50\, \sqrt{\frac{k(n-k)m(n-m)}{n^2}}\, \exp\Big(-\frac{\bar{t}^{\, 2}}{58^2\,(n-m)}\Big). \end{align} $$
The next result supplements Theorem 1.1 and extends the subgaussian bound (1.3) to a wider range of parameters
![]() $p,p'$
.
$p,p'$
.
Proposition 7.2. Let n be a positive integer, let
![]() $0<p<\frac 12 < p'\leqslant 1-p$
, and let
$0<p<\frac 12 < p'\leqslant 1-p$
, and let
![]() $\ell \leqslant pn$
be a nonnegative integer. Also let
$\ell \leqslant pn$
be a nonnegative integer. Also let
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
be two families whose cross intersections forbid
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
be two families whose cross intersections forbid
![]() $\ell $
. Set
$\ell $
. Set
![]() $t:= \min \{\ell ,pn-\ell \}$
and assume that
$t:= \min \{\ell ,pn-\ell \}$
and assume that
![]() $t\geqslant 3$
. Then we have
$t\geqslant 3$
. Then we have
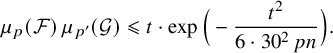 $$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) \leqslant t\cdot\exp\Big( - \frac{t^2}{6\cdot 30^2\, pn}\Big). \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) \leqslant t\cdot\exp\Big( - \frac{t^2}{6\cdot 30^2\, pn}\Big). \end{align} $$
Combining Theorem 1.1 and Proposition 7.2, we obtain the following corollary.
Corollary 7.3. Let n be a positive integer, let
![]() $\frac {6}{n}\leqslant p\leqslant p'\leqslant 1-p$
, and let
$\frac {6}{n}\leqslant p\leqslant p'\leqslant 1-p$
, and let
![]() $\ell \leqslant pn$
be a nonnegative integer. Also let
$\ell \leqslant pn$
be a nonnegative integer. Also let
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
be two families whose cross intersections forbid
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
be two families whose cross intersections forbid
![]() $\ell $
. Set
$\ell $
. Set
![]() $t:= \min \{\ell ,pn-\ell \}$
, and assume that
$t:= \min \{\ell ,pn-\ell \}$
, and assume that
![]() $t\geqslant 210 \sqrt {pn\ln (pn)}$
. Then we have
$t\geqslant 210 \sqrt {pn\ln (pn)}$
. Then we have
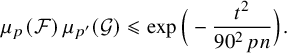 $$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) \leqslant \exp\Big( - \frac{t^2}{90^2\, pn}\Big). \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) \leqslant \exp\Big( - \frac{t^2}{90^2\, pn}\Big). \end{align} $$
We proceed to the proof of Proposition 7.2.
Proof of Proposition 7.2.
Set
![]() $m:= \frac {t}{30}$
, and observe that, by Lemma 2.3,
$m:= \frac {t}{30}$
, and observe that, by Lemma 2.3,
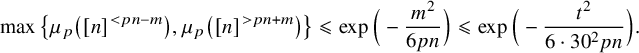 $$ \begin{align} \max\big\{ \mu_p\big([n]^{<pn-m}\big), \mu_p\big([n]^{>pn+m}\big)\big\} \leqslant \exp\Big(-\frac{m^2}{6pn}\Big) \leqslant \exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big). \end{align} $$
$$ \begin{align} \max\big\{ \mu_p\big([n]^{<pn-m}\big), \mu_p\big([n]^{>pn+m}\big)\big\} \leqslant \exp\Big(-\frac{m^2}{6pn}\Big) \leqslant \exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big). \end{align} $$
By (7.8) and the choice of m, there is a nonnegative integer
![]() $i_0$
with
$i_0$
with
![]() $pn-m\leqslant i_0\leqslant pn+m$
such that, setting
$pn-m\leqslant i_0\leqslant pn+m$
such that, setting
![]() $\mathcal {F}_{i_0}:= \mathcal {F}\cap \binom {[n]}{i_0}$
, we have
$\mathcal {F}_{i_0}:= \mathcal {F}\cap \binom {[n]}{i_0}$
, we have
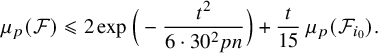 $$ \begin{align} \mu_p(\mathcal{F}) \leqslant 2\exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big)+\frac{t}{15}\, \mu_p(\mathcal{F}_{i_0}). \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F}) \leqslant 2\exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big)+\frac{t}{15}\, \mu_p(\mathcal{F}_{i_0}). \end{align} $$
Set
![]() $\overline {\mathcal {G}}:= \big \{ [n]\setminus G: G\in \mathcal {G}\big \}$
, and notice that
$\overline {\mathcal {G}}:= \big \{ [n]\setminus G: G\in \mathcal {G}\big \}$
, and notice that
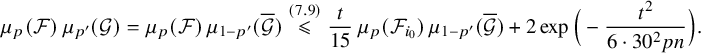 $$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G})=\mu_p(\mathcal{F})\, \mu_{1-p'}(\overline{\mathcal{G}}) \stackrel{(7.9)}{\leqslant} \frac{t}{15}\, \mu_p(\mathcal{F}_{i_0})\, \mu_{1-p'}(\overline{\mathcal{G}}) + 2\exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big). \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G})=\mu_p(\mathcal{F})\, \mu_{1-p'}(\overline{\mathcal{G}}) \stackrel{(7.9)}{\leqslant} \frac{t}{15}\, \mu_p(\mathcal{F}_{i_0})\, \mu_{1-p'}(\overline{\mathcal{G}}) + 2\exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big). \end{align} $$
Next, observe that
![]() $i_0\geqslant \ell $
and
$i_0\geqslant \ell $
and
![]() $(\mathcal {F}_{i_0},\overline {\mathcal {G}})\in \mathrm {Forbid}(n,\{i_0-\ell \})$
. Since
$(\mathcal {F}_{i_0},\overline {\mathcal {G}})\in \mathrm {Forbid}(n,\{i_0-\ell \})$
. Since
![]() $0<p\leqslant 1-p'\leqslant \frac 12$
and
$0<p\leqslant 1-p'\leqslant \frac 12$
and
![]() $i_0-\ell \leqslant pn$
, by Theorem 1.1 and (7.10), we obtain that
$i_0-\ell \leqslant pn$
, by Theorem 1.1 and (7.10), we obtain that
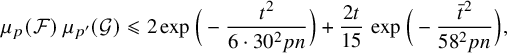 $$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) \leqslant 2\exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big) + \frac{2t}{15}\, \exp\Big(- \frac{\bar{t}^2}{58^2 pn}\Big), \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) \leqslant 2\exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big) + \frac{2t}{15}\, \exp\Big(- \frac{\bar{t}^2}{58^2 pn}\Big), \end{align} $$
where
![]() $\bar {t}:= \min \{i_0-\ell , pn-i_0+\ell \}$
.
$\bar {t}:= \min \{i_0-\ell , pn-i_0+\ell \}$
.
Claim 7.4. We have that
![]() $|\bar {t}-t|\leqslant m=\frac {t}{30}$
.
$|\bar {t}-t|\leqslant m=\frac {t}{30}$
.
Proof of Claim 7.4.
Suppose, towards a contradiction, that
![]() $|\bar {t}-t|>m$
; that is, either
$|\bar {t}-t|>m$
; that is, either
![]() $t+m<\bar {t}$
or
$t+m<\bar {t}$
or
![]() $\bar {t}<t-m$
. We recall that
$\bar {t}<t-m$
. We recall that
![]() $pn-m\leqslant i_0\leqslant pn+m$
.
$pn-m\leqslant i_0\leqslant pn+m$
.
Assume, first, that
![]() $t+m<\bar {t}$
. By the definition of t and
$t+m<\bar {t}$
. By the definition of t and
![]() $\bar {t}$
, we see that
$\bar {t}$
, we see that
-
(i)
 $\min \{\ell , pn-\ell \} +m < \bar {t} \leqslant i_0-\ell $
and
$\min \{\ell , pn-\ell \} +m < \bar {t} \leqslant i_0-\ell $
and -
(ii)
 $\min \{\ell , pn-\ell \} +m < \bar {t} \leqslant pn-i_0+\ell $
.
$\min \{\ell , pn-\ell \} +m < \bar {t} \leqslant pn-i_0+\ell $
.
If
![]() $\ell \leqslant pn-\ell $
, then, by (ii), we obtain that
$\ell \leqslant pn-\ell $
, then, by (ii), we obtain that
![]() $\ell +m<pn-i_0+\ell $
, which is a contradiction; however, if
$\ell +m<pn-i_0+\ell $
, which is a contradiction; however, if
![]() $pn-\ell \leqslant \ell $
, then, by (i), we have
$pn-\ell \leqslant \ell $
, then, by (i), we have
![]() $pn-\ell +m<i_0-\ell $
which leads, again, to a contradiction.
$pn-\ell +m<i_0-\ell $
which leads, again, to a contradiction.
Next assume that
![]() $\bar {t}<t-m$
. Then,
$\bar {t}<t-m$
. Then,
-
(iii)
 $\min \{i_0-\ell , pn-i_0+\ell \} +m < t\leqslant \ell $
and
$\min \{i_0-\ell , pn-i_0+\ell \} +m < t\leqslant \ell $
and -
(iv)
 $\min \{i_0-\ell , pn-i_0+\ell \} +m < t \leqslant pn-\ell $
.
$\min \{i_0-\ell , pn-i_0+\ell \} +m < t \leqslant pn-\ell $
.
Consequently, if
![]() $i_0-\ell \leqslant pn-i_0+\ell $
, then, by (iv), we have
$i_0-\ell \leqslant pn-i_0+\ell $
, then, by (iv), we have
![]() $i_0-\ell +m< pn-\ell $
, which is a contradiction; finally, if
$i_0-\ell +m< pn-\ell $
, which is a contradiction; finally, if
![]() $pn-i_0+\ell \leqslant i_0-\ell $
, then, by (iii), we have
$pn-i_0+\ell \leqslant i_0-\ell $
, then, by (iii), we have
![]() $pn-i_0+\ell +m<\ell $
, which is also a contradiction.
$pn-i_0+\ell +m<\ell $
, which is also a contradiction.
By (7.11) and Claim 7.4, we conclude that
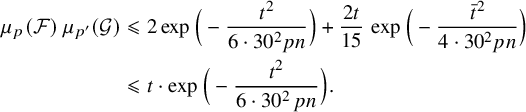 $$ \begin{align*} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) & \leqslant 2\exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big) + \frac{2t}{15}\, \exp\Big(- \frac{\bar{t}^2}{4\cdot 30^2 pn}\Big) \nonumber \\ & \leqslant t\cdot \exp\Big( - \frac{t^2}{6\cdot 30^2\, pn}\Big). \\[-44pt] \end{align*} $$
$$ \begin{align*} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) & \leqslant 2\exp\Big(- \frac{t^2}{6\cdot 30^2pn}\Big) + \frac{2t}{15}\, \exp\Big(- \frac{\bar{t}^2}{4\cdot 30^2 pn}\Big) \nonumber \\ & \leqslant t\cdot \exp\Big( - \frac{t^2}{6\cdot 30^2\, pn}\Big). \\[-44pt] \end{align*} $$
8 Optimality
We proceed to discuss the optimality of the bounds obtained by Theorem 1.1 and its extension, Corollary 7.3. Specifically, fix a positive integer n,
![]() $0<p\leqslant p'\leqslant 1-p$
and a nonnegative integer
$0<p\leqslant p'\leqslant 1-p$
and a nonnegative integer
![]() $\ell \leqslant pn$
, set
$\ell \leqslant pn$
, set
 $$ \begin{align} \varepsilon_n(p,p',\ell):= \max\!\big\{\varepsilon>0: & \, \mu_p(\mathcal{F})\,\mu_{p'}(\mathcal{G})\leqslant e^{-\varepsilon} \text{ for every pair of} \nonumber \\ & \ \ \ \ \ \ \ \ \ \ \text{nonempty families } (\mathcal{F},\mathcal{G})\in\mathrm{Forbid}(n,\{\ell\}) \big\}, \end{align} $$
$$ \begin{align} \varepsilon_n(p,p',\ell):= \max\!\big\{\varepsilon>0: & \, \mu_p(\mathcal{F})\,\mu_{p'}(\mathcal{G})\leqslant e^{-\varepsilon} \text{ for every pair of} \nonumber \\ & \ \ \ \ \ \ \ \ \ \ \text{nonempty families } (\mathcal{F},\mathcal{G})\in\mathrm{Forbid}(n,\{\ell\}) \big\}, \end{align} $$
and observe that our goal reduces to that of obtaining appropriate upper bounds for
![]() $\varepsilon _n(p,p',\ell )$
. To this end, we shall additionally assume thatFootnote
5
$\varepsilon _n(p,p',\ell )$
. To this end, we shall additionally assume thatFootnote
5
we will also use the following standard lower bounds of the biased measures of the tails of the binomial distribution (see, for example, [Reference AshAsh65, p. 115]).
Lemma 8.1. Let
![]() $k, n$
be positive integers, and let
$k, n$
be positive integers, and let
![]() $0<p\leqslant \frac 12$
. If
$0<p\leqslant \frac 12$
. If
![]() $k\leqslant pn$
, then
$k\leqslant pn$
, then
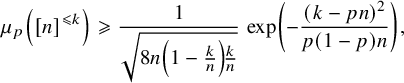 $$ \begin{align} \mu_p\left([n]^{\leqslant k}\right) \geqslant \frac{1}{\sqrt{8n\left(1-\frac{k}{n}\right)\!\frac{k}{n}}}\, \exp\left(-\frac{(k-pn)^2}{p(1-p)n}\right), \end{align} $$
$$ \begin{align} \mu_p\left([n]^{\leqslant k}\right) \geqslant \frac{1}{\sqrt{8n\left(1-\frac{k}{n}\right)\!\frac{k}{n}}}\, \exp\left(-\frac{(k-pn)^2}{p(1-p)n}\right), \end{align} $$
while if
![]() $pn\leqslant k< 2pn$
, then
$pn\leqslant k< 2pn$
, then
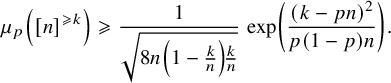 $$ \begin{align} \mu_p\left([n]^{\geqslant k}\right) \geqslant \frac{1}{\sqrt{8n\left(1-\frac{k}{n}\right)\!\frac{k}{n}}}\, \exp\left(\frac{(k-pn)^2}{p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_p\left([n]^{\geqslant k}\right) \geqslant \frac{1}{\sqrt{8n\left(1-\frac{k}{n}\right)\!\frac{k}{n}}}\, \exp\left(\frac{(k-pn)^2}{p(1-p)n}\right). \end{align} $$
8.1 The high-intersection case:
 $\ell \geqslant cpn$
for some constant
$\ell \geqslant cpn$
for some constant
 $c>0$
$c>0$
Set
![]() $\mathcal {F}:= [n]^{<\ell }$
and
$\mathcal {F}:= [n]^{<\ell }$
and
![]() $\mathcal {G}:= \{0,1\}^n$
. Then
$\mathcal {G}:= \{0,1\}^n$
. Then
![]() $(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,\{\ell \})$
and, moreover,
$(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,\{\ell \})$
and, moreover,
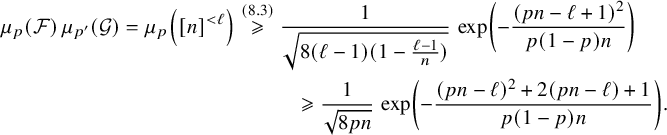 $$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) =\mu_p\left([n]^{<\ell}\right) & \stackrel{(8.3)}{\geqslant} \frac{1}{\sqrt{8(\ell-1)(1-\frac{\ell-1}{n})}}\, \exp\left(-\frac{(pn-\ell+1)^2}{p(1-p)n}\right) \nonumber \\ & \hspace{1cm} \geqslant \frac{1}{\sqrt{8pn}}\, \exp\left(-\frac{(pn-\ell)^2+2(pn-\ell)+1}{p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) =\mu_p\left([n]^{<\ell}\right) & \stackrel{(8.3)}{\geqslant} \frac{1}{\sqrt{8(\ell-1)(1-\frac{\ell-1}{n})}}\, \exp\left(-\frac{(pn-\ell+1)^2}{p(1-p)n}\right) \nonumber \\ & \hspace{1cm} \geqslant \frac{1}{\sqrt{8pn}}\, \exp\left(-\frac{(pn-\ell)^2+2(pn-\ell)+1}{p(1-p)n}\right). \end{align} $$
Next, set
![]() $C:= \max \{2,\frac {pn}{\ell }\} \leqslant \max \{2,\frac {1}{c}\}$
and
$C:= \max \{2,\frac {pn}{\ell }\} \leqslant \max \{2,\frac {1}{c}\}$
and
![]() $t:= \min \{\ell ,pn-\ell \}$
; notice that if
$t:= \min \{\ell ,pn-\ell \}$
; notice that if
![]() $\ell \geqslant \frac {pn}{2}$
, then
$\ell \geqslant \frac {pn}{2}$
, then
![]() $C=2$
and
$C=2$
and
![]() $t=pn-\ell $
, while if
$t=pn-\ell $
, while if
![]() $\ell <\frac {pn}{2}$
, then
$\ell <\frac {pn}{2}$
, then
![]() $C\leqslant \frac {1}{c}$
and
$C\leqslant \frac {1}{c}$
and
![]() $t=\ell $
. By (8.2), (8.5) and taking into account the previous observations, it is easy to see that
$t=\ell $
. By (8.2), (8.5) and taking into account the previous observations, it is easy to see that
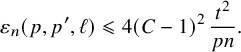 $$ \begin{align} \varepsilon_n(p,p',\ell) \leqslant 4(C-1)^2\, \frac{t^2}{pn}. \end{align} $$
$$ \begin{align} \varepsilon_n(p,p',\ell) \leqslant 4(C-1)^2\, \frac{t^2}{pn}. \end{align} $$
In particular, under (8.2), if
![]() $\ell \geqslant \frac {pn}{2}$
, then
$\ell \geqslant \frac {pn}{2}$
, then
![]() $\varepsilon _n(p,p',\ell ) \leqslant 4\, \frac {t^2}{pn}$
.
$\varepsilon _n(p,p',\ell ) \leqslant 4\, \frac {t^2}{pn}$
.
Remark 8.2. Note that if
![]() $\mathcal {F}:= [n]^{<\ell }$
, then
$\mathcal {F}:= [n]^{<\ell }$
, then
![]() $|A\cap B|\neq \ell $
for every
$|A\cap B|\neq \ell $
for every
![]() $A,B\in \mathcal {F}$
and, by (8.2) and (8.5), we have
$A,B\in \mathcal {F}$
and, by (8.2) and (8.5), we have
![]() $\mu _p(\mathcal {F})\geqslant \exp \big (- 4(C-1)^2\, \frac {t^2}{pn}\big )$
, where
$\mu _p(\mathcal {F})\geqslant \exp \big (- 4(C-1)^2\, \frac {t^2}{pn}\big )$
, where
![]() $C= \max \{2,\frac {pn}{\ell }\}$
. Thus, Theorem 1.1 and Corollary 7.3 are optimal in the regime
$C= \max \{2,\frac {pn}{\ell }\}$
. Thus, Theorem 1.1 and Corollary 7.3 are optimal in the regime
![]() $\ell \geqslant cpn$
also in the non-crossing case.
$\ell \geqslant cpn$
also in the non-crossing case.
8.2 The symmetric case:
 $p'=1-p$
$p'=1-p$
We will show that, under (8.2), we have
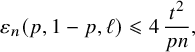 $$ \begin{align} \varepsilon_n(p,1-p,\ell) \leqslant 4\, \frac{t^2}{pn}, \end{align} $$
$$ \begin{align} \varepsilon_n(p,1-p,\ell) \leqslant 4\, \frac{t^2}{pn}, \end{align} $$
where, as usual,
![]() $t:= \min \{\ell ,pn-\ell \}$
; note that (8.7) includes the important special case
$t:= \min \{\ell ,pn-\ell \}$
; note that (8.7) includes the important special case
![]() $p=p'=\frac 12$
that corresponds to the uniform probability measure on
$p=p'=\frac 12$
that corresponds to the uniform probability measure on
![]() $\{0,1\}^n$
.
$\{0,1\}^n$
.
The subcase ‘
![]() $\ell \geqslant \frac {pn}{2}$
’ follows of course from (8.6), and so we may assume that
$\ell \geqslant \frac {pn}{2}$
’ follows of course from (8.6), and so we may assume that
![]() $\ell \leqslant \frac {pn}{2}$
. Set
$\ell \leqslant \frac {pn}{2}$
. Set
![]() $\mathcal {F}:= [n]^{>pn+\frac {\ell }{2}}$
and
$\mathcal {F}:= [n]^{>pn+\frac {\ell }{2}}$
and
![]() $\mathcal {G}:= [n]^{\geqslant (1-p)n+\frac {\ell }{2}}$
. Notice that
$\mathcal {G}:= [n]^{\geqslant (1-p)n+\frac {\ell }{2}}$
. Notice that
![]() $(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,\{\ell \})$
and
$(\mathcal {F},\mathcal {G})\in \mathrm {Forbid}(n,\{\ell \})$
and
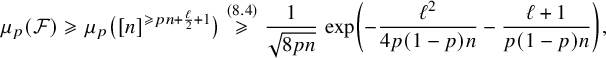 $$ \begin{align} \mu_{p}(\mathcal{F}) & \geqslant \mu_p\big([n]^{\geqslant pn+\frac{\ell}{2}+1}\big) \stackrel{({8.4})}{\geqslant} \frac{1}{\sqrt{8pn}}\, \exp\left(-\frac{\ell^2}{4p(1-p)n}-\frac{\ell+1}{p(1-p)n}\right), \end{align} $$
$$ \begin{align} \mu_{p}(\mathcal{F}) & \geqslant \mu_p\big([n]^{\geqslant pn+\frac{\ell}{2}+1}\big) \stackrel{({8.4})}{\geqslant} \frac{1}{\sqrt{8pn}}\, \exp\left(-\frac{\ell^2}{4p(1-p)n}-\frac{\ell+1}{p(1-p)n}\right), \end{align} $$
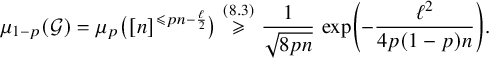 $$ \begin{align} \mu_{1-p}(\mathcal{G}) & = \mu_p\big([n]^{\leqslant pn-\frac{\ell}{2}}\big) \stackrel{(8.3)}{\geqslant} \frac{1}{\sqrt{8pn}}\, \exp\left(-\frac{\ell^2}{4p(1-p)n}\right). \end{align} $$
$$ \begin{align} \mu_{1-p}(\mathcal{G}) & = \mu_p\big([n]^{\leqslant pn-\frac{\ell}{2}}\big) \stackrel{(8.3)}{\geqslant} \frac{1}{\sqrt{8pn}}\, \exp\left(-\frac{\ell^2}{4p(1-p)n}\right). \end{align} $$
Therefore, using (8.2) and observing that in this case we have
![]() $t=\ell $
, we obtain that
$t=\ell $
, we obtain that
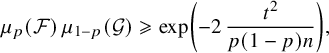 $$ \begin{align} \mu_p(\mathcal{F})\, \mu_{1-p}(\mathcal{G})\geqslant \exp\left(-2\, \frac{t^2}{p(1-p)n}\right), \end{align} $$
$$ \begin{align} \mu_p(\mathcal{F})\, \mu_{1-p}(\mathcal{G})\geqslant \exp\left(-2\, \frac{t^2}{p(1-p)n}\right), \end{align} $$
which clearly yields (8.7).
Remark 8.3. It is unclear whether the subgaussian bound (1.3) is optimal (modulo universal constants) in the low-intersection and asymmetric case – namely, when
![]() $\ell =o(pn)$
and
$\ell =o(pn)$
and
![]() $p'<1-p$
. The optimality of Theorem 1.1 in this regime is closely relatedFootnote
6
to the problem of obtaining sharp estimates of the product
$p'<1-p$
. The optimality of Theorem 1.1 in this regime is closely relatedFootnote
6
to the problem of obtaining sharp estimates of the product
![]() $\mu _p(\mathcal {F})\,\mu _p(\mathcal {G})$
of the biased measures of a pair of families
$\mu _p(\mathcal {F})\,\mu _p(\mathcal {G})$
of the biased measures of a pair of families
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
that are cross-
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
that are cross-
![]() $\ell $
-intersecting; that is, they satisfy
$\ell $
-intersecting; that is, they satisfy
![]() $|A\cap B|\geqslant \ell $
for every
$|A\cap B|\geqslant \ell $
for every
![]() $A\in \mathcal {F}$
and every
$A\in \mathcal {F}$
and every
![]() $B\in \mathcal {G}$
. The non-crossing case,
$B\in \mathcal {G}$
. The non-crossing case,
![]() $\mathcal {F}=\mathcal {G}$
, is completely understood thanks to the seminal work of Ahlswede–Khachatrian [Reference Ahlswede and KhachatrianAK97, Reference Ahlswede and KhachatrianAK99] and the more recent work of Filmus [Reference FilmusFi17]; see, also, [Reference FilmusFi13, Theorem 3.28] for some progress for general cross-intersecting families.
$\mathcal {F}=\mathcal {G}$
, is completely understood thanks to the seminal work of Ahlswede–Khachatrian [Reference Ahlswede and KhachatrianAK97, Reference Ahlswede and KhachatrianAK99] and the more recent work of Filmus [Reference FilmusFi17]; see, also, [Reference FilmusFi13, Theorem 3.28] for some progress for general cross-intersecting families.
9 Supersaturation
The main result in this section is a supersaturation version of Proposition 7.1, which is the analogue of [Reference Frankl and RödlFR87, Theorem 1.14]. To state it we need, first, to introduce some pieces of notation. Let n be a positive integer, let
![]() $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
, and let
$\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$
, and let
![]() $S\subseteq [n]$
. Given a nonnegative integer
$S\subseteq [n]$
. Given a nonnegative integer
![]() $\ell \leqslant n$
, we set
$\ell \leqslant n$
, we set
and, respectively,
We have the following theorem.
Theorem 9.1. Let
![]() $\ell ,k,n$
be positive integers with
$\ell ,k,n$
be positive integers with
![]() $\ell < k\leqslant \frac {n}{2}$
, and set
$\ell < k\leqslant \frac {n}{2}$
, and set
![]() $T:= \max \{\ell ,k-\ell \}$
. Also let
$T:= \max \{\ell ,k-\ell \}$
. Also let
![]() $\delta>0$
and assume that
$\delta>0$
and assume that
![]() $10^5 \sqrt {k} (\ln n)^{3/2}\leqslant \delta \leqslant \min \{\ell ,k-\ell \}$
. Finally, set
$10^5 \sqrt {k} (\ln n)^{3/2}\leqslant \delta \leqslant \min \{\ell ,k-\ell \}$
. Finally, set
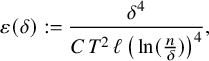 $$ \begin{align} \varepsilon(\delta):= \frac{\delta^4}{C\, T^2\, \ell\,\big(\ln(\frac{n}{\delta})\big)^4}, \end{align} $$
$$ \begin{align} \varepsilon(\delta):= \frac{\delta^4}{C\, T^2\, \ell\,\big(\ln(\frac{n}{\delta})\big)^4}, \end{align} $$
where
![]() $C:= 2^{8}\, 58^6\, 60^4$
. If
$C:= 2^{8}\, 58^6\, 60^4$
. If
![]() $\mathcal {F}\subseteq \binom {[n]}{k}$
and
$\mathcal {F}\subseteq \binom {[n]}{k}$
and
![]() $\mathcal {G}\subseteq \binom {[n]}{n-k}$
satisfy
$\mathcal {G}\subseteq \binom {[n]}{n-k}$
satisfy
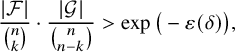 $$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot\frac{|\mathcal{G}|}{\binom{n}{n-k}}>\exp\big(-\varepsilon(\delta)\big), \end{align} $$
$$ \begin{align} \frac{|\mathcal{F}|}{\binom{n}{k}}\cdot\frac{|\mathcal{G}|}{\binom{n}{n-k}}>\exp\big(-\varepsilon(\delta)\big), \end{align} $$
then we have
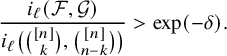 $$ \begin{align} \frac{i_{\ell}(\mathcal{F},\mathcal{G})}{i_{\ell}\big(\binom{[n]}{k},\binom{[n]}{n-k}\big)}> \exp\left(-\delta\right). \end{align} $$
$$ \begin{align} \frac{i_{\ell}(\mathcal{F},\mathcal{G})}{i_{\ell}\big(\binom{[n]}{k},\binom{[n]}{n-k}\big)}> \exp\left(-\delta\right). \end{align} $$
By Theorem 9.1, we obtain the following corollary.
Corollary 9.2. Let
![]() $\ell ,k,n, T, \delta $
be as in Theorem
9.1
and set
$\ell ,k,n, T, \delta $
be as in Theorem
9.1
and set
![]() $\varepsilon '(\delta ):= \frac {\delta ^4}{C\, T^2\, (k-\ell )\,(\ln (\frac {n}{\delta }))^4}$
, where
$\varepsilon '(\delta ):= \frac {\delta ^4}{C\, T^2\, (k-\ell )\,(\ln (\frac {n}{\delta }))^4}$
, where
![]() $C:= 2^{8}\, 58^6\, 60^4$
. If
$C:= 2^{8}\, 58^6\, 60^4$
. If
![]() $\mathcal {F}, \mathcal {G}\subseteq \binom {[n]}{k}$
satisfy
$\mathcal {F}, \mathcal {G}\subseteq \binom {[n]}{k}$
satisfy
![]() $\frac {|\mathcal {F}|}{\binom {n}{k}}\cdot \frac {|\mathcal {G}|}{\binom {n}{k}}>\exp \big (-\varepsilon '(\delta )\big )$
, then
$\frac {|\mathcal {F}|}{\binom {n}{k}}\cdot \frac {|\mathcal {G}|}{\binom {n}{k}}>\exp \big (-\varepsilon '(\delta )\big )$
, then
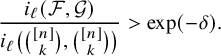 $$ \begin{align} \frac{i_{\ell}(\mathcal{F},\mathcal{G})}{i_{\ell}\big(\binom{[n]}{k},\binom{[n]}{k}\big)}> \exp\left(-\delta\right). \end{align} $$
$$ \begin{align} \frac{i_{\ell}(\mathcal{F},\mathcal{G})}{i_{\ell}\big(\binom{[n]}{k},\binom{[n]}{k}\big)}> \exp\left(-\delta\right). \end{align} $$
Proof. Set
![]() $\overline {\mathcal {G}}:= \big \{[n]\setminus G: G\in \mathcal {G}\big \}\subseteq \binom {[n]}{n-k}$
, and notice that
$\overline {\mathcal {G}}:= \big \{[n]\setminus G: G\in \mathcal {G}\big \}\subseteq \binom {[n]}{n-k}$
, and notice that
![]() $i_{\ell }(\mathcal {F},\mathcal {G})=i_{k-\ell }(\mathcal {F},\overline {\mathcal {G}})$
and
$i_{\ell }(\mathcal {F},\mathcal {G})=i_{k-\ell }(\mathcal {F},\overline {\mathcal {G}})$
and
![]() $i_{\ell }\big (\binom {[n]}{k},\binom {[n]}{k}\big )=i_{k-\ell }\big (\binom {[n]}{k},\binom {[n]}{n-k}\big )$
. The result follows from these observations and Theorem 9.1 applied to
$i_{\ell }\big (\binom {[n]}{k},\binom {[n]}{k}\big )=i_{k-\ell }\big (\binom {[n]}{k},\binom {[n]}{n-k}\big )$
. The result follows from these observations and Theorem 9.1 applied to
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\overline {\mathcal {G}}$
.
$\overline {\mathcal {G}}$
.
We proceed to the proof of Theorem 9.1.
Proof of Theorem 9.1.
We argue as in the proof of [Reference Frankl and RödlFR87, Theorem 1.14] with the main new ingredients being Theorem 1.1 and Proposition 7.1. For the reader’s convenience, we will first give a high level overview of the proof.
Our analysis is focused on the way the elements of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {G}$
are correlated with arbitrary sets of size
$\mathcal {G}$
are correlated with arbitrary sets of size
![]() $2\ell $
. More precisely, for every
$2\ell $
. More precisely, for every
![]() $A\in \binom {[n]}{2\ell }$
, we define
$A\in \binom {[n]}{2\ell }$
, we define
![]() $\mathcal {F}_A$
and
$\mathcal {F}_A$
and
![]() $\mathcal {G}_A$
to be the sets
$\mathcal {G}_A$
to be the sets
![]() $F\in \mathcal {F}$
and
$F\in \mathcal {F}$
and
![]() $G\in \mathcal {G}$
, respectively, whose intersection with A is roughly equal to
$G\in \mathcal {G}$
, respectively, whose intersection with A is roughly equal to
![]() $\ell $
. We shall informally refer to these sets as ‘good’.
$\ell $
. We shall informally refer to these sets as ‘good’.
The proof is then divided into three parts. In the first part, we show that there are many
![]() $A\in \binom {[n]}{2\ell }$
for which both
$A\in \binom {[n]}{2\ell }$
for which both
![]() $\mathcal {F}_A$
and
$\mathcal {F}_A$
and
![]() $\mathcal {G}_A$
are large – this is the content of Claim 9.3. In the second part, we work towards a contradiction, and we show that if
$\mathcal {G}_A$
are large – this is the content of Claim 9.3. In the second part, we work towards a contradiction, and we show that if
![]() $I_{\ell }(\mathcal {F},\mathcal {G})$
is small, then there exists
$I_{\ell }(\mathcal {F},\mathcal {G})$
is small, then there exists
![]() $A_0\in \binom {[n]}{2\ell }$
for which both
$A_0\in \binom {[n]}{2\ell }$
for which both
![]() $\mathcal {F}_{A_0}$
and
$\mathcal {F}_{A_0}$
and
![]() $\mathcal {G}_{A_0}$
are large, and at the same time, there are few number of pairs
$\mathcal {G}_{A_0}$
are large, and at the same time, there are few number of pairs
![]() $(F,G)\in \mathcal {F}_{A_0}\times \mathcal {G}_{A_0}$
whose intersection is of size
$(F,G)\in \mathcal {F}_{A_0}\times \mathcal {G}_{A_0}$
whose intersection is of size
![]() $\ell $
and the size of its trace on
$\ell $
and the size of its trace on
![]() $A_0$
is a specific proportion of
$A_0$
is a specific proportion of
![]() $\ell $
– this is achieved in Claim 9.4. Finally, in the third step of the proof, we arrive to a contradiction. Specifically, the properties of
$\ell $
– this is achieved in Claim 9.4. Finally, in the third step of the proof, we arrive to a contradiction. Specifically, the properties of
![]() $A_0$
imply that most of the ‘good’
$A_0$
imply that most of the ‘good’
![]() $F\in \mathcal {F}_{A_0}$
and
$F\in \mathcal {F}_{A_0}$
and
![]() $G\in \mathcal {G}_{A_0}$
are also bad in the sense that they do not form a pair whose intersection is of size
$G\in \mathcal {G}_{A_0}$
are also bad in the sense that they do not form a pair whose intersection is of size
![]() $\ell $
and its trace on
$\ell $
and its trace on
![]() $A_0$
has size specified by the previous step; this tension is enough to derive the contradiction.
$A_0$
has size specified by the previous step; this tension is enough to derive the contradiction.
We proceed to the details. We fix
![]() $\mathcal {F},\mathcal {G}$
that satisfy (9.4), and we assume, towards a contradiction, that (9.5) does not hold true. We set
$\mathcal {F},\mathcal {G}$
that satisfy (9.4), and we assume, towards a contradiction, that (9.5) does not hold true. We set
![]() $d(\mathcal {F}):= \frac {|\mathcal {F}|}{\binom {n}{k}}$
,
$d(\mathcal {F}):= \frac {|\mathcal {F}|}{\binom {n}{k}}$
,
![]() $d(\mathcal {G}):=\frac {|\mathcal {G}|}{\binom {n}{n-k}}$
and
$d(\mathcal {G}):=\frac {|\mathcal {G}|}{\binom {n}{n-k}}$
and
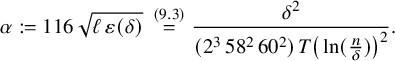 $$ \begin{align} \alpha:= 116\, \sqrt{\ell\,\varepsilon(\delta)}\, \stackrel{({9.3})}{=} \frac{\delta^2}{(2^3\,58^2\,60^2) \, T \big(\ln(\frac{n}{\delta})\big)^2}. \end{align} $$
$$ \begin{align} \alpha:= 116\, \sqrt{\ell\,\varepsilon(\delta)}\, \stackrel{({9.3})}{=} \frac{\delta^2}{(2^3\,58^2\,60^2) \, T \big(\ln(\frac{n}{\delta})\big)^2}. \end{align} $$
We also notice that for every
![]() $S\in \binom {[n]}{2\ell -\alpha }$
, we have
$S\in \binom {[n]}{2\ell -\alpha }$
, we have
-
•
 $i_{\ell }\big ( \binom {[n]}{k},\binom {[n]}{n-k}\big )=\binom {n}{k}\binom {k}{\ell }\binom {n-k}{n-k-\ell }$
,
$i_{\ell }\big ( \binom {[n]}{k},\binom {[n]}{n-k}\big )=\binom {n}{k}\binom {k}{\ell }\binom {n-k}{n-k-\ell }$
, -
•
 $i_{\ell }\big (S,\binom {[n]}{k}\big )=\binom {2\ell -\alpha }{\ell }\binom {n-2\ell +\alpha }{k-\ell }$
,
$i_{\ell }\big (S,\binom {[n]}{k}\big )=\binom {2\ell -\alpha }{\ell }\binom {n-2\ell +\alpha }{k-\ell }$
, -
•
 $i_{\ell }\big (S,\binom {[n]}{n-k}\big )=\binom {2\ell -\alpha }{\ell }\binom {n-2\ell +\alpha }{n-k-\ell }$
.
$i_{\ell }\big (S,\binom {[n]}{n-k}\big )=\binom {2\ell -\alpha }{\ell }\binom {n-2\ell +\alpha }{n-k-\ell }$
.
Next, we set
-
•
 $\mathcal {S}_{\mathcal {F}} := \big \{ S\in \binom {[n]}{2\ell -\alpha }: i_{\ell }(S,\mathcal {F})\geqslant K_{\mathcal {F}}\big \}$
and
$\mathcal {S}_{\mathcal {F}} := \big \{ S\in \binom {[n]}{2\ell -\alpha }: i_{\ell }(S,\mathcal {F})\geqslant K_{\mathcal {F}}\big \}$
and
 $\mathcal {S}_{\mathcal {G}}:= \big \{ S\in \binom {[n]}{2\ell -\alpha }: i_{\ell }(S,\mathcal {G})\geqslant K_{\mathcal {G}}\big \}$
,
$\mathcal {S}_{\mathcal {G}}:= \big \{ S\in \binom {[n]}{2\ell -\alpha }: i_{\ell }(S,\mathcal {G})\geqslant K_{\mathcal {G}}\big \}$
,
where
![]() $K_{\mathcal {F}}:= \frac {d(\mathcal {F})}{2} i_{\ell }\big (S,\binom {[n]}{k}\big )$
and
$K_{\mathcal {F}}:= \frac {d(\mathcal {F})}{2} i_{\ell }\big (S,\binom {[n]}{k}\big )$
and
![]() $K_{\mathcal {G}}:= \frac {d(\mathcal {G})}{2}i_{\ell }\big (S,\binom {[n]}{n-k}\big )$
. By [Reference Frankl and RödlFR87, Lemma 4.1], we have
$K_{\mathcal {G}}:= \frac {d(\mathcal {G})}{2}i_{\ell }\big (S,\binom {[n]}{n-k}\big )$
. By [Reference Frankl and RödlFR87, Lemma 4.1], we have
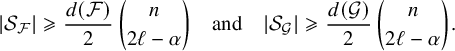 $$ \begin{align} |\mathcal{S}_{\mathcal{F}}| \geqslant \frac{d(\mathcal{F})}{2}\,\binom{n}{2\ell-\alpha} \ \ \ \text{ and } \ \ \ |\mathcal{S}_{\mathcal{G}}| \geqslant \frac{d(\mathcal{G})}{2}\, \binom{n}{2\ell-\alpha}. \end{align} $$
$$ \begin{align} |\mathcal{S}_{\mathcal{F}}| \geqslant \frac{d(\mathcal{F})}{2}\,\binom{n}{2\ell-\alpha} \ \ \ \text{ and } \ \ \ |\mathcal{S}_{\mathcal{G}}| \geqslant \frac{d(\mathcal{G})}{2}\, \binom{n}{2\ell-\alpha}. \end{align} $$
Moreover, for every
![]() $A\in \binom {[n]}{2\ell }$
, set
$A\in \binom {[n]}{2\ell }$
, set
-
•
 $\mathcal {F}_A:= \{F\in \mathcal {F}:\ell \leqslant |F\cap A|\leqslant \ell +\alpha \}$
and
$\mathcal {F}_A:= \{F\in \mathcal {F}:\ell \leqslant |F\cap A|\leqslant \ell +\alpha \}$
and
 $\mathcal {G}_A:= \{G\in \mathcal {G}:\ell \leqslant |G\cap A| \leqslant \ell +\alpha \}$
,
$\mathcal {G}_A:= \{G\in \mathcal {G}:\ell \leqslant |G\cap A| \leqslant \ell +\alpha \}$
,
and define the family
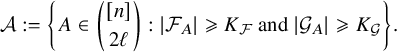 $$ \begin{align} \mathcal{A}:= \bigg\{A\in\binom{[n]}{2\ell}: |\mathcal{F}_A|\geqslant K_{\mathcal{F}} \text{ and } |\mathcal{G}_A| \geqslant K_{\mathcal{G}}\bigg\}. \end{align} $$
$$ \begin{align} \mathcal{A}:= \bigg\{A\in\binom{[n]}{2\ell}: |\mathcal{F}_A|\geqslant K_{\mathcal{F}} \text{ and } |\mathcal{G}_A| \geqslant K_{\mathcal{G}}\bigg\}. \end{align} $$
Claim 9.3. We have
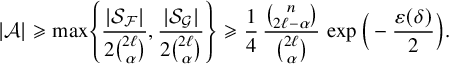 $$ \begin{align} |\mathcal{A}| \geqslant \max\left\{ \frac{|\mathcal{S}_{\mathcal{F}}|}{2\binom{2\ell}{\alpha}}, \frac{|\mathcal{S}_{\mathcal{G}}|}{2\binom{2\ell}{\alpha}}\right\} \geqslant \frac{1}{4}\, \frac{\binom{n}{2\ell-\alpha}}{\binom{2\ell}{\alpha}}\, \exp\Big(-\frac{\varepsilon(\delta)}{2}\Big). \end{align} $$
$$ \begin{align} |\mathcal{A}| \geqslant \max\left\{ \frac{|\mathcal{S}_{\mathcal{F}}|}{2\binom{2\ell}{\alpha}}, \frac{|\mathcal{S}_{\mathcal{G}}|}{2\binom{2\ell}{\alpha}}\right\} \geqslant \frac{1}{4}\, \frac{\binom{n}{2\ell-\alpha}}{\binom{2\ell}{\alpha}}\, \exp\Big(-\frac{\varepsilon(\delta)}{2}\Big). \end{align} $$
Proof of Claim 9.3.
We set
![]() $\mathcal {S}^*_{\mathcal {F}}:= \{S\in \mathcal {S}_{\mathcal {F}}:\exists S'\in \mathcal {S}_{\mathcal {G}} \text { with } |S'\setminus S|\leqslant \alpha \}$
, and we observe that
$\mathcal {S}^*_{\mathcal {F}}:= \{S\in \mathcal {S}_{\mathcal {F}}:\exists S'\in \mathcal {S}_{\mathcal {G}} \text { with } |S'\setminus S|\leqslant \alpha \}$
, and we observe that
![]() $(\mathcal {S}_{\mathcal {F}}\setminus \mathcal {S}^*_{\mathcal {F}},\mathcal {S}_{\mathcal {G}})\in \mathrm {Forbid}(n,\{2\ell -2\alpha \})$
. Also note that
$(\mathcal {S}_{\mathcal {F}}\setminus \mathcal {S}^*_{\mathcal {F}},\mathcal {S}_{\mathcal {G}})\in \mathrm {Forbid}(n,\{2\ell -2\alpha \})$
. Also note that
![]() $\varepsilon (\delta )\leqslant \frac {\ell }{2^{8}\, 58^6\, 60^4}$
, and so, by (9.7),
$\varepsilon (\delta )\leqslant \frac {\ell }{2^{8}\, 58^6\, 60^4}$
, and so, by (9.7),
![]() $\alpha =\min \{2\ell -2\alpha ,\alpha \}$
. (In fact,
$\alpha =\min \{2\ell -2\alpha ,\alpha \}$
. (In fact,
![]() $\alpha $
is significantly smaller than
$\alpha $
is significantly smaller than
![]() $\ell $
.) By part (i) of Proposition 7.1, we obtain thatFootnote
7
$\ell $
.) By part (i) of Proposition 7.1, we obtain thatFootnote
7
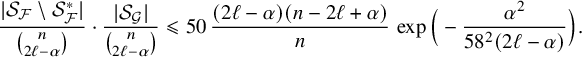 $$ \begin{align} \frac{|\mathcal{S}_{\mathcal{F}}\setminus\mathcal{S}^*_{\mathcal{F}}|}{\binom{n}{2\ell-\alpha}}\cdot \frac{|\mathcal{S}_{\mathcal{G}}|}{\binom{n}{2\ell-\alpha}} \leqslant 50\, \frac{(2\ell-\alpha)(n-2\ell+\alpha)}{n}\, \exp\Big(-\frac{\alpha^2}{58^2(2\ell-\alpha)}\Big). \end{align} $$
$$ \begin{align} \frac{|\mathcal{S}_{\mathcal{F}}\setminus\mathcal{S}^*_{\mathcal{F}}|}{\binom{n}{2\ell-\alpha}}\cdot \frac{|\mathcal{S}_{\mathcal{G}}|}{\binom{n}{2\ell-\alpha}} \leqslant 50\, \frac{(2\ell-\alpha)(n-2\ell+\alpha)}{n}\, \exp\Big(-\frac{\alpha^2}{58^2(2\ell-\alpha)}\Big). \end{align} $$
Plugging (9.4) and (9.8) into (9.11), we see that
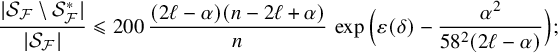 $$ \begin{align} \frac{|\mathcal{S}_{\mathcal{F}}\setminus \mathcal{S}^*_{\mathcal{F}}|}{|\mathcal{S}_{\mathcal{F}}|} \leqslant 200\, \frac{(2\ell-\alpha)(n-2\ell+\alpha)}{n}\, \exp\Big(\varepsilon(\delta)-\frac{\alpha^2}{58^2(2\ell-\alpha)}\Big); \end{align} $$
$$ \begin{align} \frac{|\mathcal{S}_{\mathcal{F}}\setminus \mathcal{S}^*_{\mathcal{F}}|}{|\mathcal{S}_{\mathcal{F}}|} \leqslant 200\, \frac{(2\ell-\alpha)(n-2\ell+\alpha)}{n}\, \exp\Big(\varepsilon(\delta)-\frac{\alpha^2}{58^2(2\ell-\alpha)}\Big); \end{align} $$
since
![]() $\varepsilon (\delta )-\frac {\alpha ^2}{58^2(2\ell -\alpha )}<-\varepsilon (\delta )$
, this in turn implies that
$\varepsilon (\delta )-\frac {\alpha ^2}{58^2(2\ell -\alpha )}<-\varepsilon (\delta )$
, this in turn implies that
![]() $|\mathcal {S}^*_{\mathcal {F}}|\geqslant \frac {|\mathcal {S}_{\mathcal {F}}|}{2}$
. Next, for every
$|\mathcal {S}^*_{\mathcal {F}}|\geqslant \frac {|\mathcal {S}_{\mathcal {F}}|}{2}$
. Next, for every
![]() $S\in \mathcal {S}^*_{\mathcal {F}}$
, we select
$S\in \mathcal {S}^*_{\mathcal {F}}$
, we select
![]() $A\in \binom {[n]}{2\ell }$
and
$A\in \binom {[n]}{2\ell }$
and
![]() $S'\in \mathcal {S}_{\mathcal {G}}$
such that
$S'\in \mathcal {S}_{\mathcal {G}}$
such that
![]() $S,S'\subseteq A$
, and we observe that for each such A, there exist at most
$S,S'\subseteq A$
, and we observe that for each such A, there exist at most
![]() $\binom {2\ell }{\alpha }$
such S’s. Therefore,
$\binom {2\ell }{\alpha }$
such S’s. Therefore,
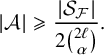 $$ \begin{align} |\mathcal{A}| \geqslant \frac{|\mathcal{S}_{\mathcal{F}}|}{2\binom{2\ell}{\alpha}}. \end{align} $$
$$ \begin{align} |\mathcal{A}| \geqslant \frac{|\mathcal{S}_{\mathcal{F}}|}{2\binom{2\ell}{\alpha}}. \end{align} $$
With identical arguments, we verify that
![]() $|\mathcal {A}| \geqslant \frac {|\mathcal {S}_{\mathcal {G}}|}{2\binom {2\ell }{\alpha }}$
. The last inequality in (9.10) follows from the previous estimates, (9.4) and (9.8). The proof of Claim 9.3 is completed.
$|\mathcal {A}| \geqslant \frac {|\mathcal {S}_{\mathcal {G}}|}{2\binom {2\ell }{\alpha }}$
. The last inequality in (9.10) follows from the previous estimates, (9.4) and (9.8). The proof of Claim 9.3 is completed.
Next, set
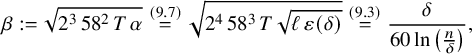 $$ \begin{align} \beta:= \sqrt{2^3\, 58^2\, T\,\alpha} \stackrel{({9.7})}{=} \sqrt{2^4\,58^3\, T\, \sqrt{\ell\, \varepsilon(\delta)}} \stackrel{(9.3)}{=} \frac{\delta}{60\ln\big(\frac{n}{\delta}\big)}, \end{align} $$
$$ \begin{align} \beta:= \sqrt{2^3\, 58^2\, T\,\alpha} \stackrel{({9.7})}{=} \sqrt{2^4\,58^3\, T\, \sqrt{\ell\, \varepsilon(\delta)}} \stackrel{(9.3)}{=} \frac{\delta}{60\ln\big(\frac{n}{\delta}\big)}, \end{align} $$
and note that
![]() $116\alpha \leqslant \beta \leqslant \frac {\ell }{30}$
and
$116\alpha \leqslant \beta \leqslant \frac {\ell }{30}$
and
![]() $10\beta \ln \big (\frac {n}{\beta }\big )\leqslant \delta $
. (Indeed,
$10\beta \ln \big (\frac {n}{\beta }\big )\leqslant \delta $
. (Indeed,
![]() $T=\max \{\ell ,k-\ell \}\geqslant \ell \geqslant \alpha $
, and so, by (9.14), we see that
$T=\max \{\ell ,k-\ell \}\geqslant \ell \geqslant \alpha $
, and so, by (9.14), we see that
![]() $\beta \geqslant 116\alpha $
; however, since
$\beta \geqslant 116\alpha $
; however, since
![]() $\delta \leqslant \min \{\ell ,k-\ell \}\leqslant \ell $
, by (9.14) again, we obtain that
$\delta \leqslant \min \{\ell ,k-\ell \}\leqslant \ell $
, by (9.14) again, we obtain that
![]() $\beta \leqslant \frac {\ell }{30}$
.) Moreover, for every
$\beta \leqslant \frac {\ell }{30}$
.) Moreover, for every
![]() $A\in \binom {[n]}{2\ell }$
, set
$A\in \binom {[n]}{2\ell }$
, set
For every
![]() $(F,G)\in I_{\ell }(\mathcal {F},\mathcal {G})$
, we can bound the number of
$(F,G)\in I_{\ell }(\mathcal {F},\mathcal {G})$
, we can bound the number of
![]() $A\in \mathcal {A}$
for which
$A\in \mathcal {A}$
for which
![]() $(F,G)$
contributes to
$(F,G)$
contributes to
![]() $y_A$
by counting the ways we can first select
$y_A$
by counting the ways we can first select
![]() $F\cap G \cap A$
, then
$F\cap G \cap A$
, then
![]() $F\cap ([n]\setminus G)\cap A$
, then
$F\cap ([n]\setminus G)\cap A$
, then
![]() $([n]\setminus F)\cap G\cap A$
, and finally
$([n]\setminus F)\cap G\cap A$
, and finally
![]() $([n]\setminus F)\cap ([n]\setminus G)\cap A$
. In particular, we have
$([n]\setminus F)\cap ([n]\setminus G)\cap A$
. In particular, we have
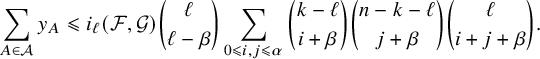 $$ \begin{align} \sum_{A\in\mathcal{A}} y_{A} \leqslant i_{\ell}(\mathcal{F},\mathcal{G}) \binom{\ell}{\ell-\beta} \sum_{0\leqslant i, j\leqslant \alpha} \binom{k-\ell}{i+\beta} \binom{n-k-\ell}{j+\beta} \binom{\ell}{i+j+\beta}. \end{align} $$
$$ \begin{align} \sum_{A\in\mathcal{A}} y_{A} \leqslant i_{\ell}(\mathcal{F},\mathcal{G}) \binom{\ell}{\ell-\beta} \sum_{0\leqslant i, j\leqslant \alpha} \binom{k-\ell}{i+\beta} \binom{n-k-\ell}{j+\beta} \binom{\ell}{i+j+\beta}. \end{align} $$
Claim 9.4. Given our starting assumption that (9.5) does not hold true, we may select
![]() $A_0\in \mathcal {A}$
such that
$A_0\in \mathcal {A}$
such that
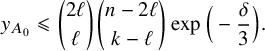 $$ \begin{align} y_{A_0} \leqslant \binom{2\ell}{\ell}\binom{n-2\ell}{k-\ell} \exp\Big(-\frac{\delta}{3}\Big). \end{align} $$
$$ \begin{align} y_{A_0} \leqslant \binom{2\ell}{\ell}\binom{n-2\ell}{k-\ell} \exp\Big(-\frac{\delta}{3}\Big). \end{align} $$
Proof of Claim 9.4.
First observe that
-
•
 $i_{\ell } \big (\binom {[n]}{k},\binom {[n]}{n-k}\big )= \binom {n}{k}\binom {k}{\ell }\binom {n-k}{n-k-\ell }=\binom {2\ell }{\ell }\binom {n-2\ell }{k-\ell }\binom {n}{2\ell }$
.
$i_{\ell } \big (\binom {[n]}{k},\binom {[n]}{n-k}\big )= \binom {n}{k}\binom {k}{\ell }\binom {n-k}{n-k-\ell }=\binom {2\ell }{\ell }\binom {n-2\ell }{k-\ell }\binom {n}{2\ell }$
.
Next, using (i) our starting assumption that (9.5) does not hold true, (ii) the fact that
![]() $\alpha +\beta \leqslant 2\alpha +\beta \leqslant \frac 12\min \{\ell ,k-\ell ,n-k-\ell \}$
, and (iii) the fact that the function
$\alpha +\beta \leqslant 2\alpha +\beta \leqslant \frac 12\min \{\ell ,k-\ell ,n-k-\ell \}$
, and (iii) the fact that the function
![]() $x\mapsto \binom {y}{x}$
is increasing for
$x\mapsto \binom {y}{x}$
is increasing for
![]() $x\leqslant \frac {y}{2}$
, we obtain that
$x\leqslant \frac {y}{2}$
, we obtain that
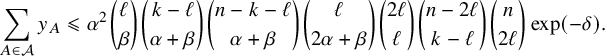 $$ \begin{align} \sum_{A\in\mathcal{A}}y_{A}\leqslant \alpha^2\binom{\ell}{\beta}\binom{k-\ell}{\alpha+\beta} \binom{n-k-\ell}{\alpha+\beta}\binom{\ell}{2\alpha+\beta} \binom{2\ell}{\ell}\binom{n-2\ell}{k-\ell}\binom{n}{2\ell}\exp(-\delta). \end{align} $$
$$ \begin{align} \sum_{A\in\mathcal{A}}y_{A}\leqslant \alpha^2\binom{\ell}{\beta}\binom{k-\ell}{\alpha+\beta} \binom{n-k-\ell}{\alpha+\beta}\binom{\ell}{2\alpha+\beta} \binom{2\ell}{\ell}\binom{n-2\ell}{k-\ell}\binom{n}{2\ell}\exp(-\delta). \end{align} $$
Therefore, by (9.10), there exists
![]() $A_0\in \mathcal {A}$
such that
$A_0\in \mathcal {A}$
such that
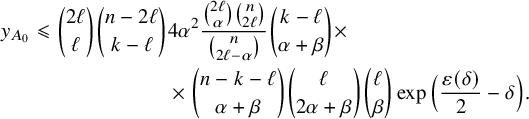 $$ \begin{align} y_{A_0} \leqslant \binom{2\ell}{\ell}\binom{n-2\ell}{k-\ell} & 4\alpha^2 \frac{\binom{2\ell}{\alpha}\binom{n}{2\ell}}{\binom{n}{2\ell-\alpha}} \binom{k-\ell}{\alpha+\beta} \times \nonumber \\ & \times \binom{n-k-\ell}{\alpha+\beta} \binom{\ell}{2\alpha+\beta}\binom{\ell}{\beta}\exp\Big(\frac{\varepsilon(\delta)}{2}-\delta\Big). \end{align} $$
$$ \begin{align} y_{A_0} \leqslant \binom{2\ell}{\ell}\binom{n-2\ell}{k-\ell} & 4\alpha^2 \frac{\binom{2\ell}{\alpha}\binom{n}{2\ell}}{\binom{n}{2\ell-\alpha}} \binom{k-\ell}{\alpha+\beta} \times \nonumber \\ & \times \binom{n-k-\ell}{\alpha+\beta} \binom{\ell}{2\alpha+\beta}\binom{\ell}{\beta}\exp\Big(\frac{\varepsilon(\delta)}{2}-\delta\Big). \end{align} $$
Now we claim that
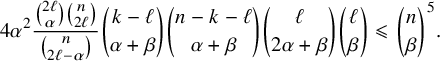 $$ \begin{align} 4\alpha^2\frac{\binom{2\ell}{\alpha}\binom{n}{2\ell}}{\binom{n}{2\ell-\alpha}} \binom{k-\ell}{\alpha+\beta}\binom{n-k-\ell}{\alpha+\beta} \binom{\ell}{2\alpha+\beta}\binom{\ell}{\beta} \leqslant \binom{n}{\beta}^5. \end{align} $$
$$ \begin{align} 4\alpha^2\frac{\binom{2\ell}{\alpha}\binom{n}{2\ell}}{\binom{n}{2\ell-\alpha}} \binom{k-\ell}{\alpha+\beta}\binom{n-k-\ell}{\alpha+\beta} \binom{\ell}{2\alpha+\beta}\binom{\ell}{\beta} \leqslant \binom{n}{\beta}^5. \end{align} $$
To this end, notice that
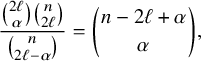 $$ \begin{align} \frac{\binom{2\ell}{\alpha}\binom{n}{2\ell}}{\binom{n}{2\ell-\alpha}}=\binom{n-2\ell+\alpha}{\alpha}, \end{align} $$
$$ \begin{align} \frac{\binom{2\ell}{\alpha}\binom{n}{2\ell}}{\binom{n}{2\ell-\alpha}}=\binom{n-2\ell+\alpha}{\alpha}, \end{align} $$
and consequently,
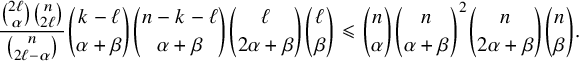 $$ \begin{align} \frac{\binom{2\ell}{\alpha}\binom{n}{2\ell}}{\binom{n}{2\ell-\alpha}} \binom{k-\ell}{\alpha+\beta}\binom{n-k-\ell}{\alpha+\beta} \binom{\ell}{2\alpha+\beta}\binom{\ell}{\beta} \leqslant \binom{n}{\alpha} \binom{n}{\alpha+\beta}^2 \binom{n}{2\alpha+\beta}\binom{n}{\beta}. \end{align} $$
$$ \begin{align} \frac{\binom{2\ell}{\alpha}\binom{n}{2\ell}}{\binom{n}{2\ell-\alpha}} \binom{k-\ell}{\alpha+\beta}\binom{n-k-\ell}{\alpha+\beta} \binom{\ell}{2\alpha+\beta}\binom{\ell}{\beta} \leqslant \binom{n}{\alpha} \binom{n}{\alpha+\beta}^2 \binom{n}{2\alpha+\beta}\binom{n}{\beta}. \end{align} $$
Moreover, by (2.6) and the fact that
![]() $2\alpha +\beta \leqslant \frac {\ell }{10}\leqslant \frac {n}{4}$
,
$2\alpha +\beta \leqslant \frac {\ell }{10}\leqslant \frac {n}{4}$
,
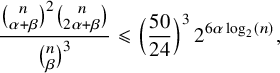 $$ \begin{align} \frac{\binom{n}{\alpha+\beta}^2 \binom{n}{2\alpha+\beta}}{\binom{n}{\beta}^3} \leqslant \Big(\frac{50}{24}\Big)^3 \, 2^{6\alpha\log_2(n)}, \end{align} $$
$$ \begin{align} \frac{\binom{n}{\alpha+\beta}^2 \binom{n}{2\alpha+\beta}}{\binom{n}{\beta}^3} \leqslant \Big(\frac{50}{24}\Big)^3 \, 2^{6\alpha\log_2(n)}, \end{align} $$
and similarly, since
![]() $\alpha \leqslant \frac {\beta }{116}$
,
$\alpha \leqslant \frac {\beta }{116}$
,
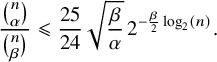 $$ \begin{align} \frac{\binom{n}{\alpha}}{\binom{n}{\beta}} \leqslant \frac{25}{24}\, \sqrt{\frac{\beta}{\alpha}}\, 2^{-\frac{\beta}{2}\log_2(n)}. \end{align} $$
$$ \begin{align} \frac{\binom{n}{\alpha}}{\binom{n}{\beta}} \leqslant \frac{25}{24}\, \sqrt{\frac{\beta}{\alpha}}\, 2^{-\frac{\beta}{2}\log_2(n)}. \end{align} $$
After observing that
we conclude that (9.20) is satisfied.
Summing up, we see that there exists
![]() $A_0\in \mathcal {A}$
such that
$A_0\in \mathcal {A}$
such that
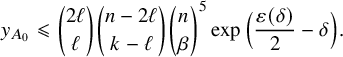 $$ \begin{align} y_{A_0}\leqslant \binom{2\ell}{\ell}\binom{n-2\ell}{k-\ell} \binom{n}{\beta}^5 \exp\Big(\frac{\varepsilon(\delta)}{2}-\delta\Big). \end{align} $$
$$ \begin{align} y_{A_0}\leqslant \binom{2\ell}{\ell}\binom{n-2\ell}{k-\ell} \binom{n}{\beta}^5 \exp\Big(\frac{\varepsilon(\delta)}{2}-\delta\Big). \end{align} $$
The claim follows from this estimate together with (2.6), and invoking the choices of
![]() $\varepsilon (\delta )$
and
$\varepsilon (\delta )$
and
![]() $\beta $
in (9.3) and (9.14), respectively.
$\beta $
in (9.3) and (9.14), respectively.
Let
![]() $A_0\in \mathcal {A}$
be as in Claim 9.4. We will show that
$A_0\in \mathcal {A}$
be as in Claim 9.4. We will show that
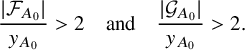 $$ \begin{align} \frac{|\mathcal{F}_{A_0}|}{y_{A_0}}>2 \ \ \ \text{ and } \ \ \ \frac{|\mathcal{G}_{A_0}|}{y_{A_0}}>2. \end{align} $$
$$ \begin{align} \frac{|\mathcal{F}_{A_0}|}{y_{A_0}}>2 \ \ \ \text{ and } \ \ \ \frac{|\mathcal{G}_{A_0}|}{y_{A_0}}>2. \end{align} $$
Indeed, by (9.9) and the choices of
![]() $K_{\mathcal {F}}$
and
$K_{\mathcal {F}}$
and
![]() $K_{\mathcal {G}}$
, we have
$K_{\mathcal {G}}$
, we have
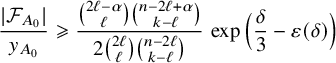 $$ \begin{align} \frac{|\mathcal{F}_{A_0}|}{y_{A_0}}\geqslant \frac{\binom{2\ell-\alpha}{\ell}\binom{n-2\ell+\alpha}{k-\ell}}{2\binom{2\ell}{\ell} \binom{n-2\ell}{k-\ell}} \, \exp\Big(\frac{\delta}{3}-\varepsilon(\delta)\Big) \end{align} $$
$$ \begin{align} \frac{|\mathcal{F}_{A_0}|}{y_{A_0}}\geqslant \frac{\binom{2\ell-\alpha}{\ell}\binom{n-2\ell+\alpha}{k-\ell}}{2\binom{2\ell}{\ell} \binom{n-2\ell}{k-\ell}} \, \exp\Big(\frac{\delta}{3}-\varepsilon(\delta)\Big) \end{align} $$
and
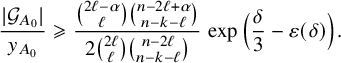 $$ \begin{align} \frac{|\mathcal{G}_{A_0}|}{y_{A_0}}\geqslant \frac{\binom{2\ell-\alpha}{\ell}\binom{n-2\ell+\alpha}{n-k-\ell}}{2\binom{2\ell}{\ell} \binom{n-2\ell}{n-k-\ell}}\, \exp\Big(\frac{\delta}{3}-\varepsilon(\delta)\Big). \end{align} $$
$$ \begin{align} \frac{|\mathcal{G}_{A_0}|}{y_{A_0}}\geqslant \frac{\binom{2\ell-\alpha}{\ell}\binom{n-2\ell+\alpha}{n-k-\ell}}{2\binom{2\ell}{\ell} \binom{n-2\ell}{n-k-\ell}}\, \exp\Big(\frac{\delta}{3}-\varepsilon(\delta)\Big). \end{align} $$
Noticing that
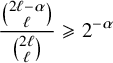 $$ \begin{align} \frac{\binom{2\ell-\alpha}{\ell}}{\binom{2\ell}{\ell}}\geqslant 2^{-\alpha} \end{align} $$
$$ \begin{align} \frac{\binom{2\ell-\alpha}{\ell}}{\binom{2\ell}{\ell}}\geqslant 2^{-\alpha} \end{align} $$
and using the previous two estimates and the choice of
![]() $\alpha $
in (9.7), we see that (9.27) is satisfied.
$\alpha $
in (9.7), we see that (9.27) is satisfied.
We introduce the families
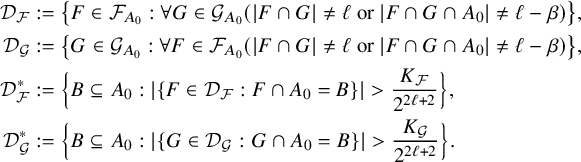 $$ \begin{align*} \mathcal{D}_{\mathcal{F}} & := \big\{F\in\mathcal{F}_{A_0}: \forall G\in\mathcal{G}_{A_0} \left(|F\cap G|\neq \ell \text{ or } |F\cap G\cap A_0|\neq \ell-\beta\right)\big\}, \\ \mathcal{D}_{\mathcal{G}} & := \big\{G\in\mathcal{G}_{A_0}: \forall F\in\mathcal{F}_{A_0} \left(|F\cap G|\neq \ell \text{ or } |F\cap G\cap A_0|\neq \ell-\beta\right)\big\}, \\ \mathcal{D}_{\mathcal{F}}^* & := \Big\{B\subseteq A_0: |\{F\in\mathcal{D}_{\mathcal{F}}:F\cap A_0=B\}|>\frac{K_{\mathcal{F}}}{2^{2\ell+2}}\Big\}, \\ \mathcal{D}_{\mathcal{G}}^* & := \Big\{B\subseteq A_0: |\{G\in\mathcal{D}_{\mathcal{G}}: G\cap A_0=B\}|>\frac{K_{\mathcal{G}}}{2^{2\ell+2}}\Big\}. \end{align*} $$
$$ \begin{align*} \mathcal{D}_{\mathcal{F}} & := \big\{F\in\mathcal{F}_{A_0}: \forall G\in\mathcal{G}_{A_0} \left(|F\cap G|\neq \ell \text{ or } |F\cap G\cap A_0|\neq \ell-\beta\right)\big\}, \\ \mathcal{D}_{\mathcal{G}} & := \big\{G\in\mathcal{G}_{A_0}: \forall F\in\mathcal{F}_{A_0} \left(|F\cap G|\neq \ell \text{ or } |F\cap G\cap A_0|\neq \ell-\beta\right)\big\}, \\ \mathcal{D}_{\mathcal{F}}^* & := \Big\{B\subseteq A_0: |\{F\in\mathcal{D}_{\mathcal{F}}:F\cap A_0=B\}|>\frac{K_{\mathcal{F}}}{2^{2\ell+2}}\Big\}, \\ \mathcal{D}_{\mathcal{G}}^* & := \Big\{B\subseteq A_0: |\{G\in\mathcal{D}_{\mathcal{G}}: G\cap A_0=B\}|>\frac{K_{\mathcal{G}}}{2^{2\ell+2}}\Big\}. \end{align*} $$
Note that
![]() $|\mathcal {D}_{\mathcal {F}}|>\frac {K_{\mathcal {F}}}{2}$
and
$|\mathcal {D}_{\mathcal {F}}|>\frac {K_{\mathcal {F}}}{2}$
and
![]() $|\mathcal {D}_{\mathcal {G}}|>\frac {K_{\mathcal {G}}}{2}$
, and so, there are
$|\mathcal {D}_{\mathcal {G}}|>\frac {K_{\mathcal {G}}}{2}$
, and so, there are
![]() $|D_{\mathcal {F}}|>\frac {K_{\mathcal {F}}}{2}$
pairs
$|D_{\mathcal {F}}|>\frac {K_{\mathcal {F}}}{2}$
pairs
![]() $(F,B)$
such that
$(F,B)$
such that
![]() $F\cap A_0=B$
. For every
$F\cap A_0=B$
. For every
![]() $F\in \mathcal {D}_{\mathcal {F}}$
, we have that
$F\in \mathcal {D}_{\mathcal {F}}$
, we have that
![]() $\ell \leqslant |F\cap A_0|\leqslant \ell +\alpha $
; therefore, there are at most
$\ell \leqslant |F\cap A_0|\leqslant \ell +\alpha $
; therefore, there are at most
![]() $2^{2\ell -1}$
such choices for
$2^{2\ell -1}$
such choices for
![]() $B=F\cap A_0$
. However, for every such B, there at most
$B=F\cap A_0$
. However, for every such B, there at most
![]() $\binom {n-2\ell }{k-\ell }$
choices for
$\binom {n-2\ell }{k-\ell }$
choices for
![]() $F\in D_{\mathcal {F}}$
. Hence,
$F\in D_{\mathcal {F}}$
. Hence,
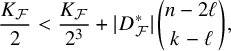 $$ \begin{align} \frac{K_{\mathcal{F}}}{2}< \frac{K_{\mathcal{F}}}{2^3}+|D_{\mathcal{F}}^*|\binom{n-2\ell}{k-\ell}, \end{align} $$
$$ \begin{align} \frac{K_{\mathcal{F}}}{2}< \frac{K_{\mathcal{F}}}{2^3}+|D_{\mathcal{F}}^*|\binom{n-2\ell}{k-\ell}, \end{align} $$
and similarly for
![]() $\mathcal {G}$
. Consequently, we have
$\mathcal {G}$
. Consequently, we have
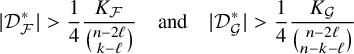 $$ \begin{align} |\mathcal{D}_{\mathcal{F}}^*|>\frac{1}{4} \frac{K_{\mathcal{F}}}{\binom{n-2\ell}{k-\ell}} \ \ \ \text{ and } \ \ \ |\mathcal{D}_{\mathcal{G}}^*|>\frac14 \frac{K_{\mathcal{G}}}{\binom{n-2\ell}{n-k-\ell}} \end{align} $$
$$ \begin{align} |\mathcal{D}_{\mathcal{F}}^*|>\frac{1}{4} \frac{K_{\mathcal{F}}}{\binom{n-2\ell}{k-\ell}} \ \ \ \text{ and } \ \ \ |\mathcal{D}_{\mathcal{G}}^*|>\frac14 \frac{K_{\mathcal{G}}}{\binom{n-2\ell}{n-k-\ell}} \end{align} $$
that implies that
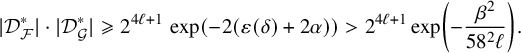 $$ \begin{align} |\mathcal{D}_{\mathcal{F}}^*|\cdot |\mathcal{D}_{\mathcal{G}}^*| \geqslant 2^{4\ell+1}\, \exp\left(-2(\varepsilon(\delta)+2\alpha)\right)> 2^{4\ell+1}\exp\left(-\frac{\beta^2}{58^2\ell}\right). \end{align} $$
$$ \begin{align} |\mathcal{D}_{\mathcal{F}}^*|\cdot |\mathcal{D}_{\mathcal{G}}^*| \geqslant 2^{4\ell+1}\, \exp\left(-2(\varepsilon(\delta)+2\alpha)\right)> 2^{4\ell+1}\exp\left(-\frac{\beta^2}{58^2\ell}\right). \end{align} $$
By Theorem 1.1 applied for ‘
![]() $p=p'=\frac 12$
’, there exist
$p=p'=\frac 12$
’, there exist
![]() $B_1\in \mathcal {D}_{\mathcal {F}}^*$
and
$B_1\in \mathcal {D}_{\mathcal {F}}^*$
and
![]() $B_2\in \mathcal {D}_{\mathcal {G}}^*$
such that
$B_2\in \mathcal {D}_{\mathcal {G}}^*$
such that
![]() $\left |B_1\cap B_2\right |=\ell -\beta $
. Next, set
$\left |B_1\cap B_2\right |=\ell -\beta $
. Next, set
![]() $x:= |B_1|-\ell $
,
$x:= |B_1|-\ell $
,
![]() $\mathcal {X}:= \{F\setminus A_0:F\in \mathcal {D}_{\mathcal {F}} \text { and } F\cap A_0=B_1\}$
and
$\mathcal {X}:= \{F\setminus A_0:F\in \mathcal {D}_{\mathcal {F}} \text { and } F\cap A_0=B_1\}$
and
![]() $y:= |B_2|-\ell $
,
$y:= |B_2|-\ell $
,
![]() $\mathcal {Y}:= \{G\setminus A_0:G\in \mathcal {D}_{\mathcal {G}} \text { and } G\cap A_0=B_2\}$
. Observe that
$\mathcal {Y}:= \{G\setminus A_0:G\in \mathcal {D}_{\mathcal {G}} \text { and } G\cap A_0=B_2\}$
. Observe that
![]() $0\leqslant x,y\leqslant \alpha $
and
$0\leqslant x,y\leqslant \alpha $
and
Therefore, by our assumption on
![]() $\delta $
and the choice of
$\delta $
and the choice of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
,
$\beta $
,
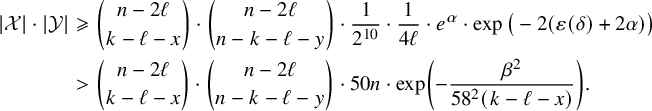 $$ \begin{align} |\mathcal{X}|\cdot |\mathcal{Y}| & \geqslant \binom{n-2\ell}{k-\ell-x}\cdot \binom{n-2\ell}{n-k-\ell-y}\cdot \frac{1}{2^{10}}\cdot \frac{1}{4\ell}\cdot e^\alpha\cdot \exp\big(-2(\varepsilon(\delta)+2\alpha)\big) \nonumber \\ &> \binom{n-2\ell}{k-\ell-x}\cdot \binom{n-2\ell}{n-k-\ell-y} \cdot 50n\cdot \exp\left(-\frac{\beta^2}{58^2(k-\ell-x)}\right). \end{align} $$
$$ \begin{align} |\mathcal{X}|\cdot |\mathcal{Y}| & \geqslant \binom{n-2\ell}{k-\ell-x}\cdot \binom{n-2\ell}{n-k-\ell-y}\cdot \frac{1}{2^{10}}\cdot \frac{1}{4\ell}\cdot e^\alpha\cdot \exp\big(-2(\varepsilon(\delta)+2\alpha)\big) \nonumber \\ &> \binom{n-2\ell}{k-\ell-x}\cdot \binom{n-2\ell}{n-k-\ell-y} \cdot 50n\cdot \exp\left(-\frac{\beta^2}{58^2(k-\ell-x)}\right). \end{align} $$
By part (i) of Proposition 7.1, there exist
![]() $H_1\in \mathcal {X}$
,
$H_1\in \mathcal {X}$
,
![]() $H_2\in \mathcal {Y}$
such that
$H_2\in \mathcal {Y}$
such that
![]() $\left |H_1\cap H_2\right |=\beta $
. It follows that
$\left |H_1\cap H_2\right |=\beta $
. It follows that
![]() $(B_1\cup H_1,B_2\cup H_2)\in (\mathcal {F}_{A_0}\times \mathcal {G}_{A_0})\cap (\mathcal {D}_{\mathcal {F}}\times \mathcal {D}_{\mathcal {G}})$
, which clearly leads to a contradiction.
$(B_1\cup H_1,B_2\cup H_2)\in (\mathcal {F}_{A_0}\times \mathcal {G}_{A_0})\cap (\mathcal {D}_{\mathcal {F}}\times \mathcal {D}_{\mathcal {G}})$
, which clearly leads to a contradiction.
Acknowledgements
The authors would like to thank the anonymous referee for numerous comments, remarks and suggestions that helped us improve the exposition.
Competing interest
The authors have no competing interests to declare.
Funding statement
The research was supported by the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the ‘2nd Call for H.F.R.I. Research Projects to support Faculty Members & Researchers’ (Project Number: HFRI-FM20-02717).