No CrossRef data available.
Article contents
REPETITIVE EQUIVALENCES AND TILTING THEORY
Published online by Cambridge University Press: 06 December 2019
Abstract
Let 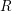 $R$ be a ring and
$R$ be a ring and 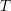 $T$ be a good Wakamatsu-tilting module with
$T$ be a good Wakamatsu-tilting module with 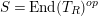 $S=\text{End}(T_{R})^{op}$. We prove that
$S=\text{End}(T_{R})^{op}$. We prove that 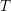 $T$ induces an equivalence between stable repetitive categories of
$T$ induces an equivalence between stable repetitive categories of 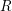 $R$ and
$R$ and 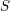 $S$ (i.e., stable module categories of repetitive algebras
$S$ (i.e., stable module categories of repetitive algebras  $\hat{R}$ and
$\hat{R}$ and 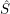 ${\hat{S}}$). This shows that good Wakamatsu-tilting modules seem to behave in Morita theory of stable repetitive categories as that tilting modules of finite projective dimension behave in Morita theory of derived categories.
${\hat{S}}$). This shows that good Wakamatsu-tilting modules seem to behave in Morita theory of stable repetitive categories as that tilting modules of finite projective dimension behave in Morita theory of derived categories.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © 2019 Foundation Nagoya Mathematical Journal
Footnotes
The author is supported by the Natural Science Foundation of China (Grant No. 11771212) and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.


