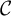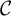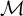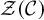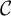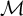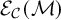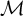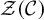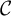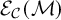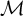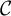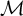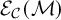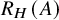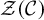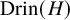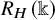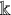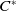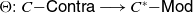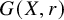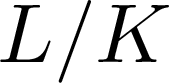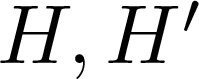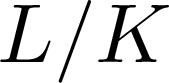Refine listing
Actions for selected content:
71 results in 16Txx
Moduli of objects in finite length abelian categories
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic structure of Dyson–Schwinger equations with multiple insertion places
- Part of
-
- Journal:
- Canadian Mathematical Communications / Volume 1 / 2025
- Published online by Cambridge University Press:
- 29 August 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FROBENIUS-PERRON DIMENSIONS OF CONJUGACY CLASSES AND AN ITO-MICHLER-TYPE RESULT IN MODULAR FUSION CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 28 August 2025, pp. 2523-2542
- Print publication:
- November 2025
-
- Article
- Export citation
Colored interacting particle systems on the ring: Stationary measures from Yang–Baxter equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1855-1922
- Print publication:
- August 2025
-
- Article
- Export citation
Reflective centers of module categories and quantum K-matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 June 2025, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Homological full-and-faithfulness of comodule inclusion and contramodule forgetful functors
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Matched pairs and Yetter–Drinfeld braces
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 April 2025, pp. 1-37
-
- Article
- Export citation
Constructing skew left braces whose additive group has trivial centre
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 30 January 2025, pp. 797-804
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From actions of an abelian group on itself to left braces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 65-79
- Print publication:
- January 2025
-
- Article
- Export citation
Addenda to “Correspondence theorems for Hopf algebroids with applications to affine groupoids”
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 347-350
- Print publication:
- February 2025
-
- Article
- Export citation
A note on right-nil and strong-nil skew braces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-9
-
- Article
- Export citation
A McKay Correspondence in Positive Characteristic
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e116
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fiber functors and reconstruction of Hopf algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 1718-1761
- Print publication:
- October 2025
-
- Article
- Export citation
Pieri rules for skew dual immaculate functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 29 April 2024, pp. 902-914
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the structure of some one-generator braces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 566-576
-
- Article
- Export citation
Finite skew braces of square-free order and supersolubility
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COEFFICIENT QUIVERS,
 ${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 561-617
- Print publication:
- September 2024
-
- Article
- Export citation
Post-Lie algebras in Regularity Structures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 October 2023, e98
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ρ-conjugate Hopf–Galois structures
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 28 April 2023, pp. 288-304
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 793-809
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation