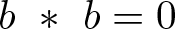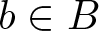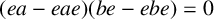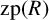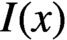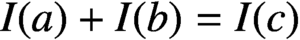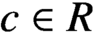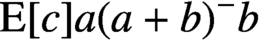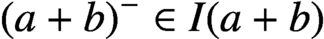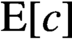Refine listing
Actions for selected content:
54 results in 16Nxx
On rings which are sums of subrings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 874-882
- Print publication:
- September 2025
-
- Article
- Export citation
The Quantitative Kurosh Problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From actions of an abelian group on itself to left braces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 65-79
- Print publication:
- January 2025
-
- Article
- Export citation
A note on right-nil and strong-nil skew braces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-9
-
- Article
- Export citation
RADICALS AND IDEMPOTENTS III: q-CENTRAL IDEMPOTENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 20 November 2024, pp. 272-282
- Print publication:
- April 2025
-
- Article
- Export citation
THE PROBABILITY OF ZERO MULTIPLICATION IN FINITE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 83-88
- Print publication:
- August 2022
-
- Article
- Export citation
TRIPLET INVARIANCE AND PARALLEL SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 25 January 2021, pp. 118-126
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
FURTHER REMARKS ON ELEMENTARY RADICALS AND ASSOCIATED FILTERS OF IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 08 October 2020, pp. 450-460
- Print publication:
- June 2021
-
- Article
- Export citation
PRIME AND SEMIPRIME QUANTUM LINEAR SPACE SMASH PRODUCTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 23 July 2020, pp. 503-514
- Print publication:
- September 2021
-
- Article
- Export citation
On the primitive ideals of nest algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 737-760
-
- Article
- Export citation
ON BASE RADICAL THEORY IN FINITE SETTINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 March 2020, pp. 510-511
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Additive n-commuting maps on semiprime rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 11 November 2019, pp. 193-216
-
- Article
- Export citation
ON THE CONNECTION BETWEEN DIFFERENTIAL POLYNOMIAL RINGS AND POLYNOMIAL RINGS OVER NIL RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 September 2019, pp. 438-441
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
On Annelidan, Distributive, and Bézout Rings
- Part of
- Chain conditions, growth conditions, and other forms of finiteness
- Radicals and radical properties of rings
- Rings and algebras arising under various constructions
- Modules, bimodules and ideals
- Local rings and generalizations
- Distributive lattices
- Conditions on elements
- Boolean algebras (Boolean rings)
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 03 May 2019, pp. 1082-1110
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Generating Adjoint Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 733-738
-
- Article
- Export citation
ON BASE RADICAL OPERATORS FOR CLASSES OF FINITE ASSOCIATIVE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 239-250
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
PRIME SPECTRA OF AMBISKEW POLYNOMIAL RINGS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 16 April 2018, pp. 49-68
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
Nilpotent, Algebraic and Quasi-Regular Elements in Rings and Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 29 December 2016, pp. 753-769
-
- Article
- Export citation
A PRIME ESSENTIAL RING THAT GENERATES A SPECIAL ATOM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 214-218
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Rings Characterized via a Class of Left Exact Preradicals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 641-653
-
- Article
- Export citation