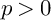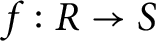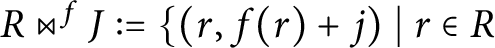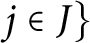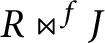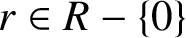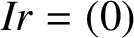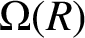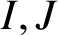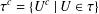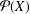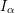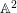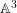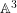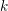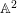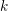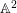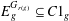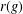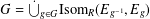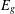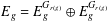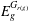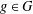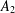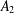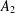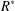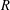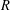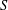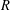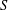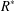Refine listing
Actions for selected content:
36 results in 13Bxx
ON THE TRIVIALITY OF AN
 $\mathbb A^2$-FIBRATION OVER A DVR
$\mathbb A^2$-FIBRATION OVER A DVR
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-7
-
- Article
- Export citation
FORMAL LIFTING OF DUALIZING COMPLEXES AND CONSEQUENCES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 219-236
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING GEOMETRIC BRANCHES VIA THE FROBENIUS MAP AND F-NILPOTENT SINGULARITIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 27 February 2024, pp. 724-741
- Print publication:
- September 2024
-
- Article
- Export citation
FORMALLY REGULAR RINGS AND DESCENT OF REGULARITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 02 January 2024, pp. 2279-2318
- Print publication:
- September 2024
-
- Article
- Export citation
HOW TO EXTEND CLOSURE AND INTERIOR OPERATIONS TO MORE MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 513-560
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A VARIANT OF PERFECTOID ABHYANKAR’S LEMMA AND ALMOST COHEN–MACAULAY ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 04 September 2023, pp. 164-215
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert rings with maximal ideals of different heights and unruly Hilbert rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 10 March 2022, pp. 196-203
- Print publication:
- March 2023
-
- Article
- Export citation
Embedding codimension of the space of arcs
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 February 2022, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE STRONG METRIC DIMENSION OF A TOTAL GRAPH OF NONZERO ANNIHILATING IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 November 2021, pp. 431-439
- Print publication:
- June 2022
-
- Article
- Export citation
Depth-graded motivic multiple zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 March 2021, pp. 529-572
- Print publication:
- March 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDS FOR INDEXES OF NILPOTENCY IN COMMUTATIVE RING THEORY: A PROOF MINING APPROACH
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 05 January 2021, pp. 257-267
- Print publication:
- December 2020
-
- Article
- Export citation
ANALYTIC SPREAD AND INTEGRAL CLOSURE OF INTEGRALLY DECOMPOSABLE MODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 245 / March 2022
- Published online by Cambridge University Press:
- 03 November 2020, pp. 166-191
- Print publication:
- March 2022
-
- Article
- Export citation
UNIFORM DEFINABILITY OF INTEGERS IN REDUCED INDECOMPOSABLE POLYNOMIAL RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1376-1402
- Print publication:
- December 2020
-
- Article
- Export citation
FROM TOPOLOGIES OF A SET TO SUBRINGS OF ITS POWER SET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 15-20
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
INTEGRAL CLOSURE OF STRONGLY GOLOD IDEALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 241 / March 2021
- Published online by Cambridge University Press:
- 18 July 2019, pp. 204-216
- Print publication:
- March 2021
-
- Article
- Export citation
ON SEPARABLE
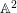 $\mathbb{A}^{2}$ AND
$\mathbb{A}^{2}$ AND 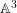 $\mathbb{A}^{3}$-FORMS
$\mathbb{A}^{3}$-FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 346-354
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
On the Integral Degree of Integral Ring Extensions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 20 August 2018, pp. 25-46
-
- Article
- Export citation
A CHARACTERISATION FOR A GROUPOID GALOIS EXTENSION USING PARTIAL ISOMORPHISMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 06 March 2017, pp. 59-68
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
FIXED ELEMENTS OF NONINJECTIVE ENDOMORPHISMS OF POLYNOMIAL ALGEBRAS IN TWO VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 20 October 2016, pp. 209-213
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
WHEN IS THE INTEGRAL CLOSURE COMPARABLE TO ALL INTERMEDIATE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 14-21
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation