1 Introduction
In this paper we define the embedding codimension of an arbitrary local ring and use it to quantify singularities of arc spaces.
The embedding codimension is a familiar notion in the Noetherian setting, where it is defined, for local rings, as the difference between the embedding dimension and the Krull dimension. It was studied, for instance, in [Reference Lech35] under the name of regularity defect. Note, however, that if the ring is not Noetherian, then both of these quantities can be infinite, and even when they are finite it can happen that the embedding dimension is smaller than the dimension. Rank ![]() $2$ valuation rings give simple examples where this phenomenon occurs.
$2$ valuation rings give simple examples where this phenomenon occurs.
Arc spaces provide a situation of geometric interest where non-Noetherian rings and rings of infinite embedding dimension naturally arise. With this in mind, we extend the definition of the embedding codimension to arbitrary local rings ![]() $(A,\mathfrak {m},k)$ by setting
$(A,\mathfrak {m},k)$ by setting
where ![]() $\gamma \colon \operatorname {\mathrm {Sym}}_k (\mathfrak {m}/\mathfrak {m}^2 ) \to \operatorname {\mathrm {gr}}(A)$ is the natural homomorphism. Geometrically, we may think of
$\gamma \colon \operatorname {\mathrm {Sym}}_k (\mathfrak {m}/\mathfrak {m}^2 ) \to \operatorname {\mathrm {gr}}(A)$ is the natural homomorphism. Geometrically, we may think of ![]() $\mathrm {ecodim}(A)$ as the codimension of the tangent cone of A inside its tangent space. Note that when A is Noetherian, this notion agrees with the classical definition of the embedding codimension, as in this case
$\mathrm {ecodim}(A)$ as the codimension of the tangent cone of A inside its tangent space. Note that when A is Noetherian, this notion agrees with the classical definition of the embedding codimension, as in this case ![]() $\dim (A)=\dim (\operatorname {\mathrm {gr}}(A))$. When A is a k-algebra, we have
$\dim (A)=\dim (\operatorname {\mathrm {gr}}(A))$. When A is a k-algebra, we have ![]() $\mathrm {ecodim}(A) = 0$ if and only if A is formally smooth over k, and therefore one can view the embedding codimension as a (rough) measure of singularity.
$\mathrm {ecodim}(A) = 0$ if and only if A is formally smooth over k, and therefore one can view the embedding codimension as a (rough) measure of singularity.
If ![]() $(A,\mathfrak {m},k)$ is equicharacteristic, then an alternative definition can be given by considering the infimum of
$(A,\mathfrak {m},k)$ is equicharacteristic, then an alternative definition can be given by considering the infimum of ![]() $\operatorname {\mathrm {ht}}(\ker (\tau ))$ for all surjective continuous
$\operatorname {\mathrm {ht}}(\ker (\tau ))$ for all surjective continuous ![]() $\tau \colon k[[x_i \mid i \in I ]] \to \widehat {A}$. We call the resulting notion the formal embedding codimension, and denote it by
$\tau \colon k[[x_i \mid i \in I ]] \to \widehat {A}$. We call the resulting notion the formal embedding codimension, and denote it by ![]() $\mathrm {fcodim}(A)$. In this paper we establish the following comparison theorem:
$\mathrm {fcodim}(A)$. In this paper we establish the following comparison theorem:
Theorem A. For every equicharacteristic local ring ![]() $(A,\mathfrak {m},k)$, we have
$(A,\mathfrak {m},k)$, we have
and equality holds in the following cases:
1. the ring A has embedding dimension
 $\mathrm {edim}(A) < \infty $ or
$\mathrm {edim}(A) < \infty $ or2. there exists a scheme X of finite type over k such that A is isomorphic to the local ring of the arc space of X at a k-rational point.
In order to prove Theorem A and related results on the formal embedding codimension, we make use of various results concerning infinite-variate power series rings and their localisations, which are of independent interest in the study of non-Noetherian rings.
Local rings of arc spaces and their completions were studied in [Reference Grinberg and Kazhdan31, Reference Drinfeld24, Reference Reguera40, Reference Reguera41, Reference Reguera42, Reference Mourtada and Reguera37, Reference de Fernex and Docampo21]; [Reference de Fernex and Docampo21] looks at the embedding dimension of the local rings to characterise stable points of arc spaces, which were originally studied in [Reference Denef and Loeser23, Reference Reguera40]. In this paper, we consider the embedding codimension.
Let X be a scheme of finite type over a field k, and let ![]() $X_{\infty }$ be its arc space. A point
$X_{\infty }$ be its arc space. A point ![]() $\alpha \in X_{\infty }$ corresponds to a formal arc
$\alpha \in X_{\infty }$ corresponds to a formal arc ![]() $\alpha \colon \operatorname {\mathrm {Spec}} K[[t]] \to X$, where K is the residue field, and defines a valuation
$\alpha \colon \operatorname {\mathrm {Spec}} K[[t]] \to X$, where K is the residue field, and defines a valuation ![]() $\operatorname {\mathrm {ord}}_\alpha $ on the local ring of X at the base point
$\operatorname {\mathrm {ord}}_\alpha $ on the local ring of X at the base point ![]() $\alpha (0)$ of the arc (the image of the closed point of
$\alpha (0)$ of the arc (the image of the closed point of ![]() $\operatorname {\mathrm {Spec}} K[[t]]$). It is convenient to denote by
$\operatorname {\mathrm {Spec}} K[[t]]$). It is convenient to denote by ![]() $\alpha (\eta )$ the image of the generic point of
$\alpha (\eta )$ the image of the generic point of ![]() $\operatorname {\mathrm {Spec}} K[[t]]$. With this notation, we can state our next theorem.
$\operatorname {\mathrm {Spec}} K[[t]]$. With this notation, we can state our next theorem.
Theorem B. Let X be a scheme of finite type over a field k, and let ![]() $\alpha \in X_{\infty }$.
$\alpha \in X_{\infty }$.
1. Assume that either k has characteristic
 $0$ or
$0$ or  $\alpha \in X_{\infty }(k)$. Then we have that
$\alpha \in X_{\infty }(k)$. Then we have that  $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) < \infty $ if and only if
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) < \infty $ if and only if  $\alpha (\eta ) \in X_{\mathrm {sm}}$.
$\alpha (\eta ) \in X_{\mathrm {sm}}$.2. Assume that k is perfect and
 $\alpha (\eta ) \in X_{\mathrm {sm}}$, and let
$\alpha (\eta ) \in X_{\mathrm {sm}}$, and let  $X^0 \subset X$ be the irreducible component containing
$X^0 \subset X$ be the irreducible component containing  $\alpha (\eta )$. Then where
$\alpha (\eta )$. Then where $$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) \le \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X^0}\right), \end{align*} $$
$$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) \le \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X^0}\right), \end{align*} $$ $\mathrm {Jac}_{X^0}$ is the Jacobian ideal of
$\mathrm {Jac}_{X^0}$ is the Jacobian ideal of  $X^0$.
$X^0$.
One of the motivations behind this result comes from the following theorem, originally conjectured by Drinfeld and proved by Grinberg and Kazhdan in characteristic ![]() $0$ and then by Drinfeld in arbitrary characteristic. Here and in the following, we exclude the trivial case where X is, locally, just a reduced point.
$0$ and then by Drinfeld in arbitrary characteristic. Here and in the following, we exclude the trivial case where X is, locally, just a reduced point.
Theorem 1.1 [Reference Grinberg and Kazhdan31, Reference Drinfeld24, Reference Drinfeld25]
Let X be a scheme of finite type over a field k, and let ![]() $\alpha \in X_{\infty }(k)$ be a k-rational point. If
$\alpha \in X_{\infty }(k)$ be a k-rational point. If ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$, then there exists a decomposition
$\alpha (\eta ) \in X_{\mathrm {sm}}$, then there exists a decomposition
 $$ \begin{align*} \widehat{X_{\infty,\alpha}} \simeq \widehat{Z_z} \hat\times \Delta^{\mathbb N}, \end{align*} $$
$$ \begin{align*} \widehat{X_{\infty,\alpha}} \simeq \widehat{Z_z} \hat\times \Delta^{\mathbb N}, \end{align*} $$where ![]() $\widehat {Z_z}$ is the formal completion of a scheme Z of finite type over k at a point
$\widehat {Z_z}$ is the formal completion of a scheme Z of finite type over k at a point ![]() $z \in Z(k)$,
$z \in Z(k)$, ![]() $\Delta ^{\mathbb N} = \operatorname {\mathrm {Spf}} (k[[x_i \mid i \in {\mathbb N}]])$ and
$\Delta ^{\mathbb N} = \operatorname {\mathrm {Spf}} (k[[x_i \mid i \in {\mathbb N}]])$ and ![]() $\hat \times $ denotes the product in the category of formal k-schemes.
$\hat \times $ denotes the product in the category of formal k-schemes.
Given the existence of an isomorphism as in Theorem 1.1, we say that ![]() $X_{\infty }$ admits a DGK decomposition at
$X_{\infty }$ admits a DGK decomposition at ![]() $\alpha $. The germ
$\alpha $. The germ ![]() $(Z,z)$ (given by
$(Z,z)$ (given by ![]() $\operatorname {\mathrm {Spec}} \mathcal {O}_{Z,z}$) and its completion
$\operatorname {\mathrm {Spec}} \mathcal {O}_{Z,z}$) and its completion  $\widehat {Z_z}=\operatorname {\mathrm {Spf}} (\widehat {\mathcal {O}_{Z_z}} )$ are often referred to as a formal model for
$\widehat {Z_z}=\operatorname {\mathrm {Spf}} (\widehat {\mathcal {O}_{Z_z}} )$ are often referred to as a formal model for ![]() $\alpha $. Drinfeld’s proof yields an algorithm for computing such a model; we will refer to it as a Drinfeld model.
$\alpha $. Drinfeld’s proof yields an algorithm for computing such a model; we will refer to it as a Drinfeld model.
Partial converses of Theorem 1.1 were obtained in [Reference Bourqui and Sebag9], where an explicit example of a k-valued constant arc through the singular locus of X is given for which a DGK decomposition does not exist, and in [Reference Chiu and Hauser19], where it is shown that in characteristic ![]() $0$, if
$0$, if ![]() $\alpha $ is any constant arc contained in the singular locus of X then there are no smooth factors in
$\alpha $ is any constant arc contained in the singular locus of X then there are no smooth factors in  $\widehat {X_{\infty ,\alpha }}$ at all. Examples of nonconstant arcs that are contained in the singular locus for which there is no DGK decomposition can easily be constructed from these results; see also [Reference Sebag43, Reference Bourqui and Sebag11] for related results. An extension of the theorem to formal schemes is given in [Reference Bourqui and Sebag10]. Formal models of toric singularities are studied in [Reference Bourqui and Sebag13].
$\widehat {X_{\infty ,\alpha }}$ at all. Examples of nonconstant arcs that are contained in the singular locus for which there is no DGK decomposition can easily be constructed from these results; see also [Reference Sebag43, Reference Bourqui and Sebag11] for related results. An extension of the theorem to formal schemes is given in [Reference Bourqui and Sebag10]. Formal models of toric singularities are studied in [Reference Bourqui and Sebag13].
As an application of our methods, we give a sharp converse to Theorem 1.1 and provide an optimal bound to the embedded codimension of the formal model.
Theorem C. Let X be a scheme of finite type over a field k, and let ![]() $\alpha \in X_{\infty }(k)$ be a k-rational point.
$\alpha \in X_{\infty }(k)$ be a k-rational point.
1. If
 $X_{\infty }$ admits a DGK decomposition at
$X_{\infty }$ admits a DGK decomposition at  $\alpha $, then
$\alpha $, then  $\alpha (\eta ) \in X_{\mathrm {sm}}$.
$\alpha (\eta ) \in X_{\mathrm {sm}}$.2. Assume that k is perfect and
 $\alpha (\eta ) \in X_{\mathrm {sm}}$, and let
$\alpha (\eta ) \in X_{\mathrm {sm}}$, and let  $X^0 \subset X$ be the irreducible component containing
$X^0 \subset X$ be the irreducible component containing  $\alpha (\eta )$. Then for any formal model
$\alpha (\eta )$. Then for any formal model  $(Z,z)$ for
$(Z,z)$ for  $\alpha $, we have Moreover, for every
$\alpha $, we have Moreover, for every $$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{Z,z}\right) \le \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X^0}\right). \end{align*} $$
$$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{Z,z}\right) \le \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X^0}\right). \end{align*} $$ $e \in {\mathbb N}$ there exist X and
$e \in {\mathbb N}$ there exist X and  $\alpha $ such that both sides in this formula are equal to e.
$\alpha $ such that both sides in this formula are equal to e.
The next result, which combines results of this paper with Theorem 1.1, provides a geometrically meaningful way of realising a DGK decomposition and gives an explicit formula for the embedding dimension of a Drinfeld model.
Theorem D. Let X be an affine scheme of finite type over a perfect field k, let ![]() $\alpha \in X_{\infty }(k)$ be a k-rational point with
$\alpha \in X_{\infty }(k)$ be a k-rational point with ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$ and let
$\alpha (\eta ) \in X_{\mathrm {sm}}$ and let ![]() $d = \dim _{\alpha (\eta )}(X)$. Let
$d = \dim _{\alpha (\eta )}(X)$. Let ![]() $f \colon X \to Y := {\mathbb A}^d$ be a general linear projection.
$f \colon X \to Y := {\mathbb A}^d$ be a general linear projection.
1. The map
 $f_{\infty } \colon X_{\infty } \to Y_{\infty }$ induces an isomorphism from the Zariski tangent space of
$f_{\infty } \colon X_{\infty } \to Y_{\infty }$ induces an isomorphism from the Zariski tangent space of  $X_{\infty }$ at
$X_{\infty }$ at  $\alpha $ to the Zariski tangent space of
$\alpha $ to the Zariski tangent space of  $Y_{\infty }$ at
$Y_{\infty }$ at  $\beta := f_{\infty }(\alpha )$, and hence a closed embedding
$\beta := f_{\infty }(\alpha )$, and hence a closed embedding  $$ \begin{align*} \widehat{f_{\infty,\alpha}} \colon \widehat{X_{\infty,\alpha}} \hookrightarrow \widehat{Y_{\infty,\beta}}. \end{align*} $$
$$ \begin{align*} \widehat{f_{\infty,\alpha}} \colon \widehat{X_{\infty,\alpha}} \hookrightarrow \widehat{Y_{\infty,\beta}}. \end{align*} $$2. For a suitable isomorphism
 $\widehat {Y_{\infty ,\beta }} \simeq \operatorname {\mathrm {Spec}} k[[u_i \mid i \in {\mathbb N}]]$, the scheme
$\widehat {Y_{\infty ,\beta }} \simeq \operatorname {\mathrm {Spec}} k[[u_i \mid i \in {\mathbb N}]]$, the scheme  $\widehat {X_{\infty ,\alpha }}$ is defined in this embedding by finitely many polynomials in the variables
$\widehat {X_{\infty ,\alpha }}$ is defined in this embedding by finitely many polynomials in the variables  $u_j$, and hence the embedding gives a DGK decomposition of
$u_j$, and hence the embedding gives a DGK decomposition of  $X_{\infty }$ at
$X_{\infty }$ at  $\alpha $.
$\alpha $.3. Let
 $X^0 \subset $X be the irreducible component containing
$X^0 \subset $X be the irreducible component containing  $\alpha (\eta )$, and set
$\alpha (\eta )$, and set  $e := \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} )$. Denote by
$e := \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} )$. Denote by  $\widehat {Y_{2e-1,\beta _{2e-1}}}$ the completion of the
$\widehat {Y_{2e-1,\beta _{2e-1}}}$ the completion of the  $(2e-1)$-jet scheme of Y at the truncation of
$(2e-1)$-jet scheme of Y at the truncation of  $\beta $. If
$\beta $. If  $(Z,z)$ is a Drinfeld model compatible with the projection f, then the composition of maps gives an embedding of
$(Z,z)$ is a Drinfeld model compatible with the projection f, then the composition of maps gives an embedding of $$ \begin{align*} \widehat{Z_z} \hookrightarrow \widehat{X_{\infty,\alpha}} \hookrightarrow \widehat{Y_{\infty,\beta}} \twoheadrightarrow \widehat{Y_{2e-1,\beta_{2e-1}}} \end{align*} $$
$$ \begin{align*} \widehat{Z_z} \hookrightarrow \widehat{X_{\infty,\alpha}} \hookrightarrow \widehat{Y_{\infty,\beta}} \twoheadrightarrow \widehat{Y_{2e-1,\beta_{2e-1}}} \end{align*} $$ $\widehat {Z_z}$ into
$\widehat {Z_z}$ into  $\widehat {Y_{2e-1,\beta _{2e-1}}}$, and this embedding induces an isomorphism at the level of continuous tangent spaces. In particular, the local ring
$\widehat {Y_{2e-1,\beta _{2e-1}}}$, and this embedding induces an isomorphism at the level of continuous tangent spaces. In particular, the local ring  $\mathcal {O}_{Z,z}$ has embedding dimension
$\mathcal {O}_{Z,z}$ has embedding dimension  $$ \begin{align*} \mathrm{edim}\left(\mathcal{O}_{Z,z}\right) = 2d \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X^0}\right). \end{align*} $$
$$ \begin{align*} \mathrm{edim}\left(\mathcal{O}_{Z,z}\right) = 2d \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X^0}\right). \end{align*} $$
By combining Theorems C and D, one sees that all Drinfeld models ![]() $(Z,z)$ have the same dimension, and this dimension satisfies
$(Z,z)$ have the same dimension, and this dimension satisfies
In general, Drinfeld models are different from the minimal formal model. Theorem D implies that ![]() $2d \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} )$ is an upper bound on the embedding dimension of the minimal formal model.
$2d \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} )$ is an upper bound on the embedding dimension of the minimal formal model.
The proofs of Theorems B and D rely on a formula on the sheaf of differentials of ![]() $X_{\infty }$ from [Reference de Fernex and Docampo21]. A result related to Theorem D(1), dealing with the case where
$X_{\infty }$ from [Reference de Fernex and Docampo21]. A result related to Theorem D(1), dealing with the case where ![]() $f \colon X \to Y$ is a generically finite morphism of equidimensional schemes with X smooth, was obtained in [Reference Ein and Mustaţă27] using a more direct computation of the map induced at the level of Zariski tangent spaces. General projections to
$f \colon X \to Y$ is a generically finite morphism of equidimensional schemes with X smooth, was obtained in [Reference Ein and Mustaţă27] using a more direct computation of the map induced at the level of Zariski tangent spaces. General projections to ![]() ${\mathbb A}^d$ are also used in [Reference Drinfeld24] to set up the proof for the Weierstrass preparation theorem; however, Drinfeld’s proof does not lead to the same conclusions about
${\mathbb A}^d$ are also used in [Reference Drinfeld24] to set up the proof for the Weierstrass preparation theorem; however, Drinfeld’s proof does not lead to the same conclusions about  $\widehat {f_{\infty ,\alpha }}$ or about the embedding of
$\widehat {f_{\infty ,\alpha }}$ or about the embedding of ![]() $\widehat {Z_z}$ into
$\widehat {Z_z}$ into  $\widehat {Y_{2e-1,\beta _{2e-1}}}$. General projections to
$\widehat {Y_{2e-1,\beta _{2e-1}}}$. General projections to ![]() ${\mathbb A}^d$ were also used in [Reference Reguera42, Reference Mourtada and Reguera37], and in fact our results give a new proof of one of the theorems of [Reference Mourtada and Reguera37].
${\mathbb A}^d$ were also used in [Reference Reguera42, Reference Mourtada and Reguera37], and in fact our results give a new proof of one of the theorems of [Reference Mourtada and Reguera37].
There have been several attempts to extend Theorem 1.1 to a more global statement; see [Reference Bouthier, Ngô and Sakellaridis16, Reference Nicaise and Sebag38, Reference Bouthier and Kazhdan15, Reference Hauser and Woblistin33] (see also the more recent [Reference Bouthier14], which supersedes [Reference Bouthier and Kazhdan15]), which at their core all rely on the Weierstrass preparation theorem. The question stems from the expectation that there should exist a well-behaved theory of perverse sheaves on arc spaces (as well as on other closely related infinite dimensional spaces). Theorem 1.1 suggests that one could try to define such perverse sheaves in terms of the intersection complexes of the formal models, but one needs a more global version of the DGK decomposition to make sense out of this. We refer to the citations already given for the motivations behind these questions.
Our interest in Theorem D comes from the observation that the same projection ![]() $f \colon X \to {\mathbb A}^d$ works for all arcs
$f \colon X \to {\mathbb A}^d$ works for all arcs ![]() $\alpha ' \in X_{\infty }(k)$ in a neighbourhood of
$\alpha ' \in X_{\infty }(k)$ in a neighbourhood of ![]() $\alpha $ and having the same order of contact with
$\alpha $ and having the same order of contact with ![]() $\mathrm {Jac}_{X^0}$. The order of contact with the Jacobian ideals of the irreducible components of X gives a stratification of
$\mathrm {Jac}_{X^0}$. The order of contact with the Jacobian ideals of the irreducible components of X gives a stratification of ![]() $X_{\infty }$, and the hope is that the theorem may turn out to be useful in understanding how the DGK decomposition varies along strata.
$X_{\infty }$, and the hope is that the theorem may turn out to be useful in understanding how the DGK decomposition varies along strata.
This paper is organised as follows. In the first few sections we review some basic properties of power series rings in an arbitrary number of indeterminates and establish various properties that we have been unable to locate in the literature. Ideals of finite definition, which provide the algebraic interpretation of a DGK decomposition, are discussed in Section 5. These sections provide some general results on non-Noetherian rings and are independent of our applications to the study of singularities of arc spaces. In the next two sections the embedding codimension and its formal counterpart are defined and general properties of these notions are studied. Starting from Section 8, we focus on the case of arc spaces, proving some technical theorems in Section 8 and then addressing the theorem of Drinfeld, Grinberg and Kazhdan in Sections 9 and 10. The last section is devoted to some applications related to Mather–Jacobian discrepancies, among others to the case of toric singularities using results of [Reference Bourqui and Sebag13].
Theorem A follows from Theorem 7.8 and Corollaries 7.5 and 9.7. Theorem B follows from Corollary 8.8 and Theorem 8.5. Theorem C follows from Theorem 9.4 and Example 9.6. Theorem D follows from Theorems 9.8 and 10.2.
2 Rings of formal power series
In this paper we will work with rings of power series in an arbitrary number of indeterminates. For our purposes, we adopt the definition of these rings as completions of polynomial rings, a definition that differs from other standard approaches to the theory. In this section, we briefly review the notions of completions, graded rings, and rings of power series. All of the material here is standard, but we want to fix notation and bring attention to some of the subtleties that appear in the infinite-dimensional setting.
Let A be a ring and ![]() $\mathfrak {m} \subset A$ an ideal. We do not assume that
$\mathfrak {m} \subset A$ an ideal. We do not assume that ![]() $\mathfrak {m}$ is a maximal ideal. We denote by
$\mathfrak {m}$ is a maximal ideal. We denote by  $\widehat {A} := \underleftarrow{\lim}_{n} A/\mathfrak {m}^n$ the
$\widehat {A} := \underleftarrow{\lim}_{n} A/\mathfrak {m}^n$ the ![]() $\mathfrak {m}$-adic completion of A and regard it as a topological ring with respect to its limit topology. Given an ideal
$\mathfrak {m}$-adic completion of A and regard it as a topological ring with respect to its limit topology. Given an ideal ![]() $\mathfrak {a} \subset A$, we denote by
$\mathfrak {a} \subset A$, we denote by ![]() $\widehat {\mathfrak {a}} \subset \widehat {A}$ the completion of
$\widehat {\mathfrak {a}} \subset \widehat {A}$ the completion of ![]() $\mathfrak {a}$ as a topological A-submodule. A basis for all neighbourhoods
$\mathfrak {a}$ as a topological A-submodule. A basis for all neighbourhoods ![]() $U\subset \widehat {A}$ of
$U\subset \widehat {A}$ of ![]() $0$ is given by the descending chain of ideals
$0$ is given by the descending chain of ideals
 $$ \begin{align*} \widehat{\mathfrak{m}^n}=\ker\left(\widehat{A}\to A/\mathfrak{m}^n\right). \end{align*} $$
$$ \begin{align*} \widehat{\mathfrak{m}^n}=\ker\left(\widehat{A}\to A/\mathfrak{m}^n\right). \end{align*} $$The ideal ![]() $\widehat {\mathfrak {a}}$ then coincides with the topological closure of
$\widehat {\mathfrak {a}}$ then coincides with the topological closure of ![]() $\mathfrak {a}$ inside
$\mathfrak {a}$ inside ![]() $\widehat {A}$ – that is,
$\widehat {A}$ – that is,
 $$ \begin{align*} \widehat{\mathfrak{a}}=\bigcap_n \left(\mathfrak{a}+\widehat{\mathfrak{m}^n}\right). \end{align*} $$
$$ \begin{align*} \widehat{\mathfrak{a}}=\bigcap_n \left(\mathfrak{a}+\widehat{\mathfrak{m}^n}\right). \end{align*} $$Note that if ![]() $\mathfrak {m}$ is not finitely generated, then the natural topology on
$\mathfrak {m}$ is not finitely generated, then the natural topology on ![]() $\widehat {A}$ may differ from the
$\widehat {A}$ may differ from the ![]() $\widehat {\mathfrak {m}}$-adic topology of
$\widehat {\mathfrak {m}}$-adic topology of ![]() $\widehat {A}$ (see Remark 2.3).
$\widehat {A}$ (see Remark 2.3).
We will denote by 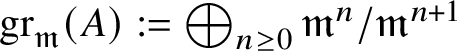 $\operatorname {\mathrm {gr}}_{\mathfrak {m}}(A) := \bigoplus _{n \ge 0} \mathfrak {m}^n/\mathfrak {m}^{n+1}$ the graded algebra of A with respect to the
$\operatorname {\mathrm {gr}}_{\mathfrak {m}}(A) := \bigoplus _{n \ge 0} \mathfrak {m}^n/\mathfrak {m}^{n+1}$ the graded algebra of A with respect to the ![]() $\mathfrak {m}$-adic filtration. If
$\mathfrak {m}$-adic filtration. If ![]() $\mathfrak {m}$ is understood from context, we simply write
$\mathfrak {m}$ is understood from context, we simply write ![]() $\operatorname {\mathrm {gr}}(A)$ for
$\operatorname {\mathrm {gr}}(A)$ for ![]() $\operatorname {\mathrm {gr}}_{\mathfrak {m}}(A)$. We will regard
$\operatorname {\mathrm {gr}}_{\mathfrak {m}}(A)$. We will regard ![]() $\widehat {A}$ as endowed with the filtration
$\widehat {A}$ as endowed with the filtration ![]() $ \{\widehat {\mathfrak {m}^n} \}$ induced by the completion, and therefore its graded algebra is given by
$ \{\widehat {\mathfrak {m}^n} \}$ induced by the completion, and therefore its graded algebra is given by  $\operatorname {\mathrm {gr}} (\widehat {A} ) := \bigoplus _{n \ge 0} \widehat {\mathfrak {m}^n}/\widehat {\mathfrak {m}^{n+1}}$. There are natural isomorphisms
$\operatorname {\mathrm {gr}} (\widehat {A} ) := \bigoplus _{n \ge 0} \widehat {\mathfrak {m}^n}/\widehat {\mathfrak {m}^{n+1}}$. There are natural isomorphisms ![]() $\widehat {\mathfrak {m}^p}/\widehat {\mathfrak {m}^q} \simeq \mathfrak {m}^p/\mathfrak {m}^q$ for all
$\widehat {\mathfrak {m}^p}/\widehat {\mathfrak {m}^q} \simeq \mathfrak {m}^p/\mathfrak {m}^q$ for all ![]() $p < q$. This gives a natural identification between
$p < q$. This gives a natural identification between ![]() $\operatorname {\mathrm {gr}} (\widehat {A} )$ and
$\operatorname {\mathrm {gr}} (\widehat {A} )$ and ![]() $\operatorname {\mathrm {gr}}(A)$. If
$\operatorname {\mathrm {gr}}(A)$. If ![]() $\mathfrak {a} \subset A$ is an ideal of A, then we write
$\mathfrak {a} \subset A$ is an ideal of A, then we write  $\operatorname {\mathrm {in}}(\mathfrak {a}) := \bigoplus _{n \geq 0} (\mathfrak {a} \cap \mathfrak {m}^n)/\mathfrak {m}^{n+1}$ for the corresponding initial ideal. Similarly, for
$\operatorname {\mathrm {in}}(\mathfrak {a}) := \bigoplus _{n \geq 0} (\mathfrak {a} \cap \mathfrak {m}^n)/\mathfrak {m}^{n+1}$ for the corresponding initial ideal. Similarly, for ![]() $\mathfrak {a} \subset \widehat {A}$, we set
$\mathfrak {a} \subset \widehat {A}$, we set  $\operatorname {\mathrm {in}}(\mathfrak {a}) := \bigoplus _{n \geq 0} (\mathfrak {a} \cap \widehat {\mathfrak {m}^n} )/\widehat {\mathfrak {m}^{n+1}}$. For an element
$\operatorname {\mathrm {in}}(\mathfrak {a}) := \bigoplus _{n \geq 0} (\mathfrak {a} \cap \widehat {\mathfrak {m}^n} )/\widehat {\mathfrak {m}^{n+1}}$. For an element ![]() $f \in A$ (or
$f \in A$ (or ![]() $f \in \widehat {A}$), we write
$f \in \widehat {A}$), we write ![]() $\operatorname {\mathrm {in}}(f) \in \operatorname {\mathrm {gr}}(A)$ for the corresponding initial form.
$\operatorname {\mathrm {in}}(f) \in \operatorname {\mathrm {gr}}(A)$ for the corresponding initial form.
Let S be a ring, and let ![]() $\{x_i \mid i\in I\}$ be a collection of indeterminates indexed by an arbitrary set I. We consider the polynomial ring
$\{x_i \mid i\in I\}$ be a collection of indeterminates indexed by an arbitrary set I. We consider the polynomial ring ![]() $P = S[x_i \mid i\in I]$ and denote by
$P = S[x_i \mid i\in I]$ and denote by ![]() $\widehat {P} = S[[ x_i \mid i \in I]]$ the completion of P with respect to the ideal
$\widehat {P} = S[[ x_i \mid i \in I]]$ the completion of P with respect to the ideal ![]() $(x_i \mid i \in I)$ – that is,
$(x_i \mid i \in I)$ – that is,
 $$ \begin{align*} S[[x_i \mid i \in I]] := \operatorname{\mathrm{\varprojlim}}_n S[x_i \mid i \in I]/(x_i \mid i\in I)^n. \end{align*} $$
$$ \begin{align*} S[[x_i \mid i \in I]] := \operatorname{\mathrm{\varprojlim}}_n S[x_i \mid i \in I]/(x_i \mid i\in I)^n. \end{align*} $$Definition 2.1. We call ![]() $S[[x_i \mid i \in I]]$ the power series ring in the indeterminates
$S[[x_i \mid i \in I]]$ the power series ring in the indeterminates ![]() $x_i$, with
$x_i$, with ![]() $i \in I$, and with coefficients in S.
$i \in I$, and with coefficients in S.
Remark 2.2. The polynomial ring ![]() $S[x_i \mid i\in I]$ is always the colimit (that is, the union) of all
$S[x_i \mid i\in I]$ is always the colimit (that is, the union) of all ![]() $S [x_j \mid j \in J ]$ with
$S [x_j \mid j \in J ]$ with ![]() $J \subset I$ finite. On the other hand, if I infinite, then
$J \subset I$ finite. On the other hand, if I infinite, then ![]() $S[[x_i \mid i \in I]]$ is not the colimit of all
$S[[x_i \mid i \in I]]$ is not the colimit of all ![]() $S [ [x_j \mid j \in J ] ]$ with
$S [ [x_j \mid j \in J ] ]$ with ![]() $J \subset I$ finite; it is, however, the colimit of all
$J \subset I$ finite; it is, however, the colimit of all ![]() $S [ [x_j \mid j \in J ] ]$ with
$S [ [x_j \mid j \in J ] ]$ with ![]() $J \subset I$ countable.
$J \subset I$ countable.
Remark 2.3. Denoting ![]() $\mathfrak {m} = (x_i \mid i\in I)$, we have the exact sequence
$\mathfrak {m} = (x_i \mid i\in I)$, we have the exact sequence
If I is infinite then ![]() $S[[x_i \mid i \in I]]$ is not
$S[[x_i \mid i \in I]]$ is not ![]() $\widehat {\mathfrak {m}}$-adically complete – that is, the natural topology on
$\widehat {\mathfrak {m}}$-adically complete – that is, the natural topology on ![]() $S[[x_i \mid i \in I]]$ coming from the completion does not coincide with the
$S[[x_i \mid i \in I]]$ coming from the completion does not coincide with the ![]() $\widehat {\mathfrak {m}}$-adic one, as for instance the inclusion
$\widehat {\mathfrak {m}}$-adic one, as for instance the inclusion ![]() $\widehat {\mathfrak {m}}^2 \subset \widehat {\mathfrak {m}^2}$ is strict in this case [44, Tag 05JA].
$\widehat {\mathfrak {m}}^2 \subset \widehat {\mathfrak {m}^2}$ is strict in this case [44, Tag 05JA].
Remark 2.4. Let us contrast the foregoing definition of ![]() $S[[x_i \mid i\in I]]$ with the ring of formal power series defined in [Reference Bourbaki8, Chapter III, Section 2.11], which we want to briefly recall. For any set I we denote by
$S[[x_i \mid i\in I]]$ with the ring of formal power series defined in [Reference Bourbaki8, Chapter III, Section 2.11], which we want to briefly recall. For any set I we denote by ![]() ${\mathbb N}^{(I)}$ the set of functions
${\mathbb N}^{(I)}$ the set of functions ![]() $I \to {\mathbb N}$ that take only finitely many nonzero values. Then
$I \to {\mathbb N}$ that take only finitely many nonzero values. Then ![]() ${\mathbb N}^{(I)}$ is a monoid, which we identify with the collection of monomials in the variables
${\mathbb N}^{(I)}$ is a monoid, which we identify with the collection of monomials in the variables ![]() $\{x_i \mid i \in I\}$ by writing
$\{x_i \mid i \in I\}$ by writing  $x^\alpha = \prod _{i\in I,\:\alpha (i)\neq 0} x_i^{\alpha (i)}$ for every
$x^\alpha = \prod _{i\in I,\:\alpha (i)\neq 0} x_i^{\alpha (i)}$ for every ![]() $\alpha \in {\mathbb N}^{(I)}$. The S-module
$\alpha \in {\mathbb N}^{(I)}$. The S-module ![]() $S^{{\mathbb N}^{(I)}}$ can be made into an S-algebra as follows: writing an element
$S^{{\mathbb N}^{(I)}}$ can be made into an S-algebra as follows: writing an element ![]() $a=(a_\alpha )_{\alpha \in {\mathbb N}^{(I)}}$ as
$a=(a_\alpha )_{\alpha \in {\mathbb N}^{(I)}}$ as ![]() $a=\sum _{\alpha \in {\mathbb N}^{(I)}} a_\alpha x^\alpha $, multiplication is defined via formal extension of
$a=\sum _{\alpha \in {\mathbb N}^{(I)}} a_\alpha x^\alpha $, multiplication is defined via formal extension of ![]() $x^\alpha \cdot x^\beta :=x^{\alpha +\beta }$. We call
$x^\alpha \cdot x^\beta :=x^{\alpha +\beta }$. We call ![]() $S^{{\mathbb N}^{(I)}}$ the ring of Bourbaki power series.
$S^{{\mathbb N}^{(I)}}$ the ring of Bourbaki power series.
Notice that there is a natural inclusion of rings  $S[[x_i \mid i\in I]] \subset S^{{\mathbb N}^{(I)}}$. This inclusion is an equality if
$S[[x_i \mid i\in I]] \subset S^{{\mathbb N}^{(I)}}$. This inclusion is an equality if ![]() $\lvert I\rvert < \infty $, and is a strict inclusion if
$\lvert I\rvert < \infty $, and is a strict inclusion if ![]() $\lvert I\rvert = \infty $, as in this case
$\lvert I\rvert = \infty $, as in this case ![]() $\sum _{i\in I} x_i$ is in
$\sum _{i\in I} x_i$ is in ![]() $S^{{\mathbb N}^{(I)}}$ but not in
$S^{{\mathbb N}^{(I)}}$ but not in ![]() $S[[x_i \mid i\in I]]$.
$S[[x_i \mid i\in I]]$.
Remark 2.5. It is often convenient to expand a formal power series in a subset of the indeterminates, but this becomes delicate in the infinite-dimensional case. Let I and J be arbitrary sets, and let ![]() $x_i$ and
$x_i$ and ![]() $y_j$ be indeterminates indexed by
$y_j$ be indeterminates indexed by ![]() $i \in I$ and
$i \in I$ and ![]() $j \in J$, respectively. Dropping for short the index sets from the notation, we have the following natural injections:
$j \in J$, respectively. Dropping for short the index sets from the notation, we have the following natural injections:
 $$ \begin{align*} S[[x_i]] \otimes_S S\left[\left[y_j\right]\right] \hookrightarrow S[[x_i]]\left[\left[y_j\right]\right] \hookrightarrow S\left[\left[x_i,y_j\right]\right] \hookrightarrow (S[[x_i]])^{{\mathbb N}^{(J)}}. \end{align*} $$
$$ \begin{align*} S[[x_i]] \otimes_S S\left[\left[y_j\right]\right] \hookrightarrow S[[x_i]]\left[\left[y_j\right]\right] \hookrightarrow S\left[\left[x_i,y_j\right]\right] \hookrightarrow (S[[x_i]])^{{\mathbb N}^{(J)}}. \end{align*} $$The first inclusion is always strict, and the other two are equalities if and only if J is finite. For example, if ![]() $x = x_{i_0}$ and
$x = x_{i_0}$ and ![]() $y = y_{i_0}$ are two respective indeterminates, then the series
$y = y_{i_0}$ are two respective indeterminates, then the series ![]() $\sum _{n \ge 0}x^ny^n$ belongs to
$\sum _{n \ge 0}x^ny^n$ belongs to ![]() $S[[x_i]] [ [y_j ] ]$ but is not in the image of
$S[[x_i]] [ [y_j ] ]$ but is not in the image of ![]() $S[[x_i]] \otimes _S S [ [y_j ] ]$, and if
$S[[x_i]] \otimes _S S [ [y_j ] ]$, and if ![]() ${\mathbb N} \subset J$ and
${\mathbb N} \subset J$ and ![]() $x = x_{i_0}$ is one of the indeterminates, then the series
$x = x_{i_0}$ is one of the indeterminates, then the series ![]() $\sum _{n \geq 1} y_n x^n$ belongs to
$\sum _{n \geq 1} y_n x^n$ belongs to ![]() $S [ [x_i, y_j ] ]$ but not to
$S [ [x_i, y_j ] ]$ but not to ![]() $S[[x_i]] [ [y_j ] ]$. Notice that Bourbaki power series are better behaved in this respect, as
$S[[x_i]] [ [y_j ] ]$. Notice that Bourbaki power series are better behaved in this respect, as  $S^{{\mathbb N}^{(I\sqcup J)}} = (S^{{\mathbb N}^{(I)}} )^{{\mathbb N}^{(J)}} = (S^{{\mathbb N}^{(J)}} )^{{\mathbb N}^{(I)}}$.
$S^{{\mathbb N}^{(I\sqcup J)}} = (S^{{\mathbb N}^{(I)}} )^{{\mathbb N}^{(J)}} = (S^{{\mathbb N}^{(J)}} )^{{\mathbb N}^{(I)}}$.
Remark 2.6. Let I be an arbitrary set, possibly infinite. We have natural identifications
Any nonzero power series ![]() $f \in S[[x_i \mid i \in I]]$ can be written as
$f \in S[[x_i \mid i \in I]]$ can be written as ![]() $f = \sum _{n=n_0}^\infty f_n$, where
$f = \sum _{n=n_0}^\infty f_n$, where ![]() $f_n \in S[x_i \mid i \in I]$ is homogeneous of degree n and
$f_n \in S[x_i \mid i \in I]$ is homogeneous of degree n and ![]() $f_{n_0} \neq 0$. Under the given identification, the initial form of f is given by
$f_{n_0} \neq 0$. Under the given identification, the initial form of f is given by ![]() $\operatorname {\mathrm {in}}(f) = f_{n_0}$. If
$\operatorname {\mathrm {in}}(f) = f_{n_0}$. If ![]() $\mathfrak {a} \subset S[[x_i \mid i \in I]]$ is an ideal, then
$\mathfrak {a} \subset S[[x_i \mid i \in I]]$ is an ideal, then ![]() $\operatorname {\mathrm {in}}(\mathfrak {a})$ gets identified with the ideal of
$\operatorname {\mathrm {in}}(\mathfrak {a})$ gets identified with the ideal of ![]() $S[x_i \mid i \in I]$ generated by the initial forms of elements of
$S[x_i \mid i \in I]$ generated by the initial forms of elements of ![]() $\mathfrak {a}$.
$\mathfrak {a}$.
Proposition 2.7. Let ![]() $P = S[x_i \mid i \in I]$ and
$P = S[x_i \mid i \in I]$ and ![]() $\widehat {P} = S[[x_i \mid i \in I]]$, where S is a ring and I a set. Let
$\widehat {P} = S[[x_i \mid i \in I]]$, where S is a ring and I a set. Let ![]() $\mathfrak {a} \subset \widehat {P}$ be an ideal such that
$\mathfrak {a} \subset \widehat {P}$ be an ideal such that ![]() $\operatorname {\mathrm {in}}(\mathfrak {a}) \subset P$ is finitely generated. Then
$\operatorname {\mathrm {in}}(\mathfrak {a}) \subset P$ is finitely generated. Then ![]() $\mathfrak {a}$ is finitely generated and is closed in
$\mathfrak {a}$ is finitely generated and is closed in ![]() $\widehat {P}$.
$\widehat {P}$.
Proof. This is proven in [Reference Eisenbud28, Proposition 7.12] for any ring R which is complete with respect to some filtration ![]() $\mathfrak {m}_i$.
$\mathfrak {m}_i$.
Question 2.8. Does the converse of Proposition 2.7 hold? That is, is the initial ideal ![]() $\operatorname {\mathrm {in}}(\mathfrak {a})$ finitely generated for any finitely generated ideal
$\operatorname {\mathrm {in}}(\mathfrak {a})$ finitely generated for any finitely generated ideal ![]() $\mathfrak {a}$ of
$\mathfrak {a}$ of ![]() $\widehat {P}$? Alternatively, is any finitely generated
$\widehat {P}$? Alternatively, is any finitely generated ![]() $\mathfrak {a}$ already closed inside
$\mathfrak {a}$ already closed inside ![]() $\widehat {P}$?
$\widehat {P}$?
3 Embedding dimension
In this section we briefly recall the notion of embedding dimension and review some basic properties.
Definition 3.1. The embedding dimension of a local ring ![]() $(A, \mathfrak {m}, k)$ is defined to be
$(A, \mathfrak {m}, k)$ is defined to be
 $$ \begin{align*} \mathrm{edim}(A) := \dim_k\left(\mathfrak{m}/\mathfrak{m}^2\right). \end{align*} $$
$$ \begin{align*} \mathrm{edim}(A) := \dim_k\left(\mathfrak{m}/\mathfrak{m}^2\right). \end{align*} $$The k-vector space ![]() $\mathfrak {m}/\mathfrak {m}^2$ is called the Zariski cotangent space of A.
$\mathfrak {m}/\mathfrak {m}^2$ is called the Zariski cotangent space of A.
When the local ring is equicharacteristic, the embedding dimension can equivalently be computed as the dimension of an embedding of the completion in a formal power series ring. Even more, if A is essentially of finite type over an infinite field k, then this embedding exists already at a Zariski-local level (see Theorem 3.15). Before we review these facts, it is convenient to introduce some terminology and discuss some general properties.
Definition 3.2. Let ![]() $(A, \mathfrak {m}, k)$ be an equicharacteristic local ring. A formal coefficient field of A is a subfield
$(A, \mathfrak {m}, k)$ be an equicharacteristic local ring. A formal coefficient field of A is a subfield ![]() $K \subset \widehat {A}$ that maps isomorphically to
$K \subset \widehat {A}$ that maps isomorphically to ![]() $\widehat {A}/\widehat {\mathfrak {m}}$ via the residue map.
$\widehat {A}/\widehat {\mathfrak {m}}$ via the residue map.
As it is well known, every equicharacteristic local ring ![]() $(A, \mathfrak {m}, k)$ admits a formal coefficient field
$(A, \mathfrak {m}, k)$ admits a formal coefficient field ![]() $K \subset \widehat {A}$ (see Remark 3.11).
$K \subset \widehat {A}$ (see Remark 3.11).
In order to talk about a well-behaved notion of cotangent map between completions of non-Noetherian rings, we make the following definition:
Definition 3.3. Let ![]() $(A, \mathfrak {m}, k)$ be a local ring. The k-vector space
$(A, \mathfrak {m}, k)$ be a local ring. The k-vector space  $\widehat {\mathfrak {m}}/\widehat {\mathfrak {m}^2}$ is called the continuous Zariski cotangent space of
$\widehat {\mathfrak {m}}/\widehat {\mathfrak {m}^2}$ is called the continuous Zariski cotangent space of ![]() $\widehat {A}$. A collection of elements
$\widehat {A}$. A collection of elements ![]() $a_i\in \widehat {A}$,
$a_i\in \widehat {A}$, ![]() $i\in I$, are called formal coordinates if their images
$i\in I$, are called formal coordinates if their images ![]() $\overline a_i$ in
$\overline a_i$ in 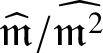 $\widehat {\mathfrak {m}}/\widehat {\mathfrak {m}^2}$ form a basis.
$\widehat {\mathfrak {m}}/\widehat {\mathfrak {m}^2}$ form a basis.
Remark 3.4. The continuous Zariski cotangent space  $\widehat {\mathfrak {m}}/\widehat {\mathfrak {m}^2}$ of
$\widehat {\mathfrak {m}}/\widehat {\mathfrak {m}^2}$ of ![]() $\widehat {A}$ is naturally isomorphic to the Zariski cotangent space
$\widehat {A}$ is naturally isomorphic to the Zariski cotangent space ![]() $\mathfrak {m}/\mathfrak {m}^2$ of A, but in general it is not the same as the Zariski cotangent space
$\mathfrak {m}/\mathfrak {m}^2$ of A, but in general it is not the same as the Zariski cotangent space ![]() $\widehat {\mathfrak {m}}/\widehat {\mathfrak {m}}^2$ of
$\widehat {\mathfrak {m}}/\widehat {\mathfrak {m}}^2$ of ![]() $\widehat {A}$, as seen in Remark 2.3.
$\widehat {A}$, as seen in Remark 2.3.
Remark 3.5. If ![]() $(A, \mathfrak {m}, k)$ is a local ring admitting a coefficient field, then the continuous cotangent space of
$(A, \mathfrak {m}, k)$ is a local ring admitting a coefficient field, then the continuous cotangent space of ![]() $\widehat {A}$ is isomorphic to
$\widehat {A}$ is isomorphic to  $\widehat \Omega _{A/k} \otimes _{\widehat {A}} k$, where
$\widehat \Omega _{A/k} \otimes _{\widehat {A}} k$, where
 $$ \begin{align*} \widehat\Omega_{A/k}:=\varprojlim_n \Omega_{\left(A/\mathfrak{m}^n\right)/k} \end{align*} $$
$$ \begin{align*} \widehat\Omega_{A/k}:=\varprojlim_n \Omega_{\left(A/\mathfrak{m}^n\right)/k} \end{align*} $$is defined as in [Reference Grothendieck32, Chapter ![]() ${0}_{\mathsf{IV}}$, Section 20.7].
${0}_{\mathsf{IV}}$, Section 20.7].
Definition 3.6. Let ![]() $(A, \mathfrak {m}, k)$ be an equicharacteristic local ring. A formal embedding of A is a surjective continuous homomorphism
$(A, \mathfrak {m}, k)$ be an equicharacteristic local ring. A formal embedding of A is a surjective continuous homomorphism ![]() $\tau \colon \widehat {P} \to \widehat {A}$, where
$\tau \colon \widehat {P} \to \widehat {A}$, where ![]() $\widehat {P} = k[[x_i \mid i\in I]]$ is a power series ring. A formal embedding
$\widehat {P} = k[[x_i \mid i\in I]]$ is a power series ring. A formal embedding ![]() $\tau $ is called efficient if the induced map at the level of continuous Zariski cotangent spaces
$\tau $ is called efficient if the induced map at the level of continuous Zariski cotangent spaces 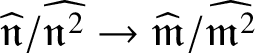 $\widehat {\mathfrak {n}}/\widehat {\mathfrak {n}^2} \to \widehat {\mathfrak {m}}/\widehat {\mathfrak {m}^2}$ is an isomorphism.
$\widehat {\mathfrak {n}}/\widehat {\mathfrak {n}^2} \to \widehat {\mathfrak {m}}/\widehat {\mathfrak {m}^2}$ is an isomorphism.
Proposition 3.7. Let ![]() $(A, \mathfrak {m}, k)$ be an equicharacteristic local ring. Let
$(A, \mathfrak {m}, k)$ be an equicharacteristic local ring. Let ![]() $K \subset \widehat {A}$ be a formal coefficient field, and let
$K \subset \widehat {A}$ be a formal coefficient field, and let ![]() $a_i\in \widehat {A}$,
$a_i\in \widehat {A}$, ![]() $i\in I$, be formal coordinates. Then there exists a unique efficient formal embedding
$i\in I$, be formal coordinates. Then there exists a unique efficient formal embedding ![]() $\tau \colon \widehat {P}=k[[ x_i \mid i\in I]] \to \widehat {A}$ such that
$\tau \colon \widehat {P}=k[[ x_i \mid i\in I]] \to \widehat {A}$ such that ![]() $\tau (k) = K$ and
$\tau (k) = K$ and ![]() $\tau (x_i) = a_i$. Every efficient formal embedding of A is of this form.
$\tau (x_i) = a_i$. Every efficient formal embedding of A is of this form.
Proof. First, note that for every ![]() $n \ge 1$ the composition
$n \ge 1$ the composition ![]() $K \to \widehat {A} \to \widehat {A}/\widehat {\mathfrak {m}^n}$ is injective (since K maps isomorphically to the residue field
$K \to \widehat {A} \to \widehat {A}/\widehat {\mathfrak {m}^n}$ is injective (since K maps isomorphically to the residue field ![]() $k = \widehat {A}/\widehat {\mathfrak {m}}$) and hence gives an embedding
$k = \widehat {A}/\widehat {\mathfrak {m}}$) and hence gives an embedding ![]() $K \subset A/\mathfrak {m}^n$ via the natural isomorphism
$K \subset A/\mathfrak {m}^n$ via the natural isomorphism ![]() $\widehat {A}/\widehat {\mathfrak {m}^n} \simeq A/\mathfrak {m}^n$. Letting
$\widehat {A}/\widehat {\mathfrak {m}^n} \simeq A/\mathfrak {m}^n$. Letting ![]() $P = k[x_i \mid i \in I]$ and
$P = k[x_i \mid i \in I]$ and ![]() $\mathfrak {n} = (x_i \mid i \in I) \subset P$, we have compatible homomorphisms
$\mathfrak {n} = (x_i \mid i \in I) \subset P$, we have compatible homomorphisms ![]() $\tau _n \colon P/\mathfrak {n}^n \to A/\mathfrak {m}^n$ such that
$\tau _n \colon P/\mathfrak {n}^n \to A/\mathfrak {m}^n$ such that ![]() $\tau _n(k) = K$ and
$\tau _n(k) = K$ and ![]() $\tau _n(x_i) = a_i+\mathfrak {m}^n$. Taking limits, these maps define
$\tau _n(x_i) = a_i+\mathfrak {m}^n$. Taking limits, these maps define ![]() $\tau $ and determine it uniquely. By construction,
$\tau $ and determine it uniquely. By construction, ![]() $\operatorname {\mathrm {gr}}(\tau )$ is surjective, and hence
$\operatorname {\mathrm {gr}}(\tau )$ is surjective, and hence ![]() $\tau $ is surjective by [Reference Bourbaki7, Chapter III, Section 2.8, Corollary 2]. Since
$\tau $ is surjective by [Reference Bourbaki7, Chapter III, Section 2.8, Corollary 2]. Since ![]() $\tau $ induces an isomorphism at the level of continuous Zariski cotangent spaces, we see that it is an efficient formal embedding. For the last statement, notice that if
$\tau $ induces an isomorphism at the level of continuous Zariski cotangent spaces, we see that it is an efficient formal embedding. For the last statement, notice that if ![]() $\tau $ is an efficient formal embedding, then clearly
$\tau $ is an efficient formal embedding, then clearly ![]() $K = \tau (k)$ is a formal coefficient field and
$K = \tau (k)$ is a formal coefficient field and ![]() $\tau (x_i)$,
$\tau (x_i)$, ![]() $i\in I$, are formal coordinates.
$i\in I$, are formal coordinates.
The map ![]() $\tau $ in Proposition 3.7 can be interpreted as follows. For short, let
$\tau $ in Proposition 3.7 can be interpreted as follows. For short, let ![]() $P := \operatorname {\mathrm {Sym}}_k (\mathfrak {m}/{\mathfrak {m}^2} )$. Every choice of formal coefficient field
$P := \operatorname {\mathrm {Sym}}_k (\mathfrak {m}/{\mathfrak {m}^2} )$. Every choice of formal coefficient field ![]() $K \subset \widehat {A}$ and formal coordinates
$K \subset \widehat {A}$ and formal coordinates ![]() $a_i \in \widehat {A}$,
$a_i \in \widehat {A}$, ![]() $i \in I$, determines an embedding
$i \in I$, determines an embedding ![]() $\mathfrak {m}/{\mathfrak {m}^2} \hookrightarrow \widehat {A}$ as a K-vector space, and hence a map
$\mathfrak {m}/{\mathfrak {m}^2} \hookrightarrow \widehat {A}$ as a K-vector space, and hence a map ![]() $\tau _0 \colon P \to \widehat {A}$. Letting
$\tau _0 \colon P \to \widehat {A}$. Letting ![]() $x_i = a_i + \mathfrak {m}^2 \in P$, we get a natural identification
$x_i = a_i + \mathfrak {m}^2 \in P$, we get a natural identification ![]() $P = k[x_i \mid i\in I]$. Then the map
$P = k[x_i \mid i\in I]$. Then the map ![]() $\tau $ is obtained from
$\tau $ is obtained from ![]() $\tau _0$ by completing the domain P.
$\tau _0$ by completing the domain P.
Remark 3.8. There is also a natural embedding ![]() $\mathfrak {m}/\mathfrak {m}^2 \hookrightarrow \operatorname {\mathrm {gr}}(A)$ as a k-vector space, which induces a map
$\mathfrak {m}/\mathfrak {m}^2 \hookrightarrow \operatorname {\mathrm {gr}}(A)$ as a k-vector space, which induces a map ![]() $\gamma \colon P \to \operatorname {\mathrm {gr}}(A)$. It is immediate from the construction that
$\gamma \colon P \to \operatorname {\mathrm {gr}}(A)$. It is immediate from the construction that ![]() $\operatorname {\mathrm {gr}}(\tau ) = \gamma $. In particular we see that
$\operatorname {\mathrm {gr}}(\tau ) = \gamma $. In particular we see that ![]() $\operatorname {\mathrm {gr}}(\tau )$ is independent of any choices. On the other hand,
$\operatorname {\mathrm {gr}}(\tau )$ is independent of any choices. On the other hand, ![]() $\tau $ itself certainly depends on the choices of the formal coefficient field K and formal coordinates
$\tau $ itself certainly depends on the choices of the formal coefficient field K and formal coordinates ![]() $a_i\in \widehat {A}$,
$a_i\in \widehat {A}$, ![]() $i\in I$.
$i\in I$.
The following result addresses the dependence of ![]() $\tau $ on K and
$\tau $ on K and ![]() $\{a_i \mid i\in I\}$:
$\{a_i \mid i\in I\}$:
Proposition 3.9. Let ![]() $(A, \mathfrak {m}, k)$ be an equicharacteristic local ring, let
$(A, \mathfrak {m}, k)$ be an equicharacteristic local ring, let ![]() $K, K' \subset \widehat {A}$ be two formal coefficient fields and let
$K, K' \subset \widehat {A}$ be two formal coefficient fields and let ![]() $\{a_i \mid i\in I\} \subset \widehat {A}$ and
$\{a_i \mid i\in I\} \subset \widehat {A}$ and  $ \{a^{\prime }_i \mid i\in I \} \subset \widehat {A}$ be two sets of formal coordinates. Consider the two maps
$ \{a^{\prime }_i \mid i\in I \} \subset \widehat {A}$ be two sets of formal coordinates. Consider the two maps ![]() $\tau \colon \widehat {P} := k[[x_i \mid i\in I]] \to \widehat {A}$ and
$\tau \colon \widehat {P} := k[[x_i \mid i\in I]] \to \widehat {A}$ and 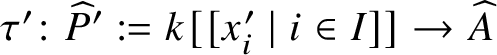 $\tau ' \colon \widehat {P}' := k [ [x_i' \mid i\in I ] ] \to \widehat {A}$ given by Proposition 3.7. Then there exists an isomorphism
$\tau ' \colon \widehat {P}' := k [ [x_i' \mid i\in I ] ] \to \widehat {A}$ given by Proposition 3.7. Then there exists an isomorphism ![]() $\varphi \colon \widehat {P}' \to \widehat {P}$ such that
$\varphi \colon \widehat {P}' \to \widehat {P}$ such that ![]() $\tau ' = \tau \circ \varphi $.
$\tau ' = \tau \circ \varphi $.
The proof of this proposition relies on the following basic property of formally smooth algebras. The statement is a natural generalisation of the definition of formal smoothness, which guarantees lifting not only via extensions with nilpotent kernel but also via extensions with topologically nilpotent kernel.
Proposition 3.10. Let ![]() $k_0$ be a topological ring and k a formally smooth
$k_0$ be a topological ring and k a formally smooth ![]() $k_0$-algebra. Let C be a complete metrisable topological
$k_0$-algebra. Let C be a complete metrisable topological ![]() $k_0$-algebra and
$k_0$-algebra and ![]() $\mathcal {I} \subset C$ a closed ideal such that
$\mathcal {I} \subset C$ a closed ideal such that ![]() $\{\mathcal {I}^n\}$ tends to zero. Then every continuous
$\{\mathcal {I}^n\}$ tends to zero. Then every continuous ![]() $k_0$-algebra homomorphism
$k_0$-algebra homomorphism ![]() $u \colon k \to C/\mathcal {I}$ factors as
$u \colon k \to C/\mathcal {I}$ factors as ![]() $k \xrightarrow {v} C \to C/\mathcal {I}$, where v is a continuous
$k \xrightarrow {v} C \to C/\mathcal {I}$, where v is a continuous ![]() $k_0$-algebra homomorphism:
$k_0$-algebra homomorphism:

Proof. See [Reference Grothendieck32, Chapter ![]() ${0}_{\mathsf{IV}}$, Proposition 19.3.10].
${0}_{\mathsf{IV}}$, Proposition 19.3.10].
Remark 3.11. Proposition 3.10 implies the existence of formal coefficient fields for any equicharacteristic local ring ![]() $(A, \mathfrak {m}, k)$. In this case,
$(A, \mathfrak {m}, k)$. In this case, ![]() $C = \widehat {A}$,
$C = \widehat {A}$, ![]() $\mathcal {I} = \widehat {\mathfrak {m}}$,
$\mathcal {I} = \widehat {\mathfrak {m}}$, ![]() $k_0$ is the prime field contained in
$k_0$ is the prime field contained in ![]() $\widehat {A}$, k is the residue field and u is the identity. Notice that
$\widehat {A}$, k is the residue field and u is the identity. Notice that ![]() $k_0$ is perfect, and therefore k is separable over
$k_0$ is perfect, and therefore k is separable over ![]() $k_0$ (hence formally smooth). Then
$k_0$ (hence formally smooth). Then ![]() $K = v(k)$ is a formal coefficient field.
$K = v(k)$ is a formal coefficient field.
Let S be any discrete topological ring. For any two topological S-algebras T and ![]() $T'$, the tensor product
$T'$, the tensor product ![]() $T\otimes _S T'$ is endowed with the final topology with respect to its natural maps. The completed tensor product
$T\otimes _S T'$ is endowed with the final topology with respect to its natural maps. The completed tensor product ![]() $T \hat {\otimes }_S T'$ is defined to be the completion of
$T \hat {\otimes }_S T'$ is defined to be the completion of ![]() $T\otimes _S T'$. Note that the operation
$T\otimes _S T'$. Note that the operation ![]() $\hat {\otimes }_S$ is the coproduct in the category of complete topological S-algebras.
$\hat {\otimes }_S$ is the coproduct in the category of complete topological S-algebras.
Lemma 3.12. Let ![]() $(S,\mathfrak {n},k)$ be a local k-algebra. Any continuous S-algebra map
$(S,\mathfrak {n},k)$ be a local k-algebra. Any continuous S-algebra map
which induces an isomorphism of continuous cotangent spaces is an isomorphism.
Proof. Note that a basis for the topology on ![]() $S \otimes _k k[[t_i \mid i \in I]]$ is given by the filtration
$S \otimes _k k[[t_i \mid i \in I]]$ is given by the filtration
 $$ \begin{align*} \mathfrak{m}_n:=\sum_{d+e=n} \mathfrak{n}^d + \big((t_i \mid i\in I)^e\big)\widehat{\phantom{t}}. \end{align*} $$
$$ \begin{align*} \mathfrak{m}_n:=\sum_{d+e=n} \mathfrak{n}^d + \big((t_i \mid i\in I)^e\big)\widehat{\phantom{t}}. \end{align*} $$Thus it follows that for the associated graded rings we have
The map ![]() $\varphi $ induces a
$\varphi $ induces a ![]() $\operatorname {\mathrm {gr}}(S)$-algebra map
$\operatorname {\mathrm {gr}}(S)$-algebra map
which by assumption is an isomorphism. Thus we can use [Reference Artin3, Lemma 10.23] to see that ![]() $\varphi $ is bijective. It is easy to check that
$\varphi $ is bijective. It is easy to check that ![]() $\varphi ^{-1}$ is continuous, and we are done.
$\varphi ^{-1}$ is continuous, and we are done.
Proof of Proposition 3.9
Let ![]() $k_0$ be the prime field contained in
$k_0$ be the prime field contained in ![]() $\widehat {A}$. Notice that k is formally smooth over
$\widehat {A}$. Notice that k is formally smooth over ![]() $k_0$. We apply Proposition 3.10 in the situation in which
$k_0$. We apply Proposition 3.10 in the situation in which ![]() $C = \widehat {P}$,
$C = \widehat {P}$, ![]() $\mathcal {I} = \ker (\tau )$ and
$\mathcal {I} = \ker (\tau )$ and ![]() $u \colon k \to \widehat {A} = C/\mathcal {I}$ is the map such that
$u \colon k \to \widehat {A} = C/\mathcal {I}$ is the map such that ![]() $u(k) = K'$. Notice that
$u(k) = K'$. Notice that ![]() $\mathcal {I} = \tau ^{-1}(0)$ is closed because
$\mathcal {I} = \tau ^{-1}(0)$ is closed because ![]() $\widehat {A}$ is separated, and that
$\widehat {A}$ is separated, and that ![]() $\{\mathcal {I}^n\}$ tends to zero because
$\{\mathcal {I}^n\}$ tends to zero because ![]() $\mathcal {I}^n \subset \widehat {\mathfrak {n}^n}$. We get a map
$\mathcal {I}^n \subset \widehat {\mathfrak {n}^n}$. We get a map ![]() $v \colon k \to \widehat {P}$ verifying
$v \colon k \to \widehat {P}$ verifying ![]() $\tau (v(k)) = K'$.
$\tau (v(k)) = K'$.
Since ![]() $\tau $ is surjective, there exist power series
$\tau $ is surjective, there exist power series ![]() $f_i \in \widehat {P}$ such that
$f_i \in \widehat {P}$ such that ![]() $\tau (f_i) = a_i'$. The map
$\tau (f_i) = a_i'$. The map ![]() $\varphi $ is given by
$\varphi $ is given by ![]() $\varphi (x_i' ) = f_i$ and
$\varphi (x_i' ) = f_i$ and ![]() $\varphi \rvert _k = v$. Lemma 3.12 shows that
$\varphi \rvert _k = v$. Lemma 3.12 shows that ![]() $\varphi $ is an isomorphism.
$\varphi $ is an isomorphism.
Remark 3.13. By the same argument as in the proof of Proposition 3.9, one can see that given any two formal embeddings ![]() $\tau \colon \widehat {P} \to \widehat {A}$ and
$\tau \colon \widehat {P} \to \widehat {A}$ and ![]() $\tau ' \colon \widehat {P}' \to \widehat {A}$ (not necessarily efficient), there is always a map
$\tau ' \colon \widehat {P}' \to \widehat {A}$ (not necessarily efficient), there is always a map ![]() $\varphi \colon \widehat {P}' \to \widehat {P}$ such that
$\varphi \colon \widehat {P}' \to \widehat {P}$ such that ![]() $\tau ' = \tau \circ \varphi $, and if
$\tau ' = \tau \circ \varphi $, and if ![]() $\tau $ is efficient then
$\tau $ is efficient then ![]() $\varphi $ is surjective.
$\varphi $ is surjective.
Proposition 3.14. For every equicharacteristic local ring ![]() $(A, \mathfrak {m}, k)$ we have
$(A, \mathfrak {m}, k)$ we have
 $$ \begin{align*} \mathrm{edim}(A) = \min_{\tau} \dim \widehat{P}, \end{align*} $$
$$ \begin{align*} \mathrm{edim}(A) = \min_{\tau} \dim \widehat{P}, \end{align*} $$where the minimum is taken over all choices of formal embeddings ![]() $\tau \colon \widehat {P} \to \widehat {A}$ and is achieved whenever
$\tau \colon \widehat {P} \to \widehat {A}$ and is achieved whenever ![]() $\tau $ is an efficient formal embedding.
$\tau $ is an efficient formal embedding.
Proof. Let ![]() $\tau \colon \widehat {P} \to \widehat {A}$ be a formal embedding, and write
$\tau \colon \widehat {P} \to \widehat {A}$ be a formal embedding, and write ![]() $P = k[x_i \mid i \in I]$ and
$P = k[x_i \mid i \in I]$ and ![]() $\mathfrak {n} = (x_i \mid i\in I) \subset P$. Since
$\mathfrak {n} = (x_i \mid i\in I) \subset P$. Since ![]() $\tau $ is continuous, we have that
$\tau $ is continuous, we have that ![]() $\tau (\widehat {\mathfrak {n}}^c ) \subset \widehat {\mathfrak {m}}$ for some c. As
$\tau (\widehat {\mathfrak {n}}^c ) \subset \widehat {\mathfrak {m}}$ for some c. As ![]() $\widehat {\mathfrak {m}}$ is maximal, this forces
$\widehat {\mathfrak {m}}$ is maximal, this forces ![]() $\tau (\widehat {\mathfrak {n}} ) \subset \widehat {\mathfrak {m}}$, and continuity gives
$\tau (\widehat {\mathfrak {n}} ) \subset \widehat {\mathfrak {m}}$, and continuity gives ![]() $\tau (\widehat {\mathfrak {n}^n} ) \subset \widehat {\mathfrak {m}^n}$ for all n. Hence we get an induced map at the level of graded rings
$\tau (\widehat {\mathfrak {n}^n} ) \subset \widehat {\mathfrak {m}^n}$ for all n. Hence we get an induced map at the level of graded rings ![]() $\operatorname {\mathrm {gr}}(\tau ) \colon P \to \operatorname {\mathrm {gr}}(A)$. Since
$\operatorname {\mathrm {gr}}(\tau ) \colon P \to \operatorname {\mathrm {gr}}(A)$. Since ![]() $\tau $ is surjective,
$\tau $ is surjective, ![]() $\operatorname {\mathrm {gr}}(\tau )$ is also surjective and
$\operatorname {\mathrm {gr}}(\tau )$ is also surjective and ![]() $\tau (\widehat {\mathfrak {n}^n} ) = \widehat {\mathfrak {m}^n}$ for every n. In particular,
$\tau (\widehat {\mathfrak {n}^n} ) = \widehat {\mathfrak {m}^n}$ for every n. In particular, ![]() $\tau $ induces a surjection at the level of Zariski cotangent spaces
$\tau $ induces a surjection at the level of Zariski cotangent spaces ![]() $\mathfrak {n}/\mathfrak {n}^2 \to \mathfrak {m}/\mathfrak {m}^2$, and we see that
$\mathfrak {n}/\mathfrak {n}^2 \to \mathfrak {m}/\mathfrak {m}^2$, and we see that ![]() $\mathrm {edim}(A) \leq \dim \widehat {P}$. If
$\mathrm {edim}(A) \leq \dim \widehat {P}$. If ![]() $\tau $ is an efficient formal embedding, then the map
$\tau $ is an efficient formal embedding, then the map ![]() $\mathfrak {n}/\mathfrak {n}^2 \to \mathfrak {m}/\mathfrak {m}^2$ is an isomorphism and we have
$\mathfrak {n}/\mathfrak {n}^2 \to \mathfrak {m}/\mathfrak {m}^2$ is an isomorphism and we have ![]() $\mathrm {edim}(A) = \dim \widehat {P}$.
$\mathrm {edim}(A) = \dim \widehat {P}$.
We finish this section by recalling the following result, which guarantees the existence of a Zariski-local minimal embedding for singular points of a scheme of finite type over an infinite field. This is well known in the case of complex varieties (see, for example, [Reference Bochnak and Kucharz6, Theorem 3]) and we provide an extension of the proof to the more general case considered here.
Theorem 3.15. Let X be a scheme of finite type over an infinite field k and let ![]() $x\in X(k)$. If
$x\in X(k)$. If ![]() $\mathrm {edim}(X,x)=d$ and X is not smooth at x, then there exist a closed subscheme
$\mathrm {edim}(X,x)=d$ and X is not smooth at x, then there exist a closed subscheme  $Y\subset {\mathbb A}^d_k$, a point
$Y\subset {\mathbb A}^d_k$, a point ![]() $y\in Y(k)$ and an isomorphism
$y\in Y(k)$ and an isomorphism
Proof. We may assume that X is projective and embedded in ![]() ${\mathbb P}^n$ for some
${\mathbb P}^n$ for some ![]() $n> d$. Denote by
$n> d$. Denote by ![]() $\bar {k}$ the algebraic closure of k and write
$\bar {k}$ the algebraic closure of k and write ![]() $\bar {X}:=X\times _k \operatorname {\mathrm {Spec}} (\bar {k} )$ and
$\bar {X}:=X\times _k \operatorname {\mathrm {Spec}} (\bar {k} )$ and ![]() $\bar {x}$ for the
$\bar {x}$ for the ![]() $\bar {k}$-point on
$\bar {k}$-point on ![]() $\bar {X}$ corresponding to x. As
$\bar {X}$ corresponding to x. As ![]() $\mathcal {O}_{\bar {X},\bar {x}}$ is not a regular ring, we have
$\mathcal {O}_{\bar {X},\bar {x}}$ is not a regular ring, we have
Suppose we can find a linear projection ![]() $\pi \colon {\mathbb P}^n \to {\mathbb P}^d$ defined over k such that if
$\pi \colon {\mathbb P}^n \to {\mathbb P}^d$ defined over k such that if ![]() $\bar {Y}$ denotes the scheme-theoretic image of
$\bar {Y}$ denotes the scheme-theoretic image of ![]() $\bar {X}$ under
$\bar {X}$ under ![]() $\pi $ and
$\pi $ and ![]() $\bar {y}=\pi (\bar {x})$, then the induced map
$\bar {y}=\pi (\bar {x})$, then the induced map ![]() $\mathcal {O}_{\bar {Y},\bar {y}}\to \mathcal {O}_{\bar {X},\bar {x}}$ is an isomorphism. Since
$\mathcal {O}_{\bar {Y},\bar {y}}\to \mathcal {O}_{\bar {X},\bar {x}}$ is an isomorphism. Since ![]() $\bar {Y}=Y\times _k \operatorname {\mathrm {Spec}} (\bar {k} )$, where Y is the scheme-theoretic image of X under the linear projection centred at x, we obtain a map
$\bar {Y}=Y\times _k \operatorname {\mathrm {Spec}} (\bar {k} )$, where Y is the scheme-theoretic image of X under the linear projection centred at x, we obtain a map ![]() $\mathcal {O}_{Y,y}\to \mathcal {O}_{X,x}$ whose base change to
$\mathcal {O}_{Y,y}\to \mathcal {O}_{X,x}$ whose base change to ![]() $\bar {k}$ gives the foregoing map. Thus, by faithfully flat descent, we get that
$\bar {k}$ gives the foregoing map. Thus, by faithfully flat descent, we get that ![]() $\mathcal {O}_{Y,y}\simeq \mathcal {O}_{X,x}$.
$\mathcal {O}_{Y,y}\simeq \mathcal {O}_{X,x}$.
Now, in order to prove the claim, let  $\bar {T}\subset {\mathbb P}^n_{\bar {k}}$ be the unique linear space passing through
$\bar {T}\subset {\mathbb P}^n_{\bar {k}}$ be the unique linear space passing through ![]() $\bar {x}$ whose tangent space at
$\bar {x}$ whose tangent space at ![]() $\bar {x}$ agrees with that of
$\bar {x}$ agrees with that of ![]() $\bar {X}$. Furthermore, let
$\bar {X}$. Furthermore, let ![]() $\bar {S}$ be the closure of the set of all lines connecting
$\bar {S}$ be the closure of the set of all lines connecting ![]() $\bar {z}$ with
$\bar {z}$ with ![]() $\bar {x}$, where
$\bar {x}$, where ![]() $\bar {z}\in \bar {X}$,
$\bar {z}\in \bar {X}$, ![]() $\bar {z}\neq \bar {x}$. Note that
$\bar {z}\neq \bar {x}$. Note that ![]() $\dim (\bar {S} )=\dim (\bar {X} )+1\leq d$. Consider now the closure
$\dim (\bar {S} )=\dim (\bar {X} )+1\leq d$. Consider now the closure ![]() $\bar {Z}$ of the set
$\bar {Z}$ of the set ![]() $\bar {X}\cup \bar {T} \cup \bar {S}$, equipped with its reduced scheme structure. Since
$\bar {X}\cup \bar {T} \cup \bar {S}$, equipped with its reduced scheme structure. Since ![]() $\dim (\bar {S} )\leq d$ the set of all linear spaces
$\dim (\bar {S} )\leq d$ the set of all linear spaces ![]() $\bar {L}$ with
$\bar {L}$ with ![]() $\bar {L}\cap \bar {Z}=\emptyset $ is open inside
$\bar {L}\cap \bar {Z}=\emptyset $ is open inside ![]() $\operatorname {\mathrm {Gr}}(n-d-1,n)\times _k \operatorname {\mathrm {Spec}} (\bar {k} )$. The preimage of this set in
$\operatorname {\mathrm {Gr}}(n-d-1,n)\times _k \operatorname {\mathrm {Spec}} (\bar {k} )$. The preimage of this set in ![]() $\operatorname {\mathrm {Gr}}(n-d-1,n)$ is a nonempty open set, and since k is infinite, it has a k-rational point, which we denote by L. Hence we have that the corresponding projection
$\operatorname {\mathrm {Gr}}(n-d-1,n)$ is a nonempty open set, and since k is infinite, it has a k-rational point, which we denote by L. Hence we have that the corresponding projection ![]() $\pi _L\colon {\mathbb P}^n\to {\mathbb P}^d$, defined over k, satisfies
$\pi _L\colon {\mathbb P}^n\to {\mathbb P}^d$, defined over k, satisfies  $\pi _{\bar {L}}^{-1} (\bar {y} ) \cap \bar {X} = \{\bar {x} \}$ set-theoretically, where
$\pi _{\bar {L}}^{-1} (\bar {y} ) \cap \bar {X} = \{\bar {x} \}$ set-theoretically, where ![]() $\bar {y}$ corresponds to the k-point
$\bar {y}$ corresponds to the k-point ![]() $y:=\pi _L(x)$. Writing
$y:=\pi _L(x)$. Writing ![]() $\bar {Y}:=\pi _{\bar {L}} (\bar {X} )$, we get that the map of local rings
$\bar {Y}:=\pi _{\bar {L}} (\bar {X} )$, we get that the map of local rings ![]() $\mathcal {O}_{\bar {Y},\bar {y}}\to \mathcal {O}_{\bar {X},\bar {x}}$ is injective and finite. Since
$\mathcal {O}_{\bar {Y},\bar {y}}\to \mathcal {O}_{\bar {X},\bar {x}}$ is injective and finite. Since ![]() $\bar {L}\cap \bar {T}=\emptyset $, the tangent spaces of
$\bar {L}\cap \bar {T}=\emptyset $, the tangent spaces of ![]() $\bar {x}$ and
$\bar {x}$ and ![]() $\bar {y}$ are isomorphic and thus
$\bar {y}$ are isomorphic and thus ![]() $\mathfrak {m}_{\bar {y}}\mathcal {O}_{\bar {X},\bar {x}}=\mathfrak {m}_{\bar {x}}$. The claim now follows from the Nakayama lemma.
$\mathfrak {m}_{\bar {y}}\mathcal {O}_{\bar {X},\bar {x}}=\mathfrak {m}_{\bar {x}}$. The claim now follows from the Nakayama lemma.
4 Flatness of completion
Let A be a ring and ![]() $\mathfrak {m}$ an ideal in A. Given an A-module E, we will consider the
$\mathfrak {m}$ an ideal in A. Given an A-module E, we will consider the ![]() $\mathfrak {m}$-adic topology on E and we will denote by
$\mathfrak {m}$-adic topology on E and we will denote by ![]() $\widehat {E}$ its
$\widehat {E}$ its ![]() $\mathfrak {m}$-adic completion. We are interested in conditions guaranteeing that the natural map
$\mathfrak {m}$-adic completion. We are interested in conditions guaranteeing that the natural map ![]() $A \to \widehat {A}$ is flat.
$A \to \widehat {A}$ is flat.
Definition 4.1. Let E be an A-module and F a submodule of E. We say that ![]() $F \subseteq E$ has the Artin–Rees property with respect to
$F \subseteq E$ has the Artin–Rees property with respect to ![]() $\mathfrak {m}$ if there exists a
$\mathfrak {m}$ if there exists a ![]() $c \in {\mathbb N}$ such that for all
$c \in {\mathbb N}$ such that for all ![]() $n> c$, we have
$n> c$, we have
The smallest such c is called the Artin–Rees index of ![]() $F \subseteq E$ with respect to
$F \subseteq E$ with respect to ![]() $\mathfrak {m}$. We say that A has the Artin–Rees property with respect to
$\mathfrak {m}$. We say that A has the Artin–Rees property with respect to ![]() $\mathfrak {m}$ if so does every finitely generated submodule of a finitely generated free A-module.
$\mathfrak {m}$ if so does every finitely generated submodule of a finitely generated free A-module.
The Artin–Rees property for ![]() $F \subseteq E$ guarantees that the
$F \subseteq E$ guarantees that the ![]() $\mathfrak {m}$-adic topology of F coincides with the topology induced by the
$\mathfrak {m}$-adic topology of F coincides with the topology induced by the ![]() $\mathfrak {m}$-adic topology of E. In this context it is natural to consider the Rees algebra
$\mathfrak {m}$-adic topology of E. In this context it is natural to consider the Rees algebra ![]() $A^* = \bigoplus _{n \geq 0} \mathfrak {m}^n$ and the graded
$A^* = \bigoplus _{n \geq 0} \mathfrak {m}^n$ and the graded ![]() $A^*$-modules
$A^*$-modules
 $$ \begin{align*} E^* = \bigoplus_{n \geq 0} \mathfrak{m}^n E \qquad\text{and}\qquad F^* = \bigoplus_{n \geq 0} \mathfrak{m}^n E \cap F. \end{align*} $$
$$ \begin{align*} E^* = \bigoplus_{n \geq 0} \mathfrak{m}^n E \qquad\text{and}\qquad F^* = \bigoplus_{n \geq 0} \mathfrak{m}^n E \cap F. \end{align*} $$Lemma 4.2. ![]() $F \subseteq E$ has the Artin–Rees property if and only if there exists a
$F \subseteq E$ has the Artin–Rees property if and only if there exists a ![]() $c \in {\mathbb N}$ such that
$c \in {\mathbb N}$ such that ![]() $F^*$ is generated as a graded
$F^*$ is generated as a graded ![]() $A^*$-module by elements of degree
$A^*$-module by elements of degree ![]() $\leq c$. Moreover, the Artin–Rees index of
$\leq c$. Moreover, the Artin–Rees index of ![]() $F \subseteq E$ is the smallest such c.
$F \subseteq E$ is the smallest such c.
Proof. This is immediate from the definitions. Compare with [Reference Bourbaki7, Chapter III, Section 3.1, Theorem 1] or [Reference Matsumura36, Theorem 8.5] or [Reference Artin3, Lemma 10.8], but notice that no finite generation hypotheses are needed for the statement of the lemma.
Remark 4.3. By the classical Artin–Rees lemma [Reference Matsumura36, Theorem 8.5], any Noetherian ring A has the Artin–Rees property with respect to any ideal ![]() $\mathfrak {m} \subset A$. By contrast, there exist non-Noetherian rings, even finite dimensional, which do not have the Artin–Rees property. A zero-dimensional example is given by
$\mathfrak {m} \subset A$. By contrast, there exist non-Noetherian rings, even finite dimensional, which do not have the Artin–Rees property. A zero-dimensional example is given by
 $$ \begin{align*} A = k[x_i \mid i \in {\mathbb N}]/\left(x_1-x_m^m \mid m \ge 2\right) + \left(x_n^{n+1} \mid n \ge 1\right), \end{align*} $$
$$ \begin{align*} A = k[x_i \mid i \in {\mathbb N}]/\left(x_1-x_m^m \mid m \ge 2\right) + \left(x_n^{n+1} \mid n \ge 1\right), \end{align*} $$with ![]() $\mathfrak {m} = (x_i \mid i \in {\mathbb N})$ and
$\mathfrak {m} = (x_i \mid i \in {\mathbb N})$ and ![]() $F = (x_1) \subset E = A$. Clearly
$F = (x_1) \subset E = A$. Clearly ![]() $x_1 \in \mathfrak {m}^n$ for all n, but there is no
$x_1 \in \mathfrak {m}^n$ for all n, but there is no ![]() $f \in \mathfrak {m}$ such that
$f \in \mathfrak {m}$ such that ![]() $x_1 = x_1 f$.
$x_1 = x_1 f$.
In complete analogy with the Noetherian case, we prove that the Artin–Rees property implies flatness of the completion. We recall that a ring is coherent if every finitely generated ideal is finitely presented.
Proposition 4.4. Let A be a coherent ring with the Artin–Rees property with respect to ![]() $\mathfrak {m} \subset A$, and let
$\mathfrak {m} \subset A$, and let ![]() $\widehat {A}$ be its
$\widehat {A}$ be its ![]() $\mathfrak {m}$-adic completion. Then
$\mathfrak {m}$-adic completion. Then ![]() $A \to \widehat {A}$ is flat. Moreover, if
$A \to \widehat {A}$ is flat. Moreover, if ![]() $\mathfrak {a} \subset A$ is a finitely generated ideal, then
$\mathfrak {a} \subset A$ is a finitely generated ideal, then ![]() $\mathfrak {a} \widehat {A}$ is closed in
$\mathfrak {a} \widehat {A}$ is closed in ![]() $\widehat {A}$ (that is,
$\widehat {A}$ (that is, ![]() $\mathfrak {a} \widehat {A} = \widehat {\mathfrak {a}}$).
$\mathfrak {a} \widehat {A} = \widehat {\mathfrak {a}}$).
Proof. Let ![]() $\mathfrak {a}$ be a finitely generated ideal of A. Since A is coherent, there exists an exact sequence
$\mathfrak {a}$ be a finitely generated ideal of A. Since A is coherent, there exists an exact sequence
Moreover, since the Artin–Rees property holds for ![]() $\ker \varphi \subset A^q$, the
$\ker \varphi \subset A^q$, the ![]() $\mathfrak {m}$-adic topology on
$\mathfrak {m}$-adic topology on ![]() $\ker \varphi $ agrees with the one induced by the inclusion
$\ker \varphi $ agrees with the one induced by the inclusion ![]() $\ker \varphi \subset A^q$. From [Reference Bourbaki7, Chapter III, Section 2.12, Lemma 2] or [Reference Artin3, Lemma 10.3], the sequence remains exact after taking
$\ker \varphi \subset A^q$. From [Reference Bourbaki7, Chapter III, Section 2.12, Lemma 2] or [Reference Artin3, Lemma 10.3], the sequence remains exact after taking ![]() $\mathfrak {m}$-adic completions, and we have a commutative diagram
$\mathfrak {m}$-adic completions, and we have a commutative diagram

with exact rows. Since taking completion commutes with finite direct sums, the map ![]() $\mathfrak {a} \otimes _A \widehat {A} \to \widehat {\mathfrak {a}}$ is an isomorphism. As the natural map
$\mathfrak {a} \otimes _A \widehat {A} \to \widehat {\mathfrak {a}}$ is an isomorphism. As the natural map ![]() $\widehat {\mathfrak {a}} \to \widehat {A}$ is an injection, the flatness of
$\widehat {\mathfrak {a}} \to \widehat {A}$ is an injection, the flatness of ![]() $A \to \widehat {A}$ follows from [Reference Matsumura36, Theorem 7.7]. The fact that
$A \to \widehat {A}$ follows from [Reference Matsumura36, Theorem 7.7]. The fact that ![]() $\mathfrak {a} \otimes _A \widehat {A} \to \widehat {\mathfrak {a}}$ is an isomorphism also shows that
$\mathfrak {a} \otimes _A \widehat {A} \to \widehat {\mathfrak {a}}$ is an isomorphism also shows that ![]() $\mathfrak {a}\widehat {A} = \widehat {\mathfrak {a}}$.
$\mathfrak {a}\widehat {A} = \widehat {\mathfrak {a}}$.
The following theorem gives a first example of a non-Noetherian ring with the Artin–Rees property. We were not able to find a reference for this statement in the literature.
Theorem 4.5. Let S be a Noetherian ring and ![]() $\mathfrak {n}$ any ideal of S. For any set I, consider
$\mathfrak {n}$ any ideal of S. For any set I, consider ![]() $P = S[x_i \mid i \in I]$ and
$P = S[x_i \mid i \in I]$ and ![]() $\mathfrak {m} = (x_i \mid i \in I) + \mathfrak {n}$. Then P has the Artin–Rees property with respect to
$\mathfrak {m} = (x_i \mid i \in I) + \mathfrak {n}$. Then P has the Artin–Rees property with respect to ![]() $\mathfrak {m}$.
$\mathfrak {m}$.
Proof. Let E be a finitely generated free P-module and ![]() $F \subseteq E$ a finitely generated submodule. Assume that E is freely generated by
$F \subseteq E$ a finitely generated submodule. Assume that E is freely generated by ![]() $e_1, \dotsc , e_s$.
$e_1, \dotsc , e_s$.
Given any subset ![]() $J \subseteq I$, we write
$J \subseteq I$, we write ![]() $P_J := S[x_i \mid i \in J]$, and for any ideal
$P_J := S[x_i \mid i \in J]$, and for any ideal ![]() $\mathfrak {a} \subseteq P$ we denote
$\mathfrak {a} \subseteq P$ we denote ![]() $\mathfrak {a}_J := \mathfrak {a} \cap P_J$. We define
$\mathfrak {a}_J := \mathfrak {a} \cap P_J$. We define ![]() $E_J := P_J \cdot e_1 \oplus \dotsb \oplus P_J \cdot e_s$, and for any P-submodule
$E_J := P_J \cdot e_1 \oplus \dotsb \oplus P_J \cdot e_s$, and for any P-submodule ![]() $G \subseteq E$ we write
$G \subseteq E$ we write ![]() $G_J := E_J \cap G$. Note that
$G_J := E_J \cap G$. Note that ![]() $P, \mathfrak {m}, \mathfrak {a}, E, G$ are the colimits of
$P, \mathfrak {m}, \mathfrak {a}, E, G$ are the colimits of ![]() $P_J, \mathfrak {m}_J, \mathfrak {a}_J, E_J, G_J$ for
$P_J, \mathfrak {m}_J, \mathfrak {a}_J, E_J, G_J$ for ![]() $J \subseteq I$ finite. We have
$J \subseteq I$ finite. We have
In particular, for all ![]() $n, d \in {\mathbb N}$ with
$n, d \in {\mathbb N}$ with ![]() $n> d$, we have
$n> d$, we have
 $$ \begin{align*} \mathfrak{m}_J^n E_J \cap F_J = (\mathfrak{m}^n E \cap F)_J \qquad\text{and}\qquad \mathfrak{m}_J^{n-d}\left(\mathfrak{m}_J^d E_J \cap F_J\right) \subseteq \left(\mathfrak{m}^{n-d}\left(\mathfrak{m}^d E \cap F\right)\right)_J. \end{align*} $$
$$ \begin{align*} \mathfrak{m}_J^n E_J \cap F_J = (\mathfrak{m}^n E \cap F)_J \qquad\text{and}\qquad \mathfrak{m}_J^{n-d}\left(\mathfrak{m}_J^d E_J \cap F_J\right) \subseteq \left(\mathfrak{m}^{n-d}\left(\mathfrak{m}^d E \cap F\right)\right)_J. \end{align*} $$ Assume that F is generated by ![]() $f_1, \dotsc , f_r$. Then there exists a finite set
$f_1, \dotsc , f_r$. Then there exists a finite set ![]() $L \subset I$ such that
$L \subset I$ such that ![]() $f_1,\dotsc ,f_r \in F_L$, and for any J with
$f_1,\dotsc ,f_r \in F_L$, and for any J with ![]() $L \subseteq J \subseteq I$ we have
$L \subseteq J \subseteq I$ we have ![]() $F_J = P_J \cdot f_1 + \dotsb + P_J \cdot f_r = P_J \cdot F_L$.
$F_J = P_J \cdot f_1 + \dotsb + P_J \cdot f_r = P_J \cdot F_L$.
Since ![]() $P_L$ is Noetherian, it has the Artin–Rees property with respect to
$P_L$ is Noetherian, it has the Artin–Rees property with respect to ![]() $\mathfrak {m}_L$, and hence there exists a
$\mathfrak {m}_L$, and hence there exists a ![]() $c \in {\mathbb N}$ such that
$c \in {\mathbb N}$ such that
for all ![]() $n> c$. The smallest such c is the Artin–Rees index of
$n> c$. The smallest such c is the Artin–Rees index of ![]() $F_L \subseteq E_L$. Since for any finite set J with
$F_L \subseteq E_L$. Since for any finite set J with ![]() $L \subseteq J \subset I$ we have
$L \subseteq J \subset I$ we have ![]() $F_J = P_J \cdot F_L$, we can apply Lemma 4.6, and we see that the Artin–Rees index of
$F_J = P_J \cdot F_L$, we can apply Lemma 4.6, and we see that the Artin–Rees index of ![]() $F_J \subseteq E_J$ is again c. This implies that
$F_J \subseteq E_J$ is again c. This implies that
Taking the colimit for all finite ![]() $J \subset I$, we get
$J \subset I$, we get
The reversed inclusion is immediate, and the theorem follows.
Lemma 4.6. Let ![]() $A_0$ be a Noetherian ring,
$A_0$ be a Noetherian ring, ![]() $\mathfrak {m}_0 \subset A_0$ an ideal,
$\mathfrak {m}_0 \subset A_0$ an ideal, ![]() $E_0$ a finitely generated
$E_0$ a finitely generated ![]() $A_0$-module and
$A_0$-module and ![]() $F_0 \subseteq E_0$ a submodule. Let z be a new variable and consider the ring
$F_0 \subseteq E_0$ a submodule. Let z be a new variable and consider the ring ![]() $A = A_0[z]$, the ideal
$A = A_0[z]$, the ideal ![]() $\mathfrak {m} = \mathfrak {m}_0 A + (z)$, the extension
$\mathfrak {m} = \mathfrak {m}_0 A + (z)$, the extension ![]() $E = A \otimes _{A_0} E_0 = E_0[z]$ and
$E = A \otimes _{A_0} E_0 = E_0[z]$ and ![]() $F = A \otimes _{A_0} F_0 = F_0[z]$. Then the Artin–Rees index of
$F = A \otimes _{A_0} F_0 = F_0[z]$. Then the Artin–Rees index of ![]() $F \subseteq E$ with respect to
$F \subseteq E$ with respect to ![]() $\mathfrak {m}$ equals the Artin–Rees index of
$\mathfrak {m}$ equals the Artin–Rees index of ![]() $F_0 \subseteq E_0$ with respect to
$F_0 \subseteq E_0$ with respect to ![]() $\mathfrak {m}_0$.
$\mathfrak {m}_0$.
Proof. Let ![]() $c_0$ and c be the Artin–Rees indexes of
$c_0$ and c be the Artin–Rees indexes of ![]() $F_0 \subseteq E_0$ and
$F_0 \subseteq E_0$ and ![]() $F \subseteq E$. As in Lemma 4.2, consider the Rees algebras
$F \subseteq E$. As in Lemma 4.2, consider the Rees algebras
 $$ \begin{align*} A_0^* = \bigoplus_{n \geq 0} \mathfrak{m}_0^n \qquad\text{and}\qquad A^* = \bigoplus_{n \geq 0} \mathfrak{m}^n \end{align*} $$
$$ \begin{align*} A_0^* = \bigoplus_{n \geq 0} \mathfrak{m}_0^n \qquad\text{and}\qquad A^* = \bigoplus_{n \geq 0} \mathfrak{m}^n \end{align*} $$and the graded modules
 $$ \begin{align*} F^*_0 = \bigoplus_{n \geq 0} \mathfrak{m}_0^n E_0 \cap F_0 \qquad\text{and}\qquad F^* = \bigoplus_{n \geq 0} \mathfrak{m}^n E \cap F. \end{align*} $$
$$ \begin{align*} F^*_0 = \bigoplus_{n \geq 0} \mathfrak{m}_0^n E_0 \cap F_0 \qquad\text{and}\qquad F^* = \bigoplus_{n \geq 0} \mathfrak{m}^n E \cap F. \end{align*} $$Then ![]() $F_0$ is generated in degree
$F_0$ is generated in degree ![]() $\leq c_0$ as a graded
$\leq c_0$ as a graded ![]() $A_0$-algebra (and not in any lower degree), and similarly for F.
$A_0$-algebra (and not in any lower degree), and similarly for F.
Any element ![]() $f \in \mathfrak {m}^n E \cap F$ can be written as
$f \in \mathfrak {m}^n E \cap F$ can be written as ![]() $f = \sum _{i=0}^n f_i z^{n-i}$, where
$f = \sum _{i=0}^n f_i z^{n-i}$, where  $f_i \in \mathfrak {m}_0^i E_0 \cap F_0$. In particular,
$f_i \in \mathfrak {m}_0^i E_0 \cap F_0$. In particular, ![]() $F^*$ is generated by
$F^*$ is generated by ![]() $F^*_0$ as an
$F^*_0$ as an ![]() $A^*$-algebra, and therefore
$A^*$-algebra, and therefore ![]() $c \leq c_0$. Conversely, if
$c \leq c_0$. Conversely, if ![]() $F^*$ is generated by homogeneous elements
$F^*$ is generated by homogeneous elements ![]() $f^{(1)}, \dotsc , f^{(r)}$ with
$f^{(1)}, \dotsc , f^{(r)}$ with  $f^{(j)} = \sum _i f_i^{(j)} z^{n_j -i}$, then
$f^{(j)} = \sum _i f_i^{(j)} z^{n_j -i}$, then ![]() $F^*_0$ is generated by
$F^*_0$ is generated by  $f^{(1)}_{n_1}, \ldots , f^{(r)}_{n_r}$. We see that
$f^{(1)}_{n_1}, \ldots , f^{(r)}_{n_r}$. We see that ![]() $c_0 \leq c$, and the result follows.
$c_0 \leq c$, and the result follows.
Remark 4.7. If A and ![]() $\mathfrak {m}$ are as in Remark 4.3, then we have
$\mathfrak {m}$ are as in Remark 4.3, then we have  $A = \operatorname {\mathrm {\varinjlim }}_m A_m$, where
$A = \operatorname {\mathrm {\varinjlim }}_m A_m$, where
 $$ \begin{align*} A_m = k[x_1,\dotsc,x_m]/\left(x_1-x_i^i,x_i^{i+1}\right), \quad 1<i\leq m. \end{align*} $$
$$ \begin{align*} A_m = k[x_1,\dotsc,x_m]/\left(x_1-x_i^i,x_i^{i+1}\right), \quad 1<i\leq m. \end{align*} $$It is easy to check that the Artin–Rees index of ![]() $(x_1) \subset A_m$ is m and A does not have the Artin–Rees property.
$(x_1) \subset A_m$ is m and A does not have the Artin–Rees property.
Recall that for any discrete topological ring S and any two topological S-algebras T and ![]() $T'$, the completed tensor product
$T'$, the completed tensor product ![]() $T \hat {\otimes }_S T'$ is defined to be the completion of
$T \hat {\otimes }_S T'$ is defined to be the completion of ![]() $T\otimes _S T'$ with respect to its natural topology.
$T\otimes _S T'$ with respect to its natural topology.
Corollary 4.8. Let ![]() $S \to T$ be a map of Noetherian rings. As before, suppose that S has the discrete topology, and let T be equipped with the
$S \to T$ be a map of Noetherian rings. As before, suppose that S has the discrete topology, and let T be equipped with the ![]() $\mathfrak {n}$-adic topology where
$\mathfrak {n}$-adic topology where ![]() $\mathfrak {n} \subset T$ is an ideal. Then the natural map
$\mathfrak {n} \subset T$ is an ideal. Then the natural map
is flat. In particular:
1. for any index set I, the completion map
 $S[x_i \mid i\in I] \to S[[x_i \mid i\in I]]$ is flat and
$S[x_i \mid i\in I] \to S[[x_i \mid i\in I]]$ is flat and2. for every finite subset
 $J\subset I$, the inclusion
$J\subset I$, the inclusion  $S [ [x_j \mid j\in J ] ] \to S[[x_i \mid i\in I]]$ is flat.
$S [ [x_j \mid j\in J ] ] \to S[[x_i \mid i\in I]]$ is flat.
Proof. Observe that a basis for the topology on ![]() $T[x_i \mid i\in I]$ is given by
$T[x_i \mid i\in I]$ is given by
which is easily seen to be equivalent to the ![]() $\mathfrak {m}$-adic one, where
$\mathfrak {m}$-adic one, where ![]() $\mathfrak {m}:=(x_i \mid i\in I)+\mathfrak {n}$. As
$\mathfrak {m}:=(x_i \mid i\in I)+\mathfrak {n}$. As ![]() $T[x_i \mid i \in I]$ is coherent (see, for example, [Reference Glaz30, Theorem 6.2.2]), the first assertion follows from Theorem 4.5 and Proposition 4.4. Regarding the last two assertions, (1) follows by observing that
$T[x_i \mid i \in I]$ is coherent (see, for example, [Reference Glaz30, Theorem 6.2.2]), the first assertion follows from Theorem 4.5 and Proposition 4.4. Regarding the last two assertions, (1) follows by observing that ![]() $S \hat {\otimes }_S S[x_i \mid i\in I] = S[[x_i \mid i\in I]]$, and (2) by taking
$S \hat {\otimes }_S S[x_i \mid i\in I] = S[[x_i \mid i\in I]]$, and (2) by taking ![]() $T = S [ [x_j \mid j\in J ] ]$ with the
$T = S [ [x_j \mid j\in J ] ]$ with the ![]() $(x_j \mid j\in J)$-adic topology and observing that the given inclusion factors as
$(x_j \mid j\in J)$-adic topology and observing that the given inclusion factors as
 $$ \begin{align*} S\left[\left[x_j \mid j\in J\right]\right] \to S\left[\left[x_j \mid j\in J\right]\right][x_i \mid i\in I \setminus J] \to S[[x_i \mid i\in I]], \end{align*} $$
$$ \begin{align*} S\left[\left[x_j \mid j\in J\right]\right] \to S\left[\left[x_j \mid j\in J\right]\right][x_i \mid i\in I \setminus J] \to S[[x_i \mid i\in I]], \end{align*} $$and so is flat.
Remark 4.9. For quotients A of ![]() $k[x_i \mid i\in I]$, the completion map
$k[x_i \mid i\in I]$, the completion map ![]() $A\to \widehat {A}$ need not be flat, even if the topology of A is separated. Consider the ideal
$A\to \widehat {A}$ need not be flat, even if the topology of A is separated. Consider the ideal
 $$ \begin{align*} \mathfrak{a}=\left(yx_1,yx_n^{n}-zx_{n-1}^{n-1} \mid n>1\right) \end{align*} $$
$$ \begin{align*} \mathfrak{a}=\left(yx_1,yx_n^{n}-zx_{n-1}^{n-1} \mid n>1\right) \end{align*} $$in ![]() $P=k [x_n,y,z \mid n\in {\mathbb N}_{>0} ]$ and the quotient
$P=k [x_n,y,z \mid n\in {\mathbb N}_{>0} ]$ and the quotient ![]() $A=P/\mathfrak {a}$. Let
$A=P/\mathfrak {a}$. Let ![]() $\mathfrak {m}= (x_n,y,z \mid n\in {\mathbb N}_{>0} )\subset A$. As
$\mathfrak {m}= (x_n,y,z \mid n\in {\mathbb N}_{>0} )\subset A$. As ![]() $\mathfrak {m}$ is weighted homogeneous with respect to the positive weights
$\mathfrak {m}$ is weighted homogeneous with respect to the positive weights ![]() $w(x_n)=w(y)=1$,
$w(x_n)=w(y)=1$, ![]() $w(z)=2$, it follows that the
$w(z)=2$, it follows that the ![]() $\mathfrak {m}$-adic topology on A is separated. Consider the element
$\mathfrak {m}$-adic topology on A is separated. Consider the element ![]() $y-z$, which is annihilated by the series
$y-z$, which is annihilated by the series ![]() $f=\sum _{n\geq 1} x_n^n$. If
$f=\sum _{n\geq 1} x_n^n$. If ![]() $\widehat {A}$ were flat over A, there would exist polynomials
$\widehat {A}$ were flat over A, there would exist polynomials ![]() $a_1,\dotsc ,a_r\in A$ annihilating
$a_1,\dotsc ,a_r\in A$ annihilating ![]() $y-z$ such that f could be written as
$y-z$ such that f could be written as  $f=\sum _{j=1}^r a_j b_j$, where
$f=\sum _{j=1}^r a_j b_j$, where  $b_j\in \widehat {A}$.
$b_j\in \widehat {A}$.
Considering this equation modulo ![]() $(y,z)$, we have written f as a linear combination of polynomials in
$(y,z)$, we have written f as a linear combination of polynomials in ![]() $k [x_n \mid n\in {\mathbb N}_{>0} ]$, which is clearly impossible.
$k [x_n \mid n\in {\mathbb N}_{>0} ]$, which is clearly impossible.
We close this section with the following analogue to Proposition 2.7 for polynomial rings:
Proposition 4.10. Let ![]() $P = S[x_i \mid i \in I]$ and
$P = S[x_i \mid i \in I]$ and ![]() $\mathfrak {m} = (x_i \mid i \in I)$, where S is a ring and I a set. Let
$\mathfrak {m} = (x_i \mid i \in I)$, where S is a ring and I a set. Let ![]() $\mathfrak {a} \subset P_{\mathfrak {m}}$ be an ideal such that
$\mathfrak {a} \subset P_{\mathfrak {m}}$ be an ideal such that ![]() $\operatorname {\mathrm {in}}(\mathfrak {a}) \subset P$ is finitely generated. Then
$\operatorname {\mathrm {in}}(\mathfrak {a}) \subset P$ is finitely generated. Then ![]() $\mathfrak {a}$ is finitely generated.
$\mathfrak {a}$ is finitely generated.
Proof. Let ![]() $f_1,\dotsc ,f_r\in \mathfrak {a}$ be such that
$f_1,\dotsc ,f_r\in \mathfrak {a}$ be such that ![]() $\operatorname {\mathrm {in}}(f_1),\dotsc ,\operatorname {\mathrm {in}}(f_r)$ generate
$\operatorname {\mathrm {in}}(f_1),\dotsc ,\operatorname {\mathrm {in}}(f_r)$ generate ![]() $\operatorname {\mathrm {in}}(\mathfrak {a})$. Since
$\operatorname {\mathrm {in}}(\mathfrak {a})$. Since ![]() $\operatorname {\mathrm {in}}(\mathfrak {a})=\operatorname {\mathrm {in}} (\widehat {\mathfrak {a}} )$, we can apply Proposition 2.7 to see that
$\operatorname {\mathrm {in}}(\mathfrak {a})=\operatorname {\mathrm {in}} (\widehat {\mathfrak {a}} )$, we can apply Proposition 2.7 to see that ![]() $\widehat {\mathfrak {a}}=(f_1,\dotsc ,f_r)\widehat {P}$. By Corollary 4.8, the map
$\widehat {\mathfrak {a}}=(f_1,\dotsc ,f_r)\widehat {P}$. By Corollary 4.8, the map ![]() $P_{\mathfrak {m}}\to \widehat {P}$ is faithfully flat and thus
$P_{\mathfrak {m}}\to \widehat {P}$ is faithfully flat and thus ![]() $\mathfrak {a}\subset \widehat {\mathfrak {a}}\cap P_{\mathfrak {m}}=(f_1,\dotsc ,f_r)P_{\mathfrak {m}}$. The other inclusion is trivial, so
$\mathfrak {a}\subset \widehat {\mathfrak {a}}\cap P_{\mathfrak {m}}=(f_1,\dotsc ,f_r)P_{\mathfrak {m}}$. The other inclusion is trivial, so ![]() $\mathfrak {a}=(f_1,\dotsc ,f_r)$.
$\mathfrak {a}=(f_1,\dotsc ,f_r)$.
5 Ideals of finite definition
In this section, we fix a field k and a set I and consider the polynomial ring ![]() $P = k[x_i \mid i \in I]$ and the power series ring
$P = k[x_i \mid i \in I]$ and the power series ring ![]() $\widehat {P} = k[[x_i \mid i \in I]]$. An important class of ideals in
$\widehat {P} = k[[x_i \mid i \in I]]$. An important class of ideals in ![]() $\widehat {P}$ are those generated by finitely many power series involving only finitely many variables. We study their properties in this section.
$\widehat {P}$ are those generated by finitely many power series involving only finitely many variables. We study their properties in this section.
For any subset ![]() $J \subset I$, we write
$J \subset I$, we write ![]() $P_J = k[x_i \mid i \in J]$ and
$P_J = k[x_i \mid i \in J]$ and ![]() $\widehat {P}_J = k[[x_i \mid i \in J]]$, and for any ideal
$\widehat {P}_J = k[[x_i \mid i \in J]]$, and for any ideal ![]() $\mathfrak {a} \subset \widehat {P}$ we denote
$\mathfrak {a} \subset \widehat {P}$ we denote ![]() $\mathfrak {a}_J := \mathfrak {a} \cap \widehat {P}_J$.
$\mathfrak {a}_J := \mathfrak {a} \cap \widehat {P}_J$.
Definition 5.1. Let ![]() $\mathfrak {a} \subset \widehat {P}$ be an ideal.
$\mathfrak {a} \subset \widehat {P}$ be an ideal.
1. We say that
 $\mathfrak {a}$ is of finite definition with respect to the indeterminates
$\mathfrak {a}$ is of finite definition with respect to the indeterminates  $x_i$ if there exists a finite subset
$x_i$ if there exists a finite subset  $J\subset I$ such that
$J\subset I$ such that  $\mathfrak {a}=\mathfrak {a}_J \widehat {P}$.
$\mathfrak {a}=\mathfrak {a}_J \widehat {P}$.2. Similarly,
 $\mathfrak {a}$ is of finite polynomial definition with respect to the indeterminates
$\mathfrak {a}$ is of finite polynomial definition with respect to the indeterminates  $x_i$ if it is generated by finitely many polynomials – that is, elements in P.
$x_i$ if it is generated by finitely many polynomials – that is, elements in P.3. We say that
 $\mathfrak {a}$ is of finite (polynomial) definition if there exists a k-isomorphism
$\mathfrak {a}$ is of finite (polynomial) definition if there exists a k-isomorphism  $\widehat {P} \simeq k [ [x^{\prime }_i \mid i\in I ] ]$ such that
$\widehat {P} \simeq k [ [x^{\prime }_i \mid i\in I ] ]$ such that  $\mathfrak {a}$ is of finite (polynomial) definition with respect to the formal coordinates
$\mathfrak {a}$ is of finite (polynomial) definition with respect to the formal coordinates  $x^{\prime }_i$.
$x^{\prime }_i$.
Definition 5.2. Let ![]() $(A, \mathfrak {m}, k)$ be an equicharacteristic local ring.
$(A, \mathfrak {m}, k)$ be an equicharacteristic local ring.
1. A weak DGK decomposition for A is an isomorphism
 $\widehat {A} \simeq k[[x_i \mid i \in I]]/\mathfrak {a}$, where
$\widehat {A} \simeq k[[x_i \mid i \in I]]/\mathfrak {a}$, where  $\mathfrak {a}$ is an ideal of finite definition.
$\mathfrak {a}$ is an ideal of finite definition.2. A DGK decomposition for A is an isomorphism
 $\widehat {A} \simeq k[[x_i \mid i\in I]]/\mathfrak {a}$ with
$\widehat {A} \simeq k[[x_i \mid i\in I]]/\mathfrak {a}$ with  $\mathfrak {a}$ of finite polynomial definition.
$\mathfrak {a}$ of finite polynomial definition.3. We say that a (weak) DGK decomposition
 $\widehat {A} \simeq k[[x_i \mid i\in I]]/\mathfrak {a}$ is efficient if the quotient map
$\widehat {A} \simeq k[[x_i \mid i\in I]]/\mathfrak {a}$ is efficient if the quotient map  $k[[x_i \mid i\in I]] \to \widehat {A}$ is an efficient formal embedding.
$k[[x_i \mid i\in I]] \to \widehat {A}$ is an efficient formal embedding.
Remark 5.3. If A has a DGK decomposition, then we have an isomorphism ![]() $\widehat {A} \simeq \widehat {B} \hat {\otimes }_k \widehat {P}$, where
$\widehat {A} \simeq \widehat {B} \hat {\otimes }_k \widehat {P}$, where ![]() $\widehat {P}$ is a power series ring and
$\widehat {P}$ is a power series ring and ![]() $(B, \mathfrak {n}, k)$ is a local k-algebra which is essentially of finite type. Geometrically, this means that
$(B, \mathfrak {n}, k)$ is a local k-algebra which is essentially of finite type. Geometrically, this means that ![]() $\operatorname {\mathrm {Spf}} (\widehat {A} ) \simeq \widehat {Z}_z \widehat \times \Delta ^I$, where
$\operatorname {\mathrm {Spf}} (\widehat {A} ) \simeq \widehat {Z}_z \widehat \times \Delta ^I$, where ![]() $\Delta ^I = \operatorname {\mathrm {Spf}} (k[[x_i \mid i \in I]])$ and
$\Delta ^I = \operatorname {\mathrm {Spf}} (k[[x_i \mid i \in I]])$ and ![]() $\widehat {Z}_z$ is the formal neighbourhood of a scheme Z of finite type over k at a point
$\widehat {Z}_z$ is the formal neighbourhood of a scheme Z of finite type over k at a point ![]() $z \in Z(k)$. If A has a weak DGK decomposition, then
$z \in Z(k)$. If A has a weak DGK decomposition, then ![]() $\widehat {A} \simeq \mathcal {B} \hat {\otimes }_k \widehat {P}$, where
$\widehat {A} \simeq \mathcal {B} \hat {\otimes }_k \widehat {P}$, where ![]() $\mathcal {B}$ is a Noetherian complete local ring with residue field k.
$\mathcal {B}$ is a Noetherian complete local ring with residue field k.
Example 5.4. The existence of a weak DGK decomposition for a ring A does not imply the existence of a DGK decomposition for A. This can be seen by considering the following example given by Whitney. Let ![]() $f(t)$ be a transcendental power series with complex coefficients and with
$f(t)$ be a transcendental power series with complex coefficients and with ![]() $f(0)=0$, and consider the equation
$f(0)=0$, and consider the equation
It is proven in [Reference Vojta46, Example 14.1] that ![]() $\mathcal B = {\mathbb C}[[x,y,t]]/(g)$ is not isomorphic to the completion of a local ring of a
$\mathcal B = {\mathbb C}[[x,y,t]]/(g)$ is not isomorphic to the completion of a local ring of a ![]() ${\mathbb C}$-scheme of finite type. In particular, any local ring A for which
${\mathbb C}$-scheme of finite type. In particular, any local ring A for which ![]() $\widehat {A} \simeq \mathcal B$ (for example,
$\widehat {A} \simeq \mathcal B$ (for example, ![]() $\mathcal B$ itself) admits a weak DGK decomposition but not a DGK decomposition.
$\mathcal B$ itself) admits a weak DGK decomposition but not a DGK decomposition.
We now give another example of a local ring A such that ![]() $\widehat {A} \simeq \mathcal B$. This example has the advantage of being explicitly presented as the localisation of a quotient of a polynomial ring in countably many variables. Write
$\widehat {A} \simeq \mathcal B$. This example has the advantage of being explicitly presented as the localisation of a quotient of a polynomial ring in countably many variables. Write ![]() $f(t)=\sum _{i\geq 1} a_i t^i \in {\mathbb C}[[t]]$. Consider the polynomial ring
$f(t)=\sum _{i\geq 1} a_i t^i \in {\mathbb C}[[t]]$. Consider the polynomial ring ![]() $P = {\mathbb C}[x,y,t,z_n \mid n \geq 0]$ and the ideal
$P = {\mathbb C}[x,y,t,z_n \mid n \geq 0]$ and the ideal
where
Let A be the localisation of ![]() $P/\mathfrak {a}$ at the ideal
$P/\mathfrak {a}$ at the ideal ![]() $(x,y,t,z_n \mid n \geq 0)$. Then in
$(x,y,t,z_n \mid n \geq 0)$. Then in ![]() $\widehat {A}$ we have, for each
$\widehat {A}$ we have, for each ![]() $m\geq 1$,
$m\geq 1$,
 $$ \begin{align*} z_0 - f(t) = z_m t^m - \sum_{i\geq m+1} a_i t^i \in \widehat{\mathfrak{m}}^{m}, \end{align*} $$
$$ \begin{align*} z_0 - f(t) = z_m t^m - \sum_{i\geq m+1} a_i t^i \in \widehat{\mathfrak{m}}^{m}, \end{align*} $$and for each ![]() $m \geq n+1$,
$m \geq n+1$,
 $$ \begin{align*} z_n - \sum_{i\geq n+1} a_i t^{i-n} = z_m t^{m-n} - \sum_{i\geq m+1} a_i t^{i-n} \in \widehat{\mathfrak{m}}^{m-n}. \end{align*} $$
$$ \begin{align*} z_n - \sum_{i\geq n+1} a_i t^{i-n} = z_m t^{m-n} - \sum_{i\geq m+1} a_i t^{i-n} \in \widehat{\mathfrak{m}}^{m-n}. \end{align*} $$Thus it follows that ![]() $\widehat {A} \simeq {\mathbb C}[[x,y,t,z_0]]/(h, z_0-f(t)) \simeq {\mathbb C}[[x,y,t]]/(g) = \mathcal B$.
$\widehat {A} \simeq {\mathbb C}[[x,y,t,z_0]]/(h, z_0-f(t)) \simeq {\mathbb C}[[x,y,t]]/(g) = \mathcal B$.
Remark 5.5. An analogous definition of finite definition can be given for ideals in a polynomial ring ![]() $P = k[x_i \mid i \in I]$. It is easy to see that the definition does not depend on the choice of indeterminates, and that an ideal of P is of finite definition if and only if it is finitely generated. By contrast, in a power series ring not every ideal of finite definition is so with respect to the given indeterminates
$P = k[x_i \mid i \in I]$. It is easy to see that the definition does not depend on the choice of indeterminates, and that an ideal of P is of finite definition if and only if it is finitely generated. By contrast, in a power series ring not every ideal of finite definition is so with respect to the given indeterminates ![]() $x_i$, and not every finitely generated ideal is of finite definition. For instance, consider
$x_i$, and not every finitely generated ideal is of finite definition. For instance, consider ![]() $\widehat {P}=k[[x_n \mid n\in {\mathbb N}]]$. The principal ideal generated by
$\widehat {P}=k[[x_n \mid n\in {\mathbb N}]]$. The principal ideal generated by ![]() $f=\sum _{n\geq 1} x_n^n$ is of finite definition by Lemma 3.12 but not in the indeterminates
$f=\sum _{n\geq 1} x_n^n$ is of finite definition by Lemma 3.12 but not in the indeterminates ![]() $x_i$. As for the second claim, an example is given by the principal ideal generated by
$x_i$. As for the second claim, an example is given by the principal ideal generated by ![]() $g=\sum _{n\geq 1} x_n^{n+1}$, which, as we shall discuss next, is not of finite definition if k is of characteristic
$g=\sum _{n\geq 1} x_n^{n+1}$, which, as we shall discuss next, is not of finite definition if k is of characteristic ![]() $0$. Indeed, assume by contradiction that there exists an isomorphism
$0$. Indeed, assume by contradiction that there exists an isomorphism ![]() $\widehat {P} \simeq k[[y_n \mid n\in {\mathbb N}]]$ such that
$\widehat {P} \simeq k[[y_n \mid n\in {\mathbb N}]]$ such that ![]() $g\widehat {P}$ is of finite definition with respect to the indeterminates
$g\widehat {P}$ is of finite definition with respect to the indeterminates ![]() $y_n$. Pick a variable
$y_n$. Pick a variable ![]() $y_r$ not appearing in the generators for
$y_r$ not appearing in the generators for ![]() $g\widehat {P}$, and consider the regular continuous derivation
$g\widehat {P}$, and consider the regular continuous derivation ![]() $d = \partial /\partial y_r$ on
$d = \partial /\partial y_r$ on ![]() $\widehat {P}$. Notice that
$\widehat {P}$. Notice that ![]() $d(g) = 0$. By regularity, we have
$d(g) = 0$. By regularity, we have ![]() $d(x_m)\in \widehat {P}^\times $ for some
$d(x_m)\in \widehat {P}^\times $ for some ![]() $m\geq 1$. Writing
$m\geq 1$. Writing ![]() $d(g)=\sum _{n\geq 1} (n+1)x_n^n d(x_n)$, we see that
$d(g)=\sum _{n\geq 1} (n+1)x_n^n d(x_n)$, we see that ![]() $\operatorname {\mathrm {ord}}_{x_m}(d(g)) < \infty $, contradicting
$\operatorname {\mathrm {ord}}_{x_m}(d(g)) < \infty $, contradicting ![]() $d(g) = 0$.
$d(g) = 0$.
Ideals of finite definition form a class of ideals of ![]() $\widehat {P}$ for which Question 2.8 has a positive answer. We give only a sketch of the proof of the next lemma here, and refer the reader to [Reference Chiu18, Section 1.5] for details.
$\widehat {P}$ for which Question 2.8 has a positive answer. We give only a sketch of the proof of the next lemma here, and refer the reader to [Reference Chiu18, Section 1.5] for details.
Lemma 5.6. Let ![]() $\mathfrak {a} \subset \widehat {P}$ be an ideal such that there exists
$\mathfrak {a} \subset \widehat {P}$ be an ideal such that there exists ![]() $J \subset I$ finite with
$J \subset I$ finite with ![]() $\mathfrak {a} = \mathfrak {a}_J \widehat {P}$. Then
$\mathfrak {a} = \mathfrak {a}_J \widehat {P}$. Then ![]() $\operatorname {\mathrm {in}}(\mathfrak {a}) = \operatorname {\mathrm {in}}(\mathfrak {a}_J) P$.
$\operatorname {\mathrm {in}}(\mathfrak {a}) = \operatorname {\mathrm {in}}(\mathfrak {a}_J) P$.
Proof. Choose a local monomial order ![]() $\prec $ compatible with the standard filtration on
$\prec $ compatible with the standard filtration on ![]() $\widehat {P}$; for example, take the order defined by
$\widehat {P}$; for example, take the order defined by ![]() $x^a \prec x^b$ if
$x^a \prec x^b$ if ![]() $x^b <_{\operatorname {\mathrm {grlex}}} x^a$, where
$x^b <_{\operatorname {\mathrm {grlex}}} x^a$, where ![]() $<_{\operatorname {\mathrm {grlex}}}$ denotes the usual graded lexicographic order. Then
$<_{\operatorname {\mathrm {grlex}}}$ denotes the usual graded lexicographic order. Then ![]() $\prec $ restricts to a local monomial order
$\prec $ restricts to a local monomial order ![]() $\prec _J$ on
$\prec _J$ on ![]() $\widehat {P}_J$. Choose a standard basis
$\widehat {P}_J$. Choose a standard basis ![]() $S = \{f_1,\dotsc ,f_r\}$ of
$S = \{f_1,\dotsc ,f_r\}$ of ![]() $\mathfrak {a}_J$ with respect to
$\mathfrak {a}_J$ with respect to ![]() $\prec _J$. By [Reference Becker4, Theorem 4.1], this is equivalent to S being closed under s-series. Note that [Reference Becker4, Theorem 4.1] extends directly to the case of infinitely many indeterminates, and thus it follows immediately that S is a standard basis of
$\prec _J$. By [Reference Becker4, Theorem 4.1], this is equivalent to S being closed under s-series. Note that [Reference Becker4, Theorem 4.1] extends directly to the case of infinitely many indeterminates, and thus it follows immediately that S is a standard basis of ![]() $\mathfrak {a}$ with respect to
$\mathfrak {a}$ with respect to ![]() $\prec $. Clearly we have
$\prec $. Clearly we have ![]() $\operatorname {\mathrm {in}}(\mathfrak {a}) = (\operatorname {\mathrm {in}}(f_1),\dotsc ,\operatorname {\mathrm {in}}(f_r))$, which proves the claim.
$\operatorname {\mathrm {in}}(\mathfrak {a}) = (\operatorname {\mathrm {in}}(f_1),\dotsc ,\operatorname {\mathrm {in}}(f_r))$, which proves the claim.
We are interested now in understanding heights of ideals of finite definition. Let us start by looking at their minimal primes.
Proposition 5.7. If ![]() $\mathfrak {a} \subset \widehat {P}$ is an ideal of finite definition, then it has a finite number of minimal primes, and each of them is of finite definition. More precisely, let
$\mathfrak {a} \subset \widehat {P}$ is an ideal of finite definition, then it has a finite number of minimal primes, and each of them is of finite definition. More precisely, let ![]() $J \subset I$ be a finite subset and assume that
$J \subset I$ be a finite subset and assume that ![]() $\mathfrak {a} = \mathfrak {a}_J \widehat {P}$. If
$\mathfrak {a} = \mathfrak {a}_J \widehat {P}$. If ![]() $\mathfrak {p} \subset \widehat {P}$ is a minimal prime of
$\mathfrak {p} \subset \widehat {P}$ is a minimal prime of ![]() $\mathfrak {a}$, then
$\mathfrak {a}$, then ![]() $\mathfrak {p} = \mathfrak {p}_J \widehat {P}$. Moreover, the assignment
$\mathfrak {p} = \mathfrak {p}_J \widehat {P}$. Moreover, the assignment ![]() $\mathfrak {p} \mapsto \mathfrak {p}_J$ gives a bijection between the minimal primes of
$\mathfrak {p} \mapsto \mathfrak {p}_J$ gives a bijection between the minimal primes of ![]() $\mathfrak {a}$ and the minimal primes of
$\mathfrak {a}$ and the minimal primes of ![]() $\mathfrak {a}_J$.
$\mathfrak {a}_J$.
Proof. Notice that if ![]() $\mathfrak {p} \subset \widehat {P}$ is a prime ideal, then
$\mathfrak {p} \subset \widehat {P}$ is a prime ideal, then ![]() $\mathfrak {p}_J \subset \widehat {P}_J$ remains prime. Moreover, by Corollary 4.8 we have that
$\mathfrak {p}_J \subset \widehat {P}_J$ remains prime. Moreover, by Corollary 4.8 we have that ![]() $\widehat {P}_J\to \widehat {P}$ is faithfully flat and thus
$\widehat {P}_J\to \widehat {P}$ is faithfully flat and thus ![]() $\mathfrak {q} = (\mathfrak {q}\widehat {P} ) \cap \widehat {P}_J$ for any ideal
$\mathfrak {q} = (\mathfrak {q}\widehat {P} ) \cap \widehat {P}_J$ for any ideal ![]() $\mathfrak {q} \subset \widehat {P}_J$. It is therefore sufficient to show that for every prime ideal
$\mathfrak {q} \subset \widehat {P}_J$. It is therefore sufficient to show that for every prime ideal ![]() $\mathfrak {q} \subset \widehat {P}_J$, the extension
$\mathfrak {q} \subset \widehat {P}_J$, the extension ![]() $\mathfrak {q} \widehat {P}$ is prime. By Remark 2.4 we have an injection
$\mathfrak {q} \widehat {P}$ is prime. By Remark 2.4 we have an injection  $\widehat {P} \to (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}}$. Since J is finite,
$\widehat {P} \to (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}}$. Since J is finite, ![]() $\widehat {P}_J$ is Noetherian and
$\widehat {P}_J$ is Noetherian and ![]() $\mathfrak {q}$ is finitely generated. This implies that
$\mathfrak {q}$ is finitely generated. This implies that  $\mathfrak {q} (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}} = \mathfrak {q}^{{\mathbb N}^{ (I \setminus J )}}$ – that is, the elements of the extension
$\mathfrak {q} (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}} = \mathfrak {q}^{{\mathbb N}^{ (I \setminus J )}}$ – that is, the elements of the extension  $\mathfrak {q} (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}}$ are precisely the Bourbaki power series that, when expanded in the variables indexed by
$\mathfrak {q} (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}}$ are precisely the Bourbaki power series that, when expanded in the variables indexed by ![]() $I \setminus J$, have coefficients in
$I \setminus J$, have coefficients in ![]() $\mathfrak {q}$. Therefore we have an injection
$\mathfrak {q}$. Therefore we have an injection
 $$ \begin{align*} \widehat{P}/\mathfrak{q} \widehat{P} \hookrightarrow \left(\widehat{P}_J/\mathfrak{q}\right)^{{\mathbb N}^{\left(I \setminus J\right)}}, \end{align*} $$
$$ \begin{align*} \widehat{P}/\mathfrak{q} \widehat{P} \hookrightarrow \left(\widehat{P}_J/\mathfrak{q}\right)^{{\mathbb N}^{\left(I \setminus J\right)}}, \end{align*} $$and the ring in the right-hand side is clearly a domain. Thus ![]() $\mathfrak {q} \widehat {P}$ is prime.
$\mathfrak {q} \widehat {P}$ is prime.
Remark 5.8. In the setup of the proof of Proposition 5.7, if J is infinite then it is no longer true that  $\mathfrak {q} (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}} = \mathfrak {q}^{{\mathbb N}^{ (I \setminus J )}}$ for an arbitrary prime
$\mathfrak {q} (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}} = \mathfrak {q}^{{\mathbb N}^{ (I \setminus J )}}$ for an arbitrary prime ![]() $\mathfrak {q} \subset \widehat {P}_J$. For example, let
$\mathfrak {q} \subset \widehat {P}_J$. For example, let ![]() $J = {\mathbb N}$, pick
$J = {\mathbb N}$, pick ![]() $i_0 \in I \setminus J$, let
$i_0 \in I \setminus J$, let ![]() $\mathfrak {q}=\widehat {\mathfrak {m}}_J$ be the maximal ideal in
$\mathfrak {q}=\widehat {\mathfrak {m}}_J$ be the maximal ideal in ![]() $\widehat {P}_J$ and consider the series
$\widehat {P}_J$ and consider the series ![]() $f = \sum _{n \in {\mathbb N}} x_n x_{i_0}^n$. Then f belongs to
$f = \sum _{n \in {\mathbb N}} x_n x_{i_0}^n$. Then f belongs to  $\mathfrak {q}^{{\mathbb N}^{ (I \setminus J )}}$ but not to
$\mathfrak {q}^{{\mathbb N}^{ (I \setminus J )}}$ but not to  $\mathfrak {q} (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}}$. We do not know if the extension
$\mathfrak {q} (\widehat {P}_J )^{{\mathbb N}^{ (I \setminus J )}}$. We do not know if the extension ![]() $\mathfrak {q} \widehat {P}$ remains prime when J is infinite.
$\mathfrak {q} \widehat {P}$ remains prime when J is infinite.
Remark 5.9. Proposition 5.7 shows that the ideal ![]() $(x_i \mid i\in J)\widehat {P}$ is prime whenever J is finite. Since colimits of prime ideals remain prime, one sees that
$(x_i \mid i\in J)\widehat {P}$ is prime whenever J is finite. Since colimits of prime ideals remain prime, one sees that ![]() $(x_i \mid i\in J)\widehat {P}$ is prime for an arbitrary subset J. In particular,
$(x_i \mid i\in J)\widehat {P}$ is prime for an arbitrary subset J. In particular, ![]() $\mathfrak {m}_0 = (x_i \mid i \in I)\widehat {P}$ is prime. Notice that
$\mathfrak {m}_0 = (x_i \mid i \in I)\widehat {P}$ is prime. Notice that ![]() $\widehat {P}/\mathfrak {m}_0$ has infinite dimension when I is infinite.
$\widehat {P}/\mathfrak {m}_0$ has infinite dimension when I is infinite.
The proof of the following theorem uses the results of the previous section and Proposition 5.13:
Theorem 5.10. If ![]() $J \subset I$ is a finite subset and
$J \subset I$ is a finite subset and ![]() $\mathfrak {a} = \mathfrak {a}_J \widehat {P}$, then
$\mathfrak {a} = \mathfrak {a}_J \widehat {P}$, then ![]() $\operatorname {\mathrm {ht}}(\mathfrak {a}) = \operatorname {\mathrm {ht}}(\mathfrak {a}_J)$.
$\operatorname {\mathrm {ht}}(\mathfrak {a}) = \operatorname {\mathrm {ht}}(\mathfrak {a}_J)$.
Proof. From Proposition 5.7 we can assume that ![]() $\mathfrak {a} = \mathfrak {p} = \mathfrak {p}_J \widehat {P}$ is a prime ideal. Notice that
$\mathfrak {a} = \mathfrak {p} = \mathfrak {p}_J \widehat {P}$ is a prime ideal. Notice that ![]() $\mathfrak {p} \subset \mathfrak {b} := (x_j \mid j\in J )$. From Proposition 5.13, the localisation
$\mathfrak {p} \subset \mathfrak {b} := (x_j \mid j\in J )$. From Proposition 5.13, the localisation ![]() $\widehat {P}_{\mathfrak {b}}$ is Noetherian, and therefore
$\widehat {P}_{\mathfrak {b}}$ is Noetherian, and therefore ![]() $\widehat {P}_{\mathfrak {p}}$, which is a further localisation of
$\widehat {P}_{\mathfrak {p}}$, which is a further localisation of ![]() $\widehat {P}_{\mathfrak {b}}$, is also Noetherian. By Corollary 4.8, the extension
$\widehat {P}_{\mathfrak {b}}$, is also Noetherian. By Corollary 4.8, the extension ![]() $\widehat {P}_J \subset \widehat {P}$ is flat, and therefore the extension
$\widehat {P}_J \subset \widehat {P}$ is flat, and therefore the extension  $ (\widehat {P}_J )_{\mathfrak {p}_J} \subset \widehat {P}_{\mathfrak {p}}$ is also flat. Since
$ (\widehat {P}_J )_{\mathfrak {p}_J} \subset \widehat {P}_{\mathfrak {p}}$ is also flat. Since ![]() $\widehat {P}_{\mathfrak {p}}$ is Noetherian, it follows from [Reference Matsumura36, Theorem 15.1] that
$\widehat {P}_{\mathfrak {p}}$ is Noetherian, it follows from [Reference Matsumura36, Theorem 15.1] that ![]() $\operatorname {\mathrm {ht}}(\mathfrak {p}) = \operatorname {\mathrm {ht}}(\mathfrak {p}_J)$.
$\operatorname {\mathrm {ht}}(\mathfrak {p}) = \operatorname {\mathrm {ht}}(\mathfrak {p}_J)$.
Corollary 5.11. Let ![]() $\mathfrak {a} \subset \widehat {P}$ be any ideal of finite definition. For every minimal prime
$\mathfrak {a} \subset \widehat {P}$ be any ideal of finite definition. For every minimal prime ![]() $\mathfrak {p}$ of
$\mathfrak {p}$ of ![]() $\mathfrak {a}$, we have
$\mathfrak {a}$, we have ![]() $\operatorname {\mathrm {ht}}(\mathfrak {p}) < \infty $.
$\operatorname {\mathrm {ht}}(\mathfrak {p}) < \infty $.
Remark 5.12. In the case of polynomial rings, the analogues of Theorem 5.10 and Corollary 5.11 are well known and easy to prove, and in fact there is a strong converse to the analogue of Corollary 5.11, since every prime ideal of finite height in a polynomial ring ![]() $P = k[x_i \mid i \in I]$ is finitely generated. To see this, suppose
$P = k[x_i \mid i \in I]$ is finitely generated. To see this, suppose ![]() $\mathfrak {p} \subset k[x_i \mid i \in I]$ is a prime ideal that is not finitely generated. Recall that
$\mathfrak {p} \subset k[x_i \mid i \in I]$ is a prime ideal that is not finitely generated. Recall that ![]() $\mathfrak {p}$ is the colimit of the ideals
$\mathfrak {p}$ is the colimit of the ideals ![]() $\mathfrak {p} \cap P_J$ as J ranges among the finite subsets of I. This implies that we can fix an embedding
$\mathfrak {p} \cap P_J$ as J ranges among the finite subsets of I. This implies that we can fix an embedding ![]() ${\mathbb N} \subset I$ and find an increasing sequence
${\mathbb N} \subset I$ and find an increasing sequence ![]() $\{r_n \mid n \in {\mathbb N}\} \subset {\mathbb N}$ such that if
$\{r_n \mid n \in {\mathbb N}\} \subset {\mathbb N}$ such that if ![]() $\mathfrak {p}_n \subset k[x_i \mid i \in I]$ is the ideal generated by
$\mathfrak {p}_n \subset k[x_i \mid i \in I]$ is the ideal generated by ![]() $\mathfrak {p} \cap k[x_1,\dotsc ,x_{r_n}]$, then
$\mathfrak {p} \cap k[x_1,\dotsc ,x_{r_n}]$, then ![]() $\mathfrak {p}_n \subsetneq \mathfrak {p}_{n+1}$ for all n. Since
$\mathfrak {p}_n \subsetneq \mathfrak {p}_{n+1}$ for all n. Since ![]() $\mathfrak {p}_n$ are all prime and are contained in
$\mathfrak {p}_n$ are all prime and are contained in ![]() $\mathfrak {p}$, it follows that
$\mathfrak {p}$, it follows that ![]() $\operatorname {\mathrm {ht}}(\mathfrak {p}) = \infty $.
$\operatorname {\mathrm {ht}}(\mathfrak {p}) = \infty $.
Moreover, for arbitrary ideals ![]() $\mathfrak {a}$ of P it is proven in [Reference Gilmer and Heinzer29, Theorem 3.3] that
$\mathfrak {a}$ of P it is proven in [Reference Gilmer and Heinzer29, Theorem 3.3] that ![]() $\mathfrak {a}$ is finitely generated if and only if it has finitely many associated primes, each of which is of finite height.
$\mathfrak {a}$ is finitely generated if and only if it has finitely many associated primes, each of which is of finite height.
Proposition 5.13. For every finite ![]() $J\subset I$, the localisation
$J\subset I$, the localisation  $\widehat {P}_{ (x_j \mid j\in J )}$ is Noetherian.
$\widehat {P}_{ (x_j \mid j\in J )}$ is Noetherian.
Proof. As discussed in Remark 2.5, since J is finite we have an isomorphism
 $$ \begin{align*} \widehat{P} \simeq k[[x_i \mid i\in I\setminus J]]\left[\left[x_j \mid j\in J\right]\right]. \end{align*} $$
$$ \begin{align*} \widehat{P} \simeq k[[x_i \mid i\in I\setminus J]]\left[\left[x_j \mid j\in J\right]\right]. \end{align*} $$The proposition now follows from the next lemma:
Lemma 5.14. For any ![]() $n\in {\mathbb N}$, let
$n\in {\mathbb N}$, let ![]() $\widehat {P}_n:=\widehat {P}[[y_1,\dotsc ,y_n]]$ and consider the ideal
$\widehat {P}_n:=\widehat {P}[[y_1,\dotsc ,y_n]]$ and consider the ideal ![]() $\mathfrak {b}_n:=(y_1, \dotsc , y_n)$ in
$\mathfrak {b}_n:=(y_1, \dotsc , y_n)$ in ![]() $\widehat {P}_n$. Then the localisation
$\widehat {P}_n$. Then the localisation  $ (\widehat {P}_n )_{\mathfrak {b}_n}$ is a Noetherian ring.
$ (\widehat {P}_n )_{\mathfrak {b}_n}$ is a Noetherian ring.
The proof of this lemma uses the following straightforward generalisation of the Weierstrass division theorem, whose proof is a simple adaptation of the proof of [Reference Bourbaki7, VII, Section 3.8] where the adic topology on ![]() $\widehat {P}_n$ is replaced with the inverse limit topology. We say that
$\widehat {P}_n$ is replaced with the inverse limit topology. We say that ![]() $f\in \widehat {P}_n$ is
$f\in \widehat {P}_n$ is ![]() $y_n$-regular of order d if its image under the canonical map
$y_n$-regular of order d if its image under the canonical map ![]() $\widehat {P}_n \to k[[y_n]]$ is nonzero of order d.
$\widehat {P}_n \to k[[y_n]]$ is nonzero of order d.
Theorem 5.15. Let ![]() $f\in \widehat {P}_{n+1}$ be
$f\in \widehat {P}_{n+1}$ be ![]() $y_{n+1}$-regular of order d. For every
$y_{n+1}$-regular of order d. For every ![]() $g\in \widehat {P}_{n+1}$ there exist unique
$g\in \widehat {P}_{n+1}$ there exist unique ![]() $q\in \widehat {P}_{n+1}$ and
$q\in \widehat {P}_{n+1}$ and ![]() $r\in \widehat {P}_{n}[y_{n+1}]$ such that
$r\in \widehat {P}_{n}[y_{n+1}]$ such that ![]() $g=q f+r$ and r has degree
$g=q f+r$ and r has degree ![]() $< r$ as a polynomial in
$< r$ as a polynomial in ![]() $y_{n+1}$.
$y_{n+1}$.
The next lemma ensures that we can apply Theorem 5.15 to prove Lemma 5.14.
Lemma 5.16. Let ![]() $f\in \widehat {P}_{n+1}=\widehat {P}[[y_1,\dotsc ,y_{n+1}]]$ be a nonzero element. Then there exists a continuous k-automorphism
$f\in \widehat {P}_{n+1}=\widehat {P}[[y_1,\dotsc ,y_{n+1}]]$ be a nonzero element. Then there exists a continuous k-automorphism ![]() $\varphi \colon \widehat {P}_{n+1} \to \widehat {P}_{n+1}$ such that
$\varphi \colon \widehat {P}_{n+1} \to \widehat {P}_{n+1}$ such that ![]() $\varphi (\mathfrak {b}_{n+1})=\mathfrak {b}_{n+1}$ and
$\varphi (\mathfrak {b}_{n+1})=\mathfrak {b}_{n+1}$ and ![]() $\varphi (f)$ is
$\varphi (f)$ is ![]() $y_{n+1}$-regular.
$y_{n+1}$-regular.
Proof. If f is already ![]() $y_{n+1}$-regular, then we are done. If not, then pick any monomial of the form
$y_{n+1}$-regular, then we are done. If not, then pick any monomial of the form  $x_{i_1}^{d_1}\dotsm x_{i_r}^{d_r} y_1^{e_1}\dotsm y_{n+1}^{e_{n+1}}$ appearing in the expansion of f. Then decompose f as
$x_{i_1}^{d_1}\dotsm x_{i_r}^{d_r} y_1^{e_1}\dotsm y_{n+1}^{e_{n+1}}$ appearing in the expansion of f. Then decompose f as
such that ![]() $f'$ cannot be decomposed further. By [Reference Asgharzadeh and Tousi1, Lemma 6.11] there exist new coordinates
$f'$ cannot be decomposed further. By [Reference Asgharzadeh and Tousi1, Lemma 6.11] there exist new coordinates  $x^{\prime }_{i_j} = x_{i_j}+y_{n+1}^{a_j}$,
$x^{\prime }_{i_j} = x_{i_j}+y_{n+1}^{a_j}$,  $y^{\prime }_l = y_l+y_{n+1}^{b_l}$ and
$y^{\prime }_l = y_l+y_{n+1}^{b_l}$ and ![]() $y^{\prime }_{n+1} := y_{n+1}$ such that
$y^{\prime }_{n+1} := y_{n+1}$ such that  $f' (x^{\prime }_{i_j},y^{\prime }_l )$ is
$f' (x^{\prime }_{i_j},y^{\prime }_l )$ is ![]() $y^{\prime }_{n+1}$-regular. We may extend this change of coordinates trivially to a continuous automorphism
$y^{\prime }_{n+1}$-regular. We may extend this change of coordinates trivially to a continuous automorphism ![]() $\varphi \colon \widehat {P}_{n+1} \to \widehat {P}_{n+1}$ by setting
$\varphi \colon \widehat {P}_{n+1} \to \widehat {P}_{n+1}$ by setting ![]() $x^{\prime }_i=x_i$ for all indices i that are different from
$x^{\prime }_i=x_i$ for all indices i that are different from ![]() $i_j$ for all j. Then clearly
$i_j$ for all j. Then clearly ![]() $\varphi (f)$ is
$\varphi (f)$ is ![]() $y_{n+1}$-regular and
$y_{n+1}$-regular and ![]() $\varphi $ fixes
$\varphi $ fixes ![]() $\mathfrak {b}_{n+1}=(y_1,\dotsc ,y_{n+1})$.
$\mathfrak {b}_{n+1}=(y_1,\dotsc ,y_{n+1})$.
Proof of Lemma 5.14
We prove the lemma by induction on n. Let  $Q_n:= (\widehat {P}_n )_{\mathfrak {b}_n}$. Clearly
$Q_n:= (\widehat {P}_n )_{\mathfrak {b}_n}$. Clearly ![]() $Q_0\simeq \operatorname {\mathrm {Quot}} (\widehat {P} )$, so let us assume that
$Q_0\simeq \operatorname {\mathrm {Quot}} (\widehat {P} )$, so let us assume that ![]() $Q_n$ is Noetherian. We have injections
$Q_n$ is Noetherian. We have injections ![]() $Q_n \to Q_{n+1}$. Let
$Q_n \to Q_{n+1}$. Let ![]() $\mathfrak {a}$ be an ideal of
$\mathfrak {a}$ be an ideal of ![]() $Q_{n+1}$ and let
$Q_{n+1}$ and let ![]() $f\in \mathfrak {a}$,
$f\in \mathfrak {a}$, ![]() $f\neq 0$. After multiplication by a unit, we may assume
$f\neq 0$. After multiplication by a unit, we may assume ![]() $f\in \widehat {P}_{n+1}$; by Lemma 5.16 we may also assume f is y-regular. Consider the ideal
$f\in \widehat {P}_{n+1}$; by Lemma 5.16 we may also assume f is y-regular. Consider the ideal ![]() $\mathfrak {a}':=\mathfrak {a}\cap Q_n[y_{n+1}]$. Since
$\mathfrak {a}':=\mathfrak {a}\cap Q_n[y_{n+1}]$. Since ![]() $Q_n$ is Noetherian, so is
$Q_n$ is Noetherian, so is ![]() $Q_n[y_{n+1}]$, and thus there exist
$Q_n[y_{n+1}]$, and thus there exist ![]() $f_1,\dotsc ,f_r\in Q_n[y_{n+1}]$ that generate
$f_1,\dotsc ,f_r\in Q_n[y_{n+1}]$ that generate ![]() $\mathfrak {a}'$. We claim that
$\mathfrak {a}'$. We claim that ![]() $\mathfrak {a}=(f,f_1,\dotsc ,f_r)Q_{n+1}$.
$\mathfrak {a}=(f,f_1,\dotsc ,f_r)Q_{n+1}$.
Let ![]() $g\in \mathfrak {a}$. By Theorem 5.15, there exist a unit
$g\in \mathfrak {a}$. By Theorem 5.15, there exist a unit ![]() $u\in Q_{n+1}$,
$u\in Q_{n+1}$, ![]() $q\in \widehat {P}_{n+1}$ and
$q\in \widehat {P}_{n+1}$ and ![]() $r\in \widehat {P}_n[y_{n+1}]$ such that
$r\in \widehat {P}_n[y_{n+1}]$ such that ![]() $u g=q f+r$. Since
$u g=q f+r$. Since ![]() $r\in \mathfrak {a}'$, we can find
$r\in \mathfrak {a}'$, we can find ![]() $v_1,\dotsc ,v_r\in Q_n$ such that
$v_1,\dotsc ,v_r\in Q_n$ such that  $r=\sum _{j=1}^r v_j f_j$. Hence we have
$r=\sum _{j=1}^r v_j f_j$. Hence we have 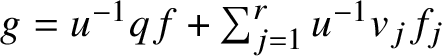 $g=u^{-1}q f+\sum _{j=1}^r u^{-1}v_j f_j$, which proves our claim.
$g=u^{-1}q f+\sum _{j=1}^r u^{-1}v_j f_j$, which proves our claim.
6 Embedding codimension
Let ![]() $(A, \mathfrak {m}, k)$ be a local ring. The inclusion of
$(A, \mathfrak {m}, k)$ be a local ring. The inclusion of ![]() $\mathfrak {m}/\mathfrak {m}^2$ in the graded ring
$\mathfrak {m}/\mathfrak {m}^2$ in the graded ring ![]() $\operatorname {\mathrm {gr}}(A)$ induces a natural surjective homomorphism of k-algebras
$\operatorname {\mathrm {gr}}(A)$ induces a natural surjective homomorphism of k-algebras
 $$ \begin{align*} \gamma \colon \operatorname{\mathrm{Sym}}_k\left(\mathfrak{m}/\mathfrak{m}^2\right) \to \operatorname{\mathrm{gr}}(A). \end{align*} $$
$$ \begin{align*} \gamma \colon \operatorname{\mathrm{Sym}}_k\left(\mathfrak{m}/\mathfrak{m}^2\right) \to \operatorname{\mathrm{gr}}(A). \end{align*} $$Definition 6.1. The embedding codimension of ![]() $(A, \mathfrak {m}, k)$ is defined to be
$(A, \mathfrak {m}, k)$ is defined to be
Proposition 6.2. For any local ring ![]() $(A, \mathfrak {m}, k)$, we have
$(A, \mathfrak {m}, k)$, we have
In particular, if A is Noetherian then ![]() $\mathrm {edim}(A) = \dim (A) + \mathrm {ecodim}(A)$.
$\mathrm {edim}(A) = \dim (A) + \mathrm {ecodim}(A)$.
Proof. This follows from the fact that for every polynomial ring ![]() $P = k[x_i \mid i \in I]$ and every ideal
$P = k[x_i \mid i \in I]$ and every ideal ![]() $\mathfrak {a} \subset P$, we have
$\mathfrak {a} \subset P$, we have ![]() $\dim (P) = \dim (P/\mathfrak {a}) + \operatorname {\mathrm {ht}}(\mathfrak {a})$ (compare Remark 5.12). For the last assertion we use the fact that
$\dim (P) = \dim (P/\mathfrak {a}) + \operatorname {\mathrm {ht}}(\mathfrak {a})$ (compare Remark 5.12). For the last assertion we use the fact that ![]() $\dim (\operatorname {\mathrm {gr}}(A)) = \dim (A)$ if A is Noetherian.
$\dim (\operatorname {\mathrm {gr}}(A)) = \dim (A)$ if A is Noetherian.
Remark 6.3. The formula in Proposition 6.2 is still valid, and informative, when some of the quantities involved are infinite.
Remark 6.4. Higher-rank valuation rings provide examples of finite-dimensional non-Noetherian rings whose embedding dimension is smaller than their dimension. For example, let ![]() $A \subset k(x,y)$ be the valuation ring associated to the valuation
$A \subset k(x,y)$ be the valuation ring associated to the valuation  $v \colon k(x,y)^* \to {\mathbb Z}^2_{\mathrm {lex}}$ given by
$v \colon k(x,y)^* \to {\mathbb Z}^2_{\mathrm {lex}}$ given by  $v(f) = (\operatorname {\mathrm {ord}}_x(f), \operatorname {\mathrm {ord}}_y (fx^{-\operatorname {\mathrm {ord}}_x(f)}\rvert _{x=0} ) )$. This is a
$v(f) = (\operatorname {\mathrm {ord}}_x(f), \operatorname {\mathrm {ord}}_y (fx^{-\operatorname {\mathrm {ord}}_x(f)}\rvert _{x=0} ) )$. This is a ![]() $2$-dimensional ring whose maximal ideal is principal, which implies that the embedding dimension is
$2$-dimensional ring whose maximal ideal is principal, which implies that the embedding dimension is ![]() $1$. In particular, the second equation in Proposition 6.2 does not hold for such rings.
$1$. In particular, the second equation in Proposition 6.2 does not hold for such rings.
Remark 6.5. The embedding codimension of a local ring was studied in the Noetherian setting in [Reference Lech35] under the name regularity defect. One of the main results proved there is that if ![]() $\mathfrak {p}$ is a prime ideal of a Noetherian local ring
$\mathfrak {p}$ is a prime ideal of a Noetherian local ring ![]() $(A,\mathfrak {m})$ such that
$(A,\mathfrak {m})$ such that ![]() $\dim (A) = \dim (A/\mathfrak {p}) + \dim (A_{\mathfrak {p}} )$, then
$\dim (A) = \dim (A/\mathfrak {p}) + \dim (A_{\mathfrak {p}} )$, then ![]() $\mathrm {ecodim} (A_{\mathfrak {p}} ) \le \mathrm {ecodim}(A)$ [Reference Lech35, Theorem 3]. It would be interesting to find suitable conditions for the same property to hold in the non-Noetherian setting.
$\mathrm {ecodim} (A_{\mathfrak {p}} ) \le \mathrm {ecodim}(A)$ [Reference Lech35, Theorem 3]. It would be interesting to find suitable conditions for the same property to hold in the non-Noetherian setting.
We now come to the main result of this section, which gives bounds for the embedding codimension of A from maps into A.
Proposition 6.6. Let ![]() $\varphi \colon (B,\mathfrak {n},k_0) \to (A,\mathfrak {m},k)$ be a homomorphism of local rings, and assume that
$\varphi \colon (B,\mathfrak {n},k_0) \to (A,\mathfrak {m},k)$ be a homomorphism of local rings, and assume that ![]() $(B,\mathfrak {n})$ has finite embedding dimension. Let
$(B,\mathfrak {n})$ has finite embedding dimension. Let ![]() $\varphi ^* \colon \mathfrak {n}/\mathfrak {n}^2 \otimes _{k_0}k \to \mathfrak {m}/\mathfrak {m}^2$ be the induced k-linear map on the Zariski cotangent spaces. Then
$\varphi ^* \colon \mathfrak {n}/\mathfrak {n}^2 \otimes _{k_0}k \to \mathfrak {m}/\mathfrak {m}^2$ be the induced k-linear map on the Zariski cotangent spaces. Then
In particular, if B is Noetherian then ![]() $\mathrm {ecodim}(A) \ge \operatorname {\mathrm {rank}}(\varphi ^*) - \dim (B)$.
$\mathrm {ecodim}(A) \ge \operatorname {\mathrm {rank}}(\varphi ^*) - \dim (B)$.
Remark 6.7. A stronger form of Proposition 6.6 is obtained by replacing ![]() $\dim (\operatorname {\mathrm {gr}}(B))$ with
$\dim (\operatorname {\mathrm {gr}}(B))$ with ![]() $\dim (\operatorname {\mathrm {gr}}(B/\ker (\operatorname {\mathrm {gr}}(\varphi ))))$ in the displayed formula. Note, in fact, that this sharper form of the proposition follows from the special case of the proposition where
$\dim (\operatorname {\mathrm {gr}}(B/\ker (\operatorname {\mathrm {gr}}(\varphi ))))$ in the displayed formula. Note, in fact, that this sharper form of the proposition follows from the special case of the proposition where ![]() $\varphi $ is assumed to be injective.
$\varphi $ is assumed to be injective.
Remark 6.8. Consider the special case where ![]() $\varphi $ is a homomorphism of local k-algebras with residue fields k (that is, such that the natural maps
$\varphi $ is a homomorphism of local k-algebras with residue fields k (that is, such that the natural maps ![]() $k \to B/\mathfrak {n}$ and
$k \to B/\mathfrak {n}$ and ![]() $k \to A/\mathfrak {m}$ are isomorphisms) and with B essentially of finite type. The geometric interpretation is the following. Let
$k \to A/\mathfrak {m}$ are isomorphisms) and with B essentially of finite type. The geometric interpretation is the following. Let ![]() $f \colon X \to Y$ be a morphism of schemes over k, with Y of finite type over k, and let
$f \colon X \to Y$ be a morphism of schemes over k, with Y of finite type over k, and let ![]() $p \in X(k)$ and
$p \in X(k)$ and ![]() $q = f(p) \in Y(k)$. Denote by
$q = f(p) \in Y(k)$. Denote by ![]() $T_pf \colon T_pX \to T_qY$ the map induced on Zariski tangent spaces. Then the proposition gives
$T_pf \colon T_pX \to T_qY$ the map induced on Zariski tangent spaces. Then the proposition gives
where ![]() $\operatorname {\mathrm {Im}}(f) \subset Y$ is the scheme-theoretic image of f. Note in particular that if X is Noetherian, then this formula reduces to the intuitive statement that
$\operatorname {\mathrm {Im}}(f) \subset Y$ is the scheme-theoretic image of f. Note in particular that if X is Noetherian, then this formula reduces to the intuitive statement that
Another special case is when f is a submersion onto Y, in which case the formula reduces to the inequality ![]() $\mathrm {ecodim} (\mathcal {O}_{X,p} ) \ge \mathrm {ecodim} (\mathcal {O}_{Y,q} )$.
$\mathrm {ecodim} (\mathcal {O}_{X,p} ) \ge \mathrm {ecodim} (\mathcal {O}_{Y,q} )$.
Proof of Proposition 6.6
We have the commutative diagram

The existence of ![]() $\sigma $ follows from the fact that
$\sigma $ follows from the fact that ![]() $\operatorname {\mathrm {Im}}(\pi ) \otimes _{k_0}k = \operatorname {\mathrm {Sym}}_k(\operatorname {\mathrm {Im}}(\varphi ^*))$. The map
$\operatorname {\mathrm {Im}}(\pi ) \otimes _{k_0}k = \operatorname {\mathrm {Sym}}_k(\operatorname {\mathrm {Im}}(\varphi ^*))$. The map ![]() $\iota $ is a linear extension of polynomial rings, and hence is faithfully flat. Since
$\iota $ is a linear extension of polynomial rings, and hence is faithfully flat. Since ![]() $\iota ^{-1}(\ker (\gamma )) = \ker (\sigma )$, we see that
$\iota ^{-1}(\ker (\gamma )) = \ker (\sigma )$, we see that
by the going-down theorem. On the other hand,
Since the inclusion ![]() $\operatorname {\mathrm {Im}}(\sigma ) \subset \operatorname {\mathrm {Im}}(\operatorname {\mathrm {gr}}(\varphi )) \otimes _{k_0}k$ is an inclusion of Noetherian local rings with the same residue field, and
$\operatorname {\mathrm {Im}}(\sigma ) \subset \operatorname {\mathrm {Im}}(\operatorname {\mathrm {gr}}(\varphi )) \otimes _{k_0}k$ is an inclusion of Noetherian local rings with the same residue field, and ![]() $\operatorname {\mathrm {Im}}(\operatorname {\mathrm {gr}}(\varphi ))$ is a quotient of
$\operatorname {\mathrm {Im}}(\operatorname {\mathrm {gr}}(\varphi ))$ is a quotient of ![]() $\operatorname {\mathrm {gr}}(B)$, we have
$\operatorname {\mathrm {gr}}(B)$, we have
Combining these formulas, we get
To conclude, notice that ![]() $\dim (\operatorname {\mathrm {gr}}(B)) = \dim (B)$ if B is Noetherian.
$\dim (\operatorname {\mathrm {gr}}(B)) = \dim (B)$ if B is Noetherian.
The following result shows that the embedding codimension of A is invariant under change of the base field, provided the residue field is already contained in A:
Proposition 6.9. Let ![]() $(A,\mathfrak {m},k)$ be a local k-algebra such that the natural map
$(A,\mathfrak {m},k)$ be a local k-algebra such that the natural map ![]() $k \to A/\mathfrak {m}$ is an isomorphism, and let
$k \to A/\mathfrak {m}$ is an isomorphism, and let ![]() $k \subset k'$ be a field extension. Denoting
$k \subset k'$ be a field extension. Denoting ![]() $A' := A \otimes _k k'$, we have
$A' := A \otimes _k k'$, we have
Proof. First, observe that ![]() $A'$ is a local
$A'$ is a local ![]() $k'$-algebra with maximal ideal
$k'$-algebra with maximal ideal ![]() $\mathfrak {m}' = \mathfrak {m} \otimes _k k'$. We have
$\mathfrak {m}' = \mathfrak {m} \otimes _k k'$. We have ![]() $\mathrm {ecodim}(A) = \operatorname {\mathrm {ht}}(\ker (\gamma ))$, where
$\mathrm {ecodim}(A) = \operatorname {\mathrm {ht}}(\ker (\gamma ))$, where
 $$ \begin{align*} \gamma \colon \operatorname{\mathrm{Sym}}_k\left(\mathfrak{m}/\mathfrak{m}^2\right) \to \operatorname{\mathrm{gr}}(A) \end{align*} $$
$$ \begin{align*} \gamma \colon \operatorname{\mathrm{Sym}}_k\left(\mathfrak{m}/\mathfrak{m}^2\right) \to \operatorname{\mathrm{gr}}(A) \end{align*} $$is defined, as at the beginning. Since for every n we have ![]() $(\mathfrak {m}')^n/(\mathfrak {m}')^{n+1} = \mathfrak {m}^n/\mathfrak {n}^{n+1} \otimes _k k'$, we see that
$(\mathfrak {m}')^n/(\mathfrak {m}')^{n+1} = \mathfrak {m}^n/\mathfrak {n}^{n+1} \otimes _k k'$, we see that ![]() $\gamma $ induces, by base change, the analogous map
$\gamma $ induces, by base change, the analogous map
 $$ \begin{align*} \gamma' \colon \operatorname{\mathrm{Sym}}_k\left(\mathfrak{m}'/(\mathfrak{m}')^2\right) \to \operatorname{\mathrm{gr}}(A'). \end{align*} $$
$$ \begin{align*} \gamma' \colon \operatorname{\mathrm{Sym}}_k\left(\mathfrak{m}'/(\mathfrak{m}')^2\right) \to \operatorname{\mathrm{gr}}(A'). \end{align*} $$The next lemma gives ![]() $\operatorname {\mathrm {ht}}(\ker (\gamma ')) = \operatorname {\mathrm {ht}}(\ker (\gamma ))$, and the assertion follows.
$\operatorname {\mathrm {ht}}(\ker (\gamma ')) = \operatorname {\mathrm {ht}}(\ker (\gamma ))$, and the assertion follows.
Lemma 6.10. Let ![]() $P = k[x_i \mid i \in I]$ and
$P = k[x_i \mid i \in I]$ and ![]() $P' = P \otimes _kk' = k'[x_i \mid i \in I]$, where
$P' = P \otimes _kk' = k'[x_i \mid i \in I]$, where ![]() $k \subset k'$ is a field extension. Then for every ideal
$k \subset k'$ is a field extension. Then for every ideal ![]() $\mathfrak {a} \subset P$ we have
$\mathfrak {a} \subset P$ we have ![]() $\operatorname {\mathrm {ht}}(\mathfrak {a}) = \operatorname {\mathrm {ht}}(\mathfrak {a} P')$.
$\operatorname {\mathrm {ht}}(\mathfrak {a}) = \operatorname {\mathrm {ht}}(\mathfrak {a} P')$.
Proof. For short, let ![]() $\mathfrak {a}' = \mathfrak {a} P'$. If I is finite, then the lemma follows from dimension theory. In general, suppose by contradiction that
$\mathfrak {a}' = \mathfrak {a} P'$. If I is finite, then the lemma follows from dimension theory. In general, suppose by contradiction that ![]() $\operatorname {\mathrm {ht}}(\mathfrak {a}) \ne \operatorname {\mathrm {ht}}(\mathfrak {a}')$. Then we can find a finite subset
$\operatorname {\mathrm {ht}}(\mathfrak {a}) \ne \operatorname {\mathrm {ht}}(\mathfrak {a}')$. Then we can find a finite subset ![]() $J \subset I$ such that
$J \subset I$ such that ![]() $\operatorname {\mathrm {ht}}(\mathfrak {a}_J) \ne \operatorname {\mathrm {ht}} (\mathfrak {a}^{\prime }_J )$ (compare Remark 5.12). Since
$\operatorname {\mathrm {ht}}(\mathfrak {a}_J) \ne \operatorname {\mathrm {ht}} (\mathfrak {a}^{\prime }_J )$ (compare Remark 5.12). Since ![]() $\mathfrak {a}^{\prime }_J = \mathfrak {a}_J P^{\prime }_J$, this contradicts the finite-dimensional case.
$\mathfrak {a}^{\prime }_J = \mathfrak {a}_J P^{\prime }_J$, this contradicts the finite-dimensional case.
7 Formal embedding codimension
In the case of equicharacteristic local rings, looking at the completion instead of the associated graded provides a different way of defining the embedding codimension. To distinguish the two, we introduce the following terminology:
Definition 7.1. The formal embedding codimension of an equicharacteristic local ring ![]() $(A, \mathfrak {m}, k)$ is defined to be
$(A, \mathfrak {m}, k)$ is defined to be
 $$ \begin{align*} \mathrm{fcodim}(A) := \inf_{\tau} \operatorname{\mathrm{ht}}(\ker(\tau)), \end{align*} $$
$$ \begin{align*} \mathrm{fcodim}(A) := \inf_{\tau} \operatorname{\mathrm{ht}}(\ker(\tau)), \end{align*} $$where the infimum is taken over all choices of formal embeddings ![]() $\tau \colon \widehat {P} \to \widehat {A}$ (see Definition 3.6).
$\tau \colon \widehat {P} \to \widehat {A}$ (see Definition 3.6).
Proposition 7.2. In this definition, we have ![]() $\mathrm {fcodim}(A) = \operatorname {\mathrm {ht}}(\ker (\tau ))$ for every efficient formal embedding
$\mathrm {fcodim}(A) = \operatorname {\mathrm {ht}}(\ker (\tau ))$ for every efficient formal embedding ![]() $\tau \colon \widehat {P} \to \widehat {A}$.
$\tau \colon \widehat {P} \to \widehat {A}$.
Proof. Given two formal embeddings ![]() $\tau \colon \widehat {P} \to \widehat {A}$ and
$\tau \colon \widehat {P} \to \widehat {A}$ and ![]() $\tau ' \colon \widehat {P}' \to \widehat {A}$ with
$\tau ' \colon \widehat {P}' \to \widehat {A}$ with ![]() $\tau $ efficient, by Remark 3.13 there is a surjection
$\tau $ efficient, by Remark 3.13 there is a surjection ![]() $\varphi \colon \widehat {P}' \to \widehat {P}$ such that
$\varphi \colon \widehat {P}' \to \widehat {P}$ such that ![]() $\tau ' = \tau \circ \varphi $, and hence
$\tau ' = \tau \circ \varphi $, and hence ![]() $\operatorname {\mathrm {ht}}(\ker (\tau ')) \ge \operatorname {\mathrm {ht}}(\ker (\tau ))$.
$\operatorname {\mathrm {ht}}(\ker (\tau ')) \ge \operatorname {\mathrm {ht}}(\ker (\tau ))$.
Remark 7.3. If A is a local k-algebra such that the residue field ![]() $A/\mathfrak {m}$ is separable over k, then it follows by [Reference Grothendieck32, Chapter
$A/\mathfrak {m}$ is separable over k, then it follows by [Reference Grothendieck32, Chapter ![]() ${0}_{\mathsf{IV}}$, Corollary 19.5.4] that the following are equivalent:
${0}_{\mathsf{IV}}$, Corollary 19.5.4] that the following are equivalent:
1. A is formally smooth over k.
2.
 $\mathrm {ecodim}(A) = 0$.
$\mathrm {ecodim}(A) = 0$.3.
 $\mathrm {fcodim}(A) = 0$.
$\mathrm {fcodim}(A) = 0$.
Proposition 7.4. For every equicharacteristic local ring ![]() $(A,\mathfrak {m},k)$, we have
$(A,\mathfrak {m},k)$, we have
 $$ \begin{align*} \mathrm{edim}(A) \ge \dim\left(\widehat{A}\right) + \mathrm{fcodim}(A), \end{align*} $$
$$ \begin{align*} \mathrm{edim}(A) \ge \dim\left(\widehat{A}\right) + \mathrm{fcodim}(A), \end{align*} $$and equality holds if A has finite embedding dimension. In particular, if A is Noetherian then ![]() $\mathrm {edim}(A) = \dim (A) + \mathrm {fcodim}(A)$.
$\mathrm {edim}(A) = \dim (A) + \mathrm {fcodim}(A)$.
Proof. Consider an efficient formal embedding ![]() $\tau \colon \widehat {P} = k[[x_i \mid i\in I]] \to \widehat {A}$. Note that
$\tau \colon \widehat {P} = k[[x_i \mid i\in I]] \to \widehat {A}$. Note that ![]() $\dim (\widehat {P} ) = \mathrm {edim}(A)$ by Proposition 3.14. The first formula follows from the simple fact that
$\dim (\widehat {P} ) = \mathrm {edim}(A)$ by Proposition 3.14. The first formula follows from the simple fact that ![]() $\dim (\widehat {P} ) \ge \operatorname {\mathrm {ht}}(\ker (\tau )) + \dim (\widehat {P}/\ker (\tau ) )$. If A has finite embedding dimension, then the set I is finite, and equality holds in the formula because a power series ring in finitely many variables is catenary of dimension equal to the number of variables. The second formula follows from the first and the fact that
$\dim (\widehat {P} ) \ge \operatorname {\mathrm {ht}}(\ker (\tau )) + \dim (\widehat {P}/\ker (\tau ) )$. If A has finite embedding dimension, then the set I is finite, and equality holds in the formula because a power series ring in finitely many variables is catenary of dimension equal to the number of variables. The second formula follows from the first and the fact that ![]() $\dim (A) = \dim (\widehat {A} )$ if A is Noetherian.
$\dim (A) = \dim (\widehat {A} )$ if A is Noetherian.
Corollary 7.5. If ![]() $(A,\mathfrak {m}, k)$ is an equicharacteristic local ring of finite embedding dimension, then
$(A,\mathfrak {m}, k)$ is an equicharacteristic local ring of finite embedding dimension, then
Proof. By Propositions 7.4 and 6.2, it suffices to show that ![]() $\dim (\operatorname {\mathrm {gr}}(A)) = \dim (\widehat {A} )$. By Proposition 3.7, the completion
$\dim (\operatorname {\mathrm {gr}}(A)) = \dim (\widehat {A} )$. By Proposition 3.7, the completion ![]() $\widehat {A}$ is the quotient of a power series ring in finitely many variables, and therefore is Noetherian and carries the
$\widehat {A}$ is the quotient of a power series ring in finitely many variables, and therefore is Noetherian and carries the ![]() $\widehat {\mathfrak {m}}$–adic topology. The result now follows from [Reference Matsumura36, Theorem 15.7] and the identification
$\widehat {\mathfrak {m}}$–adic topology. The result now follows from [Reference Matsumura36, Theorem 15.7] and the identification ![]() $\operatorname {\mathrm {gr}} (\widehat {A} ) \simeq \operatorname {\mathrm {gr}}(A)$.
$\operatorname {\mathrm {gr}} (\widehat {A} ) \simeq \operatorname {\mathrm {gr}}(A)$.
Proposition 7.6. Let ![]() $(A, \mathfrak {m}, k)$ be an equicharacteristic local ring. If A admits a DGK decomposition
$(A, \mathfrak {m}, k)$ be an equicharacteristic local ring. If A admits a DGK decomposition ![]() $\widehat {A} \simeq \widehat {B} \hat {\otimes }_k \widehat {P}$, then
$\widehat {A} \simeq \widehat {B} \hat {\otimes }_k \widehat {P}$, then
Proof. Since B is Noetherian, we have ![]() $\mathrm {edim}(B) < \infty $. By Corollary 7.5, we have that
$\mathrm {edim}(B) < \infty $. By Corollary 7.5, we have that ![]() $\mathrm {ecodim}(B) = \mathrm {fcodim}(B)$. Now we make use of the fact that
$\mathrm {ecodim}(B) = \mathrm {fcodim}(B)$. Now we make use of the fact that ![]() $A \simeq k[[x_i \mid i \in I]]/\mathfrak {a}$ with
$A \simeq k[[x_i \mid i \in I]]/\mathfrak {a}$ with ![]() $\mathfrak {a}$ of finite definition. Note that there exists
$\mathfrak {a}$ of finite definition. Note that there exists ![]() $J \subset I$ finite such that
$J \subset I$ finite such that ![]() $\mathfrak {a}$ is the extension of
$\mathfrak {a}$ is the extension of ![]() $\mathfrak {a}_J := \mathfrak {a} \cap k [ [x_j \mid j \in J ] ]$ and
$\mathfrak {a}_J := \mathfrak {a} \cap k [ [x_j \mid j \in J ] ]$ and  $\widehat {B} \simeq k [ [x_j \mid j \in J ] ]/\mathfrak {a}_J$. We may assume that the surjection
$\widehat {B} \simeq k [ [x_j \mid j \in J ] ]/\mathfrak {a}_J$. We may assume that the surjection  $\tau _{B} \colon k [ [x_j \mid j \in J ] ] \to \widehat {B}$ is an efficient formal embedding; then so is
$\tau _{B} \colon k [ [x_j \mid j \in J ] ] \to \widehat {B}$ is an efficient formal embedding; then so is ![]() $\tau _{A} \colon k[[x_i \mid i \in I]] \to \widehat {A}$. By Remark 5.3 and Theorem 5.10, it follows that
$\tau _{A} \colon k[[x_i \mid i \in I]] \to \widehat {A}$. By Remark 5.3 and Theorem 5.10, it follows that ![]() $\mathrm {fcodim}(B) = \mathrm {fcodim}(A)$. It remains to show that
$\mathrm {fcodim}(B) = \mathrm {fcodim}(A)$. It remains to show that ![]() $\mathrm {ecodim}(B) = \mathrm {ecodim}(A)$.
$\mathrm {ecodim}(B) = \mathrm {ecodim}(A)$.
To that end, note that ![]() $\operatorname {\mathrm {gr}}(\tau _A)$ factors through the natural surjection
$\operatorname {\mathrm {gr}}(\tau _A)$ factors through the natural surjection ![]() $\operatorname {\mathrm {Sym}}_k (\mathfrak {m}/\mathfrak {m}^2 ) \to \operatorname {\mathrm {gr}}(A)$, and similarly for
$\operatorname {\mathrm {Sym}}_k (\mathfrak {m}/\mathfrak {m}^2 ) \to \operatorname {\mathrm {gr}}(A)$, and similarly for ![]() $\operatorname {\mathrm {gr}}(\tau _B)$. We have the commutative diagram
$\operatorname {\mathrm {gr}}(\tau _B)$. We have the commutative diagram

and thus the claim follows by Lemma 5.6.
Remark 7.7. The analogous statement of Proposition 7.6 holds for equicharacteristic local rings ![]() $(A,\mathfrak {m},k)$ admitting a weak DGK decomposition.
$(A,\mathfrak {m},k)$ admitting a weak DGK decomposition.
The proof of Corollary 7.5 does not extend beyond the case of finite embedding dimension. Nonetheless, the following general comparison theorem holds:
Theorem 7.8. For every equicharacteristic local ring ![]() $(A,\mathfrak {m},k)$, we have
$(A,\mathfrak {m},k)$, we have
Proof. Fix an efficient formal embedding ![]() $\tau \colon \widehat {P} \to \widehat {A}$, and let
$\tau \colon \widehat {P} \to \widehat {A}$, and let ![]() $\operatorname {\mathrm {gr}}(\tau ) \colon P \to \operatorname {\mathrm {gr}}(A)$ be the induced map on associated graded rings (as in Remark 2.6, we identify
$\operatorname {\mathrm {gr}}(\tau ) \colon P \to \operatorname {\mathrm {gr}}(A)$ be the induced map on associated graded rings (as in Remark 2.6, we identify ![]() $\operatorname {\mathrm {gr}} (\widehat {P} ) = \operatorname {\mathrm {gr}}(P) = P$). As explained in Remark 3.8,
$\operatorname {\mathrm {gr}} (\widehat {P} ) = \operatorname {\mathrm {gr}}(P) = P$). As explained in Remark 3.8, ![]() $P \simeq \operatorname {\mathrm {Sym}}_k (\mathfrak {m}/\mathfrak {m}^2 )$ and
$P \simeq \operatorname {\mathrm {Sym}}_k (\mathfrak {m}/\mathfrak {m}^2 )$ and ![]() $\operatorname {\mathrm {gr}}(\tau )$ gets identified with the canonical surjection
$\operatorname {\mathrm {gr}}(\tau )$ gets identified with the canonical surjection ![]() $\gamma $. In particular, it is enough to show that
$\gamma $. In particular, it is enough to show that
Write ![]() $\mathfrak {a} = \ker (\tau )$. By [Reference Bourbaki7, Chapter III, Section 2.4, Proposition 2], we have
$\mathfrak {a} = \ker (\tau )$. By [Reference Bourbaki7, Chapter III, Section 2.4, Proposition 2], we have ![]() $\ker (\operatorname {\mathrm {gr}}(\tau )) = \operatorname {\mathrm {in}}(\mathfrak {a})$. To conclude, it is therefore enough to prove that
$\ker (\operatorname {\mathrm {gr}}(\tau )) = \operatorname {\mathrm {in}}(\mathfrak {a})$. To conclude, it is therefore enough to prove that
This follows from the next proposition.
Proposition 7.9. Let ![]() $P = k[x_i \mid i \in I]$ and
$P = k[x_i \mid i \in I]$ and ![]() $\widehat {P} = k[[x_i \mid i \in I]]$, where k is a field. Let
$\widehat {P} = k[[x_i \mid i \in I]]$, where k is a field. Let ![]() $\mathfrak {a} \subset \widehat {P}$ be an ideal and
$\mathfrak {a} \subset \widehat {P}$ be an ideal and ![]() $\operatorname {\mathrm {in}}(\mathfrak {a}) \subset P$ the corresponding initial ideal. Then
$\operatorname {\mathrm {in}}(\mathfrak {a}) \subset P$ the corresponding initial ideal. Then ![]() $\operatorname {\mathrm {ht}}(\mathfrak {a}) \ge \operatorname {\mathrm {ht}}(\operatorname {\mathrm {in}}(\mathfrak {a}))$.
$\operatorname {\mathrm {ht}}(\mathfrak {a}) \ge \operatorname {\mathrm {ht}}(\operatorname {\mathrm {in}}(\mathfrak {a}))$.
Proof. If ![]() $\operatorname {\mathrm {ht}}(\operatorname {\mathrm {in}}(\mathfrak {a})) < \infty $, then
$\operatorname {\mathrm {ht}}(\operatorname {\mathrm {in}}(\mathfrak {a})) < \infty $, then ![]() $\operatorname {\mathrm {in}}(\mathfrak {a})$ is finitely generated and there exists a finite subset
$\operatorname {\mathrm {in}}(\mathfrak {a})$ is finitely generated and there exists a finite subset ![]() $J \subset I$ such that
$J \subset I$ such that ![]() $\operatorname {\mathrm {in}}(\mathfrak {a})_J$ has the same height as
$\operatorname {\mathrm {in}}(\mathfrak {a})_J$ has the same height as ![]() $\operatorname {\mathrm {in}}(\mathfrak {a})$ (see Remark 5.12). Otherwise, if
$\operatorname {\mathrm {in}}(\mathfrak {a})$ (see Remark 5.12). Otherwise, if ![]() $\operatorname {\mathrm {ht}}(\operatorname {\mathrm {in}}(\mathfrak {a})) = \infty $, then we can pick a finite
$\operatorname {\mathrm {ht}}(\operatorname {\mathrm {in}}(\mathfrak {a})) = \infty $, then we can pick a finite ![]() $J \subset I$ such that the height of
$J \subset I$ such that the height of ![]() $\operatorname {\mathrm {in}}(\mathfrak {a})_J$ is arbitrary large. Define
$\operatorname {\mathrm {in}}(\mathfrak {a})_J$ is arbitrary large. Define ![]() $c := \operatorname {\mathrm {ht}}(\operatorname {\mathrm {in}}(\mathfrak {a})_J)$.
$c := \operatorname {\mathrm {ht}}(\operatorname {\mathrm {in}}(\mathfrak {a})_J)$.
By [Reference Bruns and Herzog17, Proposition 1.5.11], we can fix homogeneous elements ![]() $g_1,\dotsc ,g_c \in \operatorname {\mathrm {in}}(\mathfrak {a})_J$ forming a regular sequence in
$g_1,\dotsc ,g_c \in \operatorname {\mathrm {in}}(\mathfrak {a})_J$ forming a regular sequence in ![]() $P_J$. By the definition of initial ideal, there are elements
$P_J$. By the definition of initial ideal, there are elements ![]() $f_1,\dotsc ,f_c \in \mathfrak {a}$ such that
$f_1,\dotsc ,f_c \in \mathfrak {a}$ such that ![]() $\operatorname {\mathrm {in}}(f_i) = g_i$ for all i. Let
$\operatorname {\mathrm {in}}(f_i) = g_i$ for all i. Let  $R = R (\widehat {P} ) := \bigoplus _{n \in {\mathbb Z}} \widehat {\mathfrak {m}^n}u^{-n}$ be the extended Rees algebra of
$R = R (\widehat {P} ) := \bigoplus _{n \in {\mathbb Z}} \widehat {\mathfrak {m}^n}u^{-n}$ be the extended Rees algebra of ![]() $\widehat {P}$, where we set
$\widehat {P}$, where we set ![]() $\widehat {\mathfrak {m}^n} = \widehat {P}$ whenever
$\widehat {\mathfrak {m}^n} = \widehat {P}$ whenever ![]() $n < 0$. For every i, let
$n < 0$. For every i, let ![]() $\widetilde {f}_i := u^{-\operatorname {\mathrm {ord}} (f_i )}f_i \in R$. Note that
$\widetilde {f}_i := u^{-\operatorname {\mathrm {ord}} (f_i )}f_i \in R$. Note that ![]() $\widetilde {f}_i\rvert _{u=0} = \operatorname {\mathrm {in}}(f_i) = g_i$ via the identification
$\widetilde {f}_i\rvert _{u=0} = \operatorname {\mathrm {in}}(f_i) = g_i$ via the identification ![]() $R/uR \simeq P$.
$R/uR \simeq P$.
We claim that for every ![]() $1 \le r \le c$, the elements
$1 \le r \le c$, the elements ![]() $\widetilde {f}_1,\dotsc ,\widetilde {f}_r$ form a regular sequence in R and
$\widetilde {f}_1,\dotsc ,\widetilde {f}_r$ form a regular sequence in R and ![]() $R/ (\widetilde {f}_1,\dotsc ,\widetilde {f}_r )$ is flat over
$R/ (\widetilde {f}_1,\dotsc ,\widetilde {f}_r )$ is flat over ![]() $k[u]$. We argue by induction on r, the assertion being clear if
$k[u]$. We argue by induction on r, the assertion being clear if ![]() $r=0$. Setting for short
$r=0$. Setting for short ![]() $B := R/ (\widetilde {f}_1,\dotsc ,\widetilde {f}_{r-1} )$, we know by induction that B is flat over
$B := R/ (\widetilde {f}_1,\dotsc ,\widetilde {f}_{r-1} )$, we know by induction that B is flat over ![]() $k[u]$. Assume that there exists
$k[u]$. Assume that there exists ![]() $h\in \widehat {P}$ with
$h\in \widehat {P}$ with  $h=\sum _{i=1}^{r-1} a_if_i$ and
$h=\sum _{i=1}^{r-1} a_if_i$ and ![]() $\operatorname {\mathrm {in}}(h)$ not divisible by
$\operatorname {\mathrm {in}}(h)$ not divisible by ![]() $g_1,\dotsc ,g_{r-1}$. Writing
$g_1,\dotsc ,g_{r-1}$. Writing
 $$ \begin{align*} \sum_{i=1}^{r-1} u^{\operatorname{\mathrm{ord}}\left(f_i\right)}a_i \widetilde{f}_i=u^{\operatorname{\mathrm{ord}}(h)}\widetilde{h}, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{r-1} u^{\operatorname{\mathrm{ord}}\left(f_i\right)}a_i \widetilde{f}_i=u^{\operatorname{\mathrm{ord}}(h)}\widetilde{h}, \end{align*} $$Lemma 7.10 yields that B has torsion over ![]() $k[u]$, which gives a contradiction. Thus
$k[u]$, which gives a contradiction. Thus ![]() $\operatorname {\mathrm {in}}(f_1,\dotsc ,f_{r-1})=(g_1,\dotsc ,g_{r-1})$ and B is isomorphic to the algebra
$\operatorname {\mathrm {in}}(f_1,\dotsc ,f_{r-1})=(g_1,\dotsc ,g_{r-1})$ and B is isomorphic to the algebra ![]() $\bigoplus _{n \in {\mathbb Z}} \mathfrak {b}_n u^{-n}$, where
$\bigoplus _{n \in {\mathbb Z}} \mathfrak {b}_n u^{-n}$, where ![]() $\mathfrak {b}_n := (\widehat {\mathfrak {m}^n} + (f_1,\dotsc ,f_{r-1}) )/(f_1,\dotsc ,f_{r-1})$ for
$\mathfrak {b}_n := (\widehat {\mathfrak {m}^n} + (f_1,\dotsc ,f_{r-1}) )/(f_1,\dotsc ,f_{r-1})$ for ![]() $n \ge 0$ and
$n \ge 0$ and ![]() $\mathfrak {b}_n = B$ for
$\mathfrak {b}_n = B$ for ![]() $n < 0$. It follows by Proposition 2.7 that
$n < 0$. It follows by Proposition 2.7 that ![]() $\bigcap _{n \ge 1} \mathfrak {b}_n = \{0\}$. Then Lemma 7.11 implies that B is
$\bigcap _{n \ge 1} \mathfrak {b}_n = \{0\}$. Then Lemma 7.11 implies that B is ![]() $(u)$-adically separated, and Lemma 7.12 (with
$(u)$-adically separated, and Lemma 7.12 (with ![]() $t = u$) implies that the class b of
$t = u$) implies that the class b of ![]() $\widetilde {f}_r$ in B is a regular element and
$\widetilde {f}_r$ in B is a regular element and ![]() $B/bB$ is flat over
$B/bB$ is flat over ![]() $k[u]$.
$k[u]$.
The natural isomorphism ![]() $R/(u-1)R \simeq \widehat {P}$ sends
$R/(u-1)R \simeq \widehat {P}$ sends ![]() $\widetilde {f}_i$ to
$\widetilde {f}_i$ to ![]() $f_i$, and hence we see by Lemma 7.12 (with
$f_i$, and hence we see by Lemma 7.12 (with ![]() $t = u-1$) that
$t = u-1$) that ![]() $f_1,\dotsc ,f_c$ form a regular sequence in
$f_1,\dotsc ,f_c$ form a regular sequence in ![]() $\widehat {P}$. This implies that
$\widehat {P}$. This implies that ![]() $\operatorname {\mathrm {depth}} (\mathfrak {a},\widehat {P} ) \ge c$. We conclude using the fact that
$\operatorname {\mathrm {depth}} (\mathfrak {a},\widehat {P} ) \ge c$. We conclude using the fact that ![]() $\operatorname {\mathrm {ht}}(\mathfrak {a}) \ge \operatorname {\mathrm {depth}} (\mathfrak {a},\widehat {P} )$ (see, for example, [Reference Atiyah and Macdonald2, Proposition 2.3 and Lemma 3.2]).
$\operatorname {\mathrm {ht}}(\mathfrak {a}) \ge \operatorname {\mathrm {depth}} (\mathfrak {a},\widehat {P} )$ (see, for example, [Reference Atiyah and Macdonald2, Proposition 2.3 and Lemma 3.2]).
Lemma 7.10. Set ![]() $f_1,\dotsc ,f_r\in \widehat {P}$. If
$f_1,\dotsc ,f_r\in \widehat {P}$. If ![]() $h\in \widehat {P}$, then
$h\in \widehat {P}$, then ![]() $\operatorname {\mathrm {in}}(h)\in (\operatorname {\mathrm {in}}(f_1),\dotsc ,\operatorname {\mathrm {in}}(f_r))$ if and only if there exist elements
$\operatorname {\mathrm {in}}(h)\in (\operatorname {\mathrm {in}}(f_1),\dotsc ,\operatorname {\mathrm {in}}(f_r))$ if and only if there exist elements ![]() $b_1,\dotsc ,b_r$ in the Rees algebra
$b_1,\dotsc ,b_r$ in the Rees algebra ![]() $R=R (\widehat {P} )$ such that
$R=R (\widehat {P} )$ such that
 $$ \begin{align*} \widetilde{h}=\sum_i^r b_i \widetilde{f}_i. \end{align*} $$
$$ \begin{align*} \widetilde{h}=\sum_i^r b_i \widetilde{f}_i. \end{align*} $$Proof. Given ![]() $\widetilde {h}=\sum b_i \widetilde {f}_i$, we may assume that
$\widetilde {h}=\sum b_i \widetilde {f}_i$, we may assume that ![]() $b_i$ is homogeneous in R – that is, of the form
$b_i$ is homogeneous in R – that is, of the form ![]() $b_i=u^{-\operatorname {\mathrm {ord}}(h)+\operatorname {\mathrm {ord}} (f_i )}a_i$, with
$b_i=u^{-\operatorname {\mathrm {ord}}(h)+\operatorname {\mathrm {ord}} (f_i )}a_i$, with ![]() $a_i\in \widehat {P}$. But then
$a_i\in \widehat {P}$. But then ![]() $\operatorname {\mathrm {ord}}(a_i)\geq \operatorname {\mathrm {ord}}(h)-\operatorname {\mathrm {ord}}(f_i)$ and the claim follows.
$\operatorname {\mathrm {ord}}(a_i)\geq \operatorname {\mathrm {ord}}(h)-\operatorname {\mathrm {ord}}(f_i)$ and the claim follows.
Lemma 7.11. Let A be a ring and ![]() $(\mathfrak {a}_n)_{n \ge 0}$ a graded sequence of ideals of A, and let
$(\mathfrak {a}_n)_{n \ge 0}$ a graded sequence of ideals of A, and let ![]() $R(A) := \bigoplus _{n \in {\mathbb Z}} \mathfrak {a}_n u^{-n}$, where we set
$R(A) := \bigoplus _{n \in {\mathbb Z}} \mathfrak {a}_n u^{-n}$, where we set ![]() $\mathfrak {a}_n = A$ for
$\mathfrak {a}_n = A$ for ![]() $n < 0$. Assume that
$n < 0$. Assume that ![]() $\bigcap _{n \ge 1} \mathfrak {a}_n = \{0\}$. Then
$\bigcap _{n \ge 1} \mathfrak {a}_n = \{0\}$. Then ![]() $R(A)$ is
$R(A)$ is ![]() $(u)$-adically separated.
$(u)$-adically separated.
Proof. Let ![]() $a \in R(A)$ be any element. Write
$a \in R(A)$ be any element. Write  $a = \sum _{i=p}^q a_i u^{-i}$ for some
$a = \sum _{i=p}^q a_i u^{-i}$ for some ![]() $a_i \in \widehat {P}$ and
$a_i \in \widehat {P}$ and ![]() $p,q \in {\mathbb Z}$. By the definition of Rees algebra, we have
$p,q \in {\mathbb Z}$. By the definition of Rees algebra, we have ![]() $a_i \in \mathfrak {a}_i$ for all i. The condition that
$a_i \in \mathfrak {a}_i$ for all i. The condition that ![]() $a \in u^nR(A)$ is equivalent to having
$a \in u^nR(A)$ is equivalent to having ![]() $a_i \in \mathfrak {a}_{n+i}$ for all i. If
$a_i \in \mathfrak {a}_{n+i}$ for all i. If ![]() $a \in \bigcap _{n \ge 1} u^nR(A)$, then we have
$a \in \bigcap _{n \ge 1} u^nR(A)$, then we have ![]() $a_i \in \bigcap _{n \ge 1}\mathfrak {a}_n = \{0\}$ for all i, and hence
$a_i \in \bigcap _{n \ge 1}\mathfrak {a}_n = \{0\}$ for all i, and hence ![]() $a = 0$.
$a = 0$.
Lemma 7.12. Let B be a flat and ![]() $k[t]$-algebra. For any given
$k[t]$-algebra. For any given ![]() $b \in B$, consider the following properties:
$b \in B$, consider the following properties:
1. b is a regular element of B and
 $B/bB$ is flat over
$B/bB$ is flat over  $k[t]$.
$k[t]$.2. The image
 $\bar {b}$ of b in
$\bar {b}$ of b in  $B/tB$ is regular.
$B/tB$ is regular.
Then (1) ![]() $\Rightarrow $ (2), and the converse holds if B is
$\Rightarrow $ (2), and the converse holds if B is ![]() $(t)$-adically separated.
$(t)$-adically separated.
Proof. The proof is an adaptation of the proof of [Reference Matsumura36, Theorem 22.5]. The implication (1) ![]() $\Rightarrow $ (2) follows by the snake lemma applied to the commutative diagram
$\Rightarrow $ (2) follows by the snake lemma applied to the commutative diagram

after observing that the map ![]() $B \to B$ given by multiplication by b is injective, since b is regular, and so is the map
$B \to B$ given by multiplication by b is injective, since b is regular, and so is the map ![]() $B/bB \to B/bB$ given by multiplication by t, since
$B/bB \to B/bB$ given by multiplication by t, since ![]() $B/bB$ is flat over
$B/bB$ is flat over ![]() $k[t]$.
$k[t]$.
In order to prove the implication (2) ![]() $\Rightarrow $ (1) when B is
$\Rightarrow $ (1) when B is ![]() $(t)$-adically separated, suppose
$(t)$-adically separated, suppose ![]() $x \in B$ is an element such that
$x \in B$ is an element such that ![]() $bx = 0$. Then
$bx = 0$. Then ![]() $\bar {b}\bar {x} = 0$ in
$\bar {b}\bar {x} = 0$ in ![]() $B/tB$, and hence
$B/tB$, and hence ![]() $\bar {x} = 0$. This means that
$\bar {x} = 0$. This means that ![]() $x \in tB$. Suppose
$x \in tB$. Suppose ![]() $x \in t^nB$ for some positive integer n, and write
$x \in t^nB$ for some positive integer n, and write ![]() $x = t^ny$ in B. Then
$x = t^ny$ in B. Then ![]() $t^n(by) = bx = 0$ and hence
$t^n(by) = bx = 0$ and hence ![]() $by = 0$, since B is flat over
$by = 0$, since B is flat over ![]() $k[t]$. This implies that
$k[t]$. This implies that ![]() $y \in tB$, and hence
$y \in tB$, and hence ![]() $x \in t^{n+1}B$. Therefore
$x \in t^{n+1}B$. Therefore ![]() $x \in \bigcap _{n \ge 1} t^nB$, and since B is
$x \in \bigcap _{n \ge 1} t^nB$, and since B is ![]() $(t)$-adically separated, this means that
$(t)$-adically separated, this means that ![]() $x = 0$. This proves that b is a regular element. To conclude that
$x = 0$. This proves that b is a regular element. To conclude that ![]() $B/bB$ is flat over
$B/bB$ is flat over ![]() $k[t]$, we just compute
$k[t]$, we just compute  $\operatorname {\mathrm {Tor}}^{k[t]}_1(k,B/bB) = 0$ from the exact sequence
$\operatorname {\mathrm {Tor}}^{k[t]}_1(k,B/bB) = 0$ from the exact sequence ![]() $0 \to B \to B \to B/bB \to 0$ and apply [Reference Matsumura36, Theorem 22.3].
$0 \to B \to B \to B/bB \to 0$ and apply [Reference Matsumura36, Theorem 22.3].
Question 7.13. We do not know of any example where the inequality in Theorem 7.8 is strict. The question whether ![]() $\mathrm {ecodim}(A)=\mathrm {fcodim}(A)$ holds for all equicharacteristic local rings
$\mathrm {ecodim}(A)=\mathrm {fcodim}(A)$ holds for all equicharacteristic local rings ![]() $(A,\mathfrak {m},k)$ is, to our knowledge, still open.
$(A,\mathfrak {m},k)$ is, to our knowledge, still open.
8 Embedding codimension of arc spaces
Let X be a scheme of finite type over a field k. The arc space ![]() $X_{\infty }$ of X is the scheme over k representing the functor of points given, for any k-algebra R, by
$X_{\infty }$ of X is the scheme over k representing the functor of points given, for any k-algebra R, by  $R \mapsto \underleftarrow{\lim}_m X_m(R)$, where
$R \mapsto \underleftarrow{\lim}_m X_m(R)$, where ![]() $X_m(R)=\operatorname {\mathrm {Hom}}_k (\operatorname {\mathrm {Spec}} (R[t]/ (t^{m+1} ) ),X )$ is the functor of points of the mth jet scheme of X. By [Reference Bhatt5, Remark 4.6], the functor
$X_m(R)=\operatorname {\mathrm {Hom}}_k (\operatorname {\mathrm {Spec}} (R[t]/ (t^{m+1} ) ),X )$ is the functor of points of the mth jet scheme of X. By [Reference Bhatt5, Remark 4.6], the functor ![]() $X_{\infty }(R)$ is naturally isomorphic to
$X_{\infty }(R)$ is naturally isomorphic to ![]() $\operatorname {\mathrm {Hom}}_k(\operatorname {\mathrm {Spec}}(R[[t]]),X)$. A point
$\operatorname {\mathrm {Hom}}_k(\operatorname {\mathrm {Spec}}(R[[t]]),X)$. A point ![]() $\alpha \in X_{\infty }$ is called an arc on X and corresponds to a morphism
$\alpha \in X_{\infty }$ is called an arc on X and corresponds to a morphism ![]() $\operatorname {\mathrm {Spec}} (L[[t]]) \to X$, where L is the residue field of
$\operatorname {\mathrm {Spec}} (L[[t]]) \to X$, where L is the residue field of ![]() $\alpha $. A point
$\alpha $. A point ![]() $\alpha \in X_{\infty }$ is said to be constructible if it is the generic point of an irreducible constructible subset of
$\alpha \in X_{\infty }$ is said to be constructible if it is the generic point of an irreducible constructible subset of ![]() $X_{\infty }$ (compare [Reference de Fernex and Docampo21, Section 10]).
$X_{\infty }$ (compare [Reference de Fernex and Docampo21, Section 10]).
Given an arc ![]() $\alpha \colon \operatorname {\mathrm {Spec}} (k[[t]]) \to X$, we will denote by
$\alpha \colon \operatorname {\mathrm {Spec}} (k[[t]]) \to X$, we will denote by ![]() $\alpha (0)$ and
$\alpha (0)$ and ![]() $\alpha (\eta )$ the images in X of the closed point and the generic point of
$\alpha (\eta )$ the images in X of the closed point and the generic point of ![]() $\operatorname {\mathrm {Spec}} (k[[t]])$; we call
$\operatorname {\mathrm {Spec}} (k[[t]])$; we call ![]() $\alpha (0)$ the special point of
$\alpha (0)$ the special point of ![]() $\alpha $ and
$\alpha $ and ![]() $\alpha (\eta )$ the the generic point of
$\alpha (\eta )$ the the generic point of ![]() $\alpha $.
$\alpha $.
Given an open set ![]() $U \subset X$, we have
$U \subset X$, we have ![]() $\alpha (\eta ) \in U$ if and only if the morphism
$\alpha (\eta ) \in U$ if and only if the morphism ![]() $\alpha \colon \operatorname {\mathrm {Spec}} (k[[t]]) \to X$ does not factor through the complement
$\alpha \colon \operatorname {\mathrm {Spec}} (k[[t]]) \to X$ does not factor through the complement ![]() $X \setminus U$. We will be interested in the case where
$X \setminus U$. We will be interested in the case where ![]() $U = X_{\mathrm {sm}}$, the smooth locus of X. Note that if k is perfect, then the complement
$U = X_{\mathrm {sm}}$, the smooth locus of X. Note that if k is perfect, then the complement ![]() $X \setminus X_{\mathrm {sm}}$ is the singular locus
$X \setminus X_{\mathrm {sm}}$ is the singular locus ![]() $\operatorname {\mathrm {Sing}}(X)$ of X.
$\operatorname {\mathrm {Sing}}(X)$ of X.
We following result is a variant of [Reference de Fernex and Docampo21, Theorems 9.2 and 9.3]:
Theorem 8.1. Suppose that X is an affine scheme over a perfect field k. Let ![]() $\alpha \in X_{\infty }$ be an arc and let
$\alpha \in X_{\infty }$ be an arc and let ![]() $d:=\dim _{k(\alpha (\eta ))} (\Omega _{X/k}\otimes _k k(\alpha (\eta )) )$, where
$d:=\dim _{k(\alpha (\eta ))} (\Omega _{X/k}\otimes _k k(\alpha (\eta )) )$, where ![]() $k(\alpha (\eta ))$ is the residue field of
$k(\alpha (\eta ))$ is the residue field of ![]() $\alpha (\eta ) \in X$. Assume that one of the following occurs:
$\alpha (\eta ) \in X$. Assume that one of the following occurs:
1. k is a field of characteristic
 $0$ or
$0$ or2.
 $\alpha \in X_{\infty }(k)$.
$\alpha \in X_{\infty }(k)$.
Fix a closed embedding ![]() $X \subset {\mathbb A}^N$, let
$X \subset {\mathbb A}^N$, let ![]() $f \colon X \to Y :={\mathbb A}^d$ be the morphism induced by a general linear projection
$f \colon X \to Y :={\mathbb A}^d$ be the morphism induced by a general linear projection ![]() ${\mathbb A}^N \to {\mathbb A}^d$ and let
${\mathbb A}^N \to {\mathbb A}^d$ and let ![]() $\beta := f_{\infty }(\alpha ) \in Y_{\infty }$. Let
$\beta := f_{\infty }(\alpha ) \in Y_{\infty }$. Let ![]() $\mathfrak {m} \subset \mathcal {O}_{X_{\infty },\alpha }$ and
$\mathfrak {m} \subset \mathcal {O}_{X_{\infty },\alpha }$ and ![]() $\mathfrak {n} \subset \mathcal {O}_{Y_{\infty },\beta }$ be the respective maximal ideals and L and
$\mathfrak {n} \subset \mathcal {O}_{Y_{\infty },\beta }$ be the respective maximal ideals and L and ![]() $L'$ the residue fields. Then the induced L-linear map
$L'$ the residue fields. Then the induced L-linear map
is an isomorphism.
Proof. By assumption, we have that  $\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^d (\Omega _{X/k} ) )<\infty $, and by taking a general linear projection we can ensure that
$\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^d (\Omega _{X/k} ) )<\infty $, and by taking a general linear projection we can ensure that  $\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^d (\Omega _{X/k} ) )=\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^0 (\Omega _{X/Y} ) )$.
$\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^d (\Omega _{X/k} ) )=\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^0 (\Omega _{X/Y} ) )$.
Since k is perfect, we have a commutative diagram with exact rows

The main step is to understand the map ![]() $\varphi $. As in the proof of [Reference de Fernex and Docampo21, Theorem 9.2], denote for short
$\varphi $. As in the proof of [Reference de Fernex and Docampo21, Theorem 9.2], denote for short ![]() $B_L := L[[t]]$ and
$B_L := L[[t]]$ and ![]() $P_L := L(\:\!\!(t)\:\!\!)/tL[[t]]$.
$P_L := L(\:\!\!(t)\:\!\!)/tL[[t]]$.
Note that, by [Reference de Fernex and Docampo21, Theorem 5.3], there are natural isomorphisms
and
We will use these isomorphisms to study ![]() $\varphi $.
$\varphi $.
By pulling back the terms of the exact sequence
along ![]() $\alpha $, we obtain the exact sequence
$\alpha $, we obtain the exact sequence
Since Y is smooth, we see that the term ![]() $F_Y := \Omega _{Y/k} \otimes _{\mathcal {O}_Y} B_L$ is a free
$F_Y := \Omega _{Y/k} \otimes _{\mathcal {O}_Y} B_L$ is a free ![]() $B_L$-module. Write
$B_L$-module. Write ![]() $\Omega _{X/k} \otimes _{\mathcal {O}_X} B_L = F_X \oplus T_X$, where
$\Omega _{X/k} \otimes _{\mathcal {O}_X} B_L = F_X \oplus T_X$, where ![]() $F_X$ is free and
$F_X$ is free and ![]() $T_X$ is torsion. Since
$T_X$ is torsion. Since  $\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^0 (\Omega _{X/Y} ) ) < \infty $, the term
$\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^0 (\Omega _{X/Y} ) ) < \infty $, the term ![]() $T_{X/Y} := \Omega _{X/Y} \otimes _{\mathcal {O}_X} B_L$ is a torsion
$T_{X/Y} := \Omega _{X/Y} \otimes _{\mathcal {O}_X} B_L$ is a torsion ![]() $B_L$-module, and we get an exact sequence
$B_L$-module, and we get an exact sequence
Since ![]() $P_L$ is a divisible
$P_L$ is a divisible ![]() $B_L$-module, tensoring with
$B_L$-module, tensoring with ![]() $P_L$ kills torsion, and hence this sequence gives the exact sequence
$P_L$ kills torsion, and hence this sequence gives the exact sequence
 $$ \begin{align*} 0 \to \operatorname{\mathrm{Tor}}_1^{B_L}(T_X,P_L) \to \operatorname{\mathrm{Tor}}_1^{B_L}\left(T_{X/Y},P_L\right) \to F_Y \otimes_{B_L}P_L \xrightarrow{\,\varphi'\,} F_X \otimes_{B_L}P_L \to 0. \end{align*} $$
$$ \begin{align*} 0 \to \operatorname{\mathrm{Tor}}_1^{B_L}(T_X,P_L) \to \operatorname{\mathrm{Tor}}_1^{B_L}\left(T_{X/Y},P_L\right) \to F_Y \otimes_{B_L}P_L \xrightarrow{\,\varphi'\,} F_X \otimes_{B_L}P_L \to 0. \end{align*} $$Note that ![]() $\varphi ' = \varphi $ under the aforementioned isomorphisms. We have
$\varphi ' = \varphi $ under the aforementioned isomorphisms. We have  $\operatorname {\mathrm {Tor}}_1^{B_L}(T_X,P_L) \simeq T_X$, and this has dimension
$\operatorname {\mathrm {Tor}}_1^{B_L}(T_X,P_L) \simeq T_X$, and this has dimension  $\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^d (\Omega _{X/k} ) )$ over L. Similarly,
$\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^d (\Omega _{X/k} ) )$ over L. Similarly,  $\operatorname {\mathrm {Tor}}_1^{B_L} (T_{X/Y},P_L ) \simeq T_{X/Y}$ has dimension
$\operatorname {\mathrm {Tor}}_1^{B_L} (T_{X/Y},P_L ) \simeq T_{X/Y}$ has dimension  $\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^0 (\Omega _{X/Y} ) )$ over L. Since these two dimensions are equal, the map
$\operatorname {\mathrm {ord}}_\alpha (\operatorname {\mathrm {Fitt}}^0 (\Omega _{X/Y} ) )$ over L. Since these two dimensions are equal, the map ![]() $\varphi '$ in the sequence is an isomorphism. We conclude that
$\varphi '$ in the sequence is an isomorphism. We conclude that ![]() $\varphi $ is an isomorphism.
$\varphi $ is an isomorphism.
The surjectivity of ![]() $\varphi $ implies that
$\varphi $ implies that ![]() $\delta $ is surjective, and the injectivity of
$\delta $ is surjective, and the injectivity of ![]() $\delta $ follows from our assumption that either (1) or (2) holds. We conclude that
$\delta $ follows from our assumption that either (1) or (2) holds. We conclude that ![]() $(T_\alpha f_{\infty })^*$ is an isomorphism.
$(T_\alpha f_{\infty })^*$ is an isomorphism.
Corollary 8.2. Keeping the assumptions and notation from Theorem 8.1, let ![]() $\alpha _n, \beta _n$ denote the images of
$\alpha _n, \beta _n$ denote the images of ![]() $\alpha , \beta $ under the projections
$\alpha , \beta $ under the projections ![]() $X_{\infty }\to X_n$ and
$X_{\infty }\to X_n$ and ![]() $Y_{\infty }\to Y_n$, and
$Y_{\infty }\to Y_n$, and ![]() $\mathfrak {m}_n\subset \mathcal {O}_{X_n,\alpha _n}, \mathfrak {n}_n\subset \mathcal {O}_{Y_n,\beta _n}$ denote the corresponding ideals with residue fields
$\mathfrak {m}_n\subset \mathcal {O}_{X_n,\alpha _n}, \mathfrak {n}_n\subset \mathcal {O}_{Y_n,\beta _n}$ denote the corresponding ideals with residue fields ![]() $L_n, L^{\prime }_n$. Then the induced L-linear map
$L_n, L^{\prime }_n$. Then the induced L-linear map
 $$ \begin{align*} \left(T_{\alpha_n} f_n\right)^* \colon \mathfrak{n}_n/\mathfrak{n}^2_n \otimes_{L^{\prime}_n}L \to \mathfrak{m}_n/\mathfrak{m}_n^2 \otimes_{L_n} L \end{align*} $$
$$ \begin{align*} \left(T_{\alpha_n} f_n\right)^* \colon \mathfrak{n}_n/\mathfrak{n}^2_n \otimes_{L^{\prime}_n}L \to \mathfrak{m}_n/\mathfrak{m}_n^2 \otimes_{L_n} L \end{align*} $$is injective for all ![]() $n\in {\mathbb N}$.
$n\in {\mathbb N}$.
Proof. This follows from the diagram

and the fact that the top horizontal and left vertical arrows are injections.
Theorem 8.3. Let X be a scheme of finite type over a perfect field k and let ![]() $\alpha \in X_{\infty }$. Assume that one of the following occurs:
$\alpha \in X_{\infty }$. Assume that one of the following occurs:
1. k is a field of characteristic
 $0$ or
$0$ or2.
 $\alpha \in X_{\infty }(k)$.
$\alpha \in X_{\infty }(k)$.
Then we have
 $$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) \le \limsup_{n \to \infty} \mathrm{ecodim}\left(\mathcal{O}_{X_n,\alpha_n}\right), \end{align*} $$
$$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) \le \limsup_{n \to \infty} \mathrm{ecodim}\left(\mathcal{O}_{X_n,\alpha_n}\right), \end{align*} $$where ![]() $\alpha _n$ is the image of
$\alpha _n$ is the image of ![]() $\alpha $ under the truncation map
$\alpha $ under the truncation map ![]() $\pi _n \colon X_{\infty } \to X_n$.
$\pi _n \colon X_{\infty } \to X_n$.
Proof. We can assume without loss of generality that X is affine. Given a map
we let ![]() $\beta := f_{\infty }(\alpha ) \in Y_{\infty }$. For every n, we denote by
$\beta := f_{\infty }(\alpha ) \in Y_{\infty }$. For every n, we denote by ![]() $\alpha _n \in X_n$ and
$\alpha _n \in X_n$ and ![]() $\beta _n \in Y_n$ the images of
$\beta _n \in Y_n$ the images of ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $ at the respective n-jet schemes. It is convenient, within this proof, to change notation from before to let
$\beta $ at the respective n-jet schemes. It is convenient, within this proof, to change notation from before to let ![]() $A_{\infty } := \mathcal {O}_{X_{\infty },\alpha }$ and
$A_{\infty } := \mathcal {O}_{X_{\infty },\alpha }$ and ![]() $B_{\infty } := \mathcal {O}_{Y_{\infty },\beta }$, and denote by
$B_{\infty } := \mathcal {O}_{Y_{\infty },\beta }$, and denote by ![]() $\mathfrak {m}_{\infty } \subset A_{\infty }$ and
$\mathfrak {m}_{\infty } \subset A_{\infty }$ and ![]() $\mathfrak {n}_{\infty } \subset B_{\infty }$ the respective maximal ideals and by
$\mathfrak {n}_{\infty } \subset B_{\infty }$ the respective maximal ideals and by ![]() $L_{\infty } := A_{\infty }/\mathfrak {m}_{\infty }$ and
$L_{\infty } := A_{\infty }/\mathfrak {m}_{\infty }$ and ![]() $L_{\infty }' := B_{\infty }/\mathfrak {n}_{\infty }$ the residue fields. Similarly, for every
$L_{\infty }' := B_{\infty }/\mathfrak {n}_{\infty }$ the residue fields. Similarly, for every ![]() $n \in {\mathbb N}$, we let
$n \in {\mathbb N}$, we let ![]() $A_n := \mathcal {O}_{X_n,\alpha _n}$ and
$A_n := \mathcal {O}_{X_n,\alpha _n}$ and ![]() $B_n := \mathcal {O}_{Y_n,\beta _n}$, and denote by
$B_n := \mathcal {O}_{Y_n,\beta _n}$, and denote by ![]() $\mathfrak {m}_n \subset A_n$ and
$\mathfrak {m}_n \subset A_n$ and ![]() $\mathfrak {n}_n \subset B_n$ the respective maximal ideals and by
$\mathfrak {n}_n \subset B_n$ the respective maximal ideals and by ![]() $L_n := A_n/\mathfrak {m}_n$ and
$L_n := A_n/\mathfrak {m}_n$ and ![]() $L_n' := B_n/\mathfrak {n}_n$ the residue fields.
$L_n' := B_n/\mathfrak {n}_n$ the residue fields.
Note that we have direct systems ![]() $\{A_n \to A_{n+1} \mid n \in {\mathbb N}\}$ and
$\{A_n \to A_{n+1} \mid n \in {\mathbb N}\}$ and ![]() $\{B_n \subset B_{n+1} \mid n \in {\mathbb N} \}$, and
$\{B_n \subset B_{n+1} \mid n \in {\mathbb N} \}$, and  $A_{\infty } = \operatorname {\mathrm {\varinjlim }}_n A_n$ and
$A_{\infty } = \operatorname {\mathrm {\varinjlim }}_n A_n$ and  $B_{\infty } = \operatorname {\mathrm {\varinjlim }}_n B_n$. Moreover, we have commutative diagrams
$B_{\infty } = \operatorname {\mathrm {\varinjlim }}_n B_n$. Moreover, we have commutative diagrams

where ![]() $\mathfrak {n}_n = \varphi _n^{-1}(\mathfrak {m}_n)$,
$\mathfrak {n}_n = \varphi _n^{-1}(\mathfrak {m}_n)$, ![]() $\mathfrak {n}_n = \mathfrak {n}_{\infty } \cap B_n$ and
$\mathfrak {n}_n = \mathfrak {n}_{\infty } \cap B_n$ and ![]() $\mathfrak {m}_n = \mathfrak {m}_{\infty } \cap A_n$.
$\mathfrak {m}_n = \mathfrak {m}_{\infty } \cap A_n$.
For every ![]() $n \in {\mathbb N} \cup \{\infty \}$, let
$n \in {\mathbb N} \cup \{\infty \}$, let
 $$ \begin{align*} d\varphi_n \colon \mathfrak{n}_n/\mathfrak{n}_n^2 \otimes_{L^{\prime}_n}L_n \to \mathfrak{m}_n/\mathfrak{m}_n^2 \end{align*} $$
$$ \begin{align*} d\varphi_n \colon \mathfrak{n}_n/\mathfrak{n}_n^2 \otimes_{L^{\prime}_n}L_n \to \mathfrak{m}_n/\mathfrak{m}_n^2 \end{align*} $$be the induced ![]() $L_n$-linear map.
$L_n$-linear map.
We pick f as in Theorem 8.1. For every ![]() $n \in {\mathbb N} \cup \{\infty \}$, there is an associated map of graded rings
$n \in {\mathbb N} \cup \{\infty \}$, there is an associated map of graded rings ![]() $\operatorname {\mathrm {gr}}(\varphi _n) \colon \operatorname {\mathrm {gr}}(B_n) \to \operatorname {\mathrm {gr}}(A_n)$. We denote by
$\operatorname {\mathrm {gr}}(\varphi _n) \colon \operatorname {\mathrm {gr}}(B_n) \to \operatorname {\mathrm {gr}}(A_n)$. We denote by
the map induced by ![]() $\operatorname {\mathrm {gr}}(\varphi _n)$ by the indicated base changes.
$\operatorname {\mathrm {gr}}(\varphi _n)$ by the indicated base changes.
Note that  $\mathfrak {m}_{\infty } = \operatorname {\mathrm {\varinjlim }}_n \mathfrak {m}_n$ and hence
$\mathfrak {m}_{\infty } = \operatorname {\mathrm {\varinjlim }}_n \mathfrak {m}_n$ and hence 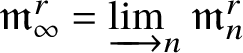 $\mathfrak {m}_{\infty }^r = \operatorname {\mathrm {\varinjlim }}_n \mathfrak {m}_n^r$ for all r. Indeed, if
$\mathfrak {m}_{\infty }^r = \operatorname {\mathrm {\varinjlim }}_n \mathfrak {m}_n^r$ for all r. Indeed, if ![]() $a \in \mathfrak {m}_{\infty }^r$ for some
$a \in \mathfrak {m}_{\infty }^r$ for some ![]() $r \ge 2$, then we can write
$r \ge 2$, then we can write ![]() $a = a_1\dotsm a_r$ with
$a = a_1\dotsm a_r$ with ![]() $a_i \in \mathfrak {m}_{\infty }$; then we can pick n such that
$a_i \in \mathfrak {m}_{\infty }$; then we can pick n such that ![]() $a_i \in \mathfrak {m}_n$ for all i, and hence
$a_i \in \mathfrak {m}_n$ for all i, and hence ![]() $a \in \mathfrak {m}_n^r$. It follows that
$a \in \mathfrak {m}_n^r$. It follows that
 $$ \begin{align*} \operatorname{\mathrm{gr}}(A_{\infty}) = \operatorname{\mathrm{\varinjlim}}_n \operatorname{\mathrm{gr}}(A_n) \otimes_{L_n}L_{\infty}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}(A_{\infty}) = \operatorname{\mathrm{\varinjlim}}_n \operatorname{\mathrm{gr}}(A_n) \otimes_{L_n}L_{\infty}, \end{align*} $$and similarly we have
 $$ \begin{align*} \operatorname{\mathrm{gr}}(B_{\infty}) = \operatorname{\mathrm{\varinjlim}}_n \operatorname{\mathrm{gr}}(B_n) \otimes_{L^{\prime}_n}L^{\prime}_{\infty}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}(B_{\infty}) = \operatorname{\mathrm{\varinjlim}}_n \operatorname{\mathrm{gr}}(B_n) \otimes_{L^{\prime}_n}L^{\prime}_{\infty}. \end{align*} $$Since ![]() $\mathfrak {n}_n^r = \varphi _n^{-1} (\mathfrak {m}_n^r )$ for all r, for every n we have a commutative diagram
$\mathfrak {n}_n^r = \varphi _n^{-1} (\mathfrak {m}_n^r )$ for all r, for every n we have a commutative diagram

For short, let ![]() $R_n := \operatorname {\mathrm {gr}}(A_n) \otimes _{L_n}L_{\infty }$,
$R_n := \operatorname {\mathrm {gr}}(A_n) \otimes _{L_n}L_{\infty }$, ![]() $S_n := \operatorname {\mathrm {gr}}(B_n) \otimes _{L^{\prime }_n}L_{\infty }$ and
$S_n := \operatorname {\mathrm {gr}}(B_n) \otimes _{L^{\prime }_n}L_{\infty }$ and ![]() $K_n := \ker (\psi _n)$.
$K_n := \ker (\psi _n)$.
Lemma 8.4. ![]() $\operatorname {\mathrm {ht}}(K_{\infty }) = \limsup _n \operatorname {\mathrm {ht}}(K_n)$.
$\operatorname {\mathrm {ht}}(K_{\infty }) = \limsup _n \operatorname {\mathrm {ht}}(K_n)$.
Proof. First, note that  $K_{\infty } = \operatorname {\mathrm {\varinjlim }}_n K_n$. Indeed, the inclusion
$K_{\infty } = \operatorname {\mathrm {\varinjlim }}_n K_n$. Indeed, the inclusion  $K_{\infty } \supset \operatorname {\mathrm {\varinjlim }}_n K_n$ is clear, and conversely, if
$K_{\infty } \supset \operatorname {\mathrm {\varinjlim }}_n K_n$ is clear, and conversely, if ![]() $b \in K_{\infty }$ and we fix
$b \in K_{\infty }$ and we fix ![]() $n \in {\mathbb N}$ such that
$n \in {\mathbb N}$ such that ![]() $b \in S_n$, then
$b \in S_n$, then ![]() $\psi _m(b)$ is in the kernel of
$\psi _m(b)$ is in the kernel of ![]() $R_m \to R_{\infty }$ for all
$R_m \to R_{\infty }$ for all ![]() $m \ge n$ and hence, since each
$m \ge n$ and hence, since each ![]() $\psi _m(b)$ maps to
$\psi _m(b)$ maps to ![]() $\psi _{m+1}(b)$ via
$\psi _{m+1}(b)$ via ![]() $R_m \to R_{m+1}$, it follows that
$R_m \to R_{m+1}$, it follows that ![]() $\psi _m(b)$ is zero for
$\psi _m(b)$ is zero for ![]() $m \gg n$, which means that
$m \gg n$, which means that ![]() $b \in K_m$ for
$b \in K_m$ for ![]() $m \gg n$.
$m \gg n$.
We are now ready to prove that
 $$ \begin{align*} \operatorname{\mathrm{ht}}(K_{\infty}) = \limsup_n\operatorname{\mathrm{ht}}(K_n). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ht}}(K_{\infty}) = \limsup_n\operatorname{\mathrm{ht}}(K_n). \end{align*} $$Note that the maps ![]() $S_n \to S_{\infty }$ are extensions of polynomial rings over the same field
$S_n \to S_{\infty }$ are extensions of polynomial rings over the same field ![]() $L_{\infty }$. Thus they are faithfully flat, and hence for every prime
$L_{\infty }$. Thus they are faithfully flat, and hence for every prime ![]() $\mathfrak {p}_n \subset S_n$ its extension
$\mathfrak {p}_n \subset S_n$ its extension ![]() $\mathfrak {p}_n S_{\infty }$ is prime.
$\mathfrak {p}_n S_{\infty }$ is prime.
Consider first the case where ![]() $\operatorname {\mathrm {ht}}(K_{\infty }) < \infty $ and let
$\operatorname {\mathrm {ht}}(K_{\infty }) < \infty $ and let ![]() $\mathfrak {p} \subset S_{\infty }$ be a minimal prime over
$\mathfrak {p} \subset S_{\infty }$ be a minimal prime over ![]() $K_{\infty }$ with
$K_{\infty }$ with ![]() $\operatorname {\mathrm {ht}}(\mathfrak {p})=\operatorname {\mathrm {ht}}(K_{\infty })$. By Remark 5.12 we have that
$\operatorname {\mathrm {ht}}(\mathfrak {p})=\operatorname {\mathrm {ht}}(K_{\infty })$. By Remark 5.12 we have that ![]() $\mathfrak {p}$ is finitely generated by elements
$\mathfrak {p}$ is finitely generated by elements ![]() $f_1,\dotsc ,f_r\in S_{\infty }$. For each
$f_1,\dotsc ,f_r\in S_{\infty }$. For each ![]() $n>0$, let
$n>0$, let ![]() $\mathfrak {p}_n$ be any minimal prime over
$\mathfrak {p}_n$ be any minimal prime over ![]() $K_n$ contained in
$K_n$ contained in ![]() $\mathfrak {p}\cap S_n$. Then
$\mathfrak {p}\cap S_n$. Then  $\mathfrak {p}':=\operatorname {\mathrm {\varinjlim }}_n \mathfrak {p}_n$ is a prime of
$\mathfrak {p}':=\operatorname {\mathrm {\varinjlim }}_n \mathfrak {p}_n$ is a prime of ![]() $S_{\infty }$ with
$S_{\infty }$ with ![]() $K_{\infty } \subset \mathfrak {p}' \subset \mathfrak {p}$, so
$K_{\infty } \subset \mathfrak {p}' \subset \mathfrak {p}$, so ![]() $\mathfrak {p}'=\mathfrak {p}$. Let
$\mathfrak {p}'=\mathfrak {p}$. Let ![]() $n_1>0$ be such that
$n_1>0$ be such that ![]() $f_1,\dotsc ,f_r\in \mathfrak {p}_{n_1}$; then
$f_1,\dotsc ,f_r\in \mathfrak {p}_{n_1}$; then ![]() $\mathfrak {p}_n=\mathfrak {p}\cap S_n$ for
$\mathfrak {p}_n=\mathfrak {p}\cap S_n$ for ![]() $n\geq n_1$. Given any chain of primes
$n\geq n_1$. Given any chain of primes
pick ![]() $s_i \in \mathfrak {q}_i \setminus \mathfrak {q}_{i-1}$ and fix
$s_i \in \mathfrak {q}_i \setminus \mathfrak {q}_{i-1}$ and fix ![]() $n_2$ such that
$n_2$ such that ![]() $s_1,\dotsc ,s_t \in S_{n_2}$. Then for every
$s_1,\dotsc ,s_t \in S_{n_2}$. Then for every ![]() $n \ge \max \{n_1,n_2\}$ we get a chain of primes
$n \ge \max \{n_1,n_2\}$ we get a chain of primes
Thus ![]() $\operatorname {\mathrm {ht}}(K_{\infty }) \le \limsup _n \operatorname {\mathrm {ht}}(K_n)$. The other inequality follows by the going-down theorem applied to
$\operatorname {\mathrm {ht}}(K_{\infty }) \le \limsup _n \operatorname {\mathrm {ht}}(K_n)$. The other inequality follows by the going-down theorem applied to ![]() $S_n \to S_{\infty }$.
$S_n \to S_{\infty }$.
If ![]() $\operatorname {\mathrm {ht}}(K_{\infty }) = \infty $, then, since
$\operatorname {\mathrm {ht}}(K_{\infty }) = \infty $, then, since ![]() $\operatorname {\mathrm {ht}}(K_{\infty }) \ge \operatorname {\mathrm {ht}}(K_nS_{\infty })$, a similar argument shows that the sequence
$\operatorname {\mathrm {ht}}(K_{\infty }) \ge \operatorname {\mathrm {ht}}(K_nS_{\infty })$, a similar argument shows that the sequence ![]() $\{\operatorname {\mathrm {ht}}(K_n)\}_n$ is unbounded.
$\{\operatorname {\mathrm {ht}}(K_n)\}_n$ is unbounded.
We can now finish the proof of the theorem. Since ![]() $B_n$ is formally smooth, for every
$B_n$ is formally smooth, for every ![]() $n \in {\mathbb N} \cup \{\infty \}$ the natural map
$n \in {\mathbb N} \cup \{\infty \}$ the natural map
 $$ \begin{align*} \operatorname{\mathrm{Sym}}_{L_n'}\left(\mathfrak{n}_n/\mathfrak{n}_n^2\right) \to \operatorname{\mathrm{gr}}(B_n) \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Sym}}_{L_n'}\left(\mathfrak{n}_n/\mathfrak{n}_n^2\right) \to \operatorname{\mathrm{gr}}(B_n) \end{align*} $$is an isomorphism (see Remark 7.3 for the case ![]() $n=\infty $). Furthermore, the diagram
$n=\infty $). Furthermore, the diagram

is commutative.
By Theorem 8.1, the map ![]() $\sigma _{\infty }$ is an isomorphism, and hence
$\sigma _{\infty }$ is an isomorphism, and hence
Similarly, by Corollary 8.2, ![]() $\sigma _n$ is an injective
$\sigma _n$ is an injective ![]() $L_{\infty }$-linear map of polynomial rings, and we have
$L_{\infty }$-linear map of polynomial rings, and we have
Then we conclude by Lemma 8.4.
Theorem 8.5. Let X be a scheme of finite type over a perfect field k and let ![]() $\alpha \in X_{\infty }$. Assume that either k is a field of characteristic
$\alpha \in X_{\infty }$. Assume that either k is a field of characteristic ![]() $0$ or
$0$ or ![]() $\alpha $ is a k-rational point. Then we have
$\alpha $ is a k-rational point. Then we have
 $$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) \le \operatorname{\mathrm{ord}}_\alpha\left(\operatorname{\mathrm{Fitt}}^d\left(\Omega_{X/k}\right)\right), \end{align*} $$
$$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) \le \operatorname{\mathrm{ord}}_\alpha\left(\operatorname{\mathrm{Fitt}}^d\left(\Omega_{X/k}\right)\right), \end{align*} $$where ![]() $d = \dim _{\alpha (\eta )}(X)$. In particular:
$d = \dim _{\alpha (\eta )}(X)$. In particular:
1. If X is a variety, then
 $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) \le \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_X)$.
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) \le \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_X)$.2. If
 $\alpha (\eta ) \in X_{\mathrm {sm}}$ and
$\alpha (\eta ) \in X_{\mathrm {sm}}$ and  $X^0 \subset X$ is the irreducible component containing
$X^0 \subset X$ is the irreducible component containing  $\alpha (\eta )$, then
$\alpha (\eta )$, then  $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) \le \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} ) < \infty $.
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) \le \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} ) < \infty $.
Proof. First note that it suffices to prove the theorem when ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$, as otherwise the right-hand side of the stated inequality is infinite and the statement is trivial. Let us therefore assume that
$\alpha (\eta ) \in X_{\mathrm {sm}}$, as otherwise the right-hand side of the stated inequality is infinite and the statement is trivial. Let us therefore assume that ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$.
$\alpha (\eta ) \in X_{\mathrm {sm}}$.
For every r, let ![]() $J_r := \operatorname {\mathrm {Fitt}}^r (\Omega _{X/k} ) \subset \mathcal {O}_X$. On the one hand, for every finite n we have by [Reference de Fernex and Docampo21, Lemma 8.1]
$J_r := \operatorname {\mathrm {Fitt}}^r (\Omega _{X/k} ) \subset \mathcal {O}_X$. On the one hand, for every finite n we have by [Reference de Fernex and Docampo21, Lemma 8.1]
 $$ \begin{align*} \mathrm{edim}\left(\mathcal{O}_{X_n,\alpha_n}\right) = (n+1)d_n - \dim\left(\overline{\{\alpha_n\}}\right) + \operatorname{\mathrm{ord}}_\alpha\left(J_{d_n}\right), \end{align*} $$
$$ \begin{align*} \mathrm{edim}\left(\mathcal{O}_{X_n,\alpha_n}\right) = (n+1)d_n - \dim\left(\overline{\{\alpha_n\}}\right) + \operatorname{\mathrm{ord}}_\alpha\left(J_{d_n}\right), \end{align*} $$where ![]() $d_n = d (\alpha _n,\Omega _{X/k} )$ is the Betti number of
$d_n = d (\alpha _n,\Omega _{X/k} )$ is the Betti number of ![]() $\Omega _{X/k}$ with respect to
$\Omega _{X/k}$ with respect to ![]() $\alpha _n$ [Reference de Fernex and Docampo21, Definition 6.1] and
$\alpha _n$ [Reference de Fernex and Docampo21, Definition 6.1] and ![]() $\overline {\{\alpha _n\}}$ the closure of
$\overline {\{\alpha _n\}}$ the closure of ![]() $\alpha _n$ in
$\alpha _n$ in ![]() $X_n$. On the other hand, since
$X_n$. On the other hand, since ![]() $\alpha $ is not in an irreducible component of
$\alpha $ is not in an irreducible component of ![]() $X_{\infty }$ that is fully contained in
$X_{\infty }$ that is fully contained in ![]() $(\operatorname {\mathrm {Sing}}(X))_{\infty }$, we have
$(\operatorname {\mathrm {Sing}}(X))_{\infty }$, we have
 $$ \begin{align*} \dim\left(\mathcal{O}_{X_n,\alpha_n}\right) \ge (n+1)d - \dim\left(\overline{\{\alpha_n\}}\right) \end{align*} $$
$$ \begin{align*} \dim\left(\mathcal{O}_{X_n,\alpha_n}\right) \ge (n+1)d - \dim\left(\overline{\{\alpha_n\}}\right) \end{align*} $$for all finite n. Since for all n large enough we have ![]() $d_n = d$, we deduce by Proposition 6.2 that
$d_n = d$, we deduce by Proposition 6.2 that ![]() $\mathrm {ecodim} (\mathcal {O}_{X_n,\alpha _n} ) \le \operatorname {\mathrm {ord}}_\alpha (J_d)$ for all
$\mathrm {ecodim} (\mathcal {O}_{X_n,\alpha _n} ) \le \operatorname {\mathrm {ord}}_\alpha (J_d)$ for all ![]() $n \gg 1$. We conclude by Theorem 8.3 that
$n \gg 1$. We conclude by Theorem 8.3 that ![]() $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) \le \operatorname {\mathrm {ord}}_\alpha (J_d)$, as stated.
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) \le \operatorname {\mathrm {ord}}_\alpha (J_d)$, as stated.
Regarding the last two assertions of the theorem, (1) follows by the fact that if X is a variety, then by definition,  $\mathrm {Jac}_X = \operatorname {\mathrm {Fitt}}^d (\Omega _{X/k} )$. As for (2), if
$\mathrm {Jac}_X = \operatorname {\mathrm {Fitt}}^d (\Omega _{X/k} )$. As for (2), if ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$, then by Lemma 8.6 we have
$\alpha (\eta ) \in X_{\mathrm {sm}}$, then by Lemma 8.6 we have  $\widehat {\mathcal {O}_{X_{\infty },\alpha }} \simeq \widehat {\mathcal {O}_{X^0_{\infty },\alpha }}$, and hence we can apply (1) to
$\widehat {\mathcal {O}_{X_{\infty },\alpha }} \simeq \widehat {\mathcal {O}_{X^0_{\infty },\alpha }}$, and hence we can apply (1) to ![]() $X^0$; note also that in this case we have
$X^0$; note also that in this case we have ![]() $\alpha \in X^0_{\mathrm {sm}}$ and hence
$\alpha \in X^0_{\mathrm {sm}}$ and hence ![]() $\operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} ) < \infty $.
$\operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} ) < \infty $.
We include a proof of the following property, which is well known to experts and is remarked in [Reference Drinfeld24]:
Lemma 8.6. Let X be a scheme of finite type over a field k and ![]() $\alpha \in X_{\infty }$ an arc with
$\alpha \in X_{\infty }$ an arc with ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$. Let
$\alpha (\eta ) \in X_{\mathrm {sm}}$. Let ![]() $X^0 \subset X$ be the irreducible component containing
$X^0 \subset X$ be the irreducible component containing ![]() $\alpha (\eta )$. Then
$\alpha (\eta )$. Then  $\widehat {\mathcal {O}_{X_{\infty },\alpha }} \simeq \widehat {\mathcal {O}_{X^0_{\infty },\alpha }}$.
$\widehat {\mathcal {O}_{X_{\infty },\alpha }} \simeq \widehat {\mathcal {O}_{X^0_{\infty },\alpha }}$.
Proof. We may assume that ![]() $X = \operatorname {\mathrm {Spec}}(R)$ is affine. By abuse of notation, we write
$X = \operatorname {\mathrm {Spec}}(R)$ is affine. By abuse of notation, we write ![]() $\alpha $ for the map
$\alpha $ for the map ![]() $R \to A[[t]]$. Let
$R \to A[[t]]$. Let ![]() $\mathfrak {a} := \ker (\alpha )$. If
$\mathfrak {a} := \ker (\alpha )$. If ![]() $(0) = \prod _i \mathfrak {q}_i \subset R$ is a primary decomposition with
$(0) = \prod _i \mathfrak {q}_i \subset R$ is a primary decomposition with ![]() $\mathfrak {q}_0$ the minimal prime defining
$\mathfrak {q}_0$ the minimal prime defining ![]() $X^0$, then the condition
$X^0$, then the condition ![]() $\alpha (\eta ) \in X^0$ translates to
$\alpha (\eta ) \in X^0$ translates to ![]() $\mathfrak {q}_0 \subset \mathfrak {a}$ and
$\mathfrak {q}_0 \subset \mathfrak {a}$ and ![]() $\mathfrak {q}_i \not \subset \mathfrak {a}$ for
$\mathfrak {q}_i \not \subset \mathfrak {a}$ for ![]() $i \ne 0$. Let A be a test-ring – that is, it is local with maximal ideal
$i \ne 0$. Let A be a test-ring – that is, it is local with maximal ideal ![]() $\mathfrak {m}$, residue field K equal to the residue field of
$\mathfrak {m}$, residue field K equal to the residue field of ![]() $\alpha \in X_{\infty }$ and
$\alpha \in X_{\infty }$ and ![]() $\mathfrak {m}^n = 0$ for some
$\mathfrak {m}^n = 0$ for some ![]() $n \in {\mathbb N}$. Let
$n \in {\mathbb N}$. Let ![]() $\alpha '$ be any A-deformation of
$\alpha '$ be any A-deformation of ![]() $\alpha $ – that is, given by a map
$\alpha $ – that is, given by a map ![]() $R \to A[[t]]$. To prove the lemma, it suffices to show that
$R \to A[[t]]$. To prove the lemma, it suffices to show that ![]() $\mathfrak {a}' := \ker (\alpha ') \supset \mathfrak {q}_0$. We have the commutative diagram
$\mathfrak {a}' := \ker (\alpha ') \supset \mathfrak {q}_0$. We have the commutative diagram

where ![]() $A((t))$ denotes the localisation of
$A((t))$ denotes the localisation of ![]() $A[[t]]$ at the ideal
$A[[t]]$ at the ideal ![]() $\mathfrak {m}$. Since
$\mathfrak {m}$. Since ![]() $A[[t]] \to A((t))$ is injective, we have
$A[[t]] \to A((t))$ is injective, we have ![]() $\mathfrak {a}' = \ker (\gamma ')$. Let
$\mathfrak {a}' = \ker (\gamma ')$. Let ![]() $f \in \mathfrak {q}_0$. Take any
$f \in \mathfrak {q}_0$. Take any ![]() $f_i \in \mathfrak {q}_i \setminus \mathfrak {a}$ for
$f_i \in \mathfrak {q}_i \setminus \mathfrak {a}$ for ![]() $i \ne 0$. Then
$i \ne 0$. Then ![]() $g := f \prod _i f_i \in \mathfrak {a}'$. Since
$g := f \prod _i f_i \in \mathfrak {a}'$. Since ![]() $\gamma '(f_i) \ne 0$ modulo
$\gamma '(f_i) \ne 0$ modulo ![]() $\mathfrak {m}$, we have that
$\mathfrak {m}$, we have that ![]() $\gamma '(f_i)$ is a unit. Thus
$\gamma '(f_i)$ is a unit. Thus ![]() $0 = \gamma '(g) = \gamma '(f)u$, where u is a unit, and in particular
$0 = \gamma '(g) = \gamma '(f)u$, where u is a unit, and in particular ![]() $f \in \mathfrak {a}'$.
$f \in \mathfrak {a}'$.
Theorem 8.7. Let X be a scheme of finite type over a perfect field k. For ![]() $\alpha \in X_{\infty }$ such that
$\alpha \in X_{\infty }$ such that ![]() $\alpha (\eta ) \in X \setminus X_{\mathrm {sm}}$, we have
$\alpha (\eta ) \in X \setminus X_{\mathrm {sm}}$, we have ![]() $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) = \infty $.
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) = \infty $.
Proof. Note that since k is perfect, we have ![]() $X \setminus X_{\mathrm {sm}} = \operatorname {\mathrm {Sing}}(X)$, and in particular the condition that
$X \setminus X_{\mathrm {sm}} = \operatorname {\mathrm {Sing}}(X)$, and in particular the condition that ![]() $\alpha (\eta ) \in X \setminus X_{\mathrm {sm}}$ is equivalent to having
$\alpha (\eta ) \in X \setminus X_{\mathrm {sm}}$ is equivalent to having ![]() $\alpha \in (\operatorname {\mathrm {Sing}}(X))_{\infty }$.
$\alpha \in (\operatorname {\mathrm {Sing}}(X))_{\infty }$.
For every ![]() $n \in {\mathbb N}$, let
$n \in {\mathbb N}$, let ![]() $\pi _n \colon X_{\infty } \to X_n$ be the truncation morphism, and let
$\pi _n \colon X_{\infty } \to X_n$ be the truncation morphism, and let ![]() $\alpha _n := \pi _n(\alpha ) \in X_n$. Note that for
$\alpha _n := \pi _n(\alpha ) \in X_n$. Note that for ![]() $n=0$ we have
$n=0$ we have ![]() $\alpha _0 = \alpha (0)$. Let L and
$\alpha _0 = \alpha (0)$. Let L and ![]() $L_n$ denote the residue fields of
$L_n$ denote the residue fields of ![]() $X_{\infty }$ at
$X_{\infty }$ at ![]() $\alpha $ and of
$\alpha $ and of ![]() $X_n$ at
$X_n$ at ![]() $\alpha _n$. By [Reference de Fernex and Docampo21, Lemma 8.3] (see also [Reference de Fernex and Docampo21, Remark 7.4]), for all n sufficiently large the differential map
$\alpha _n$. By [Reference de Fernex and Docampo21, Lemma 8.3] (see also [Reference de Fernex and Docampo21, Remark 7.4]), for all n sufficiently large the differential map
 $$ \begin{align*} (T_\alpha\pi_n)^* \colon \mathfrak{m}_{\alpha_n}/\mathfrak{m}_{\alpha_n}^2 \otimes_{L_n}L \to \mathfrak{m}_\alpha/\mathfrak{m}_\alpha^2 \end{align*} $$
$$ \begin{align*} (T_\alpha\pi_n)^* \colon \mathfrak{m}_{\alpha_n}/\mathfrak{m}_{\alpha_n}^2 \otimes_{L_n}L \to \mathfrak{m}_\alpha/\mathfrak{m}_\alpha^2 \end{align*} $$has rank at least ![]() $(n+1)d(\alpha )-\dim (\overline {\{\alpha _n\}} )$, where
$(n+1)d(\alpha )-\dim (\overline {\{\alpha _n\}} )$, where
Then by Proposition 6.6 we have
 $$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) &\ge (n+1)d(\alpha) - \operatorname{\mathrm{trdeg}}_k(L_n) - \dim\left(\mathcal{O}_{\overline{\pi_n\left(X_{\infty}\right)},\alpha_n}\right)\\ & = (n+1)d(\alpha) - \dim_{\alpha_n}\left(\overline{\pi_n(X_{\infty})}\right), \end{align*} $$
$$ \begin{align*} \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) &\ge (n+1)d(\alpha) - \operatorname{\mathrm{trdeg}}_k(L_n) - \dim\left(\mathcal{O}_{\overline{\pi_n\left(X_{\infty}\right)},\alpha_n}\right)\\ & = (n+1)d(\alpha) - \dim_{\alpha_n}\left(\overline{\pi_n(X_{\infty})}\right), \end{align*} $$where ![]() $\overline {\pi _n(X_{\infty })}$ denotes the Zariski closure of
$\overline {\pi _n(X_{\infty })}$ denotes the Zariski closure of ![]() $\pi _n(X_{\infty })$ in
$\pi _n(X_{\infty })$ in ![]() $X_n$.
$X_n$.
Since X is of finite type, ![]() $X_{\infty }$ has finitely many irreducible components (see [Reference Reguera41, Theorem 2.9] and [Reference Ngô39, Corollary 3.16]). This implies that for n sufficiently large, we have
$X_{\infty }$ has finitely many irreducible components (see [Reference Reguera41, Theorem 2.9] and [Reference Ngô39, Corollary 3.16]). This implies that for n sufficiently large, we have
 $$ \begin{align*} \dim_{\alpha_n}\left(\overline{\pi_n(X_{\infty})}\right) = \max_{C \ni \alpha} \dim\left(\overline{\pi_n(C)}\right), \end{align*} $$
$$ \begin{align*} \dim_{\alpha_n}\left(\overline{\pi_n(X_{\infty})}\right) = \max_{C \ni \alpha} \dim\left(\overline{\pi_n(C)}\right), \end{align*} $$where the maximum is taken over the irreducible components C of ![]() $X_{\infty }$ that contain
$X_{\infty }$ that contain ![]() $\alpha $.
$\alpha $.
Let C be one of the irreducible components of ![]() $X_{\infty }$ containing
$X_{\infty }$ containing ![]() $\alpha $, let
$\alpha $, let ![]() $\beta \in C$ be its generic point and let
$\beta \in C$ be its generic point and let ![]() $Z \subset X$ be the closure of
$Z \subset X$ be the closure of ![]() $\beta (\eta )$ in X. From [Reference de Fernex and Docampo21, Lemma 8.6], we have
$\beta (\eta )$ in X. From [Reference de Fernex and Docampo21, Lemma 8.6], we have
 $$ \begin{align*} \dim\left(\overline{\pi_n(C)}\right) \leq (n+1) \dim(Z) \leq (n+1) \dim_{\alpha(0)}(X). \end{align*} $$
$$ \begin{align*} \dim\left(\overline{\pi_n(C)}\right) \leq (n+1) \dim(Z) \leq (n+1) \dim_{\alpha(0)}(X). \end{align*} $$Since ![]() $\alpha (\eta )\in \operatorname {\mathrm {Sing}}(X)$, we see by the definition of
$\alpha (\eta )\in \operatorname {\mathrm {Sing}}(X)$, we see by the definition of ![]() $d(\alpha )$ that
$d(\alpha )$ that ![]() $d(\alpha )> \dim _{\alpha (0)}(X)$, and therefore
$d(\alpha )> \dim _{\alpha (0)}(X)$, and therefore
 $$ \begin{align*} \lim_{n \to \infty}\left((n+1)d(\alpha) - \dim\left(\overline{\pi_n(C)}\right)\right) \geq \lim_{n \to \infty}(n+1)\left(d(\alpha) - \dim_{\alpha(0)}(X)\right) = \infty. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty}\left((n+1)d(\alpha) - \dim\left(\overline{\pi_n(C)}\right)\right) \geq \lim_{n \to \infty}(n+1)\left(d(\alpha) - \dim_{\alpha(0)}(X)\right) = \infty. \end{align*} $$We conclude that ![]() $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) = \infty $, as claimed.
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) = \infty $, as claimed.
Corollary 8.8. Let X be a scheme of finite type over a field k and let ![]() $\alpha \in X_{\infty }$. Assume that either k has characteristic
$\alpha \in X_{\infty }$. Assume that either k has characteristic ![]() $0$ or
$0$ or ![]() $\alpha \in X_{\infty }(k)$. Then we have
$\alpha \in X_{\infty }(k)$. Then we have ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$ if and only if
$\alpha (\eta ) \in X_{\mathrm {sm}}$ if and only if ![]() $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) < \infty $.
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) < \infty $.
Proof. If k has characteristic ![]() $0$, then the corollary follows by Theorems 8.5 and 8.7.
$0$, then the corollary follows by Theorems 8.5 and 8.7.
Let then k be any field, and assume that ![]() $\alpha \in X_{\infty }(k)$. For a field extension
$\alpha \in X_{\infty }(k)$. For a field extension ![]() $k \subset k'$, we denote
$k \subset k'$, we denote ![]() $X' := X \times _{\operatorname {\mathrm {Spec}}(k)} \operatorname {\mathrm {Spec}}(k')$ and let
$X' := X \times _{\operatorname {\mathrm {Spec}}(k)} \operatorname {\mathrm {Spec}}(k')$ and let ![]() $\alpha ' \colon \operatorname {\mathrm {Spec}}(k'[[t]]) \to X'$ be the arc obtained by base change from
$\alpha ' \colon \operatorname {\mathrm {Spec}}(k'[[t]]) \to X'$ be the arc obtained by base change from ![]() $\alpha $. Since a point of X is in the smooth locus if and only if it is geometrically regular, we can find a field extension
$\alpha $. Since a point of X is in the smooth locus if and only if it is geometrically regular, we can find a field extension ![]() $k \subset k'$ such that
$k \subset k'$ such that ![]() $\alpha '$ is not a regular point of
$\alpha '$ is not a regular point of ![]() $X'$. By faithfully flat descent of regularity, we can replace
$X'$. By faithfully flat descent of regularity, we can replace ![]() $k'$ with a larger field extension and assume without loss of generality that
$k'$ with a larger field extension and assume without loss of generality that ![]() $k'$ is perfect. Note that
$k'$ is perfect. Note that ![]() $X^{\prime }_{\infty } \simeq X_{\infty } \times _{\operatorname {\mathrm {Spec}}(k)} \operatorname {\mathrm {Spec}}(k')$, and hence
$X^{\prime }_{\infty } \simeq X_{\infty } \times _{\operatorname {\mathrm {Spec}}(k)} \operatorname {\mathrm {Spec}}(k')$, and hence ![]() $\mathcal {O}_{X^{\prime }_{\infty },\alpha '} \simeq \mathcal {O}_{X_{\infty },\alpha } \otimes _k k'$. Then by Proposition 6.9 we have
$\mathcal {O}_{X^{\prime }_{\infty },\alpha '} \simeq \mathcal {O}_{X_{\infty },\alpha } \otimes _k k'$. Then by Proposition 6.9 we have
This reduces to the case of perfect fields, where the result follows again by Theorems 8.5 and 8.7.
9 On Drinfeld, Grinberg and Kazhdan’s theorem
Theorem 8.5 can be seen as a finiteness statement for singularities of the arc space at arcs that are not fully contained in the singular locus. One of the first major results in this direction is the theorem of Drinfeld, Grinberg and Kazhdan, which we will state here in its version from [Reference Drinfeld24]. Recall that for any equicharacteristic local ring ![]() $(A,\mathfrak {m},k)$, a DGK decomposition is an isomorphism
$(A,\mathfrak {m},k)$, a DGK decomposition is an isomorphism ![]() $\widehat {A}\simeq k[[t_i \mid i\in I]]/\mathfrak {a}$, where
$\widehat {A}\simeq k[[t_i \mid i\in I]]/\mathfrak {a}$, where ![]() $\mathfrak {a}$ is an ideal of finite polynomial definition.
$\mathfrak {a}$ is an ideal of finite polynomial definition.
Theorem 9.1 [Reference Grinberg and Kazhdan31, Theorem 2.1], [Reference Drinfeld24, Theorem 0.1]
Let X be a scheme of finite type over a field k, and let ![]() $\alpha \in X_{\infty }(k)$. If
$\alpha \in X_{\infty }(k)$. If ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$, then the local ring
$\alpha (\eta ) \in X_{\mathrm {sm}}$, then the local ring ![]() $\mathcal {O}_{X_{\infty },\alpha }$ admits a DGK decomposition.
$\mathcal {O}_{X_{\infty },\alpha }$ admits a DGK decomposition.
As mentioned in Remark 5.3, any DGK decomposition of ![]() $\mathcal {O}_{X_{\infty },\alpha }$ induces an isomorphism of formal schemes
$\mathcal {O}_{X_{\infty },\alpha }$ induces an isomorphism of formal schemes
 $$ \begin{align*} \widehat{X_{\infty,\alpha}} \simeq \widehat{Z_z} \hat\times \Delta^{\mathbb N}, \end{align*} $$
$$ \begin{align*} \widehat{X_{\infty,\alpha}} \simeq \widehat{Z_z} \hat\times \Delta^{\mathbb N}, \end{align*} $$with Z a scheme of finite type over k, ![]() $z\in Z(k)$ and
$z\in Z(k)$ and ![]() $\Delta =\operatorname {\mathrm {Spf}}(k[[t]])$. The formal scheme
$\Delta =\operatorname {\mathrm {Spf}}(k[[t]])$. The formal scheme ![]() $\widehat {Z_z}$ is often referred to as a formal model for
$\widehat {Z_z}$ is often referred to as a formal model for ![]() $\alpha $. While
$\alpha $. While ![]() $\widehat {Z_z}$ is not unique, there exists a unique minimal one in the following sense:
$\widehat {Z_z}$ is not unique, there exists a unique minimal one in the following sense:
Theorem 9.2 [Reference Bourqui and Sebag10, Theorem 7.1], [Reference Bourqui and Sebag12, Theorem 1.2]
Let ![]() $\widehat {Z_z}$ and
$\widehat {Z_z}$ and ![]() $\widehat {W_w}$ be two formal models for
$\widehat {W_w}$ be two formal models for ![]() $\alpha $ which are indecomposable – that is, they are not of the form
$\alpha $ which are indecomposable – that is, they are not of the form ![]() $\mathcal {Y} \hat \times \Delta $, with
$\mathcal {Y} \hat \times \Delta $, with ![]() $\mathcal {Y}$ a formal scheme. Then
$\mathcal {Y}$ a formal scheme. Then ![]() $\widehat {Z_z}\simeq \widehat {W_w}$.
$\widehat {Z_z}\simeq \widehat {W_w}$.
Definition 9.3. The indecomposable formal model of ![]() $\alpha $ is called the minimal formal model and denoted by
$\alpha $ is called the minimal formal model and denoted by ![]() $\mathcal {Z}^{\min }_\alpha $.
$\mathcal {Z}^{\min }_\alpha $.
Note that the formal model provided by Theorem 9.1 is not minimal in general, which we will see in Section 10.
Combining Theorem 9.1 with the results of this paper, we obtain the next result, which provides a characterisation of k-rational arcs admitting a DGK decomposition. The result also gives an explicit bound for the embedding codimension; we should stress that such a bound does not follow from the proofs in [Reference Grinberg and Kazhdan31, Reference Drinfeld24, Reference Drinfeld25].
Theorem 9.4. Let X be a scheme of finite type over a field k. For any ![]() $\alpha \in X_{\infty }(k)$, the following are equivalent:
$\alpha \in X_{\infty }(k)$, the following are equivalent:
1.
 $\alpha (\eta ) \in X_{\mathrm {sm}}$.
$\alpha (\eta ) \in X_{\mathrm {sm}}$.2.
 $\mathcal {O}_{X_{\infty },\alpha }$ admits a DGK decomposition.
$\mathcal {O}_{X_{\infty },\alpha }$ admits a DGK decomposition.3.
 $\mathcal {O}_{X_{\infty },\alpha }$ admits a weak DGK decomposition.
$\mathcal {O}_{X_{\infty },\alpha }$ admits a weak DGK decomposition.4.
 $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } )<\infty $.
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } )<\infty $.
Moreover, if k is perfect and ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$, then
$\alpha (\eta ) \in X_{\mathrm {sm}}$, then
where ![]() $X^0 \subset X$ is the irreducible component containing
$X^0 \subset X$ is the irreducible component containing ![]() $\alpha (\eta )$.
$\alpha (\eta )$.
Proof. The implication (1) ![]() $\Rightarrow $ (2) is Theorem 9.1, the implication (2)
$\Rightarrow $ (2) is Theorem 9.1, the implication (2) ![]() $\Rightarrow $ (3) is obvious, the implication (3)
$\Rightarrow $ (3) is obvious, the implication (3) ![]() $\Rightarrow $ (4) follows from Corollary 5.11 and finally Corollary 8.8 gives the implication (4)
$\Rightarrow $ (4) follows from Corollary 5.11 and finally Corollary 8.8 gives the implication (4) ![]() $\Rightarrow $ (1). The last statement follows from Theorem 8.5.
$\Rightarrow $ (1). The last statement follows from Theorem 8.5.
Example 9.5. Let X be the hypersurface defined by ![]() $x_0x_{n+1}+f(x_1,\dotsc ,x_n)=0$ and
$x_0x_{n+1}+f(x_1,\dotsc ,x_n)=0$ and ![]() $\alpha \in X(k)$ the arc given by
$\alpha \in X(k)$ the arc given by ![]() $(t,0,\dotsc ,0)\in k[[t]]^{n+2}$. Assume further that the hypersurface
$(t,0,\dotsc ,0)\in k[[t]]^{n+2}$. Assume further that the hypersurface ![]() $H \subset {\mathbb A}^n$ given by
$H \subset {\mathbb A}^n$ given by ![]() $f(x_1,\dotsc ,x_n) = 0$ has a singularity at
$f(x_1,\dotsc ,x_n) = 0$ has a singularity at ![]() $0$. Then, as shown in [Reference Drinfeld24], a DGK decomposition for
$0$. Then, as shown in [Reference Drinfeld24], a DGK decomposition for ![]() $\mathcal {O}_{X_{\infty },\alpha }$ is given by
$\mathcal {O}_{X_{\infty },\alpha }$ is given by
 $$ \begin{align*} \widehat{\mathcal{O}_{X_{\infty},\alpha}} \simeq k[[x_1,\dotsc,x_n]]/f(x_1,\dotsc,x_n) \,\hat{\otimes}_k\, k[[t_i \mid i\in{\mathbb N}]]. \end{align*} $$
$$ \begin{align*} \widehat{\mathcal{O}_{X_{\infty},\alpha}} \simeq k[[x_1,\dotsc,x_n]]/f(x_1,\dotsc,x_n) \,\hat{\otimes}_k\, k[[t_i \mid i\in{\mathbb N}]]. \end{align*} $$The singularity of ![]() $\alpha $ is thus again given by H and
$\alpha $ is thus again given by H and ![]() $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } )=1$. On the other hand, the order of
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } )=1$. On the other hand, the order of ![]() $\alpha $ with respect to the Jacobian ideal
$\alpha $ with respect to the Jacobian ideal ![]() $\mathrm {Jac}_X$ is
$\mathrm {Jac}_X$ is ![]() $1$, and hence the bound in Theorem 9.4 is sharp in this case.
$1$, and hence the bound in Theorem 9.4 is sharp in this case.
Example 9.6. Similar to the previous example, let X be the hypersurface defined by ![]() $x_0x_{n+1} + f(x_1,\dotsc ,x_n) = 0$, where f is a polynomial of multiplicity
$x_0x_{n+1} + f(x_1,\dotsc ,x_n) = 0$, where f is a polynomial of multiplicity ![]() $2$, and take this time
$2$, and take this time ![]() $\alpha \in X_{\infty }(k)$ to be the arc given by
$\alpha \in X_{\infty }(k)$ to be the arc given by ![]() $(t^m,0,\dotsc ,0) \in k[[t]]^{n+2}$. Denoting by
$(t^m,0,\dotsc ,0) \in k[[t]]^{n+2}$. Denoting by ![]() $g^{(j)}$ the jth Hasse–Schmidt derivative of an element
$g^{(j)}$ the jth Hasse–Schmidt derivative of an element ![]() $g \in k[x_0,\dotsc ,x_{n+1}]$ and setting for short
$g \in k[x_0,\dotsc ,x_{n+1}]$ and setting for short ![]() $I = \{0,1,\dotsc ,n+1\}$ and
$I = \{0,1,\dotsc ,n+1\}$ and ![]() $J = {\mathbb Z}_{\ge 0}$,
$J = {\mathbb Z}_{\ge 0}$, ![]() $X_{\infty }$ is defined by the ideal
$X_{\infty }$ is defined by the ideal ![]() $\mathfrak {a} = ((x_0x_{n+1} + f)^{(j)} \mid j \in J )$ of
$\mathfrak {a} = ((x_0x_{n+1} + f)^{(j)} \mid j \in J )$ of  $P := k [x_i^{(j)} \mid (i,j) \in I \times J ]$ [Reference Whitney45]. Let
$P := k [x_i^{(j)} \mid (i,j) \in I \times J ]$ [Reference Whitney45]. Let ![]() $\mathfrak {m} \subset P$ be the maximal ideal at
$\mathfrak {m} \subset P$ be the maximal ideal at ![]() $\alpha $. Since
$\alpha $. Since  $x_0^{(m)}$ is a unit in the local ring
$x_0^{(m)}$ is a unit in the local ring ![]() $P_{\mathfrak {m}}$, we see that the ideal
$P_{\mathfrak {m}}$, we see that the ideal ![]() $\operatorname {\mathrm {in}}(\mathfrak {a} P_{\mathfrak {m}})$ is generated by the elements
$\operatorname {\mathrm {in}}(\mathfrak {a} P_{\mathfrak {m}})$ is generated by the elements  $x_{n+1}^{(j)}$ for
$x_{n+1}^{(j)}$ for ![]() $j \in J$ and
$j \in J$ and ![]() $\operatorname {\mathrm {in}} (f^{(l)} )$ for
$\operatorname {\mathrm {in}} (f^{(l)} )$ for ![]() $0 \le l \le m-1$. As long as f is chosen so that
$0 \le l \le m-1$. As long as f is chosen so that ![]() $\operatorname {\mathrm {in}} (f^{(l)} )$,
$\operatorname {\mathrm {in}} (f^{(l)} )$, ![]() $0 \le l \le m-1$, form a regular sequence (for example,
$0 \le l \le m-1$, form a regular sequence (for example, ![]() $f = x_1x_2$ would work), we get that
$f = x_1x_2$ would work), we get that ![]() $\mathcal {O}_{X_{\infty },\alpha }$ has embedding codimension m. Since clearly the order of
$\mathcal {O}_{X_{\infty },\alpha }$ has embedding codimension m. Since clearly the order of ![]() $\alpha $ with respect to
$\alpha $ with respect to ![]() $\mathrm {Jac}_X$ is also m, this shows that the bound in Theorem 9.4 is sharp for all possible orders of the arc with the Jacobian ideal of X.
$\mathrm {Jac}_X$ is also m, this shows that the bound in Theorem 9.4 is sharp for all possible orders of the arc with the Jacobian ideal of X.
Let us mention here the following consequence of Theorem 9.4, which implies that the local rings of closed arcs in the arc space provide plenty of examples of non-Noetherian rings whose embedding codimension agrees with their formal embedding codimension.
Corollary 9.7. If X is a scheme of finite type over a field k, then
for every ![]() $\alpha \in X_{\infty }(k)$. If k is perfect, then the same holds for all constructible points
$\alpha \in X_{\infty }(k)$. If k is perfect, then the same holds for all constructible points ![]() $\alpha \in X_{\infty }$ with
$\alpha \in X_{\infty }$ with ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$.
$\alpha (\eta ) \in X_{\mathrm {sm}}$.
Proof. Assume first that ![]() $\alpha \in X_{\infty }(k)$. If
$\alpha \in X_{\infty }(k)$. If ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$, then the equality follows by Theorem 9.1 and Proposition 7.6. If
$\alpha (\eta ) \in X_{\mathrm {sm}}$, then the equality follows by Theorem 9.1 and Proposition 7.6. If ![]() $\alpha (\eta ) \in X \setminus X_{\mathrm {sm}}$, then we have
$\alpha (\eta ) \in X \setminus X_{\mathrm {sm}}$, then we have ![]() $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) = \infty $ by Corollary 8.8, and we conclude by Theorem 7.8. Suppose now that
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) = \infty $ by Corollary 8.8, and we conclude by Theorem 7.8. Suppose now that ![]() $\alpha \in X_{\infty }$ is a constructible point with
$\alpha \in X_{\infty }$ is a constructible point with ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$. By [Reference de Fernex and Docampo21, Theorem 10.8],
$\alpha (\eta ) \in X_{\mathrm {sm}}$. By [Reference de Fernex and Docampo21, Theorem 10.8], ![]() $\mathcal {O}_{X_{\infty },\alpha }$ has finite embedding dimension, and hence the assertion follows by Corollary 7.5.
$\mathcal {O}_{X_{\infty },\alpha }$ has finite embedding dimension, and hence the assertion follows by Corollary 7.5.
We now state the following application of Theorems 8.1 and 9.1, which says that a generic projection of the base scheme induces an efficient DGK decomposition at an arc that is not contained in the singular locus:
Theorem 9.8. Let ![]() $X \subset {\mathbb A}^N$ be an affine scheme of finite type over a perfect field k, let
$X \subset {\mathbb A}^N$ be an affine scheme of finite type over a perfect field k, let ![]() $\alpha \in X_{\infty }(k)$ with
$\alpha \in X_{\infty }(k)$ with ![]() $\alpha (\eta )\in X_{\mathrm {sm}}$ and let
$\alpha (\eta )\in X_{\mathrm {sm}}$ and let ![]() $d=\dim _{\alpha (\eta )}(X)$. Let
$d=\dim _{\alpha (\eta )}(X)$. Let ![]() $f\colon X\to Y:={\mathbb A}^d$ be the map induced by a general linear projection
$f\colon X\to Y:={\mathbb A}^d$ be the map induced by a general linear projection ![]() ${\mathbb A}^N \to {\mathbb A}^d$, and let
${\mathbb A}^N \to {\mathbb A}^d$, and let ![]() $\beta :=f_{\infty }(\alpha )$. Then the associated map
$\beta :=f_{\infty }(\alpha )$. Then the associated map
gives an efficient formal embedding of ![]() $\mathcal {O}_{X_{\infty },\alpha }$. Moreover, if k is infinite, then there exist formal coordinates
$\mathcal {O}_{X_{\infty },\alpha }$. Moreover, if k is infinite, then there exist formal coordinates  $u_i\in \widehat {\mathcal {O}_{Y_{\infty },\beta }}$,
$u_i\in \widehat {\mathcal {O}_{Y_{\infty },\beta }}$, ![]() $i\in {\mathbb N}$, such that
$i\in {\mathbb N}$, such that ![]() $\ker (\widehat {\varphi } )$ is generated by finitely many polynomials in
$\ker (\widehat {\varphi } )$ is generated by finitely many polynomials in ![]() $u_i$, and hence
$u_i$, and hence ![]() $\widehat {\varphi }$ induces an efficient DGK decomposition.
$\widehat {\varphi }$ induces an efficient DGK decomposition.
Proof. The first part follows from Theorem 8.1, together with the fact that ![]() $\mathcal {O}_{Y_{\infty },\beta }$ is formally smooth over k. Regarding the second assertion, we know by Theorem 9.1 that the map
$\mathcal {O}_{Y_{\infty },\beta }$ is formally smooth over k. Regarding the second assertion, we know by Theorem 9.1 that the map ![]() $\varphi $ induces a surjection
$\varphi $ induces a surjection
 $$ \begin{align*} \psi\colon \widehat{\mathcal{O}_{Y_{\infty},\beta}} \to \widehat{\mathcal{O}_{Z,z}} \hat{\otimes}_k k[[t_i \mid i\in {\mathbb N}]], \end{align*} $$
$$ \begin{align*} \psi\colon \widehat{\mathcal{O}_{Y_{\infty},\beta}} \to \widehat{\mathcal{O}_{Z,z}} \hat{\otimes}_k k[[t_i \mid i\in {\mathbb N}]], \end{align*} $$with Z a scheme of finite type over k and ![]() $z\in Z(k)$. If Z is smooth at z, then there is nothing to show. Otherwise, by Theorem 3.15 we may assume that
$z\in Z(k)$. If Z is smooth at z, then there is nothing to show. Otherwise, by Theorem 3.15 we may assume that ![]() $Z\subset {\mathbb A}^n$, where
$Z\subset {\mathbb A}^n$, where ![]() $n=\mathrm {edim} (\mathcal {O}_{Z,z} )$. Since
$n=\mathrm {edim} (\mathcal {O}_{Z,z} )$. Since ![]() $\psi $ induces an isomorphism of continuous cotangent spaces, the statement follows from Proposition 3.9.
$\psi $ induces an isomorphism of continuous cotangent spaces, the statement follows from Proposition 3.9.
The next example illustrates in concrete terms the content of Theorem 9.8 when X is a hypersurface in an affine space, where the existence of the efficient formal embedding as in the theorem can be verified directly from the equations.
Example 9.9. Let ![]() $f\in k[x_1,\dotsc ,x_n,y]$ and let X be the hypersurface defined by f. For the sake of convenience, we will write
$f\in k[x_1,\dotsc ,x_n,y]$ and let X be the hypersurface defined by f. For the sake of convenience, we will write ![]() $x=(x_1,\dotsc ,x_n)$. Let
$x=(x_1,\dotsc ,x_n)$. Let ![]() $\alpha =(x(t),y(t))$ be an arc on X such that
$\alpha =(x(t),y(t))$ be an arc on X such that 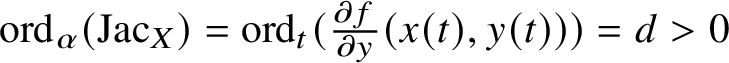 $\operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_X)=\operatorname {\mathrm {ord}}_t (\frac {\partial f}{\partial y}(x(t),y(t)) )=d>0$. We write
$\operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_X)=\operatorname {\mathrm {ord}}_t (\frac {\partial f}{\partial y}(x(t),y(t)) )=d>0$. We write  $x(t)=\sum _j a^{(j)} t^j$ and
$x(t)=\sum _j a^{(j)} t^j$ and  $y(t)=\sum _j b^{(j)} t^j$; note that
$y(t)=\sum _j b^{(j)} t^j$; note that  $a^{(j)}= (a_1^{(j)},\dotsc ,a_n^{(j)} )$. Let
$a^{(j)}= (a_1^{(j)},\dotsc ,a_n^{(j)} )$. Let ![]() $D= (D_p )_{p\geq 0}$ be the universal Hasse–Schmidt derivation on
$D= (D_p )_{p\geq 0}$ be the universal Hasse–Schmidt derivation on ![]() $k [x^{(j)},y^{(j)} \mid j\geq 0 ]$, where
$k [x^{(j)},y^{(j)} \mid j\geq 0 ]$, where  $x^{(j)}= (x_1^{(j)},\dotsc ,x_n^{(j)} )$. Then
$x^{(j)}= (x_1^{(j)},\dotsc ,x_n^{(j)} )$. Then ![]() $X_{\infty }=\operatorname {\mathrm {Spec}}(R_{\infty })$, where
$X_{\infty }=\operatorname {\mathrm {Spec}}(R_{\infty })$, where
 $$ \begin{align*} R_{\infty}=k\left[x^{(j)},y^{(j)} \mid j\geq0\right]/\left(f^{(p)} \mid p\geq0\right), \end{align*} $$
$$ \begin{align*} R_{\infty}=k\left[x^{(j)},y^{(j)} \mid j\geq0\right]/\left(f^{(p)} \mid p\geq0\right), \end{align*} $$with  $f^{(p)}:=D_p(f)$. Note that
$f^{(p)}:=D_p(f)$. Note that ![]() $f^{(p)}$ depends only on
$f^{(p)}$ depends only on ![]() $x^{(j)}, y^{(j)}$ for
$x^{(j)}, y^{(j)}$ for ![]() $j\leq p$. The arc
$j\leq p$. The arc ![]() $\alpha $ then corresponds to the ideal
$\alpha $ then corresponds to the ideal ![]() $\mathfrak {m}_\alpha $ of
$\mathfrak {m}_\alpha $ of ![]() $R_{\infty }$ given by
$R_{\infty }$ given by
 $$ \begin{align*} \mathfrak{m}_\alpha=\left(x^{(j)}-a^{(j)},y^{(j)}-b^{(j)} \mid j\geq0\right). \end{align*} $$
$$ \begin{align*} \mathfrak{m}_\alpha=\left(x^{(j)}-a^{(j)},y^{(j)}-b^{(j)} \mid j\geq0\right). \end{align*} $$Setting  $\widetilde {{f}^{(p)}} (x^{(j)},y^{(j)} ):=f^{(p)} (x^{(j)}+a^{(j)},y^{(j)}+b^{(j)} )$, we get
$\widetilde {{f}^{(p)}} (x^{(j)},y^{(j)} ):=f^{(p)} (x^{(j)}+a^{(j)},y^{(j)}+b^{(j)} )$, we get
 $$ \begin{align*} \mathcal{O}_{X_{\infty},\alpha}\simeq k\left[x^{(j)},y^{(j)}\right]_{\left(x^{(j)},y^{(j)}\right)}/\left(\widetilde{{f}^{(p)}}\right). \end{align*} $$
$$ \begin{align*} \mathcal{O}_{X_{\infty},\alpha}\simeq k\left[x^{(j)},y^{(j)}\right]_{\left(x^{(j)},y^{(j)}\right)}/\left(\widetilde{{f}^{(p)}}\right). \end{align*} $$We are going to make use of the following explicit formula from [Reference de Fernex and Docampo21, Section 5]:
 $$ \begin{align*} \frac{\partial f^{(p)}}{\partial y^{(q)}} = D_{p-q}\left(\frac{\partial f}{\partial y}\right),\quad q\leq p. \end{align*} $$
$$ \begin{align*} \frac{\partial f^{(p)}}{\partial y^{(q)}} = D_{p-q}\left(\frac{\partial f}{\partial y}\right),\quad q\leq p. \end{align*} $$The condition  $\operatorname {\mathrm {ord}}_t (\frac {\partial f}{\partial y}(x(t),y(t)) )=d$ implies that, for
$\operatorname {\mathrm {ord}}_t (\frac {\partial f}{\partial y}(x(t),y(t)) )=d$ implies that, for ![]() $p\geq d$,
$p\geq d$,
 $$ \begin{align*} \frac{\partial \widetilde{{f}^{(p)}}}{\partial y^{(q)}}(0,0) = \frac{\partial f^{(p)}}{\partial y^{(q)}}(a,b) = D_{p-q}\left(\frac{\partial f}{\partial y}\right)(a,b) \begin{cases} =0, & p-d<q\leq p, \\ \neq 0, & q=p-d. \end{cases} \end{align*} $$
$$ \begin{align*} \frac{\partial \widetilde{{f}^{(p)}}}{\partial y^{(q)}}(0,0) = \frac{\partial f^{(p)}}{\partial y^{(q)}}(a,b) = D_{p-q}\left(\frac{\partial f}{\partial y}\right)(a,b) \begin{cases} =0, & p-d<q\leq p, \\ \neq 0, & q=p-d. \end{cases} \end{align*} $$This implies that the initial forms of ![]() $f^{(p)}$, for
$f^{(p)}$, for ![]() $p\geq d$, can be written as
$p\geq d$, can be written as
 $$ \begin{align*} \operatorname{\mathrm{in}}\left(\widetilde{f^{\left(d+i\right)}}\right)=y^{(i)}+g^{(d+i)}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{in}}\left(\widetilde{f^{\left(d+i\right)}}\right)=y^{(i)}+g^{(d+i)}, \end{align*} $$where ![]() $g^{(d)} \in k [x^{(j)} \mid j\leq d ]$ and, for
$g^{(d)} \in k [x^{(j)} \mid j\leq d ]$ and, for ![]() $i> 0$,
$i> 0$, ![]() $g^{(d+i)} \in k [x^{(j)},y^{(l)} \mid j\leq d+i, l<i ]$. In particular, the elements
$g^{(d+i)} \in k [x^{(j)},y^{(l)} \mid j\leq d+i, l<i ]$. In particular, the elements ![]() $x^{(j)}$ and
$x^{(j)}$ and  $\widetilde {f^{(d+j)}}$, for
$\widetilde {f^{(d+j)}}$, for ![]() $j\geq 0$, give formal coordinates in
$j\geq 0$, give formal coordinates in ![]() $k [ [x^{(j)},z^{(j)} \mid j\geq 0 ] ]$, and hence the map
$k [ [x^{(j)},z^{(j)} \mid j\geq 0 ] ]$, and hence the map
 $$ \begin{align*} \varphi\colon k\left[\left[x^{(j)},z^{(j)} \mid j\geq0\right]\right] \to k\left[\left[x^{(j)},y^{(j)} \mid j\geq0\right]\right], \quad x^{(j)}\mapsto x^{(j)},\ z^{(j)}\mapsto \widetilde{f^{(j+d)}}, \end{align*} $$
$$ \begin{align*} \varphi\colon k\left[\left[x^{(j)},z^{(j)} \mid j\geq0\right]\right] \to k\left[\left[x^{(j)},y^{(j)} \mid j\geq0\right]\right], \quad x^{(j)}\mapsto x^{(j)},\ z^{(j)}\mapsto \widetilde{f^{(j+d)}}, \end{align*} $$is an isomorphism. Write ![]() $h_i:=\varphi ^{-1} (f^{(i)} )$ and
$h_i:=\varphi ^{-1} (f^{(i)} )$ and ![]() $\mathfrak {a}:= (\bar {h}_0,\dotsc ,\bar {h}_{d-1} )$, where
$\mathfrak {a}:= (\bar {h}_0,\dotsc ,\bar {h}_{d-1} )$, where ![]() $\bar {h}_i$ is obtained from
$\bar {h}_i$ is obtained from ![]() $h_i$ by setting
$h_i$ by setting ![]() $z^{(j)}=0$ for all
$z^{(j)}=0$ for all ![]() $j\geq 0$. Then we get
$j\geq 0$. Then we get
 $$ \begin{align*} \widehat{\mathcal{O}_{X_{\infty},\alpha}}\simeq k\left[\left[x^{(j)} \mid j\geq0\right]\right]/\widehat{\mathfrak{a}}. \end{align*} $$
$$ \begin{align*} \widehat{\mathcal{O}_{X_{\infty},\alpha}}\simeq k\left[\left[x^{(j)} \mid j\geq0\right]\right]/\widehat{\mathfrak{a}}. \end{align*} $$Observe that the map  $k [ [x^{(j)} \mid j\geq 0 ] ] \to \widehat {\mathcal {O}_{X_{\infty },\alpha }}$ is the efficient formal embedding from Theorem 9.8 with respect to the projection
$k [ [x^{(j)} \mid j\geq 0 ] ] \to \widehat {\mathcal {O}_{X_{\infty },\alpha }}$ is the efficient formal embedding from Theorem 9.8 with respect to the projection ![]() $(x,y)\mapsto x$. However, this isomorphism does not induce a DGK decomposition a priori, since the ideal
$(x,y)\mapsto x$. However, this isomorphism does not induce a DGK decomposition a priori, since the ideal ![]() $\widehat {\mathfrak {a}}$ is not necessarily of finite polynomial definition with respect to the variables
$\widehat {\mathfrak {a}}$ is not necessarily of finite polynomial definition with respect to the variables ![]() $x^{(j)}$.
$x^{(j)}$.
10 Efficient embedding of the Drinfeld model
It is useful to compare the formal embedding given by Theorem 9.8 to the one provided by the Drinfeld–Grinberg–Kazhdan theorem. This comparison is done in Theorem 10.2. We first need to recall the construction of the Drinfeld models.
Let ![]() $X \subset {\mathbb A}^N$ be an affine scheme of finite type over a field k, consider a k-rational arc
$X \subset {\mathbb A}^N$ be an affine scheme of finite type over a field k, consider a k-rational arc ![]() $\alpha \in X_{\infty }(k)$ such that
$\alpha \in X_{\infty }(k)$ such that ![]() $\alpha (\eta ) \in X_{\mathrm {sm}}$ and let
$\alpha (\eta ) \in X_{\mathrm {sm}}$ and let ![]() $d := \dim _{\alpha (\eta )}(X)$ and
$d := \dim _{\alpha (\eta )}(X)$ and ![]() $c := N-d$. Let
$c := N-d$. Let ![]() $X^0$ be the irreducible component of X containing
$X^0$ be the irreducible component of X containing ![]() $\alpha (\eta )$ (note that
$\alpha (\eta )$ (note that ![]() $d = \dim X^0$), and let
$d = \dim X^0$), and let ![]() $X' \supset X^0$ be the complete intersection scheme defined by the vanishing of c general linear combinations
$X' \supset X^0$ be the complete intersection scheme defined by the vanishing of c general linear combinations ![]() $p_1, \dotsc , p_c$ of a set of generators of the ideal of
$p_1, \dotsc , p_c$ of a set of generators of the ideal of ![]() $X^0$ in
$X^0$ in ![]() ${\mathbb A}^N$. As explained in [Reference Drinfeld24], the respective inclusions induce isomorphisms
${\mathbb A}^N$. As explained in [Reference Drinfeld24], the respective inclusions induce isomorphisms  $\widehat {\mathcal {O}_{X_{\infty },\alpha }} \simeq \widehat {\mathcal {O}_{X^0_{\infty },\alpha }} \simeq \widehat {\mathcal {O}_{X^{\prime }_{\infty },\alpha }}$ (detailed proofs are given in Lemma 8.6 and [Reference Bourqui and Sebag10, Section 4.2]). Pick coordinates
$\widehat {\mathcal {O}_{X_{\infty },\alpha }} \simeq \widehat {\mathcal {O}_{X^0_{\infty },\alpha }} \simeq \widehat {\mathcal {O}_{X^{\prime }_{\infty },\alpha }}$ (detailed proofs are given in Lemma 8.6 and [Reference Bourqui and Sebag10, Section 4.2]). Pick coordinates ![]() $x_1, \dotsc , x_d, y_1, \dotsc , y_c$ in the ambient affine space
$x_1, \dotsc , x_d, y_1, \dotsc , y_c$ in the ambient affine space ![]() ${\mathbb A}^N$. For a general choice of such coordinates, we can assume that
${\mathbb A}^N$. For a general choice of such coordinates, we can assume that
 $$ \begin{align*} \operatorname{\mathrm{ord}}_\alpha\left( \det\left( \frac {\partial (p_1,\dotsc,p_c)} {\partial (y_1,\dotsc,y_c)} \right) \right) = \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X'}\right) = \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X^0}\right) =: e < \infty. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ord}}_\alpha\left( \det\left( \frac {\partial (p_1,\dotsc,p_c)} {\partial (y_1,\dotsc,y_c)} \right) \right) = \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X'}\right) = \operatorname{\mathrm{ord}}_\alpha\left(\mathrm{Jac}_{X^0}\right) =: e < \infty. \end{align*} $$ Drinfeld defines a specific formal model for  $\widehat {\mathcal O_{X_{\infty },\alpha }}$ depending only on the choices of the coordinates
$\widehat {\mathcal O_{X_{\infty },\alpha }}$ depending only on the choices of the coordinates ![]() $x_i, y_j$, the equations
$x_i, y_j$, the equations ![]() $p_l$ and the order of contact e. Concretely, consider the affine space
$p_l$ and the order of contact e. Concretely, consider the affine space ![]() ${\mathbb A}^{m}$, where
${\mathbb A}^{m}$, where ![]() $m = e(1+2d+c)$. We denote by
$m = e(1+2d+c)$. We denote by ![]() $R[t]_{<n}$ the space of polynomials of degree
$R[t]_{<n}$ the space of polynomials of degree ![]() $< n$ with coefficients in R. Denoting by
$< n$ with coefficients in R. Denoting by ![]() $Q_n$ the scheme representing the functor
$Q_n$ the scheme representing the functor ![]() $R \mapsto t^n + R[t]_{<n}$, the space of monic polynomials of degree n with coefficients in R, we identify
$R \mapsto t^n + R[t]_{<n}$, the space of monic polynomials of degree n with coefficients in R, we identify ![]() ${\mathbb A}^m$ with the product
${\mathbb A}^m$ with the product  $Q_e \times {\mathbb A}^d_{2e-1} \times {\mathbb A}^c_{e-1}$. Under this identification, a k-rational point of
$Q_e \times {\mathbb A}^d_{2e-1} \times {\mathbb A}^c_{e-1}$. Under this identification, a k-rational point of ![]() ${\mathbb A}^m$ corresponds to a triple
${\mathbb A}^m$ corresponds to a triple
In particular, coordinates in ![]() ${\mathbb A}^m$ take the form
${\mathbb A}^m$ take the form  $q^{(n)}, \bar x_i^{(n)}, \bar y_j^{(n)}$. Consider the conditions
$q^{(n)}, \bar x_i^{(n)}, \bar y_j^{(n)}$. Consider the conditions
 $$ \begin{align} \begin{array}{rccl} p_{1}\left(\bar x(t), \bar y(t)\right) \equiv \dotsb \equiv p_{c}\left(\bar x(t), \bar y(t)\right) &\equiv &0 &\mod q(t), \\[6pt] \det\left( \dfrac {\partial (p_1,\dotsc,p_c)} {\partial (y_1,\dotsc,y_c)} \left(\bar x(t), \bar y(t)\right) \right) &\equiv &0 &\mod q(t), \\[6pt] \operatorname{\mathrm{adj}}\left( \dfrac {\partial (p_1,\dotsc,p_c)} {\partial (y_1,\dotsc,y_c)} \left(\bar x(t), \bar y(t)\right) \right) \begin{pmatrix} p_1\left(\bar x(t), \bar y(t)\right)\\ \vdots \\ p_c\left(\bar x(t), \bar y(t)\right) \end{pmatrix} &\equiv & \begin{pmatrix} 0 \\ \vdots \\ 0 \end{pmatrix} &\mod q(t)^2. \\ [2em] \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rccl} p_{1}\left(\bar x(t), \bar y(t)\right) \equiv \dotsb \equiv p_{c}\left(\bar x(t), \bar y(t)\right) &\equiv &0 &\mod q(t), \\[6pt] \det\left( \dfrac {\partial (p_1,\dotsc,p_c)} {\partial (y_1,\dotsc,y_c)} \left(\bar x(t), \bar y(t)\right) \right) &\equiv &0 &\mod q(t), \\[6pt] \operatorname{\mathrm{adj}}\left( \dfrac {\partial (p_1,\dotsc,p_c)} {\partial (y_1,\dotsc,y_c)} \left(\bar x(t), \bar y(t)\right) \right) \begin{pmatrix} p_1\left(\bar x(t), \bar y(t)\right)\\ \vdots \\ p_c\left(\bar x(t), \bar y(t)\right) \end{pmatrix} &\equiv & \begin{pmatrix} 0 \\ \vdots \\ 0 \end{pmatrix} &\mod q(t)^2. \\ [2em] \end{array} \end{align} $$Here ![]() $\operatorname {\mathrm {adj}}(B)$ denotes the classical adjoint of a matrix B. As explained in [Reference Drinfeld24] and [Reference Bourqui and Sebag10, Sections 3.3 and 3.4], the conditions in formula (10a) are polynomial in the coefficients of
$\operatorname {\mathrm {adj}}(B)$ denotes the classical adjoint of a matrix B. As explained in [Reference Drinfeld24] and [Reference Bourqui and Sebag10, Sections 3.3 and 3.4], the conditions in formula (10a) are polynomial in the coefficients of ![]() $q(t), \bar x(t), \bar y(t)$, and therefore they define a finite-type subscheme
$q(t), \bar x(t), \bar y(t)$, and therefore they define a finite-type subscheme ![]() $Z \subset {\mathbb A}^m$.
$Z \subset {\mathbb A}^m$.
Write the arc ![]() $\alpha $ in the coordinates
$\alpha $ in the coordinates ![]() $(x,y)$ of
$(x,y)$ of ![]() ${\mathbb A}^N$ as
${\mathbb A}^N$ as ![]() $\alpha = (a(t), b(t))$, where
$\alpha = (a(t), b(t))$, where ![]() $a(t) \in k[[t]]^d$ and
$a(t) \in k[[t]]^d$ and ![]() $b(t) \in k[[t]]^c$. To
$b(t) \in k[[t]]^c$. To ![]() $\alpha $ we associate the point
$\alpha $ we associate the point ![]() $z = (t^e, \bar a(t), \bar b(t) ) \in Z$ given by
$z = (t^e, \bar a(t), \bar b(t) ) \in Z$ given by
It is shown in [Reference Drinfeld24] that ![]() $\widehat {Z_z}$ gives a (finite-dimensional) formal model for
$\widehat {Z_z}$ gives a (finite-dimensional) formal model for ![]() $\alpha $ – that is,
$\alpha $ – that is,
 $$ \begin{align} \widehat{X_{\infty,\alpha}} \simeq \widehat{Z_z} \hat\times \Delta^{\mathbb N}. \end{align} $$
$$ \begin{align} \widehat{X_{\infty,\alpha}} \simeq \widehat{Z_z} \hat\times \Delta^{\mathbb N}. \end{align} $$ The isomorphism in formula (10c) can be expressed somewhat explicitly in coordinates. We identify ![]() ${\mathbb A}^d_{\infty }$ with an infinite-dimensional affine space
${\mathbb A}^d_{\infty }$ with an infinite-dimensional affine space ![]() ${\mathbb A}^{\mathbb N}$, and we use the notation
${\mathbb A}^{\mathbb N}$, and we use the notation ![]() $\xi (t)$ for points in
$\xi (t)$ for points in ![]() ${\mathbb A}^{\mathbb N}$. Hence coordinates in
${\mathbb A}^{\mathbb N}$. Hence coordinates in ![]() ${\mathbb A}^{\mathbb N}$ take the form
${\mathbb A}^{\mathbb N}$ take the form  $\xi _i^{(n)}$, with
$\xi _i^{(n)}$, with ![]() $1 \le i \le d$ and
$1 \le i \le d$ and ![]() $n \ge 0$. The disk
$n \ge 0$. The disk ![]() $\Delta ^{\mathbb N}$ appearing in formula (10c) is the formal neighbourhood of
$\Delta ^{\mathbb N}$ appearing in formula (10c) is the formal neighbourhood of ![]() $c(t)$ in
$c(t)$ in ![]() ${\mathbb A}^{\mathbb N}$, where
${\mathbb A}^{\mathbb N}$, where ![]() $c(t) := t^{-2e}(a(t))_{\geq 2e}$ is the truncation of
$c(t) := t^{-2e}(a(t))_{\geq 2e}$ is the truncation of ![]() $a(t)$ to degrees
$a(t)$ to degrees ![]() $\geq 2e$ divided by
$\geq 2e$ divided by ![]() $t^{2e}$. Summarising, we have described coordinates
$t^{2e}$. Summarising, we have described coordinates ![]() $(x(t),y(t))$ in
$(x(t),y(t))$ in  $\widehat {X_{\infty ,\alpha }}$ and coordinates
$\widehat {X_{\infty ,\alpha }}$ and coordinates ![]() $ (q(t), \bar x(t), \bar y(t), \xi (t) )$ in
$ (q(t), \bar x(t), \bar y(t), \xi (t) )$ in ![]() $\widehat {Z_z} \hat \times \Delta ^{\mathbb N}$. As explained in [Reference Drinfeld24], the isomorphism in formula (10c) gives the relation
$\widehat {Z_z} \hat \times \Delta ^{\mathbb N}$. As explained in [Reference Drinfeld24], the isomorphism in formula (10c) gives the relation
and we have
We emphasise that these relations hold only at the level of formal neighbourhoods.
Notice that the point ![]() $z \in Z$ depends on the arc
$z \in Z$ depends on the arc ![]() $\alpha $, but the scheme Z depends only on the choices of the coordinates
$\alpha $, but the scheme Z depends only on the choices of the coordinates ![]() $x_i, y_j$, the equations
$x_i, y_j$, the equations ![]() $p_l$ and the order of contact e. The choice of coordinates
$p_l$ and the order of contact e. The choice of coordinates ![]() $x_i,y_j$ also determines the linear projection
$x_i,y_j$ also determines the linear projection ![]() ${\mathbb A}^N \to {\mathbb A}^d$ given by
${\mathbb A}^N \to {\mathbb A}^d$ given by ![]() $(x,y) \mapsto x$, and hence the induced map
$(x,y) \mapsto x$, and hence the induced map ![]() $f \colon X \to {\mathbb A}^d$.
$f \colon X \to {\mathbb A}^d$.
Definition 10.1. With the foregoing notation, we say that ![]() $(Z,z)$ is a Drinfeld model of
$(Z,z)$ is a Drinfeld model of ![]() $X_{\infty }$ at
$X_{\infty }$ at ![]() $\alpha $, and that it is compatible with f.
$\alpha $, and that it is compatible with f.
We are now ready to state and prove our comparison theorem.
Theorem 10.2. Let ![]() $X \subset {\mathbb A}^N$ be an affine scheme of finite type over a perfect field k, let
$X \subset {\mathbb A}^N$ be an affine scheme of finite type over a perfect field k, let ![]() $\alpha \in X_{\infty }(k)$ with
$\alpha \in X_{\infty }(k)$ with ![]() $\alpha (\eta )\in X_{\mathrm {sm}}$ and let
$\alpha (\eta )\in X_{\mathrm {sm}}$ and let ![]() $d:=\dim _{\alpha (\eta )}(X)$. Let
$d:=\dim _{\alpha (\eta )}(X)$. Let ![]() $f \colon X \to Y := {\mathbb A}^d$ be induced by a general linear projection
$f \colon X \to Y := {\mathbb A}^d$ be induced by a general linear projection ![]() ${\mathbb A}^N \to {\mathbb A}^d$ and let
${\mathbb A}^N \to {\mathbb A}^d$ and let ![]() $\beta :=f_{\infty }(\alpha )$. Let
$\beta :=f_{\infty }(\alpha )$. Let ![]() $(Z,z)$ be a Drinfeld model compatible with f, and let
$(Z,z)$ be a Drinfeld model compatible with f, and let  $\widehat {X_{\infty ,\alpha }} \simeq \widehat {Z_z} \hat \times \Delta ^{\mathbb N}$ be the corresponding DGK decomposition.
$\widehat {X_{\infty ,\alpha }} \simeq \widehat {Z_z} \hat \times \Delta ^{\mathbb N}$ be the corresponding DGK decomposition.
1. The composition map
is the completion of a morphism $$ \begin{align*} \widehat{Z_z} \hat\times \Delta^{\mathbb N} \xrightarrow{\sim} \widehat{X_{\infty,\alpha} } \hookrightarrow \widehat{Y_{\infty,\beta}} \end{align*} $$
$$ \begin{align*} \widehat{Z_z} \hat\times \Delta^{\mathbb N} \xrightarrow{\sim} \widehat{X_{\infty,\alpha} } \hookrightarrow \widehat{Y_{\infty,\beta}} \end{align*} $$ $g\colon Z \times {\mathbb A}^{\mathbb N} \to Y_{\infty }$.
$g\colon Z \times {\mathbb A}^{\mathbb N} \to Y_{\infty }$.2. If
 $X^0 \subset X$ is the irreducible component of containing
$X^0 \subset X$ is the irreducible component of containing  $\alpha (\eta )$ and
$\alpha (\eta )$ and  $e := \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} )$, then the composition map is an efficient formal embedding. Moreover, at the level of associated graded rings, we have that
$e := \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_{X^0} )$, then the composition map is an efficient formal embedding. Moreover, at the level of associated graded rings, we have that $$ \begin{align*} \widehat{Z_z} \hookrightarrow \widehat{Z_z} \hat\times \Delta^{\mathbb N} \xrightarrow{\sim} \widehat{X_{\infty,\alpha} }\hookrightarrow \widehat{Y_{\infty,\beta}} \twoheadrightarrow \widehat{Y_{2e-1,\beta_{2e-1}}} \end{align*} $$
$$ \begin{align*} \widehat{Z_z} \hookrightarrow \widehat{Z_z} \hat\times \Delta^{\mathbb N} \xrightarrow{\sim} \widehat{X_{\infty,\alpha} }\hookrightarrow \widehat{Y_{\infty,\beta}} \twoheadrightarrow \widehat{Y_{2e-1,\beta_{2e-1}}} \end{align*} $$ $$ \begin{align*} \operatorname{\mathrm{gr}}\left(\mathcal{O}_{Z,z}\right)=\operatorname{\mathrm{Im}}\left(\operatorname{\mathrm{gr}}\left(\mathcal{O}_{Y_{2e-1},\beta_{2e-1}}\right)\to \operatorname{\mathrm{gr}}\left(\mathcal{O}_{X_{\infty},\alpha}\right)\right). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}\left(\mathcal{O}_{Z,z}\right)=\operatorname{\mathrm{Im}}\left(\operatorname{\mathrm{gr}}\left(\mathcal{O}_{Y_{2e-1},\beta_{2e-1}}\right)\to \operatorname{\mathrm{gr}}\left(\mathcal{O}_{X_{\infty},\alpha}\right)\right). \end{align*} $$
Proof. We use the notation introduced at the beginning of the section. In particular: we have coordinates ![]() $(x, y)$ in
$(x, y)$ in ![]() ${\mathbb A}^N$ such that the projection
${\mathbb A}^N$ such that the projection ![]() ${\mathbb A}^N \to Y$ is given by
${\mathbb A}^N \to Y$ is given by ![]() $(x,y) \mapsto x$; we write
$(x,y) \mapsto x$; we write ![]() $\alpha = (a(t), b(t))$, so
$\alpha = (a(t), b(t))$, so ![]() $\beta = f_{\infty }(\alpha ) = a(t)$; we have a space
$\beta = f_{\infty }(\alpha ) = a(t)$; we have a space ![]() ${\mathbb A}^m$ with coordinates
${\mathbb A}^m$ with coordinates ![]() $ (q(t), \bar x(t), \bar y(t) )$, and
$ (q(t), \bar x(t), \bar y(t) )$, and ![]() $Z \subset {\mathbb A}^m$ is defined by the conditions in formula (10a); the point
$Z \subset {\mathbb A}^m$ is defined by the conditions in formula (10a); the point ![]() $z \in Z$ is given by
$z \in Z$ is given by ![]() $z = (t^e, \bar a(x), \bar b(x) )$ as in formula (10b); the formal scheme
$z = (t^e, \bar a(x), \bar b(x) )$ as in formula (10b); the formal scheme ![]() $\widehat {Z_z} \hat \times \Delta ^{\mathbb N}$ is contained in the completion of
$\widehat {Z_z} \hat \times \Delta ^{\mathbb N}$ is contained in the completion of ![]() ${\mathbb A}^m \times {\mathbb A}^{\mathbb N}$ at
${\mathbb A}^m \times {\mathbb A}^{\mathbb N}$ at ![]() $(z,c(t))$, where
$(z,c(t))$, where ![]() $c(t) = t^{-2e}(a(t))_{\geq 2e}$; and the coordinates in this affine space have the form
$c(t) = t^{-2e}(a(t))_{\geq 2e}$; and the coordinates in this affine space have the form ![]() $ (q(t), \bar x(t), \bar y(t), \xi (t) )$.
$ (q(t), \bar x(t), \bar y(t), \xi (t) )$.
We define a map ![]() ${\mathbb A}^m \times {\mathbb A}^{\mathbb N} \to Y_{\infty }$ via
${\mathbb A}^m \times {\mathbb A}^{\mathbb N} \to Y_{\infty }$ via
and we let ![]() $g \colon Z \times {\mathbb A}^{\mathbb N} \to Y_{\infty }$ be the restriction. It is clear from the discussion surrounding formula (10d) that the completion of g gives the composition of
$g \colon Z \times {\mathbb A}^{\mathbb N} \to Y_{\infty }$ be the restriction. It is clear from the discussion surrounding formula (10d) that the completion of g gives the composition of 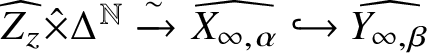 $\widehat {Z_z} \hat \times \Delta ^{\mathbb N} \xrightarrow {\sim } \widehat {X_{\infty ,\alpha } } \hookrightarrow \widehat {Y_{\infty ,\beta }}$, and the first statement of the theorem follows.
$\widehat {Z_z} \hat \times \Delta ^{\mathbb N} \xrightarrow {\sim } \widehat {X_{\infty ,\alpha } } \hookrightarrow \widehat {Y_{\infty ,\beta }}$, and the first statement of the theorem follows.
We compute the tangent map of g explicitly. With a small abuse of notation where coordinates of elements and coordinate functions are written in the same way, we denote a tangent vector on ![]() $Z \times {\mathbb A}^{\mathbb N}$ based at a point
$Z \times {\mathbb A}^{\mathbb N}$ based at a point ![]() $(z,c(t)) = (t^e, \bar a(t), \bar b(t), c(t) )$ by
$(z,c(t)) = (t^e, \bar a(t), \bar b(t), c(t) )$ by
where ![]() $dq(t) \in k[t]_{<e}$,
$dq(t) \in k[t]_{<e}$, ![]() $d{\bar x}(t) \in (k[t]_{<2e} )^d$,
$d{\bar x}(t) \in (k[t]_{<2e} )^d$, ![]() $d{\bar y}(t) \in (k[t]_{<e} )^c$,
$d{\bar y}(t) \in (k[t]_{<e} )^c$, ![]() $d\xi (t) \in k[t]^d$ and
$d\xi (t) \in k[t]^d$ and ![]() $\epsilon ^2 = 0$. The image of such a tangent vector under g is given by
$\epsilon ^2 = 0$. The image of such a tangent vector under g is given by
 $$ \begin{align*} \left(t^e + dq(t)\epsilon\right)^2 &\big(c(t) + d\xi(t) \epsilon\big) + \big(\bar x(t) + d{\bar x}(t) \epsilon\big) \\ & \quad\qquad = \big(t^{2e} c(t) + \bar x(t)\big) + \left(d{\bar x}(t) + d\xi(t)t^{2e} + 2c(t)dq(t)t^e\right) \epsilon \\ & \quad\qquad = a(t) + \left(d{\bar x}(t) + d\xi(t)t^{2e} + 2c(t)dq(t)t^e\right) \epsilon. \end{align*} $$
$$ \begin{align*} \left(t^e + dq(t)\epsilon\right)^2 &\big(c(t) + d\xi(t) \epsilon\big) + \big(\bar x(t) + d{\bar x}(t) \epsilon\big) \\ & \quad\qquad = \big(t^{2e} c(t) + \bar x(t)\big) + \left(d{\bar x}(t) + d\xi(t)t^{2e} + 2c(t)dq(t)t^e\right) \epsilon \\ & \quad\qquad = a(t) + \left(d{\bar x}(t) + d\xi(t)t^{2e} + 2c(t)dq(t)t^e\right) \epsilon. \end{align*} $$In other words, the tangent map of g at ![]() $(z,c(t))$ is given by
$(z,c(t))$ is given by
or, in coordinates – recall that ![]() $c(t) = t^{-2e}(a(t))_{\geq 2e}$ – by
$c(t) = t^{-2e}(a(t))_{\geq 2e}$ – by
 $$ \begin{align*} dx_i^{(n)} = \begin{cases} d{\bar x}_i^{(n)} & \text{if }n<e, \\ d{\bar x}_i^{(n)} + 2 \sum_{k+l=n-e} a_i^{(k+2e)}dq^{(l)} & \text{if }e \leq n<2e, \\ d\xi_i^{(n-2e)} + 2 \sum_{k+l=n-e} a_i^{(k+2e)}dq^{(l)} & \text{if }n \geq 2e. \end{cases} \end{align*} $$
$$ \begin{align*} dx_i^{(n)} = \begin{cases} d{\bar x}_i^{(n)} & \text{if }n<e, \\ d{\bar x}_i^{(n)} + 2 \sum_{k+l=n-e} a_i^{(k+2e)}dq^{(l)} & \text{if }e \leq n<2e, \\ d\xi_i^{(n-2e)} + 2 \sum_{k+l=n-e} a_i^{(k+2e)}dq^{(l)} & \text{if }n \geq 2e. \end{cases} \end{align*} $$From this we see that g induces a surjective map between associated graded rings
 $$ \begin{align*} \varphi \colon k\left[ dx^{(n)}_i \middle\vert \begin{smallmatrix} n\in{\mathbb N} \\ 1 \leq i \leq d \end{smallmatrix} \right] \simeq \operatorname{\mathrm{gr}}\left(\mathcal{O}_{Y_{\infty},\beta}\right) \longrightarrow \operatorname{\mathrm{gr}}\left(\mathcal{O}_{Z,z}\right) \otimes_k k\left[ d\xi^{(m)}_i \middle\vert \begin{smallmatrix} m\in{\mathbb N} \\ 1 \leq i \leq d \end{smallmatrix} \right]. \end{align*} $$
$$ \begin{align*} \varphi \colon k\left[ dx^{(n)}_i \middle\vert \begin{smallmatrix} n\in{\mathbb N} \\ 1 \leq i \leq d \end{smallmatrix} \right] \simeq \operatorname{\mathrm{gr}}\left(\mathcal{O}_{Y_{\infty},\beta}\right) \longrightarrow \operatorname{\mathrm{gr}}\left(\mathcal{O}_{Z,z}\right) \otimes_k k\left[ d\xi^{(m)}_i \middle\vert \begin{smallmatrix} m\in{\mathbb N} \\ 1 \leq i \leq d \end{smallmatrix} \right]. \end{align*} $$We have a commutative diagram

where ![]() $\lambda $ is the
$\lambda $ is the ![]() $\operatorname {\mathrm {gr}} (\mathcal {O}_{Z,z} )$-linear map given by
$\operatorname {\mathrm {gr}} (\mathcal {O}_{Z,z} )$-linear map given by
 $$ \begin{align*} d\xi^{(m)}_{i} \mapsto d\xi^{(m)}_{i} - 2\sum_{k+l=m-e} a_i^{(k+2e)}dq^{(l)}, \end{align*} $$
$$ \begin{align*} d\xi^{(m)}_{i} \mapsto d\xi^{(m)}_{i} - 2\sum_{k+l=m-e} a_i^{(k+2e)}dq^{(l)}, \end{align*} $$![]() $\mu $ is given by
$\mu $ is given by  $dx_i^{(n)} \mapsto d\xi _i^{(n-2e)}$ for
$dx_i^{(n)} \mapsto d\xi _i^{(n-2e)}$ for ![]() $n \ge 2e$ and
$n \ge 2e$ and ![]() $\psi $ agrees with the map
$\psi $ agrees with the map ![]() $\operatorname {\mathrm {gr}} (\mathcal {O}_{Y_{2e-1},\beta _{2e-1}} ) \to \operatorname {\mathrm {gr}} (\mathcal {O}_{Z,z} )$ induced by the composition
$\operatorname {\mathrm {gr}} (\mathcal {O}_{Y_{2e-1},\beta _{2e-1}} ) \to \operatorname {\mathrm {gr}} (\mathcal {O}_{Z,z} )$ induced by the composition
which is given by
The map ![]() $\lambda $ is invertible, and by Theorem 8.1, the map
$\lambda $ is invertible, and by Theorem 8.1, the map ![]() $\varphi $ is surjective, and thus
$\varphi $ is surjective, and thus ![]() $\psi $ is surjective as well. This implies that
$\psi $ is surjective as well. This implies that
and hence the last assertion follows. For the first part of (2), the fact that ![]() $\psi $ is surjective implies that the map induced on completions
$\psi $ is surjective implies that the map induced on completions  $\widehat {O_{Y_{2e-1},\beta _{2e-1}}}\to \widehat {\mathcal {O}_{Z,z}}$ is surjective as well. The fact that this is an efficient embedding follows from the injectivity of the corresponding tangent map.
$\widehat {O_{Y_{2e-1},\beta _{2e-1}}}\to \widehat {\mathcal {O}_{Z,z}}$ is surjective as well. The fact that this is an efficient embedding follows from the injectivity of the corresponding tangent map.
11 Applications to Mather–Jacobian discrepancies
Throughout this section, let X be a variety over a field k of characteristic ![]() $0$.
$0$.
Given a prime divisor E on a normal birational model ![]() $f \colon Y \to X$, we define the Mather discrepancy
$f \colon Y \to X$, we define the Mather discrepancy  $\widehat {k}_E := \operatorname {\mathrm {ord}}_E (\mathrm {Jac}_f)$ and the Mather–Jacobian discrepancy (or simply Jacobian discrepancy)
$\widehat {k}_E := \operatorname {\mathrm {ord}}_E (\mathrm {Jac}_f)$ and the Mather–Jacobian discrepancy (or simply Jacobian discrepancy)  $k^{\mathrm {MJ}}_E := \widehat {k}_E - \operatorname {\mathrm {ord}}_E(\mathrm {Jac}_X)$ of E over X. Note that these definitions depend only on the valuation
$k^{\mathrm {MJ}}_E := \widehat {k}_E - \operatorname {\mathrm {ord}}_E(\mathrm {Jac}_X)$ of E over X. Note that these definitions depend only on the valuation ![]() $\operatorname {\mathrm {ord}}_E$ defined by E and not by the particular model chosen. The definition extends to any divisorial valuation
$\operatorname {\mathrm {ord}}_E$ defined by E and not by the particular model chosen. The definition extends to any divisorial valuation ![]() $v = q \operatorname {\mathrm {ord}}_E$, where q is a positive integer, by setting
$v = q \operatorname {\mathrm {ord}}_E$, where q is a positive integer, by setting ![]() $\widehat {k}_v := q\widehat {k}_E$ and
$\widehat {k}_v := q\widehat {k}_E$ and  $k^{\mathrm {MJ}}_v := q k^{\mathrm {MJ}}_E$. When X is smooth, both discrepancies agree with the usual discrepancy of E over X. We say that X is MJ-terminal if
$k^{\mathrm {MJ}}_v := q k^{\mathrm {MJ}}_E$. When X is smooth, both discrepancies agree with the usual discrepancy of E over X. We say that X is MJ-terminal if  $k^{\mathrm {MJ}}_E> 0$ whenever E is exceptional over X. As proved in [Reference Ishii34, Reference de Fernex and Docampo20], this condition is equivalent to the condition that if
$k^{\mathrm {MJ}}_E> 0$ whenever E is exceptional over X. As proved in [Reference Ishii34, Reference de Fernex and Docampo20], this condition is equivalent to the condition that if ![]() $X \subset Y$ is a closed embedding with Y smooth and
$X \subset Y$ is a closed embedding with Y smooth and ![]() $c = \operatorname {\mathrm {codim}}(X,Y)$, then for any closed subset
$c = \operatorname {\mathrm {codim}}(X,Y)$, then for any closed subset ![]() $T \subsetneq X$ the pair
$T \subsetneq X$ the pair ![]() $(Y,cX)$ has minimal log discrepancy
$(Y,cX)$ has minimal log discrepancy ![]() $\operatorname {\mathrm {mld}}_T(Y,cX)> 1$. We refer to [Reference de Fernex, Ein and Ishii22, Reference Ishii34, Reference de Fernex and Docampo20, Reference Ein and Ishii26] for general studies related to these invariants.
$\operatorname {\mathrm {mld}}_T(Y,cX)> 1$. We refer to [Reference de Fernex, Ein and Ishii22, Reference Ishii34, Reference de Fernex and Docampo20, Reference Ein and Ishii26] for general studies related to these invariants.
The results of this article, together with a theorem from [Reference de Fernex and Docampo21], yield a new proof of the following theorem of Mourtada and Reguera:
Theorem 11.1 [Reference Mourtada and Reguera37, Theorem 4.1]
With the foregoing notation, let ![]() $\alpha \in X_{\infty }$ be the maximal arc defining a given divisorial valuation
$\alpha \in X_{\infty }$ be the maximal arc defining a given divisorial valuation ![]() $q\operatorname {\mathrm {ord}}_E$ (that is, such that
$q\operatorname {\mathrm {ord}}_E$ (that is, such that ![]() $\operatorname {\mathrm {ord}}_\alpha = q\operatorname {\mathrm {ord}}_E$). Then
$\operatorname {\mathrm {ord}}_\alpha = q\operatorname {\mathrm {ord}}_E$). Then 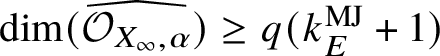 $\dim (\widehat {\mathcal {O}_{X_{\infty },\alpha }} ) \ge q (k_E^{\mathrm {MJ}} + 1 )$.
$\dim (\widehat {\mathcal {O}_{X_{\infty },\alpha }} ) \ge q (k_E^{\mathrm {MJ}} + 1 )$.
Proof. We have 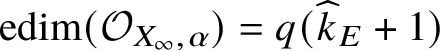 $\mathrm {edim} (\mathcal {O}_{X_{\infty },\alpha } ) = q (\widehat {k}_E+1 )$ by [Reference de Fernex and Docampo21, Theorem 11.4], and Theorem 8.5 gives us
$\mathrm {edim} (\mathcal {O}_{X_{\infty },\alpha } ) = q (\widehat {k}_E+1 )$ by [Reference de Fernex and Docampo21, Theorem 11.4], and Theorem 8.5 gives us ![]() $\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) \le \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_X)$. It follows then by Proposition 7.4 and Corollary 7.5 that
$\mathrm {ecodim} (\mathcal {O}_{X_{\infty },\alpha } ) \le \operatorname {\mathrm {ord}}_\alpha (\mathrm {Jac}_X)$. It follows then by Proposition 7.4 and Corollary 7.5 that
 $$ \begin{align*} \dim\left(\widehat{\mathcal{O}_{X_{\infty},\alpha}}\right) = \mathrm{edim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) - \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) \ge q \left(k_E^{\mathrm{MJ}} + 1\right).\\[-40pt] \end{align*} $$
$$ \begin{align*} \dim\left(\widehat{\mathcal{O}_{X_{\infty},\alpha}}\right) = \mathrm{edim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) - \mathrm{ecodim}\left(\mathcal{O}_{X_{\infty},\alpha}\right) \ge q \left(k_E^{\mathrm{MJ}} + 1\right).\\[-40pt] \end{align*} $$ Assume now that X is an affine toric variety. To fix notation, let T be an algebraic k-torus, ![]() $N := \operatorname {\mathrm {Hom}}_k({\mathbb G}_m,T)$,
$N := \operatorname {\mathrm {Hom}}_k({\mathbb G}_m,T)$, ![]() $M := \operatorname {\mathrm {Hom}}_{\mathbb Z}(M,{\mathbb Z})$,
$M := \operatorname {\mathrm {Hom}}_{\mathbb Z}(M,{\mathbb Z})$, ![]() $\sigma \subset N_{\mathbb R}$ a rational convex cone and
$\sigma \subset N_{\mathbb R}$ a rational convex cone and ![]() $X := \operatorname {\mathrm {Spec}} k[\sigma ^\vee \cap M]$. Note that every
$X := \operatorname {\mathrm {Spec}} k[\sigma ^\vee \cap M]$. Note that every ![]() $v \in \sigma \cap N$ defines a T-invariant divisorial valuation on X.
$v \in \sigma \cap N$ defines a T-invariant divisorial valuation on X.
In their recent article [Reference Bourqui and Sebag13], Bourqui and Sebag study DGK decompositions of ![]() $X_{\infty }$ at arcs that are not fully contained in the T-invariant divisor of X. The focus is on the open set
$X_{\infty }$ at arcs that are not fully contained in the T-invariant divisor of X. The focus is on the open set ![]() $X_{\infty }^\circ \subset X_{\infty }$ consisting of those arcs whose generic point is in T. They prove that for any
$X_{\infty }^\circ \subset X_{\infty }$ consisting of those arcs whose generic point is in T. They prove that for any ![]() $\alpha \in X_{\infty }^\circ $, the local ring
$\alpha \in X_{\infty }^\circ $, the local ring ![]() $\mathcal {O}_{X_{\infty },\alpha }$ depends only on the associated valuation
$\mathcal {O}_{X_{\infty },\alpha }$ depends only on the associated valuation ![]() $\operatorname {\mathrm {ord}}_\alpha $, and in particular so does the minimal formal model [Reference Bourqui and Sebag13, Corollary 3.3]. In particular, if we set
$\operatorname {\mathrm {ord}}_\alpha $, and in particular so does the minimal formal model [Reference Bourqui and Sebag13, Corollary 3.3]. In particular, if we set
 $$ \begin{align*} X_{\infty,v}^\circ := \left\{ \alpha \in X_{\infty}^\circ \mid \operatorname{\mathrm{ord}}_\alpha = v \right\}, \end{align*} $$
$$ \begin{align*} X_{\infty,v}^\circ := \left\{ \alpha \in X_{\infty}^\circ \mid \operatorname{\mathrm{ord}}_\alpha = v \right\}, \end{align*} $$then we can denote by ![]() $\mathcal {Z}^{\min }_v$ the minimal formal model of
$\mathcal {Z}^{\min }_v$ the minimal formal model of ![]() $X_{\infty }$ at any arc
$X_{\infty }$ at any arc ![]() $\alpha \in X_{\infty ,v}^\circ $.
$\alpha \in X_{\infty ,v}^\circ $.
The next theorem is one of the main results of [Reference Bourqui and Sebag13]. A similar, more general property is proved for elements v satisfying a certain property called ![]() $\mathcal {P}_v$; we refer to the original source for the precise statement.
$\mathcal {P}_v$; we refer to the original source for the precise statement.
Theorem 11.2 [Reference Bourqui and Sebag13, Corollary 6.4]
With the foregoing notation, if v is indecomposable in ![]() $\sigma \cap N$, then the associated minimal formal model
$\sigma \cap N$, then the associated minimal formal model ![]() $\mathcal {Z}^{\min }_v$ has
$\mathcal {Z}^{\min }_v$ has ![]() $\dim (\mathcal {Z}^{\min }_v ) = 0$ and
$\dim (\mathcal {Z}^{\min }_v ) = 0$ and  $\mathrm {edim} (\mathcal {Z}^{\min }_v ) = \widehat {k}_v$.
$\mathrm {edim} (\mathcal {Z}^{\min }_v ) = \widehat {k}_v$.
Indecomposable elements ![]() $v \in \sigma \cap N$ are characterised by the property that their centres on any resolution of singularity of X are irreducible components of codimension
$v \in \sigma \cap N$ are characterised by the property that their centres on any resolution of singularity of X are irreducible components of codimension ![]() $1$ of the exceptional locus [Reference Bourqui and Sebag13, Theorem 2.7]. In the terminology of the Nash problem, these form a particular class of essential valuations. By combining Theorem 11.2 with our results, we obtain the following corollary:
$1$ of the exceptional locus [Reference Bourqui and Sebag13, Theorem 2.7]. In the terminology of the Nash problem, these form a particular class of essential valuations. By combining Theorem 11.2 with our results, we obtain the following corollary:
Corollary 11.3. Let ![]() $X = \operatorname {\mathrm {Spec}} k[\sigma ^\vee \cap M]$ be an affine toric variety.
$X = \operatorname {\mathrm {Spec}} k[\sigma ^\vee \cap M]$ be an affine toric variety.
1. For any indecomposable element
 $v \in \sigma \cap N$, we have
$v \in \sigma \cap N$, we have  $k^{\mathrm {MJ}}_v \le 0$.
$k^{\mathrm {MJ}}_v \le 0$.2. If X is singular and
 ${\mathbb Q}$-factorial, then X is not MJ-terminal.
${\mathbb Q}$-factorial, then X is not MJ-terminal.
Proof. Part (1) follows immediately from Theorems 11.2 and 9.4, and (2) follows from (1) and the observation that if X is singular and ![]() ${\mathbb Q}$-factorial, then
${\mathbb Q}$-factorial, then ![]() $\sigma \cap N$ necessarily contains an exceptional indecomposable element. This is just because the exceptional locus of any resolution of singularity of a
$\sigma \cap N$ necessarily contains an exceptional indecomposable element. This is just because the exceptional locus of any resolution of singularity of a ![]() ${\mathbb Q}$-factorial variety always has pure codimension
${\mathbb Q}$-factorial variety always has pure codimension ![]() $1$, and the set of essential (toric) valuations is nonempty if X is singular.
$1$, and the set of essential (toric) valuations is nonempty if X is singular.
Acknowledgments
We wish to thank Herwig Hauser, Mel Hochster, Hiraku Kawanoue, François Loeser, Mircea Mustaţă and Karl Schwede for useful comments and discussions. We are also very grateful to the referee for their careful reading of the paper and their valuable comments and remarks.
The research of the first author was partially supported by the Austrian Science Fund project P31338 and by NWO Vici grant 639.033.514. The research of the second author was partially supported by NSF grants DMS-1700769 and DMS-2001254, and by NSF grant DMS-1440140 while in residence at MSRI in Berkeley during the spring 2019 semester. The research of the third author was partially supported by a grant from the Simons Foundation (638459, RD).
Conflicts of interest
None.











