No CrossRef data available.
Article contents
SIMPLICITY CRITERIA FOR RINGS OF DIFFERENTIAL OPERATORS
Part of:
Rings and algebras arising under various constructions
Surfaces and higher-dimensional varieties
Differential algebra
Modules, bimodules and ideals
Local theory
Published online by Cambridge University Press: 11 May 2021
Abstract
Let K be a field of arbitrary characteristic,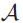 
$${\cal A}$$
be a commutative K-algebra which is a domain of essentially finite type (e.g., the algebra of functions on an irreducible affine algebraic variety), 
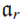$${a_r}$$
be its Jacobian ideal, and 
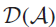$${\cal D}\left( {\cal A} \right)$$
be the algebra of differential operators on the algebra
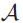$${\cal A}$$
. The aim of the paper is to give a simplicity criterion for the algebra
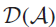$${\cal D}\left( {\cal A} \right)$$
: the algebra
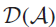$${\cal D}\left( {\cal A} \right)$$
is simple iff
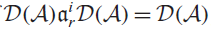$${\cal D}\left( {\cal A} \right)a_r^i{\cal D}\left( {\cal A} \right) = {\cal D}\left( {\cal A} \right)$$
for all i ≥ 1 provided the field K is a perfect field. Furthermore, a simplicity criterion is given for the algebra 
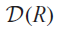$${\cal D}\left( R \right)$$
of differential operators on an arbitrary commutative algebra R over an arbitrary field. This gives an answer to an old question to find a simplicity criterion for algebras of differential operators.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
Bavula, V. V., Generalized Weyl algebras and their representations, (Russian) Algebra i Analiz
, 4(1) (1992), 75–97; translation in St. Petersburg Math. J. 4(1) (1993), 71–92.Google Scholar
Bavula, V. V., Dimension, multiplicity, holonomic modules, and an analogue of the inequality of Bernstein for rings of differential operators in prime characteristic, Represent. Theory, 13 (2009), 182–227.CrossRefGoogle Scholar
Bavula, V. V., Generators and defining relations for the ring of differential operators on a smooth algebraic variety, Algebras Represent. Theory, 13 (2010), 159–187.CrossRefGoogle Scholar
Bavula, V. V., Generators and defining relations for ring of differential operators on smooth algebraic variety in prime characteristic, J. Algebra 323 (2010), 1036–1051.CrossRefGoogle Scholar
Chamarie, M. and Stafford, J. T., When rings of differential operators are maximal orders, Math. Proc. Camb. Phil. Soc. 102 (1987), 399–410.CrossRefGoogle Scholar
Eisenbud, D., Commutative algebra. With a view toward algebraic geometry, Graduate Texts in Mathematics, vol. 150 (Springer-Verlag, New York, 1995).Google Scholar
Eriksen, E., Differential operators on monomial curves, J. Algebra 264(1) (2003), 186–198.CrossRefGoogle Scholar
McConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings. With the cooperation of L. W. Small. Revised edition, Graduate Studies in Mathematics, vol. 30 (American Mathematical Society, Providence, RI, 2001).CrossRefGoogle Scholar
Musson, I. M., Some rings of differential operators which are Morita equivalent to the Weyl algebra A 1, Proc. Amer. Math. Soc. 98(1) (1986), 29–30.Google Scholar
Smith, S. P. and Stafford, J. T., Differential operators on an affine curve. Proc. London Math. Soc. 56(2) (1988), 229–259.CrossRefGoogle Scholar