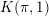 $K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements
$K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements
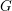 $G$-BASES
$G$-BASES
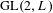 $\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF
$\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF 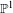 $\mathbb{P}^{1}$
$\mathbb{P}^{1}$
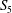 $S_5$ -FIELDS WITH A POWER SAVING ERROR TERM
$S_5$ -FIELDS WITH A POWER SAVING ERROR TERM