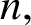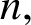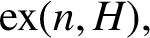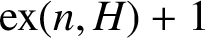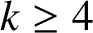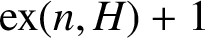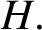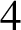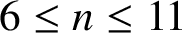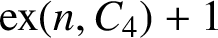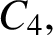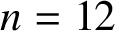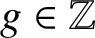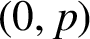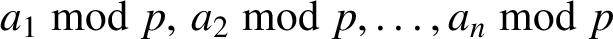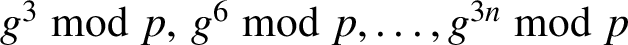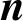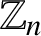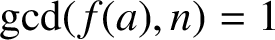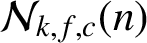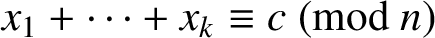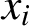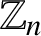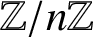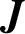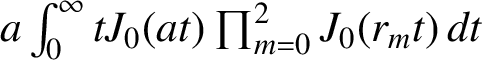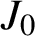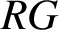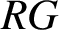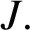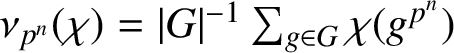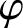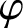Contents
Research Article
ON A PROBLEM OF ERDŐS ABOUT GRAPHS WHOSE SIZE IS THE TURÁN NUMBER PLUS ONE
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2021, pp. 177-187
-
- Article
- Export citation
CUBES IN FINITE FIELDS AND RELATED PERMUTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2021, pp. 188-196
-
- Article
- Export citation
A PROOF OF MERCA’S CONJECTURES ON SUMS OF ODD DIVISOR FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 10 September 2021, pp. 197-201
-
- Article
- Export citation
SUMS OF POLYNOMIAL-TYPE EXCEPTIONAL UNITS MODULO
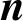 $\boldsymbol {n}$
$\boldsymbol {n}$
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2021, pp. 202-211
-
- Article
- Export citation
A UNIQUE PERFECT POWER DECAGONAL NUMBER
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2021, pp. 212-216
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONSECUTIVE SQUARE-FREE NUMBERS IN PIATETSKI-SHAPIRO SEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 13 September 2021, pp. 217-222
-
- Article
- Export citation
ON AN INTEGRAL OF
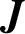 $\boldsymbol {J}$-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE
$\boldsymbol {J}$-BESSEL FUNCTIONS AND ITS APPLICATION TO MAHLER MEASURE
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2021, pp. 223-235
-
- Article
- Export citation
HEDGEHOGS IN LEHMER’S PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 07 September 2021, pp. 236-242
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON GROUP RINGS WITH TRIVIAL UNITS
- Part of:
-
- Published online by Cambridge University Press:
- 19 July 2021, pp. 243-247
-
- Article
- Export citation
EVERY GRADED IDEAL OF A LEAVITT PATH ALGEBRA IS GRADED ISOMORPHIC TO A LEAVITT PATH ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 23 August 2021, pp. 248-256
-
- Article
- Export citation
A GENERALISATION OF HIGHER-RANK GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 26 July 2021, pp. 257-266
-
- Article
- Export citation
ON HIGHER FROBENIUS–SCHUR INDICATORS
- Part of:
-
- Published online by Cambridge University Press:
- 12 July 2021, pp. 267-277
-
- Article
- Export citation
ON CERTAIN PRODUCTS OF PERMUTABLE SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 16 August 2021, pp. 278-285
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GROUPS WHOSE SUBGROUPS ARE EITHER MODULAR OR CONTRANORMAL
- Part of:
-
- Published online by Cambridge University Press:
- 18 June 2021, pp. 286-295
-
- Article
- Export citation
A FAMILY OF
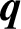 $\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
- Part of:
-
- Published online by Cambridge University Press:
- 03 September 2021, pp. 296-302
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON
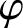 $\varphi $-AMENABILITY OF DUAL BANACH ALGEBRAS
$\varphi $-AMENABILITY OF DUAL BANACH ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2021, pp. 303-313
-
- Article
- Export citation
APPROXIMATELY MULTIPLICATIVE DECOMPOSITIONS OF NUCLEAR MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 26 July 2021, pp. 314-322
-
- Article
- Export citation
MANY FINITE-DIMENSIONAL LIFTING BUNDLE GERBES ARE TORSION
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2021, pp. 323-338
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
INTERACTING QUARTER-PLANE LATTICE WALK PROBLEMS: SOLUTIONS AND PROOFS
- Part of:
-
- Published online by Cambridge University Press:
- 05 November 2021, pp. 339-340
-
- Article
-
- You have access
- HTML
- Export citation
ON MAXIMAL SUBGROUPS OF IDEMPOTENT-GENERATED SEMIGROUPS ASSOCIATED WITH BIORDERED SETS
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2022, pp. 341-343
-
- Article
-
- You have access
- HTML
- Export citation