Hostname: page-component-7bb8b95d7b-wpx69 Total loading time: 0 Render date: 2024-09-17T18:37:34.531Z Has data issue: false hasContentIssue false
  • English
  • Français

On one-sided boundedness of normed partial sums

Published online by Cambridge University Press:  17 April 2009

R. A. Maller
R. A. Maller
Affiliation:
Division of Mathematics and Statistics, CSIRO, Private Bag, PO Wembley, Western Australia 6014, Australia.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper gives a very general sufficient condition for the existence of constants B(n), C(n) for which either 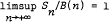almost surely or 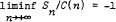almost surely, where Sn = X1 + X2 + … + Xn and Xi are independent and identically distributed random variables. The theorem is closely connected with results of Klass and Teicher on the one-sided boundedness of Sn, with the relative stability of Sn, and with a generalised law of the iterated logarithm due to Kesten. For non negative Xi the sufficient condition is shown to be necessary, and the results are partially generalised to the case when Xi form a stationary m-dependent sequence. Some connections with a generalised type of regular variation and with domains of partial attraction are also noted.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 21 , Issue 3 , June 1980 , pp. 373 - 391
Copyright
Copyright © Australian Mathematical Society 1980

References

[1]Chow, Y.S. and Robbins, Herbert, “On sums of independent random variables with infinite moments and ‘fair’ games”, Proc. Nat. Acad. Sci. 47 (1961), 330–335.CrossRefGoogle ScholarPubMed
[2]Feller, William, An introduction to probability theory and its applications. Volume II, second edition (John Wiley & Sons, New York, London, Sydney, 1971).Google Scholar
[3]Gnedenko, B.V., Kolmogorov, A.N., Limit distributions for sums of independent random variables, revised edition (translated by Chung, K. L.. Addison-Wesley, Reading, Massachusetts, London; Don Mills, Ontario; 1968).Google Scholar
[4]Hall, Peter, “On the duality between the behaviour of sums of independent random variables and the sums of their squares”, Math. Proc. Cambridge Philos. Soc. 84 (1978), 117–121.CrossRefGoogle Scholar
[5]Heyde, C.C., “A note concerning behaviour of iterated logarithm type”, Proa. Amer. Math. Soc. 23 (1969), 85–90.CrossRefGoogle Scholar
[6]Kesten, Harry, “Sums of independent random variables – without moment conditions”, Arm. Math. Statist. 43 (1972), 701–732.CrossRefGoogle Scholar
[7]Klass, M.J., “Towards a universal law of the iterated logarithm, Part I”, Z. Wahrsch. Verw. Gebiete 36 (1976), 165–178.CrossRefGoogle Scholar
[8]Klass, M.J., “Towards a universal law of the iterated logarithm, Part II”, Z. Wahrsch. Verw. Gebiete 39 (1977), 151–165.CrossRefGoogle Scholar
[9]Klass, Michael and Teicher, Henry, “Iterated logarithm laws for asymmetric random variables barely with or without finite mean”, Ann. Probab. 5 (1977), 861–874.CrossRefGoogle Scholar
[10]Lévy, Paul, Théorie de I'addition des variables alèatoires (Gauthier-Villars, Paris, 1937).Google Scholar
[11]Loève, M., Probability theory I, 4th edition (Graduate Texts in Mathematics, 45. Springer-Verlag, New York, Heidelberg, New York, 1977).Google Scholar
[12]Mailer, R.A., “A note on Karamata's generalised regular variation”, J. Austral. Math. Soc. Ser. A 24 (1977), 141–148.Google Scholar
[13]Mailer, R.A., “Relative stability and the strong law of large numbers”, Z. Wahrsch. Verw. Gebiete 43 (1978), 141–148.CrossRefGoogle Scholar
[14]Mailer, R.A., “Relative stability, characteristic functions and stochastic compactness”, J. Austral. Math. Soc. Ser. A (to appear).Google Scholar
[15]Mailer, R.A., “A note on domains of partial attraction”, Ann. Probab. (to appear).Google Scholar
[16]Maller, R.A., “An extension of Kesten's generalised law of the iterated logarithm”, Bull. Austral. Math. Soc. 21 (1980), 393–406.CrossRefGoogle Scholar
[17]Miller, H.D., “A note on sums of independent random variables with infinite first moment”, Ann. Math. Statist. 38 (1967), 751–758.CrossRefGoogle Scholar
[18]Petrov, V.V., “A generalization of an inequality of Lévy”, Theor. Prob. Appl. 20 (1975), 141–145.CrossRefGoogle Scholar
[19]Pruitt, William E., “General one-sided laws of the iterated logarithm”, Ann. Probab. (to appear).Google Scholar
[20]Rogozin, B.A., “On the existence of exact upper sequences”, Theor. Prob. Appl. 13 (1968), 667–672.CrossRefGoogle Scholar
[21]Rogozin, B.A., “The distribution of the first ladder moment and height and fluctuation of a random walk”, Theor. Prob. Appl. 16 (1971), 575–595.CrossRefGoogle Scholar
[22]Rogozin, B.A., “Relatively stable walks”, Theor. Prob. Appl. 21 (1976), 375–379.CrossRefGoogle Scholar