Article contents
ONE-POINT EXTENSIONS AND LOCAL TOPOLOGICAL PROPERTIES
Published online by Cambridge University Press: 02 August 2012
Abstract
A space 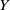 $Y$ is called an extension of a space
$Y$ is called an extension of a space 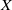 $X$ if
$X$ if 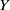 $Y$ contains
$Y$ contains 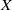 $X$ as a dense subspace. An extension
$X$ as a dense subspace. An extension 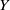 $Y$ of
$Y$ of 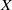 $X$ is called a one-point extension of
$X$ is called a one-point extension of 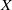 $X$ if
$X$ if 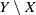 $Y\setminus X$ is a singleton. P. Alexandroff proved that any locally compact non-compact Hausdorff space
$Y\setminus X$ is a singleton. P. Alexandroff proved that any locally compact non-compact Hausdorff space 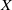 $X$ has a one-point compact Hausdorff extension, called the one-point compactification of
$X$ has a one-point compact Hausdorff extension, called the one-point compactification of 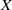 $X$. Motivated by this, Mrówka and Tsai [‘On local topological properties. II’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys.19 (1971), 1035–1040] posed the following more general question: For what pairs of topological properties
$X$. Motivated by this, Mrówka and Tsai [‘On local topological properties. II’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys.19 (1971), 1035–1040] posed the following more general question: For what pairs of topological properties 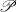 ${\mathscr P}$ and
${\mathscr P}$ and 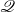 ${\mathscr Q}$ does a locally-
${\mathscr Q}$ does a locally- ${\mathscr P}$ space
${\mathscr P}$ space 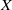 $X$ having
$X$ having 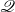 ${\mathscr Q}$ possess a one-point extension having both
${\mathscr Q}$ possess a one-point extension having both 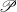 ${\mathscr P}$ and
${\mathscr P}$ and 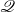 ${\mathscr Q}$? Here, we provide an answer to this old question.
${\mathscr Q}$? Here, we provide an answer to this old question.
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Australian Mathematical Publishing Association Inc.
References
- 7
- Cited by

