Article contents
Best Approximation in Riemannian Geodesic Submanifolds of Positive Definite Matrices
Published online by Cambridge University Press: 20 November 2018
Abstract
We explicitly describe the best approximation in geodesic submanifolds of positive definite matrices obtained from involutive congruence transformations on the Cartan-Hadamard manifold 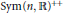 $\text{Sym(}n\text{,}\,\mathbb{R}{{\text{)}}^{++}}$ of positive definite matrices. An explicit calculation for the minimal distance function from the geodesic submanifold
$\text{Sym(}n\text{,}\,\mathbb{R}{{\text{)}}^{++}}$ of positive definite matrices. An explicit calculation for the minimal distance function from the geodesic submanifold 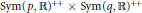 $\text{Sym(}p\text{,}\,\mathbb{R}{{\text{)}}^{++}}\,\times \,\text{Sym(}q\text{,}\,\mathbb{R}{{\text{)}}^{++}}$ block diagonally embedded in
$\text{Sym(}p\text{,}\,\mathbb{R}{{\text{)}}^{++}}\,\times \,\text{Sym(}q\text{,}\,\mathbb{R}{{\text{)}}^{++}}$ block diagonally embedded in 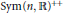 $\text{Sym(}n\text{,}\,\mathbb{R}{{\text{)}}^{++}}$ is given in terms of metric and spectral geometric means, Cayley transform, and Schur complements of positive definite matrices when
$\text{Sym(}n\text{,}\,\mathbb{R}{{\text{)}}^{++}}$ is given in terms of metric and spectral geometric means, Cayley transform, and Schur complements of positive definite matrices when 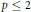 $p\,\le \,2$ or
$p\,\le \,2$ or 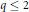 $q\,\le \,2$ .
$q\,\le \,2$ .
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
- 4
- Cited by

