Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-19T22:05:21.142Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactness of Invariant Densities for Families of Expanding, Piecewise Monotonic Transformations

Published online by Cambridge University Press:  20 November 2018

P. Góra  and
A. Boyarsky
P. Góra
Affiliation:
Warsaw University, Warsaw, Poland
A. Boyarsky
Affiliation:
Concordia University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

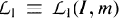Let I = [0,1] and let be the space of all integrable functions on 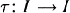I, where m denotes Lebesque measure on I. Let ∥ ∥1 be the ℒ-1-norm and let be a measurable, nonsingular transformation on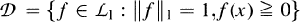 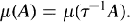I. Let denote the space of densities. The probability measure μ is invariant under τ if for all measurable sets A, The measure 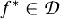μ is absolutely continuous if there exists an such that for any measurable set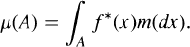 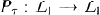A We refer to ƒ* as the invariant density of τ (with respect to m). It is well-known that ƒ * is a fixed point of the Frobenius-Perron operator defined by

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 41 , Issue 5 , 01 October 1989 , pp. 855 - 869
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Boyarsky, A., A matrix method for estimating the Lyapunov exponent of one-dimensional maps, Jour Stat. Physics, 50 (1988), 213–229.Google Scholar
2. Bugiel, P., Approximation of the measure of ergodic transformations of the real line, Z. Wahr. vern Geb. 59 (19828), 27–38.Google Scholar
3. Cornfeld, P, Fomin, S. V. and Ya. Sinai, G., Ergodic theory (Springer-Verlag, 1980).Google Scholar
4. Góra, P., Boyarsky, A.and Proppe, H., Constructive approximations to densities invariant under non-expanding maps, Jour. Stat. Phys. 57 (1988), 179–194.Google Scholar
5. Góra, P. and Schmidt, B., Un example de transformation dilatante et C1 par morceaux de l'intervalle, sans probabilité absolutement continue invariante, preprint.Google Scholar
6. Jablonski, M., Continuity of invariant measure for Rényi's transformations, Zeszyty Nauk. univ. Jagiellonskiego 530 (1979), 51–69.Google Scholar
7. Keller, G., Stochastic stability in some chaotic dynamical systems, Monats. fur Math. 94 (1982), 313–333.Google Scholar
8. Kosyakin, A. A. and Sandler, E. A., Ergodic properties of a class of piecewise-smooth tranformations of a segment, Izv. VUZ Mat. 118 (1972), 32–40. (English translation available from the British Library, Translation Service.)Google Scholar
9. Kowalski, Z. S., Invariant measures for piecewise monotonic transformations, Springer Lecture Notes in Math. 472 (1975), 77–94.Google Scholar
10. Lasota, A.and Mackey, M., Probabilistic properties of deterministic systems (Cambridge Univ. Press, 1985).Google Scholar
11. Lasota, A.and Yorke, J. A., On the existence of invariant measures for piecewise monotonie transformation, Trans. Amer. Math. Soc. 186 (1973), 481–488.Google Scholar
12. Li, T. Y., Finite approximation for the Frobenuis-Perron operator. A solution to Ulam's conjecture, J. Approx. Theory 17 (1976), 177–186.Google Scholar
13. Pianigiani, G., First return map and invariant measure, Israel Jour. Math 1-2 (1980), 32–8.Google Scholar
14. Rychlik, M., Bounded variation and invariant measures, Studia Mathematica, 76 (1983), 69–80.Google Scholar
15. Straube, E., On the existence of invariant, absolutely continuous measures, Comm. Math. Phys. 81 (1981), 27–30.Google Scholar
16. Wagner, G., The ergodic behaviour of piecewise monotonie transformations, Zeit. Wahr. Verw. Geb. 46 (1979), 317–324.Google Scholar
17. Wong, S., Some metric properties of piecewise monotonie mappings of the unit interval, Trans. Amer. Math. Soc. 246 (1978), 493–500.Google Scholar