Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T15:33:31.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Holomorphic Generation of Continuous Inverse Algebras

Published online by Cambridge University Press:  20 November 2018

Harald Biller
Harald Biller*
Affiliation:
Fachbereich Mathematik, Technische Universität Darmstadt, Schlossgartenstr. 7, 64289 Darmstadt, Germany e-mail: harald.biller@gmx.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study complex commutative Banach algebras (and, more generally, continuous inverse algebras) in which the holomorphic functions of a fixed $n$-tuple of elements are dense. In particular, we characterize the compact subsets of 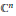${{\mathbb{C}}^{n}}$ which appear as joint spectra of such $n$ -tuples. The characterization is compared with several established notions of holomorphic convexity by means of approximation conditions.

Keywords

46H3032A3832E3041A2046J15holomorphic functional calculuscommutative continuous inverse algebraholomorphic convexityStein compactameromorphic convexityholomorphic approximation
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 1 , 01 February 2007 , pp. 3 - 35
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Arens, R. and Calderón, A. P., Analytic functions of several Banach algebra elements. Ann. of Math. (2) 62(1955), 204–216.Google Scholar
[2] Behnke, H. and Stein, K., Konvergente Folgen von Regularitätsbereichen und die Meromorphiekonvexität, Math. Ann. 116(1938), 204–216.Google Scholar
[3] Biller, Harald, Algebras of complex analytic germs. Preprint 2331, http://wwwbib.mathematik.tu-darmstadt.de/Math-Net/Preprints/Listen/shadow/pp2331.html. Google Scholar
[4] Biller, Harald, Analyticity and naturality of the multi-variable functional calculus. To appear in Expositiones Mathematicae. http://wwwbib.mathematik.tu-darmstadt.de/Math-Net/Preprints/Listen/shadow/pp2332.html. Google Scholar
[5] Biller, Harald, Continuous inverse algebras and infinite-dimensional linear Lie groups, Habilitationsschrift, Technische Universität Darmstadt, 2004, http://www.mathematik.tu-darmstadt.de/∼biller. Google Scholar
[6] Biller, Harald, Continuous inverse algebras with involution, Preprint 2346, http://wwwbib.mathematik.tu-darmstadt.de/Math-Net/Preprints/Listen/shadow/pp2346.html. Google Scholar
[7] Björk, J.-E., Holomorphic convexity and analytic structures in Banach algebras. Ark. Mat. 9(1971), 39–54.Google Scholar
[8] Blackadar, B., K-Theory for Operator Algebras. Second edition. Mathematical Sciences Research Institute Publications 5, Cambridge University Press, Cambridge, 1998.Google Scholar
[9] Bonsall, F. F. and Duncan, J., Complete Normed Algebras. Ergebnisse der Mathematik und ihrer Grenzgebiete 80, Springer-Verlag, New York, 1973.Google Scholar
[10] Bost, J.-B., Principe d’Oka, K-théorie et systèmes dynamiques non commutatifs. Invent. Math. 101(1990), no. 2, 261–333.Google Scholar
[11] Bourbaki, N., Éléments de mathématique. Fasc. XXXII. Théories spectrales. Chapitre I: Algèbres normées. Chapitre II: Groupes localement compacts commutatifs, Actualités Scientifiques et Industrielles, No. 1332, Hermann, Paris, 1967.Google Scholar
[12] Connes, A., Noncommutative differential geometry. Inst. Hautes Études Sci. Publ. Math. 62(1985), 257–360.Google Scholar
[13] Dierolf, S. and Wengenroth, J., Inductive limits of topological algebras. Linear Topol. Spaces Complex Anal. 3(1997), 45–49,Google Scholar
[14] Docquier, F. and Grauert, H., Levisches Problem und Rungescher Satz für Teilgebiete Steinscher Mannigfaltigkeiten. Math. Ann. 140(1960), 94–123.Google Scholar
[15] Dugundji, J., Topology. Allyn and Bacon, Boston, MA, 1966.Google Scholar
[16] Engelking, R., General topology. Second edition, Sigma Series in Pure Mathematics 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[17] Floret, K., Lokalkonvexe Sequenzen mit kompakten Abbildungen. J. Reine Angew.Math. 247(1971), 155–195.Google Scholar
[18] Forstnerič, F., A smooth holomorphically convex disc in C2 that is not locally polynomially convex. Proc. Amer. Math. Soc. 116(1992), no. 2, 411–415.Google Scholar
[19] Gamelin, T. W., Uniform algebras. Prentice-Hall, Englewood Cliffs, NJ, 1969.Google Scholar
[20] Glöckner, H., Algebras whose groups of units are Lie groups. Studia Math. 153(2002), no. 2, 147–177.Google Scholar
[21] Gramsch, B., Relative Inversion in der Störungstheorie von Operatoren und. -Algebren. , Math. Ann. 269(1984), no. 1, 27–71.Google Scholar
[22] Grauert, H. and Remmert, R., Theorie der Steinschen Räume. Grundlehren der Mathematischen Wissenschaften 227, Springer-Verlag, Berlin, 1977.Google Scholar
[23] Gunning, R. C. and Rossi, H., Analytic Functions of Several Complex Variables. Prentice-Hall, Englewood Cliffs, NJ, 1965.Google Scholar
[24] Harvey, R. and Wells, R. O. Jr., Compact holomorphically convex subsets of a Stein manifold. Trans. Amer. Math. Soc. 136(1969), 509–516.Google Scholar
[25] Hewitt, E. and Stromberg, K., Real and Abstract Analysis. A Modern Treatment of the Theory of Functions of a Real Variable. Graduate Texts in Mathematics 25, Springer-Verlag, New York, 1975.Google Scholar
[26] Hörmander, L., An Introduction to Complex Analysis in Several Variables. Second revised edition. North-Holland Publishing, Amsterdam, 1973.Google Scholar
[27] Hörmander, L. and Wermer, J., Uniform approximation on compact sets in Cn. Math. Scand. 23(1968), 5–21 (1968).Google Scholar
[28] Kriegl, A. and Michor, P. W., The Convenient Setting of Global Analysis. Mathematical Surveys and Monographs 53, American Mathematical Society, Providence, RI, 1997.Google Scholar
[29] Maier, P., Central extensions of topological current algebras. In: Geometry and Analysis on Finiteand Infinite-Dimensional Lie Groups, Banach Center Publ. 55, Polish Acad. Sci., Warsaw, 2002, pp. 61–76.Google Scholar
[30] Maier, P. and Neeb, K.-H., Central extensions of current groups. Math. Ann. 326(2003), no. 2, 367–415.Google Scholar
[31] Michael, E. A., Locally multiplicatively-convex topological algebras. Mem. Amer. Math. Soc., 1952(1952), no. 11.Google Scholar
[32] Neeb, K.-H., Current groups for non-compact manifolds and their central extensions. In: Infinite Dimensional Groups and Manifolds, IRMA Lect. Math. Theor. Phys. 5, de Gruyter, Berlin, 2004, pp. 109–183.Google Scholar
[33] Neeb, K.-H., Locally convex root graded Lie algebras. Travaux mathématiques 14, (Univ. du Luxembourg), 2003 pp. 25–120.Google Scholar
[34] Neeb, K.-H. and Wagemann, F., The universal central extension of the holomorphic current algebra. Manuscripta Math. 112(2003), no. 4, 441–458.Google Scholar
[35] Phillips, N. C., K-theory for Fréchet algebras. Internat. J. Math. 2(1991), no. 1, 77–129.Google Scholar
[36] Range, R. M., Holomorphic functions and integral representations in several complex variables. Graduate Texts in Mathematics 108, Springer-Verlag, New York, 1986.Google Scholar
[37] Rossi, Hugo, Holomorphically convex sets in several complex variables. Ann. of Math. (2) 74(1961), 470–493.Google Scholar
[38] Rossi, Hugo, On envelopes of holomorphy. Comm. Pure Appl. Math. 16(1963), 9–17.Google Scholar
[39] Rudin, Walter, Functional Analysis. McGraw-Hill, New York, 1973.Google Scholar
[40] Rudin, Walter, Real and Complex Analysis. Third edition. McGraw-Hill, New York, 1987.Google Scholar
[41] Šilov, G. E., On the decomposition of a commutative normed ring into a direct sum of ideals. Amer. Math. Soc. Transl. (2) 1(1955), 37–48.Google Scholar
[42] Siu, Y. T., Every Stein subvariety admits a Stein neighborhood. Invent. Math. 38(1976/77), no. 1, 89–100.Google Scholar
[43] Taylor, Joseph L., Several Complex Variables with Connections to Algebraic Geometry and LIe Groups. Graduate Studies in Mathematics 46, American Mathematical Society, Providence, RI, 2002.Google Scholar
[44] Waelbroeck, Lucien, Le calcul symbolique dans les algèbres commutatives. J. Math. Pures Appl. (9) 33(1954), 147–186.Google Scholar
[45] Waelbroeck, Lucien, Les algèbres à inverse continu. C. R. Acad. Sci. Paris 238(1954), 640–641.Google Scholar
[46] Waelbroeck, Lucien, The holomorphic functional calculus and non-Banach algebras. In: Algebras in Analysis, Academic Press, London, 1975, pp. 187–251.Google Scholar
[47] Waelbroeck, Lucien, The holomorphic functional calculus as an operational calculus. In: Spectral Theory, Banach Center Publ. 8, PWN, Warsaw, 1982, pp. 513–552.Google Scholar
[48] Wells, R. O. Jr., Holomorphic hulls and holomorphic convexity of differentiable submanifolds. Trans. Amer. Math. Soc. 132(1968), 245–262.Google Scholar
[49] Zame, William R., Holomorphic convexity of compact sets in analytic spaces and the structure of algebras of holomorphic germs. Trans. Amer. Math. Soc. 222(1976), 107–127.Google Scholar
[50] Zame, William R., Existence, uniqueness and continuity of functional calculus homomorphisms. Proc. London Math. Soc. (3) 39(1979), no. 1, 73–92.Google Scholar