Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-26T02:16:28.441Z Has data issue: false hasContentIssue false
  • English
  • Français

Khovanov–Rozansky homology for infinite multicolored braids

Part of: Low-dimensional topology

Published online by Cambridge University Press:  08 June 2020

Michael Willis
Michael Willis*
Affiliation:
Department of Mathematics, University of California Los Angeles, Los Angeles, CA90095
*
e-mail: msw188@ucla.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define a limiting 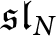${\mathfrak {sl}_N}$ Khovanov–Rozansky homology for semi-infinite positive multicolored braids. For a large class of such braids, we show that this limiting homology categorifies a highest-weight projector in the tensor product of fundamental representations determined by the coloring of the braid. This effectively completes the extension of Cautis’ similar result for infinite twist braids, begun in our earlier papers with Islambouli and Abel. We also present several similar results for other families of semi-infinite and bi-infinite multicolored braids.

Keywords

Khovanov homologycolored Khovanov homologyKhovanov–Rozansky homologycolored Khovanov–Rozansky homologycolored link homologycategorified projectorinfinite twistinfinite braids

MSC classification

Primary: 57M25: Knots and links in $S^3$
Secondary: 57M27: Invariants of knots and 3-manifolds
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 5 , October 2021 , pp. 1239 - 1277
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

References

Abel, M. and Willis, M., Colored Khovanov–Rozansky homology for infinite braids. Algebr. Geom. Topol. 19(2019), 2401–2438.CrossRefGoogle Scholar
Bar-Natan, D., Khovanov’s homology for tangles and cobordisms . Geom. Topol. 9(2005), 1443–1499. https://doi.org/10.2140/gt.2005.9.1443 CrossRefGoogle Scholar
Bondal, A. I. and Kapranov, M. M., Enhanced triangulated categories . Math. USSR-Sb. 70(1991), no. 1, 93. https://doi.org/10.1070/sm1991v070n01abeh001253 CrossRefGoogle Scholar
Cautis, S., Clasp technology to knot homology via the affine Grassmannian . Math. Ann. 363(2015), no. 3–4, 1053–1115. https://doi.org/10.1007/s00208-015-1196-x CrossRefGoogle Scholar
Cautis, S., Kamnitzer, J., and Morrison, S, Webs and quantum skew Howe duality . Math. Ann. 360(2014), no. 1–2, 351–390. https://doi.org/10.1007/s00208-013-0984-4 CrossRefGoogle Scholar
Hogancamp, M., Categorified young symmetrizers and stable homology of torus links . Geom. Topol. 22(2018), no. 5, 2943–3002.CrossRefGoogle Scholar
Islambouli, G. and Willis, M., The Khovanov homology of infinite braids . Quantum Topol. 9(2018), no. 3, 563–590. https://doi.org/10.4171/QT/114 Google Scholar
Kauffman, L. H. and Lins, S. L., Temperley-Lieb recoupling theory and invariants of 3-manifolds. In: Annals of Mathematics Studies, 134, Princeton University Press, Princeton, NJ, 1994. https://doi.org/10.1515/9781400882533 CrossRefGoogle Scholar
Khovanov, M. and Rozansky, L., Matrix factorizations and link homology . Fund. Math. 199, no. 1, 1–91, 2008. https://doi.org/10.4064/fm199-1-1 CrossRefGoogle Scholar
Queffelec, H. and Rose, D. E. V., The ${sl}_n$ foam 2-category: a combinatorial formulation of Khovanov-Rozansky homology via categorical skew Howe duality . Adv. Math . 302(2016), 1251–1339. https://doi.org/10.1016/j.aim.2016.07.027 CrossRefGoogle Scholar
Queffelec, H., Skein modules from skew Howe duality and affine extensions . SIGMA Symmetry Integr. Geom. Methods Appl . 11(2015), 36, Paper 030. https://doi.org/10.3842/SIGMA.2015.030 Google Scholar
Queffelec, H. and Wedrich, P., Khovanov homology and categorification of skein modules. Preprint, 2018. arXiv:1806.03416.Google Scholar
Rose, D. E. V., A categorification of quantum ${sl}_3$ projectors and the ${sl}_3$ Reshetikhin-Turaev invariant of tangles. Quantum Topol. 5(2014), no. 1, 1–59. https://doi.org/10.4171/QT/46 CrossRefGoogle Scholar
Rozansky, L., An infinite torus braid yields a categorified Jones-Wenzl projector . Fund. Math. 225(2014), no. 1, 305–326. https://doi.org/10.4064/fm225-1-14 CrossRefGoogle Scholar
Rozansky, L., A categorification of the stable $su(2)$ Witten-Reshetikhin-Turaev invariant of links in. ${S}^2\times {S}^1$ Preprint, 2010. arXiv:1011.1958.Google Scholar
Wenzl, H., On sequences of projections . C. R. Math. Rep. Acad. Sci. Canada 9(1987), no. 1, 5–9.Google Scholar
Willis, M., Khovanov homology for links in ${\#}^r\left({S}^2\times {S}^1\right)$ . Michigan Math. J., 2020. https://doi.org/10.1307/mmj/1594281620 CrossRefGoogle Scholar
Wu, H., A colored $sl(N)$ homology for links in ${S}^3$ . Dissertationes Math. (Rozprawy Mat.) 499(2014), 217. https://doi.org/10.4064/dm499-0-1 Google Scholar
Yonezawa, Y., Quantum $\left({sl}_n,\wedge {V}_n\right)$ link invariant and matrix factorizations . Nagoya Math. J. 204(2011), 69–123. https://doi.org/10.1215/00277630-1431840 CrossRefGoogle Scholar