Hostname: page-component-cd4964975-598jt Total loading time: 0 Render date: 2023-03-29T22:38:56.673Z Has data issue: true Feature Flags: { "useRatesEcommerce": false } hasContentIssue true
  • English

The SL(2, C) Casson Invariant for Knots and the Â-polynomial

Published online by Cambridge University Press:  20 November 2018

Hans U. Boden  and
Cynthia L. Curtis
Hans U. Boden
Affiliation:
Mathematics & Statistics, McMaster University, Hamilton, ON e-mail: boden@mcmaster.ca
Cynthia L. Curtis
Affiliation:
Mathematics & Statistics, The College of New Jersey, Ewing, NJ, USA e-mail: ccurtis@tcnj.edu
Rights & Permissions[Opens in a new window]

Abstract

HTML view is not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we extend the definition of the 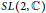$SL\left( 2,\,\mathbb{C} \right)$ Casson invariant to arbitrary knots 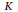$K$ in integral homology 3-spheres and relate it to the 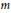$m$-degree of the 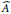$\widehat{A}$-polynomial of 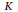$K$. We prove a product formula for the 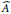$\widehat{A}$-polynomial of the connected sum 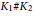${{K}_{1}}\#{{K}_{2}}$ of two knots in 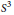${{S}^{3}}$ and deduce additivity of the 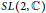$SL\left( 2,\,\mathbb{C} \right)$ Casson knot invariant under connected sums for a large class of knots in 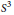${{S}^{3}}$. We also present an example of a nontrivial knot 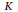$K$ in 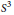${{S}^{3}}$ with trivial 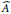$\widehat{A}$-polynomial and trivial 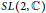$SL\left( 2,\,\mathbb{C} \right)$ Casson knot invariant, showing that neither of these invariants detect the unknot.

Keywords

57M2757M2557M05knots3-manifoldscharacter varietyCasson invariantA-polynomial
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 1 , 01 February 2016 , pp. 3 - 23
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Boden, H. U., Nontriviality of the M-degree of the A-polynomial. Proc. Amer. Math. Soc. 142(2014), no. 6, 2173–2177.http://dx.doi.org/10.1090/S0002-9939-2014-11936-8 CrossRefGoogle Scholar
[2] Boden, H. U. and Curtis, C. L., The SL2(ℂ) Casson invariant for Seifert fibered homology spheres and surgeries on twist knots. J. Knot Theory Ramific. 15(2006), no. 7, 813–837.http://dx.doi.org/10.1142/S0218216506004762 CrossRefGoogle Scholar
[3] Boden, H.U and Curtis, C.L, Splicing and the SL2(ℂ) Casson invariant. Proc. Amer. Math. Soc. 136(2008), no. 7, 2615–2623.http://dx.doi.org/10.1090/S0002-9939-08-09233-2 CrossRefGoogle Scholar
[4] Boden, H. U. and Curtis, C. L., The SL(2, ℂ) Casson invariant for for Dehn surgeries on two-bridge knots. Algebr. Geom. Topol. 12(2012), no. 4, 2095–2126.http://dx.doi.org/10.2140/agt.2012.12.2095 CrossRefGoogle Scholar
[5] Boyer, S. and Zhang, X., A proof of the finite filling conjecture. J. Differential Geom. 59(2001), 87–176.CrossRefGoogle Scholar
[6] Chesebro, E., Closed surfaces and character varieties. Algebr. Geom. Topol. 13(2013), no. 4, 2001–2037.http://dx.doi.org/10.2140/agt.2013.13.2001 CrossRefGoogle Scholar
[7] Cooper, D., Culler, M., Gillet, H., Long, D. D., and Shalen, P. B., Plane curves associated to character varieties of 3-manifolds. Invent. Math. 118(1994), no. 1, 47–84.http://dx.doi.org/10.1007/BF01231526 CrossRefGoogle Scholar
[8] Cooper, D. and Long, D. D., Remarks on the A-polynomial of a knot. J. Knot Theory Ramifications 5(1996), no. 5, 609–628.http://dx.doi.org/10.1142/S0218216596000357 CrossRefGoogle Scholar
[9] Cooper, D. and Long, D. D., The A-polynomial has ones in the corners. Bull. Lond. Math. Soc. 29(1997), no. 2, 231–238.http://dx.doi.Org/10.1112/SOO24609396002251 CrossRefGoogle Scholar
[10] Culler, M., C.|McA. Gordon, Luecke, J., and Shalen, P. B., Dehn surgery on knots. Ann. of Math. 125(1987), no. 2, 237–300.http://dx.doi.Org/10.2307/1971311 CrossRefGoogle Scholar
[11] Culler, M. and Shalen, P. B., Varieties of group representations and splittings of 3-manifolds. Ann. of Math. 117(1983), no. 1, 109–146.http://dx.doi.Org/10.2307/2006973 CrossRefGoogle Scholar
[12] Curtis, C. L., An intersection theory count of the SL(2,ℂ) -representations of the fundamental group of a 3-manifold. Topology 40(2001), 773–787.http://dx.doi.Org/10.1016/S0040-9383(99)00083-X CrossRefGoogle Scholar
[13] Curtis, C. L., Erratum to “An intersection theory count of the SL(2,ℂ) - representations of the fundamental group of a 3-manifold”. Topology 42(2003), no. 4, 929.http://dx.doi.Org/10.1016/S0040-9383(02)00101-5 CrossRefGoogle Scholar
[14] Fulton, W., Algebraic curves. An introduction to algebraic geometry. Notes written with the collaboration of Richard Weiss, Mathematics Lecture Notes Series, W. A. Benjamin, New York, 1969.Google Scholar
[15] Johnson, D. and Millson, J., Deformation spaces associated to compact hyperbolic manifolds. In: Discrete groups in geometry and analysis (New Haven, Conn., 1984), Progr. Math., 67, Birkhäuser Boston, 1987, pp. 48–106.CrossRefGoogle Scholar
[16] Kapovich, M. and Millson, J., On representation varieties of 3-manifold groups. arxiv:1303.2347Google Scholar
[17] Klassen, E. P., Representations in SU (2) of the fundamental groups of the Whitehead link and of doubled knots. Forum Math. 5(1993), 93–109.http://dx.doi.Org/10.1515/form.1993.5.93 CrossRefGoogle Scholar
[18] Le, T. L. K, Varieties of representations and their cohomology-jump subvarieties for knot groups. (Russian) Mat. Sb. 184(1993), no. 2, 57–82; translation in: Russian Acad. Sci. Sb. Math.) 78(1994), no. 1, 187–209.http://dx.doi.org/10.1070/SM1994v078n01ABEH003464 Google Scholar
[19] Le, T. K. T. and Tran, A. T., On the A] conjecture for knots. http://arxiv:1111.5258v4Google Scholar
[20] Marché, J., The skein module of torus knots. Quantum Topol. 1(2010), no. 4, 413–421.http://dx.doi.Org/10.4171/QT/11 CrossRefGoogle Scholar
[21] Shafarevich, I. R., Basic algebraic geometry I. In: Varieties in protective space. Second edition. Springer-Verlag, Berlin, 1994.Google Scholar
[22] Sikora, A. S., Character varieties. Trans. Amer. Math. Soc. 364(2012), no. 10, 5173–5208.http://dx.doi.org/10.1090/S0002-9947-2012-05448-1 CrossRefGoogle Scholar
[23] Tran, A. T., The universal character ring of the (−2, 2m + 1, 2n)-pretzel link. Internat. J. Math. 24(2013), no. 8, 1350063.http://dx.doi.org/10.1142/S0129167X13500638 CrossRefGoogle Scholar