Article contents
Tannakian Categories With SemigroupActions
Published online by Cambridge University Press: 20 November 2018
Abstract
A theorem of Ostrowski implies that 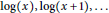 $\log \left( x \right),\,\log \left( x+1 \right),\,.\,.\,.$ are algebraically independent over
$\log \left( x \right),\,\log \left( x+1 \right),\,.\,.\,.$ are algebraically independent over 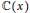 $\mathbb{C}\left( x \right)$ . More generally, for a linear differential or difference equation, it is an important problem to find all algebraic dependencies among a non-zero solution
$\mathbb{C}\left( x \right)$ . More generally, for a linear differential or difference equation, it is an important problem to find all algebraic dependencies among a non-zero solution  $y$ and particular transformations of
$y$ and particular transformations of  $y$ , such as derivatives of
$y$ , such as derivatives of  $y$ with respect to parameters, shifts of the arguments, rescaling, etc. In this paper, we develop a theory of Tannakian categories with semigroup actions, which will be used to attack such questions in full generality, as each linear differential equation gives rise to a Tannakian category. Deligne studied actions of braid groups on categories and obtained a finite collection of axioms that characterizes such actions to apply them to various geometric constructions. In this paper, we find a finite set of axioms that characterizes actions of semigroups that are finite free products of semigroups of the form
$y$ with respect to parameters, shifts of the arguments, rescaling, etc. In this paper, we develop a theory of Tannakian categories with semigroup actions, which will be used to attack such questions in full generality, as each linear differential equation gives rise to a Tannakian category. Deligne studied actions of braid groups on categories and obtained a finite collection of axioms that characterizes such actions to apply them to various geometric constructions. In this paper, we find a finite set of axioms that characterizes actions of semigroups that are finite free products of semigroups of the form 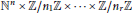 ${{\mathbb{N}}^{n}}\,\times \,\mathbb{Z}/{{n}_{1}}\mathbb{Z}\,\times \,.\,.\,.\,\mathbb{Z}/{{n}_{r}}\mathbb{Z}$ on Tannakian categories. This is the class of semigroups that appear in many applications.
${{\mathbb{N}}^{n}}\,\times \,\mathbb{Z}/{{n}_{1}}\mathbb{Z}\,\times \,.\,.\,.\,\mathbb{Z}/{{n}_{r}}\mathbb{Z}$ on Tannakian categories. This is the class of semigroups that appear in many applications.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 2
- Cited by

