Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-66d7dfc8f5-npwgr Total loading time: 0.401 Render date: 2023-02-08T17:04:21.803Z Has data issue: true Feature Flags: { "useRatesEcommerce": false } hasContentIssue true
  • English
Canadian Mathematical Bulletin Canadian Mathematical Bulletin

Article contents

Higher ℓ2-Betti Numbers of Universal Quantum Groups

Published online by Cambridge University Press:  20 November 2018

Julien Bichon ,
David Kyed  and
Sven Raum
Julien Bichon
Affiliation:
Laboratoire de Mathématiques Blaise Pascal, Université Clermont Auvergne, Campus universitaire des Cézeaux, 3 place Vasarely, 63178 Aubière cedex, Francejulien.bichon@uca.fr
David Kyed
Affiliation:
Department of Mathematics and Computer Science, University of Southern Denmark, Campusvej 22, DK-5230 Odense M, Denmarkdkyed@imada.sdu.dk
Sven Raum
Affiliation:
EPFL SB SMA, Station 8, CH-1015 Lausanne, Switzerlandsven.raum@epfl.ch
Get access Rights & Permissions[Opens in a new window]

Abstract

We calculate all 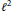${{\ell }^{2}}$-Betti numbers of the universal discrete Kac quantum groups 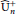$\widehat{\text{U}}_{n}^{+}$ as well as their half-liberated counterparts 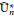$\widehat{\text{U}}_{n}^{*}$.

Keywords

16T0546L6520G42ℓ2-Betti numberfree unitary quantum grouphalf-liberated unitary quantum groupfree product formulaextension
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 225 - 235
Copyright
Copyright © Canadian Mathematical Society 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[Ban97a] Banica, T., Legroupe quantique compact libre U(n). Comm. Math. Phys. 190(1997), no. 1, 143–172.http://dx.doi.Org/10.1007/s002200050237 CrossRefGoogle Scholar
[BS09] Banica, T. and Speicher, R., Liberation orthogonal Lie groups. Adv. Math. 222(2009), no. 4, 1461–1501.http://dx.doi.Org/10.1016/j.aim.2009.06.009 CrossRefGoogle Scholar
[BV10] Banica, T. and Vergnioux, R., Invariants ofthe half-liberated orthogonal group. Ann. Inst. Fourier 60(2010), no. 6, 2137–2164.http://dx.doi.org/10.5802/aif.2579 CrossRefGoogle Scholar
[BMT01] Bédos, E., Murphy, G. J., and Tuset, L., Co-amenability of compact quantum groups. J. Geom. Phys. 40(2001), no. 2, 130–153. http://dx.doi.org/10.1016/S0393-0440(01)00024-9 CrossRefGoogle Scholar
[vdB98] van den Bergh, M., A relation between Hochschild homology and cohomology for Gorenstei rings. Proc. Amer. Math. Soc. 126(1998), no. 5,1345–1348.http://dx.doi.org/10.1090/S0002-9939-98-04210-5 CrossRefGoogle Scholar
[BDD11] Bhowmick, J., D'Andrea, F., and Dabrowski, L., Quantum isometries ofthe finite noncommutative geometry of the Standard model. Comm. Math. Phys. 307(2011), 101–131.http://dx.doi.Org/10.1007/s00220-011-1301-2 CrossRefGoogle Scholar
[Bicl6] Bichon, J., Cohomological dimensions of universal cosoverign Hopf algebras. Publicacions Matemàtiques, to appear. arxiv:1611.02069Google Scholar
[BNY15] Bichon, J., Neshveyev, S., and Yamashita, M., Graded twisting of categories and quantum groups by group actions. Ann. Inst. Fourier 66(2016), no. 6, 2299–2338.http://dx.doi.org/10.5802/aif.3064 CrossRefGoogle Scholar
[BNY16] Bichon, J., Neshveyev, S., and Yamashita, M., Graded twisting of comodule algebras and module categories. arxiv:1 604.02078Google Scholar
[Bral2] Brannan, M., Approximation properties for free orthogonal andfree unitary quantum groups. J. Reine Angew. Math. 672(2012), 223–251.Google Scholar
[Chil4] Chirvasitu, A., Cosemisimple Hopf algebras are faithfully flat over Hopf subalgebras. Algebra Number Theory 8(2014), no. 5,1179–1199.http://dx.doi.Org/10.214O/ant.2O14.8.1179 CrossRefGoogle Scholar
[CHT09] Collins, B., Härtel, Johannes, and Thom, A., Homology offree quantum groups. C. R. Math. Acad. Sei. Paris 347(2009), no. 5-6, 271–276.http://dx.doi.Org/10.1016/j.crma.2009.01.021 Google Scholar
[FimlO] Fima, P. Kazhdan's property T for discrete quantum groups. Internat. J. Math. 221(2010), no. 1, 47–65. http://dx.doi.Org/10.1142/S0129167X1000591X Google Scholar
[KVOO] Kustermans, J. and Vaes, S., Locally compact quantum groups. Ann. Sei. École Norm. Sup. (4) 33(2000), no. 6, 837–934. http://dx.doi.Org/10.1016/S0012-9593(00)01055-7Google Scholar
[KyeO8a] Kyed, D., L2-Betti numbers of coamenable quantum groups. Münster J. Math. 1(2008), 143–179.Google Scholar
[KyeO8b] Kyed, D., L2-homology for compact quantum groups. Math. Scand. 103(2008), no. 1,111–129.http://dx.doi.org/10.7146/math.scand.a-15072 CrossRefGoogle Scholar
[Kyell] Kyed, D., On the zeroth L2-homology of a quantum group. Münster J. Math. 4(2011), 119–127.Google Scholar
[Kyel2] Kyed, D., An L2-Kunneth formula for tracial algebras. J. Operator Theory 67(2012), 317–327.Google Scholar
[KR16] Kyed, D. and Raum, S., On the l2-Betti numbers of universal quantum groups. Math. Ann., to appear. arxiv:1 610.05474Google Scholar
[LücO2] Lück, W., L2-invariants: theory and applications to geometry and K-theory. Ergebnisse der Mathematik und ihrer Grenzgebiete, 44, Folge, A Series of Modern Surveys in Mathematics, Springer-Verlag, Berlin, 2002.Google Scholar
[MN06] Meyer, R. and Nest, R., The Baum-Connes conjeeture via localisation of categories. Topology 45(2006), no. 2, 209–259. http://dx.doi.Org/10.1016/j.top.2005.07.001CrossRefGoogle Scholar
[ReiOl] Reich, H., On the K-and L-theory ofthe algebra of Operators affiliated to a finite von Neumann algebra. Jf-Theory 24, no. 4, 303–326.http://dx.doi.Org/10.1023/A:1014078228859 Google Scholar
[SauO2] Sauer, R., L2-invariants of groups and discrete measured groupoids. Ph.D. Dissertation, University of Münster, 2002.Google Scholar
[Tho08] Thom, A., L2 *-cohomology for von Neumann algebras. Geom. Funct. Anal. 18(2008), no. 1, 251–270. http://dx.doi.org/10.1007/s00039-007-0634-7 CrossRefGoogle Scholar
[VW96] Van Daele, A. and Wang, S., Universal quantum groups. Internat. J. Math. 7(1996), no. 2, 255–263. http://dx.doi.Org/10.1142/S0129167X96000153 CrossRefGoogle Scholar
[VerO7] Vergnioux, R., The property of rapid decayfor discrete quantum groups. J. Operator Theory 57(2007), 303–324.Google Scholar
[Verl2] Vergnioux, R., Paths in quantum Cayley trees and L2-cohomology. Adv. Math. 229(2012), 2686–2711.http://dx.doi.Org/10.1016/j.aim.2O12.01.011 CrossRefGoogle Scholar
[Voill] Voigt, C., The Baum-Connes conjeeture for free orthogonal quantum groups. Adv. Math. 227(2011), no. 5, 1873–1913.http://dx.doi.Org/10.1016/j.aim.2O11.04.008 CrossRefGoogle Scholar
[Wan95] Wang, S., Free produets ofcompact quantum groups. Comm. Math. Phys. 167(1995), no. 3, 671–692.http://dx.doi.Org/10.1007/BF02101540 CrossRefGoogle Scholar
[Wan98] Wang, S., Quantum symmetry groups of finite Spaces. Comm. Math. Phys. 195(1998), 195–211. http://dx.doi.org/10.1007/s002200050385 CrossRefGoogle Scholar
[Wei94] Weibel, C. A., An introduction to homological algebra. Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, Cambridge, 1994.http://dx.doi.Org/10.1017/CBO9781139644136 Google Scholar
[Wor87] Woronowicz, S. L., Twisted SU(2) group. An example ofa noncommutative differential calculus. Publ. Res. Inst. Math. Sei. 23(1987), 117–181. http://dx.doi.org/10.2977/prims/1195176848 CrossRefGoogle Scholar
[Wor98] Woronowicz, S. L., Compact quantum groups. In: Symetries quantiques (Les Houches, 1995), North-Holland, Amsterdam, 1998, pp. 845–884.Google Scholar
1
Cited by

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Higher ℓ2-Betti Numbers of Universal Quantum Groups
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

Higher ℓ2-Betti Numbers of Universal Quantum Groups
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

Higher ℓ2-Betti Numbers of Universal Quantum Groups
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *