Article contents
On Differential Torsion Theories and Rings with Several Objects
Published online by Cambridge University Press: 08 April 2019
Abstract
Let 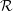 ${\mathcal{R}}$ be a small preadditive category, viewed as a “ring with several objects.” A right
${\mathcal{R}}$ be a small preadditive category, viewed as a “ring with several objects.” A right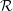 ${\mathcal{R}}$-module is an additive functor from
${\mathcal{R}}$-module is an additive functor from 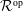 ${\mathcal{R}}^{\text{op}}$ to the category
${\mathcal{R}}^{\text{op}}$ to the category 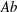 $Ab$ of abelian groups. We show that every hereditary torsion theory on the category
$Ab$ of abelian groups. We show that every hereditary torsion theory on the category 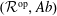 $({\mathcal{R}}^{\text{op}},Ab)$ of right
$({\mathcal{R}}^{\text{op}},Ab)$ of right 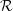 ${\mathcal{R}}$-modules must be differential.
${\mathcal{R}}$-modules must be differential.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
References
- 2
- Cited by


