Article contents
Affine Completeness of Generalised Dihedral Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
In this paper we study affine completeness of generalised dihedral groups. We give a formula for the number of unary compatible functions on these groups, and we characterise for every 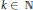 $k\in \mathbb{N}$ the
$k\in \mathbb{N}$ the  $k$-affine complete generalised dihedral groups. We find that the direct product of a 1-affine complete group with itself need not be 1-affine complete. Finally, we give an example of a nonabelian solvable affine complete group. For nilpotent groups we find a strong necessary condition for 2-affine completeness.
$k$-affine complete generalised dihedral groups. We find that the direct product of a 1-affine complete group with itself need not be 1-affine complete. Finally, we give an example of a nonabelian solvable affine complete group. For nilpotent groups we find a strong necessary condition for 2-affine completeness.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2006
References
- 3
- Cited by


