Article contents
Congruence Class Sizes in Finite Sectionally Complemented Lattices
Published online by Cambridge University Press: 20 November 2018
Abstract
The congruences of a finite sectionally complemented lattice 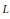 $L$ are not necessarily uniform (any two congruence classes of a congruence are of the same size). To measure how far a congruence
$L$ are not necessarily uniform (any two congruence classes of a congruence are of the same size). To measure how far a congruence 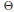 $\Theta $ of
$\Theta $ of 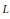 $L$ is from being uniform, we introduce Spec
$L$ is from being uniform, we introduce Spec 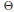 $\Theta $ , the spectrum of
$\Theta $ , the spectrum of 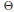 $\Theta $ , the family of cardinalities of the congruence classes of
$\Theta $ , the family of cardinalities of the congruence classes of 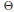 $\Theta $ . A typical result of this paper characterizes the spectrum
$\Theta $ . A typical result of this paper characterizes the spectrum 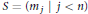 $S=({{m}_{j}}|j<n)$ of a nontrivial congruence
$S=({{m}_{j}}|j<n)$ of a nontrivial congruence 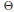 $\Theta $ with the following two properties:
$\Theta $ with the following two properties:
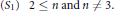 $$({{S}_{1}})\,\,\,\,2\le n\,\,\text{and }n\ne 3.\,\,\,\,$$
$$({{S}_{1}})\,\,\,\,2\le n\,\,\text{and }n\ne 3.\,\,\,\,$$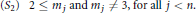 $$({{S}_{2}})\,\,\,2\le {{m}_{j}}\,\,\text{and}\,\,{{m}_{j}}\ne 3,\,\,\,\text{for}\,\text{all}\,j<n.$$
$$({{S}_{2}})\,\,\,2\le {{m}_{j}}\,\,\text{and}\,\,{{m}_{j}}\ne 3,\,\,\,\text{for}\,\text{all}\,j<n.$$
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
- 2
- Cited by

