Hostname: page-component-77f85d65b8-jkvpf Total loading time: 0 Render date: 2026-04-19T02:03:57.963Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential-free Characterisation of Smooth Mappings with Controlled Growth

Published online by Cambridge University Press:  20 November 2018

Marijan Marković
Marijan Marković*
Affiliation:
Faculty of Natural Sciences and Mathematics, University of Montenegro, Cetinjski put b.b., 81000 Podgorica, Montenegro, e-mail : marijanmmarkovic@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the 'Save PDF' action button.

In this paper we give some generalizations and improvements of the Pavlović result on the Holland–Walsh type characterization of the Bloch space of continuously differentiable (smooth) functions in the unit ball in 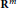${{\text{R}}^{m}}$ .

Keywords

32A1830D45Bloch type spacesLipschitz type spacesHolland-Walsh characterisationhyperbolic distanceanalytic functionMöbius transform

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 628 - 636
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Ahlfors, L. V., Möbius transformations in several dimensions. Ordway Professorship Lectures in Mathematics, University of Minnesota, School of Mathematics, Minneapolis, MN, 1981.Google Scholar
[2] Colonna, F., The Block constant of bounded harmonic mappings. Indiana Univ. Math. J. 38(1989), 829–840. http://dx.doi.Org/10.1512/iumj.1989.38.38039Google Scholar
[3] Holland, F. and Walsh, D., Criteriafor membership of Block Space and its subspace, BMOA. Math. Ann. 273(1986), 317–335. http://dx.doi.org/10.1007/BF01451410Google Scholar
[4] Pavlovic, M., On the Holland-Walsh characterization of Block functions. Proc. Edinb. Math. Soc. 51(2008), 439–441. http://dx.doi.org/10.1017/S0013091506001076Google Scholar
[5] Ren, G. and Tu, C., Block Space in the unit ball of Cn. Proc. Amer. Math. Soc. 133(2005), 719–726. http://dx.doi.org/10.1090/S0002-9939-04-07617-8Google Scholar
[6] Vuorinen, M., Conformal geometry and quasiregular mappings. Lecture Notes in Mathematics, 1319, Springer-Verlag, Berlin, 1988. http://dx.doi.Org/10.1007/BFb0077904Google Scholar
[7] Zhu, K., Distances and Banach Spaces of holomorphic functions on complex domains. J. London Math. Soc. 49(1994), 163–182. http://dx.doi.Org/10.1112/jlms/49.1.163Google Scholar
[8] Zhu, K., Bloch type Spaces of analytic functions. Rocky Mountain J. Math. 23(1993), 1143–1177. http://dx.doi.Org/10.1216/rmjm/1181072549Google Scholar