Article contents
Fundamental Solutions of Kohn Sub-Laplacians on Anisotropic Heisenberg Groups and H-type Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
We prove that the fundamental solutions of Kohn sub-Laplacians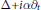 $\Delta +i\alpha {{\partial }_{t}}$ on the anisotropic Heisenberg groups are tempered distributions and have meromorphic continuation in α with simple poles. We compute the residues and find the partial fundamental solutions at the poles. We also find formulas for the fundamental solutions for some matrix-valued Kohn type sub-Laplacians on
$\Delta +i\alpha {{\partial }_{t}}$ on the anisotropic Heisenberg groups are tempered distributions and have meromorphic continuation in α with simple poles. We compute the residues and find the partial fundamental solutions at the poles. We also find formulas for the fundamental solutions for some matrix-valued Kohn type sub-Laplacians on 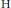 $\text{H}$-type groups.
$\text{H}$-type groups.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
- 1
- Cited by


