No CrossRef data available.
Article contents
The Global Attractor of a Damped, Forced Hirota Equation in H1
Published online by Cambridge University Press: 20 November 2018
Abstract
The existence of the global attractor of a damped forced Hirota equation in the phase space 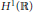 ${{H}^{1}}\left( \mathbb{R} \right)$ is proved. The main idea is to establish the so-called asymptotic compactness property of the solution operator by energy equation approach.
${{H}^{1}}\left( \mathbb{R} \right)$ is proved. The main idea is to establish the so-called asymptotic compactness property of the solution operator by energy equation approach.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010


