No CrossRef data available.
Article contents
Measures with Fourier Transforms in L 2 of a Half-space
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We prove that if the Fourier transform of a compactly supported measure is in 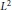 ${{L}^{2}}$ of a half-space, then the measure is absolutely continuous to Lebesgue measure. We then show how this result can be used to translate information about the dimensionality of a measure and the decay of its Fourier transform into geometric information about its support.
${{L}^{2}}$ of a half-space, then the measure is absolutely continuous to Lebesgue measure. We then show how this result can be used to translate information about the dimensionality of a measure and the decay of its Fourier transform into geometric information about its support.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
[1] Erdogan, M. B., A bilinear Fourier extension theorem and applications to the distance set problem. Int. Math. Res. Not.
2005, no. 23, 1411–1425.Google Scholar
[2] Forelli, F., Analytic and quasi-invariant measures. Acta Math.
118(1967), 33–59. doi:10.1007/BF02392475Google Scholar
[3] Forelli, F., The theorem of F. and M. Riesz for unbounded measures. In: The Madison symposium on complex analysis (Madison, WI, 1991), Contemp. Math., 137, American Mathematical Society, Providence, RI, 1992, pp. 221–234.Google Scholar
[4] Herz, C. S., Fourier transforms related to convex sets. Ann. of Math.
75(1962), 81–92. doi:10.2307/1970421Google Scholar
[5] Hofmann, S. and Iosevich, A., Circular averages and Falconer/Erdös distance conjecture in the plane for random metrics. Proc. Amer. Math. Soc.
133(2005), no. 1, 133–143. doi:10.1090/S0002-9939-04-07603-8Google Scholar
[6] Mattila, P., Spherical averages of Fourier transforms of measures with finite energy; dimension of intersections and distance sets. Mathematika
34(1987), no. 2, 207–228. doi:10.1112/S0025579300013462Google Scholar
[7] Wolff, T. H., Lectures on harmonic analysis. University Lecture Series, 29, American Mathematical Society, Providence, RI, 2003.Google Scholar

