Article contents
Variants of Korselt’s Criterion
Published online by Cambridge University Press: 20 November 2018
Abstract
Under sufficiently strong assumptions about the first term in an arithmetic progression, we prove that for any integer  $a$, there are infinitely many
$a$, there are infinitely many 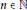 $n\,\in \,\mathbb{N}$ such that for each prime factor
$n\,\in \,\mathbb{N}$ such that for each prime factor 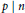 $p\,\text{ }\!\!|\!\!\text{ }\,n$, we have
$p\,\text{ }\!\!|\!\!\text{ }\,n$, we have 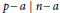 $p\,-\,a\,\text{ }\!\!|\!\!\text{ }\,n\,-\,a$. This can be seen as a generalization of Carmichael numbers, which are integers
$p\,-\,a\,\text{ }\!\!|\!\!\text{ }\,n\,-\,a$. This can be seen as a generalization of Carmichael numbers, which are integers  $n$ such that
$n$ such that 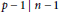 $p\,-\,1\,\text{ }\!\!|\!\!\text{ }\,n\,-\,1$ for every
$p\,-\,1\,\text{ }\!\!|\!\!\text{ }\,n\,-\,1$ for every 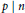 $p\,\text{ }\!\!|\!\!\text{ }\,n$.
$p\,\text{ }\!\!|\!\!\text{ }\,n$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
- 1
- Cited by


