INTRODUCTION
Evidence from the severe acute respiratory syndrome (SARS) outbreak illustrated the rapid spread of an emerging infection from one region to another by infected travellers. Thus, the risk of introduction of an infectious pathogen in a community must be assessed, in order to provide governmental authorities with timely information to help in the adoption of appropriate responses. From a risk management point of view, characterization of potentially infected travellers and prediction of their numbers is important.
Travel is a key component for importation to occur. This parameter was used in modelling works that focused on, for example, predicting the worldwide spread of influenza through the air transportation network [Reference Caley, Becker and Philp1–Reference Ferguson3]. A more recent study focused on the effect of the heterogeneity of travel frequency in the population on the global spread of infectious agents [Reference Hollingsworth, Ferguson and Anderson4]. These studies, based on ‘susceptible–infectious–recovered’ or ‘susceptible–exposed–infectious–recovered’ epidemic models structured per region, used air-travel volume data to estimate travel rate and to model the movement of individuals between regions. The number of travellers was also used by Glass et al. [Reference Glass, Becker and Clements5] to study how control measures in a source region, and entry screening and public health responses in the destination region can impact the probability and the size of a SARS outbreak. These authors estimated the probability that an infected traveller arrives undetected as a function that depends on the prevalence of infection, the delay to isolation, and the sensitivity of entry screening. This probability could be used to estimate the number of imported cases given the number of travellers. These authors applied the population's SARS prevalence to travellers heading to a destination, assuming it to be constant. However, prevalence among travellers might differ from that in the population. In addition, there are obviously some population categories that are more likely to travel than others. It is possible that within these categories, some are at a higher risk of infection than others and thus the prevalence might be different between subgroups of travellers. Health-care workers (HCWs) represent a particular group frequently exposed to in-hospital infections and susceptible to importation of infectious pathogens such as SARS [Reference Desenclos6, Reference Wilder-Smith and Paton7]. The extent of their role in the transmission and spread of influenza, for instance, has been recently analysed [Reference Barnes, Glass and Becker8].
In the present paper we estimated the cumulated number of imported SARS cases from one source region to a destination since the epidemic began, until a day, d, during an outbreak, avoiding any potential bias linked to a possible heterogeneity in the prevalence between population groups. The approach we use required two steps. First, instead of using the prevalence in the source region, we used the distribution of infected individuals by time of infection, back-calculated from the incident cases. In a second step, we performed a simple probabilistic calculation via Monte Carlo simulations, where every infected individual in the source region has a chance to travel and a probability of being undetected by entry screening in the destination region. Our aim was to estimate the number of imported SARS cases, validating this calculation using the 2003 SARS epidemic data and exploring a situation where we assumed that infected HCWs are more likely to travel than other infected individuals. We also investigated whether or not importation of SARS is affected by specific entry screening.
METHODS
We used data from the 2003 SARS epidemic to estimate the cumulated number of imported infected individuals in two scenarios: Beijing–Frankfurt and Hong Kong–London. Estimates are obtained by time interval T d=(0, d), during a number of d days since symptom onset of the first case in the source region. Both selected destinations are among the busiest European airports.
The risk of importation of SARS infection depends on the realization of some events. First, an infected individual in a source region must circulate and board a plane in order to travel to a destination. Second, the individual must indeed travel and arrive without being detected by entry screening. We assumed that there is no border screening at departure and considered entry screening for only symptomatic travellers. Thus, detection at arrival depends on the efficacy of border screening as well as on the clinical state of the infected traveller. Key parameters and assumptions are shown in Table 1 and are described in a later section.
Table 1. Data and assumptions for the parameters used in the Monte Carlo simulation calculation for the prediction of the risk of SARS importation (Beijing–Frankfurt and Hong Kong–London)

n.a., Not applicable.
* Gamma distribution is fitted to the data in both regions, and the mean and standard deviation (s.d.) are estimated.
† Constant travel rate with no seasonal variation in travel volume.
Data
The daily number of SARS cases in Beijing was obtained through the Chinese health authorities who provided us with a specific data selection including only cases aged ⩾16 years and belonging to one of the following categories: HCWs, business workers, students, retired, civil servants and staff [Reference Feng9]. According to expert judgement (D. Feng, personal communication), these professional categories are the most likely to travel. For Hong Kong, the SARS data published by the World Health Organization were used [10, 11]. Figure 1 presents the number of cases in Hong Kong by day of symptom onset and the number of cases in HCWs, who represented 22% of all cases. This proportion was high in the first stage of the outbreak, reaching 67% on 5 March 2003, then decreasing after the global alert on 12 March 2003. In Beijing 19% of the SARS cases were HCWs [Reference Feng9].
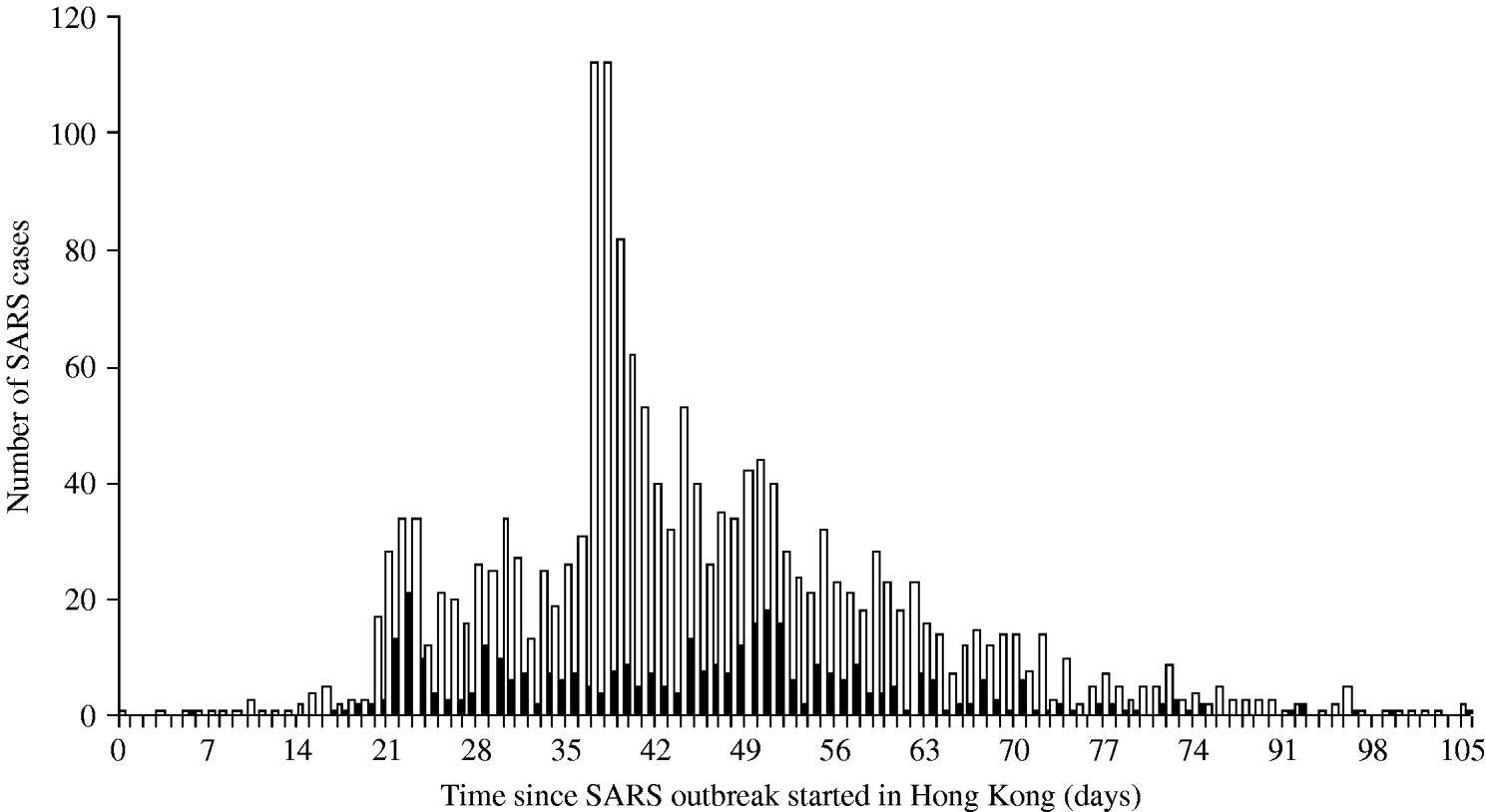
Fig. 1. Distribution of the number of SARS cases by day of symptom onset in Hong Kong. ▪, SARS health-care-worker cases; □, All SARS cases.
Back-calculation
The distribution of infected individuals by day of infection during an interval T d can be back-calculated from the incident cases in T d, using the distribution of the incubation period. This estimated distribution does not reflect the actual infection curve because individuals acquiring their infection during T d, but having developed their symptoms after day d are not accounted for. The number of these individuals corresponds to a fraction of secondary cases generated by the incident cases in T d. This number is estimated using the distribution of the serial interval as described by Cauchemez et al. [Reference Cauchemez12] (see Appendix A, section 1). Like Cauchemez and colleagues, we assumed that for SARS this distribution is similar in all regions and used a mean (standard deviation) estimate of 8·4 (s.d.=3·8) days [Reference Lipsitch13]. We applied the back-calculation method [Reference Becker, Watson and Carlin14] on the incident cases in T d and on those predicted (Appendix A, section 2). We note by ![]() (δ=0, 1, …,d) the estimated number of individuals infected δ days prior to day d (end of T d).
(δ=0, 1, …,d) the estimated number of individuals infected δ days prior to day d (end of T d).
Probabilistic Monte Carlo simulation calculation
Over T d, the risk of importation of SARS by every individual i infected δ days prior to day d (δ=0, …,d) is simulated using Monte Carlo simulation. At each simulation, we draw a random value ![]() from the gamma-distributed incubation period [Reference Donnelly15]. If
from the gamma-distributed incubation period [Reference Donnelly15]. If ![]() is less than δ, then symptom onset for individual i was δ –
is less than δ, then symptom onset for individual i was δ – ![]() days prior to d, otherwise the individual was incubating. An infected individual i with δ –
days prior to d, otherwise the individual was incubating. An infected individual i with δ – ![]() days since symptom onset to day d may travel either during the incubation period (Fig. 2, pathway P1) or after symptom onset (pathway P2). In pathway P2, the individual may be not isolated, may travel some time during the symptomatic phase and arrive undetected at the destination. The infected individual who is expected to be incubating on day d may travel during the incubation period and be undetected by entry screening (pathway P3). The potential occurrence of these events is generated using epidemiological, travel and entry screening parameters (Table 1). The way these parameters flow into the calculation is presented in Appendix A (sections 3–4).
days since symptom onset to day d may travel either during the incubation period (Fig. 2, pathway P1) or after symptom onset (pathway P2). In pathway P2, the individual may be not isolated, may travel some time during the symptomatic phase and arrive undetected at the destination. The infected individual who is expected to be incubating on day d may travel during the incubation period and be undetected by entry screening (pathway P3). The potential occurrence of these events is generated using epidemiological, travel and entry screening parameters (Table 1). The way these parameters flow into the calculation is presented in Appendix A (sections 3–4).
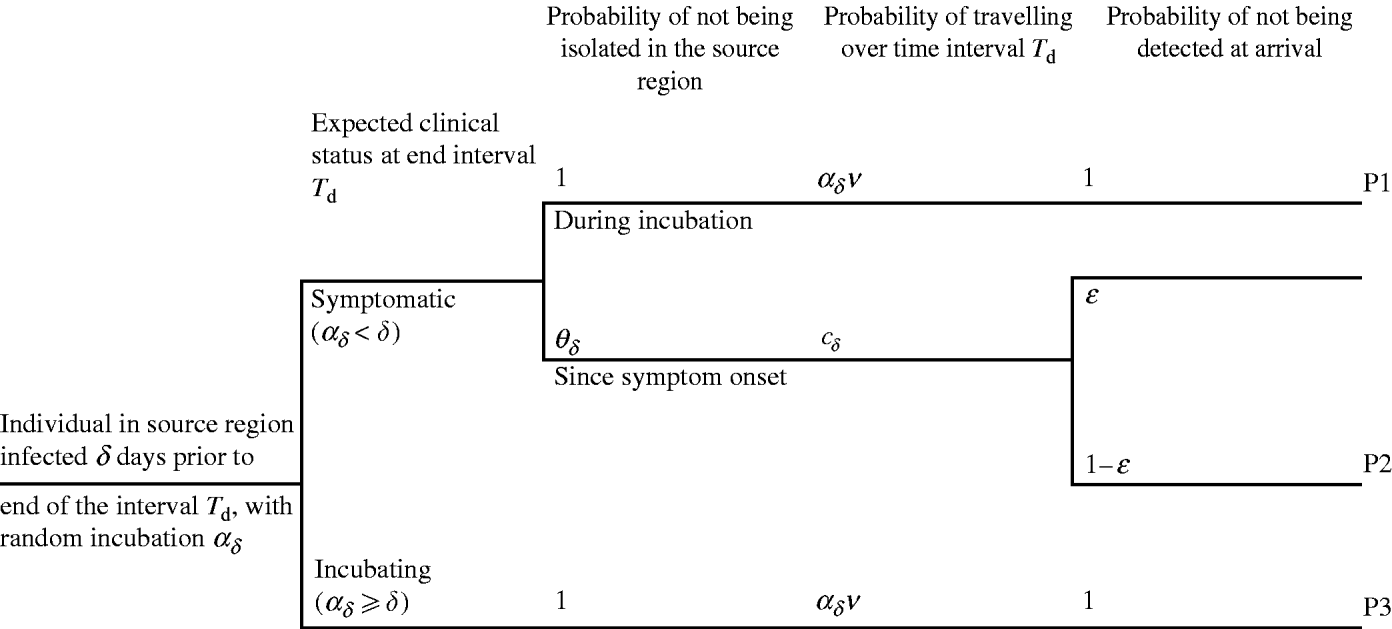
Fig. 2. The three pathways for importation of SARS during an interval T d, by an individual infected δ days since first case in source region. The probability of being isolated after symptom onset is defined by θδ. v is the probability of travelling. The probability of travelling is defined during the incubation period a δ, or during the symptomatic stage δ−a δ. ε is the probability of detecting a symptomatic traveller at entry to destination.
For an infected individual, a single Monte Carlo simulation represents a potential realization of that individual's pathway, quantified as the probability of arriving by air travel and undetected at entry within time interval T d (Appendix A, section 4). Summing these probabilities over all possible values of δ, we obtain the total cumulated number of imported infected individuals. The simulations were run with WinBUGs software [Reference Spiegelhalter16] and results are based on 40 000 runs.
Parameter description and sources
We considered hospitalization as the main reason for an infected individual to be isolated. We calculated the probability of not being isolated using the distribution of the delay between symptom onset and hospitalization (Appendix A, section 3). Estimates of this distribution are available for three time periods during the SARS outbreak in Beijing and Hong Kong, according to local control measures (Table 1). The mean time from symptom onset to hospitalization fell from 5 to 2·6 days during the outbreak in Beijing [Reference Pang17]. For Hong Kong, it fell from 4·8 to 3·7 days [Reference Donnelly15].
We considered a flight duration of 10 h for Beijing–Frankfurt and of 12 h for Hong Kong–London. We first assumed that all infected individuals can travel. Their daily probability v was estimated from the daily number of travellers divided by the size of the population in the urban areas for Beijing [18] and of the general population in Hong Kong [19]. Only direct flights from the International Civil Aviation Organization database [20] were considered (Table 1). In a second alternative, we subjectively assumed that the probability of a HCW travelling was twice that of the general population.
Possible in-flight transmissions of SARS have been documented during the SARS outbreak [Reference Desenclos6, Reference Olsen21, Reference Wilder-Smith, Leong and Villacian22]. Since SARS infectiousness starts after symptom onset, in-flight transmission from incubating travellers is unlikely while symptomatic travellers might generate infections in-flight. To investigate whether or not this impacts our results, we considered the probability of being infectious and transmitting the infection for symptomatic travellers accounting for flight duration (Appendix B).
Information on the sensitivity of symptom screening at entry is scarce. In our analysis, we used two alternatives compared with a base case of no border screening (Table 1). Entry screening with sensitivity 13·8% [95% confidence interval (CI) 3·9–31·7] was used. This value was estimated from a study aimed at detecting symptomatic travellers entering Australia during the SARS outbreak [Reference Samaan23]. In the second alternative, we assumed a mean sensitivity of 90% (95% CI 73–99) and applied the same variability (s.d.=6·9%) as in the above study [Reference Samaan23]. We considered this alternative to approximate what a near-perfect screening programme might achieve.
Our main output is the cumulated number of individuals, initially infected in Beijing or Hong Kong, and arriving undetected at their respective destinations during a time-interval T d. Results are presented in terms of a probabilistic distribution, summarized across the 40 000 runs (mean, 95% CI). We start the estimates for 7 March, 1 week before the global alert, corresponding to d=14 for Beijing–Frankfurt and d=20 for Hong Kong–London. Results are presented for several intervals T d.
RESULTS
Estimate of the number of individuals by day of infection in the source regions
For illustration we present the cumulative distribution of the new SARS infections in Hong Kong for T d where d=20, 34, 41 and 48 (Fig. 3). Each graph in Figure 3 includes two distributions: one is back-calculated based on the complete SARS epidemic data and the second is based on the adjusted data until d (Appendix A, section 1). For each T d, the two distributions are comparable except during the last week prior to day d, during which a discrepancy is noticed between the estimates based on the full epidemic data and those based on the adjusted data using Cauchemez et al.’s technique [Reference Cauchemez12]. This discrepancy reflects the uncertainty in the adjusted data that we suspected to be due to the variability in the serial interval distribution. The same conclusion is drawn from the estimated cumulative distributions of the new SARS cases in Beijing.

Fig. 3. Cumulated number of new infected SARS cases in Hong Kong since the first case's symptom onset until (a) day 20, (b) day 34, (c) day 41 and (d) day 48 during the SARS outbreak. The number of new infections is back-calculated from the complete SARS epidemic during the 2003 outbreak (–––) and from the SARS data observed until each respective day (- - - -).
SARS importation and effect of border screening at arrival
The cumulated numbers of imported SARS cases [values given are mean (95% CI)] for Hong Kong–London and Beijing–Frankfurt, assuming that all infected individuals were equally likely to travel, are presented in Tables 2a and 2b. When no entry screening was assumed, the cumulated number of SARS cases potentially imported from Hong Kong to London reaches at least one case after 21 March (T 34). A total of 0·8 imported cases (0·6–0·9) is estimated at T 34 with a 0·53 probability (0·48–0·59) that this number exceeds one case. At T 35, 1·4 cases (1·2–1·6) are estimated to be imported with a 0·75 probability (0·70–0·80) of exceeding one case. Results under each of the two other levels of entry screening (13% and 90%) are comparable to those under no screening.
Table 2a. Expected daily number of imported SARS cases (Hong Kong–London) since first case in Hong Kong
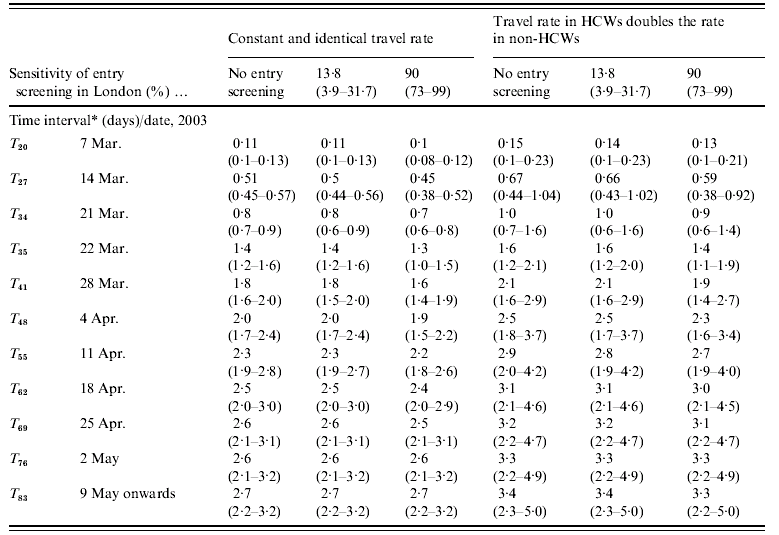
HCW, Health-care worker.
* Time interval since the first case's symptom onset in Hong Kong was in 15 February 2003.
Table 2b. Expected daily number of imported SARS cases (Beijing–Frankfurt) since first case in Beijing

HCW, Health-care worker.
* Time interval since the first case's symptom onset in Beijing which was in 21 February 2003.
For Beijing–Frankfurt (Table 2b), the cumulated number of imported SARS cases increased during the outbreak but remained <1. It was estimated as 0·7 cases (0·6–0·8) at T 63 (25 April) and stabilized at 0·8 (0·6–0·9) from T 70 onwards. Similar to Hong Kong–London, entry screening had no effect on the results.
SARS importation when infected HCWs are more likely to travel
Under the assumption that HCWs were more likely to travel, we estimated that for Hong Kong–London, at least one case arrives undetected from day 34 (Figure 4, Table 2a). The upper limit of the 95% CI of the cumulated number of imported cases reaches one case at T 27 (0·4–1·0) assuming no entry screening. For that interval, the probability that at least one case arrives in London is 0·48 (0·36–0·65). A mean of one imported case is estimated at T 34 (0·7–1·6) and there is a 95% chance that this number is between one and two cases at T 35 (1·2–2·1). One week after the epidemic peak in Hong Kong at T 41, a mean of two cases is estimated and the probability of importation of at least one case is 0·87 (0·80–0·95). From T 55 onwards, there is a 95% chance that the cumulated number of imported cases is between two and five.

Fig. 4. The mean (95% CI) of the expected cumulated number of SARS cases imported from Hong Kong to London during the outbreak. Estimates are presented by time since first symptom onset of the first case.
Under the base-case hypothesis on entry screening, the estimate for Beijing–Frankfurt is 0·5 cases at T 55 with the upper limit of the 95% CI exceeding one case (0·3–1·1). The probability that the number of imported cases exceeds one case at T 55 is 0·41 (0·25–0·65). On the following T d, the estimates come within reach of one case with the upper limit of the 95% CI reaching two cases (Table 2b). In either scenario, entry screening with 13·8% or 90% sensitivity does not affect the results.
DISCUSSION
Our results show that the transmission dynamic which defines the size of the epidemic in an affected region determines the time of a potential exportation of the infection through the air transportation network. In both scenarios, the results indicate that the risk of importation increases with amplification of local dissemination in the affected areas.
In the base case of no entry screening and when assuming all individuals in the source region have an equal probability of travelling, the method reveals no importation for Beijing–Frankfurt, which was effectively observed in 2003. For Hong Kong–London, the results indicate that importation occurred within 35 days since the time when the first case was reported in Hong Kong. This fits well with the imported case identified in the United Kingdom within this period and reported by the World Health Organization on 18 March [24]. Under the assumption that travel rate in HCWs is twofold that of the travel rate in the population in the source region, the model estimates that at least one case was imported from Beijing–Frankfurt between 11 and 18 April (T 56). This did not happen in reality, but the probability of that occurring at T 56 is 0·45 (0·26–0·71). For Hong Kong–London, importation is estimated to occur one day earlier (T 34 instead of T 35) when HCWs are assumed more likely to travel. In both scenarios, the results with no entry screening are comparable to those with 13·8% or 90% screening sensitivity, suggesting that screening which targets SARS symptomatic travellers does not markedly reduce the risk of importation, since symptomatic individuals are likely to be isolated before attempting to travel. The probability of travelling can be regarded as the probability ‘of boarding a plane and bypassing exit screening’, assuming that exit screening is already considered. Thus, in the first assumption on travel rate (equal daily chance to travel=υ), an infected HCW has a 0·5 probability of being detected at an exit border and a twofold chance of travelling (2υ). In the second assumption, HCWs have a travel rate of 2υ and can be considered as having a 100% chance of bypassing exit screening and a twofold chance of travelling (2υ). The distribution of the numbers of imported SARS cases remained unaltered when we assumed in-flight transmission (Appendix B). The expected number of generated cases during a 10–12 h flight is almost null, which is consistent with a previous analysis showing that SARS asymptomatic travellers are unlikely to develop symptoms in-flight, and subsequently would not become infectious and generate new infections in-flight [Reference Pitman25].
For a real-time application of our method, input for the epidemiological parameters (e.g. the incubation period, serial interval, infectiousness) is required. This is unlikely to be readily available in the very early stage of an outbreak of an emerging infectious disease. In addition, the role of control measures in preventing infected individuals from travelling is not instantly assessed in order to derive assumptions on the delay to isolation. However, inference on this delay from previous outbreaks could be applied. The instant risk estimate also requires the daily number of cases, which should be immediately available, but this could be difficult to achieve during an ongoing outbreak. It requires a worldwide collaboration for a global harmonization of the different surveillance systems as well as an enlarged network for a wide exchange of experiences and data.
We showed that estimates of the distribution of infected individuals by day of infection can be derived from a daily epidemic curve observed in an interval T d (using the back-calculation method) after adjusting the data by predicting the number of unobserved infected cases (e.g. cases whose symptom onset occur in the following days and their infection occurs during T d). These predicted numbers depend on the epidemiological determinants of spread of the infection in the source region. Although these factors are not well known in the early stage of an outbreak, the predictions could give satisfactory estimates of the infection curve for T d with more uncertainty in the first stage of the epidemic than in the later stage, as was seen in Cauchemez et al. [Reference Cauchemez12].
In recent studies on the effect of international travel on spread of infections, travel rates between regions were assumed constant and homogenous between peoples [Reference Cooper2, 3, 25–Reference Hufnagel, Brockmann and Geisel30]. In a more recent work, estimates of the number of exported infected cases with SARS or influenza infection were derived using simulated outbreaks distinguishing between individuals with high- and low-travel frequency [Reference Hollingsworth, Ferguson and Anderson4]. These authors studied the potential impact of the relative difference in travel frequency between these categories. Technically different from this model, our method allows for assigning of different travel patterns to different infected groups, provided that demographic information of the diseased individuals is available. In the absence of information on travel rate in HCWs (a group at risk, and a potential spreader of germs), our assumption is a subjective way of exploring the potential effect that different travel rates assigned to different population groups could have on the expected number of imported SARS case. However, we advise that the resulting risk should be interpreted with caution.
One of the key points in our analysis is that border screening has no impact on the expected number of imported SARS cases. This screening targets only symptomatic travellers who are possibly less likely to travel given the delay between their symptom onset and their hospitalization. It misses the incubating travellers who can successfully enter their destination. Thus, as a worldwide concern in delaying the spread of infection, efforts should go into promoting and strengthening interventions to reduce local spread in infected regions.
ACKNOWLEDGEMENTS
This work was part of the SARS Control project (Effective and acceptable strategies for the control of SARS and new emerging infections in China and Europe), a European Commission project, funded within the Sixth Framework Programme, Thematic priority scientific support to policies, Contract number: SP22-CT-2004-003824). We acknowledge the contribution made by Le Strat Yann and Bernillon Pascale. We also thank Dr Sake de Vlas for easing the communication between the project leaders to access some of the data. We particularly thank Martin Eichner and anonymous readers for their helpful advice and comments.
DECLARATION OF INTEREST
None.
APPENDIX A
1. Prediction of the unobserved secondary infections based on number of cases with onset currently observed
Given a set of the number of observed cases O(T) with symptom onset available up to a day T (n t, t⩽T), we predict X t+(T), the number of cases initially infected before T whose symptom onset occurs after T. We used the method of Cauchemez et al. [Reference Caley, Becker and Philp1] where the authors developed a technique to timely estimate the reproductive number (R t) of SARS. The R t is represented by the ratio of n t and the number of cases they infected, X t: X t=X t+(T)+X t−(T). X t−(T) is the number of cases initially infected before T that showed symptoms before T. As did Cauchemez and colleagues, we estimated the distribution of X t(T)/O(T) within a Bayesian framework. A decomposition of X t(T) in the number of early and secondary generated cases follows the equation:

where P[ ] indicates the probability density. The distributions of X t+(T)/X t−(T) and X t−(T)/O(T) are both estimated. The later is approximated by a sum of independent binomial distributions in the same way as in Wallinga & Teunis [Reference Cooper2]:
where ψt,k is the probability that a case detected at day k has been infected by a case detected at day t (t, k⩽T) (see supplementary material in Cauchemez et al. [Reference Caley, Becker and Philp1] for further details). A value of X t+(T)/O(T) is derived for each t(t<T) by subtracting a value of X t−(T)/O(T) from X t(T)/O(T). X t+(T)/O(T) is hence redistributed by day of symptom onset over the 10 days following T (x t(T+s), s=1–10) using the probability distribution of the serial interval.
2. Back-calculation of the observed and the predicted number of incident cases
For a given day d, we note by ![]() the number of cases by day of symptom onset t until day 10 after d:
the number of cases by day of symptom onset t until day 10 after d:
where h(t−τ, τ) is the number of individuals infected on day t – τ (prior to t), with an incubation period of τ days. h(t−τ, τ)are assumed independently Poisson-distributed with mean ![]() where
where ![]() is the expected mean of the number of individuals infected on day t and f τ is the probability that incubation time is τ. We used the Expectation Maximization algorithm that gives Smoothed (EMS) predictions [Reference Ferguson3] to estimate
is the expected mean of the number of individuals infected on day t and f τ is the probability that incubation time is τ. We used the Expectation Maximization algorithm that gives Smoothed (EMS) predictions [Reference Ferguson3] to estimate ![]() . We refer the reader to Becker et al. [Reference Ferguson3] for explicit details on the EMS algorithm. The EMS algorithm was coded with R software [Reference Hollingsworth, Ferguson and Anderson4]. In the following, we note
. We refer the reader to Becker et al. [Reference Ferguson3] for explicit details on the EMS algorithm. The EMS algorithm was coded with R software [Reference Hollingsworth, Ferguson and Anderson4]. In the following, we note ![]() by
by ![]() ; the number of individuals infected δ days prior to d (δ=0, …,d).
; the number of individuals infected δ days prior to d (δ=0, …,d).
3. Distribution of time since symptom onset to hospitalization
The probability of not being isolated equals 1 for an incubating individual. For an individual i with δ – ![]() since symptom onset, this probability is defined using the cumulative density function (F( )) of the distribution of the delay between symptom onset and hospitalization:
since symptom onset, this probability is defined using the cumulative density function (F( )) of the distribution of the delay between symptom onset and hospitalization:
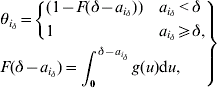
where g is the probability density function of this distribution. This is a gamma distribution specific to three time-periods during the SARS outbreak either in Beijing or Hong Kong (see Table 1 of main paper).
4. Probability of departing and arriving undetected at destination
At each simulation, for every infected individual i with incubation period ![]() , we calculated the probability of the individual travelling and arriving undetected at the destination as some time between infection and day d
, we calculated the probability of the individual travelling and arriving undetected at the destination as some time between infection and day d ![]() . Assuming ε to be the sensitivity of screening at border entry, so that 1−ε represents the probability for a symptomatic individual to bypass border control at arrival, we assumed that there is no chance of detecting an individual travelling during the incubation period.
. Assuming ε to be the sensitivity of screening at border entry, so that 1−ε represents the probability for a symptomatic individual to bypass border control at arrival, we assumed that there is no chance of detecting an individual travelling during the incubation period.
An infected individual i with δ – ![]() days since symptom onset has a probability
days since symptom onset has a probability ![]() of travelling during the incubation period
of travelling during the incubation period ![]() (see Figure 2, pathway P1 in the main paper), or a probability
(see Figure 2, pathway P1 in the main paper), or a probability ![]() of travelling after developing symptoms during time
of travelling after developing symptoms during time ![]() (pathway P2):
(pathway P2):

For an individual i likely to be incubating on day d, the probability of departing some time during the incubation period (pathway P3) is the cumulative probability of the individual travelling during incubation time ![]() . The specific probability
. The specific probability ![]() of an individual i among
of an individual i among ![]() infected cases (δ=0, …,d) is given by:
infected cases (δ=0, …,d) is given by:
We draw the time until scheduled travel from the uniform distributed over the interval (0, δ):
The sum of the probabilities ![]() approximates the expected number of initially infected individuals in the source region, arriving undetected at the region of destination during the time interval T d=(0, d); since the beginning of the outbreak until day d:
approximates the expected number of initially infected individuals in the source region, arriving undetected at the region of destination during the time interval T d=(0, d); since the beginning of the outbreak until day d:
At each simulation, ![]() is calculated and a summary statistic is derived over 40 000 runs. We assumed that SARS importation from one region to another is a non-homogenous Poisson process characterized by a time-dependent rate γ(t). The expected number of arrivals during an interval T d is defined by the integral
is calculated and a summary statistic is derived over 40 000 runs. We assumed that SARS importation from one region to another is a non-homogenous Poisson process characterized by a time-dependent rate γ(t). The expected number of arrivals during an interval T d is defined by the integral ![]() which we approximated by
which we approximated by ![]() . Therefore, the number of arrivals of undetected infected travellers in the time interval T d is regarded as a random variable, which is Poisson-distributed with mean
. Therefore, the number of arrivals of undetected infected travellers in the time interval T d is regarded as a random variable, which is Poisson-distributed with mean ![]() .
.
APPENDIX B
Transmission during flight and effect on the expected number of imported cases
For a transmission to occur during flight, an infected traveller must be infectious and transmit the infection to other passengers during the flight. We assumed that infectiousness and transmission mechanisms during flight are same as while mixing in the population. The probability of being infectious during the flight depends on the time since symptom onset to the scheduled travel. We estimated this probability using the results from the analysis of viral shedding, based on isolation of SARS coronavirus or RT–PCR detection in the respiratory secretions of 415 cases in Hong Kong [Reference Glass, Becker and Clements5]. This study indicated that viral excretion (infectiousness) was detected in the first or second day after symptom onset in 20% of cases, and in more than 33% of cases one week following symptom onset. Viral excretion was detected in only 17% of cases 2 weeks after symptom onset and in none of cases 3 weeks following symptom onset. ![]() is the probability of being infectious for an ith individual expected to be symptomatic on day d and travelling while being symptomatic (pathway P3), given time since symptom onset
is the probability of being infectious for an ith individual expected to be symptomatic on day d and travelling while being symptomatic (pathway P3), given time since symptom onset ![]() , where
, where ![]() is the time since infection to scheduled travel and ΔF is the flight duration. An infectiousness event is thus generated at each Monte Carlo simulation, using Bernoulli distribution,
is the time since infection to scheduled travel and ΔF is the flight duration. An infectiousness event is thus generated at each Monte Carlo simulation, using Bernoulli distribution, ![]() , so that a random value
, so that a random value ![]() indicates that the individual is infectious.
indicates that the individual is infectious.
Table B1. Data used to estimate transmission parameters when accounting for in-flight transmission

We first considered that all infected individuals have their own expected number of secondary cases (over each individual's infection history) given the population basic reproductive number R 0 (Table B1). For an ith infectious traveller (![]() ), the expected number of secondary cases
), the expected number of secondary cases ![]() is gamma-distributed with mean R 0 and shape α [Reference Desenclos6], and the number of secondary cases generated is considered as a random variable (Z) which is described by an offspring distribution that has a negative binomial distribution with mean
is gamma-distributed with mean R 0 and shape α [Reference Desenclos6], and the number of secondary cases generated is considered as a random variable (Z) which is described by an offspring distribution that has a negative binomial distribution with mean ![]() and dispersion parameter 1/α. The fraction of
and dispersion parameter 1/α. The fraction of ![]() caused during a flight duration ΔF is represented by
caused during a flight duration ΔF is represented by ![]() given a median infectiousness period of D days. A value
given a median infectiousness period of D days. A value ![]() is drawn from the gamma distribution at each simulation, and an estimate
is drawn from the gamma distribution at each simulation, and an estimate ![]() is obtained from equation (10). The probability of causing no secondary infections during a flight
is obtained from equation (10). The probability of causing no secondary infections during a flight ![]() is calculated from the probability distribution with mean
is calculated from the probability distribution with mean ![]() and dispersion 1/α [eqn (11)] and
and dispersion 1/α [eqn (11)] and ![]() ; the probability to generate new cases is derived, and is used drawing a value from a Bernoulli distribution:
; the probability to generate new cases is derived, and is used drawing a value from a Bernoulli distribution: ![]() . Whenever
. Whenever ![]() , a random number of generated cases during flight is drawn from the Poisson distribution with mean
, a random number of generated cases during flight is drawn from the Poisson distribution with mean ![]() [eqn (11)]:
[eqn (11)]:

The expected total number of generated cases during a flight is given by:
The cumulated number of SARS cases arriving undetected from an infected region at a destination since the beginning of the outbreak until a day d includes those imported cases who are initially infected in a source region ![]() and those generated by infectious travellers during flight
and those generated by infectious travellers during flight ![]() [eqn (12)]:
[eqn (12)]:
In the case where we account for in-flight-generated infections (Table B2), the number of arrivals of undetected infected travellers in the time-interval T d is Poisson-distributed with mean ![]() .
.
Table B2. Estimates of the number of imported SARS cases (Hong Kong–London) assuming identical travel rate, and no border screening at arrival

* Time interval (days) since the first case's symptom onset in Hong Kong on 15 February 2003.
Values are mean (95% CI).










